大学物理习题及答案
大学物理习题答案
大学物理习题答案 TYYGROUP system office room 【TYYUA16H-TYY-TYYYUA8Q8-一、 单项选择题：1. 北京正负电子对撞机中电子在周长为L 的储存环中作轨道运动。
已知电子的动量是P ，则偏转磁场的磁感应强度为： （ C ） (A)eLP π； (B)eL P π4； (C) eLPπ2； (D) 0。
2. 在磁感应强度为B的均匀磁场中，取一边长为a 的立方形闭合面，则通过该闭合面的磁通量的大小为： （ D ）(A) B a 2； (B) B a 22； (C) B a 26； (D) 0。
3．半径为R 的长直圆柱体载流为I ，电流I 均匀分布在横截面上，则圆柱体内（R r 〈）的一点P 的磁感应强度的大小为 ( B ) (A) r I B πμ20=； (B) 202R Ir B πμ=； (C) 202rIB πμ=； (D) 202RIB πμ=。
4．单色光从空气射入水中，下面哪种说法是正确的 ( A ) (A) 频率不变，光速变小； (B) 波长不变，频率变大； (C) 波长变短，光速不变； (D) 波长不变，频率不变.5.如图,在C 点放置点电荷q 1,在A 点放置点电荷q 2,S 是包围点电荷q 1的封闭曲面,P 点是S 曲面上的任意一点.现在把q 2从A 点移到B 点，则 (D )(A) 通过S 面的电通量改变,但P 点的电场强度不变；(B) 通过S 面的电通量和P 点的电场强度都改变； (C) 通过S 面的电通量和P 点的电场强度都不变； (D) 通过S 面的电通量不变,但P 点的电场强度改变。
6．如图所示，两平面玻璃板OA 和OB 构成一空气劈尖，一平面单色光垂直入射到劈尖上，当A 板与B 板的夹角θ增大时，干涉图样将 ( C )(A) 干涉条纹间距增大，并向O 方向移动； (B) 干涉条纹间距减小，并向B 方向移动； (C) 干涉条纹间距减小，并向O 方向移动； (D) 干涉条纹间距增大，并向O 方向移动.7．在均匀磁场中有一电子枪，它可发射出速率分别为v 和2v 的两个电子，这两个电子的速度方向相同，且均与磁感应强度B 垂直，则这两个电子绕行一周所需的时间之比为 ( A )(A) 1:1； (B) 1:2； (C) 2:1； (D) 4:1.8．如图所示，均匀磁场的磁感强度为B ，方向沿y 轴正向，欲要使电量为Q 的正离子沿x 轴正向作匀速直线运动，则必须加一个均匀电场E ，其大小和方向为 ( D )(A) E =νB ，E 沿z 轴正向； (B) E =vB ，E 沿y 轴正向；(C) E =B ν，E 沿z 轴正向； (D) E =B ν，E 沿z 轴负向。
大学普通物理复习题(10套)带答案
普通物理试题1－10试题1一、填空题11. 7．在与匀强磁场B垂直的平面，有一长为L 的铜杆OP ，以角速度 绕端点O 作逆时针匀角速转动，如图13—11，则OP 间的电势差为 P O U U （221L B ）。
3. 3.光程差 与相位差 的关系是（2 ）25. 1.单色光在水中传播时，与在真空中传播比较：频率(不变 )；波长( 变小 )；传播速度( 变小 )。
(选填：变大、变小、不变。
)68.17－5. 波长为 的平行单色光斜入射向一平行放置的双缝，如图所示，已知入射角为θ缝宽为a ，双缝距离为b ，产生夫琅和费衍射，第二级衍射条纹出现的角位置是（sin 2sin 1b。
33. 9. 单色平行光垂直照射在薄膜上．经上下两表面反射的两束光发生干涉、如图所示， 若薄膜的厚度为e ．且321n n n ，1 为入射光在1n 中的波长，则两束反射光的光程差为 ( 22112 n e n)。
二、选择题6. 2. 如图示，在一无限长的长直载流导线旁，有一形单匝线圈，导线与线圈一侧平行并在同一平面，问：下列几种情况中，它们的互感产生变化的有（ B ，C ，D ）（该题可有多个选择）(A) 直导线中电流不变，线圈平行直导线移动； (B) 直导线中电流不变，线圈垂直于直导线移动；(C) 直导线中电流不变，线圈绕AB 轴转动； (D) 直导线中电流变化，线圈不动12.16－1．折射率为n 1的媒质中，有两个相干光源．发出的光分别经r 1和r 2到达P 点．在r 2路径上有一块厚度为d ，折射率为n 2的透明媒质，如图所示，则这两条光线到达P 点所经过的光程是( C )。
（A ）12r r（B ） d n n r r 2112（C ） d n n n r r 12112 （D ） d n n r r 1211283. 7．用白光垂直照射一平面衍射光栅、发现除中心亮纹（0 k ）之外，其它各级均展开成一光谱．在同一级衍射光谱中．偏离中心亮纹较远的是( A )。
(完整版)《大学物理》练习题及参考答案
《大学物理》练习题一. 单选题：1．下列说法正确的是……………………………………（） 参看课本P32-36A . 惯性系中，真空中的光速与光源的运动状态无关，与光的频率有关B . 惯性系中，真空中的光速与光源的运动状态无关，与光的频率无关C . 惯性系中，真空中的光速与光源的运动状态有关，与光的频率无关D . 惯性系中，真空中的光速与光源的运动状态有关，与光的频率有关2．下列说法正确的是………………………………… （ ） 参看课本P32-36A . 伽利略变换与洛伦兹变换是等价的B . 所有惯性系对一切物理定律都是不等价的C . 在所有惯性系中，真空的光速具有相同的量值cD . 由相对论时空观知：时钟的快慢和量尺的长短都与物体的运动无关3．下列说法正确的是………………………………… （ ）参看课本P58,76,103 A . 动量守恒定律的守恒条件是系统所受的合外力矩为零 B . 角动量守恒定律的守恒条件是系统所受的合外力为零 C . 机械能守恒定律的守恒条件是系统所受的合外力不做功 D . 以上说法都不正确4. 下列关于牛顿运动定律的说法正确的是…………（ ） 参看课本P44-45A . 牛顿第一运动定律是描述物体间力的相互作用的规律B . 牛顿第二运动定律是描述力处于平衡时物体的运动规律C . 牛顿第三运动定律是描述物体力和运动的定量关系的规律D . 牛顿三条运动定律是一个整体，是描述宏观物体低速运动的客观规律5．下列关于保守力的说法错误的是…………………（ ） 参看课本P71-72 A . 由重力对物体所做的功的特点可知，重力是一种保守力B . 由弹性力对物体所做的功的特点可知，弹性力也是一种保守力C . 由摩擦力对物体所做的功的特点可知，摩擦力也是一种保守力D . 由万有引力对物体所做的功的特点可知，万有引力也是一种保守力6.已知某质点的运动方程的分量式是，，式中R 、ω是常cos x R t ω=sin y R t ω=数．则此质点将做………………………………………………（） 参看课本P19A . 匀速圆周运动B . 匀变速直线运动C . 匀速直线运动D . 条件不够，无法确定7．如图所示，三个质量相同、线度相同而形状不同的均质物体，它们对各自的几何对称轴的转动惯量最大的是………( )A . 薄圆筒B . 圆柱体 参看课本P95C . 正方体D . 一样大8．下列关于弹性碰撞的说法正确的是………………（） 中学知识在课堂已复习A . 系统只有动量守恒B . 系统只有机械能守恒C . 系统的动量和机械能都守恒D . 系统的动量和机械能都不守恒9．某人张开双臂，手握哑铃，坐在转椅上，让转椅转动起来，若此后无外力矩作用．则当此人收回双臂时，人和转椅这一系统的…………………（ ） 参看课本P104A . 转速不变，角动量变大B . 转速变大，角动量保持不变C . 转速和角动量都变大D . 转速和角动量都保持不变10.下列关于卡诺循环的说法正确的是………………（ ） 参看课本P144 A . 卡诺循环是由两个平衡的等温过程和两个平衡的绝热过程组成的B . 卡诺循环是由两个平衡的等温过程和两个平衡的等体过程组成的C . 卡诺循环是由两个平衡的等体过程和两个平衡的等压过程组成的D . 卡诺循环是由两个平衡的绝热过程和两个平衡的等压过程组成的11. 如图所示，在场强为E 的匀强电场中，有一个半径为R 的半球面，若场强E 的方向与半球面的对称轴平行，则通过这个半球面的电通量大小为…………………（ ） 参看课本P172-173A .B .2E 22R E πC . D . 02R E 12.一点电荷，放在球形高斯面的中心处，下列情况中通过高斯面的电通量会发生变化的…………………………（ ） 参看课本P173 A . 将另一点电荷放在高斯面内 B . 将高斯面半径缩小C . 将另一点电荷放在高斯面外D . 将球心处的点电荷移开，但仍在高斯面内13.如图所示，在与均匀磁场垂直的平面内有一长为l 的铜棒B MN ，设棒绕M 点以匀角速度ω转动，转轴与平行，则棒的动B 生电动势大小为……………（）参看课本P257A .B . Bl ω2BlωC .D . 12Bl ω212Blω14. 、方均v 、最概然速率为，则这气体分子的三种速率的关系是…………（p v ） A ．B 参看课本P125v >p vC ．D p v pv =15. 下列关于导体静电平衡的说法错误………………（ ） 参看课本P190-191 A . 导体是等势体，其表面是等势面 B . 导体内部场强处处为零 C . 导体表面的场强处处与表面垂直 D . 导体内部处处存在净电荷16. 下列哪种现代厨房电器是利用涡流原理工作的…（ ） 参看课本P259A . 微波炉B . 电饭锅17. 下列关于电源电动势的说法正确的是……………（） 参看课本P249-250A . 电源电动势等于电源把电荷从正极经内电路移到负极时所作的功B . 电源电动势的大小只取于电源本身的性质，而与外电路无关C . 电动势的指向习惯为自正极经内电路到负极的指向D . 沿着电动势的指向，电源将提高电荷的电势能18. 磁介质有三种，下列用相对磁导率正确表征它们各自特性的是………（ r μ）A . 顺磁质，抗磁质，铁磁质 参看课本P39-2400r μ<0r μ<1r μ?B . 顺磁质，抗磁质，铁磁质1r μ>1r μ=1r μ?C . 顺磁质，抗磁质，铁磁质0r μ>0r μ>0r μ> D . 顺磁质，抗磁质，铁磁质1r μ>1r μ<1r μ?19. 在均匀磁场中，一带电粒子在洛伦兹力作用下做匀速率圆周运动，如果磁场的磁感应强度减小，则………………………………………………（ ） 参看课本P231 A . 粒子的运动速率减小 B . 粒子的轨道半径减小 C . 粒子的运动频率不变 D . 粒子的运动周期增大20. 两根无限长的载流直导线互相平行，通有大小相等，方向相反的I 1和I 2，在两导线的正中间放一个通有电流I 的矩形线圈abcd ，如图所示. 则线圈受到的合力为…………（ ） 参看课本P221-223A . 水平向左B . 水平向右C . 零D . 无法判断21. 下列说法错误的是……………………………………（ ） 参看课本P263A . 通过螺线管的电流越大，螺线管的自感系数也越大B . 螺线管的半径越大，螺线管的自感系数也越大C . 螺线管中单位长度的匝数越多，螺线管的自感系数也越大D . 螺线管中充有铁磁质时的自感系数大于真空时的自感系数22. 一电偶极子放在匀强电场中，当电矩的方向与场强的方向不一致时，则它所受的合力F 和合力矩M 分别为…………………………………（ ） 参看课本P168-169A . F =0 ，M =0B . F ≠0 ，M ≠0C . F =0 ，M ≠0D . F ≠0 ，M =023. 若一平面载流线圈在磁场中既不受磁力，也不受磁力矩作用，这说明……（ ）A . 该磁场一定均匀，且线圈的磁矩方向一定与磁场方向平行 参看课本P223-224B . 该磁场一定不均匀，且线圈的磁矩方向一定与磁场方向平行C . 该磁场一定均匀，且线圈的磁矩方向一定与磁场方向垂直D . 该磁场一定不均匀，且线圈的磁矩方向一定与磁场方向垂直24. 下列关于机械振动和机械波的说法正确的是………（ ） 参看课本P306A . 质点做机械振动，一定产生机械波B .波是指波源质点在介质的传播过程C . 波的传播速度也就是波源的振动速度D . 波在介质中的传播频率与波源的振动频率相同，而与介质无关25. 在以下矢量场中，属保守力场的是…………………（ ） A . 静电场 B . 涡旋电场 参看课本P180,212,258C . 稳恒磁场D . 变化磁场26. 如图所示，一根长为2a 的细金属杆AB 与载流长直导线共面，导线中通过的电流为I ，金属杆A 端距导线距离为a .金属杆AB 以速度v 向上匀速运动时，杆内产生的动生电动势为……（ ） 参看课本P261 (8-8)A . ，方向由B →A B .，方向由A →B2ln 20πμεIv i =2ln 20πμεIv i =C . ，方向由B →A D . ，方向由A →B0ln 32i Iv μεπ=3ln 20πμεIv i =27．在驻波中，两个相邻波节间各质点的振动………（ ） 参看课本P325A . 振幅相同，相位相同B . 振幅不同，相位相同C . 振幅相同，相位不同D . 振幅不同，相位不同28．两个质点做简谐振动，曲线如图所示，则有（ ）A . A 振动的相位超前B 振动π/2 参看课本P291B . A 振动的相位落后B 振动π/2C . A 振动的相位超前B 振动πD . A 振动的相位与B 振动同相29．同一点光源发出的两列光波产生相干的必要条件是…（） 参看课本P336A . 两光源的频率相同，振动方向相同，相位差恒定B . 两光源的频率相同，振幅相同，相位差恒定C . 两光源发出的光波传播方向相同，振动方向相同，振幅相同D .两光源发出的光波传播方向相同，频率相同，相位差恒定30．如图所示，在一圆形电流I 所在的平面内选取一个同心圆形闭合环路L ，则由安培环路定理可知……………………………………………（ ） 参看课本P235A . ，且环路上任一点B =0d 0L B l ⋅=⎰B . ，但环路上任一点B ≠0d 0L B l ⋅=⎰ C . ，且环路上任一点B ≠0d 0 L B l ⋅≠⎰D . ，且环路上任一点B =常量d 0 LB l ⋅≠⎰二. 填空题：31. 平行板电容器充电后与电源断开，然后充满相对电容率为εr 的各向均匀电介质. 则其电容C 将______，两极板间的电势差U 将________. (填减小、增大或不变) 参看课本P195,20032. 某质点沿x 轴运动，其运动方程为: x =10t –5t 2，式中x 、t 分别以m 、s 为单位. 质点任意时刻的速度v =________，加速度a =________. 参看课本P16-1733. 某人相对地面的电容为60pF ，如果他所带电荷为，则他相对地面的电C 100.68-⨯势差为__________，他具有的电势能为_____________. 参看课本P200,20234. 一人从10 m 深的井中提水，起始时，桶中装有10 kg 的水，桶的质量为1 kg ，由于水桶漏水，每升高1m 要漏去0.1 kg 的水，则水桶匀速地从井中提到井口，人所作的功为____________．参看课本P70 (2-14)35.质量为m 、半径为R 、自转运动周期为T 的月球，若月球是密度均匀分布的实球体，则其绕自转轴的转动惯量是__________，做自转运动的转动动能是__________.参看课本P100 (3-4)36. 1mol 氢气，在温度为127℃时，氢气分子的总平均动能是_____________，总转动动能是______________，内能是_____________. 〔已知摩尔气体常量R = 8.31 J/(mol ·K ) 参看课本 P120 (4-8)37. 如图所示，两个平行的无限大均匀带电平面，其面电荷密度分别为+σ和-σ. 则区域Ⅱ的场强大小E Ⅱ=___________ . 参看课本P17738. 用一定波长的单色光进行双缝干涉实验时，要使屏上的干涉条纹间距变宽，可采用的方法是: (1) _________________________；(2) ________________________. 参看课本P34439. 通过磁场中任意闭合曲面的磁通量等于_________. 感生电场是由______________产生的，它的电场线是__________曲线. (填闭合或不闭合) 参看课本P212,25840. 子弹在枪膛中前进时受到的合力与时间关系为，子弹飞出枪口5400410N F t =-⨯的速度为200m /s ，则子弹受到的冲量为_____________. 参看课本P55-5641. 将电荷量为2.0×10-8C 的点电荷，从电场中A 点移到B 点，电场力做功6.0×10-6J . 则A 、B 两点的电势差U AB =____________ . 参看课本P18142. 如图所示，图中O 点的磁感应强度大小B =______________.参看课本P229-23043. 一个螺线管的自感L =10 mH ，通过线圈的电流I =2A ，则它所储存的磁能W =_____________. 参看课本P26744. 理想气体在某热力学过程中内能增加了ΔE =250J ，而气体对外界做功A =50J ，则气体吸收的热量Q = . 参看课本P132-13345. 一平面简谐波沿x 轴的正方向传播，波速为100 m/s ，t =0时的曲线如图所示，则简谐波的波长λ =____________,频率ν =_____________. 参看课本P30946. 两个同心的球面，半径分别为R 1、R 2(R 1R 2)，分别<带有总电量为Q 1、Q 2. 设电荷均匀分布在球面上，则两球面间的电势差U 12= ________________________.参看课本P186-187三. 计算题：47. 一正方形线圈由外皮绝缘的细导线绕成，共绕有100匝，每边长为10 cm ，放在B = 5.0T 的磁场中，当导线中通有I =10.0A 的电流时，求: (1) 线圈磁矩m 的大小；(2) 作用在线圈上的磁力矩M 的最大值. 参看课本P225 (7-7)48.如图所示，已知子弹质量为m ，木块质量为M ，弹簧的劲度系数为k，子弹以初速v o射入木块后，弹簧被压缩了L.设木块与平面间的滑动摩擦因数为μ，不计空气阻力.求初速v o.参看课本P80 (2-23)49. 一卡诺热机的效率为40％，其工作的低温热源温度为27℃.若要将其效率提高到50％，求高温热源的温度应提高多少?参看课本P148 (5-14)50. 质量均匀的链条总长为l，放在光滑的桌面上，一端沿桌面边缘下垂，其长度为a，如图所示.设开始时链条静止，求链条刚刚离开桌边时的速度.参看课本P70 (2-18)51.一平面简谐波在t =0时刻的波形如图所示，设波的频率ν=5 Hz，且此时图中P点的运动方向向下，求：(1) 此波的波函数；(2) P点的振动方程和位置坐标.参看课本P318 (10-11)52．如图所示，A和B两飞轮的轴杆可由摩擦啮合器使之连接，A轮的转动惯量J A=10 kg·m2．开始时，B轮静止，A轮以n A= 600 r/min的转速转动．然后使A和B连接，连接后两轮的转速n = 200 r/min．求: (1) B轮的转动惯量J B ；(2) 在啮合过程中损失的机械能ΔE.参看课本P105 (3-9及补充)53．如图所示，载流I的导线处于磁感应强度为B的均匀磁场中，导线上的一段是半径为R、垂直于磁场的半圆，求这段半圆导线所受安培力.参看课本P224-22554．如图所示的截面为矩形的环形均匀密绕的螺绕环，环的内外半径分别a和b，厚度为h，共有N匝，环中通有电流为I .求: (1) 环内外的磁感应强度B；(2) 环的自感L.参看课本P237-238 (7-23及补充)55.如图所示，一长直导线通有电流I，在与其相距d处放在有一矩形线框，线框长为l ，宽为a ，共有N 匝. 当线框以速度v 沿垂直于长导线的方向向右运动时，线框中的动生电动势是多少? 参看课本P255 (8-3)二. 填空题：31. 增大 减小32.33. 1000V 0.03 J1010m/s t -210m/s t -34. 1029 (或1050) J 35. 36. 4986J 3324J 8310 J 225mR 22245mR T π37. 38. (1) 将两缝的距离变小 (2) 将双缝到光屏的距离变大σε39. 零 变化的磁场 闭合 40.41.300V42.0.2N s ⋅0112I R μπ⎛⎫- ⎪⎝⎭43. 0.02 J44. 300 J45. 0.8 m 125 Hz46.1012114Q R R πε⎛⎫- ⎪⎝⎭三. 计算题：47. 线圈磁矩22100100.110A m m NIS ==⨯⨯=⋅线圈最大磁力矩max 10550N mM mB ==⨯=⋅48. 设子弹质量为m ，木块质量为M ，子弹与木块的共同速度v由动量守恒定律得①0()mv m M v =+由功能原理得 ②2211()()22m M gL kL m M v μ-+=-+由①、②式得 0v =49. 卡诺热机效率: 211T T η=-21300500K 110.4T T η⇒===--同理 21300600K 110.5T T η'==='--高温热源应提高的温度 11600500100KT T '-=-=n50. 设桌面为零势面，由机械能守恒定律得21222a a l mg mg mv l -=-+v ⇒=51. 解：(1) 由图中v P ＜0知此波沿x 轴负向传播，继而知原点此时向y 正向运动原点处0002A y v =->，023ϕπ⇒=-又x = 3m 处3300y v =>，32πϕ⇒=-由 得2x ϕπλ∆∆=2x λπϕ∆=∆30236m 223πππ-=⨯=⎛⎫--- ⎪⎝⎭此波的波函数 02cos 2x y A t ππνϕλ⎛⎫=++ ⎪⎝⎭20.10cos 10m 183t x πππ⎛⎫=+- ⎪⎝⎭(2) P 点处 P P 00y v =，<P 2πϕ⇒=P 点振动方程P P cos(2)y A t πνϕ=+0.10cos 10m 2t ππ⎛⎫=+ ⎪⎝⎭P 点位置坐标 p 363321m22x λ=+=+=52. (1) 由动量矩守恒定律得A A AB ()J J J ωω=+A A AB 2()2J n J J n ππ=+B 60020010(10)6060J ⨯=+⨯2B 20kg m J ⇒=⋅(2) 损失的机械能2222A A A B A A A B 222241111()(2)()(2)222216001200104(1020)4 1.31510J 260260E J J J J n J J n ωωππππ∆=-+=-+⎛⎫⎛⎫=⨯⨯-+⨯=⨯ ⎪ ⎪⎝⎭⎝⎭53. 依题意得 d 0x x F F =∑=d d sin d sin sin d y F F BI l BIR θθθθ===0sin d 2y F F BIR BIRπθθ===⎰54. (1)0d 2B r B r Iπμ⋅=⋅=∑⎰ 环外的磁感应强度 0B =环内的磁感应强度 02B r NIπμ⋅=02NI B rμπ=(2) 0d d d 2NIhBh r r rμΦπ==001d d ln 22b a NIh NIh br r aμμΦΦππ===⎰⎰环的自感 20ln 2N h N b L I I aμψΦπ===55. 线框的动生电动势1212()N B B lvεεε=-=-001122()NIlv NIlav d d a d d a μμππ⎛⎫=-= ⎪++⎝⎭。
《大学物理》各章练习题及答案解析
《大学物理》各章练习题及答案解析第1章 质点运动学一、选择题:1.以下五种运动中,加速度a保持不变的运动是 （ D ） (A) 单摆的运动。
(B) 匀速率圆周运动。
(C) 行星的椭圆轨道运动。
(D) 抛体运动。
(E) 圆锥摆运动。
2．下面表述正确的是（ B ）(A)质点作圆周运动,加速度一定与速度垂直； (B) 物体作直线运动,法向加速度必为零； (C)轨道最弯处法向加速度最大； (D)某时刻的速率为零,切向加速度必为零。
3.某质点做匀速率圆周运动，则下列说法正确的是（ C ）(A)质点的速度不变; (B)质点的加速度不变 (C)质点的角速度不变; (D)质点的法向加速度不变4.一运动质点在某瞬时位于矢径()y x r , 的端点处，其速度大小为（ D ）()()(()22⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛dt dy dt dx D C dtrd B dt drA5. 一质点在平面上运动,运动方程为:j t i t r222+=,则该质点作（ B ）(A)匀速直线运动 (B)匀加速直线运动(C)抛物线运动 (D)一般曲线运动6.一质点做曲线运动，r 表示位置矢量，v 表示速度，a表示加速度，s 表示路程，a t 表示切向加速度，对下列表达式,正确的是（ B ）(A)dt dr v = (B) dt ds v = (C) dtdv a = (D) dt vd a t=7. 某质点的运动方程为 3723+-=t t X （SI ）,则该质点作 [ D ](A)匀加速直线运动,加速度沿 x 轴正方向; (B)匀加速直线运动,加速度沿 x 轴负方向; (C)变加速直线运动.加速度沿 x 轴正方向; (D)变加速直线运动,加速度沿 x 轴负方向8．一质点沿x 轴运动，其运动方程为()SI t t x 3235-=，当t=2s 时，该质点正在（ A ）(A)加速 (B)减速 (C)匀速 (D)静止1.D2. B3. C4.D5.B ，6B ，7A 8 A二 、填空题1. 一质点的运动方程为x =2t ，y =4t 2-6t ，写出质点的运动方程（位置矢量）j t t i t r)64(22-+=，t =1s 时的速度j i v22+=，加速度j a 8=，轨迹方程为x x y 32-=。
(完整版)大学物理课后习题答案详解
第一章质点运动学1、(习题1.1)：一质点在xOy 平面内运动，运动函数为2x =2t,y =4t 8-。
（1）求质点的轨道方程；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。
解：（1）由x=2t 得，y=4t 2-8 可得： y=x 2-8 即轨道曲线 （2）质点的位置 ： 22(48)r ti t j =+- 由d /d v r t =则速度： 28v i tj =+ 由d /d a v t =则加速度： 8a j =则当t=1s 时，有 24,28,8r i j v i j a j =-=+= 当t=2s 时，有 48,216,8ri j v i j a j =+=+=2、（习题1.2）： 质点沿x 在轴正向运动，加速度kv a -=，k 为常数．设从原点出发时速度为0v ，求运动方程)(t x x =.解：kv dt dv-= ⎰⎰-=t vv kdt dv v 001 tk e v v -=0t k e v dtdx-=0 dt ev dx tk tx-⎰⎰=000)1(0t k e kv x --=3、一质点沿x 轴运动，其加速度为a = 4t (SI)，已知t = 0时，质点位于x 0=10 m 处，初速度v 0 = 0．试求其位置和时间的关系式． 解： =a d v /d t 4=t d v 4=t d t ⎰⎰=vv 0d 4d tt t v 2=t 2v d =x /d t 2=t 2t t x txx d 2d 020⎰⎰= x 2= t 3 /3+10 (SI)4、一质量为m 的小球在高度h 处以初速度0v 水平抛出，求：（1）小球的运动方程；（2）小球在落地之前的轨迹方程； （3）落地前瞬时小球的d d r t ，d d v t ，tv d d . 解：（1） t v x 0= 式（1）2gt 21h y -= 式（2） 201()(h -)2r t v t i gt j =+（2）联立式（1）、式（2）得 22v 2gx h y -=（3）0d -gt d rv i j t = 而落地所用时间 gh2t = 所以 0d -2gh d r v i j t =d d v g j t=- 2202y 2x )gt (v v v v -+=+= 2120212202)2(2])([gh v gh g gt v t g dt dv +=+=5、 已知质点位矢随时间变化的函数形式为22r t i tj =+，式中r 的单位为m ，t 的单位为s .求：（1）任一时刻的速度和加速度；（2）任一时刻的切向加速度和法向加速度。
大学物理习题及解答(打印版)
q V = 4πε o r
9
q .o V = o 4πε o R
q
.o
x
r
R dq
10
圆弧圆心、圆环轴线上的电场？
例题 均匀带电圆盘，半径为R，电荷面密度为 σ，求轴线上离盘心距离为x的P点的电势。(取无穷远 为电势零点) 解 将圆盘分为若干个圆环, 利用圆环公式积分。 P
例题 求半径为R、总电量为q的均匀带电球面的电 势分布。 q 解 由高斯定理求出其场强分布:
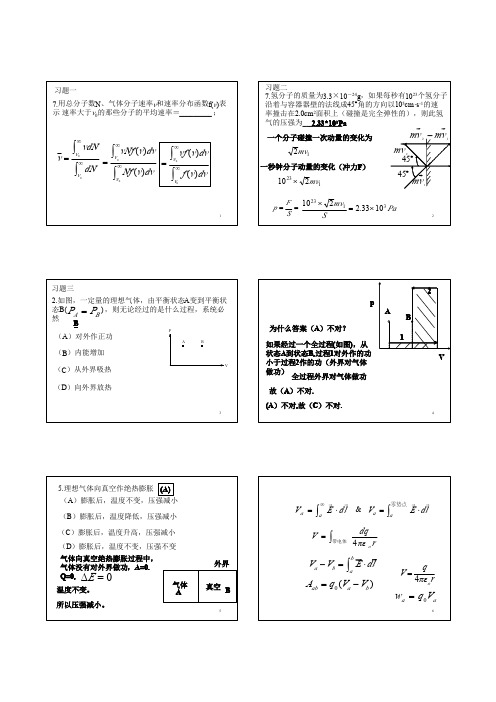
习题一 7.用总分子数N、气体分子速率v和速率分布函数f(v)表 示 速率大于v0的那些分子的平均速率＝_________ ；
习题二 7. 氢分子的质量为3.3×10－24g，如果每秒有1023个氢分子 沿着与容器器壁的法线成45°角的方向以105cm·s-1的速 率撞击在2.0cm2面积上（碰撞是完全弹性的），则此氢 气的压强为___________ *103 Pa 2.33 2.33* 一个分子碰撞一次动量的变化为
-q
a
R
+q
R o
c
R
将Vo代入功的式子，得
A∞ o = −
q πε o a
q 6 πεo R qqo 6πεo R
8
∴ Aac = −
7
例题 一均匀带电直线段，长为L，电量为q;求直 线延长线上离一端距离为d的P点的电势。(取无穷远 为电势零点) 解 将带电直线分 为许多电荷元dq(点电 荷),利用点电荷电势公 式积分：
∂V ∂V = 0, E z = − =0 ∂y ∂z
17
18
3
例题7.1 两平行金属板A、B，面积S， 相距d， 带电：QA，QB，求两板各表面上的 电荷面密度及两板间的电势差(忽略金属板的 边缘效应)。 解 (σ1+ σ2)S=QA (σ3+ σ4)S=QB P1点: P2点:
大学物理课后习题及答案(1-4章)含步骤解
，根据流量守恒
,
（2）当
（3）当
时，
时，
−
,整理可得：
可得
，即
,
图1-34所示为输液的装置。设吊瓶的截面积为1 ，针孔的截面积为2 ，且1 ≫ 2 ，开始时( = 0)，吊瓶内上下
液面距针孔的高度分别为ℎ1 和ℎ2 ，求吊瓶内药液全部输完时需要的时间。
，则针孔的流量为
液体总体积为
Ԧ =
= 2Ԧ − 2 Ԧ = −2Ԧ
1s末和2s末质点的速度为： 1 = 2Ԧ − 2Ԧ（m ∙ s−1 ），2 = 2Ԧ − 4Ԧ（m ∙ s −1 ）；
1s末和2s末质点的加速度相等：Ԧ = −2Ԧ （m ∙ s−2 ）
已知一质点做直线运动，其加速度Ԧ = 4 + 3 m ∙ s−2 , 开始运动时，0 = 5 m,
= 0.06（m）
（2）设弹簧最大压缩量为∆′ , 与碰撞粘在一起的速度为 ′，0 = ( +
) ′，代入已知条件可得 ′ = 4Τ11， + 压缩弹簧的过程中，机械能守恒，则
1
(
2
1
+ ) 2 = 2 ∆′2 ，得∆′ =
+
≈ 0.04（m）
(1)角加速度 =
由 =
∆
∆
=
0−2×1500÷60
50
由 =
=
2×1500
60
= 50 (rad ∙ s −1 )
= − (rad ∙ s−2 )
= −，得 = −，两边进行积分
得到 − 50 = − − 0,
(完整版)《大学物理》习题册题目及答案第2单元 动量守恒定律
第2单元 动量守恒定律序号 学号 姓名 专业、班级一 选择题[ B ]1. 力i F t 12=(SI)作用在质量m ＝2 kg 的物体上，使物体由原点从静止开始运动，则它在3秒末的动量应为：(A) －54i kg ⋅m ⋅s -1(B) 54i kg ⋅m ⋅s -1(C) －27i kg ⋅m ⋅s -1 (D) 27i kg ⋅m ⋅s-1[ C ]2. 如图所示，圆锥摆的摆球质量为m ，速率为v ，圆半径为R ，当摆球在轨道上运动半周时，摆球所受重力冲量的大小为：(A) mv 2 (B)()()22/2v R mg mv π+(C)vRmgπ (D) 0[ A ]3 .粒子B 的质量是粒子A 的质量的4倍。
开始时粒子A 的速度为()j i ϖϖ43+，粒子B 的速度为(j i ϖϖ72-)。
由于两者的相互作用，粒子A 的速度为()j i ϖϖ47-，此时粒子B 的速度等于：(A) j i 5- (B) j i ϖϖ72- (C) 0 (D) j i ϖϖ35-[ C ]4. 水平冰面上以一定速度向东行驶的炮车，向东南（斜向上）方向发射一炮弹，对于炮车和炮弹这一系统，在此过程中（忽略冰面摩擦及空气阻力） （A ）总动量守恒（B ）总动量在炮身前进的方向上的分量守恒，其它方向动量不守恒 (C) 总动量在水平面上任意方向的分量守恒，竖直方向分量不守恒 （D ）动量在任何方向的分量均不守恒二 填空题1. 一颗子弹在枪筒里前进时所受的合力大小为t F 31044005⨯-=(SI)，子弹从枪口射出的速率为3001s m -⋅。
假设子弹离开枪口时合力刚好为零，则(1) 子弹走完枪筒全长所用的时间 t ＝ 0.003 s ,(2) 子弹在枪筒中所受的冲量 I ＝ s N 6.0⋅ ， (3) 子弹的质量 m ＝ 2 ×10-3 kg 。
2. 质量m 为10kg 的木箱放在地面上，在水平拉力F 的作用下由静止开始沿直线运动，其拉力随时间的变化关系如图所示。
大学物理力学练习题及答案
大学物理力学练习题及答案一、选择题（每题2分，共20分）1. 一个物体质量为2kg，受到的力是3N，该物体的加速度大小为多少？A. 0.3 m/s^2B. 1.5 m/s^2C. 6 m/s^2D. 1 N/kg答案：B2. 假设一个物体在重力作用下自由下落，那么它的重力势能和动能之间的关系是？A. 重力势能和动能相等B. 重力势能大于动能C. 重力势能小于动能D. 重力势能减少，动能增加答案：A3. 力的合成是指两个或多个力合并后的结果。
如果两个力大小相等并且方向相反，则它们的合力为A. 0B. 1C. 2D. 无法确定答案：A4. 在一个力的作用下，一个物体做匀速直线运动。
可以推断出物体的状态是A. 静止状态B. 匀速运动状态C. 加速运动状态D. 不能判断答案：B5. 牛顿运动定律中，质量的作用是用来描述物体对力的抵抗程度，质量越大，则物体对力的抵抗越小。
A. 对B. 错答案：B6. 一个物体以20 m/s的速度做匀速圆周运动，周长为40π m，物体的摩擦力大小为F，那么物体受到的拉力大小为多少？A. 0B. FC. 2FD. 4F答案：C7. 一个质量为1 kg的物体向左受到3 N的力，向右受到2 N的力，则该物体的加速度大小为多少？A. 1 m/s^2B. 2 m/s^2C. 3 m/s^2D. 5 m/s^2答案：A8. 弹力是一种常见的力，它的特点是随着物体变形而产生，并且与物体的形状无关。
A. 对B. 错答案：A9. 一个物体受到两个力，力的合力为2 N，其中一个力的大小为1 N，则另一个力的大小为多少？A. 1 NB. 0 NC. -1 ND. 无法确定答案：A10. 在竖直抛体运动过程中，物体的速度在上升过程中逐渐减小，直到达到峰值后开始增大。
A. 对B. 错答案：B二、计算题（每题10分，共40分）1. 一个物体以5 m/s的初速度被一个10 N的力加速，物体质量为2 kg，求物体在2秒后的速度。
大学物理试题及答案
第1部分：选择题习题11-1 质点作曲线运动，在时刻t 质点的位矢为r r ，速度为v r，t 至()t t +∆时间内的位移为r ∆r，路程为s ∆，位矢大小的变化量为r ∆（或称r ∆r ），平均速度为v r ，平均速率为v 。
（1）根据上述情况，则必有（ ） （A ）r s r ∆=∆=∆r（B ）r s r ∆≠∆≠∆r ，当0t ∆→时有dr ds dr =≠r （C ）r r s ∆≠∆≠∆r，当0t ∆→时有dr dr ds =≠r（D ）r s r ∆=∆≠∆r ，当0t ∆→时有dr dr ds ==r（2）根据上述情况，则必有（ ） （A ）,v v v v ==r r （B ）,v v v v ≠≠r r （C ）,v v v v =≠rr（D ）,v v v v ≠=rr1-2 一运动质点在某瞬间位于位矢(,)r x y r的端点处，对其速度的大小有四种意见，即（1）dr dt ；（2）dr dt r；（3）dsdt；（4下列判断正确的是：（A ）只有（1）（2）正确 （B ）只有（2）正确 （C ）只有（2）（3）正确 （D ）只有（3）（4）正确1-3 质点作曲线运动，r r 表示位置矢量，v r 表示速度，a r表示加速度，s 表示路程，t a 表示切向加速度。
对下列表达式，即（1）dv dt a =；（2）dr dt v =；（3）ds dt v =；（4）t dv dt a =r。
下述判断正确的是（ ）（A ）只有（1）、（4）是对的 （B ）只有（2）、（4）是对的 （C ）只有（2）是对的 （D ）只有（3）是对的 1-4 一个质点在做圆周运动时，则有（ ） （A ）切向加速度一定改变，法向加速度也改变（B ）切向加速度可能不变，法向加速度一定改变 （C ）切向加速度可能不变，法向加速度不变 （D ）切向加速度一定改变，法向加速度不变*1-5 如图所示，湖中有一小船，有人用绳绕过岸上一定高度处的定滑轮拉湖中的船向岸边运动。
大学物理学第一章习题答案
习题11、1选择题(1) 一运动质点在某瞬时位于矢径的端点处,其速度大小为(A)(B)(C)(D)[答案:D](2) 一质点作直线运动,某时刻的瞬时速度,瞬时加速度,则一秒钟后质点的速度(A)等于零(B)等于-2m/s(C)等于2m/s (D)不能确定。
[答案:D](3) 一质点沿半径为R的圆周作匀速率运动,每t秒转一圈,在2t时间间隔中,其平均速度大小与平均速率大小分别为(A)(B)(C) (D)[答案:B]1、2填空题(1) 一质点,以的匀速率作半径为5m的圆周运动,则该质点在5s内,位移的大小就是;经过的路程就是。
[答案: 10m;5πm](2) 一质点沿x方向运动,其加速度随时间的变化关系为a=3+2t (SI),如果初始时刻质点的速度v0为5m·s-1,则当t为3s时,质点的速度v=。
[答案: 23m·s-1 ](3) 轮船在水上以相对于水的速度航行,水流速度为,一人相对于甲板以速度行走。
如人相对于岸静止,则、与的关系就是。
[答案:]1、3一个物体能否被瞧作质点,您认为主要由以下三个因素中哪个因素决定:(1) 物体的大小与形状;(2) 物体的内部结构;(3) 所研究问题的性质。
解:只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响,因此主要由所研究问题的性质决定。
1、4下面几个质点运动学方程,哪个就是匀变速直线运动？(1)x=4t-3;(2)x=-4t3+3t2+6;(3)x=-2t2+8t+4;(4)x=2/t2-4/t。
给出这个匀变速直线运动在t=3s时的速度与加速度,并说明该时刻运动就是加速的还就是减速的。
(x单位为m,t单位为s)解:匀变速直线运动即加速度为不等于零的常数时的运动。
加速度又就是位移对时间的两阶导数。
于就是可得(3)为匀变速直线运动。
其速度与加速度表达式分别为t=3s时的速度与加速度分别为v=20m/s,a=4m/s2。
因加速度为正所以就是加速的。
大学物理复习题(包含小题答案)
一、 选择题1．已知自由空间一均匀平面波， 其磁场强度为0cos()y H e H t z ωβ=-， 则电场强度的方向____， 能流密度的方向为____。
（ A ）A. x ，zB. -x ，zC. x ， -zD. -x ， -z2．损耗媒质中的电磁波，其传播速度随媒质电导率σ的增大而 。
（ B ）A.不变B. 减小C. 增大D.和电导率无关3．如图所示两个载流线圈，所受的电流力使两线圈间的距离 。
（ A ）A.增大B.缩小C.不变D.和力无关4．在无损耗媒质中，电磁波的相速度与波的频率 。
（ C ）A ．成正比B ．成反比C ．无关D ．线性变化5．电位移表达式D E ε= （ C ）A ．在各种电介质中适用B ．只在各向异性的电介质中适用C ．只在各向同性的、线性的均匀的电介质中适用D ．真空中适用6．恒定电流场基本方程的微分形式说明它是 （ B ）A. 有散无旋场B.无散无旋场C.无散有旋场D.有散有旋场7．已知电场中一闭合面上的电移位 D 的通量不等于零，则意味着该面内 （ D ）A ．一定存在自由磁荷B ．一定不存在自由电荷C ．不能确定D ．一定存在自由电荷8．下面表述正确的为 （ D ）A ．矢量场的散度结果为一矢量场B ．标量场的梯度结果为一标量场C ．矢量场的旋度结果为一标量场D ．标量场的梯度结果为一矢量场9．电偶极子是_ __ （ A ）A ．两个相距很小的等量异号点电荷组成的系统B ．两个相距很小的等量同号点电荷组成的系统C ．两个相距很大的等量异号点电荷组成的系统D ．两个相距很大的等量同号点电荷组成的系统10．亥姆霍兹定理表明，研究一个矢量场，必须研究它的 ，才能确定该矢量场的性质。
（ A ）A.散度和旋度B.散度和通量C.旋度和环量D.梯度和方向导数11．磁场强度表达式B H μ= （ C ）A.在各种磁介质中适用B.只在各向异性的磁介质中适用C.只在各向同性的、线性的均匀的磁介质中适用D.真空中适用12．正弦电磁场 ( 角频率为ω ) 的磁场强度复矢量H 满足的亥姆霍兹方程为 （ A ）A.22000H H ωεμ∇+=B.220r r H H ωεμ∇+=C.200r H H ωεμ∇+=D.200r H H ωεμ∇+=13．静电场中电位为零处的电场强度 （ C ）A.一定为零B.最大C.不能确定D.最小14．标量场的梯度的方向为 （ B ）A.等值面的切线方向B.等值面的法线方向C.标量增加的方向D.标量减小的方向15．下列关于电场（力）线表述正确的是 （ B ）A.由正的自由电荷出发，终止于负的自由电荷B.由正电荷出发，终止于负电荷C.正电荷逆着电场线运动D.负电荷顺着电场线运动16．矢量场的散度在直角坐标下的表示形式为 （ A ）A.y x z A A A x y z ∂∂∂++∂∂∂B.x y z Ax Ay Az e e e x y z∂∂∂++∂∂∂ C.x y z A A A e e e x y z ∂∂∂++∂∂∂ D.A A A x y z∂∂∂++∂∂∂ 17．已知自由空间一均匀平面波，其电场强度为0cos()x E e E t z ωβ=-， 则能流密度的方向____， 磁场强度的方向为____。
大学物理习题答案
大学物理练习册 参考解答第12章 真空中的静电场一、选择题1(D)，2(C)，3(C)，4(A)，5(C)，6(B)，7(C)，8(D)，9(D)，10(B)， 二、填空题(1). 电场强度和电势，0/q F E=，l E q W U aa⎰⋅==00d /(U 0=0).(2). ()042ε/q q +， q 1、q 2、q 3、q 4 ；(3). 0，λ / (2ε0) ； (4). σR / (2ε0) ； (5). 0 ； (6).⎪⎪⎭⎫ ⎝⎛-π00114r r q ε ；(7). －2×103 V ； (8).⎪⎪⎭⎫ ⎝⎛-πa br r q q 11400ε(9). 0，pE sin α ； (10). ()i a x A2+-.三、计算题1. 如图所示，真空中一长为L 的均匀带电细直杆，总电荷为q ，试求在直杆延长线上距杆的一端距离为d 的P 点的电场强度．解：设杆的左端为坐标原点O ，x 轴沿直杆方向．带电直杆的电荷线密度为λ=q / L ，在x 处取一电荷元d q = λd x = q d x / L ，它在P 点的场强：()204d d x d L q E -+π=ε()204d x d L L xq -+π=ε总场强为⎰+π=Lx d L xL q E 020)(d 4－ε()d L d q +π=04ε 方向沿x 轴，即杆的延长线方向．2．一个细玻璃棒被弯成半径为R 的半圆形，沿其上半部分均匀分布有电荷+Q ，沿其下半部分均匀分布有电荷－Q ，如图所示．试求圆心O 处的电场强度．解：把所有电荷都当作正电荷处理. 在θ处取微小电荷 d q = λd l = 2Q d θ / π它在O 处产生场强θεεd 24d d 20220R QR q E π=π=L Pd EO按θ 角变化，将d E 分解成二个分量：θθεθd sin 2sin d d 202R QE E x π==θθεθd cos 2cos d d 202RQE E y π-=-= 对各分量分别积分，积分时考虑到一半是负电荷⎥⎦⎤⎢⎣⎡-π=⎰⎰πππθθθθε2/2/0202d sin d sin 2R QE x ＝02022/2/0202d cos d cos 2R QR Q E y εθθθθεππππ-=⎥⎦⎤⎢⎣⎡-π-=⎰⎰ 所以j RQ j E i E E y x202επ-=+= 3. “无限长”均匀带电的半圆柱面，半径为R ，设半圆柱面沿轴线OO'单位长度上的电荷为λ，试求轴线上一点的电场强度．解:设坐标系如图所示．将半圆柱面划分成许多窄条．d l 宽的窄条的电荷线密度为 θλλλd d d π=π=l R取θ位置处的一条，它在轴线上一点产生的场强为θελελd 22d d 020RR E π=π=如图所示. 它在x 、y 轴上的二个分量为：d E x =d E sin θ , d E y =－d E cos θ对各分量分别积分RR E x 02002d sin 2ελθθελππ=π=⎰0d cos 2002=π-=⎰πθθελRE y 场强 i Rj E i E E y x02ελπ=+= 4. 实验表明，在靠近地面处有相当强的电场，电场强度E垂直于地面向下，大小约为100 N/C ；在离地面1.5 km 高的地方，E也是垂直于地面向下的，大小约为25 N/C ． (1) 假设地面上各处E都是垂直于地面向下，试计算从地面到此高度大气中电荷的平均体密度；(2) 假设地表面内电场强度为零，且地球表面处的电场强度完全是由均匀分布在地表面的电荷产生，求地面上的电荷面密度．(已知：真空介电常量0ε＝8.85×10-12 C 2·N -1·m -2) 解：(1) 设电荷的平均体密度为ρ，取圆柱形高斯面如图(1)(侧面垂直底面，底面∆S 平行地面)上下底面处的 场强分别为E 1和E 2，则通过高斯面的电场强度通量为：⎰⎰E·S d ＝E 2∆S -E 1∆S ＝(E 2-E 1) ∆S高斯面S 包围的电荷∑q i ＝h ∆S ρ由高斯定理(E 2－E 1) ∆S ＝h ∆S ρ /ε 0∴ () E E h1201-=ερ＝4.43×10-13 C/m 3(2) 设地面面电荷密度为σ．由于电荷只分布在地表面，所以电力线终止于地面，取高斯面如图(2)由高斯定理 ⎰⎰E·S d =∑i 01q ε-E ∆S =S ∆σε01∴ σ =－ε 0 E ＝－8.9×10-10 C/m 3 5. 一半径为R 的带电球体，其电荷体密度分布为ρ =Ar (r ≤R ) ， ρ =0 (r ＞R )， A 为一常量．试求球体内外的场强分布．解：在球内取半径为r 、厚为d r 的薄球壳，该壳内所包含的电荷为r r Ar V q d 4d d 2π⋅==ρ在半径为r 的球面内包含的总电荷为403d 4Ar r Ar dV q rVπ=π==⎰⎰ρ (r ≤R)以该球面为高斯面，按高斯定理有 0421/4εAr r E π=π⋅得到()0214/εAr E =， (r ≤R )方向沿径向，A >0时向外, A <0时向里．在球体外作一半径为r 的同心高斯球面，按高斯定理有0422/4εAR r E π=π⋅ 得到 ()20424/r AR E ε=， (r >R )方向沿径向，A >0时向外，A <0时向里．6. 如图所示，一厚为b 的“无限大”带电平板 ， 其电荷体密度分布为ρ＝kx (0≤x ≤b )，式中k 为一正的常量．求： (1) 平板外两侧任一点P 1和P 2处的电场强度大小；(2) 平板内任一点P 处的电场强度； (3) 场强为零的点在何处？解： (1) 由对称分析知，平板外两侧场强大小处处相等、方向垂直于平面且背离平面．设场强大小为E ．作一柱形高斯面垂直于平面．其底面大小为S ，如图所示． 按高斯定理∑⎰=⋅0ε/d q S E S，即22d d 12εερεkSbx x kSx S SE b b===⎰⎰得到 E = kb 2 / (4ε0) (板外两侧) (2) 过P 点垂直平板作一柱形高斯面，底面为S ．设该处场强为E '，如图所示．按高斯定理有(2)()022εεkSb xdx kSS E E x==+'⎰得到 ⎪⎪⎭⎫ ⎝⎛-='22220b x k E ε (0≤x ≤b ) (3) E '=0，必须是0222=-b x ， 可得2/b x =7. 一“无限大”平面，中部有一半径为R 的圆孔，设平面上均匀带电，电荷面密度为σ．如图所示，试求通过小孔中心O 并与平面垂直的直线上各点的场强和电势(选O 点的电势为零)．解：将题中的电荷分布看作为面密度为σ的大平面和面密度为－σ的圆盘叠加的 结果．选x 轴垂直于平面，坐标原点Ｏ在圆盘中心，大平面在x 处产生的场强为ixx E 012εσ=圆盘在该处的场强为i x R x x E ⎪⎪⎭⎫ ⎝⎛+--=2202112εσ ∴ i xR x E E E 220212+=+=εσ该点电势为 ()220222d 2x R R xR x x U x+-=+=⎰εσεσ8. 一半径为R 的“无限长”圆柱形带电体，其电荷体密度为ρ =Ar (r ≤R )，式中A 为常量．试求：(1) 圆柱体内、外各点场强大小分布； (2) 选与圆柱轴线的距离为l (l ＞R ) 处为电势零点，计算圆柱体内、外各点的电势分布．解：(1) 取半径为r 、高为h 的高斯圆柱面(如图所示)．面上各点场强大小为E 并垂直于柱面．则穿过该柱面的电场强度通量为：⎰π=⋅SrhE S E 2d为求高斯面内的电荷，r ＜R 时，取一半径为r '，厚d r '、高h 的圆筒，其电荷为r r Ah V ''π=d 2d 2ρσO R OxP则包围在高斯面内的总电荷为3/2d 2d 32Ahr r r Ah V r Vπ=''π=⎰⎰ρ由高斯定理得 ()033/22εAhr rhE π=π 解出()023/εAr E = (r ≤R )r ＞R 时，包围在高斯面内总电荷为：3/2d 2d 302AhR r r Ah V RVπ=''π=⎰⎰ρ由高斯定理 ()033/22εAhR rhE π=π 解出 ()r AR E 033/ε= (r >R )(2) 计算电势分布 r ≤R 时 ⎰⎰⎰⋅+==l R Rrl rr r AR r r A r E U d 3d 3d 0320εε ()R l AR r R A ln 3903330εε+-=r ＞R 时 rlAR r r AR r E U lrl rln 3d 3d 0303εε=⋅==⎰⎰9．一真空二极管，其主要构件是一个半径R 1＝5×10-4 m 的圆柱形阴极A 和一个套在阴极外的半径R 2＝4.5×10-3 m 的同轴圆筒形阳极B ，如图所示．阳极电势比阴极高300 V ，忽略边缘效应. 求电子刚从阴极射出时所受的电场力．(基本电荷e ＝1.6×10-19 C)解：与阴极同轴作半径为r (R 1＜r ＜R 2 )的单位长度的圆柱形高斯面，设阴极上电荷线密度为λ．按高斯定理有 2πrE = λ/ ε0得到 E = λ / (2πε0r ) (R 1＜r ＜R 2) 方向沿半径指向轴线．两极之间电势差⎰⎰π-=⋅=-21d 2d 0R R B AB A rrr E U U ελ120ln 2R R ελπ-=得到()120/ln 2R R U U A B -=πελ， 所以 ()rR R U U E A B 1/ln 12⋅-=在阴极表面处电子受电场力的大小为 ()()11211/c R R R U U eR eE F A B ⋅-==＝4.37×10-14 N 方向沿半径指向阳极．第13章 静电场中的导体和电解质一、选择题1(D)，2(D)，3(B)，4(A)，5(C)，6(B)，7(C)，8(B)，9(C)，10(B) 二、填空题(1). 4.55×105 C ；(2). σ (x ，y ，z )/ε0，与导体表面垂直朝外(σ > 0) 或 与导体表面垂直朝里(σ < 0). (3). εr ，1， εr ； (4). 1/εr ，1/εr ；(5). σ ，σ / ( ε 0ε r )； (6).Rq 04επ ；(7). P ，－P ，0； (8) (1- εr )σ / εr ； (9). 减小， 减小； (10). 增大，增大.三、计算题1. 一接地的"无限大"导体板前垂直放置一"半无限长"均匀带电直线，使该带电直线的一端距板面的距离为d ．如图所示，若带电直线上电荷线密度为λ，试求垂足O 点处的感生电荷面密度．解：如图取座标，对导体板内O 点左边的邻近一点，半无限长带电直线产生的场强为： ()⎰∞-=dx i dx E 2004/ελπ()d i 04/ελπ-= 导体板上的感应电荷产生的场强为：()0002/εσi E-='由场强叠加原理和静电平衡条件，该点合场强为零，即()[]()02/4/000=--εσελd π ∴ ()d π2/0λσ-=2．半径为R 1的导体球，带电荷q ，在它外面同心地罩一金属球壳，其内、外半径分别为R 2 = 2 R 1，R 3 = 3 R 1，今在距球心d = 4 R 1处放一电荷为Q 的点电荷，并将球壳接地(如图所示)，试求球壳上感生的总电荷．解：应用高斯定理可得导体球与球壳间的场强为 ()304/r r q E επ= (R 1＜r ＜R 2)设大地电势为零，则导体球心O 点电势为： ⎰⎰π==2121200d 4d R R R R r r q r E U ε⎪⎪⎭⎫⎝⎛-π=21114R R qε根据导体静电平衡条件和应用高斯定理可知，球壳内表面上感生电荷应为－q ． 设球壳外表面上感生电荷为Q'．以无穷远处为电势零点，根据电势叠加原理，导体球心O 处电势应为： ⎪⎪⎭⎫ ⎝⎛+-'+π=1230041R q R q R Q d Q U ε 假设大地与无穷远处等电势，则上述二种方式所得的O 点电势应相等，由此可得Q '=－3Q / 4 ， 故导体壳上感生的总电荷应是－[( 3Q / 4) +q ].3. 一圆柱形电容器，外柱的直径为4 cm ，内柱的直径可以适当选择，若其间充满各向同性的均匀电介质，该介质的击穿电场强度的大小为E 0= 200 KV/cm ．试求该电容器可能承受的最高电压． (自然对数的底e = 2.7183)解：设圆柱形电容器单位长度上带有电荷为λ，则电容器两极板之间的场强分布 为 )2/(r E ελπ= 设电容器内外两极板半径分别为r 0，R ，则极板间电压为⎰⎰⋅π==R rRr rr r E U d 2d ελ 0ln 2r Rελπ= 电介质中场强最大处在内柱面上，当这里场强达到E 0时电容器击穿，这时应有 002E r ελπ=，000ln r RE r U = 适当选择r 0的值，可使U 有极大值，即令0)/ln(/d d 0000=-=E r R E r U ，得 e R r /0=，显然有22d d r U < 0，故当 e R r /0= 时电容器可承受最高的电压 e RE U /0max = = 147 kV.4. 如图所示，一圆柱形电容器，内筒半径为R 1，外筒半径为R 2 (R 2＜2 R 1)，其间充有相对介电常量分别为εr 1和εr 2＝εr 1 / 2的两层各向同性均匀电介质，其界面半径为R ．若两种介质的击穿电场强度相同，问：(1) 当电压升高时，哪层介质先击穿？(2) 该电容器能承受多高的电压？解：(1) 设内、外筒单位长度带电荷为＋λ和－λ．两筒间电位移的大小为 D ＝λ / (2πr ) 在两层介质中的场强大小分别为E 1 = λ / (2πε0 εr 1r )， E 2 = λ / (2πε0 εr 2r ) 在两层介质中的场强最大处是各层介质的内表面处，即E 1M = λ / (2πε0 εr 1R 1)， E 2M = λ / (2πε0 εr 2R ) 可得 E 1M / E 2M = εr 2R / (εr 1R 1) = R / (2R 1)已知 R 1＜2 R 1， 可见 E 1M ＜E 2M ，因此外层介质先击穿． (2) 当内筒上电量达到λM ，使E 2M ＝E M 时，即被击穿，λM = 2πε0 εr 2RE M 此时．两筒间电压(即最高电压)为：r r r r U R R r M RR r M d 2d 221201012⎰⎰+=επελεπελ⎪⎪⎭⎫ ⎝⎛+=R R R R RE r r M r 22112ln 1ln 1εεε5. 两根平行“无限长”均匀带电直导线，相距为d ，导线半径都是R (R << d )．导线上电荷线密度分别为+λ和-λ．试求该导体组单位长度的电容．解：以左边的导线轴线上一点作原点，x 轴通过两导线并垂直于导线．两导线间x 处的场强为 x E 02ελπ=)(20x d -π+ελ两导线间的电势差为⎰--+π=Rd Rx xd x U d )11(20ελ O R 1R 2Rεr 2εr 1xx R d -R+λO-λ)ln (ln 20R d R R R d ---π=ελRRd -π=ln 0ελ 设导线长为L 的一段上所带电量为Q ，则有L Q /=λ，故单位长度的电容U LU Q C /)/(λ==RR d -π=lnε6．圆柱形电容器是由半径为a 的圆柱形导体和与它同轴的内半径为b (b ＞a )的导体圆筒构成，其间充满了相对介电常量为εr 的各向同性的均匀电介质．设圆柱导体单位长度带电荷为λ，圆筒上为－λ，忽略边缘效应．求电介质中的电极化强度P 的大小及介质内、外表面上的束缚电荷面密度σˊ．解：由D的高斯定理求出介质内的电位移大小为D = λ / (2πr ) (a ＜r ＜b ) 介质内的场强大小为E = D / (ε0εr ) = λ / (2πε0εr r ) (a ≤r ≤b ) 电极化强度 P = ε0χe E ()rr r ελεπ-=21 (a ≤r ≤b )内外表面上束缚电荷面密度a aP ='σcos180°＝()ar r ελεπ--21b bP ='σcos 0°＝()br r ελεπ-217. 一个圆柱形电容器，内圆柱半径为R 1，外圆柱半径为R 2，长为L (L >>R 2－R 1)，两圆筒间充有两层相对介电常量分别为εr 1和εr 2的各向同性均匀电介质，其界面半径为R ，如图所示．设内、外圆筒单位长度上带电荷(即电荷线密度)分别为λ和－λ，求： (1) 电容器的电容． (2) 电容器储存的能量．解：(1) 根据有介质时的高斯定理可得两筒之间的电位移的大小为D = λ / (2πr ) 介质中的场强大小分别为E 1 = D / (ε0εr 1) = λ / (2πε0εr 1r ) E 2 = D / (ε0εr 2) = λ / (2πε0εr 2r )两筒间电势差⎰⎰⋅+⋅=21221d d R RR R r E r E UR R R R r r 220110ln π2ln π2εελεελ+=()()[]21021122/ln /ln r r r r R R R R εεεεελπ+=电容 ()()R R R R L U QC r r r r /ln /ln 22112210εεεεε+π== (2) 电场能量 2102112224ln ln2r r r r R R R RL CQ W εεεεελπ⎪⎪⎭⎫ ⎝⎛+==1r 28. 如图所示，一平板电容器，极板面积为S ，两极板之间距离为d ，其间填有两层厚度相同的各向同性均匀电介质，其介电常量分别为ε1和ε2．当电容器带电荷±Q 时，在维持电荷不变下，将其中介电常量为ε1的介质板抽出，试求外力所作的功．解：可将上下两部分看作两个单独的电容器串联，两电容分别为d S C 112ε= ，d SC 222ε=串联后的等效电容为 ()21212εεεε+=d SC带电荷±Q 时，电容器的电场能量为 ()S d Q C Q W 21212242εεεε+== 将ε1的介质板抽去后，电容器的能量为 ()S d Q W 202024εεεε+='外力作功等于电势能增加，即 ⎪⎪⎭⎫⎝⎛-=-'=∆=102114εεS d Q W W W A .第14章 稳恒电流的磁场一、选择题1(B)，2(A)，3(D)，4(C)，5(B)，6(D)，7(B)，8(C)，9(D)，10(A) 二、填空题(1). 最大磁力矩，磁矩 ; (2). πR 2c ； (3). )4/(0a I μ； (4).RIπ40μ ；(5). μ0i ，沿轴线方向朝右. ； (6). )2/(210R rI πμ， 0 ; (7). 4 ; (8).BIR 2，沿y 轴正向；(9). ωλB R 3π，在图面中向上； (10). 正，负.三 计算题1. 将通有电流I 的导线在同一平面内弯成如图所示的形状，求D 点的磁感强度B的大小．解：其中3/4圆环在D 处的场 )8/(301a I B μ=AB 段在D 处的磁感强度 )221()]4/([02⋅π=b I B μ BC 段在D 处的磁感强度 )221()]4/([03⋅π=b I B μ1B 、2B、3B 方向相同，可知D 处总的B 为)223(40baI B +ππ=μ2. 半径为R 的导体球壳表面流有沿同一绕向均匀分布的面电流，通过垂直于电流方向的每单位长度的电流为K ．求球心处的磁感强度大小．解：如图 θd d d KR s K I == 2/32220])cos ()sin [(2)sin (d d θθθμR R R I B += 32302d sin RKR θθμ=θθμd sin 2120K =⎰π=020d sin 21θθμK B ⎰π-=00d )2cos 1(41θθμK π=K 041μ3. 如图两共轴线圈，半径分别为R 1、R 2，电流为I 1、I 2．电流的方向相反，求轴线上相距中点O 为x 处的P 点的磁感强度．解：取x 轴向右，那么有2/322112101])([2x b R I R B ++=μ沿x 轴正方向 2/322222202])([2x b R I R B -+=μ 沿x 轴负方向21B B B -=[2μ=2/32211210])([x b R I R ++μ]])([2/32222220x b R I R -+-μ若B > 0，则B 方向为沿x 轴正方向．若B < 0，则B的方向为沿x 轴负方向．4．一无限长圆柱形铜导体(磁导率μ0)，半径为R ，通有均匀分布的电流I ．今取一矩形平面S (长为1 m ，宽为2 R )，位置如右图中画斜线部分所示，求通过该矩形平面的磁通量．解：在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小，由安培环路定 律可得：)(220R r r RIB ≤π=μ因而，穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr r RI Rd 2020⎰π=μπ=40Iμ在圆形导体外，与导体中心轴线相距r 处的磁感强度大小为 )(20R r rIB >π=μ因而，穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S B d 2Φr r I R Rd 220⎰π=μ2ln 20π=Iμ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40I μ2ln 20π+Iμ5. 一半径为 4.0 cm 的圆环放在磁场中，磁场的方向对环而言是对称发散的，如图所示．圆环所在处的磁感强度的大小为0.10 T ，磁场的方向与环面法向成60°角．求当圆环中通有电流I =15.8 A 时，圆环所受磁力的大小和方向．解：将电流元I d l 处的B分解为平行线圈平面的B 1和垂直线圈平面的B 2两分量，则 ︒=60sin 1B B ； ︒=60cos 2B B 分别讨论线圈在B 1磁场和B 2磁场中所受的合力F 1与F 2．电流元受B 1的作用力l IB lB I F d 60sin 90sin d d 11︒=︒=方向平行圆环轴线．因为线圈上每一电流元受力方向相同，所以合力⎰=11d F F ⎰π︒=Rl IB 20d 60sin R IB π⋅︒=260sin = 0.34 N ，方向垂直环面向上．电流元受B 2的作用力l IB lB I F d 60cos 90sin d d 22︒=︒= 方向指向线圈平面中心． 由于轴对称，d F 2对整个线圈的合力为零，即02=F ． 所以圆环所受合力 34.01==F F N ， 方向垂直环面向上．6. 如图所示线框，铜线横截面积S = 2.0 mm 2，其中OA 和DO ＇两段保持水平不动，ABCD 段是边长为a 的正方形的三边，它可绕OO ＇轴无摩擦转动．整个导线放在匀强磁场B 中，B 的方向竖直向上．已知铜的密度ρ = 8.9×103kg/m 3，当铜线中的电流I =10 A 时，导线处于平衡状态，AB 段和CD段与竖直方向的夹角α =15°．求磁感强度B 的大小．解：在平衡的情况下，必须满足线框的重力矩与线框所受的磁力矩平衡(对OO ＇轴而言)．重力矩 αραρsin sin 2121gSa a a gS a M +⋅= αρsin 22g Sa =磁力矩 ααcos )21sin(222B Ia BIa M =-π=B 2d l平衡时 21M M =所以 αρsin 22g Sa αcos 2B Ia =31035.9/tg 2-⨯≈=I g S B αρ T7. 半径为R 的半圆线圈ACD 通有电流I 2，置于电流为I 1的无限长直线电流的磁场中，直线电流I 1恰过半圆的直径，两导线相互绝缘．求半圆线圈受到长直线电流I 1的磁力．解：长直导线在周围空间产生的磁场分布为 )2/(10r I B π=μ取xOy 坐标系如图，则在半圆线圈所在处各点产生的磁感强度大小为： θμsin 210R I B π=， 方向垂直纸面向里，式中θ 为场点至圆心的联线与y 轴的夹角．半圆线圈上d l 段线电流所受的力为：l B I B l I F d d d 22=⨯= θθμd sin 2210R R I I π=θsin d d F F y =．根据对称性知： F y =0d =⎰y F θcos d d F F x = ，⎰π=0x x dF F ππ=2210I I μ2210I I μ=∴半圆线圈受I 1的磁力的大小为： 2210I I F μ=，方向：垂直I 1向右．8. 如图所示．一块半导体样品的体积为a ×b ×c ．沿c 方向有电流I ，沿厚度a 边方向加有均匀外磁场B (B的方向和样品中电流密度方向垂直)．实验得出的数据为 a ＝0.10 cm 、b ＝0.35 cm 、c ＝1.0 cm 、I ＝1.0 mA 、B ＝3.0×10-1 T ，沿b 边两侧的电势差U ＝6.65 mV ，上表面电势高．(1) 问这半导体是p 型(正电荷导电)还是n 型(负电荷导电)？(2) 求载流子浓度n 0 (即单位体积内参加导电的带电粒子数)．解：(1) 根椐洛伦兹力公式：若为正电荷导电，则正电荷堆积在上表面，霍耳电场的方向由上指向下，故上表面电势高，可知是p 型半导体。
大学物理习题与答案解析
a d dvtt28j(m2/)s
大学物理
3、质点作直线运动，加速度 a2Asint，已知
t 0时质点初始状态为x 0
动学方程为xAsi n .t0
、v0 A、该质点运
解：
vv0
t
a
0
dt A
t2As
0
intdt
AAcostA
Acost
t
t
即 a2ct, t a 2c
vx vy
vvx 2vy 2a24c2t22a
大学物理
5、一飞机在跑道上跑过500米后，即升空，如果它在跑
前是静止的，以恒定加速度运动，升空前跑了30秒，则
当它升空时的速度为 v 100 m/s
.
3
解： x 1 at 2 2
a2t2x2 352 000190m2/s
答：B
v(m / s)
2
0到7秒的位移为：
0
r 2 22 2 2 2 2 3 1 i 3 .5 im1
坐标为：x23 .55 .5 m
t(s) 24 5 7
大学物理
3、一质点沿x轴运动的规律是 xt24t5,其中x以m 计，t以s计，则前3s内它的位移和路程分别是
(A)位移和路程都是3m. (B) 位移和路程都是-3m .
dvy dy
则
a vy
dvy dy
kvy2
分离变量得 :
dvy kdy vy
两边积分得 :
v dvy
y
k dy
v v0 y
0
v v0eky
大学物理
3、一质点沿半径为1 m 的圆周运动，运动方程
为 23t，3 式中以弧度计，t以秒计，求：(1) t＝2 s
大学物理练习题及答案
∙ -q OABCD关于点电荷以下说法正确的是 D(A) 点电荷是电量极小的电荷； (B) 点电荷是体积极小的电荷；(C) 点电荷是体积和电量都极小的电荷；(D) 带电体的线度与其它有关长度相比可忽略不计。
关于点电荷电场强度的计算公式E = q r / (4 π ε 0 r 3),以下说法正确的是 B(A) r →0时, E →∞；(B) r →0时, q 不能作为点电荷,公式不适用； (C) r →0时, q 仍是点电荷,但公式无意义；(D) r →0时, q 已成为球形电荷, 应用球对称电荷分布来计算电场. 如果对某一闭合曲面的电通量为S E d ⋅⎰S=0，以下说法正确的是 A(A) S 面内电荷的代数和为零; (B) S 面内的电荷必定为零； (C) 空间电荷的代数和为零； (D) S 面上的E 必定为零。
已知一高斯面所包围的空间内电荷代数和 ∑q ＝0 ，则可肯定： C(A). 高斯面上各点场强均为零． (B). 穿过高斯面上每一面元的电场强度通量均为零．(C). 穿过整个高斯面的电场强度通量为零． (D). 以上说法都不对．如图，在点电荷+q 的电场中，若取图中P 点处为 电势零点，则M 点的电势为 D(A) q /(4πε0a ) (B) −q /(4πε0a ) (C) q /(8πε0a ) (D) −q /(8πε0a )对于某一回路l ，积分l B d ⋅⎰l 等于零，则可以断定 D(A) 回路l 内一定有电流； (B) 回路l 内一定无电流；(C) 回路l 内可能有电流； (D) 回路l 内可能有电流，但代数和为零。
如图，一电量为-q 的点电荷位于圆心O 处，A 、B 、C 、D 为同一圆周上的四点，现将一试验电荷从A 点分别移动到B 、C 、D 各点，则 A(A) 从A 到各点，电场力做功相等； (B) 从A 到B ，电场力做功最大； (C) 从A 到D ，电场力做功最大；+q(D) 从A 到C ，电场力做功最大。
大学物理习题及答案3
一 选择题 (共69分)1. (本题 3分)(4468) 一定量某理想气体按pV 2＝恒量的规律膨胀，则膨胀后理想气体的温度 (A) 将升高． (B) 将降低．(C) 不变． (D)升高还是降低，不能确定． ［ ］2. (本题 3分)(4552) 若室内生起炉子后温度从15℃升高到27℃，而室内气压不变，则此时室内的分子数减少了(A)0.500． (B) 400．(C) 900． (D) 2100． ［ ］3. (本题 3分)(4304) 两个相同的容器，一个盛氢气，一个盛氦气(均视为刚性分子理想气体)，开始时它们的压强和温度都相等，现将6 J 热量传给氦气，使之升高到一定温度．若使氢气也升高同样温度，则应向氢气传递热量 (A) 12 J ． (B) 10 J ．(C) 6 J ． (D) 5 J ． ［ ］4. (本题 3分)(4014) 温度、压强相同的氦气和氧气，它们分子的平均动能ε和平均平动动能w 有如下关系：(A) ε和w 都相等． (B) ε相等，而w 不相等． (C) w 相等，而ε不相等．(D) ε和w 都不相等． ［ ］5. (本题 3分)(4651) 下列各式中哪一式表示气体分子的平均平动动能？（式中M 为气体的质量，m 为气体分子质量，N 为气体分子总数目，n 为气体分子数密度，N A 为阿伏加得罗常量）(A) pV M m23． (B)pV M M mol 23． (C) npV 23． (D) pV N MM A 23mol ． [ ]6. (本题 3分)(5335) 若在某个过程中，一定量的理想气体的内能E随压强p 的变化关系为一直线(其延长线过E －p 图的原点)，则该过程为(A) 等温过程． (B) 等压过程．(C) 等体过程． (D) 绝热过程． ［］p7. (本题 3分)(4665) 假定氧气的热力学渭度提高一倍，氧分子全部离解为氧原子，则这些氧原子的平均速率是原来氧分子平均速率的 (A) 4倍． (B) 2倍．(C) 2倍． (D) 21倍． ［ ］下列各图所示的速率分布曲线，哪一图中的两条曲线能是同一温度下氮气和氦气的分子速率分布曲线？［］vv(B(A(D(C9. (本题 3分)(5603)已知分子总数为N，它们的速率分布函数为f(v)，则速率分布在v1~v2区间内的分子的平均速率为(A) ∫21d)(vvvvv f．(B) ∫21d)(vvvvv f/∫21d)(vvvvf．(C) ∫21d)(vvvvv fN．(D) ∫21d)(vvvvv f/N．［］10. (本题 3分)(4133)关于可逆过程和不可逆过程的判断：(1) 可逆热力学过程一定是准静态过程．(2) 准静态过程一定是可逆过程．(3) 不可逆过程就是不能向相反方向进行的过程．(4) 凡有摩擦的过程,一定是不可逆过程．以上四种判断，其中正确的是(A) (1)、(2)、(3)．(B) (1)、(2)、(4)．(C)(2)、(4)．(D)(1)、(4)．［］11. (本题 3分)(4674)置于容器内的气体，如果气体内各处压强相等，或气体内各处温度相同，则这两种情况下气体的状态(A) 一定都是平衡态．(B) 不一定都是平衡态．(C) 前者一定是平衡态，后者一定不是平衡态．(D) 后者一定是平衡态，前者一定不是平衡态．［］理想气体向真空作绝热膨胀．(A) 膨胀后，温度不变，压强减小． (B) 膨胀后，温度降低，压强减小． (C) 膨胀后，温度升高，压强减小．(D) 膨胀后，温度不变，压强不变． ［ ］13. (本题 3分)(4579) 对于理想气体系统来说，在下列过程中，哪个过程系统所吸收的热量、内能的增量和对外作的功三者均为负值？(A) 等体降压过程． (B) 等温膨胀过程．(C) 绝热膨胀过程． (D) 等压压缩过程． ［ ］14. (本题 3分)(4679) 一物质系统从外界吸收一定的热量，则 (A) 系统的温度一定升高． (B) 系统的温度一定降低．(C) 系统的温度一定保持不变． (D) 系统的温度可能升高，也可能降低或保持不变．［ ］15. (本题 3分)(4310) 一定量的理想气体，其状态改变在p －T 图上沿着一条直线从平衡态a 到平衡态b (如图)．(A) 这是一个膨胀过程．(B) 这是一个等体过程．(C) 这是一个压缩过程．(D) 数据不足，不能判断这是那种过程． ［］1216. (本题 3分)(4122) 如果卡诺热机的循环曲线所包围的面积从图中的abcda 增大为da c b a ′′，那么循环abcda 与da c b a ′′所作的净功和热机效率变化情况是：(A) 净功增大，效率提高．(B) 净功增大，效率降低．(C) 净功和效率都不变．(D) 净功增大，效率不变． ［ ］c ′d T 2ab b ′c T 1Op两个卡诺热机的循环曲线如图所示，一个工作在温度为T 1 与T 3的两个热源之间，另一个工作在温度为T 2 与T 3的两个热源之间，已知这两个循环曲线所包围的面积相等．由此可知：（A ） 两个热机的效率一定相等．（B ） 两个热机从高温热源所吸收的热量一定相等．（C ） 两个热机向低温热源所放出的热量一定相等．（D ） 两个热机吸收的热量与放出的热量（绝对值）的差值一定相等． [ ]T 1 T 2T 3 T 3V p O18. (本题 3分)(5342) 一定量的理想气体，起始温度为T ，体积为V 0．后经历绝热过程，体积变为2 V 0．再经过等压过程，温度回升到起始温度．最后再经过等温过程，回到起始状态．则在此循环过程中(A) 气体从外界净吸的热量为负值． (B) 气体对外界净作的功为正值． (C) 气体从外界净吸的热量为正值．(D) 气体内能减少． ［ ］19. (本题 3分)(4125) 有人设计一台卡诺热机(可逆的)．每循环一次可从 400 K 的高温热源吸热1800 J ，向 300 K 的低温热源放热 800 J ．同时对外作功1000 J ，这样的设计是 (A) 可以的，符合热力学第一定律． (B) 可以的，符合热力学第二定律． (C) 不行的，卡诺循环所作的功不能大于向低温热源放出的热量．(D) 不行的，这个热机的效率超过理论值． ［ ］20. (本题 3分)(5074) 理想气体卡诺循环过程的两条绝热线下的面积大小(图中阴影部分)分别为S 1和S 2，则二者的大小关系是： (A) S 1 > S 2． (B) S 1 = S 2．(C) S 1 < S 2． (D) 无法确定． ［ ］21. (本题 3分)(4135) 根据热力学第二定律可知：(A) 功可以全部转换为热，但热不能全部转换为功．(B) 热可以从高温物体传到低温物体，但不能从低温物体传到高温物体 (C) 不可逆过程就是不能向相反方向进行的过程．(D) 一切自发过程都是不可逆的． ［ ］设有以下一些过程：(1) 两种不同气体在等温下互相混合．(2) 理想气体在定体下降温．(3) 液体在等温下汽化.(4) 理想气体在等温下压缩．(5) 理想气体绝热自由膨胀．在这些过程中，使系统的熵增加的过程是：(A) (1)、(2)、(3). (B) (2)、(3)、(4).(C) (3)、(4)、(5). (D) (1)、(3)、(5). ［］23. (本题 3分)(4340)气缸中有一定量的氮气(视为刚性分子理想气体)，经过绝热压缩，使其压强变为原来的2倍，问气体分子的平均速率变为原来的几倍？(A) 22/5．(B) 22/7．(C) 21/5．(D) 21/7．［］二填空题 (共77分)24. (本题 3分)(4153)下面给出理想气体的几种状态变化的关系，指出它们各表示什么过程．(1) p d V= (M / M mol)R d T表示____________________过程．(2) V d p= (M / M mol)R d T表示____________________过程．(3) p d V+V d p= 0 表示____________________过程．25. (本题 4分)(4307)分子物理学是研究________________________________________________ __________的学科．它应用的基本方法是_________________方法．26. (本题 5分)(4016)三个容器内分别贮有1 mol氦(He)、 1 mol氢(H2)和1 mol氨(NH3)(均视为刚性分子的理想气体)．若它们的温度都升高1 K，则三种气体的内能的增加值分别为：(普适气体常量R=8.31 J·mol−1·K−1)氦：△E＝___________________；氢：△E＝___________________；氨：△E＝____________________．1 mol 氧气(视为刚性双原子分子的理想气体)贮于一氧气瓶中，温度为27℃，这瓶氧气的内能为________________J ；分子的平均平动动能为____________Ｊ；分子的平均总动能为_____________________Ｊ．(摩尔气体常量 R = 8.31 J ·mol -1·K -1 玻尔兹曼常量 k = 1.38×10-23Ｊ·K -1）28. (本题 3分)(5061) 分子热运动自由度为i 的一定量刚性分子理想气体，当其体积为V 、压强为p 时，其内能E ＝______________________．29. (本题 3分)(4655) 有两瓶气体，一瓶是氦气，另一瓶是氢气(均视为刚性分子理想气体)，若它们的压强、体积、温度均相同，则氢气的内能是氦气的________倍．30. (本题 3分)(4283) 当理想气体处于平衡态时，若气体分子速率分布函数为f (v )，则分子速率处于最概然速率v p 至∞范围内的概率△N / N ＝________________．31. (本题 4分)(4459) 已知f (v )为麦克斯韦速率分布函数，N 为总分子数，则(1) 速率v > 100 m ·s -1的分子数占总分子数的百分比的表达式为_________； (2) 速率v > 100 m ·s -1的分子数的表达式为__________________．32. (本题 5分)(4037) 已知f (v )为麦克斯韦速率分布函数，v p 为分子的最概然速率．则()∫p f v v v 0d表示___________________________________________；速率v ＞v p 的分子的平均速率表达式为______________________．33. (本题 3分)(4082) 在p −V 图上(1) 系统的某一平衡态用_____________来表示； (2) 系统的某一平衡过程用________________来表示； (3) 系统的某一平衡循环过程用__________________来表示；一定量的理想气体处于热动平衡状态时，此热力学系统的不随时间变化的三个宏观量是__________________________________，而随时间不断变化的微观量是____________________________________________________________________.35. (本题 3分)(4578) 如图所示，已知图中画不同斜线的两部分的面积分别为S 1和S 2，那么(1) 如果气体的膨胀过程为a ─1─b ，则气体对外做功W ＝________； (2) 如果气体进行a ─2─b ─1─a 的循环过程，则它对外做功W ＝_______________．36. (本题 5分)(4676)设在某一过程中，系统由状态A 变为状态B ，如果__________________________________________________________________________________________________________________________，则该过程称为可逆过程；如果_____________________________________________________________________则该过程称为不可逆过程．37. (本题 3分)(4147) 同一种理想气体的定压摩尔热容C p 大于定体摩尔热容C V ，其原因是_______________________________________________________．38. (本题 3分)(4688) 刚性双原子分子的理想气体在等压下膨胀所作的功为W ，则传递给气体的热量为__________．39. (本题 5分)(4472) 一定量理想气体，从A 状态 (2p 1，V 1)经历如图所示的直线过程变到B 状态(2p 1，V 2)，则AB 过程中系统作功W ＝_________；内能改变∆E =_________．p 112气体经历如图所示的一个循环过程，在这个循环中，外界传给气体的净热量是___________．23)41. (本题 5分)(4137)热力学第二定律的克劳修斯叙述是：___________________________________；开尔文叙述是________________________________________________________．42. (本题 3分)(4141)从统计的意义来解释, 不可逆过程实质上是一个________________________ __________________________的转变过程, 一切实际过程都向着_____________ _____________________________的方向进行．43. (本题 4分)(4713)给定的理想气体(比热容比γ为已知)，从标准状态(p0、V、T)开始，作绝热膨胀，体积增大到三倍，膨胀后的温度T＝____________，压强p＝__________．三计算题 (共78分)44. (本题10分)(4070)容积为20.0 L(升)的瓶子以速率v＝200 m·s−1匀速运动，瓶子中充有质量为100g的氦气．设瓶子突然停止，且气体的全部定向运动动能都变为气体分子热运动的动能，瓶子与外界没有热量交换，求热平衡后氦气的温度、压强、内能及氦气分子的平均动能各增加多少?(摩尔气体常量R＝8.31 J·mol-1·K−1，玻尔兹曼常量k＝1.38×10-23 J·K−1)45. (本题10分)(4155)有1 mol刚性多原子分子的理想气体，原来的压强为1.0 atm，温度为27℃，若经过一绝热过程，使其压强增加到16 atm．试求：(1) 气体内能的增量；(2) 在该过程中气体所作的功；(3) 终态时，气体的分子数密度．( 1 atm= 1.013×105 Pa，玻尔兹曼常量k=1.38×10-23 J·K-1,普适气体常量R=8.31 J·mol-1·K-1 )一定量的某种理想气体，开始时处于压强、体积、温度分别为p0=1.2×106Pa，V0=8.31×10－3m3，T0 =300 K的初态，后经过一等体过程，温度升高到T1 =450 K，再经过一等温过程，压强降到p = p0的末态．已知该理想气体的等压摩尔热容与等体摩尔热容之比Cp / CV=5/3．求：(1) 该理想气体的等压摩尔热容Cp 和等体摩尔热容CV．(2) 气体从始态变到末态的全过程中从外界吸收的热量．(普适气体常量R = 8.31 J·mol－1·K－1)47. (本题10分)(4587)一定量的理想气体，由状态a经b到达c．(如图，abc为一直线)求此过程中(1) 气体对外作的功；(2) 气体内能的增量；(3) 气体吸收的热量．(1 atm＝1.013×105 Pa)48. (本题 5分)(4591)一卡诺循环的热机，高温热源温度是 400 K．每一循环从此热源吸进 100 J 热量并向一低温热源放出80 J热量．求：(1) 低温热源温度；(2) 这循环的热机效率．49. (本题10分)(4097)1 mol理想气体在T1 = 400 K的高温热源与T2 = 300 K的低温热源间作卡诺循环（可逆的），在400 K的等温线上起始体积为V1= 0.001 m3，终止体积为V2 = 0.005 m3，试求此气体在每一循环中(1) 从高温热源吸收的热量Q1(2) 气体所作的净功W(3) 气体传给低温热源的热量Q250. (本题 5分)(4703)以氢(视为刚性分子的理想气体)为工作物质进行卡诺循环，如果在绝热膨胀时末态的压强p2是初态压强p1的一半，求循环的效率．1 mol双原子分子理想气体作如图的可逆循环过程，其中1－2为直线，2－3为绝热线，3－1为等温线．已知T2 =2T1，V3=8V1试求：(1) 各过程的功，内能增量和传递的热量；(用T1和已知常量表示)(2) 此循环的效率η．(注：循环效率η=W/Q1，W为整个循环过程中气体对外所作净功，Q1为循环过程中气体吸收的热量)p12352. (本题10分)(4118)一定量的理想气体经历如图所示的循环过程，A→B和C→D是等压过程，B→C和D→A是绝热过程．已知：TC ＝ 300 K，TB＝ 400K．试求：此循环的效率．(提示：循环效率的定义式η=1－Q2 /Q1，Q1为循环中气体吸收的热量，Q2为循环中气体放出的热量）A BCDO Vp一选择题 (共69分)1. (本题 3分)(4468)(B)2. (本题 3分)(4552)(B)3. (本题 3分)(4304)(B)4. (本题 3分)(4014)(C)5. (本题 3分)(4651)(A)6. (本题 3分)(5335)(C)7. (本题 3分)(4665)(B)8. (本题 3分)(4559)(B)9. (本题 3分)(5603)(B)10. (本题 3分)(4133)(D)11. (本题 3分)(4674)(B)12. (本题 3分)(4146)(A)13. (本题 3分)(4579)(D)14. (本题 3分)(4679)(D)15. (本题 3分)(4310)(C)16. (本题 3分)(4122)(D)17. (本题 3分)(4121)(D)18. (本题 3分)(5342)(A)(D)20. (本题 3分)(5074) (B)21. (本题 3分)(4135) (D)22. (本题 3分)(5073) (D)23. (本题 3分)(4340) (D)二 填空题 (共77分)24. (本题 3分)(4153) 等压 1分 等体 1分 等温 1分25. (本题 4分)(4307) 物质热现象和热运动规律 2分统计 2分26. (本题 5分)(4016) 12.5 J 2分20.8 J 2分24.9 J 1分27. (本题 5分)(4017) 6.23×10 32分6.21×10 − 212分1.035×10 − 21 1分28. (本题 3分)(5061) ipV 213分29. (本题 3分)(4655) 5 / 3 3分30. (本题 3分)(4283)∫∞pf v v v d )( 3分31. (本题 4分)(4459) (1) ∫∞100d )(v v f 2分 (2)∫∞100d )(v v Nf 2分速率区间0 ~ v p 的分子数占总分子数的百分率； 3分∫∫∞∞=ppf f v v vv v v v v d )(d )( 2分33. (本题 3分)(4082) 一个点。
大学物理练习题及参考答案
一、填空题 1、一质点沿y 轴作直线运动，速度j t v)43(+=，t ＝0时，00=y ，采用SI 单位制，则质点的运动方程为=ymt t 223+；加速度y a ＝ 4m/s 2 。
2、一质点沿半径为R 的圆周运动，其运动方程为22t +=θ。
质点的速度大小为 2t R ，切向加速度大小为 2R 。
3、一个质量为10kg 的物体以4m/s 的速度落到砂地后经0.1s 停下来，则在这一过程中物体对砂地的平均作用力大小为 400N 。
4、在一带电量为Q 的导体空腔内部，有一带电量为-q 的带电导体，那么导体空腔的内表面所带电量为 +q ，导体空腔外表面所带电量为 Q －q 。
5、一质量为10kg 的物体，在t=0时，物体静止于原点，在作用力i x F)43(+=作用下，无摩擦地运动，则物体运动到3米处，在这段路程中力F所做的功为5J13mV 21W 2.=∆=。
6、带等量异号电荷的两个无限大平板之间的电场为0εσ，板外电场为 0 。
8、一长载流导线弯成如右图所示形状，则O 点处磁感应强度B的大小为RIR I 83400μπμ+，方向为⊗。
9、在均匀磁场B 中, 一个半径为R 的圆线圈,其匝数为N,通有电流I ，则其磁矩的大小为NIR m 2π=，它在磁场中受到的磁力矩的最大值为NIBR M 2π=。
10、一电子以v垂直射入磁感应强度B 的磁场中，则作用在该电子上的磁场力的大小为F ＝ Bqv F 0=。
电子作圆周运动，回旋半径为qBmvR =。
11、判断填空题11图中，处于匀强磁场中载流导体所受的电磁力的方向；（a ） 向下 ；（b ） 向左 ；（c ） 向右 。
12、已知质点的运动学方程为j t i t r)1(2-+=。
试求：（1）当该质点速度的大小为15-⋅s m 时，位置矢量=r i 1；（2）任意时刻切向加速度的大小τa ＝1442+t t 。
16、有一球状导体A ，已知其带电量为Q 。
大学物理第八章电磁感应部分的习题及答案
第八章 电磁感应一、简答题1、简述电磁感应定律答：当穿过闭合回路所围面积的磁通量发生变化时，不论这种变化是什么原因引起的，回路中都会建立起感应电动势，且此感应电动势等于磁通量对时间变化率的负值，即dtd i φε-=。
2、简述动生电动势和感生电动势答：由于回路所围面积的变化或面积取向变化而引起的感应电动势称为动生电动势。
由于磁感强度变化而引起的感应电动势称为感生电动势。
3、简述自感和互感答：某回路的自感在数值上等于回路中的电流为一个单位时，穿过此回路所围成面积的磁通量，即LI LI =Φ=Φ。
两个线圈的互感M M 值在数值上等于其中一个线圈中的电流为一单位时，穿过另一个线圈所围成面积的磁通量，即212121MI MI ==φφ或。
4、简述感应电场与静电场的区别？ 答：感生电场和静电场的区别5、写出麦克斯韦电磁场方程的积分形式。
答：⎰⎰==⋅svqdv ds D ρdS tB l E sL⋅∂∂-=⋅⎰⎰d0d =⋅⎰S S B dS t D j l H s l ⋅⎪⎭⎫ ⎝⎛∂∂+=⋅⎰⎰d6、简述产生动生电动势物理本质答：在磁场中导体作切割磁力线运动时，其自由电子受洛仑滋力的作用，从而在导体两端产生电势差7、 简述何谓楞次定律答：闭合的导线回路中所出现的感应电流，总是使它自己所激发的磁场反抗任何引发电磁感应的原因（反抗相对运动、磁场变化或线圈变形等）.这个规律就叫做楞次定律。
二、选择题1、有一圆形线圈在均匀磁场中做下列几种运动，那种情况在线圈中会产生感应电流 ( D )A 、线圈平面法线沿磁场方向平移B 、线圈平面法线沿垂直于磁场方向平移C 、线圈以自身的直径为轴转动，轴与磁场方向平行D 、线圈以自身的直径为轴转动，轴与磁场方向垂直2、对于位移电流，下列四种说法中哪一种说法是正确的 ( A ) A 、位移电流的实质是变化的电场 B 、位移电流和传导电流一样是定向运动的电荷 C 、位移电流服从传导电流遵循的所有规律 D 、位移电流的磁效应不服从安培环路定理3、下列概念正确的是 ( B )。
大学物理学课后习题参考答案
习题1选择题(1) 一运动质点在某瞬时位于矢径),(y x r的端点处，其速度大小为(A)dt dr (B)dtr d(C)dtr d ||(D) 22)()(dt dy dt dx +[答案：D](2) 一质点作直线运动，某时刻的瞬时速度s m v /2=，瞬时加速度2/2s m a -=，则一秒钟后质点的速度(A)等于零 (B)等于-2m/s (C)等于2m/s (D)不能确定。
[答案：D](3) 一质点沿半径为R 的圆周作匀速率运动，每t 秒转一圈，在2t 时间间隔中，其平均速度大小和平均速率大小分别为 (A)t R t R ππ2,2 (B) tRπ2,0(C) 0,0 (D)0,2tRπ [答案：B]填空题(1) 一质点，以1-⋅s m π的匀速率作半径为5m 的圆周运动，则该质点在5s 内，位移的大小是 ；经过的路程是 。
[答案： 10m ； 5πm](2) 一质点沿x 方向运动，其加速度随时间的变化关系为a=3+2t (SI)，如果初始时刻质点的速度v 0为5m ·s -1，则当t 为3s 时，质点的速度v= 。
[答案： 23m ·s -1 ](3) 轮船在水上以相对于水的速度1V 航行，水流速度为2V，一人相对于甲板以速度3V 行走。
如人相对于岸静止，则1V 、2V 和3V的关系是 。
[答案： 0321=++V V V]一个物体能否被看作质点，你认为主要由以下三个因素中哪个因素决定：(1) 物体的大小和形状；(2) 物体的内部结构；(3) 所研究问题的性质。
解：只有当物体的尺寸远小于其运动范围时才可忽略其大小的影响，因此主要由所研究问题的性质决定。
下面几个质点运动学方程，哪个是匀变速直线运动（1）x=4t-3；（2）x=-4t3+3t2+6；（3）x=-2t2+8t+4；（4）x=2/t2-4/t。
给出这个匀变速直线运动在t=3s时的速度和加速度，并说明该时刻运动是加速的还是减速的。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
x Lh书中例题：1.2, 1.6（p.7;p.17）（重点）直杆AB 两端可以分别在两固定且相互垂直的直导线槽上滑动，已知杆的倾角φ＝ωt 随时间变化，其中ω为常量。
求：杆中M 点的运动学方程。
解：运动学方程为： x=a cos(ωt)y=b sin(ωt)消去时间t 得到轨迹方程： x 2/a 2 + y 2/b 2= 1 椭圆运动学方程对时间t 求导数得速度：v x ＝dx/dt ＝-a ωsin(ωt) v y ＝dy/dt ＝b ωcos(ωt) 速度对时间t 求导数得加速度： a x ＝d v x /dt ＝－a ω2cos(ωt) a y ＝d v y /dt ＝－b ω2sin(ωt) 加速度的大小： a 2＝a x 2＋a y 2 习题指导P9. 1.4（重点） 在湖中有一小船，岸边有人用绳子跨过一高处的滑轮拉船靠岸，当绳子以v 通过滑轮时，求：船速比v 大还是比v 小？ 若v 不变，船是否作匀速运动？如果不是匀速运动,其加速度是多少？ 解：l ＝（h2＋x2）1/2221/2122()d l x d x v d t h x d t ==+ 221/2()d x h x v d t x +=当x>>h 时，dx/dt ＝v ，船速＝绳速当x →0时，dx/dt →∞ 加速度：xy M A B a b φx h220d x d t =2221/22221/2221/2221/2221/22221/2()1()11()()1112()2()d x d h x v dt dt x d h x v dt x d dx d h x dx h x v v dx x dt x dx dt dx x dx h x v v x dt x h x dt⎡⎤+=⎢⎥⎣⎦⎡⎤=∙+⎢⎥⎣⎦+⎛⎫=∙++ ⎪⎝⎭=-∙+++将221/2()d x h x vd t x +=代入得：2221/2221/2221/222221/21()112()()2()d x h x x h x h xv v v v d t x x x h x x++=-∙+++3222232222)(xvh x v v x x h dt x d -=++-= 分析： 当x ∞,变力问题的处理方法（重点）力随时间变化：F ＝f （t ） 在直角坐标系下，以x 方向为例，由牛顿第二定律：()x dv m f t dt =且：t ＝t 0 时，v x ＝v 0 ；x ＝x 0 则：1()x dv f t dt m =直接积分得：1()()x x v dv f t dt mv t c===+⎰⎰其中c 由初条件确定。
由速度求积分可得到运动学方程：2()x x v d t x t c ==+⎰其中c2由初条件确定。
例题：飞机着陆时受到的阻力为F ＝－ct ，（c 为常数） 且t ＝0时，v ＝v 0 。
求：飞机着陆时的速度。
解：根据牛顿第二定律：－ct ＝m dv / dt212c v d v td t mc t c m==-=-+⎰⎰当t ＝0时，v ＝v 0，代入得：v 0＝c 1202c v v tm =-力随速度变化：F ＝f （v ）直角坐标系中，x 方向f （v ）＝m dv ⁄ dt经过移项可得：()d vd t mf v = 等式两边同时积分得：01()()m t t d t d v m d v f v f v -===⎰⎰⎰具体给出f （v ）的函数试就可进行积分运算。
例题：（重点）质量为m 的物体以速度v 0投入粘性流体中，受到阻力f ＝－cv （c 为常数）而减速，若物体不受其它力，求：物体的运动速度。
解：根据牛顿第二定律： 移项变换： －c/m dt ＝dv/v积分得：1ln c d v d t mvct v c m-=-=+⎰⎰由初条件定c1：当t ＝0时，v ＝v 0 ∴0＝lnv 0＋c 1∴ c1＝－lnv 0dvcv m dt -=00l n c t mc v t m v v v e--==力随位移变化：F ＝f （x ） 直角坐标系中，x 方向：()d v d x d v d vf x m m m vd t d td x d x ===经过移项可得：f （x ）dx ＝mv dv等式两边同时积分得：2201()()2f x d x m v d v m v v ==-⎰⎰例题：（重点）光滑的桌面上一质量为M ，长为L 的匀质链条，有极小一段被推出桌子边缘。
求：链条刚刚离开桌面时的速度。
解：链条所受的力F 是个变力：F ＝m(x)g ()Mm x xL =根据牛顿第二定律：M d v d x d v d v x g M M M v L d t d td x d x ===0022122Lv Mg x d x M v d v L M g L M v L v g L ===⎰⎰ 书中例题3.11（p111）（重点）长为L 的匀质链条，一部分在水平桌面上，另一部分自然下垂。
链条与水平面间静摩擦因数为μ0，滑动摩擦因数为μ. 求：1）满足什么条件时，链条开始滑动？ 2）若下垂部分长度为b 时，链条开始滑动，当链条末端刚刚离开桌面时的速度是多少？解：1）最大拉力：ρb 0g ， 摩擦力：μ0ρ(L –b 0)g ρb 0g = μ0ρ(L –b 0)g2)重力和摩擦力做的功分别为：xy L b 0001μμ+=222)(1)()(21b L g dy y L g A b L g gydy A L f Lb g -=--=-==⎰⎰μρμρρρ根据动能定理：书中例题4.4（146）（重点） 已知：质量为M ，长为L 的匀质链条，上端悬挂，下端刚和称盘接触，使链条自由下落。
求：下落长度x 时，称的读数。
解： 称的读数 N ＝mg ＋Fmg 是落在称上的链条的重量，F 是链条 下落时具有速度v 的一小段与称盘碰撞， 速度由v 变成0时给称盘的冲力。
根据动量守恒定律：Fdt ＝dm v －dm 0 dm ＝M/L dx, v 2＝2gx22d m M d x M M F v v v g x d t L d t L L ====23M M M N g x g x g xL L L =+=称的读数是落在称盘上链条质量的3倍。
（参见P82，例题2.14）书中例题6.12 (P.215) （重点）质量为m 的小球系在绳子的一端，绳穿过一铅直套管，使小球限制在一光滑水平面上运动。
先使小球以速度v0绕管心作半径为r0的圆周运动，然后向下拉绳，使小球轨迹最后成为半径为r 的圆。
试求：小球距管心r 时速度v 的大小，绳从r0缩短到r 过程中，力F 所作的功。
解：绳子对小球的作用力 始终通过圆心O ，为有心 力，该力对O 点产生的力矩为0，因此，在整个过程中，质点的动量矩守恒。
mv 0r 0＝mvr∴ v ＝ v 0 r 0 /r随着半径减小，质点的速度增加，动能增加。
动能增加的原因是力F 对小球作了功。
由于系统没有耗散力，作功的结果是使动能增加。
222222200000011111122222r r A m v m v m v m v m v r r ⎡⎤⎛⎫⎛⎫=-=-=-⎢⎥ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎣⎦书中例题6.2(P.198)（重点）2222222)()(021)(21)(21b L L g b L L g v Lv b L g b L g ---=-=---μρμρρxLF vO求：质量为M ，半径为R ，高h 的圆柱或园盘对过圆心且与盘面垂直转轴的转动惯量。
解：取半径为r ，宽dr 的薄圆环，高h 。
该圆环的质量为：dm ＝ρ2π r h dr ，其中ρ是园盘的密度：2M R h ρπ= 该圆环上各个点到转轴的距离都是r ，∴圆环的转动惯量为：dJ ＝r 2dm整个园盘的转动惯量就是dJ 从0到R 积分：22322RRVJ r d m r r h d r hr dr ρππρ===⎰⎰⎰442201112422|R M h r h R M R R h πρππ===如果是圆环，则积分限从R1积到R2：221122322R R R R VJ r d m r r h d r h r dr ρππρ===⎰⎰⎰这时的密度应为：2221()MR R h ρπ=- 2144422212122211112()()42()2|R R M J h r h R R M R R R R h πρππ==-=+-（1）平行轴定理若有两个轴互相平行，其中一个轴过质心，则：J ＝J c ＋md 2其中J c 为刚体对质心的转动惯量；m 为刚体的质量；d 为两轴的垂直距离。
证明：以转轴为z 轴做坐标系oxyz ；以刚体质心为原点做质心坐标系o’x’y’z’；刚体质心在oxyz 坐标系中的坐标为：x c , y c , z c ,刚体上的任意点在oxyz 坐标系的坐标为：x i , y i , z i ； 该点在质心坐标系o’x’y’z’的坐标为：x i ’, y i ’, z i ’ 以z 轴为转轴，刚体对z 轴的转动惯量为： 22()i i i J m x y =+∑其中x i 和y i 是质点的x 坐标 和y 坐标，且：x i ＝x c ＋x i ’；y i ＝y c ＋y i ’其中x c 和y c 是刚体质心的x 坐标和y 坐标，x i ’和y i ’是质点在质心坐标系中的x’坐标和y’坐标 代入得： xyz z’ x’y’C(x c ,y c ,z c ) d22[(')(')]i c i c i J m x x y y =+++∑2222()2'2'('')i c c ci i ci i i i im x y x m x y m y m x y =+++++∑∑∑∑其中''0i icm x m x ==∑； ''0i icm y m y ==∑表示质心在质心坐标系中的坐标为0 x c 2+y c 2=d 2为质心到转轴的距离；22('')i i i cm x y J +=∑为刚体对过质心转轴的转动惯量。
∴ J ＝Jc ＋md 2例：书中例题6.1求了杆通过中心轴的转动惯量，用平行轴定理，求过端点且与杆垂直的轴的转动惯量。
解：两平行轴的间距为d ＝L/2，根据平行轴定理22221111223c J J m d m l m l ml ⎛⎫=+=+= ⎪⎝⎭ 例：过园盘边缘与园盘中心轴平行的轴的转动惯量。
园盘对其中心轴的转动惯量为：1/2 MR2 两轴之间的距离为R ，根据平行轴定理：22221322cI I m d m R m R m R =+=+=这种情况用直接积分比较困难。