模板业务量统计 (2)
医院质控分析报告模板

医院质控分析报告目录第一部分医院质量与安全管理指标 (2)1 .质量与安全主要指标统计 (2)2 .主要业务指标统计 (3)第二部分医疗病案质量 (4)1.医疗安全 (4)2.科室会诊 (5)3.输血质量 (5)4.产科质量 (6)5.科室管理 (6)6.病案管理 (6)7.其他扣款明细 (10)8.下月整改要求 (10)9三部分药事管理 (11)10部分护理质量 (16)11部分院感质量 (23)12部分消防安全管理 (28)13部分综合质量评分及考核 (29)第一部分医院质量与安全管理指标二、主要业务指标统计(-)全院完成情况(二)临床科室完成业务量第二部分医疗、病案质量一、医疗安全1.本月投诉2例(外科)。
投诉科室:外科;投诉事由:术后并发症1例,收费项目不统一引发1例。
2.医疗安全(不良)事件共上报22例。
其中:护理类11例(跌倒1例,尿管拔出受阻1例,压疮上报2例,难免压疮预报7例);药品不良反应上报3例。
3.危急值:11.1・11.30医技科室共报告并登记47例(检验科45例,放射科1例,内一科1例);临床科室共登记处理47例(内一科26例(门诊5例),内二科15例,外科4例(门诊1例),中医科2例。
抽查部分危急值处理及交班情况:各临床科室接危急值报告后均能及时登记及规范处理,病程有记录,交班本上大部分有交接记录,外科应加强危急值的交接班记录。
二、科室会诊4月院内科间会诊共计68人次。
综述如下:1.中医科会诊30次,针灸理疗科会诊29次,其他科间会诊9次。
2.内一科请会诊14人次,内二科请会诊35人次,外科请会诊16人次,妇产科请会诊1人次,理疗科请会诊2人次。
3.抽查部分病历情况如下:41)个别医生申请会诊无医嘱;52)个别医生请会诊无病程录;63)仍有个别医生请会诊医嘱不准确:如“会诊”,未注明请“XX科会诊”。
三、输血质量本月全院共使用红细胞悬液49.5U:内一科31.5U,内二科14U,外科4U,妇产科OU;共使用冰冻血浆IOOOm1:内一科60Om1,外科400m1;单采血小板1U(内一科)。
统计年度工作总结模板(7篇)

统计年度工作总结模板时间如梭,新年的钟声即将敲响。
____将告别它的光辉,____从容而至。
在这个辞旧迎新之际,第一次尝试把自己在这一年来的行动用语言表达。
下面我就做个简单的总结。
一、统计工作1、每日做好生产一线职工的个人产量与次品数据的汇总与登记,并间断性地抽查相关数据是否准确;2、每月汇总并公布职工的出勤、个人产量、次品等。
做好产量月报表上报生产经理和财务部门,包括生产车间和包装车间;3、每月月底进行一次彻底的盘库,主要有原材料、辅料、半成品、成品。
整理分析数据后上交财务部等相关部门;4、每月将生产部各种人员流动情况及考勤,奖罚,请假等数据汇总上报行政人事部;5、协助人事部门招聘、登记求职人员信息,刊出宣传橱窗;6、配合生产部发布和修改各类制度、通知、考核等;7、自从公司实行免费餐以后,每日进行就餐人数统计;8、年底将部分数据用表格的形式进行汇总与分析。
主要有《年度原材料消耗表》、《年度生产表》、《年度成品包装产量表》。
二、____的工作计划努力完成本职工作之余,学习更多有关财务、统计方面的知识,以提升自己专业学识。
积极参加一些和专业有关的培训,有效提高对统计数据的准确性,并做好数据的登记与分析。
三、总结经验与不足之处____,在原有的各种统计报表基础上,对一些没有实际意义的表格作了改进,并对统计数字的准确性进行了加强。
但也存在着不少问题,尤为突出的是“食堂就餐人数的统计”问题。
由于如今在厂职工按部门划分,人员变动情况很难在同一时间最准确地掌握,给每日的上报带来很大的麻烦。
为此经过一系列的改进与调整,我们将专属部门专职人员上报签字认可,希望能够起到更准确更及时的统计。
____月份最多统计人数相差了____人,为此我也做了检讨。
有人反映人数统计方面存在问题,那是否职工产量也是如此。
关于这个问题是我统计中的疏忽,但产量我可以大胆地说,不是百分之百的正确,却有____%的准确!工作中经常会出现这样那样的问题,我们要勇于正视错误,并且解决错误。
试用期工作业绩总结标准模板(4篇)

试用期工作业绩总结标准模板(一)养成良好的品德素质和职业道德是重中之重。
作为一名银行柜员,每天与金钱打交道,因此对员工品德修养以及职业道德上面的要求更高。
需要我们有足够的自制力,能遵纪守法,忠于职守、廉洁奉公、遵守职业道德和社会公德。
因此我对自己这方面的业务知识和工作能力方面。
在目前的工作岗位上,能够不断的去学习,积累经验,要求很高,坚决不做违反员工守则要求的事。
(二)要认真学习专业技能知识,在工作上争创佳绩。
要成为一名优秀的员工,首要条件就是成为业务技能上的骨干。
对于刚刚走出大学校门参加工作的我来说,当前的首要任务就是要努力学习、熟练掌握专业知识,始终以积极的工作态度、高度的责任感和只争朝夕的精神投入到工作中,因此,在目前的工作岗位上,我不断的跟老员工学习业务知识,积累经验,经过自己的努力,具备了一定的工作能力,能够从容的接待客户,应对柜面上面的一般业务。
在业务技能、综合分析能力、协调办事能力、文字语言表达能力等方面,都有了很大的提高。
因为我知道只有加强自己的业务技能水平,我们才能在工作中得心应手,更好的为广大客户提供方便、快捷、准确的服务。
在工作中,我是忠于职守,尽力而为的,银行属于服务行业,工作使我每天要面对众多的客户,为此,我常常提醒自己“善待别人,便是善待自己”,在繁忙的工作中,我仍然坚持做好“微笑服务”,耐心细致的解答客户的问题,遇到蛮不讲理的客户,我也试着去包容和理解他,最终也得到了客户的理解和尊重。
我始终以“客户满意、业务发展”为目标,搞好服务,树立热忱服务的良好窗口形象,做到来有迎声,问有答声,走有送声,让每个顾客都高兴而来满意而归。
(三)要扬长避短,不断完善自己。
作为一名新员工,我们的短处是业务技能上的经验不足,但我会在工作态度和勤奋敬业方面发挥自己的长处。
热爱自己的本职工作,正确,认真的去对待每一项工作任务,在工作中能够采取积极主动,能够积极参加单位组织的各项业务培训和营销任务。
客户增值服务统计(模板)

9548.38 58149.5 6071.65 39063.8 12093.9 54156.3 10264.6 53947.6
寄件增值 服务费收 入
5月 6月 7月 8月 9月 10月 11月 12月
680740.7 953113 760910.8 761662.9 927134.8 0 0 0 标准快递 482893 1374790 16020850
寄件增值服务费收入 5810089
_客户增值服务组合_月汇总(总部) 保费 35854 20480 29188 28670 33226 36918 31209 44262 55639 0 0 0 127966 包装费 22845 19665 24401 26646 31045 31939 34214 39276 50671 0 0 0 122466.6 代收货款服 签回单应用 务费 777 415 1036 930 1327 1472 1579 1928 1690 0 0 0 1598.5 1307.5 2293.5 1798.9 2560.5 2871.5 2478.5 3223.5 11473.5 0 0 0 534 265 -19 933 1348 2452 1112 946 10774 0 0 0 30032.52 14744.79 35033.82 33979.74 7521 4857 7181 7535 7763 7456 7260 7894 7926 0 0 0 7520.2 4857 7181 7535 7763 7456 7260 7894 7926 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 37601 24278.1 35895.9 37667 委托件 235 169 232 267 292 273 302 238 221 0 0 0 1433 1871.5 1480.5 3840.6 1711 1609.5 1267 1000.1 1494 0 0 0 11252 9364 11485 23679 15615 12595 11159 8481 11710 0 0 0 4700 3346 4607 5340 退货服务 超长超重费大陆偏远费 13 5 10 11 6 18 8 12 34 0 0 0 29.5 11.5 81.5 48.5 65 105 32 66 143.5 0 0 0 343 152 504 345 387 732 259 493 1096 0 0 0 65 25 50 55 19 10 15 9 8 9 6 13 39 0 0 0 612 481 392 99.5 158.5 380 106.5 1023.46 2137.5 0 0 0 3078 3539 2240 723 1011 1596 694 5797 12465 0 0 0 530 415 364 190 8 12 5 14 12 19 7 10 7 0 0 0 29.5 19.5 9 48.5 47 121 7.5 50.5 16.5 0 0 0 295 311 162 621 607 1171 154 760 270 0 0 0 80 120 50 140
上海 华东师范大学第四附属中学必修三第一章《统计》测试题(答案解析)

一、选择题1.如图1为某省2019年1~4月快递业务量统计图,图2是该省2019年1~4月快递业务收入统计图,下列对统计图理解错误的是( )A.2019年1~4月的业务量,3月最高,2月最低,差值接近2000万件B.2019年1~4月的业务量同比增长率超过50%,在3月最高C.从两图来看2019年1~4月中的同一个月快递业务量与收入的同比增长率并不完全一致D.从1~4月来看,该省在2019年快递业务收入同比增长率逐月增长2.某人研究中学生的性别与成绩、视力、智商、阅读量这4个变量之间的关系,随机抽查52名中学生,得到统计数据如表1至表4,这与性别有关联的可能性最大的变量是()A.成绩B.视力C.智商D.阅读量3.某农业科学研究所分别抽取了试验田中的海水稻以及对照田中的普通水稻各10株,测量了它们的根系深度(单位:cm ),得到了如图所示的茎叶图,其中两竖线之间表示根系深度的十位数,两边分别是海水稻和普通水稻根系深度的个位数,则下列结论中不正确的是( )A .海水稻根系深度的中位数是45.5B .普通水稻根系深度的众数是32C .海水稻根系深度的平均数大于普通水稻根系深度的平均数D .普通水稻根系深度的方差小于海水稻根系深度的方差4.若一组数据12345,,,,x x x x x 的平均数为5,方差为2,则12323,23,23x x x ---,4523,23x x --的平均数和方差分别为( )A .7,-1B .7,1C .7,2D .7,85.统计某校n 名学生的某次数学同步练习成绩,根据成绩分数依次分成六组:[)[)[)[)[)[]90,100,100,110,110,120,120,130,130,140,140,150,得到频率分布直方图如图所示,若不低于140分的人数为110.①0.031m =;②800n =;③100分以下的人数为60;④分数在区间[)120,140的人数占大半.则说法正确的是( )A .①②B .①③C .②③D .②④6.某产品的广告费用x 与销售额y 的统计数据如下表: 广告费用(万元)4235销售额(万元)49263954根据上表可得回归方程ˆˆˆybx a =+中的ˆb 为9.4,据此模型预报广告费用为6万元时销售额为A.63.6万元B.65.5万元C.67.7万元D.72.0万元7.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:父亲身高x(cm)174176176176178儿子身高y(cm)175175176177177则y对x的线性回归方程为A.y = x-1 B.y = x+1 C.y =88+12x D.y = 1768.为了了解某社区居民是否准备收看电视台直播的“龙舟大赛”,某记者分别从社区60~70岁,40~50岁,20~30岁的三个年龄段中的128,192,x人中,采用分层抽样的方法共抽出了30人进行调查,若60~70岁这个年龄段中抽查了8人,那么x为()A.64 B.96 C.144 D.1609.甲、乙两名选手参加歌手大赛时,5名评委打的分数用如图所示的茎叶图表示,s1,s2分别表示甲、乙选手分数的标准差,则s1与s2的关系是().A.s1>s2B.s1=s2C.s1<s2D.不确定10.某校为了提高学生身体素质,决定组建学校足球队,学校为了解报名学生的身体素质,对他们的体重进行了测量,将所得的数据整理后,画出了频率分布直方图(如右图),已知图中从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12,则该校报名学生总人数()A.40 B.45 C.48 D.5011.在学校组织的考试中,45名学生的数学成绩的茎叶图如图所示,则该45名学生的数学成绩的中位数为()A.127 B.128 C.128.5 D.12912.从8名女生4名男生中,选出3名学生组成课外小组,如果按性别比例分层抽样,则不同的抽取方法数为()A.112种B.100种C.90种D.80种二、填空题13.某住宅小区有居民2万户,从中随机抽取200户,调查是否安装宽带,调查结果如下表所示:宽带租户业主已安装6042未安装3662则该小区已安装宽带的居民估计有______户.14.如图是甲、乙两人在10天中每天加工零件个数的茎叶图,若这10天甲加工零件个数的中位数为a,乙加工零件个数的平均数为b,则a b+=______.15.一个车间为了规定工作原理,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如下: 零件数x (个) 15 20 30 40 50 加工时间y (分钟)6570758090由表中数据,求得线性回归方程0.66y x a =+,则估计加工70个零件时间为__________分钟(精确到0.1).16.为了了解2100名学生早晨到校时间,计划采用系统抽样的方法从全体学生中抽取容量为100栋样本,则分段间隔为__________.17.数据1x ,2x ,…,n x 的平均数是3,方差是1,则数据15x -,25x -,…,5n x -的平均数和方差之和是__________.18.某超市统计了一个月内每天光顾的顾客人数,得到如图所示的频率分布直方图,根据该图估计该组数据的中位数为__________.19.已知一组数据:5.7,5.8,6.1,6.4,6.5,则该数据的方差是__________. 20.已知某市A 社区35岁至45岁的居民有450人,46岁至55岁的居民有750人,56岁至65岁的居民有900人.为了解该社区35岁至65岁居民的身体健康状况,社区负责人采用分层抽样技术抽取若干人进行体检调查,若从46岁至55岁的居民中随机抽取了50人,试问这次抽样调查抽取的人数是________人.三、解答题21.某市政府针对全市10所由市财政投资建设的企业进行了满意度测评,得到数据如下表: 企业abcdefghij满意度x (%)21332420252124232512投资额y (万元)79 86 89 7876 72 65 62 59 44y x (2)约定:投资额y 关于满意度x 的相关系数r 的绝对值在0.7以上(含0.7)是线性相关性较强,否则,线性相关性较弱.如果没有达到较强线性相关,则根据满意度“末位淘汰”规定,关闭满意度最低的那一所企业,求关闭此企业后投资额y 关于满意度x 的线性回归方程(精确到0.1).参考数据:22.8x =,71y =,1022110248i i x x =-≈∑,10102222111010643.7i i i i x x y y ==⎛⎫⎛⎫--≈ ⎪⎪⎝⎭⎝⎭∑∑,10110406i i i x y x y =-=∑,222851984=,2287116188⨯=.附:对于一组数据()11,x y ,()22,x y ,…,(),n n x y ,其回归直线ˆˆˆybx a =+的斜率和截距的最小二乘估计公式分别为:1221ˆni ii nii x ynx y bxnx==-=-∑∑,ˆˆay bx =-.线性相关系数1222211ni ii n ni i i i x y nx yr x nx y ny ===-=⎛⎫⎛⎫-- ⎪⎪⎝⎭⎝⎭∑∑∑.22.2018年8月8日是我国第十个全民健身日,其主题是:新时代全民健身动起来.某市为了解全民健身情况,随机从某小区居民中抽取了40人,将他们的年龄分成7段:[10,20),[20,30),[30,40),[40,50),[50,60),[60,70),[70,80]后得到如图所示的频率分布直方图.(1)试求这40人年龄的平均数的估计值;(2)(i )若从样本中年龄在[50,70)的居民中任取2人赠送健身卡,求这2人中至少有1人年龄不低于60岁的概率;(ⅱ)已知该小区年龄在[10,80]内的总人数为2000,若18岁以上(含18岁)为成年人,试估计该小区年龄不超过80岁的成年人人数.23.某学校进行体验,现得到所有男生的身高数据,从中随机抽取50人进行统计(已知这50个身高介于155cm 到195cm 之间),现将抽取结果按如下方式分成八组:第一组[155,160),第二组[160,165),...,第八组[190,195],并按此分组绘制如图所示的频率分布直方图,其中第六组[180,185)和第七组[185,190)还没有绘制完成,已知第一组与第八组人数相同,第六组和第七组人数的比为5:2.(1)补全频率分布直方图;(2)根据频率分布直方图估计这50位男生身高的中位数;(3)用分层抽样的方法在身高为[170,180]内抽取一个容量为5的样本,从样本中任意抽取2位男生,求这两位男生身高都在[175,180]内的概率.24.“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的2.8%,全世界近80%人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准x (吨):一位居民的月用水量不超过x 的部分按平价收费,超出x 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照00.50.51,...,[[[44.5,),,),)分成9组,制成了如图所示的频率分布直方图.(1)求直方图中a 的值;(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;(3)若该市政府希望使82%的居民每月的用水不按议价收费,估计x 的值,并说明理由.25.为鼓励职工积极参与健康步行,某单位组织职工进行了健身走活动.根据该单位的1000名职工在健身走中行走步数(单位:百步,步数均在50到210之间)得到如图的频率分布直方图,由频率分布直方图估计出这1000名职工中有56%的职工行走步数小于130(百步).(1)计算图中的a 值,并以此估计该单位职工行走步数的中位数;(2)为鼓励职工积极参与健康步行,该单位决定对本次步数排在前200名的职工进行奖励,授予“运动达人”称号.一名职工走了160(百步),请根据频率分布直方图判断该职工能否获得“运动达人”称号.26.某学校高一100名学生参加数学竞赛,成绩均在40分到100分之间.学生成绩的频率分布直方图如图:(1)估计这100名学生分数的中位数与平均数;(精确到0.1)(2)某老师抽取了10名学生的分数:12310,,,...,x x x x ,已知这10个分数的平均数90x =,标准差6s =,若剔除其中的100和80两个分数,求剩余8个分数的平均数与标准差.(参考公式:s =(3)该学校有3座构造相同教学楼,各教学楼高均为20米,东西长均为60米,南北宽均为20米.其中1号教学楼在2号教学楼的正南且楼距为40米,3号教学楼在2号教学楼的正东且楼距为72米.现有3种型号的考试屏蔽仪,它们的信号覆盖半径依次为35,55,105米,每个售价相应依次为1500,2000,4000元.若屏蔽仪可在地下及地上任意位置安装且每个安装费用均为100元,求让各教学楼均被屏蔽仪信号完全覆盖的最小花费.(参考数据:22221044100,19236864,11012100===)【参考答案】***试卷处理标记,请不要删除一、选择题 1.D 解析:D 【分析】由题意结合所给的统计图确定选项中的说法是否正确即可. 【详解】对于选项A : 2018年1~4月的业务量,3月最高,2月最低, 差值为439724111986-=,接近2000万件,所以A 是正确的;对于选项B : 2018年1~4月的业务量同比增长率分别为55%,53%,62%,58%,均超过50%,在3月最高,所以B 是正确的;对于选项C :2月份业务量同比增长率为53%,而收入的同比增长率为30%,所以C 是正确的;对于选项D ,1,2,3,4月收入的同比增长率分别为55%,30%,60%,42%,并不是逐月增长,D 错误. 本题选择D 选项. 【点睛】本题主要考查统计图及其应用,新知识的应用等知识,意在考查学生的转化能力和计算求解能力.2.D解析:D 【解析】试题分析:由表中数据可得 表1:()25262210140.00916362032K ⨯⨯-⨯=≈⨯⨯⨯;表2: ()2524201216 1.76916362032K ⨯⨯-⨯=≈⨯⨯⨯;表3: ()252824128 1.316362032K ⨯⨯-⨯=≈⨯⨯⨯;表4: ()25214302623.4816362032K ⨯⨯-⨯=≈⨯⨯⨯.其中23.48最大,所以阅读量与性别有关联的可能性最大.故D 正确. 考点:独立性检验.3.D解析:D 【分析】选项A 求出海水稻根系深度的中位数是444745.52+=,判断选项A 正确;选项B 写出普通水稻根系深度的众数是32,判断选项B 正确;选项C 先求出海水稻根系深度的平均数,再求出普通水稻根系深度的平均数,判断选项C 正确;选项D 先求出普通水稻根系深度的方差,再求出海水稻根系深度的方差,判断选项D 错误. 【详解】解:选项A :海水稻根系深度的中位数是444745.52+=,故选项A 正确; 选项B :普通水稻根系深度的众数是32,故选项B 正确;选项C :海水稻根系深度的平均数393938434447495050514510+++++++++=,普通水稻根系深度的平均数252732323436384041453510+++++++++=,故选项C 正确;选项D :普通水稻根系深度的方差2222222211[(3845)(3945)(3945)(4345)(4445)(4745)(4945)(5045)10S =-+-+-+-+-+-+-+-+, 海水稻根系深度的方差2222222221[(2535)(2735)(3235)(3235)(3435)(3635)(3835)(4035)(10S =-+-+-+-+-+-+-+-+,故选项D 错误 故选:D. 【点睛】本题考查根据茎叶图求中位数、众数、平均数、方差,是基础题. 4.D解析:D 【分析】根据平均数的性质,方差的性质直接运算可得结果. 【详解】令23(1,2,,5)i i y x i =-=1234555x x x x x x ++++==,1234523232323232310375x x x x x y x -+-+-+-+-∴==-=-=, (也可()(23)2()32537E y E x E x =-=-=⨯-=)()()()2y 232428D D x D x =-==⨯=故选:D【点睛】本题主要考查方差及平均值的性质的简单应用,属于中档题.5.B解析:B【分析】根据频率分布直方图的性质和频率分布直方图中样本估计总体,准确运算,即可求解.【详解】由题意,根据频率分布直方图的性质得10(0.0200.0160.0160.0110.006)1m +++++=,解得0.031m =.故①正确;因为不低于140分的频率为0.011100.11⨯=,所以11010000.11n ==,故②错误; 由100分以下的频率为0.00610=0.06⨯,所以100分以下的人数为10000.06=60⨯, 故③正确;分数在区间[120,140)的人数占0.031100.016100.47⨯+⨯=,占小半.故④错误. 所以说法正确的是①③.故选B.【点睛】本题主要考查了频率分布直方图的应用,其中解答熟记频率分布直方图的性质,以及在频率分布直方图中,各小长方形的面积表示相应各组的频率,所有小长方形的面积的和等于1,着重考查了分析问题和解答问题的能力,属于基础题.6.B解析:B【详解】 试题分析:4235492639543.5,4244x y ++++++====, ∵数据的样本中心点在线性回归直线上,回归方程ˆˆˆy bx a =+中的ˆb 为9.4, ∴42=9.4×3.5+a ,∴ˆa=9.1, ∴线性回归方程是y=9.4x+9.1,∴广告费用为6万元时销售额为9.4×6+9.1=65.5考点:线性回归方程7.C解析:C【详解】 试题分析:由已知可得176,176x y ==∴中心点为()176,176,代入回归方程验证可知,只有方程y =88+12x 成立,故选C 8.D解析:D【解析】【分析】根据60~70岁这个年龄段中128人中抽查了8人,可知分层抽样的抽样比为81=12816,因为共抽出30人,所以总人数为3016=480⨯人,即可求出20~30岁年龄段的人数.【详解】根据60~70岁这个年龄段中128人中抽查了8人,可知分层抽样的抽样比为81=12816, 因为共抽出30人,所以总人数为3016=480⨯人,所以,20~30岁龄段的人有480128192160--=,故选D.【点睛】本题主要考查了分层抽样,抽样,样本容量,属于中档题 9.C解析:C【分析】先求均值,再根据标准差公式求标准差,最后比较大小.【详解】 乙选手分数的平均数分别为7885848192767780949384,84,55++++++++==== 因此s 1<s 2,选C.【点睛】本题考查标准差,考查基本求解能力.10.C解析:C【分析】根据频数关系,求出前三段每段的频数,由直方图求出四五组的频率,进而求出前三组的频率和,从而可求该校报名学生的总人数.【详解】从左到右3个小组的频率之比为1:2:3,其中第2小组的频数为12,∴从左到右3个小组的频数分别为6,12,18,共有36人,第4,5小组的频率之和为()0.03750.012550.25+⨯=,则前3小组的频率之和为10.250.75-=,则该校报名学生的总人数为360.7548÷=,故选C.【点睛】本题主要考查频率分布直方图的应用,属于中档题. 直方图的主要性质有:(1)直方图中各矩形的面积之和为1;(2)组距与直方图纵坐标的乘积为该组数据的频率;(3)每个矩形的中点横坐标与该矩形的纵坐标相乘后求和可得平均值;(4)直观图左右两边面积相等处横坐标表示中位数.11.D解析:D【解析】分析:由茎叶图得出45名学生的数学成绩,从而求出中位数.详解:根据茎叶图得出45名学生的数学成绩,可知中位数为129.故选D.点睛:本题考查了茎叶图的应用问题,解题时应根据茎叶图中的数据,进行解答,属基础题..12.A解析:A【解析】分析:根据分层抽样的总体个数和样本容量,做出女生和男生各应抽取的人数,得到女生要抽取2人,男生要抽取1人,根据分步计数原理得到需要抽取的方法数.详解:∵8名女生,4名男生中选出3名学生组成课外小组,∴每个个体被抽到的概率是14, 根据分层抽样要求,应选出8×14=2名女生,4×14=1名男生, ∴有C 82•C 41=112.故答案为:A . 点睛:本题主要考查分层抽样和计数原理,意在考查学生对这些知识的掌握水平.二、填空题13.【分析】计算出抽样中已安装宽带的用户比例乘以总人数求得小区已安装宽带的居民数【详解】抽样中已安装宽带的用户比例为故小区已安装宽带的居民有户【点睛】本小题主要考查用样本估计总体考查频率的计算属于基础题解析:10200【分析】计算出抽样中已安装宽带的用户比例,乘以总人数,求得小区已安装宽带的居民数.【详解】 抽样中已安装宽带的用户比例为604251200100+=,故小区已安装宽带的居民有512000010200100⨯=户. 【点睛】 本小题主要考查用样本估计总体,考查频率的计算,属于基础题.14.5【解析】【分析】由茎叶图直接可以求出甲的中位数和乙的平均数求和即可【详解】由茎叶图知甲加工零件个数的中位数为乙加工零件个数的平均数为则【点睛】本题主要考查利用茎叶图求中位数和平均数解析:5【解析】【分析】由茎叶图直接可以求出甲的中位数和乙的平均数,求和即可.【详解】 由茎叶图知,甲加工零件个数的中位数为()1212221.52a =⨯+=, 乙加工零件个数的平均数为()11917112124222430323010b =⨯+++++++++23=,则21.52344.5a b +=+=.【点睛】本题主要考查利用茎叶图求中位数和平均数.15.7【解析】【分析】结合题意先求出线性回归方程然后再计算出结果【详解】由题意可得则线性回归方程为当时【点睛】本题考查了求线性回归方程然后求出估计结果需要掌握解题方法较为基础解析:7【解析】【分析】结合题意先求出线性回归方程,然后再计算出结果【详解】 由题意可得1520304050315x ++++== 6570758090765y ++++==,760.6631a ∴=⨯+,55.54a =,则线性回归方程为0.66 5.4ˆ55yx =+ 当70x =时,ˆ101.7y≈ 【点睛】本题考查了求线性回归方程,然后求出估计结果,需要掌握解题方法,较为基础 16.【解析】【分析】根据系统抽样的特征求出分段间隔即可【详解】根据系统抽样的特征得:从2100名学生中抽取100个学生分段间隔为故答案是21【点睛】该题所考查的是有关系统抽样的组距问题应用总体除以样本容 解析:21【解析】【分析】根据系统抽样的特征,求出分段间隔即可.【详解】根据系统抽样的特征,得:从2100名学生中抽取100个学生,分段间隔为210021100=, 故答案是21.【点睛】该题所考查的是有关系统抽样的组距问题,应用总体除以样本容量等于组距,得到结果,属于简单题目. 17.3【解析】分析:由题意结合平均数方差的性质整理计算即可求得最终结果详解:由题意结合平均数和方差的性质可知:数据…的平均数为:方差为:则平均数和方差之和是点睛:本题主要考查均值的性质方差的性质等知识意 解析:3【解析】分析:由题意结合平均数、方差的性质整理计算即可求得最终结果.详解:由题意结合平均数和方差的性质可知:数据15x -,25x -,…,5n x -的平均数为:532-=,方差为:()2111-⨯=, 则平均数和方差之和是213+=.点睛:本题主要考查均值的性质、方差的性质等知识,意在考查学生的转化能力和计算求解能力. 18.75【解析】分析:由频率分布直方图算出各频率然后计算中位数详解:由图可知的频率为的频率为的频率为的频率为的频率为前两组频率前三组频率中位数在第三组设中位数为则解得故该组数据的中位数为点睛:本题考查了 解析:75.【解析】分析:由频率分布直方图算出各频率,然后计算中位数详解:由图可知,10~20的频率为0.1420~30的频率为0.2430~40的频率为0.3240~50的频率为0.250~60的频率为0.1前两组频率0.140.240.380.5=+=<前三组频率0.140.240.320.70.5=++=>∴中位数在第三组设中位数为x ,则()300.380.320.510x -+⨯= 解得33.75x =故该组数据的中位数为33.75点睛:本题考查了在频率分布直方图中求中位数,此类题目需要先确定中位数所在的组,然后根据公式计算求得结果,较为基础. 19.1【解析】分析:先利用平均数公式求出平均数再利用方差公式即可得结果详解:的平均数为的方差为故答案为点睛:本题考查主要考查平均数公式与方差公式属于基础题样本数据的算术平均数公式;样本方差公式标准差 解析:1【解析】分析:先利用平均数公式求出平均数,再利用方差公式即可得结果.详解:5.7,5.8,6.1,6.4,6.5的平均数为5.7+5.8+6.1+6.4+6.5 6.15=, 5.7,5.8,6.1,6.4,6.5∴的方差为()()()()()222225.7 6.1+5.8 6.1+6.1 6.1+6.4 6.1+6.5 6.10.15-----=,故答案为0.1. 点睛:本题考查主要考查平均数公式与方差公式,属于基础题. 样本数据的算术平均数公式 12n 1(x +x +...+x )x n =;样本方差公式2222121[()()...()]n s x x x x x x n=-+-++-,标准差s =20.【解析】根据题意可得抽样比为则这次抽样调查抽取的人数是即答案为140解析:140【解析】根据题意可得抽样比为501,75015= 则这次抽样调查抽取的人数是()114507509002100140,1515++=⨯= 即答案为140.三、解答题21.(1)0.63;(2)ˆ0.757.4yx =+. 【分析】(1)代入公式即可得出结果.(2)由(1)可知,因为0.630.7<,所以投资额y 关于满意度x 没有达到较强线性相关,所以要关闭j 企业.重新计算,代入公式即可求出结果.【详解】(1)由题意,根据相关系数的公式,可得10104060.63643.7ii x y x y r -=≈≈∑ (2)由(1)可知,因为0.630.7<,所以投资额y 关于满意度x 没有达到较强线性相关,所以要关闭j 企业. 重新计算得22.810122162499x ⨯-'===,7110446667499y ⨯-'===, 922222192481022.812924118.4i i xx ='-≈+⨯--⨯=∑, 9194061022.87112449247482i ii x y x y =''-≈+⨯⨯-⨯-⨯⨯=∑. 所以919221982ˆ0.690.7118.49ii i i i x y x y b xx ==''-=≈≈≈'-∑∑, ˆˆ740.692457.4457.4ay bx ''=-≈-⨯=≈. 所以所求线性回归方程为ˆ0.757.4yx =+. 22.(1)37;(2)(ⅰ)35;(ⅱ)1760. 【分析】 (1)用每组数据中间点值乘以频率相加即得;(2)(i )年龄在[50,70)的人有6人,其中年龄在[50,60)的有4人,6人分别编号后用列举法写出任选2人的所有基本事件,同时得出至少有1人年龄不低于60岁的基本事件,计数后可得概率;(ⅱ)求出18岁以上的居民所占频率即可得.【详解】解:(1)平均数()150.15250.2350.3450.15550.165750.0537x=⨯+⨯+⨯+⨯+⨯++⨯=.(2)(ⅰ)样本中,年龄在[50,70)的人共有40×0.15=6人,其中年龄在[50,60)的有4人,设为a,b,c,d,年龄在[60,70)的有2人,设为x,y.则从中任选2人共有如下15个基本事件:(a,b),(a,c),(a,d),(a,x),(a,y),(b,c),(b,d),(b,x),(b,y),(c,d),(c,x),(c,y),(d,x),(d,y),(x,y).至少有1人年龄不低于60岁的共有如下9个基本事件:(a,x),(a,y),(b,x),(b,y),(c,x),(c,y),(d,x),(d,y),(x,y).记“这2人中至少有1人年龄不低于60岁”为事件A,故所求概率()93 155P A==.(ⅱ)样本中年龄在18岁以上的居民所占频率为1-(18-10)×0.015=0.88,故可以估计,该小区年龄不超过80岁的成年人人数约为2000×0.88=1760.【点睛】本题考查频率分布直方图,考查古典概型,考查频率分布直方图的应用,考查了学生的数据处理能力,运算求解能力,属于中档题.23.(1)见解析;(2)174.5cm;(3)0.3.【详解】试题分析:(1)先分别算出第六组和第七组的人数,进而算出其频率与组距的比,补全直方图;(2)利用中位数两边频率相等,求出中位数的值;(3)先借助分层抽样的特征求出第四、第五组的人数,再运用列举法列举出所有可能数及满足题设的条件的数,运用古典概型的计算公式求解:解:(1)第六组与第七组频率的和为:∵第六组和第七组人数的比为5:2.∴第六组的频率为0.1,纵坐标为0.02;第七组频率为0.04,纵坐标为0.008.(2)设身高的中位数为,则∴估计这50位男生身高的中位数为174.5(3)由于第4,5组频率之比为2:3,按照分层抽样,故第4组中应抽取2人记为1,2,第5组应抽取3人记为3,4,5则所有可能的情况有:{1,2},{1,3},{1,4},{1,5},{2,3},{2,4},{2,5}, {3,4},{3,5},{4,5}共10种满足两位男生身高都在[175,180]内的情况有{3,4},{3,5},{4,5}共3种, 因此所求事件的概率为.24.(1)0.3;(2)16.2万;(3)2.8吨.【分析】(1)通过频率之和为1,构造方程求得结果;(2)计算出样本中不低于2.5吨人数占比,从而求得全市的人数;(3)由频率分布直方图频率分布可知2.53x <<,然后根据平均分布列方程求得相应结果.【详解】(1)由概率统计相关知识,可知各组频率之和的值为1即频率分布直方图各小矩形面积之和为1()0.50.080.160.40.520.120.080.0421a ∴⨯+++++++=解得:0.3a =(2)由图可知,不低于2.5吨人数所占百分比为()0.50.30.120.080.0427%⨯+++= ∴全市月均用水量不低于2.5吨的人数为:600.2716.2⨯=(万)(3)由(2)可知,月均用水量小于2.5吨的居民人数所占百分比为:73%即73%的居民月均用水量小于2.5吨,同理,88%的居民月均用水量小于3吨 故2.53x <<假设月均用水量平均分布,则()82%73%2.5 2.80.3x -=+=(吨) 注:本次估计默认组间是平均分布,与实际可能会产生一定误差【点睛】本题考查补全频率分布直方图、利用频率分布直方图估计总体数据特征的问题,属于基础题.25.(1)0.012a =,中位数125;(2)能.【分析】(1)由小于130步的频率是56%可计算出a ,同时也可计算出b ,由频率分布直方图可计算出中位数(频率0.5对应的步数);(2)前200人,即频率为0.2,求出频率0.2对应的步数后可得.【详解】解(1)因为1000名职工中有56%的单位职工行走步数小于130(百步).所以(0.0020.0060.008)200.56a +++⨯=.所以0.012a =.因为[]50,110的频率为(0.0020.0060.008)200.32++⨯=,又[]110,130的频率为0.24,所以中位数m 在[]110,130里面, 所以1100.500.320.75200.560.32m --==-. 所以125m =.(2)设步数为y 百步能获得称号,前200名即占1000名职工的0.20 由于[150,170]是0.16,[170,210]是0.08,所以y 应在[150,170]中取值,1500.04200.16y -=,所以155y =百步, 160155>,该职工能获得“运动达人”称号.【点睛】本题考查频率分布直方图,由频率分布直方图计算中位数,属于基础题.26.(1)中位数为71.4;平均数为71;(2)平均数为90;标准差为3)3700元.【分析】(1)利用频率分布直方图能求出中位数、平均分;(2)由题意,求出剩余8个分数的平均值,由10个分数的标准差,能求出剩余8个分数的标准差;(3)求出将3座教学楼完全包裹的球的最小直径、将一座教学楼完全包裹的球的最小直径和将1号教学楼与2号教学楼完全包裹的球的最小直径,由此能求出让各教学楼均被屏蔽仪信号完全覆盖的最小花费.【详解】(1)因为0.050.150.250.450.5++=<0.050.150.250.350.80.5+++=>所以中位数为x 满足7080x << 由80()0.350.10.10.510x -⨯++=,解得608071.47x =-≈ 设平均分为y ,则0.05450.15550.25650.35750.1850.19571y =⨯+⨯+⨯+⨯+⨯+⨯= (2)由题意,剩余8个分数的平均值为010********x x --==因为10个分数的标准差6s == 所以2222110...10(6)10(90)81360x x ++=⨯+⨯=所以剩余8个分数的标准差为0s ===(3)将3座教学楼完全包裹的球的最小直径为:210=<=因此若用一个覆盖半径为105米的屏蔽仪则总费用为4100元;70<= 因此若用3个覆盖半径为35米的屏蔽仪则总费用为4800元;将1号教学楼与2号教学楼完全包裹的球的最小直径为:110=<=70>=因此若用1个覆盖半径为55米和1个覆盖半径为35米的屏蔽仪则总费用为3700元; 所以,让各教学楼均被屏蔽仪信号完全覆盖的最小花费为3700元.【点睛】本题考查中位数、平均数、标准差、最小费用的求法,考查频率分布直方图的性质等基础知识,考查运算求解能力,是中档题.。
数据源统计表样本

作业中心经理
成本率
实际支出成本金额/实际销售收入金额
财会中心按季提供【登记表】
【考核数据登记表】
操作费用控制率
实际费用总支出/预算费用金额
实际费用总支出/财会中心按季提供【登记表】
【考核数据登记表】
客户满意度(外)
1-(客户投诉/实际业务总量(指票数))
考核者【模板】
【外部满意度调查表】
员工培训学时(公司总体)
全年员工实际培训总学时/预算培训总学时
本部门按年度提供员工培训学时(公司总体)/【登记表】
【考核数据登记表】
固定资产非正常损失件数
工程部【登记表】
【考核数据登记表】
部门协作满意度
拟定部门在进行内部服务、协作目的(涉及区域内分公司)
考核者【模板】
【部门协作满意度考核表】
内部硬件网络系统运营重大事故
拟定IT部门系统维护质量目的指标
考核者【模板】
【工程部某些指标考核表】
各业务系统运营重大故障率
拟定IT部门系统维护质量目的指标
考核者【模板】
【部门协作满意度考核表】
员工增长额度控管达到率
各单位实际新增员工额数/各单位预算新增员工额上限数
本部门按年度提供各部门实际新增员工额数/【登记表】
【考核数据登记表】
人力成本测算
精确、及时提供实际人工成本发生额
考核者【模板】
【人力成本测算考核表】
业务差错
因工作责任导致差错
考核者【模板】
【业务差错率考核表】
客户流失
客户流失数量
客户流失数/本部门按年度考核者【模板】
【营销中心客户流失考核表】
部门协作满意度
人民银行,商业银行中间业务统计制度

竭诚为您提供优质文档/双击可除人民银行,商业银行中间业务统计制度篇一:中国人民银行关于印发《商业银行中间业务统计制度》的通知20xx年03期中国人民银行文告(总第158号)gazetteoFpeople′sbankoFchina2月20日20xx年第3号(总第158号)目录中国人民银行关于印发《商业银行中间业务统计制度》的通知银发[20xx]25号(3)中国人民银行公告[20xx]第1号(22)中国人民银行关于印发《商业银行中间业务统计制度》的通知银发[20xx]25号人民银行各分行、营业管理部、省会(首府)城市中心支行、各国有独资商业银行、股份制商业银行:为了规范商业银行中间业务统计信息的收集和报送工作,中国人民银行制定了《商业银行中间业务统计制度》(见附件)。
现印发给你们,请遵照执行。
商业银行中间业务统计涉及面广,难度较大,各商业银行要加强内部各部门之间的协调与配合,做好程序开发、信息收集、数据报送等各项统计工作。
请各行于20xx年3月20日前补报20xx年全年度累计数据,如有问题,请及时与中国人民银行统计司联系。
请人民银行各分行、营业管理部、省会(首府)城市中心支行及时将此文转发至辖区内城市商业银行。
联系人:才宏远、赵铮联系电话:66194350、66194429传真电话:66012733中国人民银行二00三年一月三十日附件商业银行中间业务统计制度一、为及时、准确地了解商业银行开展中间业务的状况,规范商业银行中间业务统计信息的收集和报送工作,依据《商业银行中间业务暂行规定》(中国人民银行令[20xx]第5号),制定本统计制度。
二、本制度适用于开展中间业务的各国有独资商业银行、股份制商业银行和城市商业银行(以下称“各商业银行”)。
三、本统计制度中的指标数据从各商业银行会计科目、账户以及台账信息中取得。
四、各商业银行要按本制度的要求定期向中国人民银行报送本币及外币中间业务统计数据。
有关统计指标名称、指标编码及指标释义见附表1。
移动网信息服务业务情况表
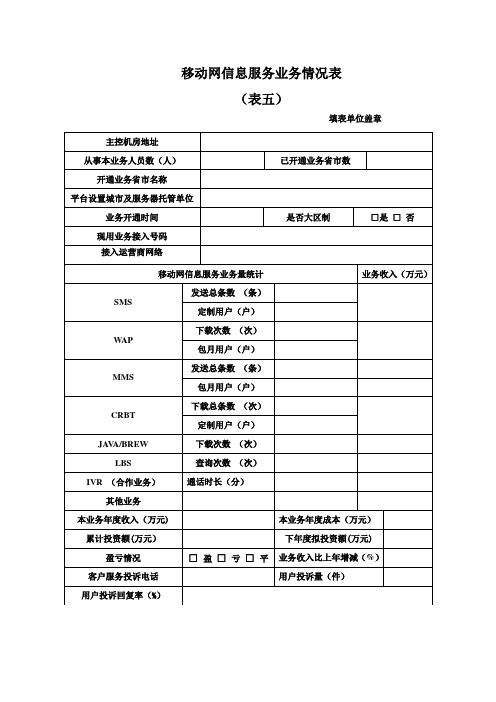
移动网信息服务业务情况表(表五)填表单位盖章填表说明1.主控机房地址管理控制整个网络的机房地址,一般该机房应承担认证、计费、管理、安全控制、数据库集中管理等功能。
2.从事本业务人员数公司从事本业务的管理及技术人员总数;3.开通业务省市数量开通业务省市数量是指已开通业务的省或直辖市数量;4.开通业务省市名称开通业务省市名称是指已开通业务的省或直辖市名称;5.平台设置城市及服务器托管单位要填写公司在哪些城市设立信息平台,并填写服务器托管的单位;6.业务开通时间公司开通本业务的时间;7.是否大区制按公司管理实际情况选择公司“是”或“否”按大区制管理,仅针对移动信息服务业务;8.现用业务接入号码特指由通信管理部门(信息产业部和地方通信管理局)核发给你公司的用于移动信息服务的短号码(如1066xxxx,1062xxxx等)。
9.接入运营商网络公司经营本业务接入与合作的基础运营商名称;10.移动网信息服务业务量和业务收入统计10.1.SMS分别填写SMS业务包含定制用户在内的发送总的条数;定制用户数;该项业务收入;10.2.W AP分别填写W AP业务含包月用户在内的总的下载次数;包月用户数;该项业务收入;10.3.MMS分别填写MMS业务包含包月用户在内的发送总的条数;包月用户数;该项业务收入;10.4.CRBT分别填写CRBT业务含定制用户在内的总的下载次数;定制用户数;该项业务收入;10.5.JA VA/BREW分别填写JA VA/BREW业务的下载次数;该项业务收入;10.6.LBS分别填写LBS业务的查询次数;该项业务收入;10.7.IVR (合作业务)IVR 属于与基础运营商合作业务,请填写本公司该项业务的总的通话时长,该项业务分成后公司应得收入;10.8.其他除以上所列业务外其他业务情况,分别填写业务量和业务收入;11.本业务年度收入(万元)是指本年度本业务的收入总额;12.本业务年度成本(万元)是指本年度用于该业务的各项费用支出总额;13.累计投资额(万元)是指历年公司用于该业务软硬件购置、机房建设等投资的累计额;14.下年度拟投资额(万元)是指下年度用于该业务软硬件购置、机房建设等投资总数的预算;15.盈亏情况是指公司运营本业务盈利情况,选择盈、亏、平之一打勾;16.业务收入比上年增减(%)公司本业务收入与上年相比增加或减少的百分比;如果07年没有数据,可填写为N/A。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
周业务量统计面试情况统计
组别初试时间电话数初试总人数其中自刷网
站数量
初试通过
人数
个人本周面谈客户详情
组别业务员姓名客户姓名面谈时间第几次面谈是否成交团队本周完成情况
组别规模标准件数人均标准产
能
人均件数
团队下周预计情况
组别规模标准件数酒会客户跟进情况
组别业务员姓名客户姓名跟进时间是否成交(意向)
金额
参加复试人数通过复试人数参与培训人数培训通过人数备注(意向)
金额下次见面时间是否有后续资金详情下次见面
时间客户对公司意见和建议详情。
