四年级下册数学加法乘法定律
四年级数学下册运算定律公式归纳

四年级下册数学——运算定律·公式归纳一、加减法运算定律:1.加法交换律:a+b=b+a2.加法结合律:(a+b)+c=a+(b+c)3.连减的性质:a-b-c=a-(b+c)二、乘除法运算定律:1.乘法交换律:a×b=b×a2.乘法结合律:(a×b)×c = a×(b×c)3.乘法分配律:①两个数的和与一个数相乘:(a+b)×c=a×c+b×c②两个数的差与一个数相乘:(a-b)×c=a×c-b×c。
4.除法的性质:a÷b÷c=a÷(b×c)5.乘法分配律的应用:①类型一:(a+b)×c= a×c+b×c (a-b)×c= a×c-b×c ②类型二:a×c+b×c=(a+b)×c a×c-b×c=(a-b)×c③类型三:a×99+a=a×(99+1)a×b-a=a×(b-1)④类型四:a×99 a×102= a×(100-1)= a×(100+2) = a×100-a×1 = a×100+a×26.商不变性质:a÷b=(a×c)÷(b×c)a÷b=(a÷c)÷(b÷c)四年级下册数学——运算定律·公式归纳一、加减法运算定律:1.加法交换律:a+b=b+a2.加法结合律:(a+b)+c=a+(b+c)3.连减的性质:a-b-c=a-(b+c)二、乘除法运算定律:1.乘法交换律:a×b=b×a2.乘法结合律:(a×b)×c = a×(b×c)3.乘法分配律:①两个数的和与一个数相乘:(a+b)×c=a×c+b×c②两个数的差与一个数相乘:(a-b)×c=a×c-b×c。
小学四年级数学下册-第三单元-运算定律
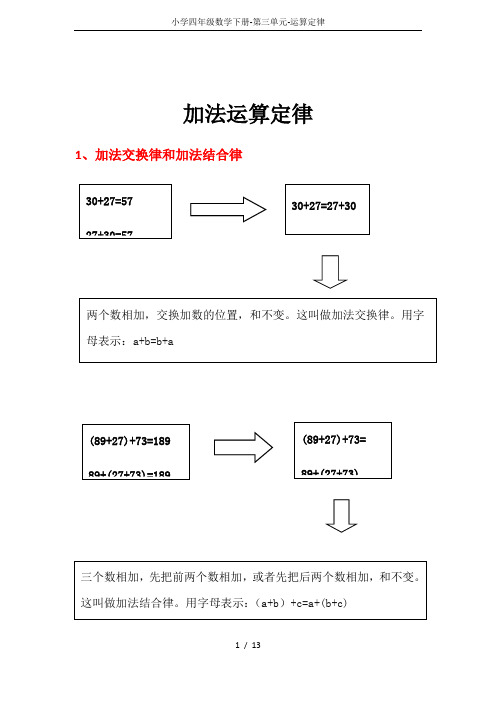
加法运算定律1、加法交换律和加法结合律知识点补充:①、几个数相加,任意交换加数的位置,和不变。
用字母表示:a+b+c=a+c+b 如:29+35+31=29+31+35 ②、加减混合运算中带着数字前面的运算符号,交换减数、加数位置,和不变。
用字母表示:a+b-c=a-c+b(a ˃c) 如:46+72-26=46-26+722、加法运算定律的应用在计算过程中,如果那两个数相加可以得到整十、整百、整千的数,就利用加法的运算定律(加法交换律、加法结合律),把这两个数先相加,这样可以使计算简便。
4.在○ 351+648+249=(351648865-246-54=865-(246496-(296+144)=496⃝296⃝1443、减法的运算性质知识点补充:①、一个数减去两个数的差,可以用这个数先减去差里的被减数,再加上减数;或用这个数加上差里的减数,再减去被减数。
用字母表示:a-(b-c)=a-b+c=a+c-b 如:50-(20-10)=50-20+10=50+10-20 ②、括号前面是加号,去掉括号不变号;加号后面添括号,括号里面不变号。
如:10+(4-3)=10+4-3括号前面是减号,去掉括号要变号;减号后面添括号,括号里面要变号。
如:10-(8+1)=10-8-1896-(375+296) 837-237-186-14 927-16-24-60乘法运算定律1、乘法交换律和乘法结合律(40+8)=586+(214+537)-(586(×8=73×538538+300-12、乘法运算定律的应用①、需要记住的特殊数的乘积5x2=10 25x4=100 125x8=1000 25x8=200 75x4=300375x8=3000 25x8=200 125x4=500②、两个数相乘的简便计算,方法不唯一。
既可以把一个因数用乘法拆分,使用乘法结合律进行简便计算,也可以把一个因数用加、减法拆分,使用乘法分配律进行简便计算。
四年级数学下册运算定律知识点梳理与思维导图

连除的性质 公式:a÷b÷c=a÷(b×c )
拆分、凑整简便运算
描述:举当例一:个33数0÷比5整÷百2=、33整0÷千(…5…×稍2大)一些时,可以将它拆成整百、
拆分法
整千……和一个较小的数的和,然后利用运算定律简便计算。
凑整法
举例:204×25=(200+4)×25 描述:当一个数比整百、整千……稍小一些时,可以将它凑成整
加法运算定律 加法交换律
定义:两个数相加,交换加数的位置,和不变。
公式:a+b=b+a 举例:40+56=56+40
加法结合律
定义:三个数相加,先把前两个数相加,或者先把后两个
数相加,和不变。 公式:(a+b)+c=a+(b+c) 举例:(88+104)+96=88+(104+96)
定义:两个数相乘,交换因数的位置,积不变。
公式:(a+b)×c=a × c+ b× c
举例:(4+2)×25=4×25+2×25
连减的性质
连减、连这个数减去两个数的和
公式:a-b-c=a -(b + c ) 举例:234-66-34=234-(66+34)
定义:一个数连续除以两个数,等于这个数除以两个数的积。
乘法交换律 公式:a×b=b×a
举例:25×4=4×25
定义:三个数相乘,先乘前两个数,或者先乘后两个数,
运
乘法运算定律 乘法结合律
积不变。 公式:(a×b)×c=a × (b × c ) 举例:(25×5)×2=25×(5×2)
数学四年级下学期第五讲-运算定律

四年级数学科辅导讲义(第讲)学生姓名:授课教师:授课时间:知识点一、加法交换律、加法结合律1、加法交换律:两个加数交换位置,和不变。
用字母表示为:a+b=b+a(a、b代表任意数)2、若干个数相加,任意交换加数的位置,和不变。
a+b+c=a+c+b3、加法结合律:三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
用字母表示为: (a +b)+c=a+(b+c)4、在一个加法算式中,当某二、乘法交换律、乘法结合律1、乘法交换律:交换两个因数的位置,积不变。
用字母表示为:a×b=b×a。
2、多个数相乘,任意交换因数的位置,积不变。
如a×b×c×d=b×d×a×c。
3、乘法结合律:三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
用字母表示为:(a×b)×c=a×(b×c)4、在乘法算式中,如果其中两个因数的积为整十、整百、整千数时,可以运用乘法交换律、乘法结合律来改变运算顺序,从而简化运算。
如:125×25×8×4=125×8×25×4…………乘法交换律=(125×8)×(25×4)…………乘法结合律=1000×100=100000些加数可以凑成整十或整百数时,运用加法交换律、加法结合律来改变运算顺序,可以使计算简便。
例:115+132+118+85=115+85+132+118…………加法交换律=(115+85)+(132+118)…………加法结合律=200+250=450三、乘法分配律1、乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再把所得的积相加。
用字母表示为:(a+b)×c=a×c+b×c2、两个数的差与一个数相乘,可以先把它们分别与这个数相乘,再把所得的积相减。
人教版四年级下册数学之运算定律

人教版四年级下册数学之运算定律一、加法运算定律1.加法交换律两个数相加,交换加数的位置,和不变。
用字母表示为a+b=b+a 。
2.加法结合律三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
用字母表示为(a+b )+c=a+(b+c )。
加法交换律和加法结合律同样适用于计算多个数连加。
加法交换律和加法结合律同样适用于计算多个数连加。
如如: 125+36+75+264=(125+75)+(36+264)=200+300=500有的算式中带有括号,先算括号里面的并不简便,根据数的特点可以先把括号去掉,再运用加法交换律和加法结合律使计算变得简便。
如:(452+36)+(48+564)=(452+48)+(36+564) =500+600 =1100注意:在计算连加算式时,不要盲目地进行计算,首先要观察算式中的数,看看有没有能凑成整十、整百、整千的数..................,.如果有...,.那么可以运用加法交换律或加法结合律进行计算.....................,.这样既简便.....又准确...。
二、减法的运算性质1.一个数连续减去两个数,等于减去这两个数的和。
用字母表示为a-b-c=a-(b+.c )。
注意:根据数据的特点逆运用减法的性质也可以使计算变......................得简便。
括号前面是减号...........,.去掉括号后.....,.括号里面的算式要改变运...........算符号...。
如:346-(146+63)=346-146-.63 =200-63 =137减法性质的逆运用:一个数减去两个数的和相当于从被减数中连续减去这两个数。
2.在连减运算中,任意交换两个减数的位置,差不变。
用字母表示为a-b-c=a-c-b 。
3.在加减混合运算中,带着数前面的运算符号交换加数、减数的位置再进行计算,其结果不变。
用字母表示为a+b-c=a-c+b (a>c )运用加法交换律可以验算加法:交换两个加数的位置再算一遍,看看和是否相等。
人教版四年级下册数学运算律课件

• 两个数相乘,交换两个因数的位置,积不变,这叫做乘法交换律。 • 用字母表示:a × b = b× a • 三个数相乘,先乘前两个数,或者先乘后两个数,积不变,这叫做乘法结合律。 • 用字母表示:(a× b)× c=a×(b×c)
4
3.4乘法运算定律-分配
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。 用字母表示:(a+b)× c=a×c+b×c
14
4、连除的性质
一个数连续除以两个数,等于除以这两个数的积。 字母表示:a÷b÷c=a÷(b×c) 【或 a÷(b×c)= a÷b÷c 】
15
谢谢
1
8
【加法运算定律】
• 三、下面各题,怎样简便就怎样计算。 • 157+78+322
554+249+146
415+187+113+285
9
【加法运算定律】
• 四、应用题。 小红一家在“十一黄金周去云南旅游,机票花了 3150元,门票花了465元,食宿费花了1235 元,小红一家此次旅游一共花了多少钱?
12
2、连减的性质
• 一个数连续减去两个数,等于减去这两个数的和。 • 字母表示:a-b-c=a-(b+c) 【或 a-(b+c)= a-b-c 】
13
3、乘法运算定律
①乘法交换律:两个数相乘,交换因数的位置,积不变。 字母表示:a×b=b×a ②乘法结合律:三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。 字母表示:(a×b) ×c=a×(b×c) • 乘法的这两个定律往往结合起来一起使用。如:125×78×8=78×(125×8) ③乘法分配律:两个数的和与一个数相乘,可以先把这两个数分别与这个数相乘,再把积 相加。 字母表示:(a+b) ×c=a×c+b×c 【或 a×c+b×c=(a+b) ×c 】
四年级下册数学讲义-第20讲 加法、乘法运算定律人教版(无答案)

【本节知识框架】知识点一:加法的运算定律知识点二:乘法法的运算定律【知识点讲解】知识点一:加法的运算定律①加法交换律:加数交换位置,和不变。
字母公式:a+b+c=____________②加法结合律:先把前两个数相加,或者先把后两个数相加,和不变。
字母公式:a+b+c=______________③加法的性质:一个加数增加多少,另一加数减少多少,和不变。
字母公式:a+b=(a+c)+__________拓展:减法的性质:a-b-c=a-(b+c) a-b-c=a-c-b加法简便运算的秘诀:凑整十、整百、整千的数。
(1)拆分法:当一个数比整百、整千稍微大一些的时候,我们可以把这个数拆分成整百、整千与一个较小数的和,然后利用加减法的交换、结合律进行简便计算。
例如:103=100+3,1006=1000+6,…(2)凑整法:当一个数比整百、整千稍微小一些的时候,我们可以把这个数写成一个整百、整千的数减去一个较小的数的形式,然后利用加减法的运算定律进行简便计算。
例如:97=100-3,998=1000-2,…例题1 简便运算(1)3+2+17 (2)25+(17+5)(3)23+4+106(4)155+657+245 (5)12+113+8 (6) 39+(61+75)+25 【变式练习】对下面式子进行简便计算:(1)63+16+84 (2)76+15+24 (5)680+485+120例题 2 运用简便运算计算下面各式:(1)528—6.5—3.5 (2)528—89—128 (3)52.8—(40+12.8)【变式练习】(1)125+8-25 (2)62+50-12 (3) 256—58+44(4)198-75-98 (5)369-45-155【随堂训练】计算题:(1)827+15+85 (2)119+81+259 (3)368+29+32 (4)9600 - 453 - 547 判断题:1、27+33+67=27+100 ()2、134-75+25=134-(75+25)()选择:56+72+28=56+(72+28)运用了()A、加法交换律B、加法结合律C、乘法结合律D、加法交换律和结合律填空题:1、用简便方法计算136+258+64,要先算(),这是根据()律。
人教版数学四年级下册【运算定律与简便计算】知识篇

加、减法的速算与巧算( 基础篇)原创不容易,为有更多动力,请【关注、关注、关注】,谢谢!落红不是无情物,化作春泥更护花。
出自龚自珍的《己亥杂诗·其五》1、加法运算定律(2个):☆加法交换律:两个数相加,交换加数的位置,和不变。
即:a + b = b + a☆加法结合律:三个数相加,可以先把前两个数相加,再加上第三个数;或者先把后两个数相加,再加上第一个数,和不变。
即:(a + b) + c = a + (b + c)(提醒:运用加法结合律时,要注意把结合的两个数用括号括起来。
)连加的简便计算方法:①使用加法交换律、结合律凑整(把和是整十、整百、整千的数先交换再结合在一起。
)②个位:1与9,2与8,3与7,4与6,5与5,结合。
③十位:0与9,1与8,2与7,3与6,4与5,结合。
连加的简便计算例题:50+98+50 488+40+60 165+93+35 65+28+35+72=50+50+98 =488+(40+60)=93+165+35=(65+35)+(28+72)=100+98 =488+100 =93+(165+35)= 100+100=198 =588 =293 = 2002、连减的性质:☆一个数连续减去几个数等于这个数减去这几个数的和。
即:a – b – c = a – (b + c)注:连减的性质逆用:a – (b + c) = a – b – c = a – c – b☆一个数连续减去两个数,可以用这个数先减去后一个数再减去前一个数。
即:a-b-c=a—c-b连减的简便计算方法:①连续减去几个数就等于减去这几个数的和。
如:106-26-74 = 106-(26+74)②连续减去两个数可以先减去后一个数再减去前一个数。
如:226-58-26=226-26-58③减去几个数的和就等于连续减去这几个数。
如:106-(26+74) = 106-26-74连减的简便计算例题:528—65—35 28—89—128 528—(150+128)=528—(65+35) =528—128—89 =528—128—150=528—100 =400—89 =400—150=428 =311 =2503、加、减法混合运算的性质:在计算没有括号的加、减混合运算时,计算时可以带着运算符号“搬家”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两个数相加,交换加数的位置,和不变。
这叫做加法交换律。
用字母表示为a+b=b+a
拓展提高:
1.若干个数相加,任意交换加数的位置,和不变。
用字母表示为a+b+c=a+c+b,
如37+25+43=37+43+25=105
2.在加减混合运算中,带有数前面的运算符号交换加数、减数的位置再进行
计算,其结果不变。
用字母表示为a+b-c=a-c+b(a>c),如
57+78-37=57-37+78=98
三个数相加,先把前两个数相加,或者先把后两个数相加,和不变。
这叫做加法结合律。
用字母表示为(a+b)+c=a+(b+c)
拓展提高:
在加减混合运算中,有时为了计算简便,可以把加数、减数用括号结合起来。
在加号后面添括号时,原来的加数、减数都不变;在减号后面添括号时,原来的减数变加数,加数变减数。
用字母表示为a+b-c=a+(b-c)(b>c),如
71+56-26=71+(56-26)=101;a-b+c=a-(b-c)(b>c)如
71-56+26=71-(56-26)=41。
运用拆分凑整法解决复杂的简算问题199999+19998+1997+196+10
分析:观察此题发现,前四个数分别加上1、2、3、4就可以凑成整十、整万、整千、整百的数,而最后一个加数10又可以分解成功+2+3+4的形式,能与前面的四个数分别相加,这样计算比较简便。
199999+19998+1997+196+10
=(199999+1)+(19998+2)+(1997+3)+(196+4)
=200000+20000+2000+200
=222200
加法交换律与加法结合律最大的区别是:交换律改变的是数的位置,结合律改变的是运算顺序。
加法结合律的重要标志是小括号的应用。
减法的运算性质:(1)一个数连续减去两个数,可以用这个数减去两个减数的和,即a-b-c=a-(b+c)。
(2)在连减运算中,任意交换减数的位置,差不变。
即a-b-c=a-c-b。
运用凑整法解决连减的问题5498-1928-387-1072-1613
分析:此题是一个边减算式,如果按从左到右的顺序计算,不够简便。
观察四个减数,发现1928和1072、387和1613相加能得到整千数。
因此,根据减法的运算性质,从被减数中连续减去两组减数的和会使计算简便。
5498-1928-387-1072-1613
=5498-(1928+1072)-(387+1613)
=5498-3000-2000
=5498-(3000+2000)
=5498-5000
=498
运用对应法解决等差数列求和的问题2+4+6+8+…+98+100
分析:观察这个连加算式,发现从第二个数开始,每一个数与前一个数的差都是2,像这样的一组数列称为等差数列。
求一组等差数列的和,可以将2+4+6+8+…+98+100这组数列前后对应的数相加。
数列中对应的每组数,和都是102,并且这组数列共有50个数,即共有25个102.从而可以计算出这组数列的和。
2+4+6+8+…+98+100
=(2+100)×50÷2
=102×50÷2
=2550
求一组等差数列的和,可以用公式“(首项+末项)×项数÷2”来解题。
用等量代换法将下面三个算式合并成一个综合算式。
840÷7=120 35×3=105 735+105=840
126+34=160 160×4=640 1280÷640=2
乘法交换律:两个数相乘,交换两个因数的位置,积不变。
用字母表示为
a×b=b×a
多个数相乘,任意交换因数的位置,积不变。
如a×b×c×d×e=a×c×e×b ×d=a×d×b×c×e
乘法结合律:三个数相乘,先乘前两个数,或者先乘后两个数,积不变。
用字母表示为(a×b)×c= a×(b×c)。
乘法分配律:两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加,这就是乘法分配律。
用字母表示为(a+b)×c=a×c+b×c,也可以表示为a×(b+c)=a×b+a×c。
拓展提高
1、两个数的差与一个数相乘,可以用被减数和减数分别与这个数相乘,
再相乘。
用字母表示为(a-b)×c=a×c-b×c。
2、多个数的和(或差)与一个数相乘,可以把这些数分别与这个数相乘,
再相加(或相减)。
用字母表示为(a±b±c)×m=a×m±b×m±c×m 3、两个数或几个数的和除以一个数,可以把和里的各个数分别除以这个
数,再相加。
用字母表示为(a+b+c)÷m=a÷m+b÷m+c÷m(m≠0)。
4、两个数的差除以一个数,可以用被减数、减数分别除以这个数,再相
减。
用字母表示为(a-b)÷c=a÷c-b÷c(c≠0)。
5、在乘加或乘减运算中,如果每个乘法算式有共同的因数,那么可以逆
用乘法分配律a×c±b×c=(a±b)×c进行简便运算。
运用转化法解决简算问题
除法的运算性质:一个数连续除以两个数,可以用这个数除以两个除数的积,即a÷b÷c=a÷(b×c)。
一个数连续除以几个数,任意交换除数的位置,商不变。
即a÷b÷c ÷d=a÷c÷b÷d=a÷d÷b÷c。
142+914+58+86 927-653-47-127 475-(255+175)
2+4+6+8+…+18+20 125×6×7×8 56×5×4×2×25
56×125 125×5×32×5 59×(101)
99×63 15×21+15×78+15 38×547-347×38-150×38 4800÷25÷4 600÷24 72×125 1000÷25÷5÷2÷4
56×7+45×7-7 888×999÷222÷333 616161×39-393939×61。
