河南省商水杨氏英语学校2012-2013第二学期九年级数学模拟试题
2013年九年级中考模拟数学试卷(2)及答案

2013年九年级中考模拟数学试卷(2)及答案姓名 得分 一、选择题(共15小题,每小题3分,满分45分)1.π+-3的绝对值是( )A .π+-3B .π--3C .π-3D .31--π 2.如图,直线a ∥b ,直线c 与a ,b 相交,∠1+∠2=66°,则∠3=( ) A .67° B .57° C .47° D .52° 3.南海是中国领土的最南端,面积为3 500 000平方公里,3 500 000用科学记数法表示为( ) A .3.5×105 B .35×105 C .3.5×106 D .0.35×106 4.下列事件中不可能事件的是( )A .在地球上,太阳从东边升起B .正常情况下,将水加热到100℃时水会沸腾C .三角形的内角和是360°D .打开电视机,正在播动画片 5.下列各式计算正确的是( )A .a 2·a 3=a 6B .a 2+a 2=2 a 2C .a 5÷a 5=aD .a 3•a 2=a 56.如图,一个几何体由5个大小相同、棱长为1的小正方形搭成,下列关于这个几何体的说法正确的是( )A .主视图的面积为5B .左视图的面积为3C .俯视图的面积为3D .三种视图的面积都是4 7.化简2x ·3x+x(1-x)结果为( )A .5x 2+xB .7xC .6x 2D .7x-x 28.四张完全相同的卡片上分别画有平行四边形、等腰三角形、正方形、等腰梯形,将有图形的一面朝下放在桌面上,从中随机抽取两张,抽到的两张卡片上图形一张中心对称一张是轴对称的概率为( ) A .43 B .32 C .16 D .65 9.如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC 的三个顶点在图中相应的格点上,则tan ∠CAB 的值为( )A .13 B .12 C .2D .3第11题图10.下列命题是真命题的是( )A .一组对角与一组对边分别相等的四边形是平行四边形B .对角线相等的梯形是等腰梯形C . 对角线相等且互相垂直的四边形的矩形D .四个角是直角的四边形是正方形 11.一次函数y 1=k 1x+b 和反比例函数y 2=xk 2错误!未找到引用源。
2012-2013第一学期初三数学期末模拟试卷2

新思维2012—2013学年度第二学期综合练习(一)初三数学 2010.4第Ⅰ卷 (机读卷共32分)一、选择题(本题共32分,每小题4分,共8个小题) 下列各题均有四个选项,其中只有一个..是符合题意的.用铅笔把“机读答题卡”上对应题目答案的相应字母涂黑.1.2-的倒数是 A . 2-B .2C .12-D .122. 2010年五月至10月,将在中国上海首次举办以“Better City, Better Life ”为主题的世界博览会。
主办机构预计吸引世界各地7000万人次参观者前往,总投资达450亿人民币,超过北京奥运会,是世界博览会史上最大规模的一次博览会。
将7000万用科学记数法表示为 A. 4710⨯万 B. 40.710⨯万 C.27010⨯万 D.3710⨯万3. 内角和与外角和相等的多边形一定是( ) A.八边形 B.六边形 C.五边形 D.四边形4. 如图,一个全透明的玻璃正方体,上面嵌有一根黑色的金属丝,金属丝在俯视图中的形状是5则这组数据的中位数与众数分别是 A .27,28 B .27.5,28 C .28,27D .26.5,276.若 2(2)30,x y -+-= 则yx 的值为 A . 8- B .8 C .18 D .18- 7. 掷一枚质地均匀的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得面朝上的点数大于4的概率为 A.16B.13C.14D.128. 在边长为2的正方形ABCD 中,对角线AC 与BD 相交于点O ,P 是BD 上一动点,过P 作EF ∥AC ,分别交正方形的两条边于点E 、F . 设BP =x ,△BEF 的面积为y ,则能反映y 与x 之间关系的图象为第Ⅱ卷 (非机读卷共88分)二、填空题:(本题共16分,每小题4分,共4个小题)9. 函数x2x y +=中,自变量x 的取值范围是 . 10.因式分解:34a a -= .11. 如图,AB 是O ⊙的直径,点C 、D 在O ⊙上,110BOC ∠=°, AD OC ∥,则AOD ∠= .12. 正方形A 1B 1C 1O ,A 2B 2C 2C 1,A 3B 3C 3C 2,…按如图所示的方式放置.点A 1,A 2,A 3,…和点C 1,C 2,C 3,…分别在直线y kx b =+(k >0)和x 轴上,已知点B 1(1,1),B 2(3,2), 其中点B 5的坐标是______________, 点B n 的坐标是______________(n三、解答题:(本题共30分,每小题5分,共6个小题) 13. 计算:(0-11()2cos302+-︒.14.求解不等式组2(1)31,213x x x +>-⎧⎪+⎨≥⎪⎩,并在所给的数轴上表示出它的解集.A. B. C. D.11题图OBDA C命运如同手中的掌纹,无论多曲折,终掌握在自己手中EFB CDA15. 将两个大小不同的含45︒角的直角三角板如图1所示放置在同一平面内.从图1中抽象出一个几何图形(如图2),B、C、E三点在同一条直线上,连结DC.求证:△ABE≌△ACD.16.已知20a a-=,求2221412211a aa a a a--÷+-+-的值.17.如图,直线xyl2:1=与直线3:2+=kxyl在同一平面直角坐标系内交于点P.(1)写出不等式2x > kx+3的解集:;(2)设直线2l与x轴交于点A,求△OAP的面积.18.列方程或方程组解应用题:有两块面积相同的小麦试验田,分别收获小麦9000kg和15000kg.已知第一块试验田每公顷的产量比第二块少3000kg,求第一块试验田每公顷的产量为多少千克?四、解答题:(本题共20分,第19、20题5分,第21题6分,第22题4分,共4个小题)19. 如图,在梯形ABCD中,AD∥BC,90B∠=,45C∠=,=3AD,CD,点,E F分别在线段AD BC,上,且AE ED=,求CF长.20.如图,在⊙O中,点A、B在圆上,BC∥OA,交⊙O于点D,且OC⊥OB,OCA B∠=∠.(1)求证:AC是⊙O的切线;(2)若OB=1,求BD的长.21. 国家通过实施政策力度大、群众受惠面广的促进家电、汽车、节能产品和住房消费等措施,优化市场消费环境,有效的挖掘了居民的消费潜力。
河南省商水外国语中学2012-2013第二学期九年级数学模拟试题

河南省商水外国语中学2012-2013第二学期九年级数学模拟试题注意事项:1.本试卷共8页,三大题,满分120分,考试时间100分钟.2.请用钢笔功圆珠笔直接答在试卷上.3.答卷前将密封线内的项目填写清楚.一、选择题(每小题3分,共18分)下列各小题均有四个答案,其中只有一个是正确的,将正确答案的代号字母填入题后括号内.1.51-的相反数是( )A. 51B. 51-C. 5-D. 52.2011年3月23日,我省残疾人工作会议在郑州举行.会议提出继续开展全省各级残联扶残助残活动,计划投入8966万元,惠及107万残疾人.8966万用科学记数法表示正确的是( ) A.9.0×107B. 9.0×106C.8.966×107D.8.966×1083. 一组数据3,4,x ,6,7的平均数是5,则这组数据的中位数和方差分别是( )A.4和2B. 5和2C. 5和4D. 4和44. 已知:四边形ABCD 的对角线AC 、BD 相交于点O ,给出下列4个条件:①AB ∥CD ;②OA =OC ;③AB =CD ;④AD ∥BC 从中任取两个条件,能推出四边形ABCD 是平行四边形的概率是( )A. 21B. 31C. 32D. 655. 方程x x 32=的根是( )A. x =3B. x =0C. x 1=3,x 2=0D. x 1=0,x 2=36. 在平面直角坐标系xoy 中,已知A (4,2),B (2,-2),以原点O 为位似中心,按位似比1:2把△OAB 缩小,则点A 的对应点A ′的坐标为( ) A. (3,1)B. (-2,-1)C. (3,1)或(-3,-1)D. (2,1)或(-2,-1)二、填空题(每小题3分,共27分)7. 分解因式m 2 - 2 (m -1) - 1为 .8. 已知:a 是5的小数部分,则代数式)25(+a 的值为.9. 一次函数)0(2<k kx y +=的图像上不重合的两点A (m 1,n 1),B (m 2,n 2),且))((2121n n m m P --=,则函数x py =的图像分布在第象限.10. 已知圆锥的侧面展开图是直径为8cm 的半圆,则这个圆锥的侧面积是cm 2.11. 如图,A 、B 、C 、D 四点在同一个圆上,AD 与BC 交于点O ,∠AOC =80°,∠B =50°,则∠C =.左视图俯视图(第11题) (第12题) (第13题)12. 已知一个直角三角板PMN ,∠MPN =30°,MN =2,使它的一边PN 与正方形ABCD 的一边AD 重合(如图放置在正方形内)把三角板绕点P 旋转,使点M 落在直线BC 上一点F 处,则CF 的长为 .13. 如图是由大小相同的小正方体组成的简单几何体的左视图和俯视图,那么组成这个几何体的小正方体的个数最少为个.(第14题) (第15题)MD B C(N)ABCODCE14. 如图,AB 是⊙O 的直径,∠CAB =45°,AB =BC =2,则图中阴影部分面积为.15. 如图,矩形纸片ABCD 中,AB =5cm ,BC =10cm ,CD 上有一点E ,EC =2cm ,AD 上有一点P ,PA =6cm ,过点P 作PF ⊥AD 交BC 于点F ,将纸片折叠,使P 与E 重合,折痕交PF 于Q ,则线段PQ 的长是cm.三、 解答题(本大题共8个小题,计75分)16. (8分)已知:A =21-x ,B =62-x x,当x 为何值时,A 与B 的值相等?17. (9分)如图,点C 是l 上任意一点,CA ⊥CB 且AC =BC ,过点A作AM ⊥l 于点M ,过点B 作BN ⊥l 于N ,则线段MN 与AM 、BN 有什么数量关系,证明你的结论:18. (9分)在“全国亿万学生阳光体育运动”启动后,小华和小敏在课外活动后,报名参加了短跑训练,在近几次百米训练中,所测成绩如图,请根据图中所给信息解答以下问题:秒(1)请补齐下面的表格:(2)小华与小敏哪次的成绩最好?最好成绩分别是多少秒?(3)分别计算他们的平均数、极差和方差,如果你是教练请综合比较他们的成绩,分别给予怎样的建议?19.(9分)如图,在梯形ABCD中,AD∥BC, AB = CD,E是AD的中点,AD=4,BC=6,点P是BC边上的动点(不与点B重合),PE与BD相交于点O,设PB的长为x.(1) 当P点在BC边上运动时,求证:△BOP∽△DOE.(2) 当x = ()时,四边形ABPE是平行四边形;当x = ()时,四边形ABPE是直角梯形;(3)当P在BC上运动的过程中,四边形ABPE会不会是等腰梯形?试说明理由.C20.(9分)某公司专销产品A,第一批产品A上市40天恰好全部售完.该公司对第一批产品A上市后的市场销售情况进行了跟踪调查,调查结果如图1和图2所示,其中图1中的折线表示是市场日销售量y(万件)与上市时间t(天)的关系,图2中的折线表示的是每件产品A的日销售利润w(元)与上市时间t(天)的关系.(1)试写出第一批产品A的市场日销售量y(万件)与上市时间t(天)的关系式;(2)第一批产品A上市后,哪一天这家公司市场日销售利润最大?最大利润是多少万元?y日销售量(万件)4020 t(天)21.(10分)如图,双曲线x ky =与直线x =k 相交于点P ,过点P 作PA ⊥y 轴于A ,y 轴上的点A 1、A 2、A 3……A n 的坐标是连续整数,分别过A 1、A 2……A n 作x 轴的平行线于双曲线x ky =(x >0)及直线x =k 分别交于点B 1、B 2,……B n ,C 1、C 2,……Cn.(1)求A 的坐标;(2)求1111B A B C 及2222B A B C 的值;(3)猜想AnBn CnBn的值(直接写答案).22.(10分)如图,在梯形ABCD中,AB∥DC,∠ABC=90°,AB=2,BC=4,tan∠ADC=2.(1)求证:DC=BC;(2)E是梯形内一点,连接DE、CE,将△DCE绕点C顺时针旋转90°,得△BCF,连接EF.判断EF与CE的数量关系,并证明你的结论;(3)在(2)的条件下,当CE=2BE,∠BEC=135°时,求cos∠BFE的值.A BEFCD23. (11分)已知:抛物线c bx ax y ++=2(a ≠0)的顶点M 的坐标为(1,-2)与y 轴交于点C (0,23-),与x 轴交于A 、B 两点(A在B 的左边).(1)求此抛物线的表达式;(2)点P 是线段OB 上一动点(不与点B 重合),点Q 在线段BM 上移动且∠MPQ =45°,设线段OP =x ,MQ =y221,求y 1与x 的函数关系式,并写出自变量x 的取值范围;(3)①在(2)的条件下是否存在点P ,使△PQB 是PB 为底的等腰三角形,若存在试求点Q 的坐标,若不存在说明理由;②在(1)中抛物线的对称轴上是否存在点F ,使△BMF 是等腰三角形,若存在直接写出所有满足条件的点F 的坐标.x2013中考数学模拟试题参考答案一、选择题(每小题3分,共18分)1. B2.C3.B4.C5.C6.D 二、填空题(每题3分,共27分)7. (m- 1)2 8. 1 9. 二、四 10. 8π 11. 30° 12. 232-或232+13. 5 14.-1 15. 625三、解答题(本大题共8个小题,计75分)16. 解:由A =B 得:6212-=-x xx………………………2分方程两边同乘以)6)(2(2--x x 得: )2(62-=-x x x解得:x =3………………………6分当x =3时,方程左边=1231=-右边=16332=-∴左边=右边∴当x =3时,A 与B 的值相等………………………8分17. 答案:MN =AM +BN ………………………1分证明:∵CA ⊥CB∴∠ACM +∠BCN = 900 又∵BN ⊥l 于N , ∴ ∠CBN + ∠BCN = 900∴ ∠ACM =∠CBN ………………………3分 又∵∠AMC =∠BNC =900,AC =BC ,∴ △AMC ≌△CNB ………………………6分 ∴AM =CN ,BN =CM , ………………………8分 ∴MN =AM +BN ………………………9分18. 解:(1)13.2,13.4 ………………………1分 (2)小华第四次成绩最好是13.2秒;小敏第三次成绩最好是13.1秒; (2)分(3)3.13)3.132.133.134.133.13(51=++++=小华x (秒) (3)分3.13)3.135.131.134.132.13(51=++++=小敏x (秒) ………………4分小华极差为:13.4-13.2=0.2(秒) 小敏极差为:13.5-13. 1=0.4(秒) ………………5分004.0)01.001.0(512=+=小华S02.0)04.004.001.001.0(512=+++=小敏S ………………8分他们成绩平均数相同,小敏成绩的极差和方差都比小华大,因此小华较稳定,小敏有潜力. ………………9分 19.(1) ∵AD ∥BC ,∴∠CBD = ∠ADB . ∵∠BOP =∠DOE ,∴△BOP ∽△DOE . ………………………………3分 (2)2;3 ………………………………5分 (3)当PB =4时,四边形ABPE 是等腰梯形. ………………6分证明:∵AD ∥BC 即DE ∥PC ,∴当PC =DE =2,即PB =BC -PC =4时,四边形PCDE 是平行四边形, ∴PE =CD .又∵AB =CD , ∴PE =AB .∵AE ∥PB 且AE 与PB 不相等,∴四边形ABPE 是等腰梯形. ………………………………9分20. 解:(1)①当0<t ≤30时,y =2t ,当30<t ≤40时,y =-6t +240 ………………2分 (2)设该公司的日销售利润为Z 万元 ①当0<t ≤20时,Z =y ·w =2t ×(3t )=6t 2当t =20时,Z最大=2400(万元) ………………4分②当20≤t ≤30时Z =2t ×60=120t当t =30时,Z最大=3600(万元) ………………6分③当30≤t ≤40时Z =(-6t +240)×60=-360t +14400∵-360<0 ∴当t =30时,Z 最大=-360×30+14400=3600(万元) …………8分由∵2400<3600∴当上市第30天时,日销售利润最大,最大利润为3600万元. ………………9分21. 解:(1)在)0(>x x ky中当x =k 时,y =1,∵PA ⊥y 轴于A ,∴A 点坐标为(0,1).………………………………2分 (2)∵A 1、A 2…A n 的坐标为连续整数, ∴A 1为(0,2),A 2(0,3).∴B 1为(2,2k ),C 1(k ,2),B 2(33,k ),C 2(k ,3).∴A 1B 1=2k ,B 1C 1=2k ,C 2B 2=32k,A 2B 2=3k ,∴11111=B A B C ,22222=B A B C . …………………………6分(3)提示:A n 为(0,n +1)∴B n 为(11++n n k,),C n (k ,n +1), ∴A n B n =1+n k ,B n C n =kn nn k k 11+=+-, ∴nn k kn nB A BC nn n n =++=11. …………………………10分22. (1)证明:作AP ⊥DC 于点P .∵AB ∥CD ,∠ABC =90°,∴四边形APCB 是矩形,………………………………1分 ∴PC =AB =2,AP =BC =4.在Rt △ADP 中,tan ∠ADC =DP AP 即DP AP=2,∴DP =2,∴DC =DP +PC =4=BC .…………………………3分 (2)EF =2CE .………………………4分 证明如下:由△DCE 绕点C 顺时针旋转90°得△BCF , ∴CF =CE ,∠ECF =90°,∴EF =CE CE CF 222=+. …………………………6分(3)由(2)得∠CEF =45°. ∵∠BEC =135°,∴∠BEF =90°. ………………………………7分 设BE =a ,则CE =2a ,由EF =2CE ,则EF =a 22 在Rt △BEF 中,由勾股定理得:BF =3a ,∴COS ∠BFE =322=BFEF . ……………………10分 23. 解:(1)∵抛物线的顶点为M (1,﹣2)可设2)1(2--=x a y , 由点(0,23-)得:232-=-a ∴21=a . ∴2)1(212--=x y 即23212--=x x y . ……………………3分 (2)在23212--=x x y 中由y =0得023212=--x x解得:11-=x ,32=x∴A 为(-1,0),B 为(3,0) ……………………4分 ∵M (1,-2)∴∠MBO =45°,MB =22 ∴∠MPQ =45° ∠MBO =∠MPQ 又∵∠M =∠M∴△MPQ ∽△MPB ……………………5分∴MP MQMB MP = ∴MQ MB MP ·2= 即12222·22)1(2y x =-+ ∴2)1(2121+-=x y (0≤x <3).…………………………7分(自变量取值范围1分)(3)①存在点Q ,使QP =QB ,即△PQB 是以PB 为底的等腰三角形,作PB 的垂直平分线交BM 于Q ,则QP =QB . ∴∠QPB =∠MBP =45° 又∵∠MPQ =45°, ∴此时MP ⊥x 轴 ∴P 为(1,0),∴PB =2.∴Q 的坐标为(2,1). …………………………9分②F 1(1,0),F 2(1,222+-),F 3(1,222--),F 4(1,2). (11)分。
2012年九年级模拟考试(二)

2012年九年级模拟考试(二) 数学参考答案及评分标准一、选择题:题号12 3 4 5 6 7 8 9 10 11 12 13 14 15 答案 CBBDCCBBCBAACCB二、填空题:16.-1 17.-3 18.1 19.2 5 20.(121n --, 12n -)三、解答题 21.(1)原式1351622=++-= …………………………………………4分 (2)解 化简:0762=+-x x ………………………………………………2分得:231+=x ,232-=x ………………………………………4分22.作图题答案:23.猜想:BE=EC ,BE ⊥EC 2分 证明: ∵AC=2AB ,点D 是AC 的中点∴AB=AD=CD∵∠EAD=∠EDA=45° ∴∠EAB=∠EDC=135° ∵EA=ED∴△EAB ≌△EDC 5分 ∴∠AEB=∠DEC ,EB=EC ∴∠BEC=∠AED=90°∴BE=EC ,BE ⊥EC 8分24.(本题8分)解: ⑴ 2 ┄┄1分⑵ 64 ┄┄2分⑶依题得第四组的频数是2,第五组的频数也是2,设第四的2名学生分别为1A 、2A 第五组的2名学生为1B 、2B ,列表(或画树状图)如下,A1 A2 B1B2A1--A1、A2 A1、B1 A1、B2A2 A2、A1--A2、B1 A2、B2 B1 B1、A1 B1、A2--B1、B2┄┄6分由上表可知共有12种结果,其中两个都是90分以上的有两种结果,所以恰好都是在90分以上的概率为61┄┄8分 25.解:(1)设二次函数的解析式为y =ax 2+bx +c ∵二次函数的图象经过点(0,3),(-3,0),(2, -5) c =3∴ 9a —3b +c =0…………………………………………………2分4a +2b +c =-5解得a =-1,b =-2,c =3,y =-x 2-2x +3 …………………………………………………4分(2)∵-(-2)2-2×(-2)+3=-4+4+3=3∴点P (-2,3)在这个二次函数的图象上…………………………6分 ∵-x 2-2x +3=0∴x 1=-3,x 2=1 ∴与轴的交点为:(-3,0),(1,0)…………7分 S △P AB =12 ×4×3=6 …………………………………………………8分26.(本题满分9分)(1)解:(1)△P 1OA 1的面积将逐渐减小. …………………………………2分 (2)作P 1C⊥OA 1,垂足为C ,因为△P 1O A 1为等边三角形,所以OC=1,P 1C=3,所以P 1)3,1(. ……………………………………3分代入xky =,得k=3,所以反比例函数的解析式为x y 3=. ……………4分作P 2D ⊥A 1 A 2,垂足为D 、设A 1D=a ,则OD=2+a ,P 2D=3a ,所以P 2)3,2(a a +.……………………………………………………………6分代入xy 3=,得33)2(=⋅+a a ,化简得0122=-+a a 解的:a= -1±2 ……………………………………………7分B2 B2、A1 B2、A2 B2、B1 --∵a >0 ∴21+-=a ………………………………8分所以点A 2的坐标为﹙22,0﹚ ………………………………………………9分27.(本题满分10分)证明:(1)连接OD . ························ 1分D Q 是劣弧»AB 的中点,120AOB ∠=° 60AOD DOB ∴∠=∠=° ···················· 2分 又∵OA=OD ,OD=OB∴△AOD 和△DOB 都是等边三角形 ········ 4分 ∴AD=AO=OB=BD ∴四边形AOBD 是菱形 ························· 5分 (2)连接AC . ∵BP =3OB ,OA=OC=OB ∴PC=OC=OA ··················································································· 6分12060AOB AOC ∠=∴∠=Q °°OAC ∴△为等边三角形∴PC=AC=OC ··················································································· 7分 ∴∠CAP =∠CP A又∠ACO =∠CP A +∠CAP 30CAP ∴∠=°90PAO OAC CAP ∴∠=∠+∠=° ······················································· 9分 又OA Q 是半径AP ∴是O ⊙的切线··········································································· 10分28.(1)2;4; 2分 (2) 当0<t ≤611时(如图),求S 与t 的函数关系式是:S=EFGH S 矩形=(2t )2=4t 2; 4分 AB CH GP E F当611<t ≤65时(如图),求S 与t 的函数关系式是: S=EFGH S 矩形-S △HMN =4t 2-12×43×[2t-34(2-t )] 2=2524-t 2+112t -32; 6分当65<t ≤2时(如图),求S 与t 的函数关系式是: S= S △ARF -S △AQE =12×34(2+t ) 2 - 12×34(2-t ) 2=3t . 8分第27题图题(3)由(2)知:若0<t≤611,则当t=611时S最大,其最大值S=144121;9分若611<t≤65,则当t=65时S最大,其最大值S=185;10分若65<t≤2,则当t=2时S最大,其最大值S=6.11分综上所述,当t=2时S最大,最大面积是6.12分。
初三年级数学第三次模拟考试试卷2012至2013下

一、选择题:(每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题3分,共24分)1.-12的相反数是( )A .-12B .12C .2D .-22.下列运算正确的是( ) A .22523a a a =+B .22623a a a =⨯C .32623a a a =⋅D .()42263a a =3.在平面直角坐标系中P (-3,1)关于x 轴对称点的坐标是( ) A .(1,-3)B .(-3,1)C .(3,-1)D .(-3,-1)4.函数y=2x-1的图像不经过( ) A .第一象限B .第二象限C .第三象限D .第四象限5.下列图形既是轴对称又是中心对称图形的是( ) A .等边三角形B .平行四边形C .等腰梯形D .矩形6.如果三角形三边为a,b,c.则能构成三角形的a,b,c 为( ) A .3, 4, 5B .1, 2, 3C .2,2, 5D .3, 4, 77.已知一元二次方程0952=+-x x 根的情况是( )A .有两个不相等的实根B .有两个不相等的实根C .无实根 D.无法判断 8.若23-=x ,231+=y ,则x 与y 的关系是( )A .互为相反数B .互为倒数C .互为负倒数D .相等二、填空题:(每小题3分,共24分.只要求填写最后结果.)10.当x 时,分式xx 1+有意义. 11. 已知直角三角形两边长是3, 4,则第三边长为 .12.PM2.5是指大气中直径小于或等于0.0000025m 的颗粒物,将0.0000025用科学技术法表示为 .13.已知圆锥底面半径为3,高为4,则圆锥侧面积为 .(用π表示)17.(本题6分)计算:020132060sin 2)1()21()3(12⋅+-+---+-π.18.(本题6分) 解分式方程4822222-=-+++x x x x x19.(本题6分)解不等式组:⎪⎩⎪⎨⎧+<-≤--212235)1(21x x x20.(本题6分)如图,有两个质地均匀的转盘A,B,转盘A 被四等分,分别标有数字1,2,3,4;转盘B 被三等分,分别标有数字5, 6, 7.小强与小华用这两个转盘玩游戏,小强说:“随机转动A,B 转盘各一次,转盘停止后,将A,B 转盘的指针所指的数字相乘,积为偶数我赢,积为奇数你赢.” (1) 小强指定的游戏规则公平吗?通过计算说明理由. (2) 请你只在转盘B 上修改其中一个数字,使游戏公平.21.(本题6分)某厂生产一种产品,图①是该厂第一季度三个月产量的统计图,图②是这三个月的产量与第一季度总产量的比例分布统计图,统计员在制作图①,图②时漏填了部分数据.根据上述信息,回答下列问题:(1)该厂第一季度哪一个月的产量最高?月. (2)该厂一月份产量占第一季度总产量的 %.(3)该厂质检科从第一季度的产品中随机抽样,抽检结果发现样品的合格率为98%.请你估计:该厂第一季度大约生产了多少件合格的产品?(写出解答过程)22.(本题6分)如图,E,C 在BF 上,A B ∥DE,AB=DE,BE=CF,求证:∠A=∠D .四、综合解答题:(共36分.解答要写出必要的文字说明、证明过程或解答步骤.)图①图②三月 38%一月二月 32%23.(本题8分)如图:一次函数y=kx+b 的图像与反比例函数xmy 交于A(3,1),B(-1, n)两点. (1)求反比例函数和一次函数的解析式; (2)求△ABO 的面积.25.(本题满分10分)某公司为了开发新产品,用A,B 两种原料各360千克和290千克试制甲,乙两种新型产品共50件.(1)设生产甲种产品x 件求x 的取值范围.(2)若甲种产品每件成本为70元,乙种产品每件成本90元,设两种产品的成本总额为y 元,写出成本总额y (元)与甲种产品件数x (件)之间的函数关系式.当甲、乙两种产品各多少件时,产品的成本总额最少?求出最少成本总额.26.(本题满分10分)已知, 如图:抛物线c bx x y ++-=2与x 轴的两个交点分别为A(1,0),B(3,0). (1):求抛物线的解析式(2):设点P 在该抛物线上滑动,且满足条件1=∆PAB S 的点P 有几个?并求出所有点P 的坐标;(3):设抛物线交y轴于点C.问该抛物线对称轴上是否存在点M,使得△MAC的周长最小. 若存在,求出点M的坐标;若不存在,请说明理由.。
2012-2013中考数学模拟试题(附答案)s

2012-2013中考数学模拟测试题(考试时间120分钟,总分120分)第I 卷 (共24分)一、选择题(在每小题给出的四个选项中,只有一项符合题目要求,请选出并在答题卡上将该项涂黑,本大题共12个小题,每小题2分)1. 5的倒数是A .51B .51- C .-5 D .52.在函数12y x =-+中,自变量x 的取值范围是A .2x -≥B .2x -≤C .2x ≠-D .2x ≠3.解集在数轴上表示为如图所示的不等式组是A .32x x >-⎧⎨⎩≥B .32x x <-⎧⎨⎩≤C .32x x <-⎧⎨⎩≥D .32x x >-⎧⎨⎩≤4.下列几何图形中,一定是中心对称图形的有A . 1个B . 2个C . 3个D . 4个5.下列运算中,结果正确的是 A .444a a a += B .325a a a = C .824a a a ÷=D .236(2)6a a -=-6.直线y=x -1的图像经过象限是( )A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限7.如图,已知△ABC 的六个元素,则下列甲、乙、丙三个三角形中和△ABC 全等的图形是2 3-3题图a ac丙︒72︒50 乙︒50甲a︒507250︒︒︒58c ba CBAA 、甲乙B 、甲丙C 、乙丙D 乙8.为建设生态城市,我市某中学在植树节那天,组织初三年级八个班的学生到西城新区植树,各班植树情况如下表: 班级 一 二 三 四 五 六 七 八 合计 棵数1518222529141819160下列说法错误的是 A .这组数据的众数是18 B .这组数据的中位数是18.5C .这组数据的平均数是20D .以平均数20(棵)为标准评价这次植树活动中各班植树任务完成情况比较合理9.如图所示的一块长方体木头,想象沿虚线所示位置截下去所得到的截面图形是10.如图10-1所示,将长为20cm ,宽为2cm 的长方形白纸条,折成图1-2所示的图形并在其一面着色,则着色部分的面积为 A .234cm B .236cm C .238cm D .240cm图10-1 图10-211.把2010个边长为1的正方形排成如右图所示的图形,则这个图形的周长是 A .4020 B. 4022 C. 4024 D.4026 12.将抛物线122--=x y 向上平移若干个单位,使抛物线与坐标轴有三个交点,(第11题图)…ABCD(第9题图)如果这些交点能构成直角三角形,那么平移的距离为 A .23个单位 B .1个单位 C .21个单位 D .2个单位 第Ⅱ卷 (共96分)二、填空题(每题3分,共18分)13. 若分式12-x 与1互为相反数,则x 的值是 . 14.如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是 °15.如图,正方形ABCD 的边长为4cm ,正方形AEFG 的边长为1cm .如果正方形AEFG 绕点A 旋转,那么C 、F 两点之间的最小距离为 cm .16.三张完全相同的卡片上分别写有函数x y 2=、xy 3=、2x y =,从中随机抽取一张,则所得卡片上函数的图象在第一象限内y随x 的增大而增大的概率是 .17.直径AB 为6的半圆,绕A 点逆时针旋转60°,此时点B 到了点B ′,则图中阴影部分的面积是______________。
2012-2013x9数学模拟试卷
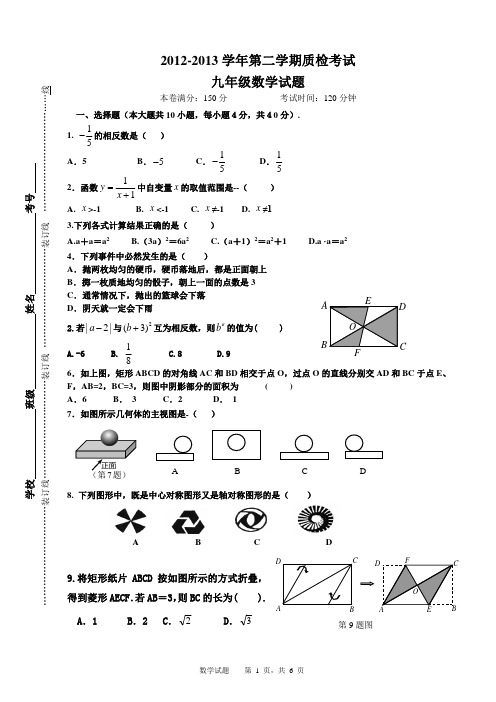
A B C2012-2013学年第二学期质检考试九年级数学试题本卷满分:150分 考试时间:120分钟一、选择题(本大题共10小题,每小题4分,共40分). 1. 15-的相反数是( ) A .5B .5-C .15-D .152.函数11+=x y 中自变量x 的取值范围是--( ) A. x >-1 B. x <-1 C. x ≠-1 D. x ≠13.下列各式计算结果正确的是( ) A.a +a =a 2 B.(3a )2=6a 2 C.(a +1)2=a 2+1 D.a ·a =a 2 4.下列事件中必然发生的是( )A .抛两枚均匀的硬币,硬币落地后,都是正面朝上B .掷一枚质地均匀的骰子,朝上一面的点数是3C .通常情况下,抛出的篮球会下落D .阴天就一定会下雨2.若|2|a -与2(3)b +互为相反数,则ab 的值为( )A.-6B. 18C.8D.96.如上图,矩形ABCD 的对角线AC 和BD 相交于点O ,过点O 的直线分别交AD 和BC 于点E 、F ,AB=2,BC=3,则图中阴影部分的面积为 ( ) A .6 B . 3 C .2 D . 1 7.如图所示几何体的主视图是-( )8. 下列图形中,既是中心对称图形又是轴对称图形的是( )A B C D9.将矩形纸片ABCD 按如图所示的方式折叠,得到菱形AECF .若AB =3,则BC 的长为( ).A .1B .2C .2D .3A B CDB第9题图10.如图2,边长为1的正三角形和边长为2的正方形在同一水平线上,正三角形沿水平线自左向右匀速穿过正方形。
下图反映了这个运动的全过程,设正三角形的运动时间为t ,正三角形与正方形的重叠部分面积为s ,则s 与t 的函数图象大致为A B C D 二、填空题(本大题共8小题,每小题3分,共24分). 11.计算:|-3|=_______.12.太阳半径大约是696000千米,用科学记数法表示为 _米.13.某学校有80名学生,参加音乐、美术、体育三个课外小组(每人只参加一项),这80人中若40%的人参加体育小组,35%的人参加美术小组,则参加音乐小组的有 人. 14. 分解因式:269ax ax a ++= 。
2012-2013学年九年级数学二次月考卷(含答题卡)

2012-2013学年九年级 第二次月考数学试卷(试卷满分为150分,考试时间为120分钟.)一、选择题(本大题共7小题,每小题4分,共28分)1、小明从上面观察下图所示的两个物体,看到的是( )2、关于x 的一元二次方程2(1)10a x x a -++-=的一个根为0,则实数a 的值为( ) A .1- B .0 C .1 D .1-或13、下列命题中,错误的是( )A.矩形的对角线互相平分且相等B.对角线互相垂直的四边形是菱形C.等腰梯形的两条对角线相等D.等腰三角形底边上的中点到两腰的距离相等 4、反比例函数y=xk与一次函数y=-kx+k 在同一直角坐标系中的图象大致是( )5、如图,在Rt △ABC 中,AB =AC ,AD ⊥BC ,垂足为D .E 、F 分别是CD 、AD 上的点,且CE =AF .如果∠AED =62º,那么∠DBF =( ) A .62º B .38º C .28º D .26º6、一个密闭不透明的盒子里有若干个白球,在不允许将球倒出来的情况下,为估计白球的个数,小刚向其中放入8个黑球,摇匀后从中随机摸出一个球记下颜色,再把它放回盒中,不断重复,共摸球400次,其中88次摸到黑球,估计盒中大约有白球( )A.28个 B.30个 C.36个 D.42个7、若点A (11x y ,)、B (22x y ,)、C (33x y ,)在反比例函数)(0k >=xk y 的图象上,且1230x x x >>>,则123y y y 、、的大小关系是( )A 、213y y y <<B 、321y y y <<C 、312y y y <<D 、123y y y << 二、填空题(本大题共8小题,每小题4分,共32分) 8、现有2类商品,每类商品各2件,其中有2件商品被损坏,求损坏的是不同类商品的概率_________.9、已知关于x 的一元二次方程01)12=++-x x m (有实数根,则m 的取值范围是 _____ 10、若反比例函数xky =的图象经过点(3,-4),则此函数在每一个象限内y 随x 的增大而 . 11、如图,在△ABC 中,BC = 8 cm ,AB 的垂直平分线交AB 于点D,交边AC 于点E ,△BCE 的周长等于18 cm ,则AC 的长等于 cm .12、如图,菱形ABCD 的对角线AC 、BD 相交于点O ,且AC=8,BD=6,过点O 作OH 丄AB ,垂足为H ,则点0到边AB 的距离OH= 13、双曲线1y 、2y 在第一象限的图像如图,14y x=,过1y 上的任意一点A ,作x 轴的平行线交2y 于B ,交y 轴于C ,若1AOB S ∆=,则2y 的解析式是 .14、如图,在矩形纸片ABCD 中,AB =2cm ,点E 在BC 上,且AE =CE .若将纸片沿AE 折叠,点B 恰好与AC 上的点B 1重合,则AC = cm .15、如图,在图(1)中,A 1、B 1、C 1分别是△ABC 的边BC 、CA 、AB 的中点,在图(2)中,A 2、B 2、C 2分别是△A 1B 1C 1的边B 1C 1、C 1 A 1、 A 1B 1的中点,…,按此规律,则第n 个图形中平行四边形的个数共有 个.三、解答题(共9小题,满分90分) 16、解方程(每小题4分,共8分)(1)3(3)x x x -=- (2)0122=-+x xD C AE 17、(8分)已知:如图,AB 、DE 是直立在地面上的两根立柱。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省商水杨氏英语学校2012-2013第二学期九年级数学模拟试题一、选择题(本题有10小题,每小题4分,共40分.每小题只有一个选项是正确的,不选、多选、错选,均不给分) 1.-3的相反数是( )A. 13- B13C. 3D. -32.不等式组431x x +>⎧⎨⎩≤的解集在数轴上可表示为( )3.下列运算正确的是 ( )A .523a a a =+B .632a a a =⋅C .22))((b a b a b a -=-+ D.222)(b a b a +=+ 4.下表是我市主要农产品总产量(单位:万吨)上述数据中中位数是( )A .81.42 B.68.25 C. 45.52 D. 54.45 5.下图所示的几何体的左视图是( )BCDA. B. C. D.6. 直线y=2x 与x 轴正半轴的夹角为α,那么下列结论正确的是( ) A. tan α=2 B. tan α=12C. sin α=2D. cos α=2 7.下列命题,正确的是( ) A.如果|a |=|b |,那么a=bB.C.D.相等的圆周角所对的弧相等8. 爷爷每天坚持体育锻炼,某天他慢跑离家到中山公园,打了一会儿太极拳后搭公交车回家。
下面能反映当天小华的爷爷离家的距离y 与时间x 的函数关系的大致图象是( )9. 在R t △ABC 中,∠C=90°,AC=8,BC=6,两等圆⊙A ,⊙B 外切,那么图中两个扇形(即阴影部分)的面积之和为( )A .258πB . 254πC .2516πD .2532π10.若实数x,y,z 满足2()4()()0x z x y y z ----=,则下列式子一定成立的是( )A.x+y+z=0B.x+y-2z=0 C y+z-2x=0 D z+x-2y=0二、填空题(本题有6小题。
每小题5分,共30分) 11.分解因式:x 2+x = .12.据报道: 2011年我国粮食产量达到640000000000千克,我们把它用科学记数法表示为:____ .(第9题)13.计算:11m nmn m +⨯=+ . 14.反比例函数xky =的图象经过点A (1,2),则该反比例函数的解析式为 .115.将量角器按如图所示的方式放置在三角形纸板上,使点C 在半圆上.点A 、B 的读数分别为86°、30°,则∠ACB 的大小为 .(15题)16.如图,已知菱形ABCD 的边AB=10,对角线BD=12,BD 边上有2012个不同的点122012,,,p p p ⋯,过(1,2,i p i =⋯,2012)作i i PE AB ⊥于i E ,i i PF AD ⊥于i F ,则111122222012201220122012PE PF P E P F P E P F ++++⋯++的值为______三、解答题(本题有8小题,共80分) 17.(本题l0分)(1)计算:011tan 45()12-+-.(2) 解方程: 210x -=18.(本题6分) 如图,已知AD 是△ABC 的角平分线,在不添加任何辅助线的前提下,要使△AE D ≌△AFD ,需添加一个条件是:_______________,并给予证明.19.(本题8分) 在一个口袋中有5个小球,这些球的形状、大小,质地等完全相同,现把它们写上标号:其中两个的标号都为1,其余三个的标号分别为2,3,4.(1)在看不到球的情况下,从袋中随机地取出一个球,BD C A EF第16题D求取到标号为1的球的概率;(2)随机地取出一个小球后不放回,再随机地取出一个小球,求第二次取出小球的标号大于第一次取出小球标号的概率(请画出树状图或列表解释) 20.(本题10分) 如图,在平面直角坐标系中,点A (0,8),点B (6,8). (1)只用直尺(没有刻度)和圆规,求作一个点P ,使点P 同时满足下列两个条件(要求保留作图痕迹,不必写出作法)①点p 到A ,B 两点的距离相等; ②点P 到∠xoy 的两边的距离相等. (2)直接写出点P 的坐标.21. (本题l0分)如图,在平面直角坐标系中,一次函数y=-2x 的图像与反比例函数ky x=的图像的一个交点为A (-1,n ). (1) 求反比例函数ky x=的解析式; (2) 若P 是坐标轴上的一点,且满足PA=0A ,直接写出P 的坐标.22.(本题l0分) 近期温州哄哄烈烈的展开了六城联创活动,抱着我为文明温州出一份力的想法,小华就公众对在餐厅吸烟的态度进行了随机抽样调查,主要有四种态度:A .顾客出面制止;B .劝说进吸烟室;C .餐厅老板出面制止;D .无所谓.他将调查结果绘制了两幅不完整的统计图.请你根据图中的信息回答下列问题:(1)这次抽样的公众有__________人;(2)请将统计图①补充完整;(3)在统计图②中,“无所谓”部分所对应的圆心角是多少度?(4)若温州全市人口有800万人,估计赞成“餐厅老板出面制止”的有多少万人?并根据统计信息,谈谈自己的感想.(不超过30个字)图①图②23.(本题l2分) 为实现区域教育均衡发展,我市计划对某县A、B两类薄弱学校全部进行改造,根据预算,共需资金1575万元,改造一所A类学校和两所B类学校共需资金230万元;改造两所A类学校和一所B类学校共需资金205万元.(1)改造一所A类学校和一所B类学校所需的资金分别是多少万元?(2)我市计划今年对该县A、B两类学校共6所进行改造,改造资金由国家财政和地方财政共同承担。
若今年国家财政拨付的改造资金不超过400万元;地方财政投入的改造资金不少于70万元,其中地方财政投入到A、B两类学校的改造资金分别为每所10万元和15万元。
请你通过计算求出有几种改造方案?24.(本题l4分) 如图①,OABC 是一张放在平面直角坐标系中的矩形纸片,O 为原点,点A 在x 轴的正半轴上,点C 在y 轴的正半轴上,OA =5,OC =4.(1)在OC 边上取一点D ,将纸片沿AD 翻折,使点O 落在BC 边上的点E 处,求D 、E 两点的坐标;(2)如图②,若AE 上有一动点P (不与A 、E 重合)自A 点沿AE 方向向E 点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为秒)50(<<t ,过P 点作ED 的平行线交AD 于点M ,过点M 作AE 的平行线交DE 于点N .求四边形PMNE 的面积S 与时间之间的函数关系式;当取何值时,S 有最大值?最大值是多少?(3)在(2)的条件下,当为何值时,以A 、M 、E 为顶点的三角形为等腰三角形,并求出相应时刻点M 的坐标.答案一、选择题(本题有10小题,每小题4分,共40分。
每小题只有一个选项是正确的,不选、多选、错选-均不给分)二、填空题(本题有6小题。
每小题5分,共30分) 11.x(x+1) 12.6.4×101113.m 14. 2y x15.28度 16.19315.2三、解答题(本题有8小题,共80分) 17.(本题l0分)(1)解:原式=1+2-1…………………………………………………………………… 3分=2…………………………………………………………………………2分(2)解:因式分解 得(x-1)(x+1)=0………………………………………………………2分∴x-1=0,x+1=0……………………………………………………2分∴x=1或x=-1………………………………………………………1分18.(本题6分)解法一:添加条件:AE =AF , ……2分证明:在△AED 与△AFD 中,∵AE =AF ,……1分B D CAEF∠EAD=∠FAD,……1分AD=AD,……1分∴△AED≌△AFD(SAS). ……1分解法二:添加条件:∠EDA=∠FDA,……2分证明:在△AED与△AFD中,∵∠EAD=∠FAD,……1分AD=AD,……1分∠EDA=∠FDA,……1分∴△AED≌△AFD(ASA). ……1分解法三:添加条件:∠DEA=∠DFA略……6分19.(本题8分)(1)取到标号为1的球的概率为25………………………………4分(2)第二次取出小球标号大于第一次取出小球标号的概率为920……4分20.(本题10分)(1)作图正确6分(2)点P坐标为(3,3)……4分21.(本题l0分)(1)∵点A(-1,n)在一次函数y=-2x图像上,∴n=-2×(-1)=2……………2分∴点A坐标为(-1,2)……1分∵点A 在反比例函数ky x=图像上 ∴ 21k=- 即 k=-2…………2分 ∴反比例函数解析式为2y x=-……1分 (2)点P 坐标为(-2,0)或(0,4)……4分22.(本题l0分)解:(1)200;……2分(2)200-20-110-10=60,补全统计图如下: ……3分60(3)18;……2分 (4)240. ……2分感想略. ……1分23.(本题l2分)(1)解:设改造一所A 类和一所B 类学校所需资金分别为x 万元和y 万元由题意得22302205x y x y +=+={…………………………4分解得6085x y =={……………………………………………2分答:改造一所A 类学校和一所B 类学校所需资金分别为60万元和85万元。
(2)设今年改造A 类学校x 所,则改造B 类学校(6-x )所,由题意得:5070(6)4001015(6)70x x x x +-≤+-≥{…………………………4分解得 14x ≤≤ ∵x 取整数 ∴ x=1,2,3,4.即共有四种方案……………………………………………2分24.(本题l4分)解:(1)依题意可知,折痕AD 是四边形OAED 的对称轴,∴在ABE Rt ∆中,45===AB AO AE , ∴3452222=-=-=AB AE BE ∴2=CE∴E 点坐标为)4,2(………………………………………………………(1分)在DCE Rt ∆中,222DE CE DC =+ 又∵OD DE =∴2222)4(OD OD =+- 解得:25=OD ∴D 点坐标为)25,0(………………………………………………………(2分)(2)如图①∵PM ∥ED ∴∽APM ∆AED ∆ ∴AE AP ED PM = 又知525==AE ED t AP ,=, ∴2255t t PM =⨯=又∵t PE -=5 而显然四边形PMNE 为矩形∴t t t t PE PM S PMNE 2521)5(22+-=-⨯=⋅=矩形…………………(3分)∴825)25(212+--=t S PMNE 矩形 又∵5250<< ∴当25=t 时,PMNE S 矩形有最大值825(面积单位)…………………(1分)(3)(i )若MA ME =(如图①)MA ME =,,AE PM ⊥ ∴P 为AE 的中点, ∴M 为AD 的中点 ∴2521==AE AP ∴25==t AP ∴4521==t PM 又∵P 与F 是关于AD 对称的两点 ∴25=M x ,45=M y∴当25=t 时(5250<<),AME ∆为等腰三角形 此时M 点坐标为)45,25(………………………………………………(3分)(ii )若5==AE AM (如图②)中,5255)25(2222=+=+=AO OD AD ∵PM ∥ED ,∴∽APM ∆AED ∆,∴AD AM AE AP = ∴5252555=⨯=⋅==AD AE AM AP t ∴521==t PM 同理可知:525-=M x , 5=M y∴当52=t 时(5520<<),此时M 点坐标为)5525(,-……………………(3分)综合(i )、(ii )可知:25=t 或52=t 时,以A 、M 、E 为顶点的三角形为等腰三角形,相应M 点的坐标为)45,25(或)5525(,-………………………………………(1分)。
