2012年黑龙江省数据理论入门
2012年黑龙江省国民经济和社会发展统计公报

2012年黑龙江省国民经济和社会发展统计公报2012年,受国际金融危机的深度影响和中国经济发展阶段性特征的制约,世界经济持续低迷,国内经济下行压力加大,省委、省政府牢牢把握“稳中求进”的工作总基调,坚定不移地推进“八大经济区”和“十大工程”建设,加快“十大重点产业”发展,我省国民经济运行呈现缓中趋稳、稳中有升、结构优化、民生改善的良好态势。
一、综合经济实力显著增强。
初步核算,我省全年实现地区生产总值(GDP)13691.6亿元,按可比价格计算比上年增长10.0%。
其中,第一产业增加值2113.7亿元,增长6.5%;第二产业增加值6456.4亿元,增长10.2%;第三产业增加值5121.4亿元,增长10.7%。
三次产业结构为15.4:47.2:37.4,第一、二、三产业对GDP增长的贡献率分别为7.8%、51.9%和40.3%。
人均地区生产总值实现35711元,比上年增长9.9%。
从行业分类看,批发和零售业增长11.0%,金融业增长20.7%,房地产业增长9.1%。
市场物价涨幅平稳回落。
全年居民消费价格(CPI)比上年上涨3.2%,低于年初调控目标(3.5%左右)。
其中,城市上涨3.3%;农村上涨 2.9%。
从商品类别看,呈现“六升二降”:食品上涨5.5%(其中粮食价格上涨4.6%,肉禽及其制品价格上涨5.4%)、居住上涨3.9%、医疗保健和个人用品价格上涨2.5%、烟酒及用品上涨3.0%;衣着价格上涨2.8%、家庭设备用品及维修服务上涨1.7%,娱乐教育文化用品及服务下降0.1%、交通和通信下降0.5%。
商品零售价格比上年上涨2.2%,农产品生产资料价格上涨5.9%,固定资产投资价格上涨0.8%。
工业生产者购进价格下降1.2%,工业生产者出厂价格与上年持平。
就业形势持续好转。
全年城镇新增就业77.3万人,下岗职工失业再就业人员59.0万人,困难群体再就业人员28.0万人。
年末城镇登记失业率为4.15%,比调控目标低0.45个百分点。
2012数农大纲

2012 全国硕士研究生入学统一考试农学门类联考数学考试大纲农学门类联考数学是为高等院校和科研院所招收农学门类的硕士研究生而设置的选拔性考试。
其目的是科学、公平、有效地测试考生是否具备农学门类各专业大学本科阶段应具备的知识、能力和素养要求,评价的标准是高等学校农学学科优秀本科毕业生所能达到的及格或及格以上水平,以利于各高等院校和科研院所择优录取,确保硕士研究生的入学质量。
考查目标农学门类数学考试涵盖高等数学、线性代数、概率论与数理统计等公共基础课程。
要求考生比较系统地理解数学的基本概念和基本理论,掌握数学的基本方法,具备抽象思维能力、逻辑推理能力、空间想像能力、运算能力能力以及综合运用所学的知识分析问题和解决问题的能力。
考试形式和试卷结构同数学三考查内容高等数学一、函数、极限、连续考试内容函数的概念及表示法,函数的有界性、单调性、周期性和奇偶性,复合函数、反函数、分段函数和隐函数,基本初等函数的性质及其图形,初等函数,函数关系的建立数列极限与函数极限的定义及其性质,函数的左极限和右极限,无穷小量和无穷大量的概念及其关系,无穷小量的性质及及无穷小量的比较,极限的四则运算,极限存在的两个准则:单调有界准则和夹逼准则,两个重要极限:函数连续的概念,函数间断点的类型,初等函数的连续性,闭区间上连续函数的性质。
考试要求1.理解函数的概念,掌握函数的表示法,会建立应用问题的函数关系。
2.了解函数的有界性、单调性、周期性和奇偶性。
3.理解复合函数及分段函数的概念,了解反函数及隐函数的概念。
4.掌握基本初等函数的性质及其图形,了解初等函数的概念。
5.了解数列极限和函数极限(包括左极限和右极限)的概念6.了解极限的性质与极限存在的两个准则,掌握极限四则运算法则,掌握利用两个重要极限求极限的方法。
7.理解无穷小量的概念和基本性质,掌握无穷小量的比较方法,了解无穷大量的概念及其无穷小量的关系。
8.理解函数连续性的概念(含左连续和右连续),会判别函数间断点的类型。
2012年统计年鉴核算主要统计指标解释

主要统计指标解释国民总收入(GNI)即国民生产总值,指一个国家(或地区)所有常住单位在一定时期内收入初次分配的最终结果。
一国常住单位从事生产活动所创造的增加值在初次分配中主要分配给该国的常住单位,但也有一部分以生产税及进口税(扣除生产和进口补贴)、劳动者报酬和财产收入等形式分配给非常住单位;同时,国外生产所创造的增加值也有一部分以生产税及进口税(扣除生产和进口补贴)、劳动者报酬和财产收入等形式分配给该国的常住单位,从而产生了国民总收入的概念。
它等于国内生产总值加上来自国外的净要素收入。
与国内生产总值不同,国民总收入是个收入概念,而国内生产总值是个生产概念。
国内生产总值(GDP) 指按市场价格计算的一个国家(或地区)所有常住单位在一定时期内生产活动的最终成果。
国内生产总值有三种表现形态,即价值形态、收入形态和产品形态。
从价值形态看,它是所有常住单位在一定时期内生产的全部货物和服务价值超过同期中间投入的全部非固定资产货物和服务价值的差额,即所有常住单位的增加值之和;从收入形态看,它是所有常住单位在一定时期内创造并分配给常住单位和非常住单位的初次收入分配之和;从产品形态看,它是所有常住单位在一定时期内最终使用的货物和服务价值与货物和服务净出口价值之和。
在实际核算中,国内生产总值有三种计算方法,即生产法、收入法和支出法。
三种方法分别从不同的方面反映国内生产总值及其构成。
一个地区(省、市、县)在使用此指标时统一称地区或某省(市、县)生产总值。
三次产业是根据社会生产活动历史发展的顺序对产业结构的划分,产品直接取自自然界的部门称为第一产业,对初级产品进行再加工的部门称为第二产业,为生产和消费提供各种服务的部门称为第三产业。
它是世界上较为通用的产业结构分类,但各国的划分不尽一致。
我国的三次产业划分是:第一产业:农业(包括种植业、林业、牧业、渔业和农林牧渔服务业)。
第二产业:工业(包括采掘业,制造业,电力、煤气及水的生产和供应业)和建筑业。
2012年东北三省数学建模A题参考资料
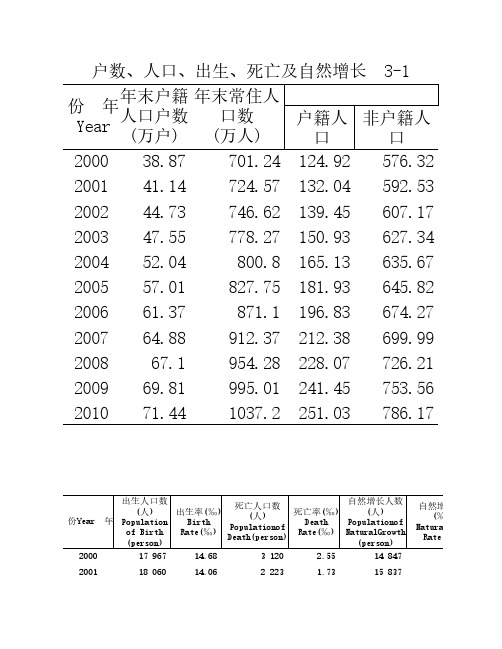
表4-3 深圳市各年龄组死亡率(1/万)
年龄组 (岁) 合计
015101520253035404550556065-
合计
6034 184 130 55 42 116 191 207 229 324 358 352 338 368 400 405
2009
男性
3644 106 69 36 29 78 122 128 150 227 244 249 224 252 258 240
神经病
1.63 6.52 0.03 0.88 0.00 0.13 0.05 0.57 1.37
循环系统疾 病
8.82 35.33
1.05 33.48
0.39 31.22
3.04 32.82
45.92
心脏病 3.9315.76 0.6922.03 0.2821.94 2.0321.95 28.91
脑血管病 4.8819.57 0.3611.45 0.12 9.29 1.0010.86 17.01
2003 47.55 778.27 150.93 627.34
2004 52.04
800.8 165.13 635.67
2005 57.01 827.75 181.93 645.82
2006 61.37
871.1 196.83 674.27
2007 64.88 912.37 212.38 699.99
传染病、寄 生虫病
0.14 0.54
0.21 6.61
0.05 4.31
0.15 1.61
1.89
肿瘤
6.9227.72 0.9429.96 0.3023.82 2.2924.71 38.13
恶性肿瘤 6.9227.72 0.9429.96 0.3023.82 2.2624.43 38.08
2012年黑龙江省数据库入门入门

1、因为后序遍历栈中保留当前结点的祖先的信息,用一变量保存栈的最高栈顶指针,每当退栈时,栈顶指针高于保存最高栈顶指针的值时,则将该栈倒入辅助栈中,辅助栈始终保存最长路径长度上的结点,直至后序遍历完毕,则辅助栈中内容即为所求。
void LongestPath(BiTree bt)//求二叉树中的第一条最长路径长度{BiTree p=bt,l[],s[]; //l, s是栈,元素是二叉树结点指针,l中保留当前最长路径中的结点int i,top=0,tag[],longest=0;while(p || top>0){ while(p) {s[++top]=p;tag[top]=0; p=p->Lc;} //沿左分枝向下if(tag[top]==1) //当前结点的右分枝已遍历{if(!s[top]->Lc && !s[top]->Rc) //只有到叶子结点时,才查看路径长度if(top>longest) {for(i=1;i<=top;i++) l[i]=s[i]; longest=top; top--;}//保留当前最长路径到l栈,记住最高栈顶指针,退栈}else if(top>0) {tag[top]=1; p=s[top].Rc;} //沿右子分枝向下}//while(p!=null||top>0)}//结束LongestPath2、对二叉树的某层上的结点进行运算,采用队列结构按层次遍历最适宜。
int LeafKlevel(BiTree bt, int k) //求二叉树bt 的第k(k>1) 层上叶子结点个数{if(bt==null || k<1) return(0);BiTree p=bt,Q[]; //Q是队列,元素是二叉树结点指针,容量足够大int front=0,rear=1,leaf=0; //front 和rear是队头和队尾指针, leaf是叶子结点数int last=1,level=1; Q[1]=p; //last是二叉树同层最右结点的指针,level 是二叉树的层数while(front<=rear){p=Q[++front];if(level==k && !p->lchild && !p->rchild) leaf++; //叶子结点if(p->lchild) Q[++rear]=p->lchild; //左子女入队if(p->rchild) Q[++rear]=p->rchild; //右子女入队if(front==last) {level++; //二叉树同层最右结点已处理,层数增1last=rear; } //last移到指向下层最右一元素if(level>k) return (leaf); //层数大于k 后退出运行}//while }//结束LeafKLevel。
2012年全国数据库入门深入

if(i==start) printf(“\n”); else Print(i,start);break;}//if
}//Print voi来自 dfs(int v) {visited[v]=1;
for(j=1;j<=n;j++ )
if (g[v][j]!=0) //存在边(v,j)
1、设T是一棵满二叉树,编写一个将T的先序遍历序列转换为后序遍历序列的递归算法。
2、假设以邻接矩阵作为图的存储结构,编写算法判别在给定的有向图中是否存在一个简单有向回路,若存在,则以顶点序列的方式输出该回路(找到一条即可)。(注:图中不存在顶点到自己的弧)
有向图判断回路要比无向图复杂。利用深度优先遍历,将顶点分成三类:未访问;已访问但其邻接点未访问完;已访问且其邻接点已访问完。下面用0,1,2表示这三种状态。前面已提到,若dfs(v)结束前出现顶点u到v的回边,则图中必有包含顶点v和u的回路。对应程序中v的状态为1,而u是正访问的顶点,若我们找出u的下一邻接点的状态为1,就可以输出回路了。
若i=1,则S1是根,这时二叉树的左子树为空,右子树的结点数是m-1,则{S2,S3,…,Sm}和{P1,P2,…,Pm-1}可以唯一确定右子树,从而也确定了二叉树。
若i=m,则Sm是根,这时二叉树的右子树为空,左子树的结点数是m-1,则{S1,S2,…,Sm-1}和{P1,P2,…,Pm-1}唯一确定左子树,从而也确定了二叉树。
2012年黑龙江省重要数据加强

1、设有一个数组中存放了一个无序的关键序列K1、K2、…、Kn。
现要求将Kn放在将元素排序后的正确位置上,试编写实现该功能的算法,要求比较关键字的次数不超过n。
51. 借助于快速排序的算法思想,在一组无序的记录中查找给定关键字值等于key的记录。
设此组记录存放于数组r[l..h]中。
若查找成功,则输出该记录在r数组中的位置及其值,否则显示“not find”信息。
请编写出算法并简要说明算法思想。
2、设t是给定的一棵二叉树,下面的递归程序count(t)用于求得:二叉树t中具有非空的左,右两个儿子的结点个数N2;只有非空左儿子的个数NL;只有非空右儿子的结点个数NR和叶子结点个数N0。
N2、NL、NR、N0都是全局量,且在调用count(t)之前都置为0.typedef struct node{int data; struct node *lchild,*rchild;}node;int N2,NL,NR,N0;void count(node *t){if (t->lchild!=NULL) if (1)___ N2++; else NL++;else if (2)___ NR++; else (3)__ ;if(t->lchild!=NULL)(4)____; if (t->rchild!=NULL) (5)____;}26.树的先序非递归算法。
void example(b)btree *b;{ btree *stack[20], *p;int top;if (b!=null){ top=1; stack[top]=b;while (top>0){ p=stack[top]; top--;printf(“%d”,p->data);if (p->rchild!=null){(1)___; (2)___;}if (p->lchild!=null)(3)___; (4)__;}}}}3、请设计一个算法,要求该算法把二叉树的叶子结点按从左到右的顺序连成一个单链表,表头指针为head。
2012年全国基础数据要领

1、有一种简单的排序算法,叫做计数排序(count sorting)。
这种排序算法对一个待排序的表(用数组表示)进行排序,并将排序结果存放到另一个新的表中。
必须注意的是,表中所有待排序的关键码互不相同,计数排序算法针对表中的每个记录,扫描待排序的表一趟,统计表中有多少个记录的关键码比该记录的关键码小,假设针对某一个记录,统计出的计数值为c,那么,这个记录在新的有序表中的合适的存放位置即为c。
(1) (3分)给出适用于计数排序的数据表定义;(2) (7分)使用Pascal或C语言编写实现计数排序的算法;(3) (4分)对于有n个记录的表,关键码比较次数是多少?(4) (3分)与简单选择排序相比较,这种方法是否更好?为什么?2、请编写一个判别给定二叉树是否为二叉排序树的算法,设二叉树用llink-rlink法存储。
3、#define maxsize 栈空间容量void InOutS(int s[maxsize])//s是元素为整数的栈,本算法进行入栈和退栈操作。
{int top=0; //top为栈顶指针,定义top=0时为栈空。
for(i=1; i<=n; i++) //n个整数序列作处理。
{scanf(“%d”,&x); //从键盘读入整数序列。
if(x!=-1) // 读入的整数不等于-1时入栈。
if(top==maxsize-1){printf(“栈满\n”);exit(0);}else s[++top]=x; //x入栈。
else //读入的整数等于-1时退栈。
{if(top==0){printf(“栈空\n”);exit(0);}else printf(“出栈元素是%d\n”,s[top--]);}}}//算法结。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、假设以邻接矩阵作为图的存储结构,编写算法判别在给定的有向图中是否存在一个简单有向回路,若存在,则以顶点序列的方式输出该回路(找到一条即可)。
(注:图中不存在顶点到自己的弧)
有向图判断回路要比无向图复杂。
利用深度优先遍历,将顶点分成三类:未访问;已访问但其邻接点未访问完;已访问且其邻接点已访问完。
下面用0,1,2表示这三种状态。
前面已提到,若dfs(v)结束前出现顶点u到v的回边,则图中必有包含顶点v和u的回路。
对应程序中v的状态为1,而u是正访问的顶点,若我们找出u的下一邻接点的状态为1,就可以输出回路了。
void Print(int v,int start ) //输出从顶点start开始的回路。
{for(i=1;i<=n;i++)
if(g[v][i]!=0 && visited[i]==1 ) //若存在边(v,i),且顶点i的状态为1。
{printf(“%d”,v);
if(i==start) printf(“\n”); else Print(i,start);break;}//if
}//Print
void dfs(int v)
{visited[v]=1;
for(j=1;j<=n;j++ )
if (g[v][j]!=0) //存在边(v,j)
if (visited[j]!=1) {if (!visited[j]) dfs(j); }//if
else {cycle=1; Print(j,j);}
visited[v]=2;
}//dfs
void find_cycle() //判断是否有回路,有则输出邻接矩阵。
visited数组为全局变量。
{for (i=1;i<=n;i++) visited[i]=0;
for (i=1;i<=n;i++ ) if (!visited[i]) dfs(i);
}//find_cycle
2、假设以I和O分别表示入栈和出栈操作。
栈的初态和终态均为空,入栈和出栈的操作序列可表示为仅由I和O组成的序列,称可以操作的序列为合法序列,否则称为非法序列。
(15分)
(1)A和D是合法序列,B和C 是非法序列。
(2)设被判定的操作序列已存入一维数组A中。
int Judge(char A[])
//判断字符数组A中的输入输出序列是否是合法序列。
如是,返回true,否则返回false。
{i=0; //i为下标。
j=k=0; //j和k分别为I和字母O的的个数。
while(A[i]!=‘\0’) //当未到字符数组尾就作。
{switch(A[i])
{case‘I’: j++; break; //入栈次数增1。
case‘O’: k++; if(k>j){printf(“序列非法\n”);exit(0);}
}
i++; //不论A[i]是‘I’或‘O’,指针i均后移。
}
if(j!=k) {printf(“序列非法\n”);return(false);}
else {printf(“序列合法\n”);return(true);}
}//算法结束。
3、请编写一个判别给定二叉树是否为二叉排序树的算法,设二叉树用llink-rlink法存储。
4、(1)p->rchild (2)p->lchild (3)p->lchild (4)ADDQ(Q,p->lchild)
(5)ADDQ(Q,p->rchild)
25. (1)t->rchild!=null (2)t->rchild!=null (3)N0++ (4)count(t->lchild) (5)count(t->rchild)
26. .(1)top++ (2) stack[top]=p->rchild (3)top++ (4)stack[top]=p->lchild
27. (1)*ppos // 根结点(2)rpos=ipos (3)rpos–ipos (4)ipos (5)ppos+1。
