正方形 (中考题)
解析中考正方形问题

黄细 把 ・
解析申考正方形 问题
正 方 形 既是 一 种特 殊 的平 行 四边形 ,又 是一 种 特殊 的矩形 ,还 是 一种 特 殊 的菱形 . 近 年来 的 中考 中 ,经 常遇 到正 方 形 问题 . 答 在 解 它 们 ,应灵 活利 用 如下性 质 :
1 正方 形 的对边 平行 ,四条边 都相 等 : .
— —
c ( 果不 取 近似值 ). m 结
分 析 : AP Q周 长 等 于胎 + Q B B P + Q,B I Q= ,那 么应 先 求船 +
的最小 值.由点尸 是对 角 线/C 一 动点 ,B、Q 点 在对 角 线4C 同 4上 两 的
一
边 ,要 求船 + 的最小 值 ,应 在对 角 线AC 另一边 找 一 定点 ,使 即 的
’ .
B
Q
…
…
…
1 3i
船 + 可取得 最 小值 ,该最 小值 等 于DQ 即 的长.
‘
. 。
C 2 QI D= ,C = , ̄D Q 9 。 C =0,
_ ^ _ ^ _ _ _ _ _ _ _ _ — — ● ● 1 _ ^ _ _ _ _ _ _ 一
・
.
.
D = D+ Q = / Q VC C x 5.
2 正方 形 的 四个 角都 是直 角 : .
3 正方 形 的两 条对 角 线互 相 垂 直平 分 且相 等 ,每 一条 对角 线 平 . 分 一组 对 角且是 正方 形 的对称 轴 . 现举 例 如下 : 例 1 ( 0 9 四川省 达 州市 中考 试题 )如 图 ,在边 长为2 m的正 20 年 c 方 形AB D中 ,点 9 C 为B 边 的 中点 ,点P C 为对 角线4C 一 动点 ,连 接 上 P B、 ,则 AP Q 长 的最小 值 为 B 周
2019年中考数学专题复习27——正方形(含答案解析)

2019年中考数学专题复习27——正方形(含答案解析)一、选择题1. 如图,将正方形放在平面直角坐标系中,是原点,若点的坐标为,则点的坐标为2. 若正方形的周长为A. B. C. D.3.C. D.4. 如图,正方形和正方形中,点在上,,,于点,那么A. B. C. D.5. 如图,在正方形外侧,作等边三角形,,相交于点,则A. B. C. D.6. 如图,正方形的边长为,点在对角线上,且,,垂足为,则A. B. C. D.7. 如图,在边长为的正方形中,为上一点,连接.过点作,交于点,若,则A. B. C. D.8. 如图,正方形的边长为,在的延长线上,四边形也为正方形,则A. B. C. D.9. 如图所示,正方形的面积为,是等边三角形,点在正方形内,在对角线上有一点,使A. B. C. D.10. 如图,将个边长都为的正方形按如图所示摆放,点,,,分别是正方形的中心,则这A. B. C. D.二、填空题11. 如图,已知,相邻两条平行线间的距离都相等,如果正方形的四个顶点分别在四条直线上,与交于点,则与正方形的面积之比为.12. 如图,在正方形中,为对角线,点在边上,于点,连接,,的周长为,则的长为.13. 如图,边长为的正方形的对角线相交于点,过点的直线分别交,于,,则阴影部分的面积是.14. 如图,将边长为的正方形绕点顺时针旋转得到正方形,则点的旋转路径长为(结果保留).15. 如图,是正方形的一条对称轴,点是直线上的一个动点,当最小时,16. 处,沿角画线,将正方形纸片分成部分,则中间一块阴影部分的面积为.17. 如图,正方形的边长为,点是对角线、的交点,点是的中点,连接.过点作,垂足是,连接,则的长为.18. 正方形,,,,按如图所示的方式放置.点,,,,和点,,,,分别在直线和轴上,已知点,,则点的坐标是.19. 如图,在正方形中,点,,,分别在边,,,上,点,,都在对角线上,且四边形和均为正方形,则的值等于.20. 如图,正方形绕点逆时针旋转后得到正方形,与相交于点,延长交于点.若正方形边长为,则.三、解答题21. 如图5,正方形的边长为,是对角线,平分,.(1)求证:.(2)求的长.22. 如图,正方形中,点在对角线上,连接、.(1)求证:;(2)延长交于点,若,求的度数.23. 如图,在正方形中,等边三角形的顶点,分别在和上.(1)求证:;(2)若等边三角形的边长为,求正方形的周长.24. 如图,点是正方形对角线的延长线上任意一点,以线段为边作一个正方形,线段和相交于点.(1)求证:;(2)判断与的位置关系,并说明理由;25. 如图,在平行四边形中,对角线,交于点,是延长线上的点,且是等边三角形.(1)求证:四边形是菱形;(2)若,求证:四边形是正方形.26. 已知:如图,平行四边形中,是的中点,连接并延长,交的延长线于点.(1)求证:;(2)连接,,当时,四边形是正方形?请说明理由.27. 中,,,点为直线上一动点(点不与,重合),以为边在右侧作正方形,连接.(1)观察猜想如图1,当点在线段上时,①与的位置关系为:.②,,之间的数量关系为:;(将结论直接写在横线上)(2)数学思考如图2,当点在线段的延长线上时,结论①,②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.(3)拓展延伸如图3,当点在线段的延长线上时,延长交于点,连接.若已知,,请求出的长.28. 如图,已知是的角平分线,交与点,交与点.(1)求证:四边形是菱形;(2)当满足什么条件时,四边形是正方形?并说明理由.29. 如图,在中,,是边上一点,,,垂足分别是,,.(1)求证:;(2)若,求证:四边形是正方形.30. 在正方形中,对角线,交于点,点在线段上(不含点),,交于点,过点作,垂足为,交于点.(1)当点与点重合时(如图).求证:;(2)结合图,通过观察、测量、猜想:,并证明你的猜想;(3)把正方形改为菱形,其他条件不变(如图),若,,直接写出的值.答案第一部分1. C 【解析】如图,过点作于点.是正方形,易证,,,所以.2. C3. A ,边长为,面积为.4. A 【解析】提示:连接,,延长交于点.易证,,,.,.5. C【解析】,的角度可求,为的外角.6. C 【解析】连接交于.四边形为正方形,,,.又,,..7. C 【解析】.8. D 【解析】设正方形的边长为,则9. A 【解析】点关于的对称点为,连接于交于一点,即为满足条件的点,此时则.由正方形的面积为,可求出.10. B,已知两个正方形可得到一个阴影部分,则个这样的正方形重叠部分即为阴影部分的和.第二部分11.12.【解析】设,根据正方形的性质及题意知,由的周长为,得,根据勾股定理得,解得.13.14.15.【解析】连接,交于点,此时最小,.16.【解析】延长小正方形的一边,与大正方形的一边交于点,连接,为直角边长为的等腰直角三角形,,阴影正方形的边长,阴影正方形的面积为:.17.【解析】在上截取,连接.四边形是正方形,,,.中,,..在与中,.,..在中,,,..根据射影定理得:,则.解得:..,..在等腰直角中,,.18.【解析】点,且四边形,,为正方形,,,..的坐标是.【解析】连接,四边形和四边形是正方形,.由旋转的性质得:,,.在和中,.,,,,.在中,,,.第三部分21. (1)证明:,;平分故又在中,故则(2)正方形的边长为对角线由(1)得,22. (1)正方形中,为对角线上一点,,.,().(2)由全等可知,.在中,,在正方形中,,有.23. (1)四边形是正方形,,.是等边三角形,,,.,.(2)在中,.设正方形的边长为,则,解得.正方形的周长.24. (1)四边形,四边形都是正方形,,,..在和中..(2).,.,,,.25. (1)四边形是平行四边形,.是等边三角形,,即,四边形是菱形.(2)是等边三角形,.,.,,.四边形是菱形,,四边形是正方形.26. (1)四边形是平行四边形,.,.又,.(2)当时,四边形是正方形.,.又,四边形是平行四边形.,,.四边形是平行四边形,,..平行四边形是菱形.,,.菱形是正方形.27. (1)①垂直.正方形中,,,.在与中..,即.②.,.,.(2)①成立②不成立.正方形中,,,.在与中,., .,,..,即 .,.(3)过作于,过作于,于 .,,...由(2)证得,,四边形是正方形,, .,,,四边形是矩形., .,..在与中,., ., .,.是等腰直角三角形....28. (1),,,.四边形是平行四边形..又是的角平分线,..四边形是菱形.(2)由(1)知,四边形是菱形.当四边形是正方形时,,即,的时,四边形是正方形.29. (1),,,,,,,,,,垂足分别是,,,在和中,.(2),,,,是边上的高,,,,,,,,四边形是矩形,,矩形是正方形.30. (1)四边形是正方形,与重合,,.,,,...(2如图,过作交于,交于.,.,..,,.()..,,.,.又,().,即.,即.(3).【解析】如图,过作交于,交于.,,.由(2)同理可得:,.,..、为菱形对角线,,,.....。
中考数学阅读说理题专题训练(正方形为背景)
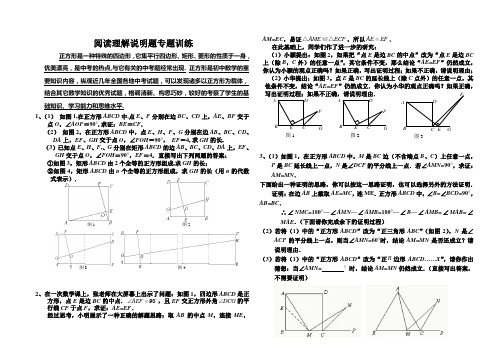
图 1 图2图 4 图3 ADF G B 图1 ADF G B 图2 ADFE B 图3阅读理解说明题专题训练正方形是一种特殊的四边形,它集平行四边形、矩形、菱形的性质于一身,优美漂亮,是中考的热点,与它有关的中考题经常出现. 正方形是初中数学的重要知识内容,纵观近几年全国各地中考试题,可以发现诸多以正方形为载体,结合其它数学知识的优秀试题,格调清新、构思巧妙,较好的考察了学生的基础知识、学习能力和思维水平.1、(1) 如图1,在正方形ABCD 中,点E 、F 分别在边BC 、CD 上,AE 、BF 交于点O ,∠AOF =90°.求证:BE =CF .(2) 如图2,在正方形ABCD 中,点E 、H 、F 、G 分别在边AB 、BC 、CD 、DA 上,EF 、GH 交于点O ,∠FOH =90°, EF =4.求GH 的长.(3)已知点E 、H 、F ,、G 分别在矩形ABCD 的边AB 、BC 、CD 、DA 上,EF 、GH 交于点O ,∠FOH =90°,EF =4. 直接写出下列两题的答案: ①如图3,矩形ABCD 由2个全等的正方形组成,求GH 的长;②如图4,矩形ABCD 由n 个全等的正方形组成,求GH 的长(用n 的代数式表示).2、在一次数学课上,张老师在大屏幕上出示了问题:如图1,四边形ABCD 是正方形,点E 是边BC 的中点.90AEF ∠=,且EF 交正方形外角DCG ∠的平行线CF 于点F ,求证:AE =EF .经过思考,小明展示了一种正确的解题思路:取AB 的中点M ,连接ME ,AM =EC ,易证AME ECF △≌△,所以AE EF =.在此基础上,同学们作了进一步的研究:(1)小颖提出:如图2,如果把“点E 是边BC 的中点”改为“点E 是边BC 上(除B ,C 外)的任意一点”,其它条件不变,那么结论“AE =EF ”仍然成立,你认为小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由; (2)小华提出:如图3,点E 是BC 的延长线上(除C 点外)的任意一点,其他条件不变,结论“AE =EF ”仍然成立.你认为小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.3、(1)如图1,在正方形ABCD 中,M 是BC 边(不含端点B 、C )上任意一点,P 是BC 延长线上一点,N 是∠DCP 的平分线上一点.若∠AMN =90°,求证:AM =MN .下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.证明:在边AB 上截取AE =MC ,连ME .正方形ABCD 中,∠B =∠BCD =90°,AB =BC .∴∠NMC =180°—∠AMN —∠AMB =180°—∠B —∠AMB =∠MAB =∠MAE .(下面请你完成余下的证明过程)(2)若将(1)中的“正方形ABCD ”改为“正三角形ABC ”(如图2),N 是∠ACP 的平分线上一点,则当∠AMN =60°时,结论AM =MN 是否还成立?请说明理由.(3)若将(1)中的“正方形ABCD ”改为“正n 边形ABCD ……X ”,请你作出猜想:当∠AMN =° 时,结论AM =MN 仍然成立.(直接写出答案,不需要证明)4、如图1,在正方形ABCD 中,E 是AB 上一点,F 是AD 延长线上一点,且DF=BE .(1)求证:CE =CF ;(2)在图1中,若G 在AD 上,且∠GCE =45°,则GE =BE +GD 成立吗?为什么? (3)运用(1)(2)解答中所积累的经验和知识,完成下题:如图2,在直角梯形ABCD 中,AD ∥BC (BC >AD ),∠B =90°,AB =BC =12,E 是AB 上一点,且∠DCE =45°,BE =4,求DE 的长.5、如图①,在正方形ABCD 中,E 、F 分别是BC 、CD 上的点,且∠EAF =45 °,则有结论EF =BE +FD 成立;(1)如图②,在四边形ABCD 中,AB =AD ,∠B =∠D =90°,E 、F 分别是BC 、CD 上的点,且∠EAF 是∠BAD 的一半,那么结论EF =BE +FD 是否仍然成立?若成立,请证明;若不成立,请说明理由;(2)若将(1)中的条件改为:在四边形ABCD 中,AB =AD ,∠B+∠D =180°,延长BC 到点E ,延长CD 到点F ,使得∠EAF 仍然是∠BAD 的一半,则结论EF =BE +FD 是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.6、已知正方形ABCD ,一等腰直角三角板的一个锐角顶点与A 重合,将此三角板绕A 点旋转时,两边分别交直线BC 、CD 于M 、N . (1)当M 、N 分别在边BC 、CD 上时(如图1),求证:BM +DN =MN ; (2)当M 、N 分别在边BC 、CD 所在的直线上时(如图2),线段BM 、DN 、MN 之间又有怎样的数量关系,请直接写出结论 ;(不用证明)(3)当M 、N 分别在边BC 、CD 所在的直线上时(如图3),线段BM 、DN 、MN 之间又有怎样的数量关系,请写出结论并写出证明过程.图1 图2B C A DE图25 - 4图25 - 3图25 - 2图25 -1D图①D 图② 图③ 图8-2图8-17、如图25-1,正方形ABCD 和正方形QMNP ,∠M =∠B ,M 是正方形ABCD 的对称中心,MN 交AB 于F ,QM 交AD 于E . ⑴求证:ME = MF .⑵如图25-2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME 与线段MF 的关系,并加以证明.⑶如图25-3,若将原题中的“正方形”改为“矩形”,且AB = m BC ,其他条件不变,探索线段ME 与线段MF 的关系,并说明理由.⑷根据前面的探索和图25-4,你能否将本题推广到一般的平行四边形情况?若能,写出推广命题;若不能,请说明理由.8、已知正方形ABCD 中,E 为对角线BD 上一点,过E 点作EF ⊥BD 交BC 于F ,连接DF ,G 为DF 中点,连接EG ,CG . (1)求证:EG =CG ;(2)将图①中△BEF 绕B 点逆时针旋转45º,如图②所示,取DF 中点G ,连接EG ,CG .问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)将图①中△BEF 绕B 点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论?(均不要求证明)9、如图8-1,已知P 为正方形ABCD 的对角线AC 上一点(不与A 、C 重合),PE ⊥BC 于点E ,PF ⊥CD 于点F. (1) 求证:BP=DP ;(2) 如图8-2,若四边形PECF 绕点C 按逆时针方向旋转,在旋转过程中是否总有BP=DP ?若是,请给予证明;若不是,请用反例加以说明;(3) 试选取正方形ABCD 的两个顶点,分别与四边形PECF 的两个顶点连结,使得到的两条线段在四边形PECF 绕点C 按逆时针方向旋转的过程中长度始终相等,并证明你的结论 .N M B E C DFG 图(1) 图(2) M B E AC DFGN10、如图(1),已知正方形ABCD 在直线MN 的上方,BC 在直线MN 上,E 是BC 上一点,以AE 为边在直线MN 的上方作正方形AEFG . (1)连接GD ,求证:△ADG ≌△ABE ;(2)连接FC ,观察并猜测∠FCN 的度数,并说明理由;(3)如图(2),将图(1)中正方形ABCD 改为矩形ABCD ,AB =a ,BC =b (a 、b 为常数),E 是线段BC 上一动点(不含端点B 、C ),以AE 为边在直线MN 的上方作矩形AEFG ,使顶点G 恰好落在射线CD 上.判断当点E 由B 向C 运动时,∠FCN 的大小是否总保持不变,若∠FCN 的大小不变,请用含a 、b 的代数式表示tan ∠FCN 的值;若∠FCN 的大小发生改变,请举例说明.11、已知, 正方形ABCD 和正方形CEFG .(1)如图①,B 、C 、E 在同一条直线上,点G 在CD 上,猜想:BG 与 DE 的数量关系为: ;BG 与DE 的位置关系是 .(2)如图②,B 、C 、E 不在同一条直线上,(1)的结论还成立吗?并说明理由. (3)若将原题中的正方形改为矩形,如图 ③且AB = a ,BC = b ,CE = ka ,CG =kb (a ≠b ,k >0) ,请你猜想:BG 与 DE 的数量关系,并证明.H① ② A DG FB C E③12、如图1,奖三角板放在正方形ABCD 上,使三角板的直角顶点E 与正方形ABCD的顶点A 重合,三角板的一边交CD 于点F ,另一边交CB 的延长线于点G .(1)求证:EF =EG ;(2)如图2,移动三角板,使顶点E 始终在正方形ABCD 的对角线AC 上,其他条件不变.(1)中的结论是否仍然成立?若成立,情给予证明;若不成立,请说明理由;(3)如图3,将(2)中的“ABCD ”改为“矩形ABCD ”,且使三角板的一边经过点B ,其他条件不变,若AB =a ,BC =b ,求EFEG 的值.图1 图2 图3A B C D GE F AE F G B D C13、正方形ABCD中,点O是对角线AC的中点,P为对角线AC上一动点,过点P作PF⊥DC于点F,如图1,当点P与点O重合时,显然有DF=CF.(1)如图2,若点P在线段AO上(不与A、O重合0,PE⊥PB且PE交CD 点E.①求证:DF=EF;②写出线段PC、PA、CE之间的一个等量关系式,并证明你的结论;(2)若点P在线段CA的延长线上,PE⊥PB且PE交直线CD于点E.请完成图3并判断(1)中的结论①、②是否成立?若不成立,写出相应的结论(所写结论均不必证明)14、数学课上,李老师出示了这样一道题目:如图1,正方形ABCD的边长为12,P为边BC延长线上的一点,E为DP的中点,DP的垂直平分线交边DC于M,交边AB的延长线于N.当CP=6时,EM与EN的比值是多少?经过思考,小明展示了一种正确的解题思路:过E作直线平行于BC交DC,AB分别于F,G,如图2,则可得:DFFC=DEEP,因为DE=EP,所以DF=FC.可求出EF和EG的值,进而可求得EM与EN的比值.(1) 请按照小明的思路写出求解过程.(2) 小东又对此题作了进一步探究,得出了DP=MN的结论.你认为小东的这个结论正确吗?如果正确,请给予证明;如果不正确,请说明理由.15、已知正方形ABCD的边长为a,两条对角线AC、BD相交于点O,P是射线AB上任意一点,过P点分别做直线AC、BD的垂线PE、PF,垂足为E、F.(1)如图1,当P点在线段AB上时,求PE+PF的值;(2)如图2,当P点在线段AB的延长线上时,求PE-PF的值.图1 图2A BCDHEFG图2E BFGD HAC图3图1ABCDH EFGA BCD E NQM O P 图2图3图4图1 ADE N Q M P16、以四边形ABCD 的边AB 、BC 、CD 、DA 为斜边分别向外侧作等腰直角三角形,直角顶点分别为E 、F 、G 、H ,顺次连结这四个点,得四边形EFGH . (1)如图1,当四边形ABCD 为正方形时,我们发现四边形EFGH 是正方形如图2,当四边形ABCD 为矩形时,请判断:四边形EFGH 的形状(不要 求证明);(2)如图3,当四边形ABCD 为一般平行四边形时,设∠ADC =α(0°<α<90°), ① 试用含α的代数式表示∠HAE ; ② 求证:HE =HG ;③ 四边形EFGH 是什么四边形?并说明理由.17、如图①,四边形ABCD 是正方形, 点G 是BC 上任意一点,DE ⊥AG 于点E ,BF ⊥AG 于点F . (1) 求证:DE -BF = EF .(2) 当点G 为BC 边中点时, 试探究线段EF 与GF 之间的数量关系, 并说明理由.(3) 若点G 为CB 延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE 、BF 、EF 之间的数量关系(不需要证明).18、在正方形ABCD 中,点E 是AD 上一动点, MN ⊥AB 分别交AB ,CD 于M ,N ,连结 BE 交MN 于点O ,过O 作OP ⊥BE 分别 交AB ,CD 于P ,Q . (1)如图1,当点E 在边AD 上时,通过测量猜测AE 与MP +NQ 之间的数量关系,并证 明你所猜测的结论;(2)如图2,若点E 在DA 的延长线上时,AE ,MP ,NQ 之间的数量关系又是怎样?请直接写出结论;(3)如图,连结BN 并延长,交AD 的延长线DG 于H ,若点E 分别在线段DH(如图3)和射线..HG (如图4)上时,请分别在图中画出符合题意的图形,并判 断AE ,MP ,NQ 之间的数量关系又分别..怎样?请直接写出结论.。
正方形与中考题

(2011青岛)如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,如此作下去,…,则所作的第n个正方形的面积S n= .解答:解:∵正方形ABCD的边长为1,∴AB=1,AC=,∴AE=AO1=,则:AO2=AB=,∴S2=,S3=,S4=,∴作的第n个正方形的面积S n=.故答案为:..(2011江西)某课题学习小组在一次活动中对三角形的内接正方形的有关问题进行了探讨:定义:如果一个正方形的四个顶点都在一个三角形的边上,那么我们就把这个正方形叫做三角形的内接正方形.结论:在探讨过程中,有三位同学得出如下结果:甲同学:在钝角、直角、不等边锐角三角形中分别存在个、个、个大小不同的内接正方形.乙同学:在直角三角形中,两个顶点都在斜边上的内接正方形的面积较大.丙同学:在不等边锐角三角形中,两个顶点都在较大边上的内接正方形的面积反而较小.任务:(1)填充甲同学结论中的数据;(2)乙同学的结果正确吗?若不正确,请举出一个反例并通过计算给予说明,若正确,请给出证明;(3)请你结合(2)的判定,推测丙同学的结论是否正确,并证明.解答:解:(1)1,2,3.(3分)(2)乙同学的结果不正确.(4分)例如:在Rt△ABC中,∠B=90°,AB=BC=1,则.如图①,四边形DEFB是只有一个顶点在斜边上的内接正方形.设它的边长为a,则依题意可得:,∴,如图②,四边形DEFH两个顶点都在斜边上的内接正方形.设它的边长为b,则依题意可得:,∴∴a>b.(3)丙同学的结论正确.设△ABC的三条边分别为a,b,c,不妨设a>b>c,三条边上的对应高分别为h a,h b,h c,内接正方形的边长分别为x a,x b,x c.依题意可得:=,∴x a=.同理x b=.∵x a﹣x b=﹣=﹣=2S(﹣)=(b+h b﹣a﹣h a).=(b+﹣a﹣).=•(b﹣a)(1﹣).=•(b﹣a)(1﹣).又∵b<a,h a<b,∴(b﹣a)(1﹣)<0,∴x a<x b,即x a2<x b2.∴在不等边锐角三角形中,两个顶点都在较大边上的内接正方形的面积反而较小.(10分)20.(2012齐齐哈尔)如图,在平面直角坐标系中有一边长为l 的正方形OABC ,边0A 、0C 分别在x 轴、y 轴上,如果以对角线OB 为边作第二个正方形OBB 1C 1,再以对角线OB l 为边作第三个正方形OB l B 2C 2,照此规律作下去,则点B 2012的坐标为。
2022年中考数学复习练习-正方形及中点四边形

课时训练(二十六) 正方形及中点四边形|夯实基础|1.根据下列条件,能判定一个四边形是正方形的是()A.对角线互相垂直且平分B.对角相等C.对角线互相垂直、平分且相等D.对角线相等2.[2022最新·滨州] 下列命题,其中是真命题的为()A.一组对边平行,另一组对边相等的四边形是平行四边形B.对角线互相垂直的四边形是菱形C.对角线相等的四边形是矩形D.一组邻边相等的矩形是正方形3.[2016·河北] 关于▱ABCD的叙述,正确的是()A.若AB⊥BC,则▱ABCD是菱形B.若AC⊥BD,则▱ABCD是正方形C.若AC=BD,则▱ABCD是矩形D.若AB=AD,则▱ABCD是正方形4.[2022最新·广安] 下列说法:①四边相等的四边形一定是菱形;②顺次连接矩形各边中点形成的四边形一定是正方形;③对角线相等的四边形一定是矩形;④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分.其中正确的个数是()A.4B.3C.2D.15.若顺次连接四边形ABCD四边的中点,得到的图形是一个矩形,则四边形ABCD一定是()A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形6.如图26-5,正方形ABCD的周长为28cm,点N在对角线BD上,则矩形MNGC的周长是()图26-5A.24cmB.14cmC.18cmD.7cm7.如图26-6,直线l过正方形ABCD的顶点B,点A,C到直线l的距离分别为1和3,则正方形ABCD的边长是()图26-6A.2√2B.3C.√10D.48.[2022最新·天津] 如图26-7,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是()图26-7A .AB B .DEC .BD D .AF9.[2022最新·枣庄] 如图26-8,把正方形纸片ABCD 沿对边中点所在的直线对折后展开,折痕为MN ,再过点B 折叠纸片,使点A 落在MN 上的点F 处,折痕为BE.若AB 的长为2,则FM 的长为()图26-8A .2B .√3C .√2D .110.[2022最新·泰安] 如图26-9,在正方形ABCD 中,M 为BC 上一点,ME ⊥AM ,ME 交AD 的延长线于点E.若AB=12,BM=5,则DE 的长为()图26-9A .18B .1095C .965D .25311.[2022最新·青岛] 如图26-10,已知正方形ABCD 的边长为5,点E ,F 分别在AD ,DC 上,AE=DF=2,BE 与AF 相交于点G ,H 为BF 的中点,连接GH ,则GH 的长为.图26-1012.[2022最新·德阳] 如图26-11,将边长为√3的正方形ABCD绕点B逆时针旋转30°得到正方形A'BC'D',那么图中阴影部分的面积为()图26-11A.3B.√3C.3-√3D.3-√3213.正方形的对角线长为2,则正方形的周长为,面积为.14.[2022最新·兰州] 在平行四边形ABCD中,对角线AC与DB相交于点O.要使四边形ABCD是正方形,还需添加一组条件.下面给出了四组条件:①AB⊥AD,且AB=AD;②AB=BD,且AB⊥BD;③OB=OC,且OB⊥OC;④AB=AD,且AC=BD.其中正确的是(填序号).15.[2015·无锡] 如图26-12,已知矩形ABCD的对角线长为8cm,E,F,G,H分别是AB,BC,CD,DA的中点,则四边形EFGH的周长等于cm.图26-1216.[2015·广安] 如图26-13,已知E,F,G,H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60°,则四边形EFGH的面积为cm2.图26-1317.[2022最新·宿迁] 如图26-14,正方形ABCD的边长为3,点E在边AB上,且BE=1.若点P在对角线BD上移动,则P A+PE的最小值是.图26-1418.[2022最新·包头样题二] 如图26-15,边长为6的大正方形中有两个小正方形,小正方形的顶点均在大正方形的边或对角线上.若两个小正方形的面积分别为S1,S2,则S1与S2的和为.图26-1519.[2022最新·常德] 如图26-16,正方形EFGH的顶点在边长为2的正方形ABCD的边上,若设AE=x,正方形EFGH 的面积为y,则y与x之间的函数关系式为(不必写出自变量的取值范围).图26-1620.[2022最新·白银] 如图26-17,已知矩形ABCD中,E是AD边上的一个动点,F,G,H分别是BC,BE,CE的中点.(1)求证:△BGF≌△FHC;(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.图26-1721.[2022最新·聊城] 如图26-18,在正方形ABCD中,E是BC上的一点,连接AE,过点B作BH⊥AE,垂足为H,延长BH交CD于点F,连接AF.(1)求证:AE=BF;(2)若正方形ABCD的边长是5,BE=2,求AF的长.图26-1822.[2022最新·潍坊] 如图26-19,M是正方形ABCD的边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.(1)求证:AE=BF;(2)已知AF=2,四边形ABED的面积为24,求∠EBF的正弦值.图26-1923.[2022最新·眉山] 如图26-20,E是正方形ABCD的边BC延长线上一点,连接DE,过顶点B作BF⊥DE,垂足为F,BF交AC于点H,交DC于点G.(1)求证:BG=DE;(2)若G为CD的中点,求HG的值.GF图26-20|拓展提升|24.[2022最新·包头样题一] 如图26-21,已知四边形ABCD 和四边形DEFG 为正方形,点E 在线段DC 上,点A ,D ,G 在同一条直线上,且AD=3,DE=1,连接CG ,AE ,并延长AE 交CG 于点H ,则EH 的长为()图26-21A .√105B .2√105C .3√55D .√55 25.[2022最新·台州] 如图26-22,在正方形ABCD 中,AB=3,点E ,F 分别在CD ,AD 上,CE=DF ,BE ,CF 相交于点G.若图中阴影部分的面积与正方形ABCD 的面积之比为2∶3,则△BCG 的周长为.图26-2226.[2022最新·青山区一模] 如图26-23,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC,DC 分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若AEAB =23,则3S△EDH=13S△DHC,其中正确的结论是(填序号).图26-2327.[2022最新·青山区二模] 如图26-24,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连接BD,DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH·PC.其中正确的是(填序号).图26-24参考答案1.C2.D3.C4.C[解析] 根据菱形的判定定理,四边相等的四边形一定是菱形,故①正确;由于矩形的对角线相等,根据三角形的中位线定理,可得顺次连接矩形各边中点所得四边形的四条边相等,由此可判定所得四边形是菱形,故②错误;对角线相等的平行四边形是矩形,故③错误;平行四边形是中心对称图形,根据中心对称图形的性质,经过对称中心的任意一条直线都把它分成两个全等形,面积当然相等,所以经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分,故④正确.综上所述,正确的说法有2个.故选C.5.D6.B7.C8.D[解析] 如图,取CD的中点E',连接AE',PE'.由正方形轴对称的性质可知EP=E'P,AF=AE',∴AP+EP=AP+E'P.∵AP+E'P≥AE',∴AP+EP的最小值是AE'的长,即AP+EP的最小值是AF的长.故选D.9.B[解析]∵四边形ABCD为正方形,AB=2,M,N分别为BC,AD的中点,过点B折叠纸片,使点A落在MN上的点F处,∴FB=AB=2,BM=1.在Rt△BMF中,FM=√BF2-BM2=√22-12=√3,故选B.10.B[解析] 在Rt△ABM中,根据勾股定理得AM=√AB2+BM2=√122+52=13,因为四边形ABCD为正方形,所以AD=AB=12.因为ME⊥AM,所以∠AME=90°,所以∠AME=∠MBA.因为AD∥BC,所以∠EAM=∠AMB,所以△ABM∽△EMA,所以BMAM =AMAE,即513=13AE,所以AE=1695,所以DE=AE-AD=1695-12=1095.11.√342[解析]∵四边形ABCD是正方形,∴AB=AD=BC=CD=5,∠BAD=∠D=∠C=90°.又∵AE=DF,∴△ABE≌△DAF,∴∠DAF=∠ABE ,∴∠ABE+∠BAG=∠DAF+∠BAG=90°,即∠BGF=90°.在Rt △BCF 中,CF=CD -DF=3,∴BF=√52+32=√34.在Rt △BGF 中,∵H 为BF 的中点,∴GH=12BF=√342.12.C[解析] 如图,连接AM.由旋转的性质可知∠1=∠4=30°,∴∠2+∠3=60°.在Rt △ABM 和Rt △C'BM 中,∵AB=C'B ,∴Rt △ABM ≌Rt △C'BM ,∴∠2=∠3=30°.在Rt △ABM 中,∵AB=√3,∠2=30°,∴AM=tan30°·AB=1.∴S △ABM =S △BMC'=√32,∴S 阴影=S 正方形A'BC'D'-(S △ABM +S △BMC')=3-√3.13.4√2214.①③④[解析]①有一个角是直角的平行四边形是矩形;有一组邻边相等的矩形是正方形,故①正确;②BD 为平行四边形的对角线,AB 为平行四边形的其中一条边,所以AB=BD 时,平行四边形不可能是正方形,故②错误; ③由OB=OC ,得AC=BD ,由OB ⊥OC 得AC ⊥BD ,∴▱ABCD 为正方形,故③正确;④由AB=AD ,得▱ABCD 为菱形.又∵AC=BD ,∴四边形ABCD 为正方形,故④正确.15.1616.9√317.√10[解析] 连接PC.根据正方形的对称性知P A=PC ,所以当点C ,P ,E 在同一条直线上时,P A+PE=PC+PE=CE 最小,根据勾股定理求得CE=√BC 2+BE 2=√32+12=√10.18.1719.y=2x 2-4x+4[解析] 由题中条件可知,图中的四个直角三角形是全等三角形,AE=x ,则AF=2-x.在Rt △EAF 中,由勾股定理可得EF 2=(2-x )2+x 2=2x 2-4x+4,即正方形EFGH 的面积y=2x 2-4x+4.20.解:(1)证明:∵F 是BC 边的中点,∴BF=FC.∵F ,G ,H 分别是BC ,BE ,CE 的中点,∴GF ,FH 是△BEC 的中位线,∴GF=HC ,FH=BG.在△BGF 和△FHC 中,{BF =FC ,BG =FH ,GF =HC ,∴△BGF ≌△FHC (SSS).(2)当四边形EGFH 是正方形时,∠BEC=90°,GF=GE=EH=FH.∵GF ,FH 是△BEC 的中位线,∴BE=CE ,∴△BEC 是等腰直角三角形.连接EF ,则EF ⊥BC ,EF=12BC=12AD=12a ,∴S 矩形ABCD =AD ·EF=a ·12a=12a 2.21.解:(1)证明:∵四边形ABCD 是正方形,∴AB=BC ,∠ABC=∠C=90°.∵BH ⊥AE ,垂足为H ,∴∠BAE+∠ABH=90°.∵∠CBF+∠ABH=90°,∴∠BAE=∠CBF .在△ABE 和△BCF 中,{∠ABE =∠C =90°,AB =BC ,∠BAE =∠CBF ,∴△ABE ≌△BCF (ASA),∴AE=BF .(2)∵△ABE ≌△BCF ,∴CF=BE=2.∵正方形的边长为5,∴AD=CD=5,∴DF=CD -CF=5-2=3.在Rt △ADF 中,AF=√AD 2+DF 2=√52+32=√34.22.解:(1)证明:∵四边形ABCD 为正方形,∴AB=AD ,∠BAD=90°,∴∠BAE+∠EAD=90°.∵BF ⊥AM ,DE ⊥AM ,∴∠DEA=∠AFB=90°,∴∠EAD+∠ADE=90°,∴∠BAE=∠ADE.∴△ABF ≌△DAE ,∴AE=BF .(2)设EF=x ,则AE=x+2,BF=AE=x+2.∵△ABF ≌△DAE ,∴S 四边形ABED =S △BEF +S △ABF +S △DAE =S △BEF +2S △ABF =24,即12x (x+2)+12×2(x+2)×2=24,解得x 1=4,x 2=-10(舍去),∴EF=4,BF=6,∴BE=√42+62=2√13,∴sin ∠EBF=EF BE =2√13=2√1313. 23.[解析](1)要证明BG=DE ,只需证明△BCG ≌△DCE ,利用AAS 或ASA 证明即可;(2)设正方形ABCD 的边长为a ,先求出BG 的长,从而得出CE ,DE 的长,分别利用△ABH ∽△CGH 和△DFG ∽△DCE ,得到HG 和GF 的长,从而求出HGGF 的值. 解:(1)证明:∵四边形ABCD 是正方形,∴BC=DC ,∠BCD=90°,∴∠DCE=180°-90°=90°,∴∠BCD=∠DCE ,∴∠CBG+∠BGC=90°.∵BF ⊥DE ,∴∠CBG+∠E=90°,∴∠BGC=∠E ,∴△BCG ≌△DCE ,∴BG=DE.(2)设正方形ABCD 的边长为a.∵G 为CD 的中点,∴CG=GD=12a.在Rt △BCG中,BG=√BC 2+CG 2=√a 2+(a 2)2=√52a. ∵△BCG ≌△DCE ,∴CE=CG=a 2,DE=BG=√52a.∵AB ∥DC ,∴△ABH ∽△CGH ,∴BH GH =AB CG =2,∴HG BG =13,∴HG=13BG=13×√52a=√56a. 又∵∠DFG=∠DCE=90°,∠FDG=∠CDE ,∴△DFG ∽△DCE ,∴GF EC =DG DE ,即GF 12a =12a √52a ,解得GF=√510a , ∴HG GF =√56a √510a =53. 24.A 25.3+√15[解析]∵在正方形ABCD 中,AB=3,∴S 正方形ABCD =32=9.∵阴影部分的面积与正方形ABCD 的面积之比为2∶3,∴空白部分的面积与正方形ABCD 的面积之比为1∶3,∴S 空白=3.∵四边形ABCD 是正方形,∴BC=CD ,∠BCE=∠CDF=90°.又∵CE=DF ,∴△BCE ≌△CDF (SAS),∴∠CBE=∠DCF .∵∠DCF+∠BCG=90°,∴∠CBE+∠BCG=90°,即∠BGC=90°,△BCG 是直角三角形.易知S △BCG =S 四边形FGED =32,∴S △BCG =12BG ·CG=32,∴BG ·CG=3.在Rt △BCG 中,根据勾股定理,得BG 2+CG 2=BC 2,即BG 2+CG 2=9,∴(BG+CG )2=BG 2+2BG ·CG+CG 2=9+2×3=15,∴BG+CG=√15,∴△BCG 的周长=BG+CG+BC=3+√15.26.①②③④[解析]∵四边形ABCD 为正方形,EF ∥AD ,∴EF=AD=DC ,∠ACD=45°,∠GFC=90°,∴△GFC 为等腰直角三角形,∴GF=CF ,∴EF -GF=DC -CF ,即EG=DF ,故①正确;∵△CFG 为等腰直角三角形,H 为CG 的中点,∴FH=CH ,∠EFH=∠DCH=45°.又∵EF=DC ,∴△EHF ≌△DHC ,故③正确;∵△EHF ≌△DHC ,∴∠FEH=∠CDH ,∴∠AEH+∠ADH=∠AEF+∠FEH+∠ADF -∠CDH=∠AEF+∠ADF=180°,故②正确;∵AE AB =23,∴AE=2BE.在△EGH 和△DFH 中,∵EG=DF ,∠EGH=∠DFH=135°,GH=FH ,∴△EGH ≌△DFH ,∴EH=DH,∠EHG=∠DHF,∴∠EHD=∠EHG+∠AHD=∠AHD+∠DHF=∠AHF=90°,∴△EHD是等腰直角三角形.DH2=13x2,过点H作HM⊥CD于点M,设HM=x,则DM=5x,CD=6x,DH=√26x,∴S△EDH=12S△DHC=1HM·CD=3x2,∴3S△EDH=13S△DHC,故④正确.227.①②④。
【精编版】中考数学专题训练——正方形的判定和性质

中考专题训练——正方形的判定和性质1.如图,在矩形ABCD中,点E,F分别在边AB,BC上,AF⊥DE,且AF=DE,AF与DE相交于点G.(1)求证:矩形ABCD为正方形:(2)若AE:EB=2:1,△AEG的面积为4,求四边形BEGF的面积.2.已知:如图,边长为4的菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.(1)求证:四边形ABCD是正方形.(2)E是OB上一点,BE=1,且DH⊥CE,垂足为H,DH与OC相交于点F,求线段OF的长.3.如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.(1)求证:∠HEA=∠CGF;(2)当AH=DG时,求证:菱形EFGH为正方形.4.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.5.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图②中补全图形,并说明理由.6.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.(1)求证:四边形MANP是正方形;(2)求证:EM=BN.7.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F 分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.8.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.9.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.10.如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的“对补点”.(1)如图1,正方形ABCD的对角线AC,BD交于点M,求证:点M是正方形ABCD 的对补点;(2)如图2,在平面直角坐标系中,正方形ABCD的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.11.已知:如图,E是正方形ABCD的对角线BD上的点,连接AE、CE.(1)求证:AE=CE;(2)若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.12.如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.(1)试判断四边形PQEF是否是正方形,并证明;(2)PE是否总过某一定点,并说明理由.13.在平面直角坐标系xOy中,OEFG为正方形,点F的坐标为(1,1).将一个最短边长大于的直角三角形纸片的直角顶点放在对角线FO上.(1)如图,当三角形纸片的直角顶点与点F重合,一条直角边落在直线FO上时,这个三角形纸片与正方形OEFG重叠部分(即阴影部分)的面积为;(2)若三角形纸片的直角顶点不与点O,F重合,且两条直角边与正方形相邻两边相交,当这个三角形纸片与正方形OEFG重叠部分的面积是正方形面积的一半时,试确定三角形纸片直角顶点的坐标(不要求写出求解过程),并画出此时的图形.14.(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.15.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图1,求证:矩形DEFG是正方形;(2)若AB=2,CE=,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.16.如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2,连接CF.(1)当DG=2时,求证:四边形EFGH是正方形;(2)当△FCG的面积为2时,求CG的值.17.已知,如图,矩形ABCD中,AD=6,DC=7,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.(1)若DG=2,求证四边形EFGH为正方形;(2)若DG=6,求△FCG的面积;(3)当DG为何值时,△FCG的面积最小.18.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.(1)∠EAF=°(直接写出结果不写解答过程);(2)①求证:四边形ABCD是正方形.②若BE=EC=3,求DF的长.(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是(直接写出结果不写解答过程).19.如图1,在正方形ABCD中,G为线段BD上一点,连接AG,过G作AG⊥GE交BC 于E,连接AE.(1)求证:BG=DG+BE;(2)如图2,AB=4,E为BC中点,P,Q分别为线段AB,AE上的动点,满足QE=AP,则在P,Q运动过程中,当以PQ为对角线的正方形PRQS的一边恰好落在△ABE 的某一边上时,直接写出正方形PRQS的面积.20.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=2,CE=2,求CG的长;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.参考答案;1.如图,在矩形ABCD中,点E,F分别在边AB,BC上,AF⊥DE,且AF=DE,AF与DE相交于点G.(1)求证:矩形ABCD为正方形:(2)若AE:EB=2:1,△AEG的面积为4,求四边形BEGF的面积.【分析】(1)根据矩形的性质得∠DAB=∠B=90°,由等角的余角相等可得∠ADE=∠BAF,利用AAS可得△ABF≌△DAE(AAS),由全等三角形的性质得AD=AB,即可得四边形ABCD是正方形;(2)根据相似三角形面积的比等于相似比的平方即可解决问题.【解答】(1)证明:∵四边形ABCD是矩形,∴∠DAB=∠B=90°,∵DE⊥AF,∴∠DAB=∠AGD=90°,∴∠BAF+∠DAF=90°,∠ADE+∠DAF=90°,∴∠BAF=∠ADE,在△ABF和△DAE中,,∴△ABF≌△DAE(AAS),∴AD=AB,∵四边形ABCD是矩形,∴四边形ABCD是正方形;(2)解:∵△ABF≌△DAE,∴BF=AE,∵AE:EB=2:1,设AE=2x,EB=x,∴BF=AE=2x,AB=3x,∴AF==x,∵∠EAG=∠F AB,∠AGE=∠B=90°,∴△AEG∽△AFB,∴△AEG的面积:△AFB的面积=AE2:AF2=4x2:13x2=4:13,∵△AEG的面积为4,∴△AFB的面积为13,∴四边形BEGF的面积=13﹣4=9.2.已知:如图,边长为4的菱形ABCD的对角线AC与BD相交于点O,若∠CAD=∠DBC.(1)求证:四边形ABCD是正方形.(2)E是OB上一点,BE=1,且DH⊥CE,垂足为H,DH与OC相交于点F,求线段OF的长.【分析】(1)由菱形的性质得出AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,得出∠BAD+∠ABC=180°,证出∠BAD=∠ABC,求出∠BAD=90°,即可得出结论;(2)由正方形的性质得出AC⊥BD,AC=BD,CO=AC,DO=BD,得出∠COB=∠DOC=90°,CO=DO,证出∠ECO=∠EDH,证明△ECO≌△FDO(ASA),即可得出结论.【解答】(1)证明:∵四边形ABCD是菱形,∴AD∥BC,∠BAD=2∠DAC,∠ABC=2∠DBC,∴∠BAD+∠ABC=180°,∵∠CAD=∠DBC,∴∠BAD=∠ABC,∴2∠BAD=180°,∴∠BAD=90°,∴四边形ABCD是正方形;(2)解:∵四边形ABCD是正方形,AB=BC=4,∴AC⊥BD,AC=BD=4,∴OB=CO=AC=2,DO=BD=2,∴∠COB=∠DOC=90°,CO=DO,∵DH⊥CE,垂足为H,∴∠DHE=90°,∠EDH+∠DEH=90°,∵∠ECO+∠DEH=90°,∴∠ECO=∠EDH,在△ECO和△FDO中,,∴△ECO≌△FDO(ASA),∴OE=OF.∵BE=1,∴OE=OF=OB﹣BE=2﹣1.3.如图,菱形EFGH的三个顶点E、G、H分别在正方形ABCD的边AB、CD、DA上,连接CF.(1)求证:∠HEA=∠CGF;(2)当AH=DG时,求证:菱形EFGH为正方形.【分析】(1)连接GE,根据正方形的性质和平行线的性质得到∠AEG=∠CGE,根据菱形的性质和平行线的性质得到∠HEG=∠FGE,解答即可;(2)证明Rt△HAE≌Rt△GDH,得到∠AHE=∠DGH,证明∠GHE=90°,根据正方形的判定定理证明.【解答】证明:(1)连接GE,∵AB∥CD,∴∠AEG=∠CGE,∵GF∥HE,∴∠HEG=∠FGE,∴∠HEA=∠CGF;(2)∵四边形ABCD是正方形,∴∠D=∠A=90°,∵四边形EFGH是菱形,∴HG=HE,在Rt△HAE和Rt△GDH中,,∴Rt△HAE≌Rt△GDH(HL),∴∠AHE=∠DGH,又∠DHG+∠DGH=90°,∴∠DHG+∠AHE=90°,∴∠GHE=90°,∴菱形EFGH为正方形;4.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)求证:矩形DEFG是正方形;(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.【分析】(1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;(2)同(1)的方法判断出△ADE≌△CDG得到CG=AE,即:CE+CG=CE+AE=AC =6.【解答】解:(1)如图,作EM⊥BC于M,EN⊥CD于N,∴∠MEN=90°,∵点E是正方形ABCD对角线上的点,∴EM=EN,∵∠DEF=90°,∴∠DEN=∠MEF,∵∠DNE=∠FME=90°,在△DEN和△FEM中,,∴△DEN≌△FEM(ASA),∴EF=DE,∵四边形DEFG是矩形,∴矩形DEFG是正方形;(2)CE+CG的值是定值,定值为6,理由如下:∵正方形DEFG和正方形ABCD,∴DE=DG,AD=DC,∵∠CDG+∠CDE=∠ADE+∠CDE=90°,∴∠CDG=∠ADE,在∴△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG,∴CE+CG=CE+AE=AC=AB=×3=6是定值.5.如图①,在正方形ABCD中,点E,F分别在AB、BC上,且AE=BF.(1)试探索线段AF、DE的数量关系,写出你的结论并说明理由;(2)连接EF、DF,分别取AE、EF、FD、DA的中点H、I、J、K,则四边形HIJK是什么特殊平行四边形?请在图②中补全图形,并说明理由.【分析】(1)根据已知利用SAS判定△DAE≌△ABF,由全等三角形的判定方法可得到AF=DE.(2)根据已知可得HK,KJ,IJ,HI都是中位线,由全等三角形的判定可得到四边形四边都相等且有一个角是直角,从而来可得到该四边形是正方形.【解答】解:(1)AF=DE.∵ABCD是正方形,∴AB=AD,∠DAB=∠ABC=90°,∵AE=BF,∴△DAE≌△ABF,∴AF=DE.(2)四边形HIJK是正方形.如下图,H、I、J、K分别是AE、EF、FD、DA的中点,∴HI=KJ=AF,HK=IJ=ED,∵AF=DE,∴HI=KJ=HK=IJ,∴四边形HIJK是菱形,∵△DAE≌△ABF,∴∠ADE=∠BAF,∵∠ADE+∠AED=90°,∴∠BAF+∠AED=90°,∴∠AOE=90°∴∠KHI=90°,∴四边形HIJK是正方形.6.如图,已知正方形ABCD,P是对角线AC上任意一点,PM⊥AD,PN⊥AB,垂足分别为点M和N,PE⊥PB交AD于点E.(1)求证:四边形MANP是正方形;(2)求证:EM=BN.【分析】(1)根据有三个角是直角的四边形是矩形证明四边形MANP是矩形,再根据角平分线的性质得:PM=PN,可得结论;(2)证明△EPM≌△BPN,可得结论.【解答】证明:(1)∵四边形ABCD是正方形,∴∠DAB=90°,AC平分∠DAB,(1分)∵PM⊥AD,PN⊥AB,∴∠PMA=∠PNA=90°,∴四边形MANP是矩形,(2分)∵AC平分∠DAB,PM⊥AD,PN⊥AB,∴PM=PN,(3分)∴四边形MANP是正方形;(4分)(2)∵四边形ABCD是正方形,∴PM=PN,∠MPN=90°,∵∠EPB=90°,∴∠MPE+∠EPN=∠NPB+∠EPN=90°,∴∠MPE=∠NPB,(5分)在△EPM和△BPN中,∵,∴△EPM≌△BPN(ASA),(6分)∴EM=BN.(7分)7.如图,在等腰直角三角形ABC中,∠ACB=90°,AC=BC=4,D是AB的中点,E,F 分别是AC,BC上的点(点E不与端点A,C重合),且AE=CF,连接EF并取EF的中点O,连接DO并延长至点G,使GO=OD,连接DE,DF,GE,GF.(1)求证:四边形EDFG是正方形;(2)当点E在什么位置时,四边形EDFG的面积最小?并求四边形EDFG面积的最小值.【分析】(1)连接CD,根据等腰直角三角形的性质可得出∠A=∠DCF=45°、AD=CD,结合AE=CF可证出△ADE≌△CDF(SAS),根据全等三角形的性质可得出DE=DF、ADE=∠CDF,通过角的计算可得出∠EDF=90°,再根据O为EF的中点、GO=OD,即可得出GD⊥EF,且GD=2OD=EF,由此即可证出四边形EDFG是正方形;(2)过点D作DE′⊥AC于E′,根据等腰直角三角形的性质可得出DE′的长度,从而得出2≤DE<2,再根据正方形的面积公式即可得出四边形EDFG的面积的最小值.【解答】(1)证明:连接CD,如图1所示.∵△ABC为等腰直角三角形,∠ACB=90°,D是AB的中点,∴∠A=∠DCF=45°,AD=CD.在△ADE和△CDF中,,∴△ADE≌△CDF(SAS),∴DE=DF,∠ADE=∠CDF.∵∠ADE+∠EDC=90°,∴∠EDC+∠CDF=∠EDF=90°,∴△EDF为等腰直角三角形.∵O为EF的中点,GO=OD,∴GD⊥EF,且GD=2OD=EF,∴四边形EDFG是正方形;(2)解:过点D作DE′⊥AC于E′,如图2所示.∵△ABC为等腰直角三角形,∠ACB=90°,AC=BC=4,∴DE′=BC=2,AB=4,点E′为AC的中点,∴2≤DE<2(点E与点E′重合时取等号).∴4≤S四边形EDFG=DE2<8.∴当点E为线段AC的中点时,四边形EDFG的面积最小,该最小值为4.8.如图,已知四边形ABCD为正方形,AB=,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE.交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.①求证:矩形DEFG是正方形;②探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.【分析】(1)作出辅助线,得到EN=EM,然后判断∠DEN=∠FEM,得到△DEN≌△FEM,则有DE=EF即可;(2)同(1)的方法证出△ADE≌△CDG得到CG=AE,得出CE+CG=CE+AE=AC=4即可.【解答】①证明:过E作EM⊥BC于M点,过E作EN⊥CD于N点,如图所示:∵正方形ABCD∴∠BCD=90°,∠ECN=45°∴∠EMC=∠ENC=∠BCD=90°且NE=NC,∴四边形EMCN为正方形∵四边形DEFG是矩形,∴EM=EN,∠DEN+∠NEF=∠MEF+∠NEF=90°∴∠DEN=∠MEF,又∠DNE=∠FME=90°,在△DEN和△FEM中,,∴△DEN≌△FEM(ASA),∴ED=EF,∴矩形DEFG为正方形,②解:CE+CG的值为定值,理由如下:∵矩形DEFG为正方形,∴DE=DG,∠EDC+∠CDG=90°∵四边形ABCD是正方形,∵AD=DC,∠ADE+∠EDC=90°∴∠ADE=∠CDG,在△ADE和△CDG中,,∴△ADE≌△CDG(SAS),∴AE=CG∴AC=AE+CE=AB=×2=4,∴CE+CG=4 是定值.9.平行四边形ABCD的对角线AC和BD交于O点,分别过顶点B,C作两对角线的平行线交于点E,得平行四边形OBEC.(1)如果四边形ABCD为矩形(如图),四边形OBEC为何种四边形?请证明你的结论;(2)如果四边形ABCD是正方形,四边形OBEC也是正方形吗?如果是,请给予证明;如果不是,请说明理由.【分析】(1)由平行线可得四边形OBEC为平行四边形,又矩形对角线互相平分且相等,则可得四边形OBEC为菱形;(2)由平行线可得四边形OBEC为平行四边形,又正方形对角线互相垂直、平分且相等,则可得四边形OBEC为正方形.【解答】解:(1)四边形OBEC是菱形.证明:∵BE∥OC,CE∥OB,∴四边形OBEC为平行四边形.又∵四边形ABCD是矩形,∴OC=OB,∴平行四边形OBEC为菱形;(2)四边形OBEC是正方形.证明:∵BE∥OC,CE∥OB,∴四边形OBEC为平行四边形.又∵四边形ABCD是正方形,∴OC=OB,∠BOC=90°,∴平行四边形OBEC为正方形.10.如果P是正方形ABCD内的一点,且满足∠APB+∠DPC=180°,那么称点P是正方形ABCD的“对补点”.(1)如图1,正方形ABCD的对角线AC,BD交于点M,求证:点M是正方形ABCD 的对补点;(2)如图2,在平面直角坐标系中,正方形ABCD的顶点A(1,1),C(3,3).除对角线交点外,请再写出一个该正方形的对补点的坐标,并证明.【分析】(1)根据四边形ABCD是正方形,得到AC⊥BD,于是得到结论;(2)如图2,延长CD交y轴于E,延长CB交x轴于F,则四边形CEOF是正方形连接OC,EF交于P,推出A,C在直线y=x上,得到A在OC上,根据全等三角形的性质得到∠APD=∠APB,得到∠CPD+∠APB=180°,于是得到结论.【解答】解:(1)∵四边形ABCD是正方形,∴AC⊥BD,∴∠AMB=∠CMD=90°,∴∠AMB+∠CMD=180°,∴点M是正方形ABCD的对补点;(2)如图2,点P(,)是该正方形的对补点,延长CD交y轴于E,延长CB交x轴于F,则四边形CEOF是正方形连接OC,EF交于P,∵A(1,1),C(3,3),∴A,C在直线y=x上,∴A在OC上,在△APD与△APB中,,∴△APD≌△APB,∴∠APD=∠APB,∴∠DPE=∠BPF,∵∠EPC+∠APF=180°,∴∠CPD+∠APB=180°,∴P(,)是该正方形的对补点.11.已知:如图,E是正方形ABCD的对角线BD上的点,连接AE、CE.(1)求证:AE=CE;(2)若将△ABE沿AB翻折后得到△ABF,当点E在BD的何处时,四边形AFBE是正方形?请证明你的结论.【分析】(1)利用正方形的性质和SAS证明△ABE≌△CBE即可;(2)由折叠的性质得出∠F=∠AEB,AF=AE,BF=BE,由直角三角形斜边上的中线性质得出AE=BD=BE=DE,证出AE=BE=AF=BF,得出四边形AFBE是菱形,AE ⊥BD,即可得出结论.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=CB,∠BAD=∠ABC=90°,∠ABE=∠CBE=45°,在△ABE和△CBE中,,∴△ABE≌△CBE(SAS),∴AE=CE.(2)解:点E在BD的中点时,四边形AFBE是正方形;理由如下:由折叠的性质得:∠F=∠AEB,AF=AE,BF=BE,∵∠BAD=90°,E是BD的中点,∴AE=BD=BE=DE,∵BF=BE,∴AE=BE=AF=BF,∴四边形AFBE是菱形,E是正方形ABCD对角线的交点,∴AE⊥BD,∴∠AEB=90°,∴四边形AFBE是正方形.12.如图所示,有四个动点P,Q,E,F分别从正方形ABCD的四个顶点出发,沿着AB,BC,CD,DA以同样速度向B,C,D,A各点移动.(1)试判断四边形PQEF是否是正方形,并证明;(2)PE是否总过某一定点,并说明理由.【分析】(1)正方形的定义:有一组邻边相等并且有一个角是直角的平行四边形叫做正方形,故可根据正方形的定义证明四边形PQEF是否使正方形.(2)证PE是否过定点时,可连接AC,证明四边形APCE为平行四边形,即可证明PE 过定点.【解答】解:(1)在正方形ABCD中,AP=BQ=CE=DF,AB=BC=CD=DA,∴BP=QC=ED=F A.又∵∠BAD=∠B=∠BCD=∠D=90°,∴△AFP≌△BPQ≌△CQE≌△DEF.∴FP=PQ=QE=EF,∠APF=∠PQB.∴四边形PQEF是菱形,∵∠FPQ=90°,∴四边形PQEF为正方形.(2)连接AC交PE于O,∵AP平行且等于EC,∴四边形APCE为平行四边形.∵O为对角线AC的中点,∴对角线PE总过AC的中点.13.在平面直角坐标系xOy中,OEFG为正方形,点F的坐标为(1,1).将一个最短边长大于的直角三角形纸片的直角顶点放在对角线FO上.(1)如图,当三角形纸片的直角顶点与点F重合,一条直角边落在直线FO上时,这个三角形纸片与正方形OEFG重叠部分(即阴影部分)的面积为;(2)若三角形纸片的直角顶点不与点O,F重合,且两条直角边与正方形相邻两边相交,当这个三角形纸片与正方形OEFG重叠部分的面积是正方形面积的一半时,试确定三角形纸片直角顶点的坐标(不要求写出求解过程),并画出此时的图形.【分析】(1)S=OE•EF=;(2)如图,正方形GFEO的面积为1,当重合的面积为正方形GFEO的面积的一半时,有两种情况:①四边形OSCB的面积为时,易证得四边形ACDO为正方形,△ABC≌△DSC,有四边形OSCB的面积与正方形ACDO的面积相等,故有OD=OA=即点C的坐标为(,).②四边形FSCB的面积为时,易证得四边形ACDF为正方形,△ABC≌△DSC,有四边形FSCB的面积与正方形ACDO的面积相等,故有AD=F A=即点C的坐标为(1﹣,1﹣).【解答】解:(1)S=OE•EF=;(2)如图,正方形GFEO的面积为1,当重合的面积为正方形GFEO的面积的一半时,有两种情况:①四边形OSCB的面积为时,易证得四边形ACOD为正方形,△ABC≌△DSC,有四边形OSCB的面积与正方形ACOD的面积相等,故有OD=OA=即点C的坐标为(,).②四边形FSCB的面积为时,易证得四边形ACDF为正方形,△ABC≌△DSC,有四边形FSCB的面积与正方形ACDO的面积相等,故有FD=F A=即点C的坐标为(1﹣,1﹣).14.(1)如图矩形ABCD的对角线AC、BD交于点O,过点D作DP∥OC,且DP=OC,连接CP,判断四边形CODP的形状并说明理由.(2)如果题目中的矩形变为菱形,结论应变为什么?说明理由.(3)如果题目中的矩形变为正方形,结论又应变为什么?说明理由.【分析】(1)根据矩形的性质得出OD=OC,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据菱形的判定推出即可;(2)根据菱形的性质得出∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据矩形的判定推出即可;(3)根据正方形的性质得出OD=OC,∠DOC=90°,根据有一组对边平行且相等的四边形是平行四边形得出四边形CODP是平行四边形,根据正方形的判定推出即可;【解答】解:(1)四边形CODP的形状是菱形,理由是:∵四边形ABCD是矩形,∴AC=BD,OA=OC=AC,OB=OD=BD,∴OC=OD,∵DP∥OC,DP=OC,∴四边形CODP是平行四边形,∵OC=OD,∴平行四边形CODP是菱形;(2)四边形CODP的形状是矩形,理由是:∵四边形ABCD是菱形,∴AC⊥BD,∴∠DOC=90°,∵DP∥OC,DP=OC,∴四边形CODP是平行四边形,∵∠DOC=90°,∴平行四边形CODP是矩形;(3)四边形CODP的形状是正方形,理由是:∵四边形ABCD是正方形,∴AC⊥BD,AC=BD,OA=OC=AC,OB=OD=BD,∴∠DOC=90°,OD=OC,∵DP∥OC,DP=OC,∴四边形CODP是平行四边形,∵∠DOC=90°,OD=OC∴平行四边形CODP是正方形.15.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图1,求证:矩形DEFG是正方形;(2)若AB=2,CE=,求CG的长度;(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.(1)作EP⊥CD于P,EQ⊥BC于Q,证明Rt△EQF≌Rt△EPD,得到EF=ED,【分析】根据正方形的判定定理证明即可;(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解决问题.(3)分两种情形考虑问题即可;【解答】(1)证明:作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,在Rt△EQF和Rt△EPD中,,∴Rt△EQF≌Rt△EPD(ASA),∴EF=ED,∴矩形DEFG是正方形;(2)如图2中,在Rt△ABC中.AC=AB=2,∵EC=,∴AE=CE,∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=.(3)①当DE与AD的夹角为30°时,点F在BC边上,∠ADE=30°,则∠CDE=90°﹣30°=60°,在四边形CDEF中,由四边形内角和定理得:∠EFC=360°﹣90°﹣90°﹣60°=120°,②当DE与DC的夹角为30°时,点F在BC的延长线上,∠CDE=30°,如图3所示:∵∠HCF=∠DEF=90°,∠CHF=∠EHD,∴∠EFC=∠CDE=30°,综上所述,∠EFC=120°或30°.16.如图,在矩形ABCD中,AD=6,CD=8,菱形EFGH的三个顶点E、G、H分别在矩形ABCD的边AB、CD、DA上,AH=2,连接CF.(1)当DG=2时,求证:四边形EFGH是正方形;(2)当△FCG的面积为2时,求CG的值.【分析】(1)由于四边形ABCD为矩形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;(2)过F作FM⊥DC于M,根据AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,利用三角形面积解答即可.【解答】(1)证明:在矩形ABCD中,有∠A=∠D=90°,∴∠DGH+∠DHG=90°.在菱形EFGH中,EH=GH∵AH=2,DG=2,∴AH=DG,∴Rt△AEH≌Rt△DHG(HL).∴∠AHE=∠DGH.∴∠AHE+∠DHG=90°.∴∠EHG=90°.∴四边形EFGH是正方形.(2)过F作FM⊥DC于M,则∠FMG=90°.∴∠A=∠FMG=90°.连接EG.由矩形和菱形性质,知AB∥DC,HE∥GF,∴∠AEG=∠MGE,∠HEG=∠FGE,∴∠AEH=∠MGF.∵EH=GF,∴△AEH≌△MGF.∴FM=AH=2.∵S△FCG=,∴CG=2.17.已知,如图,矩形ABCD中,AD=6,DC=7,菱形EFGH的三个顶点E,G,H分别在矩形ABCD的边AB,CD,DA上,AH=2,连接CF.(1)若DG=2,求证四边形EFGH为正方形;(2)若DG=6,求△FCG的面积;(3)当DG为何值时,△FCG的面积最小.【分析】(1)由于四边形ABCD为矩形,四边形HEFG为菱形,那么∠D=∠A=90°,HG=HE,而AH=DG=2,易证△AHE≌△DGH,从而有∠DHG=∠HEA,等量代换可得∠AHE+∠DHG=90°,易证四边形HEFG为正方形;(2)过F作FM⊥DC,交DC延长线于M,连接GE,由于AB∥CD,可得∠AEG=∠MGE,同理有∠HEG=∠FGE,利用等式性质有∠AEH=∠MGF,再结合∠A=∠M=90°,HE=FG,可证△AHE≌△MFG,从而有FM=HA=2(即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2),进而可求三角形面积;(3)先设DG=x,由第(2)小题得,S△FCG=7﹣x,在△AHE中,AE≤AB=7,利用勾股定理可得HE2≤53,在Rt△DHG中,再利用勾股定理可得x2+16≤53,进而可求x ≤,从而可得当x=时,△GCF的面积最小.【解答】解:(1)∵四边形ABCD为矩形,四边形HEFG为菱形,∴∠D=∠A=90°,HG=HE,又AH=DG=2,∴Rt△AHE≌Rt△DGH(HL),∴∠DHG=∠HEA,∵∠AHE+∠HEA=90°,∴∠AHE+∠DHG=90°,∴∠EHG=90°,∴四边形HEFG为正方形;(2)过F作FM⊥DC,交DC延长线于M,连接GE,∵AB∥CD,∴∠AEG=∠MGE,∵HE∥GF,∴∠HEG=∠FGE,∴∠AEH=∠MGF,在△AHE和△MFG中,∠A=∠M=90°,HE=FG,∴△AHE≌△MFG,∴FM=HA=2,即无论菱形EFGH如何变化,点F到直线CD的距离始终为定值2,因此;(3)设DG=x,则由第(2)小题得,S△FCG=7﹣x,在△AHE中,AE≤AB=7,∴HE2≤53,∴x2+16≤53,∴x≤,∴S△FCG的最小值为,此时DG=,∴当DG=时,△FCG的面积最小为().18.如图,Rt△CEF中,∠C=90°,∠CEF,∠CFE外角平分线交于点A,过点A分别作直线CE,CF的垂线,B,D为垂足.(1)∠EAF=45°(直接写出结果不写解答过程);(2)①求证:四边形ABCD是正方形.②若BE=EC=3,求DF的长.(3)如图(2),在△PQR中,∠QPR=45°,高PH=5,QH=2,则HR的长度是(直接写出结果不写解答过程).【分析】(1)根据平角的定义得到∠DFE+∠BEF=360°﹣90°=270°,根据角平分线的定义得到∠AFE=DFE,∠AEF=BEF,求得∠AEF+∠AFE=(∠DFE+∠BEF),根据三角形的内角和定理即可得到结论;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,先证明四边形ABCD 是矩形,再由角平分线的性质得出AB=AD,即可得出四边形ABCD是正方形;②设DF=x,根据已知条件得到BC=6,由①得四边形ABCD是正方形,求得BC=CD =6,根据全等三角形的性质得到BE=EG=3,同理,GF=DF=x,根据勾股定理列方程即可得到结论;(3)把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ =2,得出MG=DG=MP=PH=6,GQ=4,设MR=HR=a,则GR=6﹣a,QR=a+2,在Rt△GQR中,由勾股定理得出方程,解方程即可.【解答】解:(1)∵∠C=90°,∴∠CFE+∠CEF=90°,∴∠DFE+∠BEF=360°﹣90°=270°,∵AF平分∠DFE,AE平分∠BEF,∴∠AFE=DFE,∠AEF=BEF,∴∠AEF+∠AFE=(∠DFE+∠BEF)=270°=135°,∴∠EAF=180°﹣∠AEF﹣∠AFE=45°,故答案为:45;(2)①作AG⊥EF于G,如图1所示:则∠AGE=∠AGF=90°,∵AB⊥CE,AD⊥CF,∴∠B=∠D=90°=∠C,∴四边形ABCD是矩形,∵∠CEF,∠CFE外角平分线交于点A,∴AB=AG,AD=AG,∴AB=AD,∴四边形ABCD是正方形;②设DF=x,∵BE=EC=3,∴BC=6,由①得四边形ABCD是正方形,∴BC=CD=6,在Rt△ABE与Rt△AGE中,,∴Rt△ABE≌Rt△AGE(HL),∴BE=EG=3,同理,GF=DF=x,在Rt△CEF中,EC2+FC2=EF2,即32+(6﹣x)2=(x+3)2,解得:x=2,∴DF的长为2;(3)解:如图2所示:把△PQH沿PQ翻折得△PQD,把△PRH沿PR翻折得△PRM,延长DQ、MR交于点G,由(1)(2)得:四边形PMGD是正方形,MR+DQ=QR,MR=HR,DQ=HQ=2,∴MG=DG=MP=PH=5,∴GQ=3,设MR=HR=a,则GR=5﹣a,QR=a+2,在Rt△GQR中,由勾股定理得:(5﹣a)2+32=(2+a)2,解得:a=,即HR=;故答案为:.19.如图1,在正方形ABCD中,G为线段BD上一点,连接AG,过G作AG⊥GE交BC 于E,连接AE.(1)求证:BG=DG+BE;(2)如图2,AB=4,E为BC中点,P,Q分别为线段AB,AE上的动点,满足QE=AP,则在P,Q运动过程中,当以PQ为对角线的正方形PRQS的一边恰好落在△ABE 的某一边上时,直接写出正方形PRQS的面积.【分析】(1)过点G作GN⊥BC于点N,作GM⊥AB于点M,过点E作EF⊥BC,交BD于点F,先证明△AGM≌△EGN(ASA),从而AM=EN,再利用DG=BD﹣BG=AB﹣BM=AM,FG=BG﹣BF=BN﹣BE=EN,得出DG=FG,则BG =BF+FG=DG+BE;(2)分五种情况讨论,以点B为原点,BC所在直线为x轴,BA所在直线为y轴建立平面直角坐标系,分别求得AE和PQ的解析式,二者联立解得用含m的式子表示的点Q 的坐标,在Rt△QEF中,由勾股定理得出QE的表达式,然后结合QE=AP得出关于m的方程,解得m的值,则可得点Q的横坐标,从而可得正方形PRQS的面积,利用锐角三角函数和线段的和差关系列出方程,可求正方形的边长,即可求解.【解答】解:(1)证明:过点G作GN⊥BC于点N,作GM⊥AB于点M,过点E作EF ⊥BC,交BD于点F,如图所示:∵四边形ABCD是正方形,BD是对角线,∴BF=BE,GM=GN,∵AG⊥GE,GN⊥BC,GM⊥AB,∴∠AMG=∠ENG=90°,∠AGM+∠MGN=∠EGN+∠MGN,∴∠AGM=∠EGN,∴在△AGM和△EGN中,,∴△AGM≌△EGN(ASA),∴AM=EN,∵DG=BD﹣BG=AB﹣BM=AM,FG=BG﹣BF=BN﹣BE=EN,∴DG=FG,∴BG=BF+FG=DG+BE;(2)①若正方形PRQS的一边恰好落在AB上,如图2:当点P在点R的上方,∵AB=4,E为BC中点,∴A(0,4),E(2,0),设AE的解析式为y=kx+4,将(2,0)代入得:0=2k+4,∴k=﹣2,∴y=﹣2x+4,∵PQ与AB的夹角为45°,∴设PQ的解析式为y=﹣x+m,则P为(0,m),|AP|=4﹣m,由解得:Q(4﹣m,2m﹣4),过Q作QF⊥BC,则QF=2m﹣4,EF=m﹣2,∴在Rt△QEF中,由勾股定理得:QE==(m﹣2).∵QE=AP,∴(m﹣2)=(4﹣m),∴m=3,∴4﹣m=1,∴正方形PRQS的面积为1.如图2﹣1,当点P在点R的下方,∵tan∠RAQ==,∴AR=2RQ,∴AP=AR+RP=3RQ,∴AQ==RQ,∵BE=2,AB=4,∴AE===2,∵QE=AP,∴QE=3RQ,∴3RQ+RQ=2,∴RQ=,∴正方形PRQS的面积为.②当正方形PRQS的一边落在AE上,如图2﹣2,∵tan∠P AQ==,∴AS=2PS,∴AP==PS,∵QE=AP,∴QE=5PS,∵AE=AS+SQ+QE=2,∴2PS+PS+5PS=2,PS=,∴正方形PRQS的面积为,如图2﹣3,同理可得:AE=AR+RE=AR+QE﹣QR=(5+1)RP=2,∴PR=,∴正方形PRQS的面积为,当正方形PRQS与BC重合时,如图2﹣4,∵tan∠BAE==,∴AS=2SQ,∴AP=AS+SP=3SQ,∵sin∠AEB===,∵QE=QR,∴QE≠AP,∴这种情况不存在,故舍去,综上所述:正方形PRQS的面积为或1或或.20.四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.(1)如图,求证:矩形DEFG是正方形;(2)若AB=2,CE=2,求CG的长;(3)当线段DE与正方形ABCD的某条边的夹角是40°时,直接写出∠EFC的度数.(1)作EP⊥CD于P,EQ⊥BC于Q,证明Rt△EQF≌Rt△EPD,得到EF=ED,【分析】根据正方形的判定定理证明即可;(2)通过计算发现E是AC中点,点F与C重合,△CDG是等腰直角三角形,由此即可解决问题.(3)分两种情形考虑问题即可;【解答】(1)证明:作EP⊥CD于P,EQ⊥BC于Q,∵∠DCA=∠BCA,∴EQ=EP,∵∠QEF+∠FEC=45°,∠PED+∠FEC=45°,∴∠QEF=∠PED,在Rt△EQF和Rt△EPD中,,∴Rt△EQF≌Rt△EPD(ASA),∴EF=ED,∴矩形DEFG是正方形;(2)如图2中,在Rt△ABC中,AC=AB=4,∵EC=2,∴AE=CE,∴点F与C重合,此时△DCG是等腰直角三角形,易知CG=2;(3)①如图3,当DE与AD的夹角为40°时,∠DEC=45°+40°=85°,∵∠DEF=90°,∴∠CEF=5°,∵∠ECF=45°,∴∠EFC=130°,②如图4,当DE与DC的夹角为40°时,∵∠DEF=∠DCF=90°,∴∠EFC=∠EDC=40°,。
正方形中考拓展专题

1.如图,正方形ABCD和正方形CEFG边长分别为a和b,正方形CEFG绕点C旋转,给出下列结论:①BE=DG;②BE_LDG;®DE2+BG2=2a2+2b2,其中正确结论有()A.0个B.1个C.2个D.3个2.如图,正方形ABCD的边长为4,E为BC上的一点,BE=1,F为AB的中点,P为AC上一个动点,3.如图,四边形ABCD是边长为6的正方形,点E在边上,BE=4,过点E作EF//BC,分别交CD 于G,F两点.若N分别是OG,CE的中点,则"的长为()4.如图,正方形ABCD的边长为3,点E、F分别在边BC、CD上,将AB、AD分别沿AE、AF折叠,点B、D恰好都落在点G处,己知BE=1,则EF的长为()359A.2B.2C.4D.35.如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:©AABG^AAFG;②BG=GC;③ZEAG=45°;④AG〃CF;⑤S aecg:S a aeg=2:5,其中正确结论的个数A.2B.3C.4D.56.如图,正方形ABCD中,AB=1,M,N分别是AD,BC边的中点,沿BQ将△BCQ折叠,若点C恰好落在MN上的点P处,则PQ的长为()1^1A.2B.3C.3D.B7.如图,在正方形ABCD对角线BD上截取BE=BC,连接CE并延长交AD于点F,连接AE,过B作BG±AE 于点G,交AD于点H,则下列结论错误的是()A.AH=DFB.S四边形EFHG=S a DC f+S a aghC.ZAEF=45°D.△ABH^ADCF8.如图,正方形ABCD和正方形CEFG中,点。
在CG上,BC=L,CE=3,H是AF的中点,那么CH的长是().9.如图,在A AB C中,ZC=90°,AC=BC=4,Q是AB的中点,点E、F分别在AC、BC边上运动(点、E 不与点A、。
中考数学真题《矩形菱形正方形》专项测试卷(附答案)

中考数学真题《矩形菱形正方形》专项测试卷(附答案)学校:___________班级:___________姓名:___________考号:___________(39题)一 、单选题1.(2023·湖南·统考中考真题)如图,菱形ABCD 中 连接AC BD , 若120∠=︒,则2∠的度数为( )A .20︒B .60︒C .70︒D .80︒2.(2023·湖南常德·统考中考真题)如图1 在正方形ABCD 中 对角线AC BD 、相交于点O E F 分别为AO DO 上的一点 且EF AD ∥ 连接,AF DE .若15FAC ∠=︒,则AED ∠的度数为( )A .80︒B .90︒C .105︒D .115︒3.(2023·湖南常德·统考中考真题)下列命题正确的是( )A .正方形的对角线相等且互相平分B .对角互补的四边形是平行四边形C .矩形的对角线互相垂直D .一组邻边相等的四边形是菱形4.(2023·浙江·统考中考真题)如图,在菱形ABCD 中 160AB DAB =∠=︒,,则AC 的长为( )A .12 B .1 C 3D 35.(2023·上海·统考中考真题)在四边形ABCD 中 ,AD BC AB CD =∥.下列说法能使四边形ABCD 为矩形的是( )A .AB CD B .AD BC = C .A B ∠=∠D .A D ∠=∠6.(2023·浙江宁波·统考中考真题)如图,以钝角三角形ABC 的最长边BC 为边向外作矩形BCDE 连结,AE AD 设AED △ ABE ACD 的面积分别为12,,S S S 若要求出12S S S --的值 只需知道( )A .ABE 的面积B .ACD 的面积C .ABC 的面积D .矩形BCDE 的面积7.(2023·湖南·统考中考真题)如图所示 在矩形ABCD 中 AB AD > AC 与BD 相交于点O 下列说法正确的是( )A .点O 为矩形ABCD 的对称中心B .点O 为线段AB 的对称中心C .直线BD 为矩形ABCD 的对称轴 D .直线AC 为线段BD 的对称轴8.(2023·四川宜宾·统考中考真题)如图,边长为6的正方形ABCD 中 M 为对角线BD 上的一点 连接AM 并延长交CD 于点P .若PM PC =,则AM 的长为( )A .()331B .()3332C .)631D .()6332 9.(2023·四川乐山·统考中考真题)如图,菱形ABCD 的对角线AC 与BD 相交于点O E 为边BC 的中点 连结OE .若68AC BD ==,,则OE =( )A .2B .52C .3D .410.(2023·甘肃武威·统考中考真题)如图,将矩形ABCD 对折 使边AB 与DC BC 与AD 分别重合 展开后得到四边形EFGH .若2AB = 4BC =,则四边形EFGH 的面积为( )A .2B .4C .5D .611.(2023·浙江绍兴·统考中考真题)如图,在矩形ABCD 中 O 为对角线BD 的中点 60ABD ∠=︒.动点E 在线段OB 上 动点F 在线段OD 上 点,E F 同时从点O 出发 分别向终点,B D 运动 且始终保持OE OF =.点E 关于,AD AB 的对称点为12,E E 点F 关于,BC CD 的对称点为12,F F .在整个过程中 四边形1212E E F F 形状的变化依次是( )A .菱形→平行四边形→矩形→平行四边形→菱形B .菱形→正方形→平行四边形→菱形→平行四边形C .平行四边形→矩形→平行四边形→菱形→平行四边形D .平行四边形→菱形→正方形→平行四边形→菱形12.(2023·重庆·统考中考真题)如图,在正方形ABCD 中 O 为对角线AC 的中点 E 为正方形内一点 连接BE BE BA = 连接CE 并延长 与ABE ∠的平分线交于点F 连接OF 若2AB =,则OF 的长度为( )A .2B 3C .1D 2二 解答题13.(2023·湖南怀化·统考中考真题)如图,矩形ABCD 中 过对角线BD 的中点O 作BD 的垂线EF分别交AD BC 于点E F .(1)证明:BOF DOE ≌△△(2)连接BE DF 证明:四边形EBFD 是菱形.14.(2023·湖北随州·统考中考真题)如图,矩形ABCD 的对角线AC BD 相交于点O ,DE AC CE BD .(1)求证:四边形OCED 是菱形(2)若32BC DC ==, 求四边形OCED 的面积.15.(2023·湖南永州·统考中考真题)如图,已知四边形ABCD 是平行四边形其对角线相交于点O 3,8,5OA BD AB ===.(1)AOB 是直角三角形吗?请说明理由(2)求证:四边形ABCD 是菱形.16.(2023·新疆·统考中考真题)如图,AD 和BC 相交于点O 90ABO DCO ∠=∠=︒ OB OC =.点E F 分别是AO DO 的中点.(1)求证:OE OF =(2)当30A ∠=︒时 求证:四边形BECF 是矩形.17.(2023·云南·统考中考真题)如图,平行四边形ABCD 中 AE CF 、分别是BAD BCD ∠∠、的平分线且E F 、分别在边BC AD 、上 AE AF =.(1)求证:四边形AECF 是菱形(2)若60ABC ∠=︒ ABE 的面积等于3 求平行线AB 与DC 间的距离.18.(2023·四川遂宁·统考中考真题)如图,四边形ABCD 中 AD BC ∥ 点O 为对角线BD 的中点 过点O 的直线l 分别与AD BC 所在的直线相交于点E F .(点E 不与点D 重合)(1)求证:DOE BOF ≌(2)当直线l BD ⊥时 连接BE DF 试判断四边形EBFD 的形状 并说明理由.19.(2023·浙江嘉兴·统考中考真题)如图,在菱形ABCD 中 AE BC ⊥于点E AF CD ⊥于点F连接EF(1)求证:AE AF =(2)若=60B ∠︒ 求AEF ∠的度数.20.(2023·湖北鄂州·统考中考真题)如图,点E 是矩形ABCD 的边BC 上的一点 且AE AD =.(1)尺规作图(请用2B 铅笔):作DAE ∠的平分线AF 交BC 的延长线于点F 连接DF .(保留作图痕迹 不写作法)(2)试判断四边形AEFD 的形状 并说明理由.21.(2023·吉林长春·统考中考真题)将两个完全相同的含有30︒角的直角三角板在同一平面内按如图所示位置摆放.点A E B D 依次在同一直线上 连结AF CD .(1)求证:四边形AFDC 是平行四边形(2)己知6cm BC 当四边形AFDC 是菱形时.AD 的长为__________cm .22.(2023·湖南张家界·统考中考真题)如图,已知点A D C B 在同一条直线上 且AD BC = AE BF ==.CE DF(1)求证:AE BF∥=时求证:四边形DECF是菱形.(2)若DF FC23.(2023·湖南郴州·统考中考真题)如图,四边形ABCD是平行四边形.(1)尺规作图作对角线AC的垂直平分线MN(保留作图痕迹)(2)若直线MN分别交AD BC于E F两点求证:四边形AFCE是菱形AC BD交于点O分别以点,B C为圆心24.(2023·湖北十堰·统考中考真题)如图,ABCD的对角线,11,22AC BD 长为半径画弧 两弧交于点P 连接,BP CP .(1)试判断四边形BPCO 的形状 并说明理由(2)请说明当ABCD 的对角线满足什么条件时 四边形BPCO 是正方形?25.(2023·四川内江·统考中考真题)如图,在ABC 中 D 是BC 的中点 E 是AD 的中点 过点A 作AF BC ∥交CE 的延长线于点F .(1)求证:AF BD =(2)连接BF 若AB AC = 求证:四边形ADBF 是矩形.26.(2023·湖南岳阳·统考中考真题)如图,点M 在ABCD 的边AD 上 BM CM = 请从以下三个选项中①12∠=∠ ①AM DM = ①34∠∠= 选择一个合适的选项作为已知条件 使ABCD 为矩形.(1)你添加的条件是_________(填序号)(2)添加条件后 请证明ABCD 为矩形.27.(2023·四川乐山·统考中考真题)如图,在Rt ABC △中 90C ∠=︒ 点D 为AB 边上任意一点(不与点A B 重合) 过点D 作DE BC ∥ DF AC ∥ 分别交AC BC 于点E F 连接EF .(1)求证:四边形ECFD 是矩形(2)若24CF CE ==, 求点C 到EF 的距离.28.(2023·浙江台州·统考中考真题)如图,四边形ABCD 中 AD BC ∥ A C ∠=∠ BD 为对角线.(1)证明:四边形ABCD 是平行四边形.(2)已知AD AB > 请用无刻度的直尺和圆规作菱形BEDF 顶点E F 分别在边BC AD 上(保留作图痕迹 不要求写作法).三 填空题29.(2023·黑龙江齐齐哈尔·统考中考真题)如图,在四边形ABCD 中 AD BC = AC BD ⊥于点O .请添加一个条件:______ 使四边形ABCD 成为菱形.30.(2023·辽宁大连·统考中考真题)如图,在菱形ABCD 中 AC BD 、为菱形的对角线60,10DBC BD ︒∠== 点F 为BC 中点,则EF 的长为_______________.31.(2023·福建·统考中考真题)如图,在菱形ABCD 中 1060AB B ︒=∠=,,则AC 的长为___________.32.(2023·浙江绍兴·统考中考真题)如图,在菱形ABCD 中 40DAB ∠=︒ 连接AC 以点A 为圆心 AC 长为半径作弧 交直线AD 于点E 连接CE ,则AEC ∠的度数是________.33.(2023·甘肃武威·统考中考真题)如图,菱形ABCD 中 60DAB ∠=︒ BE AB ⊥ DF CD ⊥ 垂足分别为B D 若6cm AB =,则EF =________cm .34.(2023·山东聊城·统考中考真题)如图,在ABCD 中 BC 的垂直平分线EO 交AD 于点E 交BC 于点O 连接BE CE 过点C 作CF BE ∥ 交EO 的延长线于点F 连接BF .若8AD = 5CE =,则四边形BFCE 的面积为______..35.(2023·湖北十堰·统考中考真题)如图,在菱形ABCD 中 点E F G H 分别是AB BC CD AD 上的点 且BE BF CG AH === 若菱形的面积等于24 8BD =,则EF GH +=___________________.36.(2023·四川内江·统考中考真题)出入相补原理是我国古代数学的重要成就之一 最早是由三国时期数学家刘徽创建.“将一个几何图形 任意切成多块小图形 几何图形的总面积保持不变 等于所分割成的小图形的面积之和”是该原理的重要内容之一 如图,在矩形ABCD 中 5AB = 12AD = 对角线AC 与BD 交于点O 点E 为BC 边上的一个动点 EF AC ⊥ EG BD ⊥ 垂足分别为点F G ,则EF EG +=___________.37.(2023·山东滨州·统考中考真题)如图,矩形ABCD 的对角线,AC BD 相交于点O 点,E F 分别是线段,OB OA 上的点.若,5,1,3AE BF AB AF BE ====,则BF 的长为___________.38.(2023·山东枣庄·统考中考真题)如图,在正方形ABCD 中 对角线AC 与BD 相交于点O E 为BC 上一点 7CE = F 为DE 的中点 若CEF △的周长为32,则OF 的长为___________.39.(2023·浙江台州·统考中考真题)如图,矩形ABCD 中 4AB = 6AD =.在边AD 上取一点E 使BE BC = 过点C 作CF BE ⊥ 垂足为点F ,则BF 的长为________.参考答案一 单选题1.(2023·湖南·统考中考真题)如图,菱形ABCD 中 连接AC BD , 若120∠=︒,则2∠的度数为( )A .20︒B .60︒C .70︒D .80︒【答案】C 【分析】根据菱形的性质可得,BD AC AB CD ⊥∥,则1,290ACD ACD ∠=∠∠+∠=︒ 进而即可求解.【详解】解:①四边形ABCD 是菱形①,BD AC AB CD ⊥∥①1,290ACD ACD ∠=∠∠+∠=︒①120∠=︒①2902070∠=︒-︒=︒,故选:C .【点睛】本题考查了菱形的性质 熟练掌握是菱形的性质解题的关键.2.(2023·湖南常德·统考中考真题)如图1 在正方形ABCD 中 对角线AC BD 、相交于点O E F 分别为AO DO 上的一点 且EF AD ∥ 连接,AF DE .若15FAC ∠=︒,则AED ∠的度数为( )A .80︒B .90︒C .105︒D .115︒【答案】C 【分析】首先根据正方形的性质得到45OAD ODA ∠=∠=︒ AO DO = 然后结合EF AD ∥得到OE OF = 然后证明出()SAS AOF DOE △≌△ 最后利用三角形内角和定理求解即可.【详解】①四边形ABCD 是正方形①45OAD ODA ∠=∠=︒ AO DO =①EF AD ∥①45OEF OAD ∠=∠=︒ 45OFE ODA ∠=∠=︒①OEF OFE ∠=∠①OE OF =又①90AOF DOE ∠=∠=︒ AO DO =①()SAS AOF DOE △≌△①15ODE FAC ∠=∠=︒①30ADE ODA ODE ∠=∠-∠=︒①180105AED OAD ADE ∠=︒-∠-∠=︒故选:C .【点睛】此题考查了正方形的性质 全等三角形的性质和判定 等腰直角三角形三角形的性质等知识 解题的关键是熟练掌握以上知识点.3.(2023·湖南常德·统考中考真题)下列命题正确的是( )A .正方形的对角线相等且互相平分B .对角互补的四边形是平行四边形C .矩形的对角线互相垂直D .一组邻边相等的四边形是菱形【答案】A【分析】根据正方形 平行四边形 矩形 菱形的各自性质和构成条件进行判断即可.【详解】A 正方形的对角线相等且互相垂直平分 描述正确B 对角互补的四边形不一定是平行四边形 只是内接于圆 描述错误C 矩形的对角线不一定垂直 但相等 描述错误D 一组邻边相等的平行四边形才构成菱形 描述错误.故选:A .【点睛】本题考查平行四边形 矩形 菱形 正方形的性质和判定 解题的关键是熟悉掌握各类特殊四边形的判定和性质.4.(2023·浙江·统考中考真题)如图,在菱形ABCD 中 160AB DAB =∠=︒,,则AC 的长为( )A .12B .1C 3D 3【答案】D 【分析】连接BD 与AC 交于O .先证明ABD △是等边三角形 由AC BD ⊥ 得到1302OAB BAD ∠=∠=︒ 90AOB ∠=︒ 即可得到1122OB AB == 利用勾股定理求出AO 的长度 即可求得AC 的长度.【详解】解:连接BD 与AC 交于O .①四边形ABCD 是菱形①AB CD ∥ AB AD = AC BD ⊥ 12AO OC AC ==①60DAB ∠=︒ 且AB AD =①ABD △是等边三角形①AC BD ⊥ ①1302OAB BAD ∠=∠=︒ 90AOB ∠=︒ ①1122OB AB == ①2222111322AO AB OB ⎛⎫-= ⎪⎭=-⎝ ①23AC AO ==故选:D .【点睛】此题主要考查了菱形的性质 勾股定理 等边三角形的判定和性质 30︒角所对直角边等于斜边的一半 关键是熟练掌握菱形的性质.5.(2023·上海·统考中考真题)在四边形ABCD 中 ,AD BC AB CD =∥.下列说法能使四边形ABCD 为矩形的是( )A .AB CD B .AD BC = C .A B ∠=∠D .A D ∠=∠【答案】C【分析】结合平行四边形的判定和性质及矩形的判定逐一分析即可.【详解】A :AB CD ,AD BC AB CD =∥∴ABCD 为平行四边形而非矩形故A 不符合题意B :AD BC = ,AD BC AB CD =∥∴ABCD 为平行四边形而非矩形故B 不符合题意C :AD BC ∥180A B ∴∠+∠=︒A B ∠=∠∴90A B ∠=∠=︒AB CD =∴ABCD 为矩形故C 符合题意D :AD BC ∥180A B ∴∠+∠=︒A D ∠=∠180D B ∴∠+∠=︒∴ABCD 不是平行四边形也不是矩形故D 不符合题意故选:C .【点睛】本题主要考查平行线的性质 平行四边形的判定和性质及矩形的判定等知识 熟练掌握以上知识并灵活运用是解题的关键.6.(2023·浙江宁波·统考中考真题)如图,以钝角三角形ABC 的最长边BC 为边向外作矩形BCDE 连结,AE AD 设AED △ ABE ACD 的面积分别为12,,S S S 若要求出12S S S --的值 只需知道( )A .ABE 的面积B .ACD 的面积C .ABC 的面积D .矩形BCDE 的面积【答案】C【分析】过点A 作FG BC ∥ 交EB 的延长线于点F DC 的延长线于点G 易得:,,FG BC AF BE AG CD =⊥⊥ 利用矩形的性质和三角形的面积公式 可得1212BCDES S S +=矩形 再根据1212ABC ABC BCDE BCDE S S S S S S S -=+-=+矩形矩形 得到12ABC S S S S -=- 即可得出结论.【详解】解:过点A 作FG BC ∥ 交EB 的延长线于点F DC 的延长线于点G①矩形BCDE①,,BC BE BC CD BE CD ⊥⊥=①,FG BE FG CD ⊥⊥①四边形BFGC 为矩形①,,FG BC AF BE AG CD =⊥⊥①1211,22S BE AF S CD AG =⋅=⋅①()12111222BCDE BE AF AG BE B S C S S =+=⋅=+矩形又1212ABC ABC BCDE BCDE S S S S S S S -=+-=+矩形矩形①121122ABC ABC BCDE BCDE S S S S S S S =+---=矩形矩形 ①只需要知道ABC 的面积即可求出12S S S --的值故选C .【点睛】本题考查矩形的性质 求三角形的面积.解题的关键是得到1212BCDES S S +=矩形 7.(2023·湖南·统考中考真题)如图所示 在矩形ABCD 中 AB AD > AC 与BD 相交于点O 下列说法正确的是( )A .点O 为矩形ABCD 的对称中心B .点O 为线段AB 的对称中心C .直线BD 为矩形ABCD 的对称轴D .直线AC 为线段BD 的对称轴【答案】A 【分析】由矩形ABCD 是中心对称图形 对称中心是对角线的交点 线段AB 的对称中心是线段AB 的中点 矩形ABCD 是轴对称图形 对称轴是过一组对边中点的直线 从而可得答案.【详解】解:矩形ABCD 是中心对称图形 对称中心是对角线的交点 故A 符合题意线段AB 的对称中心是线段AB 的中点 故B 不符合题意矩形ABCD 是轴对称图形 对称轴是过一组对边中点的直线故C D 不符合题意故选A【点睛】本题考查的是轴对称图形与中心对称图形的含义 矩形的性质 熟记矩形既是中心对称图形也是轴对称图形是解本题的关键.8.(2023·四川宜宾·统考中考真题)如图,边长为6的正方形ABCD 中 M 为对角线BD 上的一点 连接AM 并延长交CD 于点P .若PM PC =,则AM 的长为( )A .()331B .()3332C .)631D .()6332 【答案】C【分析】先根据正方形的性质 三角形全等的判定证出ADM CDM ≅ 根据全等三角形的性质可得DAM DCM ∠=∠ 再根据等腰三角形的性质可得CMP DCM ∠=∠ 从而可得30DAM ∠=︒ 然后利用勾股定理 含30度角的直角三角形的性质求解即可得. 【详解】解:四边形ABCD 是边长为6的正方形6,90,45AD CD ADC ADM CDM ∴==∠=︒∠=∠=︒在ADM △和CDM 中 45DM DM ADM CDM AD CD =⎧⎪∠=∠=︒⎨⎪=⎩()SAS ADM CDM ∴≅DAM DCM ∴∠=∠PM PC =CMP DCM ∴∠=∠22APD CMP DCM DCM DAM ∴∠=∠+∠=∠=∠又18090APD DAM ADC ∠+∠=︒-∠=︒30DAM ∴∠=︒设PD x =,则22AP PD x == 6PM PC CD PD x ==-=-2236AD AP PD x ∴=-= 解得3x =663PM x ∴=-=- 243AP x ==(()43623631AM AP PM ∴=-=-= 故选:C .【点睛】本题考查了正方形的性质 勾股定理 含30度角的直角三角形的性质 等腰三角形的性质等知识点 熟练掌握正方形的性质是解题关键.9.(2023·四川乐山·统考中考真题)如图,菱形ABCD 的对角线AC 与BD 相交于点O E 为边BC 的中点 连结OE .若68AC BD ==,,则OE =( )A .2B .52C .3D .4【答案】B 【分析】先由菱形的性质得AC BD ⊥ 116322OC AC ==⨯= 118422OB BD ==⨯= 再由勾股定理求出5BC = 然后由直角 三角形斜边的中线等于斜边的一半求解.【详解】解:①菱形ABCD①AC BD ⊥ 116322OC AC ==⨯= 118422OB BD === ①由勾股定理 得225BC OB OC =+=①E 为边BC 的中点 ①1155222OE BC ==⨯= 故选:B .【点睛】本考查菱形的性质 勾股定理 直角三角形的性质 熟练掌握菱形的性质 直角三角形的性质是解题的关键.10.(2023·甘肃武威·统考中考真题)如图,将矩形ABCD 对折 使边AB 与DC BC 与AD 分别重合 展开后得到四边形EFGH .若2AB = 4BC =,则四边形EFGH 的面积为( )A .2B .4C .5D .6【答案】B 【分析】由题意可得四边形EFGH 是菱形 2FH AB == 4GE BC == 由菱形的面积等于对角线乘积的一半即可得到答案.【详解】解:①将矩形ABCD 对折 使边AB 与DC BC 与AD 分别重合 展开后得到四边形EFGH①EF GH ⊥ EF 与GH 互相平分①四边形EFGH 是菱形①2FH AB == 4GE BC ==①菱形EFGH 的面积为1124422FH GE ⋅=⨯⨯=. 故选:B【点睛】此题考查了矩形的折叠 菱形的判定和性质等知识 熟练掌握菱形的面积等于对角线乘积的一半是解题的关键.11.(2023·浙江绍兴·统考中考真题)如图,在矩形ABCD 中 O 为对角线BD 的中点 60ABD ∠=︒.动点E 在线段OB 上 动点F 在线段OD 上 点,E F 同时从点O 出发 分别向终点,B D 运动 且始终保持OE OF =.点E 关于,AD AB 的对称点为12,E E 点F 关于,BC CD 的对称点为12,F F .在整个过程中 四边形1212E E F F 形状的变化依次是( )A .菱形→平行四边形→矩形→平行四边形→菱形B .菱形→正方形→平行四边形→菱形→平行四边形C .平行四边形→矩形→平行四边形→菱形→平行四边形D .平行四边形→菱形→正方形→平行四边形→菱形【答案】A【分析】根据题意 分别证明四边形1212E E F F 是菱形 平行四边形 矩形 即可求解.【详解】①四边形ABCD 是矩形①AB CD ∥ 90BAD ABC ∠=∠=︒①60BDC ABD ∠=∠=︒ 906030ADB CBD ∠=∠=︒-︒=︒①OE OF = OB OD =①DF EB =①对称①21DF DF BF BF ==, 21,BE BE DE DE ==①1221E F E F =①对称①260F DC CDF ∠=∠=︒ 130EDA E DA ∠=∠=︒①160E DB ∠=︒同理160F BD ∠=︒①11DE BF ∥①1221E F E F ∥①四边形1212E E F F 是平行四边形如图所示当,,E F O 三点重合时 DO BO =①1212DE DF AE AE ===即1212E E E F =①四边形1212E E F F 是菱形如图所示 当,E F 分别为,OD OB 的中点时设4DB =,则21DF DF == 13DE DE ==在Rt △ABD 中 2,23AB AD ==连接AE AO①602ABO BO AB ∠=︒==,①ABO 是等边三角形①E 为OB 中点①AE OB ⊥ 1BE = ①22213AE - 根据对称性可得13AE AE =①2221112,9,3AD DE AE ===①22211AD AE DE =+①1DE A 是直角三角形 且190E ∠=︒①四边形1212E E F F 是矩形当,F E 分别与,D B 重合时 11,BE D BDF 都是等边三角形,则四边形1212E E F F 是菱形①在整个过程中 四边形1212E E F F 形状的变化依次是菱形→平行四边形→矩形→平行四边形→菱形 故选:A .【点睛】本题考查了菱形的性质与判定 平行四边形的性质与判定 矩形的性质与判定 勾股定理与勾股定理的逆定理 轴对称的性质 含30度角的直角三角形的性质 熟练掌握以上知识是解题的关键. 12.(2023·重庆·统考中考真题)如图,在正方形ABCD 中 O 为对角线AC 的中点 E 为正方形内一点 连接BE BE BA = 连接CE 并延长 与ABE ∠的平分线交于点F 连接OF 若2AB =,则OF 的长度为( )A .2B 3C .1D 2【答案】D 【分析】连接AF 根据正方形ABCD 得到AB BC BE == 90ABC ∠=︒ 根据角平分线的性质和等腰三角形的性质 求得45BFE ∠=︒ 再证明ABF EBF ≌ 求得90AFC ∠=︒ 最后根据直角三角形斜边上的中点等于斜边的一半 即可求出OF 的长度.【详解】解:如图,连接AF四边形ABCD 是正方形AB BE BC ∴== 90ABC ∠=︒ 222AC ==BEC BCE ∴∠=∠1802EBC BEC ∴∠=︒-∠290ABE ABC EBC BEC ∴∠=∠-∠=∠-︒ BF 平分ABE ∠1452ABF EBF ABE BEC ∴∠=∠=∠=∠-︒45BFE BEC EBF ∴∠=∠-∠=︒在BAF △与BEF △,AB EB ABF EBF BF BF =⎧⎪∠=∠⎨⎪=⎩()SAS BAF BEF ∴△≌△45BFE BFA ∴∠=∠=︒90AFC BAF BFE ∴∠=∠+∠=︒O 为对角线AC 的中点122OF AC ∴= 故选:D .【点睛】本题考查了等腰三角形的判定和性质 三角形内角和定理 正方形的性质 直角三角形特征 作出正确的辅助线 求得45BFE ∠=︒是解题的关键.二 解答题13.(2023·湖南怀化·统考中考真题)如图,矩形ABCD 中 过对角线BD 的中点O 作BD 的垂线EF 分别交AD BC 于点E F .(1)证明:BOF DOE ≌△△(2)连接BE DF 证明:四边形EBFD 是菱形.【答案】(1)见解析 (2)见解析【分析】(1)根据矩形的性质得出AD BC ∥,则12,34∠=∠∠=∠ 根据O 是BD 的中点 可得BO DO = 即可证明()AAS BOF DOE ≌△△(2)根据BOF DOE ≌△△可得ED BF = 进而可得四边形EBFD 是平行四边形 根据对角线互相垂直的四边形是菱形 即可得证.【详解】(1)证明:如图所示①四边形ABCD 是矩形①AD BC ∥①12,34∠=∠∠=∠①O 是BD 的中点①BO DO =在BOF 与DOE 中1234BO DO ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS BOF DOE ≌△△(2)①BOF DOE ≌△△①ED BF =又①ED BF ∥①四边形EBFD 是平行四边形①EF BD ⊥①四边形EBFD 是菱形.【点睛】本题考查了矩形的性质 全等三角形的性质与判定 菱形的判定 熟练掌握特殊四边形的性质与判定是解题的关键.14.(2023·湖北随州·统考中考真题)如图,矩形ABCD 的对角线AC BD 相交于点O ,DE AC CE BD .(1)求证:四边形OCED 是菱形(2)若32BC DC ==, 求四边形OCED 的面积.【答案】(1)见解析 (2)3【分析】(1)先根据矩形的性质求得OC OD = 然后根据有一组邻边相等的平行四边形是菱形分析推理 (2)根据矩形的性质求得OCD 的面积 然后结合菱形的性质求解.【详解】(1)解:①DE AC CE BD ∥,∥ ①四边形OCED 是平行四边形又①矩形ABCD 中 OC OD =①平行四边形OCED 是菱形(2)解:矩形ABCD 的面积为326BC DC ⋅=⨯=①OCD 的面积为13642⨯= ①菱形OCED 的面积为3232⨯=. 【点睛】本题考查矩形的性质 菱形的判定 属于中考基础题 掌握矩形的性质和菱形的判定方法 正确推理论证是解题关键.15.(2023·湖南永州·统考中考真题)如图,已知四边形ABCD 是平行四边形 其对角线相交于点O 3,8,5OA BD AB ===.(1)AOB 是直角三角形吗?请说明理由(2)求证:四边形ABCD 是菱形.【答案】(1)AOB 是直角三角形 理由见解析.(2)见解析【分析】(1)根据平行四边形对角线互相平分可得142BO BD == 再根据勾股定理的逆定理 即可得出结论(2)根据对角线互相垂直的平行四边形是菱形 即可求证.【详解】(1)解:AOB 是直角三角形 理由如下:①四边形ABCD 是平行四边形 ①142BO BD ==①222222345OA OB AB +=+==①AOB 是直角三角形.(2)证明:由(1)可得:AOB 是直角三角形①90AOB ∠=︒即AC BD ⊥①四边形ABCD 是平行四边形①四边形ABCD 是菱形.【点睛】本题主要考查了平行四边形的性质 勾股定理的逆定理 菱形的判定 解题的关键是掌握平行四边形对角线互相平分 对角线互相垂直的平行四边形是菱形.16.(2023·新疆·统考中考真题)如图,AD 和BC 相交于点O 90ABO DCO ∠=∠=︒ OB OC =.点E F 分别是AO DO 的中点.(1)求证:OE OF =(2)当30A ∠=︒时 求证:四边形BECF 是矩形.【答案】(1)见解析 (2)见解析【分析】(1)直接证明()ASA AOB DOC ≌△△ 得出OA OD = 根据E F 分别是AO DO 的中点 即可得证(2)证明四边形BECF 是平行四边形 进而根据30A ∠=︒ 推导出BOE △是等边三角形 进而可得BC EF = 即可证明四边形BECF 是矩形.【详解】(1)证明:在AOB 与DOC △中90ABO DCO OB OCAOB DOC ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩①()ASA AOB DOC ≌△△①OA OD =又①E F 分别是AO DO 的中点①OE OF =(2)①OB OC OF OE ==,①四边形BECF 是平行四边形 22BC OB EF OE ==,①E 为AO 的中点 90∠=︒ABO①EB EO EA ==①30A ∠=︒①60BOE ∠=︒①BOE △是等边三角形①OB OE =①BC EF =①四边形BECF 是矩形.【点睛】本题考查了全等三角形的性质与判定 等边三角形的性质与判定 矩形判定 熟练掌握以上知识是解题的关键.17.(2023·云南·统考中考真题)如图,平行四边形ABCD 中 AE CF 、分别是BAD BCD ∠∠、的平分线 且E F 、分别在边BC AD 、上 AE AF =.(1)求证:四边形AECF 是菱形(2)若60ABC ∠=︒ ABE 的面积等于3 求平行线AB 与DC 间的距离.【答案】(1)证明见解析 (2)3【分析】(1)先证AD BC ∥ 再证AE FC 从而四边形AECF 是平行四边形 又AE AF = 于是四边形AECF 是菱形(2)连接AC 先求得60BAE DAE ABC ∠∠∠===︒ 再证AC AB ⊥9030ACB ABC EAC ∠∠∠=︒-=︒= 3AB AC= 得3AB AC = 再证AE BE CE == 从而根据面积公式即可求得AC =43 【详解】(1)证明:①四边形ABCD 是平行四边形①AD BC ∥ BAD BCD ∠∠=①BEA DAE ∠∠=①AE CF 、分别是BAD BCD ∠∠、的平分线①BAE DAE ∠∠==12BAD ∠ BCF ∠=12BCD ∠①DAE BCF BEA ∠∠∠==①AE FC①四边形AECF 是平行四边形①AE AF =①四边形AECF 是菱形(2)解:连接AC①AD BC ∥ 60ABC ∠=︒①180120BAD ABC ∠∠=︒-=︒①60BAE DAE ABC ∠∠∠===︒①四边形AECF 是菱形①EAC ∠=1230DAE ∠=︒①90BAC BAE EAC ∠∠∠=+=︒①AC AB ⊥ 9030ACB ABC EAC ∠∠∠=︒-=︒=①AE CE = tan 30tan AB ACB AC ︒=∠=3AB AC= ①3AB AC = ①BAE ABC ∠∠=①AE BE CE ==①ABE 的面积等于43 ①211338322ABC S AC AB AC AC AC =⋅=== ①平行线AB 与DC 间的距离AC =43【点睛】本题考查了平行四边形的判定及性质 菱形的判定 角平分线的定义 等腰三角形的判定 三角函数的应用以及平行线间的距离 熟练掌握平行四边形的判定及性质 菱形的判定 角平分线的定义 等腰三角形的判定 三角函数的应用以及平行线间的距离等知识是解题的关键.18.(2023·四川遂宁·统考中考真题)如图,四边形ABCD 中 AD BC ∥ 点O 为对角线BD 的中点 过点O 的直线l 分别与AD BC 所在的直线相交于点E F .(点E 不与点D 重合)(1)求证:DOE BOF ≌(2)当直线l BD ⊥时 连接BE DF 试判断四边形EBFD 的形状 并说明理由.【答案】(1)见解析 (2)四边形EBFD 为菱形 理由见解析【分析】(1)根据AAS 证明DOE BOF ≌即可(2)连接EB FD 根据DOE BOF ≌ 得出ED BF = 根据ED BF ∥ 证明四边形EBFD 为平行四边形 根据EF BD ⊥ 证明四边形EBFD 为菱形即可.【详解】(1)证明:①点O 为对角线BD 的中点①BO DO =①AD BC ∥①ODE OBF ∠=∠ OED OFB ∠=∠在DOE 和BOF 中ODE OBF OED OFB BO DO ∠=∠⎧⎪∠=∠⎨⎪=⎩①()AAS DOE BOF ≌(2)解:四边形EBFD 为菱形 理由如下:连接EB FD 如图所示:根据解析(1)可知 DOE BOF ≌①ED BF =①ED BF ∥①四边形EBFD 为平行四边形①l BD ⊥ 即EF BD ⊥①四边形EBFD 为菱形.【点睛】本题主要考查了三角形全等的判定和性质 菱形的判定 平行线的性质 解题的关键是熟练掌握三角形全等的判定方法和菱形的判定方法.19.(2023·浙江嘉兴·统考中考真题)如图,在菱形ABCD 中 AE BC ⊥于点E AF CD ⊥于点F 连接EF(1)求证:AE AF =(2)若=60B ∠︒ 求AEF ∠的度数.【答案】(1)证明见解析 (2)60︒【分析】(1)根据菱形的性质的三角形全等即可证明AE AF =.(2)根据菱形的性质和已知条件可推出BAD ∠度数 再根据第一问的三角形全等和直角三角形的性质可求出BAE ∠和DAF ∠度数 从而求出EAF ∠度数 证明了等边三角形AEF 即可求出AEF ∠的度数.【详解】(1)证明:菱形ABCD,AB AD B D ∴=∠=∠又,AE BC AF CD ⊥⊥90AEB AFD ∴∠=∠=︒.在AEB △和AFD △中AEB AFD B DAB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩(AAS)ABE ADF ∴≌.AE AF ∴=.(2)解:菱形ABCD180B BAD ∴∠+∠=︒=60B ∠︒120BAD ∴∠=︒.又90,60AEB B ∠=︒∠=︒30BAE =∴∠︒.由(1)知ABE ADF ≌30BAE DAF ∴∠=∠=︒.120303060EAF ∴∠=︒-︒-︒=︒. =AE AFAEF ∴等边三角形.60AEF ∴∠=︒.【点睛】本题考查了三角形全等 菱形的性质 等边三角形的性质 解题的关键在于熟练掌握全等的方法和菱形的性质.20.(2023·湖北鄂州·统考中考真题)如图,点E 是矩形ABCD 的边BC 上的一点 且AE AD =.(1)尺规作图(请用2B 铅笔):作DAE ∠的平分线AF 交BC 的延长线于点F 连接DF .(保留作图痕迹 不写作法)(2)试判断四边形AEFD 的形状 并说明理由.【答案】(1)见解析 (2)四边形AEFD 是菱形 理由见解析【分析】(1)根据题意结合尺规作角平分线的方法作图即可(2)根据矩形的性质和平行线的性质得出DAF AFE ∠=∠ 结合角平分线的定义可得EFA EAF ∠=∠,则AE EF = 然后根据平行四边形和菱形的判定定理得出结论.【详解】(1)解:如图所示:(2)四边形AEFD 是菱形理由:①矩形ABCD 中 AD BC ∥①DAF AFE ∠=∠①AF 平分DAE ∠①DAF EAF ∠=∠①EFA EAF ∠=∠①AE EF =①AE AD =①AD EF =①AD EF ∥①四边形AEFD 是平行四边形又①AE AD =①平行四边形AEFD 是菱形.【点睛】本题主要考查了尺规作角平分线 矩形的性质 平行线的性质 等腰三角形的判定 平行四边形的判定以及菱形的判定等知识 熟练掌握相关判定定理和性质定理是解题的关键.21.(2023·吉林长春·统考中考真题)将两个完全相同的含有30︒角的直角三角板在同一平面内按如图所示位置摆放.点A E B D 依次在同一直线上 连结AF CD .(1)求证:四边形AFDC 是平行四边形(2)己知6cm BC 当四边形AFDC 是菱形时.AD 的长为__________cm .【答案】(1)见解析 (2)18【分析】(1)由题意可知ACB DFE △≌△易得AC DF = 30CAB FDE ∠=∠=︒即AC DF ∥ 依据一组对边平行且相等的四边形是平行四边形可证明(2)如图,在Rt ACB △中 由30︒角所对的直角边等于斜边的一半和直角三角形锐角互余易得212cm AB BC == 60ABC ∠=︒ 由菱形得对角线平分对角得30CDA FDA ∠=∠=︒ 再由三角形外角和易证BCD CDA ∠=∠即可得6cm BC BD 最后由AD AB BD =+求解即可.【详解】(1)证明:由题意可知ACB DFE △≌△AC DF =∴ 30CAB FDE ∠=∠=︒AC DF ∥∴四边形AFDC 地平行四边形(2)如图,在Rt ACB △中 90ACB ∠=︒ 30CAB ∠=︒ 6cm BC212cm AB BC ∴== 60ABC ∠=︒四边形AFDC 是菱形AD ∴平分CDF ∠30CDA FDA ∴∠=∠=︒ABC CDA BCD ∠=∠+∠603030BCD ABC CDA ∴∠=∠-∠=︒-︒=︒BCD CDA ∴∠=∠6cm BC BD ∴==18cm AD AB BD ∴=+=故答案为:18.【点睛】本题考查了全等三角形的性质 平行四边形的判定 菱形的性质 30︒角所对的直角边等于斜边的一半和直角三角形锐角互余 三角形外角及等角对等边 解题的关键是熟练掌握相关知识综合求解. 22.(2023·湖南张家界·统考中考真题)如图,已知点A D C B 在同一条直线上 且AD BC = AE BF = CE DF =.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方形
三年模拟全练
1.(2015广东河源实验学校月考,5,★☆☆)如图18-2-3-4,在正方形ABCD中,点
E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是()
图18-2-3-4
A.BE=AF
B.∠DAF=∠BEC
C.∠AFB+∠BEC=90°
D.AG⊥BE
2.(2014吉林实验中学期末,5,★★☆)顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH是正方形,需要添加的条件是()
A.AD∥BC,AC=BD
B.AC=BD
C.AC⊥BD,AC=BD
D.AD=AB
3.(2015浙江金华四中质量检测,11,★☆☆)如图18-2-3-5,在四边形ABCD
中,∠ABC=∠BCD=∠CDA=90°,对角线AC与BD相交于点O.若不增加任何字母与辅助线,要使四边形ABCD是正方形,则还需增加的一个条件是________.
图18-2-3-5
4.(2013重庆西南师大附中期末,10,★☆☆)如图18-2-3-6所示,直线a经过正方形ABCD的顶点A,分别过此正方形的顶点B、D作BF⊥a于点F、DE⊥a于点E,若DE=8,BF=5,则EF的长是________.
图18-2-3-6
五年中考全练
1.(2015山东日照,6,★☆☆)小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使▱ABCD为正方形(如图18-2-3-7),现有下列四种选法,你认为其中错误的是()
图18-2-3-7
A.①②
B.②③
C.①③
D.②④
2.(2014广东广州,8,★☆☆)将四根长度相等的细木条首尾相接,用钉子钉成四边形ABCD,转动这个四边形,使它形状改变.当∠B=90°时,如图18-2-3-8①,测得AC=2.当∠B=60°时,如图18-2-3-8②,AC=()
图18-2-3-8
A. B.2 C. D.2
3.(2015广西南宁,16,★★☆)如图18-2-3-9,在正方形ABCD的外侧,作等边
△ADE,则∠BED的度数为________°.
图18-2-3-9
4.(2014江苏宿迁,14,★★☆)如图18-2-3-10,正方形ABCD的边长为2,点E为边BC的中点,点P在对角线BD上移动,则PE+PC的最小值是________.
图18-2-3-10
5.(2015湖北恩施,18,★☆☆)如图18-2-3-11,四边形ABCD、BEFG均为正方形,连接AG、CE.(10分)
(1)求证:AG=CE;
(2)求证:AG⊥CE.
图18-2-3-11
6.(2013辽宁铁岭,20,★★☆)如图18-2-3-12,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(12
分)
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.
图18-2-3-12
探究创新全练
1.操作示例
对于边长为a的两个正方形ABCD和EFGH,按图18-2-3-13所示的方式摆放,沿虚线BD、EG剪开后,可以按图18-2-3-13所示的移动方式拼接为四边形BNED.从拼接的过程容易得到结论:
①四边形BNED是正方形;
②S
+S正方形EFGH=S正方形BNED.
正方形ABCD
图18-2-3-13
实践与探究
(1)对于边长分别为a,b(a>b)的两个正方形ABCD和EFGH,按图18-2-3-14所示的方式摆放,连接DE,过点D作DM⊥DE,交AB于点M,过点M作MN⊥DM,过点E 作EN⊥DE,MN与EN相交于点N.
①证明:四边形MNED是正方形,并用含a,b的代数式表示正方形MNED的面积;
②在图18-2-3-14中,将正方形ABCD和正方形EFGH沿虚线剪开后,能够拼接为正方形MNED,请简略说明你的拼接方法(类比图18-2-3-13,用数字表示对应的图形);
图18-2-3-14
(2)对于n(n是大于2的自然数)个任意的正方形,能否通过若干次拼接,将其拼接成为一个正方形?请简要说明你的理由.。
