2013年临沂数学中考试题
2013年临沂市初中学生学业考试试题 数 学
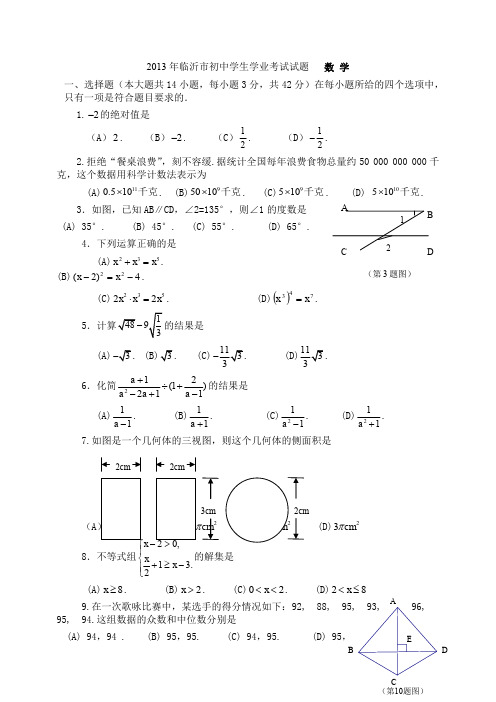
(第10题图)EDCBA(第3题图)2013年临沂市初中学生学业考试试题 数 学一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的. 1.2-的绝对值是(A )2. (B )2-. (C )12. (D )12-. 2.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学计数法表示为(A)110.510⨯千克. (B)95010⨯千克. (C)9510⨯千克. (D) 10510⨯千克. 3.如图,已知AB ∥CD ,∠2=135°,则∠1的度数是 (A) 35°. (B) 45°. (C) 55°. (D) 65°.4.下列运算正确的是(A)235x x x +=.(B)4)2(22-=-x x .(C)23522x x x ⋅=. (D)()743x x=.5(A)(C). 6.化简212(1211a a a a +÷+-+-的结果是 (A)11a -. (B)11a +. (C)211a -. (D)211a +. 7.如图是一个几何体的三视图,则这个几何体的侧面积是(A23cm π8.不等式组1 3.2x x x ⎪⎨+≥-⎪⎩的解集是(A)8x ≥. (B)2x >. (C)02x <<. (D)28x <≤ 9.在一次歌咏比赛中,某选手的得分情况如下:92, 88, 95, 93,96,95, 94.这组数据的众数和中位数分别是(A) 94,94 . (B) 95,95. (C) 94,95. (D) 95,3cmCDF)(C )(D )O1A 2A1B2BxyA (第11题图)(第12题图)94.10.如图,四边形ABCD 中,AC 垂直平分BD,垂足为E,下列 结论不一定...成立的是 (A ) AB=AD. (B) AC 平分∠BCD. (C) AB=BD. (D) △BEC ≌△DEC.11.如图,在平面直角坐标系中,点A 1 , A 2在x 轴上,点B 1,B 2在y 轴上,其坐标分别为A 1(1,0),A 2(2,0),B 1(0,1),B 2(0,2),分别以A 1A 2B 1B 2其中的任意两点与点..O .为顶点作三角形,所作三角形是等腰三角形的概率是(A ) 3 4. (B) 1 3. (C) 23. (D) 1 2.12.如图,在⊙O 中,∠CBO=45°,∠CAO=15°,则∠AOB 的度数是 (A)75°. (B)60°. (C)45°. (D)30°. 13.如图,等边三角形OAB 的一边OA 在x 轴上,双曲线xy 3在第一象限内的图像经过OB 边的中点C ,则点B 的坐标是(A )( 1, 3). (B )(3, 1 ). (C )( 2 ,32). (D )(32 ,2 ).14、如图,正方形ABCD 中,AB=8cm,对角线AC,BD 相交于点O,点E,F 分别从B,C 两点同时出发,以1cm/s 的 速度沿BC,CD 运动,到点C,D 时停止运动,设运动时间 为t(s),△OEF 的面积为s(2cm ),则s(2cm )与t(s)的 函数关系可用图像表示为(第18题图) (第17题图)DCBDB选项A B C D图1图2二、填空题(本大题共5小题,每小题3分,共15分)把答案填在题中横线上. 15.分解因式24x x -= . 16.分式方程21311x x x+=--的解是 . 17.如图,菱形ABCD 中,AB =4,o 60B ∠=,,AE BC AF CD ⊥⊥,垂足分别为E,F,连接EF,则的△AEF 的面积是 .18等腰梯形ABCD 中,//,,,AD BC DE BC BD DC ⊥⊥垂足分别为E,D,DE=3,BD=5,则腰长AB=19. 对于实数a,b,定义运算“﹡”:a ﹡b=22(),).a ab a b ab ba b ⎧-≥⎪⎨-<⎪⎩(例如4﹡2,因为4>2,所以4﹡224428=-⨯=.若12,x x 是一元二次方程2560x x -+=的两个根,则1x ﹡2x =三、开动脑筋,你一定能做对!(本大题共3小题,共21分) 20.(本小题满分7分)2013年1月1日新交通法规开始实施。
2013年山东省临沂市初中学生学业考试数学(含答案)

3 在第一象限内的图像经过 OB 边的中点 C, x
3 ). (B)( 3 , 1 ). (C)( 2 , 2 3 ). (D)( 2 3 ,2 ).
14、如图,正方形 ABCD 中,AB=8cm,对角线 AC,BD 相交 于点 O,点 E,F 分别从 B,C 两点同时出发,以 1cm/s 的速度沿 BC,CD 运动,到点 C,D 时停止运动,设运动时间为 t(s),△OEF
11
(B) 50 10 千克 .
9
(C) 5 10 千克 .
9
(D) 5 10 千克 .
10
3.如图,已知 AB∥CD,∠2=135°,则∠1 的度数是 (A) 35°. (B) 45°. (C) 55°. (D) 65°. 4.下列运算正确的是 (A) (C) 2 x x 2 x .
(D) 3 cm
(第 11 题图)
x 2 0, 8.不等式组 x 的解集是 1 x 3. 2
(第 12 题图)
第 13 题图
(A) x 8 . (B) x 2 . (C) 0 x 2 . (D) 2 x 8 9.在一次歌咏比赛中, 某选手的得分情况如下: 92, 88, 95, 93, 众数和中位数分别是 (A) 94,94 . (B) 95,95. (C) 94,95. (D) 95, 10.如图,四边形 ABCD 中,AC 垂直平分 BD,垂足为 E, 立的是 (A) AB=AD. (B) AC 平分∠BCD. (C) AB=BD. B (D) △BEC≌△DEC. 11.如图,在平面直角坐标系中,点 A1 , A2 在 x 轴上,点 B1,B2 A1(1,0),A2(2,0),B1(0,1),B2(0,2) ,分别以 A1A2B1B2 其中的任意 形,所作三角形是等腰三角形的概率是 (A) 3 . 4 (B) 1 . 3 (C). (D) 1 . 2
2013年山东省临沂市中考数学试题及答案(解析版)

2013年山东省临沂市中考数学试题及答案(解析版)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第I 卷1至4页,第II 卷5至12页.共120分.考试时间120分钟. 第Ⅰ卷(选择题 共42分)一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的. 1.2-的绝对值是(A )2.(B )2-. (C )12. (D )12-. 答案:A解析:负数的绝对值是它的相反数,故选A 。
2.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学计数法表示为(A)110.510⨯千克. (B)95010⨯千克. (C)9510⨯千克. (D) 10510⨯千克. 答案:D解析:科学记数法的表示形式为a ×10n的形式,其中1≤|a |<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数. 50 000 000 000=10510⨯千克3.如图,已知AB ∥CD ,∠2=135°,则∠1的度数是 (A) 35°. (B) 45°. (C) 55°. (D) 65°. 答案:B解析:因为∠2=135°,所以,∠2的邻补角为45°,又两直线平行,内错角相等,所以,∠1=45°4.下列运算正确的是(A)235x x x +=. (B)4)2(22-=-x x . (C)23522x x x ⋅=. (D)()743xx =.答案:C解析:对于A ,不是同类项不能相加,故错;完全平方展开后有三项,故B 也错;由幂的乘方知()4312xx =,故D 错,选C 。
5(A)(C)答案:B 解析93⨯=B 。
2013年山东省临沂市中考数学试卷-普通用卷

2013年山东省临沂市中考数学试卷学校:___________姓名:___________班级:___________考号:___________一、选择题(本大题共14小题,共42.0分)1.−2的绝对值是()A. 2B. −2C. 12D. −122.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50000000000千克,这个数据用科学记数法表示为()A. 0.5×1011千克B. 50×109千克C.5×109千克 D. 5×1010千克3.如图,已知AB//CD,∠2=135°,则∠1的度数是()A. 35°B. 45°C. 55°D. 65°4.下列运算正确的是()A. x2+x3=x5B. (x−2)2=x2−4C. 2x2⋅x3=2x5D. (x3)4=x75.计算√48−9√13的结果是()A. −√3B. √3C. −113√3 D. 113√36. 化简a+1a 2−2a+1÷(1+2a−1)的结果是( ) A. 1a−1B.1a+1C.1a 2−1D.1a 2+17. 如图是一个几何体的三视图,则这个几何体的侧面积是( )A. 12πcm 2B. 8πcm 2C. 6πcm 2D. 3πcm 28. 不等式组{x −2>0x 2+1≥x −3的解集是( )A. x ≥8B. x >2C. 0<x <2D. 2<x ≤89. 在一次歌咏比赛中,某选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是( ) A. 94,94B. 95,95C. 94,95D. 95,9410. 如图,四边形ABCD 中,AC 垂直平分BD ,垂足为E ,下列结论不一定成立的是( )A. AB =ADB. AC 平分∠BCDC. AB =BDD. △BEC≌△DEC11. 如图,在平面直角坐标系中,点A 1,A 2在x 轴上,点B 1,B 2在y 轴上,其坐标分别为A 1(1,0),A 2(2,0),B 1(0,1),B 2(0,2),分别以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形,所作三角形是等腰三角形的概率是()A. 34B. 13C. 23D. 1212.如图,在⊙O中,∠CBO=45°,∠CAO=15°,则∠AOB的度数是()A. 75°B. 60°C. 45°D. 30°13.如图,等边三角形OAB的一边OA在x轴上,双曲线y=√3x在第一象限内的图象经过OB边的中点C,则点B的坐标是()A. (1,√3)B. (√3,1)C. (2,2√3)D. (2√3,2)14.如图,正方形ABCD中,AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发,以1cm/s的速度沿BC,CD运动,到点C,D时停止运动,设运动时间为t(s),△OEF的面积为s(cm2),则s(cm2)与t(s)的函数关系可用图象表示为()A.B.C.D.二、填空题(本大题共5小题,共15.0分)15.因式分解4x−x3=.16.分式方程2xx−1+11−x=3的解是.17. 如图,菱形ABCD 中,AB =4,∠B =60°,AE ⊥BC ,AF ⊥CD ,垂足分别为E ,F ,连接EF ,则△AEF 的面积是 .18. 如图,等腰梯形ABCD 中,AD//BC ,DE ⊥BC ,BD ⊥DC ,垂足分别为E ,D ,DE =3,BD =5,则腰长AB = .19. 对于实数a ,b ,定义运算“﹡”:a ﹡b ={a 2−ab(a ≥b)ab −b 2(a <b)..例如4﹡2,因为4>2,所以4﹡2=42−4×2=8.若x 1,x 2是一元二次方程x 2−5x +6=0的两个根,则x 1﹡x 2= . 三、解答题(本大题共7小题,共63.0分)20. 2013年1月1日新交通法规开始实施.为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A :从不闯红灯;B :偶尔闯红灯;C :经常闯红灯;D :其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,解答下列问题:(1)本次调查共选取名居民;(2)求出扇形统计图中“C”所对扇形的圆心角的度数,并将条形统计图补充完整;(3)如果该社区共有居民1600人,估计有多少人从不闯红灯?21.为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A 型学习用品的单价为20元,B型学习用品的单价为30元.(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?22.如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:AF=DC;(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.23.如图,在△ABC中,∠ACB=90°,E为BC上一点,以CE为直径作⊙O,AB与⊙O相切于点D,连接CD,若BE=OE=2.(1)求证:∠A=2∠DCB;(2)求图中阴影部分的面积(结果保留π和根号).24.某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y与生产数量x之间是一次函数关系,函数y与自变量x的部分对应值如下表:(1)求y与x之间的函数关系式,并写出自变量x的取值范围;(2)求该机器的生产数量;(3)市场调查发现,这种机器每月销售量z(台)与售价a(万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价−成本)25.如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.(1)当PE⊥AB,PF⊥BC时,如图1,则PE的值为;PF(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求PE的值;PF(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,PE的值是否变化?证明你的结论.PF)三点.26.如图,抛物线经过A(−1,0),B(5,0),C(0,−52(1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N 的坐标;若不存在,请说明理由.答案和解析1.【答案】A【解析】试题分析:根据负数的绝对值等于它的相反数解答.−2的绝对值是2,即|−2|=2.故选A.2.【答案】D【解析】试题分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.将50000000000用科学记数法表示为5×1010.故选D.3.【答案】B【解析】试题分析:先求出∠3的度数,再根据平行线性质得出∠1=∠3,代入求出即可.∵AB//CD,∴∠1=∠3,∵∠2=135°,∴∠3=180°−135°=45°,∴∠1=45°,故选B.4.【答案】C【解析】A、本选项不是同类项,不能合并,错误;B、原式利用完全平方公式展开得到结果,即可作出判断;C、原式利用单项式乘单项式法则计算得到结果,即可作出判断;D、原式利用幂的乘方运算法则计算得到结果,即可作出判断.5.【答案】B【解析】试题分析:首先把两个二次根式化简,再进行加减即可.√48−9√13=4√3−3√3=√3,故选:B.6.【答案】A【解析】试题分析:首先把括号里的式子进行通分,然后把除法运算转化成乘法运算,进行约分化简.a+1a2−2a+1÷(1+2a−1)=a+1(a−1)2⋅a−1 a−1+2=1a−1.故选A .7.【答案】C【解析】试题分析:首先判断出该几何体,然后计算其面积即可. 观察三视图知:该几何体为圆柱,高为3cm ,底面直径为2cm , 侧面积为:πdℎ=2×3π=6π,故选C .8.【答案】D【解析】试题分析:先求出不等式的解集,再根据不等式的解集找出不等式组的解集即可.{x −2>0 ①x 2+1≥x −3 ② ∵解不等式①得:x >2,解不等式②得:x ≤8,∴不等式组的解集为2<x ≤8,故选D .9.【答案】D【解析】试题分析:根据众数、中位数的定义求解即可. 这组数据按顺序排列为:88,92,93,94,95,95,96, 故众数为:95,中位数为:94.故选D .10.【答案】C【解析】试题分析:根据线段垂直平分线上任意一点,到线段两端点的距离相等可得AB=AD,BC=CD,再根据等腰三角形三线合一的性质可得AC平分∠BCD,EB=DE,进而可证明△BEC≌△DEC.∵AC垂直平分BD,∴AB=AD,BC=CD,∴AC平分∠BCD,EB=DE,∴∠BCE=∠DCE,在Rt△BCE和Rt△DCE中,{BE=EDBC=CD,∴Rt△BCE≌Rt△DCE(HL),故选:C.11.【答案】D【解析】试题分析:根据题意画出树状图,进而得出以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形是等腰三角形的情况,求出概率即可.∵以A1、A2、B1、B2其中的任意两点与点O为顶点作三角形,∴画树状图得:共可以组成4个三角形,所作三角形是等腰三角形只有:△OA1B1,△OA2B2,所作三角形是等腰三角形的概率是:24=12.故选:D.12.【答案】B【解析】试题分析:首先连接OC,由OB=OC=OA,∠CBO=45°,∠CAO=15°,根据等边对等角的性质,可求得∠OCB与∠OCA的度数,即可求得∠ACB的度数,又由圆周角定理,求得∠AOB的度数.连接OC,∵OB=OC=OA,∠CBO=45°,∠CAO=15°,∴∠OCB=∠OBC=45°,∠OCA=∠OAC=15°,∴∠ACB=∠OCB−∠OCA=30°,∴∠AOB=2∠ACB=60°.故选B.13.【答案】C【解析】试题分析:过点B作BD⊥x轴,垂足为D,设点B的坐标为(a,b)(a>0),再求出b和a的关系和C点的坐标,由点C在双曲线y=√3x上,求出a的值,进而求出B点坐标.过点B作BD⊥x轴,垂足为D,设点B的坐标为(a,b)(a>0),∵三角形OAB是等边三角形,∴∠BOA=60°,在Rt△BOA中,tan60°=DBOD =ba,∴b=√3a,∵点C是OB的中点,∴点C坐标为(a2,√3a2),∵点C在双曲线y=√3x上,∴√34a2=√3,∴a=2,∴点B的坐标是(2,2√3),故选C.14.【答案】B【解析】试题分析:由点E,F分别从B,C两点同时出发,以1cm/s 的速度沿BC,CD运动,得到BE=CF=t,则CE=8−t,再根据正方形的性质的OB=OC,∠OBC=∠OCD=45°,然后根据“SAS”可判断△OBE≌△OCF,所以S△OBE=S△OCF,这样S四边形OECF =S△OBC=16,于是S=S四边形OECF−S△CEF=16−12(8−t)⋅t ,然后配方得到S =12(t −4)2+8(0≤t ≤8),最后利用解析式和二次函数的性质对各选项进行判断.根据题意BE =CF =t ,CE =8−t ,∵四边形ABCD 为正方形,∴OB =OC ,∠OBC =∠OCD =45°,∵在△OBE 和△OCF 中{OB =OC ∠OBE =∠OCF BE =CF,∴△OBE≌△OCF(SAS),∴S △OBE =S △OCF ,∴S 四边形OECF =S △OBC =14×82=16, ∴S =S 四边形OECF −S △CEF =16−12(8−t)⋅t =12t 2−4t +16=12(t −4)2+8(0≤t ≤8),∴s(cm 2)与t(s)的函数图象为抛物线一部分,顶点为(4,8),自变量为0≤t ≤8.故选B .15.【答案】−x(x +2)(x −2)【解析】试题分析:先提出公因式,再用平方差公式因式分解. 4x −x 3=−x(x 2−4)=−x(x +2)(x −2).故答案是:−x(x +2)(x −2).16.【答案】x=2【解析】【分析】此题是分式方程的解法,解分式方程的步骤是去分母,去括号,移项,合并同类项,系数化为1,最后必须检验.分式方程变形后,去分母转化为整式方程,求出整式方程得到解得到x的值,经检验即可得到分式方程的解.【解答】解:去分母得:2x−1=3(x−1),去括号得:2x−1=3x−3,解得:x=2,经检验x=2是分式方程的解.故答案为:x=217.【答案】3√3【解析】试题分析:首先利用菱形的性质及等边三角形的判定可得判断出△AEF是等边三角形,再根据三角函数计算出AE=EF的值,再过A作AM⊥EF,再进一步利用三角函数计算出AM的值,即可算出三角形的面积.∵四边形ABCD是菱形,∴BC=CD,∠B=∠D=60°,∵AE⊥BC,AF⊥CD,∴AB⋅AE=AD⋅AF,∠BAE=∠DAF=30°,∴AE=AF,∵∠B=60°,∴∠BAD=120°,∴∠EAF=120°−30°−30°=60°,∴△AEF是等边三角形,∴AE=EF,∠AEF=60°,∵AB=4,∴AE=2√3,∴EF=AE=2√3,过A作AM⊥EF,∴AM=AE⋅sin60°=3,∴△AEF的面积是:12EF⋅AM=12×2√3×3=3√3.故答案为:3√3.18.【答案】154【解析】试题分析:利用勾股定理列式求出BE的长,再利用∠CBD 的正切值列式求出CD,然后根据等腰梯形的腰长相等解答.∵DE=3,BD=5,DE⊥BC,∴BE=√BD2−DE2=√52−32=4,又∵BD⊥DC,∴tan∠CBD=CDBD =DEBE,即CD 5=34,解得CD =154,∵梯形ABCD 是等腰梯形,AD//BC ,∴AB =CD =154. 故答案为:154.19.【答案】3或−3【解析】试题分析:首先解方程x 2−5x +6=0,再根据a ﹡b ={a 2−ab(a ≥b)ab −b 2(a <b).,求出x 1﹡x 2的值即可. ∵x 1,x 2是一元二次方程x 2−5x +6=0的两个根, ∴(x −3)(x −2)=0,解得:x =3或2,①当x 1=3,x 2=2时,x 1﹡x 2=32−3×2=3; ②当x 1=2,x 2=3时,x 1﹡x 2=3×2−32=−3. 故答案为:3或−3.20.【答案】解:(1)本次调查的居民人数=56÷70%=80人;(2)为“C ”的人数为:80−56−12−4=8人, “C ”所对扇形的圆心角的度数为: ×360°=36° 补全统计图如图;(3)该区从不闯红灯的人数=1600×70%=1120人.【解析】试题分析:(1)根据为A 的人数与所占的百分比列式计算即可求出被调查的居民人数;(2)求出为C 的人数,得到所占的百分比,然后乘以360°,从而求出扇形统计图中“C ”所对扇形的圆心角的度数,然后补全条形统计图即可;(3)用全区总人数乘以从不闯红灯的人数所占的百分比,进行计算即可得解.21.【答案】解:(1)设购买A 型学习用品x 件,B 型学习用品y 件,由题意,得{x +y =100020x +30y =26000, 解得:{x =400y =600. 答:购买A 型学习用品400件,B 型学习用品600件;(2)设可以购买B 型学习用品a 件,则A 型学习用品(1000−a)件,由题意,得20(1000−a)+30a ≤28000,解得:a ≤800答:最多购买B 型学习用品800件.【解析】(1)设购买A 型学习用品x 件,B 型学习用品y 件,就有x +y =1000,20x +30y =26000,由这两个方程构成方程组求出其解就可以得出结论;(2)设可以购买B 型学习用品a 件,则A 型学习用品(1000−a)件,根据这批学习用品的钱不超过28000元建立不等式求出其解即可. 22.【答案】(1)证明:∵AF//BC ,∴∠AFE =∠DBE ,∵E 是AD 的中点,AD 是BC 边上的中线,∴AE =DE ,BD =CD ,在△AFE 和△DBE 中{∠AFE =∠DBE ∠FEA =∠BED AE =DE∴△AFE≌△DBE(AAS),∴AF =BD ,∴AF =DC .(2)四边形ADCF 是菱形,证明:AF//BC ,AF =DC ,∴四边形ADCF 是平行四边形,∵AC ⊥AB ,AD 是斜边BC 的中线,∴AD =DC ,∴平行四边形ADCF是菱形.【解析】(1)根据AAS证△AFE≌△DBE,推出AF=BD,即可得出答案;(2)得出四边形ADCF是平行四边形,根据直角三角形斜边上中线性质得出CD=AD,根据菱形的判定推出即可.23.【答案】(1)证明:连接OD,∵AB是⊙O切线,∴∠ODB=90°,∴BE=OE=OD=2,∴∠B=30°,∠DOB=60°,∵OD=OC,∴∠DCB=∠ODC=∠DOB=30°,∵在△ABC中,∠ACB=90°,∠B=30°,∴∠A=60°,∴∠A=2∠DCB;(2)解:∵∠ODB=90°,OD=2,BO=2+2=4,由勾股定理得:BD=2,∴阴影部分的面积S=S △ODB−S扇形DOE=×2×2−=2−π.【解析】(1)连接OD ,求出∠ODB =90°,求出∠B =30°,∠DOB =60°,求出∠DCB 度数,关键三角形内角和定理求出∠A ,即可得出答案;(2)根据勾股定理求出BD ,分别求出△ODB 和扇形DOE 的度数,即可得出答案.24.【答案】解:(1)设y 与x 之间的关系式为y =kx +b ,由题意,得{60=10kb 50=30kb, 解得:{k =−12b =65, ∴y =−12x +65. ∵该机器生产数量至少为10台,但不超过70台,∴10≤x ≤70;(2)由题意,得xy =2000,−12x 2+65x =2000, −x 2+130x −4000=0,解得:x 1=50,x 2=80>70(舍去).答:该机器的生产数量为50台;(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z =ma +n ,由函数图象,得{35=55mn 15=75mn , 解得:{m =−1n =90, ∴z =−a +90.当z =25时,a =65.当x =50时,y =40总利润为:25(65−40)=625万元. 答:该厂第一个月销售这种机器的利润为625万元.【解析】试题分析:(1)设y 与x 之间的关系式为y =kx +b ,运用待定系数法就可以求出其关系式,由该机器生产数量至少为10台,但不超过70台就可以确定自变量的取值范围;(2)根据每台的成本乘以生产数量等于总成本建立方程求出其解即可;(3)设每月销售量z(台)与售价a(万元∕台)之间的函数关系式为z =ma +n ,运用待定系数法求出其解析式,再将z =25代入解析式求出a 的值,就可以求出每台的利润,从而求出总利润. 25.【答案】解:(1);∵矩形ABCD ,∴AB ⊥BC ,PA =PC ;∵PE ⊥AB ,BC ⊥AB ,∴PE//BC ,∴∠APE =∠PCF ;∵PF ⊥BC ,AB ⊥BC ,∴PF//AB ,∴∠PAE=∠CPF.∵在△APE与△PCF中,∴△APE≌△PCF(ASA),∴PE=CF.在Rt△PCF中,=tan30°=,∴=.(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN.∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN,又∵∠PME=∠PNF=90°,∴△PME∽△PNF,∴.由(1)知,=,∴=.(3)答:变化.证明:如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM//BC,PN//AB.∵PM//BC,PN//AB,∴∠APM=∠PCN,∠PAM=∠CPN,∴△APM∽△PCN,∴,得CN=2PM.在Rt△PCN中,=tan30°=,∴=.∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN,又∵∠PME=∠PNF=90°,∴△PME∽△PNF,∴=.∴的值发生变化.【解析】试题分析:(1)证明△APE≌△PCF,得PE=CF;在Rt△PCF中,解直角三角形求得的值;(2)如答图1所示,作辅助线,构造直角三角形,证明△PME∽△PNF,并利用(1)的结论,求得的值;(3)如答图2所示,作辅助线,构造直角三角形,首先证明△APM∽△PCN,求得的值;然后证明△PME∽△PNF,从而由求得的值.与(1)(2)问相比较,的值发生了变化. 26.【答案】解:(1)设抛物线的解析式为y =ax 2+bx +c(a ≠0), ∵A(−1,0),B(5,0),C(0,−52)三点在抛物线上, ∴{a−bc =025a5bc =0c =−52, 解得{a =12b =−2c =−52.∴抛物线的解析式为:y =12x 2−2x −52;(2)∵抛物线的解析式为:y =12x 2−2x −52, ∴其对称轴为直线x =−b 2a =−−22×12=2,连接BC ,如图1所示,∵B(5,0),C(0,−52),∴设直线BC 的解析式为y =kx +b(k ≠0),∴{5kb =0b =−52,解得{k =12b =−52,∴直线BC 的解析式为y =12x −52,当x =2时,y =1−52=−32,∴P(2,−32);(3)存在.如图2所示,①当点N 在x 轴下方时,∵抛物线的对称轴为直线x =2,C(0,−52),∴N 1(4,−52);②当点N 在x 轴上方时,如图,过点N 2作ND ⊥x 轴于点D ,在△AN 2D 与△M 2CO 中,{∠N2AD =∠CM2OAN 2=CM 2∠AN 2D =∠M 2CO∴△AN 2D≌△M 2CO(ASA),∴N 2D =OC =52,即N 2点的纵坐标为52.∴12x 2−2x −52=52, 解得x =2+√14或x =2−√14,∴N 2(2+√14,52),N 3(2−√14,52).综上所述,符合条件的点N 的坐标为(4,−52),(2+√14,52)或(2−).√14,52【解析】(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把)三点代入求出a、b、c的值即可;A(−1,0),B(5,0),C(0,−52(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.。
2013年山东省临沂市2013年中考数学试题(解析版)

2013年临沂市初中学生学业考试试题数 学(解析)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第I 卷1至4页,第II 卷5至12页.共120分.考试时间120分钟. 第Ⅰ卷(选择题 共42分)一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的. 1.2-的绝对值是(A )2.(B )2-. (C )12. (D )12-. 答案:A解析:负数的绝对值是它的相反数,故选A 。
2.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学计数法表示为(A)110.510⨯千克. (B)95010⨯千克. (C)9510⨯千克. (D) 10510⨯千克. 答案:D解析:科学记数法的表示形式为a ×10n的形式,其中1≤|a |<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数. 50 000 000 000=10510⨯千克3.如图,已知AB ∥CD ,∠2=135°,则∠1的度数是 (A) 35°. (B) 45°. (C) 55°. (D) 65°. 答案:B解析:因为∠2=135°,所以,∠2的邻补角为45°,又两直线平行,内错角相等,所以,∠1=45°4.下列运算正确的是(A)235x x x +=. (B)4)2(22-=-x x . (C)23522x x x ⋅=. (D)()743x x =.答案:C解析:对于A ,不是同类项不能相加,故错;完全平方展开后有三项,故B 也错;由幂的乘方知()4312x x =,故D 错,选C 。
5(A)(C). 答案:B 解析=9=B 。
临沂市初中学生学业考试试题.doc

(第3题图)2013年临沂市初中学生学业考试试题数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第I 卷1至4页,第II 卷5至12页.共120分.考试时间120分钟.第Ⅰ卷(选择题 共42分)注意事项:1. 答第I 卷前,考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.2. 每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他的答案,不能答在试卷上. 3. 考试结束,将本试卷和答题卡一并收回.一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的. 1.2-的绝对值是(A )2.(B )2-. (C )12. (D )12-. 2.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学计数法表示为(A)110.510⨯千克. (B)95010⨯千克.(C)9510⨯千克. (D) 10510⨯千克.3.如图,已知AB ∥CD ,∠2=135°,则∠1的度数是 (A) 35°. (B) 45°. (C) 55°. (D) 65°.4.下列运算正确的是(A)235x x x +=. (B)4)2(22-=-x x .(C)23522x x x ⋅=. (D)()743x x =.5的结果是(A)..(C). 6.化简212(1)211a a a a +÷+-+-的结果是(A)11a -. (B)11a +. (C)211a -. (D)211a +. 7.如图是一个几何体的三视图,则这个几何体的侧面积是(A )212cm π (B )28cm π (C)26cm π (D)23cm π8.不等式组20,1 3.2x x x ->⎧⎪⎨+≥-⎪⎩的解集是3cm(第10题图)EDCBA(A)8x ≥. (B)2x >. (C)02x <<. (D)28x <≤9.在一次歌咏比赛中,某选手的得分情况如下:92, 88, 95, 93, 96, 95, 94.这组数据的众数和中位数分别是(A) 94,94 . (B) 95,95. (C) 94,95. (D) 95,94.10.如图,四边形ABCD 中,AC 垂直平分BD,垂足为E,下列结论不一定...成立的是 (A ) AB=AD. (B) AC 平分∠BCD.(C) AB=BD. (D) △BEC ≌△DEC.11.如图,在平面直角坐标系中,点A 1 , A 2在x 轴上,点B 1,B 2在y 轴上,其坐标分别为A 1(1,0),A 2(2,0),B 1(0,1),B 2(0,2),分别以A 1A 2B 1B 2其中的任意两点与点..O .为顶点作三角形,所作三角形是等腰三角形的概率是(A ) 3 4. (B) 1 3. (C) 23. (D) 1 2.12.如图,在⊙O 中,∠CBO=45°,∠CAO=15°,则∠AOB 的度数是 (A)75°. (B)60°. (C)45°. (D)30°.13.如图,等边三角形OAB 的一边OA 在x 轴上,双曲线xy 3=在第一象限内的图像经过OB 边的中点C ,则点B 的坐标是(A )( 1, 3). (B )(3, 1 ). (C )( 2 ,32). (D )(32 ,2 ).A CDF(第14题图)B(A )(B )(C )(D )O1A2A1B2BxyA(第11题图) (第12题图) 第13题图14、如图,正方形ABCD 中,AB=8cm,对角线AC,BD 相交 于点O,点E,F 分别从B,C 两点同时出发,以1cm/s 的速度沿BC,CD 运动,到点C,D 时停止运动,设运动时间为t(s),△OEF的面积为s(2cm ),则s(2cm )与t(s)的函数关系可用图像表(第18题图)(第17题图)DCBDB2013年临沂市初中学生学业考试试题数 学第Ⅱ卷(非选择题 共78分).注意事项:1.第II 卷共8页,请用钢笔或圆珠笔直接答在试卷上。
2013年山东临沂中考数学典型选择题汇总

2013年山东临沂中考数学典型选择题汇总
中考数学考什么,这是考生和家长最关心的问题。
以往的中考考题主要体现在对知识点的考查上,强调知识点的覆盖面,对能力的考查没有放在一个突出的位置上。
近几年的中考命题发生了明显的变化,既强调了由知识层面向能力层面的转化,又强调了基础知识与能力并重。
注重在知识的交汇处设计命题,对学生能力的考查也提出了较高的要求。
中考数学重点考查学生的数学思维能力已经成为趋势和共识。
初三学生可利用寒假时间对数学思想方法进行梳理、总结,逐个认识它们的本质特征、思维程序和操作程序。
有针对性地通过典型题目进行训练,能够真正适应中考命题。
2013年山东省临沂市中考数学试卷及答案解析

a
2) 1
的结果是
(
)
A. 1 a 1
B. 1 a 1
C.
1 a2
1
7.(3 分)如图是一个几何体的三视图,则这个几何体的侧面积是 (
D. 11 3 3
D.
1 a2
1
)
A.12 cm2
B. 8 cm2
C. 6 cm2
第 1页(共 31页)
D. 3 cm2
8.(3
分)不等式组
14.(3 分)如图,正方形 ABCD 中, AB 8cm ,对角线 AC , BD 相交于点 O ,点 E , F 分 别从 B , C 两点同时出发,以1cm / s 的速度沿 BC , CD 运动,到点 C , D 时停止运动,
设运动时间为 t(s) , OEF 的面积为 s(cm2 ) ,则 s(cm2 ) 与 t(s) 的函数关系可用图象表示
A.2
B. 2
C. 1 2
【分析】根据负数的绝对值等于它的相反数解答.
D. 1 2
【解答】解: 2 的绝对值是 2, 即 | 2 | 2 .
故选: A .
【点评】本题考查了绝对值的性质:正数的绝对值是它本身;负数的绝对值是它的相反数;
0 的绝对值是 0.
2.(3 分)拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约 50 000 000 000 千克,这个数据用科学记数法表示为 ( )
五、相信自己,加油呀!(本大题共 2 小题,共 24 分)
25.(11 分)如图,矩形 ABCD 中, ACB 30 ,将一块直角三角板的直角顶点 P 放在两
对角线 AC , BD 的交点处,以点 P 为旋转中心转动三角板,并保证三角板的两直角边分
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ABC D1 2 (第3题图)2013年临沂市初中学生数 学学业考试试题一、选择题(本大题共14小题,每小题3分,共42分)在每小题所给的四个选项中,只有一项是符合题目要求的.1.2-的绝对值是(A )2.(B )2-. (C )12. (D )12-. 2.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学计数法表示为(A)110.510⨯千克. (B)95010⨯千克. (C)9510⨯千克. (D) 10510⨯千克.3.如图,已知AB ∥CD ,∠2=135°,则∠1的度数是 (A) 35°. (B) 45°. (C) 55°. (D) 65°.4.下列运算正确的是(A)235x x x +=. (B)4)2(22-=-x x (C)23522x x x ⋅=. (D)()743x x =.5.计算14893-的结果是 (A)3-. (B)3. (C)1133-. (D)1133. 6.化简212(1)211a a a a +÷+-+-的结果是 (A)11a -. (B)11a +. (C)211a -. (D)211a +.7.如图是一个几何体的三视图,则这个几何体的侧面积是(A )212cm π (B )28cm π (C)26cm π (D)23cm π8.不等式组20,1 3.2x x x ->⎧⎪⎨+≥-⎪⎩的解集是(A)8x ≥. (B)2x >. (C)02x <<. (D)28x <≤2cm2cm3cm2cmA CDOEF(第14题图)B(第10题图)EDCB AO1A2A1B2B xyO BAC OABC (第11题图)(第12题图) 第13题图9.在一次歌咏比赛中,某选手的得分情况如下:92, 88, 95, 93, 96, 95, 94.这组数据的众数和中位数分别是(A) 94,94 . (B) 95,95. (C) 94,95. (D) 95,94.10.如图,四边形ABCD 中,AC 垂直平分BD,垂足为E,下列结论不.一定..成立的是 (A ) AB=AD.(B) AC 平分∠BCD.(C) AB=BD. (D) △BEC ≌△DEC.11.如图,在平面直角坐标系中,点A 1 , A 2在x 轴上,点B 1,B 2在y 轴上,其坐标分别为A 1(1,0),A 2(2,0),B 1(0,1),B 2(0,2),分别以A 1A 2B 1B 2其中的任意两点与点..O .为顶点作三角形,所作三角形是等腰三角形的概率是 (A ) 3 4. (B) 1 3. (C) 23. (D) 1 2.12.如图,在⊙O 中,∠CBO=45°,∠CAO=15°,则∠AOB 的度数是 (A)75°. (B)60°. (C)45°. (D)30°. 13.如图,等边三角形OAB 的一边OA 在x 轴上,双曲线xy 3在第一象限内的图像经过OB 边的中点C ,则点B的坐标是(A )( 1, 3). (B )(3, 1 ). (C )( 2 ,32). (D )(32 ,2 ).14、如图,正方形ABCD 中,AB=8cm,对角线AC,BD 相交 于点O,点E,F 分别从B,C 两点同时出发,以1cm/s 的速度沿BC,CD 运动,到点C,D 时停止运动,设运动时间为t(s),△OEF6O 48816 t(s) S (2cm (A )O 48816t(s)S (2cm (B )O 48816t(s) S (2cm (C )O 48816t(s)S (2cm (D )(第18题图)(第17题图)EDCBAFEDCBA的面积为s(2cm ),则s(2cm )与t(s)的函数关系可用图像表示为二、填空题(本大题共5小题,每小题3分,共15分)把答案填在题中横线上. 15.分解因式24x x -= . 16.分式方程21311x x x+=--的解是 . 17.如图,菱形ABCD 中,AB =4,o60B ∠=,,AE BC AF CD ⊥⊥,垂足分别为E,F,连接EF,则的△AEF 的面积是 .18.如图,等腰梯形ABCD 中,//,,,AD BC DE BC BD DC ⊥⊥垂足分别为E,D,DE=3,BD=5,则腰长AB=19. 对于实数a,b,定义运算“﹡”:a ﹡b=22(),).a ab a b ab b a b ⎧-≥⎪⎨-<⎪⎩(例如4﹡2,因为4>2,所以4﹡224428=-⨯=.若12,x x 是一元二次方程2560x x -+=的两个根,则1x ﹡2x =三、开动脑筋,你一定能做对!(本大题共3小题,共21分)20.(本小题满分7分)2013年1月1日新交通法规开始实施。
为了解某社区居民遵守交通法规情况,小明随机选取部分居民就“行人闯红灯现象”进行问卷调查,调查分为“A :从不闯红灯;B :偶尔闯红灯;C:经常闯红灯;D :其他”四种情况,并根据调查结果绘制出部分条形统计图(如图1)和部分扇形统计图(如图2).请根据图中信息,选项人数AB CD41256图1图2CD B A 70%FEDCBA解答下列问题:(1)本次调查共选取 名居民;(2)求出扇形统计图中“C ”所对扇形的圆心角的度数,并将条形统计图补充完整; (3)如果该社区共有居民1600人,估计有多少人从不闯红灯?21.(本小题满分7分)为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B 两种型号的学习用品共1000件,已知A 型学习用品的单价为20元,B 型学习用品的单价为30元. (1)若购买这批学习用品用了26000元,则购买A,B 两种学习用品各多少件? (2)若购买这批学习用品的钱不超过28000元,则最多购买B 型学习用品多少件?22.(本小题满分7分)如图,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F,连接CF. (1)求证:AF=DC ;(2)若AB ⊥AC,试判断四边形ADCF 的形状,并证明你的结论.(第22题图)OEDCBAaz55 751535(第24题图)四、认真思考,你一定能成功!(本大题共2小题,共18分) 23. (本小题满分9分)如图,在△ABC 中,∠ACB=o90, E 为BC 上一点,以CE 为直径作⊙O,AB 与⊙O 相切于点D ,连接CD,若BE=OE=2. (1)求证:∠A=2∠DCB ;(2)求图中阴影部分的面积(结果保留π和根号).24.(本小题满分9分)某工厂投入生产一种机器的总成本为2000万元.当该机器生产数量至少为10台,但不超过70台时,每台成本y 与生产数量x 之间是一次函数关系,函数y 与自变量x 的部分对应值如下表: x(单位:台) 10 20 30 y(单位:万元∕台)605550(1)求y 与x 之间的函数关系式,并写出自变量x 的取值范围; (2)求该机器的生产数量;(3)市场调查发现,这种机器每月销售量z (台)与售价a (万元∕台)之间满足如图所示的函数关系.该厂生产这种机器后第一个月按同一售价共卖出这种机器25台,请你求出该厂第一个月销售这种机器的利润.(注:利润=售价-成本)(第23题图)(第25题图)图3图2图1F E PCBDAFEPDCBAFEPDCBAxyAOCB(第26题图)五、相信自己,加油呀!(本大题共2小题,共24分) 25.(本小题满分11分)如图,矩形ABCD 中,∠ACB =o30,将一块直角三角板的直角顶点P 放在两对角线AC,BD 的交点处,以点P 为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC 所在的直线相交,交点分别为E,F. (1)当PE ⊥AB,PF ⊥BC 时,如图1,则PEPF的值为 . (2)现将三角板绕点P 逆时针旋转α(oo060α<<)角,如图2,求PEPF的值; (3)在(2)的基础上继续旋转,当oo6090α<<,且使AP:PC=1:2时,如图3,PEPF的值是否变化?证明你的结论.26、(本小题满分13分)如图,抛物线经过5(1,0),(5,0),(0,)2A B C --三点. (1)求抛物线的解析式;(2)在抛物线的对称轴上有一点P ,使PA+PC 的值最小,求点P 的坐标;(3)点M 为x 轴上一动点,在抛物线上是否存在一点N ,使以A,C,M,N 四点构成的四边形为平行四边形?若存在,求点N 的坐标;若不存在,请说明理由.。
