6.1.2平方根.1.2平方根课件(2)

宋木子6.1.2平方根

1 2 h gt 2
其中h的单位是m，t的单位是s，g=9.8m/s2.假设跳板的高度是3m，运动员在跳板上跳起至高出跳板 1.2m处开始下落，那么运动员下落到水面约需多长时间？
3
实际应用
解：设运动员下落到水面约需ts，根据题意，得
1 3 1.2 9.8t 2 2
t2 2 4.2 9.8
3
。
4
填一填
1、
拓展延伸
( 5)2 =
(5) =
2
.
2、
.
3、对于任意数a， a 2 一定等于a吗？
5
课堂小结
这堂课你学到了什么？
6
作业布置
拼搏使人生精彩，刻苦使生命阳光！
合肥新站寿春实验中学
H E F E I XI N Z A HN S HO UC HU N SHI YA N Z H ON GXU E
0.8571
t 0.93
因而，运动员下落到水面约需0.93s.
4
1.填空: (1)
练一练
∵ ( 0.2 )²=0.04
0.2 ，即 0.04的平方根是 0.04 0.2 ；
(2) ∵(
6 6 )²=36/25 即36/25的平方根是 5 5
。
4
练一练
2.（判断正误，若错）对）错）错）
②2的平方根可表示成。（ 2 ③(-4)2的算术平方根是-4。（
④
4 没有平方根。
（
4
填一填
1、一个数的平方根是-7，则它的另一个平方根是 2、
7
，
这个数是
49
。
0
的平方根是它本身。
3、

【人教版】精美省优课件七下数学：6.1.2-用计算器求算术平方根及其大小比较ppt课件

A. 4
B. 5
C. 6
D. 7
5.比较大小： 5 1与0.5 . 2
解：∵ 5＞4，
∴ 5 2， ∴ 5 1 2 11， ∴ 5 1 0.5 ．
2
课堂小结
使用计算器进行开方运算
用计算器开方
用计算器开方比较数的大小
语文
小魔方站作品盗版必究
谢谢您下载使用！
更多精彩内容，微信扫描二维码获取扫描二维码获取更多资源
班主任：我觉得何旋今天取得这样的成绩，我觉得，很重要的是，何旋是土生土长的北京二中的学生，二中的教育理念是综合培养学生的素质和能力。我觉得何旋，她取得今天这么好的成绩，一个来源于她的扎实的学习上的基础，还有一个非常重要的，我觉得特别想提的，何旋是一个特别充满自信，充满阳光的这样一个女孩子。在我印象当中，何旋是一个最爱笑的，而且她的笑特别感染人的。所以我觉得她很阳光，而且充满自信，这是她突出的这样一个特点。所以我觉得，这是她今天取得好成绩当中，心理素质非常好，是非常重要的。
第六章实数
6.1 平方根
第2课时用计算器求算术平方根及其大小比较
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.会用计算器求算术平方根; 2.掌握算术平方根的估算及大小比较．（重点）
导入新课
复习引入 1.什么是算术平方根？ 2.判断下列各数有没有算术平方根？如果有，请求
出它们的算术平方根.
-36 ,
1.先卡定一个大范围，再逐渐地缩小范围。 2.根据高、低提示采用取中间值的方法一步步
缩小范围，直到得到正确价格.
讲授新课
一算术平方根的估算及大小比较
合作探究

6.1.2计算机求平方根

导学
环节
课堂
流程
时间
任务驱动
问题导学
学法
指导
知识
链接
自主学习
温故
知新
3
1、算术平方根的意义及表示方法。
2、说出下列各数的算术平方根。
100 0.0049 42
1、算术平方根
2、乘方
3、有理数的运算规则
4、非负数
互助
释疑
2
对于的算术平方根部分学生有疑问，应再次讲解。
探究
出招
15
某同学用一张正方形纸片折小船，但他手头上没有现成的正方形纸片，于是他撕下一张作业本上的纸，按照如图，沿AE对折使点B落在点F的位置上,再把多余部分FECD剪下,如果他事先量得矩形ABCD的面积为90cm2,又测量剪下的多余的矩形纸片的面积为40cm2.请根据上述条件算出剪出的正方形纸片的边长是多少厘米.
（到底它为多少呢?它是一个小数吗?你有什么办法确定这个值呢?由这一系列问题进入这节课要讨论的问题.）
【活动1】
怎样用两个面积为1的正方形拼成一个面积为2的大正方形
动手画一画，若确实不会，则学生间进行交流。
问题1：画出拼成的大正方形的草图。
问题2：你能求出大正方形的边长吗？（动动脑）
把过程简要写一下。
学段
初中
年级
七年级
学科
数学
单元
第6单元
课题
6.1.2平方根（2）
课型
新授
教学
目标
1.理解有些非负数的算术平方根不是一个有理数
2.能用逼近法估算（a不是完全平方数）的算术平用逼近法估算（a不是完全平方数）的算术平方根的大小
教学
难点
通过估算能比较类似（a不是完全平方数）的数的大小

6.1平方根(课时2)课件(新人教版七年级数学下)

2 7 和27的大小．
【学习体会】
1.本节课你独立思考了那些知识？参与讨论了哪些知识？还有那些疑惑？ 2.本节课你最成功的地方是什么？说给你小组成员听听.
【当堂达标】 1. 比较下列各数的大小： (1)
65与8 ；(2)
5-1 与1 . 2
2.已知
2.3409 ＝1.53，求 23409 的值
6.2平方根（第二课时）
பைடு நூலகம்
【学习目标】
1.能用“夹值法”求一个数的平方根的近似值. 2.会用计算器求一个数的算术平方根. 3.理解被开方数扩大（缩小）与它的算数平方根扩大（缩小）的规律.
【重点难点】
重点：利用“夹值法”求一个数的算术平方根. 难点：理解被开方数扩大（缩小）与它的算术平方根扩大（缩小）的规律.
创设情景
怎样用两个面积为1的小正方形拼成一个面积为2的大正方形？大正方形的边长是多少？
2 到底有多大？
【课中探究】
数学活动一：估值根据自己的经验，你估计一下
2
大约有多大？
数学活动二：探究 ∵1² ＝1 2² ＝4 ∴1＜ 2 ＜2 ∵1.4² ＝1.96 1.5² ＝2.25 ∴1.4＜ 2 ＜1.5 ∵1.41² ＝1.9881 1.42² ＝2.0164 ∴1.41＜ 2 ＜1.42 ∵1.414² ＝1.999396 1.415² ＝2.002225 ∴1.414＜ 2 ＜1.415…… 事实上，越往下进行，得到的值就越准确。 2 ＝1.41421356…
3.用计算器计算:（如需取近似值，则精确到0.01）（ 1）
1369
；（2） 101.2036 ；（3） 5
.
它是一个无限不循环小数,像这样的数还有很多，如： 3、 5 …….

《平方根》_教学课件

25 36
（3）
1
2
4
（4）（－2 ）2
（5 ）9 （6）0 （7）－100 （8） 10
解（：1）∵ 0.920.81
∴0.81的平方根是 0. 9,即 0.810.9
（2） ∵
5 6
2
25 36
25
∴36
的平方根是
5 6
，即
25 5 36 6
（7）∵ －100 是负数，∴ －100 没有平方根；【获奖课件 ppt】《平方根》_教学课件 1-课件分析下载
【获奖课件 ppt】《平方根》_教学课件 1-课件分析下载
【获奖课件 ppt】《平方根》_教学课件 1-课件分析下载
高 1、填表： x 1 -1 2 -2 3 -3 4 -4 5 -5 6 -6 0
效 X2 预有表格可知平方等于一个正数的数有＿＿
个，它们是＿＿＿关系；_____平方等于负
思考：是不是所有的数都能进行开平方运算？
不是，只有正数和零才能进行开平方运算。
注意：由于平方与开平方互为逆运算，因此
可以通过平方运算来求一个数的平方根，也可以通过平方运算来检验一个数是不是另一个数的平方根。
【获奖课件 ppt】《平方根》_教学课件 1-课件分析下载
请同学们概括一个数的平方根的性质：【获奖课件ppt】《平方根》_教学课件1-课件分析下载
【获奖课件 ppt】《平方根》_教学课件 1-课件分析下载
练习1
【获奖课件 ppt】《平方根》_教学课件 1-课件分析下载
选择题
（1） 0.01的平方根是（ B ）

人教版七年级数学下册6.1第3课时平方根课件(共25张PPT)

∴ 3x + 5y = 25. ∴ 3x + 5y 的平方根为±5.
四课堂小结
➢ 正数有两个平方根，它们互为相反数； ➢ 0 的平方根是 0； ➢ 负数没有平方根.
课后作业
1.从课后习题中选取； 2.完成练习册本课时的习题。
5 3
2
25 9
，
因此
25 9
的平方根是
5 3
与
-5 3
.
即±
25 9
=±
5 3
.
（3）1.21. 有两个平方根
解: 由于1.12 1.21，
因此1.21的平方根是1.1与−1.1.
即± 1.21=± 1.1.
知识点2：平方与开方的关系
已知一个数，求它的平方的运算，叫作平方运算.
平方
+1
-1
1
根据上面的研究过程填表：
x2 1 16
0
49
4
25
x ±1 ±4
0
±7 ±2
5
如果我们把±1、±4、0、±7、±2 分别叫做1、
16、0、49、245
5
的平方根，你能类比算术平方根的
概念，给出平方根的概念吗？
如果有一个数 x，使得x2= a，那么我们把 x 叫作 a 的一个平方根，也叫作二次方根.
2. 判断下列说法是否正确：
（1）75
是
25 的一个平方根；
49
正确.
（2） 6是 6 的算术平方根；正确.
（3） 16 的值是±4；（4）(-4)2 的平方根是 -4.
不正确，是 4. 不正确，是 ±4.
3. 填一填。（1）a的一个平方根是3，则另一个平方根是 − 3 ，

6.1.2平方根2

要求（15分钟内完成）： 1.先自己完成导学案相关内容，再结合问题并思考解决，明确自己的疑问. 2.小组合作讨论解决个人问题.
高效展示
目标指向：1.解决前面未达到的部分。 2.训练学生规范表达，分析、解决、总结问题的能力。
问题
展示
补充质疑
1
2 3
第三组C层
第四组B层第五组B层
先组内补充最后其他组补充
学习目标
1.复习算术平方根及平方根的概念、表示和性质，并会应用其性质解决问题； 2.复习立方根的概念、表示和性质； 3.激情投入课堂自主、合作、讨论学习，学会倾听其他同学的发言，并积极参与点评和评价.
自主学习、合作探究
目标指向：1.会利用平方根和立方根的概念解题; 2.会利用算术平方根的性质解决实际问题；
先组内补充最后其他组补充先组内补充最后其他组补充
要求（15分钟内完成）：口头展示，声音洪亮、条理清楚；书面展示，书写要认真、规范，步骤要完整，注明解题方法或所用知识点或归纳规律结论。
课堂小结
1.回扣目标,总结收获 2.评出优秀小组和个人
要求(5分钟内完成)
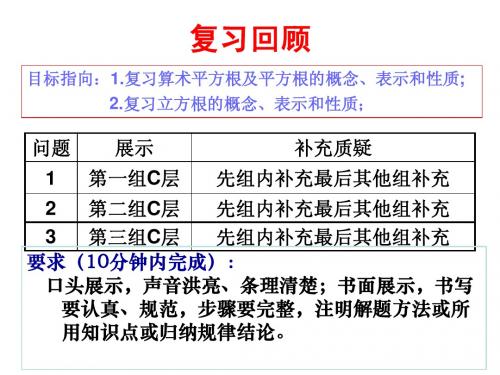
复习回顾
目标指向：1.复习算术平方根及平方根的概念、表示和性质; 2.复习立方根的概念、表示和性质；
问题 1
展示第一组C层
补充质疑先组内补充最后其他组补充 3 第三组C层先组内补充最后其他组补充要求（10分钟内完成）：口头展示，声音洪亮、条理清楚；书面展示，书写要认真、规范，步骤要完整，注明解题方法或所用知识点或归纳规律结论。

人教版初一数学下册6.1.2平方根

第六章6.1.3实数平方根学习目标1.了解平方根的概念，并理解开方与开平方的关系;2.会求非负数的平方根.（重点、难点）导入新课［回顾与思考］1・什么叫做算术平方根?2•判断下列各数有没有算术平方根，如果有请求出它们的算术平方根.100； 1；一；0; —0.0025; (-3)2 ;—25；3•填空(3) 0.82=J^£, (-0.8) 2= 0^4思考：反过来，如果已知一个数的平方，怎样求这个数？ (1) 32= 9 , (-3)曲授新课平方根的定义及性质问题如果一个数的平方等于9,这个数是多少?由于（七）今'所以这个数是3或墮甦想:3和-3有什么特彳根据上面的研究过程填表:如果我们把ztl<±4<±6士/上分别叫做1 16.36.49冬的平方根，你能给出乖方根的概念吗? 、、25—、平方根的概念根据上述问题，即要找出一个数，使它的平方等于给定的数.由此我们抽象出下述概念：如果有一个数兀，使得兀Id,那么我们把%叫作Q的一个平方根，也叫作二次方根.例如：（土1）2=1 , 1的平方根为土1.平方根的性质：如果X是正数Q的一个平方根，那么Q的平方根有且只有两个：兀与P•即平方根互为相反数.在上面的问题中，我们求平方根的数都是正数.1.零有平方根吗？如果有，它的平方根是多少？由于02=0,而非零数的平方不等于0,因此零的平方根就是0本身.2.-9有平方根吗？负数有平方根吗？由于同号两数相乘得正数，所以任何一个数的平方都不会是负数，因此-9没有平方根，进一步的，所有的负数都没有平方根.总结归纳］1•一个正数有两个平方根，它们互为相反数;2.零的平方根是0；3.负数没有平方根.练一练：判断下列各数是否有平方根，请说明理由.-4; 0; 0.000001; 100; 丄.做一做判断下列说法是否正确，并说明理由.(1)49的平方根是7；X(2)2是4的平方根；(3)-5是25的平方根；(4)64的平方根是±8；(5)T6的平方根是-4.X典例精析］例1 一个正数的两个平方根分别是2°+1和°一4, 求这个数.解：由于一个正数的两个平方根是2°+1和°—4, 则有2Q+1+Q—4=0,即3°—3=0,解得。