2017年泉州市中考数学质量检测数学试卷含答案(扫描版)
2016-2017泉州数学质检答案
人数
32 25
30
2 1 .„„„„8 分 6 3
22. (本小题 10 分) 解: 由题意得 (a 25)(400 10a) 500 , 整理得, a 65a 1050 0 , 解得 a1 30 , a2 35 .„„„„„„„„„„„„„„6 分
y B D
DN DH . DM DE
由(1)得 D3, 4 , ∴
H N
DN DH 3 . x A O E M P DM DE 4 在 RtDMN 中, DN 3 (第 24 题图 2) ∵ tan DMN , DM 4 ∴ DMN 的大小保持不变;„„„„„„„„„„„„„„„„„„„„„„„„„„12 分 DN 3 当点 P 和点 N 分别在 x 轴的正半轴和 y 轴的负半轴时,同理可求 tan DMN , DM 4 ∴ DMN 的大小同样保持不变; 综上所述,在直角 NDM 绕点 D 旋转的过程中,DMN 的大小不会发生变化.„„„„13 分
初三数学参考答案及评分标准
A -4
-2
B O (A1) 2 (A2)
(第 20 题图)
第 1 页 共 4 页
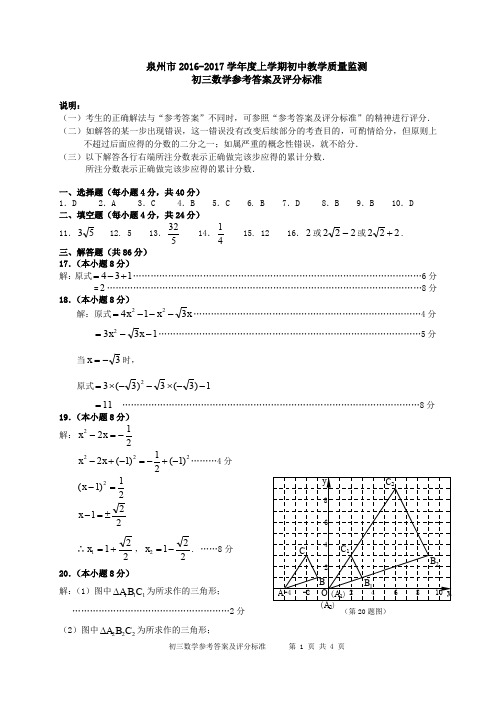
学生报名情况条形统计图
A2 (0,0) 、 B2 (9,3) 、 C2 (6,9) .„„„„„„8 分
21. (本小题 8 分) 解: (1)100,统计图如右图所示;„„„„4 分 (2) P (选中甲、乙)
BH , BC
A
∴ BH BC sin C (6 2 3 ) 在 RtABH 中, A 60 , ∵ sin A
2 3 2 6 ,„„„„„6 分 2
H
2017年福建省泉州市初中学业质量检查数学试题参考答案及评分标准(初定稿)20170516-1

解法二:画树状图如下:
女1 女 2女 3男 1男 2
女2 女 1女 3男 1男 2
女3 女 1女 2男 1男 2
男1 女 1女 2女 3男 2
男2 女 1女 2女 3男 1
…7 分
所有等可能的结果为 20 种,其中抽到一男一女的为 12 种, 所以 P (抽到 1 男 1 女)
12 3 .……………………………………………………………8 分 20 5
1 2
12. x( x 2)( x 2)
13. 8 14. (3, 2)
15. ( 3, 1) 16. 4
三、解答题(共 86 分) 17. (本小题 8 分) 解:原式 x 2 x x 1 2 x …………………………………………………………………6 分
2 2
= 2 x 1 …………………………………………………………………………………7 分
21. (本小题 8 分) (1)80,135° ;条形统计图如图所示;………3 分 (2)该校对安全知识达到“良”程度的人数:
30 25 1200 =825 (人)………………5 分 80
(3)解法一:列表如下:
女1 女1 女2 女3 男1 男2 --女 1女 2 女 1女 3 女 1男 1 女 1男 2 女2 女 2女 1 --女 2女 3 女 2男 1 女 2男 2 女3 女 3女 1 女 3女 2 --女 3男 1 女 3男 2 男1 男 1女 1 男 1女 2 男 1女 3 --男 1男 2 男2
∴ AD
3 2 3 x . ……………………………………………………………9 分 3 3 过点 P 分别作 PM x 轴,PN AD, 垂足分 y 别为 M , N , 由①得 AC 平分 OAD. D C ∴ PM PN. N P 3 2 3 F (x, x+ )(-2 x 1), 设P 3 3 P 3 2 3 M O A B x E PM PN = x+ . ………………10 分 3 3 ∵直线 DP 把阴影部分的面积分成 1: 2 的两部分
福建省2017年中考数学真题试题(含扫描答案)

24.如图,矩形 ABCD 中, AB 6, AD 8 , P, E 分别是线段 AC、BC 上的点,且四边形 PEFD 为矩形.
(Ⅰ)若 PCD 是等腰三角形时,求 AP 的长;
(Ⅱ)若 AP 2 ,求 CF 的长.
25.已知直线 y 2x m 与抛物线Y ax2 ax b 有一个公共点 M (1, 0) ,且 a b .
x 2 0
6. 不等式组:
的解集是( )
x 3 0
D.
D.136 106
A. 3 x 2
B. 3 x 2
C. x 2
D. x 3
7.某校举行“汉字听写比赛”,5 个班级代表队的正确答题数如图.这 5 个正确答题数所组成的一组数据的
中位数和众数分别是( )
A.10,15
B.13,15
A.3
B.4
C.5
D.6
10.如图,网格纸上正方形小格的边长为 1.图中线段 AB 和点 P 绕着同一个点做相同的旋转,分别得到线
段 AB 和点 P ,则点 P 所在的单位正方形区域是( )
A.1 区
B.2 区
C.3 区
D.4 区
第Ⅱ卷(共 90 分)
二、填空题:本题共6小题,每小题4分,共24分.
sin2 37o sin2 53o 0.602 0.802 1.0000 ,
sin2 45o sin2 45o ( 2 )2 ( 2 )2 1.
2
2
据此,小明猜想:对于任意锐角 ,均有 sin2 sin2 (90o ) 1.
(Ⅰ)当 30o 时,验证 sin2 sin2 (90o ) 1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,若成立,请给予证明;若不成立,请举出一个反例.
泉州市2017届初中毕业班中考模拟数学试卷(三)答案

泉州市2017届初中毕业班中考模拟数学试卷(三)参考答案及评分标准说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分.(二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分. (三)以下解答各行右端所注分数表示正确做完该步应得的累计分数.一、选择题(每小题4分,共40分)1.D 2.C 3.C 4.B 5.B 6. A 7.A 8.C 9.C 10.D 二、填空题(每小题4分,共24分)A .11.1- 12. 10% 13.6 1415. 16.2, 23或,6 三、解答题(共86分)17.(本小题8分)101()(1)12---+-解:原式=211--+………………………………………………………………………6分= 2.- ………………………………………………………………………………………8分18.(本小题8分)解:32(1)6x x --<,………………………………………………………………………………2分 32+26x x -<,…………………………………………………………………………………4分 4.x <……………………………………………………………………………………………6分………………………………………………………8分19. (本小题8分) 证明:∵AB ∥DE ,∴∠B=∠DEC.………………………………….………………………………………………2分 又∵BE =CF ,∴BC =EF . …………………………………………………………………………………4分 在△ABC 和△DEF 中,,,,AB DE B DEF BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF.………………………………………………………………………………6分 ∴∠ACB=∠F. ………………………………………………………………………………7分 ∴AC ∥DF . ……………………………………………………………………………………8分20.(本小题8分)(1)分(2)……………………………………………………………8分21. (本小题8分)(1)8.5a =,8.b = …………………………………………………………………………………2分 (2)甲班;……………………………………………………………………………………………4分 (3)解法一:列表如下:………………………………………7分所有等可能的结果为6种,其中抽到甲班、乙班各一人的结果为4种,所以P (抽到A,B)4263==.………………………………………………………………………8分 解法二:画树状图如下:……7分所有等可能的结果为6种,其中抽到甲班、乙班各一人的结果为4种, 所以P (抽到A,B)4263==.………………………………………………………………………8分 22. (本小题10分)解:(1)当1c =时,原方程为2410x x -+=,221,244)444232 3.b b ac x ±--±-±====±(-…………………………4分∴12+3x =,22 3.x =-(2)∵22112220x x x x -+=,甲 乙1 乙2甲 --- 乙1 甲 乙2 甲 乙1 甲 乙1 --- 乙2乙1 乙2 甲 乙2 乙1乙2 --- Q甲乙2乙1 甲 乙1 乙2乙2甲乙1开始∴212)0.x x -=(∴12=.x x …………………………………………………………………………………………6分 ∴=40c ∆-=2(-4).…………………………………………………………………………7分 解得:1.4c =∴1.4c =………………………………………………………………8分 23. (本小题10分)(1)证明:连结0C,…………………………………………………………………………………………1分 ∵AB 为直径, ∴∠ACB =90°. ………………………………………………………………………………………2分 ∴∠BCD +∠ECD =90°.在Rt △ADE 和Rt △ABC 中,∠E =90°-∠A ,∠ABC =90°-∠A ,∴∠E =∠ABC . …………………………………………………3分 ∵OB =OC ,∴∠ABC =∠OCB . ∴∠E =∠OCB . 又∵CD =DE , ∴∠E =∠ECD .∴∠OCB =∠ECD . …………………………………………4分 ∴∠OCB +∠BCD =90°. 即OC ⊥CD .∴CD 为⊙O 的切线…….……………………………………5分 (2)解:由(1)知:∠BCD =∠A ,∠ACB =∠BCE =90°;∴∠OBC =∠DCE ; ∵OB =OC ,CD =DE ;∴∠OBC =∠OCB =∠DCE =∠E ;……………………………………………………………………7分 在△OBC 和△DCE 中,,,OBC DCE BC CE OCB E ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△OBC ≌△DC E (ASA );………………………………………………………………………8分 ∴OC =CD =6;Rt △OCD 中,OC =CD =6,∠OCD =90°;∴OD =22666 2.+=, ………………………………………………………………………9分24. (本小题13分)解:(1)当0≤t ≤10时,∵A 的坐标分别为(10,30)∴可求直线OA 的解析式为v =3t ……………1分 当10<t ≤20时,直线AB 的解析式为v =30 …………………………………………………2分 当20<t ≤35时,∵B ,C 的坐标分别为(20,30),(35,0)∴可求直线BC 的解析式为v =-2t +70…………………………………………………………3分(2)设直线l 交v 与t 的函数图象于D 点,当0≤t ≤10时,此时OT =t ,TD =3t (如图1)∴213322S t t t =⋅⋅=…………………………4分 当10<t ≤20时,此时OT =t ,AD =ET =t ﹣10,TD =30(如图2) ∴S =S △AOE +S 矩形ADTE =12×10×30+30(t ﹣10)=30t ﹣150………………………………………5分 当20<t ≤35时,∵B ,C 的坐标分别为(20,30),(35,0) ∴直线BC 的解析式为v =﹣2t +70∴D 点坐标为(t ,﹣2t +70)∴TC =35﹣t ,TD =﹣2t +70(如图3) ∴S =DCT OABC S S-四边形=11(1035)30(35)(270)22t t +⨯---+ =2(35)675t --+ …7分 (3)∵当t =20时,S =30×20﹣150=450(km ), 当t =35时,S =﹣(35﹣35)2+675=675(km ),……………………………………………8分 ∵700(km )>675(km )∴M 城不会受到侵袭 ……………………………………………9分 又∵450<650<675,∴N 城会受到侵袭,且侵袭时间t 应在20h 至35h 之间,………10分 由﹣(35﹣t )2+675=650,解得t =30或t =40(不合题意,舍去). 所以在沙尘暴发生后30h 它将侵袭到N 城.…………………………………………………12分25. (本小题14分) 解:(1)由142y x =-+得A (0,4),B (8,0),…………………………………………………………1分 则OA =4,OB =8, ∵AD =BD ,OC =BC ∴122CD OA ==,BC =4,1.2BD AB = ……………………………………………………2分 ∵∠ABO =∠DBC ,∴∠ABO +∠ABC =∠DBC +∠ABC .图1∴∠OBC =∠ABD ……………………………………………………………………….………3分 又.∵1.2BD BC AB OB == ∴△OBC ∽△ABD . ……………………………………………………………………………4分 (2)当0°<α<180°,且A ,C ,D 三点共线时,如图, ∵∠BCD =90°,∴∠ACB =90°.∴∠ACB =∠BOA =90°. ………5分 又∵OA =BC =4,AB =BA ,∴△ACB ≌△BOA . ………6分 ∴AC =BO .∴四边形AOBC 是平行四边形 ………7分 又∵∠AOB =90°.∴平行四边形AOBC 是矩形. ∴∠AOC =90°,AC =OB =8. ………8分 ∴AC =AD +CD =8+2=10.∴OD ===………………………………………………9分(3)存在. 当180°<α<360°且A ,C ,D 三点共线时,如图, 连结OC ,同(1)可得:△ABD ∽△BOC .∴AD AB OC OB ====………10分 同(2)可得:△ACB ≌△BOA . ∴AC =BO =8.又CD =2,∴AD =6.∵2AD OC =∴62OC =∴OC =………11分 过点C 作CM ⊥y轴于M ,设OM =y ,MC =x . 在Rt △OMC 和Rt △AMC 中有:222222(4)8.x y y x ⎧+=⎪⎨⎪++=⎩解得:24,512.5x y ⎧=⎪⎪⎨⎪=⎪⎩∴点C 的坐标(245,125-)………13分设直线AC 的表达式为y kx b =+∴4,1224.55b k b =⎧⎪⎨-=+⎪⎩解得:4,34.k b ⎧=-⎪⎨⎪=⎩所以所求直线AC 的表达式为44.3y x =-+…………………………………………………14分。
2017泉州中考数学模拟试题(三)(含答案及评分标准)

.
12.为了更好的促销,某旅游纪念品连续两次降价,每件由 100 元降到了 81 元.则平均每次降价的百分率 为 .
13.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有 20 个,除颜色外其它完全相同,通过多次摸 球试验后发现其中摸到红色,黑色球的频率稳定在 20%和 50%,则口袋中白色球的个数很可 能 .
C
A
D (第 15 题图)
B
2
越努力,越幸运!
16.已知关于 x 的二次函数 y=(x-h) +3,当 1≤x≤3 时,函数有最小值 2h,则 h 的值为
2
.
三、解答题:本大题 9 小题,共 86 分.解答应写出文字说明,证明过程或演算步骤. 在答题卡的相应位置内作 答. 1- 17.(8 分) 计算:(-2) 1- 27+(-1)0+|1-3 3|.
14.有一个内角为 60°的菱形的面积是 8 3,则它的内切圆的半径为________. 15.如图,在△ABC 中,∠A=30°,D 为边 AB 上的点,且 DA=DC=2,若△DCB 绕点 D 逆时针旋转, 使 DB、DC 分别与线段 AC 相交于 M、N,则当△DMN 为等边三角形时,DM 的长值为________.
A
B
1
C
D
越努力,越幸运!
7.如 图 所 示 , 小 亮 要 判 断 △ ABC 的 面 积 是 △ DBC 的 面 积 的 几 倍 , 现 仅 有 一 把 有 刻 度 的 直 尺 , 则 至少需要测量的次数是( A.1 次
A
) C.3 次 D.4 次
A
y
B.2 次
B D
C
E F
D
C
B
O x1
x2
2017年晋江市初中数学学业质量检查答案(定稿)

2017年初中学业质量检查数学试题参考答案及评分标准说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分. (二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分.(三)以下解答各行右端所注分数表示正确做完该步应得的累计分数. 一、选择题(每小题4分,共40分) 1.B 2.C 3.B 4.A 5. A 6.C 7.D 8. B 9.D 10.C二、填空题(每小题4分,共24分)11.2 12.= 13.5± 14.︒80 15.38π16.(1)5; (2)4. 三、解答题(共86分) 17.(本小题8分) 解:原式=21214+-- …………………………………………………………………………………………7分23=…………………………………………………………………………………………………… 8分 18.(本小题8分)解:原式=()()()21322232----+⋅-+-a a a a a a a ………………………………………………………………………2分=2123-----a a a a …………………………………………………………………………………………3分 =()213----a a a ………………………………………………………………………………………4分=213-+--a a a …………………………………………………………………………………………5分=22--a ………………………………………………………………………………………………6分当4-=a 时,原式242---= …………………………………………………………………………………7分31= ……………………………………………………………………………………8分19.(本小题8分)证明:∵DE ∥BF ,AD ∥BC ,∴BFC DEA ∠=∠,C A ∠=∠…………………………………………………………………………………4分 ∵CE AF =,∴CE FE FE AF +=+≤ ≤即CF AE =…………………………………………………………………………………………………………6分 在ADE ∆和CBF ∆中,BFC DEA ∠=∠,CF AE =,C A ∠=∠,∴ADE ∆≌CBF ∆()ASA . ………………………………………………………………………………………8分 20.(本小题8分) 解:(1)矩 …………………………………………………………………………………………………………1分(2)∵四边形ADCE 是矩形,∴DC AE =,………………………………………………………………………………………………2分 ∵AC AB =,BC AD ⊥,∴AE DC BD ==.…………………………………………………………………………………………3分 设x AE DC BD ===,y CE = ∵ABC ∆的周长比AEC ∆的周长大6,∴()()6132213=++-+⨯y x x ,即7=-x y ①………………………………………………………5分 在AEC Rt ∆中,由勾股定理得:222AC CE AE =+,即16922=+y x ② …………………………7分 由② -①的平方,得:1202=xy ,60==xy S ADCE 矩形. ……………………………………………8分 21.(本小题9分)解:(1)100;………………………………………………………………………………………………………1分 (2)喜欢美术的人数在扇形统计图中所占的圆心角是:︒=⎪⎭⎫⎝⎛---⨯︒3610030%40%201360, 即喜欢美术的人数在扇形统计图中所占的圆心角是︒36;……………………………………………………2分 (3)喜欢书法的学生有:40%40100=⨯(人)喜欢美术的学生有:10%10100=⨯(人); 频数分布折线统计图示:………………………………………4分(3) 方法一:画树状图如下:…………………………………………………………………………………………………………………7分 由树状图可知,共有6种等可能结果,其中甲乙两人同被调整到美术课的有2种结果.∴P (甲乙两人被同时调整到美术课程)=3162=. ………………………………………………………8分 方法二:列表如下:甲 乙 丙 乙 甲丙 丙 甲 乙…………………………………………………………………………………………………………………7分 由树状图可知,共有6种等可能结果,其中甲乙两人同被调整到美术课的有2种结果. ∴P (甲乙两人被同时调整到美术课程)=3162=. ………………………………………………………8分 22.(本小题10分) 解:(1)121=k ……………………………………………………………3分(2) ∵ABO Rt ∆沿x 轴负半轴平移得到CDE ∆, ∴4==AB CD ,BD AC =,︒=∠=∠90ABO CDE ,…………………………………………5分在ABO Rt ∆中,由勾股定理得:5432222=+=+=AB OB OA ,……………………………6分 ∵四边形ACEO 是菱形,∴5===BD OA AC ,235=-=-=OB BD OD ,……………………………………………………………………………………7分 ∴点()4,2-C ,……………………………………………………………………………………………………8分 把点()4,2-C 代入x k y 22=得:242-=k ,8422-=⨯-=k . ……………………………………………10分 23.(本小题10分)解:(1)设乙队每天制作x 面小红旗,则甲队每天制作x 2面小红旗,依题意得:…………………………1分42400400=-xx ,…………………………………………………………………………………………………3分 解得:50=x ,经检验,50=x 是原方程的根,且符合题意, ………………………………………………4分 答:甲、乙两队每天分别能制作100面、50面小红旗. ………………………………………………………5分(2)设安排甲队制作y 天,依题意得:……………………………………………………………………………6分8000501001800250400≤-⨯+yy ……………………………………………………………………………8分(第22题图)解得:10≥y .………………………………………………………………………………………………………9分 答:至少应安排甲队制作10天. ……………………………………………………………………………10分 24.(本小题12分) 解:(1)当b y =时,a x b +-=31,解得:b a x 33-=. ∴点Q 的坐标为()b b a Q ,33-…………………………………………………………………………………3分 (2)①∵四边形OABC 是矩形,∴b a CB OA 33-== 在a x y +-=31中,当0=x 时,a y =, ∴a OC AB ==,又b AQ =, ∴b a BQ -=,∵BQC ∆与PQC ∆关于CQ 对称,∴b a PQ BQ -==,︒=∠=∠90B CPQ , ∴︒=∠+∠90APQ OPC 又︒=∠+∠90OCP OPC , ∴OCP APQ ∠=∠又︒=∠=∠90PAQ COP ,∴COP ∆∽PAQ ∆,∴PQ CPPA CO =,b a b a PAa --=33,解得:3a PA =.………………………………………………………………5分 在APQ Rt ∆中,由勾股定理得:222PQ AQ PA =+,()2223b a b a -=+⎪⎭⎫ ⎝⎛,解得:b a 49=.………………………………………………………………………………………………………………………8分②解法一: 当4=b 时,9449=⨯=a ,()1549333=-⨯=-==b a CB OA ,33==aPA ,12315=-=OP , ∴点()4,15Q ,()0,12P .取CQ 的中点I ,连接IB ,在CBQ Rt ∆中,CQ IB 21=,以点I 为圆心,IB为半径作圆由轴对称性可知:(第24题图)点P 在⊙I 上,⊙I 交x 轴、y 轴得异于C 、P 的点1M 、2M , 连接Q M 1、P M 2、Q M 2,由同弧所对的圆周角相等可得:QCB PCQ Q PM Q PM ∠=∠=∠=∠21.………………………………………………………………………9分由(1)得Q 的坐标为()b b a Q ,33-,b a BQ -=,3133tan =--==∠b a b a CB BQ QCB ∴31tan tan =∠=∠QCB PCQ . 由点()9,0C 与()4,15Q 可得中点I 的坐标为⎪⎭⎫ ⎝⎛213,215. 分两种情况讨论:当点M 在x 轴上时,即设点1M 的坐标为()0,x ,则IQ IM =1,221IQ IM =,由勾股定理可得:22224213152150213215⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x ,解得:31=x 或122=x (不合舍去),∴点()0,31M .……………………………………………………………………………………………………10分 ∴点()0,31M 关于点()0,15A 的对称点()0,274M 也符合题意. …………………………………………11分当点M 在y 轴上时,即设点2M 的坐标为()y ,0,则IQ IM =2,222IQ IM =,由勾股定理可得:22224213152152130215⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y ,解得:91=y 或42=y ,∴点()4,02M 、()9,03M .综上,点M 的坐标为()0,31M 、()4,02M 、()9,03M 、()0,274M .……………………………………12分 解法二:当4=b 时,9449=⨯=a ,1533=-===b a CP CB OA ,5=-==b a BQ PQ . i)在CQP Rt ∆中,31155tan ===∠CP PQ QCP ,(第24题图)∴点C 为符合题意的点,此时点()9,0C .………………………………………………………………………9分ii)作CQP ∆的外接圆交y 轴得异于C 点的点1M ,连接Q M 1, ∴QCP P QM ∠=∠1∵︒=∠=∠901CPQ P CM ,∴y Q M ⊥1轴,()4,01M .…………………………………………………10分 iii)在直线931+-=x y 中,令0=y ,则27=x , ∴直线CQ 与x 轴的交点()0,274M , 在A QM Rt 4∆中,3115274tan 44=-==∠AM QA A QM , ∴点()0,274M 是符合题意的点. ……………………………………………………………………………11分 iv)点()0,274M 是关于QA 的对称点为点()0,33M ,此时A QM P QM 43∠=∠, ∴点()0,33M 是符合题意的点.综上,符合题意的点M 的坐标为()9,01M 、()4,02M 、()0,33M 、()0,274M .………………………12分 25.(本小题14分) 解:解:(1)在直线3+=x y 中,令0=x ,则3=y ,∴点()3,0C ………………………………………1分把点()0,1B 与点()3,0C 代入c bx x y ++-=233,得:⎪⎩⎪⎨⎧=++-=033,3c b c ,解得:⎪⎩⎪⎨⎧=-=,3332c b ,∴抛物线的解析式为:3332332+--=x x y .……………………………………………………………3分 (2) ①连接OQ ,在直线3+=x y 中,令0=y ,则3-=x , ∴点()0,3-A .………………………………………………………4分∵AO C O CQ AO Q AQ C S S S S ∆∆∆∆-+=, ∴()33213213332333212⨯⨯--⋅⨯+⎪⎪⎭⎫ ⎝⎛+--⨯=t t t S ,∴t t S 232212+--=,……………………………………………6分 8347232212++⎪⎪⎭⎫ ⎝⎛++-=t S ,()03<<-t . ∴当232+-=t 时,8347+=最大值S .……………………8分 ②∵点()0,1B ,()3,0C ,∴1=OB ,3=OC .在BOC Rt ∆中,3tan ==∠OBOCCBO , ∴︒=∠60CBO .………………………………………………9分 作直径ET 交⊙I 于点T ,连接FT ,则︒=∠90EFT ,又︒=∠=∠60CBO FTE ,ETEFFTE =∠sin ,ET ET EF 2360sin =︒⋅=, ………………………………10分当AC BD ⊥时,此时直径BD 最小,即直径ET 最小,EF 的值最小. …………………………………11分 在AOC Rt ∆中,3==OC OA , ∴︒=∠45CAO ,在ADB Rt ∆中,()26245sin 3145sin sin +=︒--=︒=∠⋅=AB CAO AB BD , ……………12分 ∴4236262232323+=+⨯===BD ET EF ,………………………………………………13分 此时点Q 的坐标为()34,33--.……………………………………………………………………………14分。
2017年晋江市初中数学学业质量检查

2017年初中学业质量检查数 学 试 题(试卷满分:150分;考试时间:120分钟)一、选择题(每小题4分,共40分.每小题有四个答案,其中有且只有一个答案是正确的,请在答题卡上相应题目的答题区域内作答,答对的得3分,答错或不答的一律得0分.)1.72011-的相反数是( ). A .72011- B .72011C .7201D .7201-2.计算结果为6a 的是( ).A .33a a +B .32a a ⋅ C .()23aD .212a a÷3.据报道,2016年全年国内生产总值约为744000亿元,则744000亿元用科学记数法表示为( ).A .610744.0⨯亿元 B .51044.7⨯亿元 C .4104.74⨯亿元 D .310744⨯亿元 4.右图数轴上表示的是下列哪个不等式组的解集( ). A.⎩⎨⎧≤->3 ,2x x B.⎩⎨⎧<-≥3 ,2x x C.⎩⎨⎧≥-<3 ,2x x D.⎩⎨⎧>-≤3,2x x5.下列事件中是必然事件的是( ).A. 从一个装满黑球的布袋中摸出一个球是黑球B.抛掷1枚普通硬币得到正面C. 抛掷1颗正方体骰子得到的点数是偶数D.抛掷1个普通图钉一定是针尖向下 6.设2018201620172⨯-=P ,222018201840342017+⨯-=Q ,则P 与Q 的关系为( ).A .Q P >B .Q P =C .Q P <D .Q P ±= 7.正五边形的每一个外角是( ).A .︒36B .︒54C .︒72D .︒1088.如图,直线1l ∥2l ∥3l ,直线AC 分别交1l ,2l ,3l 于点A ,B ,C ,直线DF 分别交1l ,2l ,3l 于点D ,E ,F ,AC 与DF 相交于点H ,则下列式子 不正确...的是( ). A. EF DE BC AB = B. EF BCDE AB = C. DF DE AC AB = D. CFBEBC AB =1l l 3l (第4题图)9. 已知:点A 、点B 都在直线l 的上方,试用尺规作图在直线l 上求作一点P ,使得PB PA +的值最小,则下列作法正确的是( ).10. 无论m 为何值,点()m m A 23,-不可能...在( ). A.第一象限 B.第二象限 C.第三象限D.第四象限二、填空题(每小题4分,共24分):在答题卡上相应题目的答题区域内作答. 11.当_______x 时,二次根式x -2有意义.12.设数据:1,2,3,4,5的方差为21S ,数据:11,12,13,14,15的方差为22S ,则2221_____S S .(填:“>”、“<”或“=”). 13.已知19)122)(122(=-+++b a b a ,则=+b a .14.如图,ACD ∠是ABC ∆的外角,若︒=∠-∠80B ACD ,则.______︒=∠A 15.如图,在⊙O 中,圆周角︒=∠150ACB ,弦4=AB ,则扇形OAB 的面积是 . 16.如图,在ABC Rt ∆中,︒=∠90C ,4=AC ,3=BC , (1)______=AB ;(2)若经过点C 且与边AB 相切的动圆与边CB ,CA 度的取值范围是 .三、解答题(共86分):在答题卡上相应题目的答题区域内作答. 17. (8分)计算:1022)23(2132-+----⨯. 18. (8分)先化简,再求值:213249622----+⋅-+-a a a a a a a ,其中4-=a .C.B(第14题图) (第15题图)19. (8分)如图,ADE ∆与CBF ∆的边AE 、CF 在同一条直线上,DE ∥BF ,AD ∥BC ,CE AF =,求证:ADE ∆≌CBF ∆.20.(8分)如图,在ABC ∆中,cm AC AB 13==,BC AD ⊥于点D , 把线段BD 沿着BA的方向平移cm 13得到线段AE ,连接EC . 问:(1)四边形ADCE 是 形;(2)若ABC ∆的周长比AEC ∆的周长大6,求四边形ADCE 的面积.21. (8分)某校校本课程中心为了解该校学生喜欢校本课程的情况,采取抽样调查的办法,通过书法、剪纸、灯谜、足球四门课程调查若干名学生的兴趣爱好,要求每位同学只能选择一门自己喜欢的课程,并将调查结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答:(第20题图)(第19题图)(1)在这次调查研究中,一共调查了 名学生;(2)喜欢剪纸的人数在扇形统计图中所占的圆心角是多少度?请.你.补全..频数分布折线统.......计图..; (3)为了平衡各校本课程的人数,需要从喜欢书法课程的甲、乙、丙3人中调整2人到剪纸课程,求“甲乙两人被同时调整到烹饪课程”的概率,试用画树状图或列表说明.22. (10分)在平面直角坐标系中,把图中的ABO Rt ∆()︒=∠90ABO 沿x 轴负半轴平移得到CDE ∆,已知3=OB ,4=AB ,设过点A 的双曲线的解析式为()011>=x xk y . (1)直接写出双曲线xk y 11=的函数表达式; (2)设过点C 的双曲线的解析式为xky 22=,若四边形ACEO 是菱形,求2k 的值.23. (10分)为了迎接校运会开幕式,现要求甲乙两队赶制小红旗,已知甲队的工作效率是乙队的2倍,若单独赶制400面小红旗,甲队比乙队少用4天.(第22题图)(第21题图)学生喜欢课程频数分布折线统计图学生喜欢课程频数分布扇形统计图(1)问甲、乙两队每天各能制作多少面小红旗?(2)已知甲队、乙队每天的制作费用分别是400元、250元,若要制作的小红旗的数量为1800面,且总费用不超过8000元,问至少应安排甲队制作多少天?24.(12分)已知:如图,在平面直角坐标系中,矩形OABC 的直角边OA 、OC 分别在x 轴的正半轴和y 轴的正半轴上,过点C 的直线a x y +-=31交矩形的AB 边于点Q ,b AQ =.(1)求点Q 的坐标(用含a ,b 的代数式表示);(2)若把BQC ∆沿CQ 折叠,使点B 恰好落在x 轴的点, ①求a 与b 的函数关系式(不需写出b 的范围);②当4=b 时,在坐标轴上....是否存在点M ,使得31tan =∠QMP ,若存在,请求出点M 的坐标,若不存在,请说明理由.25. (14分)已知:如图,直线l :3+=x y 与x 轴负半轴、y 轴正半轴分别相交于A 、C(第24题图)两点,抛物线c bx x y ++-=233经过点()0,1B 和点C . (1)求抛物线的解析式;(2) 如图,已知点Q 是抛物线c bx x y ++-=233在第二象限内的一个动点,连接AQ ,CQ .①设点Q 的横坐标为t ,AQC ∆的面积为S ,求S 与t 的函数关系式,并求出S 的最大值;②连接BQ 交AC 于点D ,连接BC ,以BD 为直径作⊙I ,分别交BC 、AB 于点E 、F ,连接EF ,求线段EF 的最小值,并直接写出此时点Q 的坐标.(第25题图)。
2017年晋江市初中数学学业质量检查答案(定稿)

2017年初中学业质量检查数学试题参考答案及评分标准说明:(一)考生的正确解法与“参考答案”不同时,可参照“参考答案及评分标准”的精神进行评分. (二)如解答的某一步出现错误,这一错误没有改变后续部分的考查目的,可酌情给分,但原则上不超过后面应得的分数的二分之一;如属严重的概念性错误,就不给分.(三)以下解答各行右端所注分数表示正确做完该步应得的累计分数. 一、选择题(每小题4分,共40分) 1.B 2.C 3.B 4.A 5. A 6.C 7.D 8. B 9.D 10.C二、填空题(每小题4分,共24分)11.2 12.= 13.5± 14.︒80 15.38π16.(1)5; (2)4. 三、解答题(共86分) 17.(本小题8分) 解:原式=21214+-- …………………………………………………………………………………………7分23=…………………………………………………………………………………………………… 8分 18.(本小题8分)解:原式=()()()21322232----+⋅-+-a a a a a a a ………………………………………………………………………2分=2123-----a a a a …………………………………………………………………………………………3分 =()213----a a a ………………………………………………………………………………………4分=213-+--a a a …………………………………………………………………………………………5分=22--a ………………………………………………………………………………………………6分当4-=a 时,原式242---= …………………………………………………………………………………7分31= ……………………………………………………………………………………8分19.(本小题8分)证明:∵DE ∥BF ,AD ∥BC ,∴BFC DEA ∠=∠,C A ∠=∠…………………………………………………………………………………4分 ∵CE AF =,∴CE FE FE AF +=+≤ ≤即CF AE =…………………………………………………………………………………………………………6分 在ADE ∆和CBF ∆中,BFC DEA ∠=∠,CF AE =,C A ∠=∠,∴ADE ∆≌CBF ∆()ASA . ………………………………………………………………………………………8分 20.(本小题8分) 解:(1)矩 …………………………………………………………………………………………………………1分(2)∵四边形ADCE 是矩形,∴DC AE =,………………………………………………………………………………………………2分 ∵AC AB =,BC AD ⊥,∴AE DC BD ==.…………………………………………………………………………………………3分 设x AE DC BD ===,y CE = ∵ABC ∆的周长比AEC ∆的周长大6,∴()()6132213=++-+⨯y x x ,即7=-x y ①………………………………………………………5分 在AEC Rt ∆中,由勾股定理得:222AC CE AE =+,即16922=+y x ② …………………………7分 由② -①的平方,得:1202=xy ,60==xy S ADCE 矩形. ……………………………………………8分 21.(本小题9分)解:(1)100;………………………………………………………………………………………………………1分 (2)喜欢美术的人数在扇形统计图中所占的圆心角是:︒=⎪⎭⎫⎝⎛---⨯︒3610030%40%201360, 即喜欢美术的人数在扇形统计图中所占的圆心角是︒36;……………………………………………………2分 (3)喜欢书法的学生有:40%40100=⨯(人)喜欢美术的学生有:10%10100=⨯(人); 频数分布折线统计图示:………………………………………4分(3) 方法一:画树状图如下:…………………………………………………………………………………………………………………7分 由树状图可知,共有6种等可能结果,其中甲乙两人同被调整到美术课的有2种结果.∴P (甲乙两人被同时调整到美术课程)=3162=. ………………………………………………………8分 方法二:列表如下:甲 乙 丙 乙 甲丙 丙 甲 乙…………………………………………………………………………………………………………………7分 由树状图可知,共有6种等可能结果,其中甲乙两人同被调整到美术课的有2种结果. ∴P (甲乙两人被同时调整到美术课程)=3162=. ………………………………………………………8分 22.(本小题10分) 解:(1)121=k ……………………………………………………………3分(2) ∵ABO Rt ∆沿x 轴负半轴平移得到CDE ∆, ∴4==AB CD ,BD AC =,︒=∠=∠90ABO CDE ,…………………………………………5分在ABO Rt ∆中,由勾股定理得:5432222=+=+=AB OB OA ,……………………………6分 ∵四边形ACEO 是菱形,∴5===BD OA AC ,235=-=-=OB BD OD ,……………………………………………………………………………………7分 ∴点()4,2-C ,……………………………………………………………………………………………………8分 把点()4,2-C 代入x k y 22=得:242-=k ,8422-=⨯-=k . ……………………………………………10分 23.(本小题10分)解:(1)设乙队每天制作x 面小红旗,则甲队每天制作x 2面小红旗,依题意得:…………………………1分42400400=-xx ,…………………………………………………………………………………………………3分 解得:50=x ,经检验,50=x 是原方程的根,且符合题意, ………………………………………………4分 答:甲、乙两队每天分别能制作100面、50面小红旗. ………………………………………………………5分(2)设安排甲队制作y 天,依题意得:……………………………………………………………………………6分8000501001800250400≤-⨯+yy ……………………………………………………………………………8分(第22题图)解得:10≥y .………………………………………………………………………………………………………9分 答:至少应安排甲队制作10天. ……………………………………………………………………………10分 24.(本小题12分) 解:(1)当b y =时,a x b +-=31,解得:b a x 33-=. ∴点Q 的坐标为()b b a Q ,33-…………………………………………………………………………………3分 (2)①∵四边形OABC 是矩形,∴b a CB OA 33-== 在a x y +-=31中,当0=x 时,a y =, ∴a OC AB ==,又b AQ =, ∴b a BQ -=,∵BQC ∆与PQC ∆关于CQ 对称,∴b a PQ BQ -==,︒=∠=∠90B CPQ , ∴︒=∠+∠90APQ OPC 又︒=∠+∠90OCP OPC , ∴OCP APQ ∠=∠又︒=∠=∠90PAQ COP ,∴COP ∆∽PAQ ∆,∴PQ CPPA CO =,b a b a PAa --=33,解得:3a PA =.………………………………………………………………5分 在APQ Rt ∆中,由勾股定理得:222PQ AQ PA =+,()2223b a b a -=+⎪⎭⎫ ⎝⎛,解得:b a 49=.………………………………………………………………………………………………………………………8分②解法一: 当4=b 时,9449=⨯=a ,()1549333=-⨯=-==b a CB OA ,33==aPA ,12315=-=OP , ∴点()4,15Q ,()0,12P .取CQ 的中点I ,连接IB ,在CBQ Rt ∆中,CQ IB 21=,以点I 为圆心,IB为半径作圆由轴对称性可知:(第24题图)点P 在⊙I 上,⊙I 交x 轴、y 轴得异于C 、P 的点1M 、2M , 连接Q M 1、P M 2、Q M 2,由同弧所对的圆周角相等可得:QCB PCQ Q PM Q PM ∠=∠=∠=∠21.………………………………………………………………………9分由(1)得Q 的坐标为()b b a Q ,33-,b a BQ -=,3133tan =--==∠b a b a CB BQ QCB ∴31tan tan =∠=∠QCB PCQ . 由点()9,0C 与()4,15Q 可得中点I 的坐标为⎪⎭⎫ ⎝⎛213,215. 分两种情况讨论:当点M 在x 轴上时,即设点1M 的坐标为()0,x ,则IQ IM =1,221IQ IM =,由勾股定理可得:22224213152150213215⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-x ,解得:31=x 或122=x (不合舍去),∴点()0,31M .……………………………………………………………………………………………………10分 ∴点()0,31M 关于点()0,15A 的对称点()0,274M 也符合题意. …………………………………………11分当点M 在y 轴上时,即设点2M 的坐标为()y ,0,则IQ IM =2,222IQ IM =,由勾股定理可得:22224213152152130215⎪⎭⎫⎝⎛-+⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y ,解得:91=y 或42=y ,∴点()4,02M 、()9,03M .综上,点M 的坐标为()0,31M 、()4,02M 、()9,03M 、()0,274M .……………………………………12分 解法二:当4=b 时,9449=⨯=a ,1533=-===b a CP CB OA ,5=-==b a BQ PQ . i)在CQP Rt ∆中,31155tan ===∠CP PQ QCP ,(第24题图)∴点C 为符合题意的点,此时点()9,0C .………………………………………………………………………9分ii)作CQP ∆的外接圆交y 轴得异于C 点的点1M ,连接Q M 1, ∴QCP P QM ∠=∠1∵︒=∠=∠901CPQ P CM ,∴y Q M ⊥1轴,()4,01M .…………………………………………………10分 iii)在直线931+-=x y 中,令0=y ,则27=x , ∴直线CQ 与x 轴的交点()0,274M , 在A QM Rt 4∆中,3115274tan 44=-==∠AM QA A QM , ∴点()0,274M 是符合题意的点. ……………………………………………………………………………11分 iv)点()0,274M 是关于QA 的对称点为点()0,33M ,此时A QM P QM 43∠=∠, ∴点()0,33M 是符合题意的点.综上,符合题意的点M 的坐标为()9,01M 、()4,02M 、()0,33M 、()0,274M .………………………12分 25.(本小题14分) 解:解:(1)在直线3+=x y 中,令0=x ,则3=y ,∴点()3,0C ………………………………………1分把点()0,1B 与点()3,0C 代入c bx x y ++-=233,得:⎪⎩⎪⎨⎧=++-=033,3c b c ,解得:⎪⎩⎪⎨⎧=-=,3332c b ,∴抛物线的解析式为:3332332+--=x x y .……………………………………………………………3分 (2) ①连接OQ ,在直线3+=x y 中,令0=y ,则3-=x , ∴点()0,3-A .………………………………………………………4分∵AO C O CQ AO Q AQ C S S S S ∆∆∆∆-+=, ∴()33213213332333212⨯⨯--⋅⨯+⎪⎪⎭⎫ ⎝⎛+--⨯=t t t S ,∴t t S 232212+--=,……………………………………………6分 8347232212++⎪⎪⎭⎫ ⎝⎛++-=t S ,()03<<-t . ∴当232+-=t 时,8347+=最大值S .……………………8分 ②∵点()0,1B ,()3,0C ,∴1=OB ,3=OC .在BOC Rt ∆中,3tan ==∠OBOCCBO , ∴︒=∠60CBO .………………………………………………9分 作直径ET 交⊙I 于点T ,连接FT ,则︒=∠90EFT ,又︒=∠=∠60CBO FTE ,ETEFFTE =∠sin ,ET ET EF 2360sin =︒⋅=, ………………………………10分当AC BD ⊥时,此时直径BD 最小,即直径ET 最小,EF 的值最小. …………………………………11分 在AOC Rt ∆中,3==OC OA , ∴︒=∠45CAO ,在ADB Rt ∆中,()26245sin 3145sin sin +=︒--=︒=∠⋅=AB CAO AB BD , ……………12分 ∴4236262232323+=+⨯===BD ET EF ,………………………………………………13分 此时点Q 的坐标为()34,33--.……………………………………………………………………………14分。
