高中数学北师大版必修四课下能力提升(7)余弦函数的图像与性质含解析

合集下载

1.6余弦函数的图像与性质课件高中数学必修四(北师大版)

其中单调区间不必死记硬背，只要观察[0,2π]上的图像，可知[0 ，π]是余弦函数的一个减区间，[π，2π] 是余弦函数的一个增区间，然后根据余弦函数的周期为 2π 的整数倍，就可得到一般结果．
●教学流程
演示结束
1.会利用诱导公式，通过图像平移得到余弦函数的图像．课标 2．会用五点法画出余弦函数在解读 [0,2π]上的图像．(重点) 3．掌握余弦函数的性质及应用．( 重点、难点)
●重点难点重点：五点法作出余弦函数的图像，并理解图像性质．难点：余弦函数的对称性．
●教学建议关于余弦函数 y＝cos x 的性质，教科书写得比较简明，这是因为学生已经有了研究正弦函数 y＝ sin x 性质的经验．对于余弦函数的性质很容易理解，讲课时，让学生观察余弦线或余弦曲线，逐一说出余弦函数的定义域、值域、最大值和最小值以及何时取得最大值和最小值，奇偶性，单调区间．
§ 6
余弦函数的图像与性质 6．1 6．2 余弦函数的图像余弦函数的性质
教师用书独具演示
●三维目标 1．知识与技能 (1)掌握余弦函数的性质． (2)能正确使用“五点法”“几何法”“图像变换法”画出余弦函数的简图．
2．过程与方法通过图像的做法，培养运用数形结合思想分析、解决问题的能力． 3．情感、态度与价值观通过本节的学习，培养学生掌握从特殊到一般、从具体到抽象的思维方法，从而达到从感性认识到理性认识的飞跃．
图 1－6－1
五点法作余弦函数的图像
【问题导思】用五点法可以作出正弦函数的图像，利用这个方法作出余弦函数的图像吗？五个关键点是什么？
π 【提示】能．五个关键点分别为(0,1)，( ，0)，(π，－ 2 3π 1)，( 2 ，0)，(2π，1)．

(北师大版)高中数学必修四：1.6《余弦函数的图像与性质》教案(2)

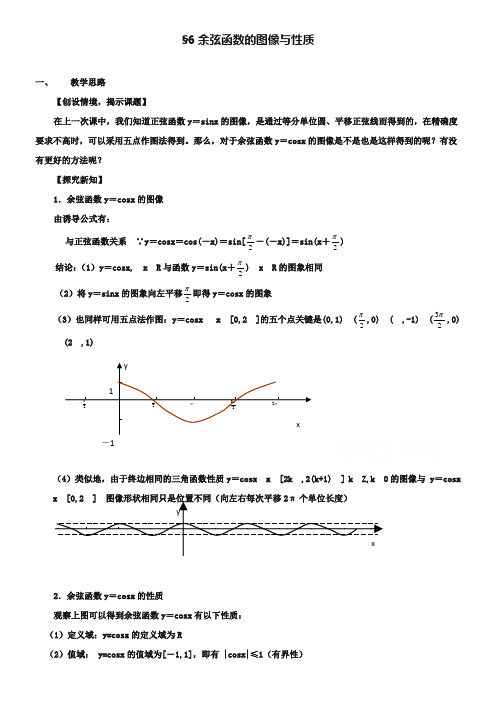
§6余弦函数的图像与性质一、教学思路【创设情境，揭示课题】在上一次课中，我们知道正弦函数y ＝sinx 的图像，是通过等分单位圆、平移正弦线而得到的，在精确度要求不高时，可以采用五点作图法得到。

那么，对于余弦函数y ＝cosx 的图像是不是也是这样得到的呢？有没有更好的方法呢？【探究新知】1．余弦函数y ＝cosx 的图像由诱导公式有：与正弦函数关系 ∵y＝cosx ＝cos(－x)＝sin[2π－(－x)]＝sin(x ＋2π) 结论：（1）y ＝与函数y ＝sin(x ＋2π的图象相同（2）将y ＝sinx 的图象向左平移2π即得y ＝cosx 的图象（3）也同样可用五点法作图：y ＝的五个点关键是(0,1) (2π-1) (23π,0)（4）类似地，由于终边相同的三角函数性质y ＝的图像与 y ＝cosx2．余弦函数y ＝cosx 的性质观察上图可以得到余弦函数y ＝cosx 有以下性质：（1）定义域：y=cosx 的定义域为R（2）值域： y=cosx 的值域为[－1,1]，即有 |cosx|≤1（有界性）－1(3)最值：对于y ＝cosx 当且仅当x ＝时 y max ＝1 当且仅当时x ＝＋π时 y min ＝－1 当-2π2π 时 y=cosx>0 当2π23π 时 y=cosx<0(4)周期性：y ＝cosx 的最小正周期为(5)奇偶性cos(－x)(6)单调性增区间为[（2k －1）π， 2k π]（k∈Z），其值从－1增至1；减区间为[2k π，（2k ＋1）π]（k∈Z），其值从1减至－1。

【巩固深化，发展思维】1．例题讲评例1．请画出函数y ＝cosx －1的简图，并根据图像讨论函数的性质。

解：（略，见教材P31-32）2．课堂练习二、归纳整理，整体认识（1）请学生回顾本节课所学过的知识内容有哪些？所涉及的主要数学思想方法有那些？（2）在本节课的学习过程中，还有那些不太明白的地方，请向老师提出。

高中数学北师大版必修4《第1章66.2余弦函数的性质》课件

8
推广到整个定义域可得当 x∈[2kπ－π，2kπ]，k∈Z 时，余弦函数 y＝cos x 是增函数，函数值由－1 增大到 1；当 x∈[2kπ，(2k＋1)π]，k∈Z 时，余弦函数 y＝cos x 是减函数，函数值由 1 减小到－1.
9
1．用五点法作出函数 y＝3－cos x 的图像，下列点中不属于五点
x
0
π 2
π
3π 2
2π
cos x
1
0 －1
0
1
－cos x －1 0
1
0
－1
14
描点并将它们用光滑的曲线连接起来，如右图．法二：作函数 y＝cos x，x∈[0,2π]的图像，然后将其作关于 x 轴对称的图像，即得 y＝－cos x， x∈[0,2π]的图像．
15
所谓的五点法是指特定的五个点，这五个点为图像的最高点、最低点或与图像的平衡位置的交点，切忌用其他的五点来代替.五点法是画正弦函数、余弦函数简图的基本方法，其他方法都由此变化而来. 函数 y＝cos x，x∈[0，2π]的图像上起关键作用的五个点坐标依次为： 0，1，π2，0，π，－1，32π，0，2π，1.
∴当 cos x＝12时，ymax＝14.
当 cos x＝－1 时，ymin＝－2.
∴函数 y＝－cos2x＋cos x 的最大值为14，最小值为－2.
32
(2)y＝3cos2x－4cos
x＋1＝3cos
x－232－13.
∵x∈π3，23π，cos x∈－12，12，
从而当 cos x＝－12，即 x＝23π时，ymax＝145；
作图中的五个关键点的是( )
A．(π，－1)
B．(0,2)

高中数学北师大版必修四余弦函数的图像与性质ppt课件(38张)

)
[答案] C
[ 解析 ] 最小正周期为 2π ， f( － x) ＝－ cos( － x) ＝－ cosx ＝ f(x)，所以f(x)是偶函数．
1 4．函数 y＝的值域是______________． 1－cosx
[答案]
1 ，＋∞ 2
[解析] ∵y－ycosx＝1，
y－1 y－1 ∴y－1＝ycosx，cosx＝ y ，∴ y ≤1， 1 1 解得y≥2，值域为2，＋∞
成才之路 ·数学
北师大版 ·必修4
路漫漫其修远兮吾将上下而求索
第一章
三角函数
第一章
§6 余弦函数的图像与性质
1
课前自主预习
3
易错疑难辨析
2
课堂典例讲练
4
课时作业
课前自主预习
现实世界中的许多运动、变化都有着循环往复、周而复始的现象，这种变化规律称为周期性．例如：地球自转引起的昼夜交替变化和公转引起的四季交替变化；月亮圆缺变化的周期性，即朔——上弦——望——下弦——朔；潮汐变化的周期性，即海
课堂典例讲练
用“五点法”作图
用“五点法”画函数 y ＝－ cosx ， x∈[0,2π]的简
图．
[思路分析] 图的关键．运用“五点法”作图，正确找出五个点是作
[规范解答] 解法一：按五个关键点列表：
x cosx －cosx
0 1 －1
π 2 0 0
π －1 1
3π 2 0 0
2π 1 －1
描点画图(如图所示)．
1 5．当 x＝________时，y＝2－2cosx 取得最大值_____．当 1 x＝______时，y＝2－2cosx 取得最小值________． 5 3 [答案] (2k＋1)π(k∈Z) 2 2kπ(k∈Z) 2

高中数学必修四北师大版第1章 §6 余弦函数的图像与性质ppt课件(44张)

[再练一题] 1 1．作出函数y＝1－3cos x在[－2π，2π]上的图像．【解】 ①列表：
x y＝cos x π 0 2 π 3π 2π 2 0 1 1 2 3
1 0 －1 4 3
1 2 1 y＝1－3cos x 3
1 ②作出y＝1－ 3 cos x在x∈[0,2π]上的图像．由于该函数为偶函数，作关于y轴 1 对称的图像，从而得出y＝1－3cos x在x∈[－2π，2π]上的图像．
2π 2π x2kπ－ ≤x≤2kπ＋，k∈Z 3 3 .
(2)要使函数有意义，
－1＋2cos x>0，则 2 9－x ≥0，
1 cos x> ， 2 即 2 x ≤9，
1 cos x>2的解集为
π π x－＋2kπ<x< ＋2kπ，k∈Z 3 3 ，
[小组合作型]
五点法作图
用“五点法”作函数y＝1－cos x(0≤x≤2π)的简图．
【精彩点拨】利用“五点法”：列表―→描点―→连线
【自主解答】列表： x cos x 0 π 2 π 3π 2π 2 0 1 1 0
1 0 －1 2
1－cos x 0 1 描点并用光滑的曲线连接起来，如图．
作函数y＝acos x＋b的图像的步骤 π 3π 1．列表：由x＝0，2，π， 2 ，2π时，cos x＝1,0，－1，0,1，求出y值． 2．描点：在同一坐标系中描五个关键点． 3．连线：用平滑曲线．
如图所示：
与余弦函数有关的定义域问题
求下列函数的定义域． (1)f(x)＝ 2cos x＋1； (2)f(x)＝log2(－1＋2cos x)＋ 9－x2.
【精彩点拨】写出使得函数有意义时所满足的条件，结合三角函数的定义

高中数学北师大版必修四课件 §6余弦函数的图像与性质

1．求三角函数的定义域，应归结为解三角不等式，其关
键就是建立使函数有意义的不等式(组)，利用三角函数的图像
直观地求得解集． 2．求三角函数的值域，要充分利用sin x和cos x的有界性，对于x有限制范围的，可结合图像求值域．
2. 求函数，的最值． 3 3
余弦函数的图像与性质
函数 y＝cos x
图像
定义域
值域
最值
R . [－1,1]. 当x＝ 2kπ(k∈Z) 时,ymax＝1; 当x＝ 2kπ+π(k∈Z) ,y ＝－1
min
续表
函数 y＝cos x
图像
周期性
2π . 周期函数，T＝
在在
奇偶性
单调性
偶函数，图像关于 y轴对称 [2kπ－π，2kπ](k∈Z)上是增加的； [2kπ，2kπ＋π](k∈Z)上是减少的
2．确定三角函数的单调区间，在理解基本三角函数的单调性的前提下，
运用整体代换的思想求解．
3．比较下列各组值的大小． 7π 7π (1)cos－与 cos ；(2)sin 194° 与 cos 160° . 8 6
7π 解：(1)cos－＝cos 8 7π π π ＝cosπ－＝－cos . 8 8 8 7π π π π π 而 cos ＝－cos ∵ 0< < < . 6 6 8 6 2 7π π π 7π ∴ cos >cos . ∴ cos－ <cos . 8 6 8 6
π 令 2kπ≤x－ ≤π＋2kπ(k∈Z)， 6 π 7π 得＋2kπ≤x≤ ＋2kπ(k∈Z)． 6 6 π －x ∴函数 y＝cos 6 的单调减区间是 π 7π ＋2kπ，＋2kπ 6 6 k∈Z.

高B数学必修四课件余弦函数的图象与性质

述光强的分布规律。
06
总结回顾与拓展延伸
关键知识点总结回顾
余弦函数定义
余弦函数是三角函数的一种，表示为y=cosx，其中x为角度，y为对应的余弦值。
余弦函数图象
余弦函数的图象是一个周期函数，周期为2π。在0到2π的区间内，余弦函数的图象呈现出一个先下降后上升的趋势，最高点为(0,1)，最低点为(π,-1)。
正切函数的图象呈现出一个周期性的上升趋势，周期为π。正切函数具有奇偶性，即tan(-x)=-tanx 。此外，正切函数在x=kπ+π/2 （k为整数）处存在间断点。
三角函数之间的关系
正弦函数、余弦函数和正切函数之间存在紧密的联系。例如， sinx=cos(x-π/2)， tanx=sinx/cosx等。这些关系式在处理复杂的三角函数问题时具有重要的应用价值。
周期性及奇偶性
周期性
余弦函数具有周期性，其最小正周期为2π。这意味着对于任意整数k，cos(x+2kπ)=cosx。
偶函数性质
余弦函数是偶函数，即cos(-x)=cosx。这意味着余弦函数的图像关于y轴对称。
02
余弦函数图像特点
振幅、周期和相位对图像影响
01
02
03
振幅
决定图像在垂直方向上的拉伸或压缩程度，振幅越大，图像在垂直方向上的变化范围越大。
THANKS
感谢观看
05
生活中实际应用举例
振动现象中余弦函数模型建立
机械振动
在机械振动中，物体围绕平衡位置做周期性往复运动，其位移随时间的变化可以用余弦函数来描述。例如，单摆的运动、弹簧振子的振动等。
VS
电磁波
电磁波是一种横波，其电场和磁场分量随时间的变化遵循余弦函数规律。在通信、广播、电视等领域，利用余弦函数的性质可以对电磁波进行调制和解调。

1-6 余弦函数的图像与性质课件高中数学必修4(北师大版)

π π x|－＋2kπ≤x≤ ＋2kπ，k∈Z. 3 3
1 (2)过0，－2、 0，
3 点分别作 x 轴的平行线，从图像中看出 2
2π 1 它们分别与余弦曲线交于点－ 3 ＋2kπ，－2 ， k ∈ Z ， 2π 1 ＋2kπ，－ 2 3 π 6＋2kπ，
自学导引 1．余弦曲线的定义余弦函数 y＝cos x(x∈R)的图像叫做
余弦曲线
(0,1)
．y＝cos x，
π ，2，0
x∈[0,2π]的图像3 ，2π，0
， (2π，1)
．
2．余弦函数的性质函数定义域值域奇偶性周期性单调性最大值与最小值对称性 y＝cos x R [－1,1] 偶函数以 2kπ 为周期(k∈Z，k≠0)，2π 为最小正周期当 x∈ [2kπ－π，2kπ](k∈Z) 当 x∈ [2kπ，2kπ＋π](k∈Z) 当 x＝ 2kπ(k∈Z) 当 x＝ 2kπ＋π(k∈Z) 时，递增；时，递减；
π π 2kπ－2，2kπ＋2k∈Z cos x，x∈ ＝ π 3π 0，x∈2kπ＋，2kπ＋ k∈Z. 2 2
函数图像如图所示：
(2)由图像知该函数的最小正周期是 2π.
π (3)由图像知函数的单调增区间为2kπ－2，2kπ(k∈Z)．
【训练 2】判断 f(x)＝sin(cos x)的奇偶性．解 f(x)＝sin(cos x)的定义域为 R，关于原点对称． f(－x)＝sin[cos(－x)]＝sin(cos x)＝f(x)． ∴f(x)＝sin(cos x)为偶函数．
题型三余弦函数“有界性”的应用【例 3】 (12 分)已知 x∈[0，π]，f(x)＝sin(cos x)的最大值为 a，最小值为 b.g(x)＝cos(sin x)的最大值为 c，最小值为 d，试判断 a、b、c、d 的大小关系．审题指导 y＝sin x，y＝cos x 都是“有界”的．当 x∈R 时，－1≤sin x≤1，－1≤cos x≤1. 【解题流程】

高中数学第一章三角函数1.6余弦函数的图像与性质课件

=
−��(��),
∴
��(��)为奇函数.
题型一
题型二
题型三
题型四
题型三余弦函数的单调性的应用
【例3】求下列函数的单调区间:
(1)y=-2cos x+3;(2)y= cos��.
分析:灵活运用y=cos x的单调性求解. 解:(1)令u=cos x,则y=-2cos x+3是由y=-2u+3和u=cos x复合而成的,而y=-2u+3在R上是减少的,故y=-2cos x+3的递增区间为 [2kπ,2kπ+π](k∈Z),递减区间为[2kπ+π,2kπ+2π](k∈Z).
2
)
A.0个 B.1个 C.2个D.3个答案:C
【做一做1-2】在区间[0,2π]内,函数y=cos x图像的五个关键点是.
答案:(0,1),
π 2
,0
, (π, −1),
3π 2
,0
, (2π, 1)
12
2.余弦函数的性质
函数性质定义域值域
最值
周期性
单调性
奇偶性
y=cos x
R [-1,1] 当 x=2kπ(k∈Z)时,y 取最大值 1;
��
=
−�� (��),
∴f (x)=c os
3 4
��
+
3π 2
为奇函数.
题型一
题型二
题型三
题型四
反思判断函数的奇偶性时,应先确定函数的定义域的对称性,再化简,最后根据定义判断.
题型一
题型二
题型三

高中数学下学期 1.6余弦函数的图象和性质课件北师大版必修4

五点法画余弦函数有关的图象画出函数 y＝－cos x,x∈[0,2π]的简图.
作简图一般利用“五点法”作图，先找出起关键作用的五个点，然后描点连线.
[解题过程] 按五个关键点列表:
x
0
π 2
π
3π 2
2π
cos x 1 0 －1 0 1
－cos x －1 0 1 0 －1
描点并将它们用光滑的曲线连接起来(如下图).
1.由诱导公式 cos(－x)＝cos x 可知余弦函数为偶函数,反映在图像上,余弦曲线关于 y 轴对称. 2.余弦曲线是中心对称图形,其所有的对称中心
坐标是kπ＋π2，0(k∈Z);余弦曲线是轴对称图形,其所有的对称轴方程是 x＝kπ(k∈Z).
3.余弦曲线的对称轴一定过余弦曲线的最高点或最低点,即此时的余弦值取最大值或最小值. 余弦曲线的对称中心一定过余弦曲线与x轴的交点,即此时的余弦值为0. 4.三角函数单调区间的确定,一般先将函数式化为基本函数的标准式,然后通过同解变形或利用数形结合的方法求解,或根据图像的直观性直接求解.
＋π8≤x≤kπ＋58π,k∈Z, 即所求的单调递增区间为kπ＋π8，kπ＋58π(k∈ Z).
【错因】上述解法忽视了复合函数的单调性的复合规律.
因为构成原函数的内层函数 u＝π4－2x 在 x∈R 上为减函数, 因此所求函数的单调递增区间为外层函数 y＝ cos u 的减区间.
【正解】因 y＝cos(π4－2x)＝cos(2x－π4) 若 y＝cos(2x－π4)递增, 则 2kπ－π≤2x－π4≤2kπ,k∈Z. 解得:kπ－38π≤x≤kπ＋π8,k∈Z. ∴函数 y＝cos(π4－2x)的递增区间为[kπ－38π,kπ ＋π8],(k∈Z).

北师大版高中数学必修四余弦函数的图像与性质教案

那么，对于余弦函数y ＝cosx 的图像是不是也是这样得到的呢？有没有更好的方法呢？【探究新知】1．余弦函数y ＝cosx 的图像由诱导公式有：与正弦函数关系 ∵y ＝cosx ＝cos(－x)＝sin[2π－(－x)]＝sin(x ＋2π) 结论：（1）y ＝cosx, x ∈R 与函数y ＝sin(x ＋2π) x ∈R 的图象相同（2）将y ＝sinx 的图象向左平移2π即得y ＝cosx 的图象（3）也同样可用五点法作图：y ＝cosx x ∈[0,2π]的五个点关键是(0,1) (2π,0) (π,-1) (23π,0) (2π,1) （4）类似地，由于终边相同的三角函数性质y ＝cosx x ∈[2k π,2(k+1)π] k ∈Z,k ≠0的图像与 y ＝cosx x ∈[0,2π] 图像形状相同只是位置不同（向左右每次平移2π个单位长2．余弦函数y ＝cosx 的性质观察上图可以得到余弦函数y ＝cosx 有以下性质：（1）定义域：y=cosx 的定义域为R（2）值域： y=cosx 的值域为[－1,1]，即有 |cosx|≤1（有界性）(3)最值：1︒对于y ＝cosx 当且仅当x ＝2k π,k ∈Z 时 y max ＝1当且仅当时x ＝2k π＋π, k ∈Z 时 y min ＝－12︒当2k π-2π<x<2k π+2π (k ∈Z)时 y=cosx>0当2k π+2π<x<2k π+23π (k ∈Z)时 y=cosx<0 (4)周期性：y ＝cosx 的最小正周期为2π(5)奇偶性cos(－x)R)是偶函数(6)单调性增区间为[（2k －1）π， 2k π]（k∈Z），其值从－1增至1；减区间为[2k π，（2k ＋1）π]（k∈Z），其值从1减至－1。

北师大版数学必修四课件：1.6余弦函数的图像和性质

2 的最大值为 ∴函数y=-3(1-cos 2x)-4cos x+4,x∈ ［ , ］ 3 3
【例】已知函数y1=a-bcosx,x∈R的最大值为
1 2
3 ，最小值 2
为，试求函数y2=b-acosx的最大值，并写出取得最大值时自变量x的集合. 【审题指导】解答本题可先利用待定系数法求出a,b的值，然后求函数y2=b-acos x的最大值.
“五点法”画函数的图像 “五点法”画函数的图像 (1)应用范围：画形如y=asin x+b (或y=acos x+b),x∈ ［0,2π ］的函数的图像.
(2)基本步骤 ①列表，取x=0，，π ，
2 3 ，2 π . 2
②求出相应的y值，确定点的坐标. ③描点. ④用光滑的曲线连线成图. 要注意用五点法画正、余弦函数图像的区别与联系.
【例1】画出y=2cos x-1在［0,2π ］上的图像.
3 【审题指导】解答本题关键是画出x=0，，π，，2π时 2 2
图像上的点的位置.
【规范解答】按五个关键点列表，描点画出图像(如下)
函数奇偶性的判断及应用
1.有关函数奇偶性的结论: (1)奇函数的图像关于原点成中心对称图形；偶函数的图像关于y轴成轴对称图形. (2)对于奇函数，当x=0属于定义域时必有f(0)=0. 对于偶函数，任意x属于定义域都有f(|x|)=f(x).
2 2 2 2
又∵y=cos x在区间［0,π］上是减少的， ∴ cos ＜cos ( ) sin .„„„„„„„„„„„„„4分
2
(2)∵cos A＜sin B, ∴ cos A＜cos ( B) .„„„„„„„„„„„„„„„6分

高中数学 1.6.1余弦函数的图象北师大版必修4

-3 5 -2 3
2
2
o - 2
2
3 2
2
5 2
3
7 2
4
-1
• 求使下列函数取得最大值的自变量x 的集合，并说出最大值是什么？
• ①y＝－2sinx，x∈R • ②y＝2-cosx，x∈R
• （1）y＝3sinx，y＝1－2cosx的值域是什么？
• 答案：［－3，3］
•
［－1，3］
再见！
余弦函数的图象
y=sinx, x[0,2] “五点法”作草
x0
2
图
3
2
2
s inx 0 11 0 1 0
. y
1
3
.
. 2 .x
o
-1
2
. 2
正弦函数的图象(正弦曲线)
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
y=sinx (xR)
y c o s x s i n ( x ) 可知把 y = s i n x 向左平移单位
根据周期性可得2kx2k
3
3
正弦、余弦函数的单调性
余弦函数的单调性 y
1
x
-3 5 -2 3
2
2
o - 2
2
3 2
2
5 2
3
7 24-1源自x -… 2
… 0… 2
…
-1
0
1
0
-1
cosx
y=cosx (xR)
增区间为 [ +2k, 2k],kZ 其值从-1增至1
减区间为 [2k, 2k， + ], kZ 其值从 1减至-1

数学北师大版必修4知识导航：1.6余弦函数含解析精品

§5 余弦函数
知识梳理
1.任意角的余弦函数（1）定义
如图1-5-1所示，单位圆与角α的终边交于P 点.设P （a ，b ）,则P 点横坐标a 是角α的函数，称为余弦函数，记为a=cosα(α∈R ).通常用x 、y 表示自变量和因变量，将余弦函数表示为y=cosx(x ∈R ).
图1-5-1
（2）余弦线
如图1-5-1所示，过点P 作x 轴的垂线PM ，垂足为M.单位圆中的有向线段OM 叫做角α的余弦线（是三角函数线之一）.当角α的终边在y 轴上时，M 与O 重合，此时余弦线变成一个点.
（3）余弦线所表示的余弦值可如下确定：
余弦线的方向是表示余弦值的符号，同x 轴一致，向上为正，向下为负；正弦线的长度是正弦值的绝对值.
（4）任意角的余弦函数定义的推广
如图1-5-2所示，设P(x,y)是α的终边上任意一点，它到原点的距离|OP|=r ，有r=2
2y x ,
则cosα=
r
x
.
图1-5-2
对于每一个确定的角α，总有唯一确定的余弦值与之对应，所以这个对应法则是以角α为自变量的函数，叫做余弦函数.余弦函数值与点P 在角α终边上的位置无关，只依赖于角α的大小.
2.余弦函数值的符号
（1）图形表示：余弦值在各象限的符号如图1-5-3所示.
图1-5-3 （2）用表格表示
3.余弦函数的图像和性质
(1)图像：如图1-5-4所示.
图1-5-4
1.复习初中学过的锐角的余弦函数，本节是锐角的余弦函数的补充和延伸.
2.任意角的余弦值的符号记忆口诀：“左负右正”.其含义是终边在y轴左侧的任意角余弦值为负，在y轴右侧的任意角余弦值为正.。

数学北师大版必修4教学设计：1.6余弦函数的图像与性质

教学设计6余弦函数的图像与性质整体设计教学分析1.上两节刚刚学习了正弦函数的图像与性质,对于本节的学习,有两个内容:一是余弦函数的图像,二是余弦函数的性质.我们可以完全类比正弦函数,只是作余弦函数图像时可通过平移的方法得到,这也是类比思想、数形结合思想、图像变换思想方法的应用.2.由于三角函数是刻画周期变化现象的重要数学模型,这也是三角函数不同于其他类型函数的最重要的地方,而且对于周期函数,只要认识清楚它在一个周期的区间上的性质,那么我们就会完全清楚它在整个定义域内的性质.教材要求我们研究三角函数性质“就是要研究这类函数性质具有的共同特点”,这是对数学思考方向的一种引导.3.余弦函数性质的难点,在于函数周期性的正确理解与运用,以下的奇偶性,无论是由图像观察,还是由诱导公式进行证明,都很容易;单调性只要求由图像观察,不要求证明.而余弦函数的最大值和最小值可以作为单调性的一个推论,只要注意引导学生利用周期进行正确归纳即可.三维目标1.通过类比正弦函数图像的作图方法,会用几何法画出余弦函数的图像;通过诱导公式能用图像平移的方法得到余弦函数的图像.2.观察函数y=cosx,x∈［0,2π］的图像上,哪些点起着关键作用,并会用关键点画出函数y=cosx 在x∈［0,2π］上的简图.3.通过类比、知识迁移的学习方法,提高探究新知的能力,并通过正弦函数和余弦函数的图像与性质的对比,理解两种函数的区别及内在联系.重点难点教学重点:会通过平移得到余弦函数的图像,并会用五点法画出余弦函数的图像;余弦函数的性质.教学难点:结合图像,余弦函数性质的灵活运用是本节的一个难点.课时安排1课时教学过程导入新课思路1.(直接导入)我们在研究了正弦函数的图像,你能类比正弦函数图像的作法作出余弦函数的图像吗？从学生画图像、观察图像入手,由此展开余弦函数性质的探究.思路2.(复习导入)研究函数就是要讨论一些性质,y＝cosx是函数,我们当然也要探讨它的一些属性.本节课,我们就来研究正弦函数、余弦函数最基本的几条性质.请同学们回想一下,一般来说,我们是从哪些方面去研究一个函数的性质的呢(定义域、值域、奇偶性、周期性、单调性、最值)?然后逐一进行探究.推进新课新知探究提出问题①你能类比作正弦函数图像的方法,用几何方法画出余弦函数的图像吗？②你能类比正弦函数性质的学习得到函数y=cosx,x∈［0,2π］的性质吗？③比较正弦函数、余弦函数的图像与性质,你能发现它们都有哪些不同？活动:先让学生充分思考、交流后再回答.对回答正确的学生,教师可鼓励他按自己的思路继续探究;对找不到思考方向的学生,教师可参与到他们中去,并适时地给予点拨、指导.在上一节中,要求学生不仅会画图,还要识图,这也是学生必须掌握的基本功.因此在研究余弦函数图像与性质时,教师要引导学生充分挖掘余弦函数曲线或单位圆中的三角函数线,当然用多媒体课件来研究三角函数性质是最理想的.因为单位圆中的三角函数线更直观地表现了三角函数中的自变量与函数值之间的关系,是研究三角函数性质的好工具.用三角函数线研究三角函数的性质,体现了数形结合的思想方法,有利于我们从整体上把握有关性质.对问题①学生不一定画准确,教师要求学生尽量画准确,能画出它们的变化趋势. 由诱导公式y=cosx=cos(-x)=sin ［2π-(-x)］=sin(2π+x)可知,y=cosx 的图像就是函数y=sin(2π+x)的图像.从而,余弦函数y=cosx 的图像可以通过将正弦曲线y=sinx 向左平移2π个单位长度得到(如图1所示).图1也可以利用描点法作出余弦函数的图像(如图2所示).余弦函数y=cosx(x ∈R )的图像叫作余弦曲线.图2教师引导学生类比正弦函数的性质学习,让学生观察余弦函数的图像,从定义域、值域、周期性、最大值与最小值、单调性、奇偶性这几个方面探究.可完全放给学生自己探究,教师仅是适时地给予引导.学生很容易得出余弦函数y ＝cosx,x ∈R 具有以下主要性质: (1)定义域余弦函数的定义域是R. (2)值域余弦函数的值域是［-1,1］. (3)周期性余弦函数是周期函数,它的最小正周期是2π.由于余弦函数具有周期性,为了研究问题方便,我们可以选取任意一个x 值,讨论余弦函数在区间［x,x+2π］上的性质,然后拓展到整个定义域(-∞,+∞)上. (4)最大值与最小值当x=2kπ(k ∈Z )时,余弦函数取得最大值1; 当x=(2k+1)π(k ∈Z )时,余弦函数取得最小值-1. (5)单调性我们选取长度为2π的区间［-π,π］.可以看出,当x 由-π增大到0时,cosx 的值由-1增大到1,当x 由0增大到π时,cosx 的值由1减小到-1.因此,余弦函数在区间［-π,0］上递增,在区间［0,π］上递减.由余弦函数的周期性可知,余弦函数在每一个区间［(2k-1)π,2kπ］(k ∈Z )上都是递增的,在每一个区间［2kπ,(2k+1)π］(k ∈Z )上都是递减的.所以这两类闭区间的每一个都是余弦函数的单调区间.(6)奇偶性余弦函数的图像关于y 轴对称,即cos(-x)=cosx.∴余弦函数是偶函数.这个变化情况可从下表及图像中直观地显示出来,教师可引导学生画图并列出下表:类比正弦函数性质的探究,学生可能通过图像已经看出来了,在余弦曲线上也有其他的对称点和对称轴,如余弦曲线还关于直线x ＝0,x ＝π等多条直线对称,余弦曲线还关于点(2π,0)等多个点对称,这是由它的周期性而来的.教师可就此引导学生进一步探讨,以开阔学生的视野.探究余弦函数的性质后,学生自然会拿它与正弦函数的性质进行比较一番,这种习惯很好.比较最能澄清问题的本质属性,比较是最好的学习方法.当我们仔细对比正弦函数、余弦函数性质后,会发现它们有很多共同之处.我们不妨把两个图像中的直角坐标系都去掉,会发现它们其实都是同样形状的曲线.所以它们的定义域相同,都为R .值域也相同,都是［-1,1］.最大值都是1,最小值都是-1,只不过由于y 轴放置的位置不同,使取得最大(或最小)值的时刻不同.它们的周期相同,最小正周期都是2π.它们的图像都是轴对称图形和中心对称图形,且都是以图像上函数值为零所对应的点为对称中心,以过最值点且垂直于x 轴的直线为对称轴.但是由于y 轴的位置不同,对称中心及对称轴与x 轴交点的横坐标也不同.它们都不具备单调性,但都有单调区间,且都是增、减区间间隔出现.也是由于y 轴的位置改变,使增、减区间的位置有所不同.也使奇偶性发生了改变.由此可以看出,图像的平移变换对函数的性质会产生怎样的影响. 讨论结果:①—③略. 应用示例例1 画出函数y=cosx-1,x ∈R 的简图,并根据图像讨论函数的性质.活动:这是课本上紧接着余弦性质后的一道例题,目的是通过这道例题直接巩固所学的余弦函数的图像与性质.课堂上可放手让学生自己去求,教师适时地指导、点拨、纠错.并提示-1对余弦函数的图像与性质的影响.让学生进一步熟悉“五点法”作图,领悟图像作法的要领,最终达到熟练掌握.从实际教学来看,“五点法”作图易学却难掌握,学生需练扎实的基本功.可先让学生按“列表、描点、连线”三步来完成.对学生出现的种种失误,教师不要着急,在学生操作中一一纠正,这对以后学习大有好处.图4让学生熟悉“五点法”.如果是多媒体教学,要突破课件教学的互动性,多留给学生一些动手操作的时间,或者增加图像纠错的环节,效果将会更加令人满意,切不可教师画图学生看.完成本例余弦后,学生从图像上就可以一目了然地说出函数的性质了.这也让学生从中体会到了数形结合的好处.例2 利用三角函数的单调性,比较cos(-523π)与cos(-417π)的大小.活动:学生很容易回忆起利用指数函数、对数函数的大小比较,这很好,充分利用学生的知识迁移有利于学生能力的快速提高.本例是余弦,只需将角化为同一个单调区间,然后根据单调性比较大小即可.课堂上仍是让学生自己独立地去操作,教师点拨、纠错,对思考方法不对的学生给予帮助指导.解:cos(-523π)=cos 523π=cos 53π,cos(-417π)=cos(417π)=cos 4π.因为0＜4π＜53π＜π,且函数y=cosx,x ∈［0,π］是减函数,所以cos4π＞cos53π,即cos(-523π)＜cos(-417π).点评:推进本例时应提醒学生注意,在今后遇到的三角函数值大小比较时,必须将已知角化为同一个单调区间.其次要注意首先大致的判断一下有没有符号不同的情况,以便快速解题,如本例中,cos4π＞0,cos53π＜0,显然大小立判. 例3 求函数y=cos(21x-6π),x ∈［-2π,2π］的单调递增区间. 活动:教师引导学生探究,可以利用余弦函数的单调性来求所给函数的单调区间.教师引导学生的思考方向:把21x-6π看成z,问题就转化为求y ＝cosz 的单调区间问题,而这就简单多了,教师应点出,这里用的是换元的思想方法.解:令z=21x-6π.函数y=cosz 的单调递增区间是［-π+2kπ,2kπ］.由-π+2kπ≤21x-6π≤2kπ,得-35π+4kπ≤x≤3π+4kπ,k ∈Z .取k=0,得-35π≤x≤3π,而［-35π,3π］［-2π,2π］,因此,函数y=cos(21x-6π),x ∈［-2π,2π］的单调递增区间是［-35π,3π］.点评:本例的求解是转化与化归思想的运用,即利用余弦函数的单调性,将问题转化为一个关于x 的不等式问题.然后通过解不等式得到所求的单调区间,要让学生熟悉并灵活运用这一数学思想方法,善于将复杂的问题简单化. 4.求函数y ＝x cos 的定义域.活动:学生探究操作,寻找解题方向,教师提醒学生充分利用函数图像.并根据实际情况进行适当的指导点拨,纠正出现的一些错误或书写不规范等. 解:由cosx≥0得-2π＋2kπ≤x≤2π＋2kπ(k ∈Z ).∴原函数的定义域为［-2π＋2kπ,2π＋2kπ］(k ∈Z ).点评:本例虽然短小,学生却易出错,本例实际上是解三角不等式,应根据余弦曲线探究适合题目要求的条件,然后解之.本例可分作两步,第一步转化,第二步利用余弦函数曲线写出解集.变式训练函数y ＝1+cosx 的图像( )A.关于x 轴对称B.关于y 轴对称C.关于原点对称D.关于直线x ＝2π对称答案:B例 5 (2007山东临沂一模,17(1))在给定的直角坐标系(如图5)中,作出函数f(x)=2cos(2x+4π)在区间［0,π］上的图像.图5解:列表取点如下:描点连线作出函数f(x)＝2cos(2x+4)在区间［0,π］上的图像如图6.图6点评:本题按说难度不大,但学生得分率却不高,画图是学生较薄弱的环节. 知能训练课本练习1-4. 课堂小结1.由学生回顾归纳并说出本节学习了哪些数学知识？学习了哪些数学思想方法？这节课我们研究了余弦函数的图像与性质.通过对两个函数从定义域、值域、最值、奇偶性、周期性、增减性、对称性等几方面的的比较,加深了我们对这两个函数的理解.同时也巩固了本节课所学的余弦函数的图像的画法及性质的理解,将我们所学内容很快地就纳入了已有的知识系统.2.进一步熟悉了数形结合的思想方法,转化与化归的思想方法,类比思想的方法及观察、归纳、特殊到一般的辩证统一的观点. 作业课本习题1—5 3、4、5、6.设计感想1.本节教案设计的容量较大,指导思想是让学生在课堂上充分探究、大量活动.作为函数的性质,从初中就开始学习,到高中学习幂、指数、对数函数后,对函数性质有了较深的认识.这是高中所学的最后一个基本初等函数.但由于以前所学的函数不是周期函数,所以理解较为容易,而正弦函数、余弦函数除具有以前所学函数的共性外,又有其特殊性,共性中包含特性,特性又离不开共性,这种普通性与特殊性的关系通过教学应让学生有所领悟.2.在学完余弦函数性质后,应着重引导学生比较正、余弦函数的性质的异同,以加深他们对两个函数的区别与联系的认识;让学生在同一坐标系中画出正弦、余弦函数的图像,在解题中突出数形结合思想,在训练中降低变化技巧的难度,提高应用图像与性质解题的力度.较好地利用图像解决问题,这也是是本节课主要强调的数学思想.3.学习正、余弦函数性质后,引导学生对过去所学的知识重新认识,例如cos(α+2π)＝cosα这个公式,以前我们只简单地把它看成一个诱导公式,现在我们认识到了它表明余弦函数的周期性,以提升学生的思维层次.备课资料备用习题1.函数y=cosx,x ∈［-6π,2π］的值域是 ( ) A.［0,1］ B.［-1,1］ C.［0,23］ D.［-21,1］ 2.(2007山东临沂)对于函数y=f(x)=⎩⎨⎧<≥,cos sin ,cos ,cos sin ,sin x x x x x x 下列命题中正确的是( )A.该函数的值域是［-1,1］B.当且仅当x=2kπ+2π(k ∈Z )时,函数取得最大值1C.该函数是以π为最小正周期的周期函数D.当且仅当2kπ+π＜x ＜2kπ+23π(k ∈Z )时,f(x)＜0 3.(2005山东潍坊)已知-6π≤x ＜3π,cosx=11+-m m ,则m 的取值范围是( ) A.m ＜-1 B.3＜m≤7+43 C.m ＞3 D.3＜m ＜7+43或m ＜-14.(2004天津,12)定义在R 上的函数f(x)既是偶函数又是周期函数,若f(x)的最小正周期是π,且当x ∈［0,2π］时,f(x)=sinx,则f(35π)的值为( ) A.-21 B.21C.-23D.23 5.(2006广东珠海)已知函数y=2cosx(0≤x≤1 000π)的图像与直线y=2围成一个封闭的平面图形,则这个封闭图形的面积是__________________.6.(2005上海,10)函数f(x)=sinx+2|sinx|,x ∈［0,2π］的图像与直线y=k 有且只有两个不同的交点,则k 的取值范围是______________.7.根据余弦函数的图像,求满足cos2x≥21的x 的集合. 参考答案:1.A 画出y=cosx,x ∈［-6π,12π］的图像,从而得出y ∈［0,1］,故选A. 2.D 画图像可知,值域为［-22,1］,x=2kπ或x=2kπ+2π时取最大值,T=2π,故选D. 3.C 由-6π≤x ＜3π,21＜cosx≤1,∴21＜11+-m m ≤1.∴m ＞3.故选C. 4.D 由f(x)的周期为π知,f(35π)=f(32π)=f(-3π). 由f(x)是偶函数知f(-3π)=f(3π).又当x ∈［0,2π］时,f(x)=sinx, ∴f(3π)=sin3π=23. 故选D.5.2 000π 由图像知y=2cosx 在［0,2π］上与直线y=2围成封闭图形的面积是2π×2=4π ∵1 000π÷2π=500,∴在0≤x≤1 000π上所围成的封闭图形的面积S=4π×500=2 000π.6.1＜k ＜3f(x)=sinx+2|sinx|=⎩⎨⎧∈-∈),2,(,sin ],,0[,sin 3πππx x x x 则k 的取值范围是1＜k ＜3.7.解:由余弦函数的图像与性质知-3π+2kπ≤2x≤3π+2kπ(k ∈Z ), 即-6π+kπ≤x≤6π+kπ(k ∈Z ).∴满足函数cos2x≥21的x 的集合是{x|-6π+kπ≤x≤6π+kπ}(k ∈Z ). (设计者：郑吉星)。

课堂新坐标高中数学北师大版必修学案余弦函数的图像与性质含解析

§6 余弦函数的图像与性质 6.1 余弦函数的图像 6.2 余弦函数的性质1．会利用诱导公式，通过图像平移得到余弦函数的图像． 2.会用五点法画出余弦函数在[0,2π]上的图像．(重点) 3．掌握余弦函数的性质及应用．(重点、难点)[基础·初探]教材整理余弦函数的图像与性质阅读教材P 31～P 33“思考交流”以上部分，完成下列问题． 1．利用图像变换作余弦函数的图像余弦函数y ＝cos x 的图像可以通过将正弦曲线y ＝sin x 向左平移π2个单位长度得到．如图1－6－1是余弦函数y ＝cos x (x ∈R )的图像，叫作余弦曲线．图1－6－12．利用五点法作余弦函数的图像画余弦曲线，通常也使用“五点法”，即在函数y ＝cos x (x ∈[0,2π])的图像上有五个关键点，为(0,1)，⎝ ⎛⎭⎪⎫π2，0，(π，－1)，⎝ ⎛⎭⎪⎫32π，0，(2π，1)，可利用此五点画出余弦函数y＝cos x，x∈R的简图(如图1－6－2)．图1－6－2 3．余弦函数的性质判断(正确的打“√”，错误的打“×”)(1)余弦函数y＝cos x的定义域为R.()(2)余弦函数y＝cos x的图像可由y＝sin x的图像向右平移π2个单位得到．()(3)在同一坐标系内，余弦函数y＝cos x与y＝sin x的图像形状完全相同，只是位置不同．()(4)正弦函数与余弦函数有相同的周期，最大值、最小值及相同的单调区间．()【解析】 (1)(3)正确；余弦函数y ＝cos x ＝sin ⎝ ⎛⎭⎪⎫π2＋x ，即可看作是y ＝sin x向左平移π2个单位得到的，因而(2)错；正、余弦函数有相同的周期(都是2π)，相同的最大值(都是1)，相同的最小值(都是－1)，也都有单调区间，但单调区间不同，因而(4)错．【答案】 (1)√ (2)× (3)√ (4)×[质疑·手记]预习完成后，请将你的疑问记录，并与“小伙伴们”探讨交流：疑问1：_________________________________________________________ 解惑：___________________________________________________________ 疑问2：_________________________________________________________ 解惑：___________________________________________________________ 疑问3：_________________________________________________________ 解惑：___________________________________________________________[小组合作型]【精彩点拨】利用“五点法”：【自主解答】列表：作函数y＝a cos x＋b的图像的步骤1．列表：由x＝0，π2，π，3π2，2π时，cos x＝1,0，－1，0,1，求出y值．2．描点：在同一坐标系中描五个关键点．3．连线：用平滑曲线．[再练一题]1．作出函数y＝1－13cos x在[－2π，2π]上的图像．【解】①列表：②作出y＝1－13cos x在x∈[0,2π]上的图像．由于该函数为偶函数，作关于y轴对称的图像，从而得出y＝1－13cos x在x∈[－2π，2π]上的图像．如图所示：(1)f(x)＝2cos x＋1；(2)f (x )＝log 2(－1＋2cos x )＋9－x 2.【精彩点拨】写出使得函数有意义时所满足的条件，结合三角函数的定义域，求若干个不等式的交集即可．【自主解答】 (1)要使y ＝2cos x ＋1有意义，则必须满足2cos x ＋1≥0，即cos x ≥－12.结合余弦函数的图像得y ＝2cos x ＋1的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π－2π3≤x ≤2k π＋2π3，k ∈Z. (2)要使函数有意义，则⎩⎨⎧－1＋2cos x >0，9－x 2≥0，即⎩⎪⎨⎪⎧cos x >12，x 2≤9，cos x >12的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－π3＋2k π<x <π3＋2k π，k ∈Z， x 2≤9的解集为{x |－3≤x ≤3}，取交集得⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪－π3<x <π3. ∴原函数的定义域为⎝ ⎛⎭⎪⎫－π3，π3.1．求三角函数的定义域时，一般要解三角不等式，其主要方法是借助于三角函数的图像，关键有两点：(1)选取一个合适的周期；(2)确定边界值．2．当函数由几部分构成时，应取使每一部分有意义的x 取值范围的公共范围，即取它们的交集．3．当三角不等式与代数不等式在一起时，在取交集时，应注意对三角不等式解集中的k 进行讨论．[再练一题]2．求下列函数的定义域．(1)y ＝32－cos x ；(2)y ＝log 12(2cos x －2)．【解】 (1)要使函数有意义，则有32－cos x ≥0， ∴cos x ≤32，可得2k π＋π6≤x ≤2k π＋11π6，k ∈Z . 故所求函数的定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π＋π6≤x ≤2k π＋11π6，k ∈Z . (2)要使函数有意义，则有2cos x －2>0， ∴cos x >22，故所求定义域为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π－π4<x <2k π＋π4，k ∈Z.(1)(2)比较大小cos 263π________cos ⎝ ⎛⎭⎪⎫－133π.【精彩点拨】 (1)y ＝1－2cos x 的单调性与y ＝－cos x 的单调性相同，与y ＝cos x 的单调性相反．(2)利用诱导公式将所给角转化到同一单调区间上比较．【自主解答】 (1)由于y ＝cos x 的单调减区间为[2k π，2k π＋π](k ∈Z )，所以函数y ＝1－2cos x 的增区间为[2k π，2k π＋π](k ∈Z )．(2)由于cos 263π＝cos ⎝ ⎛⎭⎪⎫8π＋2π3＝cos 2π3， cos ⎝ ⎛⎭⎪⎫－13π3＝cos ⎝ ⎛⎭⎪⎫13π3＝cos ⎝ ⎛⎭⎪⎫4π＋π3＝cos π3， y ＝cos x 在[0，π]上是减少的．由π3<2π3知cos π3>cos 2π3，即cos 263π<cos ⎝ ⎛⎭⎪⎫－13π3.【答案】 (1)[2k π，2k π＋π] (2)<1．形如y ＝a cos x ＋b (a ≠0)函数的单调区间 (1)当a >0时，其单调性同y ＝cos x 的单调性一致； (2)当a <0时，其单调性同y ＝cos x 的单调性恰好相反．2．比较cos α与cos β的大小时，可利用诱导公式化为[0，π]内的余弦函数值来进行．[再练一题]3．(1)比较大小：cos ⎝ ⎛⎭⎪⎫－235π与cos ⎝ ⎛⎭⎪⎫－174π；(2)求函数y ＝log 12(cos 2x )的增区间．【解】 (1)cos ⎝ ⎛⎭⎪⎫－235π＝cos 23π5＝cos ⎝ ⎛⎭⎪⎫4π＋3π5＝cos 3π5，cos ⎝ ⎛⎭⎪⎫－174π＝cos 17π4＝cos ⎝ ⎛⎭⎪⎫4π＋π4＝cos π4. ∵0<π4<3π5<π，且y ＝cos x 在[0，π]上递减， ∴cos 3π5<cos π4，即cos ⎝ ⎛⎭⎪⎫－235π<cos ⎝ ⎛⎭⎪⎫－174π.(2)由题意得cos 2x >0且y ＝cos 2x 递减． ∴x 只须满足：2k π<2x <2k π＋π2，k ∈Z ， ∴k π<x <k π＋π4，k ∈Z ，∴y ＝log 12(cos 2x )的增区间为⎝ ⎛⎭⎪⎫k π，k π＋π4，k ∈Z .[探究共研型]探究1 余弦函数在第一象限内是减函数吗？【提示】不是．余弦函数y ＝cos x 在⎣⎢⎡⎦⎥⎤0，π2内是减函数，但不能说在第一象限是减函数．如390°和60°都是第一象限角，虽然有390°>60°，却有cos 60°<cos 390°.探究2 求与余弦函数相关的最值问题时应注意什么？【提示】首先看函数的定义域，一定注意在定义域内求最值．探究3 对于y ＝A cos 2x ＋B cos x ＋C 型的函数如何求最值？【提示】利用换元法转化为在固定区间上的二次函数求最值．求下列函数的最值． (1)y ＝－cos 2x ＋cos x ；(2)y ＝3cos 2x －4cos x ＋1，x ∈⎣⎢⎡⎦⎥⎤π3，2π3.【精彩点拨】本题中的函数可以看作是关于cos x 的二次函数，可以化归为利用二次函数求最值的方法求解．【自主解答】 (1)y ＝－⎝ ⎛⎭⎪⎫cos x －122＋14.∵－1≤cos x ≤1， ∴当cos x ＝12时，y max ＝14. 当cos x ＝－1时，y min ＝－2.∴函数y ＝－cos 2x ＋cos x 的最大值为14，最小值为－2. (2)y ＝3cos 2x －4cos x ＋1 ＝3⎝ ⎛⎭⎪⎫cos x －232－13.∵x ∈⎣⎢⎡⎦⎥⎤π3，2π3，cos x ∈⎣⎢⎡⎦⎥⎤－12，12，从而当cos x ＝－12，即x ＝2π3时，y max ＝154；当cos x ＝12，即x ＝π3时，y min ＝－14.∴函数在区间⎣⎢⎡⎦⎥⎤π3，2π3上的最大值为154，最小值为－14.求值域或最大值、最小值问题，一般依据为： (1)sin x ，cos x 的有界性； (2)sin x ，cos x 的单调性；(3)化为sin x ＝f (x )或cos x ＝f (x )，利用|f (x )|≤1来确定； (4)通过换元转化为二次函数．[再练一题]4．已知函数y ＝－cos 2x ＋a cos x －12a －12的最大值为1，求a 的值.【导学号：66470018】【解】 y ＝－cos 2 x ＋a cos x －12a －12 ＝－⎝ ⎛⎭⎪⎫cos x －a 22＋a 24－a 2－12.∵－1≤cos x ≤1，于是①当a2<－1，即a <－2时，当cos x ＝－1时， y max ＝－32a －32.由－32a －32＝1，得a ＝－53>－2(舍去)；②当－1≤a 2≤1，即－2≤a ≤2时，当cos x ＝a 2时，y max ＝a 24－a 2－12. 由a 24－a 2－12＝1，得a ＝1－7或a ＝1＋7(舍去)； ③当a 2>1，即a >2时，当cos x ＝1时，y max ＝a 2－32.由a 2－32＝1，得a ＝5. 综上可知，a ＝1－7或a ＝5.[构建·体系]1．函数y ＝2cos x －1的最大值、最小值分别是( ) A ．2，－2 B ．1，－3 C ．1，－1D ．2，－1【解析】 ∵－1≤cos x ≤1， ∴－2≤2cos x ≤2， ∴－3≤2cos x －1≤1， ∴最大值为1，最小值为－3. 【答案】 B2．函数y ＝sin x 和y ＝cos x 都是减少的区间是( ) A ．⎣⎢⎡⎦⎥⎤2k π－π2，2k π(k ∈Z )B.⎣⎢⎡⎦⎥⎤2k π－π，2k π－π2(k ∈Z )C.⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋π(k ∈Z ) D.⎣⎢⎡⎦⎥⎤2k π，2k π＋π2(k ∈Z ) 【解析】结合函数y ＝sin x 和y ＝cos x 的图像知都减少的区间为⎣⎢⎡⎦⎥⎤2k π＋π2，2k π＋π(k ∈Z )．【答案】 C3．函数y ＝cos x1＋cos x的定义域是________.【导学号：66470019】【解析】由题意知1＋cos x ≠0，即cos x ≠－1，结合函数图像知{}x | x ≠2k π＋π，k ∈Z .【答案】{}x | x ≠2k π＋π，k ∈Z4．满足2＋2cos x ≥0(x ∈R )的x 的集合是________．【解析】 ∵2＋2cos x ≥0， ∴cos x ≥－22，结合图像(略)知：－34π＋2k π≤x ≤3π4＋2k π(k ∈Z )．【答案】⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪2k π－34π≤x ≤2k π＋3π4，k ∈Z5．画出y ＝1－3cos x 在[0,2π]上的简图，并指出其最值和单调区间．【解】列表：图像如下：由图像可知，函数y ＝1－3cos x 在[0,2π]上的最大值为4，最小值为－2，单调增区间为[0，π]，减区间为[π，2π]．我还有这些不足：(1)______________________________________________________________ (2)______________________________________________________________我的课下提升方案：(1)______________________________________________________________(2)______________________________________________________________。

北师大版高中数学必修四余弦函数的图像和性质PPT全文课件(18ppt)

图象的最高点 ( 0，1 )， (2π，1)
图象的最低点 (π，1)
与 x 轴的y 交点
(
π ２
，
0
)，
(３２π ，0 )
1-
五点作图法
-
-1
oπ
6
π
π 2
3
π 2 π 5 π
7π
36
6
4π 3
3π 5π
2
3
11 π 6
2π
x
-1 -
北师大版高中数学必修四余弦函数的图像和性质PPT 全文课件(18p pt)【完美课件】
3 2
2
5 2
-1
x
- …
2
cosx
-1
0
…0 1
…
2
0
3
7 2
x
4
… -1
y=cosx (xR)
单调递增区间 [ -+2k, 2k],kZ 单调递减区间 [2k, 2k + ], kZ
北师大版高中数学必修四余弦函数的图像和性质PPT 全文课件(18p pt)【完美课件】
北师大版高中数学必修四余弦函数的图像和性质PPT 全文课件(18p pt)【完美课件】
余弦曲线
由诱导公式 cos( x+2k)＝cos x，将 y＝cos x ， x[0，2 ] 的图象沿 x 轴向左、右平移2 ， 4 ，…，就可得到 y＝cos x的图象.
y
1-
-
-
6π
4π
2
o
-1 -
2π
4π
6π
x
余弦函数的图象，就叫做余弦曲线.
北师大版高中数学必修四余弦函数的图像和性质PPT 全文课件(18p pt)【完美课件】