最新人教版高中数学选修1-1《双曲线及其标准方程》温故知新(第1课时)
合集下载
人教版人教课标高中数学选修1-1 双曲线及其标准方程 课件
结 束
16
9
1.
的两种标准方程，并能熟练运用 待定系数法求解曲线的方程.
例题讲评
上 页
下 页
例3 一炮弹在某处爆炸，在 A 处听到爆炸声的时间比在 B 处晚2 s. （ 1 ）爆炸点应在什么样的曲 线上？ F1 （ 2 ）已知 A 、 B 两地相距 800 m，并且此时声速为340 m/s， 求曲线的方程.
双曲线的标准方程：
上 页
形式一： （a>0,b>0） 说明：此方程表示焦点在 x轴上的双曲线 .焦点是 F1(－c,0)、F2(c,0)，这里c2=a2+b2.
下 页
x y 2 1 2 a b
2
2
y x 形式二： a 2 b 2 1 （a>0,b>0） 说明：此方程表示焦点在 y 轴上的双曲线 . F1(0，－c)、F2(0， c)，这里c2=a2+b2.
上 页
a
b
①
因为点P1、P2在双曲线上，所以点P1、P2的坐 标适合方程①.将其分别代入方程①中，得方程 组 ( 4 2 ) 3 1
2 2
下 页
2 2 a b 9 2 ( ) 25 2 42 1 b a
解得：a2=16,b2=9.故所求双曲线的标准方程 2 2 x 为：y 说明：例 2 要求学生熟悉双曲线
4
①
下 页
a
b
因为点P1、P2在双曲线上，所以点P1、P2的坐 标适合方程①.将其分别代入方程①中，得方程 组 ( 4 2 ) 2 3 2
2 1 2 a b 9 2 ( ) 25 2 42 1 b a
结 束
解：因为双曲线的焦点在y轴上，所以设 2 2 y x 所求双曲线的标准方程为： a>0,b>0) 2 (1 2
16
9
1.
的两种标准方程，并能熟练运用 待定系数法求解曲线的方程.
例题讲评
上 页
下 页
例3 一炮弹在某处爆炸，在 A 处听到爆炸声的时间比在 B 处晚2 s. （ 1 ）爆炸点应在什么样的曲 线上？ F1 （ 2 ）已知 A 、 B 两地相距 800 m，并且此时声速为340 m/s， 求曲线的方程.
双曲线的标准方程：
上 页
形式一： （a>0,b>0） 说明：此方程表示焦点在 x轴上的双曲线 .焦点是 F1(－c,0)、F2(c,0)，这里c2=a2+b2.
下 页
x y 2 1 2 a b
2
2
y x 形式二： a 2 b 2 1 （a>0,b>0） 说明：此方程表示焦点在 y 轴上的双曲线 . F1(0，－c)、F2(0， c)，这里c2=a2+b2.
上 页
a
b
①
因为点P1、P2在双曲线上，所以点P1、P2的坐 标适合方程①.将其分别代入方程①中，得方程 组 ( 4 2 ) 3 1
2 2
下 页
2 2 a b 9 2 ( ) 25 2 42 1 b a
解得：a2=16,b2=9.故所求双曲线的标准方程 2 2 x 为：y 说明：例 2 要求学生熟悉双曲线
4
①
下 页
a
b
因为点P1、P2在双曲线上，所以点P1、P2的坐 标适合方程①.将其分别代入方程①中，得方程 组 ( 4 2 ) 2 3 2
2 1 2 a b 9 2 ( ) 25 2 42 1 b a
结 束
解：因为双曲线的焦点在y轴上，所以设 2 2 y x 所求双曲线的标准方程为： a>0,b>0) 2 (1 2
人教新课标版数学高二选修1-1课件双曲线及其标准方程
返回
(2)求双曲线的标准方程时，应注意两个问题： ①正确判断焦点的位置；②设出标准方程后，再运用待定系数法求解. 求双曲线的标准方程也是从“定形”“定式”和“定量”三个方面去考 虑.“定形”是指对称中心在原点，以坐标轴为对称轴的情况下，焦点在 哪条坐标轴上；“定式”是根据“形”设双曲线标准方程的具体形式； “定量”是指用定义法或待定系数法确定a，b的值.
解析 由题意得(10－k)(5－k)<0，解得5<k<10.
解析答案
1 2345
4.设 m 是常数，若点 F(0,5)是双曲线ym2－x92＝1 的一个焦点，则 m＝_1_6_. 解析 由已知条件知m＋9＝52，所以m＝16.
解析答案
1 2345
5.已知双曲线x92－1y62 ＝1 上一点 M 的横坐标为 5，则点 M 到左焦点的距离 34
答案
知识点二 双曲线的标准方程 (1)两种形式标准方程
焦点所在的坐标轴 标准方程
x轴 ax22－by22＝1 (a>0，b>0)
y轴 ay22－bx22＝1 (a>0，b>0)
图形
焦点坐标 a、b、c的关系式
__F__1(_－__c_,0_)_，__F_2_(c_,_0_)
__F_1_(_0_，__－__c_)，__F_2_(_0_，__c)
答案
问题2 双曲线的标准方程的推导过程是什么？
答案
问题3 双曲线中a，b，c的关系如何？与椭圆中a、b、c的关系有何不同？ 答案 双曲线标准方程中的两个参数a和b，确定了双曲线的形状和大小， 是双曲线的定形条件，这里b2＝c2－a2，即c2＝a2＋b2，其中c>a，c>b，a 与b的大小关系不确定；而在椭圆中 b2＝a2－c2，即a2＝b2＋c2，其中 a>b>0，a>c，c与b大小不确定.
(2)求双曲线的标准方程时，应注意两个问题： ①正确判断焦点的位置；②设出标准方程后，再运用待定系数法求解. 求双曲线的标准方程也是从“定形”“定式”和“定量”三个方面去考 虑.“定形”是指对称中心在原点，以坐标轴为对称轴的情况下，焦点在 哪条坐标轴上；“定式”是根据“形”设双曲线标准方程的具体形式； “定量”是指用定义法或待定系数法确定a，b的值.
解析 由题意得(10－k)(5－k)<0，解得5<k<10.
解析答案
1 2345
4.设 m 是常数，若点 F(0,5)是双曲线ym2－x92＝1 的一个焦点，则 m＝_1_6_. 解析 由已知条件知m＋9＝52，所以m＝16.
解析答案
1 2345
5.已知双曲线x92－1y62 ＝1 上一点 M 的横坐标为 5，则点 M 到左焦点的距离 34
答案
知识点二 双曲线的标准方程 (1)两种形式标准方程
焦点所在的坐标轴 标准方程
x轴 ax22－by22＝1 (a>0，b>0)
y轴 ay22－bx22＝1 (a>0，b>0)
图形
焦点坐标 a、b、c的关系式
__F__1(_－__c_,0_)_，__F_2_(c_,_0_)
__F_1_(_0_，__－__c_)，__F_2_(_0_，__c)
答案
问题2 双曲线的标准方程的推导过程是什么？
答案
问题3 双曲线中a，b，c的关系如何？与椭圆中a、b、c的关系有何不同？ 答案 双曲线标准方程中的两个参数a和b，确定了双曲线的形状和大小， 是双曲线的定形条件，这里b2＝c2－a2，即c2＝a2＋b2，其中c>a，c>b，a 与b的大小关系不确定；而在椭圆中 b2＝a2－c2，即a2＝b2＋c2，其中 a>b>0，a>c，c与b大小不确定.
新版高中数学人教A版选修1-1课件2.2.1双曲线及其标准方程
【做一做 2】 (1)已知双曲线���4���2 − 1������22=1,则其焦点坐标为
.
(2)若双曲线焦点坐标为(0,5),a=3,则其标准方程为
.
解析:(1)双曲线焦点在 x 轴上,且 c2=4+12=16,所以 c=4,故焦点
坐标为(±4,0).
(2)依题意,设双曲线标准方程为������������22 − ������������22=1(a>0,b>0), 则 c=5,a=3,b2=c2-a2=16,故方程为���9���2 − 1������62=1.
(3)若方程表示椭圆,求实数m的取值范围.
思路点拨:根据双曲线与椭圆的标准方程的特征建立不等式(组)
求解.
自主解答:(1)依题意有(m-1)(m2-4)>0,即(m-1)(m+2)(m-2)>0,解得-
2<m<1或m>2.
(2)依题意有 ������2-4 < 0,解得-2<m<1. ������-1 < 0,
答案:A
-12-
2.2.1 双曲线及其标准方程
首页
课前预习案 新知导学
课堂探究案 答疑解惑
当堂检测
探究一
探究二
探究三
思维辨析
对双曲线标准方程的理解
【例2】 已知曲线方程
������2 ������-1
−
���������2���2-4=1
.
(1)若方程表示双曲线,求实数m的取值范围;
(2)若方程表示焦点在y轴上的双曲线,求实数m的取值范围;
9 4
,5
;
(4)与双曲线1������62 − ���4���2=1 有相同的焦点,且经过点(3√2,2).
高中数学 2.2.1双曲线及其标准方程课件 新人教A版选修1-1
a
16
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
17
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
18
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
19
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
20
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
46
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
47
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
48
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
49
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
50
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
21
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
22
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
23
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
24
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
25
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
31
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
32
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a33Biblioteka 基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
a
34
基础预习点拨 要点探究归纳 知能达标演练 课后巩固作业
人教版人教课标高中数学选修1-1双曲线及其标准方程一课件
结
束 方程x2cosθ+y2sinθ=1的曲线怎样变化？
动
画上 页
音
焦点在y轴上的双曲线
乐
的标首准方程是：
y
页
M
下
页
y2 x2 a2 b2 1
F2
x
小
结
F1
结 束
定义
动 画上
页 音 乐
图象
首 页
下
页
小 结
方程
结 焦点
束
a.b.c 的关系
| |MF1|-|MF2| | =2a（2a<|F1F2|）
y
y
M
M
F2
F1 o F2 x
x
F1
x2 y2 a2 b2 1
y
y
M
M
F2
F1 o F2 x
x
F1
小 结
方程
x2 y2 a2 b2 1
y2 x2 a2 b2 1
结 焦点
束
a.b.c 的关系
F ( ±c, 0)
F(0, ± c)
c2 a2 b2
动
课本 : P108页 习题 8.3
画上
页
音 乐
第 1、2、4 题
首 页
下 页
小 结
当 0°≤θ≤180°时，
下 页
为_常__数__2_a____(小__于__|_F_1_F_2_|)_
y
M
F1 o F2 x
小 的点M的轨迹 叫做双曲线。
结
其中两个定点F1、F2叫做双曲线的焦点
结
|F1F2|=2c 叫做焦距
束
注意：在双曲线定义中必须有条件 2c >2a
束 方程x2cosθ+y2sinθ=1的曲线怎样变化？
动
画上 页
音
焦点在y轴上的双曲线
乐
的标首准方程是：
y
页
M
下
页
y2 x2 a2 b2 1
F2
x
小
结
F1
结 束
定义
动 画上
页 音 乐
图象
首 页
下
页
小 结
方程
结 焦点
束
a.b.c 的关系
| |MF1|-|MF2| | =2a（2a<|F1F2|）
y
y
M
M
F2
F1 o F2 x
x
F1
x2 y2 a2 b2 1
y
y
M
M
F2
F1 o F2 x
x
F1
小 结
方程
x2 y2 a2 b2 1
y2 x2 a2 b2 1
结 焦点
束
a.b.c 的关系
F ( ±c, 0)
F(0, ± c)
c2 a2 b2
动
课本 : P108页 习题 8.3
画上
页
音 乐
第 1、2、4 题
首 页
下 页
小 结
当 0°≤θ≤180°时，
下 页
为_常__数__2_a____(小__于__|_F_1_F_2_|)_
y
M
F1 o F2 x
小 的点M的轨迹 叫做双曲线。
结
其中两个定点F1、F2叫做双曲线的焦点
结
|F1F2|=2c 叫做焦距
束
注意：在双曲线定义中必须有条件 2c >2a
双曲线及其标准方程完整版课件
2
2
则双曲线的标准方程为20 − 16 =1.
(2)设双曲线方程为 mx2-ny2=1,
1
= 25 ,
49-72 = 1,
则有
解得
1
28-9 = 1,
= ,
75
2
2
则双曲线的标准方程为25 − 75 =1.
归纳总结
求双曲线的标准方程与求椭圆的标准方程的方法相似,可
以先根据其焦点位置设出标准方程,然后用待定系数法求出a,b
联立两方程解得 x=8(舍负),y=5 3,
所以 P(8,5 3),
kPA=tan∠PAx= 3,所以∠PAx=60°,
所以 P 点在 A 点的北偏东 30°方向.
当堂达标
1.已知两定点F1(-5,0),F2(5,0),动点P满足|PF1|-|PF2|=2a,则当a=3和5时
,P点的轨迹为(
)
A.双曲线和一条直线
情景导学
双曲线也是具有广泛应用的一种圆锥曲线，如发电厂冷却塔的外形、通过声
音时差测定定位等都要用到双曲线的性质。本节我们将类比椭圆的研究方法研究双
曲线的有关问题。
问题导学
新知探究
如图，在直线
l 上取两个定点
在平面内，取定点
F1 , F 2，以点 F1 为圆心、线段
在以 F 2 为圆心、线段
我们知道，当点
2
2
解析:∵方程1+ + -2=1,∴(m-2)(m+1)<0,
解得-1<m<2,∴m的取值范围是(-1,2).
答案:D
)
4. 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知
1
tan∠PEF=
2
则双曲线的标准方程为20 − 16 =1.
(2)设双曲线方程为 mx2-ny2=1,
1
= 25 ,
49-72 = 1,
则有
解得
1
28-9 = 1,
= ,
75
2
2
则双曲线的标准方程为25 − 75 =1.
归纳总结
求双曲线的标准方程与求椭圆的标准方程的方法相似,可
以先根据其焦点位置设出标准方程,然后用待定系数法求出a,b
联立两方程解得 x=8(舍负),y=5 3,
所以 P(8,5 3),
kPA=tan∠PAx= 3,所以∠PAx=60°,
所以 P 点在 A 点的北偏东 30°方向.
当堂达标
1.已知两定点F1(-5,0),F2(5,0),动点P满足|PF1|-|PF2|=2a,则当a=3和5时
,P点的轨迹为(
)
A.双曲线和一条直线
情景导学
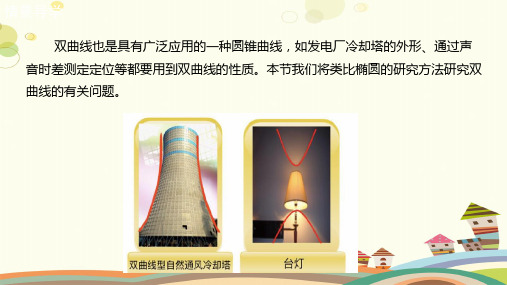
双曲线也是具有广泛应用的一种圆锥曲线，如发电厂冷却塔的外形、通过声
音时差测定定位等都要用到双曲线的性质。本节我们将类比椭圆的研究方法研究双
曲线的有关问题。
问题导学
新知探究
如图，在直线
l 上取两个定点
在平面内，取定点
F1 , F 2，以点 F1 为圆心、线段
在以 F 2 为圆心、线段
我们知道，当点
2
2
解析:∵方程1+ + -2=1,∴(m-2)(m+1)<0,
解得-1<m<2,∴m的取值范围是(-1,2).
答案:D
)
4. 一块面积为12公顷的三角形形状的农场.如图所示△PEF,已知
1
tan∠PEF=
高中数学选修1-1《双曲线及其标准方程》课件
2
结论
例题巩固
例1.（求双曲线的标准方程）
已知双曲线的焦点为F1( -5, 0 )，F2( 5 , 0 )， 双曲线上一点P到F1、F2的距离的差的绝对值等于6， 求双曲线的标准方程.
判断方程类型，确定基本参数
变式1．已知双曲线的焦点为F1(0,-5), F2(0,5)，双曲线 上一点P 到F1、F2的距离的差的绝对值等于6，求双曲 2 2 线的标准方程. y x 变式2．已知平面两个定点为F1(-5,0), F2(5,0)，动点P 到F1、F2的距离的差等于6，求点P的轨迹方程.
F1
M F2
F1
F2
金沙江上的溪洛渡水电站
双曲线的标准方程
求曲线方程的步骤： 1. 建系.
y
M
以F1,F2所在的直线为x轴，线段 F1F2的中点为原点建立直角坐标系
2.设点． 设M（x , y）,则F1(-c,0),F2(c,0) 3.列式
F
O
1
F
2
x
|MF1| - |MF2|=±2a
即
4.化简
a 1，b ，c （3）的焦点在y轴上， 1 2 5 2
x y (4) 1 3 4
2
2
（4）不是双曲线
双曲线与椭圆之间的区别与联系 椭
定义
圆
双曲线
||MF1|－|MF2||=2a
|MF1|+|MF2|=2a
方程
2 2 x2 y 2 x y 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b 2 2 y 2 x2 y x 2 1(a b 0) 2 1(a 0, b 0) 2 2 a b a b
高中数学人教A版选修1-1课件：2.2.1 双曲线及其标准方程
2-������ < 0, 或 ② |������|-3 > 0, 由①,解得-3<m<2;由②,解得 m>3. 故实数 m 的取值范围为(-3,2)∪(3,+∞).
-14-
目标导航
题型一 题型二 题型三 题型四
知识梳理
重难聚焦
典例透析
反思由方程判断曲线类型,先看其分母,再结合双曲线、椭圆的不 同要求,构造关于分母中参数的方程(组)或不等式(组)即可求得.
联立上面两式,解得 a2=20-2 10, ������2 = 2 10,
������2 ������2 ∴所求双曲线的标准方程为 − 20-2 10 2 10
= 1. −
(2)∵双曲线的焦点在
������2 ������
2
������2 y 轴上,∴设双曲线的标准方程为 ������2
= 1(������ > 0, ������ > 0). ①
������2 轴上,可设标准方程为 ������2
−
������2 ������
2
= 1(������ > 0, ������ > 0).
由双曲线的定义,得 ||MF1|-|MF2|| =| 72 + ( 15)2 − (-1)2 + ( 15)2 | =|8-4|=4=2a, 则 a=2. 又 c=4,则 b2=c2-a2=12.
������2 ������
2
= 1(������ > 0, ������ > 0), 用待定系数法求得a,b;第(2)题可
先设出标准方程,然后把点 P1,P2 的坐标代入方程,联立方程组,求出 a2,b2 的值.
-17-
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2.2双曲线
2.2.1双曲线及其标准方程
第一课时
温故知新
新知预习
1.我们把平面内与两个________F1,F2的距离的________等于常数________的点的轨迹叫做
双曲线,这两个________叫做双曲线的焦点, ________叫做双曲线的焦距.
2.在双曲线的定义中,P为动点.
(1)若|PF1|-|PF2|=2a时,曲线只表示________.
(2)若|PF1|-|PF2|=-2a时,曲线只表示________.
(3)若|F1F2|=2a时,动点的轨迹不再是双曲线,而是________.
(4)若|F1F2|<2a时,动点的轨迹________ .
3.双曲线的标准方程有两种情形.
(1)焦点在x轴上,标准方程为________ ,焦点F1 ________,F2________,这里有________.
(2)焦点在y轴上,标准方程为________,焦点F1________,F2________,这里有________.
基础示例
1.已知双曲线方程为152022yx，那么它的焦距为（ ）
A.10 B.5 C.15 D.152
解析：∵a2=20,b2=5,
∴c32=a2+b2=25.
∴c=5.故焦距2c=10.
答案：A
2.若方程14422＝kykx表示双曲线，则它的焦点坐标为（ ）
A.(2k,0),(2k,0)
B.(0,2k-),(0,2k-)
C.(k2,0),(-k2,0)
D.根据k的取值而定
解析：方程14422＝kykx表示双曲线，则（k-4）(k+4)>0,即k<-4或k>4.
(1)当k<-4时，易求得焦点坐标为（0，2k-）,(0,2k-);
(2)当k>4时，易求得焦点坐标为（2k,0）,(2k,0).
答案：D