8604运动员最佳配对问题
最佳阵容问题(向程杨)

最佳阵容问题向鹏,程春华,杨松(海军航空工程学院,烟台 264001)摘要:本文利用混合整数规划建立了最佳阵容模型,并用Lingo8.0软件进行求解。
对问题1,我们以0-1矩阵表示参赛阵容,以赛程规定作为约束条件(这里我们巧妙地通过引进0-1变量,把运动员只能参加全能或单项比赛,以及参加单项时最多只能参加三项的约束条件用线性约束条件简洁地表示出来,大大地减少了计算量),以总分为目标函数,建立了混合整数规划模型。
利用Lingo软件,可以快速求出在最悲观情况下,该队的最佳阵容,即参加全能比赛的选手为第2、5、6、9名选手,其他选手都参加单项比赛:1号选手参加跳马比赛,3号选手参加自由体操比赛,4号选手参加平衡木和跳马比赛,7号选手参加高低杠比赛,8号选手参加平衡木比赛,10号选手参加高低杠和自由体操比赛。
这时最分为212.3,反映了该队参赛所得总分的最小值。
用同样的方法,我们可以求出一般情况下(即每名运动员参加每个项目的得分按均值计算),该队的最佳阵容,即参加全能比赛的选手有2、3、9、10号选手,其他的参加单项比赛:1号、4号参加跳马比赛,5号、8号参加平衡木和自由体操比赛,6号、7号参加高低杠比赛。
这时总分为225.1。
对问题2,我们在上述问题1中模型的基础上加以改进,将夺冠团体总分不少于236.2分归为约束条件,随机的选定选手的得分情况,以夺冠前景为目标函数,建立混合整数规划模型来求夺冠前景最大时的阵容,并求其得分期望。
利用Lingo软件,我们求出了这个问题的最佳阵容,即参加全能比赛的选手有1、7、8、9号选手,其余选手参加单项比赛:2号参加高低杠和跳马,3号参加高低杠和自由体操,4号参加平衡木和跳马,5号参加自由体操,6号参加平衡木。
其夺冠前景为19×(说明夺冠的可能微乎其微),得分期望为222.90。
6.9120−10在求以该阵容出场有90%把握战胜的对手的水平(即对手的总分)时,我们首先求出了最乐观情况下,该队得分的最大值:236.6,结合最悲观情况,可以确定总分这个随机变量的取值范围为[212.3 ,236.6]。
人教版高中数学选修2-3 第一章计数原理 1-2-2-2组合的综合应用课件

【正解】 方法一:由题意,按选出女生的人数可分三类 情况:
第一类,选 1 名女生,2 名男生,有 C15·C28种选法; 第二类,选 2 名女生,1 名男生,有 C25·C18种选法; 第三类,选 3 名女生,男生不选,有 C35种选法. 故共有 C15·C28+C25·C18+C35=230 种选法. 方法二:如果没有限制条件,则有 C313种选法,而不符合 条件,即选出的全是男生(一名女生也没有)的选法是 C83种.因 此,至少要有 1 名女生的不同选法有 C313-C38=230 种.
因此分为三份,每份两本,一共有 15 种方法.
4分
(3)这是“不均匀分组”问题,一共有 C61C52C33=60 种方法.
6分
(4)在(3)的基础上再进行全排列,所以一共有 C16C25C33A33=
360 种方法.
8分
(5)可以分为三类情况:①“2、2、2 型”即(1)中的分配情
况,有 C26C24C22=90 种方法;②“1、2、3 型”即(4)中的分配 情况,有 C16C25C33A33=360 种方法;③“1、1、4 型”,有 C46A33
(1)根据分步计数原理得到:
C26C24C22=90(种).
2分
(2)分给甲、乙、丙三人,每人两本有 C62C42C22种方法,这
个过程可以分两步完成:第一步分为三份,每份两本,设学有 A33种 方法.根据分步计数原理可得:C26C24C22=xA33,所以 x=C26AC2433C22 =15.
[规律方法] 1.解排列组合的综合问题,首先要认真审 题,把握问题的实质,分清是排列还是组合问题,再注意结 合分类与分步两个原理,要按元素的性质确立分类的标准, 按事情的发生过程确定分步的顺序.
吴菊敏公开课新课件

超 越 极 (1)史冬鹏在起点前 限 到达终点;
12 13 t(秒)
6 米处起跑,
13
秒钟
(2)若刘翔在离终点仅剩8米时追上了史冬鹏,则 他追上史冬鹏用了 12 秒;刘翔跑步的速度 为 8.5 米/秒.
清华大学登山队某队员在攀登念青唐 古拉中央峰时,其海拔高度y(米)与时 间x(小时)之间的函数关系如图所示。 (假设往返均为匀速运动)
2008年奥运会已进入倒计时,为了 S(米) 让刘翔保持更好的竞技状态,孙 110 海平教练特地安排了国内110米栏 2号人物史冬鹏与他进行对抗性训 102 练。按照目前成绩看,刘翔比史 冬鹏要快。如果两人同时起跑, 肯定刘翔赢,现在孙海平教练安 6 排史冬鹏在起点前若干米起跑 0 (假设两人均为匀速运动).
0
10
20
30
40
0
10
20
30
40
甲
兔子
乌龟
乙
⑴两图中的 甲 图比较符合传统寓言故 事《龟兔赛跑》所描绘的情节.
(2) 根据甲图象你能获取哪些信息? 比比哪个小组的结论多!
注意
读取直接信息
200 100
300
挖掘间接信息
0
10
20
30
40
甲
(3)《新龟兔赛跑》故事大家说
300
200
300
200
100
100
0
10
20
30
40
0
10
20
30
40
乙
丙
(1)任选一图, 自编《新龟兔赛跑》故事; (2)图表中能确定的数值,在故事叙述中不得少于3 个,且要分别涉及时间、路程和速度这三个量,字 数不超过200字;
冬季两项运动员射击准确性“三调”要求的系统化研究

冬季两项运动员射击准确性“三调”要求的系统化研究摘要:冬季两项运动主要就是越野滑雪、射击相互结合的冬奥会竞赛项目,当前,我国的冬季两项国家队队员,滑行水平在世界中名利前茅,然而,在射击准确性与稳定性方面,与国外优秀选手相较还存在一定差异。
国外的运动员射击命中率一般在86%左右,而我国优秀运动员的射击命中率为82%,可见我国的冬季两项运动员,射击准确性较低,和国际上的水平还存在差距。
这就需要在冬季两项运动员的射击准确性方面进行系统化的分析,保证满足“三调”的要求,即动态下调姿势、调息与调意,在满足系统化要求的状况之下,只有保证射击的准确性符合要求,才能创造出非常优异的成绩。
关键词:冬季两项运动员;射击准确性;“三调”要求对于冬季两项射击而言,其具有一定特殊性的特点,运动员经过高负荷的滑行之后,需要快速的进行动静的转换,并且快速的进入到射击的这个状态,尽量以最快的速度完成高命中率动作。
在此过程中,应该满足“三调”的要求,将其作为切入点,在射击的过程中实现身心调控的目的,为运动员提升射击行为准确性、增强射击稳定性等提供准确的依据。
1冬季两项运动员射击准确性的要求冬季两项运动员,一般情况下需要进行动静的快速转换,在这个要求之下,运动员必须要确保射击的准确性,身体的姿势与呼吸节奏等均需要满足要求。
运动员需要积极参与到训练活动中,形成正确的动作认知,完整的完成相关动作,这样有助于在训练与竞赛的过程中,准确的判断、捕捉最佳射击时机。
在此过程中,应该确保运动员在射击的过程中,满足“三调”的具体准确性要求,也就是准确调整姿势、准确的调息、准确的调整意念。
对于姿势而言,主要就是按照具体的射击技术要求,保证动作的规范性,在落位以后,可以迅速的完成相关的射击姿势和动作。
而对于调息主要就是运动员主动进行呼吸节奏的调整,确保射击的稳定性,满足相关的“三调”要求。
对于调意而言,就是在射击期间进行意念的调整,有助于集中意念合理的进行射击。
数学建模
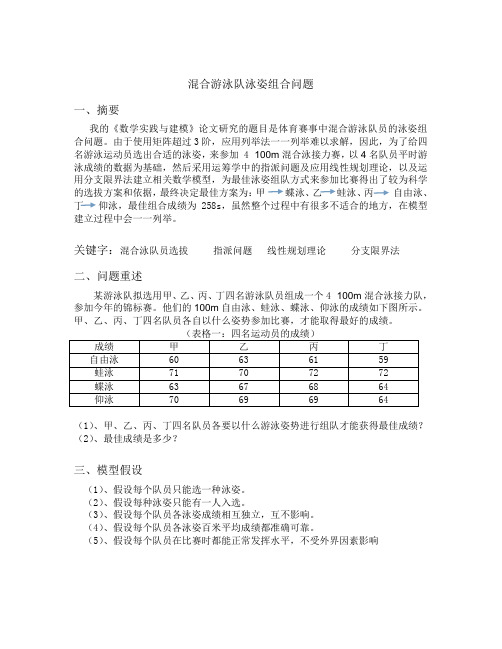
混合游泳队泳姿组合问题一、摘要我的《数学实践与建模》论文研究的题目是体育赛事中混合游泳队员的泳姿组合问题。
由于使用矩阵超过3阶,应用列举法一一列举难以求解,因此,为了给四名游泳运动员选出合适的泳姿,来参加 4×100m混合泳接力赛,以4名队员平时游泳成绩的数据为基础,然后采用运筹学中的指派问题及应用线性规划理论,以及运用分支限界法建立相关数学模型,为最佳泳姿组队方式来参加比赛得出了较为科学的选拔方案和依据,最终决定最佳方案为:甲蝶泳、乙蛙泳、丙自由泳、丁仰泳,最佳组合成绩为258s,虽然整个过程中有很多不适合的地方,在模型建立过程中会一一列举。
关键字:混合泳队员选拔指派问题线性规划理论分支限界法二、问题重述某游泳队拟选用甲、乙、丙、丁四名游泳队员组成一个4×100m混合泳接力队,参加今年的锦标赛。
他们的100m自由泳、蛙泳、蝶泳、仰泳的成绩如下图所示。
甲、乙、丙、丁四名队员各自以什么姿势参加比赛,才能取得最好的成绩。
(表格一:四名运动员的成绩)成绩甲乙丙丁自由泳60 63 61 59蛙泳71 70 72 72蝶泳63 67 68 64仰泳70 69 69 64(1)、甲、乙、丙、丁四名队员各要以什么游泳姿势进行组队才能获得最佳成绩?(2)、最佳成绩是多少?三、模型假设(1)、假设每个队员只能选一种泳姿。
(2)、假设每种泳姿只能有一人入选。
(3)、假设每个队员各泳姿成绩相互独立,互不影响。
(4)、假设每个队员各泳姿百米平均成绩都准确可靠。
(5)、假设每个队员在比赛时都能正常发挥水平,不受外界因素影响四、符号说明i B (i=1,2,3,4,)表示第i 个队员;j C (j=1,2,3,4)分别表示自由泳、蛙泳、蝶泳、仰泳等泳姿; ij M (i 、j=1,2,3,4)表示第i 名队员在j 种泳姿下所用的时间; Z :最佳组合完成比赛所用最少时间。
五、模型的建立与求解 1)、数据处理i B (i=1,2,3,4,)表示第i 个队员,j C (j=1,2,3,4)分别表示自由泳、蛙泳、蝶泳、仰泳等泳姿,然后将每个队员的比赛时间用ij M 表示,所以,由表格一得出如下表格二: i B ij M j C1B2B3B4B1C60 63 61 59 2C71 70 72 72 3C63 67 68 64 4C7069 69 64(表格二)2)、模型建立(1)、列出矩阵表示成绩:用行表示每一种泳姿中每个人所用的时间,列表示每个人在四种泳姿中的各自的时间,得出如下矩阵:M=64696970646867637272707159616360(2)、求最佳组合的上界和下界:考虑任何一个可行解,以主对角线之和为上界,即组合方式为1B 1C 、2B 2C 、3B 3C 、4B 4C 其值为:60+60+68+64=262,以每行元素最小值为下界,即组合方式为1B 3C 、2B 2C 、4B 1C 、4B 4C 其值为:59+70+63+64=256;但需要强调的是,这不是一个合理的选择,因为4B 1C 、4B 4C 来自同一列,这仅仅给出了一个参考下界,所以最优解应该在[256,262]之间的某个值。
【数据结构】男女运动员最佳组合正文终稿

东北大学信息科学与工程学院数据结构课程设计报告题目:男女运动员最佳组合课题组长王逸飞课题组成员王嘉琦李聪专业名称计算机科学与技术班级计1307指导教师:杨雷2015年1月课程设计任务书目录1课题概述 11.1 课题任务 11.2 课题原理 11.3 相关知识 32 方案设计72.1 总体功能设计72.2 数据结构设计82.3 函数原型设计102.4 主算法设计122.5 用户界面设计143 方案实现153.1 开发环境与工具 153.2 程序设计关键技术163.3 个人设计实现(按组员分工)3.3.1王逸飞设计实现173.3.2王嘉琦设计实现173.3.3李聪设计实现174 测试与调试234.1 个人测试(按组员分工)234.1.1王逸飞测试234.1.2王嘉琦测试234.1.2李聪测试234.2组装与系统测试334.3 系统运行 365 课题总结395.1 课题评价 395.2团队协作405.3团队协作415.4个人设计小结(按组员分工)425.4.1王逸飞设计小结425.4.2王嘉琦设计小结425.4.3李聪设计小结426附录A 课题任务分工 50A-1 课题程序设计分工 50A-2 课题报告分工51附录B 课题设计文档(光盘)52 B-1课程设计报告(电子版)52B-2源程序代码(*.H,*.CPP)52B-3工程与可执行文件52B-4屏幕演示录像文件(可选)52 附录C 用户操作手册(可选)53C.1 运行环境说明53C.2 操作说明541 课题概述1.1课题任务【问题描述】设有N个男羽毛球运动员和N个女羽毛球运动员,现组成N对男女混合最佳组合。
每个男运动员对每个女运动员都有一个满意度排序,用矩阵mf[0:n-1][0:n-1]表示。
mf[i][j]表示第i个男运动员对第j个女运动员的满意度,满意度值越高,满意程度越高。
同理,每个女运动员对每个男运动员也有一个满意度排序,用矩阵fm[0:n-1][0:n-1]表示。
[例1]从6名运动员中选出4人参加4×100m接力赛
![[例1]从6名运动员中选出4人参加4×100m接力赛](https://img.taocdn.com/s3/m/0997bf05580102020740be1e650e52ea5518ce2d.png)
[例1]从6名运动员中选出4人参加4×100m接力赛第一篇:[例1]从6名运动员中选出4人参加4×100 m接力赛课题:10.2排列(3)教学目标:学会分析和解决一些简单的排列应用问题.教学重点:分析和解决一些简单的排列应用问题教学难点:两个基本原理的应用.教学方法:引导式教学过程:一.知识归纳:对于排列应用题,通常有以下两种思考方法:(1)从条件出发,对问题分类或分步,应用两个基本原理,直接计算符合条件的排列数,这一思考方法叫做直接法.(2)先不考虑限制条件,求出所有排列数,然后再从中减去不符合条件的排列数,这一思考方法叫做间接法.(也叫排除法)二.典型例题:例1、从6名运动员中选出4人参加4×100 m接力赛.如果甲乙两人都不能跑第一棒,那么共有多少种不同的参赛方案?解:因为甲乙两人都不能跑第一棒,所以跑第一棒的运动员只能从其余4名运动员中选定,有A14种方法.这时跑后三棒的运动员可从余下的5名运动员中任取3名进行排列,共有13A35种方法.于是根据分步计数原理,不同的参赛方案有A4·A5=240种.例2、用0,1,2,…9(1)五位奇数?(2)大于30000的五位偶数?解:(1)要得到五位奇数,末位应从1,3,5,7,9五个数字中取,有A15种取法.取定末位数字后,首位就有除这个数字和0之外的八种不同取法.首末两位取定后,十个数字还有八3个数字可供中间的十位,百位与千位三个数位选取,共有A8种不同的安排方法.因此由分 3步计数原理共有5×8×A8=13440个没有重复数字的五位奇数.(2)要得偶数,末位应从0,2,4,6,8中选取.而要得比30000大的五位偶数,可分两类:①末位数字从0,2中选取,则首位可取3、4、5、6、7、8、9中任一个.共7种选取方法.3其余三个数位就有除首末两个数位上的数字之外的八个数字可以选取,共A8种取法.所以3共有2×7×A8种不同情况.②末位数字从4、6、8中选取,则首位应从3、4、5、6、7、8、9中除去末位数字的六个数33字中选取,其余三个数位仍有A8种选法,所以共有3×6×A8种不同情况.33由分类计数原理,共有2×7×A8+3×6×A8=10752个比30000大的无重复数字的五位偶数.例3、5男5女共10个同学排成一行.(1)女生都排在一起,有几种排法?(2)女生与男生相间,有几种排法?(3)任何两个男生都不相邻,有几种排法?(4)5名男生不排在一起,有几种排法?(5)男生甲与男生乙中间必须排而且只能排2位女生,女生又不能排在队伍的两端,有几种排法?解:(1)将5名女生看作1人,就是6个元素的全排列,有A66种排法.又5名女生内部可有65A55种排法,所以共有A6·A5=86400种排法.(2)男生自己排,女生也自己排,然后相间插入(此时有2种插法),所以女生与男生相间共5有2A55·A5=28800种排法.(3)女生先排,女生之间及首尾共有6个空隙,任取其中5个安插男生即可.因而任何两个男5生都不相邻的排法共有A55·A5=86400种.(4)直接法分类较复杂,可用间接法.即从10个人的排列总数中,减去5名男生排在一起的56排法数,得5名男生不排在一起的排法数为A1010 A5A6=3542400.2(5)先安排2个女生排在男生甲乙之间,有A5种方法;又甲、乙之间还有A2种排法.这样2就有A5·A2种排法.然后把他们4人看成一个元素,(相当于一个男生),再从这一元素及222另3名男生中,任选2人排在首尾,有A4种排法.最后再将余下的2个“男”生、3个女生25排在其间,有A55种排法.故总排法为A5A2A4A5=57600种.22三.学后反思:对于有限制条件的排列问题,要注意总结以下几种类型的问题的思考方法.1.某些元素不能排或必须排在某一位置的问题.(1)先排特殊元素或特殊位置,然后再排其他元素或位置.(2)先不考虑限制条件,求出所有的排列数,然后减去不符合条件的排列数,即间接法.2.某些元素要求相邻的问题,常用“捆帮”的办法,先看成一个元素.3.某些元素要求不相邻的问题,常用“插空”的办法.四.随堂训练:1.把3张电影票分给10人中的3人,分法种数为()A.2160B.240C.720D.120 2.五名学生站成一排,其中甲必须站在乙的左边(可以不相邻)的站法种数为()A.A4 4 B.14A4 2C.A55D.15A5 23.由0,2,5,7,9五个数字,可组成无重复数字的四位数中:(1)大于5000的有个.(2)偶数有个.4.由数字1,2,3,4,5组成没有重复数字,且数字1与2不相邻的五位数,这种五位数的个数是个.参考答案:1.C 2.D 3.72 42 4.72 五.强化训练:1.由数字0,1,2,3,4,5组成没有重复数字的六位数,其中个位数字小于十位数字的共有()A.210个 B.300个 C.464个 D.600个2.5名学生站成一排,其中A不能站在两端,B不能站在正中间,则不同的排法是()A.36 B.54 C.60 D.663.公共汽车上有5个座位,每个座位上至多坐一个人.(1)上车7个人,共有________种不同的坐法.(2)上车3个人,共有________种不同的坐法.4.6个人排成一排,甲乙两人必须站在一起的排法数为_________种.甲乙两人不得相邻的排法数为_________种.5.由4个不同的独唱节目和3个不同的合唱节目组成一台演出,要求任意两个合唱不要相邻,开始与最后一个节目必须是合唱,则这台演出编排节目的方法共有多少种?6.用0,1,2,3,4五个数字组成没有重复数字的五位数,若从小到大排列,则第86个数是几?7.九个人排成两排,第一排4人,第二排5人,规定甲不能排在第一排,乙不能排在第二排,共有几种不同的排法? 8.某一天的课程表要排入政治、语文、数学、物理、体育、美术共六门课,如果第一节课不排体育和美术,最后两节不排数学,那么共有多少种不同的排法?9.六个人排成一排,求满足下列条件的不同的排法种数:(1)若A、B、C三人必须相邻.(2)若A、B都不能与C相邻.参考答案:1.B2.C3.(1)2520(2)604.240 4805.4236.420317.1008008.3369.(1)144(2)288第二篇:从代理或科长及中选出CEO候选人(精)从代理或科长及中选出CEO候选人从代理或科长及中选出CEO候选人LG电子会针对30出头的职员启动“CEO 草”。
幼儿园科学运动员号码规范化教案设计

幼儿园科学运动员号码规范化教案设计在幼儿园教学中,科学运动员号码规范化教案设计是非常重要的。
通过科学的规范化教案设计,可以帮助幼儿建立正确的运动员号码观念,培养健康的体育活动习惯,促进儿童身心健康的全面发展。
在本文中,我们将深入探讨幼儿园科学运动员号码规范化教案设计的意义、原则和实施方法,帮助读者全面、深刻地理解这一重要主题。
1. 意义科学运动员号码规范化教案设计对幼儿的意义重大。
规范化的运动员号码教育可以培养幼儿的观察力和记忆力,通过观察和记忆不同号码的方式,提高幼儿的认知能力和学习兴趣。
运动员号码规范化教育有助于培养幼儿的团队合作意识和协调能力,通过分配不同号码的方式,让幼儿学会团结合作,培养集体荣誉感和快乐参与的精神。
科学的规范化教案设计可以为幼儿的未来体育发展打下良好的基础,促进幼儿身心健康的全面发展。
2. 原则在进行幼儿园科学运动员号码规范化教案设计时,应遵循以下原则。
要因材施教,根据幼儿的芳龄、兴趣和特点设计适合的号码规范化教育内容,保证教学的有效性和实用性。
要注重情感体验,通过有趣、生动的教学方式,让幼儿在参与运动员号码规范化教育的过程中感受快乐、获得成就感,激发幼儿对体育运动的热爱和兴趣。
要注重实践与应用,通过丰富多彩的活动设计和实际操作,帮助幼儿理解和掌握号码规范化的知识,提高实际运动能力。
3. 实施方法科学运动员号码规范化教案设计的实施方法包括以下几个方面。
可以通过一定的故事、游戏或实物展示,引导幼儿了解、认识不同号码的意义和作用,培养幼儿对号码的认知能力。
可以通过模仿和操练的方式,让幼儿亲身体验并掌握运动员号码的使用方法,提高幼儿的实际运动能力。
可以通过集体活动和比赛,让幼儿在实际运动中应用号码规范化知识,促进幼儿的团队合作意识和运动技能的提高。
总结回顾通过本文的深入探讨,我们可以看到幼儿园科学运动员号码规范化教案设计在幼儿教育中的重要作用。
规范化的运动员号码教育可以培养幼儿的认知能力、团队合作意识和实际运动能力,促进幼儿的身心健康全面发展。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8604 运动员最佳配对问题
时间限制:1000MS 内存限制:1000K
提交次数:0 通过次数:0
题型: 编程题语言: 无限制
Description
羽毛球队有男女运动员各n人。
给定2 个n×n矩阵P和Q。
P[i][j]是男运动员i和女运动员j配对组成混合双打的男运动员竞赛优势;Q[i][j]是女运动员i和男运动员j配合的女运动员竞赛优势。
由于技术配合和心理状态等各种因素影响,P[i][j]不一定等于Q[j][i]。
男运动员i和女运动员j配对组成混合双打的男女双方竞赛优势为P[i][j]*Q[j][i]。
设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
编程任务:设计一个算法,对于给定的男女运动员竞赛优势,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大。
如下面sample的数据:
P=
10 2 3
2 3 4
3 4 5
Q=
2 2 2
3 5 3
4 5 1
最大的男女双方竞赛优势总和为:10*2 + 4*5 + 4*3 = 52
最佳搭配为:(女1,男1)(女2,男3)(女3,男2)
Input
输入数据第一行有1 个正整数n (1≤n≤10)。
接下来的2n行,每行n个数。
前n行是P,后n行是Q。
Output
将计算出的男女双方竞赛优势的总和的最大值输出。
Sample Input
3
10 2 3
2 3 4
3 4 5
2 2 2
3 5 3
4 5 1
Sample Output
52
Hint
让男队员按自己编号顺序站定,女运动员和他们搭配的各种组合就是女运动员的各种排列。
(如果你让女运动员按编号顺序站定,男运动员各种排列和她们搭配,也可以!)
因此,搜索的解空间树是“排列树”。
搜索的算法可以参考书本上“批处理作业调度问题”一节或“旅行售货员问题”的解法,因为都是排列树的搜索。
Provider
zhengchan
Source Code
#include<iostream>
using namespace std;
int **P=NULL;
int **Q=NULL;
int *x=NULL;
int sum=0; //记录男女双方竞赛优势的总和的最大值
int n;
//交换两个数
void Swap(int *b,int *y)
{
int z;
z=*b;
*b=*y;
*y=z;
}
//求男女双方竞赛优势总和最大值函数
void Sum()
{
int s=0; //记录当前男女双方竞赛优势总和
for(int j=0;j<n;j++)
s+=P[j][x[j+1]-1]*Q[x[j+1]-1][j];
if(s>=sum) sum=s; //输出值
}
//回溯法搜索排列树
void Backtrack(int t)
{
if(t>n) Sum(); //当到叶子节点时
else
for(inti=t;i<=n;i++)
{
//没有约束函数和限界函数的全排列问题
Swap(&x[t],&x[i]);
Backtrack(t+1); //进行第t+1个男运动员配对
Swap(&x[t],&x[i]);
}
}
int main()
{
inti,j;
int t=1;
cin>>n;
//动态分配数组空间
x=new int[n+1];
for(i=0;i<n+1;i++)
x[i]=i;
//P,Q分配n行n列:从第0行0列到第n-1行第n-1列
P=new int*[n];
for(i=0;i<n;i++)
P[i]=new int[n];
Q=new int*[n];
for(i=0;i<n;i++)
Q[i]=new int[n];
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>P[i][j];
for(i=0;i<n;i++)
for(j=0;j<n;j++)
cin>>Q[i][j];
Backtrack(t);
cout<<sum; //输出男女双方竞赛优势的总和的最大值 //释放空间
for(int k=0;k<n;k++)
{
delete[] P[k];
P[k]=NULL;
}
for(k=0;k<n;k++)
{
delete[] Q[k];
Q[k]=NULL;
}
return 0;
}。
