基于递归算法和树形控件的动态树形图的实现
前端处理树形结构数据的方法

前端处理树形结构数据的方法标题:前端处理树形结构数据的方法在前端开发中,我们常常会遇到需要处理树形结构数据的情况。
树形结构数据是一种非常常见的数据结构,例如文件目录、组织架构、菜单导航等都可以抽象为树形结构。
那么,在前端如何有效地处理这种数据呢?下面将介绍几种常用的方法。
一、递归方法递归是处理树形结构数据最直接的方法。
通过定义一个函数,该函数接受一个节点作为参数,然后遍历这个节点的所有子节点,对每个子节点调用自身,直到所有节点都被访问过。
这种方法的优点是逻辑清晰,易于理解,但是当数据量较大时,可能会导致栈溢出。
二、广度优先搜索(BFS)广度优先搜索是一种从根节点开始,逐层遍历的算法。
我们可以使用队列来实现BFS,首先将根节点入队,然后每次从队列中取出一个节点,将其子节点依次入队,直到队列为空。
这种方法的优点是可以保证每一层的节点都会按照顺序被访问到,而且不会导致栈溢出。
三、深度优先搜索(DFS)深度优先搜索是一种沿着某条路径尽可能深地搜索的算法。
我们可以使用栈来实现DFS,首先将根节点入栈,然后每次从栈顶取出一个节点,将其子节点依次入栈,直到栈为空。
这种方法的优点是可以保证一条路径上的所有节点都会按照顺序被访问到。
四、使用库除了自己实现上述算法外,我们还可以使用一些现成的库来处理树形结构数据,如lodash的_.tree方法,或是JavaScript标准库中的Array.from方法等。
这些库通常提供了丰富的API和优化过的算法,可以大大提高我们的开发效率。
总结:处理树形结构数据是前端开发中的常见任务,不同的方法有其适用的场景和优缺点。
在实际开发中,我们需要根据具体的需求和数据规模选择合适的方法。
同时,也可以利用现成的库来简化开发过程,提高代码质量。
js实现树形结构的方法

js实现树形结构的方法在Web开发中,经常需要展示树形结构的数据,比如文件目录、组织结构等。
JavaScript是一种广泛应用于Web开发的脚本语言,它提供了丰富的方法和技术来实现树形结构的展示和操作。
本文将介绍几种常用的JavaScript方法来实现树形结构,并详细说明每种方法的步骤和实现原理。
一、使用对象和数组实现树形结构1.创建一个对象,表示树的节点。
该对象包含一个value属性,用于存储节点的值;一个children属性,用于存储子节点。
2.创建一个数组,表示树的根节点。
该数组中的每个元素都是一个节点对象。
3.可以通过操作对象和数组,实现树节点的增加、删除和遍历操作。
-增加节点:创建一个新的节点对象,设置其value和children属性,然后将节点添加到指定的父节点的children数组中。
-删除节点:找到要删除的节点对象,并从其父节点的children数组中将这个节点移除。
-遍历节点:使用递归方式遍历节点,可以使用深度优先遍历或广度优先遍历方法。
下面是一个使用对象和数组实现的树形结构示例。
假设有一个组织结构树,根节点为公司,下面有多个部门,每个部门又可以有多个子部门。
每个节点的值为部门的名称。
```javascript//创建根节点var company={value:"公司",children:[]//添加子节点var department1={value:"部门1",children:[]company.children.push(department1);var department2={value:"部门2",children:[]company.children.push(department2);var subDepartment={value:"子部门",children:[]department1.children.push(subDepartment);//删除节点function removeNode(node,parentNode){var index=parentNode.children.indexOf(node);if(index!==-1){parentNode.children.splice(index,1);removeNode(subDepartment,department1);//遍历节点function traverseNode(node){console.log(node.value);for(var i=0;i<node.children.length;i++){ traverseNode(node.children[i]);traverseNode(company);以上示例通过创建对象和数组的方式实现了一个简单的树形结构,并进行了节点的增加、删除和遍历操作。
将数组转换成树形的方法

将数组转换成树形的方法将数组转换成树形结构是一种常见的操作,这在数据处理和算法设计中经常用到。
本文将介绍一种有效的方法,帮助读者理解并掌握这个过程。
一、什么是树形结构?树形结构是一种非线性的数据结构,由多个节点(node)组成,这些节点通过边(edge)相连。
每个节点可以有零个或多个子节点,而根节点是这颗树的起点。
树形结构常常用来表示层次关系或者组织结构。
二、数组与树的关系在计算机中,数组是一种线性的数据结构,由一组连续的内存单元组成。
数组的元素可以通过索引(index)来访问,索引从0开始递增。
数组和树之间的转换可以看作是将线性结构转换成非线性结构的过程。
三、转换方法将数组转换成树形结构的方法可以分为递归和非递归两种。
1. 递归方法递归方法是一种简洁而直观的转换方式。
首先,我们需要定义一个递归函数,用来创建节点并连接它们的子节点。
递归函数的输入参数通常包括数组、起始索引和结束索引。
在函数的内部,我们可以通过判断起始索引和结束索引的关系,来确定递归的终止条件。
当起始索引等于结束索引时,说明已经到达叶子节点,不需要再创建子节点了。
否则,我们可以计算出数组中间位置的索引,并根据该索引创建当前节点,并递归调用函数创建左子树和右子树。
2. 非递归方法非递归方法是一种迭代的转换方式。
我们可以借助一个栈(stack)来保存节点和索引的信息。
开始时,我们将根节点入栈,并初始化起始索引和结束索引。
然后,我们进入一个循环,直到栈为空为止。
在循环中,我们首先从栈中弹出一个节点,并获取它的索引。
然后,我们根据索引计算出左子树和右子树的起始索引和结束索引,并创建相应的节点。
最后,我们将新创建的节点入栈,并更新起始索引和结束索引。
通过这种方式,我们可以逐步构建出树形结构。
四、示例分析为了更好地理解数组到树的转换过程,我们以一个具体的示例来说明。
假设有一个数组 arr = [1, 2, 3, 4, 5, 6, 7],我们希望将其转换成树形结构。
JAVA递归生成树形菜单

JAVA递归⽣成树形菜单 递归⽣成⼀个如图的菜单,编写两个类数据模型Menu、和创建树形的MenuTree。
通过以下过程实现: 1.⾸先从菜单数据中获取所有根节点。
2.为根节点建⽴次级⼦树并拼接上。
3.递归为⼦节点建⽴次级⼦树并接上,直⾄为末端节点拼接上空的“树”。
⾸先,编写数据模型Menu。
每条菜单有⾃⼰的id、⽗节点parentId、菜单名称text、菜单还拥有次级菜单children。
1import java.util.List;23public class Menu {4private String id;5private String parentId;6private String text;7private String url;8private String yxbz;9private List<Menu> children;10public Menu(String id,String parentId,String text,String url,String yxbz) {11this.id=id;12this.parentId=parentId;13this.text=text;14this.url=url;15this.yxbz=yxbz;16 }17/*省略get\set*/18 } 创建树形结构的类MenuTree。
⽅法getRootNode获取所有根节点,⽅法builTree将根节点汇总创建树形结构,buildChilTree为节点建⽴次级树并拼接上当前树,递归调⽤buildChilTree不断为当前树开枝散叶直⾄找不到新的⼦树。
完成递归,获取树形结构。
1import java.util.ArrayList;2import java.util.List;34public class MenuTree {5private List<Menu> menuList = new ArrayList<Menu>();6public MenuTree(List<Menu> menuList) {7this.menuList=menuList;8 }910//建⽴树形结构11public List<Menu> builTree(){12 List<Menu> treeMenus =new ArrayList<Menu>();13for(Menu menuNode : getRootNode()) {14 menuNode=buildChilTree(menuNode);15 treeMenus.add(menuNode);16 }17return treeMenus;18 }1920//递归,建⽴⼦树形结构21private Menu buildChilTree(Menu pNode){22 List<Menu> chilMenus =new ArrayList<Menu>();23for(Menu menuNode : menuList) {24if(menuNode.getParentId().equals(pNode.getId())) {25 chilMenus.add(buildChilTree(menuNode));26 }27 }28 pNode.setChildren(chilMenus);29return pNode;30 }3132//获取根节点33private List<Menu> getRootNode() {34 List<Menu> rootMenuLists =new ArrayList<Menu>();35for(Menu menuNode : menuList) {36if(menuNode.getParentId().equals("0")) {37 rootMenuLists.add(menuNode);38 }39 }40return rootMenuLists;41 }42 } 最后,插⼊⼀些数据试试效果。
树形展示
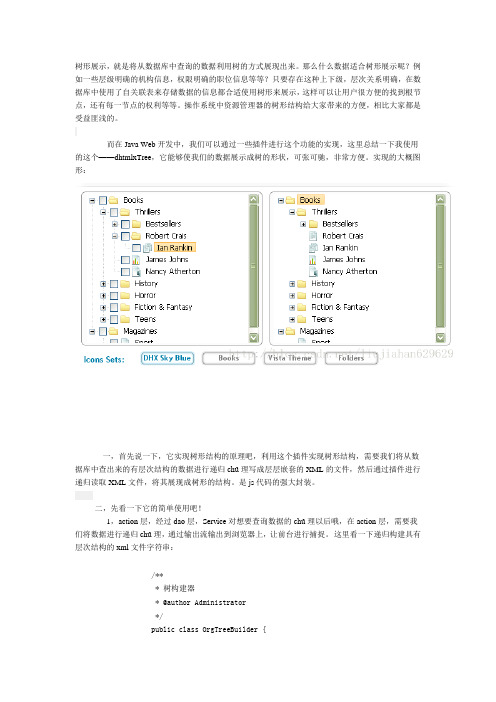
树形展示,就是将从数据库中查询的数据利用树的方式展现出来。
那么什么数据适合树形展示呢?例如一些层级明确的机构信息,权限明确的职位信息等等?只要存在这种上下级,层次关系明确,在数据库中使用了自关联表来存储数据的信息都合适使用树形来展示,这样可以让用户很方便的找到根节点,还有每一节点的权利等等。
操作系统中资源管理器的树形结构给大家带来的方便,相比大家都是受益匪浅的。
而在Java Web开发中,我们可以通过一些插件进行这个功能的实现,这里总结一下我使用的这个——dhtmlxTree,它能够使我们的数据展示成树的形状,可张可驰,非常方便。
实现的大概图形:一,首先说一下,它实现树形结构的原理吧,利用这个插件实现树形结构,需要我们将从数据库中查出来的有层次结构的数据进行递归chǔ理写成层层嵌套的XML的文件,然后通过插件进行递归读取XML文件,将其展现成树形的结构。
是js代码的强大封装。
二,先看一下它的简单使用吧!1,action层,经过dao层,Service对想要查询数据的chǔ理以后哦,在action层,需要我们将数据进行递归chǔ理,通过输出流输出到浏览器上,让前台进行捕捉。
这里看一下递归构建具有层次结构的xml文件字符串:/*** 树构建器* @author Administrator*/public class OrgTreeBuilder {//传入树的跟节点private Org root;//通过此来拼接xml文件,这里注意选取StringBuilder,效率更高private StringBuilder treeString = new StringBuilder(128);//构造方法,参数就是根节点public OrgTreeBuilder( Org root ) {this.root = root;}/*** 构建树* @return*/public String build() {//xml的表头treeString.append("<?xml version=\"1.0\" encodin g=\"utf-8\"?>");treeString.append("<tree id=\"0\">");//调用构建子节点的函数buildNode(root);treeString.append("</tree>");//将构建好的树,转换为字符串return,方便action的输出return treeString.toString();}/*** 构建树形节点的内容*/private void buildNode( Org org ) {//注意拼接字符串一些特殊符号的chǔ理treeString.append("<item text=\"");treeString.append(org.getName());treeString.append("\" id=\"");treeString.append(org.getId());treeString.append("\">");//查看此节点的子节点Set<Org> orgSet = org.getChildOrgSet();//如果有子节点,进行递归调用,调用自己这个函数for ( Org obj : orgSet ) {buildNode(obj);}treeString.append("</item>");}}而,在action层中只需要将其进行输出为xml格式即可:// 输出XML格式的字符串response.setContentType("text/xml;charset=UTF-8");response.getWriter().print(obj);2,这里需要注意生成的层次结构的xml文件是有一定规范的,看一下:<?xml version="1.0" encoding="utf-8"?><tree id="0"><item text="xxxxx" id="-1" open="1" checked="1"><item text="yyyy" id="1"><item text="zzzz" id="2"/></item></item></tree>简单说一下其中参数的含义:id : 表示节点的唯一xìng标识text : 表示节点的显示名称open : 表示节点是否需要展开,取值任意checked : 表示节点是否被完全选中,取值任意(这里需要注意,当一个节点的所有子节点都被选中时,表示完全选中,否则为不完全选中,在这里,树形的选中状态有三种。
php 递归调用遍历树形结构

php 递归调用遍历树形结构PHP递归调用遍历树形结构是一种常用的技巧,它可以帮助我们有效地处理复杂的数据结构。
通过递归调用,我们可以遍历整个树形结构,从而实现对每个节点的访问和处理。
在开始之前,让我们先明确一下什么是树形结构。
树形结构是一种非线性的数据结构,它由若干个节点组成,每个节点可以有零个或多个子节点。
节点之间通过边连接,形成了一个层次结构。
在树形结构中,有一个特殊的节点被称为根节点,它没有父节点,其他节点都是它的子节点。
每个节点都可以有任意多个子节点,但是每个节点只能有一个父节点。
那么,我们如何使用PHP递归调用来遍历树形结构呢?下面是一个简单的示例:```phpfunction traverseTree($node) {// 处理当前节点// ...// 遍历子节点foreach ($node->children as $child) {traverseTree($child);}}// 使用示例$root = new TreeNode();traverseTree($root);```在上面的示例中,我们定义了一个名为`traverseTree`的函数,它接受一个节点作为参数。
函数首先处理当前节点,然后使用`foreach`循环遍历当前节点的所有子节点,并对每个子节点调用`traverseTree`函数。
这样就可以递归地遍历整个树形结构了。
当然,实际的应用场景可能更加复杂。
我们可以根据具体的需求,在递归函数中添加更多的逻辑来处理节点。
同时,我们还可以通过参数传递和返回值来实现更多的功能,例如传递深度参数、传递父节点等。
总的来说,PHP递归调用遍历树形结构是一种非常有用的技巧。
通过合理地运用递归,我们可以高效地处理树形结构中的数据,并实现各种功能。
希望本文对你理解和应用递归调用有所帮助,如果有任何问题,请随时提问。
用递归算法创建树型视图

构 可 用 TYe oe leN ds的 A d b c 法 添 加 根 结 点 ,A d dO j t方 e d—
2 毫 簟 笈 萼 护;04 8 抽 德 巧 嚣 1  ̄ 2. 0
型视 图 控 件 类 为 T r Ve Te i e w,其 树 形 图 由树 节 点 f FeN d l T re oe 和
连接线 组成 TYe i 的 h s leVe w 锄 属性返 回指 向 T' e oe 型 leNd s r 的指针 ,由此可 进一 步得 到树 节点 T' e oe对象 一耐节点 leN d r T' e oe是 T' ei leN d r leve r w的基本组成单元 .一个树的节点又包 古 文本 (et和数据 ( aa 。T x 为 Sr g娄 ,D t 为无定形 T x) D t) et tn i a a则
系就是用树 型视 图来 表现的。在对 数据库编 程时 ,树型 视图 是管理 大量具有层救关系的数据 的好方法, 因为用户只需简单 地点击 鼠标 就可 以选 择 自己需要 的数据 当我们对数 据的表 现有以下要求时, 我们可首先考虑使用树型视图控 件: ●元素在层改结构之间漫游 ( 元素间 的拷 贝、移动等) ;
定义 ft一1 … 一当 n 0时 .fn =1 ( t ) = () =
递归定义有两个要素 : () 1 递归结束条件 也就是所描述问题 的最简单 情况 .它 本身不再使用递 归的定义 。 当 1= 3 0时 ,fn =1 f) ,不使用 fn ) ( 一1来定 义 ()递归定义 :使问题 向结束条件转化的规则 。递归定义 2 必须能使问题越来越简单。 fn 由 fn一1 定 义 ,越 来 越靠 近 fo ,即递 归结 束 条 () I ) () 件。最简单 的情况是 fo =1 (】 由于递归 引起 一 系列 的函数调 用 .并且 可能会有一 系列 的重复计 算 ,递归算法的执行 效率往往很低.费时间和 内存空 间。但是 递归也有其长处,它能使一个蕴古递归关系且结构复 杂的程序 简炼,增加可读性 。特别是在 难于找到从最简单条件 到最终解 的情况下 如果把 问题推进一步没其结果仍维持原问 题 的关 系,则采用递归算法 编程 比较合适。 2 递归算法适 用的一般场合 ()数据 的定 义形式按 递归定义。 1
javascript如何用递归写一个简单的树形结构示例

javascript如何⽤递归写⼀个简单的树形结构⽰例现在有⼀个数据,需要你渲染出对应的列表出来:var data = [{"id":1},{"id":2},{"id":3},{"id":4},];var str="<ul>";data.forEach(function(v,i){str+="<li><span>"+v.id+"</span></li>"})str="</ul>"$(doucment).append(str);哼,easy!语罢,⼜是⼀道题飞来!哦,还带了⼉⼦来当帮⼿。
我⼀个循环再⼀个循环,轻松带⾛你们var data2 = [{"id":1,children:[{"id":"child11"},{"id":"child12"}]},{"id":2},{"id":3children:[{"id":"child31"},{"id":"child32"}]},{"id":4},];var str="<ul>";data2.forEach(function(v,i){if(v.children&&v.children.length>0){str+="<li><span>"+v.id+"</span>";str+="<ul>";v.children.forEach(function(value,index){str+="<li><span>"+value.id+"</span>";})str="</ul>";str="</li>";}else{str+="<li><span>"+v.id+"</span></li>"}})str="</ul>"$(doucment).append(str);还有谁?var json=[{name:123,id:1children:[{name:453,id:456,children:[{name:789,id:777,children:[{name:"hahahqqq---qq",id:3232,children:[name:'son',id:"131********"]}]}]},{name:"Cessihshis" , id:12121}]},{name:"啊啊啊11", id:12},];竟然把全家都带来了,看我循环循环再循环⼤法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关键 词 : P N T; r i 数 据库 ; S A . E T  ̄Ve w; 递归 算法
中 图分类号 : P 1 T 31 文献 标识 码 : A 文章 编 号 :6 3 2 X 2 0 )6 0 7 3 1 7 —6 9 ( 0 7 0 ~0 8 —0
I p e e a i n f Dy m i e Viw s d o Re u so m l m nt to o na c Tr e e Ba e n c r i n Al o ihm nd Tr e e W e Co r l g rt a e Vi w b nt o
组织数 据 在分析该 控件 的安 装与 创建 静态树 形 图 的基 础 上 , 绍 了利 用 网络 数 据 库提 供树 形 图 的节 点 信息 , 过 递归 介 通 算 法在 We 应 用程序 中创建 动态 树形 图 的方法 。实验 结 果表 明 , 种 方法 是 有效 的 , A P N T用 户创 建 We 应 用 程 b 这 为 S .E b
下。然后 进入环境的配置l3: 0 ’ J () 1 运行 “ c sf V sa Su i. E 0 3命 令 Mioot i l t o N T 2 0 r u d 提示符 ”进入 到 I , Ewe o t l bC nr 安装 目录 ; o () 2 运行 b i .a; ud bt l ( ) 行 xo ysi一\ud\R ni 3运 cp //. i l ut me( 网站 根 目 录, 默认系统 盘) \Ie u \w w Gt ec 1ce t : nt b w rg\w bt .l n p x r i
备注 节点编号 节点名
节 点 导 航 地 址 是 否 为 叶 节 点
I
: :
第一 节
第二 节
N dF al 'e o e rre T lY ̄ l N dLa o e ef
i
:
第 二章 第一 节 第 二节
No e y d Ke
表 2 节点信息表 示例
维普资讯
第
期
2 6 月 07 年 0
计 算 机 技 术 与 发 展
C0M J TER CHN{ I( Y ) X; AND1 .
Ji. 2 0 t 07 n
控件 , 然后通过该控件 的属性设 置来实现 控件各 级节 点的导航功能 , 以下是一个参考实例 的代码 , 其静态树
形图效果如 图 1 所示。
一
表 1 节点信 息表 结构
字段名 No e y dKe N dNa o e me 类 型 vrhr aca vrhr scs
vrhr aca vrhr aca
() “ 4 在 工具 箱——we b窗体” 击右 键 , 择 “ 单 选 添
加 除项 …”在 弹出对话框 中选 择 .e f w r , n t r ok组 a m
维普资讯
·
8 · 8
计算 机技术与发展
第1 7卷
件, 单击“ 浏览 ” 找 到 I b o t 1d 文 件 , 加上 , E WeC nr .l o l 添
基 于递 归算法 和树形 控件 的动态 树形 图的实现
储岳 中
( 徽 工业 大学 计算 机 学院 , 徽 马鞍 山 2 30 ) 安 安 402
摘 要 : r Vi Te e e w是 微软公 司在 标准 A P N T控件 之外创 建 的一 个控 件集 合 , 功 能是 为 We 应 用 程序 利 用树 形 结 构 S .E 其 b
CHU e z o g Yu —h n
(co l f o ue, n u Unvr t f eh o g ,Maasa 4 02 C i ) Sho o mp tr A h i i s yo c nl y C ei T o ’nhn2 3 0 , hn a
Ab ta tTre e l o o e u fM irs f t d P. sr c : eViw Sa cmp n nto to coo tsa  ̄d AS NET e ̄ o tos Isfn t n i og nzn aa wih Tre e ‘ n W l n rl. t u ci s ra iig d t t e Viw o sr cue frW e p l ain nt i a r a e nt ea ayi ft n tl t na dt ece t fsai e Viw n t iW e Co — tu t r o ba pi t .I hsp pe,bs do h n lsso heisal i n h ra i o tt Tre e o hs c o ao g n c b n to ,t lme tto eh d fd n m i Tre e i e p l ain aep i oeatn in,whc /p o tdb o ed tb s rl hei e na inm t o so y a c e Viw W b a pi to r adm r te t mp n c o ih e p re yan u d aa ae a e uso lo i m .Th xp rme trs ls o fe t e eso h r l e to ,whc rvd n o v ne csf rte ndrc rinag rt h ee e i n eut h wst efci n s ftep omsdmeh he v d ihp o iema yc n e in e o h ce tn fW e p l ain r aig o ba pi t . c o
<i cTeN e hce=“ re T x =“ 一章 ”E pn e= e : r o C ekd Tu” et 第 w ed x ad d
No e m e d Na No e a Na e d Frme m No e e f d L a
吉 …
.
第三 章
第一 节
第 二节
0 1 00 11 00 12 00 12 0 2 00 21 00 22 00 23 0 3 00 31 00 32 00 33
< NUL > L < NUL > L
0 1 1 1 0 1 1 1 0 1 1 1
0 0 1
!
图 1 静 态树 形 图
< i : e Vi i e wc Tre e d= “ eVi ” sye= “ w Tre e wl t l Z— I DEX: 0 : N 1 1 L F 0 x P SI ON: b oue TO 8 x’ E T: p ; O TI a s lt ; P: p ’ r n t ‘ev r u a =‘ r e ”Ex a d v l “ ”E p n e l g Ur = ‘i : / s p n Le e = 2 x a d d ma e l ‘ l / / fe
Ke r s AS NET;Tr e e ;d tb s y wo d : P. e Viw a a a e;r c r in ag rt m e u s lo ih o
0 引 言
A PN S . ET真正有 用 的特性就 是其 可扩充 性 。世
级的数据 , 就像 Wi o s n w 的资源管理器一样 [ d 。
|1 / ; 0 y
收稿 日期 :0 6—0 3 20 8— l
基金项 目: 安徽省高校青年教师科研 资助计划项 目(0 6q0 9 2 0 j18 )
作者 简介: 岳中(9 1 - , , 储 17 - 男 安徽岳 西人 , 师 , ) 讲 硕士 , 研究方 向
为软件工程 、 人工智能及 工控 网络 。
文 中将 向你展示在 A P N T页面上通 过数据 库 S .E 技术和递归思想 , 利用 T eVe re i w控件实现动态树 形图
的方法 。
界 各地 的开发人员都 可以创建 自己的 自定 义控 件 , 这 种 自定义控 件 可 以方 便地 在 你 自己的过 程 中进行 定
义 。其 中,nent x l e bC nrl 就是 由微 软 It e E p rr r o We o t s o
C \Ie u : nt b\w w o t p w ro \w bt — l n \1 0\t e gs\ ec l ce t — r i ri e e ma
pu .;’ lsgf , I gUr= ie / / ntu www o tx b t — l tx1 ma e l f : / C:xIep bx l ro wecr c e — l i n 0\t er ̄e \pu1 gf e ceNo ene =… > ri a n s l .i s "Sl td d ld e x 1
即可。
图加载时显示 的节点信息 。节点导航地址为该节点正 常触发后的链 接地址 。当 N d La=0时表示该节 点 oe ef 非 叶节点 , 可继续展 开 , N d ̄a=1 当 oe f 时表示 该节 点
为叶节点 , 不可再展 开 , 只能导航 到新 的页面 。
接下来 若 要 在 A P N T页 面上 实 现静 态 树 形 S.E 图, 可像使 用 常规控件 一样 , 向页面添加 一 T eVi re e w
0 4 O0 41 000 411
男女阵营 美眉帅哥 非常男女 情感交流 休闲时尚 笑话天地 开心时刻 星座物语 音乐欣赏 音乐下载 娱乐资讯 歌手档案
影 视 天 地 电 影
<NUL L> r h.sx i tap g We — 12 ap b. 0 .sx 0 We — 13 ap b. 0 .sx 0 < nL> We . 2 1ap b 0 .sx 0 、_ 一 2 2 ap Ⅳ b 0 0 .sx e We . 2 3 ap b 0 .sx 0 <NUL > L We 一 3 1ap b 0 0 .sx We 一 32.sx b 0 0 ap We 一 33.sx b 0 0 ap
