判断输入数是否为质数的流程图
1.1.2 程序框图

开始
1
输入n 输入
否
i=2
r=0? 是
n不是质数 不是质数 n是质数 是质数
除以i 求n除以 除以 的余数r 的余数 i=i+1
i≥n或r=0? 或
否
结束
是 1
从上面的程序框图中,不难看出以下三种不 从上面的程序框图中 不难看出以下三种不 同的逻辑结构. 同的逻辑结构
除以i 求n除以 除以 的余数r 的余数 输入n 输入
练习:
1.流程线的功能是:…………………..( A.表示算法的起始和结束. B.表示算法的输入和输出信息. C.赋值、运算. D.按照算法顺序连接程序图框. ).
2.对程序框 表示的功能描述正确的一项 是:…( ). A.表示算法的起始和结束. B.表示算法输入和输出的信息. C.赋值、计算. 答案:D,B 答案 D. 按照算法顺序连接程序图框.
输入a,b
S=(a+b)*0.5 否 S>=60? 是
credit=2
输出credit 结束
credit=0
小结: 1、程序框图的概念
2、程序框图图例的名称和意义(作用)
3、如何用程序框图表示顺序结构、选择结构
程序框图又称流程图, 一.程序框图又称流程图,是一种用规定的图形,指向线 程序框图又称流程图 是一种用规定的图形, 及文字说明来准确、直观地表示算法的图形。 及文字说明来准确、直观地表示算法的图形。 程序框 名称 功能
终端框(起 表示一个算法的起始和结束 止框) 输入、输出 表示算法的输入和输出的信 框 息 处理框(执 赋值、计算 行框) 判断框 判断一个条件是否成立,用 “是”、“否”或“Y”、 “N”标明
输入面积S 否 S<=80 是 M=3*S M=240+5*(S-80) 开始
人教高中数学 必修三程序框图PPT(共18张PPT)

千克),
试画出计算费用f的程序框图。
第15页,共18页。
自然语言是: 第一步:输入物品重量ω; 第二步:如果ω<=50,那么f=0.53 ω,
否则f=50×0.53+(ω-50) ×0.85;
第三步:输出托运费f.
第16页,共18页。
程序框图:
求n除以i的余数r
i的值增加1,仍用i
表示
否
i>n-1或r=0
是
否
r=0?
是 输出“n不是质数”
输出“n是质数”
第3页,共18页。
结束
图形符号
名称
含义
表示一个算法的起
终端框(起止框)
始与结束
输入,输出框
表示一个算法输入 输出信息
处理框(执行框)
赋值、计算
判断框
流程线
连接点
第4页,共18页。
判断某一条件是否成立, 成立时在出口处标明“是” 或“Y”;不成立时标明 “否”或“N”
它的程序框图. B
开始
三 角 形 面 积 为 s p(pa)(pb)(pc) 其 中 pabc(a、 b、 c为 三 角 形 三 边 长 )
2
输入a,b,c
算法步骤如下:
第一步,输入三角形三条边的边长a,b,c
p 1 (abc) 2
第 二 步 ,计 算 pabc 2
sp(pa)(pb)(pc)
第 三 步 , 计 算 s p (p a )(p b )(p c )
第四步,判断△=0是否成立,若是,则输出x1=x2=p;否则, 计算x1=p+q,x2=P-q,并输出x1,x2
第11页,共18页。
质数判断

目录摘要 (1)1.方案论证 (2)1.1.设计目的和要求 (2)1.2.设计选题 (2)1.3.总体方案 (2)2 软件设计及说明 (3)2.1主程序设计说明 (3)2.2子程序流 (4)2.2.1数字输入子程序 (4)2.2.2质数判断子程序 (5)3 程序段部分说明 (6)3.1数据段定义 (6)3.2主程序部分 (6)3.3 子程序部分 (7)3.3.1数字输入子程序 (7)3.3.2质数判断子程序 (8)3.4 DOS功能调用说明 (9)4程序调试说明 (10)5心得体会 (11)参考文献 (12)附录 (13)摘要汇编语言是面向机器的程序设计语言。
在汇编语言中,用助记符代替机器指令的操作码,用地址符号或标号代替指令或操作数的地址,如此就增强了程序的可读性和编写难度。
汇编作为一门语言,具有编程语言的一般特性,既有助于透彻的理解高级语言的核心原理,又能明晰程序内部的执行过程,更重要的是能够获得直接从底层分析问题解决问题的能力,为学习高层的知识奠定基石。
质数又称素数。
指在一个大于1的自然数中,除了1和此整数自身外,不能被其他自然数整除的数。
因此我们可以对一个数不断的除以小于它的整数就可以得到结果,而用汇编语言实现这一点,需要灵活使用各种指令与结构,而输入输出还需调用一些dos功能以便打成目标。
这些都有助于加深对汇编语言的理解。
关键词:汇编语言质数质数判断汇编语言程序设计1.方案论证1.1.设计目的和要求设计目的:(1)进一步建立微机系统的概念,加深对系统的理解和认识,培养学生应用微型计算机解决实际问题的能力;(2)进一步学习和掌握汇编语言程序的编写和应用的方法,通过较大规模程序的编写,提高编写汇编语言程序的水平和学习程序调试方法。
(3)进一步熟悉微机最小系统的构成及常用接口芯片的使用,提高系统设计能力。
设计要求:本次课程设计主要为软件设计选题,要求上机调试通过。
1.2.设计选题质数判断汇编语言程序设计要求:(1)提示输入数字;输入任意数字int1 ,点击Enter 结束输入;(2)如果int1 是质数,则输出“int1 is aprime number”;如果int1 不是质数,则输出“int1 is not aprime number”;点击Enter 程序退出;。
陈景润与哥德巴赫猜想

陈景润与哥德巴赫猜想一七四二年,德国的一位中学数学教师——哥德巴赫——发现,每一个大于6的大偶数都可以写成两个素数的和。
他对许多偶数进行了检验,都说明这是确实的。
但是这需要给予证明,因为尚未经过证明,只能称之为猜想。
他自己却不能够证明它,就写信请教赫赫有名的大数学家欧拉,请他来帮忙作出证明。
但一直到死,欧拉也不能证明它。
从此这成了一道难题,吸引了成千上万数学家的注意,这就是著名的“哥德巴赫”猜想。
两百多年来,许多数学家都企图给这个猜想作出证明,但都没有成功。
一、陈氏定理陈景润(1933-1996),中国科学院数学研究所研究员。
他是世界著名解析数论学家之一,并在哥德巴赫猜想研究方面取得国际领先的成果。
1966年5月他证明了“哥德巴赫猜想”中的命题“1+2”,即“每个大于6的大偶数都是一个素数及一个不超过两个素数的乘积之和”,距摘取这颗数论皇冠上的明珠(1+ 1)只是一步之遥,将200多年来人们未能解决的哥德巴赫猜想的证明大大推进了一步。
这一结果被国际上誉为“陈氏定理”。
陈景润研究“哥德巴赫”猜想和其他数论问题的成就,至今,仍然在世界上遥遥领先。
“哥德巴赫”猜想的证明很困难,但我们可以验证,任取一个大于六的偶数,都可以将其写成两个素数之和,素数也称为质数。
对于一个相当大的偶数来说,当把它写成两个数之和的时候,这两个数本身也是很大的。
那么,这两个数是否是质数,就成了验证“哥德巴赫”猜想的核心问题了。
下面,我们就编制一个小程序用于判断我们给出的任意一个整数是否是质数。
二、判断是否质数的流程图从流程图中我们可以看出,首先输入一个要判断的数,将作为质数标志的字符串变量I的值设置为“是质数!”。
然后,这个算法用到了两个判别框。
第一个判别框的两个转向箭头都是往下的,所以,它并不代表循环结构而是分支结构。
它表示,只要n被K整除,n就不是质数。
所以,这个条件成立时,首先将作为标志的字符串变量I的值变更为“不是质数!”,然后,直接转向第二个判别框的下方。
1[1].1.2-1程序框图与顺序结构)
![1[1].1.2-1程序框图与顺序结构)](https://img.taocdn.com/s3/m/2a11b3ccbb4cf7ec4afed02e.png)
表示一个算法的起始和结束 表示一个算法输入和输出的 信息 赋值、计算
判断某一条件是否成立,成立时在 出口处标明“是”或“Y”;不成立 时标明“否”或“N”
流程线
连接程序框,表示算法步骤的 执行顺序
思考4:在逻辑结构上,“判断整数n(n>2)是否 为质数”的程序框图由几部分组成?
p( p - a )( p - b)( p - c)
输出S 结束
理论迁移 1 一个笼子里装有鸡和兔共m只,且鸡 和兔共n只脚,设计一个计算鸡和兔各有多少 只的算法,并画出程序框图表示. 算法分析:
第一步,输入m,n.
第二步,计算鸡的只数 x
= 4m - n 2
.
第三步,计算兔的只数y=m-x.
第四步,输出x,y.
思考2:我们将上述算法用下面的图形表示:
开始 输入n i=2 求n除以i的余数 i的值增加1,仍用i表示 i>n-1或r=0? 是 r=0?
否 否
输出“n是质数”
是
输出“n不是质数” 结束
上述表示算法的图形称为算法的程序框 图又称流程图,其中的多边形叫做程序 框,带方向箭头的线叫做流程线,你能 指出程序框图的含义吗?
开始 输入n i=2 求n除以i的余数 i的值增加1,仍用i表示 i>n-1或r=0? 是 r=0?
否 否
输出“n是质数”
是
输出“n不是质数” 结束
知识探究(二):算法的顺序结构 思考1:任何一个算法各步骤之间都有明确的 顺序性,在算法的程序框图中,由若干个依 次执行的步骤组成的逻辑结构,称为顺序结 构,用程序框图可以表示为:
步骤n
?
在顺序结构中可能 会用到哪几种程序 框和流程线?
常用算法表示工具
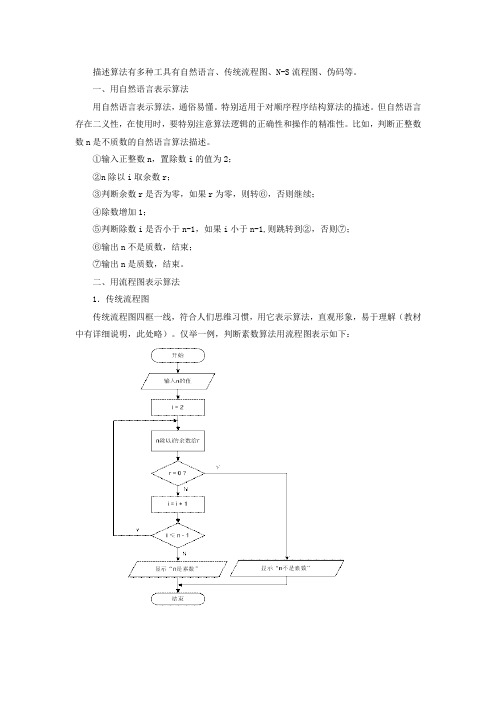
描述算法有多种工具有自然语言、传统流程图、N-S流程图、伪码等。
一、用自然语言表示算法用自然语言表示算法,通俗易懂。
特别适用于对顺序程序结构算法的描述。
但自然语言存在二义性,在使用时,要特别注意算法逻辑的正确性和操作的精准性。
比如,判断正整数数n是不质数的自然语言算法描述。
①输入正整数n,置除数i的值为2;②n除以i取余数r;③判断余数r是否为零,如果r为零,则转⑥,否则继续;④除数增加1;⑤判断除数i是否小于n-1,如果i小于n-1,则跳转到②,否则⑦;⑥输出n不是质数,结束;⑦输出n是质数,结束。
二、用流程图表示算法1.传统流程图传统流程图四框一线,符合人们思维习惯,用它表示算法,直观形象,易于理解(教材中有详细说明,此处略)。
仅举一例,判断素数算法用流程图表示如下:选择结构:当条件P成立时,则执行A语句,否则执行B语句。
当型循环结构:当条件P1成立时,则循环执行A语句。
直到型循环结构:循环执行A语句,直到条件P1成立为止。
三、伪代码表示算法用流程图表示算法,直观易懂,但画起来比较费劲,在设计一个算法时,可能要反复修改,而修改流程图是比较麻烦的,因此,流程图适用于表示一个算法,但在设计算法的过程中使用却不是很理想,尤其当算法比较复杂、需要反复修改时。
为设计算法时方便,就产生了伪代码。
伪代码是介于自然语言和机器语言之间用文字和符号来描述算法的,它不用图形符号,因此书写方便,格式紧凑,也比较好懂。
虽然伪代码不是一种实际的编程语言,但是在表达能力上类似于编程语言,同时避免了描述技术细节带来的麻烦,所以伪代码更适合描述算法,故被称为“算法语言”或“第一语言”。
伪代码便于向计算机语言算法(如C语言、Java)过渡。
伪代码的7个主要部分:(1) 算法名称(2)指令序列(3)输入/输出(4)分支选择(5)赋值(6)循环(7)算法结束1.算法名称两种表示算法的伪代码:过程(Procedure)函数(Function)过程和函数的区别是:过程是执行一系列的操作,不需要返回操作的结果,无返回数据;函数是执行一系列的操作后,要将操作的结果返回,有返回数据。
程序框图.

图形符号
名 称
终端框 (起止框)
输入、 输出框 处理框 (执行框) 判断框 流程线
功 能
表示一个算法的起始和结束 表示一个算法输入 和输出的信息 赋值、计算
判断某一条件是否成立, 成立时在出口处标明“是”或“Y”; 不成立时标明“否”或“N”。
连接程序框, 表示算法步骤的执行顺序
○
连接点
y=50
结束
循环结构
由按照一定的条件反复执行的某些步骤组成的逻辑结构
A 循环体 循环体
满足 条件
否
满足 条件
是
是
否
循环体
满足条件?
否
是
特征:在执行了一次循 环体后,对条件进行判断, 如果条件不满足,就继续 执行循环体,直到条件满 足时终止循环.
这种循环结构称为直到型循环结构,
循环体 满足条件?
S n( n 1) 2
开始
n=0 n=n+1 的值 计算
S n( n 1) 2
第四步判断“S>2007”是否
成 立,是则输出n,否则返回 到第二步
步骤A 步骤B
输出S的值
结束
练习
输出1000以内能被7整除的所有正整数
开始 k=1
算法1
n=7k k=k+1 输出n 是
第一步令k=1 第二步计算n=7k的值 第三步判断“n<1000”是否 成 立,是则执行第四步否则 结束算法 第四步输出n,将k值增加1,返回到 第二步
n<1000? 否 结束
开始 x=7 x=x+7
X (4 H F ) / 2, 解方程组,得 Y ( F 2 H ) / 2.
质数的判定方法

质数的判定方法质数是指只能被1和本身整除的正整数,如2、3、5、7等都是质数。
判定一个数是否为质数一直以来是算术领域的一个重要问题。
本文将会介绍几种判定质数的方法,以供参考。
一、试除法试除法是一种最简单有效的判断质数的方法。
所谓试除法就是将待判定的数n除以2到(n-1)中的每一个数,如果都除不尽,则n为质数;否则n为合数。
试除法出自欧几里得,是最早的找质数的方法。
代码实现如下:```pythondef is_prime(n):if n < 2:return Falsefor i in range(2, n):if n % i == 0:return Falsereturn True```虽然试除法简单易懂,但其时间复杂度较高,特别是当n为极大数时,时间复杂度将达到O(n)。
二、埃氏筛法埃氏筛法又称素数筛法,是一种较为常用的素数判定算法。
其基本思想是,从2开始,将每个质数的倍数都标记成合数,以达到筛选素数的目的。
时间复杂度为O(n log log n)。
代码实现如下:```pythondef primes(n):is_prime = [True] * nis_prime[0] = is_prime[1] = Falsefor i in range(2, int(n ** 0.5) + 1):if is_prime[i]:for j in range(i ** 2, n, i):is_prime[j] = Falsereturn [x for x in range(n) if is_prime[x]]print(primes(20))```三、Miller-Rabin素性测试Miller-Rabin素性测试是一种常见的高效素数判定算法。
其基本原理是根据费马小定理进行推导。
费马小定理指出,若p为质数,a为正整数,且a不是p的倍数,则a^(p-1) ≡ 1 (mod p)。
根据费马小定理,若对于一组给定的a和n,a^(n-1) ≢ 1 (mod n),那么n一定不是质数。
