人教版高一数学必修2 空间直线的垂直关系练习题(含答案详解)
高中数学必修2考点知识专题训练12---直线与平面垂直的性质(含答案解析)

高中数学必直线一、基础巩固1.在正方体ABCD-A 1B 1C 1D A.B 1B ⊥lB.B 1B ∥lC.B 1B 与l 异面但不垂直D.B 1B 与l 相交但不垂直解析:因为B 1B ⊥平面A 1C 1,又因答案:B2.若直线l 垂直于梯形ABCD 面的位置关系是( ) A.相交但不垂直 B.平行C.垂直 D.在平面答案:C3.如图, ADEF 的边AF ⊥平面数学必修2考点知识专题训练直线与平面垂直的性质课时过关·能力提升1中,若直线l (与直线BB 1不重合)⊥平面A 1又因为l ⊥平面A 1C 1,所以l ∥B 1B. BCD 的两腰AB 和CD ,直线m ∥l,则m 与梯形 面ABCD 内平面ABCD ,且AF=2,CD=3,则CE=( )训练C 1,则( ) 形ABCD 所在的平A.2B.3C.√√13解析:因为四边形ADEF为平行四边形,所以AF DE.因为AF⊥平面ABCD,所以DE⊥平面ABCD.所以DE⊥DC.因为AF=2,所以DE=2.又CD=3,所以CEൌ√ܥܦଶܦܧଶൌ√94ൌ√13.答案:D4.已知m,n是两条不同的直线,α,β是两个不重合的平面,给定下列四个命题,其中的真命题是()①若m⊥n,n⊂α,则m⊥α;②若m⊥α,m⊂β,则α⊥β;③若m⊥α,n⊥α,则m∥n;④若m⊂α,n⊂β,α∥β,则m∥n.A.①和②B.②和③C.③和④D.①和④解析:①中,直线m垂直于平面α内的一条直线n,则直线m与平面α不一定垂直,所以①不是真命题;②是平面与平面垂直的判定定理,所以②是真命题;③是直线与平面垂直的性质定理,所以③是真命题;④中,分别在两个平行平面α,β内的直线m,n平行或异面,所以④不是真命题.答案:B5.已知地面上有两根相距a m的竖直的旗杆,它们的高度分别是b m和c m(b>c),则它们顶端的距离为m.解析:如图,根据题意可知AD=b m,BC=c m,AB=a m.由线面垂直的性质定理可得AD∥BC.过点C向AD作垂线,设垂足为E,则在Rt△CDE中,CE=a m,DE=(b-c)m,所以CDൌටܽଶ(ܾ-ܿ)ଶሺmሻ.答案:ටܽଶ(ܾ-ܿ)ଶ6.已知直线l,m,a,b,l⊥a,l⊥b,m⊥a,m⊥b,且a,b是异面直线,求证:l∥m.证明:如图,在直线b上任取一点O,过点O作a'∥a,则直线b,a'确定一个平面α.∵a'∥a,l⊥a,∴l⊥a'.∵l⊥b,a'∩b=O,∴l⊥α.同理可证m⊥α,∴l∥m.7.如图,已知α∩β=l,EA⊥α于点A,EB⊥β于点B,a⊂α,a⊥AB.求证:a∥l.证明:因为EA⊥α,EB⊥β,α∩β=l,所以l⊥EA,l⊥EB.因为EA∩EB=E,EA⊂平面EAB,EB⊂平面EAB,所以l⊥平面EAB.因为a⊂α,EA⊥α,所以a⊥EA.因为a⊥AB,AB∩EA=A,AB⊂平面EAB,EA⊂平面EAB,所以a⊥平面EAB.所以a∥l.二、能力提升1.若a,b是互不相同的直线,α,β是不重合的平面,则下列条件中可推出a∥b的是()A.a⊂α,b⊂β,α∥βB.a∥α,b⊂αC.a⊥α,b⊥αD.a⊥α,b⊂α答案:C★2.已知直线l∩平面α=点O,A∈l,B∈l,A∉α,B∉α,且OA=AB.若AC⊥平面α,垂足为C,BD⊥平面α,垂足为D,AC=1,则BD=()A.2B.1C.ଷଶD.ଵଶ解析:因为AC⊥平面α,BD⊥平面α,所以AC∥BD.连接OD,所以ைൌ.ை因为OA=AB,所以ைൌଵଶ.ை因为AC=1,所以BD=2.答案:A3.如图,在三棱锥P-ABC中,PA⊥平面ABC,D是侧面PBC上的一点,过点D作平面ABC 的垂线DE,其中D∉PC,则DE与平面PAC的位置关系是.解析:因为DE⊥平面ABC,PA⊥平面ABC,所以DE∥PA.又DE⊄平面PAC,PA⊂平面PAC,所以DE∥平面PAC.答案:平行4.在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,AE⊥PD于点E,l⊥平面PCD.求证:l∥AE.证明:因为PA⊥平面ABCD,CD⊂平面ABCD,所以PA⊥CD.又四边形ABCD是矩形,所以CD⊥AD.因为PA∩AD=A,PA⊂平面PAD,AD⊂平面PAD,所以CD⊥平面PAD.又AE⊂平面PAD,所以AE⊥DC.因为AE⊥PD,PD∩CD=D,PD⊂平面PCD,CD⊂平面PCD,所以AE⊥平面PCD.因为l⊥平面PCD,所以l∥AE.5.如图,PA⊥平面ABD,PC⊥平面BCD,E,F分别为BC,CD上的点,且EF⊥AC.求证:ிൌா.证明:∵PA⊥平面ABD,PC⊥平面BCD,∴PA⊥BD,PC⊥BD,PC⊥EF.又PA∩PC=P,∴BD⊥平面PAC.又EF⊥AC,PC∩AC=C,∴EF⊥平面PAC,∴EF∥BD,ிൌா.★6.如图,△ABC是等边三角形,AE和CD都垂直于平面ABC,且AE=AB=2a,CD=a,F是BE的中点,求证:(1)DF∥平面ABC;(2)AF⊥BD.证明:(1)如图,取AB的中点G,连接FG,CG.因为F为BE的中点,所以FG∥AE,FGൌଵܣܧ.ଶ因为CD⊥平面ABC,AE⊥平面ABC,所以CD∥AE.因为CDൌଵܣܧ,ଶ所以FG∥CD,FG=CD.所以四边形CDFG是平行四边形,所以DF∥CG.因为CG⊂平面ABC,DF⊄平面ABC,所以DF∥平面ABC.(2)在Rt△ABE中,AE=2a,AB=2a,F为BE的中点, 所以AF⊥BE.因为△ABC是等边三角形,所以CG⊥AB,所以DF⊥AB.因为FG⊥平面ABC,所以FG⊥GC,FG⊥DF.因为FG∩AB=G,所以DF⊥平面ABE.因为AF⊂平面ABE,所以DF⊥AF.因为BE∩DF=F,所以AF⊥平面BDF.因为BD⊂平面BDF,所以AF⊥BD.。
高中数学必修二 8 6 空间直线、平面的垂直(精练)(含答案)

8.6 空间直线、平面的垂直(精练)【题组一 线面垂直】1.(2021·全国·高一课时练习)如图,在正方体ABCD ﹣A 1B 1C 1D 1中,点E 是棱BC 的中点,点F 是棱CD 上的动点.当CF FD=__时,D 1E ⊥平面AB 1F .【答案】1【解析】连接A 1B ,则A 1B 是D 1E 在面ABB 1A 内的射影,⊥AB 1⊥A 1B ,⊥D 1E ⊥AB 1,于是D 1E ⊥平面AB 1F ,又AF ⊂平面AB 1F ,所以D 1E ⊥AF .连接DE ,则DE 是D 1E 在底面ABCD 内的射影.⊥D 1E ⊥AF ,1DD AF ⊥,因为11D E DD D ⋂=,所以AF ⊥平面1DD E ,又DE ⊂平面1DD E ,所以DE ⊥AF .⊥ABCD 是正方形,E 是BC 的中点.⊥当且仅当F 是CD 的中点时,DE ⊥AF ,即当点F 是CD 的中点时,D 1E ⊥平面AB 1F .⊥CF FD=1时,D 1E ⊥平面AB 1F .故答案为:1.2.(2021·全国·高一课时练习)如图,四棱锥P ABCD -中,PA ⊥平面ABCD ,底面ABCD 是正方形,PA AD =,F 为PD 的中点.求证:AF ⊥平面PDC .【答案】证明见解析.【解析】证明:⊥PA ⊥平面ABCD ,CD ⊂平面ABCD ,⊥PA CD ⊥.⊥四边形ABCD 是正方形,⊥CD AD ⊥,又PA AD A ⋂=,PA AD ⊂、平面PAD ,⊥CD ⊥平面PAD ,⊥AF ⊂平面PAD ,⊥CD AF ⊥.⊥,PA AD FP FD ==,⊥AF PD ⊥,又CD PD D =,CD PD ⊂、平面PDC ,⊥AF ⊥平面PDC .3.(2021·全国·高一单元测试)如图,直三棱柱ABC ﹣A 1B 1C 1中,底面是边长为2的等边三角形,点D ,E 分别是BC ,AB 1的中点.(1)证明:DE ⊥平面ACC 1A 1;(2)若BB 1=1,证明:C 1D ⊥平面ADE .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)连接A 1B ,A 1C ,在直三棱柱ABC ﹣A 1B 1C 1中,侧面ABB 1A 1是矩形,因为点E 是AB 1的中点,所以点E 是A 1B 的中点,又因为点D 是BC 的中点,所以DE ⊥A 1C ,因为DE ⊥平面ACC 1A 1,A 1C ⊥平面ACC 1A 1,所以DE ⊥平面ACC 1A 1.(2)连接B 1D ,在直三棱柱ABC ﹣A 1B 1C 1中,因为BB 1⊥平面ABC ,AD ⊥平面ABC ,所以 BB 1⊥AD ,又因为底面ABC 是等边三角形,D 为BC 的中点,所以BC ⊥AD ,又BC ∩BB 1=B ,所以AD ⊥平面B 1BCC 1,又C 1D ⊥平面B 1BCC 1,所以AD ⊥C 1D ,由BC =2,得BD =1,又BB 1=CC 1=1,所以11DB C D =所以2221111DB C D B C +=,所以C 1D ⊥DB 1,DB 1AD =D ,所以C 1D ⊥平面ADB 1,即C 1D ⊥平面ADE .4.(2021·全国·高一课时练习)如图1,在直角梯形ABCD 中,1//,90,2AD BC BAD AB BC AD a ∠=︒===,E是AD 的中点,O 是AC 与BE 的交点.将ABE △沿BE 折起到图2中1A BE 的位置,得到四棱锥1A BCDE -.求证:CD ⊥平面1A OC .【答案】证明见解析【解析】证明:在题图1中, 因为12AB BC AD a ,E 是AD 的中点,90BAD ∠=︒,所以BE AC ⊥.所以在题图2中,1BE AO ⊥,BE OC ⊥, 又1AO OC O ,所以BE ⊥平面1A OC ,又//CD BE ,所以CD ⊥平面1A OC .5.(2021·广西·桂平市麻垌中学高一月考)如图,在四棱锥P -ABCD 中,底面ABCD 是菱形,⊥ABC =60°,P A ⊥平面ABCD ,点M 、N 分别为BC 、P A 中点,且P A =AB =2.(1)证明:BC ⊥平面AMN ;(2)求三棱锥N -AMC 的体积;(3)在线段PD 上是否存在一点E ,使得MN ⊥平面ACE ;若存在,求出PE 的长;若不存在,说明理由.【答案】(1)详解见解析;(3)存在点E 为PD 的中点,PE 【解析】(1)证明:因为ABCD 为菱形,所以AB =BC ,又⊥ABC =60°,所以AB =BC =AC ,又M 为BC 中点,所以BC ⊥AM ,又P A ⊥平面ABCD ,BC ⊥平面ABCD ,故P A ⊥BC又P A ∩AM =A ,所以BC ⊥平面AMN .(2)由(1)知ABC 为等边三角形,AB =BC =AC =2又M 为BC 中点,则BM =CM =1,故AM因此11122AMC S AM CM =⋅= 又P A ⊥平面ABCD ,P A =2,N 为P A 的中点,故AN =1所以11133N AMC AMC V SAN -=⋅==. (3)存在点E ,取PD 中点E ,连接NE ,EC ,AE ,如图所示:因为N ,E 分别为P A ,PD 中点,所以1//2NE AD ,且12NE AD =, 又在菱形ABCD 中,1//2CM AD ,且12CM AD =, 所以//NE MC ,且NE MC =,即MCEN 是平行四边形,故//NM EC ,又EC ⊂平面ACE ,NM ⊄平面ACE ,故//MN 平面ACE ,即在PD 上存在一点E ,使得MN //平面ACE ,此时PE =12PD【题组二 面面垂直】1.(2021·全国·高一单元测试)如图,四棱锥P ABCD -的底面是边长为a 的菱形,平面PCD ⊥平面,ABCD PC a =,,PD E =为PA 的中点.求证:平面EDB ⊥平面ABCD .【答案】证明见解析【解析】如图所示,设ACBD O =,连接EO ,则//EO PC .,PC CD a PD ===, 222,PC CD PD PC CD ∴+=∴⊥.⊥平面PCD ⊥平面ABCD ,平面PCD 平面ABCD CD =,PC ∴⊥平面,ABCD EO ∴⊥平面ABCD .又EO ⊂平面EDB ,故平面EDB ⊥平面ABCD .2.(2021·山西省长治市第二中学校高一月考)如图,在三棱锥-P ABC 中,90ACB ∠=︒,PA ⊥平面ABC .(1)求证:平面PAC ⊥平面PBC(2)若AC BC PA ==,求二面角-A PB C -的正切值【答案】(1)证明见解析;【解析】(1)PA ⊥平面ABC PA BC ∴⊥AC BC ⊥,PA AC A,PA =⊂平面,PAC AC ⊂平面PACBC ∴⊥平面PAC BC ⊂又平面PBC ,∴平面PAC ⊥平面PBC .(2)设M 是AB 的中点,过CN PB ⊥于N ,连接CM MN 、在ABC 中AC BC,CM AB,=∴⊥PA ⊥又平面ABC ∴平面PAB ⊥平面ABC ,CM ∴⊥平面,PAB CM PB ∴⊥又PB CN,CM CN C,PB ⊥=∴⊥平面CMNPB MN,MNC ∴⊥∴∠是二面角A PB C --的平面角.设1AC BC PA ===,则在Rt CMN 中,CM ===所以tan MNC ∠=3.(2021·内蒙古包头·高一期末)如图,在四棱锥P ABCD -中,已知底面ABCD 是菱形,且对角线AC 与BD 相交于点O .(1)若PB PD =,求证:平面PBD ⊥平面PAC ;(2)设点E 为BC 的中点,在棱PC 上是否存在点F ,使得PB ⊥平面AEF ?请说明理由.【答案】(1)证明见解析;(2)存在,理由见解析.【解析】证明:(1)连接PO ,底面ABCD 为菱形,,BD AC BO DO ∴⊥=.又,PB PD BD PO =∴⊥又,PO AC O BD ⋂=∴⊥平面PAC .BD ⊂平面PBD ,∴平面PAC ⊥平面PBD .(2)棱PC 上存在点F ,且F 为PC 的中点,使得PB ⊥平面AEF ,证明如下:连接,AF EF . E 是BC 的中点,EF ∴⊥PBPB ⊄平面AEF ,EF ⊂平面AEF ,PB ∴⊥平面AEF4.(2021·广东白云·高一期末)如图,PA 垂直于O 所在的平面,AC 为O 的直径,3AB =,4BC =,PA =AE PB ⊥,点F 为线段BC 上一动点.(1)证明:平面AEF ⊥平面PBC ;(2)当点F 移动到C 点时,求PB 与平面AEF 所成角的正弦值.【答案】(1)证明见解析; 【解析】(1)证明:因为PA 垂直于O 所在的平面,即PA ⊥平面ABC ,BC ⊂平面ABC , 所以PA BC ⊥,又AC 为O 的直径,所以AB BC ⊥,因为PA AB A =,所以BC ⊥平面PAB ,又AE ⊂平面PAB ,所以BC AE ⊥,因为AE PB ⊥,BC PB B =,所以AE ⊥平面PBC ,又AE ⊂平面AEF ,所以平面AEF ⊥平面PBC .(2)解:因为3AB =,PA =PB =又AE PB ⊥,所以PA AB AE PB⋅==由2AB BE PB =⋅,可得BE =如图,过点E 作//EG PA 交AB 于点G ,则EG BE PA PB=,可得EG =又4BC =,所以EC所以162ABC S AB BC =⋅=△,12AEC S AE EC =⋅=△ 设点B 到平面AEC 的距离为h ,由E ABC B AEC V V --=,可得1133ABC AEC S EG S h ⋅=⋅△△,解得h =所以当点F 移动到C 点时,PB 与平面AEF 所成角的正弦值为h BE =5.(2021·江苏·吴江汾湖高级中学高一月考)如图,在四棱锥P ABCD -中,四边形ABCD 为矩形,AB BP ⊥,M ,N 分别为AC ,PD 的中点.(1)求证://MN 平面ABP ;(2)若BP PC ⊥,求证:平面ABP ⊥平面APC .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)连结BD ,由已知,M 为AC 和BD 的中点,又N 为PD 的中点,//MN BP ∴.MN ⊄平面ABP ,BP ⊂平面ABP ,//MN ∴平面ABP .(2)AB BP ⊥,AB BC ⊥,BP BC B ⋂=,AB ∴⊥平面BPC .PC ⊂平面BPC ,AB PC ∴⊥.BP PC ⊥,AB BP B =,PC ∴⊥平面ABP .PC⊂平面APC,⊥平面ABP⊥平面APC.6(2021·山西·太原市第五十六中学校高一月考)在四棱锥P ABCD-中,底面ABCD是矩形,PA⊥平面ABCD,4PA AD==,2AB=,以BD的中点O为球心,BD为直径的球面交PD于点M.(1)求直线BD与平面P AD所成的角的正切值;(2)求证:平面ABM⊥平面PCD.【答案】(1)12;(2)证明见解析.【解析】(1)⊥ PA⊥平面ABCD,BA⊂平面ABCD,⊥ P A⊥BA,又底面ABCD是矩形,⊥BA⊥AD,又P A,AD⊂平面P AD,=PA AD A,⊥ BA⊥平面P AD,⊥ 直线BD与平面P AD内的投影为AD,⊥ ADB∠即为直线BD与平面P AD所成的角,又AB=2,AD=4,⊥1 tan2ADB=∠;⊥ 直线BD与平面P AD所成的角的正切值为12,(2)证明:依题设,M在以BD为直径的球面上,则BM PD⊥,由(1)得AB⊥平面P AD,又PD⊂平面PAD⊥ AB PD⊥⊥ =AB BM B,AB,BM⊂平面ABM,⊥ PD⊥平面ABM,又PD⊂平面PCD⊥ 平面ABM ⊥平面PCD .7.(2021·江苏如皋·高一月考)如图,在四棱锥P ABCD -中,经过AB 的平面与PD 、PC 分别交于点E 与点F ,且平面ABFE ⊥平面PCD ,AE CD ⊥,//CD 平面ABFE .(1)求证://AB EF ;(2)求证:平面PAD ⊥平面PCD .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)//CD 平面ABFE ,CD ⊂平面PCD ,平面PCD 平面ABFE EF =//CD EF ∴同理//CD AB //AB EF ∴.(2)由(1)知//CD EF ,AE CD ⊥,AE EF ∴⊥平面ABFE ⊥平面PCD ,AE EF ⊥,平面PCD 平面ABFE EF =,AE ⊂平面ABFEAE ∴⊥平面PCD ,又AE ⊂平面P AD 中,∴平面PAD ⊥平面PCD .8.(2021·江苏·滨海县八滩中学高一期中)如图,在三棱锥P ABC -中,,,D E F 分别为棱,,PC AC AB 的中点,已知PA AC AB BC ⊥⊥,,且6,8,5PA AB BC DF ====.(1)求证:平面DEF ⊥平面ABC ;(2)求直线PB 与平面PAC 所成角的正弦值.【答案】(1)证明见解析;. 【解析】(1)证明:,D E 分别为,PC AC 中点,DE ∴为PAC △的中位线//DE PA ∴,且132DE PA ==,PA AC ⊥,DE AC ∴⊥又F 为AB 中点,EF ∴为ABC 的中位线,142EF BC ∴== 又5DF =,222DE EF DF ∴+=,DE EF ∴⊥又EF AC E ⋂=,DE ∴⊥平面ABC又DE ⊂平面BDE ,所以平面DEF ⊥平面ABC(2)由(1)知DE ⊥平面ABC ,又DE ⊂平面PAC ,∴平面PAC ⊥平面ABC因为AB BC E =,为AC 中点,BE AC ∴⊥又平面PAC 平面ABC AC =,所以BE ⊥平面PAC BPE ∴∠为直线PB 与平面PAC 所成角,在直角BEP △中,10PB =,sin 45BE AB =⋅︒=所以sin 5BE BPE PB ∠==9(2021·江苏如皋·高一月考)在直三棱柱111ABC A B C -中,F 是11B C 的中点,E 是BC 上一点,线段1B E 与BF 相交于点M ,且//AE 平面1A BF .(1)证明:点M 为线段1B E 的中点;(2)若AB AC =,证明:平面1AEB ⊥平面11BCC B .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)设11AB A B N ⋂=,连接MN ,因为//AE 平面1A BF ,AE ⊂平面1AB E ,平面1AB E ⋂平面1A BF MN =所以//AE MN ,在直三棱柱111ABC A B C -中,四边形11ABB A 为平行四边形所以1AN NB =因为//AE MN ,所以1EM MB =,即点M 为线段1B E 的中点.(2)在直三棱柱111ABC A B C -中,11//BC B C因为M 为线段1B E 的中点,所以1BE B F =又因为11B C BC =,F 是11B C 的中点,所以BE EC =,因为AB AC =,所以AE BC ⊥在直三棱柱111ABC A B C -中,1BB ⊥平面ABC ,AE ⊂平面ABC所以1AE BB ⊥,因为AE BC ⊥,1BB BC B =,1BB ⊂平面11BB C C ,BC ⊂平面11BB C C ,所以AE ⊥平面11BCC B ,因为AE ⊂平面1AEB ,所以平面1AEB ⊥平面11BCC B .【题组三 线线垂直】1.(2021·安徽·六安市裕安区新安中学高一期末)如图,在长方体ABCD -A 1B 1C 1D 1的棱中,与棱AB 垂直的棱有( )A .2条B .4条C .6条D .8条【答案】D 【解析】在长方体ABCD -A 1B 1C 1D 1的棱中,与棱AB 垂直的棱有BC ,B 1C 1,A 1D 1,AD ,AA 1,BB 1,CC 1,DD 1,共8条.故选:D.2.(2021·全国·高一课时练习)如图所示,在空间四边形ABCD 中,AD =BC =2,E ,F 分别是AB ,CD 的中点,EF 求证:AD ⊥BC .【答案】证明见解析【解析】证明:如图所示,取BD的中点H,连接EH,FH.因为E是AB的中点,且AD=2,所以EH⊥AD,EH=1.同理FH⊥BC,FH=1.所以⊥EHF(或其补角)是异面直线AD,BC所成的角.因为EF,所以EH2+FH2=EF2,所以EFH是等腰直角三角形,EF是斜边,所以⊥EHF=90°,即AD与BC所成的角是90°,所以AD⊥BC.3.(2021·全国·高一单元测试)如图,已知矩形CDEF和直角梯形ABCD,AB⊥CD,⊥ADC=90°,DE=DA,M为AE的中点.(1)求证:AC⊥平面DMF;(2)求证:BE⊥DM.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)如图,连结EC交DF于点N,连结MN.因为CDEF为矩形,所以EC,DF相互平分,所以N为EC的中点.又因为M为EA的中点,所以MN⊥AC.又因为AC⊥平面DMF,且MN⊥平面DMF.所以AC⊥平面DMF.(2)因为矩形CDEF,所以CD⊥DE.又因为⊥ADC=90°,所以CD⊥AD.因为DE∩AD=D,DE,AD⊥平面ADE,所以CD⊥平面ADE.又因为DM⊥平面ADE,所以CD⊥DM.又因为AB⊥CD,所以AB⊥DM.因为AD=DE,M为AE的中点,所以AE⊥DM.又因为AB∩AE=A,AB,AE⊥平面ABE,所以MD⊥平面ABE.因为BE⊥平面ABE,所以BE⊥MD.4.(2021·天津红桥·高一学业考试)如图,在三棱锥P-ABC中,P A⊥底面ABC,BC⊥AC,M、N分别是BC、PC的中点.(1)求证:MN//平面P AB;(2)求证:BC⊥PC.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)因为M、N分别是BC、PC的中点,MN PB,所以//又MN⊄平面PAB,PB⊂平面PAB,MN平面PAB则//(2)因为P A⊥底面ABC,且BC ⊂ 平面ABC ,所以PA BC ⊥,又BC AC ⊥,且PA AC A =,,PA AC ⊂平面PAC所以BC ⊥平面PAC ,又PC ⊂平面PAC ,所以BC ⊥P C.5.(2021·全国·高一课时练习)如图,在三棱锥P ABC -中,PC ⊥底面,,,ABC AB BC D E ⊥分别是,AB PB 的中点.(1)求证://DE PA ;(2)求证://DE 平面PAC ;(3)求证:AB PB ⊥.【答案】(1) 证明见解析;(2)证明见解析 ;(3) 证明见解析.【解析】(1)在三棱锥P ABC -中,因为,D E 分别是,AB PB 的中点,根据三角形的中位线定理,可得//DE PA .(2)由(1)知//DE PA ,因为PA ⊂平面,//PAC DE PA ,且DE ⊂/平面PAC ,根据线面垂直的判定定理,可得//DE 平面PAC .(3)因为PC ⊥平面ABC ,且AB 平面ABC ,所以AB PC ⊥,又因为AB BC ⊥,且PC BC C ⋂=,所以AB ⊥平面PBC ,又由PB ⊂平面PBC ,所以AB PB ⊥.6.(2021·广西·桂平市麻垌中学高一月考)如图,在底面为平行四边形的四棱锥P -ABCD 中,AB ⊥AC ,P A ⊥平面ABCD ,且P A =AB ,点E 是PD 的中点.求证:(1)AC ⊥PB ;(2)PB //平面AEC .【答案】(1)证明见解析;(2)证明见解析.【解析】(1)四棱锥P -ABCD 中,因P A ⊥平面ABCD ,AC ⊂平面ABCD ,于是得AC ⊥P A ,而AB ⊥AC ,PA AB A =,,PA PB ⊂平面P AB ,从而得AC ⊥平面P AB ,又PB ⊂平面P AB ,所以AC ⊥PB ;(2)连接BD 交AC 于点O ,连接EO ,如图,因底面ABCD 为平行四边形,则有O 是BD 中点,又E 是PD 中点,于是得EO //PB ,而EO ⊂平面AEC ,PB ⊄平面AEC ,所以PB //平面AEC .【题组四 线线角】1.(2021·黑龙江·嫩江市第一中学校高一期末)如图,空间四边形ABCD 的对角线AC =8,BD =6,M ,N 分别为AB ,CD 的中点,并且异面直线AC 与BD 所成的角为90°,则MN =( )A .3B .4C.5D.6【答案】C【解析】取AD的中点P,连接PM,PN,则BD⊥PM,AC⊥PN,⊥⊥MPN或其补角即异面直线AC与BD所成的角,⊥⊥MPN=90°,PN=12AC=4,PM=12BD=3,⊥MN=5.故选:C.2.(2021·全国·高一课时练习)已知正四棱锥P-ABCD,P A=2,AB M是侧棱PC的中点,且BM则异面直线P A与BM所成角为________.【答案】45°【解析】如图,连接AC,BD交于点O,连接OM,则⊥OMB为异面直线P A与BM所成角.由O,M分别为AC,PC中点,得OM=12P A=1.在Rt AOB中,易得OB=AB·tan·45°=1.又BM即OB2+OM2=BM2,所以OMB为直角三角形,且⊥OMB=45°.故答案为:45°.3.(2021·全国·高一课时练习)如图,在三棱柱ABC-A1B1C1中,AA1⊥AB,AA1⊥AC.若AB=AC=AA1=1,BCA1C与B1C1所成的角为____.【答案】60°【解析】依题意,得BC⊥B 1C1,故异面直线A1C与B1C1所成的角即BC与A1C所成的角.连接A1B,在A1BC中,BC=A1C=A1B⊥A1CB=60°,即异面直线A1C与B1C1所成的角为60°.故答案为:60°.4.(2021·全国·高一课时练习)在正三棱柱ABC-A1B1C1中,D是AB的中点,则在所有的棱中与直线CD和AA1都垂直的直线有______.【答案】AB,A1B1【解析】由正三棱柱的性质可知与直线CD和AA1都垂直的直线有AB,A1B1.故答案为:AB,A1B1.5.(2021·全国·高一课时练习)若⊥AOB=135°,直线a⊥OA,a与OB为异面直线,则a和OB所成的角的大小为______.【答案】45°【解析】因为直线a//OA,a与OB为异面直线,的补角为a与OB所成角,所以AOB又135AOB ︒∠=,所以a 与OB 所成角的大小为18013545︒︒︒-=.故答案为:45︒6.(2021·全国·高一课时练习)如图,在四面体A BCD -中,AC BD a ==,AC 与BD 所成的角为60,M 、N 分别为AB 、CD 的中点,则线段MN 的长为________.【答案】2a 【解析】取BC 的中点E ,连接EM 、EN ,M 、E 分别为AB 、BC 的中点,//ME AC ∴且122a ME AC ==, 同理可得EN //BD 且122a EN BD ==, MEN ∴∠为异面直线AC 与BD 所成的角或其补角,则60MEN ∠=或120.在MEN 中,2a EM EN ==. 若60MEN ∠=,则MEN 为等边三角形,此时,2a MN =; 若120MEN ∠=,由余弦定理可得3cos1202MN ==.综上所述,2a MN =.故答案为:2a . 7.(2021·全国·高一课时练习)如图所示,空间四边形ABCD 中,两条对边3AB CD ==,,E F 分别是另外两条对边,AD BC 上的点,且1,2AE BF EF ED FC ==AB 和CD 所成角的大小为___________.【答案】90︒【解析】如图,过点E 作//EO AB ,交BD 于点O ,连接OF则AE BO ED OD = BO BF OD FC∴= //OF CD ∴ ∴异面直线AB 和CD 所成角即为EOF ∠或其补角在EOF ∆中,223OE AB ==,113OF CD ==,又EF =222EF OE OF ∴=+ 90EOF ∴∠= ∴异面直线AB 和CD 所成角的大小为90故答案为:908.(2021·全国·高一课时练习)如图所示,AB 是圆O 的直径,点C 是弧AB 的中点,D 、E 分别是VB 、VC 的中点,求异面直线DE 与AB 所成的角.【答案】45°.【解析】因为D 、E 分别是VB 、VC 的中点,所以BC ⊥DE ,因此⊥ABC 是异面直线DE 与AB 所成的角,又因为AB 是圆O 的直径,点C 是弧AB 的中点,所以⊥ABC 是以⊥ACB 为直角的等腰直角三角形,于是⊥ABC =45°,故异面直线DE 与AB 所成的角为45°.【题组五 线面角】1(2021·黑龙江·鸡西实验中学高一期中)如图,四棱锥P ABCD -的底面ABCD 是平行四边形,PA ⊥底面ABCD ,90PCD ∠=︒,2PA AB AC ===(1)证明:AC ⊥CD ;(2)若E 是棱PC 的中点,求直线AD 与平面PCD 所成的角【答案】(1)证明见解析(2)6π【解析】(1)证明:因为PA ⊥底面ABCD ,CD ⊂底面ABCD ,所以PA CD ⊥, 因为90PCD ∠=︒,所以PC CD ⊥,PA PC P =,,PA PC ⊂平面PAC ,所以CD ⊥平面PAC ,因为AC ⊂平面PAC ,所以CD AC ⊥.(2)由(1)CD ⊥平面PAC ,,AC AE ⊂平面PAC ,所以CD AE ⊥,CD AC ⊥, 因为2PA AC ==,E 为PC 的中点,所以AE PC ⊥,因为PC CD C =,,PC CD ⊂平面PCD ,所以AE ⊥平面PCD ,所以EDA ∠即为直线AD 与平面PCD 所成的角,因为2PA AB AC ===,所以AD PC =所以12AE PC ==所以1sin 2AE EDA AD ∠===,因为0,2EDA π⎛⎫∠∈ ⎪⎝⎭,所以6EDA π∠=,即直线AD 与平面PCD 所成的角为6π; 2.(2021·全国·高一课时练习)如图,在棱长均为1的直三棱柱ABC -A 1B 1C 1中,D 是BC 的中点.(1)求证:AD ⊥平面BCC 1B 1;(2)求直线AC 1与平面BCC 1B 1所成角的正弦值.【答案】(1)证明见解析;【解析】(1)直三棱柱ABC -A 1B 1C 1中,BB 1⊥平面ABC ,⊥BB 1⊥AD ,⊥AB=AC ,D 是BC 的中点, ⊥AD ⊥BC.又BC ∩BB 1=B ,⊥AD ⊥平面BCC 1B 1.(2)连接C 1D.由(1)AD ⊥平面BCC 1B 1,则⊥AC 1D 即为直线AC 1与平面BCC 1B 1所成角.在1Rt AC D 中,AC 1sin⊥AC 1D=1AD AC =, 即直线AC 1与平面BCC 1B 13.(2021·全国·高一课时练习)如图在四棱锥P ABCD -中,底面ABCD 是边长为a 的正方形,侧面PAD ⊥底面ABCD,且PA PD =,设,E F 分别为,PC BD 的中点.(1)求证://EF 平面PAD ;(2)求证:平面PAB ⊥平面PDC ;(3)求直线EF 与平面ABCD 所成角的大小.【答案】(1)证明见解析 ;(2) 证明见解析;(3) 45︒.【解析】(1)因为四边形ABCD 为正方形,连接AC ,则,AC BD F F ⋂=为AC 中点,E 为PC 中点,所以在CPA 中//EF PA ,且PA ⊂平面PAD ,EF ⊄平面PAD ,所以//EF 平面PAD .(2)因为平面PAD ⊥平面ABCD ,平面PAD 平面ABCD AD =,且四边形ABCD 为正方形,所以,CD AD CD ⊥⊂平面ABCD ,所以CD ⊥平面PAD ,所以CD PA ⊥,又PA PD AD ==, 所以PAD △是等腰直角三角形,且90APD ∠=︒,即,PA PD CD PD D ⊥⋂=,且,CD PD ⊂平面PDC ,所以PA ⊥平面PDC ,又PA ⊂平面PAB ,所以平面PAB ⊥平面PDC .(3)因为//EF PA ,所以直线EF 与平面ABCD 所成角的大小等于直线PA 与平面ABCD 所成角的大小, 因为侧面PAD ⊥底面ABCD ,所以PAD ∠就是直线PA 与平面ABCD 所成角,在APD △中,PA PD AD ==,所以45PAD ∠=︒,所以直线EF 与平面ABCD 所成角的大小为45︒. 4.(2021·浙江·镇海中学高一期中)如图,在直三棱柱111ABC A B C -中,1111,A B B C A B AC ⊥⊥.(1)求证:1111AC B C =;(2)若1B C 与1AC 的所成角的余弦值为13,求1BB 与平面11A B C 所成角的正弦值.【答案】(1)证明见解析;【解析】(1)将棱111,,AA BB CC 分别向下延长,使得112112112,,AA A A BB B B CC C C ===, 连接212,B C AB ,如图:211//B C B C ∴,2AB 与11A B 的交点E 为11A B 的中点, 11A B B C ⊥,211//B C B C ,121A B B C ∴⊥,又11A B AC ⊥,2111AC B C C =⋂,1A B ∴⊥平面21AB C ,取1BB 的中点F ,连接EF ,1//A B EF ∴,EF ∴⊥平面21AB C ,1EF C E ∴⊥,又11C E AA ⊥,1C E ∴⊥平面22AA B B ,12C E AB ∴⊥,又E 为2AB 的中点,112C A C B ∴=,1121121122,,90C A C B CC C C C CA C C B ==∠=∠=︒, 1122C CA C C B ∴≅,22AC C B =,22112211,,AC C B AC AC C B C B ===,1111A C B C ∴=(2)由(1)知1B C 与1AC 的所成角即21B C 与1AC 的所成角,211cos 3B C A ∠=±, 取AB 的中点G ,连接BG ,1//EG BB ∴,1BB 与平面11A B C 所成的角即为EG 与平面11A B C 所成的角, 当211cos 3B C A ∠=-时, 设112C A C B x ==,则22222218233AB x x x x ⎛⎫=+-⨯-= ⎪⎝⎭,2AB x ∴=, 由(1)知2EF AB ⊥,E 为2AB 的中点,故2FA FB =, ()2223AB BF BF ∴+=,1AB ∴==,令1BB y =,则AB =,22222AB BB AB +=,)()2222y ⎫⎪⎪⎝⎭∴+=,又222x AC y =+,则)()()222222y AC y ⨯⎝⎭+=+,AC y ∴=, 又11A B C 为等腰三角形,所以111C E A B ⊥, 又11CE A B ⊥,11GE A B ⊥,易得GEC ∠为EG 与平面11A B C 所成的角,2222221194B C BC BB y y y ⎫=+=+=⎪⎪⎝⎭,22222111222B E BG AB y y ⎛⎫⎛⎫==== ⎪ ⎪ ⎪⎝⎭⎝⎭,CE y ===,CG y ==sin y CG GEC CE ∠=== 当211cos 3B C A ∠=时,设112C A C B x ==,则22222214233AB x x x x =+-⨯=,2AB ∴=,1AB ,)()2222y x ⎫⎪⎪⎝⎭∴+=,则)()()222222y AC y ⨯⎝⎭+=+,AC y ∴=,2CE y =,CG =sin GEC ∠=故1BB 与平面11A B C 5.(2021·河北邢台·高一月考)如图,在直三棱柱111ABC A B C -中,底面ABC 是BC =14AA =,D 是BC 边的中点.(1)证明:AD ⊥平面11BB C C .(2)求直线1BB 与平面1ADB 所成角的正弦值.【答案】(1)证明见解析; 【解析】(1)证明:因为AB AC =,D 为BC 的中点,所以AD BC ⊥. 又1BB ⊥平面ABC ,AD ⊂平面ABC ,则1BB AD ⊥. 因为1BC BB B =,1,BC BB ⊂平面11BB C C ,所以AD ⊥平面11BB C C ;(2)解:由(1)知,AD ⊥平面11BB C C ,1B D ⊂平面11BB C C , 所以1AD B D ⊥.可求出AD =4AB =,1B D =所以111122ADB SB D AD =⋅⋅=⨯ 11422ABD S BD AD =⋅⋅=⨯=. 设点B 到平面1ADB 的距离为d ,由11B ADB B ABD V V --=,得111133ADB ABD S d S B B⋅⋅=⋅⋅,即114433d ⨯=⨯⨯,解得d =B 到平面1ADB 设1BB 与平面1ADB 所成角为θ,则1sin d BBθ==1BB 与平面1ADB 【题组六 二面角】 1.(2021·全国·高一课时练习)如图所示,在⊥ABC 中,,AB BC SA ⊥⊥平面,ABC DE 垂直平分SC ,且分别交,AC SC 于点D ,E ,,SA AB SB BC ==,求二面角E BD C --的大小.【答案】60︒.【解析】⊥E 为SC 的中点,且SB BC =,⊥BE SC ⊥.又,DE SC BE DE E ⊥=,⊥SC ⊥面BDE ,又BD ⊂面BDE ,⊥BD SC ⊥,⊥SA ⊥面ABC ,BD ⊂面ABC ,⊥SA BD ⊥,又SC SA S =,⊥BD ⊥面SAC ,,AC DE ⊂面SAC ,即,BD AC BD DE⊥⊥,⊥EDC ∠即为二面角E BD C --的平面角.设1SA AB ==.由SA AB ⊥,得SB =在⊥ABC 中,,AB BC SB BC ⊥==AC =2SC =.在Rt SAC △中,30ACS ∠=︒,故60EDC ∠=︒,即二面角E BD C --的大小为60︒.2.(2021·广东揭东·高一期末)如图,AB 是圆O 的直径,点C 是圆O 上异于A ,B 的点,直线PC ⊥平面ABC .(1)证明:平面PBC ⊥平面PAC ;(2)若点E 是PC 的中点,在AC 上找一点F 使得直线//EF 平面PAB ,并说明理由.(3)设2AB PC ==,1AC =,求二面角B PA C --的余弦值.【答案】(1)证明见解析;(2)点F 为AC 的中点,证明见解析;. 【解析】(1)证明:AB 是圆O 的直径,BC AC ∴⊥, 又PC ⊥平面ABC ,BC ⊂平面ABC ,PC BC ∴⊥,PC AC C =,且PC ,AC ⊂平面PAC ,BC ∴⊥平面PAC ,又BC ⊂平面PBC ,∴平面PBC ⊥平面PAC ;(2)F 为AC 的中点,证明如下:证明:取AC 的中点F ,由于点E 为PC 的中点,所以//EF AP ,因为EF ⊄平面PAB ,AP ⊂平面PAB ,所以//EF 平面PAB ;(3)BC ⊥平面PAC ,PA ⊂平面PAC ,PA BC ∴⊥,过C 作CM PA ⊥于M ,连结BM ,BC CM C =,且BC ,CM ⊂平面BCM ,PA ∴⊥平面BCM ,从而得PA BM ⊥,BMC ∴∠为二面角B PA C --的平面角,在Rt BMC △中,2CM =BC =∴BM ==cos MC BMC BM ∠= ∴二面角B PA C --3.(2021·河北·衡水市第十四中学高一期末)在四棱锥P ABCD -中,90ABC ACD ∠=∠=︒,30BCA CDA ∠=∠=︒,PA ⊥平面ABCD ,E ,F 分别为PD ,PC 的中点,2PA AB =.(1)求证:平面PAC ⊥平面AEF ;(2)求二面角E AC B --的余弦值.【答案】(1)证明见解析;(2)【解析】(1)由题意,设AB a ,则2PA AC a ==,4AD a =,CD =,⊥PD =,又PA ⊥平面ABCD ,AC ⊂面ABCD ,⊥PA AC ⊥,则在Rt ⊥PAC 中,PC =,在⊥PCD 中,222CD PC PD +=,则CD AC ⊥,又CD ⊂面ABCD ,有PA CD ⊥,又AC PA A ⋂=,故有CD ⊥面PAC ,又E ,F 分别为PD ,PC 的中点,即//EF CD ,⊥EF ⊥面PAC ,又EF ⊂面AEF ,则平面PAC ⊥平面AEF ;(2)过E 作EH AD ⊥,易知H 为AD 中点,若G 是AC 中点,连接,,EH HG EG ,⊥GH AC ⊥,EH AC ⊥,GH EH H ⋂=,故AC ⊥面EHG ,即EGH ∠是二面角E AC D --的平面角, ⊥由图知:二面角E AC B --为EGH π-∠,易知//EH PA ,则EH ⊥面ABCD ,GH ⊂面ABCD ,所以EH GH ⊥,在Rt ⊥EHG 中,EH a =,GH ,则2GE a =,⊥cos EGH ∠=,则二面角E AC B --的余弦值为cos()EGH π-∠=.4.(2021·湖南·武冈市第二中学高一月考)如图,在四棱锥P ABCD -中,2AD =,1AB BC CD ===,//BC AD ,90PAD ︒∠=,PBA ∠为锐角,平面PBA ⊥平面PBD .(1)证明:PA ⊥平面ABCD ;(2)若AD 与平面PBD P BD C --的余弦值.【答案】(1)证明见解析;(2) 【解析】 (1)证明:在平面PBA 内过A 作AE PB ⊥于E ,因为平面PBA ⊥平面PBD ,又平面PBA 平面PBD PB =,所以AE ⊥平面PBD ,BD ⊂平面PBD ,所以AE BD ⊥,过,B C 分别作BM CN AD ⊥、于M N 、,取AD 中点为Q ,则=BC QD ,且//BC QD ,所以四边形BCDQ 是平行四边形,=BQ CD ,所以1QD BQ QA ===,所以90ABD ∠=︒,BD AB ⊥ ,AB AE A =,且AB AE ⊂、平面PBA ,所以BD ⊥平面PBA ,PA ⊂平面PBA所以BD PA ⊥,因为PA AD ⊥,AD BD D =,PA ⊥平面ABCD .(2)二面角P BD C --的平面角与二面角P BD A --的平面角互补,由(1)可得BD AB ⊥,BD ⊥平面PBA ,因为PB ⊂平面PBA ,所以BD PB ⊥,所以PBA ∠为二面角P BD A --的平面角,连接ED ,在Rt AED △中,ADE ∠为AD 与平面PBD 2AD =,可得AE =,因为1AB =,所以BE cos PBA ∠=,所以二面角P BD C --的余弦值为2-.5.(2021·浙江衢州·高一期末)如图,平行四边形ABCD 中,⊥BAD =60°, AB =2,AD =4,将ACBD 沿BD 翻折到⊥EBD 的位置(1)当平面EBD ⊥平面ABD 时,求证:AB ⊥DE ;(2)若点F 为BE 的中点,二面角E -BD -C 的大小为60°,求直线DF 与平面BCE 所成角的正弦值.【答案】(1)证明见解析; 【解析】(1)证明:在ABD △,⊥BAD =60°, AB =2,AD =4,所以由余弦定理得2222cos BD AB AD AB AD BAD =+-⋅∠2224224cos 6020812=+-⨯⨯︒=-=所以22212416BD AB AD +=+==,所以90ABD ∠=︒所以AB ⊥BD ,因为平面EBD ⊥平面ABD ,平面EBD ∩平面ABD =BD ,AB 平面ABD所以.AB ⊥平面EBD ,因为DE ⊂平面EBD ,所以AB ⊥DE ;(2)因为四边形ABCD 为平行四边形,所以AB ⊥CD , 因为AB ⊥BD ,所以CD ⊥BD ,ED ⊥BD ,所以二面角E - BD - C 的平面角为⊥CDE =60°, 因为DC = DE ,所以⊥CDE 为正三角形,连接CE ,取CE 中点G ,连接DG ,则DG ⊥CE ,在⊥BCE 中,BC =BE ,所以BG ⊥CE ,BG ∩DG =G ,所以CE ⊥平面DBG ,因为CE ⊂平面BCE ,所以平面BCE ⊥平面DBG , . 因为平面BCE ∩平面DBG =BG ,作DH ⊥BG ,则DH ⊥平面BCE ,连接FH , 则⊥DFH 是直线DF 与平面BCE 所成的角在⊥DFH 中,DF = 2,DH⊥sin⊥DFH6(2021·江苏连云港·高一期末)在三棱柱111ABC A B C -中,AB =11BC B C ==,145CBB CBA ∠=∠=°,160ABB ∠=︒.(1)求二面角1A B B C --的余弦值;(2)求证:平面11B BCC ⊥平面ABC .【答案】(2)证明见解析. 【解析】(1)连接1AB ,在ABC中,AB =1BC =,45CBA ∠=︒,则222121451AC =+-⨯=°,故1AC =,得222AC BC AB +=,则90ACB ∠=︒, 在1BCB △中,1BC =,11B C =,145CBB ∠=°,则145CB B ∠=°,190B CB ∠=°,1B B = 1ABB △中,AB =1B B 160B BA ∠=︒,所以1AB =1B B 的中点为D ,连接AD ,CD ,则1CD B B ⊥,1AD B B ⊥, 所以CDA ∠为平面1AB B 与平面1B BC 所成的二面角, 在CDA 中,1AC =,得CD =sin 60AD AB ==°,221cos CDA +-∠== 所以二面角1A B B C --(2)由(1)知90ACB ∠=︒,190B CB ∠=°,AC BC ⊥,1B C CB ⊥,所以平面11BCC B 与平面ABC 所成的二面角为1ACB ∠,在1ACB 中,11B C =,1AB 1AC =,所以22211AC B C AB +=,故190ACB ∠=︒,所以平面11BCC B 与平面ABC 所成的二面角为90︒, 所以平面11B BCC ⊥平面ABC .。
人教版高中数学精讲精练必修二8.6.1 空间直线、平面的垂直(精讲)(解析版)
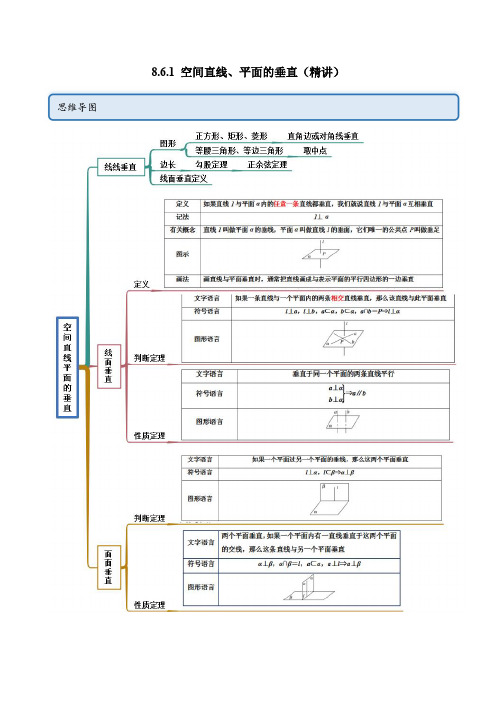
考点一 线面垂直 【例 1-1】(2022·高一课时练习)如图,正方体 ABCD A1B1C1D1 ,求证: BD1 平面 AB1C .
【答案】证明见解析 【解析】证明:∵ A1D1 平面 AA1B1B , AB1 平面 AA1B1B ∴ A1D1 AB1 ∵四边形 AA1B1B 是正方形∴ AB1 A1B 又 A1D 平面 A1BD1 , A1B 平面 A1BD1 , A1D1 A1B A1∴ AB1 平面 A1BD1 . ∵ BD1 平面 A1BD1 ∴ AB1 BD1. 同理可证: B1C BD1 . 又 AB1 平面 AB1C , B1C 平面 AB1C , AB1 B1C B1 ,∴ BD1 平面 AB1C . 【例 1-2】(2022·高一课时练习)如图,已知四棱柱 ABCD A1B1C1D1 中,各棱长都为 a ,底面 ABCD 是正方 形,顶点 A1在平面 ABCD 上的射影是正方形 ABCD 的中心,求证: A1C 平面 BDD1B1 .
【答案】证明见解析 【解析】证明:在正方形 ABCD 中, AC BD O ,则 O为 AC 、 BD 的中点,且 BD AC ,
A1O 平面 ABCD , AC 平面 ABCD , A1O AC ,则 A1C AA1 a , AC 2 AB 2a, AA12 A1C2 AC2 , A1C AA1 , 在四棱柱 ABCD A1B1C1D1 中, BB1 //AA1 , A1C BB1, A1O 平面 ABCD , BD 平面 ABCD , BD A1O , BD AC , AC A1O O , AC 、 A1O 平面 AA1C , BD 平面 AA1C , A1C 平面 AA1C , A1C BD , BB1 BD B , BD 、 BB1 平面 BDD1B1 ,因此, A1C 平面 BDD1B1 .
高中数学必修二 8 6 1 直线与直线垂直 练习(含答案)

8.6.1 直线与直线垂直一、选择题1.分别和两条异面直线相交的两条不同直线的位置关系是( )A .相交B .异面C .异面或相交D .平行【答案】C【解析】①若两条直线与两条异面直线的交点有4个,如图,直线AB 与异面直线a b ,分别相交于点A B ,,直线CD 与异面直线a b ,分别相交于点C D ,,那么A B C D ,,,四点不可能共面,否则与a b ,异面矛盾,故直线AB 与CD 异面;②若两条直线与两条异面直线的交点有3个,如图,则两条直线相交.故选:C2.在正方体1111ABCD A B C D 中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为A .2B .2CD .2【答案】C【解析】在正方体1111ABCD A B C D -中,//CD AB ,所以异面直线AE 与CD 所成角为EAB ∠, 设正方体边长为2a ,则由E 为棱1CC 的中点,可得CE a =,所以BE =,则tan 22BE EAB AB a ∠===.故选C.3.已知直三棱柱111C C AB -A B 中,C 120∠AB =,2AB =,1C CC 1B ==,则异面直线1AB 与1C B 所成角的余弦值为( )A.2 B.5 C.5 D.3【答案】C【解析】如图所示,补成直四棱柱1111ABCD A B C D -,则所求角为1111,BC D BC BD C D AB ∠=====易得22211C D BD BC =+,因此111cos BC BC D C D ∠===,故选C .4.在正方体1111ABCD A B C D -中,E 为棱CD 的中点,则( ).A .11A E DC ⊥B .1A E BD ⊥C .11AE BC ⊥ D .1A E AC ⊥【答案】C【解析】画出正方体1111ABCD A B C D -,如图所示.对于选项A ,连1D E ,若11A E DC ⊥,又111DC A D ⊥,所以1DC ⊥平面11A ED ,所以可得11DC D E ⊥,显然不成立,所以A 不正确.对于选项B ,连AE ,若1A E BD ⊥,又1BD AA ⊥,所以DB ⊥平面1A AE ,故得BD AE ⊥,显然不成立,所以B 不正确.对于选项C ,连1AD ,则11AD BC .连1A D ,则得111,AD A D AD ED ⊥⊥,所以1AD ⊥平面1A DE ,从而得11AD A E ⊥,所以11A E BC ⊥.所以C 正确.对于选项D ,连AE ,若1A E AC ⊥,又1ACAA ⊥,所以AC ⊥平面1A AE ,故得AC AE ⊥,显然不成立,所以D 不正确.故选C .5.(多选题)如图所示,在正方体1111ABCD A B C D -中,,M N 分别为棱111,C D C C 的中点,则以下四个结论正确的是( )A .直线AM 与1CC 是相交直线B .直线AM 与BN 是平行直线C .直线BN 与1MB 是异面直线D .直线AM 与1DD 是异面直线【答案】CD 【解析】直线AM 与1CC 是异面直线,直线AM 与BN 也是异面直线,故A 、B 错误直线BN 与1MB 是异面直线,直线AM 与1DD 是异面直线,故C 、D 正确.故选CD.6.(多选题)如图所示是正四面体的平面展开图,,,,G H M N 分别为,,,DE BE EF EC 的中点,在这个正四面体中,下列命题正确的是( )A .GH 与EF 平行B .BD 与MN 为异面直线C .GH 与MN 成60°角D .DE 与MN 垂直【答案】BCD 【解析】如图,把平面展开图还原成正四面体,知GH 与EF 为异面直线,A 不正确;BD 与MN 为异面直线,B 正确;//GH AD ,//MN AF ,而60DAF ∠=,60GHM ∴∠=,∴GH 与MN 成60°角,C 正确;连接,AG FG ,AG DE ⊥,FG DE ⊥DE ∴⊥平面AFG ,DE AF ∴⊥,又//MN AF∴DE 与MN 垂直,D 正确.故选:BCD二、填空题7.如图,在正方体ABCD ﹣A 1B 1C 1D 1中,E ,F ,G ,H 分别为AA 1,AB ,BB 1,B 1C 1 的中点,则异面直线EF 与GH 所成的角等于 .【答案】3π 【解析】11,EFA B GH BC ,所以异面直线EF 与GH 所成的角等于11,A B BC 所成角,11A BC ∆为正三角形,所以所成角为3π 8.已知正方体1111ABCD A B C D -中,E 为11C D 的中点,则异面直线AE 与BC 所成角的余弦值为 . 【答案】23【解析】连接DE ,设AD=2,易知AD ∥BC ,∴∠DAE 就是异面直线AE 与BC 所成角,在△RtADE 中,由于DE=,AD=2,可得AE=3,∴cos ∠DAE==.9.在直三棱柱111ABC A B C -中,90ACB ∠=,12AA =,1AC BC ==,则异面直线1A B 与1AC 所成角的余弦值是_____________.【解析】连接1AB 交1A B 于点D ,取11B C 中点E ,连接DE ,则1DE AC ,连接1A E1A DE ∴∠为异面直线1A B 与1AC 所成角在111Rt A C B 中,111AC =,1111122C E C B ==1A E ∴=同理可得12A D =,2DE =2221cos 10A DE +-∠==, ∴异面直线1A B 与1AC所成角的余弦值是1010.在正方体中,E 、F 、G 、H 分别为AA 1、AB 、BB 1、B 1C 1的中点,则所在直线与直线EF 是异面直线的是,异面直线EF 与GH 所成的角等于_____.【答案】BC ,CD ,AD ,11111111,,,,C B D A D C DD CC , 60°【解析】连接,,,由于EF ∥A 1B ,GH ∥BC 1,所以A 1B 与BC 1所成的角即为EF 与GH 所成的角,由于△A 1BC 1为正三角形,所以A 1B 与BC 1所成的角为60°,即EF 与GH 所成的角为60°.三、解答题11.空间四边形ABCD 中,2AD BC ==,,E F 分别是,AB CD 的中点,EF=求异面直线,AD BC所成的角.【答案】60【解析】设G 为AC 的中点,E 、F 分别是AB 、CD 中点//EG BC ∴且112EG BC == //FG AD 且112FG AD == EGF ∴∠为异面直线AD 、BC 所成的角(或其补角) 3EF =,EGF ∴中,1131cos 2112EGF +-∠==-⨯⨯ 120EGF ︒∴∠=, 即异面直线AD 、BC 所成的角为60︒12.如图,在四棱柱1111ABCD A B C D -中,侧面都是矩形,底面四边形ABCD 是菱形且AB BC ==,120ABC ∠=︒,若异面直线1A B 和1AD 所成的角为90︒,试求1AA 的长.【解析】连接1CD AC ,.由题意得四棱柱1111ABCD A B C D -中,11A D BC ,11A D BC =,∴四边形11A BCD 是平行四边形, 11A B CD ∴∥,1AD C ∴∠(或其补角)为1A B 和1AD 所成的角.∵异面直线1A B 和1AD 所成的角为90︒,190AD C ︒∴∠=.∵四棱柱1111ABCD A B C D -中,AB BC ==,1ACD ∴是等腰直角三角形,12AD AC ∴=.∵底面四边形ABCD 是菱形且AB BC ==,120ABC ∠=︒,sin 6026AC ︒∴=⨯=,12AD AC ==,1AA ∴===。
高中数学人教A版必修2空间中垂直关系课后练习一含解析

(同步复习精讲指导)北京市2014-2015 学年高中数学空间中的垂直关系课后练习一(含分析)新人教A版必修 2题1).在空间,以下命题正确的选项是((A)平行直线的平行投影重合(B)平行于同向来线的两个平面平行(C)垂直于同一平面的两个平面平行(D)垂直于同一平面的两条直线平行题2设平面平面,且、分别与订交于a、b,a // b.求证:平面// 平面.题3如图, P是ABC 所在平面外的一点,且PA 平面 ABC ,平面 PAC平面 PBC .求证 BC AC.题4已知在长方体ABCD A1B1C1D1中,棱 AA1 5 ,AB12 ,过点B1作B1E A1B 于E,证明 B1E平面A1BCD1,并求其长度.题5在正方体 ABCD A1B1C1D1中,E是 BB1的中点,O是底面正方形ABCD 的中心.求证: OE平面ACD1.题6如图,圆柱的轴截面ABCD 是正方形,点 E 在底面圆周上, AF DE , F 是垂足,求证:AF DB .题7如下图, P是四边形 ABCD所在平面外的一点, ABCD是∠ DAB=60°且边长为 a的菱形.侧面PAD为正三角形,其所在平面垂直于底面 ABCD.(1)若 G为 AD边的中点,求证: BG⊥平面 PAD;(2)求证: AD⊥ PB.题8已知在四棱锥 P- ABCD中,底面 ABCD是边长为4的正方形,△ PAD是正三角形,平面 PAD⊥平面 ABCD, E、 F、 G分别是 PD、 PC、 BC的中点.(I )求证:PA// 平面EFG;(II )求平面EFG 平面 PAD.题9如图,在长方形 ABCD中, AB=2,BC=1,E为 DC的中点, F为线段 EC(端点除外)上一动点.现将△ AFD沿 AF折起,使平面 ABD⊥平面 ABC.在平面 ABD内过点 D作DK⊥ AB,K为垂足.设AK= t ,则t 的取值范围是__________.题10如图, BC是Rt△ ABC的斜边, AP⊥平面 ABC,PD⊥ BC于 D点,则图中共有直角三角形的个数是() .A.8B.7C.6D.5课后练习详解题1答案: D.详解:由空间直线与平面的地点关系及线面垂直与平行的判断与性质定理能够很简单得出答案.平行直线的平行投影重合,还可能平行, A 错误;平行于同向来线的两个平面平行,两个平面可能订交,B错误;垂直于同一平面的两个平面平行,可能订交, C 错误.题2答案:见详解.证明:在平面内作直线 a 的垂线 l1,垂足为A,由于,平面平面,平面I 平面=a,因此l1在平面内作直线 b 的垂线l2,垂足为 B ,同理可证得l2l1 // l 2,又 Q l1,l 2, l1 //Q a // b a,b, a //Q l1 I a A, l1, a//题3答案:见详解.详解:在平面PAC 内作 AD PC,交 PC于D.由于平面 PAC平面 PBC 于 PC, AD平面 PAC ,且 AD PC ,因此 AD平面 PBC .又由于于是有BC 平面 PBC ,AD BC ①.此外因此PA 平面 ABC , BC平面ABC,PA BC ②.由①②及 AD PA A ,可知由于因此题4BC 平面 PAC .AC 平面 PAC ,BC AC .答案: B1E 60 13详解:∵ BC平面 A1 ABB1,且 B1 E平面 AA1 B1 B ,∴ BC B1 E ,又 B1E A1B ,又 BC A1B B ,∴ B1E平面 A1BCD1.A 1B 1 BB 15 1260,∴ BE60 在 Rt A 1 B 1 B 中, B 1 E.A 1 B52 12 2 13 113题5证明 : 连结 AE 、CE , D 1O ,设正方体 DB 1 的棱长为 a ,易证 AE CE .又∵ AO OC ,∴ OE AC .在正方体 DB 1中易求出:2D 1ODD 12DO2a22 a6a ,2222OEBE2OB2a2 a3a ,222D 1 ED 1B 12B 1E22a23a .2a22∵ D 1O 2 OE 2 D 1E 2 ,∴ D 1O OE .∵ D 1O ACO ,D 1O 、AC平面 ACD 1 ,∴ OE平面 ACD 1 .题6答案:见详解.详解:由 DA底面 ABE ,知 DABE ;又 E 为底面圆周上一点, AB 为底面圆直径,知 BE AE ,故 BE 平面 ADE ,则 BE AF ,又 AF DE ,则 AF 平面 BDE ,则 AF DB .题7答案:见详解.详解: (1) 连结 PG ,由题知△ PAD 为正三角形, G 是 AD 的中点,∴ PG ⊥AD . 又平面 PAD ⊥平面 ABCD ,∴PG ⊥平面 ABCD ,∴ PG ⊥BG .又∵四边形 ABCD 是菱形且∠ DAB =60°, ∴△ ABD 是正三角形,∴ B G ⊥AD . 又AD ∩ PG =G ,∴ BG ⊥平面 PAD .(2) 由 (1) 可知 BG ⊥ AD , PG ⊥ AD .因此 AD ⊥平面 PBG ,因此 AD ⊥PB .题8答案:见详解.详解:证明:( I )取AD的中点H,连结EH,HG.∵H, G为 AD, BC的中点,∴ HG// CD,又 EF// CD.∴ EF// HG,∴ E,F, G,H四点共面,又∵PA//EH,EH 平面EFGH,PA 平面EFGH,∴PA//平面 EFG.(II )证明:AD CD, PD CD ,∴ CD 平面PAD,∵EF// CD,∴EF平面 PAD,∵EF 平面EFG,∴平面EFG平面PAD.题91答案: ( 2,1)详解:过 K 作 KM⊥ AF于 M点,连结 DM,易得 DM⊥ AF,与折前的图形对照,可知由折前的图形中 D、M、 K 三点共线且DK⊥ AF,于是△ DAK∽△ FDA,∴AK AD t11=,又=,∴ t =.又AD DF1DF DF1DF∈(1,2),∴ t ∈(2,1) .题10答案: A.详解:所给图形中的△ PAC、△ PAD、△ PAB、△ PCD、△ PBD、△ ACD、△ ADB、△ ABC 均为直角三角形,因此共有 8 个直角三角形.。
高中数学(人教版必修2)配套练习 第二章2.3直线、平面垂直的判定及其性质试题解析

§2.3直线、平面垂直的判定及其性质2.3.1直线与平面垂直的判定一、基础过关1.已知直线a∥b,平面α∥β,a⊥α,则b与β的位置关系是() A.b⊥βB.b∥βC.b⊂βD.b⊂β或b∥β2.直线a⊥直线b,b⊥平面β,则a与β的关系是() A.a⊥βB.a∥βC.a⊂βD.a⊂β或a∥β3.空间四边形ABCD的四边相等,则它的两对角线AC、BD的关系是() A.垂直且相交B.相交但不一定垂直C.垂直但不相交D.不垂直也不相交4.如图所示,定点A和B都在平面α内,定点P∉α,PB⊥α,C是平面α内异于A和B的动点,且PC⊥AC,则△ABC为()A.锐角三角形B.直角三角形C.钝角三角形D.无法确定5. 在正方体ABCD-A 1B1C1D1中,(1)直线A1B与平面ABCD所成的角是________;(2)直线A1B与平面ABC1D1所成的角是________;(3)直线A1B与平面AB1C1D所成的角是______.6. 如图所示,在正方体ABCD-A1B1C1D1中,M、N分别是棱AA1和AB上的点,若∠B1MN是直角,则∠C1MN=______.7.如图所示,在正方体ABCD—A1B1C1D1中,E、F分别是棱B1C1、B1B的中点.求证:CF⊥平面EAB.8. 如图所示,在四棱锥P—ABCD中,底面ABCD是矩形,侧棱P A垂直于底面,E、F分别是AB、PC的中点,P A=AD.求证:(1)CD⊥PD;(2)EF⊥平面PCD.二、能力提升9. 如图所示,P A⊥平面ABC,△ABC中BC⊥AC,则图中直角三角形的个数为()A.4 B.3 C.2 D.110.已知矩形ABCD,AB=1,BC=2,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折过程中() A.存在某个位置,使得直线AC与直线BD垂直B.存在某个位置,使得直线AB与直线CD垂直C.存在某个位置,使得直线AD与直线BC垂直D.对任意位置,三对直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直11.在直三棱柱ABC—A1B1C1中,BC=CC1,当底面A1B1C1满足条件________时,有AB1⊥BC1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情况).12. 如图所示,在正方体ABCD-A1B1C1D1中,P为DD1的中点,O为ABCD的中心,求证:B1O⊥平面P AC.三、探究与拓展13.已知平面α外两点A、B到平面α的距离分别为1和2,A、B两点在α内的射影之间距离为3,求直线AB和平面α所成的角.答案1.A 2.D 3.C 4.B 5.(1)45° (2)30° (3)90° 6.90°7.证明 在平面B 1BCC 1中, ∵E 、F 分别是B 1C 1、B 1B 的中点, ∴△BB 1E ≌△CBF , ∴∠B 1BE =∠BCF ,∴∠BCF +∠EBC =90°,∴CF ⊥BE , 又AB ⊥平面B 1BCC 1,CF ⊂平面B 1BCC 1, ∴AB ⊥CF ,又AB ∩BE =B , ∴CF ⊥平面EAB .8.证明 (1)∵P A ⊥底面ABCD , ∴CD ⊥P A .又矩形ABCD 中,CD ⊥AD ,且AD ∩P A =A ,∴CD ⊥平面P AD ,∴CD ⊥PD .(2)取PD 的中点G ,连接AG ,FG .又∵G 、F 分别是PD 、PC 的中点,∴GF 綊12CD ,∴GF 綊AE ,∴四边形AEFG 是平行四边形,∴AG ∥EF . ∵P A =AD ,G 是PD 的中点, ∴AG ⊥PD ,∴EF ⊥PD , ∵CD ⊥平面P AD ,AG ⊂平面P AD . ∴CD ⊥AG .∴EF ⊥CD .∵PD ∩CD =D ,∴EF ⊥平面PCD . 9.A 10.B 11.∠A 1C 1B 1=90°12.证明 连接AB 1,CB 1,设AB =1.∴AB 1=CB 1=2,∵AO =CO ,∴B 1O ⊥AC .连接PB 1.∵OB 21=OB 2+BB 21=32, PB 21=PD 21+B 1D 21=94, OP 2=PD 2+DO 2=34,∴OB 21+OP 2=PB 21.∴B 1O ⊥PO ,又∵PO ∩AC =O ,∴B 1O ⊥平面P AC .13.解 (1)如图①,当A 、B 位于平面α同侧时,由点A 、B 分别向平面α作垂线,垂足分别为A 1、B 1,则AA 1=1,BB 1=2,B 1A 1= 3.过点A 作AH ⊥BB 1于H ,则AB 和α所成角即为∠HAB .而tan ∠BAH =2-13=33.∴∠BAH =30°.(2)如图②,当A 、B 位于平面α异侧时,经A 、B 分别作AA 1⊥α于A 1,BB 1⊥α于B 1,AB ∩α=C ,则A 1B 1为AB 在平面α上的射影,∠BCB 1或∠ACA 1为AB 与平面α所成 的角.∵△BCB 1∽△ACA 1, ∴BB 1AA 1=B 1C CA 1=2, ∴B 1C =2CA 1,而B 1C +CA 1=3,∴B 1C =233.∴tan ∠BCB 1=BB 1B 1C =2233=3,∴∠BCB 1=60°.综合(1)、(2)可知:AB 与平面α所成的角为30°或60°.2.3.2 平面与平面垂直的判定一、基础过关1.过两点与一个已知平面垂直的平面( )A .有且只有一个B .有无数个C .一个或无数个D .可能不存在 2.不能肯定两个平面一定垂直的情况是( )A .两个平面相交,所成二面角是直二面角B .一个平面经过另一个平面的一条垂线C .一个平面垂直于另一个平面内的一条直线D .平面α内的直线a 与平面β内的直线b 是垂直的 3.设有直线m 、n 和平面α、β,则下列结论中正确的是( )①若m ∥n ,n ⊥β,m ⊂α,则α⊥β; ②若m ⊥n ,α∩β=m ,n ⊂α,则α⊥β; ③若m ⊥α,n ⊥β,m ⊥n ,则α⊥β. A .①②B .①③C .②③D .①②③ 4.设l 是直线,α,β是两个不同的平面,下列结论中正确的是( )A .若l ∥α,l ∥β,则α∥βB .若l ∥α,l ⊥β,则α⊥βC .若α⊥β,l ⊥α,则l ⊥βD .若α⊥β,l ∥α,则l ⊥β5.过正方形ABCD 的顶点A 作线段AP ⊥平面ABCD ,且AP =AB ,则平面ABP 与平面CDP 所成的二面角的度数是________.6.如图所示,已知P A ⊥矩形ABCD 所在的平面,图中互相垂直的平面有________对.7.在如图所示的几何体中,四边形ABCD 是正方形,MA ⊥平面ABCD ,PD ∥MA ,E 、G 、F 分别为MB 、PB 、PC 的中点,且AD =PD =2MA .求证:平面EFG ⊥平面PDC . 8. 如图所示,四棱锥P —ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的中点,P A ⊥底面ABCD ,P A = 3.(1)证明:平面PBE ⊥平面P AB ; (2)求二面角A —BE —P 的大小. 二、能力提升9.在边长为1的菱形ABCD 中,∠ABC =60°,把菱形沿对角线AC 折起,使折起后BD =32,则二面角B -AC -D 的余弦值为( )A.13B.12C.223D.32 10.在正四面体P -ABC 中,D 、E 、F 分别是AB 、BC 、CA 的中点,下面四个结论中不成立的是( )A .BC ∥面PDFB .DF ⊥面P AEC .面PDF ⊥面ABCD .面P AE ⊥面ABC11.如图,在直三棱柱ABC —A 1B 1C 1中,E 、F 分别是A 1B 、A 1C 的中点,点D在B1C1上,A1D⊥B1C.求证:(1)EF∥平面ABC;(2)平面A1FD⊥平面BB1C1C.12.如图,在三棱锥P—ABC中,P A⊥底面ABC,P A=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.(1)求证:BC⊥平面P AC.(2)是否存在点E使得二面角A—DE—P为直二面角?并说明理由.三、探究与拓展13.如图所示,三棱锥P—ABC中,D是AC的中点,P A=PB=PC=5,AC=22,AB=2,BC= 6.(1)求证:PD⊥平面ABC;(2)求二面角P—AB—C的正切值.答案1.C 2.D 3.B 4.B5.45°6.57.证明因为MA⊥平面ABCD,PD∥MA,所以PD⊥平面ABCD.又BC⊂平面ABCD,所以PD⊥BC.因为四边形ABCD为正方形,所以BC⊥DC.又PD∩DC=D,所以BC⊥平面PDC.在△PBC中,因为G、F分别为PB、PC的中点,所以GF∥BC,所以GF⊥平面PDC.又GF⊂平面EFG,所以平面EFG⊥平面PDC.8.(1)证明如图所示,连接BD,由ABCD是菱形且∠BCD=60°知,△BCD是等边三角形.因为E是CD的中点,所以BE⊥CD.又AB∥CD,所以BE⊥AB.又因为P A⊥平面ABCD,BE⊂平面ABCD,所以P A⊥BE.而P A∩AB=A,因此BE⊥平面P AB.又BE⊂平面PBE,所以平面PBE⊥平面P AB.(2)解由(1)知,BE⊥平面P AB,PB⊂平面P AB,所以PB⊥BE.又AB⊥BE,所以∠PBA是二面角A—BE—P的平面角.在Rt△P AB中,tan∠PBA=P AAB=3,则∠PBA=60°.故二面角A—BE—P的大小是60°.9.B 10.C11.证明(1)由E、F分别是A1B、A1C的中点知EF∥BC.因为EF⊄平面ABC,BC⊂平面ABC.所以EF∥平面ABC.(2)由三棱柱ABC—A1B1C1为直三棱柱知CC1⊥平面A1B1C1.又A1D⊂平面A1B1C1,故CC1⊥A1D.又因为A1D⊥B1C,CC1∩B1C=C,故A1D⊥平面BB1C1C,又A1D⊂平面A1FD,所以平面A1FD⊥平面BB1C1C.12.(1)证明∵P A⊥底面ABC,∴P A⊥BC.又∠BCA=90°,∴AC⊥BC.又∵AC∩P A=A,∴BC⊥平面P AC.(2)解∵DE∥BC,又由(1)知,BC⊥平面P AC,∴DE⊥平面P AC.又∵AE⊂平面P AC,PE⊂平面P AC,∴DE⊥AE,DE⊥PE.∴∠AEP为二面角A—DE—P的平面角.∵P A⊥底面ABC,∴P A⊥AC,∴∠P AC=90°.∴在棱PC上存在一点E,使得AE⊥PC.这时∠AEP=90°,故存在点E,使得二面角A—DE—P为直二面角.13.(1)证明连接BD,∵D是AC的中点,P A=PC=5,∴PD⊥AC.∵AC=22,AB=2,BC=6,∴AB 2+BC 2=AC 2.∴∠ABC =90°,即AB ⊥BC .∴BD =12AC =2=AD .∵PD 2=P A 2-AD 2=3,PB =5, ∴PD 2+BD 2=PB 2.∴PD ⊥BD . ∵AC ∩BD =D ,∴PD ⊥平面ABC .(2)解 取AB 的中点E ,连接DE 、PE ,由E 为AB 的中点知DE ∥BC , ∵AB ⊥BC ,∴AB ⊥DE . ∵PD ⊥平面ABC ,∴PD ⊥AB .又AB ⊥DE ,DE ∩PD =D ,∴AB ⊥平面PDE ,∴PE ⊥AB . ∴∠PED 是二面角P —AB —C 的平面角.在△PED 中,DE =12BC =62,PD =3,∠PDE =90°,∴tan ∠PED =PDDE = 2.∴二面角P —AB —C 的正切值为 2.2.3.3 直线与平面垂直的性质 2.3.4 平面与平面垂直的性质一、基础过关1.已知两个平面互相垂直,那么下列说法中正确的个数是( )①一个平面内的直线必垂直于另一个平面内的无数条直线;②一个平面内垂直于这两个平面交线的直线必垂直于另一个平面内的任意一条直线; ③过一个平面内一点垂直于另一个平面的直线,垂足必落在交线上; ④过一个平面内的任意一点作交线的垂线,则此直线必垂直于另一个平面. A .4B .3C .2D .1 2.在圆柱的一个底面上任取一点(该点不在底面圆周上),过该点作另一底面的垂线,则这条垂线与圆柱的母线所在直线的位置关系是( ) A .相交B .平行C .异面D .相交或平行3.若m 、n 表示直线,α表示平面,则下列命题中,正确命题的个数为( )①⎭⎪⎬⎪⎫m ∥n m ⊥α⇒n ⊥α; ② ⎭⎪⎬⎪⎫m ⊥αn ⊥α⇒m ∥n ; ③⎭⎪⎬⎪⎫m ⊥αn ∥α⇒m ⊥n; ④⎭⎪⎬⎪⎫m ∥αm ⊥n ⇒n ⊥α.A .1B .2C .3D .4 4.在△ABC 所在的平面α外有一点P ,且P A =PB =PC ,则P 在α内的射影是△ABC 的( )A .垂心B .内心C .外心D .重心5. 如图所示,AF ⊥平面ABCD ,DE ⊥平面ABCD ,且AF =DE ,AD =6,则EF =________.6.若α⊥β,α∩β=AB,a∥α,a⊥AB,则a与β的关系为________.7. 如图,在三棱锥P-ABC中,P A⊥平面ABC,平面P AB⊥平面PBC.求证:BC⊥AB.8. 如图所示,在正方体ABCD—A 1B1C1D1中,M是AB上一点,N是A1C的中点,MN⊥平面A1DC.求证:(1)MN∥AD1;(2)M是AB的中点.二、能力提升9. 如图所示,平面α⊥平面β,A∈α,B∈β,AB与两平面α、β所成的角分别为π4和π6.过A、B分别作两平面交线的垂线,垂足分别为A′、B′,则AB∶A′B′等于()A.2∶1 B.3∶1 C.3∶2 D.4∶310.设α-l-β是直二面角,直线a⊂α,直线b⊂β,a,b与l都不垂直,那么() A.a与b可能垂直,但不可能平行B.a与b可能垂直,也可能平行C.a与b不可能垂直,但可能平行D.a与b不可能垂直,也不可能平行11.直线a和b在正方体ABCD-A1B1C1D1的两个不同平面内,使a∥b成立的条件是________.(只填序号)①a和b垂直于正方体的同一个面;②a和b在正方体两个相对的面内,且共面;③a和b平行于同一条棱;④a和b在正方体的两个面内,且与正方体的同一条棱垂直.12.如图所示,在多面体P—ABCD中,平面P AD⊥平面ABCD,AB∥DC,△P AD是等边三角形,已知BD=2AD=8,AB=2DC=4 5.(1)设M是PC上的一点,求证:平面MBD⊥平面P AD;(2)求四棱锥P—ABCD的体积.三、探究与拓展13.如图,直三棱柱ABC -A 1B 1C 1中,AC =BC =12AA 1,D 是棱AA 1的中点,DC 1⊥BD . (1)证明:DC 1⊥BC ;(2)求二面角A 1-BD -C 1的大小.答案1.B 2.B 3.C 4.C 5.6 6.a ⊥β7.证明 在平面P AB 内,作AD ⊥PB 于D . ∵平面P AB ⊥平面PBC , 且平面P AB ∩平面PBC =PB . ∴AD ⊥平面PBC . 又BC ⊂平面PBC , ∴AD ⊥BC .又∵P A ⊥平面ABC , BC ⊂平面ABC ,∴P A ⊥BC ,∴BC ⊥平面P AB . 又AB ⊂平面P AB , ∴BC ⊥AB .8.证明 (1)∵ADD 1A 1为正方形, ∴AD 1⊥A 1D .又∵CD ⊥平面ADD 1A 1, ∴CD ⊥AD 1. ∵A 1D ∩CD =D , ∴AD 1⊥平面A 1DC . 又∵MN ⊥平面A 1DC , ∴MN ∥AD 1.(2)连接ON ,在△A 1DC 中,A 1O =OD ,A 1N =NC .∴ON 綊12CD 綊12AB , ∴ON ∥AM .又∵MN ∥OA ,∴四边形AMNO 为平行四边形,∴ON =AM .∵ON =12AB ,∴AM =12AB , ∴M 是AB 的中点.9.A 10.C11.①②③12.(1)证明 在△ABD 中,∵AD =4,BD =8,AB =45,∴AD 2+BD 2=AB 2.∴AD ⊥BD .又∵面P AD ⊥面ABCD ,面P AD ∩面ABCD =AD ,BD ⊂面ABCD , ∴BD ⊥面P AD ,又BD ⊂面BDM ,∴面MBD ⊥面P AD .(2)解 过P 作PO ⊥AD ,∵面P AD ⊥面ABCD ,∴PO ⊥面ABCD ,即PO 为四棱锥P —ABCD 的高.又△P AD 是边长为4的等边三角形,∴PO =2 3.在底面四边形ABCD 中,AB ∥DC ,AB =2DC ,∴四边形ABCD 为梯形.在Rt △ADB 中,斜边AB 边上的高为4×845=855, 此即为梯形的高.∴S 四边形ABCD =25+452×855=24. ∴V P —ABCD =13×24×23=16 3. 13.(1)证明 由题设知,三棱柱的侧面为矩形.由于D 为AA 1的中点,故DC =DC 1.又AC =12AA 1,可得DC 21+DC 2=CC 21,所以DC 1⊥DC .而DC 1⊥BD ,CD ∩BD =D ,所以DC 1⊥平面BCD .因为BC ⊂平面BCD ,所以DC 1⊥BC .(2)解 DC 1⊥BC ,CC 1⊥BC ⇒BC ⊥平面ACC 1A 1⇒BC ⊥AC ,取A 1B 1的中点O ,过点O 作OH ⊥BD 于点H ,连接C 1O ,C 1H ,A 1C 1=B 1C 1⇒C 1O ⊥A 1B 1,面A 1B 1C 1⊥面A 1BD ⇒C 1O ⊥面A 1BD ,又∵DB ⊂面A 1DB ,∴C 1O ⊥BD ,又∵OH ⊥BD ,∴BD ⊥面C 1OH ,C 1H ⊂面C 1OH ,∴BD ⊥C 1H ,得点H 与点D 重合,且∠C 1DO是二面角A1-BD-C的平面角,设AC=a,则C1O=22a,C1D=2a=2C1O⇒∠C1DO=30°,故二面角A1-BD-C1的大小为30°.。
新教材人教A版高中数学必修第二册:8.6.1直线与直线垂直 课时练习

8.6.1 直线与直线垂直一、选择题1.已知a和b是成60°角的两条异面直线,则过空间一点且与a、b都成60°角的直线共有( )A.1条B.2条C.3条 D.4条解析:把a平移至a′与b相交,其夹角为60°.60°角的补角的平分线c与a、b成60°角.过空间这一点作直线c的平行线即满足条件.又在60°角的“平分面”上还有两条满足条件,故选C.答案:C2.在正方体ABCDA1B1C1D1中,E为棱CC1的中点,则异面直线AE与CD所成角的正切值为( )A.22B.32C.52D.72解析:本题主要考查异面直线所成的角.因为CD∥AB,所以∠BAE即为异面直线AE与CD所成的角.设正方体的棱长为2,连接BE,则BE= 5.因为AB⊥平面BB1C1C,所以AB⊥BE.在Rt△ABE中,tan∠BAE=BEAB =52.故选C.答案:C3.在三棱柱ABC-A1B1C1中,AA1⊥AB,AA1⊥AC.若AB=AC=AA1=1,BC=2,则异面直线A1C与B1C1所成的角为( )A.30° B.45°C.60° D.90°解析:由题意可知BC∥B1C1,故A1C与B1C1所成的角即BC与A1C所成的角,连接A1B,在△A1BC中,BC=A1C=A1B=2,故∠A1CB=60°.则异面直线A1C与B1C1所成的角为60°.答案:C4.如图在正三棱柱ABC-A1B1C1中,若AB=2BB1,则AB1与BC1所成的角的大小是( )A.60° B.75°C.90° D.105°解析:设BB1=1,如题图,延长CC1至点C2,使C1C2=CC1=1,连接B1C2,则B1C2∥BC1,所以∠AB1C2为AB1与BC1所成的角(或其补角).连接AC2,易知AB1=3,B1C2=3,AC2=6,所以AC22=AB21+B1C22,则∠AB1C2=90°.答案:C二、填空题5.在正方体ABCD-A1B1C1D1中,求:(1)直线AB与A1D1所成的角为________;(2)直线AD1与DC1所成的角为________.解析:(1)∵A1B1∥AB,∴∠D1A1B1就是异面直线AB与A1D1所成的角.∵∠D1A1B1=90°,∴直线AB与A1D1所成的角为90°.(2)如图,连接AB1,B1D1.∵AB1∥DC1,∴直线AB1与AD1所成的角即直线DC1与AD1所成的角.又AD1=AB1=B1D1,∴△AB1D1为正三角形,∴直线AD1与AB1所成的角为60°,即直线AD1与DC1所成的角为60°.答案:(1)90°(2)60°6.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为A1A,AB,BB1,B1C1的中点,则异面直线EF与GH所成的角等于________.解析:取A 1B 1的中点M ,连接MG ,MH ,则MG ∥EF ,MG 与GH 所成的角等于EF 与GH 所成的角. 易知△MGH 为正三角形,∠MGH =60°, ∴EF 与GH 所成的角等于60°. 答案:60°7.在三棱锥A -BCD 中,AB =AC =BD =CD =3,AD =BC =2,点M ,N 分别为AD ,BC 的中点,则异面直线AN ,CM 所成的角的余弦值是________.解析:如图,连接DN ,取DN 的中点P ,连接PM ,PC ,由M 为AD 的中点,可知PM ∥AN ,∠PMC 即为异面直线AN ,CM 所成的角(或其补角).∵AB =AC =3,BC =2,N 为BC 的中点,∴AN =32-12=22,易得PM =12AN = 2.∵CD =BD =3,∴DN =32-12=22,PN =12DN =2,易得PC =PN 2+CN 2=2+1= 3.∵AC =CD =3,M 为AD 的中点,∴CM =32-12=2 2.在△PMC 中,过点P 作PQ ⊥MC 于点Q ,则PM 2-MQ 2=PC 2-QC 2,即(2)2-MQ 2=(3)2-(22-MQ )2,解得MQ=742,则cos∠PMC =MQ PM =7422=78.即异面直线AN ,CM 所成的角的余弦值为78.答案:78三、解答题8.如图,已知空间四边形ABCD 中,AD =BC ,M ,N 分别为AB ,CD 的中点,且直线BC 与MN 所成的角为30°,求BC 与AD 所成的角.解析:连接BD ,并取其中点E ,连接EN ,EM ,则EN ∥BC ,ME ∥AD ,故∠ENM (或其补角)为BC 与MN 所成的角,∠MEN (或其补角)为BC 与AD 所成的角.由AD =BC ,知ME =EN ,∴∠EMN =∠ENM =30°,∴∠MEN =180°-30°-30°=120°,即BC 与AD 所成的角为60°.9.如图,在空间四边形ABCD 中,AD =BC =2,E ,F 分别是AB 、CD 的中点,若EF =3,求异面直线AD 、BC 所成角的大小.解析:如图,取BD 的中点M ,连接EM ,FM .因为E 、F 分别是AB 、CD 的中点,所以EM 綊12AD ,FM 綊12BC ,则∠EMF 或其补角就是异面直线AD 、BC 所成的角.因为AD=BC=2,所以EM=MF=1,在等腰△MEF中,过点M,作MH⊥EF于H,在Rt△MHE中,EM=1,EH=12EF=32,则sin∠EMH=32,于是∠EMH=60°,则∠EMF=2∠EMH=120°.所以异面直线AD、BC所成的角为∠EMF的补角,即直线AD、BC所成的角为60°.[尖子生题库]10.如图,在五面体ABCDEF中,四边形ADEF是正方形,ED⊥CD,CD=1,AD=22,求异面直线CE与AF所成的角的余弦值.解析:因为四边形ADEF 是正方形,所以FA ∥ED .因为ED ⊥CD ,所以∠CED 为锐角,则∠CED 为异面直线CE 与AF 所成的角. 在Rt△CDE 中,CD =1,ED =AD =22,CE =CD 2+ED 2=3, 所以cos∠CED =ED CE =223.所以异面直线CE 与AF 所成的角的余弦值为223.。
【课堂新坐标】高中数学人教版必修二练习:3.1.2两条直线平行与垂直的判定(含答案解析)

【课堂新坐标】高中数学人教版必修二练习:3.1.2两条直线平行与垂直的判定(含答案解析)学业分层测评(十六)(建议用时:45分钟)[达标必做]一、选择题1.若l1与l2为两条直线,它们的倾斜角分别为α1,α2,斜率分别为k1,k2,有下列说法:①若l1∥l2,则斜率k1=k2;②若斜率k1=k2,则l1∥l2;③若l1∥l2,则倾斜角α1=α2;④若倾斜角α1=α2,则l1∥l2.其中正确说法的个数是()A.1B.2C.3 D.4【解析】需考虑两条直线重合的情况,②④都可能是两条直线重合,所以①③正确.【答案】 B2.已知过(-2,m)和(m,4)两点的直线与斜率为-2的直线平行,则m的值是() A.-8 B.0C.2 D.10【解析】由题意知m≠-2,m-4-2-m=-2,得m=-8.【答案】 A3.若点A(0,1),B(3,4)在直线l1上,l1⊥l2,则直线l2的倾斜角为() A.-30°B.30°C.150°D.120°【解析】k AB=4-13-0=3,故l1的倾斜角为60°,l1⊥l2,所以l2的倾斜角为150°,故选C.【答案】 C4.以A(-1,1),B(2,-1),C(1,4)为顶点的三角形是() A.锐角三角形B.钝角三角形C.以A点为直角顶点的直角三角形D .以B 点为直角顶点的直角三角形【解析】∵k AB =-1-12+1=-23,k AC =4-11+1=32,∴k AB ·k AC =-1,∴AB ⊥AC ,∠A 为直角.【答案】 C5.设点P (-4,2),Q (6,-4),R (12,6),S (2,12),则下面四个结论:①PQ ∥SR ;②PQ ⊥PS ;③PS ∥QS ;④RP ⊥QS .正确的个数是( )A .1B .2C .3D .4 【解析】∵k PQ =-4-26+4=-35,k SR =12-62-12=-35, k PS =12-22+4=53,k QS =12+42-6=-4,k PR =6-212+4=14 . 又P 、Q 、S 、R 四点不共线,∴PQ ∥SR ,PS ⊥PQ ,RP ⊥QS .故①②④正确.【答案】 C二、填空题6.已知直线l 1过点A (-2,3),B (4,m ),直线l 2过点M (1,0),N (0,m -4),若l 1⊥l 2,则常数m 的值是______.【导学号:09960101】【解析】由l 1⊥l 2,得k AB ·k MN =-1,所以m -34--·m -40-1=-1,解得m =1或6. 【答案】 1或67.已知长方形ABCD 的三个顶点的坐标分别为A (0,1),B (1,0),C (3,2),则第四个顶点D 的坐标为________.【解析】设D 点坐标为(x ,y ),∵四边形ABCD 为长方形,∴AB ∥CD ,AD ∥BC ,即y -2x -3=-1,① y -1x =1,②联立①②解方程组得x =2,y =3,所以顶点D 的坐标为(2,3).【答案】 (2,3)三、解答题8.(2016·泰安高一检测)已知A ?1,-a +13,B 0,-13,C (2-2a,1),D (-a,0)四点,当a 为何值时,直线AB 和直线CD 垂直?【解】 k AB =-13+a +130-1=-a 3,k CD =0-1-a -2+2a =12-a(a ≠2).由-a 3×12-a =-1,解得a =32. 当a =2时,k AB =-23,直线CD 的斜率不存在.∴直线AB 与CD 不垂直.∴当a =32时,直线AB 与CD 垂直. 9.已知在?ABCD 中,A (1,2),B (5,0),C (3,4).(1)求点D 的坐标;(2)试判断?ABCD 是否为菱形.【解】(1)设D (a ,b ),由四边形为平行四边形,得k AB =k CD ,k AD =k BC ,即 0-25-1=b -4a -3,b -2a -1=4-03-5,解得a =-1,b =6,所以D (-1,6).(2)因为k AC =4-23-1=1,k BD =6-0-1-5=-1,所以k AC ·k BD =-1,所以AC ⊥BD ,故?ABCD 为菱形.[自我挑战]10.已知两点A (2,0),B (3,4),直线l 过点B ,且交y 轴于点C (0,y ),O 是坐标原点,有O ,A ,B ,C 四点共圆,那么y 的值是( )A .19 B.194C .5D .4【解析】由题意知AB ⊥BC ,∴k AB ·k BC =-1,即4-03-2×4-y 3-0=-1,解得y =194,故选B. 【答案】 B。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
必修2 空间中的垂直关系基础知识点一、选择题:1.若斜线段AB是它在平面α上的射影的长的2倍,则AB与平面α所成的角是( ).A.60°B.45°C.30°D.120°2.直线l⊥平面α,直线m⊂α,则( ).A.l⊥mB.l∥mC.l,m异面D.l,m相交而不垂直3.如图所示,PO⊥平面ABC,BO⊥AC,在图中与AC垂直的线段有( ).A.1条B.2条C.3条D.4条4.若平面α⊥平面β,平面β⊥平面γ,则( ).A.α∥γB.α⊥γC.α与γ相交但不垂直D.以上都有可能5.已知长方体ABCDA1B1C1D1,在平面AB1上任取一点M,作ME⊥AB于E,则( ).A.ME⊥平面ACB.ME ⊂平面ACC.ME∥平面ACD.以上都有可能6.如图,设P是正方形ABCD外一点,且PA⊥平面ABCD,则平面PAB与平面PBC、平面PAD的位置关系是( ).A.平面PAB与平面PBC、平面PAD都垂直B.它们两两垂直C.平面PAB与平面PBC垂直,与平面PAD不垂直D.平面PAB与平面PBC、平面PAD都不垂直二、填空题:7.在正方体A1B1C1D1ABCD中,E,F分别是棱AB,BC的中点,O是底面ABCD的中心(如图),则EF与平面BB1O的关系是________.8.若a,b表示直线,α表示平面,下列命题中正确的有________个.①a⊥α,b∥α⇒a⊥b; ②a⊥α,a⊥b⇒b∥α;③a∥α,a⊥b⇒b⊥α;④a⊥α,b⊥α⇒a∥b.9.α、β是两个不同的平面,m、n是平面α及β外的两条不同的直线,给出四个论断:①m⊥n;②α⊥β;③m⊥α;④n⊥β.以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题________.10.如图,正方体ABCDA1B1C1D1中,截面C1D1AB与底面ABCD所成二面角C1ABC的大小为________.三、解答题:11.如图所示,在Rt △AOB 中,∠ABO=π6,斜边AB=4,Rt △AOC 可以通过Rt △AOB 以直线AO 为轴旋转得到,且二面角BAOC 是直二面角,D 是AB 的中点.求证:平面COD ⊥平面AOB.12.如图,在四棱锥P ABCD 中,底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,PD=DC ,E 是PC 的中点,作EF ⊥PB 交PB 于点F.(1)求证:PA ∥平面EDB ;(2)求证:PB ⊥平面EFD.综合提高1.已知l ,m ,n 为两两垂直的三条异面直线,过l 作平面α与直线m 垂直,则直线n 与平面α的关系是( ).A.n ∥αB.n ∥α或n ⊂αC.n ⊂α或n 与α不平行D.n ⊂α2.已知平面α⊥平面β,α∩β=l ,点A ∈α,A ∉l ,直线AB ∥l ,直线AC ⊥l ,直线m ∥α,m ∥β,则下列四种位置关系中,不一定成立的是( ).A.AB ∥mB.AC ⊥mC.AB ∥βD.AC ⊥β3.一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,那么这两个二面角( ).A.相等B.互补C.相等或互补D.关系无法确定4.如图,正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,现在沿SE,SF,EF 把这个正方形折成一个四面体,使G1、G2、G3重合,重合后的点记为G.给出下列关系:①SG⊥平面EFG;②SE⊥平面EFG;③GF⊥SE;④EF⊥平面SEG.其中成立的有( ).A.①②B.①③C.②③D.③④5.如果三棱锥的三个侧面两两相互垂直,则顶点在底面的正投影是底面三角形的________心.6.已知三棱柱ABCA1B1C1的侧棱与底面边长都相等,若A1在底面ABC内的射影为△ABC的中心,则AB1与ABC底面所成的角的正弦值等于________.7.将正方形ABCD沿对角线BD折成直二面角ABDC,有如下四个结论:①AC⊥BD;②△ACD是等边三角形;③AB与平面BCD成60°的角;④AB与CD 所成的角为60°.其中真命题的编号是________(写出所有真命题的编号).8.如图,A、B、C、D为空间四点,在△ABC中,AB=2,AC=BC=2,等边三角形ADB以AB为轴运动,当平面ADB⊥平面ABC时,则CD=________.9.如图所示,四边形ABCD为正方形,SA垂直于四边形ABCD所在的平面,过点A且垂直于SC的平面分别交SB,SC,SD于点E,F,G.求证:AE⊥SB,AG⊥SD.10.如图,在四棱锥P-ABCD中,PO⊥面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=90°.(1)求证:PC⊥BC.(2)求点A到平面PBC的距离.11.如图,已知平面PAB⊥平面ABC,平面PAC⊥平面ABC,AE⊥平面PBC,E为垂足.(1)求证:PA⊥平面ABC;(2)当E为△PBC的垂心时,求证:△ABC是直角三角形.12.(创新拓展)已知△BCD 中,∠BCD=90°,BC=CD=1,AB ⊥平面BCD ,∠ADB=60°,E ,F 分别是AC ,AD 上的动点,且AE AC =AF AD=λ(0<λ<1). (1)求证:不论λ为何值,总有平面BEF ⊥平面ABC ;(2)当λ为何值时,平面BEF ⊥平面ACD?参考答案基础篇1.答案 A ;解析 斜线段、垂线段以及射影构成直角三角形.如图所示,∠ABO即是斜线AB 与平面α所成的角,又AB=2BO ,所以cos ∠ABO=OB AB =12.所以∠ABO=60°.故选A.2.答案 A ;解析 无论l 与m 是异面,还是相交,都有l ⊥m ,考查线面垂直的定义,故选A.3.答案 D ;解析 ∵PO ⊥平面ABC ,∴PO ⊥AC ,又∵AC ⊥BO ,∴AC ⊥平面PBD , ∴平面PBD 中的4条线段PB ,PD ,PO ,BD 与AC 垂直.4.答案 D ;解析 以正方体为模型:相邻两侧面都与底面垂直;相对的两侧面都与底面垂直;一侧面和一对角面都与底面垂直,故选D.5.答案 A ;解析 由于ME ⊂平面AB 1,平面AB 1∩平面AC=AB ,且平面AB 1⊥平面AC ,ME ⊥AB ,则ME ⊥平面AC.6.答案A;解析∵PA⊥平面ABCD,∴PA⊥BC.又BC⊥AB,PA∩AB=A,∴BC⊥平面PAB,∵BC⊂平面PBC,∴平面PBC⊥平面PAB.由AD⊥PA,AD⊥AB,PA∩AB=A,得AD⊥平面PAB.∵AD⊂平面PAD,∴平面PAD ⊥平面PAB.由已知易得平面PBC与平面PAD不垂直,故选A.7.答案垂直;解析由正方体性质知AC⊥BD,BB1⊥AC,∵E,F是棱AB,BC 的中点,∴EF∥AC,∴EF⊥BD,EF⊥BB1,∴EF⊥平面BB1O.8.答案2;解析由线面垂直的性质定理知①④正确.9.答案①③④⇒②或②③④⇒①;解析如图,PA⊥α,PB⊥β,垂足分别为A、B,α∩β=l,l∩平面PAB=O,连接OA、OB,可证明∠AOB为二面角αlβ的平面角,则∠AOB=90°⇔PA⊥PB.10.答案45°;解析∵AB⊥BC,AB⊥BC1,∴∠C1BC为二面角C1ABC的平面角,大小为45°.11.证明:由题意:CO⊥AO,BO⊥AO,∴∠BOC是二面角BAOC的平面角,又∵二面角BAOC是直二面角,∴CO⊥BO,又∵AO∩BO=O,∴CO⊥平面AOB,∵CO⊂平面COD,∴平面COD⊥平面AOB.12.证明:(1)连接AC,AC交BD于点O.连接EO,如图.∵底面ABCD是正方形,∴点O是AC的中点.在△PAC中,EO是中位线,∴PA∥EO.而EO⊂平面EDB且PA⊄平面EDB.所以PA∥平面EDB.(2)∵PD⊥底面ABCD且DC⊂底面ABCD.∴PD⊥DC.∵PD=DC,可知△PDC是等腰直角三角形,而DE是斜边PC的中线,∴DE⊥PC.①同样由PD⊥底面ABCD,得PD⊥BC.∵底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC.而DE⊂平面PDC,∴BC⊥DE.②由①和②推得DE⊥平面PBC.而PB⊂平面PBC,∴DE⊥PB.又EF⊥PB且DE∩EF=E,∴PB⊥平面EFD.综合提高1.答案A;解析∵l⊂α,且l与n异面,∴n⊄α,又∵m⊥α,n⊥m,∴n ∥α.2.答案D;解析如图,AB∥l∥m,AC⊥l,m∥l⇒AC⊥m,AB∥l⇒AB∥β.故选D.3.答案D;解析如图所示,平面EFDG⊥平面ABC,当平面HDG绕DG转动时,平面HDG始终与平面BCD垂直,所以两个二面角的大小关系不确定,因为二面角HDGF 的大小不确定.4.答案B;解析由SG⊥GE,SG⊥GF,得SG⊥平面EFG,排除C、D;若SE⊥平面EFG,则SG∥SE,这与SG∩SE=S矛盾,排除A,故选B.5.答案垂;解析三棱锥的三个侧面两两相互垂直,则三条交线两两互相垂直,可证投影是底面三角形的垂心.6.答案:23;解析由题意知,三棱锥A1ABC为正四面体(各棱长都相等的三棱锥),设棱长为a ,则AB 1=3a ,棱柱的高A 1O=63a(即点B 1到底面ABC 的距离),故AB 1与底面ABC 所成的角的正弦值为A 1O AB 1=23.' 7.答案 ①②④;解析 本题主要考查了空间直线与直线、直线与平面的夹角.8.答案 2;解析 取AB 的中点E ,连接DE ,CE ,因为△ADB 是等边三角形,所以DE ⊥AB.当平面ADB ⊥平面ABC 时,因为平面ADB ∩平面ABC=AB ,所以DE ⊥平面ABC.又CE ⊂平面ABC 可知DE ⊥CE. 由已知可得DE=3,EC=1,在Rt △DEC 中,CD=DE 2+CE 2=2.9.证明 因为SA ⊥平面ABCD ,所以SA ⊥BC.又BC ⊥AB ,SA ∩AB=A ,所以BC ⊥平面SAB ,又AE ⊂平面SAB ,所以BC ⊥AE.因为SC ⊥平面AEFG ,所以SC ⊥AE.又BC ∩SC=C ,所以AE ⊥平面SBC ,所以AE ⊥SB.同理可证AG ⊥SD.10.(1)证明 因为PD ⊥平面ABCD ,BC ⊂平面ABCD ,所以PD ⊥BC.因为∠BCD=90°,所以BC ⊥CD.又PD ∩CD=D ,所以BC ⊥平面PCD.而PC ⊂平面PCD ,所以PC ⊥BC.(2)解 如图,过点A 作BC 的平行线交CD 的延长线于E ,过点E 作PC 的垂线,垂足为F ,则有AE ∥平面PBC ,所以点A 到平面PBC 的距离等于点E 到平面PBC 的距离.又EF ⊥PC ,BC ⊥平面PCD ,则EF ⊥BC.BC ∩PC=C ,所以EF ⊥平面PBC.EF 即为E 到平面PBC 的距离.又因为AE ∥BC ,AB ∥CD ,所以四边形ABCE 为平行四边形.所以CE=AB=2. 又PD=CD=1,PD ⊥平面ABCD ,CD ⊂平面ABCD.所以PD ⊥CD ,∠PCD=45°. 所以EF= 2.即点A 到平面PBC 的距离为 2.11.证明 (1)在平面ABC 内取一点D ,作DF ⊥AC 于F ,∵平面PAC ⊥平面ABC ,且交线为AC ,∴DF ⊥平面PAC.又∵PA ⊂平面PAC ,∴DF ⊥PA.作DG ⊥AB 于G ,同理可证DG ⊥PA.∵DG ∩DF=D ,∴PA ⊥平面ABC.(2)连接BE 并延长交PC 于H.∵E 是△PBC 的垂心,∴PC ⊥BH ,又AE ⊥平面PBC ,故AE ⊥PC ,且AE ∩BE=E ,∴PC ⊥平面ABE.∴PC ⊥AB.又∵PA ⊥平面ABC ,∴PA ⊥AB ,且PA ∩PC=P ,∴AB ⊥平面PAC ,∴AB ⊥AC ,即△ABC 是直角三角形. 12.(1)证明 ∵AB ⊥平面BCD ,∴AB ⊥CD.∵CD ⊥BC 且AB ∩BC=B ,∴CD ⊥平面ABC.又∵AE AC =AF AD=λ(0<λ<1),∴不论λ为何值,恒有EF ∥CD ,∴EF ⊥平面ABC. 又EF ⊂平面BEF ,∴不论λ为何值恒有平面BEF ⊥平面ABC.(2)解 由(1)知,EF ⊥BE ,又平面BEF ⊥平面ACD ,∴BE ⊥平面ACD ,∴BE ⊥AC. ∵BC=CD=1,∠BCD=90°,∠ADB=60°,AB ⊥平面BCD ,∴BD=2,AB=2tan 60°= 6.AC=AB 2+BC 2=7, 由AB 2=AE ·AC 得AE=67,∴λ=AE AC =67,故当λ=67时,平面BEF ⊥平面ACD.。
