2019初三二模易错题整理 (教师答案版)

合集下载

2019初三二模易错题整理 (教师答案版)

2019初三二模易错题整理1、I will tell you my opinion on using mobile phone at school, and Jill will express ________、A、herB、hersC、sheD、herself【答案】B2、The pany started as a small business many years ago and ________ a lot since then、A、had grownB、is growingC、has grownD、was growing【答案】C3、Few people from China have ever received this honor, ______ ______?A、do theyB、don’t theyC、have theyD、haven’t they【答案】C4、The headmaster has promised ________ into the matter and give us a reply in couple of days、A、to lookB、lookC、lookingD、looked【答案】A5、Sam won’t make any progress ________ he studies harder than before、A、ifB、whenC、becauseD、unless【答案】D6、Our monitor has won the first prize in the math contest、exciting news it is!A、HowB、WhatC、What aD、What an【答案】B7、George and his team will finish the project in five weeks、(对划线部分提问)______ ______will George and his team finish the project?【参考答案】How soon8、Jack often helps to do some homework for the aged in his munity、(改为反义疑问句)Jack often helps to do some homework for the aged in his munity,_____ _____ ?【参考答案】doesn’t he9、which of the following underlined parts is different in pronunciation?A) achieve B) arrest C) admit D) ancient【正确答案】D10、Because of the heavy storm, very ______ flights could arrive on time、A) Little B) few C) a little D) a few【正确答案】B【题目解析】考察不定代词,根据语意“因为大暴雪,很少航班能准时到达。

2019上海初三优等生（二模冲刺用）英语易错题--汇编4

汇总一、单选1. ---How are you going to meet your aunt at the airport _____ Thursday morning?---I’m going there _____ my car.A. on, inB. on, byC. in, byD. in, in答案：A解析：具体某日的早、午、晚要用介词on，by car，by后无冠词或代词，in one’s car，in后有冠词或介词。

2. _____ big success the film was!A. What anB. What aC. How aD. How答案：B解析：success,pleasure等抽象名词前若有形容词修饰，要加冠词a/an。

3.______ the teachers in their school is about 200 and one fourth(四分之一) of them are________ teachers.A. A number of; womenB. A number of; womanC. The number of; womenD. The number of; woman答案：C解析：a number of“许多……”，the number of“……的数量”，两者后都接可数名词复数，名词前有woman或man限定，变复数要两者都变。

4.A lot of enjoyment is given _______many people.A.atB.forC.toD.with答案：C解析：give,offer等接双宾的动词，若将将直宾（物）提前，要加介词to或for，具体接to 还是for由动词决定。

5.Y ou should do more ____.Don‖t always be at the desk doing your _____.A.exercise,exercisesB.exercises,exercisesC.exercise,exerciseD.exercises,exercise答案：A解析：exercise当“锻炼”讲，不可数，当“练习”讲，可数。

中考数学二模试卷(含解析)

2019年中考数学二模试卷一、选择题1．下列各数是无理数的是（）A．0.5 B．﹣1 C．D．π2．观察下列图形，其中不是正方体的展开图的为（）A．B．C．D．3．下列运算正确的是（）A．x﹣2x＝x B．x8÷x2＝x4C．（ab3）2＝a2b6D．（x﹣l）2＝x2﹣14．誉为全国第三大露天碑林的“浯溪碑林”，摩崖上铭刻着500多方古今名家碑文，其中悬针篆文具有较高的历史意义和研究价值，下面四个悬针篆文文字明显不是轴对称图形的是（）A．B．C．D．5．下列说法中正确的是（）A．顺次连接一个四边形四边中点得到的四边形是平行四边形B．9的平方根为3C．抛物线y＝﹣+3的顶点坐标为（1，3）D．关于x的分式方程的解为非负数，则m的取值范围是m≥﹣16．下列说法正确的是（）A．两名同学5次成绩的平均分相同，则方差较大的同学成绩更稳定B．某班选出两名同学参加校演讲比赛，结果一定是一名男生和一名女生C．为了解我市学校“阳光体育”活动开展情况，必须采用普查的方法D．学校气象小组预报明天下雨的概率为0.8，则明天下雨的可能性较大7．方程（m﹣2）x2﹣x+＝0有两个实数根，则m的取值范围（）A．m＞B．m≤且m≠2C．m≥3D．m≤3且m≠2 8．二次函数y＝ax2+bx+c（a≠0）的图象如图，则反比例函数与一次函数y＝bx﹣c在同一坐标系内的图象大致是（）A．B．C．D．9．当a≤x≤a+1时，函数y＝x2﹣2x+1的最小值为1，则a的值为（）A．﹣1 B．2 C．0或2 D．﹣1或210．如图，正方形ABCD的边长为10，点E，F分别为BC，AB边的中点．连接AE、DF，两线交于点H，连接BH并延长，交边AD于点G．下列结论：①△ABE≌△DAF，②cos∠BAE＝，③S△AFH：S四边形CDHE＝1：11，④AG＝；其中正确的是（）A．①③④B．①②③C．①④D．②③④二、填空题（共6个小题）11．蜜蜂建造的蜂巢既坚固又省料，其厚度约为0.000073米，将0.000073用科学记数法表示为．12．一组数据：2，1，2，5，3，2的众数是．13．在平面直角坐标系中，点P（m，﹣）在第三象限内，则整数m的取值是．14．如图，某数学兴趣小组将边长为15的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得的扇形ABD的面积为．15．如图，将正方形ABCD沿AE，AF折叠后，点B、D恰好重合于点G，测得CF＝1，∠CFE ＝60°，则正方形的边长是．16．已知n是正整数，P1（x1，y1），P2（x2，y2），…，P n（x n，y n），…是反比例函数图象上的一列点，其中x1＝1，x2＝2，…，x n＝n，…．记A1＝x1y2，A2＝x2y3，…，A n＝x n y n+1，…若A1＝a（a是非零常数），则A1•A2•…•A n的值是（用含a和n的代数式表示）．三、解答题（共8个小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤）17．先化简：（﹣）÷（﹣1）．再选择你认为合适的一个x值代入求值．18．小军同学在学校组织的社会实践活动中，负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：x），并绘制了样本的频数分布表如下：月均用水量2≤x＜3 3≤x＜4 4≤x＜5 5≤x＜6 6≤x＜7 7≤x＜8 8≤x＜9 频数 2 12 ①10 ② 3 2百分比4% 24% 30% 20% ③6% 4% （1）请根据题中已有的信息补全频数分布表：①，②，③；（2）如果家庭月均用水量在5≤x＜8范围内为中等用水量家庭，请你通过样本估计，总体中的中等用水量家庭大约有多少户？（3）记月均用水量在2≤x＜3范围内的两户为a1，a2，在8≤x＜9范围内的2户为b1，b2，现从这4户家庭中任意抽取2户，请你通过列表或画树状图求出抽取的2户家庭来自不同范围的概率．19．如图，平面直角坐标系中，直线与x轴交于点A，与双曲线在第一象限内交于点B，BC丄x轴于点C，OC＝2AO．求双曲线的解析式．20．如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2m，台阶AC的坡度为1：，且B，C，E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽略不计）．21．某商店购进甲乙两种商品，甲的进货单价比乙的进货单价高20元，已知20个甲商品的进货总价与25个乙商品的进货总价相同．（1）求甲、乙商品的进货单价；（2）若甲、乙两种商品共进货100件，要求两种商品的进货总价不高于9000元，同时甲商品按进价提高10%后的价格销售，乙商品按进价提高25%后的价格销售，两种商品全部售完后的销售总额不低于10480元，问有哪几种进货方案？22．如图，矩形ABCD的对角线相交于O，E是OD的中点，DF∥AC交CE延长线于点F，连接AF．（1）求证：四边形AODF是菱形．（2）若∠AFC＝90°，AB＝2，求AD的长．23．如图，在等腰Rt△ABC中，∠ABC＝90°，AE平分∠BAC交BC于E，CD⊥AE交AE 延长线于D，连接BD，若BD＝CD，⊙O是以AE为直径的△ABE的外接圆，与AC交于点H．（1）求证：BD为⊙O的切线；（2）设⊙O的半径为1，BF平分∠ABC交AE于G，交⊙O于F；①求FG•FB的值．②求BE2的值．24．阅读下面材料，并回答问题：定义：平面内与一个定点F和一条定直线l（l不经过点F）距离相等的所有点组成的图形叫抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．应用：（1）如图1，一条抛物线的焦点为F（0，1），准线为过点（0，﹣1）且平行于x轴的直线l；设点P（x，y）为抛物线上任意一点，小聪同学在应用定义求这条抛物线的解析式时作出了如下不完整的解答，请你将余下部分补充出来．解：设点P（x，y）为抛物线上任意一点，作PM⊥l于点M，则PM＝．作PN⊥y轴于点N，则在△PFN中，有PN＝|x|，NF＝|y﹣1|，所以PF＝．∵PF＝PM∴＝，将方程两边同时平方，解得抛物线的解析式为．（2）如图2，在（1）的条件下，点A（1，3）是坐标平面内一点，则△FAP的周长最小值为．（3）在（1）（2）的条件下，如图3，点B（4，4）是坐标平面内另一点，过P作PH⊥l，垂足为H，连接PF和FH，问在抛物线上是否存在点P，使得以P，F，H为顶点的三角形与△ABO相似？若存在，求出P点的坐标；若不存在，请说明理由．参考答案一、选择题（共10个小题，每小题4分，共40分．在每小题给出的四个选项中，只有一个选项符合题意）1．下列各数是无理数的是（）A．0.5 B．﹣1 C．D．π【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．解：0.5是有限小数，属于有理数；﹣1是整数，属于有理数；，是整数，属于有理数；π是无理数．故选：D．2．观察下列图形，其中不是正方体的展开图的为（）A．B．C．D．【分析】由平面图形的折叠及正方体的展开图解题．解：由四棱柱四个侧面和上下两个底面的特征可知，A，B，C选项可以拼成一个正方体，而D选项，上底面不可能有两个，故不是正方体的展开图．故选：D．3．下列运算正确的是（）A．x﹣2x＝x B．x8÷x2＝x4C．（ab3）2＝a2b6D．（x﹣l）2＝x2﹣1【分析】根据合并同类项法则、同底数幂的除法法则、积的乘方法则、完全平方公式计算，判断即可．解：A、x﹣2x＝﹣x，本选项计算错误；B、x8÷x2＝x8﹣2＝x6，本选项计算错误；C、（ab3）2＝a2b6，本选项计算正确；D、（x﹣l）2＝x2﹣2x+1，本选项计算错误；故选：C．4．誉为全国第三大露天碑林的“浯溪碑林”，摩崖上铭刻着500多方古今名家碑文，其中悬针篆文具有较高的历史意义和研究价值，下面四个悬针篆文文字明显不是轴对称图形的是（）A．B．C．D．【分析】根据轴对称图形的概念进行判断即可．解：A、是轴对称图形，故此选项错误；B、是轴对称图形，故此选项错误；C、不是轴对称图形，故此选项正确；D、是轴对称图形，故此选项错误；故选：C．5．下列说法中正确的是（）A．顺次连接一个四边形四边中点得到的四边形是平行四边形B．9的平方根为3C．抛物线y＝﹣+3的顶点坐标为（1，3）D．关于x的分式方程的解为非负数，则m的取值范围是m≥﹣1【分析】根据各个选项中的说法，可以判断各个选项中的说法是否正确，从而可以解答本题．解：顺次连接一个四边形四边中点得到的四边形是平行四边形，故选项A正确；9的平方根是±3，故选项B错误；抛物线y＝﹣+3的顶点坐标为（﹣1，3），故选项C错误；由分式方程，得x＝，∵关于x的分式方程的解为非负数，∴≥0且≠1，得m≥﹣1且m≠1，故选项D错误；故选：A．6．下列说法正确的是（）A．两名同学5次成绩的平均分相同，则方差较大的同学成绩更稳定B．某班选出两名同学参加校演讲比赛，结果一定是一名男生和一名女生C．为了解我市学校“阳光体育”活动开展情况，必须采用普查的方法D．学校气象小组预报明天下雨的概率为0.8，则明天下雨的可能性较大【分析】利用概率的意义、全面调查与抽样调查及方差的知识进行判断即可得到正确的答案．解：A、根据方差的意义知方差越大越不稳定，故本选项错误；B、在某班中选出两名同学是随机抽取，可能是两男生或两女生或名一男生和一名女生，故本选项错误；C、为了解我市学校“阳光体育”活动开展情况，必须采用抽样调查的方法，故本选项错误；D、学校气象小组预报明天下雨的概率为0.8，则明天下雨的可能性较大，正确；故选：D．7．方程（m﹣2）x2﹣x+＝0有两个实数根，则m的取值范围（）A．m＞B．m≤且m≠2C．m≥3D．m≤3且m≠2【分析】根据一元二次方程的定义、二次根式有意义的条件和判别式的意义得到，然后解不等式组即可．解：根据题意得，解得m≤且m≠2．故选：B．8．二次函数y＝ax2+bx+c（a≠0）的图象如图，则反比例函数与一次函数y＝bx﹣c在同一坐标系内的图象大致是（）A．B．C．D．【分析】根据二次函数的图象找出a、b、c的正负，再结合反比例函数、一次函数系数与图象的关系即可得出结论．解：观察二次函数图象可知：开口向上，a＞0；对称轴大于0，﹣＞0，b＜0；二次函数图象与y轴交点在y轴的正半轴，c＞0．∵反比例函数中k＝﹣a＜0，∴反比例函数图象在第二、四象限内；∵一次函数y＝bx﹣c中，b＜0，﹣c＜0，∴一次函数图象经过第二、三、四象限．故选：C．9．当a≤x≤a+1时，函数y＝x2﹣2x+1的最小值为1，则a的值为（）A．﹣1 B．2 C．0或2 D．﹣1或2【分析】利用二次函数图象上点的坐标特征找出当y＝1时x的值，结合当a≤x≤a+1时函数有最小值1，即可得出关于a的一元一次方程，解之即可得出结论．解：当y＝1时，有x2﹣2x+1＝1，解得：x1＝0，x2＝2．∵当a≤x≤a+1时，函数有最小值1，∴a＝2或a+1＝0，∴a＝2或a＝﹣1，故选：D．10．如图，正方形ABCD的边长为10，点E，F分别为BC，AB边的中点．连接AE、DF，两线交于点H，连接BH并延长，交边AD于点G．下列结论：①△ABE≌△DAF，②cos∠BAE＝，③S△AFH：S四边形CDHE＝1：11，④AG＝；其中正确的是（）A．①③④B．①②③C．①④D．②③④【分析】①根据四边形ABCD是正方形，点E，F分别为BC，AB边的中点，即可证明△ABE≌△DAF；②根据勾股定理先求AE的长，再根据三角函数即可求cos∠BAE＝＝＝，所以可判断②错误；③先求正方形ABCD和三角形ABE的面积，再证明△HAF∽△BAE，可得三角形面积比等于相似比的平方，可得三角形AHF的面积，进而可求三角形AFH的面积，即可得S△AFH：S四边形CDHE＝1：11；④根据△HAF∽△BAE，可得对应边成比例求出AH的长，再证明△AGH∽△EBH，对应边成比例即可得AG的长．解：①∵四边形ABCD是正方形，∴AB＝BC＝AD，∠DAB＝∠ABC＝90°，∵点E，F分别为BC，AB边的中点，∴AF＝BE，∴△ABE≌△DAF（SAS），所以①正确；②∵AB＝10，BE＝5，∴AE＝＝5，∴cos∠BAE＝＝＝．所以②错误；③∵△ABE≌△DAF，∴∠DFA＝∠AEB，∵∠AEB+∠EAB＝90°，∴∠DFA+∠EAB＝90°，∴∠AHF＝90°，∴∠AHF＝∠ABE，∵∠HAF＝∠BAE，∴△HAF∽△BAE，∴＝（）2＝（）2＝，∵S△ABE＝BE•AB＝×5×10＝25，∴S△AHF＝5，∴S△ADF＝S△ABE＝25，∴S四边形BEHF＝S△ABE﹣S△AHF＝25﹣5＝20，∴S四边形CDHE＝100﹣25﹣20＝55，∴S△AFH：S四边形CDHE＝5：55＝1：11，所以③正确；④∵△HAF∽△BAE，∴＝，∴＝，∴AH＝2，∴HE＝AE﹣AH＝3，∵AG∥BE，∴△AGH∽△EBH，∴＝，∴＝，∴AG＝，所以④正确．所以其中正确的是①③④．故选：A．二、填空题（6个小题，每小题4分，共24分.）11．蜜蜂建造的蜂巢既坚固又省料，其厚度约为0.000073米，将0.000073用科学记数法表示为7.3×10﹣5．【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．解：将0.000073用科学记数法表示为7.3×10﹣5．故答案为：7.3×10﹣5．12．一组数据：2，1，2，5，3，2的众数是2．【分析】根据众数的定义即一组数据中出现次数最多的数，即可得出答案．解：在数据2，1，2，5，3，2中2出现3次，次数最多，所以众数为2，故答案为：2．13．在平面直角坐标系中，点P（m，﹣）在第三象限内，则整数m的取值是﹣1．【分析】直接利用第三象限内点的坐标特点得出m的取值范围．解：∵点P（m，﹣）在第三象限内，∴，解得：﹣2＜m＜0，∴整数m的取值是：﹣1．故答案为：﹣1．14．如图，某数学兴趣小组将边长为15的正方形铁丝框ABCD变形为以A为圆心，AB为半径的扇形（忽略铁丝的粗细），则所得的扇形ABD的面积为225．【分析】根据扇形面积公式求出弧长BD，由此即可解决问题．解：由题意的长＝CD+BC＝30，S扇形ADB＝•AB＝×30×15＝225，故答案为225．15．如图，将正方形ABCD沿AE，AF折叠后，点B、D恰好重合于点G，测得CF＝1，∠CFE ＝60°，则正方形的边长是．【分析】由CF＝1，∠CFE＝60°，得CE＝，EF＝2，由折叠可知，EG＝BE，FG＝FD，所以BE+FD＝EG+GF＝EF＝2，因此BC+CD＝（BE+FD）+（CE+CF）＝2+（1+）＝3+，则BC＝CD＝．解：∵正方形ABCD，∴∠B＝∠C＝∠D＝90°，AB＝BC＝CD＝AD，∵CF＝1，∠CFE＝60°，∴CE＝，EF＝2，由折叠可知，EG＝BE，FG＝FD，∴BE+FD＝EG+GF＝EF＝2，∴BC+CD＝（BE+FD）+（CE+CF）＝2+（1+）＝3+，∴BC＝CD＝．故答案为．16．已知n是正整数，P1（x1，y1），P2（x2，y2），…，P n（x n，y n），…是反比例函数图象上的一列点，其中x1＝1，x2＝2，…，x n＝n，…．记A1＝x1y2，A2＝x2y3，…，A n＝x n y n+1，…若A1＝a（a是非零常数），则A1•A2•…•A n的值是（用含a和n的代数式表示）．【分析】应先得到k与a之间的关系，进而根据反比例函数上的点的特点得到相应规律作答．解：易得x1y1＝k，x2y2＝k，…x n y n＝k，且由x2y2＝k得到：y2＝，∵x1＝1，x2＝2，则A1＝x1y2＝a＝＝，∴k＝2a．∵x n+1y n+1＝k，x n+1＝n+1，∴y n+1＝，又∵x1＝1，∴A1•A2•…•A n＝x1y2•x2y3…x n y n+1＝x1（y2•x2）•（y3•x3）y4•x n y n+1＝k•k…k×x1y n+1＝k•k…k×＝k n﹣1•＝＝．故答案为：．三、解答题（共8个小题，共86分．解答应写出必要的文字说明、证明过程或演算步骤）17．先化简：（﹣）÷（﹣1）．再选择你认为合适的一个x值代入求值．【分析】根据分式的减法和除法可以化简题目中的式子，然后选取一个使得原分式有意义的值代入化简后的式子即可解答本题．解：（﹣）÷（﹣1）＝[]÷＝（）＝＝，当x＝0时，原式＝＝1．18．小军同学在学校组织的社会实践活动中，负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：x），并绘制了样本的频数分布表如下：月均用水量2≤x＜3 3≤x＜4 4≤x＜5 5≤x＜6 6≤x＜7 7≤x＜8 8≤x＜9 频数 2 12 ①10 ② 3 2百分比4% 24% 30% 20% ③6% 4% （1）请根据题中已有的信息补全频数分布表：①15，②6，③12%；（2）如果家庭月均用水量在5≤x＜8范围内为中等用水量家庭，请你通过样本估计，总体中的中等用水量家庭大约有多少户？（3）记月均用水量在2≤x＜3范围内的两户为a1，a2，在8≤x＜9范围内的2户为b1，b2，现从这4户家庭中任意抽取2户，请你通过列表或画树状图求出抽取的2户家庭来自不同范围的概率．【分析】（1）根据频数的相关知识列式计算即可得出答案；（2）用总体乘以样本中中等用水量家庭的百分比即可；（3）根据题意画出树状图得出所有等情况数和抽取的2户家庭来自不同范围的情况数，再根据概率公式即可得出答案．解：（1）①50×30%＝15；②50﹣2﹣12﹣15﹣10﹣3﹣2＝6；③×100%＝12%；故答案为：15，6，12%；（2）中等用水量家庭大约有：450×（20%+12%+6%）＝171（户）；（3）根据题意画图如下：共有12种等情况数，其中抽取的2户家庭来自不同范围的有8种，则抽取出的2户家庭来自不同范围的概率：P＝＝．19．如图，平面直角坐标系中，直线与x轴交于点A，与双曲线在第一象限内交于点B，BC丄x轴于点C，OC＝2AO．求双曲线的解析式．【分析】先利用一次函数与图象的交点，再利用OC＝2AO求得C点的坐标，然后代入一次函数求得点B的坐标，进一步求得反比例函数的解析式即可．解：由题意OC＝2AO，∵当y＝0时，x+＝0，解得x＝﹣1，∴点A的坐标为（﹣1，0），∴OA＝1．又∵OC＝2OA，∴OC＝2，∴点B的横坐标为2，代入直线，得y＝，∴B（2，）．∵点B在双曲线上，∴k＝xy＝2×＝3，∴双曲线的解析式为y＝．20．如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度，他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2m，台阶AC的坡度为1：，且B，C，E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽略不计）．【分析】由于AF⊥AB，则四边形ABEF为矩形，设DE＝x，在Rt△CDE中，CE═＝＝x，在Rt△ABC中，得到＝，求出BC，在Rt△AFD中，求出AF，由AF＝BC+CE即可求出x的长．解：∵AF⊥AB，AB⊥BE，DE⊥BE，∴四边形ABEF为矩形，∴AF＝BE，EF＝AB＝2设DE＝x，在Rt△CDE中，CE＝＝＝x，在Rt△ABC中，∵＝，AB＝2，∴BC＝2，在Rt△AFD中，DF＝DE﹣EF＝x﹣2，∴AF＝＝＝（x﹣2），∵AF＝BE＝BC+CE．∴（x﹣2）＝2+x，解得x＝6．答：树DE的高度为6米．21．某商店购进甲乙两种商品，甲的进货单价比乙的进货单价高20元，已知20个甲商品的进货总价与25个乙商品的进货总价相同．（1）求甲、乙商品的进货单价；（2）若甲、乙两种商品共进货100件，要求两种商品的进货总价不高于9000元，同时甲商品按进价提高10%后的价格销售，乙商品按进价提高25%后的价格销售，两种商品全部售完后的销售总额不低于10480元，问有哪几种进货方案？【分析】（1）设甲商品的进货单价是x元，乙商品的进货单价是y元，根据“甲的进货单价比乙的进货单价高20元，20个甲商品的进货总价与25个乙商品的进货总价相同”，即可得出关于x，y的二元一次方程组，解之即可得出结论；（2）设购进甲商品m件，则购进乙商品（100﹣m）件，根据两种商品的进货总价不高于9000元且全部售完后的销售总额不低于10480元，即可得出关于m的一元一次不等式组，解之即可得出m的取值范围，再结合m为正整数即可得出各进货方案．解：（1）设甲商品的进货单价是x元，乙商品的进货单价是y元，依题意，得：，解得：．答：甲商品的进货单价是100元，乙商品的进货单价是80元．（2）设购进甲商品m件，则购进乙商品（100﹣m）件，依题意，得：，解得：48≤m≤50．又∵m是正整数，∴m＝48，49，50，∴共有3种进货方案，方案一：购进甲商品48件，乙商品52件；方案二：购进甲商品49件，乙商品51件；方案三：购进甲商品50件，乙商品50件．22．如图，矩形ABCD的对角线相交于O，E是OD的中点，DF∥AC交CE延长线于点F，连接AF．（1）求证：四边形AODF是菱形．（2）若∠AFC＝90°，AB＝2，求AD的长．【分析】（1）由“AAS”可证△DEF≌△OEC，可得DF＝OC＝OA，可证四边形AODF是平行四边形，且OA＝OD，可得结论；（2）由直角三角形的性质可求∠CAF＝60°，可得∴∠OAD＝30°，可证△AOB是等边三角形，可求解．【解答】证明：（1）∵DF∥AC，∴∠DFC＝∠OCF，∠EDF＝∠EOC，∵DE＝OE，∴△DEF≌△OEC（AAS）∴DF＝OC，∵四边形ABCD是矩形，∴OA＝OC＝OD，∴DF＝OA，且DF∥AO，∴四边形AODF是平行四边形，且OA＝OD，∴四边形AODF是菱形；（2）∵AODF是菱形，∴AF＝AO，∴AC＝2AF，∵∠AFC＝90°，∴∠CAF＝60°，∴∠OAD＝30°，∵四边形ABCD是矩形，∴∠BAD＝90°，∴∠BAC＝60°，∴△AOB是等边三角形，∵AB＝2，∴AD＝．23．如图，在等腰Rt△ABC中，∠ABC＝90°，AE平分∠BAC交BC于E，CD⊥AE交AE 延长线于D，连接BD，若BD＝CD，⊙O是以AE为直径的△ABE的外接圆，与AC交于点H．（1）求证：BD为⊙O的切线；（2）设⊙O的半径为1，BF平分∠ABC交AE于G，交⊙O于F；①求FG•FB的值．②求BE2的值．【分析】（1）连接OB．由等腰三角形的性质得出∠DBC＝∠DCB，∠OBE＝∠OEB，证出∠DEC＝∠OBE，得出∠DBC+∠OBE＝90°，则OB⊥BD，即可得出结论；（2）①由圆周角定理得出，得出∠ABF＝∠EAF，证明△AFG∽△BFA，得出FG•FB＝AF2，连接OF，则△AOF是等腰直角三角形，得出AF＝OA＝，即可得出答案；②连接EH．由圆周角定理得出∠AHE＝90°，由角平分线性质得出EH＝BE，证明△CEH是等腰直角三角形，得出EC＝EH＝BE，则AB＝BC＝（1+）BE，在△ABE中，由勾股定理得出，即可得出答案．【解答】（1）证明：连接OB．如图1所示：∵BD＝CD，∴∠DBC＝∠DCB，∵CD⊥AE交AE延长线于D，∴∠DCB+∠DEC＝90°，∵OB＝OE，∴∠OBE＝∠OEB，∵∠DEC＝∠OEB，∴∠DEC＝∠OBE，∴∠DBC+∠OBE＝90°，∴OB⊥BD，∴BD为⊙O的切线；（2）解：①∵BF平分∠ABC，∴∠ABF＝∠CBF，∴，∴∠ABF＝∠EAF，∵∠AFG＝∠BFA，∴△AFG∽△BFA，∴，∴FG•FB＝AF2，连接OF，如图2所示：∵，∴OF⊥AE，∵OA＝OF，∴△AOF是等腰直角三角形，∴AF＝OA＝，∴FB•FG＝AF2＝2，②连接EH．如图3所示：∵AE为⊙O直径，∴∠AHE＝90°，∵等腰Rt△ABC中，∠ABC＝90°，AE平分∠BAC交BC于E，∴EH＝BE，∵等腰Rt△ABC中，∠ABC＝90°，∴∠ACB＝45°，∴△CEH是等腰直角三角形，∴EC＝EH＝BE，∴AB＝BC＝BE+EC＝（1+）BE，又∵AE＝2OA＝2，∴在△ABE中，由勾股定理得：，解得：BE2＝．24．阅读下面材料，并回答问题：定义：平面内与一个定点F和一条定直线l（l不经过点F）距离相等的所有点组成的图形叫抛物线．点F叫做抛物线的焦点，直线l叫做抛物线的准线．应用：（1）如图1，一条抛物线的焦点为F（0，1），准线为过点（0，﹣1）且平行于x轴的直线l；设点P（x，y）为抛物线上任意一点，小聪同学在应用定义求这条抛物线的解析式时作出了如下不完整的解答，请你将余下部分补充出来．解：设点P（x，y）为抛物线上任意一点，作PM⊥l于点M，则PM＝y+1．作PN⊥y轴于点N，则在△PFN中，有PN＝|x|，NF＝|y﹣1|，所以PF＝．∵PF＝PM∴＝y+1，将方程两边同时平方，解得抛物线的解析式为y＝x2．（2）如图2，在（1）的条件下，点A（1，3）是坐标平面内一点，则△FAP的周长最小值为4+．（3）在（1）（2）的条件下，如图3，点B（4，4）是坐标平面内另一点，过P作PH⊥l，垂足为H，连接PF和FH，问在抛物线上是否存在点P，使得以P，F，H为顶点的三角形与△ABO相似？若存在，求出P点的坐标；若不存在，请说明理由．【分析】（1）设点P（x，y）为抛物线上任意一点，作PM⊥l于点M，则PM＝y+1．作PN⊥y轴于点N，求得PF＝．根据PF＝PM，列方程即可得到结论；（2）根据两点间的距离公式得到AF＝＝，如图2，过A作AB⊥直线l于B，交抛物线于P，则此时，PA+PB＝PA+PF最小，于是得到结论；（3）根据两点间的距离公式得到AB＝＝，AO＝＝，OB＝＝4得到AB＝OA，设点P（m，m2），则H为（m，﹣1），根据相似三角形的性质列方程即可得到结论．解：（1）设点P（x，y）为抛物线上任意一点，作PM⊥l于点M，则PM＝y+1．作PN⊥y轴于点N，则在△PFN中，有PN＝|x|，NF＝|y﹣1|，所以PF＝．∵PF＝PM，∴＝y+1，将方程两边同时平方，解得抛物线的解析式为y＝x2．故答案为：y+1，，y+1，，；（2）∵F（0，1），点A（1，3），∴AF＝＝，如图2，过A作AB⊥直线l于B，交抛物线于P，则此时，PA+PB＝PA+PF最小，且△FAP的周长最小值为＝4+，故答案为：；（3）存在，∵A（1，3），点B（4，4），∴AB＝＝，AO＝＝，OB＝＝4∴AB＝OA，∵PF＝PH，假设存在这样的点P，使得以P，F，H为顶点的三角形与△ABO相似，则PH与AB，FH与OB是对应边，∴，设点P（m，m2），则H为（m，﹣1），∴，解得m＝±1，∴点P坐标（1，）或（﹣1，）．。

2019年中考数学二模试卷(含解析)

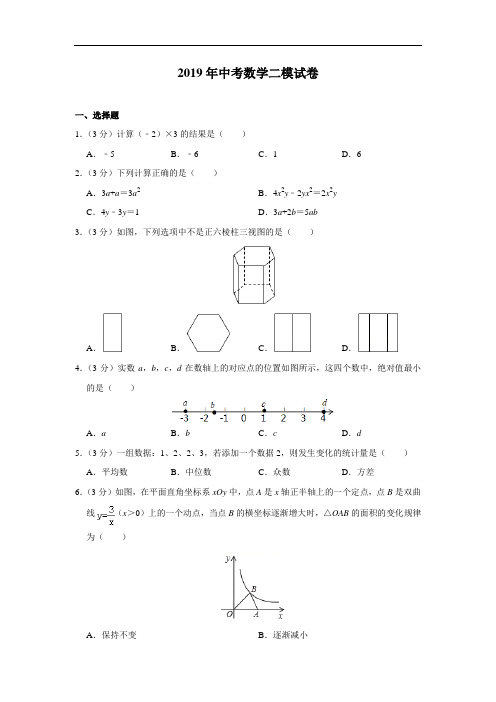
2019年中考数学二模试卷一、选择题1．（3分）计算（﹣2）×3的结果是（）A．﹣5B．﹣6C．1D．62．（3分）下列计算正确的是（）A．3a+a＝3a2B．4x2y﹣2yx2＝2x2yC．4y﹣3y＝1D．3a+2b＝5ab3．（3分）如图，下列选项中不是正六棱柱三视图的是（）A．B．C．D．4．（3分）实数a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最小的是（）A．a B．b C．c D．d5．（3分）一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是（）A．平均数B．中位数C．众数D．方差6．（3分）如图，在平面直角坐标系xOy中，点A是x轴正半轴上的一个定点，点B是双曲线（x＞0）上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积的变化规律为（）A．保持不变B．逐渐减小C．逐渐增大D．先增大后减小7．（3分）一个正多边形的每一个外角都等于45°，则这个多边形的边数为（）A．4B．6C．8D．108．（3分）为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款．已知第一次捐款总额为4800元，第二次捐款总额为5000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等，如果设第一次捐款人数是x人，那么x满足的方程是（）A．B．＝C．D．9．（3分）如图，在平面直角坐标系中，已知点A（﹣2，4），B（﹣8，﹣2），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（）A．（﹣1，2）B．（﹣9，18）C．（﹣9，18）或（9，﹣18）D．（﹣1，2）或（1，﹣2）10．（3分）下列图形中阴影部分的面积相等的是（）A．②③B．③④C．①②D．①④二、填空题11．（3分）分解因式：m2﹣9m＝．12．（3分）据报道，2018年全国普通高考报名人数约9750000人，数据9750000用科学记数法表示为9.75×10n，则n的值是．13．（3分）在一个不透明的塑料袋中装有红色、白色球共40个，除颜色外其它都相同，小明通过多次摸球实验后发现，其中摸到红色球的频率稳定在15%左右，则口袋中白色球可能有个．14．（3分）若m是方程2x2﹣3x﹣1＝0的一个根，则6m2﹣9m+2016的值为．15．（3分）填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值应是．16．（3分）已知在矩形ABCD中，AB＝6，BC＝10，沿着过矩形顶点的一条直线将∠B折叠，使点B的对应点B′落在矩形的边上，则折痕长为．三、解答题17．计算：|﹣|+（﹣1）0+2sin45°﹣2cos30°+（）﹣1．18．如图是一副扑克牌中的三张牌，将它们正面向下洗均匀，甲同学从中随机抽取一张牌后放回，乙同学再从中随机抽取一张牌，用树状图（或列表）的方法，求抽出的两张牌中，牌面上的数字都是偶数的概率．19．如图，在四边形ABCD中，E是AB的中点，AD∥EC，∠AED＝∠B．（1）求证：△AED≌△EBC．（2）当AB＝6时，求CD的长．20．某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计，并绘制如图所示的扇形统计图和条形统计图．根据图中信息解答下列问题：（1）该超市“元旦”期间共销售个绿色鸡蛋，A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是度；（2）补全条形统计图；（3）如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个，请你估计这个分店销售的B种品牌的绿色鸡蛋的个数？21．如图，AB为⊙O的直径，C为⊙O外一点，且∠CAB＝90°，BD是⊙O的弦，BD∥CO．（1）请说明：CD是⊙O的切线：（2）若AB＝4，BC＝2．则阴影部分的面积为22．如图，在东西方向的海岸线MN上有A、B两艘船，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东58°方向，船P在船B的北偏西35°方向，AP的距离为30海里（参考数据：sin32°≈0.53，sin55°≈0.82）．（1）求船P到海岸线MN的距离（精确到0.1海里）；（2）若船A、船B分别以20海里/小时、15海里/小时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处．23．如图，在平面直角坐标系中，直线DE交x轴于点E（30，0），交y轴于点D（0，40），直线AB：y＝x+5交x轴于点A，交y轴于点B，交直线DE于点P，过点E作EF⊥x 轴交直线AB于点F，以EF为一边向右作正方形EFGH．（1）求边EF的长；（2）将正方形EFGH沿射线FB的方向以每秒个单位的速度匀速平移，得到正方形E1F1G1H1，在平移过程中边F1G1始终与y轴垂直，设平移的时间为t秒（t＞0）．①当点F1移动到点B时，求t的值；②当G1，H1两点中有一点移动到直线DE上时，请直接写出此时正方形E1F1G1H1与△APE重叠部分的面积．24．在△ABC中，∠B＝45°，∠C＝30°，点D是边BC上一点，连接AD，将线段AD绕点A逆时针旋转90°，得到线段AE，连接DE．（1）如图①，当点E落在边BA的延长线上时，∠EDC＝度（直接填空）；（2）如图②，当点E落在边AC上时，求证：BD＝EC；（3）当AB＝2，且点E到AC的距离等于﹣1时，直接写出tan∠CAE的值．25．如图1，在平面直角坐标系中，直线AB：y＝kx+b（k＜0，b＞0），与x轴交于点A、与y轴交于点B，直线CD与x轴交于点C、与y轴交于点D．若直线CD的解析式为y＝﹣（x+b），则称直线CD为直线AB的”姊线”，经过点A、B、C的抛物线称为直线AB的“母线”．（1）若直线AB的解析式为：y＝﹣3x+6，求AB的”姊线”CD的解析式为：（直接填空）；（2）若直线AB的”母线”解析式为：，求AB的”姊线”CD的解析式；（3）如图2，在（2）的条件下，点P为第二象限”母线”上的动点，连接OP，交”姊线”CD于点Q，设点P的横坐标为m，PQ与OQ的比值为y，求y与m的函数关系式，并求y的最大值；（4）如图3，若AB的解析式为：y＝mx+3（m＜0），AB的“姊线”为CD，点G为AB 的中点，点H为CD的中点，连接OH，若GH＝，请直接写出AB的”母线”的函数解析式．2019年辽宁省沈阳市皇姑区中考数学二模试卷参考答案与试题解析一、选择题1．（3分）计算（﹣2）×3的结果是（）A．﹣5B．﹣6C．1D．6【分析】原式利用异号两数相乘的法则计算即可得到结果．【解答】解：原式＝﹣2×3＝﹣6，故选：B．【点评】此题考查了有理数的乘法，熟练掌握乘法法则是解本题的关键．2．（3分）下列计算正确的是（）A．3a+a＝3a2B．4x2y﹣2yx2＝2x2yC．4y﹣3y＝1D．3a+2b＝5ab【分析】根据合并同类项法则逐一计算即可得．【解答】解：A、3a+a＝4a，此选项计算错误；B、4x2y﹣2yx2＝2x2y，此选项计算正确；C、4y﹣3y＝y，此选项计算错误；D、3a与2b不是同类项，不能合并，此选项计算错误；故选：B．【点评】本题主要考查合并同类项，解题的关键是掌握“合并”是指同类项的系数的相加，并把得到的结果作为新的系数，要保持同类项的字母和字母的指数不变．3．（3分）如图，下列选项中不是正六棱柱三视图的是（）A．B．C．D．【分析】主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形．【解答】解：正六棱柱三视图分别为：三个左右相邻的矩形，两个左右相邻的矩形，正六边形．故选：A．【点评】本题考查了几何体的三种视图，注意所有的看到的棱都应表现在三视图中．4．（3分）实数a，b，c，d在数轴上的对应点的位置如图所示，这四个数中，绝对值最小的是（）A．a B．b C．c D．d【分析】根据数轴上某个数与原点的距离的大小确定结论．【解答】解：由图可知：c到原点O的距离最短，所以在这四个数中，绝对值最小的数是c．故选：C．【点评】本题考查了绝对值的定义、实数大小比较问题，熟练掌握绝对值最小的数就是到原点距离最小的数．5．（3分）一组数据：1、2、2、3，若添加一个数据2，则发生变化的统计量是（）A．平均数B．中位数C．众数D．方差【分析】依据平均数、中位数、众数、方差的定义和公式求解即可．【解答】解：A、原来数据的平均数是2，添加数字2后平均数仍为2，故A与要求不符；B、原来数据的中位数是2，添加数字2后中位数仍为2，故B与要求不符；C、原来数据的众数是2，添加数字2后众数仍为2，故C与要求不符；D、原来数据的方差＝＝，添加数字2后的方差＝＝，故方差发生了变化．故选：D．【点评】本题主要考查的是众数、中位数、方差、平均数，熟练掌握相关概念和公式是解题的关键．6．（3分）如图，在平面直角坐标系xOy中，点A是x轴正半轴上的一个定点，点B是双曲线（x＞0）上的一个动点，当点B的横坐标逐渐增大时，△OAB的面积的变化规律为（）A．保持不变B．逐渐减小C．逐渐增大D．先增大后减小【分析】作BH⊥OA于H，设点B（x，），其中x＞0，则△OAB的面积＝，根据OA固定，点B的横坐标逐渐增大，即可判断△OAB的面积的变化情况．【解答】解：如图，作BH⊥OA于H，设点B（x，），其中x＞0，则△OAB的面积＝，∵OA固定，点B的横坐标逐渐增大，∴△OAB的面积逐渐减少，故选：B．【点评】本题考查反比例函数系数k的几何意义，三角形面积的计算，解题的关键是用坐标表示出△OAB的面积．7．（3分）一个正多边形的每一个外角都等于45°，则这个多边形的边数为（）A．4B．6C．8D．10【分析】根据多边形的外角和是360度即可求得外角的个数，即多边形的边数．【解答】解：多边形的边数为：360÷45＝8．故选：C．【点评】本题主要考查了多边形的外角和定理，理解多边形外角和中外角的个数与正多边形的边数之间的关系，是解题关键．8．（3分）为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款．已知第一次捐款总额为4800元，第二次捐款总额为5000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等，如果设第一次捐款人数是x人，那么x满足的方程是（）A．B．＝C．D．【分析】如果设第一次有x人捐款，那么第二次有（x+20）人捐款，根据两次人均捐款额相等，可得等量关系为：第一次人均捐款额＝第二次人均捐款额，据此列出方程即可．【解答】解：设第一次有x人捐款，那么第二次有（x+20）人捐款，由题意，有＝，故选：B．【点评】本题考查由实际问题抽象出分式方程，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．9．（3分）如图，在平面直角坐标系中，已知点A（﹣2，4），B（﹣8，﹣2），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（）A．（﹣1，2）B．（﹣9，18）C．（﹣9，18）或（9，﹣18）D．（﹣1，2）或（1，﹣2）【分析】根据位似变换的性质计算即可．【解答】解：点A（﹣2，4），B（﹣8，﹣2），以原点O为位似中心，相似比为，把△ABO缩小，则点A的对应点A′的坐标是（﹣2×，4×）或（﹣2×（﹣），4×（﹣）），即（﹣1，2）或（1，﹣2），故选：D．【点评】本题考查的是位似变换的性质，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或﹣k．10．（3分）下列图形中阴影部分的面积相等的是（）A．②③B．③④C．①②D．①④【分析】首先根据各图形的函数解析式求出函数与坐标轴交点的坐标，进而可求得各个阴影部分的面积，进而可比较出个阴影部分面积的大小关系．【解答】解：①：图中的函数为正比例函数，与坐标轴只有一个交点（0，0），由于缺少条件，无法求出阴影部分的面积；②：直线y＝﹣x+2与坐标轴的交点坐标为：（2，0），（0，2），故S阴影＝×2×2＝2；③：此函数是反比例函数，那么阴影部分的面积为：S＝xy＝×4＝2；④：该抛物线与坐标轴交于：（﹣1，0），（1，0），（0，﹣1），故阴影部分的三角形是等腰直角三角形，其面积S＝×2×1＝1；②③的面积相等，故选：A．【点评】此题主要考查了函数图象与坐标轴交点坐标的求法以及图形面积的求法，是基础题，熟练掌握各函数的图象特点是解决问题的关键．二、填空题11．（3分）分解因式：m2﹣9m＝m（m﹣9）．【分析】直接提取公因式m即可．【解答】解：原式＝m（m﹣9）．故答案为：m（m﹣9）．【点评】此题主要考查了提公因式法分解因式，关键是正确找出公因式．12．（3分）据报道，2018年全国普通高考报名人数约9750000人，数据9750000用科学记数法表示为9.75×10n，则n的值是6．【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n 的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞10时，n是正数；当原数的绝对值＜1时，n是负数．【解答】解：数据9750000用科学记数法表示为9.75×106，则n的值是6．故答案为：6．【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．13．（3分）在一个不透明的塑料袋中装有红色、白色球共40个，除颜色外其它都相同，小明通过多次摸球实验后发现，其中摸到红色球的频率稳定在15%左右，则口袋中白色球可能有34个．【分析】设有白球有x个，利用频率约等于概率进行计算即可．【解答】解：设白球有x个，根据题意得：＝15%，解得：x＝34，即白色球的个数为34个，故答案为：34．【点评】本题考查了由频率估计概率的知识，解题的关键是了解大量重复实验中事件发生的频率等于事件发生的概率．14．（3分）若m是方程2x2﹣3x﹣1＝0的一个根，则6m2﹣9m+2016的值为2019．【分析】把x＝m代入方程，求出2m2﹣3m＝1，再变形后代入，即可求出答案．【解答】解：∵m是方程2x2﹣3x﹣1＝0的一个根，∴代入得：2m2﹣3m﹣1＝0，∴2m2﹣3m＝1，∴6m2﹣9m+2016＝3（2m2﹣3m）+2016＝3×1+2016＝2019，故答案为：2019．【点评】本题考查了求代数式的值和一元二次方程的解，能求出2m2﹣3m＝1是解此题的关键．15．（3分）填在下面各正方形中的四个数之间都有相同的规律，根据这种规律，m的值应是158．【分析】观察不难发现，左上角、左下角、右上角为三个连续的偶数，右下角的数是左下角与右上角两个数的乘积减去左上角的数的差，根据此规律先求出阴影部分的两个数，再列式进行计算即可得解．【解答】解：根据排列规律，10下面的数是12，10右面的数是14，∵8＝2×4﹣0，22＝4×6﹣2，44＝6×8﹣4，∴m＝12×14﹣10＝158，故答案为：158．【点评】本题是对数字变化规律的考查，仔细观察前三个图形，找出四个数之间的变化规律是解题的关键．16．（3分）已知在矩形ABCD中，AB＝6，BC＝10，沿着过矩形顶点的一条直线将∠B折叠，使点B的对应点B′落在矩形的边上，则折痕长为6或．【分析】分两种情形分别画出图形解决问题即可．【解答】解：①如图1中，当折痕为直线AM时，易知AB＝BM＝6，AM＝6．②如图2中，当直线CM为折痕时，在Rt△CDB′中，DB′＝＝8，∴AB′＝10﹣8＝2，设BM＝MB′＝x，在Rt△AMB′中，x2＝（6﹣x）2+22，∴x＝，∴CM＝＝，∴满足条件的折痕的长为6和．故答案为6和．【点评】本题考查翻折变换，矩形的性质等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．三、解答题17．计算：|﹣|+（﹣1）0+2sin45°﹣2cos30°+（）﹣1．【分析】原式利用零指数幂、负整数指数幂法则，以及特殊角的三角函数值计算即可求出值．【解答】解：原式＝﹣+1+2×﹣2×+2018＝2019．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．18．如图是一副扑克牌中的三张牌，将它们正面向下洗均匀，甲同学从中随机抽取一张牌后放回，乙同学再从中随机抽取一张牌，用树状图（或列表）的方法，求抽出的两张牌中，牌面上的数字都是偶数的概率．【分析】画树状图展示所有9种等可能的结果数，再找出两次抽取的牌上的数字都是偶数的结果数，然后根据概率公式求解．【解答】解：画树状图为：共有9种等可能的结果数，其中两次抽取的牌上的数字都是偶数的结果数为4，所以两次抽取的牌上的数字都是偶数的概率＝．【点评】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式求事件A或B的概率．19．如图，在四边形ABCD中，E是AB的中点，AD∥EC，∠AED＝∠B．（1）求证：△AED≌△EBC．（2）当AB＝6时，求CD的长．【分析】（1）利用ASA即可证明；（2）首先证明四边形AECD是平行四边形，推出CD＝AE＝AB即可解决问题；【解答】（1）证明：∵AD∥EC，∴∠A＝∠BEC，∵E是AB中点，∴AE＝EB，∵∠AED＝∠B，∴△AED≌△EBC．（2）解：∵△AED≌△EBC，∴AD＝EC，∵AD∥EC，∴四边形AECD是平行四边形，∴CD＝AE，∵AB＝6，∴CD＝AB＝3．【点评】本题考查全等三角形的判定和性质、平行四边形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．20．某超市对今年“元旦”期间销售A、B、C三种品牌的绿色鸡蛋情况进行了统计，并绘制如图所示的扇形统计图和条形统计图．根据图中信息解答下列问题：（1）该超市“元旦”期间共销售2400个绿色鸡蛋，A品牌绿色鸡蛋在扇形统计图中所对应的扇形圆心角是60度；（2）补全条形统计图；（3）如果该超市的另一分店在“元旦”期间共销售这三种品牌的绿色鸡蛋1500个，请你估计这个分店销售的B种品牌的绿色鸡蛋的个数？【分析】（1）用C品牌的数量除以所占的百分比，计算机求出鸡蛋的总量，再用A品牌的百分比乘以360°计算即可求出圆心角的度数；（2）求出B品牌鸡蛋的数量，然后条形补全统计图即可；（3）用B品牌所占的百分比乘以1500，计算即可得解．【解答】解：（1）共销售绿色鸡蛋：1200÷50%＝2400个，A品牌所占的圆心角：×360°＝60°；故答案为：2400，60；（2）B品牌鸡蛋的数量为：2400﹣400﹣1200＝800个，补全统计图如图；（3）分店销售的B种品牌的绿色鸡蛋为：×1500＝500个．【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．21．如图，AB为⊙O的直径，C为⊙O外一点，且∠CAB＝90°，BD是⊙O的弦，BD∥CO．（1）请说明：CD是⊙O的切线：（2）若AB＝4，BC＝2．则阴影部分的面积为π﹣【分析】（1）连接OD，易证△CAO≌△CDO（SAS），由全等三角形的性质可得∠CDO ＝∠CAO＝90°，即CD⊥OD，进而可证明CD是⊙O的切线．（2）过点O作OE⊥BD，垂足为E，首先利用勾股定理可求出AC，OC的长，证得△OBD是等边三角形，根据扇形和三角形的面积公式即可得到结论．【解答】（1）证明：如图，连接OD，∵BD∥CO，∴∠DBO＝∠COA，∠ODB＝∠COD，在⊙O中，OB＝OD，∴∠DBO＝∠ODB，∴∠COA＝∠COD，在△CAO和△CDO中，，∴△CAO≌△CDO（SAS）．，∴∠CDO＝∠CAO＝90°，即CD⊥OD，又∵OD是⊙O的半径，∴CD是⊙O的切线；（2）解：如图，过点O作OE⊥BD，垂足为E．在Rt△ABC中，AC＝＝2，∴OC＝＝4，∴∠AOC＝60°，∵△CAO≌△CDO，∴∠COD＝∠COA＝60°，∴∠BOD＝60°，∴△BOD是等边三角形，∴BD＝OD＝2，OE＝，∴阴影部分的面积＝S扇形BOD﹣S△BOD＝﹣×2×＝π﹣．故答案为：π﹣．【点评】本题考查了切线的判断和性质、全等三角形的判断和性质、勾股定理的运用，正确作出辅助线是解题的关键．22．如图，在东西方向的海岸线MN上有A、B两艘船，均收到已触礁搁浅的船P的求救信号，已知船P在船A的北偏东58°方向，船P在船B的北偏西35°方向，AP的距离为30海里（参考数据：sin32°≈0.53，sin55°≈0.82）．（1）求船P到海岸线MN的距离（精确到0.1海里）；（2）若船A、船B分别以20海里/小时、15海里/小时的速度同时出发，匀速直线前往救援，试通过计算判断哪艘船先到达船P处．【分析】（1）过点P作PE⊥AB于点E，在Rt△APE中解出PE即可；（2）在Rt△BPF中，求出BP，分别计算出两艘船需要的时间，即可作出判断．【解答】解：（1）过点P作PE⊥AB于点E，由题意得，∠P AE＝32°，AP＝30海里，在Rt△APE中，PE＝AP sin∠P AE＝AP sin32°≈15.9海里；（2）在Rt△PBE中，PE＝15.9海里，∠PBE＝55°，则BP＝≈19.4海里，A船需要的时间为：＝1.5小时，B船需要的时间为：≈1.3小时，∵1.5＞1.3，∴B船先到达．【点评】本题考查了解直角三角形的应用，解答本题的关键是理解仰角的定义，能利用三角函数值计算有关线段，难度一般．23．如图，在平面直角坐标系中，直线DE交x轴于点E（30，0），交y轴于点D（0，40），直线AB：y＝x+5交x轴于点A，交y轴于点B，交直线DE于点P，过点E作EF⊥x 轴交直线AB于点F，以EF为一边向右作正方形EFGH．（1）求边EF的长；（2）将正方形EFGH沿射线FB的方向以每秒个单位的速度匀速平移，得到正方形E1F1G1H1，在平移过程中边F1G1始终与y轴垂直，设平移的时间为t秒（t＞0）．①当点F1移动到点B时，求t的值；②当G1，H1两点中有一点移动到直线DE上时，请直接写出此时正方形E1F1G1H1与△APE重叠部分的面积．【分析】（1）根据已知点E（30，0），点D（0，40），求出直线DE的直线解析式y＝﹣x+40，可求出P点坐标，进而求出F点坐标即可；（2））①易求B（0，5），当点F1移动到点B时，t＝10÷＝10；②F点移动到F'的距离是t，F垂直x轴方向移动的距离是t，当点H运动到直线DE上时，在Rt△F'NF中，，EM＝NG'＝15﹣F'N＝15﹣3t，在Rt△DMH'中，，t＝4，S＝＝；当点G运动到直线DE上时，在Rt△F'PK中，，PK＝t﹣3，F'K＝3t﹣9，在Rt△PKG'中，，t＝7，S＝15×（15﹣7）＝120；【解答】解：（1）设直线DE的直线解析式y＝kx+b，将点E（30，0），点D（0，40），∴，∴，∴y＝﹣x+40，直线AB与直线DE的交点P（21，12），由题意知F（30，15），∴EF＝15；（2）①易求B（0，5），∴BF＝10，∴当点F1移动到点B时，t＝10÷＝10；②当点H运动到直线DE上时，F点移动到F'的距离是t，在Rt△F'NF中，，∴FN＝t，F'N＝3t，∵MH'＝FN＝t，EM＝NG'＝15﹣F'N＝15﹣3t，在Rt△DMH'中，，∴，∴t＝4，∴EM＝3，MH'＝4，∴S＝＝；当点G运动到直线DE上时，F点移动到F'的距离是t，∵PF＝3，∴PF'＝t﹣3，在Rt△F'PK中，，∴PK＝t﹣3，F'K＝3t﹣9，在Rt△PKG'中，，∴t＝7，∴S＝15×（15﹣7）＝120；【点评】本题考查一次函数图象及性质，正方形的性质；掌握待定系数法求函数解析式，利用三角形的正切值求边的关系，利用勾股定理在直角三角形中建立边之间的联系，准确确定阴影部分的面积是解题的关键．24．在△ABC中，∠B＝45°，∠C＝30°，点D是边BC上一点，连接AD，将线段AD绕点A逆时针旋转90°，得到线段AE，连接DE．（1）如图①，当点E落在边BA的延长线上时，∠EDC＝90度（直接填空）；（2）如图②，当点E落在边AC上时，求证：BD＝EC；（3）当AB＝2，且点E到AC的距离等于﹣1时，直接写出tan∠CAE的值．【分析】（1）利用三角形的外角的性质即可解决问题．（2）如图2中，作P A⊥AB交BC于P，连接PE．只要证明△BAD≌△P AE（SAS），提出BD＝PE，再证明EC＝2PE即可．（3）如图3，作EF⊥AC于F，延长FE交BC于H，作AG⊥BC于G，P A⊥AB交BC 于P，连接PE．【解答】解：（1）如图1中，∵∠EDC＝∠B+∠BED，∠B＝∠BED＝45°，∴∠EDC＝90°，故答案为90．（2）如图2中，作P A⊥AB交BC于P，连接PE．∵∠DAE＝∠BAP＝90°，∴∠BAD＝∠P AE，∵∠B＝45°，∴∠B＝∠APB＝45°，∴AB＝AP，∵AD＝AE，∴△BAD≌△P AE（SAS），∴BD＝PE，∠APE＝∠B＝45°，∴∠EPD＝∠EPC＝90°，∵∠C＝30°，∴EC＝2PE＝2BD．（3）如图3，作EF⊥AC于F，延长FE交BC于H，作AG⊥BC于G，P A⊥AB交BC于P，连接PE．设PH＝x，在Rt△EPH中，∵∠EPH＝90°，∠EHP＝60°，∴EP＝x，EH＝2PH＝2x，∴FH＝2x+﹣1，CF＝FH＝2x+3﹣，∵△BAD≌△P AE，∴BD＝EP＝x，AE＝AD，在Rt△ABG中，∵AB＝2，∴AG＝GB＝2，在Rt△AGC中，AC＝2AG＝4，∵AE2＝AD2＝AF2+EF2，∴22+（2﹣x）2＝（﹣1）2+（4﹣2x﹣3+）2，整理得：9x2﹣12x＝0，解得x＝（舍弃）或0∴PH＝0，此时E，P，H共点，∴AF＝1+，∴tan∠EAF＝＝＝2﹣．根据对称性可知当点E在AC的上方时，同法可得tan∠EAC＝．【点评】本题属于几何变换综合题，考查了等腰直角三角形的判定和性质，全等三角形的判定和性质，解直角三角形等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考压轴题．25．如图1，在平面直角坐标系中，直线AB：y＝kx+b（k＜0，b＞0），与x轴交于点A、与y轴交于点B，直线CD与x轴交于点C、与y轴交于点D．若直线CD的解析式为y＝﹣（x+b），则称直线CD为直线AB的”姊线”，经过点A、B、C的抛物线称为直线AB的“母线”．（1）若直线AB的解析式为：y＝﹣3x+6，求AB的”姊线”CD的解析式为：y＝（x+6）（直接填空）；（2）若直线AB的”母线”解析式为：，求AB的”姊线”CD的解析式；（3）如图2，在（2）的条件下，点P为第二象限”母线”上的动点，连接OP，交”姊线”CD于点Q，设点P的横坐标为m，PQ与OQ的比值为y，求y与m的函数关系式，并求y的最大值；（4）如图3，若AB的解析式为：y＝mx+3（m＜0），AB的“姊线”为CD，点G为AB 的中点，点H为CD的中点，连接OH，若GH＝，请直接写出AB的”母线”的函数解析式．【分析】（1）由题意得：k＝﹣3，b＝6，即可求解；（2）求出点A、B、C的坐标分别为（2，0）、（0，4）、（﹣4，0），即可求解；（3）设点P的横坐标为m，则点P（m，﹣m2﹣m+4）、计算出点Q坐标，则y＝，即可求解；（4）求出点H（﹣，﹣），点G（﹣，），即可求解．【解答】解：（1）由题意得：k＝﹣3，b＝6，则答案为：y＝（x+6）；（2）令x＝0，则y＝4，令y＝0，则x＝2或﹣4，点A、B、C的坐标分别为（2，0）、（0，4）、（﹣4，0），则直线CD的表达式为：y＝（x+4）＝x+2；（3）设点P的横坐标为m，则点P（m，n），n＝﹣m2﹣m+4，则直线OP的表达式为：y＝x，将直线OP和CD表达式联立并解得：点Q（，）则＝﹣m2﹣m+4，y＝＝﹣m2﹣m+3，当m＝﹣，y最大值为；（4）直线CD的表达式为：y＝﹣（x+3），令x＝0，则y＝﹣，令y＝0，则x＝﹣3，故点C、D的坐标为（﹣3，0）、（0，﹣），则点H（﹣，﹣），同理可得：点G（﹣，），则GH2＝（+）2+（﹣）2＝（）2，解得：m＝﹣3（正值已舍去），则点A、B、C的坐标分别为（1，0）、（0，3）、（﹣3，0），则“母线”函数的表达式为：y＝a（x﹣1）（x+3）＝a（x2﹣2x﹣3），即：﹣3a＝﹣3，解得：a＝1，故：“母线”函数的表达式为：y＝x2﹣2x﹣3．【点评】本题考查的是二次函数综合运用，此类新定义题目，通常按照题设顺序，逐次求解．。

2019年初中学业水平考试模拟测试(二)参考答案 .doc

2019年初中学业水平考试模拟测试（二）参考答案一、选择题（本大题共25题，每小题2分，共50分，在每小题给出的四个选项中，只有一个正确答案）50分）26．（ 12分）（1）苏联（2分）；第一个五年计划（2分）。

（2）中共十一届三中全会（2分）家庭联产承包责任制（1分）（3）国内生产总值年均增长9.5%；中国经济总量成为世界第二大经济体；贫困人口大幅度下降(3分)（4）经济建设要学会借鉴，随着发展要有所创新；坚持党的领导；坚持改革开放。

（任意两点2分）27.（ 13分）（1）瓦特。

（2分）蒸汽时代。

（2分）（2）原因：工业化时期的技术制约；人们对环境污染的漠视；“自由放任”的工业化模式．（3分）（3）科学与技术结合得更紧密了；自然科学特别是热力学、电磁学、化学等方面的新发展与工业生产紧密结合．（任答一点2分）；汽车、飞机。

（2分）（4）科技的发展的同时要重视对环境的保护；要坚持可持续发展，顺应自然，保护生态；运用科技发展可以更好地保护环境。

（2分）28.（12 分）（1）五四运动（1分）；巴黎和会失败，中国代表提出收回山东主权等正义要求，但遭到拒绝，列强还要求把德国在山东的特权转让给日本。

（1分）（2）万隆会议（2分）；提出“求同存异”的方针（1分）万隆会议十项原则。

（1分）（3）多极化趋势（2分）；提出“人类命运共同体”。

（2分）（4）①主权独立是国家外交的前提，综合国力是国家外交的基础，国家利益是外交的根本出发点。

②中国在国际事务中发挥着越来重要的作用，这和我国改革开放以来社会主义现代化建设取得巨大成就、国际地位提高分不开，我们应该坚持改革开放，努力提升综合国力。

③我国始终奉行独立自主的和平外交政策，坚持在和平共处五项原则的基础上，同其他国家发展友好合作关系。

④坚持党的领导，为世界和平、稳定与发展做出更大贡献，努力贡献中国智慧、中国方案。

（能够结合材料，言之有理，答出一点即可得1分。

）29.（ 13分）（1）秦始皇嬴政（1分）；灭六国，统一全国；建立第一个统一的、多民族的、中央集权的封建国家。

2019届河南省九年级下学期第二次模拟考试数学试卷【含答案及解析】

2019届河南省九年级下学期第二次模拟考试数学试卷【含答案及解析】姓名___________ 班级____________ 分数__________一、单选题1. 已知－2的相反数是a，则a是（）A. 2B. －C.D. －22. 函数y=的自变量x的取值范围是（）A. x>0B. x≠1C. x>1且x≠1D. x≥0且x≠13. 解集在数轴上表示为如图所示的不等式组是（）A. B. C. D.4. ．小明把如图所示的4张扑克牌放在一张桌子上,请一位同学避开他任意将其中一张牌旋转倒过来.然后小明很快辨认了哪张牌被倒过来了,那么图中被倒过来的扑克牌点数是（）A. 8B. 6C. 8和5D. 55. 如图是五个棱长为“1”的立方块组成的一个几何体，不是三视图之一的是（）A. B. C. D.6. 如图，⊙O的直径AB＝10，E在⊙O内，且OE=4，则过E点所有弦中，长度为整数的条数为（）A. 4B. 6C. 8D. 10二、填空题7. 随机从甲、乙两块试验田中各抽取100株麦苗测量高度，计算平均数和方差的结果为：=13， =13，，，则小麦长势比较整齐的试验田是 __________．8. 如图，P是∠的边OA上一点，且点P的坐标为（3，4），则sinα=__________.9. 分解因式： ______________.三、解答题10. =_________________四、填空题11. 在平面直角坐标系中，将点P（﹣1，4）向右平移2个单位长度后，再向下平移3个单位长度，得到点，则点的坐标为____________．12. 如图，Rt△AOB中，O为坐标原点，∠AOB=90°，OA∶OB＝1∶2，如果点A在反比例函数y=(x>0)的图像上运动，那么点B在函数 (填函数解析式)的图像上运动．13. 如图，直线y = kx + b经过A（–2，–1）和B（–3，0）两点，则不等式0＜kx + b的解集是___________.五、解答题14. 如图测量电线杆AB的高度，发现电线杆的影子恰好落在土坡的坡面CD和地面BC上，量得CD=4 m，BC=10 m，CD与地面成30°角，且此时测得1m杆的影子长为2 m，则电线杆的高度约为多少m？六、填空题15. 已知点A（1，5），B（3，－1），点M在x轴上，当AM－BM最大时，点M的坐标为__.七、解答题16. 先化简，再求值：，其中；17. 某公司组织部分员工到一博览会的A、B、C、D、E五个展馆参观，公司所购门票种类、数量绘制成的条形和扇形统计图如图所示．请根据统计图回答下列问题：（1）将条形统计图和扇形统计图在图中补充完整；（2）若馆门票仅剩下一张，而员工小明和小华都想要，他们决定采用抽扑克牌的方法来确定，规则是：“将同一副牌中正面分别标有数字1，2，3，4的四张牌洗匀后，背面朝上放置在桌面上，每人随机抽一次且一次只抽一张；一人抽后记下数字，不放回再由另一人抽．若小明抽得的数字比小华抽得的数字大，门票给小明，否则给小华．” 请用画树状图或列表的方法计算出小明和小华获得门票的概率，并说明这个规则对双方是否公平．18. 如图，点C为线段AB上一点，△ACM、△CBN是等边三角形，直线AN、MC交于点E，直线BM、CN交于点F．（1）求证：AN=MB；（2）求证：△CEF为等边三角形；（3）将△ACM绕点C按逆时针方向旋转90°，其他条件不变，在（2）中画出符合要求的图形，并判断（1）（2）题中的两结论是否依然成立．并说明理由．19. 因长期干旱,甲水库蓄水量降到了正常水位的最低值,为灌溉需要,由乙水库向甲水库匀速供水,20h后,甲水库打开一个排灌闸为农田匀速灌溉,又经过20h,甲水库打开另一个排灌闸同时灌溉,再经过40h,乙水库停止供水.甲水库每个排灌闸的灌溉速度相同,图中的折线表示甲水库蓄水量Q(万m3)与时间t(h)之间的函数关系.求: (1)线段BC的函数表达式;(2)乙水库供水速度和甲水库一个排灌闸的灌溉速度;(3)乙水库停止供水后,经过多长时间甲水库蓄水量又降到了正常水位的最低值?20. 台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力，据气象观测，距沿海某城市A的正南方向220千米B处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心现正以15千米/时的速度沿北偏东30°方向往C移动，且台风中心风力不变，若城市所受风力达到或超过四级，则称为受台风影响。

(优质)2019届九年级中考模拟测试卷(二)含答案解析

秘密★启用前2019年中考模拟测试卷（二）九年级物理考生注意：1．一律用黑色笔或2B铅笔将答案填写或填涂在答题卷指定位置内。

2．本试卷共4页，满分90分，答题时间75分钟。

一、选择题（共6小题，每小题3分，共18分。

每小题的4个选项中只有一个选项符合题意，多选、不选、错选均不得分）1．下列物理量中，以科学家的名字“焦耳”作为单位的物理量是A．电压B．电阻C．电流D．电功2．下列关于声现象说法中正确的是A．随着科技进步，物体不振动也能发声B．医生用“B超”给病人做检查，说明声音可以传递信息C．熟悉的人，听声音我们就知道他是谁，是根据不同人的音调来判断的D．学校路段“禁鸣喇叭”，是在传播过程中阻断噪声3．图甲测凸透镜的焦距，图乙“探究凸透镜成像的规律”,在图乙所示的位置光屏上成清晰的像，下列说法正确的是A．图乙中若用遮光板挡住凸透镜的上半部分，光屏上只出现像的下半部分B．图乙中若在凸透镜左侧“戴”上近视眼镜，光屏向右移动才能找到清晰的像C．由图甲可知凸透镜的焦距是40cmD．图乙的成像特点与照相机的成像特点相同4．下列有关热和能的说法中，正确的是A．发生热传递时，温度总是从内能大的物体传递给内能小物体B．一块0℃的冰熔化成0℃的水后，温度不变，内能变大C．内燃机的压缩冲程，主要通过热传递增加了气缸内物质的内能D．夏天在室内洒水降温，利用了水的比热容较大的性质5．图甲所示，放水地面上体，受到方向不变的水平拉F的作用F的大小与时间关如图乙示；物体运动的速度v与时间的如图丙示．则下列说法中正确的（）A．0～2s内物体受摩擦力的作用B．2～4s内物体受到的摩擦力与拉力是一对平衡力C．2～4s内物体做匀速直线运动D．4～6s内拉力做功16J6．如图所示，电源电压为4.5V且保持不变，电压表量程为0～3V，电流表量程为0～0.6A，滑动变阻器R 的规格为“20Ω 1A”，灯泡L标有“2.5V 1.25W”的字样，忽略灯丝电阻的变化，闭合开关S，为了保证各元件都安全，则下列说法中正确的是（）A．向左移动滑片，两表示数都变大B．电流表示数的变化范围是0.3A～0.5AC．滑动变阻器的阻值变化范围是4Ω～20ΩD．整个电路消耗的总功率变化范围是1W～2.25W二、填空题（共7小题，每空1分，共18分。

2019年中考模拟卷二(参考答案)

2019届九年级语文模拟卷（二）参考答案一、（共 12 分，每小题 3 分）1.D（lóu--lòu，新--心）2.D3.A（“视……”与“成为”杂糅）4.B（“居民消费需求”前的逗号改为句号。

后面是前面各项政策措施的结果。

）二、（共9分，每小题3分）5.D（只能浮于表面）6.B（没有目的性）7.B（原文说的是书，不是“书皮学”）三、（共9分，每小题3分）8.D（应为“不信”） 9.B（很惊喜，想把这位考生从众多才士中选为第一名，还是怀疑这文章是他的门客曾巩写的，只把文章列为第二。

） 10.D（欧阳修是赞美苏轼，不是“不得不”）【参考译文】苏轼，字子瞻，是眉州眉山县人。

十岁的时候，其父苏洵到外地去游学，母亲程氏则亲自教他读书，苏轼每听闻古今兴衰成败的历史，都能道出其概要。

程氏读到《后汉书·范滂传》时，发出深深的慨叹，苏轼对她说：“我如果想和范滂一样为名节而不顾生死，母亲您答应吗？”程氏说：“你如果能成为范滂一样的人，我又怎会不和范滂的母亲一样深明大义呢？”到刚成年时，就博览精通经传历史，写文章每天达几千字，喜欢贾谊、陆贽的书。

后来读《庄子》，感叹说：“我从前有些见解，不能表述出来，现在看到这本书，说到我心里了。

”嘉祐二年，参加礼部考试。

当时文章晦涩怪异的弊习很重，主考官欧阳修想加以改正，见到苏轼《刑赏忠厚论》，很惊喜，想把这位考生从众多才士中选为第一名，还是怀疑这文章是他的门客曾巩写的，只把文章列为第二；苏轼又以《春秋》经义策问取得第一，殿试中乙科。

后来苏轼写信谒见欧阳修，欧阳修对梅圣俞说：“我应当避让一下，让这个人出人头地了。

”听到的人开始哗然不服，时间久了就信服此语。

四、（6分）11.母亲程氏则亲自教他读书，苏轼每听闻古今兴衰成败的历史，都能道出其概要。

（“授”“闻”“辄”“要”各1分，语句通顺2分，共6分）五、（22分）12.（1）这个时代的人，情绪变得很多，感觉变得很少；心思变得很复杂，行为变得很单一；脑的容量变得越来越大，使用区域变得越来越小。

教师版陕西省附属中学2019届九年级下学期二模物理试题(教师解析版)

第1页共12页 ◎ 第2页共12页…外…………○学校:_…内…………○绝密★启用前陕西省***附属中学2019届九年级下学期二模物理试题试卷副标题考试范围：xxx ；考试时间：100分钟；命题人：xxx注意事项：1．答题前填写好自己的姓名、班级、考号等信息 2．请将答案正确填写在答题卡上第I 卷（选择题)请点击修改第I 卷的文字说明一、单选题1．为了让同学们养成关注生活和社会的好习惯，物理老师让同学们对身边的一些常见物理量进行估测，你认为最接近实际的是A ．人体的正常体温约37°，一名中学生的体重约50kgB ．学生书桌的高度约为80mm ，教室中日光灯的额定功率约为40WC ．正常人的脉搏是跳一次需2s ，正常步行的速度约为1.1km/hD ．一本物理课本质量约为260g ，西安地区的大气压约为0.98×105 Pa 2．2018年3月19日，我校初三年级的一千多名学生隆重举行“百日冲刺誓师大会”大家群情激昂，宣誓百日冲刺、决战中考。

如图所示为教师代表王老师激情澎湃的发言情景，下列有关说法正确的是A ．坐在后面的同学们通过音调就可判断王老师在讲话，通过扬声器增大声音的响度B ．照相机拍照时物距应大于凸透镜的2倍焦距，若想让照片中的人变大一些，应当将镜头靠近人C ．王老师手持话筒，当增大对话筒的握力时，话筒受到的摩擦力将增大D ．无线话筒是利用超声波传递信息的，速度为3×108m/s 3．如图所示为一种超声波加湿器，通电后利用超声波将水雾化成小水滴并喷出，以下说法正确是A ．水变雾与超声碎石利用了超声波相同的特点B ．加湿器制雾过程中的“白气”是液化、放热过程C ．我们能够看到加湿器底座上白底黑字的商标，是因为字发射的光进入人眼D ．加湿器在工作时将电能转化为内能4．西安交大柴东朗教授研制出目前世界上最轻的金属结构材料━━新型镁锂合金，已应用于我国研制的全球首颗二氧化碳检测科学实验卫星中的高分辨率微纳卫星上。

2019初三化学二模试题及答案

化学试卷2019．6 可能用到的相对原子质量H 1 C 12 N 14 O 16 Na 23 S 32 Ca 40 Fe 56 Cu 64 Zn 65 Ag 108第一部分选择题（每小题只有1个选项符合题意。

共20个小题，每小题1分，共20分）1．下列变化属于物理变化的是A.苹果腐烂B.榨取果汁C.面包发霉D.菜刀生锈2.以下饮品不属于溶液的是A. 啤酒B. 酸奶C. 矿泉水D.可口可乐3.下列做法不能减少PM2.5污染的是A．绿色出行 B. 使用新能源汽车 C．火力发电 D. 使用太阳能热水器4.下列用品不属于有机合成材料的是A．尼龙伞布B．塑料牙刷C．陶瓷餐具D．橡胶轮胎5.下列比较中，不符合实际的是A.空气中氮气的含量比氧气多B.苹果醋比食盐水的pH小C.铁门窗比铝合金门窗更耐腐蚀D.化肥KNO3比NH4NO3营养元素种类多[6．下列化学符号中，数字“2”表示的意义不正确的是A. 2Na：两个钠元素B. 2OH-：两个氢氧根离子C.2Mg：镁元素的化合价为+2价 D. NO2：一个二氧化氮分子含有两个氧原子7．锰丝放入稀硫酸中，有气泡产生，放入硫酸铝溶液中，表面没有金属析出。

下列关于锰活动性判断不正确的是A．Mn > Cu B．Al > Mn C．Mn > H D．Mn > Mg8．偏钛酸钡（Ba x TiO3）广泛应用于超声波发生装置中。

已知偏钛酸钡中钛元素的化合价为+4价，则其化学式中x的数值为A．1 B．2 C．3 D．49.证明汽水中含有CO2气体，最合理的做法是10．尼泊尔地震发生后，饮用水源受到污染，为保证居民正常生活，用下述方法处理饮用水源：①消毒②自然沉降③过滤。

处理的先后顺序是A．②③①B．②①③C．③②①D．③①②11.干冰用于人工降雨，当飞机喷洒干冰后，云层中不会发生变化的是A. 水分子间的间隔B. 水分子运动速率C. 二氧化碳分子间间隔D. 二氧化碳分子的大小12.下列说法不合理的是A．pH＜7的雨水称为酸雨 B．使用乙醇汽油能节约石油资源C．使用可降解塑料减少白色污染 D．温室效应主要由CO2等气体引起13．下列物质溶于水时，溶液温度明显降低的是A．氯化钠 B.硝酸铵 C.氧化钙 D.氢氧化钠14．下列实验设计不能达到目的的是15. 下列叙述正确的是A生活常识用甲醛溶液浸泡海产品保鲜B 健康常识不能吃含黄曲霉素的食物C安全常识浓硫酸沾在皮肤上，涂NaOH溶液D环保常识将煤制成煤粉燃烧，可防止空气污染16．工业上用甲、乙制备化学肥料丙，同时生成丁。

2019版中考数学二模(4月)试卷(含解析)

2019版中考数学二模（4月）试卷（含解析）一．选择题（共10小题，满分30分，每小题3分）1．下列计算正确的是（）A．＝﹣3 B．C．5×5＝5 D．＝22．阅读材料：设一元二次方程ax2+bx+c＝0（a≠0）的两根为x1，x2，则两根与方程系数之间有如下关系：x1+x2＝﹣，x1•x2＝．根据该材料填空：已知x1，x2是方程x2+6x+3＝0的两实数根，则+的值为（）A．4 B．6 C．8 D．103．已知二次函数y＝ax2+bx+c（a≠0）的图象如图，在下列代数式中（1）a+b+c＞0；（2）﹣4a＜b＜﹣2a（3）abc＞0；（4）5a﹣b+2c＜0；其中正确的个数为（）A．1个B．2个C．3个D．4个4．如图所示，直角三角形AOB中，AB⊥OB，且AB＝OB＝3．设直线l：x＝t截此三角形所得的阴影部分面积为S，则S与t之间的函数关系的图象为（如选项所示）（）A．B．C．D．5．如图所示，△ABC中，AB＝AC，过AC上一点作DE⊥AC，EF⊥BC，若∠BDE＝140°，则∠DEF＝（）A．55°B．60°C．65°D．70°6．如图△ABC绕点B顺时针旋转，旋转角是∠ABC，那么下列说法错误的是（）A．BC平分∠ABE B．AB＝BD C．AC∥BE D．AC＝DE7．在同一时刻的阳光下，小明的影子比小强的影子长，那么在同一路灯下（）A．小明的影子比小强的影子长B．小明的影子比小强的影子短C．小明的影子和小强的影子一样长D．无法判断谁的影子长8．如图，矩形ABCD中，AB＝3，AD＝，将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF，此时恰好四边形AEHB为菱形，连接CH交FG于点M，则HM＝（）A．B．1 C．D．9．如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为（）A．B．C．D．10．现定义一种变换：对于一个由有限个数组成的序列S0，将其中的每个数换成该数在S0中出现的次数，可得到一个新序列S1，例如序列S0：（4，2，3，4，2），通过变换可生成新序列S1：（2，2，1，2，2），若S0可以为任意序列，则下面的序列可作为S1的是（）A．（1，2，1，2，2）B．（2，2，2，3，3）C．（1，1，2，2，3）D．（1，2，1，1，2）二．填空题（共6小题，满分18分，每小题3分）11．若＝x﹣4+6﹣x＝2，则x的取值范围为．12．符号“”称为二阶行列式，规定它的运算法则为：＝ad﹣bc，请你根据上述规定求出下列等式中x的值．若，那么x＝．13．如图，把“QQ”笑脸放在直角坐标系中，已知左眼A的坐标是（﹣2，3），嘴唇C的坐标为（﹣1，1），若把此“QQ”笑脸向右平移3个单位长度后，则与右眼B对应的点的坐标是．14．如图，在一个正方形围栏中均匀散布着许多米粒，正方形内画有一个圆．一只小鸡在围栏内啄食，则“小鸡正在圆圈内”啄食的概率为．15．如图，在△ABC中，BC＝6，以点A为圆心，2为半径的⊙A与BC相切于点D，交AB于点E，交AC于点F，点P是优弧EF上的一点，且∠EPF＝50°，则图中阴影部分的面积是．16．△ABC中，AB＝4，AC＝2，以BC为边在△ABC外作正方形BCDE，BD、CE交于点O，则线段AO 的最大值为．三．解答题（共7小题，满分10分）17．先化简，再求值：（）•（﹣），其中x＝2+，y＝2﹣．18．解不等式组，并在数轴上表示其解集．19．如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作AF∥BC交BE的延长线于点F，连接CF．（1）求证：AF＝DC；（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．20．如图，在Rt△ACB中，∠C＝90°，AC＝3cm，BC＝4cm，以BC为直径作⊙O交AB于点D．（1）求线段AD的长度；（2）点E是线段AC上的一点，试问：当点E在什么位置时，直线ED与⊙O相切？请说明理由．21．（10分）某校八年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如下表，并绘制了如图所示的两幅不完整的统计图，已知B、E两组发言人数的比为5：2，请结合图中相关数据回答下列问题：发言次数nA0≤n＜3B3≤n＜6C6≤n＜9D9≤n＜12E12≤n＜15F15≤n＜18（1）求出样本容量，并补全直方图；（2）该年级共有学生500人，请估计全年级在这天里发言次数不少于12次的人数；（3）已知A组发言的学生中恰有1位女生，E组发言的学生中有2位男生．现从A组与E组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好是一男一女的概率．22．如图，在平面直角坐标系中，直线y＝kx﹣4k+4与抛物线y＝x2﹣x交于A、B两点．（1）直线总经过定点，请直接写出该定点的坐标；（2）点P在抛物线上，当k＝﹣时，解决下列问题：①在直线AB下方的抛物线上求点P，使得△PAB的面积等于20；②连接OA，OB，OP，作PC⊥x轴于点C，若△POC和△ABO相似，请直接写出点P的坐标．23．王华在学习相似三角形时，在北京市义务教育教科书九年级上册第31页遇到这样一道题，如图1，在△ABC中，P是边AB上的一点，连接CP，要使△ACP∽△ABC，还需要补充的一个条件是，或．请回答：（1）王华补充的条件是，或．（2）请你参考上面的图形和结论，探究，解答下面的问题：如图2，在△ABC中，∠A＝30°，AC2＝AB2+AB•BC．求∠C的度数．2019年北京市海淀区中国农业大学附属中学中考数学二模试卷（4月份）参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．【分析】根据二次根式的性质对A进行判断；根据二次根式的加减运算对B进行判断；根据二次根式的乘法法则对C进行判断；根据二次根式的除法法则对D进行判断．【解答】解：A、原式＝3，所以A选项错误；B、与不能合并，所以B选项错误；C、原式＝25，所以C选项错误；D、原式＝＝2，所以D选项正确．故选：D．【点评】本题考查了二次根式的混合运算：先把二次根式化为最简二次根式，然后合并同类二次根式即可．在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．2．【分析】根据一元二次方程的根与系数的关系得到，两根之和与两根之积，把代数式变形成与两根之和和两根之积有关的式子，代入两根之和与两根之积，求得代数式的值．【解答】解：∵x1，x2是方程x2+6x+3＝0的两实数根，∴x1+x2＝﹣＝﹣6，x1•x2＝＝3，则+＝＝＝＝10．故选：D．【点评】本题考查了一元二次方程根与系数的关系．解此类题目要会将代数式变形为两根之积或两根之和的形式，代入数值计算即可．一元二次方程ax2+bx+c＝0（a≠0）的根与系数的关系为：x1+x2＝﹣，x1•x2＝．3．【分析】由抛物线开口向上得到a大于0，再由对称轴在y轴右侧得到a与b异号，即b小于0，由抛物线与y轴交于正半轴，得到c大于0，可得出abc的符合，对于（3）作出判断；由x＝1时对应的函数值小于0，将x＝1代入二次函数解析式得到a+b+c小于0，（1）错误；根据对称轴在1和2之间，利用对称轴公式列出不等式，由a大于0，得到﹣2a小于0，在不等式两边同时乘以﹣2a，不等号方向改变，可得出不等式，对（2）作出判断；由x＝﹣1时对应的函数值大于0，将x＝﹣1代入二次函数解析式得到a﹣b+c大于0，又4a大于0，c大于0，可得出a﹣b+c+4a+c 大于0，合并后得到（4）正确，综上，即可得到正确的个数．【解答】解：由图形可知：抛物线开口向上，与y轴交点在正半轴，∴a＞0，b＜0，c＞0，即abc＜0，故（3）错误；又x＝1时，对应的函数值小于0，故将x＝1代入得：a+b+c＜0，故（1）错误；∵对称轴在1和2之间，∴1＜﹣＜2，又a＞0，∴在不等式左右两边都乘以﹣2a得：﹣2a＞b＞﹣4a，故（2）正确；又x＝﹣1时，对应的函数值大于0，故将x＝﹣1代入得：a﹣b+c＞0，又a＞0，即4a＞0，c＞0，∴5a﹣b+2c＝（a﹣b+c）+4a+c＞0，故（4）错误，综上，正确的有1个，为选项（2）．故选：A．【点评】此题考查了二次函数图象与系数的关系，利用了数形结合的思想，二次函数y＝ax2+bx+c （a≠0），a的符号由抛物线的开口决定；b的符号由a及对称轴的位置确定；c的符号由抛物线与y轴交点的位置确定，此外还有注意利用特殊点1，﹣1及2对应函数值的正负来解决问题．4．【分析】由题意得到三角形AOB为等腰直角三角形，进而确定出三角形COD为等腰直角三角形，表示出S与t的函数解析式，画出大致图象即可．【解答】解：∵Rt△AOB中，AB＝OB＝3，∴△AOB为等腰直角三角形，∵直线l∥AB，∴△OCD为等腰直角三角形，即CD＝OD＝t，∴S＝t2（0≤t≤3），画出大致图象，如图所示，．故选：D．【点评】此题考查了动点问题的函数图象，熟练掌握二次函数的图象与性质是解本题的关键．5．【分析】由DE⊥AC，∠BDE＝140°，可计算出∠A，再利用等腰三角形的性质求出∠C，最后利用EF⊥BC及同角的余角相等得到∠DEF的度数．【解答】解：∵DE⊥AC，∠BDE＝140°，∴∠A＝50°，又∵AB＝AC，∴∠C＝＝65°，∵EF⊥BC，∴∠DEF＝∠C＝65°．所以A错，B错，C对，D错．故选C．【点评】考查了垂直的性质，等腰三角形的性质和三角形的外角性质．6．【分析】由△ABC绕点B顺时针旋转，旋转角是∠ABC，根据旋转的性质得到BD＝BA，BE＝BC，∠DBE＝∠ABC，即可对选项进行判断．【解答】解：∵△ABC绕点B顺时针旋转，旋转角是∠ABC，∴BA的对应边为BD，BC的对应边为BE，∴BD＝BA，BE＝BC，∠DBE＝∠ABC，所以A，B，D选项正确，C选项不正确．故选：C．【点评】本题考查了旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．7．【分析】在同一路灯下由于位置不同，影长也不同，所以无法判断谁的影子长．【解答】解：在同一路灯下由于位置不同，影长也不同，所以无法判断谁的影子长．故选：D．【点评】本题综合考查了平行投影和中心投影的特点和规律．平行投影的特点是：在同一时刻，不同物体的物高和影长成比例．中心投影的特点是：①等高的物体垂直地面放置时，在灯光下，离点光源近的物体它的影子短，离点光源远的物体它的影子长．②等长的物体平行于地面放置时，在灯光下，离点光源越近，影子越长；离点光源越远，影子越短，但不会比物体本身的长度还短．8．【分析】由旋转的性质得到AB＝BE，根据菱形的性质得到AE＝AB，推出△ABE是等边三角形，得到AB＝3，AD＝，根据三角函数的定义得到∠BAC＝30°，求得AC⊥BE，推出C在对角线AH上，得到A，C，H共线，于是得到结论．【解答】解：∵将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF，∴AB＝BE，∵四边形AEHB为菱形，∴AE＝AB，∴AB＝AE＝BE，∴△ABE是等边三角形，∵AB＝3，AD＝，∴tan∠CAB＝＝，∴∠BAC＝30°，∴AC⊥BE，∴C在对角线AH上，∴A，C，H共线，∴AO＝OH＝AB＝，∵OC＝BC＝，∵∠COB＝∠OBG＝∠G＝90°，∴四边形OBGM是矩形，∴OM＝BG＝BC＝，∴HM＝OH﹣OM＝故选：D．【点评】本题考查了旋转的性质，矩形的性质，解直角三角形，菱形的性质，正确的作出辅助线是解题的关键．9．【分析】算出阴影部分的面积及大正方形的面积，这个比值就是所求的概率．【解答】解：设小正方形的边长为1，则其面积为1．∵圆的直径正好是大正方形边长，∴根据勾股定理，其小正方形对角线为，即圆的直径为，∴大正方形的边长为，则大正方形的面积为×＝2，则小球停在小正方形内部（阴影）区域的概率为．故选：C．【点评】用到的知识点为：概率＝相应的面积与总面积之比；难点是得到两个正方形的边长的关系．10．【分析】根据题意可知，S1中2有2的倍数个，3有3的倍数个，据此即可作出选择．【解答】解：A、∵2有3个，∴不可以作为S1，故A选项错误；B、∵2有3个，∴不可以作为S1，故B选项错误；C、3只有1个，∴不可以作为S1，故C选项错误；D、符合定义的一种变换，故D选项正确．故选：D．【点评】考查了规律型：数字的变化类，探究题是近几年中考命题的亮点，尤其是与数列有关的命题更是层出不穷，形式多样，它要求在已有知识的基础上去探究，观察思考发现规律．二．填空题（共6小题，满分18分，每小题3分）11．【分析】直接利用二次根式的性质得出关于x的不等关系进而得出答案．【解答】解：∵＝x﹣4+6﹣x＝2，∴x﹣4≥0，x﹣6≤0，解得：4≤x≤6．故答案为：4≤x≤6．【点评】此题主要考查了二次根式的性质与化简，正确掌握二次根式的性质是解题关键．12．【分析】根据已知得出分式方程﹣＝1，求出分式方程的解，再代入x﹣1和1﹣x进行检验即可．【解答】解：∵，∴﹣＝1，方程两边都乘以x﹣1得：2+1＝x﹣1，解得：x＝4，检验：当x＝4时，x﹣1≠0，1﹣x≠0，即x＝4是分式方程的解，故答案为：4．【点评】本题考查了分式方程的应用，解此题的关键是根据材料得出分式方程，题目具有一定的代表性，是一道比较好的题目．13．【分析】根据点A的坐标，在点A的右侧2个单位作y轴，点A的下方3个单位作x轴，建立平面直角坐标系，然后根据右眼的坐标，求得向右平移3个单位长度后的对应点的坐标即可．【解答】解：如图，根据左眼A的坐标是（﹣2，3），建立直角坐标系，∵右眼B的坐标为（0，3），∴向右平移3个单位后，右眼的坐标为（3，3）．故答案为：（3，3）【点评】本题以平移变换为背景，考查了坐标系中点的平移规律．在平面直角坐标系中，平移点的变化规律是：横坐标，右移加，左移减；纵坐标，上移加，下移减．确定出直角坐标系的位置是解题的关键．14．【分析】设正方形的边长为a，再分别计算出正方形与圆的面积，计算出其比值即可．【解答】解：设正方形的边长为a，则S正方形＝a2，因为圆的半径为，所以S圆＝π＝，所以“小鸡正在圆圈内”啄食的概率为：＝．【点评】解答此题的关键是求出正方形及圆的面积，用到的知识点为：概率＝相应的面积与总面积之比．15．【分析】由于BC切⊙A于D，连接AD可知AD⊥BC，从而可求出△ABC的面积；根据圆周角定理，易求得∠EAF＝2∠EPF＝100°，圆的半径为2，可求出扇形AEF的面积；图中阴影部分的面积＝△ABC的面积﹣扇形AEF的面积．【解答】解：连接AD，∵BC是切线，点D是切点，∴AD⊥BC，∴∠EAF＝2∠EPF＝100°，∴S扇形AEF＝＝π，S△ABC＝AD•BC＝×2×6＝6，∴S阴影部分＝S△ABC﹣S扇形AEF＝6﹣π．故答案为：6﹣π．【点评】本题考查了切线的性质，圆周角和圆心角的关系，扇形的面积等，求得∠EAF＝100°是关键．16．【分析】以AO为边作等腰直角△AOF，且∠AOF＝90°，由题意可证△AOB≌△FOC，可得AB＝CF＝4，根据三角形的三边关系可求AF的最大值，即可得AO的最大值．【解答】解：如图：以AO为边作等腰直角△AOF，且∠AOF＝90°∵四边形BCDE是正方形∴BO＝CO，∠BOC＝90°∵△AOF是等腰直角三角形∴AO＝FO，AF＝AO∵∠BOC＝∠AOF＝90°∴∠AOB＝∠COF，且BO＝CO，AO＝FO∴△AOB≌△FOC（SAS）∴AB＝CF＝4若点A，点C，点F三点不共线时，AF＜AC+CF；若点A，点C，点F三点共线时，AF＝AC+CF∴AF≤AC+CF＝2+4＝6∴AF的最大值为6∵AF＝AO∴AO的最大值为3．故答案为：3【点评】本题考查了旋转的性质，正方形的性质，全等三角形的判定和性质，以及三角形的三边关系，恰当添加辅助线构造全等三角形是本题的关键．三．解答题（共7小题，满分10分）17．【分析】根据分式的减法和乘法可以化简题目中的式子，然后将x、y的值代入化简后的式子即可解答本题．【解答】解：（）•（﹣）＝＝＝，当x＝2+，y＝2﹣时，原式＝＝﹣＝﹣4．【点评】本题考查分式的化简求值、分母有理化，解答本题的关键是明确分式化简求值的方法．18．【分析】分别解两个不等式，找出其解集的公共部分即不等式组的解集，再把不等式组的解集在数轴上表示出来即可．【解答】解：解不等式①，得：x＜3，解不等式②，得：x＞﹣1，则不等式组的解集为﹣1＜x＜3，将不等式的解集表示在数轴上如下：【点评】本题考查解一元一次不等式组和在数轴上表示不等式的解集，正确掌握解不等式组的方法是解决本题的关键．19．【分析】（1）证△AEF≌△DEB得AF＝DB，再证出DB＝DC即可．（2）四边形ADCF是菱形，先证明四边形ADCF是平行四边形，再证出AF＝AD即可．【解答】（1）证明：∵AF∥CD，E是AD的中点∴∠AFE＝∠DBE，EF＝EB又∠AEF＝∠DEB∴△AEF≌△DEB（ASA）∴AF＝DB∵AD是BC边上的中线∴DB＝DC∴AF＝DC，（2）四边形ADCF是菱形．证明：∵由（1）知AF＝CD，又AF∥CD∴四边形ADCF是平行四边形，∵AB⊥AC∴△ABC是直角三角形∵AD是BC边上的中线∴AD＝DC＝DB∵AF＝CD，∴AF＝AD∴四边形ADCF是菱形．【点评】本题利用了全等三角形的判定和性质、平行四边形的判定和性质、菱形的判定和性质等．20．【分析】（1）由勾股定理易求得AB的长；可连接CD，由圆周角定理知CD⊥AB，易知△ACD∽△ABC，可得关于AC、AD、AB的比例关系式，即可求出AD的长．（2）当ED与⊙O相切时，由切线长定理知EC＝ED，则∠ECD＝∠EDC，那么∠A和∠DEC就是等角的余角，由此可证得AE＝DE，即E是AC的中点．在证明时，可连接OD，证OD⊥DE即可．【解答】解：（1）在Rt△ACB中，∵AC＝3cm，BC＝4cm，∠ACB＝90°，∴AB＝5cm；连接CD，∵BC为直径，∴∠ADC＝∠BDC＝90°；∵∠A＝∠A，∠ADC＝∠ACB，∴Rt△ADC∽Rt△ACB；∴，∴；（2）当点E是AC的中点时，ED与⊙O相切；证明：连接OD，∵DE是Rt△ADC的中线；∴ED＝EC，∴∠EDC＝∠ECD；∵OC＝OD，∴∠ODC＝∠OCD；∴∠EDO＝∠EDC+∠ODC＝∠ECD+∠OCD＝∠ACB＝90°；∴ED⊥OD，∴ED与⊙O相切．【点评】此题综合考查了圆周角定理、相似三角形的判定和性质、直角三角形的性质、切线的判定等知识．21．【分析】（1）根据B、E两组的发言人数的比求出B组发言人数所占的百分比，再根据条形统计图中B组的人数为10，列式计算即可求出被抽取的学生人数，然后求出C组、F组的人数，补全直方图即可；（2）根据扇形统计图求出F组人数所占的百分比，再用总人数乘以E、F两组人数所占的百分比，计算即可得解；（3）分别求出A、E两组的人数，确定出各组的男女生人数，然后列表或画树状图，再根据概率公式计算即可得解．【解答】解：（1）∵B、E两组发言人数的比为5：2，E组发言人数占8%，∴B组发言的人数占20%，由直方图可知B组人数为10人，所以，被抽查的学生人数为：10÷20%＝50人，C组人数为：50×30%＝15人，B组人数所占的百分比为：×100%＝20%，F组的人数为：50×（1﹣6%﹣20%﹣30%﹣26%﹣8%），＝50×（1﹣90%），＝50×10%，＝5，∴样本容量为50人．补全直方图如图；（2）F组发言的人数所占的百分比为：10%，所以，估计全年级在这天里发言次数不少于12次的人数为：500×（8%+10%）＝90人；（3）A组发言的学生：50×6%＝3人，所以有1位女生，2位男生，E组发言的学生：50×8%＝4人，所以有2位女生，2位男生，列表如下：画树状图如下：共12种情况，其中一男一女的情况有6种，所以P（一男一女）＝＝．【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题，本题根据B组的人数与所占的百分比求解是解题的关键，也是本题的突破口．22．【分析】（1）变形为不定方程k（x﹣4）＝y﹣4，然后根据k为任意不为0的实数得到x﹣4＝0，y﹣4＝0，然后求出x、y即可得到定点的坐标；（2）通过解方程组得A（6，3）、B（﹣4，8）；①如图1，作PQ∥y轴，交AB于点Q，设P（x， x2﹣x），则Q（x，﹣ x+6），则PQ＝（﹣x+6）﹣（x2﹣x），利用三角形面积公式得到S△PAB＝﹣（x﹣1）2+＝20，然后解方程求出x即可得到点P的坐标；②设P（x， x2﹣x），如图2，利用勾股定理的逆定理证明∠AOB＝90°，根据三角形相似的判定，由于∠AOB＝∠PCO，则当＝时，△CPO∽△OAB，即＝；当＝时，△CPO∽△OBA，即＝，然后分别解关于x的绝对值方程即可得到对应的点P的坐标．【解答】解：（1）∵y＝kx﹣4k+4＝k（x﹣4）+4，即k（x﹣4）＝y﹣4，而k为任意不为0的实数，∴x﹣4＝0，y﹣4＝0，解得x＝4，y＝4，∴直线过定点（4，4）；（2）当k＝﹣时，直线解析式为y＝﹣x+6，解方程组得或，则A（6，3）、B（﹣4，8）；①如图1，作PQ∥y轴，交AB于点Q，设P（x， x2﹣x），则Q（x，﹣ x+6），∴PQ＝（﹣x+6）﹣（x2﹣x）＝﹣（x﹣1）2+，∴S△PAB＝（6+4）×PQ＝﹣（x﹣1）2+＝20，解得x1＝﹣2，x2＝4，∴点P的坐标为（4，0）或（﹣2，3）；②设P（x， x2﹣x），如图2，由题意得：AO＝3，BO＝4，AB＝5，∵AB2＝AO2+BO2，∴∠AOB＝90°，∵∠AOB＝∠PCO，∴当＝时，△CPO∽△OAB，即＝，整理得4|x2﹣x|＝3|x|，解方程4（x2﹣x）＝3x得x1＝0（舍去），x2＝7，此时P点坐标为（7，）；解方程4（x2﹣x）＝﹣3x得x1＝0（舍去），x2＝1，此时P点坐标为（1，﹣）；当＝时，△CPO∽△OBA，即＝，整理得3|x2﹣x|＝4|x|，解方程3（x2﹣x）＝4x得x1＝0（舍去），x2＝，此时P点坐标为（，）；解方程3（x2﹣x）＝﹣4x得x1＝0（舍去），x2＝﹣，此时P点坐标为（﹣，）综上所述，点P的坐标为：（7，）或（1，﹣）或（﹣，）或（，）．【点评】本题考查了二次函数综合题：熟练掌握二次函数图象上点的坐标特征和相似三角形的判定方法；会利用待定系数法求抛物线解析式，通过解方程组求两函数图象的交点坐标，会解一元二次方程；理解坐标与图形性质；会运用分类讨论的思想解决思想问题．23．【分析】（1）由∠A＝∠A，当∠ACP＝∠B，或∠APC＝∠ACB；或时，△ACP∽△ABC；（2）延长AB到点D，使BD＝BC，连接CD，由已知条件得出证出，由∠A＝∠A，证出△ACB∽△ADC，得出对应角相等∠ACB＝∠D，再由等腰三角形的性质和三角形内角和定理得出∠ACB+∠BCD+∠D+∠A＝180°，得出∠ACB＝50°即可．【解答】解：∵∠A＝∠A，∴当∠ACP＝∠B，或∠APC＝∠ACB；或，即AC2＝AP•AB时，△ACP∽△ABC；故答案为：∠ACP＝∠B（或∠APC＝∠ACB），或AC2＝AP•AB；（1）王华补充的条件是：∠ACP＝∠B（或∠APC＝∠ACB）；或AC2＝AP•AB；理由如下：∵∠A＝∠A，∴当∠ACP＝∠B，或∠APC＝∠ACB；或，即AC2＝AP•AB时，△ACP∽△ABC；故答案为：∠ACP＝∠B（或∠APC＝∠ACB），或AC2＝AP•AB；（2）延长AB到点D，使BD＝BC，连接CD，如图所示：∵AC2＝AB2+AB•BC＝AB（AB+BC）＝AB（AB+BD）＝AB•AD，∴，又∵∠A＝∠A，∴△ACB∽△ADC，∴∠ACB＝∠D，∵BC＝BD，∴∠BCD＝∠D，在△ACD中，∠ACB+∠BCD+∠D+∠A＝180°，∴3∠ACB+30°＝180°，∴∠ACB＝50°．【点评】本题考查了相似三角形的判定与性质、等腰三角形的性质、三角形内角和定理；本题中（2）有一定难度，需要通过作辅助线证明三角形相似才能得出结果．。

2019年上海各区初三二模数学试卷25题专题汇编(教师版)

2019年上海各区初三二模数学试卷25题专题汇编（教师版）题型一、等腰三角形的分类讨论思路点拨：出现概率较高题型，重点。

解决此类问题主要通过两个方面解决：1.一方面从边方面入手，将此三角形的三边用x y 或的表达式表示，根据腰相等建立方程求出线段长度（优点：方法简单，易理解；缺点：计算量偏大，易出错）；2.另一方面从角方面入手，利用等腰产生的底角相等转化出其他的角度关系或边长关系进而建立方程求出线段的长度（优点：计算量偏小，易计算，缺点：此方法对于孩子的分析能力要求较高，适合一部分程度较好的学生）。

25(2019崇明)、如图，在梯形ABCD 中，AD ∥BC ，AB=DC=8，BC=12，cos C=53，点E 为AB 边上一点，且BE=2，点F 是BC 边上的一个动点（与点B 、点C 不重合），点G 在射线CD 上，且∠EFG=∠B ，设BF 的长为x ，CG 的长为y .（1）当点G 在线段DC 上时，求y 与x 之间的函数关系式，并写出自变量x 的取值范围；（2）当以点B 为圆心，BF 长为半径的⊙B 与以点C 为圆心，CG 长为半径的⊙C 相切时，求线段BF 的长；（3）当△CFG 为等腰三角形时，直接写出线段BF 的长.题型二、动点产生的相似综合思路点拨：1.首先寻找题目中特殊的条件和不变的量，并找出由条件引发的一些相等角、相等线段等特殊条件；（挖掘题目中的隐藏条件）2.然后注意分类讨论，先找到对应相等的角，再决定分类讨论情况：3.相似三角形的边如果能直接求出列等式最好，如果不能求出，注意转化相似（是否产生新的相似、等腰、平行四边形等更特殊的条件）.25(2019黄浦)．（本题满分14分）已知四边形ABCD 中，AD ⊙BC ，2ABC C ∠=∠，点E 是射线AD 上一点，点F 是射线DC 上一点，且满足BEF A ∠=∠.（1）如图8，当点E 在线段AD 上时，若AB=AD ，在线段AB 上截取AG=AE ，联结GE .求证：GE=DF ；（2）如图9，当点E 在线段AD 的延长线上时，若AB =3，AD =4，1cos 3A =，设AE x =，DF y =，求y 关于x 的函数关系式及其定义域；（3）记BE 与CD 交于点M ，在（2）的条件下，若⊙EMF 与⊙ABE 相似，求线段AE 的长.25.解：（1）∵AG AE =，∴1802AAGE ︒-∠∠=.∵AD ∥BC ，∴180A ABC ∠+∠=︒， ∵2ABC C ∠=∠，∴1802AC ︒-∠∠=，∴AGE C ∠=∠，---------------------------------（1分）∵AD ∥BC ，∴180D C ∠+∠=︒，又180BGE AGE ∠+∠=︒，∴BGE D ∠=∠.----------（1分） ∵BEF FED A GBE ∠+∠=∠+∠，∵BEF A ∠=∠，∴FED GBE ∠=∠ .--------------（1分）又AB=AD ，AG=AE ，∴BG=ED ，∴GBE ∆≌DEF ∆，∴GE=DF . --------------------------（1分）（2）在射线AB 上截取AH=AE ，联结EH . ------------------------------------------------------------（1分）∵HBE A AEB ∠=∠+∠，DEF BEF AEB ∠=∠+∠，又BEF A ∠=∠，∴HBE DEF ∠=∠. ∵AD ∥BC ，∴EDC C ∠=∠，180A ABC ∠+∠=︒.∵AH=AE ，∴1802AH ︒-∠∠=，又2ABC C ∠=∠，∴H C ∠=∠，∴H EDC ∠=∠，∴BHE ∆∽EDF ∆.-------------------（1分） ∴BH EH ED DF =.过点H 作HP ⊥AE ，垂足为点P .∵1cos 3A =，AE AH x ==， ∴13AP x =，223PH x =，23PE x =，∴233EH x =.-------------------------------------（1分） ∵AB =3，AD =4，AE x =，DF y =，∴23334xx x y -=-，∴()22383439x x y x x -=>-.（2分）（3）记EH 与BC 相交于点N .∵EMF ∆∽ABE ∆，BEF A ∠=∠，∴AEB EMF ∠=∠，或AEB EFM ∠=∠.-------------（1分）若AEB EMF ∠=∠，又AEB EMF ∠<∠，矛盾，∴此情况不存在. -----------------------------（1分）若AEB EFM ∠=∠，∵BHE ∆∽EDF ∆，∴BEH EFM ∠=∠，∴AEB BEH ∠=∠.------（1分） ∵AD ∥BC ，∴AEB EBC ∠=∠，∴BEH EBC ∠=∠，∴3BN EN BH x ===-,D A BCEF 图9ABCE F G D图8∵AD ∥BC ，∴AB ENAH EH=，∴3x =，∴3x =.----------------------------------（2分） ∴线段AE的长为3.25(2019金山)、如图，在Rt △ABC 中，∠CC=90°，AC=16cm ，AB=20cm ，动点D 由点C 向点A 以每秒1cm 速度在边AC 上运动，动点E 由点C 向点B 以每秒34cm 速度在边BC 上运动，若点D 、点E 从点C 同时出发，运动t 秒（t > 0），联结DE. （1）求证：△DCE ∽△BCA ；（2）设经过点D 、C 、E 三点的圆为⊙P. ① 当⊙P 与边AB 相切时，求t 的值；② 在点D 、点E 运动过程中，若⊙P 与边AB 交于点F 、G （点F 在点G 左侧），联结CP 并延长CP 交边AB 于点M ，当△PFM 与△CDE 相似时，求t 的值.25（2019长宁）、如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，点P在边AC上（点P与点A不重合），以点P为圆心，PA为半径作⊙P交边AB于另一点D，ED⊥DP，交边BC于点E.（1）求证：BE=DE；（2）若BE=x，AD=y，求y关于x的函数关系式并写出定义域；（3）延长ED交CA延长线于点F，联结BP，若△BDP与△DAF相似，求线段AD的长.题型三、动点产生的面积问题思路点拨：首先考虑底乘以高。

2019年中考数学二模试卷(含解析)

2019年中考数学二模试卷一、选择题（本大题共8小题，每小题3分，共24分，在每小题所给出的四个选项中，只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置上）1．（3分）下列四个数，表示无理数的是（）A．sin30°B．πC．D．2．（3分）下列四种标志图案中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．3．（3分）下列各式正确的是（）A．6a2﹣5a2＝a2B．（2a）2＝2a2C．﹣2（a﹣1）＝﹣2a+1D．（a+b）2＝a2+b24．（3分）如图所示，直线a、b、c、d的位置如图所示，若∠1＝125°，∠2＝125°，∠3＝135°，则∠4的度数为（）A．45°B．55°C．60°D．65°5．（3分）某工艺品厂草编车间共有16名工人，为了了解每个工人的日均生产能力，随机调查了某天每个工人的生产件数，获得数据如下表：则这一天16名工人生产件数的众数和中位数分别是（）A．5件、11件B．12件、11件C．11件、12件D．15件、14件6．（3分）如图，▱ABCD的周长为22m，对角线AC、BD交于点O，过点O与AC垂直的直线交边AD于点E，则△CDE的周长为（）A．8cm B．9cm C．10cm D．11cm7．（3分）一个圆锥的主视图是边长为6cm的正三角形，则这个圆锥的侧面积等于（）A．36 πcm2B．24πcm2C．18πcm2D．12 πcm28．（3分）如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF ⊥AB交AC于点G，反比例函数y＝（x＞0）经过线段DC的中点E，若BD＝4，则AG的长为（）A．B．+2C．2+1D．+1二、填空题（本大题共有8小题，每小题3分，共24分不需写出解答过程，请将答案直接写在答题卡相应位置上）9．（3分）要使有意义，则实数x的取值范围是．10．（3分）若x＝﹣1是关于x的方程2x+3m﹣7＝0的解，则m的值为．11．（3分）青盐铁路（青岛一盐城），是我国“八纵八横”高速铁路网中第一纵“沿海通道”的一部分，全长428.752千米．数据428.752千米用科学记数法表示为米．12．（3分）在一个不透明的盒子中装有红、白两种除颜色外完全相同的球，其中有a个白球和3个红球，若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则a的值约为．13．（3分）边长为a、b的长方形，它的周长为14，面积为10，则a2b+ab2的值为．14．（3分）如图，CE、BF分别是△ABC的高线，连接EF，EF＝6，BC＝10，D、G分别是EF、BC的中点，则DG的长为．15．（3分）如图，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝1．将边BA绕点B顺时针旋转90°得线段BD，再将边CA绕点C顺时针旋转90°得线段CE，连接DE，则图中阴影部分的面积是．16．（3分）如图，已知△ABC中，∠BAC＝120°，AB＝AC＝2．D为BC边一点，且BD：DC＝1：2．以D为一个点作等边△DEF，且DE＝DC连接AE，将等边△DEF绕点D旋转一周，在整个旋转过程中，当AE取得最大值时AF的长为．三、解答题（本大题共有11小题，共102分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式，并把它的解集在数轴上表示出来：18．（6分）先化简，再求值：（x﹣3）2+2（x﹣2）（x+7）﹣（x+2）（x﹣2），其中x2+2x﹣3＝0．19．（8分）已知关于x方程x2﹣6x+m+4＝0有两个实数根x1，x2（1）求m的取值范围；（2）若x1＝2x2，求m的值．20．（8分）某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图，请结合以上信息解答下列问题：（1）求m的值；（2）请补全上面的条形统计图；（3）在图2中，“乒乓球”所对应扇形的圆心角的度数为多少度？（4）已知该校共有1200名学生，请你估计该校约有多少名学生最喜爱足球活动？21．（8分）“2019大洋湾盐城马拉松”的赛事共有三项：A，“全程马拉松”、B，“半程马拉松”、C．“迷你健身跑”，小明和小刚参与了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．（1）小明被分配到“迷你健身跑”项目组的概率为；（2）求小明和小刚被分配到不同项目组的概率．22．（10分）如图，在四边形ABCD中，AD∥BC，∠ABC＝∠ADC，对角线AC、BD交于点O，AO＝BO，DE平分∠ADC交BC于点E，连接OE．（1）求证：四边形ABCD是矩形；（2）若AB＝2，求△OEC的面积．23．（10分）某公司研发生产的560件新产品需要精加工后才能投放市场．现由甲、乙两个工厂来加工生产，已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍，并且加工生产240件新产品甲工厂比乙工厂少用4天．（1）求甲、乙两个工厂每天分别可加工生产多少件新产品？（2）若甲工厂每天的加工生产成本为2.8万元，乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元，至少应安排甲工厂加工生产多少天？24．（10分）如图，以AB为直径作半圆O，点C是半圆上一点，∠ABC的平分线交⊙O于E，D为BE延长线上一点，且DE＝FE．（1）求证：AD为⊙O切线；（2）若AB＝20，tan∠EBA＝，求BC的长．25．（10分）甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线OBCDA 表示轿车离甲地距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：（1）当轿车刚到乙地时，此时货车距离乙地千米；（2）当轿车与货车相遇时，求此时x的值；（3）在两车行驶过程中，当轿车与货车相距20千米时，求x的值．26．（12分）【操作发现】如图（1），在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB ＝∠COD＝45°，连接AC，BD交于点M．①AC与BD之间的数量关系为；②∠AMB的度数为；【类比探究】如图（2），在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC，交BD的延长线于点M．请计算的值及∠AMB的度数；【实际应用】如图（3），是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE 组成的图形，其中∠ACB＝∠DCE＝90°，∠A＝∠D＝30°且D、E、B在同一直线上，CE＝1，BC＝，求点A、D之间的距离．27．（14分）如图，二次函数y＝ax2﹣3ax+c的图象与x轴交于点A、B，与y轴交于点C直线y＝﹣x+4经过点B、C．（1）求抛物线的表达式；（2）过点A的直线交抛物线于点M，交直线BC于点N．①点N位于x轴上方时，是否存在这样的点M，使得AM：NM＝5：3？若存在，求出点M的坐标；若不存在，请说明理由．②连接AC，当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时，请求出点M的横坐标．2019年江苏省盐城市建湖县中考数学二模试卷参考答案与试题解析一、选择题（本大题共8小题，每小题3分，共24分，在每小题所给出的四个选项中，只有一个选项是正确的，请将正确选项的字母代号填涂在答题卡相应位置上）1．（3分）下列四个数，表示无理数的是（）A．sin30°B．πC．D．【分析】无限不循环小数叫做无理数，根据无理数的定义逐个排除即可．【解答】解：A、sin30°＝，不是无理数，故本选项不符合题意；B、π是无限不循环小数，是无理数，符合题意；C、＝4，不是无理数，故本选项不符合题意；D．＝﹣2，不是无理数，故本选项不符合题意；故选：B．【点评】本题考查了无理数，正确理解无理数的意义是解题的关键．2．（3分）下列四种标志图案中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【分析】根据轴对称图形与中心对称图形的概念判断即可．【解答】解：A、不是轴对称图形，是中心对称图形；B、是轴对称图形，是中心对称图形；C、不是轴对称图形，是中心对称图形；D、不是轴对称图形，不是中心对称图形．故选：B．【点评】本题考查的是中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．3．（3分）下列各式正确的是（）A．6a2﹣5a2＝a2B．（2a）2＝2a2C．﹣2（a﹣1）＝﹣2a+1D．（a+b）2＝a2+b2【分析】根据合并同类项法则、积的乘方、单项式乘多项式法则及完全平方公式逐一判断即可得．【解答】解：A．6a2﹣5a2＝a2，正确；B．（2a）2＝4a2，错误；C．﹣2（a﹣1）＝﹣2a+2，错误；D．（a+b）2＝a2+2ab+b2，错误；故选：A．【点评】本题主要考查幂的乘方与积的乘方，解题的关键是掌握合并同类项法则、积的乘方、单项式乘多项式法则及完全平方公式．4．（3分）如图所示，直线a、b、c、d的位置如图所示，若∠1＝125°，∠2＝125°，∠3＝135°，则∠4的度数为（）A．45°B．55°C．60°D．65°【分析】先依据同位角相等，判定a∥b，再根据平行线的性质，即可得出∠4＝45°．【解答】解：如图所示，∵∠1＝125°，∠2＝125°，∴a∥b，∴∠4＝∠5，又∵∠3＝135°，∴∠5＝45°，∴∠4＝45°，故选：A．【点评】本题考查了平行线的判定和性质的应用，能求出a∥b是解此题的关键．5．（3分）某工艺品厂草编车间共有16名工人，为了了解每个工人的日均生产能力，随机调查了某天每个工人的生产件数，获得数据如下表：则这一天16名工人生产件数的众数和中位数分别是（）A．5件、11件B．12件、11件C．11件、12件D．15件、14件【分析】根据众数和中位数的概念求解可得．【解答】解：这组数据的众数为11件，中位数为＝12（件），故选：C．【点评】此题考查了众数与中位数，中位数是将一组数据从小到大（或从大到小）重新排列后，最中间的那个数（最中间两个数的平均数），众数是一组数据中出现次数最多的数．6．（3分）如图，▱ABCD的周长为22m，对角线AC、BD交于点O，过点O与AC垂直的直线交边AD于点E，则△CDE的周长为（）A．8cm B．9cm C．10cm D．11cm【分析】由平行四边形的性质可得AB＝CD，AD＝BC，AO＝CO，可得AD+CD＝11cm，由线段垂直平分线的性质可得AE＝CE，即可求△CDE的周长＝CE+DE+CD＝AE+DE+CD＝AD+CD＝11cm．【解答】解：∵四边形ABCD是平行四边形∴AB＝CD，AD＝BC，AO＝CO，又∵EO⊥AC，∴AE＝CE，∵▱ABCD的周长为22cm，∴2（AD+CD）＝22cm∴AD+CD＝11cm∴△CDE的周长＝CE+DE+CD＝AE+DE+CD＝AD+CD＝11cm故选：D．【点评】本题考查了平行四边形的性质，线段垂直平分线的性质，熟练运用平行四边形的性质是本题的关键．7．（3分）一个圆锥的主视图是边长为6cm的正三角形，则这个圆锥的侧面积等于（）A．36 πcm2B．24πcm2C．18πcm2D．12 πcm2【分析】根据视图的意义得到圆锥的母线长为6cm，底面圆的半径为3cm，然后根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长和扇形的面积公式求解．【解答】解：根据题意得圆锥的母线长为6cm，底面圆的半径为3cm，所以这个圆锥的侧面积＝×6×2π×3＝18π（cm2）．故选：C．【点评】本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．8．（3分）如图，菱形ABCD的四个顶点均在坐标轴上，对角线AC、BD交于原点O，DF ⊥AB交AC于点G，反比例函数y＝（x＞0）经过线段DC的中点E，若BD＝4，则AG的长为（）A．B．+2C．2+1D．+1【分析】过E作y轴和x的垂线EM，EN，证明四边形MENO是矩形，设E（b，a），根据反比例函数图象上点的坐标特点可得ab＝，进而可计算出CO长，根据三角函数可得∠DCO＝30°，再根据菱形的性质可得∠DAB＝∠DCB＝2∠DCO＝60°，∠1＝30°，AO＝CO＝2，然后利用勾股定理计算出DG长，进而可得AG长．【解答】解：过E作y轴和x的垂线EM，EN，设E（b，a），∵反比例函数y＝（x＞0）经过点E，∴ab＝，∵四边形ABCD是菱形，∴BD⊥AC，DO＝BD＝2，∵EN⊥x，EM⊥y，∴四边形MENO是矩形，∴ME∥x，EN∥y，∵E为CD的中点，∴DO•CO＝4，∴CO＝2，∴tan∠DCO＝＝．∴∠DCO＝30°，∵四边形ABCD是菱形，∴∠DAB＝∠DCB＝2∠DCO＝60°，∠1＝30°，AO＝CO＝2，∵DF⊥AB，∴∠2＝30°，∴DG＝AG，设DG＝r，则AG＝r，GO＝2﹣r，∵AD＝AB，∠DAB＝60°，∴△ABD是等边三角形，∴∠ADB＝60°，∴∠3＝30°，在Rt△DOG中，DG2＝GO2+DO2，∴r2＝（2﹣r）2+22，解得：r＝，∴AG＝．故选：A．【点评】此题主要考查了反比例函数和菱形的综合运用，关键是掌握菱形的性质：菱形对角线互相垂直平分，且平分每一组对角，反比例函数图象上的点横纵坐标之积＝k二、填空题（本大题共有8小题，每小题3分，共24分不需写出解答过程，请将答案直接写在答题卡相应位置上）9．（3分）要使有意义，则实数x的取值范围是x≥﹣1．【分析】根据二次根式的性质可以得到x﹣1是非负数，由此即可求解．【解答】解：依题意得x+1≥0，∴x≥﹣1．故答案为：x≥﹣1．【点评】此题主要考查了二次根式有意义的条件，根据被开方数是非负数即可解决问题．10．（3分）若x＝﹣1是关于x的方程2x+3m﹣7＝0的解，则m的值为3．【分析】使方程左右两边的值相等的未知数的值是该方程的解．将方程的解代入方程可得关于m的一元一次方程，从而可求出m的值．【解答】解：根据题意得：2×（﹣1）+3m﹣7＝0解得：m＝3，故答案为：3．【点评】本题考查了一元一次方程的解的定义．已知条件中涉及到方程的解，把方程的解代入原方程，转化为关于m字母系数的方程进行求解，注意细心．11．（3分）青盐铁路（青岛一盐城），是我国“八纵八横”高速铁路网中第一纵“沿海通道”的一部分，全长428.752千米．数据428.752千米用科学记数法表示为 4.28752×105米．【分析】用科学记数法表示较大的数时，一般形式为a×10﹣n，其中1≤|a|＜10，n为整数，据此判断即可．【解答】解：428.752千米＝428752米＝4.28752×105米．故答案为：4.28752×105．【点评】此题主要考查了用科学记数法表示较大的数，一般形式为a×10﹣n，其中1≤|a|＜10，确定a与n的值是解题的关键．12．（3分）在一个不透明的盒子中装有红、白两种除颜色外完全相同的球，其中有a个白球和3个红球，若每次将球充分搅匀后，任意摸出1个球记下颜色再放回盒子．通过大量重复试验后，发现摸到红球的频率稳定在20%左右，则a的值约为12．【分析】在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近，可以从摸到红球的频率稳定在20%左右得到比例关系，列出方程求解即可．【解答】解：由题意可得，×100%＝20%，解得a＝12．经检验：a＝12是原分式方程的解，所以a的值约为12，故答案为：12．【点评】本题利用了用大量试验得到的频率可以估计事件的概率．关键是根据红球的频率得到相应的等量关系．13．（3分）边长为a、b的长方形，它的周长为14，面积为10，则a2b+ab2的值为70．【分析】先把所给式子提取公因式ab，再整理为与题意相关的式子，代入求值即可．【解答】解：根据题意得：a+b＝7，ab＝10，则a2b+ab2＝ab（a+b）＝70．故答案为70．【点评】本题既考查了对因式分解方法的掌握，又考查了代数式求值的方法，同时还隐含了数学整体思想和正确运算的能力．14．（3分）如图，CE、BF分别是△ABC的高线，连接EF，EF＝6，BC＝10，D、G分别是EF、BC的中点，则DG的长为4．【分析】连接EG、FG，根据直角三角形的性质得到EG＝FG＝BC＝5，根据等腰三角形的性质求出ED，根据勾股定理计算，得到答案．【解答】解：连接EG、FG，∵CE，BF分别是△ABC的高线，∴∠BEC＝90°，∠BFC＝90°，∵G是BC的中点，∴EG＝FG＝BC＝5，∵D是EF的中点，∴ED＝EF＝3，GD⊥EF，由勾股定理得，DG＝＝4，故答案为：4．【点评】本题考查的是直角三角形的性质，掌握在直角三角形中，斜边上的中线等于斜边的一半是解题的关键．15．（3分）如图，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝1．将边BA绕点B顺时针旋转90°得线段BD，再将边CA绕点C顺时针旋转90°得线段CE，连接DE，则图中阴影部分的面积是﹣．【分析】作EF⊥CD于F，根据勾股定理骑车AC，根据旋转变换的性质求出EF，根据扇形面积公式、三角形的面积公式计算，得到答案．【解答】解：作EF⊥CD于F，由旋转变换的性质可知，EF＝BC＝1，CD＝CB+BD＝4，由勾股定理得，CA＝＝＝，则图中阴影部分的面积＝△ABC的面积+扇形ABD的面积+△ECD的面积﹣扇形ACE的面积＝×1×3++﹣＝﹣，故答案为：﹣．【点评】本题考查的是扇形面积计算、旋转变换的性质，掌握扇形面积公式：S＝是解题的关键．16．（3分）如图，已知△ABC中，∠BAC＝120°，AB＝AC＝2．D为BC边一点，且BD：DC＝1：2．以D为一个点作等边△DEF，且DE＝DC连接AE，将等边△DEF绕点D旋转一周，在整个旋转过程中，当AE取得最大值时AF的长为2．【分析】点E，F在以D为圆心，DC为半径的圆上，当A，D，E在同一直线上时AE 取最大值，过点A作AH⊥BC交BC于H，通过解直角三角形求出DH，BH，CH的长度，∠ADH的度数，证明四边形DEFC是菱形，△ACF为直角三角形，通过勾股定理可求出AF的长度．【解答】解：如图，点E，F在以D为圆心，DC为半径的圆上，当A，D，E在同一直线上时AE取最大值，过点A作AH⊥BC交BC于H，∴∠BAC＝120°，AB＝AC＝2，∴∠B＝∠ACB＝30°，BH＝CH，∴在Rt△ABH中，AH＝AB＝，BH＝AH＝3，∴BC＝2BH＝6，∵BD：DC＝1：2，∴BD＝2，CD＝4，∴DH＝BH﹣BD＝1，在Rt△ADH中，AH＝，DH＝1，∴tan∠DAH＝＝，∴∠DAH＝30°，∠ADH＝60°，∵△DEF是等边三角形，∴∠E＝60°，DE＝EF＝DC，∵∠ADC＝∠E＝60°，∴DC∥EF，∵DC＝EF，∴四边形DEFC为平行四边形，又∵DE＝DC，∴平行四边形DEFC为菱形，∴FC＝DC＝4，∠DCF＝∠E＝60°，∴∠ACF＝ACB+∠DCF＝90°，在Rt△ACF中，AF＝＝＝2，故答案为：2．【点评】本题考查了等腰三角形的性质，解直角三角形，勾股定理，菱形的判定与性质等，解题关键是能够确定AE取最大值时的位置．三、解答题（本大题共有11小题，共102分.请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）17．（6分）解不等式，并把它的解集在数轴上表示出来：【分析】先去分母，然后去括号，再移项、合并同类项，系数化为1即可，再用数轴表示解集．【解答】解：去分母得3（2+x）≤2（2x﹣1）+6，去括号得6+3x≤4x﹣2+6，移项得3x﹣4x≤﹣2+6﹣6，合并得﹣x≤﹣2，系数化为1得，x≥2，用数轴表示为：【点评】本题考查了解一元一次不等式：根据不等式的性质解一元一次不等式，基本操作方法与解一元一次方程基本相同，都有如下步骤：①去分母；②去括号；③移项；④合并同类项；⑤化系数为1．也考查了在数轴上表示不等式的解集．18．（6分）先化简，再求值：（x﹣3）2+2（x﹣2）（x+7）﹣（x+2）（x﹣2），其中x2+2x﹣3＝0．【分析】原式利用完全平方公式，平方差公式，以及多项式乘以多项式法则计算，去括号合并得到最简结果，求出方程的解得到x的值，代入计算即可求出值．【解答】解：原式＝x2﹣6x+9+2x2+10x﹣28﹣x2+4＝4x﹣15，由x2+2x﹣3＝0，即（x﹣1）（x+3）＝0，得到x＝1或x＝﹣3，当x＝1时，原式＝4﹣15＝﹣11；当x＝﹣3时，原式＝﹣12﹣15＝﹣27．【点评】此题考查了整式的混合运算﹣化简求值，熟练掌握运算法则是解本题的关键．19．（8分）已知关于x方程x2﹣6x+m+4＝0有两个实数根x1，x2（1）求m的取值范围；（2）若x1＝2x2，求m的值．【分析】（1）根据方程的系数结合根的判别式△≥0，即可得出关于m的一元一次不等式，解之即可得出m的取值范围；（2）根据根与系数的关系可得出x1+x2＝6，x1x2＝m+4，结合x1＝2x2可求出x1，x2的值，再将其代入x1x2＝m+4中可求出m的值．【解答】解：（1）∵关于x方程x2﹣6x+m+4＝0有两个实数根，∴△＝（﹣6）2﹣4×1×（m+4）≥0，解得：m≤5．（2）∵关于x方程x2﹣6x+m+4＝0有两个实数根x1，x2，∴x1+x2＝6，x1x2＝m+4．又∵x1＝2x2，∴x2＝2，x1＝4，∴4×2＝m+4，∴m＝4．【点评】本题考查了根与系数的关系以及根的判别式，解题的关键是：（1）牢记“当△≥0时，方程有实数根”；（2）根据根与系数的关系结合x1＝2x2，求出x1，x2的值．20．（8分）某校开展“我最喜爱的一项体育活动”调查，要求每名学生必选且只能选一项，现随机抽查了m名学生，并将其结果绘制成如下不完整的条形图和扇形图，请结合以上信息解答下列问题：（1）求m的值；（2）请补全上面的条形统计图；（3）在图2中，“乒乓球”所对应扇形的圆心角的度数为多少度？（4）已知该校共有1200名学生，请你估计该校约有多少名学生最喜爱足球活动？【分析】（1）根据排球人数及其所占百分比可得总人数；（2）求得“足球“的人数＝150×20%＝30人，补全上面的条形统计图即可；（3）360°×乒乓球”所占的百分比即可得到结论；（4）用总人数乘以样本中足球所占的百分比．【解答】解：（1）m＝21÷14%＝150；（2）足球的人数为150×20%＝30，补全图形如下：（3）在图2中，“乒乓球”所对应扇形的圆心角的度数为360°×＝36°；（4）估计该校最喜爱足球活动的学生约有1200×20%＝240人．【点评】本题考查扇形统计图、条形统计图、用样本估计总体．一般来说，用样本去估计总体时，样本越具有代表性、容量越大，这时对总体的估计也就越精确．解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．21．（8分）“2019大洋湾盐城马拉松”的赛事共有三项：A，“全程马拉松”、B，“半程马拉松”、C．“迷你健身跑”，小明和小刚参与了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．（1）小明被分配到“迷你健身跑”项目组的概率为；（2）求小明和小刚被分配到不同项目组的概率．【分析】（1）利用概率公式直接计算即可；（2）先画树状图展示所有9种等可能的结果数，再找出其中小明和小刚被分配到不同项目组的结果数，然后根据概率公式计算．【解答】解：（1）∵共有A，B，C三项赛事，∴小明被分配到“迷你健身跑”项目组的概率是，故答案为：；（2）画树状图为：共有9种等可能的结果数，其中小明和小刚被分配到不同项目组的结果数为6，所以小明和小刚被分配到不同项目组的概率＝．【点评】本题考查了列表法与树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B 的概率．22．（10分）如图，在四边形ABCD中，AD∥BC，∠ABC＝∠ADC，对角线AC、BD交于点O，AO＝BO，DE平分∠ADC交BC于点E，连接OE．（1）求证：四边形ABCD是矩形；（2）若AB＝2，求△OEC的面积．【分析】（1）证出∠BAD＝∠BCD，得出四边形ABCD是平行四边形，得出OA＝OC，OB＝OD，证出AC＝BD，即可解决问题；（2）作OF⊥BC于F．求出EC、OF即可解决问题；【解答】（1）证明：∵AD∥BC，∴∠ABC+∠BAD＝180°，∠ADC+∠BCD＝180°，∵∠ABC＝∠ADC，∴∠BAD＝∠BCD，∴四边形ABCD是平行四边形，∴OA＝OC，OB＝OD，∵OA＝OB，∴AC＝BD，∴四边形ABCD是矩形．（2）解：作OF⊥BC于F，如图所示．∵四边形ABCD是矩形，∴CD＝AB＝2，∠BCD＝90°，AO＝CO，BO＝DO，AC＝BD，∴AO＝BO＝CO＝DO，∴BF＝FC，∴OF＝CD＝1，∵DE平分∠ADC，∠ADC＝90°，∴∠EDC＝45°，在Rt△EDC中，EC＝CD＝2，∴△OEC的面积＝•EC•OF＝1．【点评】本题考查矩形的性质、三角形的面积、三角形中位线定理等知识，解题的关键是学会添加常用辅助线，构造三角形中位线解决问题，属于中考常考题型．23．（10分）某公司研发生产的560件新产品需要精加工后才能投放市场．现由甲、乙两个工厂来加工生产，已知甲工厂每天加工生产的新产品件数是乙工厂每天加工生产新产品件数的1.5倍，并且加工生产240件新产品甲工厂比乙工厂少用4天．（1）求甲、乙两个工厂每天分别可加工生产多少件新产品？（2）若甲工厂每天的加工生产成本为2.8万元，乙工厂每天的加工生产成本为2.4万元要使这批新产品的加工生产总成本不超过60万元，至少应安排甲工厂加工生产多少天？【分析】（1）设乙工厂每天可加工生产x件新产品，则甲工厂每天可加工生产1.5x件新产品，根据题意列出方程，求出方程的解即可得到结果；（2）设甲工厂加工生产y天，根据题意列出不等式，求出不等式的解集即可得到结果．【解答】解：（1）设乙工厂每天可加工生产x件新产品，则甲工厂每天可加工生产1.5x 件新产品，根据题意得：+4＝，去分母得：240+6x＝360，解得：x＝20，经检验x＝20是分式方程的解，且符合题意，∴1.5x＝30，则甲、乙两个工厂每天分别可加工生产30件、20件新产品；（2）设甲工厂加工生产y天，根据题意得：2.8y+2.4×≤60，解得：y≥9，则少应安排甲工厂加工生产9天．【点评】此题考查了分式方程的应用，以及一元一次不等式的应用，弄清题意是解本题的关键．24．（10分）如图，以AB为直径作半圆O，点C是半圆上一点，∠ABC的平分线交⊙O于E，D为BE延长线上一点，且DE＝FE．（1）求证：AD为⊙O切线；（2）若AB＝20，tan∠EBA＝，求BC的长．【分析】（1）先利用角平分线定义、圆周角定理证明∠4＝∠2，再利用AB为直径得到∠2+∠BAE＝90°，则∠4+∠BAE＝90°，然后根据切线的判定方法得到AD为⊙O切线；（2）解：根据圆周角定理得到∠ACB＝90°，设AE＝3k，BE＝4k，则AB＝5k＝20，求得AE＝12，BE＝16，连接OE交AC于点G，如图，解直角三角形即可得到结论．【解答】（1）证明：∵BE平分∠ABC，∴∠1＝∠2，∵AB为直径，∴AE⊥BD，∵DE＝FE，∴∠3＝∠4，∵∠1＝∠3，∴∠4＝∠2，∵AB为直径，∴∠AEB＝90°，∵∠2+∠BAE＝90°∴∠4+∠BAE＝90°，即∠BAD＝90°，∴AD⊥AB，∴AD为⊙O切线；（2）解：∵AB为直径，∴∠ACB＝90°，在Rt△ABC中，∵tan∠EBA＝，∴设AE＝3k，BE＝4k，则AB＝5k＝20，∴AE＝12，BE＝16，连接OE交AC于点G，如图，∵∠1＝∠2，∴＝，∴OE⊥AC，∵∠3＝∠2，∴tan∠EBA＝tan∠3＝，∴设AG＝4x，EG＝3x，∴AE＝5x＝12，∴x＝，∴AG＝，∵OG∥BC，∴AC＝2AG＝，∴BC＝＝．【点评】本题考查了切线的判定与性质：经过半径的外端且垂直于这条半径的直线是圆的切线；圆的切线垂直于经过切点的半径．判定切线时“连圆心和直线与圆的公共点”或“过圆心作这条直线的垂线”；有切线时，常常“遇到切点连圆心得半径”．也考查了圆周角定理、垂径定理和解直角三角形．25．（10分）甲、乙两地相距300千米，一辆货车和一辆轿车先后从甲地出发驶向乙地，如图，线段OA表示货车离甲地距离y（千米）与时间x（小时）之间的函数关系；折线OBCDA 表示轿车离甲地距离y（千米）与时间x（小时）之间的函数关系．请根据图象解答下列问题：（1）当轿车刚到乙地时，此时货车距离乙地30千米；（2）当轿车与货车相遇时，求此时x的值；（3）在两车行驶过程中，当轿车与货车相距20千米时，求x的值．【分析】（1）根据图象可知货车5小时行驶300千米，由此求出货车的速度为60千米/时，再根据图象得出货车出发后4.5小时轿车到达乙地，由此求出轿车到达乙地时，货车行驶的路程为270千米，而甲、乙两地相距300千米，则此时货车距乙地的路程为：300﹣270＝30千米；（2）先求出线段CD对应的函数关系式，再根据两直线的交点即可解答；（3）分两种情形列出方程即可解决问题．【解答】解：（1）根据图象信息：货车的速度V货＝，∵轿车到达乙地的时间为货车出发后4.5小时，∴轿车到达乙地时，货车行驶的路程为：4.5×60＝270（千米），此时，货车距乙地的路程为：300﹣270＝30（千米）．所以轿车到达乙地后，货车距乙地30千米．故答案为：30；（2）设CD段函数解析式为y＝kx+b（k≠0）（2.5≤x≤4.5）．∵C（2.5，80），D（4.5，300）在其图象上，，解得，∴CD段函数解析式：y＝110x﹣195（2.5≤x≤4.5）；易得OA：y＝60x，，解得，∴当x＝3.9时，轿车与货车相遇；（3）当x＝2.5时，y货＝150，两车相距＝150﹣80＝70＞20，由题意60x﹣（110x﹣195）＝20或110x﹣195﹣60x＝20，解得x＝3.5或4.3小时．答：在两车行驶过程中，当轿车与货车相距20千米时，x的值为3.5或4.3小时．【点评】本题考查了一次函数的应用，对一次函数图象的意义的理解，待定系数法求一次函数的解析式的运用，行程问题中路程＝速度×时间的运用，本题有一定难度，其中求出货车与轿车的速度是解题的关键．26．（12分）【操作发现】如图（1），在△OAB和△OCD中，OA＝OB，OC＝OD，∠AOB ＝∠COD＝45°，连接AC，BD交于点M．①AC与BD之间的数量关系为AC＝BD；②∠AMB的度数为45°；【类比探究】如图（2），在△OAB和△OCD中，∠AOB＝∠COD＝90°，∠OAB＝∠OCD＝30°，连接AC，交BD的延长线于点M．请计算的值及∠AMB的度数；【实际应用】如图（3），是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE 组成的图形，其中∠ACB＝∠DCE＝90°，∠A＝∠D＝30°且D、E、B在同一直线上，CE＝1，BC＝，求点A、D之间的距离．【分析】【操作发现】如图（1），证明△COA≌△DOB（SAS），即可解决问题．【类比探究】如图（2），证明△COA∽△ODB，可得＝＝，∠MAK＝∠OBK，已解决可解决问题．【实际应用】分两种情形解直角三角形求出BE，再利用相似三角形的性质解决问题即可．【解答】解：【操作发现】如图（1）中，设OA交BD于K．。

(精品)2019年初三数学二模试卷(含详细答案)

2019届初三二模数学试卷一. 选择题（本大题共6题，每题4分，共24分）1. 下列实数中，是无理数的是（）A. 3.14B.13C.3D. 92. 下列二次根式中，与a 是同类二次根式的是（）A.3aB.22aC.3aD.4a3. 函数1y kx （常数0k ）的图像不经过的象限是（）A. 第一象限B. 第二象限C. 第三象限D. 第四象限4. 某幢楼10户家庭某月的用电量如下表所示：用电量（度）140 160 180 200 户数13 42那么这10户家庭该月用电量的众数和中位数分别是（）A. 180、180B. 180、160C. 160、180D. 160、1605. 已知两圆的半径分别为1和5，圆心距为4，那么两圆的位置关系是（）A. 外离B. 外切C. 相交D. 内切6. 如图，已知△ABC 和△DEF ，点E 在BC 边上，点A 在DE 边上，边EF 和边AC 交于点G ，如果AEEC ，AEGB . 那么添加下列一个条件后，仍无法判定△DEF 与△ABC 一定相似的是（）A.AB DE BC EF B.AD GF AE GE C. AG EG ACEFD.ED EG EFEA二. 填空题7. 计算：2a a8. 因式分解：22x x 9. 方程82xx 的根是10. 函数3()2xf x x 的定义域是11. 如果关于x 的方程220x x m 有两个实数根，那么m 的取值范围是12. 计算：12()3a ab 13. 将抛物线221yx x 向上平移4个单位后，所得新抛物线的顶点坐标是14. 一个不透明的袋子里装有3个白球、1个红球，这些球除颜色外无其他的差异，从袋子中随机摸出1个球，恰好是白球的概率是15. 正五边形的中心角是16. 如图，圆弧形桥拱的跨度16AB 米，拱高4CD 米，那么圆弧形桥拱所在圆的半径是米17. 如果一个三角形一边上的中线的长与另两边中点的连线段的长相等，我们称这个三角形为“等线三角形”，这条边称为“等线边”.在等线三角形ABC 中，AB 为等线边，且3AB ，2AC ，那么BC18. 如图，矩形ABCD 中，4AB ，7AD，点E 、F 分别在边AD 、BC 上，且点B 、F关于过点E 的直线对称，如果以CD 为直径的圆与EF 相切，那么AE三. 解答题19. 计算：1321|22|8221.20. 解不等式组：3(21)4531122x x x x①②21. 如图，在平面直角坐标系xOy 中，点A 在x 轴正半轴上，点B 、C 在第一象限，且四边形OABC 是平行四边形，25OC，2sin 55AOC，反比例函数k yx的图像经过点C 以及边AB 的中点 D. 求：（1）这个反比例函数的解析式；（2）四边形OABC 的面积.22. 某文具店有一种练习簿出售，每本的成本价为2元，在销售的过程中价格有调整，按原价格每本8.25元，卖出36本，后经两次涨价，按第二次涨价后的价格卖出了25本. 发现按原价格和第二次涨价后的价格销售，分别获得的销售利润恰好相等.（1）求第二次涨价后每本练习簿的价格；（2）在两次涨价过程中，假设每本练习簿平均获得利润的增长率完全相同，求这个增长率.（注：=100%（后一次的利润-前一次的利润）利润增长率前一次的利润）23. 如图，在直角梯形ABCD 中，AD ∥BC ，90C ，BCCD ，点E 、F 分别在边BC 、CD 上，且BEDF AD ，联结DE ，联结AF 、BF 分别与DE 交于点G 、P. （1）求证：AB BF ；（2）如果2BEEC ，求证：DGGE .24. 已知抛物线23y axbx 经过点(7,3)A ，与x 轴正半轴交于(,0)B m 、(6,0)C m 两点，与y 轴交于点 D.（1）求m 的值；（2）求这条抛物线的表达式；（3）点P 在抛物线上，点Q 在x 轴上，当90PQD 且2PQ DQ ，求P 、Q 坐标.MON，点P是MON内一点，过点P作PA OM于点A、25. 如图所示，45PB，取OP的中点C，联结AC并延长，交OB于点 D. PB ON于点B，且22（1）求证：ADB OPB；（2）设PA x，OD y，求y关于x的函数解析式；（3）分别联结AB、BC，当△ABD与△CPB相似时，求P A的长.2019年第二学期初三教学质量检测数学参考答案及评分说明一、选择题：（本大题共6题，每题4分，满分24分）1．C；2．C；3．B；4．A；5．D；6．C．二、填空题：（本大题共12题，每题4分，满分48分）7．3a ；8．2xx ；9．4x ；10．2x ；11．1m ；12．b a 3137；13．2,1；14．43；15．72；16．10；17．5；18．3．三、解答题：（本大题共7题，满分78分）19．（本题满分10分）解：原式=1241222．………………………………………………………各2分=43．………………………………………………………………………………2分20．（本题满分10分）解：由①得:5436x x．…………………………………………………………………2分22x ．……………………………………………………………………2分1x．……………………………………………………………………1分由②得:x x 23．………………………………………………………………………2分22x ．………………………………………………………………………1分1x．………………………………………………………………………1分∴原不等式组的解集是11x ．……………………………………………………2分21．（本题满分10分，每小题各5分）解：（1）过点C 作CH ⊥OA 于点H ．………………………………………………………1分在△COH 中，∠CHO=90°,∴sin ∠AOC=552OCCH ．………………………1分∵52OC，∴CH=4．………………………………………………………………1分在△COH 中，∠CHO=90°,∴222CHOCOH ．∵点C 在第一象限，∴点C 的坐标是（2，4）．………………………………………1分∵反比例函数x ky的图像过点C （2，4），∴k =8．即xy 8．…………………1分（2）过点D 作DG ⊥OA 于点G ．……………………………………………………………1分∵四边形ABCD 是平行四边形，∴AB=OC=52．……………………………………1分∵点D 是边AB 的中点，∴AD =5．…………………………………………………1分在△DAG 中，∠DGA=90°,∴sin ∠DAG =sin ∠AOC=552DA DG．∴DG=2，AG=1．∴设点D 的坐标为（a ，2）．∵反比例函数xy8的图像过点D （a ，2），∴a =4．即OG=4．…………………1分∴OA=OG －AG=3．∴四边形OABC 的面积为12．……………………………………1分22．（本题满分10分，其中第（1）小题4分，第（2）小题6分）解：（1）设第二次涨价后每本练习簿的价格为x 元．………………………………………1分由题意得：25236225.8x ．…………………………………………2分解得：11x．答：第二次涨价后每本练习簿的价格为11元．……………………………………1分（2）设每本练习簿平均获得利润的增长率为y ．………………………………………1分由题意得：2111225.82y．…………………………………………2分解得：2.0y或2.2y（不合题意，舍去）．…………………………………2分答：每本练习簿平均获得利润的增长率为20%．…………………………………1分23．（本题满分12分，每小题各6分）证明：（1）∵AD ∥BC ，AD=BE ，∴四边形ABED 是平行四边形．………………………1分∴AB=DE ．………………………………………………………………………………1分∵BE=DF ，BC=CD ，∴CE=CF ．……………………………………………………1分又∵∠BCF=∠DCE=90o ，BC=CD ．∴△BCF ≌△DCE ．……………………………2分∴DE =BF ．………………………………………………………………………………1分∴AB=BF ．（2）延长AF 与BC 延长线交于点H ．………………………………………………………1分∵BE=2CE ，BE=DF=AD ，CE=CF ，∴DF =2CF ，AD=2CE ．…………………………………………………………………1分∵AD ∥BC ，∴CFDF CHAD ．……………………………………………………………1分∴AD=2CH ．………………………………………………………………………………1分∴AD=2CE=2CH ．又∵EH =CE +CH ．∴AD=EH ．…………………………………………………………1分∵AD ∥BC ，∴EHAD GEDG ．……………………………………………………………1分∴DG=GE ．24．（本题满分12分，其中第（1）小题3分，第（2）小题4分，第（3）小题5分）解：（1）抛物线32bxaxy与y 轴的交点D （0，3）．……………………………1分∵抛物线经过点A （7，3），∴抛物线的对称轴为直线27x．…………………1分∴2726m m ．解得1m ．…………………………………………………………1分（2）由1m 得B （1，0）．将A （7，3）、B （1，0）代入抛物线解析式得：.03,33749bab a ……………2分解得：.27,21ba…………………………………………………………………………1分∴这条抛物线的表达式为：327212x x y．……………………………………1分（3）①当点Q 在原点时，抛物线与x 轴的交点）（0,6即为点P ，90PQD且PQ=2DQ ．∴）（0,6P ，）（0,0Q ．…………………………………………………………1分②当点Q 不在原点时，过点P 作轴x PH于点H ．∵90QHP DOQ ，QPH DQO，∴△DOQ ∽△QHP ．…………………………………………………………………1分∵PQ=2DQ ，∴21QPDQ PHOQ QHOD ．∴62OD QH，OQ PH 2．………………………………………………………1分由题意，设）（0,k Q ，那么)26(k k P ，．∵点)26(k k P ，在抛物线327212xxy 上，∴kk k 23)6(27)6212（解得01k ，12k ．………………………………………………………………1分当0k时，点Q 与点O 重合，舍去．∴）（2,5P ，）（0,1Q ．………………………………………………………………1分∴）（0,6P ，）（0,0Q 或）（2,5P ，）（0,1Q ．25．（本题满分14分，其中第（1）小题5分，第（2）小题5分，第（3）小题4分）（1）证明：记COA∵PAOM ，C 是OP 的中点，∴PC OC AC ．……………………………1分∴COA CAO ．……………………………………………………………1分又∵45MON ，∴45ADB AOD CAO o ．……………………………………………1分45POBMON COAo．……………………………………………1分又∵PBON ，∴在△POB 中，∠PBO=90°,∴9045OPB POB oo．……………1分∴ADB OPB ．（2）解：延长AP ，交ON 于点E ，过点A 作AFON 于点F ．……………………1分∵PA OM ，∠MON=45°,PB ON ，∴∠AEO=45°．即△AOE 、△PBE 均为等腰直角三角形．又PA=x ，PB =22，∴PE=4，AO=AE=4x ．…………………………………1分∴OE=242x ．∴OF=EF=AF =2222x ，OB=222x，DF =y x 2222．………1分∵ADB OPB ，∴cot cot ADB OPB ．∴DF PB AFOB．………………1分即2222222222222xyxx．∴422422xx xy ．………………………………………………………………1分（3）∵PBON ，C 是OP 的中点，∴CB CP ．∴CBP CPB ，即△CBP 为等腰三角形．又∵△ABD 与△CBP 相似，且ADBCPB ．∴ADB ABD或ADB DAB ．即AD AB 或BD AB ．…………………………………………………………1分∵CA COCP CB ，∴2ACPCOA ，2BCPBOC ．∴902AOB ACB．又∵CACB ，∴45DAB．………………………………………………1分①如果AB AD ，那么1804567.52ADBABDooo．∴67.5OPB o．∴22.5AOP BOP o．又∵OM PA 于点A 、ON PB 于点B ，∴22PB PA．……………………………………………………………1分②如果BA BD ，那么90ABD o．∵90PBD ，∴点A 在直线PB 上．又∵OM PA 于点A ，∴点P 与点A 重合．而点P 是MON 内一点，∴点P 与点A 不重合．此情况不成立．………1分综上所述，当△ABD 与△CBP 相似时，22PA．参考答案一. 选择题1. C2. C3. B4. A5. D6. C二. 填空题7. 3a8. (2)x x 9. 4x 10. 2x 11. 1m 12. 7133a b 13. (1,2)14.3415. 7216. 1017.518. 3三. 简答题19.34；20.11x ；21.（1）8yx；（2）12；22.（1）11；（2）20%；23. 略；24.（1）1m；（2）217322yxx ；（3）(6,0)P 、(0,0)Q 或(5,2)P 、(1,0)Q ；25.（1）略；（2）224224xxyx ；（3）4.。

2019九年级中考二模数学精选试题包含参考答案

2019年中考模拟考试试卷数学请将答案写在答题卡相应的位置上总分120分时间100分钟一、选择题(本大题10小题，每小题3分，共30分)在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑.1. 2019的相反数是( ▲ )A．2019 B．-2019 C．12019D．120192. 2018年汕头市龙湖区的GDP总量约为389亿元，其中389亿用科学记数法表示为( ▲ ) A．3.89×1011 B.0.389×1011 C．3.89×1010D．38.9×10103.如图是一个由5A．B．C．D4.已知实数a，b在数轴上的位置如图所示，下列结论中正确的是( ▲ )A．a＞b B．|a|＜|b|C．ab＞0 D．﹣a＞b5.如图，AB∥CD，∠D=42°，∠CBA=64°，则∠CBD的度数是( ▲ )A．42°B．64°C．74°D．106°6.某篮球运动员在连续7场比赛中的得分(单位：分)依次为2117，23，20，20，23，则这组数据的平均数与中位数分别是( ▲ )A．20分，17分B．20分，22分C．20分，19分D．20分，20分7.下列所述图形中，既是中心对称图形，又是轴对称图形的是( ▲ )A．矩形B．平行四边形C．正五边形D．等边三角形8.下列运算正确的是( ▲ )A．a2+a3=a5B．a2×a3=a6C．(a+b)2=a2+b2D．(a2)3=a6 9．已知一个多边形的内角和为1080°，则这个多边形是( ▲ )A．九边形B．八边形C．七边形D．六边形10.如图，等边△ABC的边长为3cm，动点P从点A出发，以每秒度，沿A→B→C的方向运动，到达点Cy=PC2，则y关于x的函数的图象大致为(( ▲ )A B D二、填空题(本大题6小题，每小题4分，共24分)请将下列各题的正确答案填写在答题卡相应的位置上.)11.要使分式1x1有意义，x的取值应满足▲．12.因式分解：2x2﹣8=▲．13.若关于x的一元二次方程x2+mx+2n=0有一个根是2，则m+n=▲．14.如图，在Rt△ABC中，∠C=90°，BC=4，AC=3，则sinB=▲．15.如图，在平行四边形ABCD中，AB＜AD，∠C=150°CD=4，以AB为直径的⊙O交BC于点E，则阴影部分的面积为▲．16.如图，在平面直角坐标系中，△P 1OA1，△P2A1A2△P3A2A3，…都是等腰直角三角形，其直角顶点P1(3，3)，P2，P3，…均在直线y=﹣13x+4上．设△P1OA1，△P2A1A2，△P3A2A3，…的面积分别为S1S2，S3，…，依据图形所反映的规律，S2019=▲．三、解答题(一)(本大题3小题，每小题6分，共18分)17.计算：|﹣3|+(π﹣2019)0﹣2sin 30°+(13)﹣1．18.先化简，再求值：(1x1--1)÷22x2x1x1++-，其中x=2.19.如图，点D在△ABC的AB边上.(1)作∠BDC的平分线DE，交BC于点E(保留作图痕迹，不要求写作法)；(2)在(1)的条件下，若DE∥AC, 求证：∠ACD=∠A四、解答题(二)(本大题3小题，每小题7分，共21分)20.某图书馆计划选购甲、乙两种图书．已知甲图书每本价格是乙图书每本价格的2.5倍，用800元单独购买甲图书比用800元单独购买乙图书要少24本．(1)甲、乙两种图书每本价格分别为多少元？(2)如果该图书馆计划购买乙图书的本数比购买甲图书本数的2倍多8本，且用于购买甲、乙两种图书的总经费不超过1060元，那么该图书馆最多可以购买多少本乙图书？21.随着信息技术的迅猛发展，人们去商场购物的支付方式更加多样、便捷．某校数学兴趣小组设计了一份调查问卷，要求每人选且只选一种你最喜欢的支付方式．现将调查结果进行统计并绘制成如下两幅不完整的统计图，请结合图中所给的信息解答下列问题：(1)这次活动共调查了人；在扇形统计图中，表示“支付宝”支付的扇形圆心角的度数为；(2)将条形统计图补充完整．观察此图，支付方式的“众数”是；(3)在一次购物中，小明和小亮都想从“微信”、“支付宝”、“银行卡”三种支付方式中选一种方式进行支付，则两人恰好选择同一种支付方式的概率为．22.在正方形ABCD中，对角线BD所在的直线上有两点E、F满足BE=DF，连接AE、AF、CE、CF，如图所示．(1)求证：△ABE≌△ADF；(2)试判断四边形AECF的形状，并说明理由．五、解答题(三)(本大题3小题，每小题9分，共27分)23.如图，A(4，3)是反比例函数y=kx在第一象限图象上一点，连接OA，过A作AB∥x轴，截取AB=OA(B在A右侧)，连接OB，交反比例函数y=kx的图象于点P．(1)求反比例函数y=kx的表达式；(2)求点B的坐标及OB所在直线解析式；(3)求△OAP的面积．24.如图，在△ABC中，∠C=90°，∠ABC的平分线交AC于点E，过点E作BE的垂线交AB于点F，⊙O是△BEF的外接圆．(1)求证：AC是⊙O的切线；(2)过点E作EH⊥AB，垂足为H，求证：CD=HF；(3)若CD=1，EH=3，求BF及AF长．25.把Rt△ABC和Rt△DEF按如图①摆放(点C与E重合)，点B、C(E)、F在同一条直线上．已知：∠ACB=∠EDF=90°，∠DEF=45°，AC=8，BC=6，EF=10．如图②，△DEF从图①的位置出发，以每秒1个单位的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点A出发，以每秒1个单位的速度沿AB向点B匀速移动；当点P移动到点B时，点P停止移动，△DEF也随之停止移动．DE与AC交于点Q，连接PQ，设移动时间为t(s)．(1)△DEF在平移的过程中，AP=CE= (用含t的代数式表示);当点D落在Rt△ABC的边AC上时，求t的值.(2)在移动过程中，当0＜t≤5时，连接PE,①设四边形APEQ的面积为y，求y与t之间的函数关系式并试探究y的最大值；②是否存在△PQE为直角三角形？若存在，请直接写出t的值；若不存在，请说明理由．2019年中考模拟考试试卷数学参考答案一．选择题1. B2. C3.B4.D5. C6.D7. A8.D9. B 10.C二．填空题11. x≠1 12. 2(x+2)(x ﹣2) 13. ﹣2 14.35 15. 43π- 16. 201894三．解答题(一)17．解：(1)原式=3+1﹣2×12+3…………4分=6 …………6分18. 解：原式=112)111-x (22-++÷---x x x x x x …………1分 =x-x+1x 1+·2(x+1)(x-1)(x 1)+ …………3分=11+x …………4分当x=2时，原式=1-2121=+ …………6分 19. 解：解：(1)如图射线DE 为所示； …………3分 (2)∵DE 平分∠BDC ，∴∠BDE =∠CDC ， …………4分∵DE ∥AC∴∠BDE =∠A ，∠CDC =∠ACD ， …………5分∴∠A =∠ACD ． …………6分四．解答题(二)20. 解：(1)设乙图书每本价格为x 元，则甲图书每本价格是2.5x 元，根据题意可得：800800x 2.5x-=24， …………2分解得：x=20，…………3分经检验得：x=20是原方程的根，则2.5x=50，…………4分答：乙图书每本价格为20元，则甲图书每本价格是50元；(2)设购买甲图书本数为a ，则购买乙图书的本数为：2a+8，根据题意可得：50a+20(2a+8)≤1060，…………5分解得：a≤10，故2a+8≤28， …………6分答：该图书馆最多可以购买28本乙图书． …………7分 21. (1)200、81°；…………2分 (2)微信人数为200×30%=60人，银行卡人数为200×15%=30人，补全图形如下：…… 4分由条形图知，支付方式的“众数”是“微信”. …………5分 (3)31…………7分22. 证明：(1)∵正方形ABCD ，∴AB=AD ，∴∠ABD=∠ADB ，…………1分∴∠ABE=∠ADF ， …………2分在△ABE 与△ADF 中，∴△ABE ≌△ADF(SAS)； …………4分(2)连接AC ，四边形AECF 是菱形． …………5分理由：∵正方形ABCD ， ∴OA=OC ，OB=OD ，AC ⊥EF ， ∴OB+BE=OD+DF ，即OE=OF ，∵OA=OC ，OE=OF ，∴四边形AECF 是平行四边形， …………6分 ∵AC ⊥EF ，∴四边形AECF 是菱形．…………7分五．解答题(三)23. 解：(1)将点A(4，3)代入y=kx(k≠0)，得：k=12， …………1分则反比例函数解析式为y=12x； …………2分 (2)如图，过点A 作AC ⊥x 轴于点C ，则OC=4、AC=3，∴， …………3分∵AB ∥x 轴，且AB=OA=5， ∴点B 的坐标为(9，3)； …………4分设OB 所在直线解析式为y=mx(m≠0)将点B(9，3)代入得m=31…………5分∴OB 所在直线解析式为y=31x ， …………6分(3)由可得点P 坐标为(6，2)， …………7分过点P 作PD ⊥x 轴，延长DP 交AB 于点E ，则点E 坐标为(6，3)，∴AE=2,PE=1,PD=2， …………8分则△OAP 的面积=12×(2+6)×3﹣12×6×2﹣12×2×1=5． …………9分 24．(1)证明：如图，连接OE ．∵BE ⊥EF ， ∴∠BEF=90°， ∴BF 是圆O 的直径． ∵BE 平分∠ABC ，∴∠CBE=∠OBE ， …………1分∵OB=OE ， ∴∠OBE=∠OEB ， ∴∠OEB=∠CBE ，∴OE ∥BC ， …………2分 ∴∠AEO=∠C=90°，∴AC 是⊙O 的切线； …………3分 (2)证明：如图，连结DE ．∵∠CBE=∠OBE ，EC ⊥BC 于C ，EH ⊥AB 于H ， ∴EC=EH ．∵∠CDE+∠BDE=180°，∠HFE+∠BDE=180°， ∴∠CDE=∠HFE ． …………4分在△CDE 与△HFE 中，，∴△CDE ≌△HFE(AAS)， …………5分∴CD=HF …………6分 (3)由(2)得CD=HF ，又CD=1，∴HF=1，在Rt △HFE 中，EF= =，∵EF ⊥BE ， ∴∠BEF=90°， ∴∠EHF=∠BEF=90°， ∵∠EFH=∠BFE ， ∴△EHF ∽△BEF ，∴=，即=， ∴BF=10， ………… 7分∴OE=21BF=5，OH=5﹣1=4，∴Rt △OHE 中，cos ∠EOA= 54，∴Rt △EOA 中，cos ∠EOA= OA OE = 54， ∴OA 5= 54，∴OA= 425， …………8分 ∴AF= 425﹣5= 45 …………9分25.…………1分当D 在AC 上时，…………2分 …………3分(2)如图4，过点P 作PM ⊥BE 于M ，∴∠BMP=∠ACB =90°…………4分又∵∠EDF=90°，∠DEF=45°∴∠EQC=∠DEF=45°…………5分y 最大值=45512932532)932(109-2=⨯+⨯ …………6分7分 9分附：(3)的参考做法：如图4，过点P 作PH ⊥BE 于H ，过点P 作PW ⊥AC 于W当∠PQE=90°，在Rt △PEQ 中当∠PEQ=90°，解得：t 1=0(舍去) t 2=20(舍去)∴此时不存在；当∠EPQ=90°时 PQ 2+PE 2=EQ 2，。

2019初三二模易错题整理 (教师答案版)