《 离散数学》期中考试试卷(2006—2007学年第2学期)
北京大学 离散数学 2007下学期期中考试试卷
2007下学期期中考试试卷姓名___________________学号 _____________________三总分一二(15) (16.1) (16.2) (17)(18)(19)(20)(21)(22)(23)一 选择题（20%）:将所选择的答案填入下面表格中。
(1) (2) (3) (4) (5) (6) (7) (8) (9) (10)(1) 下面“p→q”的等价说法，不正确的是( )：(A) p是q的充分条件；(B) q是p的必要条件；(C) q仅当p；(D) 只有q才p。
(2) 下面不是命题的是：(A) ∀xP(x) (B) x∈{x}∪{{x}} (C) A-B=∅⇔A=B (D) ∀x(P(x)∨P(y))(3) 谓词公式∀x∃yP(x,y)的否定式为( )：(A) ∀x∃y(¬P(x,y)) (B) ∀x∀y(¬P(x,y)) (C) ∃x∀y(¬P(x,y)) (D) ∃x∃y(¬P(x,y))(4) 下面是一些运算的分配性表达式，不成立是( )(A) A∩(B⊕C) = (A∩B)⊕ (A∩C) (B) A∪ (B⊕C) = (A∪B)⊕ (A∪C)(C) (A⊕B)×C = (A×C)⊕(B×C) (D) (A－B)×C = (A×C)－(B×C)(5) 有关关系的逆关系的说法不正确的是( )：等价关系和相容关系的逆关系就是其本身；(A)(B) 偏序关系的逆关系仍然是偏序关系；全序关系的逆关系仍然是全序关系；(C)(D) 良序关系的逆关系仍然是良序关系；(6) 下面推理中，不正确的是(A) p⇒ p∨q (B) q⇒p→q (C) ¬q∧( p→q) ⇒q (D) ¬(p→q) ⇒¬q(7) 命题公式(p→q) ∨( p→q)的成真赋值有___个：(A) 1 (B) 2 (C) 3 (D) 4(8) 下列集合运算中( )是正确的。
离散数学 期中试题
《离散数学》期中试题姓名：______________ 学号：______________ 一、确定下列各命题的真、假；（1）∅⊆∅（2）∅⊂∅（3）∅∈∅（4）∅⊆｛∅｝（5）∅∈｛∅｝（6）｛a, b｝⊆｛a , b , c,｛a，b，c｝｝（7）｛a, b｝∈｛a，b，c，｛a，b，c｝｝（8）｛a, b｝⊆｛｛a，b｝，｛｛a，b｝｝｝（9）｛a, b｝∈｛｛a，b｝，｛｛a，b｝｝｝（10）{{a, b}}⊂｛｛a，b｝，｛｛a，b｝｝｝（11）对任意集合A，B，C，、若A∈B，B ⊆ C则A∈C。
（12）对任意集合A，B，C，若A∈B，B ⊆C则A ⊆ C。
（13）对任意集合A，B，C，若A ⊆ B，B∈ C则A ∈ C。
（l4）对任意集合A，B，C，若A ⊆ B，B ∈ C则A ⊆ C。
二、对任意集合A，B，C，证明：（1）（A - B）⊕ B = A ⋃ B （2）（A ⊗ B）⋃ C =（A ⋃ C）⊗（B ⋃ C）（3）A ⋃ B = A ⊕（B ⊕（A ⋂ B））证三、归纳定义下列集合：（1）谓词公式。
（2）命题公式（3）十进制非负有穷小数。
（4）全体十进制有理数。
解四、判断下列语句是否是命题，若是命题则请将其形式化：（1）x>0（2）所有的人都是要死的，但有人不怕死。
（3）我明天或后天去苏州的说法是谣传。
（4）如果买不到飞机票，我哪儿也不去。
（5）除非你陪伴我或代我雇辆车子，否则我不去。
（6）如果只有懂得希腊文才能了解柏拉图，那么我不了解柏拉图。
五、用四种不同方法证明下列逻辑等价式：（1）A→(A→B)┝┥A→B（2）A→(B→C)┝┥(A→B)→(A→C)六、用四种不同方法证明下列逻辑蕴涵式：（1）A∧B┝ A↔B（2）(A→B)→A┝ A七、. 设整数集为个体域，判定下列公式的真值(*表示数乘运算)：（1）∀x ∃y(x*y=x)（2）∀x∃y (x*y=1)（3）∀x ∃y(x+y=1)八、. 用谓词公式将下列语句形式化：（1）高斯是数学家，但不是文学家。
离散数学试卷06-07(上)A
合肥学院2007至2008学年第二学期《离散数学》课程考试（ A ）卷计算机 系 06 级 网络工程 专业 学号 姓名一、选择题：(每小题2分，计22分)1.前提,,p q q r r ⌝∨⌝∨⌝的结论是（A.qB.p ⌝C. p q ∨D p q ⌝→2.集合A={1，2，3，4}，下列关系R 中不是等价关系的是（ ） A. {1,1,2,2,3,3}R =〈〉〈〉〈〉；B.{1,1,2,2,3,3,3,2,2,3}R =〈〉〈〉〈〉〈〉〈〉；C.{1,1,2,2,3,3,1,4}R =〈〉〈〉〈〉〈〉；D.{1,2,2,1,1,3,3,1,2,3,3,2}A R I =〈〉〈〉〈〉〈〉〈〉〈〉⋃。
. 3.下列语句中哪个是命题（ ）A.我正在说谎。
B. 5x y + 。
C.地球之外还存在有智慧的动物。
D.请勿践踏草地！ 4．设F(x)：x 是火车，G(x)：y 是汽车，H(x,y)：x 比y 快。
命题“某些汽车比所有的火车慢”的符号化公式是（ ）.(()(()(,)))A y G y x F x H x y ∃→∀∧ .(()(()(,)B y G y x F x H x y ∃∧∀→ .(()(()(,)))C x y G y F x H x y ∀∃→∧ .(()(()(,)D y G y x F x H x y ∃→∀→ 5．利用谓词的约束变元的更名规则和自由变元的代人规则，可将公式(()(,))(,)x P x Q x y R x y ∀→∧改写为（ ）。
.(()(,))(,)A x P y Q x y R z s ∀→∧ .(()(,))(,)B z P z Q z s R x s ∀→∧ .(()(,))(,)C x P s Q x s R x s ∀→∧ .(()(,))(,)D z P s Q z s R z s ∀→∧6.下列公式中正确的等价式是（ ）。
.()()A xA x x A x ∃⇔∃⌝ .()()B xA x x A x ⌝∀⇔∃⌝.(,)(,)C x yA x y y xA x y ∀∃⇔∃∀.(()())(()())D x A x B x x A x B x ∀∧⇔∀∨7．设{},(())A B P P A =∅=，以下不正确的式子是（ ）。
离散数学期中考试
离散数学期中考试试卷班级————姓名————学号————一、单项选择题（每题４分，共３２分。
）1、前提┐P∨Q, ┐Q∨R, ┐R的结论是（）。
A. QB. ┐PC. P∨QD. ┐P→R2、下列语句为命题的是（）。
Ａ．暮春三月，江南草长。
Ｂ．这是多么可爱的风景啊！Ｃ．大家想做什么，就做什么，行吗？Ｄ．请勿践踏草坪！3、下列复合命题为真命题的是（）。
A．如果３＋３≠６，则３是奇数。
B．３是有理数当且仅当加拿大在亚洲。
C．只要乌鸦是黑色的，就有中国是世界上面积最大的国家。
D．２是偶素数是不对的。
４、下列关于谓词公式的论述不正确的是（）。
A．闭式在任何解释下都是命题。
B．可满足式是指存在一个解释使得在该解释下对任一赋值公式都为真。
C．命题公式中的重言式的代换实例是永真式。
D．命题公式中的矛盾式的代换实例是矛盾式。
，Ｂ＝P(P(A))，以下不正确的是（）。
Ａ．｛｝∈ＢＢ．｛｝∈ＢＣ．｛｝包含于ＢＤ．｛｛｛｝｝｝包含于Ｂ６、设集合｛１，２，３｝，下列关系Ｒ中不是等价关系的是（）。
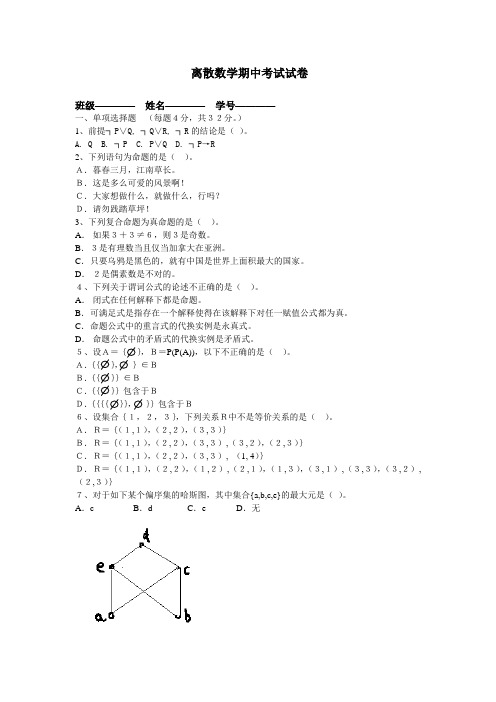
Ａ．Ｒ＝｛（１,１），（２,２），（３,３）｝Ｂ．Ｒ＝｛（１,１），（２,２），（３,３）,（３,２），（２,３）｝Ｃ．Ｒ＝｛（１,１），（２,２），（３,３）, （1, 4）｝Ｄ．Ｒ＝｛（１,１），（２,２），（１,２）,（２,１），（１,３），（３,１）,（３,３），（３,２）,（２,３）｝７、对于如下某个偏序集的哈斯图，其中集合{a,b,c,e}的最大元是（）。
A．c B．d C．e D．无８、命题公式A和B是等值的，是指（）。
A．A和B有相同的命题变项。
B．A和B都是可满足的。
C．当A对某一赋值为真时，B对该赋值也为真。
D．A和B有相同的真值表。
二、填空题（每题３分，共15 分。
）1、设R为非空集合A上的二元关系，如果R满足（）、（）、（），则称R为A上的一个偏序关系。
２、若集合A={1, 2, 3}上的二元关系R1和R2的关系图如下所示，则R1o R2 =（），R2o R1=（）。
离散数学期中考试（含答案）
《离散数学》期中考试参考答案一、填空题（本题共10个空，每空2分，共20分）1. 设A为任意的公式，B为重言式，则A∨B的公式类型为重言式。
2. 设个体域为非负实数集，A(x,y)表示x+y=y，则∃x∀yA(x,y)的真值为 T ，∀x∃yA(x,y)的真值为 F 。
3. ∀x∃yA(x,y)的否定式是∃x∀y⌝A(x,y) 。
4. 命题公式P→(Q∧⌝R)的成真赋值有 000, 001, 010, 011, 110 ，成假赋值有 100, 101, 111 。
5. {⌝,∧}，或{⌝,∧}，或{↑} 或{↓} 或{⌝,→} 是一个最小联结词组。
6. 由n个命题变元组成不等价的命题公式的个数为22n。
7. 设A是含有n(n≥1)个命题变元的公式，若A为重演式，则A的主析取范式含有2n个小项。
8. 设解释I为：个体域D={a,b},F(x)与G(x)为2个一元谓词，且F(a)=0,G(b)=1,G(a)=1,G(b)=0.在I下，公式∀x(F(x)→G(x))的真值为 F 。
二、简答题（本大题共5个小题，共计60分）1. 在命题逻辑中，把下列命题符号化（每个小题5分，共25分）（1）除非天下大雨，否则小王不会迟到。
P: 天下大雨，Q：小王迟到。
[2分]Q→P [3分]（后面的相同）（2）仅当你走，我将留下。
P: 你走，Q：我留下。
Q→P（3）他一面吃饭，一面听音乐。
P: 他吃饭，Q：他听音乐。
P ∧ Q（4）老王是山东人或河北人。
P: 老王是山东人，Q：老王是河北人。
P∨Q 或 (P∧⌝Q)∨(⌝P∧Q) 或 P∨Q （5）一个数是素数当且仅当它只能被1和它自身整除。
P: 一个数是素数，Q：一个数被1整除，R：一个数被它自身整除。
S：一个数能被除1和它自身以外的数整除P ⇄（Q∧R∧⌝S）2. 在一阶谓词逻辑中，把下列命题符号化（每个小题5分，共10分）（1）尽管有人聪明，但未必一切人都聪明.M(x):x是人，P(x):x聪明。
《离散数学》考试试卷(试卷库14卷)及答案
第 1 页/共 4 页《离散数学》考试试卷（试卷库14卷）试题总分： 100 分 考试时限：120 分钟一、选择题（每题2分，共20分）1. 下述命题公式中，是重言式的为( )（A ）)()(q p q p ∨→∧ （B ）q p ∨))()((p q q p →∨→⇔（C ）q q p ∧→⌝)(（D ）q q p →⌝∧)(2. 对任意集合A,B,C,下列结论正确的是（ ）（A ）若A ⊆B,B ∈C,则A ⊆C ； （B ）若A ∈B,B⊆C,则A ⊆C ； （C ）若A ⊆B,B ∈C,则A ∈C ； （D ）若A ∈B,B ⊆C,则A ∈C ； 3. 设} 3 ,2 ,1 {=S ，定义S S ⨯上的等价关系,,则由R 产生的S S ⨯上一个划分共有( )个分块。
（A ）4（B ）5（C ）6（D ）94. 下列偏序集( )能构成格5. 连通图G 是一棵树当且仅当G 中( )（A ）有些边是割边 （B ）每条边都是割边（C ）所有边都不是割边 （D ）图中存在一条欧拉路径6. 有n 个结点)3(≥n ，m 条边的连通简单图是平面图的必要条件( )（A ） 63-≤n m（B ）63-≤m n （C ）63-≥n m （D ） 63-≥m n7. 设P,Q 的真值为0,R,S 的真值为1,则下面命题公式中真值为1的是（ ）（A ）R →P （B ）Q ∧S （C ）P S （D ）Q ∨R 8. 在图G=<V,E>中,结点总度数与边数的关系是（ ）（A ）deg()2||i v E =（B ）deg()||i v E =（C ）deg()2||iv Vv E ∈=∑（D ）deg()||iv Vv E ∈=∑9. 设有33盏灯,拟公用一个电源,则至少需有五插头的接线板数（ ）（A ）７ （B ）８ （C ）９ （D ）１４ 10. 设集合A 上有四个元素,则A 上的不同的等价关系的个数为（ ）（A ）11 （B ）14 （C ）17（D ）15二、填空题（每题2分，共20分）1. 设A={a ，b ，c ，d}，其上偏序关系R 的哈斯图为则R= 。
离散数学考试题及答案
离散数学考试题及答案一、选择题1. 关于图论的基本概念，以下哪个说法是正确的？A. 无向图中的边无方向性，有向图中的边有方向性。
B. 有向图中的边无方向性，无向图中的边有方向性。
C. 无向图和有向图都是由顶点和边组成的。
D. 无向图和有向图都只由边组成。
答案：A2. “若顶点集合为V，边集合为E，那么图G可以表示为G(V, E)”是关于图的哪个基本概念的描述？A. 图的顶点B. 图的边C. 图的邻接D. 图的表示方法答案：D3. 以下哪个命题是正确的？A. 若集合A和B互相包含，则A和B相等。
B. 若集合A和B相交为空集，则A和B相等。
C. 若集合A和B相等，则A和B互相包含。
D. 若集合A和B相等，则A和B相交为空集。
答案：C二、填空题1. 有一个集合A = {1, 2, 3, 4}，则集合A的幂集的元素个数为__________。
答案：162. 设A = {a, b, c}，B = {c, d, e}，则集合A和B的笛卡尔积为__________。
答案：{(a, c), (a, d), (a, e), (b, c), (b, d), (b, e), (c, c), (c, d), (c, e)}3. 若p为真命题，q、r为假命题，则合取范式(p ∨ q ∨ r)的值为__________。
答案：真三、计算题1. 计算集合A = {1, 2, 3, 4}和集合B = {3, 4, 5, 6}的交集、并集和差集。
答案：交集：{3, 4}并集：{1, 2, 3, 4, 5, 6}差集：{1, 2}2. 计算下列命题的真值：(~p ∨ q) ∧ (p ∨ ~q)，其中p为真命题，q为假命题。
答案：真四、证明题证明：对于任意集合A和B，如果A和B互相包含，则A和B相等。
证明过程：假设A和B互相包含，即A包含于B且B包含于A。
设x为集合A中的任意元素，则x也必然存在于集合B中，即x属于B。
同理，对于集合B中的任意元素y，y也属于集合A。
离散数学考试题及答案
离散数学考试题及答案一、选择题（每题5分，共20分）1. 下列哪个选项不是离散数学的研究对象？A. 图论B. 组合数学C. 微积分D. 逻辑学答案：C2. 在逻辑学中，下列哪个命题是真命题？A. 如果今天是周一，那么明天是周二。
B. 如果今天是周一，那么明天是周三。
C. 如果今天是周一，那么明天是周四。
D. 如果今天是周一，那么明天是周五。
答案：A3. 在集合论中，下列哪个符号表示集合的并集？A. ∩B. ∪C. ⊆D. ⊂答案：B4. 在图论中，下列哪个术语描述的是图中的顶点集合？A. 边B. 路径C. 子图D. 顶点答案：D二、填空题（每题5分，共20分）1. 如果一个集合A包含5个元素，那么它的子集个数是______。
答案：322. 在逻辑学中，如果命题P和命题Q都是真命题，那么复合命题“P且Q”的真值是______。
答案：真3. 在图论中，如果一个图的顶点数为n，那么它的最大边数是______。
答案：n(n-1)/24. 如果一个二叉树的深度为3，那么它最多包含______个节点。
答案：7三、简答题（每题10分，共30分）1. 请简述什么是图的连通性，并给出一个例子。
答案：图的连通性是指在图中任意两个顶点之间都存在一条路径。
例如，在一个完全图K3中，任意两个顶点之间都可以通过一条边直接连接，因此它是连通的。
2. 解释什么是逻辑蕴含，并给出一个例子。
答案：逻辑蕴含是指如果一个命题P为真，则另一个命题Q也必须为真。
例如，命题P：“如果今天是周一”，命题Q：“明天是周二”。
如果今天是周一，那么根据逻辑蕴含，明天必须是周二。
3. 请描述什么是二叉搜索树，并给出它的一个性质。
答案：二叉搜索树是一种特殊的二叉树，其中每个节点的左子树只包含小于当前节点的数，右子树只包含大于当前节点的数。
它的一个性质是中序遍历可以得到一个有序序列。
四、计算题（每题15分，共30分）1. 给定一个集合A={1, 2, 3, 4, 5}，请计算它的幂集，并列出所有元素。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《离散数学J》考试试卷（期中）
课程代码143140320命题单位学院：计算机学院信息教研室
学院:_______________班级:_____________姓名:_______________学号:____________ 1．将下列命题将其符号化。
（4分）
①.李平不是不聪明，而是不用功。
假设p:李平聪明，q:李平用功
②.如果只有懂得希腊文才能了解柏拉图，那么我不了解柏拉图。
假设p：我懂得希腊文，q：我了解柏拉图
2．在一阶逻辑中将下列命题符号化。
（9分）
①.整数都是有理数，并不是每个有理数一定是整数，有些有理数不是整数。
假设I(x)：x是整数，Q(x)：x是有理数。
②.某些汽车比所有的火车慢。
假设F(x)：x是火车。
G(x)：y是汽车。
H(x,y)：x比y快
③.谁要是游戏人生，他就一事无成；谁不能主宰自己，他就是一个奴隶。
假设：M(x)表示“x是人”，K(x)表示“x游戏人生”，L(x)表示“x 一事无成”，H(x,y)表示“x主宰y”，N(x)表示“x是奴隶”。
3．试证明：
(┐P∧(┐Q∧R))∨((Q∧R)∨(P∧R))=R(10分)
4．求公式G＝(P→Q)∧R的主析取范式和主合取范式。
(12分)
5．先将些列论断符号化，再证明论断的正确性。
（15分）
所有的大一学生都要学习英语；并非所有的大一学生都要学习离散数学；故有些学习英语的不学习离散数学。
假设谓词如下：P(x)：x是大一学生；Q(x)：x要学习英语；
R(x)：x要学习离散数学。
6．某班学生50人，会排球的有40人，会篮球的35人，会足球的10人，以上三种运动都会的5人，都不会的没有，问只会两种运动的有几人？
《离散数学J》考试试卷（期中）
假设A表示会排球的人的集合，B表示会篮球的人的集合，C表示会足球的人的集合。
(12分)
7．设R,S分别是从集合A到集合B，集合B到集合C的二元关系，试证明：(R o S)-1＝S-1o R-1(12分)
8．设集合A＝{2,4}，B＝{2,3，8}，设R={<2,3>,<3,8>}是集合B上的二元关系.(26分)
1)求A×B；
2)求r(R)，s(R)，t(R))，st(R)和ts(R)；
3)画出集合B的幂集P(B)上定义的“包含于”关系的哈斯图，并指出集合
{{3},{2,3},{3,8}}的最小元、最大元、极小元、极大元、上界、最小上界、下界和最大下界。