第二章晶体衍射和倒格子案例
合集下载
倒格空间晶体的X射线衍射演示文稿
设A为任一格点，格矢
S0
A
Rl l1 a1l2 a2l3 a3
S
Rl
波程差
CO D
C O O D R lS 0R lSR lSS0
衍射加强条件为：
R lS S 0 (为)整劳数 厄衍射方程
波矢 k02πS0,k2πS
λ
λ
R lk k 0 2 π μ
R lk k 0 2 π μ
*(2)3a2a3(a3a 1a 1a2)
A B C (A C ) B (A B ) C
a 3 a 1 a 1 a 2
a 3 a 1 a 2 a 1 a 3 a 1 a 1 a 2 Ω a 1
Ω * 2π 3a2a3Ω a1(2)3
Ω
正点阵中晶面族与倒易位矢的关系
倒格空间晶体的X射线衍射演示文稿
晶体结构是怎么测定的？
晶体结构与衍射图样的对应关系？
晶体的X光衍射
按照衍射理论，当辐射的波长与晶格中原子的间距 相同或更小时，即可发生显著的衍射现象。
晶体衍射的基本方法
1、X射线衍射
X射线是由被高电压V
加速了的电子，打击在
hmaxeU
h
c
min
eU
“靶极”物质上而产生
(1)证明 Khh1b1h2b2h3b3 与晶面族(h1h2h3)正交。
设ABC为晶面族(h1h2h3)中离原点最近的晶面，
ABC在基矢
a1,a2,a3上的 截距分别为
a1 , a2 , a3 。
h1 h2 h3
a3
由图可知： CAOAOCa1 a3
C Kh
h1 h3 CBOBOCa2 a3
h2 h3
h12 h22 h32
23布里渊区
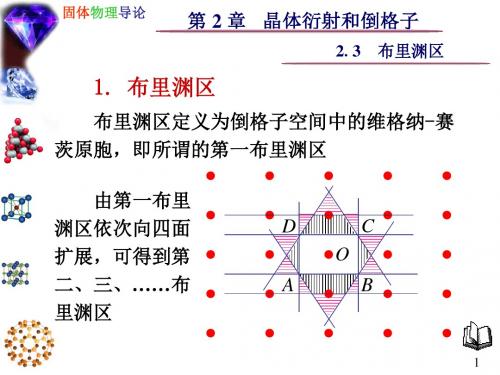
将任一布里渊 区的各部分平移适 当的位矢就可合并 成第一布里渊区
D
O A
C
B
由于倒格子的周期性，很多时候我们 只需关心第一布里渊区
2
固体物理导论
第 2 章 晶体衍射和倒格子
2.3 布里渊区
2. 衍射条件的布里渊区诠释
2k G G 2
D
GD
k1
1 1 2 k G G 2 2
体心立方
x
a3
Ω a1 (a2 a3 ) 1 3 a 2
Ω b1 (b2 b3 )
*
4π a
2( 2 π ) 3 / a 3
5
固体物理导论
第 2 章 晶体衍射和倒格子
2.3 布里渊区
倒格矢可以表示为
G v1b1 v2b2 v3b3 4π 2π [(v2 v3 )i (v3 v1 ) j (v1 v2 )k ] a a
最短的倒格矢是以下12个矢量
2π 2π 2π ( j k ); ( k i ); (i j ) a a a
第一布里渊区由上述12个矢量的 垂直平分面围成，是一个正十二面体
6
固体物理导论
第 2 章 晶体衍射和倒格子
2.3 布里渊区
体心立方晶格的布里渊区中一些 具有较高对称性的点或轴的坐标
其中
2π X: (1,0,0) a 2π 1 1 1 L: ( , , ) a 2 2 2 2π 3 3 K: ( , ,0 ) a 4 4 1 3 0 1, 0 , 0 2 4
10
k2
O
GC
C
任何从原点到 G 的垂直平分面的矢量都满足衍射 条件，这些平面正是布里渊区的边界。布里渊区包含 了所有能在晶体上发生布拉格反射的波的波矢 k
第二部分 倒易点阵和晶体衍射-总结与习题指导
ϕG = ∑ f j ( G ) exp ( −iG ⋅ r j )
j
(2.11)
其中 rj 是基元中第 j 原子的坐标，
r j = x j a1 + y j a2 + z j a3 , ( 0 ≤ x j , y j , z j < 1) f j 是第 j 原子的形状因子，
4
f j = ∫ dVn j ( r ) exp ( −iG ⋅ r )
j
(2.13)
当基元的几何结构因子为零时，空间点阵所允许的反射消失，而根据消失了 的反射(即消光规则)又可以帮助我们确定晶体结构．
5
例题
2．1 体心立方和面心立方点阵的倒易点阵 证明体心立方点阵的倒易点阵
是面心立方点阵．反之，面心立方点阵的倒易点阵是体心立方点阵．
[证明]
选体心立方点阵的初基矢量如图 1．8 所示，
2
2
{
}
这里引用了公式： ( A × B ) × ( C × D ) = ⎡ ⎣( A × B ) ⋅ D ⎤ ⎦C − ⎡ ⎣( A × B ) ⋅ C ⎤ ⎦D。 由于 ( a3 × a1 ) ⋅ a1 = 0 ，故有
⎛ 2π ⎞ b2 × b3 = ⎜ ⎟ ⎡ ⎣( a3 × a1 ) ⋅ a2 ⎤ ⎦ a1 ⎝ Vc ⎠
2k ⋅ G + G 2 = 0
或
(2.9a)
2k ⋅ G = G 2
(2.9b)
可以证明，布喇格定律和劳厄条件完全是等价的。
相应于倒易点阵矢量 G 所给出的波矢改变 Δk = G ，有劳厄衍射的峰值，这 个劳厄衍射峰正好相当于来自和 G 相垂直的晶面族的布喇格反射，而出现在布 喇格定律中的反射级 n 正是倒易点阵矢量 G 除以和它平行的最短倒易点阵矢量 而得的倍数。
固体01-04倒格子
a 1 ⋅ b1 = 2π a1 ⋅ b2 = 0
a i ⋅ b j = 2πδ ij =
2π ( i = j )
0 (i ≠ j )
a 2 ⋅ b1 = 0 a 2 ⋅ b2 = 2π
2π b1 = i a 2π b2 = j a
2π a
2π a
G h = h1 b1 + h2 b 2
2π 的正方形格子。 倒格是边长为 的正方形格子。 a
b1 =
2
2π
2
3
1 = a1 ⋅ a2 ×a3 = a3 2
(
)
3
1
3
1
2
a2 ×a3 =
i a 2 a 2
j a − 2 a 2
a k − a =i 2 a 2 a 2 − 2
a a 2 + j 2 a a − − 2 2
一、倒格子点阵
一个具有晶格点阵周期的函数 n(r) = n(r + R) 展开成傅里 叶级数后，其傅里叶级数中的波矢在傅里叶空间中表现为 叶级数后， 一系列规则排列的点， 一系列规则排列的点，这些点排列的规律性只决定于函数 n(r)的周期性而与函数的具体形式无关。 n(r)的周期性而与函数的具体形式无关。 的周期性而与函数的具体形式无关 我们把在傅里叶空间中规则排列着的点的列阵称为倒格子 我们把在傅里叶空间中规则排列着的点的列阵称为倒格子 点阵（或倒易点阵） 点阵（或倒易点阵）。倒格子点阵是晶体结构周期性在傅 里叶空间中的数学抽象。 里叶空间中的数学抽象。如果把晶体点阵本身看作一个周 期函数，我们可以说， 期函数，我们可以说，倒格子点阵就是晶体点阵的傅里叶 变换。反之，晶体点阵就是倒格子点阵的傅里叶逆变换。 变换。反之，晶体点阵就是倒格子点阵的傅里叶逆变换。
a i ⋅ b j = 2πδ ij =
2π ( i = j )
0 (i ≠ j )
a 2 ⋅ b1 = 0 a 2 ⋅ b2 = 2π
2π b1 = i a 2π b2 = j a
2π a
2π a
G h = h1 b1 + h2 b 2
2π 的正方形格子。 倒格是边长为 的正方形格子。 a
b1 =
2
2π
2
3
1 = a1 ⋅ a2 ×a3 = a3 2
(
)
3
1
3
1
2
a2 ×a3 =
i a 2 a 2
j a − 2 a 2
a k − a =i 2 a 2 a 2 − 2
a a 2 + j 2 a a − − 2 2
一、倒格子点阵
一个具有晶格点阵周期的函数 n(r) = n(r + R) 展开成傅里 叶级数后，其傅里叶级数中的波矢在傅里叶空间中表现为 叶级数后， 一系列规则排列的点， 一系列规则排列的点，这些点排列的规律性只决定于函数 n(r)的周期性而与函数的具体形式无关。 n(r)的周期性而与函数的具体形式无关。 的周期性而与函数的具体形式无关 我们把在傅里叶空间中规则排列着的点的列阵称为倒格子 我们把在傅里叶空间中规则排列着的点的列阵称为倒格子 点阵（或倒易点阵） 点阵（或倒易点阵）。倒格子点阵是晶体结构周期性在傅 里叶空间中的数学抽象。 里叶空间中的数学抽象。如果把晶体点阵本身看作一个周 期函数，我们可以说， 期函数，我们可以说，倒格子点阵就是晶体点阵的傅里叶 变换。反之，晶体点阵就是倒格子点阵的傅里叶逆变换。 变换。反之，晶体点阵就是倒格子点阵的傅里叶逆变换。
晶体的周期性结构(2)(倒格矢)
波恩-卡曼边界条件
• 电荷密度、势能等物理量满足迭加原理，如
V (r )
V
l
原子
r R l
• 理想的无限大晶体具有平移周期性，这样的物 理量满足
F (r R l ) F (r )
• 实际的晶体都是有限大小的， 并不满足严格的 平移对称性
F (r R l ) F (r )
2
N 3是 原 胞 的 总 数 ，
k 是 满 足 波 恩 -卡 曼 周 期 性 边 界 条 件 的 波 矢 量
k
l1 N1
b1
+
l2 N
2
b2+
l3 N
3
b3
• 对于布里渊区中许可波矢 k 的求和可化为对
k 的连续积分
kBZ
(.....)
V ( 2 )
3
( . . . . )d
3
k
正、倒对应关系
• 互为正格子、倒格子
b 1 2 b 2 2 b 3 2 a2 a3 a 1 (a 2 a 3 ) a 3 a1 a 1 (a 2 a 3 ) a1 a 2 a 1 (a 2 a 3 )
a 1 2 a 2 2 a 3 2 b2 b3 b 1 (b 2 b 3 ) b 3 b1 b 1 (b 2 b 3 ) b1 b 2 b 1 (b 2 b 3 )
j
bi a
2
ij
• 那确实可以满足上述关系，确实可以满足Kh所 有的段点为格点（即有可用基矢和整数表示的 平移周期性）
• bi就是倒格子基矢
• 如果确定了正格子基矢，倒格子基矢就不是任 意的。利用矢量关系
-倒格子
C
a3/h3
a3
G
B a2
O
a2/h2
a1/h1
A
a1
(2)晶面族（h1h2h3)的面间距d为
d
2
Gh
证明：由前面的证明
可知，原点到面ABC 的距离即为所求面间 距(设为d)。
d OA cos
又OAGh OA Gh cos
a3
Gh
C
a3/h3
d
B a2
O
a2/h2
倒格子空间
又称状态空间或
简称为k空间
描述微观粒子运动状态的波矢k具有和倒格子空间
同样的量纲。
—— 倒格子与正格子间的关系 1) 正格子原胞体积反比于倒格子原胞体积
* (2 )3
2）正格子中一簇晶面
和
正交
—— 可以证明
Gh1h2h3 CA 0 Gh1h2h3 CB 0
与晶面族正交
a1 cos a1, n h1d a2 cos a2 , n h2d a3 cos a3 , n h3d
cos a1 , n
h1 d a1
cos a 2 , n h2 d a2
cos a 3 , n h3 d a3
对于立方晶系：
2π
a
h1 i h2 j h3 k
2π K a h1h2h3
h12 h22 h32
d K2π h1h2h3
h1h2h3
a
h12 h22 h32
法二： 设ABC为晶面族(h1h2h3)中离原点最近的晶面，
ABC在基矢
a1 , a2 ,上a的3 截距分别为
第二章++X射线衍射和倒格子
第⼆章++X射线衍射和倒格⼦第⼆章 X 射线衍射和倒格⼦⼤多数探测晶体中原⼦结构的⽅法都是以辐射的散射概念为基础的。
早在1895年伦琴发现X 射线不久，劳厄在1912年就意识到X 射线的波长量级与晶体中原⼦的间距相同，⼤约是0.1nm 量级，晶体必然可以成为X 射线的衍射光栅。
随后布拉格⽤X 射线衍射证明了NaCl 等晶体具有⾯⼼⽴⽅结构，从⽽奠定了⽤X 射线衍射测定晶体中的原⼦周期性长程有序结构的地位。
随着科学技术的不断发展，电⼦、中⼦衍射有为⼈类认识晶体提供了有效的探测⽅法。
但到⽬前为⽌，X 射线衍射仍然是确定晶体结构、甚⾄是只具有短程有序的⽆定形材料结构的重要⼯具。
本章以X 射线衍射为例介绍晶体的衍射理论，引⼊倒格⼦的概念，在此基础上介绍原⼦形状因⼦和⼏何结构因⼦，并介绍⼏种确定晶格结构的实验⽅法。
§2.1 晶体衍射理论⼀、布拉格定律（Bragg ’s Law ）X 射线是⼀种可以⽤来探测晶体结构的辐射，其波长可以⽤下式来估算012.4()()hcE h A E KeV νλλ==?= （2.1.1）能量为2~10KeV 的X 射线适⽤于晶体结构的研究。
在固体中，X 射线与原⼦的电⼦壳层相互作⽤，电⼦吸收并重新发射X 射线，重新发射的X 射线可以探测得到，⽽原⼦核的质量相对较⼤，对这个过程没有响应。
X 射线的反射率⼤约是10-3~10-5量级，在固体中穿透⽐较深，所以X 射线可以作为固体探针。
1912年劳厄（/doc/eb1ccaba1a37f111f1855b71.html ul ）等发现了X 射线通过晶体的衍射现象之后，布拉格（W.L.Bragg ）⽗⼦测定了NaCl 、KCl 的晶体结构，⾸次给出了晶体中原⼦规则排列的实验数据，发现了晶态固体反射X 射线特征图像，推导出了⽤X 射线与晶体结构关系的第⼀个公式，著名的布拉格定律（Bragg ’s Law ）。
布拉格对于来⾃晶体的衍射提出了⼀个简单的解释。
第二章——晶体衍射和倒格子
插播知识点1
傅里叶分析
For a set of R and a plane wave eikr , the set of all wave
vectors G that yield plane waves with the periodicity of a given
Bravais lattice － reciprocal lattice
a2 h2
a3 h3
0
所以 K h h1b1 h2 b2 h3 b3 与晶面族(h1h2h3)正交。
b）
证明 K h h1b1 h2 b2 h3 b3 的长度等于
2π 。 d h1h2h3
由平面方程： X n d 得：
dh h h 123
a1 h1
Kh Kh
a1 h1 b1 h2 b2 h3 b3
d h1h2h3
a） 证明 K h h1 b1 h2 b2 h3 b3 与晶面族(h1h2h3)正交。
b） 证明
K h h1b1 h2 b2 h3 b3
的长度等于 2π d h1h2h3
。
a）
设ABC为晶面族(h1h2h3)中离原点最近的晶面，
ABC在基矢 a1,a2 ,a3 上的 截距分别为
其中 a1 , a 2 , a 3 是正格基矢，
Ω a1 a 2 a 3
是固体物理学原胞体积
与 K n h1b1 h2b2 h3b3 (h1, h2, h3为整数)所联系的各点
的列阵即为倒格。
倒格基矢的方向和长度如何呢？
b1 2π a2 a3 Ω
b2 2π a3 a1 Ω
eiGr
R
eiGr
eiGR
1
G belongs to the reciprocal lattice of a Bravais lattice of points R
第二章晶体的X射线衍射
证明：
* b 1 [ b 2 b 3 ] ( 2 3 ) 3 [ a 2 a 3 ] [ a 3 a 1 ] [ a 1 a 2 ]
利用： A (B C )(A C )B(A B )C
[ a 3 a 1 ] [ a 1 a 2 ] { a 3 a [ 1 ] a 2 } a 1 { a 3 a [ 1 ] a 1 } a 2 a 1
∴2dhSin＝n 布拉格方程（正空间）
N k
nkh
实际上：劳厄方程和布拉格方程是等价的
x-ray作用于多原子面上
• 经两相邻原子面反射的反射波光程差： R = 2d sinθ
布拉格方程：
• 干涉加强条件（布拉格方程）为：
2dsinn
式中：n —整数，“反射”级数（衍射级数） 一组（hkl）随n值的不同，可产生n个
2） K hkl 2
d hk l
3） RlKhkl 2m
其中
R l m an blc
所以倒格矢 K hkl 可以代表 （h，k，l）晶面。
三、布里渊区
定义： 任选一倒格点为原点，从原点向它的第 一、第二、第三……近邻倒格点画出倒格矢，并 作这些倒格矢的中垂面，这些中垂面绕原点所围 成的多面体称第一B.Z，其“体积”为倒格子原 胞体积
？ ？
X射线分析仪
世界闻名的事件：
1953年，用于测定“DNA”脱氧核糖核酸的 双螺旋结构就是用的此法。
• X 射线的波长 0.01—100 nm
• 用于测定晶体结构的X—ray 的波长 0.05—0.25 nm
• 用X 光管在高压下加速电子,冲击Mo靶或Cu靶产生X 射线，
固体物理2(1)
8
CA =
a1 a3 − ⇒CA⋅ Kh = 0 h1 h3
同 CB⋅ Kh = 0 理 ⇒ Kh垂 于 直 ABC面 。
Kh
a1/h1 返回
dh1h2h3
a1 Kh a1 (h1b1 + h2b2 + h3b3 ) 2π = ⋅ = ⋅ = h Kh h Kh Kh 1 1
9
2-2 X射线衍射
6
小结2
• 光波通过光栅衍射的过程，其实质是把 光栅从坐标空间(坐标域)变换到了状态空 间(频率域)，晶体的X射线衍射照片上的 斑点分布或图谱分布，一定程度上是晶 体结构在状态空间的化身。 • 倒格子是晶格在状态空间的化身。
7
倒格子与正格子间的关系
• 正格子晶胞体积Ω=a1⋅[a2×a3]，倒格子晶胞体积 Ω*=b1⋅[b2×b3]， Ω*=2π/ Ω； • 晶面(h1h2h3)与倒格矢Kh= h1b1+h2b2+h3b3正交 (证明在下页)； • 晶面(h1h2h3) 间距d h1h2h3= 2π/Kh； • 把晶格的一族晶面转化为倒格子中的一点，这 在处理晶格的问题上有很大的意义，晶体的衍 射是由于晶格和波的互相作用，一族晶面干涉 的结果，在照片上得出一点。倒格点的平移可 得出倒格子空间。
π
π
e4 1+ cos2 2θ 求和⇒ Ie = I0 2 2 4 mRc 2 汤 孙 Thom )公 姆 ( son 式
说明电子散射强度随2θ而变，IPZ在2θ为0o和180o 的方向上，其强度为90o方向上强度的2倍，IPY 不变，故一束非偏振的X射线被电子散射后偏振 31 化了，偏振化程度取决于2θ角度大小。
19
劳厄法
• 对应于λ极小和λ极大间的任一波长的反射球 介于这两反射球之间； • 所有反射球的球心都在入射线方向上， 图中的阴影部分的倒格点和各球心的联 线都表示晶体可以产生的反射的方向。
CA =
a1 a3 − ⇒CA⋅ Kh = 0 h1 h3
同 CB⋅ Kh = 0 理 ⇒ Kh垂 于 直 ABC面 。
Kh
a1/h1 返回
dh1h2h3
a1 Kh a1 (h1b1 + h2b2 + h3b3 ) 2π = ⋅ = ⋅ = h Kh h Kh Kh 1 1
9
2-2 X射线衍射
6
小结2
• 光波通过光栅衍射的过程，其实质是把 光栅从坐标空间(坐标域)变换到了状态空 间(频率域)，晶体的X射线衍射照片上的 斑点分布或图谱分布，一定程度上是晶 体结构在状态空间的化身。 • 倒格子是晶格在状态空间的化身。
7
倒格子与正格子间的关系
• 正格子晶胞体积Ω=a1⋅[a2×a3]，倒格子晶胞体积 Ω*=b1⋅[b2×b3]， Ω*=2π/ Ω； • 晶面(h1h2h3)与倒格矢Kh= h1b1+h2b2+h3b3正交 (证明在下页)； • 晶面(h1h2h3) 间距d h1h2h3= 2π/Kh； • 把晶格的一族晶面转化为倒格子中的一点，这 在处理晶格的问题上有很大的意义，晶体的衍 射是由于晶格和波的互相作用，一族晶面干涉 的结果，在照片上得出一点。倒格点的平移可 得出倒格子空间。
π
π
e4 1+ cos2 2θ 求和⇒ Ie = I0 2 2 4 mRc 2 汤 孙 Thom )公 姆 ( son 式
说明电子散射强度随2θ而变，IPZ在2θ为0o和180o 的方向上，其强度为90o方向上强度的2倍，IPY 不变，故一束非偏振的X射线被电子散射后偏振 31 化了，偏振化程度取决于2θ角度大小。
19
劳厄法
• 对应于λ极小和λ极大间的任一波长的反射球 介于这两反射球之间； • 所有反射球的球心都在入射线方向上， 图中的阴影部分的倒格点和各球心的联 线都表示晶体可以产生的反射的方向。
固体物理第二章第四节 倒格子.
h1 Gh h1 Gh h1 Gh Gh
2
d h1h2h3 Gh
表明,对任一倒格矢Gh h1b1 h2b2 h3b3
以其在倒易空间的坐标数(h1，h2，h3)表征的
正格子空间中的晶面族(h1h2h3)，一定以 Gh
为法线方向，且面间距为 2 / Gh
这个关系很重要,后面分析XRD时要用
3.倒格子基矢的方向和长度
许多的固体书中把上述描述作为倒格子的定义
2. 与正格子空间的平面波 类eiG似h•r，可以把
看成ei倒g•R空l 间的平面波， 是倒空间g的任一矢量
e e • e e i(gGh )•Rl
ig • Rl
iGh •Rl
ig • Rl
所以，在倒空间中，矢量 与g
代表相同的波或相同的状态。
g Gh
b1
2π a
j k
b2
2π a
i k
b3
2π a
i
j
体心立方的倒格子是边长为4/a的面心立方 。
例3：证明简立方晶面(h1h2h3)的面间距为
a
d h1h2h3
证明：
h12 h22 h32
由于 a为1,基a2,矢a3，互不共面，则由
bi • aj 2可知ij
亦b应1, b该2 , b不3 共面，从而可以用
描述倒格子Gh。 h1b1 h2b2 h3b3
由于 Gh h1b1 h2为b2 倒 h格3b3矢，如果把倒格矢所在 的空间称为倒格子空间，或倒易空间(reciprocal
2
a
a a a
2
2 j 2
a
a
2
2
2 k 2 aa 22
2 a 2
22
2
2
d h1h2h3 Gh
表明,对任一倒格矢Gh h1b1 h2b2 h3b3
以其在倒易空间的坐标数(h1，h2，h3)表征的
正格子空间中的晶面族(h1h2h3)，一定以 Gh
为法线方向，且面间距为 2 / Gh
这个关系很重要,后面分析XRD时要用
3.倒格子基矢的方向和长度
许多的固体书中把上述描述作为倒格子的定义
2. 与正格子空间的平面波 类eiG似h•r，可以把
看成ei倒g•R空l 间的平面波， 是倒空间g的任一矢量
e e • e e i(gGh )•Rl
ig • Rl
iGh •Rl
ig • Rl
所以，在倒空间中，矢量 与g
代表相同的波或相同的状态。
g Gh
b1
2π a
j k
b2
2π a
i k
b3
2π a
i
j
体心立方的倒格子是边长为4/a的面心立方 。
例3：证明简立方晶面(h1h2h3)的面间距为
a
d h1h2h3
证明：
h12 h22 h32
由于 a为1,基a2,矢a3，互不共面，则由
bi • aj 2可知ij
亦b应1, b该2 , b不3 共面，从而可以用
描述倒格子Gh。 h1b1 h2b2 h3b3
由于 Gh h1b1 h2为b2 倒 h格3b3矢，如果把倒格矢所在 的空间称为倒格子空间，或倒易空间(reciprocal
2
a
a a a
2
2 j 2
a
a
2
2
2 k 2 aa 22
2 a 2
22
2
固体物理第二章
由于k0=2π/ λ, (2)式:
R ∙(k0 - k)=2 πn
由平移矢量R和倒格式G的关系: R ∙G=2 πm (3) 比较(2)和(3): k0 – k=G (4)
(4)被称为劳厄方程
4.衍射极大条件 劳厄方程 （Laue Equation） a. 坐标空间中的劳厄方程
晶格中任一格点为O，格点A的位矢 Rl=l1a1+l2a2+l3a3, S0和S为单位矢量。 光程差 衍射加强的条件 A
可以证明，每个布里渊区的体积均相等，都等于第一布里渊区的体积， 即倒格子原胞的体积b
立方晶系的简约区
正格子 格常数 倒格子 格常数 简约区
sc
a
sc
2 a
由6个{100}*面 围成的立方体
由12个{110}*面 围成的菱形12面体 由8个{111}*面和6个{100}*面围 成的14面体
bcc
S=2f 当v1 ＋v2 ＋v3＝偶数
7. 晶体衍射
当辐射的波长与晶格中原子间距可以比较或更小时，可发生显著的衍射现象 。 （1）x射线 一种电磁波，由被高电压加速了的电子撞击靶极物质产生。X射线的光子能量为：
SG=celldV j nj(r-rj) exp(-iG•r)
= j exp(-iG•rj) dV nj() exp(-iG• ),
= r-rj . 原子形状因子 (atomic form factor) : fj= dV nj() exp(-iG• ), SG= j fj exp(-iG•rj) rj =xja1+ yja2+ zja3 , G= v1b1+ v2b2+ v3b3 SG(v1 v2 v3) = j fj exp[-2 i (v1xj + v2yj +v3zj )] 例如：体心立方 S=0 当v1 ＋v2 ＋v3＝奇数
第二章 晶体衍射
0 k
R
0 k R
0 k ' R
0 k '
劳厄衍射图
假设X射线沿 k 0 方向从无穷远处入射，
波长为
波矢为
2 0 k k
散射为弹性散射，那么沿着方向 k 0 ' 的散射波与入射波 有相同的波长，其波矢为 2 0 k ' k '
与它相对应的点阵称为正格子（direct lattice），格矢 R
则称作是正格矢（direct lattice vectors）。
注意：倒矢量或倒格子空间的长度量纲是［L－1］，即1／米，这与 波矢的量纲是一样的。所以，也将倒格子称作是波矢空间。
二、倒矢量（reciprocal vectors）
ij 1
（i,j=1,2,3）
R l l1 a 1 l 2 a 2 l 3 a 3
G h R l ( h1b1 h 2 b 2 h3 b3 ) ( l1 a1 l 2 a 2 l 3 a 3 ) 2 ( h1l1 h 2 l 2 h 3 l 3 )
0 这里 k 和 k 0 ' 分别为入射和散射方向的单位矢量。
由这两个散射体反射的X射线要发生相长干涉，入射和反射波的 波程差必须是波长的整数倍。由图可知，相长干涉的条件是：
0 0 k 'R k R m
其中 m 是整数。 给（2.1.3）式两边同乘以
2
（2.1.3）
在固体中，X 射线与原子的电子壳层相互作用，电子吸收并重新 发射X射线，重新发射的 X 射线可以探测得到，而原子核的质量相对 较大，对这个过程没有响应。X射线的反射率大约是10-3~10-5量级，在 固体中穿透比较深，所以 X 射线可以作为固体探针。
倒易格子与电子衍射
倒易格子对电子衍射的深入理解
理解电子衍射原理
倒易格子有助于深入理解电子衍射的原 理，通过将复杂的电子衍射过程简化为 倒易格子中的数学运算，有助于更好地 掌握电子衍射的基本概念和理论。
探索新型材料
利用倒易格子可以探索新型材料，通 过分析电子衍射图谱，可以研究材料 的原子结构和分子排列，从而发现具 有潜在应用价值的材料。
倒易格子与电子衍射
• 引言 • 倒易格子基础 • 电子衍射原理 • 倒易格子与电子衍射的关系 • 实际应用案例 • 结论
目录
01
引言
主题简介
倒易格子
倒易格子是晶体学中的基本概念，用于描述晶体中原子或分 子的排列方式。它是一个抽象的数学模型，通过将原子或分 子的位置映射到一个连续的空间格子上，可以方便地描述和 预测晶体中的各种性质。
布拉格定律
当电子束满足布拉格定律时，即电子束方向与晶体中原子面网法线方向 平行，且入射角等于晶面间距与波长的比值，将产生衍射。
03
倒易格子
倒易格子是描述晶体中原子排列周期性的数学工具，通过倒易格子可以
方便地计算出电子衍射图样中各衍射斑点的位置和强度。
电子衍射与晶体结构
晶体结构分析
点阵常数测量
通过电子衍射图样中各衍射斑点的位 置和强度，可以反推出晶体的结构信 息，如晶面间距、晶胞参数等。
通过电子衍射技术可以观察金属材料的微观结构，如晶粒大小、晶界特征等，进一步研究 这些结构特征对金属材料力学性能的影响。
陶瓷材料的电子衍射分析
陶瓷材料的晶体结构和相变
利用电子衍射技术可以研究陶瓷材料的晶体结构、相变过 程以及晶体缺陷等，有助于理解陶瓷材料的物理和化学性 质。
陶瓷材料的微观结构和性能
通过电子衍射技术可以观察陶瓷材料的微观结构，如晶粒 大小、晶界特征等，进一步研究这些结构特征对陶瓷材料 性能的影响。
第二章晶体衍射-总结
G
如何寻找满足条件的矢量组 G ？
n(r
T)
nG
ex
p[iG
(r
T )]
G
nG exp(iG r ) exp(iG T ) n(r )
G
bbb123222πππaaa231ΩΩΩaaa31倒2 格子与W正(((3Ω21*)格))为* G子倒bΩbi格T*1a子(jb原(222胞nπ2πb)的π,33)体/nijΩ积 Z
正格矢 ：
T u1a1 u2a2 u3a3
倒格 矢：
G v1b1 v2b2 v3b3, v1, v2,v3 Z
倒格子：
简单立方 体心立方结构 面心立方结构 六角密堆结构
晶面间距
倒格子空间中任一倒格点都体现了正格子中一族晶面的 特征，倒格点位矢的方向是这族晶面的法向，而它的大 小比例于该晶面族面间距的倒数。
k
晶胞的散射振幅
FG
N
dVn(r ) exp( iG r )
cell
NSG
结构因子可以利用原子的形状因子重新写为
SG f j exp(iG rj )
j
SG (v1v2v3) f j exp[i2π(v1xj v2 y j v3z j )]
j
衍射波强度
I | FG |2 N 2 | SG |2
为零，相应的反射消失。
例3： 金刚石结构的几何结构因子
金刚石结构平均每个布拉维原胞包含8个原子，将其坐标：
000, 1 1 0, 1 0 1 ,0 1 1 , 22 2 2 22
1 1 1,1 3 3,3 31,31 3, 444 444 444 444
代入 Fhkl
f e i 2πn hu j kv j lw j j
第二部分倒易点阵和晶体衍射-总结与习题指导教学文稿
第二部分倒易点阵和晶体衍射-总结与习题指导教学文稿第二部分倒易点阵和晶体衍射-总结与习题指导竭诚为您提供优质文档/双击可除第二部分倒易点阵和晶体衍射-总结与习题指导篇一：第十二章习题答案new1、分析电子衍射与x衍射有何异同？答：相同点：①都是以满足布拉格方程作为产生衍射的必要条件。
②两种衍射技术所得到的衍射花样在几何特征上大致相似。
不同点：①电子波的波长比x射线短的多，在同样满足布拉格条件时，它的衍射角很小，约为10-2rad。
而x射线产生衍射时，其衍射角最大可接近2。
②在进行电子衍射操作时采用薄晶样品，增加了倒易阵点和爱瓦尔德球相交截的机会，使衍射条件变宽。
③因为电子波的波长短，采用爱瓦尔德球图解时，反射球的半径很大，在衍射角θ较小的范围内反射球的球面可以近似地看成是一个平面，从而也可以认为电子衍射产生的衍射斑点大致分布在一个二维倒易截面内。
④原子对电子的散射能力远高于它对x射线的散射能力，故电子衍射束的强度较大，摄取衍射花样时曝光时间仅需数秒钟。
2、倒易点阵与正点阵之间关系如何？倒易点阵与晶体的电子衍射斑点之间有何对应关系？答：倒易点阵是与正点阵相对应的量纲为长度倒数的一个三维空间点阵，通过倒易点阵可以把晶体的电子衍射斑点直接解释成晶体相对应晶面的衍射结果，可以认为电子衍射斑点就是与晶体相对应的倒易点阵某一截面上阵点排列的像。
关系：①倒易矢量ghkl垂直于正点阵中对应的（hkl）晶面，或平行于它的法向nhkl②倒易点阵中的一个点代表正点阵中的一组晶面③倒易矢量的长度等于点阵中的相应晶面间距的倒数，即ghkl=1/dhkl④对正交点阵有a*//a，b*//b，c*//c，a*=1/a，b*=1/b，c*=1/c。
⑤只有在立方点阵中，晶面法向和同指数的晶向是重合的，即倒易矢量ghkl是与相应指数的晶向[hkl]平行⑥某一倒易基矢量垂直于正交点阵中和自己异名的二基矢所成平面。
3、用爱瓦尔德图解法证明布拉格定律。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一格点A的格矢则为
0
R ll1 a 1l2 a 2l3 a 3
劳厄衍射方程
从图中看出，光程差为CO+OD
Rl •(SS0)
当光程差为波长整数倍时则衍射加强，即
R l•(SS0)n
考 则虑劳到厄衍射方k程0 也和可2表S示0 为
，k
2
S
S0
CO Rl • S0 A OD Rl • S
R l•(kk0)2n
[110]方向记作Σ： [111]方向记作Λ：
H 2 a
N 2 2 2a
P 3 2 2a
4）面心立方正格子的布里渊区 晶格的基矢和倒格子的基矢为
可见其倒格子为体心立 方结构
a1
a2
a jk
2
a k + i
2
b1
2
a
-i
b2
2
a
i
+ -
j k j+k
a3
a 2
i
j
b3
2
a
i
j
的垂直平分线
同第I布里渊区边界线围成的区域 称为第II布里渊区，其大小为
( 2 )2 a
(4 )
(1 )
b2 b1
(2 )
(3 )
第三布里渊区 由4个倒格点
2b1, 2b2
(2 )
2b1, 2b2
的垂直平分线
同第Ｉ区的边界线和第二II区的边 界线围成第III区，其大小为
( 2 )2 a
(3 )
§2.2.1 倒格子的定义
假设晶格的原胞基矢为 、、，
原胞体积 a 1 a 2 a 3
a1(a2a3)
构建一新的空间，其基 矢为
由这组基矢构成的格子称为对应于以 、 、 为基矢的正格子的倒易格子(简称倒格子)
a1
b1
2
a2 a3
b2
2
a3 a1
b3
2
a1 a2
a2 a3
b
、
1
b、2
b称为倒格子基矢 3
X-射线是由被高电压V加速了的电子，打击在“靶级”物质上而产生的一种电磁波，这 样为产生的X-射线，最大的光子能量h最大等于电子的能量eV，因此，X-射线的最短波长
m ine cV h12 V 00 (V:V , m in:nm )
实验上多采用40千伏，所产生的最短波长为0.03nm
V104V,m in~0.1nm
推论
2(l1h 1l2h2l3h3) 2
(0,1,2...)
如 其果 中两 一个 个矢 为量 正满 格足 矢关 ，系则式另一个必为倒格矢Rl Kh2
§2.3 布里渊区
在倒格子中，以某一倒格点为原点，作所有倒格矢G的垂直平分面，这些平面把倒易空间 分割成许多包围原点的多面体，其中离原点最近的多面体称为第一布里渊区，离原点次近 的多面体与第一布里渊区的表面所围成的区域称为第二布里渊区，以此类推，可得到第三、 第四等各布里渊区。
从数学上讲，倒易点阵和布喇菲点阵是互相对应的傅里叶空间
倒易空间中每个格点的位置由倒格子矢量（又称倒 格矢）给出
K h h 1 b 1 h 2 b 2 h 3 b 3
§2.2.2 倒格子与正格子间的关系
1、正、倒格子基矢间的关系
ai bj 2ij20
(ij) (ij)
i, j 1,2,3
作为习题验证该关系
由前面证明可知，倒格矢
K 是晶面族
的法线方向
h1 h2 h3
（ h1h2h3）
dh1h2h3
a1 h1
Kh1h2h3 Kh1h2h3
a1 (h1b1h2b2 h3b3)
h1
Kh1h2h3
2 K h1h2h3
aibj 2ij
d h1h2h3
K h1h2h3
R 5、正格矢 与倒格矢 l
的关系 K h
2、倒格子原胞体积反比于正格子原胞体积倒数
正格子原胞体积 倒格子原胞体积
a1(a2a3)
*b1(b2b3)
* (2 )3
作为习题验证该关系
3、正格子中晶面指数为
的晶面（和h1倒h2格h3）矢 正交
Kh
意味着
倒格矢 是K晶h 面指数为
其 中 K h h 1 b 1 h 2 b 2 h 3 b 3
1）一维晶格
晶格基矢
a ai
倒格子基矢
b 2 i a
2）二维 正方格子
正方格子基矢
倒格子原胞基矢
可见倒格子的结构也是正方格子，晶格 常数为：
2 a
其倒格矢可以表示为：
Kh h1b1h2b2 2a(h1i h2j)
(h1和h2为整数)
a 1a i 2
b1 a i
a 2a j 2
b2 a j
b2 b1
Rl
C
S
OD
§2.1.3 衍射波的波幅与强度
由上面分析可知，在k方向上，两个原子产生的散射波的相位差为
2 光 程 差 R l•(kk0)
因此，k方向上散射波的幅度应当为来自两个原子散射波的幅度之和，即
A (k)0A e i(k k 0)• R l
其中 为第i个原子散射波幅度 i
若计及所有原子对散射波的贡献，则k方向散
基本判据：辐射的波长同晶格常数相当或小于晶格常数 晶体中的原子间距在0.1nm左右
图中给出了X-射线光子、电子和中子的波长与 能量的关系，可以看到，这三种粒子束的波长 都满足同晶格常数相当或小于晶格常数的判据
X-射线
1895年伦琴发现X-射线， 1912年劳厄意识到其波长在0.1nm量级，与晶体中的原子间距相 当，因此，晶体必可成为X射线的衍射光栅，随后布拉格用X射线证实NaCl等晶体具有 面心立方结构。
MnO具有NaCl结构，其中Mn2+可看成由(111) 密排面叠成的面心立方结构
同一(111）面内各离子的磁矩是平行的，而相 邻（111）面上的离子的磁矩是反平行的 。
§2.1.2 衍射方程
假设射线源与晶体距离以及观测点与晶体的距离都比晶体的线度大得多，因此，将入射波和
衍射波均可看成平面波，其传播方向分别用单位矢量S 和S表示，取格点O为原点，晶格中任
射波的幅度为
N
A(k)
ei(kk0)•Rj
j
j1
由此可得k方向的衍射强度为 2
I(k ) A(k )
k0
A
ei(k k0 )•(Rj Rj ' ) j j' j, j ' j
Rl
k
§2.2 倒格子
由于晶格周期性，一些物理量具有周期性，若Γ代表晶 体的某一物理性质（如电场强度、电子云密度、势能 等），由于晶格的周期性，则有
R ll1 a 1l2 a 2l3 a 3
K h h 1 b 1 h 2 b 2 h 3 b 3
R lK h 2 ( 0 , 1 , 2 . . . )
证明
R lK h ( l 1 a 1 l 2 a 2 l 3 a 3 ) ( h 1 b 1 h 2 b 2 h 3 b 3 )
l 1 a 1 h 1 b 1 l 2 a 2 h 2 b 2 l 3 a 3 h 3 b 3
表明：一个重复单元中任一r 处的物理性质同另一个重复单
元相应处的物理性质相同
( r ) ( r l 1 a 1 l 2 a 2 l 3 a 3 )
例如图中A和A’处的物理性质相同
或者说，物理性质为是周以期的三维周期函a数1、a2、a3
引入倒格子，可以将三维周期函数展开为傅里叶级数，
例如
V(r) V(Km)eiKmr m
中子 中子质量约为电子质量的2000倍，如果能量和电子束一样，则中子波长约为电子波长的 1/2000，因此，对中子束，只需0.1eV能量的中子就可产生0.1nm的波。
中子没有电荷但有磁矩，与晶体中电子自旋的相互作用，使得中子衍射成为探测晶体磁有序 结构的独特的手段
图 是 根 据 中 子 衍 射 推 断 出 MnO 晶 体 的 晶 体 结 构及其Mn2+离子的磁矩的有序排列
b2
(1 )
b1
(4 )
第一、第二和第三布里渊区
正方格子其它布里渊区的形成
正方格子其它布里渊区的形状
—— 每个布里渊区经 过适当的平移之后和 第一布里渊区重合
2）二维斜格子 第一布里渊区
其它布里渊区的形成
其它布里渊区的形状
—— 每个布里渊区经 过适当的平移之后和 第一布里渊区重合
3）体心立方格子的第一布里渊区
第二章 晶体衍射和倒格子
§2.1 晶体衍射 §2.2 倒格子 §2.3 布里渊区 §2.4 布拉格反射 §2.5 原子散射因子 §2.6 几何结构因子
如何确定晶体结构
§2.1 晶体衍射
晶体的特点是其内部原子的周期性排列，形成不同方向等间 隔的晶面族
每组晶面族可以作为波的衍射光栅，因此，选择适当波长的 波入射到晶体上就有可能观察到衍射现象
直到今天，X射线衍射（XRD）仍为确定晶体结构的重要工具，但由于X射线穿透能力 太强，在某些方面，例如在研究晶体表面结构中，难以发挥作用。
电子
电子波动性的发现给人类确定晶体结构增添了另外一种手段
电子衍射是以电子束直接打在晶体上而形成的，电子束的德布罗意波的波长=h/p，利用 p2/2m=eV，V是电子的加速电压，因此有
同理可证
h1b1
ah11 h3b3
a3 h3
0
Kh1h2h3 CB0
所以晶面族
（与h和1h2倒h3格）矢
正交
K h1h2h3
K h1h2h3
4、倒格矢
K的长度正比于晶面族 h1 h2 h3
面间距 （的倒h1h数2h3）