运筹学05━06学年第一学期期末考试试卷B
运筹学期末考试试卷(B)卷

福建农林大学考试试卷 ( B )卷学年 第 学期课程名称: 运 筹 学 考试时间 120分钟专业 年级 班 学号 姓名1. 目标规划模型中,目标约束ax d d g -++-=中的g 称为 目标值 。
2. 线性规划问题的单纯形法中,有最优解的判别准则是 所有检验数非负且最优值为常数 。
3. 如果流{}ij f f =中所有0ij f =,则称f 是 零 流。
4. 如果001020(,,...,)m B P P P =,t B 为最优基,则1t B -为01020(,,...,)tttm P P P 。
5. 无向图中的环是 端点重合的边 。
二、单项选择题(选择正确答案的字母填入空格处,每小题2分,共10分)1.线性规划的非对称形式的原问题和对偶问题数学模型中,互补松弛性的描述式为 C 。
A. ****0,0s s y x y x == B. **0s y x = C. **0s y x = D .**0y x =2. 若11(,)V V 为最大截集,则 C 。
A. 11(,)c V V 为最小截量B. 11(,)c V V 为最大流流量C. 11(,)c V V 为11(,)V V 的截量D. 11(,)c V V 为最小截量 3. 最短路求解的主要内容是 D 。
A. 关键路线B. 最短路线C. 最短路长D. 最短路线和最短路长 4. 线性规划问题的价值系数变化后,当最优表中 B 不发生变化。
A. 非基变量检验数B. 限定常数、技术系数和基变量检验数一、填空题(每空2分,共10分)C. 检验数D. 目标函数值的相反数 5. 网络计划中关键工序a ij 的TF ij C 。
A.>0B.<0C.=L j -E i -T ijD.=L j三、判断题(正确打“√”;错误打“×”;每小题2分,共10分)1. 在增广链上确定的流量调整量只能是负的。
( × )2. 目标规划模型中必须有目标约束。
运筹学试卷及参考问题详解
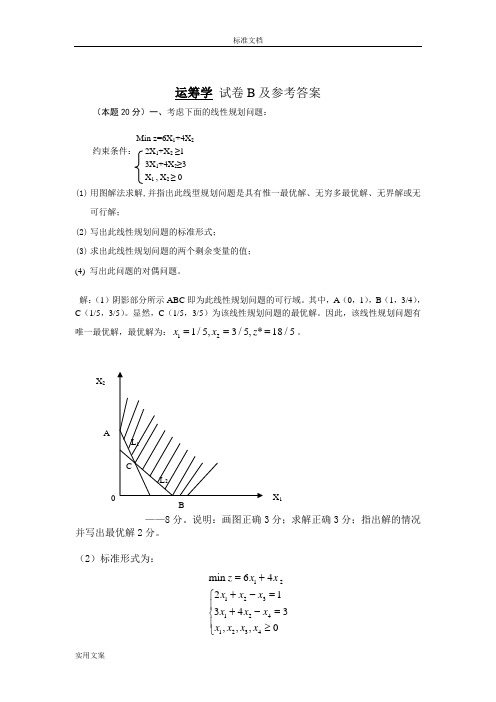
运筹学 试卷B 及参考答案(本题20分)一、考虑下面的线性规划问题:Min z=6X 1+4X 2约束条件: 2X 1+X 2 ≥13X 1+4X 2≥3 X 1 , X 2 ≥ 0(1) 用图解法求解,并指出此线型规划问题是具有惟一最优解、无穷多最优解、无界解或无可行解;(2) 写出此线性规划问题的标准形式; (3) 求出此线性规划问题的两个剩余变量的值; (4) 写出此问题的对偶问题。
解:(1)阴影部分所示ABC 即为此线性规划问题的可行域。
其中,A (0,1),B (1,3/4),C (1/5,3/5)。
显然,C (1/5,3/5)为该线性规划问题的最优解。
因此,该线性规划问题有唯一最优解,最优解为:121/5,3/5,*18/5x x z ===。
——8分。
说明:画图正确3分;求解正确3分;指出解的情况并写出最优解2分。
(2)标准形式为:121231241234min 6421343,,,0z x x x x x x x x x x x x =++-=⎧⎪+-=⎨⎪≥⎩ X 1 X 2 AB——4分 (3)两个剩余变量的值为:340x x =⎧⎨=⎩——3分(4)直接写出对偶问题如下:12121212max '323644,0z y y y y y y y y =++≤⎧⎪+≤⎨⎪≥⎩——5分(本题10分)二、前进电器厂生产A 、B 、C 三种产品,有关资料下表所示:学模型,不求解)解:设生产A 、B 、C 三种产品的数量分别为x 1,x 2和x 3,则有:——1分123123123123123max 810122.0 1.5 5.030002.0 1.5 1.21000200250100,,0z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤⎪⎨≤⎪⎪≤⎪≥⎪⎩ ——14分,目标函数和每个约束条件2分(本题10分)三、某电子设备厂对一种元件的年需求为2000件,订货提前期为零,每次订货费为25元。
运筹学教材编写组《运筹学》期末考试试卷(B)

《运筹学》期末考试试卷(B)学院 班级 姓名 学号考生注意∶1.本试题共 七 题,共 3 页,请考生认真检查;一、用单纯形法求解下述线性规划问题(20分)⎧⎨⎪⎪⎩⎪⎪0,824424m ax 2121212121≥≤-≤-≤+-+=x x x x x x x x x x z二、设一线性规划问题为(25分)⎧⎨⎪⎩⎪m a x ,,z x x x x x x x x x j j =-+++≤-+≤≥=27624013123121232 目标函数变为max z x x x =++23123;3 约束条件右端项由(6,4)T 变为(3,5)T;4 增加一个约束条件-+≥x x 1322三、某种产品今后四周的需求量分别为300,700,900,600件,必须得到满足。
已知每件产品的成本在起初两周是10元,以后两周是15元。
工厂每周能生产这种产品700件,且在第二、三周能加班生产。
加班后,每周可增产200件产品,但成本每件增加5元。
产品如不能在本周交货,则每件每周存贮费是3元。
问如何安排生产计划,使总成本最小,要求建立运输问题数学模型求解。
(25分)四、某校蓝球队准备从以下6名预备队员中选拔3名为正式队员,并使平均身高尽可能高,这6名预备队员情况如下表所示,试建立数学模型。
(20分)队员的挑选要满足下列条件:2少补充一名后卫队员;3大李或小田中间只能入选一名;4最多补充一名中锋;5如果大李或小赵入选,小周就不能入选。
五、某高校拟开设文学、艺术、音乐、美术四个学术讲座。
每个讲座每周下午举行一次。
经调查知,每周星期一至星期五不能出席某一讲座的学生数如下表:(20分)学生总数。
六、某飞行队有5名正驾驶员和5名副驾驶员。
由于种种原因,某些正、副驾驶员不能同机飞行,某些则可以,如下表所示。
每架飞机出航时需正,副驾驶员各一人。
问最多能有几架飞机同时出航?应如何安排正,副驾驶员?用图论方法求解。
(20分)七、填空:(20分)1.某工程公司拟从四个项目中选择若干项目,若令11,2,3,40i i i ix ìïï==íïïïî,第个项目被选中;,第个项目未被选中;用i x 的线性表达式表示下列要求:(1)从1,2,3项目中至少选2个: ;(2)只有项目2被选中,项目4才能被选中: ;2.用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经济意义是 ,若从该空格出发进行调整,设调整量为2,则调后可使总运费下降 ;3. 动态规划中的Bellman 最优性原理是。
运筹学期末试卷B卷

福建农林大学考试试卷( B )卷学年第学期课程名称:运筹学考试时间专业年级班学号姓名1.目标规划模型中,目标约束正偏差变量和负偏差变量的乘积为零。
2.在求极大化的线性规划问题中,无可行解的判别特征是。
3.约束条件的价值系数c r变化后,最优单纯形表中不发生变化。
4.存贮论的随机性存贮模型中,费用由构成。
5.最短路算法的求解内容为和。
6.若f*为满足下列条件的流:各条弧上的流量非负切不大于对应的容量,中间点净流出量为零,发点和收点净流出量互为相反数,则称f*为网络D的。
7.对互为对偶的两个线性规划问题,如果其中一个无有限最优解,则另一个。
8.存贮论的研究对象为。
9.网络计划中工序的总时差指的是。
二、单项选择题(选择正确答案的字母填入括号,每小题1分,共10分)1.一个矩阵对策策略意义下的解。
A.一定存在纯 B.不一定存在纯C.不可能存在混合 D.不可能存在纯2. 如果目标规划的硬约束中有相互矛盾的约束,则该问题 。
A .有唯一的最优解 B .有最优解 C .无可行解 D .无有限最优解3.在约束为0,0≥≥X b AX =的线性规划中,设 A = 111222⎡⎤⎢⎥⎣⎦,⎪⎪⎭⎫ ⎝⎛-=21b ,则该问题 。
A .基至多有3个B .可行基有3个C .每个基下,有3个基变量D .没有基4.最小费用最大流问题 有最优解。
A .不一定B .一定C .不可能D .可能5.若线性规划问题的原问题具有n 个无约束变量,则它的对偶问题的约束组具有 等于型约束。
A .m 个B .大于n 个C .n 个D .小于n 个 6.线性规划的大M 法中,人工变量的价值系数是 。
A .-M ,求极小化 B .M ,求极小化 C .-M ,求极大化 D .M ,求极大化 7.目标规划模型中要求尽量接近目标值的目标函数是。
。
A .min Z d d +-=+ B .min Z d -= C .min Z d += D .min Z d d +-=-8.具有m 个产地、n 个销地和的产销平衡运输问题,用表上作业法求解时有___________。
管理运筹学期末试卷B

一、填空题(每小题4分,共20分)1、设原LP问题为则它的标准形和对偶规划问题分别为: 和。
2、用分枝定界法求整数规划的解时,求得放松问题的解为x1=18/11,x2=40/11,则可将原问题分成如下两个子问题与求解.3、右图的最小支撑图是。
4、右边的网络图是标号算法中的图,其中每条弧上的数表示其容量和流量。
该图中得到的可行流的增广链为:,在其上可增的最大流量为。
5、则其最优解为:,最优值。
二、单项选择题(每小题2分,共10分)1、下列表格是对偶单纯形表的是(A )ABCD2A 、可行域必有界; B 、可行域必然包括原点; C 、可行域必是凸的; D 、可行域内必有无穷多个点.3、在运输问题中如果总需求量大于总供应量,则求解时应( ) A 、虚设一些供应量; B 、虚设一个供应点; C 、根据需求短缺量,虚设多个需求点; D 、虚设一个需求点。
4、下列规划问题不可用动态规划方法求解的是( ) A 、背包问题; B 、最短路径问题 C 、线性规化: D 、5、下列关于图的论述正确地是( ) A 、有向图的邻接矩阵是对称矩阵;B 、图G 是连通的,当且仅当G 中的任意两点之间至少存在一条链;C 、任何一个连通图,都存在唯一的最小支撑树;D 、若图是图一个支撑子图,则。
三、判断题(每小题2分,共10分)( )1、若原始问题是利润最大化的生产计划问题,则对偶问题是资源定价问题,对偶问题的最优解称为原始问题中资源的影子价格。
影子价格越大说明这种资源越是相对紧缺,影子价格越小说明这种资源相对不紧缺.( )2、对max 型整数规划,若其松弛问题最优解对应的目标函数值为Z c ,而其最优整数解对应的目标值为Z d ,那么一定有Z c ≤Z d .( )3、任何一个无圈的图G 都是一个树图。
( )4、一个可行流满足平衡条件是指:所有中间结点处流出量=流入量,收点流出量=0, 发点流入量=0,收点流入量=发点流出量。
2006级运筹学试题B参考答案及评分标准

2006级运筹学试题B参考答案及评分标准一、单项选择题(每题2分,共20分)1. 运筹学中,线性规划问题的目标函数是()。
A. 最小化B. 最大化C. 任意化D. 固定化答案:B2. 以下哪个不是线性规划问题的约束条件()。
A. 线性不等式B. 线性等式C. 非线性不等式D. 非线性等式答案:C3. 单纯形法中,若某变量的检验数大于0,则该变量()。
A. 可以增加B. 可以减少C. 不能增加D. 不能减少答案:A4. 在整数规划问题中,目标函数的值()。
A. 总是整数B. 总是实数C. 可以是整数或实数D. 不确定答案:A5. 动态规划中,状态转移方程的目的是()。
A. 确定最优解B. 确定最优路径C. 确定最优策略D. 确定最优解的值答案:D6. 以下哪个方法不是用于解决非线性规划问题的()。
A. 梯度下降法B. 牛顿法C. 单纯形法D. 内点法答案:C7. 在图论中,最短路径问题的解通常指的是()。
A. 最短距离B. 最短时间C. 最短成本D. 最短路径答案:D8. 网络流问题中,最大流问题的目标是()。
A. 最大化流量B. 最小化流量C. 最大化成本D. 最小化成本答案:A9. 对于一个决策树,其根节点表示()。
A. 最终决策B. 初始状态C. 决策变量D. 决策结果答案:B10. 以下哪个不是排队论中的主要参数()。
A. 到达率B. 服务率C. 等待时间D. 决策变量答案:D二、填空题(每题2分,共20分)1. 在线性规划问题中,目标函数的系数称为_________。
答案:目标系数2. 单纯形法中,如果某变量的检验数小于0,则该变量称为_________。
答案:进基变量3. 动态规划的基本原理是_________。
答案:最优子结构4. 整数规划问题中,如果变量的取值只能是0或1,则该问题称为_________。
答案:0-1整数规划5. 在图论中,如果一个图中的任意两个顶点都可以通过边相连,则称该图为_________。
《运筹学》期末考试试题及参考答案

《运筹学》试题参考答案一、填空题(每空2分,共10分)1、在线性规划问题中,称满足所有约束条件方程和非负限制的解为 可行解 。
2、在线性规划问题中,图解法适合用于处理 变量 为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是 设立虚供地或虚需求点,化为供求平衡的标准形式 。
4、在图论中,称 无圈的 连通图为树。
5、运输问题中求初始基本可行解的方法通常有 最小费用法 、 西北角法 两种方法。
二、(每小题5分,共10分)用图解法求解下列线性规划问题: 1)max z = 6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x , 解:此题在“《运筹学》复习参考资料.doc ”中已有,不再重复。
2)min z =-3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解:⑴ ⑵ ⑶ ⑷ ⑸ ⑹、⑺⑴⑵ ⑶ ⑷ ⑸、⑹可行解域为abcda ,最优解为b 点。
由方程组⎩⎨⎧==+02242221x x x 解出x 1=11,x 2=0∴X *=⎪⎪⎭⎫ ⎝⎛21x x =(11,0)T ∴min z =-3×11+2×0=-33三、(15分)某厂生产甲、乙两种产品,这两种产品均需要A 、B 、C 三种资源,每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示:A B C 甲 9 4 3 70 乙 4 6 10 1203602003001)建立使得该厂能获得最大利润的生产计划的线性规划模型;(5分)2)用单纯形法求该问题的最优解。
(10分) 解:1)建立线性规划数学模型:设甲、乙产品的生产数量应为x 1、x 2,则x 1、x 2≥0,设z 是产品售后的总利润,则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x , 2)用单纯形法求最优解:加入松弛变量x 3,x 4,x 5,得到等效的标准模型:max z =70x 1+120x 2+0 x 3+0 x 4+0 x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下:∴X *=(11,11,11,0,0)T∴max z =70×11100+120×11300=1143000四、(10分)用大M 法或对偶单纯形法求解如下线性规划模型:min z =5x 1+2x 2+4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x解:用大M 法,先化为等效的标准模型:max z / =-5x 1-2x 2-4x 3 s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7,得到:max z / =-5x 1-2x 2-4x 3-M x 6-M x 7 s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下:∴x *=(32,2,0,0,0)T最优目标函数值min z =-max z / =-(-322)=322五、(15分)给定下列运输问题:(表中数据为产地A i 到销地B j 的单位运费)1)用最小费用法求初始运输方案,并写出相应的总运费;(5分) 2)用1)得到的基本可行解,继续迭代求该问题的最优解。
管理运筹学期末试卷题目B卷

运筹学 期末试卷(B 卷)系别: 工商管理学院 专业: 考试日期: 年 月 日姓名: 学号: 成 绩:. 分 匹克公司要安排 个工人去做 项不同的工作,每个工人要求: ( )建立线性规划模型 只建模型 不求解( )写出基于 软件的源程序。
分 某公司下属甲、乙两个厂,有 原料 斤, 原料 斤。
甲厂用 、 两种原料生产 两种产品,乙厂也用 、 两种原料生产两种产品。
每种单位产品所消耗各种原料的数量及产值、分配等如下( ) 建立规划模型获取各厂最优生产计划。
( ) 试用图解法 求解最优结果。
. 分 考虑下面的线性规划问题 目标函数:约束条件:利用教材附带软件求解如下最优解如下目标函数最优值为 变量 最优解 相差值约束 松弛 剩余变量 对偶价格目标函数系数范围变量 下限 当前值 上限无上限 常数项数范围约束 下限 当前值 上限无上限试回答下列问题:13123123123300.56153420,,0x x x x x x x x x x x +≤-+≥+-≥≥( )第二个约束方程的对偶价格是一个负数 为 ,它的含义是什么( ) 有相差值为 它的含义是什么( )请对右端常数项范围的上、下限给予具体解释,应如何应用这些数据?( )当目标函数系数在什么范围内变化时,最优购买计划不变?( )当目标函数中 的系数从 降为 而 的系数从 升为 时 最优解是否发生变化. 分 某工厂每年需要甲零件 件,每件零件 元,每个部件的年存储费为每个部件价格的 ,每批订货费为 元。
试求经济订货批量及订货周期。
分 城市 到城市 的交通道路如下图所示,线上标注的数字为两点间距离 单位:公里 。
某公司现需从 市紧急运送一批货物到 市。
假设各条线路的交通状况相同,请为该公司寻求一条最佳路线。
分 用单纯形法求解如下线性规划问题目标:1231341234212333115s.t.- -333,,,0x x xx x xx x x x⎧++=⎪⎪⎪+=⎨⎪≥⎪⎪⎩. 分 试求解下面网络图中的最小费用最大流。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东外语外贸大学
运筹学2005━2006学年第一学期期末考试试卷(B)
考试时间:2小时
班级: 学号: 姓名:
一. 单选题(以下各题的备选答案中,只有一个答案是正确的,请将你选择的答案的
编号填在以下表格中)(每小题2分,共20分)
1. 运筹学模型是以( )模型为其主要形式。
A. 图表
B. 图形
C. 模拟
D. 数学 2.假设用对偶单纯形法对某线性规划问题求解,所得的最优解表中目标函数的值为Z ,则( )。
A. Z 为该线性规划问题的最优值
B. -Z 为该线性规划问题的最优值 A. Z 为该线性规划对偶问题的最优值 B. -Z 为该线性规划对偶问题的最优值 3.在目标规划中,求解的基本原则是首先满足高级别的目标,但当高级别目标不能满足时(d )。
A. 其后的所有低级别目标一定不能被满足
B. 其后的所有低级别目标一定能被满足
C. 其后的某些低级别目标一定不能被满足
D. 其后的某些低级别目标有可能被满足 4.如果要使目标规划实际实现值不超过目标值,则相应的偏离变量应满足( )。
A .0>+d ;
B .0=+d ;
C .0=-
d ; D ..0,0>>+-d d 5.动态规划问题中最优策略具有性质:( ) A . 每个阶段的决策都是最优的 B . 当前阶段以前的各阶段决策是最优的
C . 无论初始状态与初始决策如何,对于先前决策所形成的状态而言,其以后的所有决
策应构成最优策略 D . 它与初始状态无关
6.树是( )的图。
A. 任两顶点之间有一条链相连接
B. 有两个顶点之间存在一条链相连接
C. 任两顶点之间有唯一一条链相连接
D. 有两顶点之间存在唯一一条链相连接 7. 在网络中,设通过弧),(j i v v 的流量和容量分别为ij f 和ij c ,若弧),(j i v v 是饱和弧,则( )。
A. 0>ij f
B. ij ij c f =
C. ij ij c f <
D. ij ij c f > 8. 决策问题中包含的三个基本因素为( )。
A. 自然状态、策略和结果
B. 自然状态、策划和结果
C. 自然状态、决策和结果 C. 自然状态、对策和结果
9. 在灵敏度分析中,若转折概率与对应的自然状态原概率差别较大时,则原最优方案是( )。
A. 不稳定的
B. 稳定的
C. 不确定的
D. 确定的 10. 各自然状态发生可能性的大小为已知的决策问题是(B )决策问题。
A. 确定型 B. 风险 C. 非确定型 D. 不确定型
二. 试用对偶单纯形法求解以下线性规划问题(15分)
⎪⎩⎪
⎨⎧≥≥≥≥+≥++++=0
,0,06
238232min 321
21321321x x x x x x x x x x x s
三. 应用动态规划的原理求解资金分配问题:即有3万元资金,如何分配给A、B、C 三个项目,使总产量最大(资金投入产出表见下表)。
ⅰ)将以上问题按项目的顺序分为______ 3_________个阶段(1分);
表示第k阶段可能的________投入的总资金________________(1分);ⅱ)状态变量S
k
表示________投给第k个项目的资金______________________(1分);ⅲ)决策变量u
k
ⅳ)转移方程为:_________________________(1分);ⅴ)基本方程为:_________________________(1分);
ⅵ)求解(10分):
四. 用破圈法和求以下网络中的最小生成树:(1)写出计算步骤(5分),(2)用双线将最小生成树在图中标出(5分)。
S
A
B
C
D
E
T 2
5
4
1
3
3 1
4
3
6
5
6
2
五. 某企业要投资生产一种新产品,投资方案为A、B、C,不同的经济形势下利润表如下表所示,如果经济形势各状况的概率未知, 试用
(1)悲观法进行决策(8分);
(2)后悔值法进行决策(要求给出后悔值矩阵)(10分);
如果已知经济形势好与差的概率分别为0.5和0.2, 试用决策树方法进行决策(要求先建立决策树模型)(12分)。
••••••••
六. 某工厂生产A 、B 两种产品,如果售出一个产品A 和B 的利润分别为7元和8元,已知产品A 和B 需经过Ⅰ、Ⅱ两个工序加工,其中每天每个产品A 、B 所需工时,以及各工序可提供的生产能力如下表所示,
要求:1)一天内的利润达到50元;
2)在完成利润50元的前提下,工序Ⅰ剩余的工时越多越好;
问如何安排产品A 、B 的产量(只要求建立以上问题的目标规划模型(10分))。
⎪⎪⎪⎩
⎪
⎪⎪⎨⎧≥≤+≤+=-++=-++-++=+
-+-+
-+--++-0,,,,,12
3 30 3430345087)
()(min 2211212
1
2122211121222111d d d d x x x x x x d d x x d d x x d d P d d P Z。
