2014年绵阳一诊(高2015届)理数
四川省绵阳南山实验高中2015届高三一诊模拟考试试题数学理Word含答案

数学阶段性测试题一、选择题(本大题共10小题,每小题5分。
1. 集合 M 2,0,1,2, N x 2x1 1 ,则 N M=()A. {-2,1,2 }B. {0,2}C. {-2 , 2}D. [-2 , 2]2. 已知 a=(2,1), b x,3 ,且 a//b ,则 x 的值为()A.2B.1C.3D.63. 在各项均为正数的等比数列 a n 中,3a 1,-a 3,2a 2成等差数列,则■a11—岂()2a 8 a10A. 1或3B.3C.1 或 27D.27 4.卜列 J 说法错误的是( ) A. 若p : xR,:x 2x 1 0,贝U p: x R, x 2 x 1 0;B.sin1 ” 2是“30: ”的充分不必要条件;C. 命题“若 a 0,则 ab 0”的否命题是:“若a 0,则ab 0D.若 p: x R,cosx 1,q : x R,x 2 x 10,则“ p q ”为假命题.5. 为了得到函数y cos(2x )的图象,只需将函数y sin 2x 的图象()3A.向左平移—个单位B •向右平移—个单位12 12 C.向左平移5个单位D•向右平移5个单位666. 设x R ,若函数f(x)为单调递增函数,且对任意实数x ,都有f f (x) e x e 1 ( e 是自然对数的底数),则f (ln 2)的值等于()A. 1 B . e 1 C.3 D . e 32x 3y 57.若实数x, y 满足约束条件2x y 5 0 ,则函数z | x y 1|的最小值是()x 0A.0B.4C.8 D.7328.已知函数f xsin x ,0x 1log2014x , x1若a,b,c 互不相等,且f a f b f c ,则a b c 的取值范围是(). A.(1,2014) B.(1,2015)C.[2,2015]D.(2,2015)二、填空题(本大题共5小题,每小题5分,共25分.) 11.幕函数y (m 2 3m 3)x m 过点 112.计算 log 3 6 log 3 2 42 3叫4点,且在A,B 两点处的切线互相平行,则$的取值范围为亠X 1三、解答题(解答应写出文字说明,证明过程或演算步骤共 75分)16.(本小题满分12分)数m 的取值范围.17.(本小题满分12分) 设公差不为0的等差数列a n 的首项为1,且32,35,3!4构成等比数列.9.已知定义为R 的函数f x 满足f 4,且函数f x 在区间2,上单调递增.如果x 12 x 2,且x 1X 2 4,则f 捲f X 2的值( A.恒小于0 B.恒大于 C.可能为0 D.可正可负10.设函数f x的导函数为fx ,对任意x R 都有fA. 3f(ln2) 2f (l n3)B. 3f (l n2) 2f(l n3)C. 3f (ln2)2f (l n3) D.3f (l n 2)与2f (l n3)的大小不确定2,4,贝U m =的结果为13已知菱形ABCD 的边长为2, 若 A E A F BC 3BE , DC DF .14.已知x,y R , x 22y_ 215.已知ABAD 120,点 E,F 分别在边 BC, DC 上,1,则的值为j 则決口的最大值为 X 2』2咅 x 2是函数f x 3 x 图象上的两个不同已知函数f x 2cos x -sin x 3玉sx 「(I )求f x 的值域和最小正周期;(U )若对任意°,「使得mfx2 0恒成立,求实(I)求数列a n的通项公式;(U)若数列b n满足P直…%1 A,n a i a2 a n 218. (本小题满分12分)已知函数f(x) .3 sin( x )( 0,2 2)的图像关于直线x-对称,且图像上相邻两个最高点的距离为.(I)求和的值;(II)若电)4 ,( 6 3),求COS( 2)的值.19. (本小题满分12分)已知二次函数f(x) Ax2 Bx(A 0), f(1) 3,其图象关于x 1对称,数列a n的前n项和为S n,点n,S n n N*均在y f (x)图象上.(I)求数列a n的通项公式,并求S n的最小值;1 11 3 1 (n)数列b n , b n - , b n的前n项和为T n ,求证:-一T n --.S n 3 4n 4 n 3 20. (本小题满分13分)N*,求b n的前n项和T n1 a 设函数f (x) x2ax ln x ( a R).(I)当a 1时,求函数f (x)的极值;(U)当a R时,讨论函数f(x)的单调性;(川)若对任意a (2,3)及任意x i , X2 1,2,恒有ma ln2 f(xjf(X2)成立, 求实数m的取值范围.21. (本小题满分14分)已知 f (x) In x mx(m R).(I)若曲线y f (x)过点P(1, 1),求曲线在P点处的切线方程;(U)求f (x)在区间1,e上的最大值;(川)若函数f (x)有两个不同的零点X1,X2,求证X1X2 e2.绵阳南山中学.南山中学实验学校绵阳市“一诊”模拟考试试题理科数学参考答案一、 C DDBA CADAB 二、 填空题 11.2 12. -1 13 . 2 14. 3 2 15. (-1,0 )8三、 解答题 16.解:(1)f(x) = 2sin x +"3 cos x + -3 — 2 3cos2 x + -3n r — n2X +~3 < 1. /.— 2 — 3< 2sin 2x+p — 3< 2— 3, T = 今=冗,即卩f(x)的值域为[—2 — , 3, 2— ,3],最小正周期为n .. n r n n 2n,, n\/3⑵当 x € 0,舌时,2x + -3 € -3, -3,故 sin 2x +§ € 电,1 ,此时 f(x) + 3= 2sin 2x +nn € [ 3,2].由 m[f(x) + 3] + 2= 0知,帀0, /• f(x)m 的取值范围是一^3^,— 117. 解:(I )设等差数列a n 的公差为d,(d 0),则还%a 52,即(1 4d )2 (1 d ))1 13d )解得 d=0 (舍去)或 d=2, a n 1+2(n-1)=2n-12n=sin 2X +~32ncos 2X +~3 + 1 = sin2 n 厂 2 n 2x +3 — 3cos 2x +~3=2sin 2x + 3 —"』3. I — 1w sin+ 3= — m 即 3< — m 2,即m+ 3< 0,2+ 2> 0, m解得-2.331.即实数a 2, a 5, a 14构成等比数列,.3分(II 由已知 b ,云b n a1-(n2n(当n=1时,牛1 ;2时,b n a n (1(1一)=丄12n'b n a n丄,(n N * )2n由(I ), a n 2n-1 b n2n 1 2n 2n1 ~22n 1两式相减得 2 24 2n 2n 11 2n 12n 2n 2n 2n.1218.解 由题可知, 二 f(x) = . 3 2 n T = 一| 3|sin 2(x- )= .. 3 sin(2x--n ), ©二 12 6 周期 w = 2nn T n n n_为对称轴f (_-_)= f ( ) = 0,且-_ wg _33 412227t 12 -丄所以,3=2, 6n (^=-— 6(II )f (》=彳.3 sin( a - ” = —,即 sin( a -n ) = 14 6 4 3 n n n n -J 3 cos(a + —) = sin a = Sin[( a-—) + 6] = sin( a - —) 2-2 + j n 2 n . n n n 15 < a < .I 0< a - —< ,COS (a-—)=6 3 6 2 6 4 ■■- 3+15 审 所以,cos(a+——)= n 1 COS (a-—) ?— 6 2 3 / .3n_ - --COS(a + ---- )= 2 4 1?2』?丄= 2 3n .3+、15 2, 8 19.解:(1) f (1)3,2AA 1,B 2,, f (x )x 22x..1分点 n, S h n 均在y=f(x) 图象上, S nn 2 2n ① ..2分S n 1(n1)22;n 1) (n 2[②①-②得S nS n 12n 1,即 a n =2n+1 (.4 分,又 a 1 s 1 a n =2n+1 (n N )⑵b n1n ( n 2)丄).7分1 T n 尹1 1)(14) 4(丄 n宀]1 =2[(1 )]丄)即证- n (n丄), -,所以右边成立 2 10分,1又T n 随n 的增大而增大,T n T 1 - 3 14n ,左边成立..11 分所以,原不等式成立 . ................ 20.解:(I)函数的定义域为(0,),当a .12分1时, f(x) x In x, f '(x) 1 1 —•令 f'(x) x x0,得x 1.,当 0 x 1 时,f '(x) 0 ;当x 1时, f'(x) f(x)在(0,1)单调递减,在(1,)单调递增, f (x)极小值 f(1) 无极大值; f'(x) (1 a)x a (1 a)x 2ax 1 [(1 a)x 1](x 1) x (1 a)(x1七(x 1)a 1 _____ x① a 1 时,(1 a )x 10,f (x )在(0,1)单减,(1,)单增;1②1 a 2时, ------------ a 1(川)由(U)知,当a (2,3)时,f(x)在[1,2]上单调递减,当x 1时,f (x)有a 3最大值,当 x 2 时,f (x)有最小值,|f(x ,) f (x 2)| f (1) f (2)ln2,2 2a 3 ma ln 2In 2 ,2 2而a 0经整理得m I—由2 a 3得11— 0, m 0.……13分 22a 4 2 2a21.解:(1)因为点P (1, -1 )在曲线上,所以f(1)=-1,得m=11-f /(x )— 1, f /(1)=0,故切线方程为y=-1.……3分 x1④当 m 1 即 m 1 时,x(1,e ),f/(x)f (x )在]1,e ]上的最大值f (x )max =I 1 mx/(x )- m=- 一①当 mO 时,x(1, e )x x1③当丄1即a 2时,f'(x) a 1(x 1)2 x0, f (x)在(0,)上是减函数;④当1 a 1 1 a 11, 即 a 2时,令 f'(x) x 10,得 0 x 丄 或x 1,令 f'(x)a 1 ................ 9分0,得x (1, e ),f /(x )>0, ②当1 e m ,即0 m1时 ef(X )max :=f(e)=1-me ;③当111 1e 时,即—一 1时,me m单减,1f (X )max =f (―)= ln m m 1x (1, e ), f /(x ) >0, f (x )单增,1 1x (1, e ),f (x )在(1,—)单增,在(-,e )0,f (x)单减,f (X )max = f(1)=-mf (x )单增,f (x )max =f(e)=1-me ;8分f (x 2) 0, In X r mx 0 ,1 , f (x )在(0,1)单增,在(1,单减,,)单增;a 1 a 1要证 x 1x 2 e 2,即证In x 1InX22 ,即证m j x 1 X 2)2,......... 10分 In x 1 In m x 1 x 2 X 2In 2,即证 X 1 In x 2 2即证X 1X 2X 1 X 2In x 1In x 2心1 X 2)x即证In 」X2X 1X21)…12分X 1 x 21X2x令亠=t,则tx1,即证In tt 1 (t )In tt1t 1,t 1,1 则 /(t )1 4 9(t1)290, 函数 (t)在 (1,)单增0, In x r In x 2m j x 1x 2) , In x r In x 2 m (X i X 2), t (t 1)2t (t 1)(t ) (1)=0, 原不等式成立.14分r1 — me,—fiwn — 1, 1(-<m<I)伽 A 1).....(3)不妨设x 1X20,: f(xjIn x 2 m>。
绵阳市高2014届数学第一次诊断考试(理科)含答案

括整数本身)变化时,至少含有 2 个周期,则最小的正整数 k 为 A.50 B.51 C.12 D.13
4 5 , sin( ) ,则 tan 为 5 5
9.已知 , 都是锐角,且 cos A.2 B.
2 11
2 2 或2 D. 或-2 11 11 1 10.已知 O 为△ABC 的外心, cos A ,若 AO AB AC ,则 的最 3
1 2 sin(2 x ) , 4
∴ f ( x)max 1 2 . „„„„„„„„„„„„„„„„„„„„„„„8 分 (II)由题意得 1 2 sin(2 x ) ≥0,即 sin(2 x ) ≤
π 4
π 4
2 , 2
3π π 9π ≤ 2 x ≤ 2kπ ,k∈Z, 4 4 4 π 整理得 kπ ≤x≤ kπ π ,k∈Z. 4
O 1
3
OD=4,折线段 BCD 为可变线路,但为保证驾驶安全,限定∠BCD=120º.
数学(理科)试题第 3 页(共 10 页)
19. (本题满分 12 分)已知函数 f (x)=x2+bx+2,g(x)=|x2-1|,x∈R. (Ⅰ)若函数 f (x)满足 f (3+x)=f (-x),求使不等式 f (x)≥g(x)成立的 x 的取 值集合; (Ⅱ)若函数 h(x)= f (x)+g(x)+2 在(0,2)上有两个不同的零点 x1,x2,求实 数 b 的取值范围.
b1 (1 q 2 ) b (1 q 3 ) , S3 1 , 1 q 1 q
数学(理科)试题第 5 页(共 10 页)
于是 2 2
绵阳一诊成绩分析
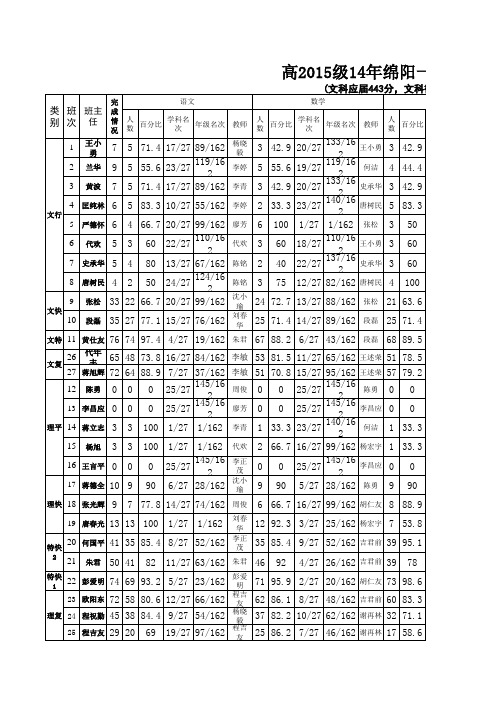
52 70.3 4/14 96/162 64 88.9 1/14 37/162 35 77.8 3/14 74/162 24 82.8 2/14 60/162
73 98.6 62 86.1 33 73.3 24 82.8
17/27 117/162 王洪英 26 89.7 1/14 32/162
地理(生物) 学科名 年级名次 教师 次
17 蒋德全 10 9
理快
9
9
18 张光辉 9
7 77.8 14/27 74/162 1/27 1/162
6 66.7 16/27 99/162 12 92.3 3/27 25/162
8 88.9 7 53.8
19 唐春光 13 13 100
特快2
20 何国平 41 35 85.4 8/27 52/162 李正茂 35 85.4 9/27 52/162 吉君前 39 95.1 21
27 81.8 27 77.1 69 90.8 56 86.2 53 73.6 0 0 0 100 100 0 90
24 68.6 9/13 98/162 67 88.2 5/13 43/162 58 89.2 3/13 34/162 67 93.1 2/13 24/162 0 0
25/27 145/162 陈晓东 0 25/27 145/162 张晓霞 0
杨旭
1 33.3 23/27 140/162 2 66.7 16/27 99/162 0 90
1 33.3 1 33.3 0 90
3
16 王言平 0
25 刘春华
25/27 145/162 李昌应 0 5/27 28/162
陈勇 胡仁友 杨宏宇
5 83.3 3 2 3 4 50 40 60 100
四川省绵阳市高中高三数学第一次诊断性考试试题 理 新人教A版

四川省绵阳市高中2014届高三数学第一次诊断性考试试题 理 新人教A 版一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项 是符合题目要求的.1.若集合A ={x |1<x <4},集合B ={y |y 2<4},则A ∩B =( ) (A)∅ (B){1,2} (C)(1,2) (D)(1,4)2.对于非零向量a ,b ,“a ∥b ”是“a +b =0”的( ) (A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分又不必要条件3.若向量a =(1,2),b =(1,-1),则2a +b 与b 的夹角为( ) (A)0 (B)3π (C)2π(D)π4.已知命题p q :空集是集合A 的子集,下列判断正确的是( ) (A)p q ∨为假命题 (B)p q ∧真命题 (C)()()p q ⌝∨⌝为假命题 (D)()()p q ⌝∧⌝为假命题5.下列不等式中,正确的是( )(A)sin1°>cos1 (B)sin1>cos1° (C)sin1<sin2 (D)sin2<sin36.已知函数f (x )=k (01)x x a a a a --≠>且在R 上是奇函数,且是增函数,则函 数g (x )=log a (x -k )的大致图象是( )7.若正数a,b满足的最小值为( )(A)1 (B)6 (C)9 (D)168.已知函数其中k>0,若当自变量x在任何两个整数间(包括整数本身)变化时,至少含有2个周期,则最小的正整数k为( )(A)50 (B)51 (C)12 (D)139.已知,αβ都是锐角,且4cos)5ααβ=+=,则tanβ为( )(A)2 (B)-211(C)-211或2 (D)211或-210.已知O 为△ABC 的外心, 1cos ,,3A AO AB AC αβαβ==++若则的最大值为( ) (A)13 (B)12 (C)23 (D)34第Ⅱ卷(共90分)二、填空题(每题4分,满分16分,将答案填在答题纸上) 11.设数列{n a }的前n 项和为2n S n =,中5a =___.12.计算:=_____.13.已知变量x,y满足约束条件则z=2x+y的最大值为___.14.已知f(x)是R上的减函数,A(3,-1),B(0,1)是其图象上两个点,则不等式|f(1+lnx)|<1的解集是____.15.对于定义域为[0,1]的函数f(x),如果同时满足以下三条:①对任意的x∈[0,1],总有f(x)≥0;②f(1)=1;③若x1≥0,x2≥0,x1+x2≤1,都有f(x1+x2)≥f (x1)+f(x2)成立,则称函数f(x)为“美好函数”,给出下列结论:(1)若函数f(x)为美好函数,则f(0)=0;(2)函数g(x)=2x-1(x∈[0,1])不是美好函数;(3)函数是美好函数;(4)若函数f(x)为美好函数,且∃x0∈[0,1],使得f(f(x0))=x0,则f(x0)=x0.以上说法中正确的是______(写出所有正确的结论的序号)显然=在[0,1]满足条件①()0()h x xαg=.若g x≥,也满足条件②(1)三、解答题(本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.已知函数sin2(sin cos) ()cosx x xf xx-= .(I)求函数f(x)的定义域及最大值;(II)求使f(x)≥0成立的x的取值集合.17.已知{n a }为等差数列,且45814,48a a a =+=. (I )求{n a }的通项公式;(II )设n S 是等比数列{n b }的前n 项和,若成等差数列,求S 4.18.安通驾校拟围着一座山修建一条环形训练道路OASBCD,道路的平面图如图所示(单位:km),已知曲线ASB为函数的图象,且最高点为S(1,2),折线段AOD为固定线路,其中AO OD=4,折线段BCD为可变线路,但为保证驾驶安全,限定∠BCD=120°. (I)求的值;(II)应如何设计,才能使折线段道路BCD最长?19.(本题满分12分)已知函数(I)若函数f(x)满足f(3+x)=f(-x),求使不等式f(x)≥g(x)成立的x的取值集合;(II)若函数h(x)=f(x)+g(x)+2在(0,2)上有两个不同的零点求实数b的取值范围.20.(本题满分13分).已知函数y=lg(1+tx-x2)的定义域为M,其中t R(I)若,求函数在M上的最小值及相应的x的值;(II)若对任意函数满足求t的取值范围.【解析】21.(本题满分14分)已知函数(I)若函数f(x)的图象在x=0处的切线方程为y=2x+b,求a,b的值;(II)若函数f(x)在R上是增函数,求实数a的取值范围;(III)如果函数恰好有两个不同的极值点证明:【解析】。
四川省绵阳南山实验高中2015届高三一诊模拟考试试题 数学理 Word含答案

绵阳南山中学. 南山中学实验学校绵阳市“一诊”模拟考试试题理科数学本试卷分I 卷(选择题)和第II 卷(非选择题)两部分,满分150分,考试时间为120分钟。
考试结束后,将试卷和答题卡一并交回。
注意事项:1.答题前,考生必须将自己的姓名、准考证号填写清楚,将条形码准确粘贴在条形码区域内。
2.选择题必须用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
第I 卷(共50分)一、选择题(本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.集合{}2,0,1,2M -=,{}211N x x =->,则N M ⋂=( ) A.{-2,1,2} B.{0,2} C.{-2,2} D.[-2,2]2.已知a =(2,1), (),3b x =,且 b a//,则x 的值为( )A.2B.1C.3D.63.在各项均为正数的等比数列{}n a 中,13213,,22a a a 成等差数列,则1113810a aa a +=+( )A.1-或3B.3C.1或27D.27 4.下列说法错误的是 ( )A .若2:,10p x R x x ∃∈-+=,则 2:,10p x R x x ⌝∀∈-+≠;B .“1sin 2θ=”是“30θ=”的充分不必要条件;C .命题“若0a =,则0ab =”的否命题是:“若0a ≠,则0ab ≠”;D .若1cos ,:=∈∃x R x p ,01,:2>+-∈∀x x R x q ,则“q p ⌝∧”为假命题.8.已知函数(){2014sin ,01log ,1x x x x f x π≤≤>=若,,a b c 互不相等,且()()()f a f b f c ==,则a b c++的取值范围是( ).A.(1,2014)B.(1,2015)C.[2,2015]D.(2,2015)9.已知定义为R 的函数()f x 满足()()4f x f x -=-+,且函数()f x 在区间()2,+∞上单调递增.如果122x x <<,且124x x +<,则()()12f x f x +的值( ) A. 恒小于0B.恒大于0C .可能为0D .可正可负10.设函数()f x 的导函数为()'f x ,对任意x R ∈都有()()'f x f x >成立,则( ) A. 3(ln 2)2(ln3)f f > B. 3(ln 2)2(ln3)f f <C. 3(ln 2)2(ln3)f f =D. 3(ln 2)f 与2(ln 3)f 的大小不确定第Ⅱ卷二、填空题(本大题共5小题,每小题5分,共25分.) 11.幂函数2(33)m y m m x =-+过点()2,4,则m = . 12. 计算31log 4233log 6log 243-+- 的结果为 .13已知菱形ABCD 的边长为2,120BAD ︒∠=,点,E F 分别在边,BC DC 上,3BC BE =,DC DF λ=. 若1AE AF ⋅=,则λ的值为 .14.已知22,,12y x y R x +∈+=,则12的最大值为 . 15.已知()()()112212,,,A x y B x y x x >是函数()3f x x x=-图象上的两个不同点,且在,A三、解答题(解答应写出文字说明,证明过程或演算步骤共75分) 16. (本小题满分12分)已知函数()2cos sin 333f x x x x πππ⎡⎤⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.(Ⅰ)求()f x 的值域和最小正周期;(Ⅱ)若对任意0,6x π⎡⎤∈⎢⎥⎣⎦,使得()20m f x ⎡++=⎣恒成立,求实数m 的取值范围.17.(本小题满分12分)设公差不为0的等差数列{}n a 的首项为1,且2514,,a a a 构成等比数列. (Ⅰ)求数列{}n a 的通项公式; (Ⅱ)若数列{}n b 满足12121 (12)n n n b b b a a a +++=-,*n N ∈,求{}n b 的前n 项和n T18. (本小题满分12分)已知函数())(0,)22f x x ππωϕωϕ=+>-≤<的图像关于直线3x π=对称,且图像上相邻两个最高点的距离为π. (I )求ω和ϕ的值;(II )若()2f α= ,( 263ππα<<),求3cos()2πα+的值.19. (本小题满分12分)已知二次函数2()(0),(1)3,f x Ax Bx A f =+≠=其图象关于1x =-对称,数列{}n a 的前n 项和为n S ,点()()*,n n S n N ∈均在()y f x =图象上. (Ⅰ)求数列{}n a 的通项公式,并求n S 的最小值; (Ⅱ)数列{}n b , 1n nb S =, {}n b 的前n 项和为n T ,求证:11313443n T n n -<<-+.20.(本小题满分13分)设函数x ax x a x f ln 21)(2-+-=(R a ∈). (Ⅰ)当1=a 时,求函数)(x f 的极值; (Ⅱ)当R a ∈时,讨论函数)(x f 的单调性;(Ⅲ)若对任意(2,3)a ∈及任意1x ,[]2,12∈x ,恒有12ln 2()()ma f x f x +>-成立,求实数m 的取值范围.21.(本小题满分14分) 已知()ln ()f x x mx m R =-∈.(Ⅰ)若曲线()y f x =过点P(1,1)-,求曲线在P 点处的切线方程; (Ⅱ)求()f x 在区间[]1,e 上的最大值;(Ⅲ)若函数()f x 有两个不同的零点12,x x ,求证212x x e >.绵阳南山中学. 南山中学实验学校绵阳市“一诊”模拟考试试题理科数学参考答案一、CDDBA CADAB 二、填空题11.2 12. -1 13.2 14. 3815.(-1,0)三、解答题16.解: (1)f(x)=2sin ⎝ ⎛⎭⎪⎫x +π3cos ⎝ ⎛⎭⎪⎫x +π3-23cos2⎝ ⎛⎭⎪⎫x +π3=sin ⎝ ⎛⎭⎪⎫2x +2π3-3⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫2x +2π3+1=sin ⎝ ⎛⎭⎪⎫2x +2π3-3cos ⎝ ⎛⎭⎪⎫2x +2π3- 3=2sin ⎝ ⎛⎭⎪⎫2x +π3- 3.∵-1≤sin ⎝⎛⎭⎪⎫2x +π3≤1. ∴-2-3≤2sin ⎝ ⎛⎭⎪⎫2x +π3-3≤2-3,T =2π2=π,即f(x)的值域为[-2-3,2-3],最小正周期为π. (2)当x ∈⎣⎢⎡⎦⎥⎤0,π6时,2x +π3∈⎣⎢⎡⎦⎥⎤π3,2π3,故sin ⎝ ⎛⎭⎪⎫2x +π3∈⎣⎢⎡⎦⎥⎤32,1,此时f(x)+3=2sin ⎝⎛⎭⎪⎫2x +π3∈[3,2].由m[f(x)+3]+2=0知,m≠0,∴f(x)+3=-2m,即3≤-2m ≤2,即⎩⎪⎨⎪⎧2m +3≤0,2m +2≥0,解得-233≤m≤-1.即实数m 的取值范围是⎣⎢⎡⎦⎥⎤-233,-1.17.解:(I )设等差数列{}n a 的公差为d,(d 0≠),则2514,,a a a 构成等比数列,∴22145a a a =,即2(14)(1))113)d d d +=++ 解得d=0(舍去)或d=2, ∴n a =1+2(n-1)=2n-1 ……………….3分(II )由已知1212...n nb b b a a a +++112n =-(*n N ∈) 当n=1时,11b a =12; 当2n ≥时,n nb a =(112n -)11(1)2n ---=12n ,∴n nb a ==12n ,(*n N ∈) 由(I ),n a =2n-1(*n N ∈),∴212n nn b -=(*n N ∈)…………7分 12313521...2222n nn T -=++++ 2341113521 (22222)n n n T +-=++++ 两式相减得234111222221(...)2222222n n n n T +-=+++++-,=113121222n n n -+---, ∴n T =2332nn +- …………….12分 18.解:(I )6π-φ2ω,.6π-φ)6π-2sin(3)12π-(2sin 3f(x)∴2πφ≤2π-0)12π()4-3π(∴3π2ω⇒|ω|π2∴π=====<======,所以,,且为对称轴由题可知,周期x x f T f x T T ………………………….5分(II )8153)23παcos(,.8153214152341)23παcos(∴.415)6π-αcos(2π6π-α0∴32πα6π21)6π-αcos(23)6π-αsin(]6π)6π-αsin[(αsin )23παcos(41)6π-αsin(43)6π-αsin(3∴43)2α(+=++=•+•=+=<<<<•+•=+==+===所以,,即 f……………………12分 19.解:(1)(1)3,12Bf A B A=+=-=-, ∴21,2,,()2A B f x x x ===+ ……………..1分点()()*,n n S n N ∈均在y=f(x)图象上,∴22n S n n =+①………………..2分21(1)2(1)n S n n -=-+-(2n ≥)②①-②得121n n S S n --=+,即n a =2n+1 (2n ≥)……………………….4分, 又113a s == ……………5分∴n a =2n+1(*n N ∈) ………………6分 (2)211111()(2)222n b n n n n n n===-+++ ………………….7分 111111[(1)()...()23242n T n n =-+-++-+] =1111[(1)]2212n n +--++=3111()4212n n -+++ ………9分即证313111()434212n n n ->-++++ 即证211()312n n n <++++, 1111,3132n n n n <<++++,所以右边成立……..10分, 又n T 随n 的增大而增大,1111334n T T n>=>-,左边成立…………..11分 所以,原不等式成立 . ……………………….12分 20.解:(Ⅰ)函数的定义域为(0,)+∞,当1a =时,11()ln ,'()1.x f x x x f x x x-=-=-= 令'()0, 1.f x x ==得,当01x <<时,'()0f x <;当1x >时,'()0f x >,()(0,1)f x ∴在单调递减,在(1,)+∞单调递增,()(1)1f x f ∴==极小值,无极大值 ;…… 4分 (Ⅱ)21(1)1[(1)1](1)'()(1)a x ax a x x f x a x a x x x-+--+-=-+-==1(1)()(1)1a x x a x----=………………5分 ①1a ≤时,(1)10a x -+>,()f x 在(0,1)单减,(1,)+∞单增; ②12a <<时,111a >-,()f x 在(0,1)单增,在1(1,)1a -单减,1(,)1a +∞-单增;③当111a =-即2a =时,2(1)'()0,()(0,)x f x f x x -=-≤+∞在上是减函数;④当111a <-,即2a >时,令'()0f x <,得1011x x a <<>-或,令'()0f x >,得111x a <<- ……………9分 (Ⅲ)由(Ⅱ)知,当(2,3)a ∈时,()[1,2]f x 在上单调递减,当1x =时,()f x 有最大值,当2x =时,()f x 有最小值,123|()()|(1)(2)ln 222a f x f x f f ∴-≤-=-+,3ln 2ln 222a ma ∴+>-+ , 而0a >经整理得13113230,22422m a a a>-<<-<-<由得 0m ∴≥.……13分 21.解:(1)因为点P (1,-1)在曲线上,所以f(1)=-1,得m=1/1()1f x x=-,∴/(1)f =0,故切线方程为y=-1. ……3分 (2) /1()f x m x=-=1mxx-①当m ≤0时,(1,)x e ∈; (1,)x e ∈,/()f x >0, ()f x 单增,max ()f x =f(e)=1-me ; ② 当1e m ≥,即10m e<≤时,(1,)x e∈,/()f x >0, ()f x 单增,max ()f x =f(e)=1-me ;③ 当11e m <<时,即111e m <<时,(1,)x e ∈,()f x 在1(1,)m 单增,在1(,)e m单减, max ()f x =1()f m=ln 1m --④当11m≤即1m ≥时,(1,)x e ∈,/()f x 0<,()f x 单减,max ()f x = f(1)=-m∴()f x 在[1,e ]上的最大值max ()f x=………………………………8分(3)不妨设120x x >>,12()()0f x f x ==,∴11ln 0x mx -=,22ln 0,x mx -=1212ln ln ()x x m x x +=+,1212ln ln ()x x m x x -=-, 要证212x x e >,即证12ln ln x x +2>,即证12()m x x +2>,………10分1212ln ln x x m x x -=-,即证1212ln ln x x x x --122x x >+,即证12ln ln x x -12)122(x x x x ->+,即证1121222(1)ln 1x x x x x x ->+,……………12分 令12x x =t,则1t >,即证1ln 1t t t ->+,1()ln 1t t t t ϕ-=-+,则/()t ϕ=22214(1)0(1)(1)t t t t t --=>--,函数()t ϕ在(1,)+∞单增,∴()t ϕ(1)ϕ>=0,∴原不等式成立. ……………………14分。
绵阳市高中2014-2015学年第一学期高二期末教学质量测试数学试题(理科)(含详细解答)

绵阳市高中2014-2015学年第一学期高二期末教学质量测试数学试题(理科)一、选择题(本大题共10小题,每小题4分,满分40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1、刘徽是我国古代最伟大的数学家之一,他的 是极限思想的开始,他计算体积的思想是积分学的萌芽.( )A .割圆术B .勾股定理C .大衍求一术D .辗转相除法2、在极坐标系中,极坐标方程4sin ρθ=表示的曲线是( )A .圆B .直线C .椭圆D .抛物线3、直线l 310y +-=,则直线l 的倾斜角为( )A .30B .60C .120D .1504、下列关于统计的说法正确的是( )A .一组数据只能有一个众数B .一组数据可以有两个中位数C .一组数据的方差一定是非负数D .一组数据中的每一个数据都加上同一非零常数后,平均数不会发生变化5、有5件产品,其中3件正品,2件次品,从中任取2件,则互斥而不对立的两个事件是( )A .至少有1件次品与至多有1件正品B .至少有1件次品与都是正品C .至少有1件次品与至少有1件正品D .恰有1件次品与恰有2件正品6、某市要对辖区内的中学教师的年龄进行调查,现从中随机抽出200名教师,已知抽到的教师年龄都在[)25,50岁之间,根据调查结果得出教师的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市辖区内中学教师的年龄的中位数大约是( )A .37.1岁B .38.1岁C .38.7岁D .43.1岁7、执行右图的程序框图,任意输入一次x (x ∈Z ,22x -≤≤)与y (y ∈Z ,22y -≤≤),则能输出数对(),x y 的概率为( )A .725 B .825 C .925D .258、已知O 为坐标原点,F 为抛物线C :2y =的焦点,P 为C 上一点,若F ∆PO 的面积为F P =( )A .B .C .D .92x m =+有实数解,则实数m 的取值范围是( )A .)[)2,⎡+∞⎣B .)(0,3⎡⎤⎣⎦C .([),2,-∞+∞D .(][),22,-∞-+∞10、已知点P 是椭圆221135x y +=(0x ≠,0y ≠)上的动点,1F ,2F 为椭圆的两个焦点,O 是坐标原点,若M 是以线段1F P 为直径的圆上一点,且M 到12F F ∠P 两边的距离相等,则OM 的取值范围是( )A .(B .(0,C .D .(3,二、填空题(本大题共5小题,每小题4分,共20分.)11、设()3,2,1A ,()1,0,5B ,则AB 的中点M 的坐标为 .12、右面算法最后输出的结果是 . 13、质检部门对某超市甲、乙、丙三种商品共750件进行分层抽样检查,抽检员制作了如下的统计表格:表格中甲、丙商品的有关数据已被污染看不清楚(分别用1x ,2x ,3x ,4x 表示),若甲商品的样本容量比丙商品的样本容量多6,则根据以上信息可求得丙商品数量2x 的值为 .14、已知1F 是双曲线22221x y a b-=(0a >,0b >)的左焦点,以线段1F O 为边作正三角形1F OM ,若顶点M 在双曲线上,则双曲线的离心率是 .15、已知椭圆22221x y a b+=(0a b >>)及内部面积为S ab π=,1A ,2A 是长轴的两个顶点,1B ,2B 是短轴的两个顶点,在椭圆上或椭圆内部随机取一点P ,给出下列命题:①12∆PA A 为钝角三角形的概率为1;②12∆PB B 为钝角三角形的概率为b a ; ③12∆PA A 为钝角三角形的概率为b a ; ④12∆PB B 为锐角三角形的概率为a b a -. 其中正确的命题有 .(填上你认为所有正确的命题序号)三、解答题(本大题共4小题,每小题10分,共40分.解答应写出文字说明、证明过程或演算步骤.)16、直线l 经过两直线240x y -+=与50x y -+=的交点,且与直线1:l 60x y +-=平行.()1求直线l 的方程;()2若点(),1a P 到直线l 的距离与直线1l 到直线l 的距离相等,求实数a 的值.17、甲、乙两个竞赛队都参加了10场比赛,比赛得分情况记录如下(单位:分): 甲队:57,41,51,40,49,39,52,43,45,53乙队:30,50,67,47,66,34,46,30,64,66()1根据得分情况记录,请将茎叶图补充完整,并求乙队得分的中位数;()2如果从甲、乙两队的10场得分中,各随机抽取一场不小于50分的得分,求甲的得分大于乙的得分的概率.18、已知圆C :22230x y x ++-=.()1求过点()1,3P 且与圆C 相切的直线方程;()2问是否存在斜率为1的直线l ,使以l 被圆C 截得的弦AB 为直线的圆经过原点?若存在,请求出的方程;若不存在,请说明理由.19、已知椭圆C :22221x y a b+=(0a b >>)的左焦点为()F 1,0-,O 为坐标原点,点G 1,2⎛ ⎝⎭在椭圆上,过点F 的直线l 交椭圆于不同的两点A 、B .()1求椭圆C 的方程;()2求弦AB 的中点M 的轨迹方程;()3设过点F 且不与坐标轴垂直的直线交椭圆于A 、B 两点,P 为x 轴上一点,若PA 、PB 是菱形的两条邻边,求点P 横坐标的取值范围.。
四川省绵阳市2014届高三第一次诊断性考试理科数学压轴题总结

2014年四川省高考模拟试题9(关于2014届绵阳一诊10向量压轴讨论版)2013.11.9 理科数学第I 卷一.选择题:本大题共10小题,每小题5分,共50分. 在每小题给出的四个备选项中,只有一项是符合题目要求的.1.设△ABC ,P 0是边AB 上一定点,满足P 0B =14AB ,且对于AB 上任一点P ,恒有→PB ∙→PC ≥→P 0B ∙→P 0C ,则 A .∠ABC =90︒ B .∠BAC =90︒ C .AB =AC D .AC =BC2. 已知△ABC 为等边三角形,=2AB ,设点P ,Q 满足=AP AB λ ,=(1)AQ AC λ-,R λ∈,若3=2BQ CP ⋅- ,则=λA.12B.122±C.1102±D.3222-±3. 在平面直角坐标系中,o 是坐标原点,两定点,A B 满足2,OA OB OA OB ===则点集,1,,|P OP OA OB R λμλμλμ==++≤∈所表示的区域的面积是A.22B.23C. 42D.43 4.对任意两个非零的平面向量α和β,定义αβαβββ⋅=⋅ 。
若平面向量,a b 满足||||0a b ≥>,a 与b 的夹角(0,)4πθ∈,且a b 和b a 都在集合{|}2∈nn Z 中,则a b = A .12 B. 1 C. 32 D. 525.已知非零向量AB →与AC →满足(AB →|AB →| +AC →|AC →| )·BC →=0且AB →|AB →| ·AC →|AC→| =12 , 则△ABC 为( )A.三边均不相等的三角形B.直角三角形C.等腰非等边三角形D.等边三角形6.在平面上,12AB AB ⊥ ,121OB OB == ,12AP AB AB =+ .若12OP < ,则OA 的取值范围是A.5(0,]2 B.57(,]22 C.5(,2]2 D.7(,2]27. 如图1:OM ∥AB ,点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内(不含边界).且OB y OA x OP +=,则实数对(x ,y )可以是A .)43,41( B. )32,32(- C. )43,41(- D. )57,51(-第七题 第八题8.如题八图,在直角梯形ABCD 中,,1,3,AB AD AD DC AB ⊥===动点P 在以点C 为圆心且与直线BD 相切的圆内运动,设(,)AP AD AB R αβαβ=+∈,则αβ+的取值范围是( )A .4(0,)3B .5(0,)3C .4(1,)3D .5(1,)39.已知A 、B 、C 是平面上不共线的三点,O 为△ABC 的外心,动点P 满足3])21()1(1[(OC OB OA OP λλλ++-+-=)(λ∈R ), 则P 的轨迹一定过△ABC 的A 、内心B 、垂心C 、重心D 、AC 边的中点10.【2014届绵阳一诊10题】已知O 为△ABC 的外心,1cos 3A =,若AO AB AC αβ=+ ,则αβ+的最大值为 A .13B .21 C .32 D .43 第II 卷二.填空题(共5个小题,每小题5分,共25分.将答案直接填写在各题中的横线上) 11.设E D ,分别是ABC ∆的边BC AB ,上的点,AB AD 21=,BC BE 32=,若AC AB DE 21λλ+=(21λλ,为实数),则21λλ+的值为 . 12.在平行四边形ABCD 中,3π=∠A ,边AB 、AD 的长分别为2、1,若M 、N 分别是边BC 、CD上的点,且满足||||||||CD CN BC BM =,则AN AM ⋅的取值范围是13.如图2,两块斜边长相等的直角三角板拼在一起,若AD xAB y AC =+,则x = ,y =A B O M 图1图1314、给定两个长度为1的平面向量OA 和OB ,它们的夹角为120o.如图所示,点C 在以O 为圆心的圆弧AB 上变动.若,OC xOA yOB =+其中,x y R ∈,则x y +的最大值是________.15.已知O 是ABC ∆的外心,2=AB ,1=AC ,︒=∠120BAC ,若AC AB AO 21λλ+=,则21λλ+的值为三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.已知数列{}n a 中,13a =,25a =,其前n 项和n S 满足()121223n n n n S S S n ---+=+≥.令11n n n b a a +=⋅.(1)求数列{}n a 的通项公式;(2)若()12x f x -=,求证:()()()121126n n T b f b f b f n =+++< (1n ≥); (3)令()2312312n n n T b a b a b a b a =++++ (0a >),求同时满足下列两个条件的所有a 的值:①对于任意正整数n ,都有16n T <;②对于任意的10,6m ⎛⎫∈ ⎪⎝⎭,均存在0n N *∈,使得0n n ≥时,n T m >2014年四川省高考模拟试题9(关于2014届绵阳一诊10向量压轴讨论版:参考答案)【1解析】D 由题意,设|→AB |=4,则|→P 0B |=1,过点C 作AB 的垂线,垂足为H ,在AB 上任取一点P ,设HP 0=a ,则由数量积的几何意义可得,→PB ∙→PC =|→PH ||→PB |=(|→PB | −(a +1))|→PB |,→P 0B ∙→P 0C =−|→P 0H ||→P 0B |=−a ,于是→PB ∙→PC≥→P 0B ∙→P 0C 恒成立,相当于(|→PB |−(a +1))|→PB |≥−a 恒成立,整理得|→PB |2−(a +1)|→PB |+a ≥0恒成立,只需∆=(a +1)2−4a =(a −1)2≤0即可,于是a =1,因此我们得到HB =2,即H 是AB 的中点,故△ABC 是等腰三角形,所以AC =BC【2解析】A.∵=BQ AQ AB - =(1)AC AB λ-- ,=CP AP AC -=AB AC λ- ,又∵3=2BQ CP ⋅- ,且||=||A B A C ,0<,>=60AB AC ,0=||||cos 60=2AB AC AB AC ⋅⋅ ,∴3[(1)]()=2AC AB AB AC λλ---- ,2223||+(1)+(1)||=2AB AB AC AC λλλλ--⋅- ,所以234+2(1)+4(1)=2λλλλ---,解得1=2λ. CBAPQ第1题图【3解析】D 1,,,,=++=μλμλ其中是线外一点则三点共线若PC PB PA P C B A .在本题中,32cos 4cos ||||πθθθ=⇒==⋅⋅=⋅OB OA OB OA .建立直角坐标系,设A(2,0),).(10,0).31(含边界内在三角形时,,则当OAB P B ≤+≥≥μλμλ344=⨯=的面积三角形的面积根据对称性,所求区域OAB S 所以选D【4解析】B :因为||2cos cos ||2θθ⋅==≥>⋅ a b a a b b b b ,||cos cos 1||θθ⋅==≤<⋅ b a b b a a a a 且a b 和b a 都在集合{|}2∈nn Z 中所以,||1c o s ||2θ== b b a a ,||1||2cos θ=b a ,所以2||cos 2cos 2||θθ==< a a b b 所以222≤< a b ,故有1= a b 【答案】B【5解析】D 已知非零向量AB →与AC →满足(||||AB AC AB AC +)·BC →=0,即角A 的平分线垂直于BC ,∴ AB =AC ,CABHP 0P又cos A =||||AB AC AB AC ⋅=12,∠A =3π,所以△ABC 为等边三角形,选D . 【6解析】D 因为1AB ⊥2AB ,所以可以A 为原点,分别以1AB ,2AB所在直线为x 轴,y 轴建立平面直角坐标系.设B 1(a,0),B 2(0,b ),O (x ,y ),则AP =1AB +2AB=(a ,b ),即P (a ,b ).由|1OB |=|2OB |=1,得(x -a )2+y 2=x 2+(y -b )2=1.所以(x -a )2=1-y 2≥0,(y -b )2=1-x 2≥0.由|OP |<12,得(x -a )2+(y -b )2<14,即0≤1-x 2+1-y 2<14.所以74<x 2+y 2≤2,即22722x y <+≤. 所以|OA |的取值范围是7,22⎛⎤⎥ ⎝⎦,故选D . 【7解析】C 如图,OM ∥AB ,点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内(不含边界).且OB y OA x OP +=,由图知,x<0,当x=-41时,即OC =-41OA,P 点在线段DE 上,CD =41OB ,CE =45OB ,而41<43<45,∴ 选C.【9解析】根据向量的加法的平行四边形法则向量的运算法则,对3])21()1(1[(OC OB OA OP λλλ++-+-=)进行化简,得到根据三点共线的充要条件知道P 、C 、D 三点共线,从而得到点P 的轨迹一定经过△ABC 的重心.【11解析】)(32213221AC BA AB BC AB BE DB DE ++=+=+= AC AB AC AB 213261λλ+=+-=所以,611-=λ,322=λ,=+21λλ12 .【13解析】作DF AB ⊥,设12AB AC BC DE ==⇒==,60DEB ∠= ,6,2BD ∴=由45DBF ∠=解得623,222DF BF ==⨯=故31,2x =+3.2y = 【14解析】设AOC α∠= ,,OC OA xOA OA yOB OA OC OB xOA OB yOB OB ⎧∙=∙+∙⎪⎨∙=∙+∙⎪⎩,即01cos 21cos(120)2x y x y αα⎧=-⎪⎪⎨⎪-=-+⎪⎩∴02[cos cos(120)]cos 3sin 2sin()26x y πααααα+=+-=+=+≤【15解析思路】更简单了变得!建立直角坐标系,求出三角形各顶点的坐标,因为O 为△ABC 的外心,把AB 的中垂线 m 方程和AC 的中垂线 n 的方程,联立方程组,求出O 的坐标,利用已知向量间的关系,待定系数法求λ1和λ2 的值.答案为:13616.【解】(Ⅰ)由题意知()111223n n n n n S S S S n -----=-+≥即()1123n n n a a n --=+≥……1′∴()()()112322n n n n n a a a a a a a a ---=-+-++-+()1221222225222212213n n n n n n ----=++++=++++++=+ ≥……2′检验知1n =、2时,结论也成立,故21n n a =+.…………3′(Ⅱ)由于()()()()()()()11111212111111222212121212121n nn n n n n n n n b f n +-++++-+⎛⎫=⋅=⋅=- ⎪++++++⎝⎭ 故()()()1222311111111122121212122121n n n n T b f b f b f n +⎡⎤⎛⎫⎛⎫⎛⎫=+++=-+-++- ⎪ ⎪ ⎪⎢⎥++++++⎝⎭⎝⎭⎝⎭⎣⎦ 1111111212212126n +⎛⎫=-<⋅= ⎪+++⎝⎭.…………6′ (Ⅲ)(ⅰ)当2a =时,由(Ⅱ)知:16n T <,即条件①满足;又106m <<,∴1211113321110212211616n n n T m m n log m m ++⎛⎫⎛⎫>⇔->⇔>-⇔>--> ⎪ ⎪++--⎝⎭⎝⎭.取0n 等于不超过23116log m ⎛⎫- ⎪-⎝⎭的最大整数,则当0n n ≥时,n T m >.…9′(ⅱ)当2a >时,∵1n ≥,222nn n a a a ⎛⎫= ⎪⎝⎭≥,∴22n n a a ⋅≥,∴2222n n n n n n a ab a b b ⋅⋅⋅=⋅⋅≥.∴()11111111222221221nni i n i i n i i a a T b a b -+==⎛⎫⎛⎫=⋅=⋅- ⎪ ⎪++⎝⎭⎝⎭∑∑≥.由(ⅰ)知存在0n N *∈,当0n n ≥时,11111212213n a +⎛⎫->⎪++⎝⎭, 故存在0n N *∈,当0n n ≥时,111111221221236n n a a T a +⎛⎫=⋅->⋅= ⎪++⎝⎭,不满足条件. …12′ (ⅲ)当02a <<时,∵1n ≥,222n n n a a a ⎛⎫= ⎪⎝⎭≤,∴22n n a a ⋅≤,∴2222n n n n n n a ab a b b ⋅⋅⋅=⋅⋅≤.∴()()11111111222221221n nii n i i n i i a a T b a b -+==⎛⎫==⋅- ⎪++⎝⎭∑∑≤.取10,126a m ⎛⎫=∈ ⎪⎝⎭,若存在0n N *∈,当0n n ≥时,n T m >,则111122122112n a a+⎛⎫⋅->⎪++⎝⎭. ∴111112213n +->++矛盾. 故不存在0n N *∈,当0n n ≥时,n T m >.不满足条件. 综上所述:只有2a =时满足条件,故2a =.…………14′ 。
2015届绵阳市高三“一诊”试题及答案

保密 ★ 启用前 【考试时间:2014年11月1日上午9∶00~11∶30】绵阳市高中2012级第一次诊断性考试理科综合·化学理科综合考试时间共150分钟,满分300分。
其中,物理110分,化学100分,生物90分。
化学试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)。
第Ⅰ卷5至6页,第Ⅱ卷7至8页,共4页。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
考试结束后,将答题卡交回。
可能用到的相对原子质量:H 1 C 12 O 16 S 32 Na 23 Cu 64第Ⅰ卷(选择题 共42分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑。
第Ⅰ卷共7题,每题6分。
每题给出的四个选项中,只有一项是符合题目要求的。
1. 由塑化剂引起的食品、药品问题受到广泛关注。
下列关于塑化剂DBP (结构如下图)的说法不.正确..的是 A .属于芳香族化合物,能溶于水 B .其核磁共振氢谱共有6种吸收峰 C .分子中一定有12个原子位于同一平面上 D .水解得到的酸性产物能与乙二醇发生缩聚反应 2. 下列关于物质分类的说法正确的是A .油脂、糖类、蛋白质均是天然高分子化合物B .三氯甲烷、氯乙烯、三溴苯酚均是卤代烃C .CaCl 2、烧碱、聚苯乙烯均为化合物D .稀豆浆、硅酸、雾霾均为胶体 3. 下列离子方程式正确的是A .向Fe(NO 3)3溶液中滴入少量的HI 溶液:2Fe 3++2I -==2Fe 2++I 2B .向苯酚钠溶液中通入少量CO 2气体:2C 6H 5O -+CO 2+H 2O —→2C 6H 5OH↓+CO 2-3C .Cu(OH)2沉淀溶于氨水得到深蓝色溶液:Cu(OH)2+4NH 3== [Cu(NH 3)4]2++2OH -D .澄清石灰水中加入少量NaHCO 3溶液:Ca 2++2OH -+2HCO -3==CaCO 3↓+CO 2-3 +2H 2OOO O O4. 短周期主族元素R 、T 、Q 、W 在元素周期表中的相对位置如右下图所示,T 元素的最高正价与最低负价的代数和为0。
