实验2 基本命令与工具(一)
实验报告2 常用网络命令的使用

计算机网络实验报告班级信工(2)班日期 2016-5-12学号 20130702047 姓名李格实验名称常用网络命令的使用一、实验目的1. 掌握几种常用的网络命令,通过使用这些命令能检测常见网络故障。
2. 理解各命令的含义,并能解释其显示内容的意义。
二、实验步骤(一)ping 命令的使用1、单击开始按钮,输入cmd 并按回车键,进入windows DOS环境。
2、输入ping/? 回车,了解ping命令的基本用法。
结果如下:最常用的ping命令是在ping后面直接跟域名或IP地址。
测试内网或外网的联通情况。
3、依次输入以下命令并查看分析结果。
(1)输入ping 并回车查看分析结果。
结果如下:分析:(2)输入ping 218.197.176.10并回车查看分析结果。
结果如下:分析:(3)输入ping 并回车查看分析结果。
结果如下:分析:(3)输入pi ng 121.14.1.189 并回车查看分析结果。
结果如下:分析:4、使用不同的参数测试ping命令。
结果如下:分析:(二)ipconfig 命令的使用1、单击开始按钮,输入cmd 并按回车键,进入windows DOS环境。
2、输入ipconfig/? 回车,了解ipconfig 命令的基本用法。
结果如下:3、依次输入以下命令并查看分析结果。
(1)输入ipconfig 并回车查看并分析结果。
结果如下:分析:(2)输入ipconfig/all 并回车查看分析结果。
结果:分析:ipconfig/all显示详细信息(3)输入ipconfig/displaydns 并回车查看分析结果。
结果:分析:ipconfig/displaydns 显示DNS解析程序缓存的内容。
由于显示内容太多所以没有全部截图展示出来。
(三)tracert 命令的使用1、单击开始按钮,输入cmd 并按回车键,进入windows DOS环境。
2、输入tracert/? 回车,了解tracert命令的基本用法。
贵州大学计算机网络实验报告-实验二-TCPIP 协议常用网络工具的使用

实验课程名称计算机网络实验报告实验项目名称TCP/IP 协议常用网络工具的使用专业班级电子信息科学与技术08级1班学生姓名学号指导教师理学院实验时间:2010年4月22日实验名称:实验二TCP/IP协议常用网络工具的使用实验目的:●了解系统网络命令及其所代表的含义,以及所能对网络进行的操作。
●通过网络命令了解运行系统网络状态,并利用网络命令对网络进行简单的操作。
实验器材:连接到因特网的计算机,个人电脑Windows XP sp3系统。
实验内容(步骤):学习使用windows环境下常用的网络命令:1)Ipconfig:IP地址与以太网卡硬件地址查看命令2)Ping:网络连接测试命令3)ARP:地址解析命令4)FTP:文件传输命令5)Netstat:显示协议及其端口信息和当前的TCP/IP 网络连接6)Route:控制网络路由表7)TFTP:简单文件传输命令8)Tracert:该诊断实用程序将包含不同生存时间(TTL) 值的Internet 控制消息协议(ICMP) 回显数据包发送到目标,以决定到达目标采用的路由。
9)Net:网络服务等1. ipconfigIpconfig命令应该是最最基础的命令了,主要功能就是显示用户所在主机内部的IP协议的配置信息等资料。
它的主要参数有:all:显示与TCP/IP协议相关的所有细节信息,其中包括测试的主机名、IP地址、子网掩码、节点类型、是否启用IP路由、网卡的物理地址、默认网关等。
renew all:更新全部适配器的通信配置情况,所有测试重新开始。
release all:释放全部适配器的通信配置情况。
renew n:更新第n号适配器的通信配置情况,所有测试重新开始。
命令格式是:C:\>ipconfig/(参数)分析:Windows IP 配置主机名:b5469b44b6904d3主DNS后缀:节点类型:混合IP路由已启用:否WINS代理已启用:否以太网适配器本地连接:媒体类型:媒体未连接描述:Intel(R) 82566MM Gigabit Network Connection 物理地址:00-21-85-4E-30-42以太网适配器无线网络连接:连接特定的DNS后缀:描述:802.11g Mini Card Wireless Adapter物理地址:00-1D-92-CF-AA-57DHCP已启用:是自动配置已启动:是IP地址:192.168.1.7子网掩码:255.255.255.0缺省路径:192.168.1.1DHCP服务器:192.168.1.1DNS服务器:221.13.30.242 221.13.28.234租赁通行:2010年4月26日23:19:54租赁期满:2010年4月27日23:19:542. ping命令PING命令是一个在网络中非常重要的并且常用的命令,主要是用来测试网络是否连通。
大学计算机基础实验指导与习题 第2章 Windows操作系统

14
实验2-2 Windows XP资源 管理器的应用
四、练习实验 1.在E:盘上建立文件夹,名为“计算机基础”。 2.查找“sunset.jpg”所在位置,并将其复制到 “计算机基础”文件夹中。 3.将“计算机基础”文件夹中的“sunset.jpg”改 名为“我的图片.jpg”。 4.在桌面上为“我的图片.jpg”创建快捷方式,并尝 试用新建立的快捷方式打开该文件。 5.查看“我的图片.jpg”文件的信息,包括文件的大 小、文件的名称(包括文件主名和扩展名)、文件建 立与修改日期等。 6.在E:盘中,分别以连续成组、非连续、反向和全 选方式选择文件或文件夹。
2
实验2-1 Windows XP基本操作
2.掌握窗口的基本操作。 (1)打开“我的电脑”窗口,熟悉窗口的组成。 窗口是由标题栏、菜单栏、工具栏、状态栏、工作 区域及滚动条等几部分组成。 (2)练习下列窗口操作操作: ①移动窗口。 ②适当调整窗口的大小,使滚动条出现。利用滚动 条来改变窗口显示的内容。 ③先将窗口最小化,然后再将窗口复原。 ④先将窗口最大化,然后再将窗口复原。 ⑤关闭窗口。
实验2-1 Windows XP基本操作
一、实验目的 1.掌握Windows XP的启动和退出。 2.熟悉Windows XP的桌面布局。 3.了解对话框中的常见组成元素。 4.熟悉窗口的基本操作。 5.熟悉菜单的使用。
1
实验2-1 Windows XP基本操作
二、实验内容和步骤 1.启动Windows XP,熟悉桌面、对话框的组成, 学会对桌面的图标和对话框等进行操作。 (1)打开计算机,进入Windows XP。观察桌面 的组成,认识应用程序和图标。 ①查看任务栏的属性。 ②改变任务栏及各区域大小。 ③熟悉桌面常用的图标。 ④熟悉“开始”菜单的使用。 (2)熟悉对话框的组成要素,了解基本操作。
实验二 GCC 及GDB的使用

实验二GCC 及GDB的使用一、实验目的和要求a)掌握VI编译环境。
b)掌握GCC编译命令。
c)掌握多个文件共同编译方法。
d)掌握GDB调试命令。
二、实验内容和原理(可参照课件第五章)a)在VI编辑器里编写简单的“hello,world,I am 13050141XX XXX”,利用GCC编译为可执行文件,执行,观察运行结果。
b)在VI编辑器里编写多个文件(至少两个,其中一个为主程序,一个为需要调用的子程序),为其书写头文件,共同编译为可执行文件,执行,观察运行结果。
学习书写MAKEFILE文件,编译,执行,观察结果。
c)编写循环结构的程序,利用GCC 编译(加参数-g)为可执行文件,利用GDB调试,学习GDB调试命令。
三、实验环境a)硬件:PC机b)软件:LINUX操作系统、虚拟机四、实验步骤vi hello.c i:C语言编程Esc :wq gcc hello.c gdb file a.out run a实验三交叉编译环境配置一、实验目的和要求熟悉 Linux 开发环境,学会基于S3C2410 的Linux 开发环境的配置和使用。
使用Linux 的armv4l-unknown-linux-gcc 编译,使用基于NFS 方式的下载调试,了解嵌入式开发的基本过程。
二、实验内容a)配置网络,包括配置IP 地址、NFS 服务、防火墙。
b)安装交叉编译器c)配置超级终端,下载文件到目标机上。
三、实验设备及工具(包括软件调试工具)硬件:UP-TECH S2410/P270 DVP 嵌入式实验平台、PC 机Pentium 500 以上, 硬盘10G 以上。
软件:REDHAT LINUX 9.0+超级终端+ARM-LINUX 开发环境四、实验步骤(所有的内容截图)1、虚拟机设置为桥接模式。
2、配置IP地址,设置为192.168.0.xxx参照实验指导书图1.4.1-1.4.3. 自己截图,说明3、关闭防火墙,参照实验指导书图1.4.4自己截图,说明4、打开桌面超级终端(HyperTerminal),配置COM1,115200波特率,8N1,实验箱插上电源线,网线与主机相连,串口线与主机串口1相连,开机,看bootloader程序VIVI是否自动加载,回车后进入命令提示符。
实验二 Windows常用网络设置与命令实验指导

实验二 Windows网络配置与常用网络命令(实验指导)一、实验目的学习在Windows系统中进行网络配置、用ping ipconfig/winipcfg命令工具来进行网络测试、使用tracert路由跟踪命令、使用netstat、arp、nslookup 命令查看网络状态。
本实验目的在于使学生更好地熟悉计算机网络设置的基本操作,掌握WINDOWS 环境常用网络命令的用法,学会使用网络命令查看网络信息,解决网络故障。
二、实验工具PC机,Packet Tracer软件三、实验要求熟悉TCP/IP协议标准,准确理解IP地址及其子网划分方法,理解网关和子网掩码及其DNS的概念和原理;学习使用各种网络设备,掌握TCP/IP配置方法,学会使用常用的网络命令。
四、实验内容学习在windows环境下对TCP/IP协议的属性进行设置。
1、IP地址与子网掩码的设置;2、网关的设置3、DNS的设置学习使用常用的网络命令:1、掌握ipconfig命令的含义;2、掌握ping命令的含义;3、理解Netstat命令的含义与应用;4、理解tracert命令的含义与应用;5、理解nslookup命令的含义与应用;6、理解ARP命令的含义与应用;7、理解Telnet的含义与应用;1、ipconfig/all命令的使用注释:Config命令是我们经常使用的命令,它可以查看网络连接的情况,比如本机的ip 地址,子网掩码,dns配置,dhcp配置等等/all参数就是显示所有配置的参数。
在“开始”——“运行”弹出的对话框重输入“cmd”回车,弹出窗口,然后输入”ipconfig/all”回车,如图上图显示相应的地址例如IP地址子网掩码等等。
如图:显示这些表明不能上网。
数据报:发送=4 接受=0 丢失=42、ping的使用常用参数选项ping IP -t--连续对IP地址执行Ping命令,直到被用户以Ctrl+C中断。
-a 以IP地址格式来显示目标主机的网络地址-l 2000--指定Ping命令中的数据长度为2000字节,而不是缺省的323字节。
02实验二(1)Visio绘制l流程图、数据流图
实验二( 1 )软件开发绘图工具Visio一、背景知识1 . Visio 功能特色Microsoft Visio 为我们提供了强大的绘图功能,使用Visio 中提供的图形模板,我们可以轻松绘制数据流图、系统流程、程序流程图、ER 图、UML 类图、Gantt 图等图形,这些图形是我们在软件工程系统分析和设计过程中使用的非常重要的系统描述工具。
下面介绍一下Visio 的主要特性。
(1)拖拽式绘图。
只要用鼠标把需要的元素拖到绘图区中,就生成该元素的实例。
(2)提供了适应不同行业设计需求的解决方法,为不同的设计用户定制了对应的模板库和图纸初始化,方便快速的进入工作。
如图2-1 所示,对话框左边列出了可供选择的解决方案目录,每个目录中可以选择的模板库在右边,并且带有相应的图形提示。
图2-1 可供选择的解决方案(3)完全兼容Office 系列的其他产品。
用户可以非常方便地将Visio 图形插入这些产品中进行编辑和整合。
(4)所有Visio 产品都具有开放式的程序架构,支持自定义智慧图元。
用户可以为特定的工作制定不同的图元,并可以在图形符号列表(ShapeShee)t 中修改和设置特定的图原型为。
(5)完善的网络应用。
可以方便地将超级链接加入到Visio 的图形和绘图页中。
这样用户可以方便的按照预定的路线跳转到其他绘图页、其他文件或Web 站点。
2.Visio 基本绘图知识启动Visio 后,首先启动图2-2 所示的“开始”界面,该界面的主窗中的Template Previews (模板浏览区),展示了当前系统中可以应用的各类解决方案。
单击某个目录后,Template 区中将显示该目录下包含的各个模板名称和缩略示意图。
单击某一模板后,在左下角的模板简介区中会给对应模板的简要介绍。
图2-2 Visio “开始”界面“开始”界面支持用户通过多种方式开始Visio 的绘图编辑工作。
用户可以选择任意目录中的一个模板开始设计,或者根据自己的需要建立个性化的新模板。
实验2--微分方程(基础实验)

实验2--微分方程(基础实验)119 项目四 无穷级数与微分方程实验2 微分方程(基础实验)实验目的 理解常微分方程解的概念以及积分曲线和方向场的概念,掌握利用Mathematica 求微分方程及方程组解的常用命令和方法.基本命令1. 求微分方程的解的命令DSolve对于可以用积分方法求解的微分方程和微分方程组,可用Dsolve 命令来求其通解或特解.例如,求方程023=+'+''y y y 的通解, 输入DSolve[y ''[x]+3y '[x]+2y[x]==0,y[x],x]则输出含有两个任意常数C[1]和C[2]的通解:{}{}]2[C e ]1[C e ]x [y x x 2--+→注:在上述命令中,一阶导数符号 ' 是通过键盘上的单引号 ' 输入的,二阶导数符号 '' 要输入两个单引号,而不能输入一个双引号.又如,求解微分方程的初值问题:,10,6,03400='==+'+''==x x y y y y y输入Dsolve[{y''[x]+4 y'[x]+3y[x]==0,y[0]==6, y'[0]==10},y[x],x](*大括号把方程和初始条件放在一起*)则输出{}{}x 2x 3e 148(e ]x [y +-→-2. 求微分方程的数值解的命令NDSolve对于不可以用积分方法求解的微分方程初值问题,可以用NDSolve 命令来求其特解.例如要求方程5.0,032=+='=x y x y y的近似解)5.10(≤≤x , 输入NDSolve[{y'[x]==y[x]^2+x^3,y[0]==0.5},y[x],{x,0,1.5}](*命令中的{x,0,1.5}表示相应的区间*)则输出{{y->InterpolatingFunction[{{0.,1.5}},< >]}}注:因为NDSolve 命令得到的输出是解)(x y y =的近似值. 首先在区间[0,1.5]内插入一系 列点n x x x ,,,21Λ, 计算出在这些点上函数的近似值n y y y ,,,21Λ, 再通过插值方法得到 )(x y y =在区间上的近似解.3. 一阶微分方程的方向场一般地,我们可把一阶微分方程写为),(y x f y ='的形式,其中),(y x f 是已知函数. 上述微分方程表明:未知函数y 在点x 处的斜率等于函数120f 在点),(y x 处的函数值. 因此,可在Oxy 平面上的每一点, 作出过该点的以),(y x f 为斜率 的一条很短的直线(即是未知函数y 的切线). 这样得到的一个图形就是微分方程),(y x f y ='的方向场. 为了便于观察, 实际上只要在Oxy 平面上取适当多的点,作出在这些点的函数的 切线. 顺着斜率的走向画出符合初始条件的解,就可以得到方程),(y x f y ='的近似的积分曲 线.例如, 画出0)0(,12=-=y y dxdy 的方向场. 输入<<Graphics`PlotField`g1=PlotVectorField[{1,1-y^2},{x,-3,3},{y,-2,2}, Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25}];则输出方向场的图形(图2.1), 从图中可以观察到, 当初始条件为2/10=y 时, 这个微分方程的解介于1-和1之间, 且当x 趋向于-∞或∞时, )(x y 分别趋向于1-与1.-3-2-10123-2-1012 -3-2-10123-2-112下面求解这个微分方程, 并在同一坐标系中画出方程的解与方向场的图解. 输入sol=DSolve[{y'[x]==1-y[x]^2,y[0]==0},y[x],x];g2=Plot[sol[[1,1,2]],{x,-3,3},PlotStyle->{Hue[0.1],Thickness[0.005]}];Show[g2,g1,Axes->None,Frame->True];则输出微分方程的解xxe e x y 2211)(++-=,以及解曲线与方向场的图形(图2.2). 从图中可以看到, 微分方程的解与方向场的箭头方向相吻合.实验内容用Dsolve 命令求解微分方程例2.1 (教材 例2.1) 求微分方程 22x xe xy y -=+'的通解.输入Clear[x,y];DSolve[y '[x]+2x*y[x]==x*Exp[-x^2],y[x],x]或DSolve[D[y[x],x]+2x*y[x]==x*Exp[-x^2],y[x],x]则输出微分方程的通解:121 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+→--]1[C e x e 21]x [y 22x 2x 其中C[1]是任意常数.例2.2 (教材 例2.2) 求微分方程0=-+'x e y y x 在初始条件e y x 21==下的特解. 输入Clear[x,y];DSolve[{x*y ' [x]+y[x]-Exp[x]==0,y[1]==2 E},y[x],x]则输出所求特解:⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧+→x e e ]x [y x 例2.3 (教材 例2.3) 求微分方程x e y y y x 2cos 52=+'-''的通解.输入DSolve[y ''[x]-2y '[x]+5y[x]==Exp[x]*Cos[2 x],y[x],x]//Simplify则输出所求通解:⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧-++→])x 2[Sin ])1[c 4x (2]x 2[Cos ])2[c 81((e 81]x [y x 例2.4 (教材 例2.4) 求解微分方程x e x y +=''2, 并作出其积分曲线.输入g1=Table[Plot[E^x+x^3/3+c1+x*c2,{x,-5,5},DisplayFunction->Identity],{c1,-10,10,5},{c2,-5,5,5}];Show[g1,DisplayFunction->$DisplayFunction]; -4-224-40-20204060图2.3例2.5 (教材 例2.5) 求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++02y x dtdy e y x dt dx t 在初始条件0,100====t t y x 下的特解.输入122Clear[x,y,t];DSolve[{x' [t]+x[t]+2 y[t]==Exp[t], y'[t] -x[t]- y[t]==0,x[0]==1,y[0]==0},{x[t],y[t]},t]则输出所求特解:⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+-→→])t [Sin ]t [Cos e (21]t [y ],t [Cos ]t [x t例2.6 验证c y y x =+--)3305(15152是微分方程2)(42-='y x x y 的通解. 输入命令<<Graphics`PlotField`<<Graphics`ImplicitPlot`sol=(-5x^3-30y+3y^5)/15==C;g1=ImplicitPlot[sol/.Table[{C->n},{n,-3,3}],{x,-3,3}];g2=PlotVectorField[{1,x^2/(y^4-2)},{x,-3,3},{y,-3,3},Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25}];g=Show[g2,g1,Axes->None,Frame->True];Show[GraphicsArray[{g1,g2,g}]];则分别输出积分曲线如图 2.4(a), 微分方程的方向场如图 2.4(b). 以及在同一坐标系中画出积分曲线和方向场的图形如下图2.4 (c).-3-2-1123-2-112-3-2-10123-3-2-10123-3-2-10123-3-2-10123图2.4从图 2.4(c)中可以看出微分方程的积分曲线与方向场的箭头方向吻合, 且当∞→x 时, 无论初始条件是什么, 所有的解都趋向于一条直线方程.例2.7 (教材 例2.6) 求解微分方程,)1(122/5+=+-x x y dx dy 并作出积分曲线. 输入<<Graphics`PlotField`DSolve[y' [x]-2y[x]/(x+1)==(x+1)^(5/2),y[x],x]则输出所给积分方程的解为 ⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧+++→]1[C )x 1()x 1(32]x [y 22/7123 下面在同一坐标系中作出这个微分方程的方向场和积分曲线(设),3,2,1,0,1,2,3---=C 输入t=Table[2(1+x)^(7/2)/3+(1+x)^2c,{c,-1,1}];g1=Plot[Evaluate[t],{x,-1,1},PlotRange->{{-1,1},{-2,2}},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];g2=PlotVectorField[{1,-2y/(x+1)+(x+1)^(5/2)},{x,-0.999,1},{y,-4,4},Frame->True,ScaleFunction->(1&), ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25},DisplayFunction->Identity];Show[g1,g2,Axes->None,Frame->True,DisplayFunction->$DisplayFunction];则输出积分曲线的图形(图2.5).-0.75-0.5-0.2500.250.50.751-1.5-1-0.50.511.52图2.5例2.8 求解微分方程,2)21(22-+='-y x y xy 并作出其积分曲线.输入命令<<Graphics`PlotField`DSolve[1-2*x*y[x]*y' [x]==x^2+(y[x])^2-2,y[x],x]则得到微分方程的解为.)2(323C y x x y ++-+= 我们在33≤≤-C 时作出积分曲线, 输入命令t1=Table[(3+Sqrt[3])Sqrt[3+24x^2-4x^4-4*c*x]/(6*x),{c,-3,3}];t2=Table[(3-Sqrt[3])Sqrt[3+24x^2-4x^4-4*c*x]/(6*x),{c,-3,3}];gg1=Plot[Evaluate[t1],{x,-3,3},PlotRange->{{-3,3},{-3,3}},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];124gg2=Plot[Evaluate[t2],{x,-3,3},PlotRange->{{-3,3},{-3,3}},PlotStyle->RGBColor[1,0,0],DisplayFunction->Identity];g1=ContourPlot[y-x^3/3-x*(-2+y^2),{x,-3,3},{y,-3,3},PlotRange->{-3,3},Contours->7,ContourShading->False,PlotPoints->50,DisplayFunction->Identity];g2=PlotVectorField[{1,(x^2+y^2-2)/(1-2*x*y)},{x,-3,3},{y,-3,3},Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25},DisplayFunction->Identity];Show[g1,g2,Axes->None,Frame->True,DisplayFunction->$DisplayFunction];Show[gg1,gg2,g2,Axes->None,Frame->True,DisplayFunction->$DisplayFunction];则输出微分方程的向量场与积分曲线, 并输出等值线的图2.6.-3-2-10123-2-10123-2-10123-2-1123图2.6用NDSolve 命令求微积分方程的近似解例2.9 (教材 例2.7) 求初值问题:1,0)1()1(2.1=='-++=x y y xy y xy 在区间[1.2,4]上的近似解并作图.输入fl=NDSolve[{(1+x*y[x])*y[x]+(1-x*y[x])*y'[x]==0,y[1.2]==1},y,{x,1.2,4}]则输出为数值近似解(插值函数)的形式:{{y->InterpolatingFunction[{{1.2,4.}},< >]}}用Plot 命令可以把它的图形画出来.不过还需要先使用强制求值命令Evalu-ate, 输入 Plot[Evaluate[y[x]/.fl],{x,1.2,4}]则输出近似解的图形(图2.7).125 1.5 2.53 3.5410203040图2.7如果要求区间[1.2,4]内某一点的函数的近似值, 例如8.1=x y ,只要输入y[1.8]/.fl则输出所求结果{3.8341}例2.10 (教材 例2.8) 求范德波尔(Van der Pel)方程5.0,0,0)1(002-='==+'-+''==x x y y y y y y在区间[0,20]上的近似解.输入 Clear[x,y];NDSolve[{y''[x]+(y[x]^2-1)*y'[x]+y[x]==0,y[0]==0,y'[0]==-0.5},y,{x,0,20}];Plot[Evaluate[y[x]/.%],{x,0,20}]可以观察到近似解的图形(图2.8).5101520-2-112图2.8126 ⎪⎩⎪⎨⎧==+-'1)1(01sin 2y x y x y x 的数值解, 并作出数值解的图形.输入命令<<Graphics`PlotField`sol=NDSolve[{x*y'[x]-x^2*y[x]*Sin[x]+1==0,y[1]==1},y[x],{x,1,4}];f[x_]=Evaluate[y[x]/.sol];g1=Plot[f[x],{x,1,4},PlotRange->All,DisplayFunction->Identity];g2=PlotVectorField[{1,(x^2*y*Sin[x]-1)/x},{x,1,4},{y,-2,9},Frame->True,ScaleFunction->(1&),ScaleFactor->0.16,HeadLength->0.01,PlotPoints->{20,25},DisplayFunction->Identity];g=Show[g1,g2,Axes->None,Frame->True];Show[GraphicsArray[{g1,g}],DisplayFunction->$DisplayFunction];则输出所给微分方程的数值解及数值解的图2.9.1.522.533.544681 1.52 2.53 3.54-22468例2.11 (教材 例2.9) 求出初值问题⎪⎩⎪⎨⎧='==+'+''0)0(,1)0(cos sin 22y y xy x y y的数值解, 并作出数值解的图形.输入NDSolve[{y''[x]+Sin[x]^2*y'[x]+y[x]==Cos[x]^2,y[0]==1,y'[0]==0},y[x],{x,0,10}]127 Plot[Evaluate[y[x]/.%],{x,0,10}];则输出所求微分方程的数值解及数值解的图形(图2.10).2468100.20.40.60.8图2.10例2.12 (教材 例2.10) 洛伦兹(Lorenz)方程组是由三个一阶微分方程组成的方程组.这三个方程看似简单, 也没有包含复杂的函数, 但它的解却很有趣和耐人寻味. 试求解洛伦兹方程组,0)0(,4)0(,12)0()(4)()()()()(45)()()()(16)(16)(⎪⎪⎩⎪⎪⎨⎧===-='-+-='-='z y x t z t y t x t z t y t x t z t x t y t x t y t x 并画出解曲线的图形.输入Clear[eq,x,y,z]eq=Sequence[x'[t]==16*y[t]-16*x[t],y'[t]==-x[t]*z[t]-y[t]+45x[t],z'[t]==x[t]*y[t]-4z[t]];sol1=NDSolve[{eq,x[0]==12,y[0]==4,z[0]==0},{x[t],y[t],z[t]},{t,0,16},MaxSteps->10000];g1=ParametricPlot3D[Evaluate[{x[t],y[t],z[t]}/.sol1],{t,0,16},PlotPoints->14400,Boxed->False,Axes->None];则输出所求数值解的图形(图2.11(a)). 从图中可以看出洛伦兹微分方程组具有一个奇异吸引子, 这个吸引子紧紧地把解的图形“吸”在一起. 有趣的是, 无论把解的曲线画得多长, 这些曲线也不相交.128图2.11改变初值为,10)0(,10)0(,6)0(=-==z y x 输入sol2=NDSolve[{eq,x[0]==6,y[0]==-10,z[0]==10}, {x[t],y[t],z[t]},{t,0,24},MaxSteps->10000];g2=ParametricPlot3D[Evaluate[{x[t],y[t],z[t]}/.sol2],{t,0,24},PlotPoints->14400,Boxed->False,Axes->None];Show[GraphicsArray[{g1,g2}]];则输出所求数值解的图形(图2.11(b)). 从图中可以看出奇异吸引子又出现了, 它把解“吸”在某个区域内, 使得所有的解好象是有规则地依某种模式缠绕.实验习题1. 求下列微分方程的通解:(1) ;0136=+'+''y y y(2) ();024=+''+y y y(3) ;2sin 52x e y y y x =+'-''(4) .)1(963x e x y y y +=+'-''2. 求下列微分方程的特解:(1) ;15,0,029400='==+'+''==x x y y y y y(2) .1,1,02sin ='==++''==ππx x y yx y y 3. 求微分方程0cos 2)1(2=-+'-x xy y x 在初始条件10==x y 下的特解.分别求精确解和数值解)10(≤≤x 并作图.4. 求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++t t e y x dt dy e y x dt dx 235的通解.129 5. 求微分方程组⎪⎪⎩⎪⎨⎧==+-==-+==4,081,0300t t y y x dt dyxy x dt dx 的特解. 6. 求欧拉方程组324x y y x y x =-'+''的通解.7. 求方程5,0,011='==+'+''==x x y y y y x y 在区间[0,4]上的近似解.。
实验二、ERDAS实用菜单操作
实验二、ERDAS实用菜单操作内容一数据输入实习目的:掌握TM图像数据输入的主要方法。
实习内容:主要包括单波段TM图像数据输入、多波段组合文件的生成。
从地面站购买的TM图像数据或其它图像数据,不一定都是img格式,要通过数据输入输出得到img格式。
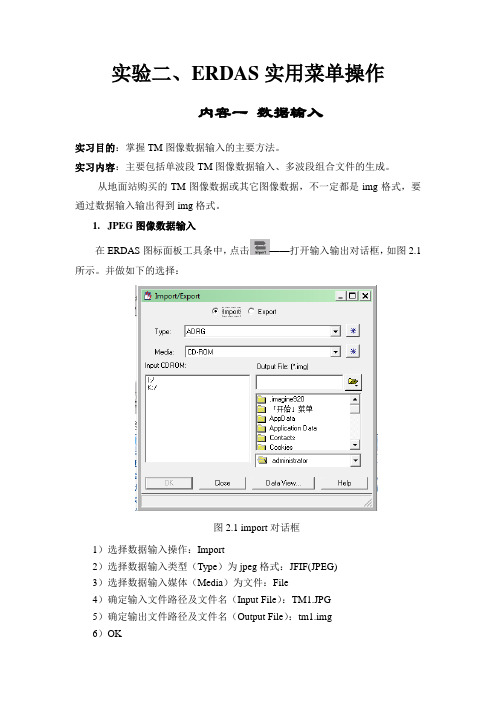
1.JPEG图像数据输入在ERDAS图标面板工具条中,点击——打开输入输出对话框,如图2.1所示。
并做如下的选择:图2.1 import对话框1)选择数据输入操作:Import2)选择数据输入类型(Type)为jpeg格式:JFIF(JPEG)3)选择数据输入媒体(Media)为文件:File4)确定输入文件路径及文件名(Input File):TM1.JPG5)确定输出文件路径及文件名(Output File):tm1.img6)OK图2.2 import对话框参数设置打开Import JFIF Files对话框,如图2.3所示图2.3 Import JFIF Files对话框在Import JFIF Files对话框中点击OK执行输入操作,完成数据输入,如图2.4所示。
图2.4 进程状态条重复上述过程,可依此将多波段数据全部输入,转换为.IMG文件。
2. 组合多波段数据为了图像处理与分析,需要将上述转换的单波段IMG文件组合为一个多波段图像文件。
第一步:在ERDAS图标面板工具条中,点击Interpreter|Utilities|Layer Stack。
出现波段叠加对话框,如图2.5所示。
图2.5 Layer Selection and Stacking对话框第二步:在Layer Selection and Stacking对话框中,依此选择并加载(Add)单波段IMG图像:1)输入单波段图像文件(Input File: *.img):tm1.img——Add2)输入单波段图像文件(Input File: *.img):tm2.img——Add重复上述步骤3)输入组合多波段图像文件(Output File:*.img):bandstack.img4)OK执行并完成波段组合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东技术师范学院实验报告学院: 计科院 专业:班级: 成绩:姓名:学号:组别:组员:实验地点: 工业中心204 实验日期:指导教师签名:实验 2 项目名称: 基本命令与工具(一)1、 实验目的学习Linux 命令的基本结构,掌握Linux 操作系统的基本命令使用方法,为进一步学习Linux 高级命令的使用做准备。
2、 实验内容2.1 回顾:UNIX 系统的基本结构硬件层尽管我们在《操作系统原理》中已经了解过UNIX 系统,但在这里仍有必要对UNIX 系统的基本结构作简单的回顾,目的是要更好地理解AIX 操作系统基本工作原理。
UNIX 系统包括两级:用户级和核心级。
用户程序通过系统调用界面获得内核的服务。
核心级中包括进程控制子系统、文件子系统,设备系统等,底层是操作系统对硬件层的控制。
如果要对UNIX 系统结构做一个最简单的划分,就是内核(kernel )和“外壳”(shell )了。
系统管理的大部分工作,都需要通过字符终端在shell下完成。
Shell就是用户使用操作系统各种功能的基本界面。
课程实验的许多内容,都是在shell中展开的。
Linux系统初始化时就会自动启动shell。
用户是通过一个所谓的字符终端去从用户登录到用户退出登录,用户输入的每个命令都要由shell接收,并由shell 去解释输入的命令。
如果用户输入的命令正确,shell会去调用相应的命令或程序,并由内核负责其执行,从而实现用户所要求的功能。
UNIX的Shell有许多种,有Bourne Shell,C Shell,Bourne-Again Shell(简称Bash,最流行的shell),korn Shell(简称k shell)。
Linux默认使用Bash,但也有使用k shell等其他shell的。
要知道现在所在系统的shell类型,可利用字符终端登录系统后用命令查看当前系统使用的shell类型:$ echo $SHELL/bin/bash2.2 字符终端的概念一谈到字符终端,许多人就会贴上“落后”的标签,毕竟图形界面已经广泛使用,有许多用户已不能接受输入命令的方式。
事实上,随着现今Linux桌面的不断发展,应用程序的逐渐丰富,因此字符终端在许多场合中并不是必须的。
不过,从上述UNIX结构中,你会发现shell在UNIX中的作用远非一个用户操作的界面那么简单。
总的来说,SHELL是一个解释器,对命令进行解释并交由内核执行,在字符终端上用户能利用SHELL语言编写具有强大系统管理功能的脚本,这些功能是图形界面说不具备的。
此外,作为一个复杂的应用程序,图形界面出错的可能性比字符终端要高得多,字符终端的稳定性在一些关键的应用场合还是很有必要的。
在字符终端下,用户是通过一定的协议实现远程登录并使用机器,主要有telnet协议和SSH协议。
由于Telnet的不安全性,Linux下多用SSH协议。
SSH 为Secure Shell 的缩写,是专为远程登录会话和其他网络服务提供安全性的协议。
参见的使用ssh协议的远程访问工具有SecureShellClient等。
2.3 命令的基本格式当你通过字符终端登录后,便进入命令提示符,命令提示符有许多表达形式,可以附带用户名和主机名称等信息,但也可以很简洁。
下图是一个典型的命令提示UNIX中一个基本命令包含三个要素:命令名、选项、参数。
本质上命令名是指用户要运行的程序的名称。
用户通过设定选项指出命令要执行的特定功能,参数是命令执行时需要的输入值。
选项和参数不是一定要填写的。
命令名、选项、参数都区分大小写,它们通过空格或制表符(TAB键)隔开。
初学者经常容易犯的一个错误是把选项和参数混淆,一般来说,选项带有符号“-”,如“-a”,而参数没有,但也有特例,在学习具体例子时会指出。
此外,选项和参数都是可以多个的。
如果需要多个选项,可把选项连续表示,如“-abc”,也可以单独表示,如“-a -b -c”,但选项间需要用空格区分开来。
多个参数也是需要用空格隔开。
为什么要用空格把命令名、参数、选项隔开?因为shell作为解释器,以空格或制表符作为间隔标志来读取命令,如果没有空格隔开,shell就会认为是一个独立的整体而对其进行解释。
下面是一些命令的例子,大家指出哪部分是命令名,选项和参数:# wc -cl /etc/inittab# find . -name "unix" –print# kill -9 230942.4 一些常用的基本命令下面介绍一些常用的基本命令,这些命令是一些日常系统管理时经常用到的工具,掌握这些命令以及下面所提及的选项是系统管理所必需的(课程要求能熟练使用)。
注意由于不同发行版本的Linux安装的shell命令有所不同,所以下面部分shell命令未必在你所使用的Linux中已安装,如遇此情况请尝试安装该命令。
(1)who命令功能:列出当前系统注册的用户,另外有whoami命令选项:无参数:无例子:注意看系统有多少人在线,并思考以下问题,如何自动统计在线人数?#who#whoami(2)ls命令功能:显示目录内容格式:ls [选项] [文件或目录]选项:-a:列出目录中所有项,包括以“.”开始的项(以点开头的为隐藏文件)-l:以列表形式显示文件-R:递归列出所有例子:注意对比三个命令的结果差异# ls -a /etc# ls -al /etc# ls -R /etc(3)pwd功能:显示当前目录选项:无例子:# pwd(4)cd命令功能:更改当前目录格式:cd [选项] [文件或目录]选项:无例子:注意三个cd命令的区别和结果# cd /proc# ls# cd ~# ls# cd ..# ls(5)stat命令和file命令功能:获得关于某文件的基本信息格式:stat 文件/ file命令例子:stat命令和file命令在功能上的差异# stat /etc/environment# file /etc/environment(6)touch命令功能:更新一个文件的访问和修改时间,如果没有对应文件则新建该文件格式:touch 文件名例子:注意前一次使用stat命令和后一次使用stat命令的返回结果的差异# cd ~# touch tt# stat tt# touch tt# stat tt(7)mv命令功能:移动或重命名文件或目录格式:mv [选项] 源文件或目录目的文件或目录选项:-b:若存在同名文件,覆盖前先备份(backup)原来的文件-f:强制(force)覆盖同名文件例子:留意最后目录中是否多了一个备份文件(文件末尾有“~”符号)# cd ~# touch ttt# touch tt# mv –b tt ttt# ls(8)cp命令功能:复制文件或目录格式:cp [选项] 源文件或源目录目的文件或目的目录选项:-f:强制(force)覆盖同名文件-b:若存在同名文件,覆盖前先备份(backup)原来的文件-r:-r选项是以递归方式复制文件# cd ~# cp a acopy# ls(9)rm命令功能:删除文件或目录格式:rm [选项] 文件或目录选项:-f:强制(force)删除文件-r:rm命令默认只删除文件,-r选项是以递归方式删除目录例子:# cd ~# touch a b c# rm a b# rm –f b(10)mkdir命令和rmdir命令功能:增加文件夹和删除文件夹格式:mkdir [选项] 目录/ rmdir选项:无例子:注意要删除的文件夹要求是空的,如果里面有文件,则使用“rm –r 文件夹”# cd ~# mkdir testdir# cd testdir# touch a b c# ls# cd ..# rmdir testdir# rm -r testdir(11)cat功能:连接或显示文件格式:ls [选项] [文件cat-ls] 选项:-n:显示行号# cat /etc/environment(12)more命令功能:分屏显示文本文件的内容。
首先显示一屏后若还有内容,按回车键再显示下一行,按空格键显示另一屏。
格式:more 文件# more /etc/environment(13)tail命令功能:显示文本文件的结尾部分,默认显示文件的最后10行格式:tail [选项] [行数] [文件]选项:-n:指定显示的行数# tail -n 5 /etc/environment(14)grep命令功能:从指定文件或标准输出中中查找符合条件的字符串。
格式:grep [选项] 字符串文件列表例子:# grep init /etc/inittab(15)wc(WordCount)命令功能:依次显示文本文件的行数、字数和字符数格式:wc [选项] 文件列表选项:-c(character):显示文件的字节数-l(line):显示文件的行数-w(word):显示文件的单词数例子:# wc /etc/inittab# wc -l /etc/profile /etc/environment(16)date命令功能:查看或修改系统时间格式:date例子:# date(17)clear命令功能:清除当前终端的屏幕内容格式:clear例子:# clear(18)man(manual)命令功能:显示对应命令的帮助手册格式:man 命令名例子:查询一个命令有哪些选项可以简单的采用--help选项,但最完整的信息在该命令的manual中。
# man cat# cat --help(19)history命令功能:查看shell命令的历史记录,如果不使用数字参数,则将查看所有shell命令的历史记录。
如果使用数字参数,则将查看最近执行过指定个数的shell命令。
# history# history 52.3 vi工具的使用在系统管理工作中,经常需要阅读各类配置文件、日志和说明手册,同时也需要编写各种脚本以满足系统管理的需要。
vi编辑器相当于Windows中的“记事本”,但由于是在字符终端下使用编辑器,因此其使用方法与图形界面上的编辑器的使用方法有所不同(最大的不同是鼠标没用了)。
vi编辑器是系统管理员必须熟练掌握的基本工具之一。
UNIX下还有许多编辑器供人们使用,如vim(vi 的变种)、Emacs等。
感兴趣的同学可以查阅相关资料。
vi编辑器有三种工作模式:命令模式、文本编辑模式、最后行模式。
下面分别对该三种模式进行讨论。
(1)命令模式vi编辑器启动后即进入命令模式,vi的命令往往只有一个字母,而且按下该命令的字母后也不会在屏幕上显示,而是直接处理该命令。
常用的命令有:i:从当前的光标位置开始输入字符,vi编辑器进入文本编辑模式a:从当前的光标的下一个位置开始输入字符,vi编辑器进入文本编辑模式o:在光标所在行之下新增一行u:撤销上一步操作/字符串:按下“/”键后,屏幕底部出现“/”,在其后输入要查找的字符串,按Enter后,vi讲从光标当前位置开始向文件尾查找,并定位在第一个匹配的单词的地方。
