2004美国数学竞赛题更正
美国大学生数学建模竞赛数据及评阅分析_吴孟达
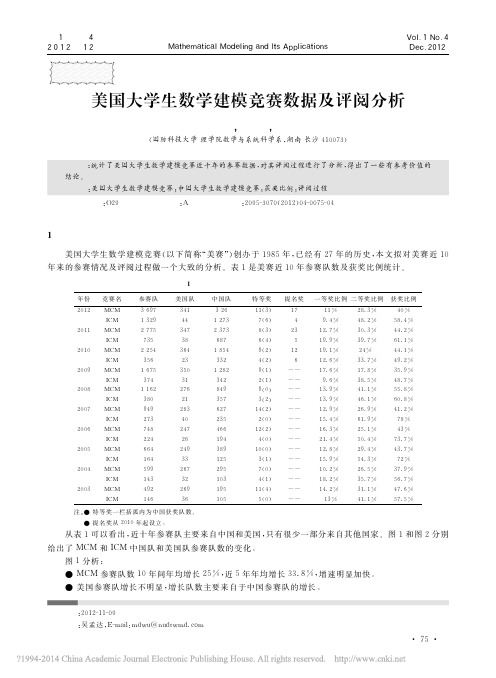
给出了 MCM 和ICM 中国队和美国队参赛队数的变化。
图1分析:
● MCM 参赛队数10年间年均增长25%,近5年年均增长33.8%,增速明显加快。
● 美国参赛队增长不明显,增长队数主要来自于中国参赛队的增长。
收 稿 日 期 :2012-11-09 通 讯 作 者 :吴 孟 达 ,E-mail:mdwu@nudtwmd.com
摘 要:统计了美国大学生数学建模竞赛近十年的参赛数据,对其评阅过程进行 了 分 析,得 出 了 一 些 有 参 考 价 值 的 结论。 关 键 词 :美 国 大 学 生 数 学 建 模 竞 赛 ;中 国 大 学 生 数 学 建 模 竞 赛 ;获 奖 比 例 ;评 阅 过 程
中 图 分 类 号 :O29 文 献 标 志 码 :A 文 章 编 号 :2095-3070(2012)04-0075-04
3 26 1 273 2 373 687 1 854 332 1 282 342 849 357 627 235 466 194 389 125 295 103 195 105
11(3) 7(6) 8(3) 6(4) 9(2) 4(2) 9(1) 2(1) 9(0) 3(2)
图2 ICM 参赛队数变化图 图3 MCM 获奖比例 图4 ICM 获奖比例
2 评 阅 过 程 分 析
据 美 赛 “评 委 评 论 ”介 绍 ,美 赛 评 阅 过 程 大 致 分 为 三 轮 。 第一轮可以称为“淘汰轮(the Triage Round)”。此轮评阅主要以摘要信息以及论文整体结构为 评 判 依 据 ,时 间 大 约 是 5~10 分 钟 。 每 个 评 委 以 “通 过 ”、“不 通 过 ”计 分 ,事 先 应 当 设 置 有 大 致 的 “通 过 ”比 例 (此 轮 与 国内研赛的网评阶段相类似)。当两位 评 委 意 见 不 一 致 时 可 以 协 商 达 成 一 致 意 见,如 果 仍 不 能 达 成 一 致 意 见 ,则 请 第 三 位 评 委 评 阅 。 有 “评 论 ”介 绍 说 ,这 一 轮 的 淘 汰 率 大 约 为 45% ,通 过 这 一 轮 评 审 的 参 赛 队 大 约 有 80% 的 获 奖 概 率 。 关 于 如 何 通 过 这 一 轮 评 审 ,评 委 给 出 的 建 议 是 : 1)摘 要 至 关 重 要 ,必 须 清 晰 且 信 息 量 充 分 。 评 委 关 心 的 是 你 对 问 题 的 理 解 是 否 准 确 ,你 建 立 的 模 型 及 使 用的方法是否恰当,以及根据你所建模型得到的主要结果和主要结论是否合理 。 过 于 冗 长 的 技 术 性 描 述 将 · 76 ·
历届美国数学建模竞赛赛题(汉语版)

历届美国数学建模竞赛赛题, 1985-2006AMCM1985问题-A 动物群体的管理AMCM1985问题-B 战购物资储备的管理AMCM1986问题-A 水道测量数据AMCM1986问题-B 应急设施的位置AMCM1987问题-A 盐的存贮AMCM1987问题-B 停车场AMCM1988问题-A 确定毒品走私船的位置AMCM1988问题-B 两辆铁路平板车的装货问题AMCM1989问题-A 蠓的分类AMCM1989问题-B 飞机排队AMCM1990问题-A 药物在脑内的分布AMCM1990问题-B 扫雪问题AMCM1991问题-A 估计水塔的水流量AMCM1992问题-A 空中交通控制雷达的功率问题AMCM1992问题-B 应急电力修复系统的修复计划AMCM1993问题-A 加速餐厅剩菜堆肥的生成AMCM1993问题-B 倒煤台的操作方案AMCM1994问题-A 住宅的保温AMCM1994问题-B 计算机网络的最短传输时间AMCM1995问题-A 单一螺旋线AMCM1995问题-B A1uacha Balaclava学院AMCM1996问题-A 噪音场中潜艇的探测AMCM1996问题-B 竞赛评判问题AMCM1997问题-A Velociraptor(疾走龙属)问题AMCM1997问题-B为取得富有成果的讨论怎样搭配与会成员AMCM1998问题-A 磁共振成像扫描仪AMCM1998问题-B 成绩给分的通胀AMCM1999问题-A 大碰撞AMCM1999问题-B “非法”聚会AMCM1999问题- C 大地污染AMCM2000问题-A空间交通管制AMCM2000问题-B: 无线电信道分配AMCM2000问题-C:大象群落的兴衰AMCM2001问题- A: 选择自行车车轮AMCM2001问题-B:逃避飓风怒吼(一场恶风…)AMCM2001问题-C我们的水系-不确定的前景AMCM2002问题-A风和喷水池AMCM2002问题-B航空公司超员订票AMCM2002问题-C蜥蜴问题AMCM2003问题-A: 特技演员AMCM2003问题-C航空行李的扫描对策AMCM2004问题-A:指纹是独一无二的吗?AMCM2004问题-B:更快的快通系统AMCM2004问题-C:安全与否?AMCM2005问题-A:.水灾计划AMCM2005问题-B:TollboothsAMCM2005问题-C:.Nonrenewable ResourcesAMCM2006问题-A:用于灌溉的自动洒水器的安置和移动调度AMCM2006问题-B:通过机场的轮椅AMCM2006问题-C:在与HIV/爱滋病的战斗中的交易AMCM85问题-A 动物群体的管理在一个资源有限,即有限的食物、空间、水等等的环境里发现天然存在的动物群体。
amc12数学题

amc12数学题篇一:AMC12数学题是指美国数学竞赛(AMC)12级的数学题目。
AMC12是一项面向高中生的数学竞赛,旨在鼓励学生对数学的深入学习和探索。
这些数学题目涵盖了广泛的数学概念和技巧,并要求学生通过逻辑推理和解题技巧来解决问题。
AMC12数学题的难度较高,常常需要学生具备扎实的数学基础和解题能力。
这些题目涉及的数学领域包括代数、几何、数论和概率等。
许多题目都要求学生运用多个数学概念进行综合分析和解答。
因此,参加AMC12数学竞赛是考验学生数学能力和解题能力的良好机会。
解答AMC12数学题需要学生具备良好的数学思维和解题技巧。
学生需要能够正确理解问题并找出解决问题的方法。
在解答过程中,学生需要通过分析和推理来得出结论,同时要注意细节和逻辑的严谨性。
有时候,解答AMC12数学题还需要一些创造性思维和巧妙的数学变换。
参加AMC12数学竞赛对学生有很多好处。
首先,它可以提高学生的数学能力和解题能力,培养学生的数学思维和分析能力。
其次,参加竞赛可以增强学生对数学的兴趣和热爱,激发学生对数学的探索欲望。
此外,竞赛还可以培养学生的竞争意识和团队合作精神。
最重要的是,参加AMC12数学竞赛可以为学生在大学申请中增加一份优势,显示出学生在数学方面的才能和成就。
总之,AMC12数学题是一系列挑战性的数学问题,要求学生具备扎实的数学基础和解题能力。
通过参加AMC12数学竞赛,学生能够提高数学能力,培养数学思维,并为将来的学术和职业发展奠定坚实的基础。
篇二:AMC12(美国数学竞赛12级)是由美国数学协会举办的一项数学竞赛,面向高中学生。
这项竞赛旨在鼓励学生培养解决复杂数学问题的能力,并提供一个展示自己数学才能的平台。
AMC12数学题目通常涵盖广泛的数学领域,包括代数、几何、概率与统计、数论等。
这些题目要求学生在有限的时间内思考、分析和解决问题,考察他们的数学思维能力、推理能力和解决问题的能力。
举一个例子,假设有一道AMC12的几何问题:如图所示,一个直径为12的圆与一个半径为8的圆相切。
美国数学竞赛AMC题目及答案

2.3.What is the value of ?4.Eight friends ate at a restaurant and agreed to share the bill equally. Because Judi forgot her money, each of her seven friends paid an extra $2.50 to cover her portion of the total bill. What was the total bill?5.Hammie is in the grade and weighs 106 pounds. His quadruplet sisters are tiny babies and weigh 5, 5, 6, and 8 pounds. Which is greater, the average (mean) weight of these five children or the median weight, and by how many pounds?6.The number in each box below is the product of the numbers in the two boxes that touch it in the row above. For example, . What is the missing number in the top row?7.Trey and his mom stopped at a railroad crossing to let a train pass. As the train began to pass, Trey counted 6 cars in the first 10 seconds. It took the train 2 minutes and 45 seconds to clear the crossing at a constant speed. Which of the following was the most likely number of cars in the train?8.A fair coin is tossed 3 times. What is the probability of at least two consecutive heads?9.The Incredible Hulk can double the distance he jumps with each succeeding jump. If his first jump is 1 meter, the second jump is 2 meters, the third jump is 4 meters, and so on, then on which jump will he first be able to jump more than 1 kilometer?10.What is the ratio of the least common multiple of 180 and 594 to the greatest common factor of 180 and 594?11. Ted's grandfather used his treadmill on 3 days this week. He went 2 miles each day. On Monday he jogged at a speed of 5 miles per hour. He walked at the rate of 3 miles per hour on Wednesday and at 4 miles per hour on Friday. If Grandfather had always walked at 4 miles per hour, he would have spent less time on the treadmill. How many minutes less?12. At the 2013 Winnebago County Fair a vendor is offering a "fair special" on sandals. If you buy one pair of sandals at the regular price of $50, you get a second pair at a 40% discount, and a third pair at half the regular price. Javier took advantage of the "fair special" to buy three pairs of sandals. What percentage of the $150 regular price did he save?13. When Clara totaled her scores, she inadvertently reversed the units digit and the tens digit of one score. By which of the following might her incorrect sum have differed from the correct one?14. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .15. If , , and , what is the product of , , and ?16. A number of students from Fibonacci Middle School are taking part in a community service project. The ratio of -graders to -graders is , and the the ratio of -graders to -graders is . What is the smallest number of students that could be participating in the project?17. The sum of six consecutive positive integers is 2013. What is the largest of these six integers?18. Isabella uses one-foot cubical blocks to build a rectangular fort that is 12 feet long, 10 feet wide, and 5 feet high. The floor and the four walls are all one foot thick. How many blocks does the fort contain?--Arpanliku 16:22, 27 November 2013 (EST) Courtesy of Lord.of.AMC19. Bridget, Cassie, and Hannah are discussing the results of their last math test. Hannah shows Bridget and Cassie her test, but Bridget and Cassie don't show theirs to anyone. Cassie says, 'I didn't get the lowest score in our class,' and Bridget adds, 'I didn't get the highest score.' What is the ranking of the three girls from highest to lowest?20. A rectangle is inscribed in a semicircle with longer side on the diameter. What is the area of the semicircle?21. Samantha lives 2 blocks west and 1 block south of the southwest corner of City Park. Her school is 2 blocks east and 2 blocks north of the northeast corner of City Park. On school days she bikes on streets to the southwest corner of City Park, then takes a diagonal path through the park to the northeast corner, and then bikes on streets to school. If her route is as short as possible, how many different routes can she take?22. Toothpicks are used to make a grid that is 60 toothpicks long and 32 toothpicks wide. How many toothpicks are used altogether?23. Angle of is a right angle. The sides of are the diameters of semicircles as shown. The area of the semicircle on equals , and the arc of the semicircle on has length .What is the radius of the semicircle on ?24. Squares , , and are equal in area. Points and are the midpoints of sidesand , respectively. What is the ratio of the area of the shaded pentagon to the sum of the areas of the three squares?25. A ball with diameter 4 inches starts at point A to roll along the track shown. The track is comprised of 3 semicircular arcs whose radii are inches, inches, and inches, respectively. The ball always remains in contact with the track and does not slip. What is the distance the center of theball travels over the course from A to B?1.2.The 50% off price of half a pound of fish is $3, so the 100%, or the regular price, of a half pound of fish is $6. Consequently, if half a pound of fish costs $6, then a whole pound of fish is dollars.3.Notice that we can pair up every two numbers to make a sum of 1:Therefore, the answer is .4.Each of her seven friends paid to cover Judi's portion. Therefore, Judi's portion must be . Since Judi was supposed to pay of the total bill, the total bill must be .5.The median here is obviously less than the mean, so option (A) and (B) are out.Lining up the numbers (5, 5, 6, 8, 106), we see that the median weight is 6 pounds.The average weight of the five kids is .Therefore, the average weight is bigger, by pounds, making the answer.6.Solution 1: Working BackwardsLet the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We see that , making .It follows that , so .Solution 2: Jumping Back to the StartAnother way to do this problem is to realize what makes up the bottommost number. This method doesn't work quite as well for this problem, but in a larger tree, it might be faster. (In this case, Solution 1 would be faster since there's only two missing numbers.)Again, let the value in the empty box in the middle row be , and the value in the empty box in the top row be . is the answer we're looking for.We can write some equations:Now we can substitute into the first equation using the two others:7.If Trey saw , then he saw .2 minutes and 45 seconds can also be expressed as seconds.Trey's rate of seeing cars, , can be multiplied by on the top and bottom (and preserve the same rate):. It follows that the most likely number of cars is . Solution 2minutes and seconds is equal to .Since Trey probably counts around cars every seconds, there are groups of cars that Trey most likely counts. Since , the closest answer choice is .8.First, there are ways to flip the coins, in order.The ways to get two consecutive heads are HHT and THH.The way to get three consecutive heads is HHH.Therefore, the probability of flipping at least two consecutive heads is .9.This is a geometric sequence in which the common ratio is 2. To find the jump that would be over a 1000 meters, we note that .However, because the first term is and not , the solution to the problem is10. To find either the LCM or the GCF of two numbers, always prime factorize first.The prime factorization of .The prime factorization of .Then, find the greatest power of all the numbers there are; if one number is one but not the other, use it (this is ). Multiply all of these to get 5940.For the GCF of 180 and 594, use the least power of all of the numbers that are in both factorizations and multiply. = 18.Thus the answer = = .We start off with a similar approach as the original solution. From the prime factorizations, the GCF is .It is a well known fact that . So we have,.Dividing by yields .Therefore, .11. We use that fact that . Let d= distance, r= rate or speed, and t=time. In this case, let represent the time.On Monday, he was at a rate of . So, .For Wednesday, he walked at a rate of . Therefore, .On Friday, he walked at a rate of . So, .Adding up the hours yields + + = .We now find the amount of time Grandfather would have taken if he walked at per day. Set up the equation, .To find the amount of time saved, subtract the two amounts: - = . To convert this to minutes, we multiply by .Thus, the solution to this problem is12. First, find the amount of money one will pay for three sandals without the discount. We have.Then, find the amount of money using the discount: .Finding the percentage yields .To find the percent saved, we have13. Let the two digits be and .The correct score was . Clara misinterpreted it as . The difference between the two is which factors into . Therefore, since the difference is a multiple of 9, the only answerchoice that is a multiple of 9 is .14. The probability that both show a green bean is . The probability that both show a red bean is . Therefore the probability is15.Therefore, .Therefore, .To most people, it would not be immediately evident that , so we can multiply 6's until we get the desired number:, so .Therefore the answer is .16. Solution 1: AlgebraWe multiply the first ratio by 8 on both sides, and the second ratio by 5 to get the same number for 8th graders, in order that we can put the two ratios together:Therefore, the ratio of 8th graders to 7th graders to 6th graders is . Since the ratio is in lowest terms, the smallest number of students participating in the project is .Solution 2: FakesolvingThe number of 8th graders has to be a multiple of 8 and 5, so assume it is 40 (the smallest possibility). Then there are 6th graders and 7th graders. The numbers of students is17. Solution 1The mean of these numbers is . Therefore the numbers are, so the answer isSolution 2Let the number be . Then our desired number is .Our integers are , so we have that.Solution 3Let the first term be . Our integers are . We have,18. Solution 1There are cubes on the base of the box. Then, for each of the 4 layers above the bottom (as since each cube is 1 foot by 1 foot by 1 foot and the box is 5 feet tall, there are 4 feet left), there arecubes. Hence, the answer is .Solution 2We can just calculate the volume of the prism that was cut out of the original box. Each interior side of the fort will be feet shorter than each side of the outside. Since the floor is foot, the height will be feet. So the volume of the interior box is .The volume of the original box is . Therefore, the number of blocks contained inthe fort is .19. If Hannah did better than Cassie, there would be no way she could know for sure that she didn't get the lowest score in the class. Therefore, Hannah did worse than Cassie. Similarly, if Hannah did worse than Bridget, there is no way Bridget could have known that she didn't get the highest in the class.Therefore, Hannah did better than Bridget, so our order is .20.A semicircle has symmetry, so the center is exactly at the midpoint of the 2 side on the rectangle, making the radius, by the Pythagorean Theorem, . The area is .21.The number of ways to get from Samantha's house to City Park is , and the number of ways toget from City Park to school is . Since there's one way to go through City Park (just walking straight through), the number of different ways to go from Samantha's house to City Park to school .22. There are vertical columns with a length of toothpicks, and there are horizontal rows with a length of toothpicks. An effective way to verify this is to try a small case, i.e. a grid of toothpicks.Thus, our answer is .23. Solution 1If the semicircle on AB were a full circle, the area would be 16pi. Therefore the diameter of the first circle is 8. The arc of the largest semicircle would normally have a complete diameter of 17. The Pythagoreantheorem says that the other side has length 15, so the radius is .Solution 2We go as in Solution 1, finding the diameter of the circle on AC and AB. Then, an extended version of the theorem says that the sum of the semicircles on the left is equal to the biggest one, so the area of thelargest is , and the middle one is , so the radius is .24.First let (where is the side length of the squares) for simplicity. We can extend until it hits theextension of . Call this point . The area of triangle then is The area of rectangle is . Thus, our desired area is . Now, the ratio of the shaded area to thecombined area of the three squares is .Let the side length of each square be .Let the intersection of and be .Since , . Since and are vertical angles, they are congruent. We also have by definition.So we have by congruence. Therefore, .Since and are midpoints of sides, . This combined with yields.The area of trapezoid is .The area of triangle is .So the area of the pentagon is .The area of the squares is .Therefore, .Let the intersection of and be .Now we have and .Because both triangles has a side on congruent squares therefore .Because and are vertical angles .Also both and are right angles so .Therefore by AAS(Angle, Angle, Side) .Then translating/rotating the shaded into the position ofSo the shaded area now completely covers the squareSet the area of a square asTherefore, .25. Solution 1The radius of the ball is 2 inches. If you think about the ball rolling or draw a path for the ball (see figure below), you see that in A and C it loses inches, and it gains inches on B.So, the departure from the length of the track means that the answer is . Solution 2The total length of all of the arcs is . Since we want the path from the center, the actual distance will be shorter. Therefore, the only answer choice less than is . Thissolution may be invalid because the actual distance can be longer if the path the center travels is on the outside of the curve, as it is in the middle bump.古希腊哲学大师亚里士多德说:人有两种,一种即“吃饭是为了活着”,一种是“活着是为了吃饭”.一个人之所以伟大,首先是因为他有超于常人的心。
美国数学建模竞赛题目(1985--2009年)

美国数学建模竞赛题目1985年:A题:动物群体的管理B题:战略物资储备的管理问题1986年:A题:海底地型测量问题B题:应急设施的优化选址问题1987年:A题:堆盐问题(盐堆稳定性问题)B题:停车场安排问题1988年:A题:确定毒品走私船位置B题:平板列车车厢的优化装载1989年:A题:蠓虫识别问题;最佳分类与隔离B题:飞机排队模型1990年:A题:脑中多巴胺的分布B题:铲雪车的路径与效率问题1991年:A题:估计水塔的水流量B题:通信网络费用问题1992年:A题:雷达系统的功率与设计式样B题:紧急修复系统的研制1993年:A题:堆肥问题B题:煤炭装卸场的最优操作1994年:A题:保温房屋设计问题B题:计算机网络的最小接通时间1996年:A题:大型水下物体的探测B题:快速遴选优胜者问题1997年:A题:恐龙捕食问题B题:会议混合安排问题1998年:A题:MRI图象处理问题B题:分数贬值问题1999年:A题:小星体撞击地球问题B题:公用设施的合法容量问题C题:确定环境污染的物质、位置、数量和时间的问题2000年:A题:空间交通管制B题:无线电信道分配C题:大象群落的兴衰2001年:A题:选择自行车车轮B题:逃避飓风怒吼C题:我们的水系-不确定的前景2002年:A题:风和喷水池B题:航空公司超员订票C题:如果我们过分扫荡自己的土地,将会失去各种各样的蜥蜴。
2003年:A题:特技演员B题:Gamma刀治疗方案C题:航空行李的扫描对策2004年:A题:指纹是独一无二的吗?B题:更快的快通系统C题:安全与否?2005年:A题:flood planningB题:tollboothsC题: Nonrenewable Resources2006年:A题:Positioning and Moving SprinklerSystems for IrrigationB题:Wheel Chair Access at AirportsC题:Trade-offs in the fight againstHIV/AIDS2007年:A题:GerrymanderingB题:The Airplane Seating ProblemC题:Organ Transplant: The Kidney Exchange Problem2008年:A题:Take a BathB题:Creating Sudoku PuzzlesC题:Finding the Good in Health Care Systems2009年:A题:Designing a Traffic CircleB题:Energy and the Cell PhoneC题:Creating Food Systems: Re-Balancing Human-Influenced Ecosystems。
AMC 美国数学竞赛 2004 AMC 10B 试题及答案解析

2004 AMC 10BProblem 1Each row of the Misty Moon Amphitheater has 33 seats. Rows 12 through 22 are reserved for a youth club. How many seats are reserved for this club?SolutionThere are rows of seats, giving seats.Problem 2How many two-digit positive integers have at least one 7 as a digit?SolutionTen numbers () have as the tens digit. Nine numbers () have it as the ones digit. Number is in both sets. Thus the result is .Problem 3At each basketball practice last week, Jenny made twice as many free throws as she made at the previous practice. At her fifth practice she made 48 free throws. How many free throws did she make at the first practice?SolutionAt the fourth practice she made throws, at the third one it was , then we get throws for the second practice, and finally throws at the first one.Problem 4A standard six-sided die is rolled, and P is the product of the five numbers that are visible. What is the largest number that is certain to divide P?Solution 1The product of all six numbers is . The products of numbers that can be visible are , , ..., . The answer to this problem is their greatest common divisor -- which is , where is the least common multiple of . Clearly and the answer is .Solution 2Clearly, can not have a prime factor other than , and .We can not guarantee that the product will be divisible by , as the number can end on the bottom.We can guarantee that the product will be divisible by (one of and will always be visible), but not by .Finally, there are three even numbers, hence two of them are always visible and thus the product is divisible by . This is the most we can guarantee, as when the is on the bottom side, the two visible even numbers are and , and their product is not divisible by .Hence .SolutionProblem 5In the expression , the values of , , , and are , , , and , although not necessarily in that order. What is the maximum possible value of the result?SolutionIf or , the expression evaluates to .If , the expression evaluates to .Case remains.In that case, we want to maximize where .Trying out the six possibilities we get that the best one is, where .Problem 6Which of the following numbers is a perfect square?SolutionUsing the fact that , we can write:▪▪▪▪▪Clearly is a square, and as , , and are primes, none of the other four are squares.Problem 7On a trip from the United States to Canada, Isabella took U.S.dollars. At the border she exchanged them all, receiving Canadian dollars for every U.S. dollars. After spending Canadian dollars, she had Canadian dollars left. What is the sum of the digits of ?SolutionSolution 1Isabella had Canadian dollars. Setting up an equation we get , which solves to , and the sum of digits of isSolution 2Each time Isabelle exchanges U.S. dollars, she gets Canadian dollars and Canadian dollars extra. Isabelle received a total of Canadian dollars extra, therefore she exchanged U.S. dollars times. Thus .Problem 8Minneapolis-St. Paul International Airport is 8 miles southwest of downtown St. Paul and 10 miles southeast of downtown Minneapolis. Which of the following is closest to the number of miles between downtown St. Paul and downtown Minneapolis?SolutionThe directions "southwest" and "southeast" are orthogonal. Thus the described situation is a right triangle with legs 8 miles and 10 miles long. The hypotenuse length is , and thus the answeris .Without a calculator one can note that . Problem 9A square has sides of length 10, and a circle centered at one of its vertices has radius 10. What is the area of the union of the regions enclosed by the square and the circle?SolutionThe area of the circle is , the area of the square is .Exactly of the circle lies inside the square. Thus the total area is.Problem 10A grocer makes a display of cans in which the top row has one can and each lower row has two more cans than the row above it. If the display contains cans, how many rows does it contain?SolutionThe sum of the first odd numbers is . As in our case , we have .Problem 11Two eight-sided dice each have faces numbered 1 through 8. When the dice are rolled, each face has an equal probability of appearing on the top. What is the probability that the product of the two top numbers is greater than their sum?SolutionSolution 1We have , hence if at least one of the numbers is , the sum is larger. There such possibilities.We have .For we already have , hence all other cases are good.Out of the possible cases, we found that in the sum is greater than or equal to the product, hence in it is smaller. Therefore the answer is .Solution 2Let the two rolls be , and .From the restriction:Since and are non-negative integers between and , either , , orif and only if or .There are ordered pairs with , ordered pairs with , and ordered pair with and . So, there areordered pairs such that .if and only if and or equivalently and . This gives ordered pair .So, there are a total of ordered pairs with .Since there are a total of ordered pairs , there are ordered pairs with .Thus, the desired probability is .Problem 12An annulus is the region between two concentric circles. The concentric circles in the figure have radii and , with . Let be a radius of the larger circle, let be tangent to the smaller circle at , and let be the radius of the larger circle that contains . Let , , and . What is the area of the annulus?SolutionThe area of the large circle is , the area of the small one is , hence the shaded area is .From the Pythagorean Theorem for the right triangle we have , hence and thus the shaded area is . Problem 13In the United States, coins have the following thicknesses: penny, mm; nickel, mm; dime, mm; quarter, mm. If a stack of these coins is exactly mm high, how many coins are in the stack?SolutionAll numbers in this solution will be in hundreds of a millimeter.The thinnest coin is the dime, with thickness . A stack of dimes has height .The other three coin types have thicknesses , , and . By replacing some of the dimes in our stack by other, thicker coins, we can clearly create exactly all heights in the set.If we take an odd , then all the possible heights will be odd, and thus none of them will be . Hence is even.If the stack will be too low and if it will be too high. Thus we are left with cases and .If the possible stack heights are , with the remaining ones exceeding .Therefore there are coins in the stack.Using the above observation we can easily construct such a stack. A stack of dimes would have height , thus we need to add . This can be done for example by replacing five dimes by nickels (for ), and one dime by a penny (for ).Problem 14A bag initially contains red marbles and blue marbles only, with moreblue than red. Red marbles are added to the bag until only of the marbles in the bag are blue. Then yellow marbles are added to the baguntil only of the marbles in the bag are blue. Finally, the number of blue marbles in the bag is doubled. What fraction of the marbles now in the bag are blue?SolutionWe can ignore most of the problem statement. The only important information is that immediately before the last step blue marbles formed of the marbles in the bag. This means that there were blue and other marbles, for some . When we double the number ofblue marbles, there will be blue and other marbles, hence blue marbles now form of all marbles in the bag.Problem 15Patty has coins consisting of nickels and dimes. If her nickels were dimes and her dimes were nickels, she would have cents more. How much are her coins worth?SolutionSolution 1She has nickels and dimes. Their total cost iscents. If the dimes were nickels and vice versa, she would havecents. This value should be cents more than the previous one. We get , which solves to . Her coins are worth .Solution 2Changing a nickel into a dime increases the sum by cents, and changing a dime into a nickel decreases it by the same amount. As the sum increased by cents, there are more nickels than dimes. As the total count is , this means that there are nickels and dimes.Problem 16Three circles of radius are externally tangent to each other and internally tangent to a larger circle. What is the radius of the large circle?SolutionThe situation in shown in the picture below. The radius we seek is . Clearly . The point is clearly the center of the equilateral triangle , thus is of the altitude of this triangle. We get that . Therefore the radius we seek is.WARNING. Note that the answer does not correspond to any of the five options. Most probably there is a typo in option D.Problem 17The two digits in Jack's age are the same as the digits in Bill's age, but in reverse order. In five years Jack will be twice as old as Bill will be then. What is the difference in their current ages?SolutionSolution 1If Jack's current age is , then Bill's current age is .In five years, Jack's age will be and Bill's age will be .We are given that . Thus .For we get . For and the value is not an integer, and for it is more than . Thus the only solution is , and the difference in ages is .Solution 2Age difference does not change in time. Thus in five years Bill's age will be equal to their age difference.The age difference is , hence it is a multiple of . Thus Bill's current age modulo must be .Thus Bill's age is in the set .As Jack is older, we only need to consider the cases where the tens digit of Bill's age is smaller than the ones digit. This leaves us with the options .Checking each of them, we see that only works, and gives the solution .Problem 18In the right triangle , we have , , and . Points , , and are located on , , and , respectively, so that , , and . What is the ratio of the area of to that of ?SolutionFirst of all, note that , and therefore.Draw the height from onto as in the picture below:Now consider the area of . Clearly the triangles and are similar, as they have all angles equal. Their ratio is ,hence . Now the area of can be computed as= . Similarly we can find that as well.Hence , and the answer is .Problem 19In the sequence , , , , each term after the third is found by subtracting the previous term from the sum of the two terms that precede that term. For example, the fourth term is. What is the term in this sequence?SolutionSolution 1We already know that , , , and . Let's compute the next few terms to get the idea how the sequence behaves. We get ,, , and so on.We can now discover the following pattern: and . This is easily proved by induction. It follows that.Solution 2Note that the recurrence can be rewritten as.Hence we get that and also From the values given in the problem statement we see that .From we get that .From we get that .Following this pattern, we get.Problem 20In points and lie on and , respectively. If and intersect at so that and , what isSolutionSolution (Triangle Areas)We use the square bracket notation to denote area.Without loss of generality, we can assume . Then , and . We have , so we need to find the area of quadrilateral .Draw the line segment to form the two triangles and . Let , and . By considering trianglesand , we obtain , and by considering triangles and , we obtain . Solving, we get , , so the area of quadrilateral is .ThereforeSolution (Mass points)The presence of only ratios in the problem essentially cries out for mass points.As per the problem, we assign a mass of to point , and a mass of to . Then, to balance and on , has a mass of .Now, were we to assign a mass of to and a mass of to , we'd have . Scaling this down by (to get , which puts and in terms of the masses of and ), we assign a mass of to and a mass of to .Now, to balance and on , we must give a mass of . Finally, the ratio of to is given by the ratio of the mass of tothe mass of , which is .Solution (Coordinates)Affine transformations preserve ratios of distances, and for any pair of triangles there is an affine transformation that maps the first one onto the second one. This is why the answer is the same for any , and we just need to compute it for any single triangle.We can choose the points , , and . This way we will have , and . The situation is shown in the picture below:The point is the intersection of the lines and . The points on the first line have the form , the points on the second line have the form . Solving for we get , hence.The ratio can now be computed simply by observing the coordinates of , , and :Problem 21Let ; ; and ; ; be two arithmetic progressions. The set is the union of the first terms of each sequence. How many distinct numbers are in ?SolutionThe two sets of terms are and.Now . We can compute. We will now find .Consider the numbers in . We want to find out how many of them lie in . In other words, we need to find out the number of valid values of for which .The fact "" can be rewritten as ", and ".The first condition gives , the second one gives .Thus the good values of are , and their count is .Therefore , and thus .Problem 22A triangle with sides of 5, 12, and 13 has both an inscribed and a circumscribed circle. What is the distance between the centers of those circles?SolutionThis is obviously a right triangle. Pick a coordinate system so that the right angle is at and the other two vertices are at and .As this is a right triangle, the center of the circumcircle is in the middle of the hypotenuse, at .The radius of the inscribed circle can be computed using the well-known identity , where is the area of the triangle and its perimeter. In our case, and , thus . As the inscribed circle touches both legs, its center must be at .The distance of these two points is then.Problem 23Each face of a cube is painted either red or blue, each with probability 1/2. The color of each face is determined independently. What is the probability that the painted cube can be placed on a horizontal surface so that the four vertical faces are all the same color?SolutionLabel the six sides of the cube by numbers to as on a classic dice. Then the "four vertical faces" can be: , , or .Let be the set of colorings where are all of the same color, similarly let and be the sets of good colorings for the other two sets of faces.There are possible colorings, and there are goodcolorings. Thus the result is . We need to compute .Using the Principle of Inclusion-Exclusion we can writeClearly , as we have two possibilities for the common color of the four vertical faces, and two possibilities for each of the horizontal faces.What is ? The faces must have the same color, and at the same time faces must have the same color. It turns out thatthe set containing just the two cubes where all six faces have the same color.Therefore , and the result is .Problem 24In we have , , and . Point is on the circumscribed circle of the triangle so that bisects . What is the value of ?SolutionProblem 25A circle of radius is internally tangent to two circles of radius at points and , where is a diameter of the smaller circle. What is the area of the region, shaded in the picture, that is outside the smaller circle and inside each of the two larger circles?SolutionThe area of the small circle is . We can add it to the shaded region, compute the area of the new region, and then subtract the area of the small circle from the result.Let and be the intersections of the two large circles. Connect them to and to get the picture below:Now obviously the triangles and are equilateral with side .Take a look at the bottom circle. The angle is , hence the sector is of the circle. The same is true for the sector of the bottom circle, and sectors and of the top circle.If we now sum the areas of these four sectors, we will almost get the area of the new shaded region - except that each of the two equilateral triangles will be counted twice.Hence the area of the new shaded region is, and the area of the original shared region is .- 21 -。
美国大联盟数学竞赛答题填写要求

美国大联盟数学竞赛答题填写要求美国大联盟数学竞赛分成不同的年级组,答题卡的要求略有不同。
3-9年纪年级学生使用答题说明如下:必须使用2B铅笔在答题卡上填涂。
答题卡填涂要求:1.机读卡基本信息填写用笔不限,准考证号码和作答区域必须使用2B铅笔进行填涂,如需修改,一定用橡皮擦拭干净,不要留下原填涂痕迹,以免造成误判。
2.机读卡必须保持卷面整洁,不可折叠,不允许使用修正带或涂改液,右侧和下侧条形码决不允许涂抹,如遇到以上情况,考生机读卡将无法识别,会出现无分或0分现象。
3.涂卡说明:(1)姓名:填写考生姓名,不能写昵称;学校:填写考生的公立学校;年级:填写考生参赛的年级。
填写这三项时可使用铅笔或者签字笔。
(2)考号位置:必须用2B铅笔按照桌贴或准考证上的考号涂写。
注意从左到右对准每个考号的数字位置填涂。
填涂完毕后仔细检查一遍,确保所填写的数字与所涂数字一致。
考号说明:本次考号为考桌左上角或准考证上的14位数字,即18开头的14位数字。
(3)如需修改,一定要用橡皮将答题卡上涂错的部分擦拭干净,不要留下原填涂痕迹。
(4)不得折叠、污损答题卡,保持机读卡整洁,否则会出现无分数及0分的现象。
(5)答题卡必须使用2B铅笔填涂,填涂时要正确填涂。
(6)答案填涂说明:本次考试共计40题选择题,考生只填写1~40题。
正确答案为A、B、C、D四个选项之一。
请考生将正确答案涂在相应的A、B、C、D选项上,请考生一定仔细看清楚选项再填涂答案。
答案涂错、涂反全部按照0分处理。
例:你的答案是A,那么请把【A】【B】【C】【D】中的【A】选项涂黑即可。
10-12年级学生使用答题说明如下:1.必须使用黑色或蓝色的钢笔、签字笔在答题纸上答题,请务必填写工整。
禁止使用其他类型笔涂写,禁止使用修正液、涂改带。
2.请考生把答案工整的填写到对应题号的横线上。
数学竞赛典型题目(一)

数学竞赛典型题目(一)1.(2004美国数学竞赛)设n a a a ,,,21 是整数列,并且他们的最大公因子是1.令S 是一个整数集,具有性质:(1)),,2,1(n i S a i =∈(2) }),,2,1{,(n j i S a a j i ∈∈-,其中j i ,可以相同(3)对于S y x ∈,,若S y x ∈+,则S y x ∈-证明:S 为全体整数的集合。
2.(2004美国数学竞赛)c b a ,,是正实数,证明:3252525)()3)(3)(3(c b a c c b b a a ++≥+-+-+-3.(2004加拿大数学竞赛)T 为1002004的所有正约数的集合,求集合T 的子集S 中的最大可能的元素个数。
其中S 中没有两个元素,一个是另一个的倍数。
4.(2004英国数学竞赛)证明:存在一个整数n 满足下列条件:(1)n 的二进制表达式中恰好有2004个1和2004个0;(2)2004能整除n .5.(2004英国数学竞赛)在0和1之间,用十进制表示为 21.0a a 的实数x 满足:在表达式中至多有2004个不同的区块形式,)20041(20031≤≤++k a a a k k k ,证明:x 是有理数。
6.(2004亚太地区数学竞赛)求所有由正整数组成的有限非空数集S ,满足:如果S n m ∈,,则S n m n m ∈+),( 7.(2004亚太地区数学竞赛)平面上有2004个点,并且无三点共线,S 为通过任何两点的直线的集合。
证明:点可以被染成两种颜色使得两点同色当且仅当S 中有奇数条直线分离这两点。
8.(2004亚太地区数学竞赛)证明:)()!1(*2N n n n n ∈⎥⎦⎤⎢⎣⎡+-是 偶数。
9.(2004亚太地区数学竞赛)z y x ,,是正实数,证明:)(9)2)(2)(2(222zx yz xy z y x ++≥+++10.(2003越南数学竞赛)函数f 满足)0(2sin 2cos )(cot π<<+=x x x x f ,令 )11)(1()()(≤≤--=x x f x f x g ,求)(x g 在区间]1,1[-的上最值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5th AMC 10 A 2004
1. 你与5位朋友要为慈善捐款筹募1500元, 若每一个人要筹募的金额相同, 则每一个人需筹募多少元? (A) 250 (B) 300 (C) 1500 (D) 7500 (E)
9000
2. 对任意的三个实数,,a b c , 其中b c ≠, 令
(,,)a q a b c b c
=
-.
试问 ((1,2,3),(2,3,1),(3,1,2))q q q q 之值是多少?
(A) 12
-
(B)
14
-
(C) 0 (D)
14
(E)
12
3. 爱丽每小时的工资为美金20元, 其中的1.45%要缴地方税, 试问爱丽每小时的工资中要付地方税美金多少分?(美金1元 = 美金100分)
(A) 0.0029 (B) 0.029 (C) 0.29 (D) 2.9 (E) 29
4. 若12
x x -=-, 则x 值为何?
(A)
12
- (B) 12
(C) 1 (D)
32
(E) 2
5. 在下图中随机任选三点, 若每组三点被取到的机率都相等, 则所取三点在一直在线的机率为多少?
(A) 1
21(B) 1
14
(C) 2
21
(D) 1
7
(E) 2
7
6. 白婆婆有6个女儿、没有儿子, 有些女儿也恰有6个女儿, 其它的女儿没有孩子. 白婆婆有女儿及外孙女共30位, 没有外曾孙女. 试问白婆婆的女儿及外孙女中有多少位没有女儿?
(A) 22 (B) 23 (C) 24 (D) 25 (E) 26
7. 将橘子堆成像金字塔形, 底部的长方形是由5列8行的橘
子所排成的, 上层的每一个橘子是放在下层的四个橘子所
形成袋状凹处上, 最上层是一列橘子. 试问此堆橘子有多
少个?
(A) 96 (B) 98 (C) 100 (D) 101 (E) 134
8. 一种代币的游戏, 其规则如下:每回持有最多代币者须分
给其它每一位参与游戏者一枚代币, 并放一枚代币于回收
桶中; 当有一位游戏参与者没有代币时, 则游戏结束. 假
设A 、B 、C 三人玩此游戏, 在游戏开始时分别持有15、14及13枚代币. 试问游戏从开始到结束, 共进行了多少回? (A) 36 (B) 37 (C) 38 (D) 39 (E) 40
9. 如图所示,
EAB ∠及ABC ∠为直角, 4AB =, 6BC =, 8AE =, AC
与BE 交于D 点. 试问ADE ∆与BDC ∆面积之差为多少?
(A) 2 (B) 4 (C)5
(D) 8 (E) 9
10. 设A 、B 为两枚公正的硬币, 将硬币A 投掷3次, 硬币B 投掷4次. 试问两枚硬币出现人头次数相同的机率为多少? (A) 19128
(B)
23128
(C)
14
(D)
35128
(E)
12
4
6
D
E
A
B
C
11. 有一个将花生酱装在圆桶状瓶子内出售的公司. 市场研
究建议瓶子较粗时可增加销售量. 若瓶子的直径增加25%, 而体积仍维持不变, 则瓶子的高度应减少百分之多少?
(A) 10 (B) 25 (C) 36 (D) 50 (E) 60
12. 亨利汉堡店对其出售的汉堡供应下列佐料:蕃茄酱、芥
末、美奶滋、蕃茄、生菜、腌黄瓜、吉士及洋葱. 每位顾客可以任意选用一片、两片或三片肉饼及任意组合的佐料.
试问可以搭配出多少种不同汉堡?
(A) 24 (B) 256 (C) 768 (D) 40,320 (E)
120,960
13. 在某个舞会中, 每位男士恰与三位女士跳舞, 而每位女
士恰与两位男士跳舞. 已知有12位男士参加这场舞会, 试问有几位女士参加这场舞会?
(A) 8 (B) 12 (C) 16 (D) 18 (E) 24
14. 某国的硬币中有1分、5分、10分及25分四种, 已知在保菈的皮包内硬币的平均值为20分. 若再增加一枚25分的硬币, 平均值则增为21分. 试问她的皮包内有多少枚10分的硬币? (A) 0 (B) 1 (C) 2 (D) 3 (E) 4
15. 已知42x -≤≤-且24y ≤≤. 试问x y x
+可能的最大值为何? (A) 1- (B)
12
-
(C) 0 (D)
12
(E) 1
16. 在下图中有多少个边长由1到5的正方形可盖住中间阴
影正方形? (A) 12 (B) 15 (C) 17 (D) 19 (E) 20
17. 小美与小雯在一个圆形的跑道上向相反的方向跑, 开始
两人分别从圆形跑道直径的两端起跑. 小美跑了100公尺时她们第一次相遇; 在第一次相遇后小雯跑了150公尺时她们第二次相遇. 假设她们跑的速度都分别维持固定不变, 试问此圆形跑道的长度是多少公尺?
(A) 250 (B) 300 (C) 350 (D) 400 (E)
500
18. 三个实数的数列形成一个等差数列, 首项是9. 若将第二
项加2、第三项加20可使得这三个数变为等比数列, 则这个等比数列中第三项最小可能的数是多少?
(A) 1 (B) 4 (C) 36 (D) 49 (E) 81
19. 如图所示, 一个白色圆柱的直径为30呎, 高为80呎. 绕
着白色圆柱的外围漆上一条水平宽度为3呎的红色长条带, 已知此长条带恰绕圆柱两圈. 试问此长条带的面积为多少平方呎?
A
C
E (A) 120 (B) 180 (C) 240 (D) 360 (E)
480
20. 如图ABCD 为正方形,
BEF
∆为正三角形. 试问DEF ∆与
ABE ∆面积的比值是多少?
(A)
43
(B)
32
(C) (D) 2 (E) 1
D
C
E 21. 如图三同心圆, 其半径分别为3、2、1. 已知图中阴影区域的面积是非阴影区域面积的
813
. 试问两直线所夹锐角
的弧度为多少?(注意:π弧度=180︒) (A) 8
π (B)
7
π (C)
6
π (D)
5
π (E)
4
π
22. 如图所示, ABCD 是边长2的正方形. 在正方形的内部作一个以AB 为直径的半圆, 且自C 点引此半圆的切线交AD 边于E 点. 试问CE 的长度是多少?
(A) 22
(B)
(C) (D)
52
(E) 5
23. 如图所示, A 、B 、C 三圆彼此外切且均内切于圆D . 已知B 、C 两圆全等, 圆A 的半径为1且通过圆D 的圆心. 试问圆B 的半径是多少?
(A)
23
(B)
2
(C)
78
(D)
89
(E)
13
-
24. 设数列12,,a a 满足下列条件: (i)
11a =,
且
(ii)对于任意的正整数n ,恒有 2n n a n a =⋅.
试问100
2a 之值是多少?
(A) 1 (B) 992 (C) 1002 (D) 49502 (E) 99992
25. 三个半径为1的球彼此外切且放置在同一水平面上, 一个半径为2的大球放在它们的上面.试问大球的最高点至平面的距离是多少?
(A) 32
+
(B)
33
+
(C)
34
+
(D)
529
(E)
3+
答 案:
1 ( A )
2 ( B )
3 ( E )
4 ( D )
5 ( C )
6 ( E )
7 ( C )
8 ( B )
9 ( B )
10
( D )
11 ( C ) 12 ( C ) 13 ( D ) 14 ( A ) 15 ( D ) 16 ( D ) 17 ( C ) 18 ( A ) 19 ( C ) 20 ( D ) 21 ( B ) 22 ( D )
23 ( D )
24 ( D )
25 ( B )。
