有理数的除法课件
合集下载
《有理数的除法》有理数PPT优秀课件
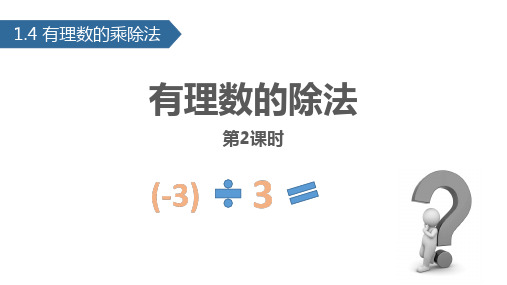
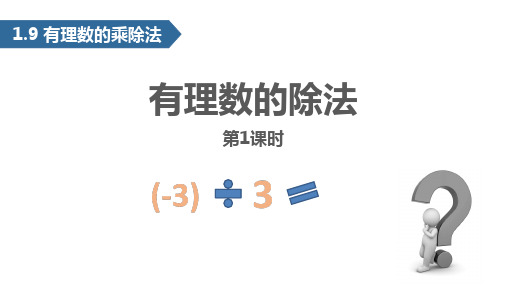
答案:(-1-3)÷(0.8)×100=(4)÷(0.8)×100=5×100=500米; 答:这个山峰高500米.
【讲解】 此题考查有理数的混合运算, 主要搞清规定上升为正,下降 为负.首先算出山脚与山顶的温 度差,再进一步算出下降了多 少个0.8℃,再乘100即可.
课后作业
1.计算8-(-3)×(-7)的值为( )
教学新知
例9 某公司去年1~3月平均每月亏损1.5万元,4~6月平均每月
盈利2万元,7~10月平均每月盈利1.7万元,11~12月平均每月 亏损2.3万元.这个公司去年总的盈亏情况如何?
解:记盈利额为正数,亏损额为负数,这个公司去年全年亏盈额(单位: 万元)为:
−15 × 3 + 2 × 3 + 1.7 × 4 + −2.3 × 2 = −4.5 + 6 + 6.8 − 4.6 = 3.7 答:这个公司去年全年盈利3.7万元.
=
144 5
【剖析】错解受乘法分配律的影响,误认为除法也能用分配律,其实, 除法没有分配律.
课堂练习
1.计算:
11 1 1 3 5 1 5 × (3 − 2) × 11 ÷ 4
3 2 − 3 − [−5 + (1 − 0.2 × 5) ÷ −2 ]
2 = −(25)
11 = 2 25
75 3 3 (9 − 6 + 18) × 18 − 1.45 × 6 + 3.95 ×=6 17
知识梳理
知识点1:有理数的混合运算
【例】计算:
(1) (-3)×4-42÷(-7)
(2) 20-8÷(-4)×(-0.25)
1 61 (3) 2 4 × (− 7) ÷ (2 − 2)
【讲解】 此题考查有理数的混合运算, 主要搞清规定上升为正,下降 为负.首先算出山脚与山顶的温 度差,再进一步算出下降了多 少个0.8℃,再乘100即可.
课后作业
1.计算8-(-3)×(-7)的值为( )
教学新知
例9 某公司去年1~3月平均每月亏损1.5万元,4~6月平均每月
盈利2万元,7~10月平均每月盈利1.7万元,11~12月平均每月 亏损2.3万元.这个公司去年总的盈亏情况如何?
解:记盈利额为正数,亏损额为负数,这个公司去年全年亏盈额(单位: 万元)为:
−15 × 3 + 2 × 3 + 1.7 × 4 + −2.3 × 2 = −4.5 + 6 + 6.8 − 4.6 = 3.7 答:这个公司去年全年盈利3.7万元.
=
144 5
【剖析】错解受乘法分配律的影响,误认为除法也能用分配律,其实, 除法没有分配律.
课堂练习
1.计算:
11 1 1 3 5 1 5 × (3 − 2) × 11 ÷ 4
3 2 − 3 − [−5 + (1 − 0.2 × 5) ÷ −2 ]
2 = −(25)
11 = 2 25
75 3 3 (9 − 6 + 18) × 18 − 1.45 × 6 + 3.95 ×=6 17
知识梳理
知识点1:有理数的混合运算
【例】计算:
(1) (-3)×4-42÷(-7)
(2) 20-8÷(-4)×(-0.25)
1 61 (3) 2 4 × (− 7) ÷ (2 − 2)
《有理数的除法》有理数及其运算PPT课件 (共15张PPT)

随堂练习:
一. 填空.
(1)
(2)-6的倒数是 (3)
的倒数是-2,1/2 -0.1的倒数是
,相反数是 . 的相反数
.
的倒数等于它本身,
等于它本身,
的绝对值等于它本身.
(4)若一个数的相反数与这个数的倒数的和等于0,则这 个数是 .
二.判断题
(1)a+b的倒数是1/a+b
(2)0÷a=0 (3)两个数相除,商是正数,则和一定为正数 (4)两个数互为相反数,那么它们的商一定存在 三.计算题
发现:
做完以后, 有什么发现?
对有理数仍有:乘积是 1的两个数互为倒数。
用式子表示就是:
1 如果a 1( a 0), 则 a 1 a的倒数为 . 因为任意 a 一个数与零相乘都得 零,所以0没有倒数.
注意:倒数与相反数符号的区别。
倒数 正数 正 相反数 负 正 零
负数
零
负
不存在
练习:P60 第一题
观察上面各式,注意商的符号及绝对值与 被除数和除数的关系,你能否得到与有理数 乘法法则类似的除法法则?
有理数除法运算的第二种方法: 有理数除法法则:
1. 两数相除,同号得
正
,异号得
负
,
并把绝对值 相除 。
2. 零除以任何一个非零的数,都得 零
。
例2. 化简下列分数。
12 (1) 3
例3 法:
有理数除法运算的第一种方法:
除以一个数等于乘上这个数的倒数。 注意:零不能作除数
练一练: (1)(-18)÷3 (3)(-27)÷(-9)
1 2 (5)( )÷( ) 7 7 1 (2)5÷( ) 5
(4)0÷(-2)
人教版七年级数学上册课件1.4.2有理数的除法(共50张PPT)

=(–30)÷(–45)
2
= 30÷45 = 3.
(3) 0 = __0___.
75
探究新知
知识点 2 有理数的乘除混合运算
例3 计算
(1) 125 5 5
7
解:原式 125 5 5 7
(125 5) 1 75
125 1 5 1 5 75
25 1 25 1
7
7
(2) 2.5 5 ( 1)
探究新知
–4×(2÷8)和 –4×2÷8
8÷ (–4)=_–_2_ 1+1+3×4+5×6+7×8=100
(2)(+6)÷(–2)=
8 ×(– )=_–_2_
已知该地区高度每增加100米,气温大约降低0.
8÷ (–4)=___
–36÷ 6=_–_6_ 解:450+20×60–12×120
5万元,4~6月平均盈利2万元,7~10月平均盈利1.
探究新知
利用上面的除法法则计算下列各题:
(1)–54 (–9);6 (2)–27 3;–9
(3)0 (–7); 0
(4)–24 (–6). 4
思考:从上面我们能发现商的符号有什么规律?
探究新知
有理数除法法则(二)
两数相除,同号得正,异号得负,并把绝对值 相除.
0除以任何一个不等于0的数,都得0.
原式的倒数为 ( 2 1 1 2) ( 1 ) =( 2 1 1 2) (30)
3 10 6 5 30 3 10 6 5
= 20 35 12=10. 故( 1 ) ( 2 1 1 2)= 1 .
30 3 10 6 5 10
简便计算, 先取倒数
巩固练习
《有理数的除法》初中课件PPT
因为 (- 2)×(- 4)=8
所以 8÷(- 4)=- 2
①
1
另外,我们知道,8×(- )= - 2 ②
4
1
由①、②得 8÷(- 4)=8× (- ) ③
4
1
③式表明,一个数除以-4可以转化为乘以- 来进行,即一个数除
4
1
以-4,等于乘以-4的倒数4
探究新知
【探究】根据“除法是乘法的逆运算”填空.
5
( ) ( ) =____
5
25
3
1
–8
(–72)× =___
9
探究新知
【思考】上面各组数计算结果有什么关系?
由此你能得到有理数的除法法则了吗?
探究新知
观察下列两组式子,你能找到它们的共同点吗?
“÷ ”变 “× ”
(1)(+6)÷(+2) = +3
1
6 +3
2
互为倒数
“÷ ”变 “× ”
30
3 10 6 5
10
=
10
简便计算,
先取倒数。
巩固练习
选择合适的方法计算:
1
1 3 2 2
( ) (
).
42
6 14 3 7
巩固练习
1 3 2 2
1
解:原式的倒数为 ( ) ( )
6 14 3 7
42
1 3 2 2
(
) (42)
6 14 3 7
7 9 28 12
14
1
1 3 2 2
1
故 ( ) ( )
42
6 14 3 7
《有理数除法》有理数PPT课件 (共10张PPT)

1 1 1 (3)能否用上述方法解决: 12 ( ) 6 2 3
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
挫折的名言 1、 我觉得坦途在前,人又何必因为一点小障碍而不走路呢?——鲁迅 2、 “不耻最后”。即使慢,弛而不息,纵会落后,纵会失败,但一定可以达到他所向的目标。——鲁迅 3、 故天将降大任于是人也,必先苦其心志,劳其筋骨,饿其体肤,空乏其身,行拂乱其所为,所以动心忍性,曾益其所不能。 战胜挫折的名言 1、卓越的人一大优点是:在不利与艰难的遭遇里百折不饶。——贝多芬 2、每一种挫折或不利的突变,是带着同样或较大的有利的种子。——爱默生 3、我以为挫折、磨难是锻炼意志、增强能力的好机会。——邹韬奋 4、斗争是掌握本领的学校,挫折是通向真理的桥梁。——歌德 激励自己的座右铭 1、 请记得,好朋友的定义是:你混的好,她打心眼里为你开心;你混的不好,她由衷的为你着急。 2、 要有梦想,即使遥远。 3、 努力爱一个人。付出,不一定会有收获;不付出,却一定不会有收获,不要奢望出现奇迹。 4、 承诺是一件美好的事情,但美好的东西往往不会变为现实。 工作座右铭 1、 不积跬步,无以至千里;不积小流,无以成江海。——《荀子劝学》 2、 反省不是去后悔,是为前进铺路。 3、 哭着流泪是怯懦的宣泄,笑着流泪是勇敢的宣言。 4、 路漫漫其修远兮,吾将上下而求索。——屈原《离骚》 5、 每一个成功者都有一个开始。勇于开始,才能找到成功的路。 国学经典名句 1、知我者,谓我心忧,不知我者,谓我何求。(诗经王风黍离) 2、人而无仪,不死何为。 (诗经风相鼠) 3、言者无罪,闻者足戒。 (诗经大序) 4、他山之石,可以攻玉。 (诗经小雅鹤鸣) 5、投我以桃,报之以李。 (诗经大雅抑) 6、天作孽,犹可违,自作孽,不可活。(尚书) 7、满招损,谦受益。 (尚书大禹谟) 青春座右铭 1、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。 2、把手握紧,什么也没有;把手伸开,你就拥有了一切。 3、不在打击面前退缩,不在困难面前屈服,不在挫折面前低头,不在失败面前却步。勇敢前进! 4、当你能飞的时候就不要放弃飞。 5、当你能梦的时候就不要放弃梦。 激励向上人生格言 1、实现自己既定的目标,必须能耐得住寂寞单干。 2、世界会向那些有目标和远见的人让路。 3、为了不让生活留下遗憾和后悔,我们应该尽可能抓住一切改变生活的机会。 4、无论你觉得自己多么的不幸,永远有人比你更加不幸。 5、无论你觉得自己多么的了不起,也永远有人比你更强。 6、打击与挫败是成功的踏脚石,而不是绊脚石。 激励自己的名言 1、忍别人所不能忍的痛,吃别人所别人所不能吃的苦,是为了收获得不到的收获。 2、销售是从被别人拒绝开始的。 3、好咖啡要和朋友一起品尝,好机会也要和朋友一起分享。 4、生命之灯因热情而点燃,生命之舟因拼搏而前行。 5、拥有梦想只是一种智力,实现梦想才是一种能力。 6、有识有胆,有胆有识,知识与胆量是互相促进的。 7、体育锻炼可以(有时可以迅速)使人乐观(科学实验证明)。 8、勤奋,机会,乐观是成功的三要素。(注意:传统观念认为勤奋和机会是成功的要素,但是经过统计学和成功人士的分析得出,乐观是成功的第三要素) 9、自信是人格的核心。 10、获得的成功越大,就越令人高兴。
有理数的除法-完整版课件

先确定结果的符号, 再根据法则进行绝 对值的运算。
例2 计算:
畅谈所得 感悟提升
1.做有理数的除法有哪些方法?
(1)直接应用有理数除法的法则进行 计算 (2)把除法转化为乘法
2.做有理数的除法时应注意什么?
先确定结果的符号,再把除法转化为乘法,使运算更简便合理。
倒数与相反数的区别和联系: (1)符号上区别:互为相反数(0除外)的两数的符号相反,而互为倒数的两数的符号相同; (2)0减去一个数得到这个数的相反数,也就是说a与-a互为相反数。1除以一个不为0的数得到这个数的倒数,也就是说当a≠0时,a与1/a互为倒数; (3)互为相反数的两数的和为0,互为倒数的两数的积为1;0的相反数是0,但0没有倒数;相反数是本身的数只有一个0,倒数是本身的数有+1和-1两个。
想一想
1、小学学过的除法的意义?
除法是已知两个因数的积与其中一个因数,求另一个因数的运算。除法是乘法的逆运算。
2、有理数的乘法法则?
两数相乘,同号得正,异号得负,并把绝对值相乘。
3、什么是倒数?
乘积是1的两个数互为倒数。
做一做
☞
(1)由9 ×(-2)=-18,得(-18)÷(-2)=( ), (-18)÷9=( ). (2)由(-9)× 2 =-18,得(-18)÷(-9)=( ), (-18)÷2=( ). (3)由(-9)×(-2)=18,得 18÷≠0),得0÷a=( )
观察上面的结果,两个 有理数相除,商的符号 有什么规律?商的绝对 值呢?
9
-2
2
-9
-2
-9
0
有理数的除法法则:
两数相除,同号得正,异号得负, 并把绝对值相除; 零除以任何一个不等于零的数都是零。
有理数除法ppt课件

有理数除法ppt课件
汇报人: 202X-12-30
目 录
• 有理数除法的基本概念 • 有理数除法的运算方法 • 有理数除法的应用 • 有理数除法中的常见错误及纠正方法 • 有理数除法的练习题及解析
01
有理数除法的基本概念
有理数除法的定义
有理数除法是一种数学运算,通 过除法运算可以将一个数表示为
另一个数的倍数。
有理数除法运算的结果是一个有 理数,这个有理数可以是整数、
分数或小数。
有理数除法运算可以用除法符号 “÷”表示,例如,a÷b表示a
除以b。
有理数除法的性质
有理数除法具有交换 律和结合律,即 a÷b=b÷a和 (a÷b)÷c=a÷(b×c) 。
有理数除法还具有零 性质,即任何数除以 零都是无意义的。
倒数法
利用倒数的性质,将除法转化为乘法,简化计算进程 。
输入 标题
详细描写
倒数是指与给定数的乘积为1的数。通过将被除数和 除数的倒数相乘,可以将除法运算转化为乘法运算, 从而简化计算进程。
总结词
适用范围
例如,求8除以2,可以找到2的倒数为1/2,因此8除 以2等于8乘以1/2,即4。
举例说明
适用于有理数范围内的除法运算。
运算顺序错误
总结词
运算顺序错误是有理数除法中常见的错误之一。
详细描写
在进行有理数除法时,学生需要遵循正确的运算顺序,即先进行乘法和除法,再进行加法和减法。如果运算顺序 错误,会导致计算结果不正确。因此,需要强调运算顺序的重要性,并让学生通过练习来加深理解和记忆。
05
有理数除法的练习题及解析
基础练习题
总结词:巩固基础
详细描写:基础练习题主要涉及有理数除法的基本规则和运算,包括正数、负数 和零的除法。这些题目旨在帮助学生掌握除法的基本概念和运算方法。
汇报人: 202X-12-30
目 录
• 有理数除法的基本概念 • 有理数除法的运算方法 • 有理数除法的应用 • 有理数除法中的常见错误及纠正方法 • 有理数除法的练习题及解析
01
有理数除法的基本概念
有理数除法的定义
有理数除法是一种数学运算,通 过除法运算可以将一个数表示为
另一个数的倍数。
有理数除法运算的结果是一个有 理数,这个有理数可以是整数、
分数或小数。
有理数除法运算可以用除法符号 “÷”表示,例如,a÷b表示a
除以b。
有理数除法的性质
有理数除法具有交换 律和结合律,即 a÷b=b÷a和 (a÷b)÷c=a÷(b×c) 。
有理数除法还具有零 性质,即任何数除以 零都是无意义的。
倒数法
利用倒数的性质,将除法转化为乘法,简化计算进程 。
输入 标题
详细描写
倒数是指与给定数的乘积为1的数。通过将被除数和 除数的倒数相乘,可以将除法运算转化为乘法运算, 从而简化计算进程。
总结词
适用范围
例如,求8除以2,可以找到2的倒数为1/2,因此8除 以2等于8乘以1/2,即4。
举例说明
适用于有理数范围内的除法运算。
运算顺序错误
总结词
运算顺序错误是有理数除法中常见的错误之一。
详细描写
在进行有理数除法时,学生需要遵循正确的运算顺序,即先进行乘法和除法,再进行加法和减法。如果运算顺序 错误,会导致计算结果不正确。因此,需要强调运算顺序的重要性,并让学生通过练习来加深理解和记忆。
05
有理数除法的练习题及解析
基础练习题
总结词:巩固基础
详细描写:基础练习题主要涉及有理数除法的基本规则和运算,包括正数、负数 和零的除法。这些题目旨在帮助学生掌握除法的基本概念和运算方法。
2024年秋人教七年级数学上册2.2.2 第1课时 有理数的除法(课件)

72÷9 =__8___,
(-4)×3 =_-__1_2_,
(-12)÷3 =_-__4__,
2×(-3) =__-__6_,
(-6)÷2 =_-__3__,
(-4)×(-3) =__1_2__, 12÷(-4) =_-__3__,
0×(-6) =___0__,
0÷(-6) =___0__.
观察右侧算式,思考两个有理数相除时:
的绝对值等于被除数的绝对值除以除数的绝对值的商.
0 除以任何一个不等于 0 的数,都得__0__.
(1)如果 a<0,b>0,那么 ab__<__0, a __<__0.
b
(2)如果 a>0,b<0,那么 ab__<__0, a __<__0.
b
(3)如果 a<0,b<0,那么 ab__>__0, a __>__0.
p 这样,有理数就是形如 q (p,q 是整数,q ≠ 0) 的数.
巩固练习
化简:(1)53
;(2)412
;(3)
8 2.4
.
解:(1)53
=
(-3)÷5
=
-(3÷5)
=
3;
5
(2)412
=
4÷(-12)
=
-(4÷12)
=
1 3
;
(3) 8
2.4
=
-[(-8)÷2.4]
=
8÷2.4
=
10 3
.
a a a b b b
1)
4
.
8÷(-4)= 8×(- 1 ) .
4
一个数除以 -4,等于乘 -4 的倒数 - 1 . 4
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a
1 3 −1 计算: 9、计算:(1)( − )×( 2 4
)÷(− 2
1 ); 4
11 25) (2)-6÷(-0.25)× 14
.
c 10、 10、当 a = −3 , = −2 , = 5 b
−b+c 的值. 时求 − a 的值.
小结: 小结:
定义 1、倒数: 倒数: 1、0没有倒数,0有 没有倒数, 相反数。 相反数。
例2、化简下列分数:
(1) (2)
解: (1)
=(-12)÷3= -4
= (-45)÷(-15)=3
(2)
倒数与相反数的区别和联系: 倒数与相反数的区别和联系: 符号上区别:互为相反数( (1)符号上区别:互为相反数(0 除外)的两数的符号相反, 除外)的两数的符号相反,而互为 倒数的两数的符号相同; 倒数的两数的符号相同; (2)0减去一个数得到这个数的相 反数,也就是说a 反数,也就是说a与-a互为相反数 除以一个不为0 。1除以一个不为0的数得到这个数 的倒数,也就是说当a≠0 a≠0时 的倒数,也就是说当a≠0时,a与 1/a互为倒数 互为倒数; 1/a互为倒数; 互为相反数的两数的和为0 (3)互为相反数的两数的和为0, 互为倒数的两数的积为1 互为倒数的两数的积为1;0的相反 数是0 没有倒数; 数是0,但0没有倒数;相反数是本 身的数只有一个0 身的数只有一个0,倒数是本身的数 +1和 两个。 有+1和-1两个。
0 的相反数是它本身; (2)______的相反数是它本身 (2)______的相反数是它本身;
或正数 的绝对值是它本身. ______的绝对值是它本身 (3)0或正数 的绝对值是它本身. ______
求下列各数的倒数: 例1 、求下列各数的倒数: ( 1) - 3 ( 2) - 1 (3 )( 4) - 1 ( 5) 0. 2 ( 6) 1. 2
课堂练习
1.计算:
5 1 (1) 21 ÷ − 7 ;
1 (2) (−12) ÷ 3
5 (3) 15÷(- ) 6
2 2 (4) (− ) ÷ (− ) 15 3
1 4
2、求下列各数的倒数: 求下列各数的倒数: (1) − 4
7
;(2)4
;(3) .2 0 (6)1.
;
(4) 0.25 ;(5)-5; −
分析:欲求某数的倒数, 分析:欲求某数的倒数,就是要确定与 这个数相乘积为1的数是什么? 这个数相乘积为1的数是什么?
解:(1) ∵(- 3)×(:(1 (3)∵- 1 。 (5) ∵ 0.2= ==)=1,∴- 3的倒数是 =1,
)=1,的倒数是, - × ( )=1,-1 的倒数是求小数的倒数时, 求小数的倒数时,要先把小数化成分 数; 5=1, 0. 的倒数是5 = , ×5=1,∴ 0.2的倒数是5 求带分数的倒数时, 求带分数的倒数时,要先把带分数化 成假分数。 成假分数。
(1)(+12)÷(+4) 1)(+12) (+4) (+12 (2)(-57)÷(+3) 2)(-57)÷(+3) (-57) (3)(-36)÷(-9) 3)(-36)÷(-9 (-36) (4)(+96)÷(-16) 4)(+96) (-16)
练一练: 练一练: (1) 84 ÷ (− 14 ); (2 ) (− 1 . 6 ) ÷ 0 . 4 ;
做 一 做
(1)由 (1)由9×(-2)=-18,得 2)=-18, (-18)÷(-2)=( 9 18)÷ (-18) ÷9 =( -2 ) ), ),
(2)由 =-18, (2)由(- 9) × 2 =-18,得 (-18)÷2=( -9 18)÷ ), ), )
(-18) ÷ (- 9 )=( 2 观察上面的结果 两个有理数相除, (3)由(- 9) ×(-2) = 18,得 ,两个有理数相除, (3)由 18, 商的符号有什么规律 18÷ ), 18÷(-2)=( -9 ), 商的绝对值呢? ?商的绝对值呢? 18÷ 18÷ (- 9 )=( -2 ) (4)由 a=0(a表示不等于零的有 (4)由0 ×a=0(a表示不等于零的有 理数), ),得 理数),得 0 ÷ a=( 0 )
3、化简下列分数 −12 −45 (1) 3 ;(2) ; −15
3 36) (3) 或3:(-36) −36
1 (4) − ;(5) 0 . 4 −5 5 计算: 4、计算:
(− 15) ÷ (− 3) (− 0.75 ) ÷ 0.25
1 (− 12 ) ÷ − 4
1 (− 12 ) ÷ − ÷ (− 100 12
1.8 有理数的除法
小学学过的除法的意义? 1、小学学过的除法的意义?
前 提 测 评
除法是已知两个因数的积与其 中一个因数,求另一个因数的 运算。除法是乘法的逆运算。 有理数的乘法法则? 2、有理数的乘法法则? 两数相乘,同号得正,异号得 负,并把绝对值相乘。
什么是倒数? 3、什么是倒数?
乘积是1的两个数互为倒数。
口答 ( 1 )( − 3 ) × 4 (2 )3 × (− 1 ) 3 ( 3 )( − 9 ) × ( − 3 ) (4 )0 × (− 2 )
想一想: 想一想: 已知一因数与- 相乘所得的积等于-12, 已知一因数与-3相乘所得的积等于-12, 求这个因数。 求这个因数。 你用什么运算来计算呢? 你用什么运算来计算呢?
有理数除法法则 两个有理数相除, 两个有理数相除,同号得 正 ,异号得 负 , 并把绝对值 相除 。 0除以任何非0的数都 零 。 除以任何非0
例1 (1) (− 8) ÷ (− 4); (2) (− 3.2) ÷ 0.08;
1 2 (3) − ÷ 6 3
口答:先说出商的符号, 口答:先说出商的符号,再说出商
倒数与相反数的区别: 倒数与相反数的区别: 2、a,b互为倒数 a,b互为倒数 ab=1 a,b互为相反 3、 a,b互为相反 数 除法法则 (一) a+b=0 2、有理数的除法法则: 有理数的除法法则: 除法法则( 除法法则(二)
注意
a
1 1 -1 1
31 3
-0.5 -2
-1 -1 1 1
1 6
− 7 8
填 一 填
a的倒数 a的相反数 a的倒数与a 的倒数与a 的积
3 10
6
−
1 6
8 7
− 3 1 0.5 3
1 1
−
1
7 8
1
± 1 的倒数是它本身 (1)______的倒数是它本身; (1)______的倒数是它本身;
)
达标评: 达标测评:
1、如果两个有理数的乘积是1,那么 这两个有理数互为 倒数 2、如果两个有理数的和是0,那么这 两个有理数互为 相反 数 3、(()的相反数的倒数是
)的倒数的相反数是 的绝对值与它的倒数的和
4、 -1 为0。
5、当x= ,
3 时,
没有意义, 没有意义,当x= ±3
时
的值为0 的值为0。
在进行有理数除法运 算时, 算时,你认为何时用法则 一般在不能整 一,何时用法则二会比较 除的情况下应 方便? 方便? 第一法则, 用 第一法则,
在能整除的情 请选用合适的法则进行计算: 况下应用第二 5 1 ⑴ -÷(--); 法则。 法则。 21 7
⑵ (-15)÷(-5); 2 1 ⑶ (-3)÷(--)÷(--); 5 4 2 1 ⑷ (-3)÷〔(--)÷(--)〕 5 4
7 (3 ) 0 ÷ − ; 83 3 3 (4 ) − ÷ − . 5 25
做一做: 做一做:
比较下列各组数的计算结果: 比较下列各组数的计算结果:
5) 2 )与1× (1) 1 ÷ (- (- 5 2 (2) 0.8 ÷ (- 3 ) 0.8× 与 (- 3 ) 10 10 注意: 注意: 1) 1 ) (- 1 ) 60) (3)(- ÷ (- 与 × (- 0不能做除数 4 60 4
____( 6. 的倒数是____( a ≠ _____ ); a 的倒数是____
a 7. ÷ b = a × __________ _ ;
a b 同号, 8.若 a 、 同号,则 _____ 0 ; b
a b 异号, 若 、 异号,则 _____ 0 ; b a = 0 , ≠ 0 时,则 a _____ 0 。 b 若 b
有理数的除法法则( 有理数的除法法则(二) 一个数除以另一个数, 一个数除以另一个数,等于 乘以这个数的倒数。 乘以这个数的倒数。
想 一 想 (1)怎样求负数的倒数? 乘以这个数的倒数 (2) 除以一个数等于_____________ 。 1、倒数:乘积是1的两数互为倒数,一 般地,a· =1(a≠0)。也就是说,如 果 a是不等于0的有理数,那么a的倒数是 没有倒数。 (1)0没有倒数。 求分数的倒数, (2)求分数的倒数,只要把这个 分数的分子,分母颠倒位置即可。 分数的分子,分母颠倒位置即可。 正数的倒数是正数, (3)正数的倒数是正数,负数 的倒数是负数。 的倒数是负数。
