2013高考理科数学二轮训练20
2013年高考理科数学(新课标Ⅱ卷)

2013年普通高等学校招生全国统一考试(新课标Ⅱ卷)数 学(理科)注意事项:1. 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答卷前考生将自己的姓名\准考证号填写在本试卷和答题卡相应位置。
2. 回答第Ⅰ卷时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号标黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在本试卷上无效。
3. 答第Ⅱ卷时,将答案写在答题卡上,写在本试卷上无效。
4. 考试结束,将试题卷和答题卡一并交回。
第Ⅰ卷(选择题 共50分)一、选择题:本大题共10小题。
每小题5分,共50分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合M={x|(x-1)2< 4,x ∈R},N={-1,0,1,2,3},则M ∩N = (A ){0,1,2} (B ){-1,0,1,2}(C ){-1,0,2,3} (D ){0,1,2,3} (2)设复数z 满足(1-i )z=2 i ,则z=(A )-1+i(B )-1-i (C )1+i(D )1-i(3)等比数列{a n }的前n 项和为S n ,已知S 3 = a 2 +10a 1 ,a 5 = 9,则a 1=( ) (A )13 (B )13- (C )19(D )19-(4)已知m ,n 为异面直线,m ⊥平面α,n ⊥平面β。
直线l 满足l ⊥m ,l ⊥n ,,l l αβ⊄⊄,则(A )α∥β且l ∥α(B )α⊥β且l ⊥β(C )α与β相交,且交线垂直于l (D )α与β相交,且交线平行于l (5)已知(1+ɑx)(1+x)5的展开式中x 2的系数为5,则ɑ = (A )-4(B )-3 (C )-2(D )-1(6)执行右面的程序框图,如果输入的N=10,那么输出的S=(A )11112310++++ (B )11112!3!10!++++ (C )11112311++++ (D )11112!3!11!++++(7)一个四面体的顶点在空间直角坐标系O-xyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画该四面体三视图中的正视图时,以zOx平面为投影面,则得到正视图可以为(8)设a=log36,b=log510,c=log714,则(A)c>b>a (B)b>c>a (C)a>c>b (D)a>b>c(9)已知a>0,x,y满足约束条件()133xx yy a x⎧≥⎪+≤⎨⎪≥-⎩,若z=2x+y的最小值为1,则a= (A)14(B)12(C)1 (D)2(10)已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是(A)∃xα∈R,f(xα)=0(B)函数y=f(x)的图像是中心对称图形(C)若xα是f(x)的极小值点,则f(x)在区间(-∞,xα)单调递减(D)若x0是f(x)的极值点,则()0'0f x=(11)设抛物线y2=3px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为(A)y2=4x或y2=8x (B)y2=2x或y2=8x(C)y2=4x或y2=16x (D)y2=2x或y2=16x(12)已知点A(-1,0);B(1,0);C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是(A)(0,1)(B)112⎛⎫⎪⎪⎝⎭(C)113⎛⎤⎥⎦⎝(D)11,32⎡⎫⎪⎢⎣⎭第Ⅱ卷本卷包括必考题和选考题,每个试题考生都必修作答。
2013届高考理科数学复习演练套题(含答案)

2013届高考理科数学复习演练套题(含答案)(时间:40分钟满分:60分)一、填空题(每小题5分,共40分)1.不等式|2x-1|<3的解集为________.解析①当2x-1≥0,即x≥12时,不等式变为2x-1<3,得x<2,∴12≤x <2.②当2x-1<0即x<12时,不等式变为-(2x-1)<3即x>-1,∴-1<x<12,综上不等式解集为{x|-1<x<2}.答案(-1,2)2.已知x>0,则函数y=x(1-x2)的最大值为________.解析∵y=x(1-x2),∴y2=x2(1-x2)2=2x2(1-x2)(1-x2)•12.∵2x2+(1-x2)+(1-x2)=2,∴y2≤122x2+1-x2+1-x233=427.当且仅当2x2=1-x2,即x=33时取等号.∴y≤239.∴y的最大值为239.答案2393.(2011•江西卷)对于x∈R,不等式|x+10|-|x-2|≥8的解集为________.解析法一(零点分段法)由题意可知,x≤-10,-x-10+x-2≥8或-10<x<2,x+10+x-2≥8或x≥2,x+10-x+2≥8,解得x≥0,故原不等式的解集为{x|x≥0}.法二(几何意义法)如图,在数轴上令点A、B的坐标分别为-10,2,在x轴上任取一点P,其坐标设为x,则|PA|=|x+10|,|PB|=|x-2|,观察数轴可知,要使|PA|-|PB|≥8,则只需x≥0.故原不等式的解集为{x|x≥0}.答案{x|x≥0}4.(2011•陕西)若不等式|x+1|+|x-2|≥a对任意x∈R恒成立,则a 的取值范围是________.解析由于|x+1|+|x-2|≥|(x+1)-(x-2)|=3.所以只需a≤3即可.答案(-∞,3]5.若不等式|x+1|+|x-3|≥a+4a对任意的实数x恒成立,则实数a 的取值范围是________.解析当a<0时,显然成立;当a>0时,∵|x+1|+|x-3|的最小值为4,∴a+4a≤4.∴a=2..综上可知a的取值范围是(-∞,0)∪{2}.答案(-∞,0)∪{2}6.设x,y,z∈R,若x2+y2+z2=4,则x-2y+2z的最小值为________时,(x,y,z)=________.解析∵(x-2y+2z)2≤(x2+y2+z2)12+(-2)2+22]=4×9=36,∴x-2y +2z最小值为-6,此时x1=y-2=z2.又∵x2+y2+z2=4,∴x=-23,y=43,z=-43.答案-6-23,43,-437.若对任意x>0,xx2+3x+1≤a恒成立,则a的取值范围是________.解析∵a≥xx2+3x+1=1x+1x+3对任意x>0恒成立,设u=x+1x+3,∴只需a≥1u恒成立即可.∵x>0,∴u≥5(当且仅当x=1时取等号).由u≥5,知0<1u≤15,∴a≥15.答案15,+∞8.已知h>0,a,b∈R,命题甲:|a-b|<2h:命题乙:|a-1|<h 且|b-1|<h,则甲是乙的________条件.解析|a-b|=|a-1+1-b|≤|a-1|+|b-1|<2h,故由乙能推出甲成立,但甲成立不能推出乙成立,所以甲是乙的必要不充分条件.答案必要不充分二、解答题(共20分)9.(10分)已知关于x的不等式|ax-2|+|ax-a|≥2(a>0).(1)当a=1时,求此不等式的解集;(2)若此不等式的解集为R,求实数a的取值范围.解(1)当a=1时,不等式为|x-2|+|x-1|≥2.由绝对值的几何意义知,不等式的意义可解释为数轴上的点x到1、2的距离之和大于等于2.∴x≥52或x≤12.∴不等式的解集为xx≤12或x≥52.注也可用零点分段法求解.(2)∵|ax-2|+|ax-a|≥|a-2|,∴原不等式的解集为R等价于|a-2|≥2,∴a≥4或a≤0,又a>0,∴a≥4.10.(10分)对于任意实数a(a≠0)和b,不等式|a+b|+|a-2b|≥|a|(|x -1|+|x-2|)恒成立,试求实数x的取值范围.解原不等式等价于|a+b|+|a-2b||a|≥|x-1|+|x-2|,设ba=t,则原不等式变为|t+1|+|2t-1|≥|x-1|+|x-2|对任意t恒成立.因为|t+1|+|2t-1|=3t,t≥12,-t+2,-1<t<12,-3t,t≤-1,在t=12时取到最小值为32.所以有32≥|x-1|+|x-2|=2x-3,x≥2,1,1<x<2,3-2x,x≤1,解得x∈34,94.。
2013年4月高三理科数学二轮复习试题(含答案)

2013年4月高三理科数学二轮复习试题(含答案)山东省济南一中2013届高三二轮复习质量检测数学试题(理工类)2013.4本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,其中第Ⅱ卷第22~24题为选考题,其它题为必考题。
考生作答时,将答案答在答题卡上,在本试卷上答题无效。
考试结束后,将本试卷和答题卡一并交回。
注意事项:1.答题前,考生务必先将自己的姓名、准考证号填写在答题卡上,认真核对条形码上的姓名、准考证号,并将条形码粘贴在答题卡的指定位置上。
2.选择题答案使用2B铅笔填涂,如需改动,用橡皮擦干净后,再选涂其他答案的标号;非选择题答案使用0.5毫米的黑色中性(签字)笔或碳素笔书写,字体工整、笔迹清楚。
3.请按照题号在各题的答题区域(黑色线框)内作答,超出答题区域书写的答案无效。
4.保持卡面清洁,不折叠,不破损。
5.做选考题时,考生按照题目要求作答,并用2B铅笔在答题卡上把所选题目对应的题号涂黑。
第I卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知U={1,2,3,4,5,6,7,8},A={1,3,5,7},B={2,4,5},则CU(A∪B)等于A.{6,8}B.{5,7}C.{4,6,7}D.{1,3,5,6,8}2.已知为虚数单位,复数z=,则复数的虚部是A.B.C.D.3.函数y=与y=图形的交点为(a,b),则a所在区间是A.(0,1)B.(1,2)C.(2,3)D.(3,4)4.已知F1、F2是双曲线x2a2-y2b2=1(a>0,b>0)的两个焦点,以线段F1F2为边作正△MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率为A.4+23B.3-1C.3+12D.3+15.阅读右边的程序框图,若输出S的值为-14,则判断框内可填写A.iC.i6.函数f(x)=A.在上递增,在上递减B.在上递增,在上递减C.在上递增,在上递减D.在上递增,在上递减7.若某空间几何体的三视图如图所示,则该几何体的体积是A.13B.23C.1D.28.已知点是边长为1的等边的中心,则等于A.B.C.D.9.从6名同学中选4人分别到A、B、C、D四个城市游览,要求每个城市有一人游览,每人只游览一个城市,且这6人中甲、乙两人不去D 城市游览,则不同的选择方案共有A.96种B.144种C.240种D.300种10.在直角坐标系xOy中,已知△AOB三边所在直线的方程分别为x=0,y=0,2x+3y=30,则△AOB内部和边上整点(即横、纵坐标均为整数的点)的总数是A.95B.91C.88D.7511.已知抛物线上存在关于直线对称的相异两点、,则等于A.3B.4C.D.12.设函数f(x)=x-,对任意恒成立,则实数m的取值范围是A.(-1,1)B.C.D.或(第Ⅱ卷本卷包括必考题和选考题两部分.第13题~第21题为必考题,每个试题考生都必须做答.第22题~第24题为选考题,考生根据要求做答.二、填空题:本大题共4小题,每小题5分.13.已知函数f(x)=ax+1x+2在区间(-2,+∞)上为增函数,则实数a 的取值范围是________________.14.已知向量则的值为.15.在三次独立重复试验中,事件A在每次试验中发生的概率相同,若事件A至少发生一次的概率为,则事件A恰好发生一次的概率为。
2013二模理科数学答案.doc

永州市2013年高考第二次模拟考试 数学(理科)参考答案及评分标准一、选择题(每小题5分,共40分)D ADC BAAC二、填空题(每小题5分,共35分)(一)选做题(9-11题,考生只能从中选做2题,如果多做则按前两题计分)9. 2cos 0ρθ+= 10.1(1,)3-- 11. (二)必做题(12-16题)12. 90 13. i 14. -10 15. <16. (1)15(2)7 三、解答题(本大题共6小题,共75分,解答须写出文字说明、证明过程或演算步骤) 17.(本题满分12分)解:(1)20人只有2人过关,过关率为110,估计100名学员中有11001010⨯=人一次过关; …………3分(2)设“过科目一、二、三”分别为事件A 、B 、C ,过科目一的12人中有2人过了科目二却没过科目三,故P =21(|)126P BC A ==;…6分 (3)设这个学员一次过关的科目数为η,则η的分布列为: …………………8分E η=22119012355101010⨯+⨯+⨯+⨯=, ………………10分 ξ=100η,E (ξ)=E (100η)=100 ×E (η)=100×910=90. ………………12分18.(本小题满分12分)解法一(1)证明:连接OE ,OF ,由图1知:OE //AC ,OF //AD ,而OE ,OF 不在平面ACD 上,且OE 交OF 于O ,故平面OEF //平面ACD ,所以EF //平面ACD . ………………5分(2)取AD 的中点G ,连接OG ,则∠CGO 就是二面角C -AD -O 的平面角, OGCO =2,………………9分90oCOG ∠=,tan CO CGO OG∠===, ………………11分故二面角C -AD -O.……………12分解法二:证明(1)如图建立空间直角坐标系,A (0,-2,0),C (0,0,2),D,-1,0), E(0,),,1,0),(0,2,2),AC =(3,1,0)AD =, (3,1EF =设平面ACD 的法向量(,,)m x y z =,依题意有:m AC m AD ⊥⊥⎧⎪⎨⎪⎩(,,)(0,2,2)220(,,)0)0m AC x y z y z m AD x y z y ⋅=⋅=+=⇒⊥=⋅=+=⎧⎪⎨⎪⎩,令x =-1,则y,z =,则(m =-,………………3分因为(m EF ⋅=-⋅-0==,所以m EF ⊥,又EF 不在平面ACD 上,故EF//平面ACD . ………………6分 (2)易求得平面OAD 的一个法向量(0,0,1)n =,设二面角C -AD -O 的大小为θ,由图知θ为锐角,(1,cos ||||||mn m n θ⋅-===,………………9分tan cos 3θθ===………………11分故二面角C -AD -O的正切值为3. ………………12分19.(本小题满分12分) 解:(1) 由|f (x )|=|2sin(3πx +6π)|=2得sin(3πx +6π)=±1, 即3πx +6π=k π+2π,∴ x =3k +1,k ∈N ,∴ {a n }是首项为1,公差为3的等差数列,∴ a n =3n -2,n ∈N *, …………4分3222n a n n b -==,{n b }是首项是2,公比是8的等比数列,其前n 项和2(18)2(81)187n nn S -==--; ………………6分 (2) 12231tan tan tan tan tan tan n n n T a a a a a a +=+++tan1tan 4tan 4tan 7tan(32)tan(31)n n =⋅+⋅++-⋅+, ………………8分由tan(31)tan(32)tan 3tan[(31)(32)]1tan(31)tan(32)n n n n n n +--=+--=++⋅-, ………………9分有tan(31)tan(32)tan(32)tan(31)1tan 3n n n n +---⋅+=-, ………………10分14473231n T n n =⋅+⋅++-⋅+tan tan tan tan tan()tan()4174107111333---=-+-+-+tan tan tan tan tan tan ()()()tan tan tan313213n n +--+-tan()tan()[]tan 3113n n +-=-tan()tan tan . ……………12分20.(本小题满分13分)解:(1) 设B (x 1,y 1),C (x 2,y 2),直线BC 过焦点F (0,1), 故设BC 的直线方程为y =kx +1,由 ⎩⎨⎧=+=yx kx y 412 得x 2-4kx -4=0,故x 1+x 2=4k ,x 1x 2=-4, ……………3分 ∴ |x 1-x 2|=212214)(x x x x -+=16162+k ∴ S △EBC =S △EBF +S △CEF =21|x 1| |EF |+21|x 2| |EF | =|x 1-x 2|=142+k =5,求得k =34±,此时,BC 方程为314y x =±+, 点 B 的坐标为(±4,4),故l 的方程为514y x =±-; ………………6分 (2)设B (x 1,y 1),A (x 3,y 3),l 方程:y =kx -1,由⎩⎨⎧=-=yx kx y 412, 得x 2-4kx +4=0,△=16k 2-16>0,k 2>1,故x 1+x 3=4k ,x 1x 3=4,又A 在E 与B 之间, ∴0<∣x 3∣<∣x 1∣, ∴0<|x 3|2<∣x 1 x 3∣=4, ∴0<∣x 3∣<2,x 1=34x ,直线BC 的方程为1111y y x x -=+, ………………9分 设M (3x ,y o ),点M 在直线BC 上,有13111o y y x x -=+,即2131141o x y x x -=+,整理得y o =2-234x ,M (3x ,2-234x ), (-2<3x <2且3x ≠0)|EM|==,令234x =t ,则(0,1)t ∈,|EM|==. ………………12分 线段EM长的取值范围为. ………………13分 21.(本题满分13分)解:(1)连结 OP ,因30o BAP ∠=,120o ABP ∠=30oAPB ∴∠=.在三角形PBO 中,222102021020cos120700OP =+-⨯⨯=22(1012)OP >+ 即22OP >故该外轮未进入我领海主权范围内. ………………5分 (2)作PQ AN ⊥于Q ,PS AB ⊥于S,则AQ SP ==30PQ =,因60oNAP ∠=,NMP θ∠=,首先应有60oθ>, 30sin PM θ=,30cos sin AM θθ=,设MP 方向的船速为V ,则我救助船全速到达P 点共所需时间为130cos 13030cos ()]sin sin sin T VV VVθλθθλθθλθ-=+⋅=⨯, ……………7分221cos 301cos 30()sin sin T VVθλθλθλθθ--'=⨯=⨯,令()0T θ'=得1cos θλ=.设使1cos θλ=的那个锐角为λθ,则当(60,)oλθθ∈时,()0T θ'<,当(,90)o λθθ∈时,()0T θ'>,()T θ在(60,)oλθ位减函数,在(,90)o λθ位增函数,(注:将(60,)o λθ写成 (0,)oλθ 不扣分)所以当1cos θλ=时()T θ能取得最小值. ………………9分另一方面,延长PC 与AN 交于0M ,须0QM QM ≥(即0QM P θ≥∠)救助船才能沿直线MP 航行.0cos cos QM P θ∠===≤,由1λ≤解得λ≥.此时0Q M P λθ≥∠,而当λ<时,0Q M P λθ<∠,由()T θ的单调性知θ取0QM P ∠时()T θ最小. ………………11分综上知,为使到达P 点的时间最短,当λ≥时,救助船选择的拐角θ应满足1cos θλ=;当λ<时,救助船应在0M 处拐头直朝P 点航行,此时cosθ=. ………………13分22.(本题满分13分)解:(1)∵()2ln()f x a x b =+,∴2()af x x b'=+,则()f x 在切点(0,2ln )A a b 处切线的 斜率2(0)a k f b '==,则()f x 在点(0,2ln )A a b 处切线方程为22ln a y x a b b =+.又由2()1x g x e =-,得2()2x g x e '=,则()g x 在切点B(0,0)处切线的斜率(0)2k g '==, 则()g x 在点B 处切线方程为2y x =. 由22ab= 和2ln 0a b =解得1a =,1b =. ()2ln(1)(1)f x x x =+>-,2()1xg x e =-. ………………4分(2)由002[1g(x x m ->+202x m x e <-, 令2()2h x x e =-要使22m x e <-[0,)+∞上有解,只需max [()]m h x <. ………………5分 ①当0x =时,(0)0h =,所以0m <; ………………6分②当0x >时,2()2x h x e '=-,∵0x >,有2≥,e 1x >,∴2()20x h x e '=-<函数2()2h x x e =-[0,)+∞上单调递减,所以max ()(0)0h x h ==, 所以0m <综合①②得实数m 的取值范围是(,0)-∞ ……………8分(3)令2()()()12ln(1)(1)x u x g x f x e x x =-=--+>-,则2222(1)2()211xx e x u x e x x +-'=-=++.∴当0x ≥时,由于21,11xex ≥+≥,所以 22(1)2x e x +≥∴()0u x '≥在0x ≥上恒成立, 函数()u x 在区间(0,)+∞上单调递增, ∴当0x >时,()(0)0u x u >=恒成立,故对于任意210x x >>,有2121()()g x x f x x ->-. ………………10分 又∵212121111()1011x x x x x x x x +--+-=>++,∴2212111ln(1)ln ln(1)ln(1)1x x x x x x +-+>=+-++. ∴2121()()()f x x f x f x ->-, ………………12分 从而2121()()()g x x f x f x ->-. ………………13分方法2:也可按下面思路:先证明212()2112()x x e x x -->- [构造2()12x u x e x =--,求导再分析单调性] 再证明2121ln(1)ln(1)x x x x ->+-+ [通过构造()ln(x 1)v x x =-+,求导后分析单调性](详略)。
2013届高考理科数学复习演练系列试题(附答案)

2013届高考理科数学复习演练系列试题(附答案)A级基础达标演练(时间:40分钟满分:60分)一、选择题(每小题5分,共25分)1.下列命题中的假命题是().A.∃x0∈R,lgx0=0B.∃x0∈R,tanx0=1C.∀x∈R,x3>0D.∀x∈R,2x>0解析对于A,当x0=1时,lgx0=0正确;对于B,当x0=π4时,tanx0=1,正确;对于C,当x<0时,x3<0错误;对于D,∀x∈R,2x>0,正确.答案C2.(2012•杭州高级中学月考)命题“∀x>0,x2+x>0”的否定是().A.∃x0>0,x20+x0>0B.∃x0>0,x20+x0≤0C.∀x>0,x2+x≤0D.∀x≤0,x2+x>0解析根据全称命题的否定是特称命题,可知该命题的否定是:∃x0>0,x20+x0≤0.答案B3.(★)(2012•郑州外国语中学月考)ax2+2x+1=0至少有一个负的实根的充要条件是().A.0<a≤1B.a<1C.a≤1D.0<a≤1或a<0解析(筛选法)当a=0时,原方程有一个负的实根,可以排除A、D;当a=1时,原方程有两个相等的负实根,可以排除B,故选C.答案C4.(2012•合肥质检)已知p:|x-a|<4;q:(x-2)(3-x)>0,若綈p 是綈q的充分不必要条件,则a的取值范围为().A.a<-1或a>6B.a≤-1或a≥6C.-1≤a≤6D.-1<a<6解析解不等式可得p:-4+a<x<4+a,q:2<x<3,因此綈p:x≤-4+a或x≥4+a,綈q:x≤2或x≥3,于是由綈p是綈q的充分不必要条件,可知2≥-4+a且4+a≥3,解得-1≤a≤6.答案C5.若函数f(x)=x2+ax(a∈R),则下列结论正确的是().A.∀a∈R,f(x)在(0,+∞)上是增函数B.∀a∈R,f(x)在(0,+∞)上是减函数C.∃a∈R,f(x)是偶函数D.∃a∈R,f(x)是奇函数解析对于A只有在a≤0时f(x)在(0,+∞)上是增函数,否则不成立;对于B,如果a≤0就不成立;对于D若a=0,则f(x)为偶函数了,因此只有C是正确的,即对于a=0时有f(x)=x2是一个偶函数,因此存在这样的a,使f(x)是偶函数.答案C二、填空题(每小题4分,共12分)6.(2012•西安模拟)若命题“∃x0∈R,2x20-3ax0+9<0”为假命题,则实数a的取值范围是________.解析因为“∃x0∈R,2x20-3ax0+9<0”为假命题,则“∀x∈R,2x2-3ax+9≥0”为真命题.因此Δ=9a2-4×2×9≤0,故-22≤a≤22.答案-22≤a≤227.已知命题p:x2+2x-3>0;命题q:13-x>1,若綈q且p为真,则x的取值范围是________.解析因为綈q且p为真,即q假p真,而q为真命题时,x-2x-3<0,即2<x<3,所以q假时有x≥3或x≤2;p为真命题时,由x2+2x-3>0,解得x>1或x<-3,由x>1或x<-3,x≥3或x≤2,得x≥3或1<x≤2或x<-3,所以x的取值范围是x≥3或1<x≤2或x<-3.故填(-∞,-3)∪(1,2]∪3,+∞).答案(-∞,-3)∪(1,2]∪3,+∞)8.(2012•南京五校联考)令p(x):ax2+2x+a>0,若对∀x∈R,p(x)是真命题,则实数a的取值范围是________.解析∵对∀x∈R,p(x)是真命题.∴对∀x∈R,ax2+2x+a>0恒成立,当a=0时,不等式为2x>0不恒成立,当a≠0时,若不等式恒成立,则a>0,Δ=4-4a2<0,∴a>1.答案a>1三、解答题(共23分)9.(11分)已知命题p:∀x∈1,2],x2-a≥0,命题q:∃x0∈R,x20+2ax0+2-a=0,若“p且q”为真命题,求实数a的取值范围.解由“p且q”为真命题,则p,q都是真命题.p:x2≥a在1,2]上恒成立,只需a≤(x2)min=1,所以命题p:a≤1;q:设f(x)=x2+2ax+2-a,存在x0∈R使f(x0)=0,只需Δ=4a2-4(2-a)≥0,即a2+a-2≥0⇒a≥1或a≤-2,所以命题q:a≥1或a≤-2.由a≤1,a≥1或a≤-2得a=1或a≤-2∴实数a的取值范围是a=1或a≤-2.10.(12分)写出下列命题的否定,并判断真假.(1)q:∀x∈R,x不是5x-12=0的根;(2)r:有些质数是奇数;(3)s:∃x0∈R,|x0|>0.解(1)綈q:∃x0∈R,x0是5x-12=0的根,真命题.(2)綈r:每一个质数都不是奇数,假命题.(3)綈s:∀x∈R,|x|≤0,假命题.B级综合创新备选(时间:30分钟满分:40分)一、选择题(每小题5分,共10分)1.下列命题错误的是().A.命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0无实数根,则m≤0”B.“x=1”是“x2-3x+2=0”的充分不必要条件C.若p∧q为假命题,则p,q均为假命题D.对于命题p:∃x0∈R,使得x20+x0+1<0,则綈p:∀x∈R,均有x2+x+1≥0解析依次判断各选项,易知只有C是错误的,因为用逻辑联结词“且”联结的两个命题中,只要一个为假整个命题为假.答案C2.(★)(2011•广东广雅中学模拟)已知p:∃x0∈R,mx20+2≤0.q:∀x∈R,x2-2mx+1>0,若p∨q为假命题,则实数m的取值范围是().A.1,+∞)B.(-∞,-1]C.(-∞,-2]D.-1,1]解析(直接法)∵p∨q为假命题,∴p和q都是假命题.由p:∃x0∈R,mx20+2≤0为假,得∀x∈R,mx2+2>0,∴m≥0.①由q:∀x∈R,x2-2mx+1>0为假,得∃x0∈R,x20-2mx0+1≤0,∴Δ=(-2m)2-4≥0⇒m2≥1⇒m≤-1或m≥1.②由①和②得m≥1.答案A【点评】本题采用直接法,就是通过题设条件解出所求的结果,多数选择题和填空题都要用该方法,是解题中最常用的一种方法.二、填空题(每小题4分,共8分)3.命题“∃x0∈R,x0≤1或x20>4”的否定是______________.解析已知命题为特称命题,故其否定应是全称命题.答案∀x∈R,x>1且x2≤44.(2012•太原十校联考)已知命题“∀x∈R,x2-5x+152a>0”的否定为假命题,则实数a的取值范围是________.解析由“∀x∈R,x2-5x+152a>0”的否定为假命题,可知命题“∀x∈R,x2-5x+152a>0”必为真命题,即不等式x2-5x+152a>0对任意实数x恒成立.设f(x)=x2-5x+152a,则其图象恒在x轴的上方.故Δ=25-4×152a<0,解得a>56,即实数a的取值范围为56,+∞.答案56,+∞三、解答题(共22分)5.(10分)已知两个命题r(x):sinx+cosx>m,s(x):x2+mx+1>0.如果对∀x∈R,r(x)与s(x)有且仅有一个是真命题.求实数m的取值范围.解∵sinx+cosx=2sinx+π4≥-2,∴当r(x)是真命题时,m<-2.又∵对∀x∈R,当s(x)为真命题时,即x2+mx+1>0恒成立有Δ=m2-4<0,∴-2<m<2.∴当r(x)为真,s(x)为假时,m<-2,同时m≤-2或m≥2,即m≤-2.当r(x)为假,s(x)为真时,m≥-2且-2<m<2,即-2≤m<2.综上,实数m的取值范围是m≤-2或-2≤m<2.6.(12分)已知c>0,设命题p:函数y=cx为减函数.命题q:当x∈12,2时,函数f(x)=x+1x>1c恒成立.如果p或q为真命题,p且q为假命题.求c的取值范围.解由命题p知:0<c<1.由命题q知:2≤x+1x≤52要使此式恒成立,则2>1c,即c>12.又由p或q为真,p且q为假知,p、q必有一真一假,当p为真,q为假时,c的取值范围为0<c≤12.当p为假,q为真时,c≥1.综上,c的取值范围为c0<c≤12或c≥1.。
2013年高考理科数学全国新课标卷2试题与答案word解析版
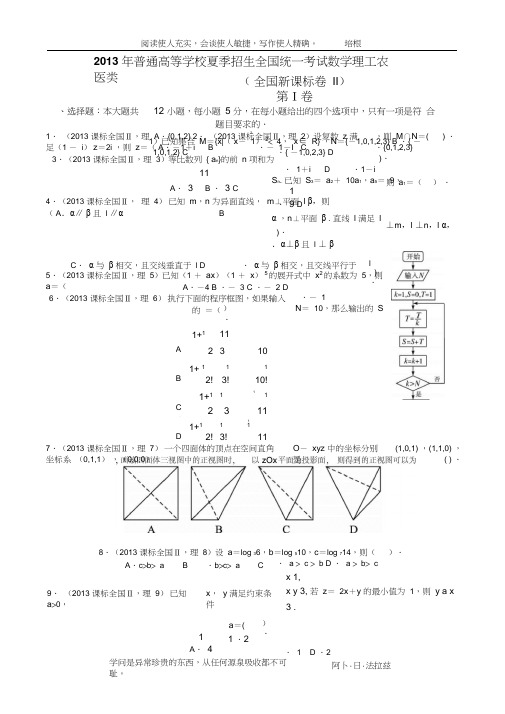
2013 年普通高等学校夏季招生全国统一考试数学理工农医类、选择题:本大题共 ( 全国新课标卷 II )第Ⅰ卷12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符 合题目要求的. 21)已知集合 M ={x |( x - 1) 2< 4, x ∈ R} ,N ={-1,0,1,2,3} B .{ -1,0,1,2} C .{ -1,0,2,3} D 1. (2013 课标全国Ⅱ,理 A .{0,1,2} 2. (2013 课标全国Ⅱ,理 2)设复数 z 满足(1 - i ) z =2i ,则 z =( A .-1+i B .- 1-I C3.(2013 课标全国Ⅱ,理 3)等比数列 { a n }的前 n 项和为 11A . 3B . 3C 4.(2013 课标全国Ⅱ, 理 4) 已知 m ,n 为异面直线, m ⊥平面 l β,则 ( A .α∥ β 且 l ∥α B,则 M ∩N =( ) . .{0,1,2,3} ). . 1+i D .1-i S n . 已知 S 3= a 2+ 10a 1,a 5= 9, 1. 9 D α ,n ⊥平面 β . 直线 l 满足 l )..α⊥β 且 l ⊥ β则 a 1=( ) .⊥m ,l ⊥n ,l α, C . α 与 β 相交,且交线垂直于 l D . α 与 β 相交,且交线平行于 5.(2013 课标全国Ⅱ,理 5)已知(1 + ax )(1 + x ) 5的展开式中 x 2的系数为 5,则a =( .- 1 N = 10,那么输出的 S A .-4 B .- 3 C .- 2 D6.(2013 课标全国Ⅱ,理 6) 执行下面的程序框图,如果输入的 =().A. 2 3 101+ 1 11B .2! 3!10!1+1 111C . 2 3111+1 1 1 1D 2! 3! 11 1+1 11 l ). 7.(2013 课标全国Ⅱ,理 7) 一个四面体的顶点在空间直角坐标系 (0,1,1) ,(0,0,0) O - xyz 中的坐标分别是 (1,0,1) ,(1,1,0) ,( ) .8.(2013 课标全国Ⅱ,理 8)设 a =log 36,b =log 510,c =log 714,则( ).. a > c > b D . a > b > cx 1,x y 3, 若 z = 2x +y 的最小值为 1,则 y a x 3 .A .c >b > aB .b >c > a C9. (2013 课标全国Ⅱ,理 9) 已知a >0,x , y 满足约束条件 a =( 1 .2). 1 A . 4 . 1 D .210.(2013 课标全国Ⅱ,理10)已知函数f(x) =x 3+ax2+bx+ c ,下列结论中错误的是( ).A.x0∈R,f(x0) =0B.函数y =f(x) 的图像是中心对称图形C.若x0 是f(x) 的极小值点,则f(x) 在区间( -∞,x0) 单调递减D.若x0 是f(x) 的极值点,则f′ (x0) =011.(2013 课标全国Ⅱ,理11)设抛物线C:y2=2px( p> 0)的焦点为F,点M在C上,| MF| =5,若以MF为直径的圆过点(0,2) ,则C的方程为( ) .A.y2 =4x 或y2=8x B .y2=2x 或y2=8xC.y2=4x 或y2=16x D .y2=2x 或y2=16x12.(2013 课标全国Ⅱ,理12)已知点A(-1,0) ,B(1,0) ,C(0,1) ,直线y=ax+b(a>0)将△ ABC分割为面积相等的两部分,则 b 的取值范围是( ) .12 , 11,12 ,11,1,1 A.(0,1) B.2 2 C . 2 3 D .3,2第Ⅱ卷本卷包括必考题和选考题两部分,第13题~第21 题为必考题,每个试题考生都必须做答。
山东省2013届高三高考模拟卷(二)理科数学.pdf

山东省2013届高三高考模拟卷(二) 数学()本试卷分第Ⅰ卷选择题和第Ⅱ卷非选择题两部分全卷满分150分考试时间120分钟 第Ⅰ卷 一选择题:本大题共1小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 满足,那么复数的虚部为 A.1 B. C. D. 2.已知集合,,,,,则 A.P=M B.Q=S 3.某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该种日用品中随机抽取200件,对其等级系数进行统计分析,得到频率的分布表如下: 则在所取的200件日用品中,等级系数X=1的件数为 A.40 B.20 C.30 D.60 :,,则 A.:, B.:, C.:, D.:, 5.如图所示,已知向量,,,,则下列等式中成立的是 A. B. C. D. 6.如图,若程序框图输出的S是254,则判断框①处应为 A. B. C. D. 7.在△ABC中角A,B,C的对边分别为,已知,且,,则△ABC的面积为 A. B. C. D. 8.已知函数是定义在R上的奇函数,当时,为常数),则函数的大致图象为 9.箱中装有标号为1,2,3,4,5,6且大小相同的6个球,从箱中一次摸出两个球,记下号码并放回,如果两球号码之积是4的倍数,则获奖.现有4人参与摸奖,恰好有3人获奖的概率是 A. B. C. D. 10.设O为坐标原点,点M的坐标为(2,1),若点满足不等式组,则使取得最大值的点N有 A.1个 B.2个 C.3个 D.无数个 11.若P是双曲线:和圆:的一个交点且,其中是双曲线的两个焦点,则双曲线的离心率为 A. B. C.2 D.3 12.已知函数,若存在正实数,使得方程在区间(2,+)上有两个根,其中,则的取值范围是 A. B. C. D. 第Ⅱ卷二、填空题:本大题共小题,每小题分. 13.设,则曲线在点处的切线的斜率为__________. 14.已知一个三棱锥的三视图如图所示,其中俯视图是等腰直角三角形,该三棱锥的外接球的半径为2,则该三棱锥的体积为_______. 15.的展开式中各项系数的和为1458,则该展开式中项的系数为_______. 16.设函数,其中表示不超过的最大整数,如,,若直线与函数的图象有三个不同的交点,则的取值范围是__________. 三、解答题:解答应写文字说明证明过程或演算步骤. 已知函数. (1)求的最小正周期及其单调增区间: (2)当时,求的值域. 18.(本小题满分12分) 如图,在三棱锥A-BCD中,△ABD和△BCD是两个全等的等腰直角三角形,O为BD的中点,且AB=AD=CB=CD=2,AC=. (1)当时,求证:AO⊥平面BCD; (2)当二面角的大小为时,求二面角的正切值. 19.(本小题满分12分) 某批发市场对某种商品的日销售量(单位:吨)进行统计,最近50天的统计结果如下表: 日销售量(吨)11.52天数102515(1)计算这50天的日平均销售量; (2)若以频率为概率,且每天的销售量相互独立. ①求5天中该种商品恰有2天的销售量为1.5吨的概率; ②已知每吨该商品的销售利润为2万元,X表示该种商品两天销售利润的和,求X的分布列和数学期望. 20.(本小题满分12分) 已知等差数列的首项,公差,且第2项、第5项、第14项分别是等比数列的第2项、第3项、第4项. (1)求数列、的通项公式; (2)设数列对任意的,均有成立,求. 21.(本小题满分13分) 已知中心在原点的椭圆C:的一个焦点为,为椭圆C上一点,的面积为. (1)求椭圆C的方程; (2)是否存在平行于OM的直线,使得直线与椭圆C相交于A,B两点,且以线段AB为直径的圆恰好经过原点?若存在,求出直线的方程;若不存在,请说明理由. 22.(本小题满分13分) 已知函数,. (1)若,求函数的单调区间; (2)若恒成立,求实数的取值范围; (3)设,若对任意的两个实数满足,总存在,使得成立,证明:. 数学() 一选择题: 14.2 15.61 16. 三、计算题 17.【解析】 . (1)函数的最小正周期. 由正弦函数的性质知,当, 即时,函数为单调增函数,所以函数的单调增区间为,. (2)因为,所以,所以, 所以,所以的值域为[1,3]. 18.【解析】(1)根据题意知,在△AOC中,,, 所以,所以AO⊥CO. 因为AO是等腰直角E角形ABD的中线,所以AO⊥BD. 又BDCO=O,所以AO⊥平面BCD. (2)法一 由题易知,CO⊥OD.如图,以O为原点, OC、OD所在的直线分别为轴、轴建立如图所示的空间直角坐标系, 则有O(0,0,0),,,. 设,则,. 设平面ABD的法向量为, 则即 所以,令,则. 所以. 因为平面BCD的一个法向量为, 且二面角的大小为,所以, 即,整理得. 因为,所以, 解得,,所以, 设平面ABC的法向量为, 因为,, 则即 令,则,.所以. 设二面角的平面角为,则 . 所以,即二面角的正切值为. 法二 在△ABD中,BD⊥AO,在△BCD中,BD⊥CO, 所以∠AOC是二面角的平面角,即∠AOC=. 如图,过点A作CO的垂线交CO的延长线于点H, 因为BD⊥CO,BD⊥AO,且COAO=O, 所以BD⊥平面AOC. 因为AH平面AOC,所以BD⊥AH. 又CO⊥AH,且COBD=O,所以AH⊥平面BCD. 过点A作AK⊥BC,垂足为K,连接HK. 因为BC⊥AH,AKAH=A,所以BC⊥平面AHK. 因为HK平面AHK,所以BC⊥HK, 所以∠AKH为二面角的平面角. 在△AOH中,∠AOH=,,则,, 所以. 在Rt△CHK中,∠HCK=,所以. 在Rt△AHK中,, 所以二面角的正切值为. 19.【解析】(1)日平均销售量为(吨). (2)①日销售量为1.5吨的概率. 设5天中该商品有Y天的销售量为1.5吨,则, 所以. ②X的所有可能取值为4,5,6,7,8.又日销售量为1吨的概率为,日销售量为2吨的概率为,则 ; ; ; ; . 所以X的分布列为 数学期望. 20.【解析】(1)由已知得,,, 所以,解得或. 又因为,所以. 所以. 又,,所以等比数列的公比, 所以. (2)由 ①,得当时, ②, ①-②,得当时,,所以2). 而时,,所以.所以. 所以 . 21.【解析】(1)因为椭圆C的一个焦点为, 所以,则椭圆C的方程为, 因为,所以,解得. 故点M的坐标为(1,4). 因为M(1,4)在椭圆上,所以,得, 解得或(不合题意,舍去),则. 所以椭圆C的方程为. (2)假设存在符合题意的直线与椭圆C相交于,两点,其方程为(因为直线OM的斜率, 由消去,化简得. 进而得到,. 因为直线与椭圆C相交于A,B两点, 所以, 化简,得,解得. 因为以线段AB为直径的圆恰好经过原点, 所以,所以. 又, , 解得. 由于,所以符合题意的直线存在,且所求的直线的方程为或. 22.【解析】(1)当时,函数, 则. 当时,,当时,1, 则函数的单调递减区间为(0,1),单调递增区间为(1,. (2)恒成立,即恒成立,整理得恒成立. 设,则,令,得.当时,,函数单调递增,当时,,函数单调递减,因此当时,取得最大值1,因而. (3),. 因为对任意的总存在,使得成立, 所以, 即, 即 . 设,其中,则,因而在区间(0,1)上单调递增,,又. 所以,即.。
2013届江苏省高三数学二轮专题训练解答题(20)

江苏省2013届高三数学二轮专题训练:解答题(20)本大题共6小题,解答时应写出文字说明、证明过程或演算步骤。
1. (本题满分14分)在平面直角坐标系xOy 中,已知点,sin ,cos ),0,56()(ααP A 其中20πα<<.(1)若,65cos =α求证:;PQ PA ⊥ (2)42sin(πα+的值.2. (本题满分14分)设集合{}32|≤≤-=x x A ,函数)34(log)(26+++=k x kx x f (1)当1-=k 时, 求函数)(x f 的值域.(2)若 B 为函数)(x f 的定义域,当A B ⊆时,求实数k 的取值范围.3. (本题满分14分)已知函数2()2cos cos f x x x x =+.(1)求函数()f x 在区间[,]63ππ-上的值域;(2)在△ABC 中,若()2f C =,2sin cos()cos()B A C A C =--+,求tan A 的值.BP4. (本题满分14分)已知函数()23x x f x a b =⋅+⋅,其中常数,a b 满足0a b ⋅≠(1)若0a b ⋅>,判断函数()f x 的单调性;(2)若b a 3-=,求(1)()f x f x +>时的x 的取值范围.5. (本题满分16分)如图△ABC 为正三角形,边长为2,以点A 为圆心,1为半径作圆,PQ 为圆A 的任意一条直径.⑴若12CDDB =,求||AD ; ⑵求CP BQ ⋅的最小值.⑶判断CQ BP ⋅+CP BQ ⋅的值是否会随点P 的变化而变化,请说明理由.6. (本题满分18分)已知函数||()2x m f x -=和函数()||28g x x x m m =-+-. (1)若2m =,写出函数)(x f 的对称轴方程、并求函数()g x 的单调区间;(2)若对任意1(,4]x ∈-∞,均存在2[4,)x ∈+∞,使得12()()f x g x =成立,求实数m 的取值范围.1. 解:(1)(方法一)由题设知).sin ,cos (),sin ,cos 56(a a PO a a PA --=--=所以2sin ()cos )(cos 56()a a a POPA -+--=⋅ .1cos 56sin cos cos 5622+-=++-=a a a a ……………………6分因为,65cos =a 所以.0=⋅PO PA 故.PO PA ⊥……………………7分(方法二)因为,65cos =a ,20π<<a 所以611sin =a ,故.611,65()P 因此).611,65(),611,3011(--=-=PO PA 因为.0)611()65(30112=-+-⨯=⋅PO PA所以.PO PA ⊥(2)因为,PO PA ⊥所以,22PO PA =即.sin cos sin )56cos 2222a a a a +=+-(解得.53cos =a ……………………9分因为,20π<<a 所以.54sin =a因此.2571cos 22cos ,2524cos sin 22sin 2-=-===a a a a a ……………………12分从而.50217)257(222524222cos 222sin 2242sin(=-⨯+⨯=+=+a a a )π……………14分2. 解:(1) 当1-=k 时, 66)2(3422≤+--=+++x k x kx ……………2分 ∴26log)(6=≤x f ……………4分∴函数)(x f 的值域为]2,(-∞……………5分(2)设g (x)=kx 2+4x+k+3,则B={x|g(x)>0}.①当k=0时,B=(-,+∞)⊈A,不合题意,故舍去. ……………7分②当k>0时,注意到g(x)的图象开口向上,显然B ⊈A,故舍去. ……………9分 ③当k<0时,由A B ⊆知解得-4<k ≤-.综上知k ∈(-4,-]. ……………14分3. 解:(1)f (x )=1+cos2x +3sin2x =2sin(2x +π6)+1. ………………………………3分因为-π6≤x ≤π3,所以-π6≤2x +π6≤5π6.……………………………………………5分所以-12≤sin(2x +π6)≤1.所以-1≤2sin(2x +π6)≤2所以f (x )∈[0,3].即函数f (x )在[-π6,π3]上的值域为[0,3].………………………7分(2)由f (C )=3得,2sin(2C +π6)+1=2,所以sin(2C +π6)=12.在△ABC 中,因为0<C <π,所以π6<2C +π6<13π6.所以2C +π6=5π6.所以C =π3,所以A +B =2π3. ………………………………………9分 因为2sin B =cos(A -C )-cos(A +C ).所以2sin B =2sin A sin C . …………………11分因为B =2π3-A , C =π3.所以2sin(2π3-A )=3sin A . 即3cos A +sin A =3sin A .即(3-1)sin A =3cos A .所以tan A =sin A cos A =33-1=3+32.………………14分4. 解:⑴ 当0,0a b >>时,任意1212,,x x R x x ∈<,则121212()()(22)(33)x x x x f x f x a b -=-+-∵121222,0(22)0x x x x a a <>⇒-<,121233,0(33)0x x x x b b <>⇒-<,∴12()()0f x f x -<,函数()f x 在R 上是增函数……………6分 当0,0a b <<时,同理函数()f x 在R 上是减函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
训练20 统计及其与概率的交汇问题
(时间:45分钟 满分:75分)
一、选择题(每小题5分,共25分)
1.(2012·珠海三模)要完成下列两项调查:①从某社区125户高收入家庭、200户中等收入家庭、95户低收入家庭中选出100户,调查社会购买能力的某项指标;②从某中学的5名艺术特长生中选出3名调查学习负担情况.宜采用的方法依次为
( ).
A .①简单随机抽样调查,②系统抽样
B .①分层抽样,②简单随机抽样
C .①系统抽样,②分层抽样
D .①②都用分层抽样
2.(2012·陕西五校联考)已知x 与y 之间的几组数据如下表:
则y 与x 的线性回归方程y =bx +a 必过
( ).
A .(1,3)
B .(2,5)
C .(1.5,4)
D .(3,7)
3.(2012·湖南)设某大学的女生体重y (单位:k g)与身高x (单位:cm)具有线性相关关系,根据一组样本数据(x i ,y i )(i =1,2,…,n ),用最小二乘法建立的回归方程为y ^
=0.85x -85.71,则下列结论中不正确的是
( ).
A .y 与x 具有正的线性相关关系
B .回归直线过样本点的中心(x ,y )
C .若该大学某女生身高增加1 cm ,则其体重约增加0.85 k g
D .若该大学某女生身高为170 cm ,则可断定其体重必为58.79 k g
4.“母亲节”当天某种鲜花进货价是每束2.5元,销售价是每束5元;当天卖不出去的鲜花以每束1.6元的价格处理.根据前四年销售情况预测,“母亲
节”当天这种鲜花的需求量X 服从如下表所示的分布列:
( ).
A .706元
B .690元
C .754元
D .720元
5.(2012·潍坊一模)随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图.现从乙班这10名同学中随机抽取两名身高不低于173 cm 的同学,则身高为176 cm 的同学被抽中的概率为
( ).
A.15
B.25
C.35
D.45 二、填空题(每小题5分,共15分)
6.(2012·泗县质检)防疫站对学生进行身体健康调查,采用分层抽样法抽取,泗县一中高三有学生1600人,抽取一个容量为200的样本,已知女生比男生少抽10人,则该校的女生人数应该有________.
7.将容量为n 的样本中的数据分为6组,绘制频率分布直方图,若第一组至第六组的数据的频率之比为2∶3∶4∶6∶4∶1,且前三组数据的频数之和为27,则n =________.
8.(2012·宝鸡三模)某产品的广告费用x 与销售额y 的统计数据如下表:
根据上表可得回归方程:y =b x +a 中的b 为7.据此模型,若广告费用为10元,则预报销售额等于________.
三、解答题(本题共3小题,共35分)
9.(11分)某班甲、乙两学生的高考备考成绩如下:
甲:512554528549536556534541522
538
乙:515558521543532559536548527
531
(1)用茎叶图表示两学生的高考备考成绩;
(2)分别求两学生的高考备考成绩的中位数和平均分.
10.(12分)(2012·合肥三模)某市对该市小微企业资金短缺情况统计如下表:
(2)某银行为更好的支持小微企业健康发展,从其第一批注资的A行业4家小
微企业和B行业的3家小微企业中随机选取4家小微企业,进行跟踪调研.设选取的4家小微企业中是B行业的小微企业的个数为随机变量ξ,求ξ的分布列.
11.(12分)(2012·北京)近年来,某市为了促进生活垃圾的分类处理,将生活垃圾分为厨余垃圾、可回收物和其他垃圾三类,并分别设置了相应的垃圾箱.为调查居民生活垃圾分类投放情况,现随机抽取了该市三类垃圾箱中总计1 000吨生活垃圾,数据统计如下(单位:吨):
(2)试估计生活垃圾投放错误的概率;
(3)假设厨余垃圾在“厨余垃圾”箱、“可回收物”箱、“其他垃圾”箱的投
放量分别为a,b,c,其中a>0,a+b+c=600.当数据a,b,c的方差s2最
大时,写出a ,b ,c 的值(结论不要求证明),并求此时s 2的值.
(注:s 2=1
n [(x 1-x )2+(x 2-x )2+…+(x n -x )2],其中x 为数据x 1,x 2,…,x n 的平均数)
参考答案
训练20 统计及其与概率的交汇问题
1.B
2.C [由题意知:样本中心点⎝ ⎛⎭
⎪⎫
32,4一定在回归直线上.]
3.D [由于回归直线的斜率为正值,故y 与x 具有正的线性相关关系,选项A 中的结论正确;回归直线过样本点的中心,选项B 中的结论正确;根据回归直线斜率的意义易知选项C 中的结论正确;由于回归分析得出的是估计值,故选项D 中的结论不正确.]
4.A [前四年“母亲节”当天售出鲜花的期望EX =200×0.2+300×0.35+400×0.3+500×0.15=340,则“母亲节”当天利润的均值为340×2.5+160×(-0.9)=706.]
5.B [从乙班这10名同学中随机抽取两名身高不低于173 cm 的同学,共有10种不同的取法.设A 表示随机事件“抽到身高为176 cm 的同学”,则A 中的基本事件有4个.故所求概率为P (A )=410=2
5.]
6.解析 设该校的女生为x 人,男生为(1 600-x )人,则按照分层抽样,各层的比例为2001 600=18,所以女生抽取x 8,男生抽取1 600-x 8,所以x
8+10=1 600-x 8,
解得x =760. 答案 760
7.解析 设第一组至第六组数据的频率分别为2x,3x,4x,6x,4x ,x ,则2x +3x +4x +6x +4x +x =1,解得,x =120,所以前三组数据的频率分别是110,320,1
5,故前三组数据的频数之和⎝ ⎛⎭⎪⎫110+320+15n =27,解得n =60. 答案 60
8.解析x=4.5,y=35,∴^
a=y-b x=3.5,
∴当x=10时,^
y=70+3.5=73.5(元)
答案73.5(元)
9.解(1)两学生的高考备考成绩的茎叶图如图所示:
(2)将甲、乙两学生的高考备考成绩从小到大排列为:
甲:512522528534536538541549554556 乙:515521527531532536543548558559 从以上排列可知
甲学生的高考备考成绩的中位数为
536+538
2=537.
乙学生的高考备考成绩的中位数为
532+536
2=534.
甲学生的高考备考成绩的平均分为
500+12+22+28+34+36+38+41+49+54+56
10=537;
乙学生的高考备考成绩的平均分为
500+15+21+27+31+32+36+43+48+58+59
10=537.
10.解(1)由统计表得,该市小微企业资金缺额的平均值约为x=10×0.05+30×0.1+50×0.35+70×0.3+90×0.2=60(万元).
(2)ξ的可能值为0,1,2,3则P(ξ=0)=C44
C47=
1
35,P(ξ=1)=
C34·C13
C47=
12
35,P(ξ=2)=
C24·C23 C47=18
35,P(ξ=3)=
C14·C33
C47=
4
35;
∴ξ的分布列为:
11.解 (1)“厨余垃圾”箱里厨余垃圾量厨余垃圾总量=400400+100+100
=2
3.
(2)设生活垃圾投放错误为事件A ,则事件A 表示生活垃圾投放正确.事件A 的概率约为“厨余垃圾”箱里厨余垃圾量、“可回收物”箱里可回收物量与“其他垃圾”箱里其他垃圾量的总和除以生活垃圾总量,即P (A )约为400+240+60
1 000=0.7,所以P (A )约为1-0.7=0.3.
(3)当a =600,b =c =0时,s 2取得最大值. 因为x =1
3(a +b +c )=200,
所以s 2=1
3[(600-200)2+(0-200)2+(0-200)2]=80 000. 即s 2的最大值为80 000.。
