2016-2017学年北京市东直门中学高二上学期期中考试数学(理)试题 解析版
北京市东城区2016-2017学年高二(上)期末数学试卷(解析版)(理科)

2016-2017学年北京市东城区高二(上)期末数学试卷(理科)一、选择题:(共大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线x﹣y+1=0的倾斜角的大小为()A.30°B.60°C.120° D.150°2.已知a∈R,命题“∀x∈(0,+∞),等式lnx=a成立”的否定形式是()A.∀x∈(0,+∞),等式lnx=a不成立B.∀x∈(﹣∞,0),等式lnx=a不成立C.∃x0∈(0,+∞),等式lnx0=a不成立D.∃x0∈(﹣∞,0),等式lnx0=a不成立3.若焦点在x轴上的椭圆的离心率为,则a的值为()A.9 B.6 C.3 D.24.某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是()A.B.C.D.85.设m,n是两条不同的直线,α,β是两个不同的平面,且m⊂α,n⊂β,下列命题中正确的是()A.若α⊥β,则m⊥n B.若α∥β,则m∥n C.若m⊥n,则α⊥βD.若n ⊥α,则α⊥β6.如图,长方体ABCD﹣A1B1C1D1中,,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为()A.2 B.C.D.7.已知A(﹣3,0),B(0,4),点P为直线y=x上一点,过A,B,P三点的圆记作圆C,则“点P为原点”是“圆C的半径取得最小值”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件8.图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是()A.B.C.D.二、填空题(本大题共6小题,每小题4分,共24分.请把答案填在答题卡中相应题中横线上)9.点(﹣1,1)到直线x+y﹣2=0的距离为.10.双曲线的渐近线方程为.11.若x,y满足约束条件则z=x+2y的最小值为.12.已知球的体积为36π,球的表面积是.13.已知点,点F为抛物线y2=2px(p>0)的焦点,点P是该抛物线上的一个动点.若|PF|+|PM|的最小值为5,则p的值为.14.已知直线l k:y=kx+k2(k∈R),下列说法中正确的是.(注:把你认为所有正确选项的序号均填上)①l k与抛物线均相切;②l k与圆x2+(y+1)2=1均无交点;③存在直线l,使得l与l k均不相交;④对任意的i,j∈R,直线l i,l j相交.三、解答题(本大题共6个小题,共52分,解答应写出文字说明,证明过程或演算步骤.)15.(9分)已知△ABC的顶点A(5,1),AB边上的中线CM所在的直线方程为2x﹣y﹣5=0,AC边上的高BH所在的直线方程为x﹣2y﹣5=0.求(Ⅰ)AC所在的直线方程;(Ⅱ)点B的坐标.16.(8分)三棱柱ABC﹣A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.(Ⅰ)求证:B1C1∥面BEF;(Ⅱ)过点A存在一条直线与平面BEF垂直,请你在图中画出这条直线(保留作图痕迹,不必说明理由).17.(9分)已知圆C的圆心在直线x﹣3y=0上,且与y轴相切于点(0,1).(Ⅰ)求圆C的方程;(Ⅱ)若圆C与直线l:x﹣y+m=0交于A,B两点,分别连接圆心C与A,B两点,若CA⊥CB,求m的值.18.(9分)如图1,在等边△ABC中,D,E,F分别为AB,AC,BC的中点.将△ABF沿AF折起,得到如图2所示的三棱锥A﹣BCF.(Ⅰ)证明:AF⊥BC;(Ⅱ)当∠BFC=120°时,求二面角A﹣DE﹣F的余弦值;(Ⅲ)在(Ⅱ)的条件下,在线段BC上是否存在一点N,使得平面ABF⊥平面FDN?若存在,求出的值;若不存在,说明理由.19.(9分)已知动点P到点A(﹣2,0)与点B(2,0)的斜率之积为,点P的轨迹为曲线C.(Ⅰ)求曲线C的轨迹方程;(Ⅱ)过点D(1,0)作直线l与曲线C交于P,Q两点,连接PB,QB分别与直线x=3交于M,N两点.若△BPQ和△BMN的面积相等,求直线l的方程.20.(8分)在平面直角坐标系中,设A(x1,y1),B(x2,y2).定义:,其中α∈R+(R+表示正实数).(Ⅰ)设A(1,1),B(2,3),求d1(A,B)和d2(A,B)的值;(Ⅱ)求证:对平面中任意两点A和B都有;(Ⅲ)设M(x,y),O为原点,记.若0<α<β,试写出Dα与Dβ的关系(只需写出结论,不必证明).2016-2017学年北京市东城区高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题:(共大题共8小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.直线x﹣y+1=0的倾斜角的大小为()A.30°B.60°C.120° D.150°【考点】直线的倾斜角.【分析】设直线x﹣y+1=0的倾斜角为θ,则tanθ=,θ∈[0°,180°).即可得出.【解答】解:设直线x﹣y+1=0的倾斜角为θ,则tanθ=,θ∈[0°,180°).∴θ=60°,故选:B.【点评】本题考查了直线的倾斜角与斜率的关系,考查了推理能力与计算能力,属于基础题.2.已知a∈R,命题“∀x∈(0,+∞),等式lnx=a成立”的否定形式是()A.∀x∈(0,+∞),等式lnx=a不成立B.∀x∈(﹣∞,0),等式lnx=a不成立C.∃x0∈(0,+∞),等式lnx0=a不成立D.∃x0∈(﹣∞,0),等式lnx0=a不成立【考点】命题的否定.【分析】根据全称命题的否定是特称命题进行求解判断.【解答】解:命题是全称命题,则命题的否定是:∃x0∈(0,+∞),等式lnx0=a不成立,故选:C【点评】本题主要考查含有量词的命题的否定,比较基础.3.若焦点在x轴上的椭圆的离心率为,则a的值为()A.9 B.6 C.3 D.2【考点】椭圆的简单性质.【分析】利用椭圆的离心率,列出方程求解即可.【解答】解:焦点在x轴上的椭圆,可得c=,离心率为,可得:,解得a=3.故选:C.【点评】本题考查椭圆的简单性质的应用,考查计算能力.4.某几何体的三视图如图所示,其中正视图是边长为2的正方形,俯视图是正三角形,则这个几何体的体积是()A.B.C.D.8【考点】棱柱、棱锥、棱台的体积;由三视图求面积、体积.【分析】由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱柱,代入柱体体积公式,可得答案.【解答】解:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱柱,底面是一个边长为2的等边三角形,故底面面积S==,高h=2,故体积V=Sh=2,故选:A【点评】本题考查的知识点是棱柱的体积和表面积,棱锥的体积和表面积,简单几何体的三视图,难度基础.5.设m,n是两条不同的直线,α,β是两个不同的平面,且m⊂α,n⊂β,下列命题中正确的是()A.若α⊥β,则m⊥n B.若α∥β,则m∥n C.若m⊥n,则α⊥βD.若n ⊥α,则α⊥β【考点】空间中直线与平面之间的位置关系;空间中直线与直线之间的位置关系.【分析】对4个命题分别进行判断,即可得出结论.【解答】解:对于A,若α⊥β,则m、n位置关系不定,不正确;对于B,若α∥β,则m∥n或m,n异面,不正确;对于C,若m⊥n,则α、β位置关系不定,不正确;对于D,根据平面与平面垂直的判定可知正确.故选D.【点评】本题考查了空间线面、面面平行和垂直关系,面面平行的判定定理,线面垂直的定义及其应用,空间想象能力6.如图,长方体ABCD﹣A1B1C1D1中,,E为BC的中点,则异面直线A1E与D1C1所成角的正切值为()A.2 B.C.D.【考点】异面直线及其所成的角.【分析】以D原点,DA为x轴,AC为y轴,DD1为z轴,建立空间直角系,利用向量法能求出异面直线A1E与D1C1所成角的正切值.【解答】解:以D原点,DA为x轴,AC为y轴,DD1为z轴,建立空间直角系,设=1,则A1(1,0,2),E(,1,0),C1(0,1,2),D1(0,0,2),=(﹣,1,﹣2),=(0,1,0),设异面直线A1E与D1C1所成角为θ,则cosθ===,sinθ==,∴tanθ==.∴异面直线A1E与D1C1所成角的正切值为.故选:C.【点评】本题考查异面直线所成角的正切值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.7.已知A(﹣3,0),B(0,4),点P为直线y=x上一点,过A,B,P三点的圆记作圆C,则“点P为原点”是“圆C的半径取得最小值”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】结合直线和圆的位置关系以及充分条件和必要条件的定义进行判断即可.【解答】解:当点P为原点时,三角形AOB是直角三角形,此时AB是圆的直径,此时圆C的半径最小,即充分性成立,当C的半径取得最小值,AB是圆的直径,当以AB为直径的圆和直线y=x相切时,切点不是O,即必要性不成立,则点P为原点”是“圆C的半径取得最小值”的充分不必要条件,故选:A【点评】本题主要考查充分条件和必要条件的判断,结合直线和圆的位置关系是解决本题的关键.8.图中的两条曲线分别表示某理想状态下捕食者和被捕食者数量随时间的变化规律.对捕食者和被捕食者数量之间的关系描述正确的是()A.B.C.D.【考点】函数的图象.【分析】由已知可得:捕食者和被捕食者数量与时间以10年为周期呈周期性变化,故捕食者和被捕食者数量之间的关系应为环状,进而得到答案.【解答】解:由已知中某理想状态下捕食者和被捕食者数量随时间的变化规律.可得捕食者和被捕食者数量与时间以10年为周期呈周期性变化,故捕食者和被捕食者数量之间的关系应为环状,故选:B【点评】本题考查的知识点是函数的图象,复变函数的图象和性质,本题比较抽象,理解起来有一定的难度.二、填空题(本大题共6小题,每小题4分,共24分.请把答案填在答题卡中相应题中横线上)9.点(﹣1,1)到直线x+y﹣2=0的距离为.【考点】点到直线的距离公式.【分析】利用点到直线的距离公式求解.【解答】解:点(﹣1,1)到直线x+y﹣2=0的距离为d==,故答案为.【点评】本题考查点到直线的距离公式的求法,是基础题.10.双曲线的渐近线方程为y=±x.【考点】双曲线的简单性质.【分析】先确定双曲线的焦点所在坐标轴,再确定双曲线的实轴长和虚轴长,最后确定双曲线的渐近线方程.【解答】解:∵双曲线的a=2,b=1,焦点在x轴上而双曲线的渐近线方程为y=±∴双曲线的渐近线方程为y=±故答案为:y=±【点评】本题考察了双曲线的标准方程,双曲线的几何意义,特别是双曲线的渐近线方程,解题时要注意先定位,再定量的解题思想11.若x,y满足约束条件则z=x+2y的最小值为3.【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用z的几何意义即可得到结论.【解答】解:作出不等式组对应的平面区域,由z=x+2y,得y=,平移直线y=,由图象可知当直线经过点C 时,直线y=的截距最小,此时z最小,由,得,即C(3,0)此时z=3+2×0=3.故答案为:3【点评】本题主要考查线性规划的应用,利用图象平行求得目标函数的最小值,利用数形结合是解决线性规划问题中的基本方法.12.已知球的体积为36π,球的表面积是36π.【考点】球的体积和表面积.【分析】通过球的体积求出球的半径,然后求出球的表面积.【解答】解:因为球的体积为36π,所以=36π,球的半径为:r=3,所以球的表面积为:4π×32=36π.故答案为:36π.【点评】本题考查球的表面积与体积的求法,考查计算能力.13.已知点,点F为抛物线y2=2px(p>0)的焦点,点P是该抛物线上的一个动点.若|PF|+|PM|的最小值为5,则p的值为2或6.【考点】直线与抛物线的位置关系.【分析】分类讨论,利用|PF|+|PM|的最小值为5,求出p的值.【解答】解:M在抛物线的内部时,∵抛物线上的点到焦点距离=到准线的距离,∴|PM|+|PF|=|PM|+P到准线的距离≤M到到准线的距离l=2+=5,解得p=6,M在抛物线的外部时,|MF|=5,=5,∴p=2综上所述,p=2或6.故答案为:2或6.【点评】本题考查抛物线的方程与定义,考查分类讨论的数学思想,属于中档题.14.已知直线l k:y=kx+k2(k∈R),下列说法中正确的是①③④.(注:把你认为所有正确选项的序号均填上)①l k与抛物线均相切;②l k与圆x2+(y+1)2=1均无交点;③存在直线l,使得l与l k均不相交;④对任意的i,j∈R,直线l i,l j相交.【考点】命题的真假判断与应用.【分析】根据已知中直线l k:y=kx+k2(k∈R),逐一分析四个结论的真假,可得答案.【解答】解:由得:,由△=0恒成立,可得方程组恒有一解,即l k与抛物线均相切,故①正确;圆x2+(y+1)2=1的圆心(0,﹣1)到直线l k:y=kx+k2的距离d==≥1恒成立,当且仅当k=0时,l k与圆x2+(y+1)2=1相切,故②错误;存在直线l:y=x+1,y=﹣x+1,y=0,与直线l k:y=kx+k2(k∈R)均不相交,故③正确;对任意的i,j∈R,直线l i,l j的斜率不相等,两直线必相交,故④正确;故答案为:①③④【点评】本题以命题的真假判断与应用为载体,考查了直线与直线的位置关系,直线与圆的位置关系等知识点,难度中档.三、解答题(本大题共6个小题,共52分,解答应写出文字说明,证明过程或演算步骤.)15.已知△ABC的顶点A(5,1),AB边上的中线CM所在的直线方程为2x﹣y ﹣5=0,AC边上的高BH所在的直线方程为x﹣2y﹣5=0.求(Ⅰ)AC所在的直线方程;(Ⅱ)点B的坐标.【考点】直线的一般式方程.【分析】(Ⅰ)设AC所在的直线方程为2x+y+t=0,代入A(5,1),即可AC 所在的直线方程;(Ⅱ)设B(x0,y0),则AB的中点为.联立方程组,即可求出点B的坐标.【解答】解:(Ⅰ)因为AC⊥BH,所以设AC所在的直线方程为2x+y+t=0.把A(5,1)代入直线方程为2x+y+t=0,解得t=﹣11.所以AC所在的直线方程为2x+y﹣11=0.…(Ⅱ)设B(x0,y0),则AB的中点为.联立方程组化简得解得即B(﹣1,﹣3).…(9分)【点评】本题考查直线方程,考查直线与直线的位置关系,考查学生的计算能力,属于中档题.16.三棱柱ABC﹣A1B1C1中,AB=AC,侧棱AA1⊥平面ABC,E,F分别为A1B1,A1C1的中点.(Ⅰ)求证:B1C1∥面BEF;(Ⅱ)过点A存在一条直线与平面BEF垂直,请你在图中画出这条直线(保留作图痕迹,不必说明理由).【考点】直线与平面平行的判定;直线与平面垂直的判定.【分析】(Ⅰ)利用已知及三角形的中位线定理可证EF∥B1C1,进而利用线面平行的判定定理即可得证.(Ⅱ)利用线面垂直的性质及判定定理即可作图得解.【解答】(本题满分8分)证明:(Ⅰ)∵E,F分别为A1B1,A1C1的中点,∴EF∥B1C1.又∵EF⊂面BEF,B1C1⊄面BEF,∴B1C1∥面BEF.…(Ⅱ)作图如下:…(8分)【点评】本题主要考查了三角形的中位线定理,线面平行的判定定理,线面垂直的性质及判定定理的综合应用,考查了数形结合思想,考查了空间想象能力和推理论证能力,属于中档题.17.已知圆C的圆心在直线x﹣3y=0上,且与y轴相切于点(0,1).(Ⅰ)求圆C的方程;(Ⅱ)若圆C与直线l:x﹣y+m=0交于A,B两点,分别连接圆心C与A,B两点,若CA⊥CB,求m的值.【考点】圆方程的综合应用;直线与圆的位置关系.【分析】(Ⅰ)设圆心坐标为C(a,b),推出a=3b.利用切点坐标,求出圆心与半径,然后求出圆的方程.(Ⅱ)判断△ABC为等腰直角三角形.利用点到直线的距离公式化简求解即可.【解答】(本题满分9分)解:(Ⅰ)设圆心坐标为C(a,b),圆C的圆心在直线x﹣3y=0上,所以a=3b.因为圆与y轴相切于点(0,1),则b=1,r=|a﹣0|.所以圆C的圆心坐标为(3,1),r=3.则圆C的方程为(x﹣3)2+(y﹣1)2=9.…(Ⅱ)因为CA⊥CB,|CA|=|CB|=r,所以△ABC为等腰直角三角形.因为|CA|=|CB|=r=3,则圆心C到直线l的距离.则,求得m=1或﹣5.…(9分)【点评】本题考查直线与圆的位置关系的应用,考查转化思想以及计算能力.18.如图1,在等边△ABC中,D,E,F分别为AB,AC,BC的中点.将△ABF 沿AF折起,得到如图2所示的三棱锥A﹣BCF.(Ⅰ)证明:AF⊥BC;(Ⅱ)当∠BFC=120°时,求二面角A﹣DE﹣F的余弦值;(Ⅲ)在(Ⅱ)的条件下,在线段BC上是否存在一点N,使得平面ABF⊥平面FDN?若存在,求出的值;若不存在,说明理由.【考点】二面角的平面角及求法;直线与平面垂直的性质.【分析】(Ⅰ)推导出AF⊥BF,AF⊥FC.由此能证明AF⊥BC.(II)以点F为原点,在平面BCF内过点F作FC的垂线作为x轴,FC为y轴,FA为z轴,建立空间直角坐标系.利用向量法能求出二面角A﹣DE﹣F的余弦值.(III)在平面BCF内,过F作FN⊥BF交BC于N,推导出AF⊥FN,从而FN⊥面ABF,进而面ABF⊥面DFN.由此能求出在线段BC上存在一点N,满足面ABF⊥面DFN,且.【解答】(本题满分9分)证明:(Ⅰ)∵等边△ABC,F为BC的中点,∴AF⊥BC.即AF⊥BF,AF⊥FC.又∵BF∩FC=F,∴AF⊥面BCF.又∵BC⊂面BCF,∴AF⊥BC.…解:(II)如图,以点F为原点,在平面BCF内过点F作FC的垂线作为x轴,FC为y轴,FA为z轴,建立空间直角坐标系.设FC=2,则有F(0,0,0),,,C(0,2,0),∴,.∴,,,.设平面DEF的法向量为=(x1,y1,z1),因此,即,令z1=1,则=(﹣3,﹣,1).设平面ADE的法向量为=(x2,y2,z2),因此有,即,令z2=1,则=(3,,1).∴cos<>===﹣.∴二面角A﹣DE﹣F的余弦值为.…(6分)(III)在线段BC上存在一点N,满足面ABF⊥面DFN,且.证明如下:在平面BCF内,过F作FN⊥BF交BC于N,∵AF⊥面BCF,FN⊂面BCF,∴AF⊥FN.又∵FN⊥BF,AF∩BF=F,∴FN⊥面ABF.又∵FN⊂面DFN,∴面ABF⊥面DFN.设FN=a,∵∠BFC=120°,BF=FC,∴∠FBC=∠FCB=30°.又∵FN⊥BF,∴BN=2a.∵∠NFC=∠FCN=30°,∴FN=NC=a.∴BC=3a.∴.…(9分)【点评】本题考查线线垂直的证明,考查二面角的余弦值的求法,考查满足条件的点的位置的判断与求法,是中档题,解题时要认真审题,注意向量法的合理运用.19.已知动点P到点A(﹣2,0)与点B(2,0)的斜率之积为,点P的轨迹为曲线C.(Ⅰ)求曲线C的轨迹方程;(Ⅱ)过点D(1,0)作直线l与曲线C交于P,Q两点,连接PB,QB分别与直线x=3交于M,N两点.若△BPQ和△BMN的面积相等,求直线l的方程.【考点】直线与圆锥曲线的综合问题;轨迹方程.【分析】(Ⅰ)设P点的坐标为(x,y),求出直线的斜率,利用斜率乘积,化简求解即可.(Ⅱ)当直线l的斜率不存在时,直线的方程为x=1,求出两个三角形的面积,判断相等,当直线l的斜率存在时,法1:设直线的方程为y=k(x﹣1),P(x1,y1),Q(x2,y2).联立直线与椭圆方程,求出M,N坐标,通过△BPQ和△BMN的面积不相等,推出结果.法2:设直线的方程为y=k(x﹣1),P(x1,y1),Q(x2,y2).联立直线与椭=S△BMN,得到.推出﹣1=0.说明△BPQ和△BMN 圆方程,通过S△BPQ的面积不相等.【解答】(本题满分9分)解:(Ⅰ)设P点的坐标为(x,y),则,.∵,∴.化简得曲线C的轨迹方程为.…(Ⅱ)当直线l的斜率不存在时,直线的方程为x=1,则.直线PB的方程为,解得.直线QB的方程为,解得.则,.此时△BPQ和△BMN的面积相等…(6分)当直线l的斜率存在时,法1:设直线的方程为y=k(x﹣1),P(x1,y1),Q(x2,y2).由得(1+4k2)x2﹣8k2x+4k2﹣4=0.,.直线PB的方程为,求得.直线QB的方程为,求得.,.=S△BMN,则(2﹣x1)(2﹣x2)=1,即x1x2﹣2(x1+x2)+3=0.若S△BPQ∴,化简得﹣1=0.此式不成立.所以△BPQ和△BMN的面积不相等综上,直线l的方程为x=1.…(9分)法2:设直线的方程为y=k(x﹣1),P(x1,y1),Q(x2,y2).由得(1+4k2)x2﹣8k2x+4k2﹣4=0.,.,,=S△BMN,因为∠PBQ=∠MBN,S△BPQ所以|BQ||BP|=|BM||BN|,即.则有,化简得x1x2﹣2(x1+x2)+3=0.∴,化简得﹣1=0.此式不成立.所以△BPQ和△BMN的面积不相等综上,直线l的方程为x=1.…(9分)【点评】本题考查直线与椭圆的位置关系的综合应用,轨迹方程的求法,考查转化思想以及计算能力.20.在平面直角坐标系中,设A(x1,y1),B(x2,y2).定义:,其中α∈R+(R+表示正实数).(Ⅰ)设A(1,1),B(2,3),求d1(A,B)和d2(A,B)的值;(Ⅱ)求证:对平面中任意两点A和B都有;(Ⅲ)设M(x,y),O为原点,记.若0<α<β,试写出Dα与Dβ的关系(只需写出结论,不必证明).【考点】函数与方程的综合运用.【分析】(Ⅰ)dα(A,B)的定义代入即可得出.(Ⅱ)设A(x1,y1),B(x2,y2),则d1(A,B)=|x1﹣x2|+|y1﹣y2|,.通过计算展开即可证明.(Ⅲ)Dα⊂Dβ真子集.任取(x0,y0)∈Dα,.对x0,y0分类讨论,即可证明.【解答】(Ⅰ)解:d1(A,B)=|1﹣2|+|1﹣3|=3,d2(A,B)===.(Ⅱ)证明:设A(x1,y1),B(x2,y2),则d1(A,B)=|x1﹣x2|+|y1﹣y2|,.=.=.所以d2(A,B)≤d1(A,B)成立.因为,所以===.所以成立.(Ⅲ)Dα⊂Dβ真子集.证明如下:任取(x0,y0)∈Dα,.当x0=1,y0=0时,dα(M,O)=0,dβ(M,O)=0,此时Dα⊆Dβ.当|x0|=1,|y0|=0时,,dβ(M,O)=1.此时Dα⊆Dβ.同理可得,当|x0|=0,|y0|=1时,Dα⊆Dβ.当|x0|≠1,|y0|≠1时,因为,所以.又因为0<α<β,所以.此时Dα⊆Dβ.反之不成立.所以Dα⊂Dβ.【点评】本题考查了新定义、集合之间的关系、两点之间的距离公式、分类讨论方法、不等式的解法,考查了推理能力与计算能力,属于难题.。
2017北京市东直门中学高三(上)期中数学(理)

2017北京市东直门中学高三(上)期中数 学(理)一、选择题:本大题共8小题,每小题5分满分40分.在每小题给出的四个选项中,只有一项符合要求.1.设集合{}|1P x x =>,{}2|0Q x x x =−>,则下列结论正确的是( ).A .P Q =B .P Q =RC .Q P ÜD .P Q Ü 2.复数z 满足i 3i z ⋅=−,则在复平面内,复数z 对应的点位于( ).A .第一象限B .第二象限C .第三象限D .第四象限3.如果平面向量(2,0)a =,(1,1)b =,那么下列结论中正确的是( ).A .||||a b =B .22a b ⋅=C .()a b b −⊥D .a b4.设函数π()sin 23f x x ⎛⎫=− ⎪⎝⎭的图象为C ,下面结论中正确的是( ).A .函数()f x 满足π()2f x f x ⎛⎫−= ⎪⎝⎭B .图象C 关于点π,06⎛⎫⎪⎝⎭对称C .图象C 可由函数()sin 2g x x =的图象向右平移π3个单位得到 D .函数()f x 在区间ππ,122⎛⎫− ⎪⎝⎭上是增函数5.在ABC 中,π4A =,2BC =,则“3AC =”是“π3B =”的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知函数x y a =,b y x =,log c y x =的图象如图所示,则( ).A .a b c >>B .a c b >>C .c a b >>D .c b a >>7.已知函数,0,(),0.x x f x x x −<⎧⎪=⎨⎪⎩≥若关于x 的方程()(1)f x a x =+有三个不相等的实数根,则实数a 的取值范围是( ).A .1,2⎡⎫+∞⎪⎢⎣⎭B .(0,)+∞C .(0,1)D .10,2⎛⎫⎪⎝⎭8.如图所示,正方体ABCD A B C D ''''−的棱长为1,E ,F 分别是棱AA ',CC '的中点,过直线E ,F 的平面分别与棱BB ',DD '交于M ,N ,设BM x =,(0,1)x ∈,给出以下四个命题:①四边形MENF 为平行四边形;②若四边形MENF 面积()S f x =,(0,1)x ∈,则()f x 有最小值; ③若四棱锥A MENF −的体积()V p x =,(0,1)x ∈,则()p x 是常函数; ④若多面体ABCD MENF −的体积()V h x =,1,12x⎛⎫∈ ⎪⎝⎭,则()h x 为单调函数.其中假命题...为( ). A .①B .②C .③D .④二、填空题:本大题共6小题,每小题5分,满分30分9.已知命题:0p c ∃>,方程20x x c −+=有解,则p ⌝为__________. 10.已知π02α−<<,且4cos 5α=,则πtan 4α⎛⎫+ ⎪⎝⎭的值等于__________.11.若||3a =,||2b =,且a 与b 的夹角为π3,则||a b −=__________. 12.ππ(sin )d x x x −+=⎰__________. 13.如图,11AB C ,122C B C ,233C B C 是三个边长为2的等边三角形,且有一条边在同一直线上,边33B C 上有2个不同的点1P ,2P ,则212()AB AP AP ⋅+=__________.14.已知函数()f x 的定义域为R ,a ∀,b ∈R ,若此函数同时满足: ①当0a b +=时有()()0f a f b +=;②当0a b +>时有()()0f a f b +>,则称函数()f x 为Ω函数. 在下列函数中:①sin y x x =+;②133xx y ⎛⎫=− ⎪⎝⎭;③0,01,0x y x x=⎧⎪=⎨−≠⎪⎩是Ω函数的为__________(填出所有符合条件的函数序号).三、解答题:本大题共6小题,满分80分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13分) 已知函数3()cos (sin 3cos )2f x x x x =+−,x ∈R . (1)求()f x 的最小正周期和单调递增区间.如图所示,在四边形ABCD 中,2D B ∠=∠,且1AD =,3CD =,3cos 3B =.(1)求ACD 的面积.(2)若23BC =,求AB 的长.17.(本小题满分13分)手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间.为了解A ,B 两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A ,B 两个型号的手机各7台,在相同条件下进行测试,统计结果如下, 手机编号1234 5 6 7 A 型待机时间(h ) 120 125 122 124 124 123 123 B 型待机时间(h ) 118 123 127 120 124 a b其中,a ,b 是正整数,且a b <.(1)该卖场有56台A 型手机,试估计其中待机时间不少于123小时的台数.(2)从A 型号被测试的7台手机中随机抽取4台,记待机时间大于123小时的台数为X ,求X 的分布列及其数学期望.(3)设A ,B 两个型号被测试手机待机时间的平均值相等,当B 型号被测试手机待机时间的方差最小时,写出a ,b 的值(结论不要求证明).在如图所示的几何体中,四边形ABCD 为正方形,四边形ABEF 为直角梯形,且AF BE ,AB BE ⊥,平面ABCD平面ABEF AB =,22AB BE AF ===.(1)求证:AC 平面DEF .(2)若二面角D AB E −−为直二面角, (i )求直线AC 与平面CDE 所成角的大小.(ii )棱DE 上是否存在点P ,使得BP ⊥平面DEF ?若存在,求出DPDE的值;若不存在,请说明理由.19.(本小题满分14分) 已知函数2()e ()x f x x ax a =++.(1)当1a =时,求曲线()y f x =在点(0,(0))f 处的切线方程. (2)求()f x 的单调区间.(3)求证:当4a ≥时,函数()f x 存在最小值.20.(本小题满分13分) 已知集合{}123,,,,n A a a a a =,其中i a ∈R ,1i n ≤≤,2n >.()l A 表示(1)i j a a i j n +<≤≤中所有不同值的个数.(1)设集合{}2,4,6,8P =,{}2,4,8,16Q =,分别求()l P 和()l Q . (2)若集合{}2,4,8,,2n A =,求证:(1)()2n n l A −=. (3)()l A 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.数学试题答案一、选择题:本大题共8小题,每小题5分满分40分.在每小题给出的四个选项中,只有一项符合要求. 1. 【答案】D【解析】∵集合{}|1P x x =>,集合{}{2|0|0Q x x x x x =−>=<或}1x >,∴P Q Ü. 故选D . 2. 【答案】C【解析】∵i 3i z ⋅=−,∴223i (3i)i 3i i 13i 1i 1z −−−====−−−, ∴其对应的点是(1,3)−−,位于第三象限. 故选C . 3. 【答案】C【解析】由平面向量(2,0)a =,(1,1)b =知: 在A 中,||2a =,||2b =, ∴||||a b ≠,故A 错误; 在B 中,2a b ⋅=,故B 错误; 在C 中,(1,1)a b −=−, ∴()110a b b −⋅=−=, ∴()a b b −⊥,故C 正确; 在D 中,∵2011≠, ∴a 与b 不平行,故D 错误. 综上所述. 故选C . 4 【答案】B【解析】A 项.∵π()sin 23f x x ⎛⎫=− ⎪⎝⎭,∴πππsin 2πsin 2()233f x x x f x ⎛⎫⎛⎫⎛⎫−=−−=−−=− ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故A 错误;B 项.∵πππsin 2sin 00663f ⎛⎫⎛⎫=⨯−== ⎪ ⎪⎝⎭⎝⎭,∴()f x 的图象C 关于点π,06⎛⎫⎪⎝⎭对称,故B 正确;∴()f x 的图象C 由函数()sin 2g x x =的图象向右平移π6个单位得到,故C 错误; D 项,当ππ,122x ⎛⎫∈− ⎪⎝⎭时,ππ2π2,323x ⎛⎫−∈− ⎪⎝⎭,∴函数()f x 在区间ππ,122⎛⎫− ⎪⎝⎭上先增后减,故D 错误.5. 【答案】B【解析】由正弦定理可得sin sin AC BCB A=, ∴若π3B =,则2ππsin sin 34AC =,得π2sin33πsin 4AC ==,必要性成立;若3AC =,则32πsin sin 4B =,得π3sin34sin 22B ==,π3B =或2π3,充分性不成立, ∴“3AC =”是“π3B =”的必要不充分条件. 故选B . 6. 【答案】C【解析】根据函数的图象知,函数x y a =是指数函数, 且当1x =时,(1,2)y a =∈;函数b y x =是幂函数,且2x =时,2(1,2)b y =∈, ∴(0,1)b ∈;函数log c y x =是对数函数,且当2x =时,log 2(0,1)c y =∈, ∴2c >.综上所述,a ,b ,c 的大小是c a b >>. 故选C . 7. 【答案】D【解析】作出函数()y f x =的图象,如图所示,作出函数(1)y a x =+, 则直线恒过点(1,0)−,关于x 的方程()(1)f x a x =+有三个不相等的实数根, 即为直线与曲线y x =相交时, 当()f x 的图象有三个交点,当直线与曲线y x =相切时,设切点为(,)m m , 则112y x'=⋅, 则切线斜率为112a m⋅=, 又(1)a m m +=, 由此解得12a =(负值舍去), 所以实数a 的取值范围是10,2⎛⎫⎪⎝⎭.故选D . 8. 【答案】D【解析】对于①,∵平面ADD A ''平面BCC B '', ∴ENMF ,同理:FNEM ,∴四边形MENF 为平行四边形,故①正确;对于②,四边形MENF 的面积1()()2S f x EF MN ==⨯,当M 为BB '的中点时,即12x =时,MN 最短, 此时面积最小,故②正确; 对于③,则四棱锥分割为两个小棱锥,它们是以AEF 为底,以M ,N 为顶点的两个小棱锥, 因为AEF 的面积是个常数,M ,N 到平面AEF 的距离和是个常数,所以四棱锥C MENF '−的体积()V P x =是常函数,故③正确;对于④,多面体ABCD MENF −的体积11()22ABCD A B C D V h x V ''''−===为常数函数,故④错误.综上所述,假命题为④. 故选D .二、填空题:本大题共6小题,每小题5分,满分30分 9.【答案】0c ∀>,方程20x x c −+=无解【解析】在否定特称命题时,需将存在量词改为全称量词,同时否定结论, 故命题:0p c ∃>,方程20x x c −+=有解,则p ⌝为:0c ∀>,方程20x x c −+=无解. 10. 【答案】17【解析】∵π02α−<<,且4cos 5α=, ∴23sin 1cos 5αα=−−=−,3tan 4α=−,∴π1tan 1tan 41tan 7ααα+⎛⎫+== ⎪−⎝⎭. 11. 【答案】7【解析】由题意可得π||||cos ,32cos 33a b a b a b ⋅=⋅=⨯⨯=, ∴222||29467a b a b a b −=+−⋅=+−=, ∴||7a b −=. 12. 【答案】0【解析】π2π22ππ111(sin )d cos πcos ππcos(π)0222x x x x x −−⎛⎫⎛⎫+=−=−−−−= ⎪⎪⎝⎭⎝⎭⎰. 13. 【答案】36 【解析】∵11AB C ,122C B C ,233C B C 是三个边长为2的等边三角形,且有一条边在同一直线上,∴四边形121AC B B 为菱形, ∴21π6B AC ∠=,211AB B C ⊥, ∴213AB PC ⊥,23AB BC ⊥,∴21223313223π()(2)22236cos 366AB AP AP AB AC C P C P AB AC ⋅+=⋅++=⋅=⨯⨯⨯=. 14.【答案】①②【解析】若()f x 为Ω函数,则由0a b +=时有()()0f a f b +=可得()f x 为奇函数, 又0a b +>时,()()0f a f b +>,故a b >−时,()()f a f b >−, 即()()f a f b >−, 故()f x 为增函数,∴若函数()y f x =是定义在R 上的奇函数,且单调递增,则函数()f x 为Ω函数. 易知,①②③都是奇函数,当sin y x x =+时,1cos 0y x '=−≥; 当133xxy ⎛⎫=− ⎪⎝⎭时,ln3(33)0x x y −'=⋅+>;∴①②都在定义域R 上单调递增; ③在定义域R 上没有单调性. 故是Ω函数的为:①②.三、解答题:本大题共6小题,满分80分.解答应写出文字说明,证明过程或演算步骤. 15.【答案】见解析.【解析】解:(1)∵3()cos (sin 3cos )2f x x x x =+−, 23sin cos 3cos 2x x x =+−, 13sin 2cos 222x x =+, πsin 23x ⎛⎫=+ ⎪⎝⎭,∴函数()f x 的最小正周期2ππ2T ==, 令πππ2π22π232k x k −++≤≤,k ∈Z , 得5ππππ1212k x k −+≤≤,k ∈Z , ∴函数()f x 的单调递增区间是5πππ,π1212k k ⎡⎤−+⎢⎥⎣⎦,k ∈Z .(2)由题意得,π()()sin 223g x f x x αα⎛⎫=+=++ ⎪⎝⎭,∵函数()g x 为奇函数,且x ∈R , ∴(0)0g =,即πsin 203α⎛⎫+= ⎪⎝⎭,∴π2π3k α+=,k ∈Z ,又∵0α>, ∴α的最小值为π3. 16.【答案】见解析.【解析】解:(1)∵2C B ∠=∠,3cos 3B =, ∴21cos cos 22cos 13D B B ==−=−,222sin 1cos 3D D =−=,又∵1AD =,3CD =,∴ACD 的面积1122sin 132223S AD CD D =⋅⋅=⨯⨯⨯=. (2)在ACD 中,由余弦定理得:2222cos 12AC AD DC AD DC D =+−⋅⋅=,∴23AC =, 又∵23BC =, ∴由正弦定理得sin sin AC AB B ACB=∠, 即23sin sin(π2)ABB B =−, ∴23sin sin 2ABB B=, 即23sin 2sin cos ABB B B=,即232cos AB B =, ∴343cos 4343AB B ==⨯=. 17.【答案】见解析.【解析】解:(1)被检测的7台手机中有5台的待机时间不少于123小时, 因此,估计56台A 型手机中有556407⨯=台手机的待机时间不少于123小时. (2)由题意,X 可能的取值为0,1,2,3, 4711(0)C 35P X ===, 133447C C 12(1)C 35P X ===, 223447C C 18(2)C 35P X ===, 3447C 4(3)C 35P X ===, ∴X 的分布列为: X 0123P112184数学期望1121846012()012335353535357E X =⨯+⨯+⨯+⨯==. (3)124a =,125b =.18.【答案】见解析.【解析】(1)证明:连接BD 交AC 于O ,∵四边形ABCD 为正方形,∴D 是BD 中点,设G 是DE 的中点,连接OG ,FG ,则OG BE ,且12OG BE =, ∵四边形ABEF 为直角梯形,且AF BE ,22BE AF ==, ∴AF BE ,且12AF BE =, ∴AF OG ,且AF OG =,∴四边形AOGF 为平行四边形,∴AO FG ,即AC FG ,又∵AC ⊄平面DEF ,FG ⊂平面DEF ,∴AC 平面DEF .(2)(i )由已知,AF BE ,AB BE ⊥,∴AF AB ⊥,∵二面角D AB E −−为直二面角,∴平面ABCD ⊥平面ABEF ,∴AF ⊥平面ABCD ,∴AF AD ⊥,AF AB ⊥,又四边形ABCD 为正方形,∴AB AD ⊥,∴AD ,AB ,AF 两两垂直,以A 为原点,AD ,AB ,AF 分别为x ,y ,z 轴建立空间直角坐标系,如图所示,由22AB BE AF ===得:(0,0,0)A ,(0,2,0)B ,(2,2,0)C ,(2,0,0)D ,(0,2,2)E ,(0,0,1)F . ∴(2,2,0)AC =,(0,2,0)CD =,(2,0,2)CE =−.设平面CDE 的一个法向量为(,,)n x y z =,则:00n CD n CE ⎧⋅=⎪⎨⋅=⎪⎩,即20220y x z −=⎧⎨+=⎩, 取1x =,则0y =,1z =−,∴(1,0,1)n =,设直线AC 与平面CDE 所成的角为θ,则有:21sin |cos ,|2222AC n θ===⨯, ∵090θ︒≤≤,∴30θ=︒,即直线AC 与平面CDE 所成角的大小为30︒.(ii )假设棱DE 上存在点P ,使得BP ⊥平面DEF ,设(01)DP DE λλ=≤≤,则DP DE λ=, 设(,,)P x y z ,则(2,,)DP x y z =−,∵(2,2,2)DE =−,∴(2,,)(2,2,2)x y z λ−=−,∴22x λ−=−,2y λ=,2z λ=,解得22x λ=−,2y λ=,2z λ=,即P 点坐标为(22,2,2)λλλ−,∵(0,2,0)B ,∴(22,22,2)BP λλλ−−,又(2,0,1)DF =−,(0,2,1)EF =−−,∴00BP DF BP EF ⎧⋅=⎪⎨⋅=⎪⎩,即2(22)202(22)20λλλλ−−+=⎧⎨−−−=⎩, 解得23λ=. ∵2[0,1]3∈, ∴DE 上存在点P ,使得BP ⊥平面DEF ,且23DP DE =.19.【答案】见解析.【解析】解:(1)当1a =时,2()e (1)x f x x x =++,2()e (32)x f x x x '=++, ∴(0)1f =,(0)2f '=,∴曲线()y f x =在点(0,(0))f 处的切线方程为:12(0)y x −=−,即21y x =+.(2)由2()e ()x f x x ax a =++得2()e [(2)2]e ()(2)x x f x x a x a x a x '=+++=++, 令()0f x '=,解得:2x =−或x a =,①当2a −=−,即2a =时,2()e (2)0x f x x '=+≥,()f x 在R 上单调递增;②当2a −>−,即2a <时,令()0f x '>,得2x <−或x a >−;令()0f x '<,得2x a −<<−,∴()f x 的单调增区间是(,2)−∞−和(,)a −+∞,单调减区间是(2,)a −−;③当2a −<−,即2a >时,令()0f x '>,得x a <−或2x >−;令()0f x '<,得2a x −<<−,∴()f x 的单调增区间是(,)a −∞−和(2,)−+∞,单调减区间是(,2)a −−.综上所述,当2a =时,函数()f x 在R 上递增;当2a <时,()f x 的单调增区间是(,2)−∞−和(,)a −+∞,单调减区间是(2,)a −−; 当2a >时,()f x 的单调增区间是(,)a −∞−和(2,)−+∞,单调减区间是(,2)a −−. (3)由(1)得:当4a ≥时,函数()f x 在[),x a ∈−+∞上有()(2)f x f −≥, 且2(2)e (4)0f a −−=−≤,∵4a ≥,∴(,)x a ∈−∞−时,()0x x a +≥,e 0x >,()e [()]0x f x x x a a =++>,∴4a ≥时,函数()f x 存在最小值(2)f −.20.【答案】见解析.【解析】解:(1)由246+=,268+=,2810+=,4610+=,4812+=,6814+=得()5l P =, 由246+=,2810+=,21618+=,4812+=,41620+=,81624+=得()6l Q =.(2)证明:∵(1)i j a a i j n +<≤≤最多有2(1)C 2n n n −=个值, ∴(1)()2n n l A −≤, 又集合{}2,4,8,,2n A =,任取i j a a +,(1,1)k l a a i j n k l n +<<≤≤≤≤,当j l ≠时,不妨设j l <,则22j i i j j l k l a a a a a a ++<=<+≤,即i j k l a a a a +≠+,当j l =,i k ≠时,i j k l a a a a +≠+,∴当且仅当i k =,j l =时,i j k l a a a a +=+,即所有(1)i j a a i j n +<≤≤的值两两不同, ∴(1)()2n n l A −=. (3)()l A 存在最小值,且最小值为23n −, 不妨设123n a a a a <<<<,可得1213121n n n n a a a a a a a a a a −+++<<+<<<<+, ∴(1)i j a a i j n +<≤≤中至少有23n −个不同的数,即()23l A n −≥, 取{}1,2,3A n =,则{}3,4,5,21i j a a n +∈−,即i j a a +的不同值共有23n −个, 故()l A 的最小值为23n −.word 下载地址。
北京市东城东直门中学2017-2018学年高三上期中数学试题(解析版)

北京市东直门中学2017-2018年度高三第一学期期中试题(数学理科)项符合要求.一、选择题:本大题共8小题,每小题5分满分40分•在每小题给出的四个选项中,i•设集合「〔y乂弋;,则下列结论正确的是()•A. .B. ;:•「丿•:C. . .D. l x;./【答案】D【解析】T集合■■:->1:,集合* ;八」、:■:: :■:或,•••齐匚•故选•2•复数满足,则在复平面内,复数对应的点位于()•A.第一象限B.第二象限C.第三象限D.第四象限【答案】C【解析】试题分析:由x :|得,'':|,对应点为I :,位于第三象限,选C.1考点:复数运算3•如果平面向量,I; ; .1,,那么下列结论中正确的是().A. I计一打B. I- ':. ■:C. | "丄卜D. ■■ I 、【答案】C【解析】由平面向量^ =;-,:”:;,I;;. I,知:在中,卜一「,很=.,••卜密】,故错误;在中,:「匕•,故错误;在中,】=;「;]卜‘、' I•」丄I■,故正确;••• 的图象关于点 对称,故正确;扩呷胡],/ 3E 皿\•函数 在区间 上先增后减,故错误.故选B.点睛:本题考查的是三角函数的图象变换•三角函数中函数图象的平移变化是常考知识点,也是易错题型 项必须看清题目中是由哪个函数平移,平移后是哪个函数;其次,在平移时,还要注意自变量否为1,如果x 有系数,需要将系数提出来求平移量,平移时遵循“左加右减”•兀 L L 兀5•在.中,•, .,则 “ .•”是“:”的( )•在中,T ,1 ]•与不平行,故错误. 综上所述. 故选•A.函数 满足B.图象关于点 对称兀C.图象 可由函数L •'■|1-'':的图象向右平移 个单位得到/ 兀 3T 1.D.函数在区间【答案】B,故错误;「•ii"的图象 由函数「•’•:的图象向右平移个单位得到,故错误;•首x 的系数是 4•设函数=F 面结论中正确的是(【解析】处6S1O项,当; 时,:A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B【解析】AC Qr t .兀 ----••右..=» ,贝 y, 3 sin- siri-3 4得一 ---------- L ,必要性成立;sin —斗Tj'3sm- 得 • ■ sinB = —= {- x 2?c.',或.,充分性不成立,:—JJ2丸C=&”是P = f”的必要不充分条件.A. a > b > c B . a > c > bC . c > a > bD . c > b > a【答案】C 【解析】试题分析:由图象有 •• 1' I ■■■ I ,所以 最小,对于];=『「.=〔 .< = F ,看图象有I V :;,所以II"〔:对于/ n 1 ■-:,,看图象有 ,所以:,故 ,选C .考点:基本初等函数的图象.7•已知函数若关于 的方程■:-有三个不相等的实数根,则实数 的取值范围是()若..•,则,sinB sinA故选.A. | :'B. J 十。
2023-2024学年北京市东城区东直门中学高二(上)期中数学试卷【答案版】

2023-2024学年北京市东城区东直门中学高二(上)期中数学试卷一.选择题:(本题有12道小题,每小题4分,共48分) 1.已知α∈(π2,π),且sin α=35,则tan α=( ) A .34B .−34C .43D .−432.在等差数列{a n }中,a 2=1,a 4=5,则a 8=( ) A .9B .11C .13D .153.已知数列{a n }是公比为正数的等比数列,S n 是其前n 项和,a 2=2,a 4=8,则S 7=( ) A .31B .63C .127D .2554.已知α,β是两个不同的平面,直线m ⊂α,下列命题中正确的是( ) A .若α⊥β,则m ∥β B .若α⊥β,则m ⊥βC .若m ∥β,则α∥βD .若m ⊥β,则α⊥β5.向量a →=(2,1,x ),b →=(2,y ,﹣1),若|a →|=√5,且a →⊥b →,则x +y 的值为( ) A .﹣1B .1C .﹣4D .46.在△ABC 中,a =2,B =π3,△ABC 的面积等于√32,则b 等于( ) A .√32B .1C .√3D .27.设{a n }是公差不为0的无穷等差数列,则“{a n }为递增数列”是“存在正整数N 0,当n >N 0时,a n >0”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件8.在平面直角坐标系xOy 中,角α以Ox 为始边,终边与单位圆交于点P(x 0,√63),则cos2α=( ) A .−13B .±13C .2√33D .139.如图,正方体ABCD ﹣A 1B 1C 1D 1的棱长为1,线段B 1D 1上有两个动点E ,F ,且EF =12,给出下列三个结论: ①AC ⊥BE ;②△AEF 的面积与△BEF 的面积相等; ③三棱锥A ﹣BEF 的体积为定值. 其中,所有正确结论的个数是( )A .0B .1C .2D .310.已知公差不为零的等差数列{a n },首项a 1=﹣7,若a 5,a 6,a 9成等比数列,记T n =a 1•a 2•⋯•a n (n =1,2,3,⋯),则数列{T n }( ) A .有最小项,无最大项 B .有最大项,无最小项 C .无最大项,无最小项D .有最大项,有最小项11.ISO 216是国际标准化组织所定义的纸张尺寸国际标准,该标准定义了A ,B 系列的纸张尺寸.设型号为A i (i =0,1,2,3,4,5,6)的纸张面积分别是a i (i =0,1,2,3,4,5,6),它们组成一个公比为12的等比数列,设型号为B i (i =1,2,3,4,5,6)的纸张的面积分别是b i (i =1,2,3,4,5,6),已知b i 2=a i−1a i (i =1,2,3,4,5,6),则a 4b 5的值为( )A .12B .√22 C .√2D .212.已知数列{a n }满足a n+1=14(a n −6)3+6(n =1,2,3,⋯),则( ) A .当a 1=3时,{a n }为递减数列,且存在常数M ≤0,使得a n >M 恒成立 B .当a 1=5时,{a n }为递增数列,且存在常数M ≤6,使得a n <M 恒成立 C .当a 1=7时,{a n }为递减数列,且存在常数M >6,使得a n >M 恒成立 D .当a 1=9时,{a n }为递增数列,且存在常数M >0,使得a n <M 恒成立 二.填空题:(本题有6道小题,每小题5分,共30分)13.已知函数f(x)=√3sinx −cosx ,则f(π3)= ;若将f (x )的图象向右平行移动π6个单位长度后得到g (x )的图象,则g (x )的一个对称中心为 . 14.在△ABC 中,若BC =3,AC =2√6,B =2A ,则B = .15.已知数列{a n }满足a 1=1,a 2=﹣2,且a n +1=a n +a n +2,n ∈N *,则a 5= ;数列{a n }的前2023项的和为 .16.已知平面α和三条不同的直线m ,n ,l .给出下列六个论断:①m ⊥α;②m ∥α;③m ∥l ;④n ⊥α;⑤n ∥α;⑥n ∥l .以其中两个论断作为条件,使得m ∥n 成立.这两个论断可以是 .(填上你认为正确的一组序号)17.我国度量衡的发展有着悠久的历史,战国时期就出现了类似于砝码的用来测量物体质量的“环权”.已知9枚环权的质量(单位:铢)从小到大构成项数为9的数列{a n },该数列的前3项成等差数列,后7项成等比数列,且a 1=1,a 5=12,a 9=192,则a 7= ,数列{a n }的所有项的和为 . 18.已知函数f(x)=λsin(π2x +φ)(λ>0,0<φ<π)的部分图象如图1所示,A ,B 分别为图象的最高点和最低点,过A 作x 轴的垂线,交x 轴于点A ',点C 为该部分图象与x 轴的交点.将绘有该图象的纸片沿x 轴折成直二面角,如图2所示,此时|AB|=√10,则λ= .给出下列四个结论: ①φ=π3;②图2中,AB →⋅AC →=5;③图2中,过线段AB 的中点且与AB 垂直的平面与x 轴交于点C ;④图2中,S 是△A 'BC 及其内部的点构成的集合.设集合T ={Q ∈S ||AQ |≤2},则T 表示的区域的面积大于π4.其中所有正确结论的序号是 . 三.解答题:(本题有6小题,共72分)19.(10分)已知{a n }是等差数列,{b n }是等比数列,且b 2=3,b 3=9,a 1=b 1,a 14=b 4. (1)求{a n }和{b n }的通项公式;(2)设c n =a n +b n ,求数列{c n }的前n 项和.20.(10分)已知函数f (x )=A sin x cos x −√3cos2x 的一个零点为π6.(1)求A 和函数f (x )的最小正周期;(2)当x ∈[0,π2]时,若f (x )≤m 恒成立,求实数m 的取值范围.21.(12分)在△ABC 中,2asinB =√2b . (1)求A ;(2)若b =2√6,从下列三个条件中选出一个条件作为已知,使得△ABC 存在且唯一确定,求△ABC 的面积.条件①:cosC =−√1010;条件②:a =2;条件③:sinB =√55. 注:如果选择了不合适的条件,则第(2)问记0分.22.(12分)如图,在四棱锥P ﹣ABCD 中,底面ABCD 为矩形,PD ⊥平面ABCD ,PD =AD =2,AB =4,点E 在线段AB 上,且AE =34AB . (1)求证:CE ⊥平面PBD ; (2)求二面角P ﹣CE ﹣D 的余弦值; (3)求点A 到平面PCE 的距离.23.(14分)如图,在多面体ABCDEF 中,平面ADEF ⊥平面ABCD ,四边形ADEF 为正方形,四边形ABCD 为梯形,且AD ∥BC ,∠BAD =90°,AB =AD =1,BC =3. (Ⅰ)求证:AF ⊥CD ;(Ⅱ)求直线BF 与平面CDE 所成角的正弦值;(Ⅲ)线段BD 上是否存在点M ,使得直线CE ∥平面AFM ?若存在,求BM BD的值;若不存在,请说明理由.24.(14分)设λ为正实数,若各项均为正数的数列{a n }满足:∀n ∈N *,都有a n +1≥a n +λ.则称数列{a n }为P (λ)数列.(Ⅰ)判断以下两个数列是否为P (2)数列:数列A :3,5,8,13,21; 数列B :log 25,π,5,10.(Ⅱ)若数列{b n }满足b 1>0且b n +1=b n +√n +3−√n +1,是否存在正实数λ,使得数列{b n }是P (λ)数列?若存在,求λ的取值范围;若不存在,说明理由.(Ⅲ)若各项均为整数的数列{a n }是P (1)数列,且{a n }的前m (m ≥2)项和a 1+a 2+a 3+⋯+a m 为150,求a m +m 的最小值及取得最小值时a m 的所有可能取值.2023-2024学年北京市东城区东直门中学高二(上)期中数学试卷参考答案与试题解析一.选择题:(本题有12道小题,每小题4分,共48分) 1.已知α∈(π2,π),且sin α=35,则tan α=( ) A .34B .−34C .43D .−43解:α∈(π2,π),且sinα=35,∴cos α<0,cos α=−√1−sin 2α=−√1−(35)2=−45, ∴tan α=sinαcosα=−34. 故选:B .2.在等差数列{a n }中,a 2=1,a 4=5,则a 8=( ) A .9B .11C .13D .15解:在等差数列{a n }中,a 2=1,a 4=5,∴{a 1+d =1a 1+3d =5,解得a 1=﹣1,d =2,则a 8=a 1+7d =﹣1+14=13. 故选:C .3.已知数列{a n }是公比为正数的等比数列,S n 是其前n 项和,a 2=2,a 4=8,则S 7=( ) A .31B .63C .127D .255解:设等比数列{a n }的公比为q (q >0),由a 4=a 2q 2,得8=2q 2,解得q =2或q =﹣2(舍去),又a 1=a 2q =22=1,所以S 7=1−271−2127.故选:C .4.已知α,β是两个不同的平面,直线m ⊂α,下列命题中正确的是( )A .若α⊥β,则m ∥βB .若α⊥β,则m ⊥βC .若m ∥β,则α∥βD .若m ⊥β,则α⊥β解:对于选项A :若α⊥β,则m ∥β也可能m ⊥β,故错误. 对于选项B :若α⊥β,则m ⊥β也可能m ∥β,故错误. 对于选项C :若m ∥β,则α∥β也可能α与β相交,故错误. 对于选项D ,直线m ⊂α,m ⊥β,则α⊥β是面面垂直的判定,故正确. 故选:D .5.向量a →=(2,1,x ),b →=(2,y ,﹣1),若|a →|=√5,且a →⊥b →,则x +y 的值为( ) A .﹣1B .1C .﹣4D .4解:向量a →=(2,1,x ),若|a →|=√5, 则√22+12+x 2=√5,解得x =0; 又向量b →=(2,y ,﹣1),且a →⊥b →, 则a →•b →=4+y +0=0,解得y =﹣4; 所以x +y =﹣4. 故选:C .6.在△ABC 中,a =2,B =π3,△ABC 的面积等于√32,则b 等于( ) A .√32B .1C .√3D .2解:∵a =2,B =π3,△ABC 的面积等于√32=12ac sin B =12×2×c ×√32, ∴解得:c =1,∴由余弦定理可得:b =√a 2+c 2−2accosB =√4+1−2×2×1×12=√3. 故选:C .7.设{a n }是公差不为0的无穷等差数列,则“{a n }为递增数列”是“存在正整数N 0,当n >N 0时,a n >0”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件解:因为数列{a n }是公差不为0的无穷等差数列,当{a n }为递增数列时,公差d >0,令a n =a 1+(n ﹣1)d >0,解得n >1−a 1d ,[1−a1d ]表示取整函数,所以存在正整数N0=1+[1−a1d],当n>N0时,a n>0,充分性成立;当n>N0时,a n>0,a n﹣1<0,则d=a n﹣a n﹣1>0,必要性成立;是充分必要条件.故选:C.8.在平面直角坐标系xOy中,角α以Ox为始边,终边与单位圆交于点P(x0,√63),则cos2α=()A.−13B.±13C.2√33D.13解:∵平面直角坐标系xOy中,角α以Ox为始边,终边与单位圆交于点P(x0,√63 ),∴OP2=x02+69=1,∴x0=±√33,∴cosα=±√33,则cos2α=2cos2α﹣1=2×x02−1=−1 3,故选:A.9.如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E,F,且EF=12,给出下列三个结论:①AC⊥BE;②△AEF的面积与△BEF的面积相等;③三棱锥A﹣BEF的体积为定值.其中,所有正确结论的个数是()A.0B.1C.2D.3解:对于①,根据题意,结合图形知,AC⊥面DD1B1B,BE⊂平面DD1B1B,∴AC⊥BE,命题①正确;对于②,∵点B到直线EF的距离与点A到直线EF的距离不相等,∴△AEF与△BEF的面积不相等,命题②错误;对于③,三棱锥A ﹣BEF 的体积为V 三棱锥A ﹣BEF =13•S △BEF •h =13×12×12×1×√22=√224, ∴三棱锥A ﹣BEF 的体积为定值,命题③正确; 对于综上,正确的命题有2个. 故选:C .10.已知公差不为零的等差数列{a n },首项a 1=﹣7,若a 5,a 6,a 9成等比数列,记T n =a 1•a 2•⋯•a n (n =1,2,3,⋯),则数列{T n }( ) A .有最小项,无最大项 B .有最大项,无最小项 C .无最大项,无最小项D .有最大项,有最小项解:在等差数列{a n }中,由a 5,a 6,a 9成等比数列,得a 62=a 5⋅a 9,即(﹣7+5d )2=(﹣7+4d )(﹣7+8d ), 解得d =2或d =0(舍),则a n =2n ﹣9,当n ≤4,n ∈N *时,a n <0;当n ≥5,n ∈N *时,a n >0. ∴{a n }的前6项为:﹣7,﹣5,﹣3,﹣1,1,3, 又T n =a 1•a 2•⋯•a n ,故T 3最小,没有最大值. 故选:A .11.ISO 216是国际标准化组织所定义的纸张尺寸国际标准,该标准定义了A ,B 系列的纸张尺寸.设型号为A i (i =0,1,2,3,4,5,6)的纸张面积分别是a i (i =0,1,2,3,4,5,6),它们组成一个公比为12的等比数列,设型号为B i (i =1,2,3,4,5,6)的纸张的面积分别是b i (i =1,2,3,4,5,6),已知b i 2=a i−1a i (i =1,2,3,4,5,6),则a 4b 5的值为( )A .12B .√22C .√2D .2解:∵b i 2=a i−1a i ,令i =5,∴b 52=a 4a 5,又∵a 0,a 1,a 2,a 3,a 4,a 5,a 6组成一个公比为12的等比数列,∴b 52=a 4a 5=a 4⋅a 4⋅12=12a 42, 又a 4>0,b 5>0, ∴a 4b 5=√2.故选:C .12.已知数列{a n }满足a n+1=14(a n −6)3+6(n =1,2,3,⋯),则( )A .当a 1=3时,{a n }为递减数列,且存在常数M ≤0,使得a n >M 恒成立B .当a 1=5时,{a n }为递增数列,且存在常数M ≤6,使得a n <M 恒成立C .当a 1=7时,{a n }为递减数列,且存在常数M >6,使得a n >M 恒成立D .当a 1=9时,{a n }为递增数列,且存在常数M >0,使得a n <M 恒成立 解:因为a n+1=14(a n −6)3+6,故a n+1−6=14(a n −6)3, 对于A ,若a 1=3,可用数学归纳法证明:a n ﹣6≤﹣3,即a n ≤3, 证明:当n =1时,a 1﹣6=﹣3≤﹣3,此时不等关系a n ≤3成立; 设当n =k 时,a k ﹣6≤﹣3成立, 则a k+1−6=14(a k −6)3∈(−54,−274),故a k +1﹣6≤﹣3成立, 由数学归纳法可得a n ≤3成立.而a n+1−a n =14(a n −6)3−(a n −6)=(a n −6)[14(a n −6)2−1],14(a n −6)2−1≥94−1=54>0,a n ﹣6<0,故a n +1﹣a n <0,故a n +1<a n ,故{a n }为减数列,注意a k +1﹣6≤﹣3<0,故a n+1−6=14(a n −6)3=(a n −6)×14(a n −6)2≤94(a n −6),结合a n +1﹣6<0, 所以6−a n+1≥94(6−a n ),故6−a n+1≥3(94)n−1,故a n+1≤6−3(94)n−1, 若存在常数M ≤0,使得a n >M 恒成立,则6−3(94)n−1>M , 故6−M 3>(94)n−1,故n <1+log 946−M3,故a n >M 恒成立仅对部分n 成立, 故A 不成立.对于B ,若a 1=5,可用数学归纳法证明:﹣1≤a n ﹣6<0,即5≤a n <6, 证明:当n =1时,﹣1≤a 1﹣6=﹣1≤0,此时不等关系5≤a n <6成立; 设当n =k 时,5≤a k <6成立,则a k+1−6=14(a k −6)3∈(−14,0),故﹣1≤a k +1﹣6<0成立, 即由数学归纳法可得5≤a k +1<6成立.而a n+1−a n =14(a n −6)3−(a n −6)=(a n −6)[14(a n −6)2−1],14(a n −6)2−1<0,a n ﹣6<0,故a n +1﹣a n >0,故a n +1>a n ,故{a n }为增数列,若M =6,则a n <6恒成立,故B 正确.对于C ,当a 1=7时,可用数学归纳法证明:0<a n ﹣6≤1,即6<a n ≤7, 证明:当n =1时,0<a 1﹣6≤1,此时不等关系成立; 设当n =k 时,6<a k ≤7成立,则a k+1−6=14(a k −6)3∈(0,14],故0<a k +1﹣6≤1成立,即6<a k +1≤7 由数学归纳法可得6<a n ≤7成立.而a n+1−a n =(a n −6)[14(a n −6)2−1]<0,故a n +1<a n ,故{a n }为减数列,又a n+1−6=(a n −6)×14(a n −6)2≤14(a n −6),结合a n +1﹣6>0可得:a n+1−6≤(a 1−6)(14)n ,所以a n+1≤6+(14)n ,若a n+1≤6+(14)n ,若存在常数M >6,使得a n >M 恒成立,则M −6≤(14)n 恒成立,故n ≤log 14(M −6),n 的个数有限,矛盾,故C 错误.对于D ,当a 1=9时,可用数学归纳法证明:a n ﹣6≥3即a n ≥9, 证明:当n =1时,a 1﹣6=3≥3,此时不等关系成立; 设当n =k 时,a k ≥9成立, 则a k+1−6=14(a k −6)3≥274>3,故a k +1≥9成立 由数学归纳法可得a n ≥9成立.而a n+1−a n =(a n −6)[14(a n −6)2−1]>0,故a n +1>a n ,故{a n }为增数列,又a n+1−6=(a n −6)×14(a n −6)2>94(a n −6),结合a n ﹣6>0可得:a n+1−6>(a 1−6)(94)n−1=3(94)n−1,所以a n+1≥6+3(94)n−1,若存在常数M >0,使得a n <M 恒成立,则M >6+3(94)n−1, 故M >6+3(94)n−1,故n <log 94(M−63)+1,这与n 的个数有限矛盾,故D 错误. 故选:B .二.填空题:(本题有6道小题,每小题5分,共30分)13.已知函数f(x)=√3sinx −cosx ,则f(π3)= 1 ;若将f (x )的图象向右平行移动π6个单位长度后得到g (x )的图象,则g (x )的一个对称中心为 (π3,0)(答案不唯一) . 解:f(x)=√3sinx −cosx =2sin(x −π6),f(π3)=2sin π6=1,则g(x)=2sin(x−π3),取x−π3=kπ,k∈Z,即x=π3+kπ,k∈Z,取k=0,x=π3,此时对称中心为(π3,0).故答案为:1;(π3,0)(答案不唯一).14.在△ABC中,若BC=3,AC=2√6,B=2A,则B=arccos13.解:由正弦定理得BCsinA =ACsinB,即3sinA=2√6sin2A,所以cos A=√63,所以cos B=cos2A=2cos2A﹣1=13,因为0<B<π,所以B=arccos 1 3.故答案为:arccos 1 3.15.已知数列{a n}满足a1=1,a2=﹣2,且a n+1=a n+a n+2,n∈N*,则a5=2;数列{a n}的前2023项的和为1.解:依题意,由a n+1=a n+a n+2,可得a n+2=a n+1﹣a n,则a1=1,a2=﹣2,a3=a2﹣a1=﹣2﹣1=﹣3,a4=a3﹣a2=﹣3﹣(﹣2)=﹣1,a5=a4﹣a3=﹣1﹣(﹣3)=2,a6=a5﹣a4=2﹣(﹣1)=3,a7=a6﹣a5=3﹣2=1,a8=a7﹣a6=1﹣3=﹣2,…∴数列{a n}是以6为最小正周期的周期数列,∵2023÷6=337……1,∴a2023=a1=1,a1+a2+a3+a4+a5+a6=1﹣2﹣3﹣1+2+3=0,∴数列{a n}的前2023项的和为:a1+a2+…+a2023=(a1+a2+a3+a4+a5+a6)+(a7+a8+a9+a10+a11+a12)+…+(a2017+a2018+a2019+a2020+a2021+a2022)+a2023=0+0+…+0+1=1.故答案为:2;1.16.已知平面α和三条不同的直线m,n,l.给出下列六个论断:①m⊥α;②m∥α;③m∥l;④n⊥α;⑤n∥α;⑥n∥l.以其中两个论断作为条件,使得m∥n成立.这两个论断可以是①④(或③⑥).(填上你认为正确的一组序号)解:由平面α和三条不同的直线m,n,l.①m⊥α;②m∥α;③m∥l;④n⊥α;⑤n∥α;⑥n∥l.得:若①m⊥α,④n⊥α,则由线面垂直的性质得m∥n,若③m∥l,⑥n∥l,则由平行公理得m∥n.∴以其中两个论断作为条件,使得m∥n成立.这两个论断可以是①④(或③⑥).故答案为:①④(或③⑥).17.我国度量衡的发展有着悠久的历史,战国时期就出现了类似于砝码的用来测量物体质量的“环权”.已知9枚环权的质量(单位:铢)从小到大构成项数为9的数列{a n},该数列的前3项成等差数列,后7项成等比数列,且a1=1,a5=12,a9=192,则a7=48,数列{a n}的所有项的和为384.解:∵数列{a n}的后7项成等比数列,a n>0,∴a7=√a5a9=√12×192=48,∴a3=a52a7=12248=3,∴公比q=√a5a3=√123=2.∴a4=3×2=6,又该数列的前3项成等差数列,∴数列{a n}的所有项的和为3(a1+a3)2+6×(26−1)2−1=3×(1+3)2+378=384.故答案为:48;384.18.已知函数f(x)=λsin(π2x+φ)(λ>0,0<φ<π)的部分图象如图1所示,A,B分别为图象的最高点和最低点,过A作x轴的垂线,交x轴于点A',点C为该部分图象与x轴的交点.将绘有该图象的纸片沿x轴折成直二面角,如图2所示,此时|AB|=√10,则λ=√3.给出下列四个结论: ①φ=π3;②图2中,AB →⋅AC →=5;③图2中,过线段AB 的中点且与AB 垂直的平面与x 轴交于点C ;④图2中,S 是△A 'BC 及其内部的点构成的集合.设集合T ={Q ∈S ||AQ |≤2},则T 表示的区域的面积大于π4.其中所有正确结论的序号是 ②③ . 解:在图2中,过B 作BD 垂直x 轴于D , 由题意可得T =2ππ2=4,∴A ′D =2,∴A ′B =√λ2+4,∴AB =√A′B 2+AA′2=√2λ2+4=√10,解得λ=√3或λ=−√3(舍去),∴f (x )=√3sin (π2x +φ),当x =0时,√3sin φ=√32,∵0<φ<π,∴φ=π6或φ=5π6,当φ=π6显然不符合图象的变化情况,故舍去, ∴φ=5π6,故①错误; 由题意可得AC =√3+1=2,BC =2, ∴cos ∠BAC =10+4−42√10×2=√104,∴AB →•AC →=|AB →|•|AC →|•cos ∠BAC =√10×2×√104=5,故②正确;∵AC =BC =2,∴过线段AB 的中点且与AB 垂直的平面与x 轴交于点C ,故③正确; ∵|AQ |≤2,二面角为直二面角可得|A ′Q |≤1,∴T 表示的区域的面积为π×12×∠BA′C 2π<π4,故④错误. 故答案为:√3;②③.三.解答题:(本题有6小题,共72分)19.(10分)已知{a n }是等差数列,{b n }是等比数列,且b 2=3,b 3=9,a 1=b 1,a 14=b 4. (1)求{a n }和{b n }的通项公式;(2)设c n =a n +b n ,求数列{c n }的前n 项和. 解:(1)设{a n }是公差为d 的等差数列, {b n }是公比为q 的等比数列, 由b 2=3,b 3=9,可得q =b 3b 2=3, b n =b 2q n ﹣2=3•3n ﹣2=3n ﹣1; 即有a 1=b 1=1,a 14=b 4=27, 则d =a 14−a 113=2, 则a n =a 1+(n ﹣1)d =1+2(n ﹣1)=2n ﹣1; (2)c n =a n +b n =2n ﹣1+3n ﹣1,则数列{c n }的前n 项和为[1+3+…+(2n ﹣1)]+(1+3+9+…+3n ﹣1)=12n •2n +1−3n 1−3=n 2+3n−12.20.(10分)已知函数f (x )=A sin x cos x −√3cos2x 的一个零点为π6.(1)求A 和函数f (x )的最小正周期;(2)当x ∈[0,π2]时,若f (x )≤m 恒成立,求实数m 的取值范围. 解:(1)∵f (x )=A sin x cos x −√3cos2x =A2sin2x −√3cos2x 的一个零点为π6,∴f (π6)=A 2×√32−√32=0, ∴A =2,f (x )=sin2x −√3cos2x =2sin (2x −π3), ∴T =2π2=π; (2)当x ∈[0,π2]时,2x −π3∈[−π3,2π3],2sin (2x −π3)∈[−√3,2],∴f (x )max =2,∴m ≥2,即m ∈[2,+∞).21.(12分)在△ABC 中,2asinB =√2b .(1)求A;(2)若b=2√6,从下列三个条件中选出一个条件作为已知,使得△ABC存在且唯一确定,求△ABC的面积.条件①:cosC=−√1010;条件②:a=2;条件③:sinB=√55.注:如果选择了不合适的条件,则第(2)问记0分.解:(1)在△ABC中,2asinB=√2b⇒2sinAsinB=√2sinB,因为B∈(0,π),sin B>0,所以2sinA=√2⇒sinA=√22,又A∈(0,π),所以A=π4或A=3π4.(2)若选①,即cosC=−√1010,则π2<C<π,所以0<A<π2,0<B<π2,sinC=3√1010,则A=π4,则sinB=sin(π−(A+C))=sin(A+C)=sin(π4+C)=√22×(−√1010)+3√1010×√22=√55,由正弦定理得:a sinA =bsinB=csinC,a=2655√22=2√15,c=26553√1010=6√3,则△ABC存在且唯一确定,△ABC面积为S=12acsinB=12×2√15×6√3×√55=18.若选②,即a=2,又b=2√6,2asinB=√2b,所以sinB=√3,矛盾,所以②不成立.若选③,由sinB=√55,b=2√6,2asinB=√2b,得a=2√15,由余弦定理可得:a2=b2+c2﹣2bc cos A,当A=π4时,60=24+c2﹣2bc cos A,得c2−4√3c−36=0⇒c=6√3或c=−2√3舍;当A=3π4时,60=24+c2﹣2bc cos A,得c2+4√3c−36=0⇒c=2√3或c=−6√3舍,此时△ABC存在但不唯一确定,所以不合题意.22.(12分)如图,在四棱锥P﹣ABCD中,底面ABCD为矩形,PD⊥平面ABCD,PD=AD=2,AB=4,点E在线段AB上,且AE=34 AB.(1)求证:CE ⊥平面PBD ; (2)求二面角P ﹣CE ﹣D 的余弦值; (3)求点A 到平面PCE 的距离.解:(1)证明:因为PD ⊥平面ABCD ,CE ⊂平面ABCD ,所以PD ⊥CE , 因为AB =4,AE =34AB ,所以AE =3,BE =1, 所以ABAD=BC BE=2,∠ABC =∠EBC ,所以Rt △CBE ∽Rt △BAD ,所以BD ⊥CE ,又因为PD ⊥CE ,PD ∩BD =D ,PD ,BD ⊂平面PBD , 所以CE ⊥平面PBD ;(2)因为PD ⊥平面ABCD ,AD ⊂平面ABCD ,CD ⊂平面ABCD , 所以PD ⊥AD ,PD ⊥CD ,又因为ABCD 是矩形,AD ⊥CD , 所以AD ,CD ,PD 两两垂直,如图建立空间直角坐标系D ﹣xyz ,则C (0,4,0),P (0,0,2),E (2,3,0),A (2,0,0), 所以PC →=(0,4,﹣2),CE →=(2,﹣1,0), 设平面PCE 的一个法向量为n →=(x ,y ,z ), 则有{n →⋅PC →=4y −2z =0n →⋅CE →=2x −y =0,令x =1,则y =2,z =4,于是n →=(1,2,4),因为PD ⊥平面ABCD ,取平面CED 的法向量为m →=(0,0,1),则cos <m →,n →>=m →⋅n →|m →||n →|=41×1+4+16=4√2121,由图可知二面角P ﹣CE ﹣D 为锐角, 所以二面角P ﹣CE ﹣D 的余弦值为4√2121; (3)由(2)知AP →=(﹣2,0,2), 而平面PCE 的一个法向量为n →=(1,2,4),所以点A 到平面PCE 的距离为|AP⋅n →||n →|=√1+4+16=2√217. 23.(14分)如图,在多面体ABCDEF 中,平面ADEF ⊥平面ABCD ,四边形ADEF 为正方形,四边形ABCD 为梯形,且AD ∥BC ,∠BAD =90°,AB =AD =1,BC =3. (Ⅰ)求证:AF ⊥CD ;(Ⅱ)求直线BF 与平面CDE 所成角的正弦值;(Ⅲ)线段BD 上是否存在点M ,使得直线CE ∥平面AFM ?若存在,求BM BD的值;若不存在,请说明理由.解:(Ⅰ)证明:∵四边形ADEF 为正方形, ∴AF ⊥AD ,又∵平面ADEF ⊥平面ABCD , ∴AF ⊥平面ABCD , ∴AF ⊥CD ;(Ⅱ)取BC 的三等分点G ,H 如图,连接EG ,可由EF ∥AD ,AD ∥BC ,得EF ∥BG , 且EF =AD =BG =1,∴四边形BGEF 为平行四边形, ∴GE ∥BF , ∵DE ∥AF , ∴DE ⊥平面ABCD , ∴平面EDC ⊥平面ABCD , 作GN ⊥CD 于N , 则GN ⊥平面EDC , 连接EN ,则∠GEN 为GE 与平面EDC 所成的角, 在Rt △CGD 中,求得GN =2√5, 又GE =BF =√2, ∴sin ∠GEN =GNGE =√105,故直线BF 与平面CDE 所成角的正弦值为:√105;(Ⅲ)连接FH ,易证四边形EFHC 为平行四边形, ∴EC ∥FH , ∴EC ∥平面AFH , 连接AH 交BD 于M , 则CE ∥平面AFM , 此时BM MD=BH AD=2,∴BM BD=23.24.(14分)设λ为正实数,若各项均为正数的数列{a n }满足:∀n ∈N *,都有a n +1≥a n +λ.则称数列{a n }为P (λ)数列.(Ⅰ)判断以下两个数列是否为P (2)数列: 数列A :3,5,8,13,21; 数列B :log 25,π,5,10.(Ⅱ)若数列{b n }满足b 1>0且b n +1=b n +√n +3−√n +1,是否存在正实数λ,使得数列{b n }是P (λ)数列?若存在,求λ的取值范围;若不存在,说明理由.(Ⅲ)若各项均为整数的数列{a n }是P (1)数列,且{a n }的前m (m ≥2)项和a 1+a 2+a 3+⋯+a m 为150,求a m +m 的最小值及取得最小值时a m 的所有可能取值. 解:(Ⅰ)根据定义,P (2)数列应满足∀n ∈N *,a n +1≥a n +2, 即a n +1﹣a n ≥2恒成立,对于数列A :有5﹣3=2≥2,8﹣5=3≥2,13﹣8=5≥2,21﹣13=8≥2, 均满足,∴数列A 是P (2)数列;对于数列B :∵5﹣π<2,不满足,∴数列B 不是P (2)数列; (Ⅱ)不存在正实数λ,使得数列{b n }是P (λ)数列. 理由如下:假设存在正实数λ,使得数列{b n }是P (λ)数列, 则∀n ∈N *,都有b n +1≥b n +λ,∴b n +1﹣b n ≥λ恒成立, ∵b n+1=b n +√n +3−√n +1, ∴b n +1﹣b n =√n +3−√n +1=2√n+3+√n+11√n , 当n >1λ2时,b n +1﹣b n 1√n λ,这与假设矛盾,∴不存在正实数λ,使得数列{b n }是P (λ)数列; (Ⅲ)∵数列{a n }是P (1)数列,∴a n +1≥a n +1, ∴a m ≥a m ﹣1+1≥a m ﹣2+2≥…≥a 1+m ﹣1≥m ,∴a m ﹣1≤a m ﹣1,a m ﹣2≤a m ﹣1﹣1,a m ﹣3≤a m ﹣2﹣1≤a m ﹣3,…,a 2≤a 3﹣1≤a m ﹣(m ﹣2), a 1≤a 2﹣1≤a m ﹣(m ﹣1),∴a 1+a 2+a 3+…+a m ≤ma m ﹣[1+2+3+…+(m ﹣1)]=ma m −m(m−1)2,∴150≤ma m −m(m−1)2,∴a m ≥150m +m 2−12, ∴a m +m ≥150m +m 2−12=30−12=592, ∵数列{a n }是整数数列,∴a m +m 的最小值不小于30, 假设a m +m =30,必有150m+3m 2−12≤30,解得253≤m ≤12,∵m ∈N *,∴m 可取9,10,11,12, 当m =9时,a m =21,存在满足条件的数列,a 1=10,a 2=14,a 3=15,a 4=16,a 5=17,a 6=18,a 7=19,a 8=20,a 9=21, 当m =10时,a m =20,存在满足条件的数列,a 1=6,a 2=12,a 3=13,a 4=14,a 5=15,a 6=16,a 7=17,a 8=18,a 9=19,a 10=20, 当m =11时,a m =19,存在满足条件的数列,a 1=5,a 2=10,a 3=11,a 4=12,a 5=13,a 6=14,a 7=15,a 8=16,a 9=17,a 10=18,a 11=19, 当m =12时,a m =18,存在满足条件的数列,a 1=7,a 2=8,a 3=9,a 4=10,a 5=11,a 6=12,a 7=13,a 8=14,a 9=15,a 10=16,a 11=17,a 12=18, 以上都是a m +a n =30的充分条件, ∴a m +m 的最小值为30,此时取得最小值时a m 的所有可能取值为18,19,20,21.。
2017北京市东直门中学高三(上)期中数 学(理)

2017北京市东直门中学高三(上)期中数 学(理)一、选择题:本大题共8小题,每小题5分满分40分.在每小题给出的四个选项中,只有一项符合要求.1.设集合{}|1P x x =>,{}2|0Q x x x =->,则下列结论正确的是( ).A .P Q =B .P Q =RC .Q P ÜD .P Q Ü 2.复数z 满足i 3i z ⋅=-,则在复平面内,复数z 对应的点位于( ). A .第一象限 B .第二象限 C .第三象限D .第四象限 3.如果平面向量(2,0)a =,(1,1)b =,那么下列结论中正确的是( ).A .||||a b =B .22a b ⋅=C .()a b b -⊥D .a b ∥4.设函数π()sin 23f x x ⎛⎫=- ⎪⎝⎭的图象为C ,下面结论中正确的是( ). A .函数()f x 满足π()2f x f x ⎛⎫-= ⎪⎝⎭ B .图象C 关于点π,06⎛⎫ ⎪⎝⎭对称 C .图象C 可由函数()sin 2g x x =的图象向右平移π3个单位得到 D .函数()f x 在区间ππ,122⎛⎫- ⎪⎝⎭上是增函数 5.在ABC △中,π4A =,2BC =,则“3AC =”是“π3B =”的( ). A .充分不必要条件 B .必要不充分条件C .充要条件D .既不充分也不必要条件6.已知函数x y a =,b y x =,log c y x =的图象如图所示,则( ).A .a b c >>B .a c b >>C .c a b >>D .c b a >> 7.已知函数,0,(),0.x x f x x x -<⎧⎪=⎨⎪⎩≥若关于x 的方程()(1)f x a x =+有三个不相等的实数根,则实数a 的取值范围是( ).A .1,2⎡⎫+∞⎪⎢⎣⎭B .(0,)+∞C .(0,1)D .10,2⎛⎫ ⎪⎝⎭8.如图所示,正方体ABCD A B C D ''''-的棱长为1,E ,F 分别是棱AA ',CC '的中点,过直线E ,F 的平面分别与棱BB ',DD '交于M ,N ,设BM x =,(0,1)x ∈,给出以下四个命题:①四边形MENF 为平行四边形;②若四边形MENF 面积()S f x =,(0,1)x ∈,则()f x 有最小值;③若四棱锥A MENF -的体积()V p x =,(0,1)x ∈,则()p x 是常函数;④若多面体ABCD MENF -的体积()V h x =,1,12x ⎛⎫∈ ⎪⎝⎭,则()h x 为单调函数. 其中假命题...为( ). A .① B .② C .③ D .④二、填空题:本大题共6小题,每小题5分,满分30分9.已知命题:0p c ∃>,方程20x x c -+=有解,则p ⌝为__________.10.已知π02α-<<,且4cos 5α=,则πtan 4α⎛⎫+ ⎪⎝⎭的值等于__________. 11.若||3a =,||2b =,且a 与b 的夹角为π3,则||a b -=__________. 12.ππ(sin )d x x x -+=⎰__________. 13.如图,11AB C △,122C B C △,233C B C △是三个边长为2的等边三角形,且有一条边在同一直线上,边33B C 上有2个不同的点1P ,2P ,则212()AB AP AP ⋅+=__________.14.已知函数()f x 的定义域为R ,a ∀,b ∈R ,若此函数同时满足:①当0a b +=时有()()0f a f b +=;②当0a b +>时有()()0f a f b +>,则称函数()f x 为Ω函数.在下列函数中:①sin y x x =+;②133x x y ⎛⎫=- ⎪⎝⎭;③0,01,0x y x x=⎧⎪=⎨-≠⎪⎩ 是Ω函数的为__________(填出所有符合条件的函数序号).三、解答题:本大题共6小题,满分80分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分13分) 已知函数3()cos (sin 3cos )2f x x x x =+-,x ∈R . (1)求()f x 的最小正周期和单调递增区间.如图所示,在四边形ABCD 中,2D B ∠=∠,且1AD =,3CD =,3cos 3B =.(1)求ACD △的面积.(2)若23BC =,求AB 的长.17.(本小题满分13分)手机完全充满电量,在开机不使用的状态下,电池靠自身消耗一直到出现低电量警告之间所能维持的时间称为手机的待机时间.为了解A ,B 两个不同型号手机的待机时间,现从某卖场库存手机中随机抽取A ,B 两个型号的手机各7台,在相同条件下进行测试,统计结果如下, 手机编号 1 2 3 4 5 6 7A 型待机时间(h ) 120 125 122 124 124 123 123B 型待机时间(h ) 118 123 127 120 124 a b其中,a ,b 是正整数,且a b <.(1)该卖场有56台A 型手机,试估计其中待机时间不少于123小时的台数.(2)从A 型号被测试的7台手机中随机抽取4台,记待机时间大于123小时的台数为X ,求X 的分布列及其数学期望.(3)设A ,B 两个型号被测试手机待机时间的平均值相等,当B 型号被测试手机待机时间的方差最小时,写出a ,b 的值(结论不要求证明).在如图所示的几何体中,四边形ABCD 为正方形,四边形ABEF 为直角梯形,且AF BE ∥,AB BE ⊥,平面ABCD平面ABEF AB =,22AB BE AF ===.(1)求证:AC ∥平面DEF .(2)若二面角D AB E --为直二面角,(i )求直线AC 与平面CDE 所成角的大小.(ii )棱DE 上是否存在点P ,使得BP ⊥平面DEF ?若存在,求出DP DE 的值;若不存在,请说明理由.19.(本小题满分14分)已知函数2()e ()x f x x ax a =++.(1)当1a =时,求曲线()y f x =在点(0,(0))f 处的切线方程.(2)求()f x 的单调区间.(3)求证:当4a ≥时,函数()f x 存在最小值.20.(本小题满分13分)已知集合{}123,,,,n A a a a a =,其中i a ∈R ,1i n ≤≤,2n >.()l A 表示(1)i j a a i j n +<≤≤中所有不同值的个数. (1)设集合{}2,4,6,8P =,{}2,4,8,16Q =,分别求()l P 和()l Q .(2)若集合{}2,4,8,,2n A =,求证:(1)()2n n l A -=. (3)()l A 是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.数学试题答案一、选择题:本大题共8小题,每小题5分满分40分.在每小题给出的四个选项中,只有一项符合要求. 1.【答案】D【解析】∵集合{}|1P x x =>,集合{}{2|0|0Q x x x x x =->=<或}1x >, ∴P Q Ü.故选D .2.【答案】C【解析】∵i 3i z ⋅=-, ∴223i (3i)i 3i i 13i 1i 1z ---====---, ∴其对应的点是(1,3)--,位于第三象限.故选C .3.【答案】C【解析】由平面向量(2,0)a =,(1,1)b =知:在A 中,||2a =,||2b =,∴||||a b ≠,故A 错误;在B 中,2a b ⋅=,故B 错误;在C 中,(1,1)a b -=-,∴()110a b b -⋅=-=,∴()a b b -⊥,故C 正确; 在D 中,∵2011≠, ∴a 与b 不平行,故D 错误.综上所述.故选C .4【答案】B 【解析】A 项.∵π()sin 23f x x ⎛⎫=- ⎪⎝⎭, ∴πππsin 2πsin 2()233f x x x f x ⎛⎫⎛⎫⎛⎫-=--=--=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,故A 错误; B 项.∵πππsin 2sin 00663f ⎛⎫⎛⎫=⨯-== ⎪ ⎪⎝⎭⎝⎭, ∴()f x 的图象C 关于点π,06⎛⎫ ⎪⎝⎭对称,故B 正确;∴()f x 的图象C 由函数()sin 2g x x =的图象向右平移π6个单位得到,故C 错误; D 项,当ππ,122x ⎛⎫∈- ⎪⎝⎭时,ππ2π2,323x ⎛⎫-∈- ⎪⎝⎭, ∴函数()f x 在区间ππ,122⎛⎫- ⎪⎝⎭上先增后减,故D 错误.5.【答案】B 【解析】由正弦定理可得sin sin AC BC B A=, ∴若π3B =,则2ππsin sin 34AC =, 得π2sin 33πsin 4AC ==,必要性成立; 若3AC =,则32πsin sin 4B =, 得π3sin 34sin 22B ==,π3B =或2π3,充分性不成立, ∴“3AC =”是“π3B =”的必要不充分条件. 故选B .6.【答案】C【解析】根据函数的图象知,函数x y a =是指数函数,且当1x =时,(1,2)y a =∈;函数b y x =是幂函数,且2x =时,2(1,2)b y =∈,∴(0,1)b ∈;函数log c y x =是对数函数,且当2x =时,log 2(0,1)c y =∈,∴2c >.综上所述,a ,b ,c 的大小是c a b >>.故选C .7.【答案】D【解析】作出函数()y f x =的图象,如图所示,作出函数(1)y a x =+,则直线恒过点(1,0)-,关于x 的方程()(1)f x a x =+有三个不相等的实数根, 即为直线与曲线y x =相交时,当()f x 的图象有三个交点, 当直线与曲线y x =相切时,设切点为(,)m m , 则112y x'=⋅, 则切线斜率为112a m⋅=, 又(1)a m m +=, 由此解得12a =(负值舍去), 所以实数a 的取值范围是10,2⎛⎫ ⎪⎝⎭. 故选D .8.【答案】D【解析】对于①,∵平面ADD A ''∥平面BCC B '',∴EN MF ∥,同理:FN EM ∥,∴四边形MENF 为平行四边形,故①正确;对于②,四边形MENF 的面积1()()2S f x EF MN ==⨯, 当M 为BB '的中点时,即12x =时,MN 最短, 此时面积最小,故②正确;对于③,则四棱锥分割为两个小棱锥,它们是以AEF 为底,以M ,N 为顶点的两个小棱锥, 因为AEF △的面积是个常数,M ,N 到平面AEF 的距离和是个常数,所以四棱锥C MENF '-的体积()V P x =是常函数,故③正确;对于④,多面体ABCD MENF -的体积11()22ABCD A B C D V h x V ''''-===为常数函数,故④错误. 综上所述,假命题为④.故选D .二、填空题:本大题共6小题,每小题5分,满分30分9.【答案】0c ∀>,方程20x x c -+=无解【解析】在否定特称命题时,需将存在量词改为全称量词,同时否定结论,故命题:0p c ∃>,方程20x x c -+=有解,则p ⌝为:0c ∀>,方程20x x c -+=无解.10. 【答案】17【解析】∵π02α-<<,且4cos 5α=, ∴23sin 1cos 5αα=--=-,3tan 4α=-, ∴π1tan 1tan 41tan 7ααα+⎛⎫+== ⎪-⎝⎭.11. 【答案】7 【解析】由题意可得π||||cos ,32cos33a b a b a b ⋅=⋅=⨯⨯=, ∴222||29467a b a b a b -=+-⋅=+-=, ∴||7a b -=.12.【答案】0【解析】π2π22ππ111(sin )d cos πcos ππcos(π)0222x x x x x --⎛⎫⎛⎫+=-=----= ⎪ ⎪⎝⎭⎝⎭⎰.13.【答案】36【解析】∵11AB C △,122C B C △,233C B C △是三个边长为2的等边三角形,且有一条边在同一直线上, ∴四边形121AC B B 为菱形,∴21π6B AC ∠=,211AB B C ⊥, ∴213AB PC ⊥,23AB BC ⊥,∴21223313223π()(2)22236cos366AB AP AP AB AC C P C P AB AC ⋅+=⋅++=⋅=⨯⨯⨯=.14. 【答案】①②【解析】若()f x 为Ω函数,则由0a b +=时有()()0f a f b +=可得()f x 为奇函数, 又0a b +>时,()()0f a f b +>,故a b >-时,()()f a f b >-,即()()f a f b >-,故()f x 为增函数,∴若函数()y f x =是定义在R 上的奇函数,且单调递增,则函数()f x 为Ω函数. 易知,①②③都是奇函数,当sin y x x =+时,1cos 0y x '=-≥; 当133xx y ⎛⎫=- ⎪⎝⎭时,ln 3(33)0x x y -'=⋅+>; ∴①②都在定义域R 上单调递增;③在定义域R 上没有单调性.故是Ω函数的为:①②.三、解答题:本大题共6小题,满分80分.解答应写出文字说明,证明过程或演算步骤. 15.【答案】见解析.【解析】解:(1)∵3()cos (sin 3cos )2f x x x x =+-, 23sin cos 3cos 2x x x =+-, 13sin 2cos222x x =+, πsin 23x ⎛⎫=+ ⎪⎝⎭, ∴函数()f x 的最小正周期2ππ2T ==, 令πππ2π22π232k x k -++≤≤,k ∈Z , 得5ππππ1212k x k -+≤≤,k ∈Z , ∴函数()f x 的单调递增区间是5πππ,π1212k k ⎡⎤-+⎢⎥⎣⎦,k ∈Z . (2)由题意得,π()()sin 223g x f x x αα⎛⎫=+=++ ⎪⎝⎭, ∵函数()g x 为奇函数,且x ∈R ,∴(0)0g =,即πsin 203α⎛⎫+= ⎪⎝⎭, ∴π2π3k α+=,k ∈Z ,又∵0α>,∴α的最小值为π3.16.【答案】见解析.【解析】解:(1)∵2C B ∠=∠,3cos 3B =, ∴21cos cos22cos 13D B B ==-=-,222sin 1cos 3D D =-=, 又∵1AD =,3CD =,∴ACD △的面积1122sin 132223S AD CD D =⋅⋅=⨯⨯⨯=. (2)在ACD △中,由余弦定理得:2222cos 12AC AD DC AD DC D =+-⋅⋅=, ∴23AC =, 又∵23BC =, ∴由正弦定理得sin sin AC AB B ACB =∠, 即23sin sin(π2)AB B B =-, ∴23sin sin 2AB B B =, 即23sin 2sin cos AB B B B=,即232cos AB B =, ∴343cos 4343AB B ==⨯=.17.【答案】见解析.【解析】解:(1)被检测的7台手机中有5台的待机时间不少于123小时,因此,估计56台A 型手机中有556407⨯=台手机的待机时间不少于123小时. (2)由题意,X 可能的取值为0,1,2,3,4711(0)C 35P X ===, 133447C C 12(1)C 35P X ===, 223447C C 18(2)C 35P X ===, 3447C 4(3)C 35P X ===, ∴X 的分布列为: X 01 2 3 P 112184数学期望1121846012()012335353535357E X =⨯+⨯+⨯+⨯==. (3)124a =,125b =.18.【答案】见解析.【解析】(1)证明:连接BD 交AC 于O ,∵四边形ABCD 为正方形,∴D 是BD 中点,设G 是DE 的中点,连接OG ,FG ,则OG BE ∥,且12OG BE =, ∵四边形ABEF 为直角梯形,且AF BE ∥,22BE AF ==, ∴AF BE ∥,且12AF BE =, ∴AF OG ∥,且AF OG =, ∴四边形AOGF 为平行四边形,∴AO FG ∥,即AC FG ∥,又∵AC ⊄平面DEF ,FG ⊂平面DEF ,∴AC ∥平面DEF .(2)(i )由已知,AF BE ∥,AB BE ⊥,∴AF AB ⊥,∵二面角D AB E --为直二面角,∴平面ABCD ⊥平面ABEF ,∴AF ⊥平面ABCD ,∴AF AD ⊥,AF AB ⊥,又四边形ABCD 为正方形,∴AB AD ⊥,∴AD ,AB ,AF 两两垂直,以A 为原点,AD ,AB ,AF 分别为x ,y ,z 轴建立空间直角坐标系,如图所示,由22AB BE AF ===得:(0,0,0)A ,(0,2,0)B ,(2,2,0)C ,(2,0,0)D ,(0,2,2)E ,(0,0,1)F . ∴(2,2,0)AC =,(0,2,0)CD =,(2,0,2)CE =-.设平面CDE 的一个法向量为(,,)n x y z =,则:00n CD n CE ⎧⋅=⎪⎨⋅=⎪⎩,即20220y x z -=⎧⎨+=⎩, 取1x =,则0y =,1z =-,∴(1,0,1)n =,设直线AC 与平面CDE 所成的角为θ,则有:21sin |cos ,|2222AC n θ===⨯, ∵090θ︒≤≤,∴30θ=︒,即直线AC 与平面CDE 所成角的大小为30︒.(ii )假设棱DE 上存在点P ,使得BP ⊥平面DEF ,设(01)DP DEλλ=≤≤,则DP DE λ=, 设(,,)P x y z ,则(2,,)DP x y z =-,∵(2,2,2)DE =-,∴(2,,)(2,2,2)x y z λ-=-,∴22x λ-=-,2y λ=,2z λ=,解得22x λ=-,2y λ=,2z λ=,即P 点坐标为(22,2,2)λλλ-,∵(0,2,0)B ,∴(22,22,2)BP λλλ--,又(2,0,1)DF =-,(0,2,1)EF =--,∴00BP DF BP EF ⎧⋅=⎪⎨⋅=⎪⎩,即2(22)202(22)20λλλλ--+=⎧⎨---=⎩, 解得23λ=. ∵2[0,1]3∈, ∴DE 上存在点P ,使得BP ⊥平面DEF ,且23DP DE =.19.【答案】见解析.【解析】解:(1)当1a =时,2()e (1)x f x x x =++,2()e (32)x f x x x '=++, ∴(0)1f =,(0)2f '=,∴曲线()y f x =在点(0,(0))f 处的切线方程为:12(0)y x -=-,即21y x =+.(2)由2()e ()x f x x ax a =++得2()e [(2)2]e ()(2)x x f x x a x a x a x '=+++=++, 令()0f x '=,解得:2x =-或x a =,①当2a -=-,即2a =时,2()e (2)0x f x x '=+≥,()f x 在R 上单调递增;②当2a ->-,即2a <时,令()0f x '>,得2x <-或x a >-;令()0f x '<,得2x a -<<-,∴()f x 的单调增区间是(,2)-∞-和(,)a -+∞,单调减区间是(2,)a --;③当2a -<-,即2a >时,令()0f x '>,得x a <-或2x >-;令()0f x '<,得2a x -<<-,∴()f x 的单调增区间是(,)a -∞-和(2,)-+∞,单调减区间是(,2)a --.综上所述,当2a =时,函数()f x 在R 上递增;当2a <时,()f x 的单调增区间是(,2)-∞-和(,)a -+∞,单调减区间是(2,)a --; 当2a >时,()f x 的单调增区间是(,)a -∞-和(2,)-+∞,单调减区间是(,2)a --. (3)由(1)得:当4a ≥时,函数()f x 在[),x a ∈-+∞上有()(2)f x f -≥, 且2(2)e (4)0f a --=-≤,∵4a ≥,∴(,)x a ∈-∞-时,()0x x a +≥,e 0x >,()e [()]0x f x x x a a =++>,∴4a ≥时,函数()f x 存在最小值(2)f -.20.【答案】见解析.【解析】解:(1)由246+=,268+=,2810+=,4610+=,4812+=,6814+=得()5l P =, 由246+=,2810+=,21618+=,4812+=,41620+=,81624+=得()6l Q =.(2)证明:∵(1)i j a a i j n +<≤≤最多有2(1)C 2n n n -=个值, ∴(1)()2n n l A -≤, 又集合{}2,4,8,,2n A =,任取i j a a +,(1,1)k l a a i j n k l n +<<≤≤≤≤,当j l ≠时,不妨设j l <,则22j i i j j l k l a a a a a a ++<=<+≤,即i j k l a a a a +≠+,当j l =,i k ≠时,i j k l a a a a +≠+,∴当且仅当i k =,j l =时,i j k l a a a a +=+,即所有(1)i j a a i j n +<≤≤的值两两不同, ∴(1)()2n n l A -=. (3)()l A 存在最小值,且最小值为23n -, 不妨设123n a a a a <<<<,可得1213121n n n n a a a a a a a a a a -+++<<+<<<<+, ∴(1)i j a a i j n +<≤≤中至少有23n -个不同的数,即()23l A n -≥, 取{}1,2,3A n =,则{}3,4,5,21i j a a n +∈-,即i j a a +的不同值共有23n -个, 故()l A 的最小值为23n -.。
北京东直门中学2016—2017学年高三上学期期中考试理科数学试题

北京东直门中学2016—2017学年高三上学期期中考试理科数学试题数学试题(理)1.已知集合{}|12A x x =-<,{}211B x og x =,则A B =( ). A. (1,3)-B. (0,3)C. (2,3)D. (1,4)-2.“0x >”是“20x x +>”的( ) . A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件D. 既不充分也不必要条件3.设命题:0p x ∃>,sin 21x x >-,则p ⌝为( ). A. 0x ∀>,sin 21x x ≤- B. 0x ∃>,sin 21x x <- C. 0x ∀>,sin 21x x <-D. 0x ∃>,sin 21x x ≤-4.已知π3sin 25α⎛⎫+= ⎪⎝⎭,π0,2α⎛⎫∈ ⎪⎝⎭,则sin(π)α+=( ). A. 35B. 35-C.45D. 45-,5.函数2()1log f x x =+与1()2x g x -+=在同一直角坐标系下的图象大致是( )6.为得到sin3cos3y x x =+ 图象,可将y x = 的图象A. 向右平移π4个单位B. 向左平移π4个单位C. 向右平移π12个单位D. 向左平移π12个单位7.设,a b 是两个非零向量,则下列命题为真命题的是 A. 若a b a b a b +=-⊥,则 B. 若,a b a b a b ⊥+=-则C. 若a b a b +=-,则存在实数λ,使得a b λ=D. 若存在实数λ,使得a b λ=,则a b a b +=-8.已知函数()f x 满足:()f x x ≥且()2,xf x x R ≥∈.( ) A. 若()f a b ≤,则a b ≤ B. 若()2bf a ≤,则a b ≤ C. 若()f a b ≥,则a b ≥ D. 若()2bf a ≥,则a b ≥9.定积分21d 1x x ⎰-的值为__________. 10.在三个数12,122-,3log 2中,最小的数是__________. 11.设π02θ<<,向量(sin 2,cos )a θθ=,(1,cos )b θ=-,若0a b ⋅=,则t a n θ=__________.12.已知函数()f x 的定义域为R ,当0x <时,3()1f x x =-;当11x -≤≤时,()()f x f x -=-;当12x >时,1122f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭.则(6)f =__________.13.已知函数2,()24,x x m f x x mx m x m⎧≤=⎨-+>⎩ 其中0m >,若存在实数b ,使得关于x 的方程f (x )=b 有三个不同的根,则m 的取值范围是________________. 14.如图,正方形ABCD 的边长为6,点E ,F 分别在边AD ,BC 上,且2DE AE =,2CF BF =.如果对于常数λ,在正方形ABCD 的四条边上,有且只有6个不同的点P 使得PE PF λ⋅=成立.那么λ的取值范围是__________.15.已知函数22()(sin cos )2cos f x x x x =+-.(1)求函数()f x 的最小正周期和单调递增区间. (2)求函数()f x 在π3π,44⎡⎤⎢⎥⎣⎦上的值域.16.已知数列{}(1,2,3,)n a n =满足12n n a a +=,且1a ,21a +,3a 成等差数列,设23log 10n n b a =-.(1)求数列{}n a ,{}n b 的通项公式. (2)求数列{}n b 前n 项和n T .17.在ABC △中,内角A 、B 、C 、所对边长分别为a 、b 、c ,且1cos 2B =-. (1)若2a =,b =求角C 的大小. (2)求sin sin A C ⋅的取值范围.18.已知函数1()e xxf x -=. (1)求曲线()y f x =在点(0,(0))f 处的切线方程. (2)求函数()f x 的零点和极值.(3)若对任意1x ,2[,)x a ∈+∞都有1221()()ef x f x -≥-成立,求实数a 最小值.的19.如图,椭圆2222:1(0)x y E a b a b+=>>经过点(0,1)A -,且离心率2. (I )求椭圆E 的方程;(II )经过点(1,1),且斜率为k 的直线与椭圆E 交于不同两点,P Q (均异于点A ), 问:直线AP 与AQ 的斜率之和是否为定值?若是,求出此定值;若否,说明理由。
北京市东城区东直门中学2017届高三上学期期中考试数学(理)试题含解析

北京东直门中学2016—2017学年度第一学期期中考试高三数学(理)2016.11 考试时间:120分钟总分 150分第一部分(选择题)一、选择题(本大题共8小题,每小题5分,共40分). 1.已知集合{}|12A x x =-<,{}2|1og 1B x x =>,则A B =( ).A .(1,3)-B .(0,3)C .(2,3)D .(1,4)-【答案】C【解析】{}{}|1|213A x x x x =-<=-<<,{}{}2log 12B x x x x =>=>, ∴{}23A B x x =<<.故选C .2.“0x >"是“20x x +>”的( ) . A .充分不必要条件 B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【解析】201x x x +>⇔<-或0x >,∴“0x >”是“20x x +>"的充分不必要条件.故选A .3.设命题:0p x ∃>,sin 21x x >-,则p ⌝为( ). A .0x ∀>,sin 21x x -≤B .0x ∃>,sin 21x x <-C .0x ∀>,sin 21x x <-D .0x ∃>,sin 21x x -≤【答案】A【解析】特称命题的否定为全称命题,∴p ⌝为“0x ∀>,sin 21x x -≤".故选A . 4.已知π3sin 25α⎛⎫+= ⎪⎝⎭,π0,2α⎛⎫∈ ⎪⎝⎭,则sin(π)α+=( ).A .35B .35-C .45D .45-,【答案】D 【解析】∵π3sin 25α⎛⎫+= ⎪⎝⎭,π0,2α⎛⎫∈ ⎪⎝⎭,∴3cos 5α=,4sin 5α=,∴4sin(π)sin 5αα+=-=-.故选D .5.函数2()1log f x x =+与1()2x g x -=在同一直角坐标系下的图像大致是( ).A.B.C.D.【答案】C【解析】对于函数1()2x g x -=,当0x =时,函数值为2,过点(0,2),排除B ,D . 对于函数2()1log f x x =+,当1x =时,函数值为1,过点(1,1),排除A . 综上,故选C .6.为了得到函数sin3cos3y x x =+的图像,可以将函数y x =的图像( ).A .向右平移π4个单位 B .向左平移π4个单位 C .向右平移π12个单位D .向左平移π12个单位【答案】D【解析】ππsin3cos333412y x x x x ⎡⎤⎛⎫⎛⎫=+++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,所以为了得到函数sin3cos3y x x =+的图象,可以将y x 的图象向左平移π12个单位.故选D .7.设a ,b 是两个非零向量( ). A .若||||||a b a b +=-,则a b ⊥B .若a b ⊥,则||||||a b a b +=-C .若||||||a b a b +=-,则存在实数λ,使得a b λ=D .若存在实数λ,使得a b λ=,则||||||a b a b +=-【答案】C【解析】根据向量加法的几何意义,|||||a b a b +-≥|,其中等号当且仅当向量a ,b 共线时成立,所以由||||||a b a b +=-,可得存在实数λ,使得a b λ=.故选C .8.已知函数()f x 满足:()f x x ≥且()2x f x ≥,x ∈R .( ). A .若()f a b ≤,则a b ≤ B .若()2b f a ≤,则a b ≤C .若()f a b ≥,则a b ≥D .若()2b f a ≥,则a b ≥【答案】B【解析】由题意可得下图:A 项,1()||f a b '<,1a b '>,故A 项错误;B 项,若()f a b ≠,如图,1()2b f a <,1a b <,若()2bf a =,则等号成立,故B 项正确;C 项,2()||f a b >,2a b <,故C 项错误;D 项,2()2bf a >,2a b <,故D 项错误.综上所述,故选B .第二部分(非选择题)二、填空题(本大题共6小题,每小题5分,共30分) 9.定积分21d 1x x -⎰的值为__________. 【答案】23【解析】1231111112d |3333x x x --⎛⎫==--= ⎪⎝⎭⎰10.在三个数12,122-,3log 2中,最小的数是__________. 【答案】12【解析】12122-==>,31log 2log 2>.故三个数12,122-,3log 2中最小的数是12.11.设π02θ<<,向量(sin2,cos )a θθ=,(1,cos )b θ=-,若0a b ⋅=,则tan θ=__________. 【答案】12【解析】∵22(sin2,cos )(1,cos )sin2cos 2sin cos cos 0a b θθθθθθθθ⋅=⋅-=-=-=, ∴22sin cos cos θθθ=, ∵π02θ<<,∴cos 0θ>,∴2tan 1θ=,解得1tan 2θ=.12.已知函数()f x 的定义域为R ,当0x <时,3()1f x =x -;当11x -≤≤时,()()f x f x -=-;当12x >时,1122f x f x ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭.则(6)f =__________.【答案】2 【解析】当12x >时,1122f x f x ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭+,所以当1x >时,()(1)f x f x =-,故(6)(1)f f =;当11x -≤≤时,()()f x f x -=-,所以(1)(1)f f =-. 当0x <时,3()1f x x =-,所以(1)2f =-,故(1)2f =.13.已知函数2,()24,x x mf x x mx m x m⎧⎪=⎨-+>⎪⎩≤,其中0m >,若存在实数b ,使得关于x 的方程()f x b =有三个不同的根,则m 的取值范围是__________. 【答案】(3,)+∞ 【解析】)=x 22mx+4m (x>m )m m 2当0m >,函数2||,()24,x x mf x x mx m x m ⎧=⎨->⎩≤+的图象如图:∵x m >时,2222()24()44f x x mx m x m m m m m =-=-->-++, ∴y 要使得关于x 的方程()f x b =有三个不同的根,则:24(0)m m m m -<>,即23(0)m m m >>,解得,3m >. 故m 的取值范围是(3,)∞+.14.如图,正方形ABCD 的边长为6,点E ,F 分别在边AD ,BC 上,且2DE AE =,2CF BF =.如果对于常数λ,在正方形ABCD 的四条边上,有且只有6个不同的点P 使得PE PF λ⋅=成立.那么λ的取值范围是__________.FEB【答案】(0,4)【解析】以DC 为x 轴,以DA 为y 轴建立平面直角坐标系,如图,则(0,4)E ,6,4F (),①若P 在CD 上,设(,0)P x ,06x ≤≤,则(,4)PE x ==-,(6,4)PF x =-. ∴2616PE PF x x ⋅=-+,∵[]0,6x <,∴716PE PF ⋅≤≤.∴当7λ=时有一解,当716λ<≤时有两解.②若P 在AD 上,设(0,)P y ,06y ≤≤,则(0,4)PE y =-,(6,4)PF y =-. ∴22(4)816PE PF y y y ⋅=-=-+. ∵06y ≤≤,∴016PE PF ⋅≤≤.当0λ=或416λ<≤,有一解,当04λ<≤时有两解.③若P 在AB 上,设(,6)x x ,06x ≤≤,则(,2)PE x =--,(6,2)PF x =--, ∴2=64PE PF x x ⋅-+.∵06x ≤≤,∴74PE PF -⋅≤≤.∴当7λ=-时有一解,当72λ-<≤时有两解.④若P 在BC 上,设(6,)P y ,06y ≤≤,则(6,4)PE y =--,(0,4)PF y =-. ∴22(4)816PE PF y y y ⋅=-=-+. ∵06y ≤≤,∴16PE PF ⋅0≤≤.∴当0λ=或416λ<≤,有一解,当04λ<≤时有两解. 综上所述,∴04λ<<.三、解答题(本大题共6小题,共80分) 15.已知函数22()(sin cos )2cos f x x x x =+-. (1)求函数()f x 的最小正周期和单调递增区间. (2)求函数()f x 在π3π,44⎡⎤⎢⎥⎣⎦上的值域.【答案】(1)根据题意得:222()sin 2sin cos cos 2cos f x x x x x x =-++ 21sin 22cos x x =-+ sin 2cos 2x x =-π24x ⎛⎫=- ⎪⎝⎭故函数()f x 的最小正周期2ππ2T ==. 由πππ2π22π+242k x k --≤≤,k ∈Z ,可得:3πππ88k x k λ-≤≤+,k ∈Z故函数()f x 的单调递增区间是π3ππ,π88k k ⎡⎤-⎢⎥⎣⎦+,()k ∈Z .(2)∵π3π,44x ⎡⎤∈⎢⎥⎣⎦,∴ππ5π2,444x ⎡⎤-∈⎢⎥⎣⎦,∴πsin 24x ⎡⎤⎛⎫-∈⎢⎥ ⎪⎝⎭⎣⎦π24x ⎛⎫⎡-∈- ⎪⎣⎝⎭,即()f x ⎡∈-⎣,故函数()f x 在π3π,44⎡⎤⎢⎥⎣⎦上的值域为⎡-⎣.16.已知数列{}(1,2,3,)n a n =满足12n n a a +=,且1a ,21a +,3a 成等差数列,设23log 10n n b a =-. (1)求数列{}n a ,{}n b 的通项公式. (2)求数列{}n b 的前n 项和n T . 【答案】【解析】(1)12n n a a =+,∴{}n a 为等比数列,其公比为2.∵1a ,21a +,3a 成等差数列,∴2132(1)a a a =++,即1112(21)4a a a =++,解得:12a =. ∴112n n n a a q -==,222log 103log 210310n n n b a n =-=-=-, 故2n n a =,310n b n =-.(2)由310n b n =-,可得{}n b 的前几项和为1(317)2n S n n =-.当13n -≤≤时,0n b <,即1(317)2n n T S n n =-=--;当4n ≥时,可得:231317482(317)2422n n n n T S S n n -=-=-=++.综上可得,22317,132()31748,42n n nn T n n n n ⎧-⎪⎪=∈⎨-⎪⎪⎩N ≤≤≥++.17.在ABC △中,内角A 、B 、C 、所对边的长分别为a 、b 、c ,且1cos 2B =-.(1)若2a =,b =求角C 的大小. (2)求sin sin A C ⋅的取值范围. 【答案】【解析】(1)在ABC △中,1cos 2B =-,(0,π)B ∈,∴2π3B =,sin B =. 由正弦定理sin sin a b A B=,可得:2sin A ,∴1sin 2A =,∴π6A =. ∴ππ6C A B =--=.(2)π1sin sin sin sin sin sin 32A C C C C C C ⎫⎛⎫⋅=-⋅=-⋅⎪ ⎪⎪⎝⎭⎝⎭111π12cos2sin 244264C C C ⎛⎫=-=- ⎪⎝⎭++. ∵π0,3C ⎛⎫∈ ⎪⎝⎭,∴ππ5π2,666C ⎛⎫∈ ⎪⎝⎭+.∴π1sin 2,162C ⎛⎫⎛⎤∈ ⎪ ⎥⎝⎭⎝⎦+,∴1π11sin 20,2644C ⎛⎫⎛⎤-∈ ⎪ ⎥⎝⎭⎝⎦+,即1sin sin 0,4A C ⎛⎤⋅∈ ⎥⎝⎦. 故sin sin A C ⋅的取值范围是10,4⎛⎤ ⎥⎝⎦.18.已知函数1()e xxf x -=. (1)求曲线()y f x =在点(0,(0))f 处的切线方程. (2)求函数()f x 的零点和极值.(3)若对任意1x ,2[,)x a ∈+∞都有1221()()e f x f x --≥成立,求实数a 的最小值. 【答案】【解析】(1)∵1()e x x f x -=,2()e xx f x -'=,∴(0)1f =,(0)2f '=-, ∴()f x 在点(0,(0))f 处的切线的斜率为2-,切点为(0,1), ∴切线方程为:21y x =-+,即210x y -=+. (2)由()0f x =,可得1x =,即零点为1;由2x >时,()0f x '>,()f x 递增,2x <时,()0f x '<,()f x 递减,可得:当2x =时,()f x 取得极小值,21()(2)e f x f ==-极小值,无极大值.【注意有文字】 (3)当1x >时,1()0e x x f x -=<,当1x <时,1()0e x xf x -=>,若1a <,令12x =,2[,1)x a ∈,则1x ,[)2,x a ∈∞+,由于22()()0f x f x ⇔-<,则有121221()()()()e f x f x f x f x -<==-,不符合题意; 若1a ≥时,对任意1x ,[)2,x a ∈∞+,都有1()0f x ≤,2()0f x ≤,则有2()0f x -≥, 所以121221()()()()e f x f x f x f x -=-≥≥, 即1a ≥时,对任意1x ,[)2,x a ∈∞+,都有1221()()e f x f x --≥成立. 综上所述,实数a 的最小值是1.19.如图,椭圆2222:1(0)x y E a b a b +=>>经过点(0,1)A -.(1)求椭圆E 的方程.(2)经过点(1,1),且斜率为k 的直线与椭圆E 交于不同的两点P ,Q (均异于点A ),判断直线AP 与AQ 的斜率之和是否为定值?若是定值,求出改定值;若不是定值,请说明理由.【答案】【解析】根据题意知:c a =1b =,结合222a b =+c ,解得:a =,1b =,1c =,∴椭圆的方程为:2212x y =+.(2)由题设知,直线PQ 的方程为(1)1(2)y k x k =-≠+,将直线方程与椭圆方程联立,22(1)1,(2)12y k x k x y =≠⎧⎪⎨=⎪⎩+++,得22(12)4(1)2(2)0k x k k x k k ---=++. 由已知0∆>,设11(,)P x y ,22(,)Q x y ,120x x ≠,则1224(1)12k k x x k -=++,1222(2)12k k x x k -=+, 从而直线AP ,AQ 的斜率之和: 12121212121211222(2)AP AQ y y kx k kx k x xk k k k x x x x x x --===-+++++++++ 4(1)2(2)22(1)22(2)k k k k k k k k -=-⋅=--=-+.故直线AP 、AQ 斜率之和为定值2.20.在数列{}n a 中,10a =,21n n a a m +=+,其中m ∈R ,n *∈N . (1)当1m =时,求2a ,3a ,4a 的值.(2)是否存在实物m ,使2a ,3a ,4a 构成公差不为0的等差数列?证明你的结论. (3)当14m >时,证明:存在k *∈N ,使得2016k a >. 【答案】【解析】(1)当1m =时,211n na a =++,10a =, ∴21a =,32a =,45a =.(2)∵2a ,3a ,4a 成等差数列,∴3243a a a a -=-,即222233a m a a m a -=-++,∴223232()()0a a a a ---=, ∴320a a -≠,∴3210a a -=+.将2a m =,23a m m =+,代入上式,解得1m =- 经检验,此时2a ,3a ,4a 的公差不为0.∴存在1m =-2a ,3a ,4a 构成公差不为0的等差数列. (3)∵221111244n n n n n a a a m a a m m ⎛⎫⎛⎫-=-=--- ⎪ ⎪⎝⎭⎝⎭≥+++,又14m >,∴令104d m =->. ∵1n n a a d --≥,12n n a a d ---≥,,21a a d -≥,∴1(1)n a a n d --≥,即(1)n a n d -≥. 取正整数20161k d>+,则: 2016(1)2016k a k d d d ⎛⎫->⋅= ⎪⎝⎭≥.故当14m >时,存在*k ∈N ,使得2016k a >.。
2016-2017学年高二上学期期中考试数学试题Word版含答案
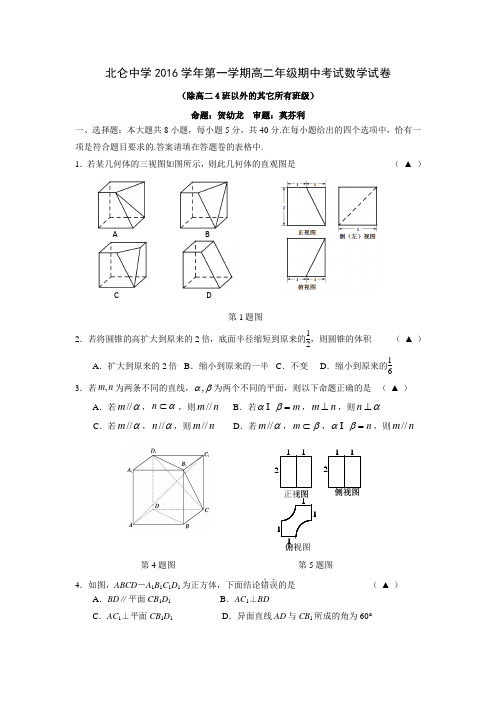
北仑中学2016学年第一学期高二年级期中考试数学试卷(除高二4班以外的其它所有班级) 命题:贺幼龙 审题:莫芬利一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,恰有一项是符合题目要求的.答案请填在答题卷的表格中.1.若某几何体的三视图如图所示,则此几何体的直观图是 ( ▲ )第1题图2.若将圆锥的高扩大到原来的2倍,底面半径缩短到原来的12,则圆锥的体积 ( ▲ )A .扩大到原来的2倍B .缩小到原来的一半C .不变D .缩小到原来的163.若,m n 为两条不同的直线,,αβ为两个不同的平面,则以下命题正确的是 ( ▲ ) A .若α//m ,α⊂n ,则n m // B .若m =βα ,n m ⊥,则α⊥nC .若α//m ,α//n ,则n m //D .若α//m ,β⊂m ,n =βα ,则n m //第4题图 第5题图4.如图,ABCD -A 1B 1C 1D 1为正方体,下面结论错误..的是 ( ▲ )A .BD ∥平面CB 1D 1 B .AC 1⊥BDC .AC 1⊥平面CB 1D 1 D .异面直线AD 与CB 1所成的角为60°A BC D5.某几何体三视图如图所示,则该几何体的体积为 ( ▲ ) A .82π- B .8π- C .82π- D .84π-6.如果一个水平放置的图形的斜二测直观图是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是 ( ▲ )A .2+2 B.1+22 C.2+22D .1+ 27.下列四个命题中正确的命题有 ( ▲ ) ①过空间任何一点P 可以作无数条直线与已知的异面直线b a ,都相交; ②三个平面两两相交,有三条交线,则此三条交线或交于一点,或互相平行;③直线a α⊥平面,直线b β⊥平面,则直线b a ,所成角与平面βα,所成角相等或互补; ④αβ⊥平面平面,,,m n m n αβ⊂⊂⊥,则β⊥m 或α⊥n .A.1个B.2个C.3个D.4个8.如图,正方体1111ABCD A B C D -的棱长为1,点A 在平面α内,点E 是底面ABCD 的中心.若1C E ⊥平面α,则1C AB ∆在平面α内的射影的面积为 ( ▲ )ABCD第8题图 第11题图 第12题图二、填空题:本大题共7小题,前4题每空3分,后3题每空4分,共36分.将正确答案填在答题卷的横线上.9.正方体1111ABCD A B C D -的棱长为1,则其表面积为 ▲ ,其内切球的体积为 ▲ . 10.将一个边长分别是2 cm 和3 cm ,两邻边夹角为60°的平行四边形绕其3 cm 边上的高所在直线旋转一周形成的简单几何体是 ▲ ,其体积为 ▲ cm 3.11.如图,P 是正方形ABCD 外一点,且PA ABCD ⊥平面,则此几何体的5个面中互相垂直的面有 ▲ 对;若PA AB =,则直线PC 与平面PAB 所成角的正切值为 ▲ .1C 1A 1D 1B CDABαE12.一个几何体的三视图及部分数据如图所示,正视图、侧视图和俯视图都是等腰直角三角形,则该几何体体积为 ▲ ,表面积为 ▲ .第13题图 第15题图13.如图,已知正三棱锥A —BCD 侧面的顶角为45°,侧棱长为a ,动点E 在侧棱AC 上运动,则线段BE 、ED 长度和的最小值为 ▲ .14,a b ,则a,b 所满足的等量关系式是 ▲ .15.如图,已知平面⊥α平面β,、A B 是平面α与β的交线上的两个定点,β⊂DA ,β⊂CB ,且6,8,4,,===⊥⊥AB BC AD CB DA αα,在平面α上有一个动点P ,使得BPC APD ∠=∠,则PAB ∆的面积的最大值为 ▲ .三、解答题:本大题共5小题,共74分.解答应写出文字说明,证明过程或演算步骤.16.(本题满分14的正四棱锥P -ABCD 中,侧棱与底面所成角的大小为60°. (1)求侧棱的长度;(2)求正四棱锥P -ABCD 的外接球的表面积.第16题图 第17题图17.(本题满分15分)如图所示,在直三棱柱ABC -A 1B 1C 1中,AB =BC =AA 1=1,∠ABC=PDCBABCDAE90°. 点E 、F 分别是棱AB 、BB 1的中点. (1)求三棱锥B -AFC 的体积; (2)求异面直线EF 和BC 1所成的角.18.(本题满分15分)如图1,平面四边形 ABCD 关于直线AC 对称,2=CD ,60,90,A C ︒︒∠=∠=把ABD ∆沿BD 折 起(如图2)使二面角C BD A --的余弦值 为33.对于图2 (1)求AC 的长;(2)证明:⊥AC 平面BCD ;(3)求直线AC 与平面ABD 所成角的正弦值.第18题图19.(本题满分15分)如图,两矩形ABCD ,ABEF 所在平面互相垂直,DE 与平面ABCD 及平面ABEF 所成角分别为0030,45,N M ,分别为DB DE 、的中点,且1=MN . (1)求证:⊥MN 平面ABCD ; (2)求二面角B DE A --的正弦值.第19题图 第20题图20.(本题满分15分)如图,矩形ABCD 所在的半平面和直角梯形CDEF 所在的半平面 成60的二面角,.45,6,23,2,,// =∠===⊥CFE CF EF AD DE CD CF DE (1)求证:BF ∥平面ADE ;A CDB图1CABD图2FACB ED(2)试问在线段CF 上是否存在一点G ,使锐二面角D EG B --的余弦值为41.若存在,请求出CG 的值;若不存在,请说明理由.北仑中学2016学年第一学期高二年级期中考试数学参考答案(除高二4班以外的其它所有班级)一.选择题二.填空题9._____6______ ___6π____ 10.__圆台_____ ___3319π__ 11.______5_____ ____22___ 12.___ 31____ ____32+__13. 14. 822=+b a15. 12三.解答题16.(本题满分14分) (1)2 (2)316π17. (本题满分15分)PDCBA(1)1/12(2)318.(本题满分15分)解:(Ⅰ)取的中点,连接,由,得:就是二面角的平面角,在中,(Ⅱ)由,,又平面(Ⅲ)方法一:由(Ⅰ)知平面平面∴平面平面平面平面,作交于,则平面,就是与平面所成的角方法二:设点到平面的距离为,∵于是与平面所成角的正弦为.19. (本题满分15分)(1)证明:∵平面ABCD⊥平面ABEF,且平面ABCD∩平面ABEF=AB,EB ⊥AB,∴EB⊥平面ABCD,又MN∥EB,∴MN⊥面ABCD.(2)解:过B作BO⊥AE于O点,过O作OH⊥DE于H,连BH,∵AD⊥平面ABEF,BO面ABEF,∴BO⊥平面ADE,∴OH为BH在平面ADE内的射影,∴BH⊥DE,即∠BHO为所求二面角的平面角,在Rt△ABE中,BO=,在Rt△DBE中,由BH·DE=DB·OE得BH=,∴sin∠BHO= .MOGFACBEDHOH20. (本题满分15分)证明:(1)∵在矩形ABCD 中BC ∥AD , AD ⊂平面ADE BC ⊄平面ADE , ∴BC ∥平面ADE , 同理CF ∥平面ADE , 又∵BC∩CF=C , ∴平面BCF ∥平面ADE , 而BF ⊂平面BCF , ∴BF ∥平面ADE . (2)∵CD ⊥AD ,CD ⊥DE∴∠ADE 即为二面角A-CD-F 的平面角, ∴∠ADE=60° 又∵AD∩DE=D , ∴CD ⊥平面ADE , 又∵CD ⊂平面CDEF ∴平面CDEF ⊥平面ADE ,作AO ⊥DE 于O ,则AO ⊥平面CDEF .过O 作EH OH ⊥于H,连接BH,易得BHO ∠是锐二面角D EG B --的平面角 因为3=BO ,易求得55=OH 取CF 中点M,易知OHG ∆与EMG ∆相似,设x OG =(x>0),则EGEMOG OH =,即2)2(9355x x -+=,解得21=x 或2213-=x (舍)因此存在符合题意的点G,使得CG=23.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
北京市东直门中学2016-2017学年度第一学期期中考试高二数学2016.11.8一、选择题:(本大题共15小题,每小题3分,共45分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.点(3,4,5)P ,在yOz 平面上的射影P '的坐标是( ).A .(0,4,5)B .(3,0,5)C .(3,4,0)D .(3,0,0) 【答案】A【解析】点P 在yOz 平面上的射影P '和点P 的y 坐标相同,z 坐标相同,x 坐标为O , ∴P '坐标为(0,4,5),故选A .2.已知全集{},,,U a b c d =,集合{},A a b =,{},B b c =,则()U A B ð等于( ).A .{}bB .{}dC .{},,a c dD .{},,a b c 【答案】B【解析】∵{,}A a b =,{,}B b c =,∴{,,}A B a b c = ,∴(){}U A B d = ð.故选B .3.πsin 6⎛⎫-= ⎪⎝⎭( ). A .32 B .32- C .12 D .12- 【答案】D 【解析】ππ1sin sin 662⎛⎫-=-=- ⎪⎝⎭.故选D .4.已知两条相交直线a 、b ,a ∥平面α,则b 与α的位置关系是( ).A .b ⊂平面αB .b ⊥平面αC .b ∥平面αD .b 与平面α相交,或b ∥平面α 【答案】D【解析】根据空间中直线与平面的位置关系的可得:b 与平面α相交或b ∥平面α.故选D .5.已知命题21:p x x ∀>,2122x x >,则p ⌝是( ).A .21x x ∀>,2122x x <B .21x x ∃>,2122x x ≤C .21x x ∀≤,2122x x ≤D .21x x ∃≤,2122x x < 【答案】B【解析】命题p 是全称命题,其否定为特称命题,所以:p ⌝“21x x ∃>,2122x x ≤”.故选B .6.“tan 0α>”是“角α是第一象限的角”的( ).A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B 【解析】若“角α是第一象限角”,则“tan 0α>”,“若tan 0α>”,则“角α是第一象限角或第三象限角”,所以“tan 0α>”是“角α是第一象限角”的必要不充分条件.故选B . 7.已知向量(2,3,1)a = ,(1,2,0)b = ,则||a b + 等于( ).A .3B .3C .35D .9 【答案】C 【解析】∵(2,3,1)a = ,(1,2,0)b = ,(3,5,1)a b += , ∴||925135a b +=++= .故选C .8.命题p :x ∀∈R ,220x ax a ++≥;命题q :向量(2,3,0)e = ,(0,0,0)f = 不平行,则下列命题中为真命题的是( ).A .p q ∧B .p q ∨C .()p q ⌝∨D .()()p q ⌝∧⌝【答案】B【解析】∵p 是真命题,q 是假命题,所以p q ∨是真命题.故选B .9.已知向量(0,1,1)a =- ,(1,0,2)b = ,若向量ka b + 与向量a b - 互相垂直,则实数k 的值是( ). A .32B .2C .54D .74 【答案】D 【解析】∵(0,1,1)a =- ,(1,0,2)b = ,∴(1,,2)ka b k k +=-+ ,(1,1,3)a b -=-- ,∵ka b + 与a b - 互相垂直,∴13(2)0k k -+--+=, 解得:74k =. 故选D .10.在四面体O ABC -中,点P 为棱BC 的中点,设OA a = ,OB b = ,OC c = 那么向量AP 用基底{},,a b c 可表示为( ). AB COPA .111222a b c -++B .111222a b c ++ C .12a b c ++ D .1122a b c -++ 【答案】D 【解析】111111()()222222AP AB AC OB OA OC OA OA OB OC =+=-+-=-++ ∴1122AP a b c =-++ .故选D .11.已知3cos 5α=,π,02α⎛⎫∈- ⎪⎝⎭,则sin 2α的值为( ). A .2425- B .2425 C .725- D .725【答案】A 【解析】∵3cos 5α=,π,02α⎛⎫∈- ⎪⎝⎭, ∴4sin 5α=-, ∴24sin 22sin cos 25ααα==-. 故选A .12.已知(2,5,1)A -,(2,2,4)B -,(1,4,1)C -,则向量AB 与AC 的夹角为( ).A .30︒B .45︒C .60︒D .90︒ 【答案】C【解析】∵(2,5,1)A -,(2,2,4)B -,(1,4,1)C -,∴(0,3,3)AB = ,(1,1,0)AC =- , ∴31cos ,2||||322AB AC AB AC AB AC ⋅<>===⋅ , ∴AB 与AC 的夹角为60︒,故选C .13.设m 、n 是不同的直线,α、β、γ是不同的平面,有以下四个命题:①a αββγγ⎫⇒⎬⎭∥∥∥;②m m αββα⎫⇒⎬⎭⊥⊥∥;③m m ααββ⎫⇒⎬⎭⊥⊥∥;④m n m n αα⎫⇒⎬⊂⎭∥∥ 其中为真命题的是( ).A .①④B .①③C .②③D .②④ 【答案】B【解析】①利用平面与平面平行的性质定理可知:αβ∥,a γ∥,则βγ∥,故①正确; ②αβ⊥,m α∥,则m 与β可能平行,也可能相交,故②错误;③m n ββ⇒∃⊂∥,且m n ∥,因为m α⊥,所以n α⊥,所以αβ⊥,故③正确; ④m n ∥,n m αα⊂⇒∥或m α⊂,故④错误.综上所述,真命题是:①③.故选B .14.某三棱锥的三视图如图所示,则该三棱锥的体积是( ).1112正视图侧视图俯视图A .13B .12C .1D .32【答案】A 【解析】三棱锥如图所示,1CD =,2BC =,CD BC ⊥,且1A BCD h -=, ∴底面积11212BCD S =⨯⨯=, ∴11111333A BCD BCD V S h -=⋅⋅=⨯⨯=.故选A . D ABC h15.已知正方体1111ABCD A B C D -,点E ,F ,G 分别是线段1B B ,AB 和1A C 上的动点,观察直线CE 与1D F ,CE 与1D G .给出下列结论:①对于任意给定的点E ,存在点F ,使得1D F CE ⊥;②对于任意给定的点F ,存在点E ,使得1CE D F ⊥;③对于任意给定的点E ,存在点G ,使得1D G CE ⊥;④对于任意给定的点G ,存在点E ,使得1CE D G ⊥.其中正确结论的个数是( ). A 1B 1C 1D 1F E C BA G DA .4个B .3个C .2个D .1个【答案】C【解析】①只有1D F ⊥平面11BCC B ,即1D F ⊥平面11ADD A 时,才能满足对于任意,给定的点E ,存在点F ,使得1D F CE ⊥,∵过1D 点与平面11ADD A 垂直的直线只有一条11D C ,而11D C AB ∥,故①错误.②当点E 与1B 重合时,CE AB ⊥且1CE AD ⊥,∴CE ⊥平面1ABD ,∵对于任意给定的点F ,存在点E ,使得1CE D F ⊥,故②正确.③只有CE 垂直于1D G 在平面1BCC B 中的射影时,1D G CE ⊥,故③正确.④只有CE ⊥平面11A CD 时,④才正确,因为过C 点的平面11A CD 的垂线与1BB 无交点,故④错误.综上,正确的结论是②③,故选C .每二部分(非选择题)二、填空题:(本大题共7小题,每小题4分,共28分) 16.已知向量(3,5,1)a = ,(2,2,3)b = ,(4,1,3)c =-- ,则向量234a b c -+ 的坐标为___________.【答案】(16,0,19)- 【解析】∵(3,5,1)a = ,(2,2,3)b = ,(4,1,3)c =-- ,∴2342(3,5,1)3(2,2,3)4(4,1,3)(16,0,19)a b c -+=-+--=- .17.已知向量(2,1,3)a =- ,(4,,)b x y =- ,若a b ∥则实数x y +=___________.【答案】4- 【解析】∵(2,1,3)a =- ,(4,,)b x y =- ,a b ∥,∴2x =,6y =-,4x y +=-.18.空间不共线的四点,可能确定___________个平面.【答案】1或4【解析】空间四点中,任意三点都不共线时,可确定4个平面,当四点共面时,可确定1个平面,故空间不共线四点,可确定1个或4个平面.19.若圆锥的侧面积为2π,底面积为π,则该圆锥的体积为___________. 【答案】3π3【解析】∵底面面积是π,∴底面半径是1,又∵圆锥侧面积为π2πrl =,1r =,∴2l =,且圆锥高3h =, ∴圆锥的体积为:13π3π33V =⨯⨯=.20.下图的正方体平面展开图,在这个正方体中①BM 与ED 平行;②CN 与BE 是异面直线;③CN 与BM 成45︒角;④DM 与BN 垂直. 其中正确结论的是___________.M NFE C BA D【答案】④【解析】将正方体还原,如图所示:BM ED ⊥,故①错;CN BE ∥,故②错;CN 和BM 所成角为60︒,故③错;DM BN ⊥,故④正确.综上,正确结论是④.M NF EDA B C21.一个棱长为4的正方体,被一个平面截去一部分后,所得几何体的三视图如图所示,则该截面的面积是___________.2正(主)视图侧(左)视图俯视图2【答案】6 【解析】三视图对应的几何体如图所示,截面是一个等腰三角形,腰长为25,底为22,所以截面的面积为:22122(25)(2)62⨯⨯-=.22.高三年级267位学生参加期末考试,某班37位学生的语文成绩、数学成绩与总成绩在全年级中的排名情况如下图所示,甲、乙、丙为该班三位学生.从这次考试成绩看,①在甲、乙两人中,其语文成绩名次比其总成绩名次靠前的学生是__________.②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是__________. 乙甲267总成绩年级名次语文成绩年级名次267丙267267总成绩年级名次数学成绩年级名次 【答案】乙;数学 【解析】①观察散点图可知,甲、乙两人中,语文成绩名次比总成绩名次靠前的学生是乙. ②观察散点图,作出对角线y x =,发现丙的坐标横坐标大于纵坐标,说明数学成绩的名次小于总成绩名次,所以在语文和数学两个科目中,丙的成绩名次靠前的科目是数学.三、解答题(本大题共4小题,共47分.解答应写出文字说明,证明过程或演算步骤) 23.(本题满分10分)如图,在四棱锥P ABCD -中,平面PAD ⊥平面ABCD ,AB AD =,60BAD =︒∠,E 、F 分别是AP 、AD 的中点.求证:(Ⅰ)直线EF ∥平面PCD .(Ⅱ)平面BEF ⊥平面PAD .F EC BAPD【答案】见解析【解析】(Ⅰ)证明:∵E 、F 分别是AP 、AD 的中点,∴EF PD ∥,又EF ⊄平面PCD ,PD ⊂平面PCD ,∴EF ∥平面PCD .(Ⅱ)连接BD ,∵AB AD =,60BAD =︒∠,∴ABD △是等边三角形,∴BF AD ⊥,又平面PAD ⊥平面ABCD 且平面PAD 平面ABCD AD =,BF ⊂平面ABCD , ∴BF ⊥平面PAD ,又∵BF ⊂平面BEF ,∴平面BEF ⊥平面PAD .DPA BCEF24.(本题满分13分) 已知函数2()23sin cos 2sin f x x x x =-.(Ⅰ)求函数()f x 的最小正周期.(Ⅱ)求函数()f x 在π0,4⎡⎤⎢⎥⎣⎦上的最大值与最小值.【答案】见解析【解析】(Ⅰ)2()23sin cos 2sin 3sin 2cos21f x x x x x x =-=+-31π2sin 2cos212sin 21226x x x ⎛⎫⎛⎫=+-=+- ⎪ ⎪ ⎪⎝⎭⎝⎭.∴()f x 的最小正周期2ππ2T ==. (Ⅱ)∵π04x ≤≤,∴ππ2π2663x +≤≤, ∴1πsin 2126x ⎛⎫+ ⎪⎝⎭≤≤, ∴π02sin 2116x ⎛⎫+- ⎪⎝⎭≤≤,即:0()1f x ≤≤.当且仅当0x =时,()f x 取最小值,()min (0)0f x f ==. 当且仅当ππ262x +=,即π6x =时,()f x 取最大值,max π()16f x f ⎛⎫== ⎪⎝⎭.25.(本题满分14分)在如图所示的多面体中,EA ⊥平面ABC ,DB ⊥平面ABC ,AC BC ⊥,且22AC BC BD AE ====,M 是AB 的中点.(Ⅰ)求证:CM EM ⊥.(Ⅱ)求平面EMC 与平面BCD 所成的锐二面角的余弦值.(Ⅲ)在棱DC 上是否存在一点N ,使得直线MN 与平面EMC 所成的角是60︒.若存在,指出点N 的位置;若不存在,请说明理由.MECBA D【答案】见解析【解析】(Ⅰ)证明:∵AC BC =,M 是AB 的中点,∴CM AB ⊥,又EA ⊥平面ABC ,∴CM EA ⊥,∵EA AB A = ,∴CM ⊥平面AEM ,∴CM EM ⊥.(Ⅱ)以M 为原点,分别以MB ,MC 为x ,y 轴,如图建立坐标系M xyz -.则:(0,0,0)M ,(0,2,0)C ,(2,0,0)B ,(2,0,2)D ,(2,0,1)E -,(2,0,1)ME =- ,(0,2,0)MC = ,(0,0,2)BD = ,(2,2,0)BC =- ,设平面EMC 的一个法向量111(,,)m x y z = , 则:1112020x z y ⎧-+=⎪⎨=⎪⎩,取11x =,10y =,12z =,所以(1,0,2)m =,设平面DBC 的一个法向量222(,,)n x y z = ,则:222220,20,x y y ⎧-+=⎪⎨=⎪⎩取11x =,11y =,10z =,所以(1,1,0)n =,16cos 6||||23m n m n m n ⋅<⋅>===⨯.故平面EMC 与平面BCD 所成的锐二面角的余弦值为66.(Ⅲ)在棱DC 上存在一点N ,使得直线MN 与平面EMC 所成的角是60︒, 设(,,)N x y z 且DN DC λ= ,(01)λ≤≤, ∴(2,,2)(2,2,2)x y z λ--=--, ∴22x λ=-,2y λ=,22z λ=-, ∴(22,2,22)MN λλλ=-- ,若直线MN 与平面EMC 所成的的角为60︒,则:222222(22)3cos ,sin 60232(1)24(1)MN m λλλλλ-+-<>==︒=⋅-++- , 解得12λ=,所以在棱DC 上存在一点N ,使直线MN 与平面EMC 所成的角是60︒, 点N 为棱DC 的中点.xyz DA B C EM26.(本题满分10分)已知数列{}1212,,(1,2)n n A a a a a a a n =<<< ≤≥具有性质P :对任意i ,(1)j i j n ≤≤≤,i j a a ⋅与jiaa 两数至少有一个属于A .(Ⅰ)分别判断数集{}1,3,4与{}1,2,3,6是否具有性质P ,并说明理由. (Ⅱ)求证:11a =. (Ⅲ)求证:1211112nn na a a a a a a ---++=+++ .【答案】见解析【解析】(Ⅰ)由于34⨯与43均不属于数集{}1,3,4,所以该数集不具有性质P ,由于12⨯,13⨯,16⨯,23⨯,62,63,11,22,33,66,都属于数集{}1,2,3,6,所以该数集具有性质P .(Ⅱ)因为123{,,}n A a a a a = 具有性质P ,11 所以n n a a 与nnaa 中至少有一个属于A ,由于121n a a a << ≤,所以n n n a a a >,故n n a a A ∉, 从而1nna A a =∈,所以11a =.(Ⅲ)因为121n a a a =<<< ,所以k n n a a a >,故(2,3)k n a a A k n ∉= . 由A 具有性质P 可知(1,2,)nka A k n a ∈= , 又因为121nn n n n n a a a a a a a a -<<< , 所以1nn a a =,21n n a a a -=, ,12n n a a a -=,1nn a a a =, 从而121n n n n n n a a a aa a a a -++++121n n a a a a -=++++ , 所以1211112nn na a a a a a a ---+++=++ .。
