【配套K12】[学习]2019年高考数学一轮复习 第十五单元 点、线、面的位置关系单元B卷 文
2019版高考数学文一轮复习课时跟踪检测三十九 空间点、线、面之间的位置关系普通高中 含解析 精品

课时跟踪检测(三十九)空间点、线、面之间的位置关系(一)普通高中适用作业A级——基础小题练熟练快1.a,b是两条异面直线,a⊂平面α,b⊂平面β.若α∩β=c,则直线c必定() A.与a,b均相交B.与a,b都不相交C.至少与a,b中的一条相交D.至多与a,b中的一条相交解析:选C假设直线c与直线a,b都不相交,则直线c与直线a,b都平行.根据公理4,直线a,b平行,与已知条件中的a,b是两条异面直线矛盾,所以直线c至少与a,b中的一条相交.故选C.2.在空间中,有如下四个命题:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面α内有不共线的三点到平面β的距离相等,则α∥β;④过平面α的一条斜线,有且只有一个平面与平面α垂直.其中正确的命题是()A.①③B.②④C.①④D.②③解析:选B①平行于同一个平面的两条直线,可能平行,相交或异面,不正确;②由面面平行的判定定理知正确;③若平面α内有不共线的三点到平面β的距离相等,则α与β可能平行,也可能相交,不正确;易知④正确.故选B.3.若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是()A.l1⊥l4B.l1∥l4C.l1与l4既不垂直也不平行D.l1与l4的位置关系不确定解析:选D构造如图所示的正方体ABCD-A1B1C1D1,取l1为AD,l2为AA1,l3为A1B1,当取l4为B1C1时,l1∥l4,当取l4为BB1时,l1⊥l4,故排除A、B、C,选D.4.在正方体ABCD-A1B1C1D1中,E,F分别是线段BC,CD1的中点,则直线A1B与直线EF的位置关系是()A.相交B.异面C.平行D.垂直解析:选A由BC綊AD,AD綊A1D1知,BC綊A1D1,从而四边形A1BCD1是平行四边形,所以A1B∥CD1,又EF⊂平面A1BCD1,EF∩D1C=F,则A1B与EF相交.5.已知A,B,C,D是空间四点,命题甲:A,B,C,D四点不共面,命题乙:直线AC和BD不相交,则甲是乙成立的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析:选A若A,B,C,D四点不共面,则直线AC和BD不共面,所以AC和BD 不相交;若直线AC和BD不相交,若直线AC和BD平行时,A,B,C,D四点共面,所以甲是乙成立的充分不必要条件.6.到空间不共面的四点距离相等的平面的个数为()A.1 B.4C.7 D.8解析:选C当空间四点不共面时,则四点构成一个三棱锥.①当平面一侧有一点,另一侧有三点时,如图 1.令截面与四棱锥的四个面之一平行,第四个顶点到这个截面的距离与其相对的面到此截面的距离相等,这样的平面有4个;②当平面一侧有两点,另一侧有两点时,如图2,当平面过AB,BD,CD,AC的中点时,满足条件.因为三棱锥的相对棱有三对,则此时满足条件的平面有3个.所以满足条件的平面共有7个,故选C.7.若平面α,β相交,在α,β内各取两点,这四点都不在交线上,这四点能确定________个平面.解析:如果这四点在同一平面内,那么确定一个平面;如果这四点不共面,则任意三点可确定一个平面,所以可确定四个.答案:1或4B1C1D1中,既与AB共面又与CC18.如图,平行六面体ABCD-A共面的棱有________条.解析:依题意,与AB 和CC 1都相交的棱有BC ;与AB 相交且与CC 1平行有棱AA 1,BB 1;与AB 平行且与CC 1相交的棱有CD ,C 1D 1.故符合条件的有5条.答案:59.如图所示,在空间四边形ABCD 中,点E ,H 分别是边AB ,AD 的中点,点F ,G 分别是边BC ,CD 上的点,且CF CB =CG CD =23,则下列说法正确的是______(填序号).①EF 与GH 平行;②EF 与GH 异面;③EF 与GH 的交点M 可能在直线AC 上,也可能不在直线AC 上;④EF 与GH 的交点M 一定在直线AC 上.解析:连接EH ,FG ,如图所示.依题意,可得EH ∥BD ,FG ∥BD ,故EH ∥FG ,所以E ,F ,G ,H 共面.因为EH =12BD ,FG =23BD ,故EH ≠FG , 所以EFGH 是梯形,EF 与GH 必相交,设交点为M .因为点M 在EF 上,故点M 在平面ACB 上.同理,点M 在平面ACD 上,∴点M 是平面ACB 与平面ACD 的交点,又AC 是这两个平面的交线,所以点M 一定在直线AC 上.答案:④10.如图为正方体表面的一种展开图,则图中的AB ,CD ,EF ,GH 在原正方体中互为异面直线的有________对.解析:平面图形的翻折应注意翻折前后相对位置的变化,则AB ,CD ,EF 和GH 在原正方体中,显然AB 与CD ,EF 与GH ,AB 与GH 都是异面直线,而AB 与EF 相交,CD 与GH 相交,CD 与EF 平行.故互为异面直线的有3对.答案:3B 级——中档题目练通抓牢1.如图,ABCD -A 1B 1C 1D 1是长方体,O 是B 1D 1的中点,直线A 1C 交平面AB 1D 1于点M ,则下列结论正确的是( )A .A ,M ,O 三点共线B .A ,M ,O ,A 1不共面C .A ,M ,C ,O 不共面D .B ,B 1,O ,M 共面解析:选A 连接A 1C 1,AC ,则A 1C 1∥AC ,所以A 1,C 1,C ,A四点共面,所以A 1C ⊂平面ACC 1A 1,因为M ∈A 1C ,所以M ∈平面ACC 1A 1,又M ∈平面AB 1D 1,所以M 在平面ACC 1A 1与平面AB 1D 1的交线上,同理O 在平面ACC 1A 1与平面AB 1D 1的交线上,所以A ,M ,O 三点共线.2.平面α过正方体ABCD -A 1B 1C 1D 1的顶点A ,α∥平面CB 1D 1,α∩平面ABCD =m ,α∩平面ABB 1A 1=n ,则m ,n 所成角的正弦值为( ) A.32 B.22 C.33 D.13解析:选A 如图,在正方体ABCD -A1B 1C 1D 1的上方接一个同等大小的正方体ABCD -A 2B 2C 2D 2,则过A 与平面CB 1D 1平行的是平面AB 2D 2,即平面α就是平面AB 2D 2,平面AB 2D 2∩平面ABB 1A 1=AB 2,即直线n 就是直线AB 2,由面面平行的性质定理知直线m 平行于直线B 2D 2,故m ,n 所成的角就等于AB 2与B 2D 2所成的角,在等边三角形AB 2D 2中,∠AB 2D 2=60°,故其正弦值为32. 3.过正方体ABCD -A 1B 1C 1D 1的顶点A 作直线l ,使l 与棱AB ,AD ,AA 1所成的角都相等,这样的直线l 可以作( )A .1条B .2条C .3条D .4条解析:选D 如图,连接体对角线AC1,显然AC 1与棱AB ,AD ,AA 1所成的角都相等,所成角的正切值都为 2.联想正方体的其他体对角线,如连接BD 1,则BD 1与棱BC ,BA ,BB 1所成的角都相等,∵BB 1∥AA 1,BC ∥AD ,∴体对角线BD 1与棱AB ,AD ,AA 1所成的角都相等,同理,体对角线A 1C ,DB 1也与棱AB ,AD ,AA 1所成的角都相等,过A 点分别作BD 1,A 1C ,DB 1的平行线都满足题意,故这样的直线l 可以作4条.4.如图,在三棱锥A -BCD 中,AB =AC =BD =CD =3,AD =BC =2,点M ,N 分别为AD ,BC 的中点,则异面直线AN ,CM 所成角的余弦值是________.解析:如图所示,连接DN ,取线段DN 的中点K ,连接MK ,CK .∵M 为AD 的中点,∴MK ∥AN ,∴∠KMC (或其补角)为异面直线AN ,CM 所成的角.∵AB =AC =BD =CD =3,AD =BC =2,N 为BC 的中点,由勾股定理易求得AN =DN =CM =22,∴MK = 2.在Rt △CKN 中,CK = (2)2+12= 3.在△CKM 中,由余弦定理,得cos ∠KMC =(2)2+(22)2-(3)22×2×22=78, 所以异面直线AN ,CM 所成角的余弦值是78. 答案:785.α,β是两个平面,m ,n 是两条直线,有下列四个命题:①如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β.②如果m ⊥α,n ∥α,那么m ⊥n .③如果α∥β,m ⊂α,那么m ∥β.其中正确的命题有________.(填写所有正确命题的编号)解析:对于①,α,β可能平行,也可能相交但不垂直,故错误.对于②,由线面平行的性质定理知存在直线l ⊂α,n ∥l ,又m ⊥α,所以m ⊥l ,所以m ⊥n ,故正确.对于③,因为α∥β,所以α,β没有公共点.又m ⊂α,所以m ,β没有公共点,由线面平行的定义可知m ∥β,故正确.答案:②③6.如图所示,在正方体ABCD -A 1B 1C 1D 1中,M ,N 分别是A 1B 1,B 1C 1的中点.问:(1)AM 与CN 是否是异面直线?说明理由;(2)D 1B 与CC 1是否是异面直线?说明理由.解:(1)AM 与CN 不是异面直线.理由如下:如图,连接MN ,A 1C 1,AC .因为M ,N 分别是A 1B 1,B 1C 1的中点,所以MN ∥A 1C 1.又因为A 1A 綊C 1C ,所以四边形A 1ACC 1为平行四边形,所以A 1C 1∥AC ,所以MN ∥AC ,所以A ,M ,N ,C 在同一平面内,故AM 和CN 不是异面直线.(2)D 1B 与CC 1是异面直线.理由如下:因为ABCD -A 1B 1C 1D 1是正方体,所以B ,C ,C 1,D 1不共面.假设D 1B 与CC 1不是异面直线,则存在平面α,使D 1B ⊂平面α,CC 1⊂平面α,所以D 1,B ,C ,C 1∈α,这与B ,C ,C 1,D 1不共面矛盾.所以假设不成立,即D 1B 与CC 1是异面直线.7.如图所示,在三棱锥P -ABC 中,PA ⊥底面ABC ,D 是PC 的中点.已知∠BAC =90°,AB =2,AC =23,PA =2.求:(1)三棱锥P -ABC 的体积;(2)异面直线BC 与AD 所成角的余弦值.解:(1)S △ABC =12×2×23=23, 故三棱锥P -ABC 的体积为V =13·S △ABC ·PA =13×23×2=433. (2)如图所示,取PB 的中点E ,连接DE ,AE ,则DE ∥BC ,所以∠ADE (或其补角)是异面直线BC 与AD 所成的角.在△ADE 中,DE =12BC =12AB 2+AC 2=2, AE =AB 2-BE 2=2,AD =AC 2+CD 2-2AC ·CD ·cos 30°=2,则cos ∠ADE =DE 2+AD 2-AE 22DE ·AD =22+22-22×2×2=34. 即异面直线BC 与AD 所成角的余弦值为34. C 级——重难题目自主选做1.如图是三棱锥D -ABC 的三视图,点O 在三个视图中都是所在边的中点,则异面直线DO 和AB 所成角的余弦值等于( )A.33B.12C. 3D.22解析:选A 由三视图及题意得如图所示的直观图,从A 出发的三条线段AB ,AC ,AD 两两垂直且AB =AC =2,AD =1,O 是BC 中点,取AC 中点E ,连接DE ,DO ,OE ,则OE =1,又可知AE =1,由于OE ∥AB ,故∠DOE 即为所求两异面直线所成的角或其补角.在直角三角形DAE 中,DE =2,由于O 是BC 的中点,在直角三角形ABC 中可以求得AO =2,在直角三角形DAO 中可以求得DO = 3.在三角形DOE 中,由余弦定理得cos ∠DOE =1+3-22×1×3=33,故所求异面直线DO 与AB 所成角的余弦值为33.2.如图所示,在三棱柱ABC -A 1B 1C 1中,底面是边长为2的正三角形,侧棱A 1A ⊥底面ABC ,点E ,F 分别是棱CC 1,BB 1上的点,点M 是线段AC 上的动点,EC =2FB =2.(1)当点M 在何位置时,BM ∥平面AEF?(2)若BM ∥平面AEF ,判断BM 与EF 的位置关系,说明理由;并求BM 与EF 所成的角的余弦值.解:(1)法一:如图所示,取AE 的中点O ,连接OF ,过点O 作OM⊥AC 于点M .因为侧棱A 1A ⊥底面ABC ,所以侧面A 1ACC 1⊥底面ABC .又因为EC =2FB =2,所以OM ∥EC ∥FB 且OM =12EC =FB , 所以四边形OMBF 为矩形,BM ∥OF .因为OF ⊂平面AEF ,BM ⊄平面AEF ,故BM ∥平面AEF ,此时点M 为AC 的中点.法二:如图所示,取EC 的中点P ,AC 的中点Q ,连接PQ ,PB ,BQ.因为EC=2FB=2,所以PE綊BF,所以PQ∥AE,PB∥EF,所以PQ∥平面AFE,PB∥平面AEF,因为PB∩PQ=P,PB⊂平面PBQ,PQ⊂平面PBQ,所以平面PBQ∥平面AEF.又因为BQ⊂平面PBQ,所以BQ∥平面AEF.故点Q即为所求的点M,此时点M为AC的中点.(2)由(1)知,BM与EF异面,∠OFE(或∠MBP)就是异面直线BM与EF所成的角或其补角.易求AF=EF=5,MB=OF=3,OF⊥AE,所以cos∠OFE=OFEF=35=155,所以BM与EF所成的角的余弦值为15 5.。
2019年高考理科数学一轮单元卷:第十五单元点、线、面的位置关系A卷(含答案)

一轮单元训练金卷▪高三▪数学卷(A ) 第十五单元 点、线、面的位置关系注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试题卷和答题卡一并上交. 一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )A .B .C .D .2.已知直线l ⊥平面,直线m ∥平面β,则下列命题正确的是( ) A .若αβ⊥,则l m ∥B .若αβ∥,则l m ⊥C .若l β∥,则m α⊥D .若l m ⊥,则αβ∥3.如图,在正方体ABCD A B C D '-'''中,M ,N 分别是BB ',CD 中点,则异面直线AM 与D N '所成的角是( )A .30︒B .45︒C .60︒D .90︒4.已知m ,n 是两条不重合的直线,α,β,γ是三个两两不重合的平面,给出下列四个命题: ①若m α⊥,m β⊥,则αβ∥; ②若αγ⊥,βγ⊥,则αβ∥;③若m α⊂,n β⊂,m n ∥,则αβ∥;④若m ,n 是异面直线,m α⊂,m β∥,n α∥,则αβ∥. 其中真命题是( ) A .①和④B .①和③C .③和④D .①和②5.如图是正方体的平面展开图,则在这个正方体中,AM 与BN 所成角的大小为( )A .0︒B .45︒C .60︒D .90︒6.已知直线1l 、2l ,平面α,12l l ∥,1l α∥,那么2l 与平面α的关系是( ) A .1l α∥B .2l α⊂C .2l α∥或2l α⊂D .2l 与α相交7.如图,在正四棱锥S ABCD -中,E ,M ,N 分别是BC ,CD ,SC 的中点,动点P 在线段MN 上运动时,下列四个结论:①EP AC ⊥;②EP BD ∥;③EP ∥面SBD ;④EP ⊥面SAC ,其中恒成立的为( )A .①③B .③④C .①②D .②③④8.已知m ,n 表示两条不同直线,α表示平面,下列说法中正确的是( ) A .若m α⊥,n α⊂,则m n ⊥ B .若m α∥,n α∥,则m n ∥ C .若m α⊥,m n ⊥,则n α∥D .若m α∥,m n ⊥,则n α⊥9.如图,正方体1111ABCD A B C D -的棱长为1,E ,F 是线段11B D 上的两个动点,且下列结论错误..的是 ( )A .AC BF ⊥B .直线AE 、BF 所成的角为定值C .EF ∥平面ABCDD .三棱锥A BEF -的体积为定值10.如图,在直四棱柱1111A B C D A B C D -中,四边形ABCD 为梯形,AD BC ∥,13AA =,AB BC CD ==120BCD ∠=︒,则直线1A B 与1B C 所成的角的余弦值为( )A .78 B .58C D 11.已知正方体1111ABCD A B C D -的棱长为1,E ,F 分别为棱1BB 、1CC 的中点,P 为棱BC 上的一点,且()01BP m m =<<,则点P 到平面AEF 的距离为( )A B C D 12.如图,已知四边形ABCD 是正方形,ABP △,BCQ △,CDR △,DAS △都是等边三角形,E 、F 、G 、H 分别是线段AP 、DS 、CQ 、BQ 的中点,分别以AB 、BC 、CD 、DA 为折痕将四个等边三角形折起,使得P 、Q 、R 、S 四点重合于一点P ,得到一个四棱锥.对于下面四个结论: ①EF 与GH 为异面直线; ②直线EF 与直线PB 所成的角为60︒ ③EF ∥平面PBC ; ④平面EFGH ∥平面ABCD ;其中正确结论的个数有( )A .0个B .1个C .2个D .3个二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.已知α,β,γ是三个互不重合的平面,l 是一条直线,给出下列四个命题:①若αβ⊥,l β⊥,则l α∥; ②若l α⊥,l β⊥,则αβ∥; ③若αγ⊥,βγ∥,则αβ⊥;④若m α⊂,n α⊂,m β∥,n β∥,则αβ∥. 其中所有..正确命题的序号是_____. 14.如图所示,AB ⊥平面BCD ,BC CD ⊥,图中互相垂直的平面共有______对.15.正四面体ABCD 中, E ,F 分别为边AB ,BD 的中点,则异面直线AF ,CE 所成角的余弦值为__________.16.如图所示,在四棱锥P ABCD -,PA ⊥底面ABCD ,且底面各边都相等,M 是PC 上的一动点,请你补充一个条件__________,使平面MBD ⊥平面PCD .①DM PC ⊥ ②DM BM ⊥③BM PC ⊥④PM MC =(填写你认为是正确的条件对应的序号).三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)如图,在四棱锥E ABCD -中,平面EAB ⊥平面ABCD ,四边形ABCD 为矩形,EA EB ⊥,M ,N 分别为AE ,CD 的中点.求证:(1)直线MN ∥平面EBC ; (2)直线EA ⊥平面EBC .18.(12分)如图,已知四棱锥P ABCD -的底面ABCD 是菱形,60ABC ∠=︒,PA ⊥平面ABCD ,2AB =,2PA =,点F 为PC 的中点.(1)求证:平面PAC ⊥平面BDF ; (2)求三棱锥P BDF -的体积.19.(12分)如图,在直四棱柱1111ABCD A B C D -中,1AB BD ==,AD ,12AA BC ==,AD BC ∥. (1)证明:平面1BDB ⊥平面11ABB A ;(2)比较四棱锥11D ABB A -与四棱锥1111D A B C D -的体积的大小.20.(12分)如图所示的多面体中,底面ABCD 为正方形,GAD △为等边三角形,BF ⊥平面ABCD ,90GDC ∠=︒,点E 是线段GC 上除两端点外的一点,若点P 为线段GD 的中点.(1)求证:AP ⊥平面GCD ; (2)求证:平面ADG ∥平面FBC .21.(12分)如图,三棱锥B ACD -的三条侧棱两两垂直,2BC BD ==,E ,F ,G 分别是棱CD ,AD ,AB 的中点.(1)证明:平面ABE ⊥平面ACD ; (2)若四面体BEFG 的体积为12,且F 在平面ABE 内的正投影为M ,求线段CM 的长.22.(12分)在如图如示的多面体中,平面AEFD ⊥平面BEFC ,四边形AEFD 是边长为2的正方形,BC(1)若M ,N 分别是AE ,CF 中点,求证:MN ∥平面ABCD (2)求此多面体ABCDEF 的体积一轮单元训练金卷▪高三▪数学卷答案(A)第十五单元点、线、面的位置关系一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.【答案】A【解析】对于B,易知AB MQ∥,∥,则直线AB∥平面MNQ;对于C,易知AB MQ则直线AB∥平面MNQ;对于D,易知AB NQ∥,则直线AB∥平面MNQ.故排除B,C,D,选A.2.【答案】B【解析】A中l与m位置不确定,D中α与β可能相交,C中m与α的位置不确定,B正确,故选B.3.【答案】D【解析】如图,平移直线D N '到A H ',则直线A H '与直线AM 所成角,由于点M ,H 都是中点, 所以ABM A AH ≅'△△,则BAM AA H ∠=∠',而90A HA AA H '∠+∠='︒, 所以90A HA BAM ∠+∠='︒,即A H AM '⊥,应选答案D . 4.【答案】A【解析】由线面角的定义可知答案①中的直线m α⊥,m β⊥,则平面αβ∥是正确的; 因为答案②中的两个平面α,β也可能相交,故不正确;答案③中的两个平面m α⊂,n β⊂可以推出两个平面α,β相交,故也不正确;对于答案④,可将直线n 平移到到平面α内,借助异面直线平移后不相交的结论及面面平行的判定定理可知αβ∥,是正确命题,所以应选答案A . 5.【答案】D【解析】AM 与BN 为正方体两相对平面的对角线,且不平行,所以AM 与BN 所成角的大小为90︒,故选D . 6.【答案】C【解析】在正方体1111ABCD A B C D -中,取1AB l =,2CD l =,当取面11CDD C 为平面α时,∴满足12l l ∥,1l α∥,此时2αl ⊂;当取面1111B A D C 为平面α时,∴满足12l l ∥,1l α∥,此时2l α∥,∴当直线1l 、2l ,平面α,12l l ∥,1l α∥时, 2l 与平面α的关系是2l α∥或2l α⊂,故选C .7.【答案】A 【解析】连接AC ,BD 相交于点O ,连接EM ,EN . 在①中,由正四棱锥S ABCD -,可得SO ⊥底面ABCD AC BD ⊥,∴SO AC ⊥.∵SOBD O =,∴AC ⊥面SBD .∵E ,M ,N 分别是BC ,CD ,SC 的中点,∴EM BD ∥,MN SD ∥,EM MN N =,∴平面EMN ∥平面SBD ,∴AC ⊥平面EMN ,∴AC EP ⊥,故①正确;在②中,由异面直线的定义可知,EP 和BD 是异面直线,不可能EP BD ∥,因此不正确; 在③中,由①可知,平面EMN ∥平面SBD ,∴EP ∥平面SBD ,因此正确; 在④中,由①同理可得,EM ⊥平面SAC ,若EP ⊥平面SAC ,则EP EM ∥, 与EPEM E =相矛盾,因此当P 与M 不重合时,EP 与平面SAC 不垂直,即不正确.故选A . 8.【答案】A【解析】逐一考查所给的线面关系:A .若m α⊥,n α⊂,由线面垂直的定义,则m n ⊥,B .若m α∥,n α∥,不一定有m n ∥,如图所示的正方体中, 若取m ,n 为AB ,AD ,平面α为上底面1111A BCD 即为反例;C .若m α⊥,m n ⊥,不一定有n α∥,如图所示的正方体中,若取m ,n 为1A A ,11AD ,平面α为上底面1111A B C D 即为反例;D .若m α∥,m n ⊥,不一定有n α⊥如图所示的正方体中,若取m ,n 为AD ,BC ,平面α为上底面1111A B C D 即为反例;故选A . 9.【答案】B【解析】在A 中,∵正方体1111ABCD A B C D -的棱长为1,E ,F 是线段11B D 上的两个动点, 2EF =,∴AC BD ⊥,1AC BB ⊥, ∵1BDBB B =,∴AC ⊥平面11BDD B ,∵BF ⊂平面11BDD B ,∴AC BF ⊥,故A 正确;在B 中,异面直线AE 、BF 所成的角不为定值, 由图知,当F 与1B 重合时,令上底面顶点为O ,则此时两异面直线所成的角是1A AO ∠,当E 与1D 重合时,此时点F 与O 重合, 则两异面直线所成的角是1OBC ∠,此二角不相等, 故异面直线AE 、BF 所成的角不为定值.故B 错误;在C 中,∵EF BD ∥,BD ⊂平面ABCD ,EF ⊄平面ABCD ,∴EF ∥平面ABCD ,故C 正确; 在D 中,∵AC ⊥平面11BDD B ,∴A 到平面BEF 的距离不变,B 到EF 的距离为1,∴BEF △的面积不变, ∴三棱锥A BEF -的体积为定值,故D 正确. 10.【答案】A 【解析】如图所示,过点C 作1CE BA ∥,连接1B E ,则1B CE ∠就是直线1A B 与1B C 所成的角或其补角, 由题得123B C CE =,13B E =1121237cos 2128B CE +-∠==⨯,故选A .11.【答案】B【解析】由BC EF ∥可知BC ∥平面AEF ,则点P 到平面AEF 的距离即点B 到平面AEF 的距离, 直线EF ⊥平面11ABB A ,则平面AEF ⊥平面11ABB A , 结合平面AEF平面11ABB A AE =可知原问题可转换为点B 到直线AE 的距离,利用面积相等可得点P 到平面AEF 的距离为:B 选项. 12.【答案】D【解析】①错误.所得四棱锥中,设AS 中点为I ,则E 、I 两点重合, ∵FI GH ∥,即EF GH ∥,即EF 与GH 不是异面直线;②正确.∵FI GH ∥,PB 与BQ 重合,且GH 与BQ 所成角为60︒, 说明EF 与PB 所成角为60︒;③正确.∵FI GH BC ∥∥,BC ⊂平面PBC ,FI ⊄平面PBC ,∴FI ∥平面PBC ,∴FE ∥平面PBC ;④正确.∵FI ∥平面ABCD , IH ∥平面ABCD ,FIHI I =点,∴平面FIHG ∥平面ABCD ,即平面EFGH ∥平面ABCD ,故选D .二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】②③【解析】若αβ⊥,l β⊥,则l α∥,l α⊂; 若l α⊥,l β⊥,则αβ∥; 若αγ⊥,βγ,则αβ⊥;若m α⊂,n α⊂,m β∥,n β∥,则αβ∥或,αβ相交, 所以正确命题的序号是②③ 14.【答案】3【解析】由AB ⊥平面BCD ,又AB ⊂平面ABC 、平面ABD , 所以平面ABC ⊥平面BCD ,平面ABD ⊥平面BCD ;由AB ⊥平面BCD 可得CD AB ⊥,又CD BC ⊥,所以CD ⊥平面ABC , 又CD ⊂平面ACD ,故平面ABC ⊥平面ACD .故答案为3. 15.【解析】取BF 中点G ,连CG ,EG ,不妨设正四面体的棱长为2,EG =,CG =,异面直线AF,CE 16.【答案】①③【解析】由定理可知,BD PC ⊥,∴当DM PC ⊥(或BM PC ⊥)时,即有PC ⊥平面MBD , 而PC ⊂平面PCD ,∴平面MBD ⊥平面PCD ,则DM PC ⊥或BM PC ⊥正确, 故答案为①③.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【答案】(1)见解析;(2)见解析. 【解析】证明:(1)取BE 中点F ,连结CF ,MF ,又M 是AE 的中点,所以12MF AB ∥,且12MF AB =,因为N 是矩形ABCD 的边CD 的中点,所以NC AB ∥,且12NC AB =. 所以MF NC ∥且MF NC =,所以四边形MNCF 是平行四边形.所以MN CF ∥.又MN ⊄平面EBC ,CF ⊂平面EBC ,所以直线MN ∥平面EBC . (2)在矩形ABCD 中,BC AB ⊥. 又平面EAB ⊥平面ABCD ,平面ABCD 平面EAB AB =,BC ⊂平面ABCD ,所以BC ⊥平面EAB .又EA ⊂平面EAB ,所以BC EA ⊥. 又EA EB ⊥,BCEB B =,EB ,BC ⊂平面EBC ,所以直线EA ⊥平面EBC .18.【答案】(1)见解析;(2. 【解析】(1)连接AC ,BC 与AC 交于点O ,连接OF , 因为PA ⊥平面ABCD ,AC ⊂平面ABCD ,所以PA AC ⊥, 因为点F 为PC 的中点,所以OF PA ∥.因为OF AC ⊥,因为ABCD 是菱形,所以AC BD ⊥, 因为OFBD O =,所以AC ⊥平面BDF ,因为AC ⊂平面PAC ,所以平面PAC ⊥平面BDF .(2)由(1)可知PA ⊥平面ABCD ,OF PA ∥,所以11133P BCD BCD V OF S -=⋅⋅=⨯=△,所以11233P ABD ABD V PA S -=⋅⋅=⨯△,所以P BDF P ABCD F BCD A BDP V V V V ----=--.19.【答案】(1)见解析;(2)111111D A B C D D ABB A V V -->. 【解析】(1)证明:∵2222AB BD AD +==,∴AB BD ⊥, 又1AA ⊥平面ABCD ,∴1AA BD ⊥, ∵1ABAA A =,∴BD ⊥平面11ABB A .又BD ⊂平面1BDB ,∴平面1BDB ⊥平面11ABB A . (2)解:∵AB BD =且AB BD ⊥,∴45ADB ∠=︒,又AD BC ∥,∴45CBD ADB ∠=∠=︒,∴1sin4522BCD S BD BC =⨯⨯︒=△∴四边形ABCD 的面积为12+∴111111232D A B C D V -⎛=⨯⨯= ⎝⎭又1111112112333D ABB A ABB A V BD S -=⨯⨯=⨯⨯⨯=矩形,∵23>∴111111D A B C D D ABB A V V -->. 20.【答案】(1)见解析;(2)见解析.【解析】(1)证明:因为GAD △是等边三角形,点P 为线段GD 的中点,故AP GD ⊥. 因为AD CD ⊥,GD CD ⊥,且AD GD D =,AD ,GD ⊂平面GAD ,故CD ⊥平面GAD , 又AP ⊂平面GAD ,故CD AP ⊥,又CD GD D =,CD ,GD ⊂平面GCD ,故AP ⊥平面GCD . (2)证明:∵BF ⊥平面ABCD ,∴BF CD ⊥, ∵BC CD ⊥,BFBC B =,BF ,BC ⊂平面FBC ,∴CD ⊥平面FBC ,由(1)知CD ⊥平面GAD ,∴平面ADG ∥平面FBC .21.【答案】(1)见解析;(2. 【解析】(1)证明:因为BC BD =,E 是棱CD 的中点,所以BE CD ⊥, 又三棱锥B ACD -的三条侧棱两两垂直,且BC BD B =,所以AB ⊥平面BCD ,则AB CD ⊥, 因为ABBE B =,所以CD ⊥平面ABE ,又CD ⊂平面ACD ,所以平面ABE ⊥平面ACD . (2)由(1)知CD ⊥平面ABE ,因为MF ⊥平面ABE , 所以MF CD ∥,又F 为AD 的中点,所以M 为AE 的中点,因为2BE 122MF DE =所以四面体体BEFG 的体积为11326BG BE BG MF ⨯⨯⨯⨯==12,则3BG =.在Rt ABE △中,26AB BG ==,AE ==在Rt CEM △中,12ME AE ==CM =.22.【答案】(1)见解析;(2. 【解析】(1)证明:在平面CDF 中,作NH CF ⊥交DC 于H ,连接AH . ∵M ,N 是AE ,CF 中点,且AEFD 是正方形,∴NH DF ∥又AM DF ∥,,∴NH AM =,NH AM ∥, ∴四边形AMNH 是平行四边形,∴MN AH ∥,又AH ⊂平面ABCD ,MN ⊄平面ABCD ,∴MN ∥平面ABCD . (2)解:如图,连BD ,BF ,过F 作FG EF ⊥,交BC 于点G .∵四边形BEFC FG =. ∵平面AEFD ⊥平面BEFC ,平面AEFD 平面BEFC EF =,FG EF ⊥,DF EF ⊥,∴GF ⊥平面AEFD , DF ⊥平面BEFC . 1143。
2019版高考数学(文)一轮复习课时跟踪检测(三十九)+空间点、线、面之间的位置关系(普通高中)+.docx

课时跟踪检测(三十九)空间点、线、面之间的位置关系(一)普通高中适用作业A级——基础小题练熟练快1. (I, b是两条异面直线,“U平面么,bU平面0?若aQ0=c,则直线c必定()A.与“,b均相交B.与a, b都不相交C.至少与°, 〃中的一条相交D.至多与“,b中的一条相交解析:选C 假设直线C与直线“,b都不相交,则直线C与直线4,方都平行?根据公理4,直线“,方平行,与已知条件中的°, 〃是两条异面直线矛盾,所以直线c至少与a, b中的一条相交.故选C?2.在空间中,有如下四个命题:①平行于同一个平面的两条直线是平行直线;②垂直于同一条直线的两个平面是平行平面;③若平面么内有不共线的三点到平面"的距离相等,则④过平面么的一条斜线,有且只有一个平面与平面么垂直. 其中正确的命题是()A.①③B.②④C.①④D.②③解析:选B ①平行于同一个平面的两条直线,可能平行,相交或异面,不正确;②由面面平行的判定定理知正确;③若平面a内有不共线的三点到平面p的距离相等,则 a 与0可能平行,也可能相交,不正确;易知④正确.故选B.厶丄/4,则下列结3.若空间中四条两两不同的直线/i,I"厶,厶,满足/i丄厶,厶丄厶,论一定正确的是()/4A. /!±C.厶与人既不垂直也不平行D. A与人的位置关系不确定解析:选D 构造如图所示的正方体ABCD-AxB^Dx,取人为力0, ?2为AA lf厶为AM,当取人为BiCi时,71/7/4,当取人为时,人丄人, 故排除A、B、C,选D.4.在正方体ABCD-AiB.C.D,中,E, F分别是线段BC, CQ的中点,则直线力0与直线EF的位置关系是()解析:选A 由BC 統AD, AD^A.D.知,BC 統力山】,从而四边形A X BCD X 是平行四边形,所以A\B//CD\,又EFU 平面AiBCDr, £FnPiC=F, 则A X B 与EF 相交.5?已知力,B, C, D 是空间四点,命题甲:A t B, C, D 四点不共面,命题乙:直线/C 和不相交,则甲是乙成立的()A.充分不必要条件B.必要不充分条件C ?充要条件D.既不充分也不必要条件解析:选A 若力,B, C, Q 四点不共面,则直线力(7和〃。
2019届高考数学(浙江版)一轮配套讲义:8.2空间点线面的位置关系

面的位置关 点 , 那么它们有且只有一条过该点的公共直
系
线.
公理 4: 平行于同一条直线的两条直线互相
平行 .
定理 : 空间中如果一个角的两边与另一个角
的两边分别平行 , 那么这两个角相等或互
补.
2. 理解两条异面直线所成角的概念 .
要求 理解
2013
10,5 分
4( 文 ) ,
5分
浙江省五年高考统计 2014 2015 2016
点 , 当正四面体以 AB为轴旋转时 , 线段 EF在平面 α上的射影长的取值范围是
.
答案 [3,3 ]
7.(2016 浙江高考冲刺卷 ( 三),13) 已知平面 α 和不重合的直线 m、n, 下列命题中真命题是 有真命题的序号 ).
( 写出所
①如果 m? α ,n ?α ,m、 n 是异面直线 , 那么 n∥ α . ②如果 m? α ,n 与 α相交 , 那么 m、 n 是异面直线 . ③如果 m? α ,n ∥ α,m、 n 共面 , 那么 m∥ n. ④如果 m⊥α ,n ⊥ m,那么 n∥α . 答案 ③
行翻折 , 将△ CDE沿 DE所在的直线进行翻折 , 则在翻折的过程中 ( ) A. 点 A 与点 C 在某一位置可能重合
B. 点 A 与点 C 的最大距离为 AB
C. 直线 AB与直线 CD可能垂直
D. 直线 AF 与直线 CE可能垂直
答案 D
5.(2017 浙江镇海中学第一学期期中 ,7) 如图 , 四边形 ABCD中 ,AB=BD=DA=2,BC=CD= , 现将△ ABD沿 BD折起 ,
C. 若 m⊥ α,m⊥ n, 则 n∥ α
D. 若 m∥ α,m⊥ n, 则 n⊥ α
【配套K12】[学习](福建专用)2019高考数学一轮复习 课时规范练33 基本不等式及其应用 理
2019高考数学一轮复习 课时规范练33 基本不等式及其应用 理](https://img.taocdn.com/s3/m/add19e3b14791711cc7917f5.png)
课时规范练33 基本不等式及其应用一、基础巩固组1.设0<a<b,则下列不等式正确的是()A.a<b<B.a<<bC.a<<b<D.<a<<b2.(2017山东枣庄一模)若正数x,y满足=1,则3x+4y的最小值是()A.24B.28C.25D.263.已知a>0,b>0,a,b的等比中项是1,且m=b+,n=a+,则m+n的最小值是()A.3B.4C.5D.64.函数y=(x>-1)的图象的最低点的坐标是()A.(1,2)B.(1,-2)C.(1,1)D.(0,2)5.(2017山东日照一模)已知圆x2+y2+4x-2y-1=0上存在两点关于直线ax-2by+2=0(a>0,b>0)对称,则的最小值为()A.8B.9C.16D.186.要制作一个容积为4 m3,高为1 m的无盖长方体容器.已知该容器的底面造价是每平方米20元,侧面造价是每平方米10元,则该容器的最低总造价是()A.80元B.120元C.160元D.240元7.若两个正实数x,y满足=1,并且x+2y>m2+2m恒成立,则实数m的取值范围是()A.(-∞,-2)∪[4,+∞)B.(-∞,-4]∪[2,+∞)C.(-2,4)D.(-4,2)8.设x,y∈R,a>1,b>1,若a x=b y=3,a+b=2,则的最大值为()A.2B.C.1D.9.若直线=1(a>0,b>0)过点(1,2),则2a+b的最小值为.10.若直线ax+by-1=0(a>0,b>0)过曲线y=1+sin πx(0<x<2)的对称中心,则的最小值为.11.(2017山西临汾二模)近来鸡蛋价格起伏较大,假设第一周、第二周鸡蛋价格分别为a元/千克、b元/千克,家庭主妇甲和乙买鸡蛋的方式不同:家庭主妇甲每周买3千克鸡蛋,家庭主妇乙每周买10元钱的鸡蛋,试比较谁的购买方式更优惠(两次平均价格低视为实惠).(在横线上填甲或乙即可) 〚导学号21500548〛12.设a,b均为正实数,求证:+ab≥2.二、综合提升组13.已知不等式|y+4|-|y|≤2x+对任意实数x,y都成立,则实数a的最小值为()A.1B.2C.3D.414.(2017天津河东区一模,理13)已知x>0,y>0,lg 2x+lg 8y=lg 2,则的最小值是.15.如果a,b满足ab=a+b+3,那么ab的取值范围是.16.某工厂某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x)(单元:万元),当年产量不足80千件时,C(x)=x2+10x(单位:万元).当年产量不少于80千件时,C(x)=51x+-1 450(单位:万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L(x)(单位:万元)关于年产量x(单位:千件)的函数解析式;(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?〚导学号21500549〛三、创新应用组17.若正实数x,y满足x+y+=5,则x+y的最大值是()A.2B.3C.4D.518.(2017山东德州一模,理8)圆:x2+y2+2ax+a2-9=0和圆:x2+y2-4by-1+4b2=0有三条公切线,若a∈R,b∈R,且ab≠0,则的最小值为()A.1B.3C.4D.5 〚导学号21500550〛课时规范练33基本不等式及其应用1.B∵0<a<b,∴a<<b,故A,C错误;-a=)>0,即>a,D错误,故选B.2.C∵正数x,y满足=1,∴3x+4y=(3x+4y)=13+13+3×2=25,当且仅当x=2y=5时等号成立.∴3x+4y的最小值是25.故选C.3.B由题意知ab=1,则m=b+=2b,n=a+=2a,∴m+n=2(a+b)≥4=4,当且仅当a=b=1时,等号成立.4.D∵x>-1,∴x+1>0.∴y==(x+1)+2,当且仅当x+1=,即x=0时等号成立,即当x=0时,该函数取得最小值2.所以该函数图象最低点的坐标为(0,2).5.B由圆的对称性可得,直线ax-2by+2=0必过圆心(-2,1),所以a+b=1.所以(a+b)=5+5+4=9,当且仅当,即2a=b=时等号成立,故选B. 6.C设底面矩形的长和宽分别为a m,b m,则ab=4(m2).容器的总造价为20ab+2(a+b)×10=80+20(a+b)≥80+40=160(元)(当且仅当a=b=2时等号成立).故选C.7.D x+2y=(x+2y)=2++2≥8,当且仅当,即x=2y=4时等号成立.由x+2y>m2+2m恒成立,可知m2+2m<8,即m2+2m-8<0,解得-4<m<2.8.C由a x=b y=3,因为a>1,b>1,所以ab=3,所以lg(ab)≤lg 3,从而=1,当且仅当a=b=时等号成立.9.8∵直线=1过点(1,2),=1.∵a>0,b>0,∴2a+b=(2a+b)=4+4+2=8.当且仅当b=2a时等号成立.10.3+2由正弦函数的图象与性质可知,曲线y=1+sin πx(0<x<2)的对称中心为(1,1),故a+b=1.则(a+b)=3+3+2=3+2,当且仅当,即a=-1,b=2-时等号成立,此时的最小值为3+211.乙甲购买产品的平均单价为,乙购买产品的平均单价为0,且两次购买的单价不同,∴a≠b,>0,∴乙的购买方式的平均单价较小.故答案为乙.12.证明因为a,b均为正实数,所以2,当且仅当,即a=b时等号成立,又因为+ab≥2=2,当且仅当=ab时等号成立,所以+ab+ab≥2,当且仅当即a=b=时等号成立.13.D令f(y)=|y+4|-|y|,则f(y)≤|y+4-y|=4,即f(y)max=4.∵不等式|y+4|-|y|≤2x+对任意实数x,y都成立,∴2x+f(y)max=4,∴a≥-(2x)2+4×2x=-(2x-2)2+4恒成立;令g(x)=-(2x)2+4×2x,则a≥g(x)max=4,∴实数a的最小值为4.14.2+4x>0,y>0,lg 2x+lg 8y=lg 2,可得x+3y=1.+4≥2+4=2+4.当且仅当x=y,x+3y=1,即y=,x=时等号成立.的最小值是2+4.15.(-∞,1)∪(9,+∞)∵ab=a+b+3,∴a+b=ab-3,∴(a+b)2=(ab-3)2.∵(a+b)2≥4ab,∴(ab-3)2≥4ab,即(ab)2-10ab+9≥0,故ab≤1或ab≥9.16.解 (1)因为每件商品售价为0.05万元,则x千件商品销售额为0.05×1 000x万元,依题意得,当0<x<80时,L(x)=(0.05×1 000x)-x2-10x-250=-x2+40x-250;当x≥80时,L(x)=(0.05×1 000x)-51x-+1 450-250=1 200-,则L(x)=(2)当0<x<80时,L(x)=-(x-60)2+950,此时,当x=60时,L(x)取得最大值L(60)=950.当x≥80时,L(x)=1 200-≤1 200-2=1 200-200=1 000,当且仅当x=时,即x=100时,L(x)取得最大值1 000.因为950<1 000,所以当年产量为100千件时,该厂在这一商品的生产中所获利润最大.最大利润为1 000万元.17.C∵x>0,y>0,xy,,即,∴x+y+x+y+即x+y+5.设x+y=t,则t>0,∴t+5,得到t2-5t+4≤0,解得1≤t≤4,∴x+y的最大值是4.18.A由题意可得两圆相外切,两圆的标准方程分别为(x+a)2+y2=9,x2+(y-2b)2=1,圆心分别为(-a,0),(0,2b),半径分别为3和1,故有a2+4b2=16,(a2+4b2)=(8+8)=1,当且仅当,即a2=8,b2=2时,等号成立,故选A.。
【中小学资料】备战2019年高考数学一轮复习 第十五单元 点、线、面的位置关系单元A卷 理
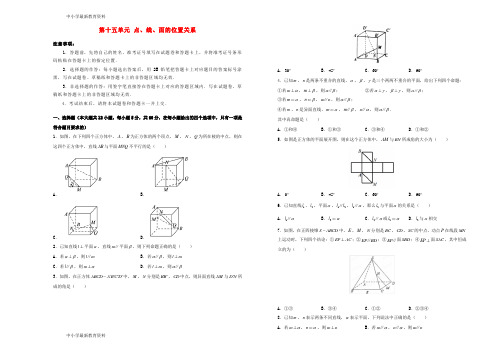
中小学最新教育资料第十五单元 点、线、面的位置关系注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效.3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内.写在试题卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试题卷和答题卡一并上交.一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )A .B .C .D .2.已知直线l ⊥平面α,直线m ∥平面β,则下列命题正确的是( ) A .若αβ⊥,则l m ∥ B .若αβ∥,则l m ⊥ C .若l β∥,则m α⊥D .若l m ⊥,则αβ∥3.如图,在正方体ABCD A B C D '-'''中,M ,N 分别是BB ',CD 中点,则异面直线AM 与D N '所成的角是( )A .30︒B .45︒C .60︒D .90︒4.已知m ,n 是两条不重合的直线,α,β,γ是三个两两不重合的平面,给出下列四个命题: ①若m α⊥,m β⊥,则αβ∥;②若αγ⊥,βγ⊥,则αβ∥;③若m α⊂,n β⊂,m n ∥,则αβ∥;④若m ,n 是异面直线,m α⊂,m β∥,n α∥,则αβ∥. 其中真命题是( ) A .①和④B .①和③C .③和④D .①和②5.如图是正方体的平面展开图,则在这个正方体中,AM 与BN 所成角的大小为( )A .0︒B .45︒C .60︒D .90︒6.已知直线1l 、2l ,平面α,12l l ∥,1l α∥,那么2l 与平面α的关系是( ) A .1l α∥B .2l α⊂C .2l α∥或2l α⊂D .2l 与α相交7.如图,在正四棱锥S ABCD -中,E ,M ,N 分别是BC ,CD ,SC 的中点,动点P 在线段MN上运动时,下列四个结论:①EP AC ⊥;②EP BD ∥;③EP ∥面SBD ;④EP ⊥面SAC ,其中恒成立的为( )A .①③B .③④C .①②D .②③④8.已知m ,n 表示两条不同直线,α表示平面,下列说法中正确的是( ) A .若m α⊥,n α⊂,则m n ⊥B .若m α∥,n α∥,则m n ∥中小学最新教育资料C .若m α⊥,m n ⊥,则n α∥D .若m α∥,m n ⊥,则n α⊥9.如图,正方体1111ABCD A B C D -的棱长为1,E ,F 是线段11B D 上的两个动点,且下列结论错误..的是 ( )A .AC BF ⊥B .直线AE 、BF 所成的角为定值C .EF ∥平面ABCDD .三棱锥A BEF -的体积为定值10.如图,在直四棱柱1111ABCD A B C D -中,四边形ABCD 为梯形,AD BC ∥,13AA =,AB BC CD ===120BCD ∠=︒,则直线1A B 与1B C 所成的角的余弦值为( )A .78B .58CD11.已知正方体1111ABCD A B C D -的棱长为1,E ,F 分别为棱1BB 、1CC 的中点,P 为棱BC 上的一点,且()01BP m m =<<,则点P 到平面AEF 的距离为( )ABCD12.如图,已知四边形ABCD 是正方形,ABP △,BCQ △,CDR △,DAS △都是等边三角形,E 、F 、G 、H 分别是线段AP 、DS 、CQ 、BQ 的中点,分别以AB 、BC 、CD 、DA 为折痕将四个等边三角形折起,使得P 、Q 、R 、S 四点重合于一点P ,得到一个四棱锥.对于下面四个结论: ①EF 与GH 为异面直线; ②直线EF 与直线PB 所成的角为60︒ ③EF ∥平面PBC ; ④平面EFGH ∥平面ABCD ;其中正确结论的个数有( )A .0个B .1个C .2个D .3个二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.已知α,β,γ是三个互不重合的平面,l 是一条直线,给出下列四个命题: ①若αβ⊥,l β⊥,则l α∥; ②若l α⊥,l β⊥,则αβ∥; ③若αγ⊥,βγ∥,则αβ⊥;④若m α⊂,n α⊂,m β∥,n β∥,则αβ∥. 其中所有..正确命题的序号是_____. 14.如图所示,AB ⊥平面BCD ,BC CD ⊥,图中互相垂直的平面共有______对.15.正四面体ABCD 中, E ,F 分别为边AB ,BD 的中点,则异面直线AF ,CE 所成角的余弦值为__________.16.如图所示,在四棱锥P ABCD -,PA ⊥底面ABCD ,且底面各边都相等,M 是PC 上的一动点,请你补充一个条件__________,使平面MBD ⊥平面PCD .①DM PC ⊥②DM BM ⊥③BM PC ⊥④PM MC =(填写你认为是正确的条件对应的序号).中小学最新教育资料三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)如图,在四棱锥E ABCD -中,平面EAB ⊥平面ABCD ,四边形ABCD 为矩形,EA EB ⊥,M ,N 分别为AE ,CD 的中点.求证: (1)直线MN ∥平面EBC ; (2)直线EA ⊥平面EBC .18.(12分)如图,已知四棱锥P ABCD -的底面ABCD 是菱形,60ABC ∠=︒,PA ⊥平面ABCD ,2AB =,2PA =,点F 为PC 的中点. (1)求证:平面PAC ⊥平面BDF ; (2)求三棱锥P BDF -的体积.19.(12分)如图,在直四棱柱1111ABCD A B C D -中,1AB BD ==,AD =,12AA BC ==,AD BC ∥. (1)证明:平面1BDB ⊥平面11ABB A ;(2)比较四棱锥11D ABB A -与四棱锥1111D A B C D -的体积的大小.20.(12分)如图所示的多面体中,底面ABCD 为正方形,GAD △为等边三角形,BF ⊥平面ABCD ,90GDC ∠=︒,点E 是线段GC 上除两端点外的一点,若点P 为线段GD 的中点.(1)求证:AP ⊥平面GCD ; (2)求证:平面ADG ∥平面FBC .中小学最新教育资料21.(12分)如图,三棱锥B ACD -的三条侧棱两两垂直,2BC BD ==,E ,F ,G 分别是棱CD ,AD ,AB 的中点.(1)证明:平面ABE ⊥平面ACD ; (2)若四面体BEFG 的体积为12,且F 在平面ABE 内的正投影为M ,求线段CM 的长.22.(12分)在如图如示的多面体中,平面AEFD ⊥平面BEFC ,四边形AEFD 是边长为2的正方形,BC ,且(1)若M ,N 分别是AE ,CF 中点,求证:MN ∥平面ABCD (2)求此多面体ABCDEF 的体积中小学最新教育资料单元训练金卷▪高三▪数学卷答案(A ) 第十五单元 点、线、面的位置关系一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】A【解析】对于B ,易知AB MQ ∥,则直线AB ∥平面MNQ ;对于C ,易知AB MQ ∥, 则直线AB ∥平面MNQ ;对于D ,易知AB NQ ∥,则直线AB ∥平面MNQ . 故排除B ,C ,D ,选A . 2.【答案】B【解析】A 中l 与m 位置不确定,D 中α与β可能相交,C 中m 与α的位置不确定,B 正确,故选B . 3.【答案】D 【解析】如图,平移直线D N '到A H ',则直线A H '与直线AM 所成角,由于点M ,H 都是中点, 所以ABM A AH ≅'△△,则BAM AA H ∠=∠',而90A HA AA H '∠+∠='︒, 所以90A HA BAM ∠+∠='︒,即A H AM '⊥,应选答案D . 4.【答案】A【解析】由线面角的定义可知答案①中的直线m α⊥,m β⊥,则平面αβ∥是正确的; 因为答案②中的两个平面α,β也可能相交,故不正确;答案③中的两个平面m α⊂,n β⊂可以推出两个平面α,β相交,故也不正确;对于答案④,可将直线n 平移到到平面α内,借助异面直线平移后不相交的结论及面面平行的判定定理可知αβ∥,是正确命题,所以应选答案A . 5.【答案】D【解析】AM 与BN 为正方体两相对平面的对角线,且不平行,所以AM 与BN 所成角的大小为90︒,故选D . 6.【答案】C【解析】在正方体1111ABCD A B C D -中,取1AB l =,2CD l =,当取面11CDD C 为平面α时,∴满足12l l ∥,1l α∥,此时2αl ⊂;当取面1111B A D C 为平面α时,∴满足12l l ∥,1l α∥,此时2l α∥,∴当直线1l 、2l ,平面α,12l l ∥,1l α∥时, 2l 与平面α的关系是2l α∥或2l α⊂,故选C .7.【答案】A 【解析】连接AC ,BD 相交于点O ,连接EM ,EN . 在①中,由正四棱锥S ABCD -,可得SO ⊥底面ABCD AC BD ⊥,∴SO AC ⊥.∵SOBD O =,∴AC ⊥面SBD .∵E ,M ,N 分别是BC ,CD ,SC 的中点,∴EM BD ∥,MN SD ∥,EM MN N =,∴平面EMN ∥平面SBD ,∴AC ⊥平面EMN ,∴AC EP ⊥,故①正确;在②中,由异面直线的定义可知,EP 和BD 是异面直线,不可能EP BD ∥,因此不正确; 在③中,由①可知,平面EMN ∥平面SBD ,∴EP ∥平面SBD ,因此正确; 在④中,由①同理可得,EM ⊥平面SAC ,若EP ⊥平面SAC ,则EP EM ∥,中小学最新教育资料与EPEM E =相矛盾,因此当P 与M 不重合时,EP 与平面SAC 不垂直,即不正确.故选A . 8.【答案】A【解析】逐一考查所给的线面关系:A .若m α⊥,n α⊂,由线面垂直的定义,则m n ⊥,B .若m α∥,n α∥,不一定有m n ∥,如图所示的正方体中, 若取m ,n 为AB ,AD ,平面α为上底面1111A BCD 即为反例;C .若m α⊥,m n ⊥,不一定有n α∥,如图所示的正方体中,若取m ,n 为1A A ,11AD ,平面α为上底面1111A B C D 即为反例;D .若m α∥,m n ⊥,不一定有n α⊥如图所示的正方体中,若取m ,n 为AD ,BC ,平面α为上底面1111A B C D 即为反例;故选A . 9.【答案】B【解析】在A 中,∵正方体1111ABCD A B C D -的棱长为1,E ,F 是线段11B D 上的两个动点,AC BD ⊥,1AC BB ⊥,∵1BDBB B =,∴AC ⊥平面11BDD B ,∵BF ⊂平面11BDD B ,∴AC BF⊥,故A 正确;在B 中,异面直线AE 、BF 所成的角不为定值, 由图知,当F 与1B 重合时,令上底面顶点为O ,则此时两异面直线所成的角是1A AO ∠,当E 与1D 重合时,此时点F 与O 重合, 则两异面直线所成的角是1OBC ∠,此二角不相等, 故异面直线AE 、BF 所成的角不为定值.故B 错误;在C 中,∵EF BD ∥,BD ⊂平面ABCD ,EF ⊄平面ABCD ,∴EF ∥平面ABCD ,故C 正确;在D 中,∵AC ⊥平面11BDD B ,∴A 到平面BEF 的距离不变,B 到EF 的距离为1,∴BEF △的面积不变, ∴三棱锥A BEF -的体积为定值,故D 正确.10.【答案】A 【解析】如图所示,过点C 作1CE BA ∥,连接1B E ,则1B CE ∠就是直线1A B 与1B C 所成的角或其补角,由题得1B C CE =,1B E =1121237cos 2128B CE +-∠==⨯,故选A .11.【答案】B【解析】由BC EF ∥可知BC ∥平面AEF ,则点P 到平面AEF 的距离即点B 到平面AEF 的距离, 直线EF ⊥平面11ABB A ,则平面AEF ⊥平面11ABB A , 结合平面AEF平面11ABB A AE =可知原问题可转换为点B 到直线AE 的距离,利用面积相等可得点P 到平面AEF 的距离为:B 选项. 12.【答案】D【解析】①错误.所得四棱锥中,设AS 中点为I ,则E 、I 两点重合,∵FI GH ∥,即EF GH ∥,即EF 与GH 不是异面直线;②正确.∵FI GH ∥,PB 与BQ 重合,且GH 与BQ 所成角为60︒, 说明EF 与PB 所成角为60︒;③正确.∵FI GH BC ∥∥,BC ⊂平面PBC ,FI ⊄平面PBC , ∴FI ∥平面PBC ,∴FE ∥平面PBC ;④正确.∵FI ∥平面ABCD , IH ∥平面ABCD ,FIHI I =点,∴平面FIHG ∥平面ABCD ,即平面EFGH ∥平面ABCD ,故选D .中小学最新教育资料二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】②③【解析】若αβ⊥,l β⊥,则l α∥,l α⊂; 若l α⊥,l β⊥,则αβ∥; 若αγ⊥,βγ,则αβ⊥;若m α⊂,n α⊂,m β∥,n β∥,则αβ∥或,αβ相交, 所以正确命题的序号是②③ 14.【答案】3【解析】由AB ⊥平面BCD ,又AB ⊂平面ABC 、平面ABD , 所以平面ABC ⊥平面BCD ,平面ABD ⊥平面BCD ;由AB ⊥平面BCD 可得CD AB ⊥,又CD BC ⊥,所以CD ⊥平面ABC , 又CD ⊂平面ACD ,故平面ABC ⊥平面ACD .故答案为3. 15.【解析】取BF 中点G ,连CG ,EG ,不妨设正四面体的棱长为2,EG =,CG异面直线AF ,CE16.【答案】①③【解析】由定理可知,BD PC ⊥,∴当DM PC ⊥(或BM PC ⊥)时,即有PC ⊥平面M BD , 而PC ⊂平面PCD ,∴平面MBD ⊥平面PCD ,则DM PC ⊥或BM PC ⊥正确, 故答案为①③.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【答案】(1)见解析;(2)见解析. 【解析】证明:(1)取BE 中点F ,连结CF ,MF ,又M 是AE 的中点,所以12MF AB ∥,且12MF AB =,因为N 是矩形ABCD 的边CD 的中点,所以NC AB ∥,且12NC AB =. 所以MF NC ∥且MF NC =,所以四边形MNCF 是平行四边形.所以MN CF ∥.又MN ⊄平面EBC ,CF ⊂平面EBC ,所以直线MN ∥平面EBC . (2)在矩形ABCD 中,BC AB ⊥. 又平面EAB ⊥平面ABCD ,平面ABCD 平面EAB AB =,BC ⊂平面ABCD ,所以BC ⊥平面EAB .又EA ⊂平面EAB ,所以BC EA ⊥. 又EA EB ⊥,BCEB B =,EB ,BC ⊂平面EBC ,所以直线EA ⊥平面EBC . 18.【答案】(1)见解析;(2. 【解析】(1)连接AC ,BC 与AC 交于点O ,连接OF , 因为PA ⊥平面ABCD ,AC ⊂平面ABCD ,所以PA AC ⊥, 因为点F 为PC 的中点,所以OF PA ∥.因为OF AC ⊥,因为ABCD 是菱形,所以AC BD ⊥, 因为OFBD O =,所以AC ⊥平面BDF ,因为AC ⊂平面PAC ,所以平面PAC ⊥平面BDF . (2)由(1)可知PA ⊥平面ABCD ,OF PA ∥,所以11133P BCD BCD V OF S -=⋅⋅=⨯=△,所以11233P ABD ABD V PA S -=⋅⋅=⨯△,所以P BDF P ABCD F BCD A BDP V V V V ----=--==.19.【答案】(1)见解析;(2)111111D A B C D D ABB A V V -->.【解析】(1)证明:∵2222AB BD AD +==,∴AB BD ⊥,中小学最新教育资料又1AA ⊥平面ABCD ,∴1AA BD ⊥, ∵1ABAA A =,∴BD ⊥平面11ABB A .又BD ⊂平面1BDB ,∴平面1BDB ⊥平面11ABB A . (2)解:∵AB BD =且AB BD ⊥,∴45ADB ∠=︒, 又AD BC ∥,∴45CBD ADB ∠=∠=︒,∴1sin452BCD S BD BC =⨯⨯︒△ ∴四边形ABCD的面积为12,∴111111232D A B C D V -⎛=⨯⨯+= ⎝⎭又1111112112333D ABB A ABB A V BD S -=⨯⨯=⨯⨯⨯=矩形,∵1233>∴111111D A B C D D ABB A V V -->.20.【答案】(1)见解析;(2)见解析.【解析】(1)证明:因为GAD △是等边三角形,点P 为线段GD 的中点,故AP GD ⊥. 因为AD CD ⊥,GD CD ⊥,且AD GD D =,AD ,GD ⊂平面GAD ,故CD ⊥平面GAD , 又AP ⊂平面GAD ,故CD AP ⊥,又CD GD D =,CD ,GD ⊂平面GCD ,故AP ⊥平面GCD . (2)证明:∵BF ⊥平面ABCD ,∴BF CD ⊥, ∵BC CD ⊥,BFBC B =,BF ,BC ⊂平面FBC ,∴CD ⊥平面FBC ,由(1)知CD ⊥平面GAD ,∴平面ADG ∥平面FBC . 21.【答案】(1)见解析;(2. 【解析】(1)证明:因为BC BD =,E 是棱CD 的中点,所以BE CD ⊥, 又三棱锥B ACD -的三条侧棱两两垂直,且BC BD B =,所以AB ⊥平面BCD ,则AB CD ⊥, 因为ABBE B =,所以CD ⊥平面ABE ,又CD ⊂平面ACD ,所以平面ABE ⊥平面ACD . (2)由(1)知CD ⊥平面ABE ,因为MF ⊥平面ABE , 所以MF CD ∥,又F 为AD 的中点,所以M 为AE 的中点,因为BE =12MF DE ==, 所以四面体体BEFG 的体积为11326BG BE BG MF ⨯⨯⨯⨯==12,则3BG =.在Rt ABE △中,26AB BG ==,AE == 在Rt CEM △中,12ME AE =,CM =. 22.【答案】(1)见解析;(2. 【解析】(1)证明:在平面CDF 中,作NH CF ⊥交DC 于H ,连接AH . ∵M ,N 是AE ,CF 中点,且AEFD 是正方形,∴NH DF ∥又AM DF ∥,,∴NH AM =,NH AM ∥, ∴四边形AMNH 是平行四边形,∴MN AH ∥,又AH ⊂平面ABCD ,MN ⊄平面ABCD ,∴MN ∥平面ABCD . (2)解:如图,连BD ,BF ,过F 作FG EF ⊥,交BC 于点G .∵四边形BEFCFG =. ∵平面AEFD ⊥平面BEFC ,平面AEFD 平面BEFC EF =,FG EF ⊥,DF EF ⊥,∴GF ⊥平面AEFD , DF ⊥平面BEFC .。
【新】2019年高考数学一轮复习第十五单元点、线、面的位置关系单元B卷理

小中高 精品 教案 试卷制作不易 推荐下载 第十五单元 点、线、面的位置关系注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在四面体P ABC -中,PA ,PB ,PC 两两垂直,M 是面ABC 内一点,M 到三个面PAB PBC ,PCA 的距离分别是2,3,6,则M 到P 的距离是( )A .7B .8C .9D .102.平面α∥平面β的一个充分条件是( )A .存在一条直线a ,a α∥,a β∥B .存在一条直线a ,a α⊂,a β∥C .存在两条平行直线a ,b ,a α⊂,b β⊂,a β∥,b α∥D .存在两条异面直线a ,b ,a α⊂,b β⊂,a β∥,b α∥3.“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的( )条件A .充要B .充分非必要C .必要非充分D .既非充分又非必要4.下列命题中错误的是( )A .如果平面⊥α平面β,那么平面α内一定存在直线平行于平面βB .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC .如果平面⊥α平面γ,平面⊥β平面γ,l αβ=,那么⊥l 平面γD .如果平面⊥α平面β,那么平面α内所有直线都垂直于平面β5.已知α,β,γ为互不重合的平面,命题p :若βα⊥,γβ⊥,则αγ∥;命题q :若α上不共线的三点到平面β的距离相等,则αβ∥.则下列命题正确的是( ) A .p q ∧ B .q p ∨ C .q p ∧⌝)( D .)(q p ⌝∨ 6.设α,β是两个不同的平面,l 是一条直线,以下命题正确的是( ) A .若l α⊥,αβ⊥,则l β⊂ B .若l α∥,αβ∥,则l β⊂ C .若l α⊥,αβ∥,则l β⊥ D .若l α∥,αβ⊥,则l β⊥ 7.右图是一个正方体的平面展开图,在这个正方体中有以下结论: ①BM ED ∥; ②CN 与BE 是异面直线; ③CN 与BM 成60︒角; ④DM 与BN 垂直.以上四个命题中,正确命题的序号的是( )A .①②B .②③C .①④D .③④ 8.如图所示,在正方形ABCD 中,E ,F 分别是AB 、BC 的中点,沿DE 、DF 及EF 把ADE △、CDF △和BEF △折起,使A 、B 、C 三点重合,设重合后的点为P ,则四面体DEF P -中必有( )A .DP ⊥平面PEFB .DF ⊥平面PEFC .PE ⊥平面DEFD .PF ⊥平面DEF 9.设α,β为两个不重合的平面,l ,m ,n 为两两不重合的直线,给出下列四个命题: ①若αβ∥,l α⊂,则l β∥ ②若m α⊂,n α⊂,m β∥,n β∥,则αβ∥ ③若l α∥,l β⊥,则αβ⊥ ④若m α⊂,n α⊂,且l m ⊥,l n ⊥,则l α⊥ 其中真命题的序号是( ) A .①③④ B .①②③ C .①③ D .②④ 10.如图,正方体1111D C B A ABCD -的棱长为1,E ,F 分别为线段1AA ,1B C 上的点,小中高 精品 教案 试卷制作不易 推荐下载 则三棱锥EDF D -1的体积为( )A .31B .41C .61D .12111.如图,正方体1111D C B A ABCD -的棱长为1,线段11B D 有两个动点E ,F,且EF ,则下列结论中错误的是( )A .AC BE ⊥B .EF ∥平面ABCDC .三棱锥A BEF -的体积为定值D .异面直线AE ,BF 所成的角为定值12.如图所示,在正方体1111D C B A ABCD -的侧面1AB 内有一动点P 到直线11A B 、BC 的距离相等,则动点P 所在曲线的形状为( )A. B .C .D . 二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.已知平面α∥平面β,P 是α,β外一点,过P 点的两条直线AC ,BD 分别交α于A ,B ,交β于C ,D ,且6=PA ,9=AC ,8=AB ,则CD 的长为________. 14.如图,在正四棱柱1111ABCD A B C D -中,E 、F 、G 、H 、N 分别是棱1CC 、11D C 、D D 1、DC 、BC 的中点,点M 在四边形EFGH 及其内部运动,则满足条件_____时,有MN ∥平面11BDD B .15.如图是一体积为31的正四面体,连结两个面的重心E 、F ,则线段EF 的长为_____.16.已知正三棱柱111C B A ABC -的棱长都相等,M 是侧棱1CC 的中点,则异面直线1AB 和BM 所成的角的大小是 . 三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(10分)如图,三棱柱111C B A ABC -,1A A ⊥底面ABC ,且ABC △为正三角形,D 为AC 中点. (1)求证:直线1AB ∥平面1BC D ,小中高 精品 教案 试卷制作不易 推荐下载 (2)求证:平面1BC D ⊥平面11ACC A ;18.(12分)如图,四边形ABCD 为矩形,⊥BC 平面ABE ,F 为CE 上的点,且⊥BF 平面ACE .(1)求证:BE AE ⊥;(2)设点M 为线段AB 的中点,点N 为线段CE 的中点,求证:MN ∥平面DAE .19.(12分)如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,⊥BE 平面ABCD .(1)证明:平面⊥AEC 平面BED ;(2)若120ABC ∠=︒,EC AE ⊥,三棱锥ACD E -的体积为36,求该三棱锥的侧面积.20.(12分)如图,四棱锥P ABCD -的底面ABCD 是正方形,侧棱PD ⊥底面ABC D ,3cm PD DC ==,E 为PC 的中点; (1)证明:PA ∥平面BDE ; (2)在棱PC 上是否存在点F ,使三棱锥C BDF -的体积为33cm ?并说明理由.小中高 精品 教案 试卷制作不易 推荐下载21.(12分)已知ABCD 是边长为a ,60BAD ∠=︒的菱形,点P 为ABCD 所在平面外一点, PAD △为正三角形,其所在平面垂直于平面ABCD .(1)若G 为AD 边的中点,求证:⊥BG 平面PAD ;(2)求证:PB AD ⊥;(3)若E 为BC 的中点,能否在PC 上,找到一点F 使平面⊥DEF 平面ABCD .22.(12分)如图所示,一个棱柱的直观图和三视图,主视图和俯视图是边长为a 的正方形,左视图是等腰直角三角形,直角边为a .M ,N 分别是AB ,AC 的中点,G 是DF 上的一动点.(1)求证:AC GN ⊥; (2)求三棱锥MCE F -的体积; (3)当GD FG =时,证明AG ∥平面FMC .小中高精品教案试卷制作不易推荐下载小中高 精品 教案 试卷制作不易 推荐下载 单元训练金卷▪高三▪数学卷答案(B )第十五单元 点、线、面的位置关系一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.【答案】A【解析】由题目的条件可知,M 到P 的距离即为以2、3、6为长、宽、高的长方体的对角线, ∴M 到P7=,故选A .2.【答案】D【解析】对于A ,B ,C 选项均有可能出现平面α与平面β相交的情况,故选D .3.【答案】C【解析】“直线l 与平面α内无数条直线都垂直”不能推出“直线l 与平面α垂直”;反之,能推出.故条件“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的必要非充分条件,选C .4.【答案】D【解析】平面α与平面β垂直时,平面α内所有与交线不垂直的直线都与平面β不垂直, 故D 错误,答案为D .5.【答案】D【解析】易知p 、q 均为假命题,从而p ⌝、q ⌝均为真命题,所以)(q p ⌝∨为真命题,故选D .6.【答案】C【解析】对于A 、B 、D 均可能出现l β∥,根据面面平行的性质可知选项C 是正确的.7.【答案】D【解析】展开图可以折成如图所示的正方体,由此可知①②不正确;③④正确.故选D .8.【答案】A【解析】折叠前,AE DA ⊥,CF DC ⊥,FB EB ⊥,折叠后这些垂直关系都未发生变化,因此,DP ⊥平面PEF ,故选A . 9.【答案】C 【解析】②是假命题,∵m ,n 不一定相交,∴α,β不一定平行;④是假命题, ∵m ,n 不一定相交,∴l 与α不一定垂直,故选C . 10.【答案】C 【解析】=-ED F D V 11F D ED V -,又112D ED S =△,点F 到面ED D 1的距离为1, ∴111111326D EDF F D ED V V --==⨯⨯=.故选C . 11.【答案】D 【解析】∵AC ⊥平面11B BDD ,⊂BE 平面11B BDD ,∴AC BE ⊥,A 正确; 易知EF ∥平面ABCD ,B 正确; 设点A 到平面11B BDD 的距离为d,d =,112BEF S EF BB =⨯⨯=△ ∴11d 312A BEF BEF V S -=⋅=.所以三棱锥A BEF -的体积为定值.C 正确;故结论中错误的是D . 12.【答案】C 【解析】如图,在平面1AB 内过P 点作PE 垂直于11A B 于E ,连接PB ,∵BC 垂直于侧面1AB ,∴PB BC ⊥,由题意PE PB =,故P 点在以1BB 的中点O 为顶点,以B 为焦点的抛物线上, 并且该抛物线过A 点,故选C . 二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】4或20 【解析】若P 在平面α,β的同侧,由于平面α∥平面β,故AB CD ∥,则CD AB PC PA =, 可求得20=CD ;若P 在平面α,β之间,同理可求得4=CD .小中高 精品 教案 试卷制作不易 推荐下载 14.【答案】M ∈线段FH【解析】∵HN BD ∥,1HF DD ∥,∴平面N H F ∥平面11B D D B ,又平面NHF 平面E F G H FH =,故线段FH 上任意点M 与N 相连,有MN ∥平面11BDD B ,故填M ∈线段FH .15.【答案】32【解析】设正四面体的棱长为a ,则正四面体的高为a h 36=,体积231133V ===,∴223=a ,∴2=a,∴2132EF =⨯.16.【答案】90︒【解析】取BC 的中点N ,连结AN ,则AN ⊥平面11B BCC ,∴AN BM ⊥.∵正三棱柱111C B A ABC -的棱长都相等,∴11B BCC 是正方形.连结N B 1则易证1B N BM ⊥, ∴BM ⊥平面N AB 1,∴1BM AB ⊥,异面直线1AB 和BM 所成的角的大小是90︒.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.【答案】(1)见解析;(2)见解析.【解析】(1)连结1B C 交1BC 于O ,连结OD ,在1B AC △中,D AC 为中点,O 为1B C 中点,所以1OD AB ∥,又OD ⊂平面1BC D ,∴直线1AB ∥平面1BC D . (2)∵1A A ⊥底面ABC ,∴1A A BD ⊥. 又BD AC ⊥,∴BD ⊥平面11ACC A 又BD ⊂平面1BC D ,∴平面1BC D ⊥平面11ACC A . 18.【答案】(1)见解析;(2)见解析. 【解析】(1)证明:∵⊥BC 平面ABE ,⊂AE 平面ABE ,∴BC AE ⊥, 又⊥BF 平面ACE ,⊂AE 平面ACE ,∴BF AE ⊥. 又B BC BF = ,∴⊥AE 平面BCE , 又⊂BE 平面BCE ,∴BE AE ⊥. (2)取DE 的中点P ,连结PA ,PN ,∵点N 为线段CE 的中点,∴PN DC ∥,且DC PN 21=,又四边形ABCD 是矩形,点M 为线段AB 的中点,∴AM DC ∥,且DC AM 21=, ∴PN AM ∥,且AM PN =,∴四边形AMNP 是平行四边形, ∴MN AP ∥,而⊂AP 平面DAE ,⊄MN 平面DAE ,∴MN ∥平面DAE .19.【答案】(1)见解析;(2)3+ 【解析】(1)证明:∵⊥BE 平面ABCD ,⊂AC 平面ABCD ,∴AC BE ⊥. 又∵四边形ABCD 为菱形,∴BD AC ⊥.∵B BE BD = , ∴⊥AC 平面BED ,∵⊂AC 平面AEC ,∴平面⊥AEC 平面BED . (2)∵⊥BE 平面ABCD ,∴AB BE ⊥,BC BE ⊥, ∵BC AB =,∴Rt Rt ABE CBE ≅△△,∴CE AE =. 在Rt ACE △中,22222AE CE AE AC =+=, 又∵22222cos 3AC AB BC AB BC ABC AB =+-⋅∠=,小中高 精品 教案 试卷制作不易 推荐下载 ∴2232AB AE =,∴AB AE 26=,∴AB BE 22=, ∴111sin 332E ACD ACD V BE S BE AB BC ABC -=⋅=⋅⋅⋅∠△311sin12032AB AB AB AB =⋅⋅⋅︒=,3AB =2=AB .∴12ABE CBE S S AB BE ==⨯=△△∵EC ED AE ==2CD AD ==,∴3ACE S =△,DAE CDE S S =△△所以该三棱锥的侧面积为3ACE DAE CDE S S S ++=+△△△.20.【答案】(1)见解析;(2)存在且F 是线段PC 的靠近P 点的一个三等分点,见解析.【解析】(1)连接AC 交BD 于O 点,连接OE ,在APC △中,O 、E 分别为AC ,PC 的中点,∴OE ∥PA ;∵OE ⊂平面BDE ,PA ⊄平面BDE ,∴PA ∥平面BDE ;(2)∵侧棱PD ⊥⊥底面ABCD ,∴PD CD ⊥,设F 为PC 上一点,过F 作FG CD ⊥于G ,则FG PD ∥,∴FG ⊥平面ABCD .若11133333322C BDF F BDC BDC V V S FG FG FG --==⋅=⨯⨯⨯⨯==△,则2FG =,∴在棱PC 上存在点F 使三棱锥C BDF -的体积为33cm .且F 是线段PC 的靠近P 点的一个三等分点.21.【答案】(1)见解析;(2)见解析;(3)能,见解析.【解析】(1)连结BD ,则在正三角形ABD 中,AD BG ⊥,又平面⊥PAD 平面ABCD 于AD ,所以⊥BG 平面PAD .(2)连结PG ,在正三角形PAD 中,AD PG ⊥,又AD BG ⊥,∴⊥AD 平面PBG .∵⊂PB 平面PBG ,∴PB AD ⊥.(3)能在PC 上,找到一点F 使平面⊥DEF 平面ABCD ,且F 为PC 中点. 证明如下:连结ED ,GC 交于点O ,易知O 为GC 的中点, 在平面PGC 内,作OF GP ∥,交PC 于点F ,则F 为PC 中点,⊥FO 平面ABCD , ∴平面⊥DEF 平面ABCD . 22.(12分)如图所示,一个棱柱的直观图和三视图,主视图和俯视图是边长为a 的正方形,左视图是等腰直角三角形,直角边为a .M ,N 分别是AB ,AC 的中点,G 是DF 上的一动点.【答案】(1)见解析;(2)316a ;(3)见解析. 【解析】(1)由三视图可知,多面体是直三棱柱, 且底面是直角边为a 的等腰直角三角形, ∴侧面ABCD ,CDEF 是边长为a 的正方形. 连结DN ,因为CD FD ⊥,AD FD ⊥,所以⊥FD 平面ABCD , ∴AC FD ⊥,又∵DN AC ⊥,∴⊥AC 平面GND , ∵⊂GN 平面GND ,∴AC GN ⊥.(2)∵⊥AD 平面CEF ,∴2311113326F MCE M CEF CEF V V AD S a a a --==⋅=⨯⨯=△. (3)连结DE 交FC 于Q ,连结QG , ∵Q ,G 分别是FD ,FC 的中点,∴GQ CD ∥,且12GQ CD =, ∵M 是AB 的中点,∴AM CD ∥,且CD AM 21=, ∴AM GQ ∥=,∴AMQC 是平行四边形,∴AG QM ∥,小中高 精品 教案 试卷制作不易 推荐下载 ∵⊄AG 平面FMC .⊂MQ 平面FMC ,∴AG ∥平面FMC .。
【新】2019年高考数学一轮复习第十五单元点、线、面的位置关系单元B卷文

小中高 精品 教案 试卷制作不易 推荐下载 第十五单元 点、线、面的位置关系注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在四面体P ABC -中,PA ,PB ,PC 两两垂直,M 是面ABC 内一点,M 到三个面PAB PBC ,PCA 的距离分别是2,3,6,则M 到P 的距离是( )A .7B .8C .9D .102.平面α∥平面β的一个充分条件是( )A .存在一条直线a ,a α∥,a β∥B .存在一条直线a ,a α⊂,a β∥C .存在两条平行直线a ,b ,a α⊂,b β⊂,a β∥,b α∥D .存在两条异面直线a ,b ,a α⊂,b β⊂,a β∥,b α∥3.“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的( )条件A .充要B .充分非必要C .必要非充分D .既非充分又非必要4.下列命题中错误的是( )A .如果平面⊥α平面β,那么平面α内一定存在直线平行于平面βB .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC .如果平面⊥α平面γ,平面⊥β平面γ,l αβ=,那么⊥l 平面γD .如果平面⊥α平面β,那么平面α内所有直线都垂直于平面β5.已知α,β,γ为互不重合的平面,命题p :若βα⊥,γβ⊥,则αγ∥;命题q :若α上不共线的三点到平面β的距离相等,则αβ∥.则下列命题正确的是( ) A .p q ∧ B .q p ∨ C .q p ∧⌝)( D .)(q p ⌝∨ 6.设α,β是两个不同的平面,l 是一条直线,以下命题正确的是( ) A .若l α⊥,αβ⊥,则l β⊂ B .若l α∥,αβ∥,则l β⊂ C .若l α⊥,αβ∥,则l β⊥ D .若l α∥,αβ⊥,则l β⊥ 7.右图是一个正方体的平面展开图,在这个正方体中有以下结论: ①BM ED ∥; ②CN 与BE 是异面直线; ③CN 与BM 成60︒角; ④DM 与BN 垂直.以上四个命题中,正确命题的序号的是( )A .①②B .②③C .①④D .③④ 8.如图所示,在正方形ABCD 中,E ,F 分别是AB 、BC 的中点,沿DE 、DF 及EF 把ADE △、CDF △和BEF △折起,使A 、B 、C 三点重合,设重合后的点为P ,则四面体DEF P -中必有( )A .DP ⊥平面PEFB .DF ⊥平面PEFC .PE ⊥平面DEFD .PF ⊥平面DEF 9.设α,β为两个不重合的平面,l ,m ,n 为两两不重合的直线,给出下列四个命题: ①若αβ∥,l α⊂,则l β∥ ②若m α⊂,n α⊂,m β∥,n β∥,则αβ∥ ③若l α∥,l β⊥,则αβ⊥ ④若m α⊂,n α⊂,且l m ⊥,l n ⊥,则l α⊥ 其中真命题的序号是( ) A .①③④ B .①②③ C .①③ D .②④ 10.如图,正方体1111D C B A ABCD -的棱长为1,E ,F 分别为线段1AA ,1B C 上的点,小中高 精品 教案 试卷制作不易 推荐下载 则三棱锥EDF D -1的体积为( )A .31B .41C .61D .12111.如图,正方体1111D C B A ABCD -的棱长为1,线段11B D 有两个动点E ,F,且EF ,则下列结论中错误的是( )A .AC BE ⊥B .EF ∥平面ABCDC .三棱锥A BEF -的体积为定值D .异面直线AE ,BF 所成的角为定值12.如图所示,在正方体1111D C B A ABCD -的侧面1AB 内有一动点P 到直线11A B 、BC 的距离相等,则动点P 所在曲线的形状为( )A. B .C .D . 二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.已知平面α∥平面β,P 是α,β外一点,过P 点的两条直线AC ,BD 分别交α于A ,B ,交β于C ,D ,且6=PA ,9=AC ,8=AB ,则CD 的长为________. 14.如图,在正四棱柱1111ABCD A B C D -中,E 、F 、G 、H 、N 分别是棱1CC 、11D C 、D D 1、DC 、BC 的中点,点M 在四边形EFGH 及其内部运动,则满足条件_____时,有MN ∥平面11BDD B .15.如图是一体积为31的正四面体,连结两个面的重心E 、F ,则线段EF 的长为_____.16.已知正三棱柱111C B A ABC -的棱长都相等,M 是侧棱1CC 的中点,则异面直线1AB 和BM 所成的角的大小是 . 三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.(10分)如图,三棱柱111C B A ABC -,1A A ⊥底面ABC ,且ABC △为正三角形,D 为AC 中点. (1)求证:直线1AB ∥平面1BC D ,小中高 精品 教案 试卷制作不易 推荐下载 (2)求证:平面1BC D ⊥平面11ACC A ;18.(12分)如图,四边形ABCD 为矩形,⊥BC 平面ABE ,F 为CE 上的点,且⊥BF 平面ACE .(1)求证:BE AE ⊥;(2)设点M 为线段AB 的中点,点N 为线段CE 的中点,求证:MN ∥平面DAE .19.(12分)如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,⊥BE 平面ABCD .(1)证明:平面⊥AEC 平面BED ;(2)若120ABC ∠=︒,EC AE ⊥,三棱锥ACD E -的体积为36,求该三棱锥的侧面积.20.(12分)如图,四棱锥P ABCD -的底面ABCD 是正方形,侧棱PD ⊥底面ABC D ,3cm PD DC ==,E 为PC 的中点; (1)证明:PA ∥平面BDE ; (2)在棱PC 上是否存在点F ,使三棱锥C BDF -的体积为33cm ?并说明理由.小中高 精品 教案 试卷制作不易 推荐下载21.(12分)已知ABCD 是边长为a ,60BAD ∠=︒的菱形,点P 为ABCD 所在平面外一点, PAD △为正三角形,其所在平面垂直于平面ABCD .(1)若G 为AD 边的中点,求证:⊥BG 平面PAD ;(2)求证:PB AD ⊥;(3)若E 为BC 的中点,能否在PC 上,找到一点F 使平面⊥DEF 平面ABCD .22.(12分)如图所示,一个棱柱的直观图和三视图,主视图和俯视图是边长为a 的正方形,左视图是等腰直角三角形,直角边为a .M ,N 分别是AB ,AC 的中点,G 是DF 上的一动点.(1)求证:AC GN ⊥; (2)求三棱锥MCE F -的体积; (3)当GD FG =时,证明AG ∥平面FMC .小中高精品教案试卷制作不易推荐下载小中高 精品 教案 试卷制作不易 推荐下载 单元训练金卷▪高三▪数学卷答案(B )第十五单元 点、线、面的位置关系一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.【答案】A【解析】由题目的条件可知,M 到P 的距离即为以2、3、6为长、宽、高的长方体的对角线, ∴M 到P7=,故选A .2.【答案】D【解析】对于A ,B ,C 选项均有可能出现平面α与平面β相交的情况,故选D .3.【答案】C【解析】“直线l 与平面α内无数条直线都垂直”不能推出“直线l 与平面α垂直”;反之,能推出.故条件“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的必要非充分条件,选C .4.【答案】D【解析】平面α与平面β垂直时,平面α内所有与交线不垂直的直线都与平面β不垂直, 故D 错误,答案为D .5.【答案】D【解析】易知p 、q 均为假命题,从而p ⌝、q ⌝均为真命题,所以)(q p ⌝∨为真命题,故选D .6.【答案】C【解析】对于A 、B 、D 均可能出现l β∥,根据面面平行的性质可知选项C 是正确的.7.【答案】D【解析】展开图可以折成如图所示的正方体,由此可知①②不正确;③④正确.故选D .8.【答案】A【解析】折叠前,AE DA ⊥,CF DC ⊥,FB EB ⊥,折叠后这些垂直关系都未发生变化,因此,DP ⊥平面PEF ,故选A . 9.【答案】C 【解析】②是假命题,∵m ,n 不一定相交,∴α,β不一定平行;④是假命题, ∵m ,n 不一定相交,∴l 与α不一定垂直,故选C . 10.【答案】C 【解析】=-ED F D V 11F D ED V -,又112D ED S =△,点F 到面ED D 1的距离为1, ∴111111326D EDF F D ED V V --==⨯⨯=.故选C . 11.【答案】D 【解析】∵AC ⊥平面11B BDD ,⊂BE 平面11B BDD ,∴AC BE ⊥,A 正确; 易知EF ∥平面ABCD ,B 正确; 设点A 到平面11B BDD 的距离为d,d =,112BEF S EF BB =⨯⨯=△ ∴11d 312A BEF BEF V S -=⋅=.所以三棱锥A BEF -的体积为定值.C 正确;故结论中错误的是D . 12.【答案】C 【解析】如图,在平面1AB 内过P 点作PE 垂直于11A B 于E ,连接PB ,∵BC 垂直于侧面1AB ,∴PB BC ⊥,由题意PE PB =,故P 点在以1BB 的中点O 为顶点,以B 为焦点的抛物线上, 并且该抛物线过A 点,故选C . 二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】4或20 【解析】若P 在平面α,β的同侧,由于平面α∥平面β,故AB CD ∥,则CD AB PC PA =, 可求得20=CD ;若P 在平面α,β之间,同理可求得4=CD .小中高 精品 教案 试卷制作不易 推荐下载 14.【答案】M ∈线段FH【解析】∵HN BD ∥,1HF DD ∥,∴平面N H F ∥平面11B D D B ,又平面NHF 平面E F G H FH =,故线段FH 上任意点M 与N 相连,有MN ∥平面11BDD B ,故填M ∈线段FH .15.【答案】32【解析】设正四面体的棱长为a ,则正四面体的高为a h 36=,体积231133V ===,∴223=a ,∴2=a,∴2132EF =⨯.16.【答案】90︒【解析】取BC 的中点N ,连结AN ,则AN ⊥平面11B BCC ,∴AN BM ⊥.∵正三棱柱111C B A ABC -的棱长都相等,∴11B BCC 是正方形.连结N B 1则易证1B N BM ⊥, ∴BM ⊥平面N AB 1,∴1BM AB ⊥,异面直线1AB 和BM 所成的角的大小是90︒.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.【答案】(1)见解析;(2)见解析.【解析】(1)连结1B C 交1BC 于O ,连结OD ,在1B AC △中,D AC 为中点,O 为1B C 中点,所以1OD AB ∥,又OD ⊂平面1BC D ,∴直线1AB ∥平面1BC D . (2)∵1A A ⊥底面ABC ,∴1A A BD ⊥. 又BD AC ⊥,∴BD ⊥平面11ACC A 又BD ⊂平面1BC D ,∴平面1BC D ⊥平面11ACC A . 18.【答案】(1)见解析;(2)见解析. 【解析】(1)证明:∵⊥BC 平面ABE ,⊂AE 平面ABE ,∴BC AE ⊥, 又⊥BF 平面ACE ,⊂AE 平面ACE ,∴BF AE ⊥. 又B BC BF = ,∴⊥AE 平面BCE , 又⊂BE 平面BCE ,∴BE AE ⊥. (2)取DE 的中点P ,连结PA ,PN ,∵点N 为线段CE 的中点,∴PN DC ∥,且DC PN 21=,又四边形ABCD 是矩形,点M 为线段AB 的中点,∴AM DC ∥,且DC AM 21=, ∴PN AM ∥,且AM PN =,∴四边形AMNP 是平行四边形, ∴MN AP ∥,而⊂AP 平面DAE ,⊄MN 平面DAE ,∴MN ∥平面DAE .19.【答案】(1)见解析;(2)3+ 【解析】(1)证明:∵⊥BE 平面ABCD ,⊂AC 平面ABCD ,∴AC BE ⊥. 又∵四边形ABCD 为菱形,∴BD AC ⊥.∵B BE BD = , ∴⊥AC 平面BED ,∵⊂AC 平面AEC ,∴平面⊥AEC 平面BED . (2)∵⊥BE 平面ABCD ,∴AB BE ⊥,BC BE ⊥, ∵BC AB =,∴Rt Rt ABE CBE ≅△△,∴CE AE =. 在Rt ACE △中,22222AE CE AE AC =+=, 又∵22222cos 3AC AB BC AB BC ABC AB =+-⋅∠=,小中高 精品 教案 试卷制作不易 推荐下载 ∴2232AB AE =,∴AB AE 26=,∴AB BE 22=, ∴111sin 332E ACD ACD V BE S BE AB BC ABC -=⋅=⋅⋅⋅∠△311sin12032AB AB AB AB =⋅⋅⋅︒=,3AB =2=AB .∴12ABE CBE S S AB BE ==⨯=△△∵EC ED AE ==2CD AD ==,∴3ACE S =△,DAE CDE S S =△△所以该三棱锥的侧面积为3ACE DAE CDE S S S ++=+△△△.20.【答案】(1)见解析;(2)存在且F 是线段PC 的靠近P 点的一个三等分点,见解析.【解析】(1)连接AC 交BD 于O 点,连接OE ,在APC △中,O 、E 分别为AC ,PC 的中点,∴OE ∥PA ;∵OE ⊂平面BDE ,PA ⊄平面BDE ,∴PA ∥平面BDE ;(2)∵侧棱PD ⊥⊥底面ABCD ,∴PD CD ⊥,设F 为PC 上一点,过F 作FG CD ⊥于G ,则FG PD ∥,∴FG ⊥平面ABCD .若11133333322C BDF F BDC BDC V V S FG FG FG --==⋅=⨯⨯⨯⨯==△,则2FG =,∴在棱PC 上存在点F 使三棱锥C BDF -的体积为33cm .且F 是线段PC 的靠近P 点的一个三等分点.21.【答案】(1)见解析;(2)见解析;(3)能,见解析.【解析】(1)连结BD ,则在正三角形ABD 中,AD BG ⊥,又平面⊥PAD 平面ABCD 于AD ,所以⊥BG 平面PAD .(2)连结PG ,在正三角形PAD 中,AD PG ⊥,又AD BG ⊥,∴⊥AD 平面PBG .∵⊂PB 平面PBG ,∴PB AD ⊥.(3)能在PC 上,找到一点F 使平面⊥DEF 平面ABCD ,且F 为PC 中点. 证明如下:连结ED ,GC 交于点O ,易知O 为GC 的中点, 在平面PGC 内,作OF GP ∥,交PC 于点F ,则F 为PC 中点,⊥FO 平面ABCD , ∴平面⊥DEF 平面ABCD . 22.(12分)如图所示,一个棱柱的直观图和三视图,主视图和俯视图是边长为a 的正方形,左视图是等腰直角三角形,直角边为a .M ,N 分别是AB ,AC 的中点,G 是DF 上的一动点.【答案】(1)见解析;(2)316a ;(3)见解析. 【解析】(1)由三视图可知,多面体是直三棱柱, 且底面是直角边为a 的等腰直角三角形, ∴侧面ABCD ,CDEF 是边长为a 的正方形. 连结DN ,因为CD FD ⊥,AD FD ⊥,所以⊥FD 平面ABCD , ∴AC FD ⊥,又∵DN AC ⊥,∴⊥AC 平面GND , ∵⊂GN 平面GND ,∴AC GN ⊥.(2)∵⊥AD 平面CEF ,∴2311113326F MCE M CEF CEF V V AD S a a a --==⋅=⨯⨯=△. (3)连结DE 交FC 于Q ,连结QG , ∵Q ,G 分别是FD ,FC 的中点,∴GQ CD ∥,且12GQ CD =, ∵M 是AB 的中点,∴AM CD ∥,且CD AM 21=, ∴AM GQ ∥=,∴AMQC 是平行四边形,∴AG QM ∥,小中高 精品 教案 试卷制作不易 推荐下载 ∵⊄AG 平面FMC .⊂MQ 平面FMC ,∴AG ∥平面FMC .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精品K12教育教学资料第十五单元 点、线、面的位置关系注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.在四面体P ABC -中,PA ,PB ,PC 两两垂直,M 是面ABC 内一点,M 到三个面PAB PBC ,PCA 的距离分别是2,3,6,则M 到P 的距离是( )A .7B .8C .9D .102.平面α∥平面β的一个充分条件是( ) A .存在一条直线a ,a α∥,a β∥ B .存在一条直线a ,a α⊂,a β∥C .存在两条平行直线a ,b ,a α⊂,b β⊂,a β∥,b α∥D .存在两条异面直线a ,b ,a α⊂,b β⊂,a β∥,b α∥3.“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的( )条件 A .充要B .充分非必要C .必要非充分D .既非充分又非必要4.下列命题中错误的是( )A .如果平面⊥α平面β,那么平面α内一定存在直线平行于平面βB .如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面βC .如果平面⊥α平面γ,平面⊥β平面γ,l αβ=,那么⊥l 平面γD .如果平面⊥α平面β,那么平面α内所有直线都垂直于平面β5.已知α,β,γ为互不重合的平面,命题p :若βα⊥,γβ⊥,则αγ∥;命题q :若α上不共线的三点到平面β的距离相等,则αβ∥.则下列命题正确的是( ) A .p q ∧B .q p ∨C .q p ∧⌝)(D .)(q p ⌝∨6.设α,β是两个不同的平面,l 是一条直线,以下命题正确的是( )A .若l α⊥,αβ⊥,则l β⊂B .若l α∥,αβ∥,则l β⊂C .若l α⊥,αβ∥,则l β⊥D .若l α∥,αβ⊥,则l β⊥7.右图是一个正方体的平面展开图,在这个正方体中有以下结论: ①BM ED ∥;②CN 与BE 是异面直线; ③CN 与BM 成60︒角;④DM 与BN 垂直.以上四个命题中,正确命题的序号的是( )A .①②B .②③C .①④D .③④8.如图所示,在正方形ABCD 中,E ,F 分别是AB 、BC 的中点,沿DE 、DF 及EF 把ADE △、CDF △和BEF △折起,使A 、B 、C 三点重合,设重合后的点为P ,则四面体DEF P -中必有( )A .DP ⊥平面PEFB .DF ⊥平面PEFC .PE ⊥平面DEFD .PF ⊥平面DEF9.设α,β为两个不重合的平面,l ,m ,n 为两两不重合的直线,给出下列四个命题: ①若αβ∥,l α⊂,则l β∥ ②若m α⊂,n α⊂,m β∥,n β∥,则αβ∥ ③若l α∥,l β⊥,则αβ⊥ ④若m α⊂,n α⊂,且l m ⊥,l n ⊥,则l α⊥其中真命题的序号是( ) A .①③④B .①②③C .①③D .②④10.如图,正方体1111D C B A ABCD -的棱长为1,E ,F 分别为线段1AA ,1B C 上的点, 则三棱锥EDF D -1的体积为( )精品K12教育教学资料A .31B .41C .61D .12111.如图,正方体1111D C B A ABCD -的棱长为1,线段11B D 有两个动点E ,F,且EF , 则下列结论中错误的是( )A .AC BE ⊥B .EF ∥平面ABCDC .三棱锥A BEF -的体积为定值D .异面直线AE ,BF 所成的角为定值12.如图所示,在正方体1111D C B A ABCD -的侧面1AB 内有一动点P 到直线11A B 、BC 的距离相等,则动点P 所在曲线的形状为( )A .B .C. D .二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上)13.已知平面α∥平面β,P 是α,β外一点,过P 点的两条直线AC ,BD 分别交α于A ,B ,交β于C ,D ,且6=PA ,9=AC ,8=AB ,则CD 的长为________.14.如图,在正四棱柱1111ABCD A B C D -中,E 、F 、G 、H 、N 分别是棱1CC 、11D C 、D D 1、DC 、BC 的中点,点M 在四边形EFGH 及其内部运动,则满足条件_____时,有MN ∥平面11BDD B .15.如图是一体积为31的正四面体,连结两个面的重心E 、F ,则线段EF 的长为_____.16.已知正三棱柱111C B A ABC -的棱长都相等,M 是侧棱1CC 的中点,则异面直线1AB 和BM 所成的角的大小是 .三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)如图,三棱柱111C B A ABC -,1A A ⊥底面ABC ,且ABC △为正三角形,D 为AC 中点.(1)求证:直线1AB ∥平面1BC D , (2)求证:平面1BC D ⊥平面11ACC A ;精品K12教育教学资料18.(12分)如图,四边形ABCD 为矩形,⊥BC 平面ABE ,F 为CE 上的点, 且⊥BF 平面ACE . (1)求证:BE AE ⊥;(2)设点M 为线段AB 的中点,点N 为线段CE 的中点,求证:MN ∥平面DAE .19.(12分)如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,⊥BE 平面ABCD . (1)证明:平面⊥AEC 平面BED ;(2)若120ABC ∠=︒,EC AE ⊥,三棱锥ACD E -的体积为36,求该三棱锥的侧面积.20.(12分)如图,四棱锥P ABCD -的底面ABCD 是正方形,侧棱PD ⊥底面ABCD ,3cm PD DC ==,E 为PC 的中点;(1)证明:PA ∥平面BDE ;(2)在棱PC 上是否存在点F ,使三棱锥C BDF -的体积为33cm ?并说明理由.21.(12分)已知ABCD是边长为a,60BAD∠=︒的菱形,点P为ABCD所在平面外一点,PAD△为正三角形,其所在平面垂直于平面ABCD.(1)若G为AD边的中点,求证:⊥BG平面PAD;(2)求证:PBAD⊥;(3)若E为BC的中点,能否在PC上,找到一点F使平面⊥DEF平面ABCD.22.(12分)如图所示,一个棱柱的直观图和三视图,主视图和俯视图是边长为a的正方形,左视图是等腰直角三角形,直角边为a.M,N分别是AB,AC的中点,G是DF上的一动点.(1)求证:ACGN⊥;(2)求三棱锥MCEF-的体积;(3)当GDFG=时,证明AG∥平面FMC.精品K12教育教学资料精品K12教育教学资料单元训练金卷▪高三▪数学卷答案(B ) 第十五单元 点、线、面的位置关系一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的) 1.【答案】A【解析】由题目的条件可知,M 到P 的距离即为以2、3、6为长、宽、高的长方体的对角线, ∴M 到P7,故选A . 2.【答案】D【解析】对于A ,B ,C 选项均有可能出现平面α与平面β相交的情况,故选D .3.【答案】C【解析】“直线l 与平面α内无数条直线都垂直”不能推出“直线l 与平面α垂直”;反之,能推出.故条件“直线l 与平面α内无数条直线都垂直”是“直线l 与平面α垂直”的必要非充分条件,选C . 4.【答案】D【解析】平面α与平面β垂直时,平面α内所有与交线不垂直的直线都与平面β不垂直, 故D 错误,答案为D . 5.【答案】D【解析】易知p 、q 均为假命题,从而p ⌝、q ⌝均为真命题,所以)(q p ⌝∨为真命题,故选D . 6.【答案】C【解析】对于A 、B 、D 均可能出现l β∥,根据面面平行的性质可知选项C 是正确的. 7.【答案】D 【解析】展开图可以折成如图所示的正方体,由此可知①②不正确;③④正确.故选D . 8.【答案】A【解析】折叠前,AE DA ⊥,CF DC ⊥,FB EB ⊥,折叠后这些垂直关系都未发生变化,因此,DP ⊥平面PEF ,故选A .9.【答案】C【解析】②是假命题,∵m ,n 不一定相交,∴α,β不一定平行;④是假命题, ∵m ,n 不一定相交,∴l 与α不一定垂直,故选C . 10.【答案】C【解析】=-ED F D V 11F D ED V -,又112D ED S =△,点F 到面ED D 1的距离为1, ∴111111326D EDF F D ED V V --==⨯⨯=.故选C .11.【答案】D【解析】∵AC ⊥平面11B BDD ,⊂BE 平面11B BDD ,∴AC BE ⊥,A 正确;易知EF ∥平面ABCD ,B 正确;设点A 到平面11B BDD 的距离为d,d =,112BEF S EF BB =⨯⨯=△ ∴11d 312A BEF BEF V S -=⋅=.所以三棱锥A BEF -的体积为定值.C 正确;故结论中错误的是D .12.【答案】C 【解析】如图,在平面1AB 内过P 点作PE 垂直于11A B 于E ,连接PB ,∵BC 垂直于侧面1AB ,∴PB BC ⊥, 由题意PE PB =,故P 点在以1BB 的中点O 为顶点,以B 为焦点的抛物线上, 并且该抛物线过A 点,故选C .二、填空题(本大题有4小题,每小题5分,共20分.请把答案填在题中横线上) 13.【答案】4或20【解析】若P 在平面α,β的同侧,由于平面α∥平面β,故AB CD ∥,则CDABPC PA =, 可求得20=CD ;若P 在平面α,β之间,同理可求得4=CD . 14.【答案】M ∈线段FH【解析】∵HN BD ∥,1HF DD ∥,∴平面NHF ∥平面11BDD B ,又平面NHF平面EFGH FH =,故线段FH 上任意点M 与N 相连,有MN ∥平面11BDD B ,故填M ∈线段FH .精品K12教育教学资料15.【答案】32【解析】设正四面体的棱长为a ,则正四面体的高为a h 36=,体积231133V ===,∴223=a ,∴2=a,∴2132EF =⨯. 16.【答案】90︒【解析】取BC 的中点N ,连结AN ,则AN ⊥平面11B BCC ,∴AN BM ⊥.∵正三棱柱111C B A ABC -的棱长都相等,∴11B BCC 是正方形.连结N B 1则易证1B N BM ⊥, ∴BM ⊥平面N AB 1,∴1BM AB ⊥,异面直线1AB 和BM 所成的角的大小是90︒.三、解答题(本大题有6小题,共70分.解答应写出文字说明、证明过程或演算步骤) 17.【答案】(1)见解析;(2)见解析. 【解析】(1)连结1B C 交1BC 于O ,连结OD ,在1B AC △中,D AC 为中点,O 为1B C 中点,所以1OD AB ∥,又OD ⊂平面1BC D ,∴直线1AB ∥平面1BC D . (2)∵1A A ⊥底面ABC ,∴1A A BD ⊥. 又BD AC ⊥,∴BD ⊥平面11ACC A又BD ⊂平面1BC D ,∴平面1BC D ⊥平面11ACC A .18.【答案】(1)见解析;(2)见解析.【解析】(1)证明:∵⊥BC 平面ABE ,⊂AE 平面ABE ,∴BC AE ⊥,又⊥BF 平面ACE ,⊂AE 平面ACE ,∴BF AE ⊥.又B BC BF = ,∴⊥AE 平面BCE , 又⊂BE 平面BCE ,∴BE AE ⊥.(2)取DE 的中点P ,连结PA ,PN ,∵点N 为线段CE 的中点,∴PN DC ∥,且DC PN 21=,又四边形ABCD 是矩形,点M 为线段AB 的中点,∴AM DC ∥,且DC AM 21=, ∴PN AM ∥,且AM PN =,∴四边形AMNP 是平行四边形,∴MN AP ∥,而⊂AP 平面DAE ,⊄MN 平面DAE ,∴MN ∥平面DAE .19.【答案】(1)见解析;(2)3+【解析】(1)证明:∵⊥BE 平面ABCD ,⊂AC 平面ABCD ,∴AC BE ⊥. 又∵四边形ABCD 为菱形,∴BD AC ⊥.∵B BE BD = , ∴⊥AC 平面BED ,∵⊂AC 平面AEC ,∴平面⊥AEC 平面BED . (2)∵⊥BE 平面ABCD ,∴AB BE ⊥,BC BE ⊥, ∵BC AB =,∴Rt Rt ABE CBE ≅△△,∴CE AE =. 在Rt ACE △中,22222AE CE AE AC =+=, 又∵22222cos 3AC AB BC AB BC ABC AB =+-⋅∠=,∴2232AB AE =,∴AB AE 26=,∴AB BE 22=, ∴111sin 332E ACD ACD V BE S BE AB BC ABC -=⋅=⋅⋅⋅∠△311sin12032AB AB AB AB =⋅⋅⋅︒=,3=2=AB .∴12ABE CBE S S AB BE ==⨯△△∵EC ED AE ===,2CD AD ==,精品K12教育教学资料∴3ACE S =△,DAE CDE S S ==△△所以该三棱锥的侧面积为3ACE DAE CDE S S S ++=+△△△.20.【答案】(1)见解析;(2)存在且F 是线段PC 的靠近P 点的一个三等分点,见解析. 【解析】(1)连接AC 交BD 于O 点,连接OE ,在APC △中,O 、E 分别为AC ,PC 的中点,∴OE ∥PA ; ∵OE ⊂平面BDE ,PA ⊄平面BDE ,∴PA ∥平面BDE ; (2)∵侧棱PD ⊥⊥底面ABCD ,∴PD CD ⊥,设F 为PC 上一点,过F 作FG CD ⊥于G ,则FG PD ∥,∴FG ⊥平面ABCD .若11133333322C BDF F BDC BDC V V S FG FG FG --==⋅=⨯⨯⨯⨯==△,则2FG =,∴在棱PC 上存在点F 使三棱锥C BDF -的体积为33cm . 且F 是线段PC 的靠近P 点的一个三等分点.21.【答案】(1)见解析;(2)见解析;(3)能,见解析. 【解析】(1)连结BD ,则在正三角形ABD 中,AD BG ⊥, 又平面⊥PAD 平面ABCD 于AD ,所以⊥BG 平面PAD .(2)连结PG ,在正三角形PAD 中,AD PG ⊥,又AD BG ⊥,∴⊥AD 平面PBG . ∵⊂PB 平面PBG ,∴PB AD ⊥.(3)能在PC 上,找到一点F 使平面⊥DEF 平面ABCD ,且F 为PC 中点. 证明如下:连结ED ,GC 交于点O ,易知O 为GC 的中点,在平面PGC 内,作OF GP ∥,交PC 于点F ,则F 为PC 中点,⊥FO 平面ABCD , ∴平面⊥DEF 平面ABCD .22.(12分)如图所示,一个棱柱的直观图和三视图,主视图和俯视图是边长为a 的正方形,左视图是等腰直角三角形,直角边为a .M ,N 分别是AB ,AC 的中点,G 是DF 上的一动点. 【答案】(1)见解析;(2)316a ;(3)见解析.【解析】(1)由三视图可知,多面体是直三棱柱, 且底面是直角边为a 的等腰直角三角形, ∴侧面ABCD ,CDEF 是边长为a 的正方形.连结DN ,因为CD FD ⊥,AD FD ⊥,所以⊥FD 平面ABCD , ∴AC FD ⊥,又∵DN AC ⊥,∴⊥AC 平面GND , ∵⊂GN 平面GND ,∴AC GN ⊥.(2)∵⊥AD 平面CEF ,∴2311113326F MCE M CEF CEF V V AD S a a a --==⋅=⨯⨯=△.(3)连结DE 交FC 于Q ,连结QG ,∵Q ,G 分别是FD ,FC 的中点,∴GQ CD ∥,且12GQ CD =,∵M 是AB 的中点,∴AM CD ∥,且CD AM 21=, ∴AM GQ ∥=,∴AMQC 是平行四边形,∴AG QM ∥,∵⊄AG 平面FMC .⊂MQ 平面FMC ,∴AG ∥平面FMC .。
