数学倍长中线法
倍长中线法经典例题较难

倍长中线法经典例题较难在说到倍长中线法,大家可能会觉得这是什么神秘的东西,其实并没有那么复杂。
想象一下,我们在课堂上,老师拿着一个三角形,指着那根中线,眼睛闪闪发光,像是在说:“看,这就是你们的未来!”这时的我们,或许有点懵,心里想着:“我能干嘛呢?”可这玩意儿就像一块儿美味的蛋糕,切开来让大家分享,越吃越觉得香。
倍长中线法的核心就像是我们生活中的很多道理,简单明了。
想象一个三角形,边边角角都各有千秋,老师告诉我们,长的那条中线就像是三角形的心脏,连接着两个顶点,恰到好处。
这时候,你可能会想:“这和我有什么关系?”可实际上,这就是几何的魅力所在!你看,学习数学就像是打怪升级,每个定理、每条公式都是你在游戏中的技能点,越多越好。
说到倍长中线,得先搞清楚中线是啥。
简单来说,三角形的中线是连接一个顶点和对边中点的线段。
它像个桥,把三角形的两边连成一体,真是个绝佳的搭档。
老师总爱用“中线”来解释一些深奥的道理,仿佛在说:“只要你找到这个点,生活就会变得简单。
”可这条中线可不止是个连接的角色,它还能让我们看见美丽的几何图形之舞,优雅而又有趣。
再说说倍长的意思。
倍长中线法的“倍长”其实就是中线的长度变成了原来的两倍。
这时候,想象一下我们平常买的衣服,如果腰围从30寸变成了60寸,那可就得赶紧去找裁缝了。
这种变化让我们不仅能观察到三角形的变化,更能思考背后隐藏的数学美感。
倍长中线法就像是一种魔法,把简单的三角形变成了充满可能的世界。
有人会问,倍长中线法到底有什么用呢?这就像问“为什么要吃水果”,答案是让我们更健康。
用倍长中线法,我们可以求得三角形的周长、面积,还能算出各种角度。
学会这招,就像拥有了打开数学大门的钥匙。
数学不仅仅是书本上的公式,更是我们生活中的每一个细节。
在解题时,倍长中线法也特别好用。
拿个简单的例子来说,给你个三角形,让你找出它的面积。
用倍长中线法,你只需简单几步,仿佛在解密一样,轻松搞定,心里那种成就感,简直就像是打通了一个难关,爽得不行。
倍长中线法(经典例题)
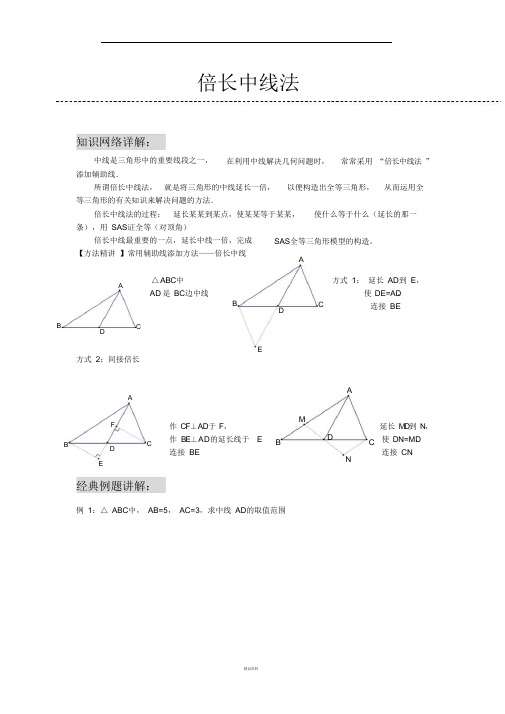
倍长中线法例 1:△ ABC 中, AB=5, AC=3,求中线 AD 的取值范围知识网络详解:中线是三角形中的重要线段之一, 添加辅助线.在利用中线解决几何问题时, 常常采用 “倍长中线法 ”所谓倍长中线法, 就是将三角形的中线延长一倍, 以便构造出全等三角形, 从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程: 延长某某到某点,使某某等于某某, 使什么等于什么(延长的那一条),用 SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成 【方法精讲 】常用辅助线添加方法——倍长中线SAS 全等三角形模型的构造。
AA△ ABC 中 AD 是 BC 边中线BDC方式 1: 延长 AD 到 E ,使 DE=AD ,连接 BEB DCE方式 2:间接倍长AAF 作 CF ⊥ AD 于 F , MDB D C作 BE ⊥ AD 的延长线于 连接 BEE BC 延长 MD 到 N , 使 DN=M ,D 连接 CNEN经典例题讲解:例2:已知在△ABC中,AB=AC,D 在AB上,E 在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CEADBFCE例3:已知在△ ABC中,AD是BC边上的中线, E 是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EFAFEBD C例4:已知:如图,在ABC 中,AB 交AE于点F,DF=AC.求证:AE平分BAC AC ,D、E 在BC上,且DE=EC,过D作DF // BAAFB D E C例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAEABCE D自检自测:1、如图,△ABC中,BD=DC=AC,E是DC的中点,求证,AD平分∠BAE.2、在四边形ABCD中,AB∥DC,E 为BC边的中点,∠BAE=∠EAF,AF 与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论.ADBE CF3、如图,AD为ABC 的中线,DE平分BDA 交AB于E,DF平分ADC 交AC于F. 求证:BE CF EFAEFB CD第14 题图4、已知:如图,ABC中,C=90 ,CM AB于M,AT 平分BAC交CM于D,交BC于T,过D作DE//AB 交BC于E,求证:CT=BE.A MD BETCWelcome To Download !!!欢迎您的下载,资料仅供参考!。
数学倍长中线法
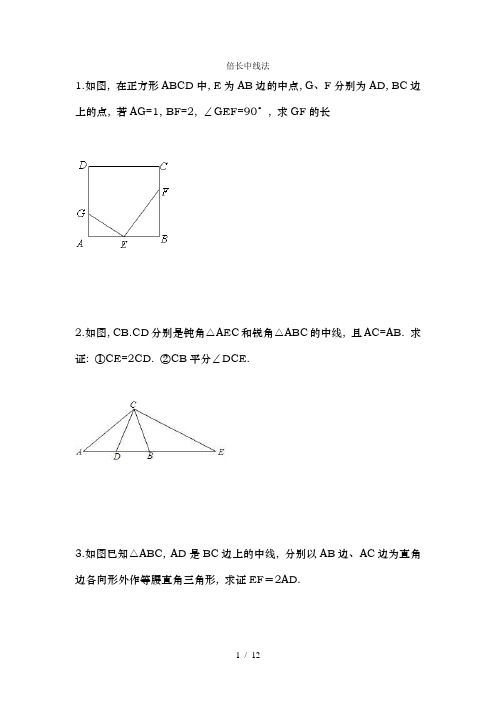
倍长中线法1.如图, 在正方形ABCD中, E为AB边的中点, G、F分别为AD, BC边上的点, 若AG=1, BF=2, ∠GEF=90°, 求GF的长2.如图, CB.CD分别是钝角△AEC和锐角△ABC的中线, 且AC=AB. 求证: ①CE=2CD. ②CB平分∠DCE.3.如图已知△ABC, AD是BC边上的中线, 分别以AB边、AC边为直角边各向形外作等腰直角三角形, 求证EF=2AD.4.如图, 在△ABC中, D是BC边的中点, E是AD上一点, BE=AC, BE 的延长线交AC于点F, 求证: ∠AEF=∠EAF5..如图, 在△ABC中, AD交BC于点D, 点E是BC中点, EF∥AD交CA的延长线于点F, 交EF于点G, 若BG=CF, 求证: AD为△ABC的角平分线.6..如图, △ABC中, BD=DC=AC,E是DC的中点, 求证, AD平分∠BAE.7.: 已知在△ABC中, AB=AC, D在AB上, E在AC的延长线上, DE交BC于F, 且DF=EF, 求证: BD=CEA9.在四边形ABCD 中, AB ∥DC, E 为BC 边的中点, ∠BAE=∠EAF, AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系, 并证明你的结论10.已知: 如图, XXXABC 中, XXXC=90XXX, CMXXXAB 于M, AT 平分XXXBAC 交CM 于D, 交BC 于T, 过D 作DE//AB 交BC 于E, 求证: CT=BE.DABCMTEGDE12.13.四边形ABCD是矩形, 将沿着直线AE翻折, 点A落在点F处, 直线AF与直线CD交于点G,如图1, 若E为BC的中点, 请探究线段AB、AG、DG之间的关系FGB.。
八年级数学全等三角形--倍长中线法经典例题

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC中方式1:延长AD到E,AD是BC边中线使DE=AD,连接BE方式2:间接倍长作CF⊥AD于F,延长MD到N,作BE⊥AD的延长线于使DN=MD,连接BE 连接CN经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE过D 作DG//AC例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠BABFDEC例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.E D ABF EAB C3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.第 14 题图DF CBEADABCMTE。
初中数学全等专题倍长中线法(含答案)

初中数学全等专题倍长中线法1.如图,在△ABC中,AC=5,中线AD=7,则AB边的取值范围是( )<AB<12 <AB<12 <AB<19 <AB<19 答案:C解题思路:延长AD至E,使DE=AD,连接CE,可先证明△ABD≌△ECD,则AB=CE,在△ACE中,根据三角形的三边关系,得AE-AC<CE<AE+AC,即9<CE<19.则9<AB<19.故选C.2.如图,已知CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB,给出下列结论:①AE=2AC;②CE=2CD;③∠ACD=∠BCE;④CB平分∠DCE,则以上结论正确的是()A.①②④B.①③④C.①②③D.①②③④ 答案:A解题思路:①正确,延长CD至点F,使得DF=CD,连接AF,可先证明△ADF≌△BDC,再证明△ACF≌△BEC,由这两个三角形全等可以得知②、④正确。
由△ACF≌△BEC,得∠ACD=∠E,若要∠ACD=∠BCE,则需∠E=∠BCE,则需BC=BE,显然不成立,故③选项错误3.如图,点E是BC的中点,∠BAE=∠CDE,延长DE到点F使得EF=DE,连接BF,则下列说法正确的是()①BF∥CD ②△BFE≌△CDE ③AB=BF ④△ABE为等腰三角形A.①②③B.②③④C.①③④D.①②③④ 答案:A解题思路:可以先证明△BEF≌△CED,可以得到②正确,进而得到∠F=∠D,BF∥CD,①正确,又∵∠BAE=∠CDE=∠F,∴AB=BF,③正确。
④不正确。
4.如图,在正方形ABCD中,E为AB边的中点,G、F分别为AD,BC边上的点,若AG=1,BF=2,∠GEF=90°,则GF的长为()答案:C解题思路:延长FE交DA的延长线于点M,则可证△AEM≌△BEF,再证明△GEM≌△GEF,可以得到GF=GM=GA+BF=3,答案选C5.如图,在△ABC中,点D、E为边BC的三等分点,则下列说法正确的有()①BD=DE=EC ②AB+AE>2AD ③AD+AC>2AE ④AB+AC>AD+AE 个个个个答案:D解题思路:点D、E为边BC的三等分点,∴BD=DE=CE延长AD至点M,AE至点N,使得DM=AD,EN=AE,连接EM、CN,则可证明△ABD≌△MED,进而可得AB+AE>2AD,再证明△ADE≌△NCE,进而可得AD+AC>2AE,将两式相加可得到AB+AE+AD+AC>2AD+2AE,即AB+AC>AD+AE.∴①②③④均正确。
初中数学倍长中线法,经典题型解析

初中数学倍长中线法,经典题型解析《初中数学倍长中线法》小朋友们,今天我来给大家讲讲初中数学里一个很有趣的方法,叫倍长中线法。
比如说,有一个三角形,中间有条中线把三角形分成了两半。
那如果我们把这条中线延长一倍,会发生什么神奇的事情呢?就像有一次,小明在做数学题的时候,遇到了一个三角形,怎么都解不出来。
后来老师告诉他可以用倍长中线法,他一试,哇,一下子就找到答案啦!其实啊,倍长中线法就像是给我们打开了一扇神奇的门,能让我们更容易地解决三角形的问题。
只要我们认真学,也能像小明一样变得很厉害哟!小朋友们,你们学会了吗?再给大家讲一个例子。
小花也遇到了一个三角形的难题,怎么都想不明白。
后来她想到了倍长中线法,把中线延长一倍后,她突然就发现了其中的秘密,很快就把题目做出来啦。
所以呀,这个倍长中线法真的很有用,大家要好好记住哦!《初中数学倍长中线法》小朋友们,今天咱们来认识一个初中数学里的好方法,叫倍长中线法。
举个例子,假如有个三角形,就像一个小蛋糕被切成了两半,中间切的那一刀就是中线。
那如果我们把这中线变得更长,两倍那么长,会怎么样呢?有个叫小军的同学,数学题总是做不好。
有一次碰到一个三角形的题目,怎么都解不出来,急得都快哭了。
这时候老师教了他倍长中线法,小军一下子就明白了,很快就把答案算出来了,高兴得又蹦又跳。
再比如说,小美的数学也不太好。
有一回考试,就有一道三角形的题,她不会。
后来老师讲了倍长中线法,小美记住了,下次再遇到类似的题,一下子就做出来啦。
所以呀,倍长中线法能帮我们解决很多三角形的难题,小朋友们以后上了初中可要好好学哟!《经典题型解析》小朋友们,今天来给大家讲讲数学里的经典题型。
比如说,有这样一道题:小明有 5 个苹果,小红的苹果比小明多3 个,那小红有几个苹果呀?这是不是很简单?其实经典题型就是这样,看着不难,但能让我们学会很多知识。
还有一次,老师出了一道题:树上有 10 只鸟,飞走了 3 只,又飞来了 2 只,现在树上有几只鸟?小朋友们都积极思考,很快就算出了答案。
八年级数学全等三角形--倍长中线法经典例题

八年级数学全等三角形--倍长中线法经典例题中线是三角形中的重要线段之一。
为了解决几何问题,常常采用“倍长中线法”添加辅助线。
倍长中线法的过程是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题。
倍长中线最重要的一点是延长中线一倍,完成SAS全等三角形模型的构造。
常用的辅助线添加方法有两种:一是将中线延长到某一点,使其等于另一条边,然后连接这两个点构造全等三角形;二是通过作垂线和延长线来间接倍长中线。
例1:在△ABC中,已知AB=5,AC=3,求中线AD的取值范围。
例2:在△ABC中,已知AB=AC,D在AB上,E在AC 的延长线上,DE交BC于F,且DF=EF,求证BD=CE。
例3:在△ABC中,已知AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证AF=EF。
例4:在△ABC中,已知AB≠AC,D、E在BC上,且DE=EC。
过D作DF//BA交AE于点F,DF=AC。
求证AE平分∠BAC。
例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证∠C=∠BAE。
自检自测:1、在△ABC中,已知BD=DC=AC,E是DC的中点,求证AD平分∠BAE。
2、在四边形ABCD中,已知AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论。
3、在△ABC中,已知AD为中线,DE平分∠BDA交AB于E,DF平分∠ADC交AC于F。
求证BE+CF>EF。
4、在直角△ABC中,已知CM⊥XXX于M,AT平分∠BAC交CM于D,交BC于T,XXX于E。
求证CT=BE。
倍长中线法经典例题

倍长中线法经典例题倍长中线法是一种常见的数学解题方法,运用它可以轻松解决很多简单的数学问题。
这种方法也被称作双倍长中线法,下面我们就这一方法来讲解一下,以帮助大家迅速掌握该方法,并应用于实际问题中。
倍长中线法的具体操作步骤如下:1.需要求解的数学问题转化为倍长的等式(如:x=a+b+c),其中a、b、c均为常数;2.出倍长等式对应的图形,其中x表示一条中线,长度为2a+2b+2c;3. 从图形上画出相等的三角形,分别用1、2、3标记,其中:三角形1的边长等于a+2b+2c,三角形2的边长等于2a+b+2c,三角形3的边长等于2a+2b+c;4.三角形1、2、3平移至倍长等式中,依次放置左边,中间,右边,即倍长等式变为:a+2b+2c=1,2a+b+2c=2,2a+2b+c=3;5.三角形1、2、3进行运算,得出结果,即a=1,b=1,c=1。
通过以上操作,我们可以得出结果,即:x=a+b+c=1+1+1=3。
以上就是倍长中线法的具体操作步骤,下面来看一个实际的例子,来详细说明倍长中线法的用法。
例题一:已知a=2,求x的值解:将原等式x=a+b+c转化为倍长等式:2a+2b+2c=x,其中a =2,即2×2+2b+2c=x,画出对应的图形,用1、2、3表示三角形,其边长分别为4+2b+2c,4+b+2c,4+2b+c,并将三角形移动至倍长等式中,即4+2b+2c=1,4+b+2c=2,4+2b+c=3,再依次运算,可得到:b=1,c=1,从而可得出:x=2a+2b+2c=2+2+2=6。
以上就是倍长中线法的简单介绍和经典例题,大家可以结合实际问题来练习,以加深对该方法的理解,掌握运用倍长中线法轻松解决各类数学问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倍长中线法
1. 如图,在正方形 ABCD中,E为AB边的中点,G、F分别为AD, BC边上的点,若AG=1, BF=2,
/ GEF=90,求 GF 的长
2. 如图,CB、CD分别是钝角 △ AEC和锐角△ ABC的中线,且 AC=AB.求证:①CE=2CD②CB平 分/
DCE.
3. 如图已知△ ABC, AD是BC边上的中线,分别以 AB边、AC边为直角边各向形外作等腰直角三 角形,
求证EF= 2AD.
C
4. 如图,在 △ ABC中,D是BC边的中点,E是AD上一点,BE= AC, BE的延长线交 AC于点F, 求
证:/ AEF=Z EAF
5..如图,在 △ ABC中,AD交BC于点D,点E是BC中点,EF// AD交CA的延长线于点 F,交EF 于点G,
若BG=CF,求证:AD ABC的角平分线.
6..如图,△ ABC中,BD=DC=AC,E是 DC 的中点,求证, AD平分/ BAE.
7.:已知在△ ABC中,AB=AC, D在AB 上, E在AC的延长线上,
BD=CE
DE交BC于F,A且DF=EF,求证:
A
D
F
Sfiffl:如图,在中,AB^AC, D、E在EC 上,且 DE=EC,过D 作 DF1/BA交
AE 于点F,DW|
求证! AE平分乙嘶
9.
在四边形 ABCD中,AB// DC, E为BC边的中点,/ BAE=/ EAF, AF与DC的延长线相交于点 F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论
10.
已知:如图, ABC 中,C=90,CMAB 于 M, AT 平分 BAC 交CM于D,交BC于T,过D作DE
第1题图
D
B
C
11. "眈中,分别以AB、AC芮直角边向外做等膜直角三弟三角形MBD、^ACS, F
0C中舄FA朗延畏线交DE于点G,求证匕DE=2AF,氏口丄DE
12.
12如图空 3C中,&二勿:D为斜边EC的中点,E, F分别九AB, AC ±的貳 且
药丄若BE* CF-4
(
试求ET的长,
13.四边形ABCD是矩形,将 VABE沿着直线AE翻折,点A落在点F处,直线AF与直线CD交
于点G,
如图1,若E为BC的中点,请探究线段 AB、AG、DG之间的关系
15如图'是佔亡的中线I ^=k-AC,点卫是用亡延长线上一点,且厶&戸=如耳
即农珈延长銭于点F.採究丿E.卫尸的敌量关系.
17如图,等搀直角 3C与等睡直角ABDE9 P为CE中点连接刊、PD 探究阳、肋的关系.
]8 如图,AAEC 与 LBDE 中,ZCXB= Z.BDE =90°, AC^ k-ABf DE = k -DB 9 P 为 CE 中
点,连接血、PD.
探究刃1、卩D的数董关系.
A
1
19•如图,两个正方^ABDE^ACGF,点卩为的中点,连接刊交EF于点0 探究曲与商的关系.
20.⑴如图1,两个矩形ABDE^ ACGF相似,AE^k-AB,点F为眈的中点,连接血交EF
于点◎探究AP^EF的关系.
(2劝图2,若将'俩个矩形肋D陋加®相似”改为“两几平行四辺形ABDE^ ACGF^ 似匕 且Z^ = a.
探究处与防的关系.
« 1
B
图
2
2L已知:如图,正牙形廊J和正方形朋点M是线段DF的中点 试说明线段砲与恥的关系.
22.如图,若将上题中正芳形阳前绕点8顺时针旋转a度数(乂《90。),其他条件不变,上 述
结论还正确吗?若正确,请你证朋;若不正确,请说明理由.
23•如图1,正右形肋UD中,对角线力C、0Q交于点
操作:将三第板中的% °肃的顶点与点°重合,使这个角落注倔C的內部,两边分别与正 方形
朋QD的边.肋、交于只 罗当几 左的位置发生变化时,诘你通过测量并回答, 鉛纽加\ FE、聽
三条銭段中,哪一条线段是中始终最长
1
24. 在23题条件下,以人〃、血、EC这三条线段能否生成以FE为斜边的直甬三角形? 若能.
谣你证明;若不能,谣你说明理由.
25. 探究如图2, AXPC, ZB.90-,点0是斜线71C的中為 当90。角的顶点与点。重合, 便这个角在
仙C的內部绕点O转动时,⑵中的结论是否仍然成立?请你证日月
26. (1)如图1,操作:把正方形CGM的对角线皿啟在正方^ABCD的边比的延长线上( CG>BC}
取鮭段应的中占P
探究 线段pQ' PF的关系,并加以证明.
(2曲图2将正椰C関F绕点C旋转任意角度后,其他条件不变.探究:线段"、卅的 关系,并加以
证明.
图
1
B
图
2 &
刃•已知△ABC, AQ杲BC辺上的屮线,分别以AB辺、At辺沖直角辺各向外作寻腰宜角 三角
形,如图5・2,求证EF=2AD.
图5- 2
28•如图 7,在4ABC 中,ZBAC=90° , AB = AC. M 是 AC 边的中点。ADIBM^BC 于 D,交 BM
于 E。求证:ZAMB = ZDMC.
29•已知:如图,D为线段AB的中点,在AB ±任取一点C (不与点A, B, D重合),分别 以
AC, BC为斜边在AB同测作等曉RtZkACEZ等腫RtABCF, ZAEJZCFBTO。,连 接 DE, DF,
EF・
求证:ADEF汁弄彌直伯三伯彫.
30.在四边形ABCD中.AB〃DC\ E为BC边的中点、,NBAE=2EAF, AF与DC的延檢线 相交于点
F.试探究线段Ab与AF、CF之「可的数垦关系,并证明你的结I它。
