(完整版)倍长中线法(经典例题)
倍长中线法(经典例题)

倍长中线法知识网络详解:中线是三角形中的重要线段之一,中线是三角形中的重要线段之一,在利用中线解决几何问题时,在利用中线解决几何问题时,在利用中线解决几何问题时,常常采用常常采用“倍长中线法”添加辅助线.添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,就是将三角形的中线延长一倍,以便构造出全等三角形,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.等三角形的有关知识来解决问题的方法.倍长中线法的过程:倍长中线法的过程:延长某某到某点,使某某等于某某,延长某某到某点,使某某等于某某,延长某某到某点,使某某等于某某,使什么等于什么(延长的那一使什么等于什么(延长的那一条),用SAS 证全等(对顶角)证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC 中 方式1: 延长AD 到E ,AD 是BC 边中线边中线 使DE=AD ,连接BE 方式2:间接倍长:间接倍长作CF ⊥AD 于F , 延长延长MD 到N ,作BE ⊥AD 的延长线于E E 使使DN=MD DN=MD,, 连接BE 连接CN 经典例题讲解:经典例题讲解:例1:△ABC 中,AB=5,AC=3,求中线AD 的取值范围的取值范围D ABCE DAB C F EDC B AN DC B AM例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE 例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF 例4:已知:如图,在ABC D 中,AC AB ¹,D 、E 在BC 上,且DE=EC DE=EC,过,过D 作BA DF //交AE 于点F ,DF=AC.DF=AC.求证:AE 平分BAC ÐFED ABCFEC ABD AB F D E C例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△是△ABD ABD 的中线,求证:∠C=∠BAE 自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE. 2、在四边形ABCD 中,AB ∥DC DC,,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
倍长中线法证明全等例题

选择题在三角形ABC中,AD是中线,倍长AD至点E,连接BE,若要证明三角形ADC与三角形EDB 全等,需要添加的条件是?A. 角ADC = 角EDBB. AD = BDC. 角CAD = 角EBD(正确答案)D. AC = BE已知三角形ABC中,D是BC的中点,AD是中线,延长AD至E使得DE = AD,连接BE。
若角ADC = 角EDB,则下列哪一对三角形全等?A. 三角形ABD与三角形ECDB. 三角形ADC与三角形EDB(正确答案)C. 三角形ABC与三角形EBDD. 三角形ABD与三角形EBD在三角形ABC中,D为BC的中点,AD为中线。
延长AD到E,使得DE = AD,连接BE。
若AC平行于BE,则下列结论正确的是?A. 三角形ADC与三角形EDB不全等B. 三角形ADC与三角形EDB全等(正确答案)C. 三角形ABC与三角形EBD全等D. 无法判断三角形ADC与三角形EDB的全等关系在三角形ABC中,D是BC的中点,AD是中线。
延长AD到E,使得DE = AD,连接BE。
若要证明三角形ADC全等于三角形EDB,可依据的判定定理是?A. SSSB. ASAC. SAS(正确答案)D. AAA已知三角形ABC,D为BC的中点,AD为中线。
延长AD至E,使DE = AD,连接BE。
若角C = 角E,则下列哪一对三角形一定全等?A. 三角形ABD与三角形ECDB. 三角形ABC与三角形EBDC. 三角形ADC与三角形EDB(正确答案)D. 三角形ABC与三角形ADC在三角形ABC中,D是BC的中点,AD是中线。
延长AD到E,使得DE = AD,连接BE。
若三角形ADC与三角形EDB全等,则它们的对应角一定相等,即?A. 角ADC = 角EBD(正确答案)B. 角ADC = 角EDCC. 角CAD = 角CDED. 角BAC = 角E已知三角形ABC,D是BC的中点,AD是中线。
延长AD至E,使得DE = AD,连接BE。
倍长中线最全总结 例题+练习(附答案)
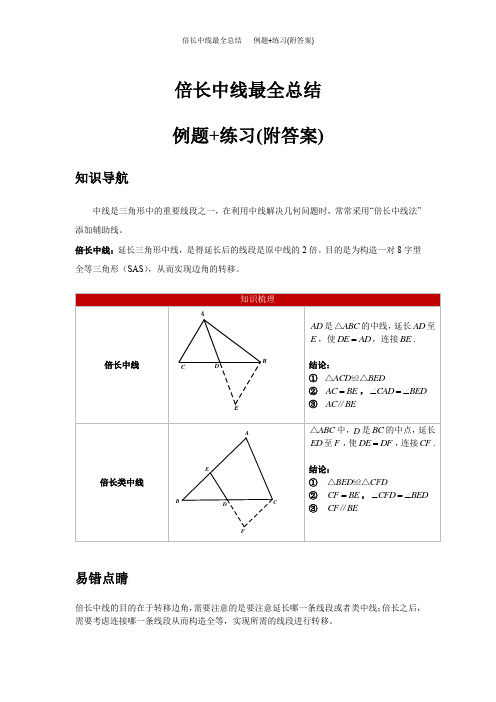
倍长中线最全总结 例题+练习(附答案)知识导航中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线。
倍长中线:延长三角形中线,是得延长后的线段是原中线的2倍。
目的是为构造一对8字型全等三角形(SAS ),从而实现边角的转移。
易错点睛倍长中线的目的在于转移边角,需要注意的是要注意延长哪一条线段或者类中线;倍长之后,需要考虑连接哪一条线段从而构造全等,实现所需的线段进行转移。
DAB C模块一 有关倍长中线的全等模型【范例】(2014秋•江汉区校级月考)如图,在ABC ∆中,AD 为中线,求证:2AB AC AD +>.【分析】延长AD 至E ,使DE AD =,构造ADC EDB ∆≅∆,再根据三角形的三边关系可得 2AB AC AD +>。
【解答】证明:由BD CD =,再延长AD 至E ,使DE AD =,D 为BC 的中点,DB CD ∴=,在ADC ∆和EDB ∆中AD DE ADC BDE DB CD =⎧⎪∠=∠⎨⎪=⎩,()ADC EDB SAS ∴∆≅∆, BE AC ∴=,在ABE ∆中,AB BE AE +>,2AB AC AD ∴+>;BB【核心考点1】倍长中线1.(2016秋•五莲县期中)如图,ABC ∆中,D 为BC 的中点. (1)求证:2AB AC AD +>;(2)若5AB =,3AC =,求AD 的取值范围.【分析】(1)再延长AD 至E ,使DE AD =,构造ADC EDB ∆≅∆,再根据三角形的三边关 系可得2AB AC AD +>;(2)直接利用三角形的三边关系:三角形两边之和大于第三边,三角形的两边差小于第三 边可得53253AD -<<+,再计算即可. 【解答】(1)证明:由BD CD =,再延长AD 至E ,使DE AD =,D 为BC 的中点,DB CD ∴=,在ADC ∆和EDB ∆中AD DEADC BDE DB CD =⎧⎪∠=∠⎨⎪=⎩,()ADC EDB SAS ∴∆≅∆, BE AC ∴=,在ABE ∆中,AB BE AE +>,2AB AC AD ∴+>;(2)5AB =,3AC =,53253AD ∴-<<+,14AD ∴<<.ABC2.如图,ABC ∆中,BD DC AC ==,E 是DC 的中点,求证:AD 平分BAE ∠.【分析】延长AE 到M ,使EM AE =,连结DM ,由SAS 证明DEM CEA ∆≅∆,得出C MDE ∠=∠,DM AC =,证出DM BD =,ADM ADB ∠=∠,由SAS 证明ADB ADM ∆≅∆,得出BAD MAD ∠=∠即可.【解答】证明:延长AE 到M ,使EM AE =,连结DM ,如图所示:E 是DC 的中点,DE CE ∴=,在DEM ∆和CEA ∆中,EM AE DEM CEADE CE =⎧⎪∠=∠⎨⎪=⎩,()DEM CEA SAS ∴∆≅∆, C MDE ∴∠=∠,DM AC =,又BD DC AC ==,DM BD ∴=,ADC CAD ∠=∠,又ADB C CAD ∠=∠+∠,ADM MDE ADC ∠=∠+∠,ADM ADB ∴∠=∠,在ADB ∆和ADM ∆中,AD AD ADB ADMBD DM =⎧⎪∠=∠⎨⎪=⎩,()ADB ADM SAS ∴∆≅∆,BAD MAD ∴∠=∠,即AD 平分BAE ∠。
倍长中线法(经典例题)

N作 BE! AD 的延长线于倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时, 常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全 等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么 等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模 型的构造。
【方法精讲】常用辅助线添加方法倍长中线△ ABC 中式1:延长AD 到E,B --------------- ■ ------------- CDAD 是E BC使 DE=AD接BE方式2:间接倍长 AB 延长MD 到N, CE连接CN 经典例题讲解:例〔:△ ABC 中,AB=5 AC=3求中线 AD 的取值范围例2:已知在△ ABC 中,AB=AC D 在AB 上,E 在AC 的延长线上,DE 交 BC 于 F ,且 DF=EF 求证:BD=CE例3:已知在△ ABC 中 , AD 是 BC 边上的中线,E 是AD 上一点,且BE 二AC例4:已知:如图,在- ABC 中,AB = AC , DE 在 BC 上 ,且 DE 二EC 过 D 作 DF//BA 交 AE 于点 F , DF=AC.例 5:已知 CD=AB Z BDA M BAD AE 是A ABD 的中线,求证:/ C=Z BAE自检自测:1、如图,△ ABC 中 , BD=DC=AC,是 DC 的中点,求证,AD 平分/ BAE.使 DN=M ,BE延长BE 交AC 于F ,求证:AF=EF求证:AE 平分.BACDEAECCFAC2、在四边形ABCD K AB// DC E 为BC 边的中点,/ BAE K EAF AF与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关 系,并证明你的结论.3、如图,AD 为 MBC 的中线,DE 平分.BDA 交AB 于E,DF 平分.AD 交 AC 于 F.求证:BE CF EF4、已知:如图, ABC 中, C=90,CM AB 于 M AT 平 分 BAC 交 CM 于 D,交 BC 于 T ,过 D 作 DE//AB 交 BC 于 E ,求证:CT=BE.ADBF。
倍长中线最全总结。例题+练习(附答案)

倍长中线最全总结。
例题+练习(附答案)中线是三角形中的重要线段之一。
在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线。
倍长中线指的是延长三角形中线,使得延长后的线段是原中线的2倍。
其目的是为了构造一对8字型全等三角形(SAS),从而实现边角的转移。
以三角形ABC为例,延长中线AD至点E,使得DE=AD,连接BE。
根据三角形的SAS全等条件,可以得出结论:△ACD≌△BED,AC=BE,∠CAD=∠BED,AC∥BE。
同样地,延长中线CD至点F,使得DE=DF,连接CF。
根据三角形的SAS全等条件,可以得出结论:△BED≌△CFD,CF=BE,∠CFD=∠BED,CF∥BE。
在利用倍长中线法时,需要注意延长哪一条线段或者类中线。
倍长之后,需要考虑连接哪一条线段从而构造全等,实现所需的线段进行转移。
举例来说,如图所示,在三角形ABC中,需要证明AB+AC>2AD。
延长中线AD至点E,使得DE=AD,构造△ADC和△EDB,根据三角形的三边关系可得AB+AC>2AD。
另外,还有一道题目是需要求解AD的取值范围。
在三角形ABC中,D为BC的中点。
根据三角形的三边关系可得5-3<2AD<5+3,即AD的取值范围为1<AD<4.证明:延长AD到F,使DF=AD,连接BF(如图)。
因为AD是中线,所以BD=DC=AC,又因为DF=AD,所以BD=BF,所以AB>BF。
由三角形的三边关系,在三角形ABF中,有AB+BF>AF,即2AD<AB+AC,证毕。
2)因为AD是中线,所以BD=DC=AC,又因为DF=AD,所以BD=BF,所以AB>BF。
由相似三角形ADC和FDB,得到∠CAD=∠F,由边的大小关系可得到∠BAD>∠DAC,证毕。
3)同(2),由相似三角形ADC和FDB,得到AE/AD=BF/BD<1,即AE<AD,证毕。
倍长中线法经典例题

倍长中线法(加倍法)知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围。
例2:已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于F,且DF=EF,求证:BD=CE例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE第 14 题图DF CBEAB自检自测:1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE 。
2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.3、已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC.求证:AE 平分BAC ∠F EAB C DABFDEC4、如图,CB、CD分别是钝角△AEC和锐角△ABC的中线,且AC=AB.求证:①CE=2CD.②CB平分∠DCE.5、如图已知△ABC,AD是BC边上的中线,分别以AB边、AC边为直角边各向形外作等腰直角三角形,求证EF=2AD.4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.倍长中线法(加倍法)知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS 证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS 全等三角形模型的构造。
倍长中线法(经典例题)

倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC中方式1:延长AD到E, AD是BC边中线使DE=AD,连接BE方式2:间接倍长作CF⊥AD于F,延长MD到作BE⊥AD的延长线于使DN=MD,连接BE 连接CN经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE过D 作DG//AC例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC,延长BE 交AC 于F,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠BABFDEC例5:已知CD=AB ,∠BDA=∠BAD,AE 是△ABD 的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证,AD 平分∠BAE.2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论。
E DABF EAB C3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F 。
倍长中线法(经典例题)
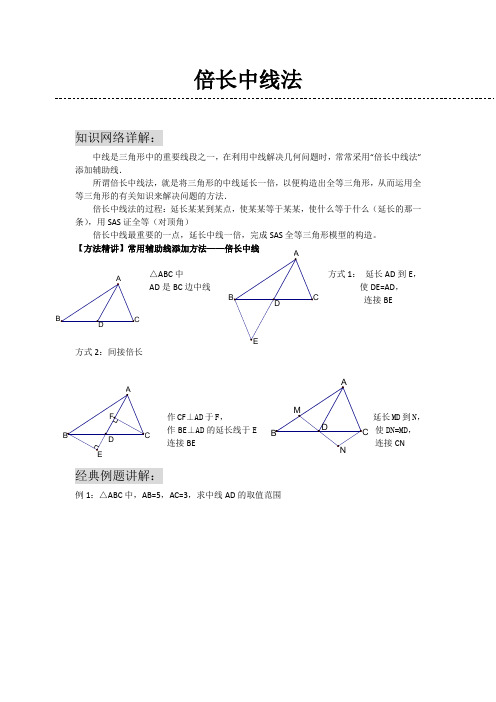
倍长中线法知识网络详解:中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线△ABC中方式1:延长AD到E,AD是BC边中线使DE=AD,连接BE方式2:间接倍长作CF⊥AD于F,延长MD到N,作BE⊥AD的延长线于使DN=MD,连接BE 连接CN经典例题讲解:例1:△ABC中,AB=5,AC=3,求中线AD的取值范围例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE过D 作DG//AC例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠BABFDEC例5:已知CD=AB,∠BDA=∠BAD,AE是△ABD的中线,求证:∠C=∠BAE自检自测:1、如图,△ABC中,BD=DC=AC,E是DC的中点,求证,AD平分∠BAE.2、在四边形ABCD中,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F。
试探究线段AB与AF、CF之间的数量关系,并证明你的结论.ABFEAB C3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.(范文素材和资料部分来自网络,供参考。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
倍长中线法
知识网络详解:
中线是三角形中的重要线段之一,在利用中线解决几何问题时,常常采用“倍长中线法”添加辅助线.
所谓倍长中线法,就是将三角形的中线延长一倍,以便构造出全等三角形,从而运用全等三角形的有关知识来解决问题的方法.
倍长中线法的过程:延长某某到某点,使某某等于某某,使什么等于什么(延长的那一条),用SAS证全等(对顶角)
倍长中线最重要的一点,延长中线一倍,完成SAS全等三角形模型的构造。
【方法精讲】常用辅助线添加方法——倍长中线
△ABC中
方式1:延长AD
到E,AD是BC边中线
使DE=AD,
连接BE
方式2:间接倍长
作CF⊥AD于F,延长MD到N,
作BE⊥AD的延长线于使DN=MD,
连接BE 连接CN
经典例题讲解:
例1:△ABC中,AB=5,AC=3,求中线AD的取值范围
例2:已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于F ,且DF=EF ,求证:BD=CE
例3:已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF
例4:已知:如图,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠
B
A
B
F
D
E
C
例5:已知CD=AB ,∠BDA=∠BAD ,AE 是△ABD 的中线,求证:∠C=∠BAE
自检自测:
1、如图,△ABC 中,BD=DC=AC,E 是DC 的中点,求证,AD 平分∠BAE.
2、在四边形ABCD 中,AB ∥DC ,E 为BC 边的中点,∠BAE=∠EAF ,AF 与DC 的延长线相交于点F 。
试探究线段AB 与AF 、CF 之间的数量关系,并证明你的结论.
E D A
B
F E
A
B C
3、如图,AD 为ABC ∆的中线,DE 平分BDA ∠交AB 于E ,DF 平分ADC ∠交AC 于F. 求证:EF CF BE >+
4、已知:如图,∆ABC 中,∠C=90︒,CM ⊥AB 于M ,AT 平分∠BAC 交CM 于D ,交BC 于T ,过D 作DE//AB 交BC 于E ,求证:CT=BE.
第 14 题图
D
F C
B
E
A
D
A
B
C
M
T
E。
