第5章 列联表分析与对数线性模型
对数线性模型

对于分类数据的分析,最简单也是最广泛使用的是卡方检验,但卡方检验在处理分类数据时,有两个局限:1.卡方检验只能简单描述变量间的相关关系,而无法分析出具体的因果关系或变量间相互作用(效应)大小2.卡方检验通常用于2*2列联表,而对于高维列联表,则无法系统的评价变量间的关系,而对数线性模型则是分析高维列联表的常用方法。
基于以上问题,我们除了可以使用Logistic模型之外,还可以使用对数线性模型进行分析。
对数线性模型的结构类似于方差分析,思想也和方差分析一样,不同的是方差分析用于连续变量,而对数线性模型用于分类变量。
在方差分析中,观测值y 的变异由各因素的主效应、各因素之间的交互效应、随机误差三者之和组成。
而对于分类变量也可以采用这种方法进行分解,只不过此时的观测值y为频数而不是实际的观测值,最终观测值变异的组成也不是相加关系,而是乘积关系。
以两个分类变量α、β为例:M ij代表第i行第j列的频数αi代表变量α的主效应βj代表变量β的主效应(αβ)ij代表变量αβ的交互作用εij代表随机误差分类数据的频数分布一般分为多项式分布、二项式分布、泊松分布,取值在0—+∞之间,因此等式两边都取其对数ln,这样可以使期望频数取值在-∞—+∞,这就是所谓的对数线性模型。
模型的独立参数和自由度:独立参数个数=分类数-限制条件数数据提供的信息量=列联表中网格的数量模型自由度=信息量-独立参数个数对数线性模型的一个假设前提是:每个分类变量各水平的效应之和等于0========================================== ===对数线性模型的统计检验:对数线性模型的假设检验都是基于Pearson卡方检验和似然比卡方检验L2,当样本规模较大时,这两个统计值很接近,但似然比卡方更加稳健1.对模型的整体检验也就是拟合优度检验,两种卡方的零假设是:检验模型的频数估计与观测频数无差异,也就是拟合度良好2.分层效应检验类似于逐步回归的筛选自变量,分层效应检验就是逐步筛选交互作用,每剔除一种交互作用,就检验一次,主要是:某一阶及更高阶所有交互作用项的集体检验,检验是否显著表明这一阶及更高阶中是否至少有一项分类的效应是有意义的。
08列联表及对数线性模型

下面就是SPSS计算机对于这个问题的输出
Chi-Square Tests Value 20.456a 21.190 20.713 20.290
b
df 2 2 1
Pearson Chi-Square Likelihood Ratio Fisher's Exact Test Linear-by-Linear Association N of Valid Cases
•研究列联表的一个主 要目的是看这些变量 是否相关。比如前面 例子中的收入和观点 是否相关。 •这需要形式上的检验
二维列联表的检验
• 下面表是把该例的三维表简化成只有收入 和观点的二维表(这是SPSS自动转化 的:Analyze-Descriptive StatisticsCrosstabs-…..).
(多项分布)对数线性模型
• 注意,这里的估计之所以打引号是 因为一个变量的各个水平的影响是 相对的, • 只有事先固定一个参数值(比如 1=0),或者设定类似于Si=0这样 的约束,才可能估计出各个的值。 • 没有约束,这些参数是估计不出来 的。
(多项分布)对数线性模型
• 二维列联表的更完全的对数线性模型为
二维列联表的检验
• 聪明的同学必然会问,既然有精确检 验为什么还要用近似的2检验呢? • 这是因为当数目很大时,超几何分布 计算相当缓慢(比近似计算会差很多 倍的时间);而且在计算机速度不快 时,根本无法计算。因此人们多用大 样本近似的2统计量。而列联表的有关 检验也和2检验联系起来了。
具体运算:先加权,加权之后,按照次序选 Analyze-Descriptive Statistics-Crosstabs。 在打开的对话框中,把opinion和income分别选入 Row(行)和Column(列);至于哪个放入行或 哪个放入列是没有关系的。 如果要Fisher精确检验则可以点Exact,另外在 Statistics中选择Chi-square,以得到2检验结果。 最后点击OK之后,就得到有关Pearson 2统计量、 似然比2统计量以及Fisher统计量的输出了(这里 的Sig就是p-值)。
对数线性模型

此模型包括主效应、因素A与B的交互作用,称为饱和模 型(saturated model)。
如果模型中的交互项为0,则模型为
此 模型称为不饱和模型(unsaturated model)或简约模 型(reduced model)。
在对数线性模型中,通过交互效应项反映各因素是否有关 及其效应大小。
•对数线性模型不区分各因素为因变量和自变量,综合考虑
通过迭代法估计一组参数(0, 1 , 2 ….. m),使L达 到最大。
4.模型及自变量的统计检验 (1)模型检验(拟合优度检验):当P>0.05,说明可以
接受拟合的模型。
•似然比检验(the likelihood ratio test)
•Pearson卡方检验
评价模型拟和的好坏:大多数单元格的标准化残差或调整 残差的 绝对值小于2。
四种独立性间的关系
•若A、B、C相互独立,则一定有A与B、C联合独立,B与A、
C联合独立,且C与A、B联合独立。
•若C与A、B联合独立,则一定有C与A、C与B边际独立,并 有给定A,C与B条件独立;给定B,C与A条件独立。 •注意:若A、B条件独立,则不一定有A、B边际独立;A、 B边际独立;也不一定有A、B条件独立。
结论:
生育史与工作姿势无关,与是否子宫后倾也无关,但工 作姿势(是坐姿还是立姿)与子宫是否后倾有关,不过这种 关系不受生育史状态影响(即有、无生育史并不影响工作 姿势与子宫后倾的关系)。
变量间的四种独立性
• 边际独立(marginally independent):不考虑 A的影响下,
X与Y对给定Z条件独立,此资料属于条件独立模型(XZ,YZ)。
ORXY=(7/42)/(76/849)=1.86
对数线性模型剖析

极大似然法与最小二乘法的区别于联系
最小二乘法所要解决的问题是:为了选出似的模型输出 与系统输出尽可能接近的参数估计,用误差平方和即离 差平方和的大小来表示接近程度。使离差平方和最小的 参数值即为估计值。简单来说,已知点,自己拟合模型 也即分布函数(概率密度函数的积分),进行预测。
极大似然估计所要解决的问题是:选择参数Ɵ,使已知 数据在某种意义下最可能出现。某种意义指的是似然函 数最大,此处似然函数就是概率密度函数。也就是经常 提到的“模型已知,参数未定”。
对数线性模型的统计检验
举例说明:
由图可知,自由度变为1,L2由0增大到10.284,显著性水平α为0.01(P)(拒绝原假设), 说明简略模型和饱和模型存在十分显著的差异,即拟合程度受到很大影响。 显著=不能剔除该交互因素 在因素很多的复杂饱和模型中,通过此方法删减多个不显著效应项来形成简略模型。
上两式的数学变换使各种效应项相乘的关系被转换成相 加的关系,使各项效应独立化了。
常数效应;
A因素效应;
B因素效应;(主效应)
A、B两因素的交互效应;
主效应和多元交互列表涉及因素数量相等;
交互效应的总数则为所有因素各阶组合数之和。
对数线性模型有一个限制条件:
模型中每一项效应的各类参数之和等于0; 如果每项效应中只有一类的参数未知,那么可以由已知参数推 算出来。
ɯ1=π12/π11
ɯ2=π22/π21
同理我们可以测量两个两个类别间的比值,称作比数比。
Ɵ= ɯ1/ ɯ2=π22π21/π12π21=F11 F22/ F12 F21 一个大于1 的比数比意味着行变量和列变量的第二个(或者第一个) 存在正相关;等于1无关;小于1负相关。
第5章列联表分析与对数线性模型
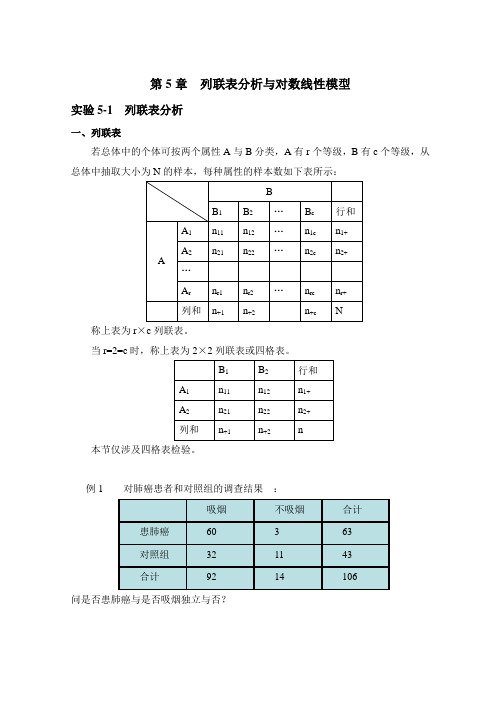
第5章列联表分析与对数线性模型实验5-1 列联表分析一、列联表若总体中的个体可按两个属性A与B分类,A有r个等级,B有c个等级,从总体中抽取大小为N的样本,每种属性的样本数如下表所示:称上表为r×c列联表。
当r=2=c时,称上表为2×2列联表或四格表。
本节仅涉及四格表检验。
例1 对肺癌患者和对照组的调查结果:问是否患肺癌与是否吸烟独立与否?例2 1976年至1977年美国佛罗里达州29个区的凶杀案件中凶手的肤色和是否被判死刑的326个犯人的情况如下,问是否存在种族歧视与审判不公?二、实验内容数据来源:wushujiance.sav某防疫站观察当地一个污水排放口在高温和低温季节中伤寒病菌检出情况。
其中高温和低温季节各观测12次,数据有24个观测样本,有两个属性变量degree 和test,degree有1(高温季节)和2(低温季节)两个等级;test有1(+)和2(-)两个等级。
问:两个季节的伤寒菌检出率有无差别?数据如下图所示:意为:Degree1(高温) 2(低温) 合计 test1(检出)17 8 2(没有检出) 115 16合计121224设A :高温季节;A :低温季节;B :检出;B :没有检出。
记)|(1A B P p =,2p =)|(A B P 此处欲检验0H :21p p =1H ↔:21p p ≠检验统计量:Pearson 卡方统计量=21212211222112)(++++-=n n n n n n n n n χ~)(12χ (渐进)称此检验为卡方检验。
此外,可以证明:卡方检验等价于独立性检验(A 属性与B 属性独立),即:0H :21p p =1H ↔:21p p ≠等价于0H :j i ij p p p ⋅⋅=1H ↔:j i ij p p p ••≠,.2,1,=j i其中nn p ij ij =,nn p i i +•=,n n p j j +•=,.2,1,=j i实验过程:(1)打开数据文件;(2)分析->描述统计->交叉表;相依系数:其数值在0~1之间,但不能达到1,是行变量和列变量相关性的度量指标。
对数线性模型剖析课件

与逻辑回归模型比较
对数线性模型和逻辑回归模型都适用于处理 二分类问题。逻辑回归模型在对数几率尺度 上建模,而标准对数线性模型在概率单位尺 度上建模。逻辑回归模型通常更易于解释, 并且在数据不平衡时表现更好,但对数线性 模型在某些情况下可能提供更好的拟合。
对数线性模型在未来的应用前景
自然语言处理
随着深度学习和自然语言处理技术的不断发展,对数线性模型在文本分类、情感分析等领 域的应用前景广阔。通过结合先进的特征提取方法和深度学习技术,对数线性模型有望在 自然语言处理领域取得更好的效果。
对数线性模型剖析课件
contents
目录
• 对数线性模型概述 • 对数线性模型的原理 • 对数线性模型的建立与实现 • 对数线性模型的应用案例 • 对数线性模型的扩展与展望
01
对数线性模型概述
对数线性模型的定义
总结词
对数线性模型是一种统计模型,用于 研究分类变量之间的关联。
详细描述
对数线性模型是一种统计模型,用于 研究分类变量之间的关联。它通过对 数函数将概率与解释变量相联系,从 而分析变量之间的关系。
总结词
对数线性模型具有简单易用、可解释性强等优点,但 也存在对数据分布和样本量要求较高、无法处理非线 性关系等局限性。
详细描述
对数线性模型具有简单易用、可解释性强等优点,能够 方便地分析分类变量之间的关系,并给出概率估计值。 此外,它还可以用于探索性数据分析,帮助研究者了解 数据分布和变量之间的关系。然而,对数线性模型也存 在一些局限性,如对数据分布和样本量要求较高,无法 处理非线性关系等。此外,当数据存在违反独立性假设 的情况时,对数线性模型可能产生偏差。因此,在使用 对数线性模型时需要注意其适用条件和局限性。
9_对数线性模型分析

19
3)用对数线性模型来分析这组数据。 A:护理地点 B:护理量 C:婴儿存活情况
20
4)用Logistic回归模型来分析这组数据。 A:护理地点 (自变量) B:护理量 (自变量) C:婴儿存活情况(因变量)
21
对数线性模型的缺点: 1)对数线性模型更强调的是变量之间的交互 效应,它不能直接将因变量用自变量的函 数表示出来。 2)对数线性模型抽象复杂,特别是高维模型,
27
② MAXIMUM-LIKELIHOOD ANALYSIS-OF-VARIANCE TABLE Source DF Chi-Square Prob -------------------------------------------------HP 3 16.63 0.0008 TRT 3 5.03 0.1694 HP*TRT 9 1.10 0.9992 SEV 2 93.62 0.0000 HP*SEV 6 4.90 0.5563 TRT*SEV 6 12.58 0.0502 LIKELIHOOD RATIO 18 13.43 0.7651 --------------------------------------------------
3
第一节 对数线性模型的基本概念
一、频数分布:
1、列联表 (contingency table)
2、 维数 (dimension)
3、行(row)、列(column)、层(layer)变量
4、网格频数 (cell frequency)
4
第二节 对数线性模型
二维对数线性模型:
总均值
主效应A 主效应B
24
其中,变量HP 表示医院(hospital:1,2,3,4) ,变量 TRT 表示手术处理方法(treatment:A,B,C,D) , 变量SEV表示术后并发症的严重程度(severity:0= 没有,1=轻度,2=中度) ,变量WT表示频数。
对数线性模型

由比数计算而来。那么什么叫做比数呢?比数 是一个事件发生的概率与其不发生概率之比,测 量了一个事件发生的可能性。这个数值越高说 明结果2相对于结果1发生的可能性就越高。
• F, ji)j代有表关某的模期型望fij的概期率望值,令πij 代表与单元格(i • 上表可转化为
互效应就很繁杂,可 以解决logistic回归分
能需要建立很多哑变 析中多个自变量的交
量
互效应问题
2、列联表的四种类型
• 双向无序列联表; • 单向有序列联表; • 双向有序且属性不同的列联表; • 双向有序且属性相同的列联表
3、列联表的优势
• 约束条件少 • 清晰 • 可以快速准确进行判断
4、列联表的劣势:对于多关系变量(两个 以上)研究:不能被清晰解读
对数多元线社会性统计分回析 归
一、对数线性模型简介
• 1、对数线性模型基本思想
• 对数线性模型分析是把列联表资料的网格频数
的对数表示为各变量及其交互效应的线性模型 ,然后运用类似方差分析的基本思想,以及逻 辑变换来检验各变量及其交互效应的作用大小
区别
方法
作用
优缺点
列联表
逻辑回归
对数线性模型
分析定类变量和定类 分析尺度变量(也可 综合运用方差分析和
联。
• 饱和性:将多元频数分布分解成具体的各项主效应和各项交互效应
,以及高阶效应,不会漏项。(饱和模型与不饱和模型)
• 定量性:以发生比的形式来表示自变量的类型不同反映在因变量频
数分布上的差异。
• 可检验性:不仅可以对所有参数估计进行检验,使抽样数据可以推
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章列联表分析与对数线性模型
实验5-1 列联表分析
一、列联表
若总体中的个体可按两个属性A与B分类,A有r个等级,B有c个等级,从总体中抽取大小为N的样本,每种属性的样本数如下表所示:
称上表为r×c列联表。
当r=2=c时,称上表为2×2列联表或四格表。
本节仅涉及四格表检验。
例1 对肺癌患者和对照组的调查结果:
问是否患肺癌与是否吸烟独立与否?
例2 1976年至1977年美国佛罗里达州29个区的凶杀案件中凶手的肤色和是否被判死刑的326个犯人的情况如下,问是否存在种族歧视与审判不公?
二、实验内容
数据来源:wushujiance.sav
某防疫站观察当地一个污水排放口在高温和低温季节中伤寒病菌检出情况。
其中高温和低温季节各观测12次,数据有24个观测样本,有两个属性变量degree 和test,degree有1(高温季节)和2(低温季节)两个等级;test有1(+)和2(-)两个等级。
问:两个季节的伤寒菌检出率有无差别?
数据如下图所示:
意为:
设A :高温季节;A :低温季节;B :检出;B :没有检出。
记)|(1A B P p =,2p =)|(A B P 此处欲检验
0H :21p p =1H ↔:21p p ≠
检验统计量:
Pearson 卡方统计量=2
1212211222112
)(++++-=n n n n n n n n n χ ~)
(12
χ (渐进) 称此检验为卡方检验。
此外,可以证明:卡方检验等价于独立性检验(A 属性与B 属性独立),即:
0H :21p p =1H ↔:21p p ≠等价于0H :j i ij p p p ⋅⋅=1H ↔:j i ij p p p ∙∙≠,.2,1,=j i 其中n
n p ij ij =,n n p i i +
∙=
,n
n p j j +∙=,.2,1,=j i
实验过程:
(1)打开数据文件;
(2)分析->描述统计->交叉表;
相依系数:其数值在0~1之间,但不能达到1,是行变量和列变量相关性的度量指标。
Phi和Cramer变量:也可以刻画相关性。
Lambda:取“1”时表明自变量完全预测因变量,取“0”时表示预测完全没有效果。
不定性系数:表示用一个变量来预测其他变量时降低错误的比例。
输出结果:
[数据集1] K:\SPSS教程\sample\Chap05\wushuijiance.sav
季节* 检验结果交叉制表
检验结果合计
阳性阴性
季节高温
计数 1 11 12
期望的计数 4.0 8.0 12.0
季节中的 % 8.3% 91.7% 100.0%
检验结果中的 % 12.5% 68.8% 50.0%
总数的 % 4.2% 45.8% 50.0%
残差-3.0 3.0
标准残差-1.5 1.1
调整残差-2.6 2.6
低温
计数7 5 12
期望的计数 4.0 8.0 12.0
季节中的 % 58.3% 41.7% 100.0%
检验结果中的 % 87.5% 31.3% 50.0%
总数的 % 29.2% 20.8% 50.0%
残差 3.0 -3.0
标准残差 1.5 -1.1
调整残差 2.6 -2.6
合计计数8 16 24 期望的计数8.0 16.0 24.0 季节中的 % 33.3% 66.7% 100.0% 检验结果中的 % 100.0% 100.0% 100.0% 总数的 % 33.3% 66.7% 100.0%
上表的sig值均小于0.05,说明高低温两组检出率有显著差别。
直接分析列联表的方法(加权个案)
若无个案,直接分析下表
检验结果合计
阳性阴性
高温 1 11 12
季节
低温7 5 12
合计8 16 24
本例的完成方法:在SPSS中,定义数据为:
要让SPSS识别列联表,必须加权个案:
输出结果:
交叉表
[数据集0] C:\Documents and Settings\wangkun\桌面\未标题1.sav
气温* 检出交叉制表
计数
检出合计
阴性高温
低温 5 7 12
气温
高温11 1 12
合计16 8 24
可以看到上表中
由于sig值小于0.05,所以认为高温和低温检出率有显著差别。
实验5-2 对数线性模型 一、对数线性模型
2×2维交叉列联表
对应概率表为:
其中n
n p ij ij =
将概率取对数:
ij ij p ln =η
⎪⎪⎭
⎫ ⎝
⎛=⋅⋅⋅⋅j i ij
j
i p p p p p ln j
i ij j i p p p p p ⋅⋅⋅⋅++=ln ln ln ,2,1,=j i
将上式视为:
()ij j i ij AB B A ++=η
接下来引入方差分析模型
这是一个有交互效应的双因素方差分析数学模型。
二、实验内容
数据来源:qiguanyan.sav
实验过程:
(1)打开数据
(2)分析—>对数线性模型—>常规
输出结果
数据信息
N
案例有效 4 缺失0 加权有效206
单元格定义的单元格 4 结构中的无效单元0 采样无效单元0
类别
吸烟状况 2
治疗效果 2
收敛信息a,b
最大迭代次数20
收敛容限度.00100
最终最大绝对差值.00150
最终最大相对差值.00071c
迭代次数 5
a. 模型:泊松
b. 设计:常量 + smoke * effect +
smoke + effect
c. 由于参数估计的最大相对变化
小于指定的收敛条件,导致迭代已
收敛。
三、任意r×c列联表分析(对数线性模型)如:数据来源:qiguanyan.sav
意为:
下面要检验吸烟和治疗效果是否独立?实验过程:
定义范围
输出结果:
层次对数线性分析
附注
创建的输出19-JUN-2016 09:20:10 注释
输入数据
M:\2015-2016学年下学期\20131101+统计软
件与应用\自编讲义
\sample\Chap05\qiguanyan.sav
活动的数据集数据集1
过滤器<none>
权重频数
拆分文件<none>
工作数据文件中的 N 行 4
缺失值处理缺失的定义用户自定义缺失值被视为缺失。
使用的个案
对于模型中的所有变量而言,统计量以带有有
效数据的所有个案为基础。
语法HILOGLINEAR smoke(0 1) effect(0 1) /CWEIGHT=freq
/METHOD=BACKWARD
/CRITERIA MAXSTEPS(10) P(.05) ITERATION(20) DELTA(.5)
/PRINT=FREQ RESID ESTIM
/DESIGN.
资源处理器时间00:00:00.02 已用时间00:00:00.01
[数据集1] M: \sample\Chap05\qiguanyan.sav
数据信息
N
个案有效 4 超出范围a0 缺失0 加权有效206
类别
吸烟状况 2
治疗效果 2
a. 由于超过因子值范围,个案被拒绝。
设计 1
收敛信息
生成类smoke*effect
迭代数 1 “观测边际”与“拟合边际”之间
的最大差异
.000 收敛性准则10.404
似然比.000 0 . Pearson .000 0 .。
