一元线性回归模型案例分析
第三章 一元线性回归模型

第三章 一元线性回归模型一、预备知识(一)相关概念对于一个双变量总体,若由基础理论,变量和变量之间存在因果),(i i x y x y 关系,或的变异可用来解释的变异。
为检验两变量间因果关系是否存在、x y 度量自变量对因变量影响的强弱与显著性以及利用解释变量去预测因变量x y x ,引入一元回归分析这一工具。
y 将给定条件下的均值i x i yi i i x x y E 10)|(ββ+=(3.1)定义为总体回归函数(PopulationRegressionFunction,PRF )。
定义为误差项(errorterm ),记为,即,这样)|(i i i x y E y -i μ)|(i i i i x y E y -=μ,或i i i i x y E y μ+=)|(i i i x y μββ++=10(3.2)(3.2)式称为总体回归模型或者随机总体回归函数。
其中,称为解释变量x (explanatory variable )或自变量(independent variable );称为被解释y 变量(explained variable )或因变量(dependent variable );误差项解释μ了因变量的变动中不能完全被自变量所解释的部分。
误差项的构成包括以下四个部分:(1)未纳入模型变量的影响(2)数据的测量误差(3)基础理论方程具有与回归方程不同的函数形式,比如自变量与因变量之间可能是非线性关系(4)纯随机和不可预料的事件。
在总体回归模型(3.2)中参数是未知的,是不可观察的,统计计10,ββi μ量分析的目标之一就是估计模型的未知参数。
给定一组随机样本,对(3.1)式进行估计,若的估计量分别记n i y x i i ,,2,1),,( =10,),|(ββi i x y E 为,则定义3.3式为样本回归函数^1^0^,,ββi y ()i i x y ^1^0^ββ+=n i ,,2,1 =(3.3)注意,样本回归函数随着样本的不同而不同,也就是说是随机变量,^1^0,ββ它们的随机性是由于的随机性(同一个可能对应不同的)与的变异共i y i x i y x 同引起的。
一元线性回归模型案例分析

一元线性回归模型案例分析一元线性回归是最基本的回归分析方法,它的主要目的是寻找一个函数能够描述因变量对于自变量的依赖关系。
在一元线性回归中,我们假定存在满足线性关系的自变量与因变量之间的函数关系,即因变量y与单个自变量x之间存在着线性关系,可表达为:y=β0+ β1x (1)其中,β0和β1分别为常量,也称为回归系数,它们是要由样本数据来拟合出来的。
因此,一元线性回归的主要任务就是求出最优回归系数和平方和最小平方根函数,从而评价模型的合理性。
下面我们来介绍如何使用一元线性回归模型进行案例分析。
数据收集:首先,研究者需要收集自变量和因变量之间关系的相关数据。
这些数据应该有足够多的样本观测值,以使统计分析结果具有足够的统计力量,表示研究者所研究的关系的强度。
此外,这些数据的收集方法也需要正确严格,以避免因相关数据缺乏准确性而影响到结果的准确性。
模型构建:其次,研究者需要利用所收集的数据来构建一元线性回归模型。
即建立公式(1),求出最优回归系数β0和β1,即最小二乘法拟合出模型方程式。
模型验证:接下来,研究者需要对所构建的一元线性回归模型进行验证,以确定模型精度及其包含的统计意义。
可以使用F检验和t检验,以检验回归系数β0和β1是否具有统计显著性。
另外,研究者还可以利用R2等有效的拟合检验统计指标来衡量模型精度,从而对模型的拟合水平进行评价,从而使研究者能够准确无误地判断其研究的相关系数的统计显著性及包含的统计意义。
另外,研究者还可以利用偏回归方差分析(PRF),这是一种多元线性回归分析技术,用于计算每一个自变量对相应因变量的贡献率,使研究者能够对拟合模型中每一个自变量的影响程度进行详细的分析。
模型应用:最后,研究者可以利用一元线性回归模型进行应用,以实现实际问题的求解以及数据挖掘等功能。
例如我们可以使用这一模型来预测某一物品价格及销量、研究公司收益及投资、检测影响某一地区经济发展的因素等。
综上所述,一元线性回归是一种利用单变量因变量之间存在着线性关系来拟合出回归系数的回归分析方法,它可以应用于许多不同的问题,是一种非常实用的有效的统计分析方法。
一元线性回归案例

S=963.191+18.501R
例9. CEO薪水与股本回报率
OLS回归线为 S=963.191+18.501R N=209, R^2=0.0132
企业股本回报率只能解释薪水变异中的 1.3%.
例2. 一个简单的工资方程
美国研究者以1976年的526名美国工人为样 本,OLS回归方程为:
W=-0.90 +0.54 E 这里W单位为美元/小时,E单位为年. E平均工资计算为5.90美元/小时. 根据消费者价格指数,这一数值相当于2003
年的19.06美元.
例2. 一个简单的工资方程
对同样的数据,但是把log(w)作为因变量, 得到的回归方程为:
Log(invpc)=-0.550+1.24log(price) (0.043) (0.382)
N=42 R^2=0.208 显著性检验不明显,事实上这一关系也是错误的,未
来我们将加上时间序列分析中特有的趋势分析说 名这个问题.
例8. 集装箱吞吐量与外贸额
2001-2006年中国集装箱吞吐量增长与外贸 额增长的弹性分析.以Y表示集装箱吞吐量( 百万标准箱),X表示外贸额(百亿美元).
出勤率无关,但这几乎不可能.
例5. 学校的数学成绩与学校午餐项目
以math10表示高中十年级学生在一次标准化 数学考试中通过的百分比.lnchprg表示有资 格接受午餐计划的学生的百分比.
若其他条件不变,若学生太贫穷不能保证正常 饮食,可以有资格接受学校午餐项目的资助, 他的成绩应有所提高.
例5. 学校的数学成绩与学校午餐项目
1992-1993学年美国密歇根州408所高中的 数据的OLS回归方程:
一元线性回归分析案例

i=1
(2)当 r>0 时,称两个变量_正__相___关__;
当 r<0 时,称两个变量_负__相__关__;
当 r=0 时,称两个变量线性不相关.
【教材拓展】 1.相关关系与函数关系的异同 共同点:二者都是指两个变量间的关系; 不同点:函数关系是一种确定性关系,体现的是因果关系,而相关关系是一种非确 定性关系,体现的不一定是因果关系,也可能是伴随关系. 2.从散点图看相关性 正相关:样本点分布在从左下角到右上角的区域内; 负相关:样本点分布在从左上角到右下角的区域内. 3.回归直线 y=bx+a 必过样本点的中心.
答案:68
1.四名同学根据各自的样本数据研究变量 x,y 之间的相关关系,并求得回归直线方
程,分别得到以下四个结论:
①y 与 x 负相关且 y=2.347x-6.423;②y 与 x 负相关且 y=-3.476x+5.648;③y 与
x 正相关且 y=5.437x+8.493;④y 与 x 正相关且 y=-4.326x-4.578.
(1)根据数据绘制的散点图能够看出可用线性回归模型拟合 y 与 x 的关系,请用相关
系数 r 加以说明;(系数精确到 0.001)
(2)建立 y 关于 x 的回归方程 y=bx+a(系数精确到 0.01);如果该公司计划在 9 月份
实现产品销量超 6 万件,预测至少需投入促销费用多少万元(结果精确到 0.01).
4.线性回归方程
假设样本点为(x1,y1),(x2,y2),…,(xn,yn),如果用x-表示x1+x2+n …+xn,用-y表
示y1+y2+n …+yn,则可以求得 b=
(x1-x-)(y1--y)+(x2-x-)(y2--y)+…+(xn-x-)(yn--y) (x1-x-)2+(x2-x-)2+…+(xn-x-)2
一元线性回归模型典型例题分析

第二章 一元线性回归模型典型例题分析例1、令kids 表示一名妇女生育孩子的数目,educ 表示该妇女接受过教育的年数。
生育率对教育年数的简单回归模型为μββ++=educ kids 10(1)随机扰动项μ包含什么样的因素?它们可能与教育水平相关吗?(2)上述简单回归分析能够揭示教育对生育率在其他条件不变下的影响吗?请解释。
例2.已知回归模型μβα++=N E ,式中E 为某类公司一名新员工的起始薪金(元),N 为所受教育水平(年)。
随机扰动项μ的分布未知,其他所有假设都满足。
如果被解释变量新员工起始薪金的计量单位由元改为100元,估计的截距项与斜率项有无变化?如果解释变量所受教育水平的度量单位由年改为月,估计的截距项与斜率项有无变化?例3.对于人均存款与人均收入之间的关系式t t t Y S μβα++=使用美国36年的年度数据得如下估计模型,括号内为标准差:)011.0()105.151(067.0105.384ˆtt Y S +==0.538 023.199ˆ=σ (1)β的经济解释是什么?(2)α和β的符号是什么?为什么?实际的符号与你的直觉一致吗?如果有冲突的话,你可以给出可能的原因吗?(3)对于拟合优度你有什么看法吗? (4)检验统计值?例4.下列方程哪些是正确的?哪些是错误的?为什么?⑴ y xt n t t=+=αβ12,,, ⑵ yx t n t tt=++=αβμ12,,, ⑶ y x t n t t t=++= ,,,αβμ12⑷ ,,,y x t n t t t =++=αβμ12 ⑸ y x t n t t =+= ,,,αβ12 ⑹ ,,,y x t n t t=+=αβ12 ⑺ y x t n t t t =++= ,,,αβμ12 ⑻ ,,,y x t n t t t=++=αβμ12 其中带“^”者表示“估计值”。
例5.对于过原点回归模型i i i u X Y +=1β ,试证明∑=∧221)(iu X Var σβ例6、对没有截距项的一元回归模型i i i X Y μβ+=1称之为过原点回归(regression through the origin )。
一元线性回归案例spss
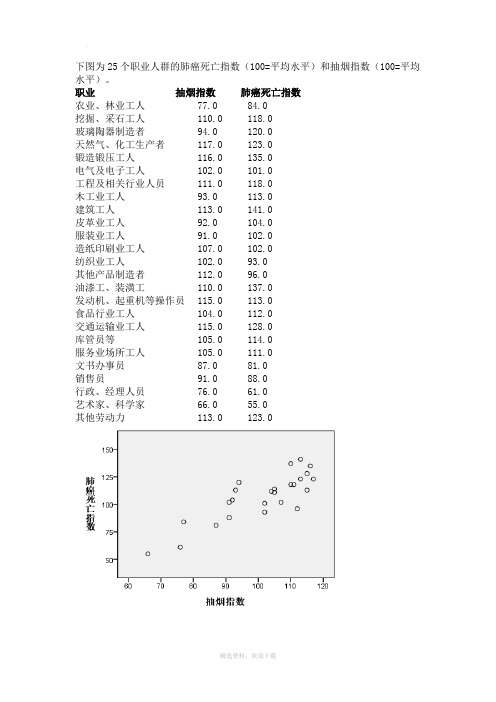
下图为25个职业人群的肺癌死亡指数(100=平均水平)和抽烟指数(100=平均水平)。
职业抽烟指数肺癌死亡指数农业、林业工人77.0 84.0挖掘、采石工人110.0 118.0玻璃陶器制造者94.0 120.0天然气、化工生产者117.0 123.0锻造锻压工人116.0 135.0电气及电子工人102.0 101.0工程及相关行业人员111.0 118.0木工业工人93.0 113.0建筑工人113.0 141.0皮革业工人92.0 104.0服装业工人91.0 102.0造纸印刷业工人107.0 102.0纺织业工人102.0 93.0其他产品制造者112.0 96.0油漆工、装潢工110.0 137.0发动机、起重机等操作员115.0 113.0食品行业工人104.0 112.0交通运输业工人115.0 128.0库管员等105.0 114.0服务业场所工人105.0 111.0文书办事员87.0 81.0销售员91.0 88.0行政、经理人员76.0 61.0艺术家、科学家66.0 55.0其他劳动力113.0 123.0散点图呈线性关系令Y=肺癌死亡指数,X=抽烟指数,做线性回归分析如下:表2中R=0.839 表示两变量高度相关R方=0.703 表示拟合较好,散点相对集中于回归线表3中sig.<0.05 则自变量与因变量具有显著的线性关系,即可以用回归模型表示表4中自变量sig.<0.05 则自变量对因变量的线性影响是显著的由此得到抽烟指数及肺癌死亡指数的一元回归方程:Y=-24.421+1.301X即抽烟指数每变动一个单位则肺癌死亡指数平均变动1.301个单位Welcome !!! 欢迎您的下载,资料仅供参考!。
一元线性回归分析案例

求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为 172cm的女大学生的体重。
解:1、选取身高为自变量x,体重为因变量y,作散点图:
2、由散点图知道身高和体重有比较好的线性相 关关系,因此可以用线性回归方程刻画它们之间 的关系。
第17页/共39页
课题:选修2-3 8.5 回归分析案例
分析:由于问题中要求根 据身高预报体重,因此选 取身高为自变量,体重为 因变量.
再冷的石头,坐上三年也会暖 !
1. 散点图;
2.回归方程: yˆ 0.849x 85.172 身高172cm女大学生体重 yˆ = 0.849×172 - 85.712 = 60.316(kg)
本例中, r=0.798>0.75.这表明体重与身高有很强的线性相关关系,从而也表明我们 建立的回归模型是有意义的。
xi2
2
nx
,......(2)
i 1
i 1
其中x
1 n
n i 1
xi ,
y
1 n
n i 1
yi .
(x, y) 称为样本点的中心。
第8页/共39页
课题:选修2-3 8.5 回归分析案例
再冷的石头,坐上三年也会暖 !
1、回归直线方程
1、所求直线方程叫做回归直线方程;
相应的直线叫做回归直线。
2、对两个变量进行的线性分析叫做线性回归分析。
然后,我们可以通过残差 e1, e2 , , en 来判断模型拟合的效果,
判断原始数据中是否存在可疑数据,这方面的分析工作称为残差分析。
表3-2列出了女大学生身高和体重的原始数据以及相应的残差数据。
编号 1
2
3
4
5
数据分析线性回归报告(3篇)

第1篇一、引言线性回归分析是统计学中一种常用的数据分析方法,主要用于研究两个或多个变量之间的线性关系。
本文以某城市房价数据为例,通过线性回归模型对房价的影响因素进行分析,以期为房地产市场的决策提供数据支持。
二、数据来源与处理1. 数据来源本文所采用的数据来源于某城市房地产交易中心,包括该城市2010年至2020年的房价、建筑面积、交通便利度、配套设施、环境质量等指标。
2. 数据处理(1)数据清洗:对原始数据进行清洗,去除缺失值、异常值等。
(2)数据转换:对部分指标进行转换,如交通便利度、配套设施、环境质量等指标采用五分制评分。
(3)变量选择:根据研究目的,选取建筑面积、交通便利度、配套设施、环境质量等指标作为自变量,房价作为因变量。
三、线性回归模型构建1. 模型假设(1)因变量与自变量之间存在线性关系;(2)自变量之间不存在多重共线性;(3)误差项服从正态分布。
2. 模型建立(1)选择合适的线性回归模型:根据研究目的和数据特点,采用多元线性回归模型。
(2)计算回归系数:使用最小二乘法计算回归系数。
(3)检验模型:对模型进行显著性检验、方差分析等。
四、结果分析1. 模型检验(1)显著性检验:F检验结果为0.000,P值小于0.05,说明模型整体显著。
(2)回归系数检验:t检验结果显示,所有自变量的回归系数均显著,符合模型假设。
2. 模型结果(1)回归系数:建筑面积、交通便利度、配套设施、环境质量的回归系数分别为0.345、0.456、0.678、0.523,说明这些因素对房价有显著的正向影响。
(2)R²:模型的R²为0.876,说明模型可以解释约87.6%的房价变异。
3. 影响因素分析(1)建筑面积:建筑面积对房价的影响最大,说明在房价构成中,建筑面积所占的比重较大。
(2)交通便利度:交通便利度对房价的影响较大,说明在购房时,消费者对交通便利性的需求较高。
(3)配套设施:配套设施对房价的影响较大,说明在购房时,消费者对生活配套设施的需求较高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一元线性回归模型案例分析一、研究的目的要求居民消费在社会经济的持续发展中有着重要的作用。
居民合理的消费模式和居民适度的消费规模有利于经济持续健康的增长,而且这也是人民生活水平的具体体现。
改革开放以来随着中国经济的快速发展,人民生活水平不断提高,居民的消费水平也不断增长。
但是在看到这个整体趋势的同时,还应看到全国各地区经济发展速度不同,居民消费水平也有明显差异。
例如,2002年全国城市居民家庭平均每人每年消费支出为6029.88元, 最低的黑龙江省仅为人均4462.08元,最高的上海市达人均10464元,上海是黑龙江的2.35倍。
为了研究全国居民消费水平及其变动的原因,需要作具体的分析。
影响各地区居民消费支出有明显差异的因素可能很多,例如,居民的收入水平、就业状况、零售物价指数、利率、居民财产、购物环境等等都可能对居民消费有影响。
为了分析什么是影响各地区居民消费支出有明显差异的最主要因素,并分析影响因素与消费水平的数量关系,可以建立相应的计量经济模型去研究。
二、模型设定我们研究的对象是各地区居民消费的差异。
居民消费可分为城市居民消费和农村居民消费,由于各地区的城市与农村人口比例及经济结构有较大差异,最具有直接对比可比性的是城市居民消费。
而且,由于各地区人口和经济总量不同,只能用“城市居民每人每年的平均消费支出”来比较,而这正是可从统计年鉴中获得数据的变量。
所以模型的被解释变量Y 选定为“城市居民每人每年的平均消费支出”。
因为研究的目的是各地区城市居民消费的差异,并不是城市居民消费在不同时间的变动,所以应选择同一时期各地区城市居民的消费支出来建立模型。
因此建立的是2002年截面数据模型。
影响各地区城市居民人均消费支出有明显差异的因素有多种,但从理论和经验分析,最主要的影响因素应是居民收入,其他因素虽然对居民消费也有影响,但有的不易取得数据,如“居民财产”和“购物环境”;有的与居民收入可能高度相关,如“就业状况”、“居民财产”;还有的因素在运用截面数据时在地区间的差异并不大,如“零售物价指数”、“利率”。
因此这些其他因素可以不列入模型,即便它们对居民消费有某些影响也可归入随即扰动项中。
为了与“城市居民人均消费支出”相对应,选择在统计年鉴中可以获得的“城市居民每人每年可支配收入”作为解释变量X。
从2002年《中国统计年鉴》中得到表2.5的数据:表2.52002年中国各地区城市居民人均年消费支出和可支配收入如图2.12:图2.12从散点图可以看出居民家庭平均每人每年消费支出(Y)和城市居民人均年可支配收入(X)大体呈现为线性关系,所以建立的计量经济模型为如下线性模型:12i i i Y X u ββ=++ 三、估计参数假定所建模型及随机扰动项i u 满足古典假定,可以用OLS 法估计其参数。
运用计算机软件EViews 作计量经济分析十分方便。
利用EViews 作简单线性回归分析的步骤如下: 1、建立工作文件首先,双击EViews 图标,进入EViews 主页。
在菜单一次点击File\New\Workfile ,出现对话框“Workfile Range ”。
在“Workfile frequency ”中选择数据频率:Annual (年度) Weekly ( 周数据 )Quartrly (季度) Daily (5 day week ) ( 每周5天日数据 ) Semi Annual (半年) Daily (7 day week ) ( 每周7天日数据 ) Monthly (月度) Undated or irreqular (未注明日期或不规则的) 在本例中是截面数据,选择“Undated or irreqular ”。
并在“Start date ”中输入开始时间或顺序号,如“1”在“end date ”中输入最后时间或顺序号,如“31”点击“ok ”出现“Workfile UNTITLED ”工作框。
其中已有变量:“c ”—截距项 “resid ”—剩余项。
在“Objects ”菜单中点击“New Objects”,在“New Objects”对话框中选“Group”,并在“Name for Objects”上定义文件名,点击“OK ”出现数据编辑窗口。
若要将工作文件存盘,点击窗口上方“Save ”,在“SaveAs ”对话框中给定路径和文件名,再点击“ok ”,文件即被保存。
4000600080001000012000400060008000100001200014000XY2、输入数据在数据编辑窗口中,首先按上行键“↑”,这时对应的“obs”字样的空格会自动上跳,在对应列的第二个“obs”有边框的空格键入变量名,如“Y ”,再按下行键“↓”,对因变量名下的列出现“NA ”字样,即可依顺序输入响应的数据。
其他变量的数据也可用类似方法输入。
也可以在EViews 命令框直接键入“data X Y ”(一元时) 或 “data Y 1X 2X … ”(多元时),回车出现“Group”窗口数据编辑框,在对应的Y 、X 下输入数据。
若要对数据存盘,点击 “fire/Save As”,出现“Save As ”对话框,在“Drives ”点所要存的盘,在“Directories ”点存入的路径(文件名),在“Fire Name ”对所存文件命名,或点已存的文件名,再点“ok ”。
若要读取已存盘数据,点击“fire/Open”,在对话框的“Drives”点所存的磁盘名,在“Directories”点文件路径,在“Fire Name”点文件名,点击“ok”即可。
3、估计参数方法一:在EViews 主页界面点击“Quick ”菜单,点击“Estimate Equation ”,出现“Equation specification ”对话框,选OLS 估计,即选击“Least Squares”,键入“Y C X ”,点“ok ”或按回车,即出现如表2.6那样的回归结果。
表2.6在本例中,参数估计的结果为:^282.24340.758511i i Y X =+ (287.2649) (0.036928) t=(0.982520) (20.54026)20.935685r = F=421.9023 df=29方法二:在EViews 命令框中直接键入“LS Y C X ”,按回车,即出现回归结果。
若要显示回归结果的图形,在“Equation ”框中,点击“Resids ”,即出现剩余项(Residual )、实际值(Actual )、拟合值(Fitted )的图形,如图2.13所示。
图2.13四、模型检验1、经济意义检验所估计的参数^20.758511β=,说明城市居民人均年可支配收入每相差1元,可导致居民消费支出相差0.758511元。
这与经济学中边际消费倾向的意义相符。
2、拟合优度和统计检验用EViews 得出回归模型参数估计结果的同时,已经给出了用于模型检验的相关数据。
拟合优度的度量:由表2.6中可以看出,本例中可决系数为0.935685,说明所建模型整体上对样本数据拟合较好,即解释变量“城市居民人均年可支配收入”对被解释变量“城市居民人均年消费支出”的绝大部分差异作出了解释。
对回归系数的t 检验:针对01:0H β=和02:0H β=,由表2.6中还可以看出,估计的回归系数^1β的标准误差和t 值分别为:^1()287.2649SE β=,^1()0.982520t β=;^2β的标准误差和t 值分别为:^2()0.036928SE β=,^2()20.54026t β=。
取0.05α=,查t 分布表得自由度为231229n -=-=的临界值0.025(29) 2.045t =。
因为^10.025()0.982520(29) 2.045t t β=<=,所以不能拒绝01:0H β=;因为^20.025()20.54026(29) 2.045t t β=>=,所以应拒绝02:0H β=。
这表明,城市人均年可支配收入对人均年消费支出有显著影响。
五、回归预测由表2.5中可看出,2002年中国西部地区城市居民人均年可支配收入除了西藏外均在8000以下,人均消费支出也都在7000元以下。
在西部大开发的推动下,如果西部地区的城市居民人均年可支配收入第一步争取达到1000美元(按现有汇率即人民币8270元),第二步再争取达到1500美元(即人民币12405元),利用所估计的模型可预测这时城市居民可能达到的人均年消费支出水平。
可以注意到,这里的预测是利用截面数据模型对被解释变量在不同空间状况的空间预测。
用EViews 作回归预测,首先在“Workfile ”窗口点击“Range ”,出现“Change Workfile Range ”窗口,将“End data”由“31”改为“33”,点“OK ”,将“Workfile ”中的“Range ”扩展为1—33。
在“Workfile ”窗口点击“sampl”,将“sampl”窗口中的“1 31”改为“1 33”,点“OK ”,将样本区也改为1—33。
为了输入18270f X =,212405f X =在EViews 命令框键入data x /回车, 在X 数据表中的“32”位置输入“8270”,在“33”的位置输入“12405”,将数据表最小化。
然后在“E quation ”框中,点击“Forecast ”,得对话框。
在对话框中的“Forecast name ”(预测值序列名)键入“fY ”, 回车即得到模型估计值及标准误差的图形。
双击“Workfile ”窗口中出现的“Yf ”,在“Yf ”数据表中的“32”位置出现预测值16555.132f Y =,在“33”位置出现29691.577f Y =。
这是当18270f X =和212405f X =时人均消费支出的点预测值。
为了作区间预测,在X 和Y 的数据表中,点击“View”选“Descriptive Stats\Cmmon Sample”,则得到X 和Y 的描述统计结果,见表2.7: 表2.7根据表2.7的数据可计算:2221()(1)2042.68230125176492.59niX i XX n σ=-=-=⨯=∑221()(82707515.026)569985.74f X X -=-=222()(124057515.026)23911845.72f X X -=-=fY 置信度95%的预测区间为:2221()11()f fni i X X Y t nX X ασ=-++-∑ 18270f X =时1569985.746555.13 2.045413.1593131125176492.59⨯⨯++6555.13860.32=212405f X =时123911845.729691.58 2.045413.1593131125176492.59⨯⨯++9691.58934.49=即是说,当第一步18270f X =时,1f Y 个别值置信度95%的预测区间为(5694.81,7415.45)元。
