泄漏源及扩散模式
泄漏源与扩散模式

u C0
2 Pg
2gz 2 Pg 2gz
(6.9) (6.10)
7
Q uA AC0
6.3储罐中液体经小孔泄漏的源模式(2)
由式(6. 9) 和式(6. 10) 知,随着泄漏过程的延续,z , u Q 。如果储罐通过呼吸阀或弯管与大气连通, 则 ΔP=0 。
Q uA AC0 2gz
u C0 2 RT0 1 M P 1 1 ( ) P0 2 RT0 1 M
(6.32)
Q uA C0 A 0
P 2 P 1 ( ) ( ) (6.33) P0 P0
14
6.5气体或蒸气经小孔泄漏的源模式(4)
Q uAC0 AC0 2P 1
(6.7)
6
6.3储罐中液体经小孔泄漏的源模式(1)
图 6.4 所示的液体储罐,距液位高度 Z 0 处有一小孔 ,在静压能和势能的作用下,储罐中的液体经小孔 向外泄漏。 P 2 P gz F C0( gz) (6.8)
将式(6.8)代入式(6.3),得
dp
F C
2 0
dp
(6.29)
将式(6.29)代人式(6.28) ,忽略气体或蒸气的初 始动能,得到:
2 C0 p
dp
p0
u2 0 2
(6.30)
13
6.5气体或蒸气经小孔泄漏的源模式(3) 由式(6.27) 得到:
1 p ( ) 0 p0
(6.31)
将式(6.31)代入式(6.30),积分 得:
4
6.2液体经小孔泄漏的源模式(2)
第7章 化学品泄露与扩散模型 - 2

100
向运动较小。
0
图7-9 昼间和夜间空气温度随高度的变化,
-1
1
3
5
7
9
11
温度梯度影响空气的垂直运动
温度 摄氏度
7. 3 扩散方式及扩散模型
7.3.1 扩散方式及其影响因素 稳定度划分:不稳定、中性和稳定 划分标准:对地面加热速度与地面散热速度相对快慢 (1)加热速度>地面散热速度 地面附近的空气温度比高处的空气温度高,地表附近空气的密度小,上层空 气密度大,密度小的空气在这种浮力作用下上升,导致大气不稳定。[晴天上 午9、10点后,肉眼会观测到地表升腾;春秋早晨水雾消散]。F浮>F重 (2)加热速度=散热速度。热量对大气扰动很小,但很难长久保持。F浮=F重 (3)加热速度<散热速度。地面附近的温度比高处空气的温度低,地表附近 空气密度大于高处空气的密度。F浮<F重。重力影响抑制了大气机械湍流。
• 求解液体蒸发比例,有:
fv mv / m 1 exp Cp (T0 Tb ) / Hv
(7-60) (7-61)
7.2.3 液体闪蒸
【例7-6】闪蒸计算 • 1 kg饱和水储存在温度为177°C的容器中,容器破裂,压力下降到
1atm,计算水的蒸发比例。 • 解:
• 对于100◦C下的液体水: Cp=4.2 kJ/(kg·◦C ); △Hv=2252.2 kJ/kg
预测的Ma1 式子左边的值
0.20 -8.48
0.25 -0.007
• 根据最近一次预测的Ma1值计算结果接近于零,因此由式(728):
7.2.2 气体或蒸气泄露
• 由式(7-35)和式(7-36)得:
7.2.2 气体或蒸气泄露
• 为确保是塞流,管道出口处的压力必须小于340kPa,由式(7-38) 计算单位面积质量流量:
泄露扩散模型
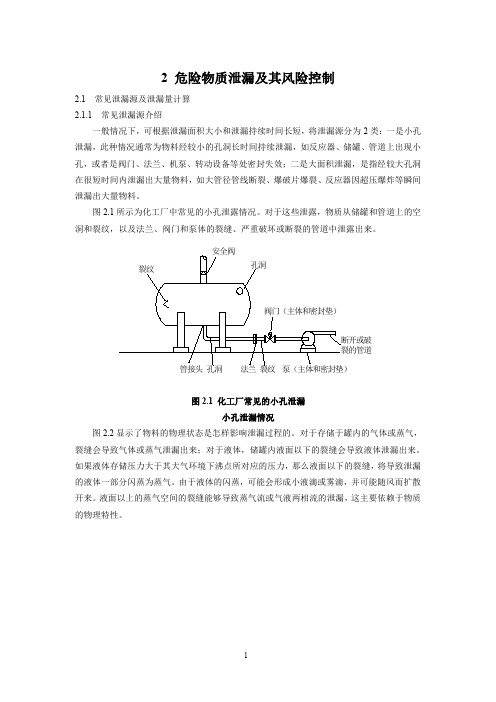
Q AC0 2 gz0
2 pg
gC02 A2
A0
t
储罐
(2.15)
根据式(2.15)可以求出不同时间的泄漏质量流量。 【例 3-2 】如图 3-7 所示为某一盛装丙酮液体的储罐,上部装有呼 吸阀与大气连通。在其下部有一泄漏孔,直径 4cm,已知丙酮的密度为 800kg·m-3 (1)最大泄漏量; (2)泄漏质量流量随时间变化的表达式; (3)最大泄漏时间; (4)总泄漏量随时间变化的表达式。 图 2.7
附件 弯头 90° 附件描述 标准(r/D=1)的,带螺纹的
K1
K
0.40
800
7
标准(r/D=1)的,用法兰连接/焊接 长半径(r/D=1.5) ,所有类型 斜接的(r/D=1.5) :1. 焊缝(90°) 2. 焊缝(45°) 3. 焊缝(30°) 4. 焊缝(22.5°) 5. 焊缝(18°) 标准(r/D=1)的,所有类型 45° 长半径(r/D=1.5) 斜接的:1. 焊缝(45°) 2. 焊缝(22.5°) 标准(r/D=1)的,带螺纹的 180° 标准(r/D=1)的,用法兰连接/焊接 长半径(r/D=1.5) ,所有类型 标准的,带螺纹的 长半径,带螺纹的 作弯头 用 标准的,用法兰连接/焊接 短分支 带螺纹的 用法兰连接/焊接 短分支 附件 闸阀、 球 阀、 旋塞 阀 球心阀 阀门 隔膜阀、 蝶阀 全尺寸, 1.0 缩减尺寸, 0.9 缩减尺寸, 标准的 斜角或 Y 形 Dam(闸坝)类型 提升阀 止回阀 回转阀 倾斜片状阀 附件描述
Pg
10m 4m A0
储罐上的小孔泄漏
3)液体经过管道泄漏的泄漏量计算 如图 2.8 所示,在化工生产中,通常采用圆形管道输送液体,沿管道的压力梯度是液体
化工安全工程课件第六章泄漏源及扩散模式

第八节 湍流扩散模型 一、湍流扩散微分方程的推导
若风向与X轴方向一致
二、无边界点源扩散模型
1. 瞬时泄漏点源的扩散模型 U=0 即无风条件下
U≠0 有风条件下
2. 连续泄漏点源的扩散模型 U=0 即无风条件下,连续泄漏各位置点浓度与时间无关
U≠0 有风条件下,连续泄漏各位置点浓度与时间无关
三、有边界点源扩散模型
第六节 易挥发液体蒸发的源模式
泄漏液体向大气蒸发,该蒸发过程的传质推动力为蒸发物质 的气液界面与大气间的浓度差。液体蒸发为气体的摩尔通量:
第七节 扩散模式(有毒有害ቤተ መጻሕፍቲ ባይዱ质在空气中扩散)
连续泄漏源泄漏 的扩散模式
瞬间泄漏源泄漏 的扩散模式
风速、大气稳定度、地面情况、泄漏源高度、泄漏物质的初 始状态、物料性质等因素均会对泄漏物质在大气中的扩散产 生影响。
a 对于光滑管,λ由雷诺数Re决定 (经验公式) b 对于粗糙管,λ由雷诺数Re和相对粗糙度ε/d决定(经验公式、查图)
U= 0→u Z= 5 →0
第四节 气体或蒸气经小孔泄露的源模式
泄漏后密度发生变化 可压缩流体
(势能变化忽略) 定义孔流系数:
令
第五节 闪蒸液体的泄漏源模式
闪蒸:瞬间完成的减压气化,不需加热。近似为绝热过程。
第一节 液体经小孔泄露的源模式
泄露形式
容器内流速忽略, 不考虑摩擦损失和 液位变化
考虑到因惯性引起的截面收缩及摩擦引起的速度减小,引入孔流系数C0。 C0=实际流量/理论流量
C0约为1
薄壁小孔C0约0.61
厚壁小孔或孔外伸有 一段短管C0约0.81
通常情况下C0难以求取,为保持足够的安全余量,可取1.
第二节 储罐中液体经小孔泄露的源模式
第六章 泄漏源

大气污染源的分类方法: 按空间分布 (1)点源-污染物集中于一点或相当于一点的小范围排放 源,如工厂烟囱排放源。 (2)线源-交通干线两侧汽车尾气污染源。 (3)面源-即在相当大面积范围内有许多个污染排放源, 如一个大城市内的许多污染物排放源。
2. 扩散模式
2.1 扩散影响因素
释放发生后,空气中的毒物被风以烟羽方式、云团方 式带走,有毒物质的最大浓度是在释放处。众多因素 影响有毒物质在大气中的扩散: •风速; •大气稳定度; •地面条件(建筑物、水、树); •释放距离地面高度; •物质释放的初始动量和浮力。
大气稳定度(atmospheric stability) 1) 空气在上升过程中的绝热变化是大气中降温最快 的过程; 2) 上升过程中的绝热变化会导致水汽的凝结,这是 大气中云、雾、雨、雪形成的最重要的原因; 3) 因此,判断大气中是否会产生云雾,主要就是看 大气中是否会产生上升运动; 判断空气是否会产生上升运动,就要看空气在铅直 方向上位置稳定的程度,即大气稳定度。
Qm AC0 2 pg / 2 gz0
gC02 A2
At
t
思考:如果容器内的压力为大气压,上式可以化简为? 容器液面降到孔洞所在高度时所需时间?
圆柱型储罐,高20ft,直径8ft,里面有苯。储罐内有氮气为防
止爆炸,罐内表压1atm且恒定不变。目前,储罐内液面高度为
17ft,由于疏忽,铲车驾驶员将距离地面5ft的管壁上撞出一个 直径为1in的小孔。该条件下苯的相对密度为0.8794。请估算: (1) 将流出多少苯? (2) 苯流到泄漏孔高度时所需要的时间? (3) 苯通过小孔的最大质量流率。 注:1ft=0.3048m;1in=2.54×10-2m。
u C0 2Pg /
第7章 化学品泄露与扩散模型-1

P2 <P1 u2 =u1 Z2
P1
ρ=常数
u1
d
Z1
流体经管道流出
7.2 化学品泄露模型
7.2 化学品泄露模型
• (3)通过管道泄漏
• 对流经管道的液体,Kf为
f:范宁摩擦系数,L: 管长,d:管径 。 范宁摩擦系数f 是雷诺数Re和管道粗糙度ε的函数。具体关系式
及取值见表7-2与图7-3。
• (3)通过管道泄漏
• 2-K方法
管道附件,阀门及其他流动阻碍物;传统方法是在式(7-12) 中使用当量管长。一种改进的方法是使用2-K方法,使用实际 的流程长度而不是当量长度。
2-K方法由两个常数来定义压差损失系数。这两个常数即雷诺 数和管道内径。
������������
=
K1 ������������
7.2 化学品泄露模型
• (2)通过储罐上的孔洞泄漏 • 对于恒定截面积为A的储罐,储罐中小孔以上的液体总质量为:
• 储罐中的质量变化率为:
7.2 化学品泄露模型
• (2)通过储罐上的孔洞泄漏 • 将上式从初始高度hL0到任意高度hL进行积分,得到储罐中液面高
度随时间的变化函数:
• 得到任意时刻t所泄漏液体的质量流量:
7.2 化学品泄露模型
• (3)通过管道泄漏 • 2-K方法也可以用来描述液体通过孔洞的流出,流出系数的表达
式为 :
• ∑Kf为所有压差损失相之和,包括:进口、出口、管长和附件。
7.2 化学品泄露模型
• (3)通过管道泄漏
• 如对于没有管道连接或附件的贮罐上的一个简单的孔,摩擦仅仅
是由孔的进口和出口效应引起的,对Re>100000,进口的
第7章 化学品泄露与扩散模型
泄漏源及扩散模式汇总

第六章泄漏源及扩散模式很多事故是由于物料的泄漏引起的。
因泄漏而导致事故的危害,很大程度上取决于有毒有害,易燃易爆物料的泄漏速度和泄漏量。
物料的物理状态在其泄漏至空气中后是否发生改变,对其危害范围也有非常明显的影响,泄漏物质的扩散不仅由其物态、性质所决定,又为当时气象条件、当地的地表情况所影响。
6.1常见泄漏源泄漏源分为两类:一是小孔泄漏:通常为物料经较小的孔洞,长时间持续泄漏。
如反应器、管道、阀门等出现小孔或密封失效;二是大面积泄漏:在短时间内,经较大的孔洞泄漏大量物料。
如管线断裂、爆破片爆裂等。
为了能够预测和估算发生泄漏时的泄漏速度、泄漏量、泄漏时间等,建立如下泄漏源模型,描述物质的泄漏过程:1.流体流动过程中液体经小孔泄漏的源模式;2.储罐中液体经小孔泄漏的源模式;3.液体经管道泄漏的源模式;4.气体或蒸汽经小孔泄漏的源模式;5.闪蒸液体的泄漏源模式;6.易挥发液体蒸发的源模式。
针对不同的工艺条件和泄漏源情况,应选用相应的泄漏源模式进行泄漏速度、泄漏量、泄漏时间的求取。
6.2 流体流动过程中液体经小孔泄漏的源模式系统与外界无热交换,流体流动的不同能量形式遵守如下的机械能守恒方程:(6—1)式中:P——压力,Pa;ρ——流体密度,kg/m3;α——动能校正因子,无因次;α≈1U ——流体平均速度,m/s;g ——重力加速度,g = 9.81 m/s2;z ——高度,m;F ——阻力损失,J/kg;W s ——轴功率,J;m ——质量,kg。
对于不可压缩流体,密度ρ恒为常数,有:(6—2)泄漏过程暂不考虑轴功率,W s =0,则有:(6—3)液体在稳定的压力作用下,经薄壁小孔泄漏,如图6.1所示。
容器内的压力为p1,小孔直径为d,面积为A,容器外为大气压力。
此种情况,容器内液体流速可以忽略,不考虑摩擦损失和液位变化,可得到:式中,Q为单位时间内流体流过任一截面的质量,称为质量流量,其单位为kg/s。
泄漏气体扩散模型的研究与应用

( I . 辽 宁石 油化 工大 学 机 械工 程学 院 , 辽 宁 抚顺 I 1 3 0 0 1 ; 2 . 三 一重 型装 备有 限公 司 ,辽宁 沈 阳 1 0 0 0 2 7)
摘
要 :通 过对 泄漏 源模 式及 泄漏 影响因素的分 析 ,以湍流扩散微分方程为基础 ,对泄漏气体扩散行为模
2 . S a n y He a v y Eq u i p me n t Co . , Lt d . ,L i a o n i n g S h e n y a n g 1 0 0 0 2 7 , Ch i n a )
Ab s t r a c t : Th r o u g h a n a l y z i n g t h e mo d e o f l e a k a g e s o u r c e a n d f a c t o r s t o i n l f u e n c e t h e l e a k a g e ,t h e d i f f u s i o n mo d e l o f l e a k a g e g a s wa s e s t a b l i s h e d b a s e d o n t u r b u l e n t d i f f u s i o n d i fe r e n t i a l e q u a t i o n s ,b o u n d e d a n d u n b o u n d e d p u f a n d p l u me mo d e l s we r e o b t a i n e d . a n d a e x a mp l e a n a l y s i s wa s c a  ̄i e d o u t . T h e s t u d y o f t h e d i f f u s i o n mo d e l c a n b e u s e d t o d e t e r mi n e t h e i n f l u e n c e s c o p e a n d d a ma g e d e g r e e o f t h e a c c i d e n t , wh i c h c a n p r o v i d e a r e f e r e n c e f o r e me r g e n c y r e s c u e
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章泄漏源及扩散模式很多事故是由于物料的泄漏引起的。
因泄漏而导致事故的危害,很大程度上取决于有毒有害,易燃易爆物料的泄漏速度和泄漏量。
物料的物理状态在其泄漏至空气中后是否发生改变,对其危害范围也有非常明显的影响,泄漏物质的扩散不仅由其物态、性质所决定,又为当时气象条件、当地的地表情况所影响。
6.1常见泄漏源泄漏源分为两类:一是小孔泄漏:通常为物料经较小的孔洞,长时间持续泄漏。
如反应器、管道、阀门等出现小孔或密封失效;二是大面积泄漏:在短时间内,经较大的孔洞泄漏大量物料。
如管线断裂、爆破片爆裂等。
为了能够预测和估算发生泄漏时的泄漏速度、泄漏量、泄漏时间等,建立如下泄漏源模型,描述物质的泄漏过程:1.流体流动过程中液体经小孔泄漏的源模式;2.储罐中液体经小孔泄漏的源模式;3.液体经管道泄漏的源模式;4.气体或蒸汽经小孔泄漏的源模式;5.闪蒸液体的泄漏源模式;6.易挥发液体蒸发的源模式。
针对不同的工艺条件和泄漏源情况,应选用相应的泄漏源模式进行泄漏速度、泄漏量、泄漏时间的求取。
6.2 流体流动过程中液体经小孔泄漏的源模式系统与外界无热交换,流体流动的不同能量形式遵守如下的机械能守恒方程:(6—1)式中:P——压力,Pa;ρ——流体密度,kg/m3;α——动能校正因子,无因次;α≈1U ——流体平均速度,m/s;g ——重力加速度,g = 9.81 m/s2;z ——高度,m;F ——阻力损失,J/kg;W s ——轴功率,J;m ——质量,kg。
对于不可压缩流体,密度ρ恒为常数,有:(6—2)泄漏过程暂不考虑轴功率,W s =0,则有:(6—3)液体在稳定的压力作用下,经薄壁小孔泄漏,如图6.1所示。
容器内的压力为p1,小孔直径为d,面积为A,容器外为大气压力。
此种情况,容器内液体流速可以忽略,不考虑摩擦损失和液位变化,可得到:式中,Q为单位时间内流体流过任一截面的质量,称为质量流量,其单位为kg/s。
考虑到因惯性引起的截面收缩以及摩擦引起的速度减低,引入孔流系数C0,则经小孔泄漏的实际质量流量为:kg /s(6—7)式中:Q——质量流量,kg / s;A——泄漏孔面积,m2;C0——孔流系数;p1——容器内的压力,Pa;ρ——流体密度,kg / m3。
C0的取值:1、薄壁小孔( 壁厚≤d / 2 ),Re > 105C0 = 0.612、厚壁小孔( d / 2 < 壁厚≤4d ),或在孔处伸有一段短管(见图6.3 ) C0 = 0.813、修圆小孔( 见图6.2 ) C0 = 1但在很多情况下难以确定泄漏孔口的孔流系数,为了保证安全裕量,确保估算出最大的泄漏量和泄漏速度,Co值可取为1。
例:某液体在容器中以稳定的0.2MPa的压力完全湍流流动,液体的密度为1000kg / m3,因时久腐蚀的原因,容器底部有一小孔发生泄漏,孔径为5mm,壁厚≤d/2,孔流系数C0 = 0.62,容器外部为大气压;问经小孔泄漏的实际质量流量为多少?解:按液体经小孔的泄漏源模式(6—7)计算:Q = AC0(2 p1ρ)1/2= 0.7854×0.0052×0.62(2×0.2×106×1000)= 0.24 kg / s6.3 储罐中液体经小孔泄漏的源模式如图6.4所示的液体储罐,距液体位高度Z0处有一小孔,在静压能和势能的作用下,液体经小孔向外泄漏,泄漏过程可由机械能守恒方程描述,罐内液体流速忽略,罐内液体压力为P g,外部为大气压(表压P=0),如前面定义孔流系数C0,由下式表达:(6—8)将式(6—8)代入式(6—3)中,可求泄漏速度U:(6—9)小孔截面积为A,则质量流量Q为:(6—10)但是储罐内液位高度z0不断下降,泄漏速度和质量流量也随之减少,假定储罐与大气相通,则内外压差Δp为0,则上式简化为:(6—11)若储罐的横截面积为A0,则经小孔泄漏的最大液体量m为:(6—12)取一微元时间内液体的泄漏量:(6—13)并且罐内液体质量的变化速率,即为泄漏质量:(6—14)将式(6—11)、(6—13)代入(6—14)式,得到:(6—15)设定边界条件:t=0,t=t,z=z0 ,z=z,对上式进行积分,有:(6—16)当液体泄漏到泄漏点位置时,泄漏停止,z=0,为此,得到总的泄漏时间:(6—17)将式(6—16)代入式(6—11)中得到随时间变化的质量流量关系:(6—18)式中:ρ——流体密度,kg / m3;C0——孔流系数;A ——泄漏孔面积,m2;A0——储罐截面积,m2;z0 ——泄漏点以上液体的高度,m;g ——重力加速度,9.81m / s2;t ——泄漏时间,s。
如果储罐内盛装的是易燃液体,为防止可燃蒸汽大量泄漏至空气中,或空气大量进入储罐内的气相空间,形成爆炸性混合物,通常情况下会采取通氮气保护的措施。
液体表压为P g,外部为大气压(表压P=0),内外压差即为P g,则根据式(6—10)、式(6—12)、式(6—13)、式(6—14)可同理得到:将式(6—20)代入式(6—10)得到任意时刻的质量流量Q:式中:P g——储罐内液体表压,Pa。
根据上式(6—21)可求出不同时间的泄漏质量流量。
例:有一常压甲苯储罐,内径1 m,下部因腐蚀产生一个小孔,孔直径为10mm,小孔上方甲苯液位初始高度为3 m,巡检人员于上午7:00发现泄漏,马上进行堵漏处理,完工后,小孔上方液位高度1.8 m,请计算已泄漏掉甲苯的量kg和泄漏始于何时?已知甲苯的密度ρ =900 kg / m3, C0=1。
解:(1)求泄漏质量流量随时间的变化式C0 = 1Q =ρC0A(2gz0)1/2-(ρgC02A2/A0) tz0 = 3m ρ= 900kg/m3g = 9.81A = 0.012×π/4 = 7.854×10-5 m2A0 = 12×π/4 = 0.7854 m2将有关数据代入计算:Q = 900×1×7.854×10-5 (2×9.81×3)1/2-[900×9.81×12×(7.854×10-5)2/0.7854] t整理后得:Q = 0.5423-0.00006934t(2)求任一时间内总的泄漏量W为泄漏质量流量对时间的积分:W =∫0t Qdt =∫0t (0.5423-0.00006934t) dt而W =π/4×D2z1ρ=π/4×12×(3-1.8)×900 = 848.23 kg所以848.23 = ∫0t (0.5423-0.00006934t) dt积分后得:848.23 = 0.5423t-0.00003467t2(a)式(a)为一元二次方程:0.00003467t2-0.5423t + 848.23 = 0求解:根据t =[-b±(b2-4ac)1/2] / 2aa = 0.00003467b =-0.5423c = 848.23t = 0.5423±(0.54232-4×0.00003467×848.23)1/2 /(2×0.00003467)解得:t1 = 13878 s t2 = 1764 s用t1代入(a)式不符,舍去,取t2 = 1764 s (也就是说泄漏掉848.23kg甲苯用时1764秒)1764 / 60 = 29.4 min(3)已知早上7:00发现泄漏并即时堵漏,则泄漏约始于早上6:31分左右,总泄漏掉的甲苯为848.23 kg。
6.4 液体经管道泄漏的源模式化工生产中,通常采用圆形管道输送流体。
如果管道发生爆裂、折断等,可造成液体经管口泄漏,其泄漏过程可用来描述。
其中阻力损失F的计算是估算泄漏速度和泄漏量的关键。
流动阻力分为直管阻力和局部阻力:1、直管阻力F1的计算:(范宁公式) (6—22)式中:λ——摩擦系数,无因次;l——管长,m;d ——管径,m;U ——流速,m/s。
λ的计算与Re数有关,Re≤2000时,属层流,λ=64/Re2000≤Re≤4000时,属过渡流,λ=0.0025Re1/3Re>4000时,属湍流,λ=f ( Re,ε/ d ),ε/d称相对粗糙度,ε为管壁粗糙度,d 为圆管内径。
ε值可由表6.1查得。
对于光滑管:以上是采用一些公式对λ值进行计算,λ也可根据Re和ε/d,查图6.7查得λ值,此图也称莫迪图。
图6.7 莫迪图上图按雷诺准数范围可分为如下四个区域:a、滞流区(Re≤2000),λ=64/Re,与ε/d无关,λ和Re准数成直线关系。
b、过渡区(2000<Re<4000),流动处于不稳定状态,在此区域内滞流或湍流的λ~Re 曲线都可应用。
为安全起见,对于流动阻力的计算,一般将湍流时的曲线延伸,以查取λ值。
c、湍流区(Re≥4000及虚线以下的区域), λ与Re和ε/d均有关,在这个区域内对于不同的ε/d标绘出一系列曲线;其中最下面的一条曲线为流体通过光滑管的摩擦系数λ与Re的关系曲线。
d、完全湍流区(在图中虚线以上的区域),λ与Re无关,仅与ε/d有关。
2、局部阻力F2的计算:可将局部阻力按当量长度或动能折合来计算。
按当量长度计算:(6—23)式中: le——当量长度,m。
按动能计算:(6—24)式中:ξ——局部阻力系数。
ξ值可由表6.2和表6.3查得。
3、总的阻力损失F的计算:总的阻力损失为直管阻力损失和局部阻力损失之和:F=F直管+F局部或F=λ(l/d)×(U2/2)+Σξ(U2/2)(6—25)将已知数据代入(6.3)式并整理(Z是减少,取“-”号):U2/2 +(-gZ)+1.78U1.75 +0.085U2 = 0U2/2 +1.78U1.75 +0.085U2 = 9.8×5将等式两边同乘以2,得:1.17U2+3.56U1.75 = 98再设定流速U的数值,代入上式,直到上等式两端相等:初设U = 5.6 m/s 等式左端为109.3, 等式右端为98,显然不符;重设U = 5.4 m/s 等式左端为102.2, 等式右端为98,显然不符;再设U = 5.3 m/s 等式左端为98.8, 等式右端为98,基本符合;误差:(98.8-98)/98×100 % = 0.8 % 已很小;计算结果显示Re = 5.3×105 在4000 <Re <106 内,说明U选择正确。
泄漏的最大质量流量Q为:Q = ΡUA = 1000×5.3×0.12×π/4 = 41.62 kg/s6.5 气体或蒸汽经小孔泄漏的源模式气体或蒸汽是可压缩气体,工程上通常将气体或蒸汽近似为理想气体,它们的压力、密度、温度等参数遵循理想气体状态方程。
