身高体重分析
体质监测测试数据分析报告

体质监测测试数据分析报告一、引言二、测试数据及分析1.性别:男年龄:30岁2. 身高:180cm 体重:75kg3.体质指数(BMI):23.15BMI=体重(kg)/身高^2(m^2)根据以上测试数据,我们得知被测试个体的体质指数为23.15,属于正常范围。
三、体质指数(BMI)的解读体质指数(BMI)是衡量体重与身高之间关系的指标,是一种判断体重是否偏低或偏高的简单有效方法。
根据世界卫生组织(WHO)的分类,BMI的解读如下:-BMI<18.5体重过轻-18.5<=BMI<24正常范围-24<=BMI<28超重-BMI>=28肥胖据此,我们可以看出该被测试个体的体重处于正常范围内,属于健康水平。
四、其他数据分析除了体质指数之外,还可以根据不同指标的数据进一步评估个体的体质状况。
以下是一些常见测试指标及其分析结果:1. 血压:120/80mmHg(正常范围为90/60mmHg到140/90mmHg)被测试个体的血压值为120/80mmHg,处于正常范围内,说明心血管系统工作正常。
2.体脂率:15%(男性正常范围为10%-20%)被测试个体的体脂率为15%,处于男性正常范围内,说明脂肪分布较为均衡。
3.心率:65次/分钟(正常范围为60-100次/分钟)被测试个体的心率为65次/分钟,处于正常范围内,说明心脏健康。
综合以上数据分析,被测试个体的血压、体脂率和心率等指标均处于正常范围内,属于良好的体质状况。
五、健康建议基于以上测试结果,我们可以给被测试个体一些相应的健康建议:1.保持正常的体重:目前的体重处于正常范围,可以维持现状,避免过度减肥或增肥。
2.均衡饮食:保持饮食均衡,控制热量摄入,注重营养摄取的多样化。
3.运动锻炼:定期进行适量的运动,如有条件,可选择有氧运动、力量训练等。
4.健康生活方式:保持良好的生活习惯,避免熬夜、过度劳累和不健康的饮食习惯。
六、结论通过对被测试个体的体质监测测试数据分析,得出的结论是被测试个体的体质状况良好。
幼儿园身高体重测量分析总结范文(通用15篇)

幼儿园身高体重测量分析总结范文(通用15篇)1. 这次幼儿园身高体重测量分析显示,所有幼儿在生长方面都有了明显的进步。
他们的身高都有了显著的增长,说明他们的饮食和健康状况都有所改善。
同时,他们的体重也有了适当的增加,说明他们获得了足够的营养。
这些结果表明我们的幼儿园在提供健康的生活环境和饮食方面取得了良好的成果。
2. 在这次幼儿园身高体重测量分析中,我们发现一些幼儿的身高和体重增长较慢。
这可能与他们的饮食和生活习惯有关。
在接下来的日子里,我们将加强对这些幼儿的饮食管理和健康指导,确保他们能够获得足够的营养和健康成长。
3. 我们幼儿园这次身高体重测量结果显示了一些令人担忧的情况。
有些幼儿的身高和体重增长过快,可能意味着他们的饮食不够健康。
同时,还有一些幼儿的身高和体重增长过慢,可能与他们的饮食摄入不足有关。
我们将与家长合作,制定健康的饮食计划和生活习惯,确保每个幼儿能够健康成长。
4. 幼儿园身高体重测量分析结果显示,大部分幼儿的身高和体重增长都符合正常范围。
这表明我们幼儿园提供了良好的饮食和生活环境,帮助幼儿们健康成长。
然而,仍然有一小部分幼儿的身高和体重增长不理想。
我们将密切关注他们的饮食和生活习惯,并提供必要的健康指导,确保他们能够健康成长。
5. 在这次身高体重测量分析中,我们观察到一些幼儿的身高增长超过了体重增长,可能表示他们身体状况良好但缺少适当的营养。
相反,还有一些幼儿的体重增长超过身高增长,可能意味着他们摄入了过多的卡路里。
我们将与家长密切合作,提供健康饮食指导,确保每个幼儿都能够取得平衡的身高体重增长。
6. 根据幼儿园身高体重测量分析结果,我们发现大部分幼儿的身高和体重增长都是适宜的。
这显示了我们幼儿园的饮食和生活管理取得了良好的效果。
然而,仍有一些幼儿的身高和体重增长较慢。
我们将关注他们的饮食习惯和生活方式,提供适当的指导和支持,以促进他们的健康成长。
7. 通过这次幼儿园身高体重测量分析,我们发现幼儿的身高和体重增长比例大多数较为均衡。
学生体检情况综合分析报告

学生体检情况综合分析报告尊敬的领导:经过对学生体检情况的全面分析,我将就体检结果中较为突出的几个方面进行分析和总结,以期能为学校更好地开展健康教育和促进学生身心健康提供参考。
一、身高和体重方面根据体检结果统计,学生的平均身高和体重均处于正常范围内,但也存在一些特殊情况。
在身高方面,一些学生的身高明显低于均值,这可能与个体差异、生活习惯以及遗传等因素有关。
对于身高低于正常范围的学生,我们应建议他们改善饮食结构,增加运动锻炼,保证充足的睡眠等,以促进身高的发育。
在体重方面,有一部分学生的体重超过了正常范围,其中一些学生存在肥胖问题。
肥胖问题已成为当今社会的主要健康问题之一,容易导致多种慢性疾病的发生。
因此,我们应该加强对学生的健康教育,提倡健康饮食、合理膳食结构和适量运动,帮助学生养成良好的生活习惯,预防肥胖问题的发生。
二、视力和听力方面眼睛和耳朵是学生学习的重要器官,对于学习能力的影响较大。
在体检中,我们发现学生中有不少视力和听力存在问题。
视力问题主要表现为近视居多,可能与学生过多时间接触电子产品、长时间处于高度集中注意力状态、缺乏户外活动等有关。
要解决视力问题,除了学校和家庭应共同关注,提供良好的学习环境、防控过度疲劳等外,还应加强对学生的眼睛健康教育,引导他们正确使用电子产品、科学用眼,避免近视进一步加深。
听力问题主要集中在一部分学生身上,这可能与学生的生活环境、噪音污染、过度使用耳机等因素有关。
学校应该提供安静的学习环境,防止噪音对学生的听力造成影响。
另外,加强学生耳朵健康教育,告诉他们正确用耳机、远离噪音等措施也是很有必要的。
三、心理健康方面四、运动健康方面随着现代科技的发展,学生的体育锻炼时间逐渐减少,这导致了学生运动健康状况的下降。
体检结果显示,有很多学生体育成绩不达标,体力较差。
为了改善这一状况,学校应加强体育课程的开展,提高学生的体育锻炼兴趣,培养他们的体育习惯。
此外,学校还应组织各类体育活动,增加学生体育锻炼的机会,提高学生的身体素质。
BMI分析与指导

BMI分析与指导BMI(Body Mass Index)是通过身高和体重两个指标来评估一个人是否体重正常、偏瘦还是超重肥胖的一个指标。
它可以帮助我们了解自己的体重状况,并采取相应的行动以维持健康的生活方式。
本文将对BMI的分析和指导进行详细介绍。
首先,让我们了解一下如何计算BMI。
BMI的计算公式为:体重(kg)/身高(m)的平方。
具体来说,计算BMI可以按照以下步骤进行:1.将体重以公斤为单位记下。
2.将身高以米为单位记下。
3.将身高的值平方。
4.用第一步得到的体重值除以第三步得到的身高平方值。
5.得出的结果即为BMI。
了解了如何计算BMI后,接下来是如何分析BMI的结果。
根据世界卫生组织(WHO)的标准,BMI的结果可分为以下几个级别:1.BMI<18.5:体重过轻2.18.5≤BMI<24.9:体重正常3.25≤BMI<29.9:超重4.BMI≥30:肥胖根据自己的BMI结果,可以进行相应的健康指导。
下面是一些建议:1.体重过轻:-增加摄入的卡路里,通过增加蛋白质和健康油脂的摄入来增加肌肉质量。
-增加饮食次数和食量,避免长时间禁食。
-参加适量的运动,如力量训练和有氧运动,以增加肌肉质量。
2.体重正常:-继续保持健康的饮食习惯,包括均衡的营养摄入和适量的能量摄入。
-继续进行适量的运动,至少每周进行150分钟的有氧运动和两次力量训练。
3.超重:-控制饮食,减少高热能和高脂肪食物的摄入。
-增加运动,每周至少进行150分钟的有氧运动和两次力量训练。
-注意避免过度饮食和过度运动,保持适中的健康生活方式。
4.肥胖:-在饮食方面,控制能量摄入,减少高热能、高脂肪和高糖食物的摄入。
-增加运动,每周至少进行150分钟的有氧运动和两次力量训练。
-寻求专业医生的帮助,进行更详细的评估和治疗方案。
此外,BMI也存在一些局限性。
例如,对于一些体肥肌瘦的人来说,BMI可能会高估其体重问题。
因此,在一些特殊情况下,其他更准确的指标如体脂率可能更有意义。
幼儿园幼儿身高体重分析总结【三篇】

幼儿园幼儿身高体重分析总结【三篇】篇一:幼儿园幼儿身高体重的分析总结随着社会的发展,人们的生活方式和饮食习惯也发生了改变。
这些改变以及其他因素都会对幼儿的身高和体重产生影响。
在幼儿园中,身高和体重是常被家长和老师关注的方面之一。
首先,幼儿的身高和体重受到多种因素的影响。
其中包括遗传、环境、饮食、锻炼等。
对于身高而言,遗传因素最为重要,但同时,饮食和运动也是决定身高的重要因素。
对于体重而言,饮食摄入和运动消耗是主要的影响因素。
如果幼儿长期处于高热量、高脂肪的饮食中,同时又缺乏运动,那么很容易导致体重偏胖。
其次,在幼儿园中,我们可以通过定期的身高、体重测量来了解幼儿的身高和体重情况。
通过这些数据,我们可以判断幼儿是否存在身高或体重异常,如果存在异常,我们可以采取一些措施,如调整幼儿的饮食、增加运动等。
此外,我们还可以通过对幼儿的身高和体重进行分类统计,得出某个年龄段或某个性别中身高和体重的平均值,以此来了解幼儿的整体情况。
最后,我们需要注意的是,幼儿期的身高和体重是处于不断增长和发育中的,因此我们不能仅仅根据数据上的大小而做出判断。
如果幼儿身高或体重超过了平均值,当然需要关注,但我们也应该充分考虑孩子的家庭和个人特征,以及年龄和性别等因素,做出科学合理的评估和处理。
总之,在幼儿园中,身高和体重是需要时刻被关注和记录的,它们不仅关乎孩子的身体健康,还涉及家庭、学校、社会等多个层面。
我们应该采取科学合理的方法,全面了解和管理孩子的身高和体重,让他们健康成长。
篇二:幼儿园幼儿身高体重的分析总结在幼儿园中,我们经常会进行身高、体重的测量,以了解孩子们的生长发育情况。
除此之外,身高体重的数据也可以为我们提供一定的参考,以制定幼儿园健康教育和营养膳食计划。
下面,我们来对幼儿园幼儿身高体重的测量数据做一个简要的分析总结。
首先,从幼儿园幼儿总体来看,身高和体重两个指标均呈正态分布。
也就是说,大部分幼儿身高和体重都处于正常水平范围内,少部分幼儿存在身高或体重偏高或偏低的情况。
幼儿身高 体重分析表
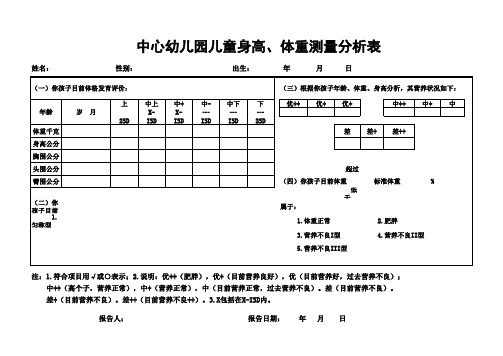
中心幼儿园儿童身高、体重测量分析表
姓名:
性别:
出生:
年
月
日
(一)你孩子目前体格发育评价:
年龄
体重千克 身高公分 胸围公分 头围公分 臂围公分
岁月
上
中上 中+
X-
X-
2SD
ISD
ISD
(二)你 孩子目前
1. 匀称型
(三)根据你孩子年龄、体重、身高分析,其营养状况如下:
中- 中下
下
┄
┄
┄
ISD#43; 优+
中++
中+
中
差 差+ 差++
超过 (四)你孩子目前体重
低 于 属于:
1.体重正常
3.营养不良I型
5.营养不良III型
标准体重
%
2.肥胖 4.营养不良II型
注:1.符合项目用√或○表示;2.说明:优++(肥胖),优+(目前营养良好),优(目前营养好,过去营养不良); 中++(高个子,营养正常),中+(营养正常),中(目前营养正常,过去营养不良)。差(目前营养不良)。 差+(目前营养不良)。差++(目前营养不良++)。3.X包括在X-ISD内。
报告人:
报告日期: 年 月 日
测量我们的身高和体重实验报告单

测量我们的身高和体重实验报告单实验报告标题:身高和体重的测量与分析摘要:本实验旨在通过测量身高和体重的实验数据,分析身高和体重之间的相关性,并探讨其对个体的健康和发育的影响。
实验中共选取了100名年龄在18至25岁的学生参与身高和体重的测量,所有数据均经过统计分析和可视化处理,结果表明身高和体重之间存在一定的正相关性。
引言:身高和体重是人体健康和发育的重要指标,身高通常反映了个体的生长水平和遗传潜力,而体重则反映了个体的整体营养状况和代谢能力。
因此,通过测量身高和体重的数据并分析其相关性,可以更好地了解个体的生长发育情况,从而为改善个体的健康提供科学依据。
材料与方法:1.实验对象:选取100名年龄在18至25岁的学生作为实验对象。
2.测量仪器:身高测量使用的是标准尺子和墙上的高度刻度,体重测量使用的是电子体重秤。
3.测量过程:实验对象站立直立,背部贴紧墙壁,头部保持平直,由实验人员使用标准尺子进行身高测量;然后实验对象脱鞋、脱袜,站到电子体重秤上进行体重测量。
每个实验对象进行身高和体重测量各两次,然后取两次测量结果的平均值。
结果与讨论:1.身高与体重的测量数据统计分析结果如下表所示:编号身高 (cm) 体重 (kg)117267216560317873416055517669.........[插入散点图,横轴为身高,纵轴为体重]3.通过计算身高和体重数据的相关系数,得到相关系数为0.67,表明身高和体重之间存在一定的正相关关系。
结论:通过对100名年龄在18至25岁学生的身高和体重测量实验数据的分析,我们发现身高和体重之间呈现一定的正相关性,即身高较高者体重较重的趋势较为明显。
这一结果支持了生物学理论中身高和体重之间的正相关关系。
因此,在关注个体健康和发育的过程中,不仅要重视营养的供给和代谢的平衡,还需要注重个体生长潜力的发挥和遗传因素的影响。
限制与展望:本实验的样本仅选取了18至25岁的学生,未涵盖其他年龄段的个体,因此不能代表整个人群的身高和体重情况。
幼儿园身高体重测量分析总结

幼儿园身高体重测量分析总结随着社会的进步,人们对幼儿身高体重的关注日益增加。
幼儿园身高体重测量是一项重要的工作,通过对身高体重数据的测量和分析,可以帮助了解幼儿们成长的状态,为幼儿的身体健康提供及时的干预和促进。
本文通过对幼儿园身高体重测量分析总结,探讨幼儿园身高体重测量的重要性以及如何进行科学有效的测量工作。
一、身高体重测量的重要性1.及时掌握幼儿的生长发展状态身高体重是幼儿成长过程中最基本的身体指标,通过测量身高体重可以及时掌握幼儿的生长发育状态,判断是否存在身体偏差、发育滞后等情况,为及时发现问题提供依据。
2.为儿童的健康提供基础数据通过身高体重数据的基础分析,可以发现儿童身体发育是否正常,分析其体型结构,帮助家长和教育工作者了解幼儿成长的状况,为儿童的健康提供基础数据,指导育儿。
3.为幼儿提供有针对性的调整和食谱通过身高体重数据的测量和分析,幼儿园可以根据幼儿的身高体重指数,量身定制合适的食谱和营养搭配,使幼儿获得更加安全健康的生活。
4.促进幼儿自我意识的逐步形成幼儿通过身高体重测量了解自己的身体基本情况,对自己的身体表现和身体感觉有更加清晰的认识,从而有利于形成自我意识,对于幼儿的身体认知、健康习惯培养与提高有着极为积极的推动作用。
二、身高体重测量的操作方法1.测量身高(1)测量前应将幼儿身上的衣物松开,保持稳定站立姿势,双脚分开,两肩平行,头部正对前方。
(2)使用测量身高的标尺,将标尺紧贴幼儿头顶,使其平行于地面。
(3)测量人员仔细观察幼儿头部与标尺之间的尺度读数,将读数记录在体重测量单上。
2.测量体重(1)将幼儿放在体重测量仪上,充分放松。
(2)测量人员使用体重测量仪进行测量,记录幼儿的体重测量值。
(3)注意:在测量体重时,应注意幼儿体重的变化和波动,尤其在儿童生长发育、季节变化、用药、患病、运动性活动等情况下,体重的测量会有所变化,应给予相应的调整。
三、身高体重测量后分析的应用工具1.标准成长曲线标准成长曲线可以根据幼儿的生长发育指标,结合现有疾病、营养知识,制作相应的成长图表,直观地展示幼儿的生长状态,帮助医生、教育工作者和家长及时了解并掌握幼儿的生长发育情况。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经济运行模拟:身高体重分析姓名:***学号:***********指导老师:***院系:经济学院身高体重分析王萌萌(河南财经政法大学经济学院郑州 450000)一、实验目的为了研究河南财经政法大学09级经济学院同学身高体重的关系,同时考虑性别因素对体重的影响。
建立身高体重模型,首先对经济二班同学的身高体重回归分析。
为了进一步说明身高对于体重的影响,同时对经济学院四个班同学的身高体重进行回归分析。
二、数据说明表 1:09级经济学院四个班学生身高体重数据以上数据由09级经济学院学生登记提供三、实证分析(一)09级经济二班同学的身高体重简单回归分析1.建立模型为了分析09级经济二班身高体重的关系。
估计模型如下:u H W +∂+∂=10其中W 代表体重(kg ),H 代表身高(cm),10∂∂、代表回归系数,u 代表随机误差项。
2.估计结果通过运行Eviews5.0估计结果如下:表二:二班同学身高h (cm )体重w (kg )估计结果Dependent Variable: W Method: Least Squares Date: 05/11/12 Time: 08:41 Sample: 1 43Included observations: 43Variable Coefficient Std. Error t-Statistic Prob.H 1.238985 0.152011 8.150606 0.0000 C-150.488425.78017-5.8373730.0000R-squared 0.618365 Mean dependent var 59.41860 Adjusted R-squared 0.609056 S.D. dependent var 12.28284 S.E. of regression 7.679906 Akaike info criterion 6.960487 Sum squared resid 2418.219 Schwarz criterion 7.042403 Log likelihood -147.6505 F-statistic 66.43238 Durbin-Watson stat1.950340 Prob(F-statistic)0.000000估计方程为: H W238985.14884.150ˆ+-= 25.78017 0.152011 t 值 -5.837373 8.150606 P 值 0.0000 0.00002R =0.618365,2R =0.609056,F=66.43238(P=0.0000)3.模型检验P 检验:由表一可知,p 值(0.0000),在0.05的显著水平下,p 值小于0.05,拒绝原假设。
说明二班同学身高对体重的影响是显著的。
(二)二班数据加虚拟变量回归(加法模型)1.建立模型为了研究二班同学身高体重关系,并考虑性别因素建立模型如下 加法模型u S H W +∂+∂+∂=210其中W 代表体重(kg ),H 代表身高(cm ),S代表性别, ⎩⎨⎧=女男10S 为虚拟变量,10∂∂、是回归系数,u 是随机误差项。
表三:二班同学身高体重模型考虑性别因素估计结果(加法模型)Dependent Variable: W Method: Least Squares Date: 05/11/12 Time: 09:12 Sample: 1 43Included observations: 43VariableCoefficient Std. Error t-Statistic Prob. S -7.591082 4.365116 -1.739033 0.0897 H 0.820754 0.282592 2.904375 0.0060 C -75.5721249.89161 -1.5147260.1377R-squared 0.645190 Mean dependent var 59.41860 Adjusted R-squared 0.627450 S.D. dependent var 12.28284 S.E. of regression 7.497065 Akaike info criterion 6.934114 Sum squared resid 2248.239 Schwarz criterion 7.056989 Log likelihood -146.0835 F-statistic 36.36825 Durbin-Watson stat2.039081 Prob(F-statistic)0.0000002.估计结果估计结果如下:S H W591082.7820754.057212.75ˆ-+-= (49.89161) (0.282592) (4.365116)t 值 -1.514726 2.904375 -1.739033 p 值 0.1377 0.0060 0.08972R =0.645190,2R =0.627450,F=36.36825(P=0.0000)3.模型检验通过OLS 法引入虚拟变量估计结果可知,在0.05的显著水平下,p 值(0.0897)>0.05,接受原假设。
即可认为性别对体重无显著影响。
(三)二班数据加虚拟变量回归(乘法模型)1.建立模型为了研究二班同学身高体重的关系,同时考虑性别因素的影响。
按照乘法方式引入虚拟变量,建立模型如下:u SHH W +∂+∂+∂=210,⎩⎨⎧=女男10S其中W 代表体重(kg),H 代表身高(cm ),S 代表性别,10∂∂、是回归系数,u 是随机误差项。
2.估计结果通过运行eviews5.0估计结果如下:表四:二班同学身高体重模型考虑性别因素的估计结果(乘法模型)Dependent Variable: W Method: Least Squares Date: 05/11/12 Time: 09:32Sample: 1 43Included observations: 43VariableCoefficientStd. Error t-Statistic Prob.SH -0.046104 0.025911 -1.779349 0.0828 H 0.828742 0.274053 3.024024 0.0043 C-76.9585248.36264-1.5912810.1194R-squared 0.646356 Mean dependent var 59.41860 Adjusted R-squared 0.628674 S.D. dependent var 12.28284 S.E. of regression 7.484737 Akaike info criterion 6.930823 Sum squared resid 2240.851 Schwarz criterion 7.053697 Log likelihood -146.0127 F-statistic 36.55409 Durbin-Watson stat2.038843 Prob(F-statistic)0.000000估计方程为:SH H W046104.0828742.095852.76ˆ-+-= (48.36264)(0,274053)(0.025911)t 值 -1.591281 3.024024 -1.779349p 值 0.1194 0.0043 0.08282R =0.646356,2R =0.628674,F=36.55409(p=0.0000)3.模型检验p 检验:由表四知,S 的p 值为0.0828大于0.05,所以接受原假设。
即认为性别对体重无显著影响。
根据常识,身高对体重有影响的。
但根据二班数据,我们得出性别对体重无影响的结论,结果与常识相违背。
这可能是因为样本容量太小的原因,样本容量太小可能会因为其他因素干扰,导致性别因素不显著(四)经济学院学生身高体重数据简单回归1.建立模型为了分析经济学院学生身高与体重关系建立模型如下(模型四):u H W ++=1101ββ其中H 表示身高(cm ),W 表示体重(kg ),10 ββ,代表回归系数,u 代表随机误差项。
2.估计结果通过运行eviews5.0估计结果如下:表 五:经济学院同学身高体重回归模型估计结果Dependent Variable: W1 Method: Least Squares Date: 05/14/12 Time: 15:28Sample: 1 167Included observations: 167Variable Coefficient Std. Error t-Statistic Prob.H1 1.088517 0.068225 15.95490 0.0000 C-124.137911.46084-10.831490.0000R-squared0.606730 Mean dependent var 58.55689 Adjusted R-squared 0.604346 S.D. dependent var 9.899711 S.E. of regression 6.227018 Akaike info criterion 6.507576 Sum squared resid 6398.000 Schwarz criterion 6.544917 Log likelihood -541.3826 F-statistic 254.5588 Durbin-Watson stat1.931333 Prob(F-statistic) 0.000000下面是利用OLS 法估计模型得到的回归结果:(11.46084) (0.068225) t 值-10.83149 15.95490p 值0.0000 0.00002R =0.606730,2R =0.604346,F=254.5588(P=0.0000)3.模型检验P 检验:由表五可知,1H 的p 值为0.0000小于0.05,所以拒绝原假设。
即认为身高对体重有显著影响。
(五)经济学院学生身高体重加虚拟变量数据回归(加法模型)1.建立模型为了分析经济学院同学性别因素对体重的影响以加法方式加入性别虚拟变量建立模型如下:u S H W +++=121101βββ其中1H 表示身高(cm),1W 表示体重(kg),1S 的代表性别,当性别为女时1S =0,11088517.11379.-124ˆH W +=性别为男时1S =1,210 βββ,,代表回归系数,u 代表随机误差项。
2.估计结果由eviews5.0估计结果如下:表 六:经济学院同学身高体重以加法方式引入虚拟变量函数估计结果Dependent Variable: W1 Method: Least Squares Date: 05/14/12 Time: 15:56 Sample: 1 167Included observations: 167Variable Coefficient Std. Error t-Statistic Prob.H1 0.840822 0.110912 7.580987 0.0000 S1 4.407906 1.574893 2.798861 0.0057 C-84.5448818.06213-4.6807820.0000R-squared0.624658 Mean dependent var 58.55689 Adjusted R-squared 0.620081 S.D. dependent var 9.899711 S.E. of regression 6.101942 Akaike info criterion 6.472892 Sum squared resid 6106.325 Schwarz criterion 6.528904 Log likelihood -537.4865 F-statistic 136.4676 Durbin-Watson stat2.026940 Prob(F-statistic) 0.000000下面是利用OLS 法估计模型得到的回归结果:111407906.4840822.054488.-84ˆS H W ++= (18.06213)(0.110912) (1.574893)t 值 -4.680782 7.580987 2.798861 P 值 0.0000 0.0000 0.0057)0000.0(4676.136,620081.0,624658.022====值P F R R3.模型检验在05.0=α对2α进行显著性检验,1S 对应的P 统计量为0.0057, P >α,故02≠α显著成立,得到1S 对体重1W 具有显著影响。
