2013年挑战中考数学压轴题预测附(精选中考题训练)

合集下载

2013年中考数学压轴题精选

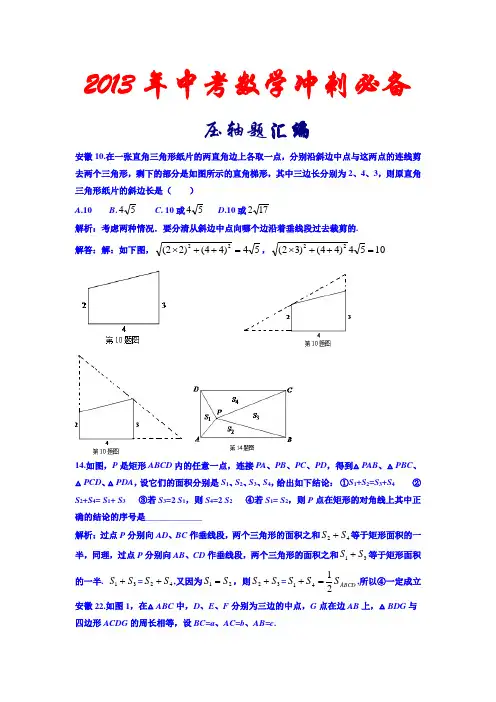
2013年中考数学冲刺必备压轴题汇编安徽10.在一张直角三角形纸片的两直角边上各取一点，分别沿斜边中点与这两点的连线剪去两个三角形，剩下的部分是如图所示的直角梯形，其中三边长分别为2、4、3，则原直角三角形纸片的斜边长是（）A .10B .54C . 10或54D .10或172解析：考虑两种情况．要分清从斜边中点向哪个边沿着垂线段过去裁剪的.解答：解：如下图，54)44()22(22=++⨯，1054)44()32(22=++⨯14.如图，P 是矩形ABCD 内的任意一点，连接PA 、PB 、PC 、PD ，得到△PAB 、△PBC 、△PCD 、△PDA ，设它们的面积分别是S 1、S 2、S 3、S 4，给出如下结论： ①S 1+S 2=S 3+S 4 ② S 2+S 4= S 1+ S 3 ③若S 3=2 S 1，则S 4=2 S 2 ④若S 1= S 2，则P 点在矩形的对角线上其中正确的结论的序号是_____________解析：过点P 分别向AD 、BC 作垂线段，两个三角形的面积之和42S S +等于矩形面积的一半，同理，过点P 分别向AB 、CD 作垂线段，两个三角形的面积之和31S S +等于矩形面积的一半. 31S S +=42S S +,又因为21S S =，则32S S +=ABCD S S S 2141=+,所以④一定成立安徽22.如图1，在△ABC 中，D 、E 、F 分别为三边的中点，G 点在边AB 上，△BDG 与四边形ACDG 的周长相等，设BC =a 、AC =b 、AB =c .（1）求线段BG 的长；（2）求证：DG 平分∠EDF ;（3）连接CG ，如图2，若△BDG 与△DFG 相似，求证：BG ⊥CG . 解（1）∵D 、C 、F 分别是△ABC 三边中点 ∴DE ∥21AB ,DF ∥21AC ，又∵△BDG 与四边形ACDG 周长相等即BD +DG +BG =AC +CD +DG +AG∴BG =AC +AG ∵BG =AB －AG ∴BG =2AC AB +=2cb +（2）证明：BG =2c b +，FG =BG －BF =2c b +－22bc = ∴FG =DF ,∴∠FDG =∠FGD 又∵DE ∥AB∴∠EDG =∠FGD ∠FDG =∠EDG ∴DG 平分∠EDF （3）在△DFG 中，∠FDG =∠FGD , △DFG 是等腰三角形,∵△BDG 与△DFG 相似,∴△BDG 是等腰三角形,∴∠B =∠BGD ,∴BD =DG , 则CD = BD =DG ,∴B 、CG 、三点共圆, ∴∠BGC =90°,∴BG ⊥CG23.如图，排球运动员站在点O 处练习发球，将球从O 点正上方2m 的A 处发出，把球看成点，其运行的高度y （m ）与运行的水平距离x (m )满足关系式y =a (x －6)2+h .已知球网与O 点的水平距离为9m ，高度为2.43m ，球场的边界距O 点的水平距离为18m 。

挑战中考数学压轴题[2013中考版]

图1
动感体验
请打开几何画板文件名―12 黄冈 25‖，拖动点 C 在 x 轴正半轴上运动，观察左图，可以体验到，EC 与 BF 保持平行，但是∠BFC 在无限远处也不等于 45° ．观察右图，可以体验到，∠CBF 保持 45° ，存在 ∠BFC＝∠BCE 的时刻．
思路点拨
1．第（3）题是典型的―牛喝水‖问题，当 H 落在线段 EC 上时，BH＋EH 最小． 2．第（4）题的解题策略是：先分两种情况画直线 BF，作∠CBF＝∠EBC＝45° ，或者作 BF//EC．再用含 m 的式子表示点 F 的坐标．然后根据夹角相等，两边对应成比例列关于 m 的方程．
满分解答
4
b )． 4 （2）如图 2，过点 P 作 PD⊥x 轴，PE⊥y 轴，垂足分别为 D、E，那么△PDB≌△PEC．因此 PD＝PE．设点 P 的坐标为(x, x)．如图 3，联结 OP． 1 b 1 5 所以 S 四边形 PCOB＝S△PCO＋S△PBO＝ x b x bx ＝2b． 2 4 2 8 16 16 16 解得 x ．所以点 P 的坐标为( , )． 5 5 5
所以 C、Q、B 三点共线．因此
BO QA ，即 b QA ．解得 QA 4 ．此时 Q(1,4)． b CO OA 1 4
图4
图5
考点伸展
第（3）题的思路是，A、C、O 三点是确定的，B 是 x 轴正半轴上待定的点，而∠QOA 与∠QOC 是互余的，那么我们自然想到三个三角形都是直角三角形的情况．这样，先根据△QOA 与△QOC 相似把点 Q 的位置确定下来，再根据两直角边对应成比例确定点 B 的位置．如图中，圆与直线 x＝1 的另一个交点会不会是符合题意的点 Q 呢？如果符合题意的话，那么点 B 的位置距离点 A 很近，这与 OB＝4OC 矛盾．

2013年全国部分地市中考数学压轴题集(含答案)

2013年全国各地中考压轴试题精选代数几何综合1、（2013年潍坊市压轴题）如图，抛物线c bx ax y ++=2关于直线1=x 对称，与坐标轴交于C B A 、、三点，且4=AB ,点⎪⎭⎫ ⎝⎛232，D 在抛物线上，直线是一次函数()02≠-=k kx y 的图象，点O 是坐标原点.（1）求抛物线的解析式；（2）若直线平分四边形OBDC 的面积，求k 的值.（3）把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线与直线交于N M 、两点，问在y 轴正半轴上是否存在一定点P ，使得不论k 取何值，直线PM 与PN 总是关于y 轴对称？若存在，求出P 点坐标；若不存在，请说明理由.答案：（1）因为抛物线关于直线x =1对称，AB =4，所以A (－1，0),B (3，0), 由点D (2，1.5)在抛物线上，所以⎩⎨⎧=++=+-5.1240c b a c b a ，所以3a +3b =1.5,即a +b =0.5,又12=-a b ，即b=－2a,代入上式解得a =－0.5,b =1,从而c =1.5,所以23212++-=x x y . （2）由（1）知23212++-=x x y ，令x =0,得c (0,1.5),所以CD //AB ,令kx －2=1.5,得l 与CD 的交点F (23,27k )，令kx －2=0，得l 与x 轴的交点E (0,2k)，根据S 四边形OEFC =S 四边形EBDF 得：OE +CF =DF +BE , 即：,511),272()23(272=-+-=+k k k k k 解得（3）由（1）知,2)1(21232122+--=++-=x x x y 所以把抛物线向左平移1个单位，再向下平移2个单位，所得抛物线的解析式为221x y -= 假设在y 轴上存在一点P (0，t )，t ＞0，使直线PM 与PN 关于y 轴对称，过点M 、N 分别向y 轴作垂线MM 1、NN 1，垂足分别为M 1、N 1，因为∠MPO =∠NPO ,所以Rt △MPM 1∽Rt △NPN 1, 所以1111PN PM NN MM =,………………(1) 不妨设M (x M ,y M )在点N (x N ,y N )的左侧，因为P 点在y 轴正半轴上，则（1）式变为NMN M y t y t x x --=-,又y M =k x M －2, y N =k x N －2, 所以（t +2）(x M +x N )=2k x M x N ,……(2) 把y =kx －2(k ≠0)代入221x y -=中，整理得x 2+2kx －4=0, 所以x M +x N =－2k , x M x N =－4,代入（2）得t =2,符合条件，故在y 轴上存在一点P （0,2），使直线PM 与PN 总是关于y 轴对称.考点：本题是一道与二次函数相关的压轴题，综合考查了考查了二次函数解析式的确定，函数图象交点及图形面积的求法，三角形的相似，函数图象的平移，一元二次方程的解法等知识，难度较大.点评：本题是一道集一元二次方程、二次函数解析式的求法、相似三角形的条件与性质以及质点运动问题、分类讨论思想于一体的综合题，能够较好地考查了同学们灵活应用所学知识，解决实际问题的能力。

2013年中考压轴题预测

12013中考数学压轴题预测(第28题，12分）函数图象中点的存在性问题1.1 因动点产生的相似三角形问题例1、如图1，已知抛物线211(1)444b y x b x =-++（b 是实数且b ＞2）与x 轴的正半轴分别交于点A 、B （点A 位于点B 是左侧），与y 轴的正半轴交于点C ．（1）点B 的坐标为______，点C 的坐标为__________（用含b 的代数式表示）；（2）请你探索在第一象限内是否存在点P ，使得四边形PCOB 的面积等于2b ，且△PBC 是以点P 为直角顶点的等腰直角三角形？如果存在，求出点P 的坐标；如果不存在，请说明理由；（3）请你进一步探索在第一象限内是否存在点Q ，使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点Q 的坐标；如果不存在，请说明理由．图11.2 因动点产生的等腰三角形问题例1、如图1，抛物线y＝ax2＋bx＋c经过A(－1,0)、B(3, 0)、C(0 ,3)三点，直线l是抛物线的对称轴．（1）求抛物线的函数关系式；（2）设点P是直线l上的一个动点，当△P AC的周长最小时，求点P的坐标；（3）在直线l上是否存在点M，使△MAC为等腰三角形，若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．图12例2、如图1，点A在x轴上，OA＝4，将线段OA绕点O顺时针旋转120°至OB的位置．（1）求点B的坐标；（2）求经过A、O、B的抛物线的解析式；（3）在此抛物线的对称轴上，是否存在点P，使得以点P、O、B为顶点的三角形是等腰三角形？若存在，求点P的坐标；若不存在，请说明理由．图1341.3 因动点产生的直角三角形问题例1、如图1，抛物线233384y xx =--+与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ．（1）求点A 、B 的坐标；（2）设D 为已知抛物线的对称轴上的任意一点，当△ACD 的面积等于△ACB 的面积时，求点D 的坐标；（3）若直线l 过点E (4, 0)，M 为直线l 上的动点，当以A 、B 、M 为顶点所作的直角三角形有且只有．．．．三个时，求直线l 的解析式．图11.4 因动点产生的平行四边形问题例1、如图1，在平面直角坐标系中，已知抛物线经过A(－4,0)、B(0,－4)、C(2,0)三点．（1）求抛物线的解析式；（2）若点M为第三象限内抛物线上一动点，点M的横坐标为m，△MAB的面积为S，求S关于m的函数关系式，并求出S的最大值；（3）若点P是抛物线上的动点，点Q是直线y＝－x上的动点，判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形，直接写出相应的点Q的坐标．图1 图251.5 因动点产生的梯形问题例1、如图1，把两个全等的Rt△AOB和Rt△COD方别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A(1，2)，过A、C两点的直Array线分别交x轴、y轴于点E、F．抛物线y＝ax2＋bx＋c经过O、A、C三点．（1）求该抛物线的函数解析式；（2）点P为线段OC上的一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由；（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移的过程中与△COD重叠部分的面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．671.6 因动点产生的面积问题例 1、如图1，在平面直角坐标系中，直线112y x =+与抛物线y ＝ax 2＋bx －3交于A 、B两点，点A 在x 轴上，点B 的纵坐标为3．点P 是直线AB 下方的抛物线上的一动点（不与点A 、B 重合），过点P 作x 轴的垂线交直线AB 于点C ，作PD ⊥AB 于点D ．（1）求a 、b 及sin ∠ACP 的值；（2）设点P 的横坐标为m ．①用含m 的代数式表示线段PD 的长，并求出线段PD 长的最大值；②连结PB ，线段PC 把△PDB 分成两个三角形，是否存在适合的m 的值，使这两个三角形的面积比为9∶10？若存在，直接写出m 的值；若不存在，请说明理由．图18。

2013年中考数学压轴题专项练习

2013年中考数学压轴题专项练习1，观察下列一组等式： 11×2＝1－12，12×3＝12－13，13×4＝13－14，…．解答下列问题：将以上三个等式两边分别相加得： 11×2＋12×3＋13×4＝1－12＋12－13＋13－14．(1)对于任意的正整数n：1n(n＋1)＝．【证】(2)计算： 11×2＋12×3＋13×4＋…＋12011×2012＝．【解】(3)已知m为正整数化简： 11×3＋13×5＋15×7＋…＋1(2m－1)(2m＋1)＝．2、在△ABC中，AB＝AC，D是线段BC的延长线上一点，以AD为一边在AD的右侧．．作△ADE，使AE＝AD，∠DAE＝∠BAC，连接CE．(1)如图1，点D在线段BC的延长线上移动，若∠BAC＝30°，则∠DCE＝．(2)设∠BAC＝α，∠DCE＝β：①如图1，当点D在线段BC的延长线上移动时，α与β之间有何的数量关系？请说明理由；②当点D在直线BC上(不与B、C重合)移动时，α与β之间有何的数量关系？请直接写出你的结论．AB C D EB C B CA A备用图备用图3、某商业公司为指导某种应季商品的生产和销售，对三月份至七月份该商品的售价和生产进行了调研，结果如下：一件商品的售价M(元)与时间t(月)的关系可用一条线段上的点来表示(如图甲)，一件商品的成本Q(元)与时间t(月)的关系可用一条抛物线上的点来表示，其中6月份成本最高(如图乙)．根据图象提供的信息解答下面问题：(1)一件商品在3月份出售时的利润是多少元?(利润＝售价－成本)(2)求出图(乙)中表示的一件商品的成本Q(元)与时间t(月)之间的函数关系式；(3)你能求出3月份至7月份一件商品的利润W(元)与时间t(月)之间的函数关系式吗?若该公司能在一个月内售出此种商品30000件，请你计算该公司在一个月内最少获利多少元?4、阅读下列材料：我们知道|x|的几何意义是在数轴上数x对应的点与原点的距离；即，也就是说，|x|表示在数轴上数x与数0对应点之间的距离；这个结论可以推广为表示在数轴上，对应点之间的距离；例1:解方程，容易看出，在数轴下与原点距离为2点的对应数为±2，即该方程的解为x=±2例2:解不等式▏x-1▏＞2，如图，在数轴上找出▏x-1▏=2的解，即到1的距离为2的点对应的数为－1、3，则▏x-1▏＞2的解为x<－1或x>3例3:解方程。

2013中考数学压轴题(含答案)

1、如图12，已知直线12y x =与双曲线(0)k y k x =>交于A B ，两点，且点A 的横坐标为4．（1）求k 的值；（2）若双曲线(0)ky k x =>上一点C 的纵坐标为8，求A O C △的面积；（3）过原点O 的另一条直线l 交双曲线(0)ky k x =>于P Q ，两点（P 点在第一象限），若由点A B P Q ，，，为顶点组成的四边形面积为24，求点P 的坐标．解：(1)∵点A 横坐标为4 , ∴当 x = 4时，y = 2 .∴ 点A 的坐标为（ 4，2 ）.∵ 点A 是直线与双曲线（k>0）的交点 , ∴ k = 4 ×2 = 8 .(2) 解法一：如图12-1，∵ 点C 在双曲线上，y = 8时，x = 1∴ 点C 的坐标为 ( 1, 8 ) .过点A 、C 分别做x 轴、y 轴的垂线，垂足为M 、N ，得矩形DMON .S 矩形ONDM = 32 ， S △ONC = 4 ， S △CDA = 9， S △OAM = 4 .S △AOC = S 矩形ONDM - S △ONC - S △CDA - S △OAM = 32 - 4 - 9 - 4 = 15 .解法二：如图12-2，过点 C 、A 分别做x 轴的垂线，垂足为E 、F ，∵ 点C 在双曲线8y x =上，当y = 8时，x = 1 .∴ 点C 的坐标为 ( 1, 8 ).图12O x A y B x y 21x y 8=∵ 点C 、A 都在双曲线8y x =上 ,∴ S △COE = S △AOF = 4 。

∴ S △COE + S 梯形CEFA = S △COA + S △AOF .∴ S △COA = S 梯形CEFA .∵ S 梯形CEFA = 12×（2+8）×3 = 15 ,∴ S △COA = 15 .（3）∵ 反比例函数图象是关于原点O 的中心对称图形 ,∴ OP=OQ ，OA=OB .∴ 四边形APBQ 是平行四边形 .∴ S △POA = S 平行四边形APBQ = ×24 = 6 .设点P 的横坐标为m （m > 0且4m ≠）,得P ( m , ) .过点P 、A 分别做x 轴的垂线，垂足为E 、F ，∵ 点P 、A 在双曲线上，∴S △POE = S △AOF = 4 .若0＜m ＜4，如图12-3，∵ S △POE + S 梯形PEFA = S △POA + S △AOF ,∴ S 梯形PEFA = S △POA = 6 .∴ 18(2)(4)62m m +⋅-=.4141m8解得m = 2，m = - 8(舍去) .∴ P （2，4）.若 m ＞ 4，如图12-4，∵ S △AOF + S 梯形AFEP = S △AOP + S △POE ,∴ S 梯形PEFA = S △POA = 6 .∴18(2)(4)62m m +⋅-=，解得m = 8，m = - 2 (舍去) .∴ P （8，1）.∴ 点P 的坐标是P （2，4）或P （8，1）.2、如图，抛物线212y x mx n =++交x 轴于A 、B 两点，交y 轴于点C ，点P 是它的顶点，点A的横坐标是-3，点B 的横坐标是1．(1)求m 、n 的值；(2）求直线PC 的解析式；(3）请探究以点A 为圆心、直径为5的圆与直线 PC 的位置关系，并说明理由．(参考数：2 1.41≈，3 1.73≈，5 2.24≈) 解： (1)由已知条件可知：抛物线212y x mx n =++经过A (-3，0)、B (1，0)两点． ∴ 903,210.2m n m n ⎧=-+⎪⎪⎨⎪=++⎪⎩ ……………………………………2分解得 31,2m n ==-． ………………………3分 (2) ∵21322yx x =+-， ∴ P (-1，-2)，C 3(0,)2-． …………………4分设直线PC 的解析式是y kx b =+，则2,3.2k b b -=-+⎧⎪⎨=-⎪⎩ 解得13,22k b ==-． ∴ 直线PC 的解析式是1322yx =-． …………………………6分说明：只要求对1322k b ==-，，不写最后一步，不扣分．(3) 如图，过点A 作AE ⊥PC ，垂足为E ．设直线PC 与x 轴交于点D ，则点D 的坐标为(3，0)． ………………………7分在Rt△O CD 中，∵ O C =32，3O D =， ∴ 2233()3522C D =+=． …………8分∵ O A =3，3O D =，∴AD =6． (9)分 ∵ ∠C O D =∠AED =90o ，∠CD O 公用，∴ △C O D ∽△AED ． ……………10分 ∴ OCC D AEAD =，即335226AE =． ∴ 655AE =． …………………11分 ∵ 65 2.688 2.55> ，∴ 以点A 为圆心、直径为5的圆与直线PC 相离． …………12分。

中考数学压轴题100题精选(21-30题)2013

中考数学压轴题100题精选（21-30题）（答案在本人文辑中寻找）【021】如图，点P 是双曲线11(00)k y k x x=<<，上一动点，过点P 作x 轴、y 轴的垂线，分别交x 轴、y 轴于A 、B 两点，交双曲线y =xk 2（0＜k 2＜|k 1|）于E 、F 两点．（1）图1中，四边形PEOF 的面积S 1= ▲ (用含k 1、k 2的式子表示)；（2）图2中，设P 点坐标为（－4，3）．①判断EF 与AB 的位置关系，并证明你的结论；②记2PEF OEF S S S ∆∆=-，S 2是否有最小值？若有，求出其最小值；若没有，请说明理由。

【022】一开口向上的抛物线与x 轴交于A (m －2，0)，B (m ＋2，0)两点，记抛物线顶点为C ，且AC ⊥BC ．(1)若m 为常数，求抛物线的解析式；(2)若m 为小于0的常数，那么(1)中的抛物线经过怎么样的平移可以使顶点在坐标原点？(3)设抛物线交y 轴正半轴于D 点，问是否存在实数m ，使得△BCD 为等腰三角形？若存在，求出m 的值；若不存在，请说明理由．【023】如图，在梯形ABCD 中，24AD BC AD BC ==∥，，，点M 是AD 的中点，MBC △是等边三角形．（1）求证：梯形ABCD 是等腰梯形；（2）动点P 、Q 分别在线段BC 和MC 上运动，且60MPQ =︒∠保持不变．设PC x MQ y ==，，求y 与x 的函数关系式；（3）在（2）中：①当动点P 、Q 运动到何处时，以点P 、M 和点A 、B 、C 、D 中的两个点为顶点的四边形是平行四边形？并指出符合条件的平行四边形的个数；②当y 取最小值时，判断PQC △的形状，并说明理由．【024】如图，已知ABC ∆为直角三角形，90ACB ∠=︒，AC BC =,点A 、C 在x 轴上，点B 坐标为（3，m ）（0m >），线段AB 与y 轴相交于点D ，以P （1，0）为顶点的抛物线过点B 、D ．（1）求点A 的坐标（用m 表示）；（2）求抛物线的解析式；（3）设点Q 为抛物线上点P 至点B 之间的一动点，连结PQ 并延长交BC 于点E ，连结 BQ 并延长交AC 于点F ，试证明：()FC AC EC +为定值．ADCB P MQ60°【025】如图12，直线4+-=x y 与两坐标轴分别相交于A 、B 点，点M 是线段AB 上任意一点（A 、B 两点除外），过M 分别作MC ⊥OA 于点C ，MD ⊥OB 于D ．（1）当点M 在AB 上运动时，你认为四边形OCMD 的周长是否发生变化？并说明理由；（2）当点M 运动到什么位置时，四边形OCMD 的面积有最大值？最大值是多少？（3）当四边形OCMD 为正方形时，将四边形OCMD 沿着x 轴的正方向移动，设平移的距离为)40<<a a （，正方形OCMD 与△AOB 重叠部分的面积为S ．试求S 与a 的函数关系式并画出该函数的图象．图12（1）图12（2）图12（3）【026】如图11，在△ABC中，∠C=90°，BC=8，AC=6，另有一直角梯形DEFH（HF∥DE，∠HDE=90°）的底边DE落在CB上，腰DH落在CA上，且DE=4，∠DEF=∠CBA，AH∶AC=2∶3（1）延长HF交AB于G，求△AHG的面积.（2）操作：固定△ABC，将直角梯形DEFH以每秒1个单位的速度沿CB方向向右移动，直到点D与点B重合时停止，设运动的时间为t秒，运动后的直角梯形为DEFH′（如图12）.探究1：在运动中，四边形CDH′H能否为正方形？若能，请求出此时t的值；若不能，请说明理由.探究2：在运动过程中，△ABC与直角梯形DEFH′重叠部分的面积为y，求y与t的函数关系.【027】阅读材料：如图12-1，过△ABC 的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC 的“水平宽”(a )，中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”.我们可得出一种计算三角形面积的新方法：ah S ABC 21=∆，即三角形面积等于水平宽与铅垂高乘积的一半. 解答下列问题：如图12-2，抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0)，交y 轴于点B . (1)求抛物线和直线AB 的解析式；(2)点P 是抛物线(在第一象限内)上的一个动点，连结PA ，PB ，当P 点运动到顶点C 时，求△CAB 的铅垂高CD 及CAB S ∆； (3)是否存在一点P ，使S △PAB =89S △CAB ，若存在,求出P 点的坐标；若不存在，请说明理由.图12-2xC Oy ABD 1 1【028】如图，已知抛物线与x 交于A(－1，0)、E(3，0)两点，与y 轴交于点B(0，3)。

2013年中考数学压轴题 2-含答案

1.如图，抛物线的顶点为A （2，1），且经过原点O ，与x 轴的另一个交点为B ．（1）求抛物线的解析式；（2）在抛物线上求点M ，使△MOB 的面积是△AOB 面积的3倍；（3）连结OA ，AB ，在x 轴下方的抛物线上是否存在点N ，使△OBN 与△OAB 相似？若存在，求出N 点的坐标；若不存在，说明理由．解：（1）由题意，可设抛物线的解析式为y ＝a (x －2)2＋1．∵抛物线经过原点，∴a (0－2)2＋1＝0，∴a ＝－41． ∴抛物线的解析式为y ＝－41(x －2)2＋1＝－41x 2＋x ． ························· 3分（2）△AOB 和所求△MOB 同底不等高，若S △MOB ＝3S △AOB ，则△MOB 的高是△AOB 高的3倍，即M 点的纵坐标是－3． ············································································· 5分∴－41x 2＋x ＝－3，整理得x 2－4x －12＝0，解得x 1＝6，x 2＝－2． ∴满足条件的点有两个：M 1(6，－3)，M 2(－2，－3) ····························· 7分（3）不存在． ········································································································ 8分理由如下：由抛物线的对称性，知AO ＝AB ，∠AOB ＝∠ABO ．若△OBN ∽△OAB ，则∠BON ＝∠BOA ＝∠BNO ．设ON 交抛物线的对称轴于A ′ 点，则A ′ (2，－1)．∴直线ON 的解析式为y ＝－21x ．由21x ＝－41x 2＋x ，得x 1＝0，x 2＝6． ∴N (6，－3)．过点N 作NC ⊥x 轴于C ．在Rt △BCN 中，BC ＝6－4＝2，NC ＝3∴NB ＝2232＋＝13．∵OB ＝4，∴NB ≠OB ，∴∠BON ≠∠BNO ，∴△OBN 与△OAB 不相似．同理，在对称轴左边的抛物线上也不存在符合条件的N 点．∴在x 轴下方的抛物线上不存在点N ，使△OBN 与△OAB 相似． ····· 10分2.如图，在直角坐标系中，点A 的坐标为(－2，0)，连结OA ，将线段OA 绕原点O 顺时针旋转120°，得到线段OB ．（1）求点B 的坐标；（2）求经过A 、O 、B 三点的抛物线的解析式；（3）在（2）中抛物线的对称轴上是否存在点C ，使△BOC 的周长最小？若存在，求出点C 的坐标；若不存在，请说明理由．（4）如果点P 是（2）中的抛物线上的动点，且在x 轴的下方，那么△PAB 是否有最大面积？若有，求出此时P 点的坐标及△PAB 的最大面积；若没有，请说明理由．（1）如图1，过点B 作BM ⊥x 轴于M ．由旋转性质知OB ＝OA ＝2．∵∠AOB ＝120°，∴∠BOM ＝60°．∴OM ＝OB ·cos60°＝2×21＝1，BM ＝OB ·sin60°＝2×23＝3． ∴点B 的坐标为(1，3)． ··········································· 1分（2）设经过A 、O 、B 三点的抛物线的解析式为y ＝ax 2＋bx ＋c∵抛物线过原点，∴c ＝0． ∴⎪⎩⎪⎨⎧=+=-3024b a b a 解得⎪⎪⎩⎪⎪⎨⎧==33233b a ∴所求抛物线的解析式为y ＝33x 2＋332x ． ······································ 3分（3）存在． ·········································································································· 4分如图2，连接AB ，交抛物线的对称轴于点C ，连接OC ．∵OB 的长为定值，∴要使△BOC 的周长最小，必须BC ＋OC 的长最小． ∵点A 与点O 关于抛物线的对称轴对称，∴OC ＝AC ．∴BC ＋OC ＝BC ＋AC ＝AB ．由“两点之间，线段最短”的原理可知：此时BC ＋OC 最小，点C 的位置即为所求．设直线AB 的解析式为y ＝kx ＋m ，将A (－2，0)，B (1，3)代入，得⎪⎩⎪⎨⎧=+=+-302m k m k 解得⎪⎪⎩⎪⎪⎨⎧==33233m k∴直线AB 的解析式为y ＝33x ＋332．抛物线的对称轴为直线x ＝332332⨯-＝－1，即x ＝－1．将x ＝－1代入直线AB 的解析式，得y ＝33×(－1)＋332＝33． ∴点C 的坐标为(－1，33)． ································································· 6分（4）△PAB 有最大面积． ·················································································· 7分如图3，过点P 作y 轴的平行线交AB 于点D ．∵S △PAB ＝S △PAD ＋S △PBD＝21(y D －y P )(x B －x A ) ＝21[(33x ＋332)－(33x 2＋332x )](1＋2) ＝－23x 2－23x ＋3 ＝－23(x ＋21)2＋839 ∴当x ＝－21时，△PAB 的面积有最大值，最大值为839．··············· 8分此时y P ＝33×(－21)2＋332×(－21)＝－43． ∴此时P 点的坐标为(－21，－43)． ···················································· 9分。

2013年中考数学预测压轴题精选及答案

（第2题）中考数学预测压轴题精选及答案1、已知，在平行四边形OABC 中，OA=5，AB=4，∠OCA=90°，动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动，同时动点Q 从A 点出发沿射线AB 方向以每秒1个单位的速度移动．设移动的时间为t 秒．（1）求直线AC 的解析式；（2）试求出当t 为何值时，△OAC 与△PAQ 相似；（3）若⊙P 的半径为58，⊙Q 的半径为23；当⊙P 与对角线AC 相切时，判断⊙Q 与直线AC 、BC 的位置关系，并求出Q 点坐标。

解：（1）42033y x =-+ （2）①当0≤t≤2.5时，P 在OA 上，若∠OAQ=90°时，故此时△OAC 与△PAQ 不可能相似．当t>2.5时，①若∠APQ=90°，则△APQ ∽△OCA ，∵t>2.5，∴符合条件．②若∠AQP=90°，则△APQ ∽△∠OAC ，∵t>2.5，∴符合条件．综上可知，当时，△OAC 与△APQ 相似．（3）⊙Q 与直线AC 、BC 均相切，Q 点坐标为（109,531）。

2、如图，以矩形OABC 的顶点O 为原点，OA 所在的直线为x 轴，OC 所在的直线为y 轴，建立平面直角坐标系．已知OA ＝3，OC ＝2，点E 是AB 的中点，在OA 上取一点D ，将△BDA 沿BD 翻折，使点A 落在BC 边上的点F 处．（1）直接写出点E 、F 的坐标；（2）设顶点为F 的抛物线交y 轴正半轴．．．于点P ，且以点E 、F 、P 为顶点的三角形是等腰三角形，求该抛物线的解析式；（3）在x 轴、y 轴上是否分别存在点M 、N ，使得四边形MNFE 的周长最小？如果存在，求出周长的最小值；如果不存在，请说明理由．解：（1）(31)E ，；(12)F ，．（2）在Rt EBF △中，90B ∠=，EF ∴===设点P 的坐标为(0)n ，，其中0n >，顶点(12)F ，， ∴设抛物线解析式为2(1)2(0)y a x a =-+≠．①如图①，当EF PF =时，22EF PF =，221(2)5n ∴+-=．解得10n =（舍去）；24n =．(04)P ∴，．24(01)2a ∴=-+．解得2a =．∴抛物线的解析式为22(1)2y x =-+②如图②，当EP FP =时，22EP FP =，22(2)1(1)9n n ∴-+=-+．解得52n =-（舍去）． ③当EF EP =时，3EP =<，这种情况不存在．综上所述，符合条件的抛物线解析式是22(1)2y x =-+．（3）存在点M N ，，使得四边形MNFE 的周长最小．如图③，作点E 关于x 轴的对称点E '，CBCBCB作点F 关于y 轴的对称点F '，连接E F ''，分别与x 轴、y 轴交于点M N ，，则点M N ，就是所求点．(31)E '∴-，，(12)F NF NF ME ME '''-==，，，．43BF BE ''∴==，FN NM ME F NNM ME F E ''''∴++=++=5=．又EF = ，∴5FN NM ME EF +++=，此时四边形MNFE 的周长最小值是53、如图，在边长为2的等边△ABC 中，AD ⊥BC,点P 为边AB 上一个动点，过P 点作PF//AC 交线段BD 于点F,作PG ⊥AB 交AD 于点E,交线段CD 于点G,设BP=x .（1）①试判断BG 与2BP 的大小关系,并说明理由;②用x 的代数式表示线段DG 的长,并写出自变量x 的取值范围;（2）记△DEF 的面积为S,求S 与x 之间的函数关系式,并求出S 的最大值;（3）以P 、E 、F 为顶点的三角形与△EDG 是否可能相似？如果能相似，请求出BP 的长，如果不能，请说明理由。

2013中考数学压轴题练习

2013中考数学压轴题练习1.某数学兴趣小组开展了一次活动，过程如下：设∠BAC =θ（0°＜θ＜90°）.现把小棒依次摆放在两射线AB ，AC 之间，并使小棒两端分别落在两射线上. 活动一：如图甲所示，从点A 1开始，依次向右摆放小棒，使小棒与小棒在两端点处互相垂直，A 1A 2为第1根小棒. 数学思考：（1）小棒能无限摆下去吗？答： .（填“能”或“不能”）（2）设AA 1=A 1A 2=A 2A 3=1. ①θ= 度；②若记小棒A 2n-1A 2n 的长度为a n （n 为正整数，如A 1A 2=a 1,A 3A 4=a 2,）,求此时a 2，a 3的值，并直接写出a n （用含n 的式子表示）.图甲活动二：如图乙所示，从点A 1开始，用等长的小棒依次向右摆放，其中A 1A 2为第1根小棒，且A 1A 2= AA 1.数学思考：（3）若已经向右摆放了3根小棒，则1θ= ，2θ= ，3θ= ；（用含θ的式子表示）（4）若只能．．摆放4根小棒，求θ的范围.图乙2.数学课上，李老师出示了如下框中的题目.在等边三角形ABC 中，点E 在AB 上，点D 在CB 的延长线上，且ED=EC ，如图.试确定线段AE 与DB 的大小关系，并说明理由.EABCD小敏与同桌小聪讨论后，进行了如下解答：（1）特殊情况，探索结论当点E 为AB 的中点时，如图1，确定线段AE 与DB 的大小关系，请你直接写出结论： AE DB （填“>”,“<”或“=”）.EA BCDEA BCD（2）特例启发，解答题目解：题目中，AE 与DB 的大小关系是：AE DB （填“>”,“<”或“=”）.理由如下：如图2，过点E 作//EF BC ，交AC 于点F . （请你完成以下解答过程）（3）拓展结论，设计新题在等边三角形ABC 中，点E 在直线AB 上，点D 在直线BC 上，且ED EC =.若ABC ∆的边长为1，2AE =，求CD 的长（请你直接写出结果）.3.已知：二次函数y =x 2＋bx －3的图像经过点P （－2,5）．（1）求b 的值，并写出当1＜x ≤3时y 的取值范围；（2）设点P 1（m ,y 1）、P 2（m +1,y 2）、P 3(m +2,y 3)在这个二次函数的图像上． ①当m =4时，y 1、y 2、y 3能否作为同一个三角形的三边的长？请说明理由；②当m 取不小于5的任意实数时，y 1、y 2、y 3一定能作为同一个三角形三边的长，请说明理由．第2题图1 第2题图24.已知抛物线:y=x²-2x +m-1 与x 轴只有一个交点，且与y 轴交于A 点, 如图，设它的顶点为B (1)求m 的值；(2)过A 作x 轴的平行线，交抛物线于点C ，求证是△ABC 是等腰直角三角形；yxCEA O BF(3)将此抛物线向下平移4个单位后，得到抛物线C'，且与x 轴的左半轴交于E 点，与y 轴交于F 点，如图.请在抛物线C'上求点P ，使得△EFP 是以EF 为直角边的直角三角形.5.如图（1），矩形ABCD 的一边BC 在直角坐标系中x 轴上，折叠边AD,使点D 落在x 轴上点F 处，折痕为AE ，已知AB=8，AD=10，并设点B 坐标为（m,0），其中m ＞0.（1）求点E 、F 的坐标（用含m 的式子表示）；（2）连接OA ，若△OAF 是等腰三角形，求m 的值；（3）如图（2），设抛物线y=a(x －m －6)2+h 经过A 、E 两点，其顶点为M ，连接AM ，若∠OAM=90°，求a 、h 、m 的值.。

2013年中考数学中考最后压轴题训练---折叠旋转问题

数学重点压轴之折叠旋转一．折叠类1. （12江苏徐州卷）在平面直角坐标系中，已知矩形ABCD 中，边2A B =，边1A D =，且AB 、AD 分别在x 轴、y 轴的正半轴上，点A 与坐标原点重合．将矩形折叠，使点A 落在边DC 上，设点A '是点A 落在边DC 上的对应点．（1）当矩形ABCD 沿直线12yx b=-+折叠时（如图1），求点A '的坐标和b 的值；（2）当矩形ABCD 沿直线y kx b=+折叠时，① 求点A '的坐标（用k 表示）；求出k 和b 之间的关系式； ② 如果我们把折痕所在的直线与矩形的位置分为如图2、3、4所示的三种情形，请你分别写出每种情形时k 的取值范围．（将答案直接填在每种情形下的横线上）k 的取值范围是； k 的取值范围是；k 的取值范围是； [解] （1）如图答5，设直线12y x b=-+与OD 交于点E ，与OB 交于点F ，连结A O '，则OE = b ，OF = 2b ，设点A '的坐标为（a ，1）因为90D O A A O F ''∠+∠=︒，90O F E A O F '∠+∠=︒，所以D O A O F E'∠=∠，所以△D O A '∽△OFE ．所以D A D O O EO F'=，即12a b b=，所以12a=．所以点A '的坐标为（12，1）．连结A E '，则A E O E b'==．在R t △D EA '中，根据勾股定理有222A E A D D E''=+ ，即2221()(1)2b b =+-，解得58b=．（2）如图答6，设直线y kx b=+与OD 交于点E ，与OB 交于点F ，连结A O '，则OE = b ，b O Fk=-，设点A '的坐标为（a ，1）．因为90D O A A O F ''∠+∠=︒，90O F E A O F '∠+∠=︒．所以D O A O F E'∠=∠，所以△D O A '∽△OFE ．（图1）所以D A D O O EO F'=，即1a b bk=-，所以ak=-．所以A '点的坐标为（k -，1）．连结A E '，在Rt △D EA '中，D A k'=-，1D Eb=-，A Eb'=．因为222A E A D D E''=+，所以222()(1)bk b =-+-．所以212kb+=．在图答6和图答7中求解参照给分．（3）图13﹣2中：21k -≤≤-；图13﹣3中：1-≤k≤2-+图13﹣4中：20k -+≤≤[点评]这是一道有关折叠的问题，主要考查一次函数、四边形、相似形等知识，试题中贯穿了方程思想和数形结合的思想，请注意体会。

2013年中考数学压轴题及答案【最新】

2012中考数学压轴题及答案1.（2011年四川省宜宾市）已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.（1）求该抛物线的解析式；（2）若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；（3） △AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）2. （11浙江衢州）已知直角梯形纸片OABC 在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，32)，C(0，32)，点T 在线段OA 上(不与线段端点重合)，将纸片折叠，使点A 落在射线AB 上(记为点A ′)，折痕经过点T ，折痕TP 与射线AB 交于点P ，设点T 的横坐标为t ，折叠后纸片重叠部分(图中的阴影部分)的面积为S ；(1)求∠OAB 的度数，并求当点A ′在线段AB 上时，S 关于t 的函数关系式；(2)当纸片重叠部分的图形是四边形时，求t 的取值范围；(3)S 存在最大值吗？若存在，求出这个最大值，并求此时t 的值；若不存在，请说明理由.3. （11浙江温州）如图，在Rt ABC △中，90A ∠=，6AB =，8AC =，D E ，分别是边AB AC ，的中点，点P 从点D 出发沿DE 方向运动，过点P 作PQ BC ⊥于Q ，过点Q 作QR BA ∥交AC 于R ，当点Q 与点C 重合时，点P 停止运动．设BQ x =，QR y =．（1）求点D 到BC 的距离DH 的长；（2）求y 关于x 的函数关系式（不要求写出自变量的取值范围）；（3）是否存在点P ，使P Q R △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由．4.（11山东省日照市）在△ABC 中，∠A ＝90°，AB ＝4，AC ＝3，M 是AB 上的动点（不与A ，B 重合），过M 点作MN ∥BC 交AC 于点N ．以MN 为直径作⊙O ，并在⊙O 内作内接矩形AMPN ．令AM ＝x ．（1）用含x 的代数式表示△ＭNP 的面积S ；（2）当x 为何值时，⊙O 与直线BC 相切？（3）在动点M 的运动过程中，记△ＭNP 与梯形BCNM 重合的面积为y ，试求y 关于x 的函数表达式，并求x 为何值时，y 的值最大，最大值是多少？5、（2007浙江金华）如图1，已知双曲线y=xk (k>0)与直线y=k ′x 交于A ，B 两点，点A 在第一象限.试解答下列问题：(1)若点A 的坐标为(4，2).则点B 的坐标为；若点A 的横坐标为m ，则点B 的坐标可表示为；（2）如图2，过原点O 作另一条直线l ，交双曲线y=xk (k>0)于P ，Q 两点，点P 在第一象限.①说明四边形APBQ 一定是平行四边形；②设点A.P 的横坐标分别为m ，n ，四边形APBQ 可能是矩形吗?可能是正方形吗?若可能，直接写出mn 应满足的条件；若不可能，请说明理由.8. (2011浙江义乌)如图1所示，直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l ．将直线l 平移，平移后的直线l 与x 轴交于点D ，与y 轴交于点E ．（1）将直线l 向右平移，设平移距离CD 为t (t ≥0)，直角梯形OABC 被直线l 扫过的面积（图中阴影部份）为s ，s 关于t 的函数图象如图2所示， OM 为线段，MN 为抛物线的一部分，NQ 为射线，N 点横坐标为4．①求梯形上底AB 的长及直角梯形OABC 的面积；②当42<<t 时，求S 关于t 的函数解析式；（2）在第（1）题的条件下，当直线l 向左或向右平移时（包括l 与直线BC 重合），在直线．．AB ．．上是否存在点P ，使PDE ∆为等腰直角三角形?若存在，请直接写出所有满足条件的点P 的坐标;若不存在，请说明理由．9.(2011山东烟台)如图，菱形ABCD 的边长为2，BD=2，E 、F 分别是边AD ，CD 上的两个动点，且满足AE+CF=2.（1）求证：△BDE ≌△BCF ；（2）判断△BEF 的形状，并说明理由；（3）设△BEF 的面积为S ，求S 的取值范围.10.(2011山东烟台)如图，抛物线21:23L y x x =--+交x 轴于A 、B 两点，交y 轴于M 点.抛物线1L 向右平移2个单位后得到抛物线2L ，2L 交x 轴于C 、D 两点.（1）求抛物线2L 对应的函数表达式；（2）抛物线1L 或2L 在x 轴上方的部分是否存在点N ，使以A ，C ，M ，N 为顶点的四边形是平行四边形.若存在，求出点N 的坐标；若不存在，请说明理由；（3）若点P 是抛物线1L 上的一个动点（P 不与点A 、B 重合），那么点P 关于原点的对称点Q 是否在抛物线2L 上，请说明理由.13.（2011山东威海）如图，在梯形ABCD 中，AB ∥CD ，AB ＝7，CD ＝1，AD ＝BC ＝5．点M ，N 分别在边AD ，BC 上运动，并保持MN ∥AB ，ME ⊥AB ，NF ⊥AB ，垂足分别为E ，F ．（1）求梯形ABCD 的面积；（2）求四边形MEFN 面积的最大值．（3）试判断四边形MEFN 能否为正方形，若能，求出正方形MEFN 的面积；若不能，请说明理由．16.(2011年浙江省绍兴市)将一矩形纸片OABC 放在平面直角坐标系中，(00)O ，，(60)A ，，(03)C ，．动点Q 从点O 出发以每秒1个单位长的速度沿OC 向终点C 运动，运动23秒时，动点P 从点A 出发以相等的速度沿AO 向终点O 运动．当其中一点到达终点时，另一点也停止运动．设点P 的运动时间为t （秒）．（1）用含t 的代数式表示OP OQ ，；（2）当1t 时，如图1，将OPQ △沿PQ 翻折，点O 恰好落在CB 边上的点D 处，求点D 的坐标；（4）连结AC ，将OPQ △沿PQ 翻折，得到EPQ △，如图2．问：PQ 与AC 能否平行？PE 与AC能否垂直？若能，求出相应的t 值；若不能，说明理由．17.(2011年辽宁省十二市)如图16，在平面直角坐标系中，直线33y x =--与x 轴交于点A ，与y 轴交于点C ，抛物线223(0)3y ax x c a =-+≠经过A B C ，，三点．（1）求过A B C ，，三点抛物线的解析式并求出顶点F 的坐标；（2）在抛物线上是否存在点P ，使ABP △为直角三角形，若存在，直接写出P 点坐标；若不存在，请说明理由；（3）试探究在直线AC 上是否存在一点M ，使得MBF △的周长最小，若存在，求出M 点的坐标；若不存在，请说明理由．18.(2011年沈阳市)如图所示，在平面直角坐标系中，矩形ABOC 的边BO 在x 轴的负半轴上，边OC 在y 轴的正半轴上，且1AB =，3OB =，矩形ABOC 绕点O 按顺时针方向旋转60后得到矩形EFOD ．点A 的对应点为点E ，点B 的对应点为点F ，点C 的对应点为点D ，抛物线2y ax bx c =++过点A E D ，，．（1）判断点E 是否在y 轴上，并说明理由；（2）求抛物线的函数表达式；（3）在x 轴的上方是否存在点P ，点Q ，使以点O B P Q ，，，为顶点的平行四边形的面积是矩形ABOC 面积的2倍，且点P 在抛物线上，若存在，请求出点P ，点Q 的坐标；若不存在，请说明理由．19.(2011年四川省巴中市) 已知：如图14，抛物线2334y x =-+与x 轴交于点A ，点B ，与直线34y x b =-+相交于点B ，点C ，直线34y x b =-+与y 轴交于点E ．（1）写出直线BC 的解析式．（2）求ABC △的面积．（3）若点M 在线段AB 上以每秒1个单位长度的速度从A 向B 运动（不与A B ，重合），同时，点N 在射线BC 上以每秒2个单位长度的速度从B 向C 运动．设运动时间为t 秒，请写出MNB △的面积S 与t 的函数关系式，并求出点M 运动多少时间时，MNB △的面积最大，最大面积是多少？20.(2011年成都市)如图，在平面直角坐标系xOy 中，△OAB 的顶点Ａ的坐标为（10，0），顶点B 在第一象限内，且AB =35，sin ∠OAB=55. （1）若点C 是点B 关于x 轴的对称点，求经过O 、C 、A 三点的抛物线的函数表达式；（2）在(1)中，抛物线上是否存在一点P ，使以P 、O 、C 、A 为顶点的四边形为梯形？若存在，求出点P 的坐标；若不存在，请说明理由；（3）若将点O 、点A 分别变换为点Q （ -2k ,0）、点R （5k ，0）（k>1的常数），设过Q 、R 两点，且以QR 的垂直平分线为对称轴的抛物线与y 轴的交点为N ，其顶点为M ，记△QNM 的面积为QMN S ∆，△QNR 的面积Q NR S ∆，求QMN S ∆∶Q NR S ∆的值.22.(2011年四川省宜宾市)已知:如图,抛物线y=-x 2+bx+c 与x 轴、y 轴分别相交于点A （-1，0）、B （0，3）两点，其顶点为D.(1)求该抛物线的解析式；(2)若该抛物线与x 轴的另一个交点为E. 求四边形ABDE 的面积；(3)△AOB 与△BDE 是否相似？如果相似，请予以证明；如果不相似，请说明理由.（注：抛物线y=ax 2+bx+c(a ≠0)的顶点坐标为⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22）．24.(2011年大庆市)如图①，四边形AEFG 和ABCD 都是正方形，它们的边长分别为a b ，（2b a ≥），且点F 在AD 上（以下问题的结果均可用a b ，的代数式表示）．（1）求DBF S △；（2）把正方形AEFG 绕点A 按逆时针方向旋转45°得图②，求图②中的DBF S △；（3）把正方形AEFG 绕点A 旋转一周，在旋转的过程中，DBF S △是否存在最大值、最小值？如果存在，直接写出最大值、最小值；如果不存在，请说明理由．25. （2011年上海市）已知24AB AD ==，，90DAB ∠=，AD BC ∥（如图13）．E 是射线BC 上的动点（点E 与点B 不重合），M 是线段DE 的中点．（1）设BE x ，ABM △的面积为y ，求y 关于x 的函数解析式，并写出函数的定义域；（2）如果以线段AB 为直径的圆与以线段DE 为直径的圆外切，求线段BE 的长；（3）联结BD ，交线段AM 于点N ，如果以A N D ，，为顶点的三角形与BME △相似，求线段BE 的长．27. （2011年山东省青岛市）已知：如图①，在Rt △ACB 中，∠C ＝90°，AC ＝4cm ，BC ＝3cm ，点P 由B 出发沿BA 方向向点A 匀速运动，速度为1cm/s ；点Q 由A 出发沿AC 方向向点C 匀速运动，速度为2cm/s ；连接PQ ．若设运动的时间为t （s ）（0＜t ＜2），解答下列问题：（1）当t 为何值时，PQ ∥BC ？（2）设△AQP 的面积为y （2cm ），求y 与t 之间的函数关系式；（3）是否存在某一时刻t ，使线段PQ 恰好把Rt △ACB 的周长和面积同时平分？若存在，求出此时t 的值；若不存在，说明理由；（4）如图②，连接PC ，并把△PQC 沿QC 翻折，得到四边形PQP ′C ，那么是否存在某一时刻t ，使四边形PQP ′C 为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．28.（2011年江苏省南通市）已知双曲线kyx=与直线14y x=相交于A、B两点.第一象限上的点M（m，n）（在A点左侧）是双曲线kyx=上的动点.过点B作BD∥y轴于点D.过N（0，－n）作NC∥x轴交双曲线kyx=于点E，交BD于点C.（1）若点D坐标是（－8，0），求A、B两点坐标及k的值.（2）若B是CD的中点，四边形OBCE的面积为4，求直线CM的解析式.（3）设直线AM、BM分别与y轴相交于P、Q两点，且MA＝pMP，MB＝qMQ，求p－q的值.29.（2011年江苏省无锡市）一种电讯信号转发装置的发射直径为31km．现要求：在一边长为30km的正方形城区选择若干个安装点，每个点安装一个这种转发装置，使这些装置转发的信号能完全覆盖这个城市．问：（1）能否找到这样的4个安装点，使得这些点安装了这种转发装置后能达到预设的要求？（2）至少需要选择多少个安装点，才能使这些点安装了这种转发装置后达到预设的要求？答题要求：请你在解答时，画出必要的示意图，并用必要的计算、推理和文字来说明你的理由．（下面给出了几个边长为30km的正方形城区示意图，供解题时选用）压轴题答案1.解：（ 1）由已知得：310c b c =⎧⎨--+=⎩解得c=3,b =2∴抛物线的线的解析式为223y x x =-++(2)由顶点坐标公式得顶点坐标为（1，4）所以对称轴为x=1,A,E 关于x=1对称，所以E(3,0)设对称轴与x 轴的交点为F所以四边形ABDE 的面积=ABO DFE BOFD S S S ∆∆++梯形 =111()222AO BO BO DF OF EF DF ⋅++⋅+⋅ =11113(34)124222⨯⨯++⨯+⨯⨯ =9 （3）相似如图，BD=2222112BG DG +=+= BE=22223332BO OE +=+= DE=22222425DF EF +=+=所以2220BD BE +=, 220DE =即： 222BD BE DE +=,所以BDE ∆是直角三角形所以90AOB DBE ∠=∠=︒,且22AO BO BD BE ==, 所以AOB DBE ∆∆.2. (1) ∵A ，B 两点的坐标分别是A(10，0)和B(8，32)，∴381032OAB tan =-=∠， ∴︒=∠60OAB当点A ´在线段AB 上时，∵︒=∠60OAB ，TA=TA ´，∴△A ´TA 是等边三角形，且A T TP '⊥，∴)t 10(2360sin )t 10(T P -=︒-=，)t 10(21AT 21AP P A -==='，○2当6t 2<≤时，由图○1，重叠部分的面积EB A TP A S S S '∆'∆-=∵△A ´EB 的高是︒'60sin B A ， ∴23)4t 10(21)t 10(83S 22⨯----= 34)2t (83)28t 4t (8322+--=++-=当t=2时，S 的值最大是34；○3当2t 0<<，即当点A ´和点P 都在线段AB 的延长线是(如图○2，其中E 是TA ´与CB 的交点，F 是TP 与CB 的交点)，∵ETF FTP EFT ∠=∠=∠，四边形ETAB 是等腰形，∴EF=ET=AB=4， ∴3432421OC EF 21S =⨯⨯=⋅= 综上所述，S 的最大值是34，此时t 的值是2t 0≤<.3. 解：（1）Rt A ∠=∠，6AB =，8AC =，10BC ∴=．点D 为AB 中点，132BD AB ∴==． 90DHB A ∠=∠=，B B ∠=∠．BHD BAC ∴△∽△，DH BD AC BC ∴=，3128105BD DH AC BC ∴==⨯=．（2）QR AB ∥，90QRC A ∴∠=∠=． C C ∠=∠，RQC ABC ∴△∽△，RQ QC AB BC ∴=，10610y x -∴=，即y 关于x 的函数关系式为：365y x =-+．（3）存在，分三种情况：①当PQ PR =时，过点P 作PM QR ⊥于M ，则QM RM =．1290∠+∠=，290C ∠+∠=，1C ∴∠=∠．84cos 1cos 105C ∴∠===，45QM QP ∴=， 1364251255x ⎛⎫-+ ⎪⎝⎭∴=，185x ∴=． ②当PQ RQ =时，312655x -+=， 6x ∴=．③当PR QR =时，则R 为PQ 中垂线上的点，于是点R 为EC 的中点，11224CR CE AC ∴===． tan QR BA C CR CA ==， 366528x -+∴=，152x ∴=．综上所述，当x 为185或6或152时，PQR △为等腰三角形．4.解：（1）∵MN ∥BC ，∴∠AMN =∠B ，∠ANM ＝∠C ．∴ △AMN ∽ △ABC ．∴ AM AN AB AC =，即43x AN =． ∴ AN ＝43x ． ……………2分 ∴ S =2133248MNP AMN S S x x x ∆∆==⋅⋅=．（0＜x ＜4） ……………3分（2）如图2，设直线BC 与⊙O 相切于点D ，连结AO ，OD ，则AO =OD =21MN ．在Rt △ABC 中，BC ＝22AB AC +=5．由（1）知 △AMN ∽ △ABC ．∴ AM MN AB BC =，即45x MN =． ∴ 54MN x =， ∴ 58OD x =． …………………5分过M 点作MQ ⊥BC 于Q ，则58MQ OD x ==．在Rt △BMQ 与Rt △BCA 中，∠B 是公共角，∴ △BMQ ∽△BCA ．∴ BM QM BC AC=． ∴ 55258324x BM x ⨯==，25424AB BM MA x x =+=+=．∴ x ＝4996． ∴ 当x ＝4996时，⊙O 与直线B C 相切．…………………………………7分故以下分两种情况讨论：① 当0＜x ≤2时，2Δ83x S y PMN ==． ∴ 当x ＝2时，2332.82y =⨯=最大 ……………………………………8分② 当2＜x ＜4时，设PM ，PN 分别交BC 于E ，F ．∵ 四边形AMPN 是矩形，∴ PN ∥AM ，PN ＝AM ＝x ．又∵ MN ∥BC ，∴ 四边形MBFN 是平行四边形．∴ FN ＝BM ＝4－x ．∴ ()424PF x x x =--=-．又△PEF ∽ △ACB ．∴ 2PEF ABC S PF AB S ∆∆⎛⎫= ⎪⎝⎭． ∴ ()2322PEF S x ∆=-． ……………………………………………… 9分 MNP PEF y S S ∆∆=-＝()222339266828x x x x --=-+-．……………………10分当2＜x ＜4时，29668y x x =-+-298283x ⎛⎫=--+ ⎪⎝⎭． ∴ 当83x =时，满足2＜x ＜4，2y =最大． ……………………11分综上所述，当83x =时，y 值最大，最大值是2． …………………………12分 5. 解：（1）（-4，-2）；（-m,-k m） (2) ①由于双曲线是关于原点成中心对称的，所以OP=OQ,OA=OB,所以四边形APBQ一定是平行四边形②可能是矩形，mn=k 即可不可能是正方形，因为Op 不能与OA 垂直.解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23，∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-,的以直线AB 的解析式为 343y x =-+（2）由旋转知，AP=AD, ∠PAD=60o, ∴ΔAPD 是等边三角形，PD=PA=2219AO OP +=6. 解：（1）作BE ⊥OA ，∴ΔAOB 是等边三角形∴BE=OB ·sin60o =23，∴B(23,2)∵A(0,4),设AB 的解析式为4y kx =+,所以2342k +=,解得33k =-, 以直线AB 的解析式为343y x =-+ （2）由旋转知，AP=AD, ∠PAD=60o ,∴ΔAPD 是等边三角形，PD=PA=2219AO OP +=（1）①2AB = ……………………………………………………………………………2分842OA ==，4OC =，S 梯形OABC =12 ……………………………………………2分 ②当42<<t 时，直角梯形OABC 被直线l 扫过的面积=直角梯形OABC 面积－直角三角开DOE 面积2112(4)2(4)842S t t t t =--⨯-=-+-…………………………………………4分（2）存在 ……………………………………………………………………………………1分123458(12,4),(4,4),(,4),(4,4),(8,4)3P P P P P --- …（每个点对各得1分）……5分对于第（2）题我们提供如下详细解答（评分无此要求）.下面提供参考解法二： ① 以点D 为直角顶点，作1PP x ⊥轴同理在③二图中分别可得P点的生标为P（－4，4）（与①情形二重合舍去）、P（4，4），E点在A点下方不可能.综上可得P点的生标共5个解，分别为P（－12，4）、P（－4，4）、P（－83，4）、P（8，4）、P（4，4）．下面提供参考解法二：以直角进行分类进行讨论（分三类）：第一类如上解法⑴中所示图22P DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) 的中点坐标为b (-,b)2，直线DE 的中垂线方程：1()22by b x -=-+，令4y =得3(8,4)2b P -．由已知可得2PE DE =即222232(8)(42)42b b b b ⨯-+-=+化简得2332640b b -+=解得 121883b b P P ==∴=3b，将之代入（-8，4）（4，4)、22(4,4)P -；第二类如上解法②中所示图22E DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) ，直线PE 的方程：122y x b =-+，令4y =得(48,4)P b -．由已知可得PE DE =即2222(48)(42)4b b b b -+-=+化简得22(28)b b =-解之得，123443b b P P ==∴=，将之代入（4b-8，4）（8，4)、48(,4)3P - 第三类如上解法③中所示图22D DE y x b ∠=+为直角：设直线：，D 此时（-b,o)，E(O,2b) ，直线PD 的方程：1()2y x b =-+，令4y =得(8,4)P b --．由已知可得PD DE =即2222844b b +=+解得12544b b P P ==-∴=，将之代入（-b-8，4）（-12，4)、 6(4,4)P -（6(4,4)P -与2P 重合舍去）．综上可得P 点的生标共5个解，分别为P （－12，4）、P （－4，4）、P （－83，4）、 P （8，4）、P （4，4）．事实上，我们可以得到更一般的结论：如果得出AB a OC b ==、、OA h =、设b ak h-=，则P 点的情形如下∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ．即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFNS 正方形． ∴ 6494738)2(7342+⎪⎭⎫ ⎝⎛--=-=⋅=x x x EF ME S MEFN矩形． ……………………8分当x ＝47时，ME ＝37＜4，∴四边形MEFN 面积的最大值为649．……………9分（3）能． ……………………………………………………………………10分由（2）可知，设AE ＝x ，则EF ＝7－2x ，ME ＝x 34．若四边形MEFN 为正方形，则ME ＝EF ．即=34x 7－2x ．解，得 1021=x ． ……………………………………………11分 ∴ EF ＝21147272105x -=-⨯=＜4． ∴ 四边形MEFN 能为正方形，其面积为251965142=⎪⎭⎫ ⎝⎛=MEFN S 正方形．（2）当1t =时，过D 点作1DD OA ⊥，交OA 于1D ，如图1，则53DQ QO ==，43QC =，1CD ∴=，(13)D ∴，．（3）①PQ 能与AC 平行．若PQ AC ∥，如图2，则OP OAOQ OC=，即66233t t -=+，149t ∴=，而703t ≤≤， 149t ∴=． ②PE 不能与AC 垂直．若PE AC ⊥，延长QE 交OA 于F ，如图3，则23335t QF OQ QFAC OC +==．253QF t ⎛⎫∴=+ ⎪⎝⎭．EF QF QE QF OQ ∴=-=-22533t t ⎛⎫⎛⎫=+-+ ⎪ ⎪⎝⎭⎝⎭2(51)(51)3t =-+-．又Rt Rt EPF OCA △∽△，PE OCEF OA∴=， 6326(51)3t t -∴=⎛⎫-+ ⎪⎝⎭，3.45t ∴≈，而703t ≤≤，t ∴不存在．17. 解：（1）直线33y x =--与x 轴交于点A ，与y 轴交于点C ．(10)A ∴-，，(03)C -， ··························································································· 1分点A C ，都在抛物线上，23033a c c ⎧=++⎪∴⎨⎪-=⎩ 333a c ⎧=⎪∴⎨⎪=-⎩∴抛物线的解析式为2323333y x x =-- ·························································· 3分 ∴顶点4313F ⎛⎫- ⎪ ⎪⎝⎭， ································································································ 4分（2）存在 ················································································································ 5分 1(03)P -， ·············································································································· 7分2(23)P -， ·············································································································· 9分（3）存在 ·············································································································· 10分理由：解法一：延长BC 到点B '，使BC B C '=，连接B F '交直线AC 于点M ，则点M 就是所求的点．····················································································· 11分在Rt BB H '△中，1232B H BB ''==， 36BH B H '==，3OH ∴=，(323)B '∴--， ·················································· 12分设直线B F '的解析式为y kx b =+233433k b k b ⎧-=-+⎪∴⎨-=+⎪⎩ 解得36332k b ⎧=⎪⎪⎨⎪=-⎪⎩33362y x ∴=- ································································································· 13分 3333362y x y x ⎧=--⎪∴⎨=-⎪⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩，310377M ⎛⎫∴- ⎪ ⎪⎝⎭，∴在直线AC 上存在点M ，使得MBF △的周长最小，此时310377M ⎛⎫- ⎪ ⎪⎝⎭，． ····· 14分03533k b b =+⎧⎪⎨=-⎪⎩ 解得539533k b ⎧=⎪⎪⎨⎪=-⎪⎩ 553393y ∴=- ································································································· 13分 55339333y x y x ⎧=-⎪∴⎨⎪=--⎩ 解得371037x y ⎧=⎪⎪⎨⎪=-⎪⎩310377M ⎛⎫∴- ⎪ ⎪⎝⎭， ∴在直线AC 上存在点M ，使得MBF △的周长最小，此时310377M ⎛⎫- ⎪ ⎪⎝⎭，． 1 18. 解：（1）点E 在y 轴上 ···················································································· 1分理由如下：连接AO ，如图所示，在Rt ABO △中，1AB =，3BO =，2AO ∴=1sin 2AOB ∴∠=，30AOB ∴∠= 由题意可知：60AOE ∠=306090BOE AOB AOE ∴∠=∠+∠=+=点B 在x 轴上，∴点E 在y 轴上． ······································································· 3分（2）过点D 作DM x ⊥轴于点M1OD =，30DOM ∠=∴在Rt DOM △中，12DM =，32OM = 点D 在第一象限， ∴点D 的坐标为3122⎛⎫ ⎪ ⎪⎝⎭， ························································································ 5分由（1）知2EO AO ==，点E 在y 轴的正半轴上∴点E 的坐标为(02)，∴点A 的坐标为(31)-， ·························································································· 6分抛物线2y ax bx c =++经过点E ，2c ∴= 由题意，将(31)A -，，3122D ⎛⎫ ⎪ ⎪⎝⎭，代入22y ax bx =++中得33213312422a b a b ⎧-+=⎪⎨++=⎪⎩ 解得89539a b ⎧=-⎪⎪⎨⎪=-⎪⎩∴所求抛物线表达式为：2853299y x x =--+ ······················································ 9分（3）存在符合条件的点P ，点Q ． ······································································ 10分理由如下：矩形ABOC 的面积3AB BO ==∴以O B P Q ，，，为顶点的平行四边形面积为23．由题意可知OB 为此平行四边形一边，又3OB =OB ∴边上的高为2 ································································································ 11分依题意设点P 的坐标为(2)m ，点P 在抛物线2853299y x x =--+上 28532299m m ∴--+= 解得，10m =，2538m =-1(02)P ∴，，25328P ⎛⎫- ⎪ ⎪⎝⎭，以O B P Q ，，，为顶点的四边形是平行四边形，PQ OB ∴∥，3PQ OB ==，∴当点1P 的坐标为(02)，时，点Q 的坐标分别为1(32)Q -，，2(32)Q ，；当点2P 的坐标为5328⎛⎫- ⎪ ⎪⎝⎭，时，点Q 的坐标分别为313328Q ⎛⎫-⎪ ⎪⎝⎭，，43328Q ⎛⎫ ⎪ ⎪⎝⎭，． ·············································· 14分（以上答案仅供参考，如有其它做法，可参照给分）19.解：（1）在2334y x =-+中，令0y = 23304x ∴-+=12x ∴=，22x =-(20)A ∴-，，(20)B ， ··················································· 1分又点B 在34y x b =-+上 302b ∴=-+ 32b = BC ∴的解析式为3342y x =-+ ················································································ 2分（2）由23343342y x y x ⎧=-+⎪⎪⎨⎪=-+⎪⎩，得11194x y =-⎧⎪⎨=⎪⎩ 2220x y =⎧⎨=⎩ ······················································· 4分 914C ⎛⎫∴- ⎪⎝⎭，，(20)B ， 4AB ∴=，94CD = ································································································ 5分 1994242ABC S ∴=⨯⨯=△ ··························································································· 6分（3）过点N 作NP MB ⊥于点PEO MB ⊥NP EO ∴∥BNP BEO ∴△∽△ ································································································· 7分 BN NP BE EO∴= ··········································································································· 8分由直线3342y x =-+可得：302E ⎛⎫ ⎪⎝⎭，∴在BEO △中，2BO =，32EO =，则52BE = 25322t NP ∴=，65NP t ∴= ························································································· 9分 16(4)25S t t ∴=- 2312(04)55S t t t =-+<< ······················································································ 10分 2312(2)55S t =--+ ······························································································· 11分此抛物线开口向下，∴当2t =时，125S =最大 ∴当点M 运动2秒时，MNB △的面积达到最大，最大为125． 20. 解：（1）如图，过点B 作BD ⊥OA 于点D.在Rt △ABD 中，∵∣AB ∣=35,sin ∠OAB=55, ∴∣BD ∣=∣AB ∣·sin ∠OAB =35×55=3. 又由勾股定理，得22A D AB B D =- 22(35)36=-=∴∣OD ∣=∣OA ∣-∣AD ∣=10-6=4.∵点B 在第一象限，∴点B 的坐标为（4，3）. ……3分。

2013年中考数学压轴题及解析分类汇编(优选.)

2013年中考数学压轴题及解析分类汇编2013年中考数学压轴题及解析分类汇编2013中考数学压轴：相似三角形问题2013中考数学压轴题函数相似三角形问题(一)2013中考数学压轴题函数相似三角形问题(二)2013中考数学压轴题函数相似三角形问题(三)2013中考数学压轴：等腰三角形问题2013中考数学压轴题函数等腰三角形问题(一)2013中考数学压轴题函数等腰三角形问题(二)2013中考数学压轴题函数等腰三角形问题(三)2013中考数学压轴：直角三角形问题2013中考数学压轴题函数直角三角形问题(一)2013中考数学压轴题函数直角三角形问题(二)2013中考数学压轴题函数直角三角形问题(三)2013中考数学压轴：平行四边形问题2013中考数学压轴题函数平行四边形问题(一)2013中考数学压轴题函数平行四边形问题(二)2013中考数学压轴题函数平行四边形问题(三)2013中考数学压轴：梯形问题2013中考数学压轴题函数梯形问题(一)2013中考数学压轴题函数梯形问题(二)2013中考数学压轴题函数梯形问题(三)2013中考数学压轴：面积问题2013中考数学压轴题函数面积问题(一)2013中考数学压轴题函数面积问题(二)2013中考数学压轴题函数面积问题(三)2013中考数学压轴题:函数相似三角形问题(一) 例1直线113y x=-+分别交x轴、y轴于A、B两点，△AOB绕点O按逆时针方向旋转90°后得到△COD，抛物线y＝ax2＋bx＋c经过A、C、D三点．(1) 写出点A、B、C、D的坐标；(2) 求经过A、C、D三点的抛物线表达式，并求抛物线顶点G的坐标；(3) 在直线BG上是否存在点Q，使得以点A、B、Q为顶点的三角形与△COD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．图1动感体验请打开几何画板文件名“11闸北25”，拖动点Q在直线BG上运动，可以体验到，△ABQ的两条直角边的比为1∶3共有四种情况，点B上、下各有两种．思路点拨1．图形在旋转过程中，对应线段相等，对应角相等，对应线段的夹角等于旋转角．2．用待定系数法求抛物线的解析式，用配方法求顶点坐标．3．第（3）题判断∠ABQ＝90°是解题的前提．4．△ABQ与△COD相似，按照直角边的比分两种情况，每种情况又按照点Q与点B的位置关系分上下两种情形，点Q共有4个．满分解答（1）A (3，0)，B (0，1)，C (0，3)，D (－1，0)．（2）因为抛物线y ＝ax 2＋bx ＋c 经过A (3，0)、C (0，3)、D (－1，0) 三点，所以930,3,0.a b c c a b c ++=⎧⎪=⎨⎪-+=⎩ 解得1,2,3.a b c =-⎧⎪=⎨⎪=⎩所以抛物线的解析式为y ＝－x 2＋2x ＋3＝－(x －1)2＋4，顶点G 的坐标为(1，4)．（3）如图2，直线BG 的解析式为y ＝3x ＋1，直线CD 的解析式为y ＝3x ＋3，因此CD //BG ．因为图形在旋转过程中，对应线段的夹角等于旋转角，所以AB ⊥CD ．因此AB ⊥BG ，即∠ABQ ＝90°．因为点Q 在直线BG 上，设点Q 的坐标为(x ，3x ＋1)，那么22(3)10BQ x x x =+=±． Rt △COD 的两条直角边的比为1∶3，如果Rt △ABQ 与Rt △COD 相似，存在两种情况：①当3BQ BA =时，10310x ±=．解得3x =±．所以1(3,10)Q ，2(3,8)Q --． ②当13BQ BA =时，101310x ±=．解得13x =±．所以31(,2)3Q ，41(,0)3Q -．图2 图3考点伸展第（3）题在解答过程中运用了两个高难度动作：一是用旋转的性质说明AB ⊥BG ；二是BQ ==．我们换个思路解答第（3）题：如图3，作GH ⊥y 轴，QN ⊥y 轴，垂足分别为H 、N ．通过证明△AOB ≌△BHG ，根据全等三角形的对应角相等，可以证明∠ABG ＝90°．在Rt △BGH 中，sin 1∠=cos 1∠=①当3BQ BA=时，BQ =．在Rt △BQN 中，sin 13QN BQ =⋅∠=，cos 19BN BQ =⋅∠=．当Q 在B 上方时，1(3,10)Q ；当Q 在B 下方时，2(3,8)Q --．②当13BQ BA =时，BQ =31(,2)3Q ，41(,0)3Q -．例2Rt △ABC 在直角坐标系内的位置如图1所示，反比例函数(0)k y k x=≠在第一象限内的图像与BC 边交于点D （4，m ），与AB 边交于点E （2，n ），△BDE 的面积为2．（1）求m 与n 的数量关系；（2）当tan ∠A ＝12时，求反比例函数的解析式和直线AB 的表达式；（3）设直线AB 与y 轴交于点F ，点P 在射线FD 上，在（2）的条件下，如果△AEO 与△EFP 相似，求点P 的坐标．图1动感体验请打开几何画板文件名“11杨浦24”，拖动点A 在x 轴上运动，可以体验到，直线AB 保持斜率不变，n 始终等于m 的2倍，双击按钮“面积BDE ＝2”，可以看到，点E 正好在BD 的垂直平分线上，FD //x 轴．拖动点P 在射线FD 上运动，可以体验到，△AEO 与△EFP 相似存在两种情况．思路点拨1．探求m 与n 的数量关系，用m 表示点B 、D 、E 的坐标，是解题的突破口．2．第（2）题留给第（3）题的隐含条件是FD //x 轴．3．如果△AEO 与△EFP 相似，因为夹角相等，根据对应边成比例，分两种情况．满分解答（1）如图1，因为点D （4，m ）、E （2，n ）在反比例函数k y x=的图像上，所以4,2.m k n k =⎧⎨=⎩ 整理，得n ＝2m ．（2）如图2，过点E 作EH ⊥BC ，垂足为H ．在Rt △BEH 中，tan ∠BEH ＝tan ∠A ＝12，EH ＝2，所以BH ＝1．因此D (4，m )，E (2，2m )，B (4，2m ＋1)．已知△BDE 的面积为2，所以11(1)2222BD EH m ⋅=+⨯=．解得m ＝1．因此D (4，1)，E (2，2)，B (4，3)．因为点D （4，1）在反比例函数k y x =的图像上，所以k ＝4．因此反比例函数的解析式为4y x=．设直线AB的解析式为y＝kx＋b，代入B(4，3)、E(2，2)，得34,22.k bk b=+⎧⎨=+⎩解得12k=，1 b=．因此直线AB的函数解析式为112y x=+．图2 图3 图4（3）如图3，因为直线112y x=+与y轴交于点F（0，1），点D的坐标为（4，1），所以FD// x轴，∠EFP＝∠EAO．因此△AEO与△EFP相似存在两种情况：①如图3，当EA EFAO FP=时，255=．解得FP＝1．此时点P的坐标为（1，1）．②如图4，当EA FPAO EF=时，255=．解得FP＝5．此时点P的坐标为（5，1）．考点伸展本题的题设部分有条件“Rt△ABC在直角坐标系内的位置如图1所示”，如果没有这个条件限制，保持其他条件不变，那么还有如图5的情况：第（1）题的结论m与n的数量关系不变．第（2）题反比例函数的解析式为12yx=-，直线AB为172y x=-．第（3）题FD不再与x轴平行，△AEO与△EFP也不可能相似．图52013中考数学压轴题函数相似三角形问题(二) 例3如图1，已知梯形OABC，抛物线分别过点O（0，0）、A（2，0）、B（6，3）．（1）直接写出抛物线的对称轴、解析式及顶点M的坐标；（2）将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移，分别交抛物线于点O1、A1、C1、B1，得到如图2的梯形O1A1B1C1．设梯形O1A1B1C1的面积为S，A1、B1的坐标分别为(x1，y1)、(x2，y2)．用含S的代数式表示x2－x1，并求出当S=36时点A1的坐标；（3）在图1中，设点D的坐标为(1，3)，动点P从点B出发，以每秒1个单位长度的速度沿着线段BC运动，动点Q从点D出发，以与点P相同的速度沿着线段DM运动．P、Q两点同时出发，当点Q到达点M时，P、Q两点同时停止运动．设P、Q两点的运动时间为t，是否存在某一时刻t，使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似？若存在，请求出t的值；若不存在，请说明理由．图1 图2动感体验请打开几何画板文件名“10义乌24”，拖动点I上下运动，观察图形和图像，可以体验到，x2－x1随S的增大而减小．双击按钮“第（3）题”，拖动点Q在DM上运动，可以体验到，如果∠GAF＝∠GQE，那么△GAF与△GQE相似．思路点拨1．第（2）题用含S 的代数式表示x 2－x 1，我们反其道而行之，用x 1，x 2表示S ．再注意平移过程中梯形的高保持不变，即y 2－y 1＝3．通过代数变形就可以了．2．第（3）题最大的障碍在于画示意图，在没有计算结果的情况下，无法画出准确的位置关系，因此本题的策略是先假设，再说理计算，后验证．3．第（3）题的示意图，不变的关系是：直线AB 与x 轴的夹角不变，直线AB 与抛物线的对称轴的夹角不变．变化的直线PQ 的斜率，因此假设直线PQ 与AB 的交点G 在x 轴的下方，或者假设交点G 在x 轴的上方．满分解答（1）抛物线的对称轴为直线1x =，解析式为21184y x x =-，顶点为M （1，18-）．（2）梯形O 1A 1B 1C 1的面积12122(11)3()62x x S x x -+-⨯3==+-，由此得到1223s x x +=+．由于213y y -=，所以22212211111138484y y x x x x -=--+=．整理，得212111()()384x x x x ⎡⎤-+-=⎢⎥⎣⎦．因此得到2172x x S -=．当S =36时，212114,2.x x x x +=⎧⎨-=⎩ 解得126,8.x x =⎧⎨=⎩ 此时点A 1的坐标为（6，3）．（3）设直线AB 与PQ 交于点G ，直线AB 与抛物线的对称轴交于点E ，直线PQ 与x 轴交于点F ，那么要探求相似的△GAF 与△GQE ，有一个公共角∠G ．在△GEQ 中，∠GEQ 是直线AB 与抛物线对称轴的夹角，为定值．在△GAF 中，∠GAF 是直线AB 与x 轴的夹角，也为定值，而且∠GEQ ≠∠GAF ．因此只存在∠GQE ＝∠GAF 的可能，△GQE ∽△GAF ．这时∠GAF ＝∠GQE ＝∠PQD ．由于3tan 4GAF ∠=，tan 5DQ t PQD QP t ∠==-，所以345t t =-．解得207t =．图3 图4 考点伸展第（3）题是否存在点G 在x 轴上方的情况？如图4，假如存在，说理过程相同，求得的t 的值也是相同的．事实上，图3和图4都是假设存在的示意图，实际的图形更接近图3．例4如图1，已知点A (-2，4) 和点B (1，0)都在抛物线22y mx mx n =++上．（1）求m 、n ；（2）向右平移上述抛物线，记平移后点A 的对应点为A ′，点B 的对应点为B ′，若四边形A A ′B ′B 为菱形，求平移后抛物线的表达式；（3）记平移后抛物线的对称轴与直线AB ′ 的交点为C ，试在x 轴上找一个点D ，使得以点B ′、C 、D 为顶点的三角形与△ABC 相似．图1动感体验请打开几何画板文件名“10宝山24”，拖动点A ′向右平移，可以体验到，平移5个单位后，四边形A A ′B ′B 为菱形．再拖动点D 在x 轴上运动，可以体验到，△B ′CD 与△ABC 相似有两种情况．思路点拨1．点A 与点B 的坐标在3个题目中处处用到，各具特色．第（1）题用在待定系数法中；第（2）题用来计算平移的距离；第（3）题用来求点B ′ 的坐标、AC 和B ′C 的长．2．抛物线左右平移，变化的是对称轴，开口和形状都不变．3．探求△ABC 与△B ′CD 相似，根据菱形的性质，∠BAC ＝∠CB ′D ，因此按照夹角的两边对应成比例，分两种情况讨论．满分解答(1) 因为点A (-2，4) 和点B (1，0)都在抛物线22y mx mx n =++上，所以444,20.m m n m m n -+=⎧⎨++=⎩ 解得43m =-，4n =． (2)如图2，由点A (-2，4) 和点B (1，0)，可得AB ＝5．因为四边形A A ′B ′B 为菱形，所以A A ′＝B ′B ＝ AB ＝5．因为438342+--=x x y ()2416133x =-++，所以原抛物线的对称轴x ＝－1向右平移5个单位后，对应的直线为x ＝4．因此平移后的抛物线的解析式为()3164342,+--=x y ．图2(3) 由点A (-2，4) 和点B′(6，0)，可得A B′＝45．如图2，由AM//CN，可得''''B N B CB M B A=，即2845=．解得'5B C=．所以35AC=．根据菱形的性质，在△ABC与△B′CD中，∠BAC＝∠CB′D．①如图3，当''AB B CAC B D=时，535=，解得'3B D=．此时OD＝3，点D的坐标为（3，0）．②如图4，当''AB B DAC B C=时，355=，解得5'3B D=．此时OD＝133，点D的坐标为（133，0）．图3 图4考点伸展在本题情境下，我们还可以探求△B′CD与△AB B′相似，其实这是有公共底角的两个等腰三角形，容易想象，存在两种情况．我们也可以讨论△B′CD与△C B B′相似，这两个三角形有一组公共角∠B，根据对应边成比例，分两种情况计算．2013中考数学压轴题函数相似三角形问题(三) 例5如图1，抛物线经过点A(4，0)、B（1，0)、C（0，－2）三点．（1）求此抛物线的解析式；（2）P是抛物线上的一个动点，过P作PM⊥x轴，垂足为M，是否存在点P，使得以A、P、M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC上方的抛物线是有一点D，使得△DCA的面积最大，求出点D的坐标．,图1动感体验请打开几何画板文件名“09临沂26”，拖动点P在抛物线上运动，可以体验到，△PAM的形状在变化，分别双击按钮“P在B左侧”、“P在x轴上方”和“P在A右侧”，可以显示△PAM与△OAC相似的三个情景．双击按钮“第(3)题”，拖动点D在x轴上方的抛物线上运动，观察△DCA的形状和面积随D变化的图象，可以体验到，E是AC的中点时，△DCA的面积最大．思路点拨1．已知抛物线与x轴的两个交点，用待定系数法求解析式时，设交点式比较简便．2．数形结合，用解析式表示图象上点的坐标，用点的坐标表示线段的长． 3．按照两条直角边对应成比例，分两种情况列方程． 4．把△DCA 可以分割为共底的两个三角形，高的和等于OA ．满分解答（1）因为抛物线与x 轴交于A (4，0)、B （1，0)两点，设抛物线的解析式为)4)(1(--=x x a y ，代入点C 的坐标（0，－2），解得21-=a ．所以抛物线的解析式为22521)4)(1(212-+-=---=x x x x y ．（2）设点P 的坐标为))4)(1(21,(---x x x ．①如图2，当点P 在x 轴上方时，1＜x ＜4，)4)(1(21---=x x PM ，x AM -=4．如果2==CO AO PM AM ，那么24)4)(1(21=----x x x ．解得5=x 不合题意．如果21==CO AO PM AM ，那么214)4)(1(21=----x x x ．解得2=x ．此时点P 的坐标为（2，1）．②如图3，当点P 在点A 的右侧时，x ＞4，)4)(1(21--=x x PM ，4-=x AM ．解方程24)4)(1(21=---x x x ，得5=x ．此时点P 的坐标为)2,5(-．解方程214)4)(1(21=---x x x ，得2=x 不合题意．③如图4，当点P 在点B 的左侧时，x ＜1，)4)(1(21--=x x PM ，x AM -=4．解方程24)4)(1(21=---xx x ，得3-=x ．此时点P 的坐标为)14,3(--．解方程214)4)(1(21=---xxx，得0=x．此时点P与点O重合，不合题意．综上所述，符合条件的点P的坐标为（2，1）或)14,3(--或)2,5(-．图2 图3 图4（3）如图5，过点D作x轴的垂线交AC于E．直线AC的解析式为221-=xy．设点D的横坐标为m)41(<<m，那么点D的坐标为)22521,(2-+-mmm，点E的坐标为)221,(-mm．所以)221()22521(2---+-=mmmDE mm2212+-=．因此4)221(212⨯+-=∆mmSDACmm42+-=4)2(2+--=m．当2=m时，△DCA的面积最大，此时点D的坐标为（2，1）．图5 图6第（3）题也可以这样解：如图6，过D 点构造矩形OAMN ，那么△DCA 的面积等于直角梯形CAMN 的面积减去△CDN 和△ADM 的面积．设点D 的横坐标为（m ，n ）)41(<<m ，那么42)4(21)2(214)22(21++-=--+-⨯+=n m m n n m n S ．由于225212-+-=m m n ，所以m m S 42+-=．例6如图1，△ABC 中，AB ＝5，AC ＝3，cos A ＝310．D 为射线BA 上的点（点D 不与点B 重合），作DE //BC 交射线CA 于点E .．(1) 若CE ＝x ，BD ＝y ，求y 与x 的函数关系式，并写出函数的定义域； (2) 当分别以线段BD ，CE 为直径的两圆相切时，求DE 的长度；(3) 当点D 在AB 边上时，BC 边上是否存在点F ，使△ABC 与△DEF 相似？若存在，请求出线段BF 的长；若不存在，请说明理由．图1 备用图备用图动感体验请打开几何画板文件名“09闸北25”，拖动点D 可以在射线BA 上运动．双击按钮“第（2）题”，拖动点D 可以体验到两圆可以外切一次，内切两次．双击按钮“第（3）题”，再分别双击按钮“DE 为腰”和“DE 为底边”，可以体验到，△DEF 为等腰三角形．1．先解读背景图，△ABC是等腰三角形，那么第（3）题中符合条件的△DEF也是等腰三角形．2．用含有x的式子表示BD、DE、MN是解答第（2）题的先决条件，注意点E的位置不同，DE、MN表示的形式分两种情况．3．求两圆相切的问题时，先罗列三要素，再列方程，最后检验方程的解的位置是否符合题意．4．第（3）题按照DE为腰和底边两种情况分类讨论，运用典型题目的结论可以帮助我们轻松解题．满分解答（1）如图2，作BH⊥AC，垂足为点H．在Rt△ABH中，AB＝5，cosA＝310 AHAB=，所以AH＝32＝12AC．所以BH垂直平分AC，△ABC为等腰三角形，AB＝CB＝5．因为DE//BC，所以AB ACDB EC=，即53y x=．于是得到53y x=，（0x>）．（2）如图3，图4，因为DE//BC，所以DE AEBC AC=，MN ANBC AC=，即|3|53DE x-=，1|3|253xMN-=．因此5|3|3xDE-=，圆心距5|6|6xMN-=．图2 图3 图4 在⊙M中，115226Mr BD y x===，在⊙N中，1122Nr CE x==．①当两圆外切时，5162x x +5|6|6x -=．解得3013x =或者10x =-．如图5，符合题意的解为3013x =，此时5(3)15313x DE -==． ②当两圆内切时，5162x x -5|6|6x -=．当x ＜6时，解得307x =，如图6，此时E 在CA 的延长线上，5(3)1537x DE -==；当x ＞6时，解得10x =，如图7，此时E 在CA 的延长线上，5(3)3533x DE -==．图5 图6 图7（3）因为△ABC 是等腰三角形，因此当△ABC 与△DEF 相似时，△DEF 也是等腰三角形．如图8，当D 、E 、F 为△ABC 的三边的中点时，DE 为等腰三角形DEF 的腰，符合题意，此时BF ＝2.5．根据对称性，当F 在BC 边上的高的垂足时，也符合题意，此时BF ＝4.1．如图9，当DE 为等腰三角形DEF 的底边时，四边形DECF 是平行四边形，此时12534BF =．图8 图9 图10 图11考点伸展第（3）题的情景是一道典型题，如图10，如图11，AH 是△ABC 的高，D 、E 、F 为△ABC 的三边的中点，那么四边形DEHF 是等腰梯形．例 7如图1，在直角坐标系xOy 中，设点A （0，t ），点Q （t ，b ）．平移二次函数2tx y -=的图象，得到的抛物线F 满足两个条件：①顶点为Q ；②与x 轴相交于B 、C 两点（∣OB ∣<∣OC ∣），连结A ，B ．（1）是否存在这样的抛物线F ，使得OC OB OA ⋅=2？请你作出判断，并说明理由；（2）如果AQ ∥BC ，且tan ∠ABO ＝23，求抛物线F 对应的二次函数的解析式．图1动感体验请打开几何画板文件名“08杭州24”，拖动点A 在y 轴上运动，可以体验到，AQ 与BC 保持平行，OA ∶OB 与OA ∶OB ′保持3∶2．双击按钮“t ＝3”，“t ＝0．6”，“t ＝－0．6”，“t ＝－3”，抛物线正好经过点B （或B ′）．思路点拨1．数形结合思想，把OC OB OA ⋅=2转化为212t x x =⋅．2．如果AQ ∥BC ，那么以OA 、AQ 为邻边的矩形是正方形，数形结合得到t ＝b ． 3．分类讨论tan ∠ABO ＝23，按照A 、B 、C 的位置关系分为四种情况．A 在y 轴正半轴时，分为B 、C 在y 轴同侧和两侧两种情况；A 在y 轴负半轴时，分为B 、C 在y 轴同侧和两侧两种情况．满分解答（1）因为平移2tx y -=的图象得到的抛物线F 的顶点为Q （t ，b ），所以抛物线F 对应的解析式为b t x t y +--=2)(．因为抛物线与x 轴有两个交点，因此0>b t ．令0=y ，得-=t OB t b，+=t OC tb ．所以-=⋅t OC OB (|||||tb)( +t t b)|-=2|t 22|OA t tb ==．即22bt t t-=±．所以当32t b =时，存在抛物线F 使得||||||2OC OB OA ⋅=．（2）因为AQ //BC ，所以t ＝b ，于是抛物线F 为t t x t y +--=2)(．解得1,121+=-=t x t x ．①当0>t 时，由||||OC OB <，得)0,1(-t B ．如图2，当01>-t 时，由=∠ABO tan 23=||||OB OA =1-t t ，解得3=t ．此时二次函数的解析式为241832-+-=x x y ．如图3，当01<-t 时，由=∠ABO tan 23=||||OB OA =1+-t t ，解得=t 53．此时二次函数的解析式为-=y 532x ＋2518x ＋12548．图2 图3②如图4，如图5，当0<t 时，由||||OC OB <，将t -代t ,可得=t 53-，3-=t ．此时二次函数的解析式为=y 532x ＋2518x －12548或241832++=x x y ．图4 图5考点伸展第（2）题还可以这样分类讨论：因为AQ //BC ，所以t ＝b ，于是抛物线F 为2()y t x t t =--+．由3tan 2OA ABO OB ∠==，得23OB OA =． ①把2(,0)3B t 代入2()y t x t t =--+，得3t =±（如图2，图5）． ②把2(,0)3B t -代入2()y t x t t =--+，得35t =±（如图3，图4）．2013中考数学压轴题函数等腰三角形问题(一) 例1如图1，已知正方形OABC的边长为2，顶点A、C分别在x、y轴的正半轴上，M 是BC的中点．P(0,m)是线段OC上一动点（C点除外），直线PM交AB的延长线于点D．（1）求点D的坐标（用含m的代数式表示）；（2）当△APD是等腰三角形时，求m的值；（3）设过P、M、B三点的抛物线与x轴正半轴交于点E，过点O作直线ME的垂线，垂足为H（如图2）．当点P从O向C运动时，点H也随之运动．请直接写出点H 所经过的路长（不必写解答过程）．图1 图2动感体验请打开几何画板文件名“11湖州24”，拖动点P在OC上运动，可以体验到，△APD的三个顶点有四次机会可以落在对边的垂直平分线上．双击按钮“第(3)题”，拖动点P由O向C运动，可以体验到，点H在以OM为直径的圆上运动．双击按钮“第(2)题”可以切换．思路点拨1．用含m的代数式表示表示△APD的三边长，为解等腰三角形做好准备．2．探求△APD是等腰三角形，分三种情况列方程求解．3．猜想点H的运动轨迹是一个难题．不变的是直角，会不会找到不变的线段长呢？Rt△OHM的斜边长OM是定值，以OM为直径的圆过点H、C．满分解答（1）因为PC //DB ，所以1CP PM MC BD DM MB ===．因此PM ＝DM ，CP ＝BD ＝2－m ．所以AD ＝4－m ．于是得到点D 的坐标为(2，4－m )．（2）在△APD 中，22(4)AD m =-，224AP m =+，222(2)44(2)PD PM m ==+-． ①当AP ＝AD 时，2(4)m -24m =+．解得32m =（如图3）． ②当PA ＝PD 时，24m +244(2)m =+-．解得43m =（如图4）或4m =（不合题意，舍去）．③当DA ＝DP 时，2(4)m -244(2)m =+-．解得23m =（如图5）或2m =（不合题意，舍去）．综上所述，当△APD 为等腰三角形时，m 的值为32，43或23．图3 图4 图5（3）点H 5．考点伸展第（2）题解等腰三角形的问题，其中①、②用几何说理的方法，计算更简单： ①如图3，当AP ＝AD 时，AM 垂直平分PD ，那么△PCM ∽△MBA ．所以12PC MB CM BA ==．因此12PC =，32m =．②如图4，当PA ＝PD 时，P 在AD 的垂直平分线上．所以DA ＝2PO ．因此42m m -=．解得43m =．第（2）题的思路是这样的：如图6，在Rt △OHM 中，斜边OM 为定值，因此以OM 为直径的⊙G 经过点H ，也就是说点H 在圆弧上运动．运动过的圆心角怎么确定呢？如图7，P 与O 重合时，是点H 运动的起点，∠COH ＝45°，∠CGH ＝90°．图6 图7例2如图1，已知一次函数y ＝－x ＋7与正比例函数43y x =的图象交于点A ，且与x 轴交于点B ．（1）求点A 和点B 的坐标；（2）过点A 作AC ⊥y 轴于点C ，过点B 作直线l //y轴．动点P 从点O 出发，以每秒1个单位长的速度，沿O—C —A 的路线向点A 运动；同时直线l 从点B 出发，以相同速度向左平移，在平移过程中，直线l 交x 轴于点R ，交线段BA 或线段AO 于点Q ．当点P 到达点A 时，点P和直线l 都停止运动．在运动过程中，设动点P 运动的时间为t 秒．①当t 为何值时，以A 、P 、R 为顶点的三角形的面积为8？②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形？若存在，求t 的值；若不存在，请说明理由．图1动感体验请打开几何画板文件名“11盐城28”，拖动点R由B向O运动，从图像中可以看到，△APR的面积有一个时刻等于8．观察△APQ，可以体验到，P在OC上时，只存在AP＝AQ的情况；P在CA上时，有三个时刻，△APQ是等腰三角形．思路点拨1．把图1复制若干个，在每一个图形中解决一个问题．2．求△APR的面积等于8，按照点P的位置分两种情况讨论．事实上，P在CA上运动时，高是定值4，最大面积为6，因此不存在面积为8的可能．3．讨论等腰三角形APQ，按照点P的位置分两种情况讨论，点P的每一种位置又要讨论三种情况．满分解答（1）解方程组7, 4,3y xy x=-+⎧⎪⎨=⎪⎩得3,4.xy=⎧⎨=⎩所以点A的坐标是(3，4)．令70y x=-+=，得7x=．所以点B的坐标是(7，0)．（2）①如图2，当P在OC上运动时，0≤t＜4．由8APR ACP PORCORAS S S S=--=△△△梯形，得1113+7)44(4)(7)8222t t t t-⨯-⨯⨯--⨯-=（．整理，得28120t t-+=．解得t＝2或t＝6（舍去）．如图3，当P在CA上运动时，△APR的最大面积为6．因此，当t＝2时，以A、P、R为顶点的三角形的面积为8．图2 图3 图4②我们先讨论P 在OC 上运动时的情形，0≤t ＜4．如图1，在△AOB 中，∠B ＝45°，∠AOB ＞45°，OB ＝7，42AB =，所以OB ＞AB ．因此∠OAB ＞∠AOB ＞∠B ．如图4，点P 由O 向C 运动的过程中，OP ＝BR ＝RQ ，所以PQ //x 轴．因此∠AQP ＝45°保持不变，∠PAQ 越来越大，所以只存在∠APQ ＝∠AQP 的情况．此时点A 在PQ 的垂直平分线上，OR ＝2CA ＝6．所以BR ＝1，t ＝1．我们再来讨论P 在CA 上运动时的情形，4≤t ＜7．在△APQ 中， 3cos 5A ∠=为定值，7AP t =-，5520333AQ OA OQ OA OR t =-=-=-．如图5，当AP ＝AQ 时，解方程520733t t -=-，得418t =．如图6，当QP ＝QA 时，点Q 在PA 的垂直平分线上，AP ＝2(OR －OP )．解方程72[(7)(4)]t t t -=---，得5t =．如7，当PA ＝PQ 时，那么12cos AQ A AP∠=．因此2cos AQ AP A =⋅∠．解方程52032(7)335t t -=-⨯，得22643t =．综上所述，t ＝1或418或5或22643时，△APQ 是等腰三角形．图5 图6 图7考点伸展当P 在CA 上，QP ＝QA 时，也可以用2cos AP AQ A =⋅∠来求解．2013中考数学压轴题函数等腰三角形问题(二) 例3如图1，在直角坐标平面内有点A(6, 0)，B(0, 8)，C(－4, 0)，点M、N分别为线段AC和射线AB上的动点，点M以2个单位长度/秒的速度自C向A方向作匀速运动，点N以5个单位长度/秒的速度自A向B方向作匀速运动，MN交OB于点P．(1)求证：MN∶NP为定值；(2)若△BNP与△MNA相似，求CM的长；(3)若△BNP是等腰三角形，求CM的长．图1动感体验请打开几何画板文件名“10闸北25”，拖动点M在CA上运动，可以看到△BNP 与△MNA的形状随M的运动而改变．双击按钮“△BNP∽△MNA”，可以体验到，此刻两个三角形都是直角三角形．分别双击按钮“BP＝BN，N在AB上”、“NB＝NP”和“BP＝BN，N在AB的延长线上”，可以准确显示等腰三角形BNP的三种情况．思路点拨1．第（1）题求证MN∶NP的值要根据点N的位置分两种情况．这个结论为后面的计算提供了方便．2．第（2）题探求相似的两个三角形有一组邻补角，通过说理知道这两个三角形是直角三角形时才可能相似．3．第（3）题探求等腰三角形，要两级（两层）分类，先按照点N 的位置分类，再按照顶角的顶点分类．注意当N 在AB 的延长线上时，钝角等腰三角形只有一种情况．4．探求等腰三角形BNP ，N 在AB 上时，∠B 是确定的，把夹∠B 的两边的长先表示出来，再分类计算．满分解答(1)如图2，图3，作NQ ⊥x 轴，垂足为Q ．设点M 、N 的运动时间为t 秒．在Rt △ANQ 中，AN ＝5t ，NQ ＝4t ，AQ ＝3t ．在图2中，QO ＝6－3t ，MQ ＝10－5t ，所以MN ∶NP ＝MQ ∶QO ＝5∶3．在图3中，QO ＝3t －6，MQ ＝5t －10，所以MN ∶NP ＝MQ ∶QO ＝5∶3．(2)因为△BNP 与△MNA 有一组邻补角，因此这两个三角形要么是一个锐角三角形和一个钝角三角形，要么是两个直角三角形．只有当这两个三角形都是直角三角形时才可能相似．如图4，△BNP ∽△MNA ，在Rt △AMN 中，35AN AM =，所以531025t t =-．解得3031t =．此时CM 6031=．图2 图3 图4(3)如图5，图6，图7中，OP MP QN MN =，即245OP t =．所以85OP t =． ①当N 在AB 上时，在△BNP 中，∠B 是确定的，885BP t =-，105BN t =-．(Ⅰ)如图5，当BP ＝BN 时，解方程881055t t -=-，得1017t =．此时CM 2017=． (Ⅱ)如图6，当NB ＝NP 时，45BE BN =．解方程()1848105255t t ⎛⎫-=- ⎪⎝⎭，得54t =．此时CM 52=． (Ⅲ)当PB ＝PN 时，1425BN BP =．解方程()1481058255t t ⎛⎫-=- ⎪⎝⎭，得t 的值为负数，因此不存在PB ＝PN 的情况．②如图7，当点N 在线段AB 的延长线上时，∠B 是钝角，只存在BP ＝BN 的可能，此时510BN t =-．解方程885105t t -=-，得3011t =．此时CM 6011=．图5 图6 图7考点伸展如图6，当NB ＝NP 时，△NMA 是等腰三角形，1425BN BP =，这样计算简便一些．例4如图1，在矩形ABCD中，AB＝m（m是大于0的常数），BC＝8，E为线段BC上的动点（不与B、C重合）．连结DE，作EF⊥DE，EF与射线BA交于点F，设CE＝x，BF＝y．（1）求y关于x的函数关系式；（2）若m＝8，求x为何值时，y的值最大，最大值是多少？（3）若12ym，要使△DEF为等腰三角形，m的值应为多少？图1动感体验请打开几何画板文件名“10南通27”，拖动点E在BC上运动，观察y随x变化的函数图像，可以体验到，y是x的二次函数，抛物线的开口向下．对照图形和图像，可以看到，当E是BC的中点时，y取得最大值．双击按钮“m＝8”，拖动E到BC的中点，可以体验到，点F是AB的四等分点．拖动点A可以改变m的值，再拖动图像中标签为“y随x”的点到射线y＝x上，从图形中可以看到，此时△DCE≌△EBF．思路点拨1．证明△DCE∽△EBF，根据相似三角形的对应边成比例可以得到y关于x的函数关系式．2．第（2）题的本质是先代入，再配方求二次函数的最值．3．第（3）题头绪复杂，计算简单，分三段表达．一段是说理，如果△DEF为等腰三角形，那么得到x＝y；一段是计算，化简消去m，得到关于x的一元二次方程，解出x的值；第三段是把前两段结合，代入求出对应的m的值．满分解答(1)因为∠EDC 与∠FEB 都是∠DEC 的余角，所以∠EDC ＝∠FEB ．又因为∠C ＝∠B ＝90°，所以△DCE ∽△EBF ．因此DC EB CE BF =，即8m x x y -=．整理，得y 关于x 的函数关系为218y x x m m =-+． (2)如图2，当m ＝8时，2211(4)288y x x x =-+=--+．因此当x ＝4时，y 取得最大值为2．(3) 若12y m =，那么21218x x m m m=-+．整理，得28120x x -+=．解得x ＝2或x ＝6．要使△DEF 为等腰三角形，只存在ED ＝EF 的情况．因为△DCE ∽△EBF ，所以CE ＝BF ，即x ＝y ．将x ＝y ＝2代入12y m =，得m ＝6（如图3）；将x ＝y ＝6代入12y m =，得m ＝2（如图4）．图2 图3 图4考点伸展本题中蕴涵着一般性与特殊性的辩证关系，例如：由第（1）题得到218y x x m m =-+221116(8)(4)x x x m m m=--=--+，那么不论m 为何值，当x ＝4时，y 都取得最大值．对应的几何意义是，不论AB 边为多长，当E 是BC 的中点时，BF 都取得最大值．第（2）题m ＝8是第（1）题一般性结论的一个特殊性．再如，不论m 为小于8的任何值，△DEF 都可以成为等腰三角形，这是因为方程218x x x m m=-+总有一个根8x m =-的．第（3）题是这个一般性结论的一个特殊性．2013中考数学压轴题函数相似三角形问题(三)例5已知：如图1，在平面直角坐标系xOy 中，矩形OABC 的边OA 在y 轴的正半轴上，OC 在x 轴的正半轴上，OA ＝2，OC ＝3，过原点O 作∠AOC 的平分线交AB 于点D ，连接DC ，过点D 作DE ⊥DC ，交OA 于点E ．（1）求过点E 、D 、C 的抛物线的解析式；（2）将∠EDC 绕点D 按顺时针方向旋转后，角的一边与y 轴的正半轴交于点F ，另一边与线段OC 交于点G ．如果DF 与（1）中的抛物线交于另一点M ，点M 的横坐标为56，那么EF ＝2GO 是否成立？若成立，请给予证明；若不成立，请说明理由；（3）对于（2）中的点G ，在位于第一象限内的该抛物线上是否存在点Q ，使得直线GQ 与AB 的交点P 与点C 、G 构成的△PCG 是等腰三角形？若存在，请求出点Q 的坐标；若不存在成立，请说明理由．图1动感体验请打开几何画板文件名“09重庆26”，拖动点G 在OC 上运动，可以体验到，△DCG 与△DEF 保持全等，双击按钮“M 的横坐标为1.2”，可以看到，EF ＝2，GO ＝1．拖动点P 在AB 上运动的过程中，可以体验到，存在三个时刻，△PCG 可以成为等腰三角形．。

挑战中考数学压轴题详解(115页)

目录第一部分函数图象中点的存在性问题1.1 因动点产生的相似三角形问题例1 上海市中考第24题例2 苏州市中考第29题例3 黄冈市中考第25题例4 义乌市中考第24题例5 临沂市中考第26题例6 苏州市中考第29题1.2 因动点产生的等腰三角形问题例1 上海市虹口区中考模拟第25题例2 扬州市中考第27题例3 临沂市中考第26题例4 湖州市中考第24题例5 盐城市中考第28题例6 南通市中考第27题例7 江西省中考第25题1.3 因动点产生的直角三角形问题例1 山西省中考第26题例2 广州市中考第24题例3 杭州市中考第22题例4 浙江省中考第23题例5 北京市中考第24题例6 嘉兴市中考第24题例7 河南省中考第23题1.4 因动点产生的平行四边形问题例1 上海市松江区中考模拟第24题例2 福州市中考第21题例3 烟台市中考第26题例4 上海市中考第24题例5 江西省中考第24题例6 山西省中考第26题例7 江西省中考第24题1.5 因动点产生的梯形问题例1 上海市松江中考模拟第24题例2 衢州市中考第24题例4 义乌市中考第24题例5 杭州市中考第24题例7 广州市中考第25题1.6 因动点产生的面积问题例1 苏州市中考第29题例2 菏泽市中考第21题例3 河南省中考第23题例4 南通市中考第28题例5 广州市中考第25题例6 扬州市中考第28题例7 兰州市中考第29题1.7 因动点产生的相切问题例1 上海市杨浦区中考模拟第25题例2 河北省中考第25题例3 无锡市中考第28题1.8 因动点产生的线段和差问题例1 天津市中考第25题例2 滨州市中考第24题例3 山西省中考第26题第二部分图形运动中的函数关系问题2.1 由比例线段产生的函数关系问题例1 宁波市中考第26题例2 上海市徐汇区中考模拟第25题例3 连云港市中考第26题例4 上海市中考第25题2.2 由面积公式产生的函数关系问题例1 菏泽市中考第21题例2 广东省中考第22题例3 河北省中考第26题例4 淮安市中考第28题例5 山西省中考第26题例6 重庆市中考第26题第三部分图形运动中的计算说理问题3.1 代数计算及通过代数计算进行说理问题例1 南京市中考第26题例2 南昌市中考第25题3.2几何证明及通过几何计算进行说理问题例1 上海市黄浦区中考模拟第24题例2 江西省中考第24题第一部分函数图象中点的存在性问题1.1 因动点产生的相似三角形问题例1 上海市中考第24题如图1，在平面直角坐标系xOy 中，顶点为M 的抛物线y ＝ax 2＋bx （a ＞0）经过点A 和x 轴正半轴上的点B ，AO ＝BO ＝2，∠AOB ＝120°．（1）求这条抛物线的表达式；（2）连结OM ，求∠AOM 的大小；（3）如果点C 在x 轴上，且△ABC 与△AOM 相似，求点C 的坐标．图1动感体验请打开几何画板文件名“13上海24”，拖动点C 在x 轴上运动，可以体验到，点C 在点B 的右侧，有两种情况，△ABC 与△AOM 相似．请打开超级画板文件名“13上海24”，拖动点C 在x 轴上运动，可以体验到，点C 在点B 的右侧，有两种情况，△ABC 与△AOM 相似．点击按钮的左部和中部，可到达相似的准确位置。

2013中考数学压轴题及答案40例

中考数学压轴题及答案40例1.如图：抛物线经过A （-3，0）、B （0，4）、C （4，0）三点.（1）求抛物线的解析式.（2）已知AD = AB （D 在线段AC 上），有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动；同时另一个动点Q 以某一速度从点B 沿线段BC 移动，经过t 秒的移动，线段PQ 被BD 垂直平分，求t 的值；（3）在（2）的情况下，抛物线的对称轴上是否存在一点M ，使MQ+MC 的值最小？若存在，请求出点M 的坐标；若不存在，请说明理由。

（注：抛物线2y ax bx c =++的对称轴为2b x a=-）解：设抛物线的解析式为2(0)y ax bx c a =++≠，依题意得：c=4且934016440a b a b -+=⎧⎨++=⎩ 解得1313a b ⎧=-⎪⎪⎨⎪=⎪⎩所以所求的抛物线的解析式为211433y x x =-++ （2）连接DQ ，在Rt △AOB 中，2222345AB AO BO =+=+=所以AD=AB= 5，AC=AD+CD=3 + 4 = 7，CD = AC - AD = 7 – 5 = 2因为BD 垂直平分PQ ，所以PD=QD ，PQ ⊥BD ，所以∠PDB=∠QDB因为AD=AB ，所以∠ABD=∠ADB ，∠ABD=∠QDB ，所以DQ ∥AB所以∠CQD=∠CBA 。

∠CDQ=∠CAB ，所以△CDQ ∽ △CABDQ CD AB CA = 即210,577DQ DQ ==所以AP=AD – DP = AD – DQ=5 –107=257 ，2525177t =÷= 所以t 的值是257（3）答对称轴上存在一点M ，使MQ+MC 的值最小理由：因为抛物线的对称轴为122b x a =-=所以A （- 3，0），C （4，0）两点关于直线12x =对称连接AQ 交直线12x =于点M ，则MQ+MC 的值最小过点Q 作QE ⊥x 轴，于E ，所以∠QED=∠BOA=90 DQ ∥AB ，∠ BAO=∠QDE ， △DQE ∽△ABO QE DQ DE BO AB AO == 即 107453QE DE ==所以QE=87，DE=67，所以OE = OD + DE=2+67=207，所以Q （207，87）设直线AQ 的解析式为(0)y kx m k =+≠则2087730k m k m ⎧+=⎪⎨⎪-+=⎩ 由此得8412441k m ⎧=⎪⎪⎨⎪=⎪⎩ 所以直线AQ 的解析式为8244141y x =+ 联立128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 由此得128244141x y x ⎧=⎪⎪⎨⎪=+⎪⎩ 所以M 128(,)241则：在对称轴上存在点M 128(,)241，使MQ+MC 的值最小。

精选2013年数学中考压轴题

精选2013年数学中考压轴题25．（10分）（2013•常德）如图，已知二次函数的图象过点A（0，﹣3），B（，），对称轴为直线x=﹣，点P是抛物线上的一动点，过点P分别作PM⊥x轴于点M，PN⊥y轴于点N，在四边形PMON上分别截取PC=MP，MD=OM，OE=ON，NF=NP．（1）求此二次函数的解析式；（2）求证：以C、D、E、F为顶点的四边形CDEF是平行四边形；（3）在抛物线上是否存在这样的点P，使四边形CDEF为矩形？若存在，请求出所有符合条件的P点坐标；若不存在，请说明理由．26．（10分）（2013•常德）已知两个共一个顶点的等腰Rt△ABC，Rt△CEF，∠ABC=∠CEF=90°，连接AF，M是AF的中点，连接MB、ME．（1）如图1，当CB与CE在同一直线上时，求证：MB∥CF；（2）如图1，若CB=a，CE=2a，求BM，ME的长；（3）如图2，当∠BCE=45°时，求证：BM=ME．20．（10分）（2013•成都）如图，点B在线段AC上，点D，E在AC同侧，∠A=∠C=90°，BD⊥BE，AD=BC．（1）求证：AC=AD+CE；（2）若AD=3，CE=5，点P为线段AB上的动点，连接DP，作PQ⊥DP，交直线BE于点Q；（i）当点P与A，B两点不重合时，求的值；（ii）当点P从A点运动到AC的中点时，求线段DQ的中点所经过的路径（线段）长．（直接写出结果，不必写出27．（10分）（2013•成都）如图，⊙O的半径r=25，四边形ABCD内接圆⊙O，AC⊥BD于点H，P为CA延长线上的一点，且∠PDA=∠ABD．（1）试判断PD与⊙O的位置关系，并说明理由；（2）若tan∠ADB=，PA=AH，求BD的长；（3）在（2）的条件下，求四边形ABCD的面积．28．（12分）（2013•成都）在平面直角坐标系中，已知抛物线y=x2+bx+c（b，c为常数）的顶点为P，等腰直角三角形ABC的顶点A的坐标为（0，﹣1），C的坐标为（4，3），直角顶点B在第四象限．（1）如图，若该抛物线过A，B两点，求该抛物线的函数表达式；（2）平移（1）中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q．（i）若点M在直线AC下方，且为平移前（1）中的抛物线上的点，当以M、P、Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；（ii）取BC的中点N，连接NP，BQ．试探究是否存在最大值？若存在，求出该最大值；若不存在，请说明理由．23．（10分）（2013•大连）如图，AB是⊙O的直径，CD与⊙O相切于点C，DA⊥AB，DO及DO的延长线与⊙O 分别相交于点E、F，EB与CF相交于点G．（1）求证：DA=DC；（2）⊙O的半径为3，DC=4，求CG的长．24．（11分）（2013•大连）如图，一次函数y=﹣x+4的图象与x轴、y轴分别相交于点A、B．P是射线BO上的一个动点（点P不与点B重合），过点P作PC⊥AB，垂足为C，在射线CA上截取CD=CP，连接PD．设BP=t．（1）t为何值时，点D恰好与点A重合？（2）设△PCD与△AOB重叠部分的面积为S，求S与t的函数关系式，并直接写出t的取值范围．25．（12分）（2013•大连）将△ABC绕点B逆时针旋转α得到△DBE，DE的延长线与AC相交于点F，连接DA、BF．（1）如图1，若∠ABC=α=60°，BF=AF．①求证：DA∥BC；②猜想线段DF、AF的数量关系，并证明你的猜想；（2）如图2，若∠ABC＜α，BF=mAF（m为常数），求的值（用含m、α的式子表示）．26．（12分）（2013•大连）如图，抛物线y=﹣x2+x﹣4与x轴相交于点A、B，与y轴相交于点C，抛物线的对称轴与x轴相交于点M．P是抛物线在x轴上方的一个动点（点P、M、C不在同一条直线上）．分别过点A、B作（2）△MDE能否为等腰直角三角形？若能，求此时点P的坐标；若不能，说明理由；（3）若将“P是抛物线在x轴上方的一个动点（点P、M、C不在同一条直线上）”改为“P是抛物线在x轴下方的一个动点”，其他条件不变，△MDE能否为等腰直角三角形？若能，求此时点P的坐标（直接写出结果）；若不能，说明理由．25．（12分）（2013•南平）在矩形ABCD中，点E在BC边上，过E作EF⊥AC于F，G为线段AE的中点，连接BF、FG、GB．设=k．（1）证明：△BGF是等腰三角形；（2）当k为何值时，△BGF是等边三角形？（3）我们知道：在一个三角形中，等边所对的角相等；反过来，等角所对的边也相等．事实上，在一个三角形中，较大的边所对的角也较大；反之也成立．利用上述结论，探究：当△BGF分别为锐角、直角、钝角三角形时，k的取值范围．26．（14分）（2013•南平）如图，已知点A（0，4），B（2，0）．（1）求直线AB的函数解析式；（2）已知点M是线段AB上一动点（不与点A、B重合），以M为顶点的抛物线y=（x﹣m）2+n与线段OA交于点C．①求线段AC的长；（用含m的式子表示）②是否存在某一时刻，使得△ACM与△AMO相似？若存在，求出此时m的值．24．（12分）（2013•莆田）如图，抛物线y=ax2+bx+c的开口向下，与x轴交于点A（﹣3，0）和点B（1，0）．与y 轴交于点C，顶点为D．（1）求顶点D的坐标．（用含a的代数式表示）；（2）若△ACD的面积为3．①求抛物线的解析式；②将抛物线向右平移，使得平移后的抛物线与原抛物线交于点P，且∠PAB=∠DAC，求平移后抛物线的解析式．25．（14分）（2013•莆田）在Rt△ABC，∠C=90°，D为AB边上一点，点M、N分别在BC、AC边上，且DM⊥DN．作MF⊥AB于点F，NE⊥AB于点E．（1）特殊验证：如图1，若AC=BC，且D为AB中点，求证：DM=DN，AE=DF；（2）拓展探究：若AC≠BC．①如图2，若D为AB中点，（1）中的两个结论有一个仍成立，请指出并加以证明；②如图3，若BD=kAD，条件中“点M在BC边上”改为“点M在线段CB的延长线上”，其它条件不变，请探究AE 与DF的数量关系并加以证明．25．（12分）（2013•泉州）如图，直线y=﹣x+2分别与x、y轴交于点B、C，点A（﹣2，0），P是直线BC 上的动点．（1）求∠ABC的大小；（2）求点P的坐标，使∠APO=30°；（3）在坐标平面内，平移直线BC，试探索：当BC在不同位置时，使∠APO=30°的点P的个数是否保持不变？若不变，指出点P的个数有几个？若改变，指出点P的个数情况，并简要说明理由．22．（12分）（2013•三明）如图①，AB是半圆O的直径，以OA为直径作半圆C，P是半圆C上的一个动点（P与点A，O不重合），AP的延长线交半圆O于点D，其中OA=4．（1）判断线段AP与PD的大小关系，并说明理由；（2）连接OD，当OD与半圆C相切时，求的长；（3）过点D作DE⊥AB，垂足为E（如图②），设AP=x，OE=y，求y与x之间的函数关系式，并写出x的取值范围．23．（14分）（2013•三明）如图，△ABC的顶点坐标分别为A（﹣6，0），B（4，0），C（0，8），把△ABC沿直线BC翻折，点A的对应点为D，抛物线y=ax2﹣10ax+c经过点C，顶点M在直线BC上．（1）证明四边形ABCD是菱形，并求点D的坐标；（2）求抛物线的对称轴和函数表达式；（3）在抛物线上是否存在点P，使得△PBD与△PCD的面积相等？若存在，直接写出点P的坐标；若不存在，请说明理由．25．（12分）（2013•天水）如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）两点．（1）求抛物线的解析式；（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB的点P 坐标（点P、O、D分别与点N、O、B对应）．26．（12分）（2013•天水）如图1，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B 在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．（1）求直线AB的解析式；（2）当点P运动到点（，0）时，求此时DP的长及点D的坐标；（3）是否存在点P，使△OPD的面积等于？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．4. 25(广东省)有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=3将这副直角三角板按如题25图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.(1)如题25图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC=______度；(2)如题25图（3），在三角板DEF运动过程中,当EF经过点C时,求FC的长;(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围.23．（11分）（2013•梅州）用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P．（1）当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；（2）当点P在运动的过程中出现PA=FC时，求∠PAB的度数．探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF 的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．26．（12分）（2013•百色）如图，在平面直角坐标系xOy中，将抛物线C1：y=x2+3先向右平移1个单位，再向下平移7个单位得到抛物线C2．C2的图象与x轴交于A、B两点（点A在点B的左侧）．（1）求抛物线C2的解析式；（2）若抛物线C2的对称轴与x轴交于点C，与抛物线C2交于点D，与抛物线C1交于点E，连结AD、DB、BE、EA，请证明四边形ADBE是菱形，并计算它的面积；（3）若点F为对称轴DE上任意一点，在抛物线C2上是否存在这样的点G，使以O、B、F、G四点为顶点的四边形是平行四边形？如果存在，请求出点G的坐标；如果不存在，请说明理由．25．（广西河池卷）如图（1），在Rt△ABC, ∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED，连结AD、CF，AD与CF交于点M。

2013年中考数学压轴题70题精选(含答案)

1. alter v. 改变，改动，变更2. burst vi. n. 突然发生，爆裂3. dispose vi. 除掉；处置；解决；处理(of)4. blast n. 爆炸；气流vi. 炸，炸掉5. consume v. 消耗，耗尽6. split v. 劈开；割裂；分裂a. 裂开的7. spit v. 吐(唾液等)；唾弃8. spill v. 溢出，溅出，倒出9. slip v. 滑动，滑落；忽略10. slide v. 滑动，滑落n. 滑动；滑面；幻灯片11. bacteria n. 细菌12. breed n. 种，品种v. 繁殖，产仔13. budget n. 预算v. 编预算，作安排14. candidate n. 候选人15. campus n. 校园16. liberal a. 慷慨的；丰富的；自由的17. transform v. 转变，变革；变换18. transmit v. 传播，播送；传递19. transplant v. 移植20. transport vat. 运输，运送n. 运输，运输工具21. shift v. 转移；转动；转变22. vary v. 变化，改变；使多样化23. vanish vi. 消灭，不见（记：“瘟神”消失不见）24. swallow v. 吞下，咽下n. 燕子25. suspicion n. 怀疑，疑心26. suspicious a. 怀疑的，可疑的27. mild a. 温暖的，暖和的；温柔的，味淡的28. tender a. 温柔的；脆弱的29. nuisance n. 损害，妨害，讨厌(的人或事物)（记：“牛绅士”——>让人讨厌）30. insignificant a. 无意义的，无足轻重的；无价值的31. accelerate vt. 加速，促进32. absolute a. 绝对的，无条件的；完全的33. boundary n. 分界线，边界34. brake n. 刹车，制动器v. 刹住(车)35. catalog n. 目录(册) v. 编目36. vague a. 模糊的，不明确的37. vain n. 徒劳，白费38. extinct a. 绝灭的，熄灭的39. extraordinary a. 不平常的，特别的，非凡的（记：新概念3 的passage2里出现过的）40. extreme a. 极度的，极端的n. 极端，过分41. agent n. 代理人，代理商；动因，原因42. alcohol n. 含酒精的饮料，酒精43. appeal n. /vi. 呼吁，恳求44. appreciate vt. 重视，赏识，欣赏45. approve v. 赞成，同意，批准46. stimulate vt. 刺激，激励47. acquire vt. 取得，获得；学到48. accomplish vt . 完成，到达；实行49. network n. 网状物；广播网，电视网；网络50. tide n. 潮汐；潮流51. tidy a. 整洁的，整齐的52. trace vt. 追踪，找到n. 痕迹，踪迹53. torture n. /vt. 拷打，折磨（记：“讨吃的”就会受到别人的折磨和拷打= =）54. wander vi. 漫游，闲逛55. wax n. 蜡56. weave v. 织，编57. preserve v. 保护，保存，保持，维持61. abuse v. 滥用，虐待；谩骂62. academic a. 学术的；高等院校的；研究院的63. academy n. (高等)专科院校；学会64. battery n. 电池(组)65. barrier n. 障碍；棚栏66. cargo n. (船、飞机等装载的)货物67. career n. 生涯，职业68. vessel n. 船舶；容器，器皿；血管69. vertical a. 垂直的70. oblige v. 迫使，责成；使感激71. obscure a. 阴暗，模糊72. extent n. 程度，范围，大小，限度73. exterior n. 外部，外表a. 外部的，外表的74. external a. 外部的，外表的，外面的75. petrol n. 汽油76. petroleum n. 石油（记：一直搞错的两个单词：petrol & petroleum）77. delay vt. /n. 推迟，延误，耽搁78. decay vi. 腐烂，腐朽（记：近义词“rotten”）79. decent a. 像样的，体面的80. route n. 路；路线；航线81. ruin v. 毁坏，破坏n. 毁灭，[pl. ]废墟ruins82. sake n. 缘故，理由83. satellite n. 卫星84. scale n. 大小，规模；等级；刻度85. temple n. 庙宇86. tedious a. 乏味道，单调的，87. tend vi. 易于，趋向88. tendency n. 趋向，趋势89. ultimate a. 极端的，最大的，最终的n. 极端90. undergo v. 经历，遭受91. abundant a. 丰富的，充裕的，大量的92. adopt v. 收养；采用；采纳93. adapt vi. 适应，适合；改编，改写vt. 使适应94. bachelor n. 学士，学士学位；单身汉95. casual a. 偶然的，碰巧的；临时的；非正式的96. trap n. 陷阱，圈套v. 设陷阱捕捉97. vacant a. 空的，未占用的98. vacuum n. 真空，真空吸尘器99. oral a. 口头的，口述的，口的100. optics n. (单、复数同形)光学101. organ n. 器官，风琴102. excess n. 过分，过量，过剩103. expel v. 驱逐，开除，赶出104. expend v. 消费105. expenditure n. 支出，消费；经费106. expense n. 开销，费用107. expensive a. 花钱多的；价格高贵的108. expand v. 扩大，扩张；展开，膨胀109. expansion n. 扩大，扩充；发展，膨胀110. private a. 私人的，个人的111. individual a. 个别的，单独的n. 个人，个体112. personal a. 个人的，私人的；亲自的114. personnel n. [总称] 人员，员工；人事部门115. the Pacific Ocean 太平洋116. the Atlantic Ocean 大西洋117. the Arctic Ocean 北冰洋118. the Antarctic Ocean 南冰洋119. grant vt. 授予，同意，准予119. grand a. 宏伟大，壮丽的，重大的120. invade v. 侵入，侵略，侵袭121. acid n. 酸，酸性物质a. 酸的；尖刻的122. acknowledge v. 承认；致谢123. balcony n. 阳台124. calculate vt. 计算，核算125. calendar n. 日历，月历126. optimistic a. 乐观127. optional a. 可以任选的，非强制的128. outstanding a. 杰出的，突出的，显著的129. export n. 出口(物) v. 出口，输出130. import n. 进口(物) v. 进口，输入131. impose vt. 把. . . 加强(on)；采用，利用132. religion n. 宗教，宗教信仰133. religious a. 宗教的134. victim n. 牺牲品，受害者135. video n. 电视，视频a. 电视的，录像的136. videotape n. 录像磁带v. 把. . . 录在录像带上137. offend v. 冒犯，触犯138. bother v. 打搅，麻烦139. interfere v. 干涉，干扰，妨碍140. internal a. 内部的，国内的141. beforehand ad. 预先，事先142. racial a. 人种的种族的143. radiation n. 放射物，辐射144. radical a. 根本的；激进的145. range n. 幅度，范围v. (在某范围内)变动146. wonder n. 惊奇，奇迹v. 想知道，对. . . 感到疑惑147. isolate vt. 使隔离，使孤立148. issue n. 问题，争论点；发行，(报刊)一期149. hollow a. 空的，中空的，空虚道150. hook n. 钩vt. 钩住151. adequate a. 适当地；足够152. adhere vi. 粘附，附着；遵守，坚持153. ban vt. 取缔，禁止154. capture vt. 俘虏，捕获155. valid a. 有效的，有根据的；正当的156. valley n. 山谷，峡谷157. consistent a. 坚固定；一致的，始终如一的158. continuous a. 继续的，连续(不断)的159. continual a. 不断地，频繁的160. explode v. 爆炸；爆发；激增161. exploit v. 剥削；利用，开采162. explore v. 勘探163. explosion n. 爆炸；爆发；激增164. explosive a. 爆炸的；极易引起争论的165. remote a. 遥远的，偏僻的166. removal n. 除去，消除167. render vt. 使得，致使167. render 解释比较长，可要仔细体会啊！（记：??? ）168. precaution n. 预防，防备，警惕169. idle a. 懒散的，无所事事的170. identify vt. 认出，鉴定171. identify n. 身份；个性，特性172. poverty n. 贫穷173. resistant a. (to) 抵抗的，抗. . . 的，耐. . . 的174. resolve vt. 解决；决定，决意175. barrel n. 桶176. bargain n. 便宜货vi. 讨价还价177. coarse a. 粗的，粗糙的，粗劣的178. coach n. 教练；长途公共汽车179. code n. 准则，法规，密码180. coil n. 线圈v. 卷，盘绕181. adult n. 成年人182. advertise v. 为. . . 做广告183. advertisement n. 广告184. agency n. 代理商，经销商185. focus v. (使)聚集n. 焦点，中心，聚焦186. forbid vt. 不许，禁止187. debate n. /v. 辩论，争论188. debt n. 欠债189. decade n. 十年190. enclose vt. 围住；把. . . 装入信封191. encounter vt. /n. 遭遇，遭到192. globe n. 地球，世界；地球仪193. global a. 全球的；总的194. scan vt. 细看；扫描；浏览195. scandal n. 丑事，丑闻196. significance n. 意义；重要性197. subsequent a. 随后的，后来的198. virtue n. 美德，优点199. virtual a. 实际上的，事实上的200. orient vt. 使适应。