2017年挑战中考数学压轴题(全套含答案)
2017年天津市中考数学试卷压轴题
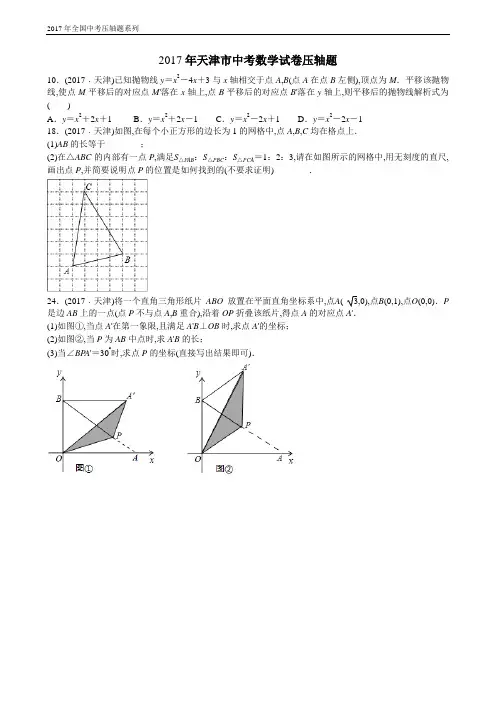
2017年天津市中考数学试卷压轴题10.(2017﹒天津)已知抛物线y=x2-4x+3与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,则平移后的抛物线解析式为()A.y=x2+2x+1 B.y=x2+2x-1 C.y=x2-2x+1 D.y=x2-2x-118.(2017﹒天津)如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.(1)AB的长等于________;(2)在△ABC的内部有一点P,满足S△P AB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)________.24.(2017﹒天津)将一个直角三角形纸片ABO放置在平面直角坐标系中,点A( 3,0),点B(0,1),点O(0,0).P 是边AB上的一点(点P不与点A,B重合),沿着OP折叠该纸片,得点A的对应点A'.(1)如图①,当点A'在第一象限,且满足A'B⊥OB时,求点A'的坐标;(2)如图②,当P为AB中点时,求A'B的长;(3)当∠BP A'=30°时,求点P的坐标(直接写出结果即可).25.(2017﹒天津)已知抛物线y=x2+bx-3(b是常数)经过点A(-1,0).(1)求该抛物线的解析式和顶点坐标;(2)P(m,t)为抛物线上的一个动点,P关于原点的对称点为P'.①当点P'落在该抛物线上时,求m的值;②当点P'落在第二象限内,P'A2取得最小值时,求m的值.2017年天津市中考数学试卷压轴题参考答案10.(2017﹒天津)已知抛物线y=x2-4x+3与x轴相交于点A,B(点A在点B左侧),顶点为M.平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,则平移后的抛物线解析式为()A.y=x2+2x+1 B.y=x2+2x-1 C.y=x2-2x+1 D.y=x2-2x-1解:当y=0,则0=x2-4x+3,(x-1)(x-3)=0,解得:x1=1,x2=3,∴A(1,0),B(3,0),y=x2-4x+3=(x-2)2-1,∴M点坐标为:(2,-1),∵平移该抛物线,使点M平移后的对应点M'落在x轴上,点B平移后的对应点B'落在y轴上,∴抛物线向上平移一个单位长度,再向左平移3个单位长度即可,∴平移后的解析式为:y=(x+1)2=x2+2x+1.选A.18.(2017﹒天津)如图,在每个小正方形的边长为1的网格中,点A,B,C均在格点上.(1)AB的长等于________;(2)在△ABC的内部有一点P,满足S△P AB:S△PBC:S△PCA=1:2:3,请在如图所示的网格中,用无刻度的直尺,画出点P,并简要说明点P的位置是如何找到的(不要求证明)________.解:(1)AB=12+42=17.故答案为17.(2)如图AC与网格相交,得到点D、E,取格点F,连接FB并且延长,与网格相交,得到M,N,G.连接DN,EM,DG,DN与EM相交于点P,点P即为所求.理由:平行四边形ABME 的面积:平行四边形CDNB 的面积:平行四边形DEMG 的面积=1:2:3,△P AB 的面积=12平行四边形ABME 的面积,△PBC 的面积=12平行四边形CDNB 的面积,△P AC 的面积=△PNG 的面积=12△DGN 的面积=12平行四边形DEMG 的面积, ∴S △P AB :S △PBC :S △PCA =1:2:3.24.(2017﹒天津)将一个直角三角形纸片ABO 放置在平面直角坐标系中,点A ( 3,0),点B (0,1),点O (0,0).P 是边AB 上的一点(点P 不与点A ,B 重合),沿着OP 折叠该纸片,得点A 的对应点A '.(1)如图①,当点A '在第一象限,且满足A 'B ⊥OB 时,求点A '的坐标;(2)如图②,当P 为AB 中点时,求A 'B 的长;(3)当∠BP A '=30°时,求点P 的坐标(直接写出结果即可).解:(1)∵点A (3,0),点B (0,1),∴OA =3,OB =1,由折叠的性质得:OA '=OA =3,∵A 'B ⊥OB ,∴∠A 'BO =90°,在Rt △A 'OB 中,A 'B =OA ′2-OB 2=2,∴点A '的坐标为(2,1);(2)在Rt △ABO 中,OA =3,OB =1,∴AB =OA 2+OB 2=2,∵P 是AB 的中点,∴AP =BP =1,OP =12AB =1, ∴OB =OP =BP∴△BOP 是等边三角形,∴∠BOP =∠BPO =60°,∴∠OP A =180°-∠BPO =120°,由折叠的性质得:∠OP A '=∠OP A =120°,P A '=P A =1,∴∠BOP +∠OP A '=180°,∴OB ∥P A ',又∵OB =P A '=1,∴四边形OP A 'B 是平行四边形,∴A 'B =OP =1;(3)设P (x ,y ),分两种情况:①如图③所示:点A '在y 轴上,在△OP A '和△OP A 中,⎩⎪⎨⎪⎧OA ′=OAP A ′=P A OP =OP, ∴△OP A '≌△OP A (SSS ),∴∠A 'OP =∠AOP =12∠AOB =45°, ∴点P 在∠AOB 的平分线上,设直线AB 的解析式为y =kx +b ,把点A (3,0),点B (0,1)代入得:⎩⎨⎧3k +b =0b =1, 解得:⎩⎪⎨⎪⎧k =-33b =1, ∴直线AB 的解析式为y =-33x +1, ∵P (x ,y ),∴x =-33x +1, 解得:x =3-32, ∴P ⎛⎪⎫3-3,3-3;②如图④所示:由折叠的性质得:∠A '=∠A =30°,OA '=OA ,∵∠BP A '=30°,∴∠A '=∠A =∠BP A ',∴OA '∥AP ,P A '∥OA ,∴四边形OAP A '是菱形,∴P A =OA =3,作PM ⊥OA 于M ,如图④所示:∵∠A =30°,∴PM =12P A =32, 把y =32代入y =-33x +1得:32=-33x +1, 解得:x =23-32, ∴P ⎝ ⎛⎭⎪⎫23-32,32;综上所述:当∠BP A '=30°时,点P 的坐标为⎝⎛⎭⎪⎫3-32,3-32或⎝ ⎛⎭⎪⎫23-32,32.25.(2017﹒天津)已知抛物线y =x 2+bx -3(b 是常数)经过点A (-1,0).(1)求该抛物线的解析式和顶点坐标;(2)P (m ,t )为抛物线上的一个动点,P 关于原点的对称点为P '.①当点P '落在该抛物线上时,求m 的值;②当点P '落在第二象限内,P 'A 2取得最小值时,求m 的值.解:(1)∵抛物线y =x 2+bx -3经过点A (-1,0),∴0=1-b -3,解得b =-2,∴抛物线解析式为y =x 2-2x -3,∵y =x 2-2x -3=(x -1)2-4,∴抛物线顶点坐标为(1,-4);(2)①由P (m ,t )在抛物线上可得t =m 2-2m -3,∵点P ′与P 关于原点对称,∴P ′(-m ,-t ),∵点P ′落在抛物线上,∴-t =(-m )2-2(-m )-3,即t =-m 2-2m +3, ∴m 2-2m -3=-m 2-2m +3,解得m =3或m =-3;∴-m <0,-t >0,即m >0,t <0,∵抛物线的顶点坐标为(1,-4),∴-4≤t <0,∵P 在抛物线上,∴t =m 2-2m -3,∴m 2-2m =t +3,∵A (-1,0),P ′(-m ,-t ),∴P ′A 2=(-m +1)2+(-t )2=m 2-2m +1+t 2=t 2+t +4=⎝⎛⎭⎫t +122+154; ∴当t =-12时,P ′A 2有最小值, ∴-12=m 2-2m -3,解得m =2-142或m =2+142, ∵m >0,∴m =2-142不合题意,舍去, ∴m 的值为2+142.。
2017年河北省中考数学压轴试卷及解析答案word版(一)

2017年河北省中考数学压轴试卷(一)一、选择题(本大题共16个小题,1-10小题,每小题3分,11-16小题,每小题3分,共42分.在每小题给出的四个选项中只有一项是符合题目要求的,请把正确的答案涂在答题卡上.1.(3分)﹣3的相反数是()A.3 B.﹣3 C.D.﹣2.(3分)如图,数轴上的A、B、C、D四点中,与数﹣表示的点最接近的是()A.点A B.点B C.点C D.点D3.(3分)下列运算正确的是()A.a2⋅a3=a6 B.(a2)3=a6C.(﹣ab2)6=a6b6D.(a+b)2=a2+b24.(3分)下列图形中,不是中心对称图形的是()A. B.C. D.5.(3分)的算术平方根是()A.2 B.±2 C.D.±6.(3分)要使分式有意义,则x的取值应满足()A.x=﹣2 B.x≠2 C.x>﹣2 D.x≠﹣27.(3分)在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的()A.众数B.方差C.平均数D.中位数8.(3分)将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是()A.B.C.D.9.(3分)如图几何体的俯视图是()A.B.C.D.10.(3分)下列等式从左到右的变形,属于因式分解的是()A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1C.(x+1)(x+3)=x2+4x+3 D.x3﹣x=x(x+1)(x﹣1)11.(2分)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是()A.3 B.6 C.9 D.1212.(2分)解分式方程+=3时,去分母后变形正确的是()A.2+(x+2)=3(x﹣1)B.2﹣x+2=3(x﹣1)C.2﹣(x+2)=3 D.2﹣(x+2)=3(x﹣1)13.(2分)将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有()A.4个 B.3个 C.2个 D.1个14.(2分)如图,点A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD 的面积为6,则k的值为()A.6 B.﹣6 C.3 D.﹣315.(2分)如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是()A.OE=BE B.=C.△BOC是等边三角形D.四边形ODBC是菱形16.(2分)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高()A.600﹣250米B.600﹣250米C.350+350米D.500米二、填空题(本大题共4个小题,每小题3分,共12分.把答案写在题中的横线上)17.(3分)若|a|=20160,则a=.18.(3分)如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为.19.(3分)在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A 向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,则A3表示的数是按照这种移动规律移动下去,第n次移动到点A N,如果点A N与原点的距离不小于20,那么n的最小值是.三、解答题(本大题6个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(9分)计算:(﹣2015)0+|1﹣|﹣2cos45°++(﹣)﹣2.21.(9分)先化简,再求值:,其中x=+1.22.(10分)为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:(1)该校初四学生共有多少人?(2)求表中a,b,c的值,并补全条形统计图.(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.23.(9分)我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=的一部分,请根据图中信息解答下列问题:(1)求k的值;(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?24.(10分)已知一次函数y=﹣x+6的图象与坐标轴交于A、B点(如图),AE 平分∠BAO,交x轴于点E.(1)求点B的坐标;(2)求直线AE的表达式;(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB 的面积.25.(10分)如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.(1)试判断线段AB与AC的数量关系,并说明理由;(2)若PC=2,求⊙O的半径和线段PB的长;(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.26.(12分)抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y轴交于点C(0,﹣3)(1)求抛物线的解析式;(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m 经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.2017年河北省中考数学压轴试卷(一)参考答案与试题解析一、选择题(本大题共16个小题,1-10小题,每小题3分,11-16小题,每小题3分,共42分.在每小题给出的四个选项中只有一项是符合题目要求的,请把正确的答案涂在答题卡上.1.(3分)﹣3的相反数是()A.3 B.﹣3 C.D.﹣【解答】解:﹣3的相反数是3,故选:A.2.(3分)如图,数轴上的A、B、C、D四点中,与数﹣表示的点最接近的是()A.点A B.点B C.点C D.点D【解答】解:∵≈1.732,∴﹣≈﹣1.732,∵点A、B、C、D表示的数分别为﹣3、﹣2、﹣1、2,∴与数﹣表示的点最接近的是点B.故选:B.3.(3分)下列运算正确的是()A.a2⋅a3=a6 B.(a2)3=a6C.(﹣ab2)6=a6b6D.(a+b)2=a2+b2【解答】解:A、同底数幂的乘法底数不变值数相加,故A错误;B、幂的乘方底数不变指数相乘,故B正确;C、积的乘方等于乘方的积,故C错误;D、和的平方等于平方和加积的二倍,故D错误;故选:B.4.(3分)下列图形中,不是中心对称图形的是()A. B.C. D.【解答】解:A、是中心对称图形,故本选项不符合题意;B、不是中心对称图形,故本选项符合题意;C、是中心对称图形,故本选项不符合题意;D、是中心对称图形,故本选项不符合题意.故选B.5.(3分)的算术平方根是()A.2 B.±2 C.D.±【解答】解:∵=2,而2的算术平方根是,∴的算术平方根是,故选:C.6.(3分)要使分式有意义,则x的取值应满足()A.x=﹣2 B.x≠2 C.x>﹣2 D.x≠﹣2【解答】解:∵分式有意义,∴x+2≠0,∴x≠﹣2,即x的取值应满足:x≠﹣2.故选:D.7.(3分)在某校“我的中国梦”演讲比赛中,有9名学生参加比赛,他们决赛的最终成绩各不相同,其中的一名学生要想知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的()A.众数B.方差C.平均数D.中位数【解答】解:由于总共有9个人,且他们的分数互不相同,第5的成绩是中位数,要判断是否进入前5名,故应知道中位数的多少.故选:D.8.(3分)将一张长与宽的比为2:1的长方形纸片按如图①、②所示的方式对折,然后沿图③中的虚线裁剪,得到图④,最后将图④的纸片再展开铺平,则所得到的图案是()A.B.C.D.【解答】解:严格按照图中的顺序向右翻折,向右上角翻折,剪去右上角,展开得到结论.故选A.9.(3分)如图几何体的俯视图是()A.B.C.D.【解答】解:该几何体的俯视图为,故选D10.(3分)下列等式从左到右的变形,属于因式分解的是()A.a(x﹣y)=ax﹣ay B.x2+2x+1=x(x+2)+1C.(x+1)(x+3)=x2+4x+3 D.x3﹣x=x(x+1)(x﹣1)【解答】解:A、右边不是整式积的形式,不是因式分解,故本选项错误;B、右边不是整式积的形式,不是因式分解,故本选项错误;C、右边不是整式积的形式,不是因式分解,故本选项错误;D、符合因式分解的定义,故本选项正确;故选:D.11.(2分)△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是()A.3 B.6 C.9 D.12【解答】解:∵△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,△ABC的面积是3,∴△ABC与△A′B′C′的面积比为:1:4,则△A′B′C′的面积是:12.故选:D.12.(2分)解分式方程+=3时,去分母后变形正确的是()A.2+(x+2)=3(x﹣1)B.2﹣x+2=3(x﹣1)C.2﹣(x+2)=3 D.2﹣(x+2)=3(x﹣1)【解答】解:方程变形得:﹣=3,去分母得:2﹣(x+2)=3(x﹣1),故选D13.(2分)将直角三角尺的直角顶点靠在直尺上,且斜边与这根直尺平行,那么,在形成的这个图中与∠α互余的角共有()A.4个 B.3个 C.2个 D.1个【解答】解:∵斜边与这根直尺平行,∴∠α=∠2,又∵∠1+∠2=90°,∴∠1+∠α=90°,又∠α+∠3=90°∴与α互余的角为∠1和∠3.故选:C.14.(2分)如图,点A是反比例函数y=(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD 的面积为6,则k的值为()A.6 B.﹣6 C.3 D.﹣3【解答】解:作AE⊥BC于E,如图,∵四边形ABCD为平行四边形,∴AD∥x轴,∴四边形ADOE为矩形,∴S=S矩形ADOE,平行四边形ABCD=|﹣k|,而S矩形ADOE∴|﹣k|=6,而k<0,即k<0,∴k=﹣6.故选B.15.(2分)如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是()A.OE=BE B.=C.△BOC是等边三角形D.四边形ODBC是菱形【解答】解:∵AB⊥CD,AB过O,∴DE=CE,=,根据已知不能推出OE=BE,△BOC是等边三角形,四边形ODBC是菱形.故选:B.16.(2分)小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为60°,求山高()A.600﹣250米B.600﹣250米C.350+350米D.500米【解答】解:∵BE:AE=5:12,=13,∴BE:AE:AB=5:12:13,∵AB=1300米,∴AE=1200米,BE=500米,设EC=x米,∵∠DBF=60°,∴DF=x米.又∵∠DAC=30°,∴AC=CD.即:1200+x=(500+x),解得x=600﹣250.∴DF=x=600﹣750,∴CD=DF+CF=600﹣250(米).答:山高CD为(600﹣250)米.故选:B.二、填空题(本大题共4个小题,每小题3分,共12分.把答案写在题中的横线上)17.(3分)若|a|=20160,则a=±1.【解答】∵|a|=20160,∴|a|=1,∴a=±1.故答案为:±1.18.(3分)如图,在△ABC中,CA=CB,∠ACB=90°,AB=2,点D为AB的中点,以点D为圆心作圆心角为90°的扇形DEF,点C恰在弧EF上,则图中阴影部分的面积为﹣.【解答】解:连接CD,作DM⊥BC,DN⊥AC.∵CA=CB,∠ACB=90°,点D为AB的中点,∴DC=AB=1,四边形DMCN是正方形,DM=.则扇形FDE的面积是:=.∵CA=CB,∠ACB=90°,点D为AB的中点,∴CD平分∠BCA,又∵DM⊥BC,DN⊥AC,∴DM=DN,∵∠GDH=∠MDN=90°,∴∠GDM=∠HDN,在△DMG和△DNH中,,∴△DMG≌△DNH(AAS),∴S=S四边形DMCN=.四边形DGCH则阴影部分的面积是:﹣.故答案为﹣.19.(3分)在数轴上,点A表示1,现将点A沿x轴做如下移动,第一次点A 向左移动3个单位长度到达点A1,第二次将点A1向右移动6个单位长度到达点A2,第三次将点A2向左移动9个单位长度到达点A3,则A3表示的数是﹣5按照这种移动规律移动下去,第n次移动到点A N,如果点A N与原点的距离不小于20,那么n的最小值是13.【解答】解:第一次点A向左移动3个单位长度至点A1,则A1表示的数,1﹣3=﹣2;第2次从点A1向右移动6个单位长度至点A2,则A2表示的数为﹣2+6=4;第3次从点A2向左移动9个单位长度至点A3,则A3表示的数为4﹣9=﹣5;第4次从点A3向右移动12个单位长度至点A4,则A4表示的数为﹣5+12=7;第5次从点A4向左移动15个单位长度至点A5,则A5表示的数为7﹣15=﹣8;…;则A7表示的数为﹣8﹣3=﹣11,A9表示的数为﹣11﹣3=﹣14,A11表示的数为﹣14﹣3=﹣17,A13表示的数为﹣17﹣3=﹣20,A6表示的数为7+3=10,A8表示的数为10+3=13,A10表示的数为13+3=16,A12表示的数为16+3=19,所以点A N与原点的距离不小于20,那么n的最小值是13,故答案为:﹣5,13.三、解答题(本大题6个小题,共66分.解答应写出文字说明、证明过程或演算步骤)20.(9分)计算:(﹣2015)0+|1﹣|﹣2cos45°++(﹣)﹣2.【解答】解:原式=1+﹣1﹣2×+2+9=2+9.21.(9分)先化简,再求值:,其中x=+1.【解答】解:∵x=+1,∴x=3+1=4,原式=×=,当x=4时,原式==2.22.(10分)为了解今年初四学生的数学学习情况,某校在第一轮模拟测试后,对初四全体同学的数学成绩作了统计分析,绘制如下图表:请结合图表所给出的信息解答系列问题:(1)该校初四学生共有多少人?(2)求表中a,b,c的值,并补全条形统计图.(3)初四(一)班数学老师准备从成绩优秀的甲、乙、丙、丁四名同学中任意抽取两名同学做学习经验介绍,求恰好选中甲、乙两位同学的概率.【解答】解:(1)由题意可得:该校初四学生共有:105÷0.35=300(人),答:该校初四学生共有300人;(2)由(1)得:a=300×0.3=90(人),b==0.15,c==0.2;如图所示;(3)画树形图得:∴一共有12种情况,抽取到甲和乙的有2种,∴P(抽到甲和乙)==.23.(9分)我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线y=的一部分,请根据图中信息解答下列问题:(1)求k的值;(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?【解答】解:(1)把B(12,20)代入y=中得:k=12×20=240(2)设AD的解析式为:y=mx+n把(0,10)、(2,20)代入y=mx+n中得:解得∴AD的解析式为:y=5x+10当y=15时,15=5x+10,x=115=,x==16∴16﹣1=15答:恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有15小时.24.(10分)已知一次函数y=﹣x+6的图象与坐标轴交于A、B点(如图),AE 平分∠BAO,交x轴于点E.(1)求点B的坐标;(2)求直线AE的表达式;(3)过点B作BF⊥AE,垂足为F,连接OF,试判断△OFB的形状,并求△OFB 的面积.【解答】解:(1)当y=﹣x+6=0时,x=8,∴点B的坐标为(8,0).(2)当x=0时,y=﹣x+6=6,∴点A的坐标为(0,6),∴OA=6,OB=8,∴AB==10.∵AE平分∠BAO,交x轴于点E,∴=,∴OE=BE.∵OE+BE=OB=8,∴OE=3,BE=5,∴点E的坐标为(3,0).设直线AE的表达式为y=kx+b,将A(0,6)、E(3,0)代入y=kx+b,,解得:,∴直线AE的表达式为y=﹣2x+6.(3)过点F作FG⊥x轴于点G,如图所示.∵BF⊥AE,∴∠BFE=90°=∠AOE.∵∠AEO=∠BEF,∴△AOE∽△BFE,∴==.∵OA=6,OE=3,∴AE=3.∵BE=5,∴BF=2,EF=.同理可得:△BEF∽△BFG,∴BG=4,FG=2.∵OB=8,∴OG=4=BG,∴△OFB为等腰三角形,∴S=OB•FG=8.△OFB25.(10分)如图,已知直线l与⊙O相离,OA⊥l于点A,OA=5.OA与⊙O相交于点P,AB与⊙O相切于点B,BP的延长线交直线l于点C.(1)试判断线段AB与AC的数量关系,并说明理由;(2)若PC=2,求⊙O的半径和线段PB的长;(3)若在⊙O上存在点Q,使△QAC是以AC为底边的等腰三角形,求⊙O的半径r的取值范围.【解答】解:(1)AB=AC,理由如下:连接OB.∵AB切⊙O于B,OA⊥AC,∴∠OBA=∠OAC=90°,∴∠OBP+∠ABP=90°,∠ACP+∠APC=90°,∵OP=OB,∴∠OBP=∠OPB,∵∠OPB=∠APC,∴∠ACP=∠ABC,∴AB=AC;(2)延长AP交⊙O于D,连接BD,设圆半径为r,则OP=OB=r,PA=5﹣r,则AB2=OA2﹣OB2=52﹣r2,AC2=PC2﹣PA2=﹣(5﹣r)2,∴52﹣r2=﹣(5﹣r)2,解得:r=3,∴AB=AC=4,∵PD是直径,∴∠PBD=90°=∠PAC,又∵∠DPB=∠CPA,∴△DPB∽△CPA,∴=,∴=,解得:PB=.∴⊙O的半径为3,线段PB的长为;(3)作出线段AC的垂直平分线MN,作OE⊥MN,则可以推出OE=AC=AB=又∵圆O与直线MN有交点,∴OE=≤r,≤2r,25﹣r2≤4r2,r2≥5,∴r≥,又∵圆O与直线相离,∴r<5,即≤r<5.26.(12分)抛物线y=x2+bx+c与x轴交于A、B两点,B点坐标为(3,0),与y 轴交于点C(0,﹣3)(1)求抛物线的解析式;(2)点P在抛物线位于第四象限的部分上运动,当四边形ABPC的面积最大时,求点P的坐标(3)直线l经过A、C两点,点Q在抛物线位于y轴左侧的部分上运动,直线m 经过点B和点Q,是否存在直线m,使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似?若存在,求出直线m的解析式,若不存在,请说明理由.【解答】(1)把B、C两点坐标代入抛物线解析式可得,解得,∴抛物线解析式为y=x2﹣2x﹣3;(2)如图1,连接BC,过Py轴的平行线,交BC于点M,交x轴于点H,在y=x2﹣2x﹣3中,令y=0可得0=x2﹣2x﹣3,解得x=﹣1或x=3,∴A点坐标为(﹣1,0),∴AB=3﹣(﹣1)=4,且OC=3,∴S=AB×OC=×4×3=6,△ABC∵B(3,0),C(0,﹣3),∴直线BC解析式为y=x﹣3,设P点坐标为(x,x2﹣2x﹣3),则M点坐标为(x,x﹣3),∵P点在第四限,∴PM=x﹣3﹣(x2﹣2x﹣3)=﹣x2+3x,=PM•OH+PM•HB=PM(OH+HB)=PM•OB=PM,∴S△PBC∴当PM有最大值时,△PBC的面积最大,则四边形ABPC的面积最大,∵PM=﹣x2+3x=﹣(x﹣)2+,∴当x=时,PM max=,则S△PBC=×=,此时P点坐标为(,﹣)(3)如图2,设直线m交y轴于点N,交直线l于点G,则∠AGP=∠GNC+∠GCN,当△AGB和△NGC相似时,必有∠AGB=∠CGB,又∠AGB+∠CGB=180°,∴∠AGB=∠CGB=90°,∴∠ACO=∠OBN,在Rt△AON和Rt△NOB中,∴Rt△AON≌Rt△NOB(ASA),∴ON=OA=1,∴N点坐标为(0,﹣1),设直线m解析式为y=kx+d,把B、N两点坐标代入可得,解得,∴直线m解析式为y=x﹣1,即存在满足条件的直线m,其解析式为y=x﹣1.赠送:初中数学几何模型【模型一】半角型:图形特征:FAB正方形ABCD中,∠EAF=45°∠1=12∠BAD推导说明:1.1在正方形ABCD中,点E、F分别在BC、CD上,且∠FAE=45°,求证:EF=BE+DFE-aa B E1.2在正方形ABCD中,点E、F分别在BC、CD上,且EF=BE+DF,求证:∠FAE=45°E-a aBE挖掘图形特征:x-aa-a运用举例:1.正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.(1)求证:EF=FM(2)当AE=1时,求EF的长.E3.如图,梯形ABCD中,AD∥BC,∠C=90°,BC=CD=2AD=4,E为线段CD上一点,∠ABE=45°.(1)求线段AB的长;(2)动点P从B出发,沿射线..BE运动,速度为1单位/秒,设运动时间为t,则t为何值时,△ABP为等腰三角形;(3)求AE-CE的值.。
2017中考数学《压轴题》专题训练含答案解析

压轴题1、已知,在平行四边形OABC 中,OA=5,AB=4,∠OCA=90°,动点P 从O 点出发沿射线OA 方向以每秒2个单位的速度移动,同时动点Q 从A 点出发沿射线AB 方向以每秒1个单位的速度移动.设移动的时间为t 秒. (1)求直线AC 的解析式;(2)试求出当t 为何值时,△OAC 与△PAQ 相似; (3)若⊙P 的半径为58,⊙Q 的半径为23;当⊙P 与对角线AC 相切时,判断⊙Q 与直线AC 、BC 的位置关系,并求出Q 点坐标。
解:(1)42033y x =-+ (2)①当0≤t≤2.5时,P 在OA 上,若∠OAQ=90°时, 故此时△OAC 与△PAQ 不可能相似.当t>2.5时,①若∠APQ=90°,则△APQ ∽△OCA ,∵t>2.5,∴符合条件.②若∠AQP=90°,则△APQ ∽△∠OAC ,∵t>2.5,∴符合条件.综上可知,当时,△OAC 与△APQ 相似.(3)⊙Q 与直线AC 、BC 均相切,Q 点坐标为(109,531)。
2、如图,以矩形OABC 的顶点O 为原点,OA 所在的直线为x 轴,OC 所在的直线为y 轴,建立平面直角坐标系.已知OA =3,OC =2,点E 是AB 的中点,在OA 上取一点D ,将△BDA 沿BD 翻折,使点A 落在BC 边上的点F 处. (1)直接写出点E 、F 的坐标;(2)设顶点为F 的抛物线交y 轴正半轴...于点P ,且以点E 、F 、P 为顶点的三角形是等腰三角形,求该抛物线的解析式;(3)在x 轴、y 轴上是否分别存在点M 、N ,使得四边形MNFE 的周长最小?如果存在,求出周长的最小值;如果不存在,请说明理由.解:(1)(31)E ,;(12)F ,.(2)在Rt EBF △中,90B ∠=o, 2222125EF EB BF ∴=+=+=.设点P 的坐标为(0)n ,,其中0n >,Q 顶点(12)F ,, ∴设抛物线解析式为2(1)2(0)y a x a =-+≠.①如图①,当EF PF =时,22EF PF =,221(2)5n ∴+-=.解得10n =(舍去);24n =.(04)P ∴,.24(01)2a ∴=-+.解得2a =. ∴抛物线的解析式为22(1)2y x =-+(第2题)②如图②,当EP FP =时,22EP FP =,22(2)1(1)9n n ∴-+=-+. 解得52n =-(舍去).③当EF EP =时,53EP =<,这种情况不存在. 综上所述,符合条件的抛物线解析式是22(1)2y x =-+. (3)存在点M N ,,使得四边形MNFE 的周长最小. 如图③,作点E 关于x 轴的对称点E ',作点F 关于y 轴的对称点F ',连接E F '',分别与x 轴、y 轴交于点M N ,,则点M N ,就是所求点.(31)E '∴-,,(12)F NF NF ME ME '''-==,,,.43BF BE ''∴==,.FN NM ME F N NM ME F E ''''∴++=++=22345+=.又5EF =Q ,∴55FN NM ME EF +++=+,此时四边形MNFE 的周长最小值是553、如图,在边长为2的等边△ABC 中,A D ⊥BC,点P 为边AB 上一个动点,过P 点作PF//AC 交线段BD 于点F,作PG ⊥AB 交AD 于点E,交线段CD 于点G,设BP=x . (1)①试判断BG 与2BP 的大小关系,并说明理由;②用x 的代数式表示线段DG 的长,并写出自变量x 的取值范围;(2)记△DEF 的面积为S,求S 与x 之间的函数关系式,并求出S 的最大值;(3)以P 、E 、F 为顶点的三角形与△EDG 是否可能相似?如果能相似,请求出BP 的长,如果不能,请说明理由。
2017中考数学压轴题及答案精选

A O C
Bx
y = a(x + 1) ( x − 3) ( a ≠ 0 ),
-
把 C(0, ∴C1:
1 3 a= 2 2 )代入可得 1 2 3 x −x− 2 2
…………………………………………………………4 分
y=
1 2 3 n −n− 2) 设 P( n , 2
∴ △ PBC 3 3 2 27 − (n − ) + 4 2 16 = S = S △ POC + S △ BOP – S △ BOC
…………………………………6 分 3 3 27 a=− n= 16 4 2 ∵ <0, ∴当 时, S△PBC 最大值为 . ……………………………………7 分 (3)由 C2 可知: B(3,0),D(0, −3m ),M(1, − 4m )
2 2 2 BD2= 9m + 9 , BM2= 16m + 4 ,DM2= m + 1 ,
图 12
3 1 5 y = x2 − x + 4 4 2 (2)sin ∠ ACB= 5 ,
--------------4 分
P
N
90° , (3)证明:因为 D 为圆心,A 在圆周上,DA=r=5,故只需证明 ∠DAF =
9 25 9 2 15 9 2 (5, − ) DF = 4 + = , AF = 3 + ( ) = 4 4 4 4 , 4 , 抛物线顶点坐标:F
1
∵2.25<4, ∴x 轴下方不存在 B 点, ∴点 B 的坐标为:(4,4); ③∵点 B 的坐标为:(4,4), ∴∠BOD=45°,BO= =4 ,
当∠POB=90°, ∴∠POD=45°, 设 P 点横坐标为:﹣x,则纵坐标为:x2﹣3x, 即﹣x=x2﹣3x, 解得 x=2 或 x=0, ∴在抛物线上仅存在一点 P (2,﹣2). ∴OP= =2 ,
2017年河北中考压轴题数学含答案

2017年河北中考压轴题【17·河北·25·11分】平面内,如图,在▱ABCD中,AB=10,AD=15,tan A=,点P为AD边上任意点,连接PB,将PB绕点P逆时针旋转90°得到线段PQ.(1)当∠DPQ=10°时,求∠APB的大小;(2)当tan∠ABP:tan A=3:2时,求点Q与点B间的距离(结果保留根号);(3)若点Q恰好落在▱ABCD的边所在的直线上,直接写出PB旋转到PQ所扫过的面积.(结果保留π)【解答】解:(1)如图1中,①当点Q在平行四边形ABCD内时,∠AP′B=180°﹣∠Q′P′B﹣∠Q′P′D=180°﹣90°﹣10°=80°,②当点Q在平行四边形ABCD外时,∠APB=180°﹣(∠QPB﹣∠QPD)=180°﹣(90°﹣10°)=100°,综上所述,当∠DPQ=10°时,∠APB的值为80°或100°.(2)如图2中,连接BQ,作PE⊥AB于E.∵tan∠ABP:tan A=3:2,tan A=,∴tan∠ABP=2,在Rt△APE中,tan A==,设PE=4k,则AE=3k,在Rt△PBE中,tan∠ABP==2,∴EB=2k,∴AB=5k=10,∴k=2,∴PE=8,EB=4,∴PB==4,∵△BPQ是等腰直角三角形,∴BQ=PB=4.(3)①如图3中,当点Q落在直线BC上时,作BE⊥AD于E,PF⊥BC于F.则四边形BEPF是矩形.在Rt△AEB中,∵tan A==,∵AB=10,∴BE=8,AE=6,∴PF=BE=8,∵△BPQ是等腰直角三角形,PF⊥BQ,∴PF=BF=FQ=8,∴PB=PQ=8,∴PB旋转到PQ所扫过的面积==32π.②如图4中,当点Q落在CD上时,作BE⊥AD于E,QF⊥AD交AD的延长线于F.设PE=x.易证△PBE≌△QPF,∴PE=QF=x,EB=PF=8,∴DF=AE+PE+PF﹣AD=x﹣1,∵CD∥AB,∴∠FDQ=∠A,∴tan∠FDQ=tan A==,∴=,∴x=4,∴PE=4,=4,在Rt△PEB中,PB==4,∴PB旋转到PQ所扫过的面积==20π③如图5中,当点Q落在AD上时,易知PB=PQ=8,∴PB旋转到PQ所扫过的面积==16π,综上所述,PB旋转到PQ所扫过的面积为32π或20π或16π.。
上海市2017年中考数学压轴题专项训练(含答案).docx

上海市 2017 年中考数学压轴题专项训练( 含答案 )上海市 2017 年中考数学压轴题专项训练1. (本分 12分,第( 1)小分 3 分,第( 2)小分 4 分,第( 3)小分 5分)如,已知抛物y x2bx cA 0, 1 、 B4, 3两点 .(1)求抛物的解析式;(2 求tan ABO 的;y(3)点 B 作 BC x ,垂足点C,点 M 是抛物上一点,直 MN 平行于y交直 AB 于点 N,如果 M、 N、 B、 C点的四形是平行四形,求点N 的坐 .oxAB(第 24 题图)1.解:( 1)将 A( 0, -1)、 B( 4, -3)分代入y x2bx cc1,,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)得4b c316解,得b 91⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分 ) , c29 x所以抛物的解析式y x21⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)2( 2)点 B 作 BC x ,垂足C,点A作AH OB,垂足点 H ⋯⋯⋯( 1 分)在 Rt AOH 中,OA=1,sin AOH sin OBC4,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)5∴ AH OA sin AOH 4,∴ OH3, BH OB OH22,⋯⋯⋯⋯⋯⋯(1 分)555在 Rt ABH 中,tan ABO AH4222⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)BH5511(3)直 AB 的解析式y 1 x1,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)2点 M 的坐(m, m29 m1) ,点N坐 (m, 1 m1)22那么 MN= (m29 m1)( 1 m1)m24m ;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)22∵ M、 N、 B、 C 点的四形是平行四形,∴MN =BC=3解方程m24m =3得m27 ;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)解方程 m 24m3 得 m 1或 m3 ;⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)所以符合 意的点N 有 4 个 (27,7 7 3 5 22),(27,2),(1, ),(3,)222⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)2. (本 分 14 分,第( 1)小 分 4 分,第( 2)小 分 5分,第( 3)小 分 5分)在 Rt △ABC 中,∠ ACB = 90 °, 点 B 的直 l ( l 不与直 AB 重合)与直BC 的角等于∠ ABC ,分 点 C 、点 A 作直 l 的垂 ,垂足分 点D 、点E .(1)如 1,当点 E 与点 B 重合 ,若 AE=4,判断以 C 点 心 CD 半径的C 与直 AB 的位置关系并 明理由;(2)如 2,当点 E 在 DB 延 上 ,求 :AE=2CD ;ACF 5(3) 直 CE 与直 AB 相交于点 F ,若EF, CD = 4,求 BD 的 .6ACCDB(E)lD Bl(第 25 题图 1)E(第 25 题图 2 )2.解:( 1) 点 C 作 CF ⊥ AB ,垂足 点 F. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵∠ AED =90°,∠ ABC=∠ CBD ,∴∠ ABC=∠ CBD =45°,∵∠ ACB=90 °,∠ ABC=45°, AE=4,∴ CF=2 ,BC= 2 2 ,⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) 又∵∠ CBD=∠ ABC=45°, CD ⊥ l ,∴ CD =2, ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) ∴CD =CF=2,∴ C 与直 AB 相切 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分) (2) 明:延 AC 交直 l 于点 G . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵∠ ACB = 90 °,∠ ABC =∠GBC ,∴∠ BAC =∠BGC .∴AB = GB .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ ( 1 分) ∴AC = GC .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)∵AE ⊥l ,CD ⊥ l ,∴ AE ∥ CD .∴CD GC 1. ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯AE GA 2∴AE = 2CD . ⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(3)( I )如 1,当点 E 在 DB 延 上 :点 C 作 CG ∥ l 交 AB 于点 H ,交 AE 于点 G , ∠ CBD =∠ HCB .∵∠ ABC =∠CBD ,∴∠ ABC =∠ HCB .∴ CH = BH .⋯⋯⋯( 1 分)∵∠ ACB = 90 °,∴∠ ABC +∠BAC =∠ HCB +∠ HCA = 90 °. CH∴∠ BAC =∠HCA .∴ CH = AH = BH .F∵CG ∥ l ,∴CHCF 5FBEEF.D B6(第 25 题图CH = 5x , BE = 6x , AB = 10 x .( 1 分)( 1 分)AGlE1)在 Rt △ ABE 中, AEAB 2BE 28x .由( 2)知 AE = 2CD = 8,∴ 8x 8 ,得 x 1 .∴CH = 5 , BE = 6 ,AB = 10.∵CG ∥ l ,∴HGAH 1 ,∴ HG=3.⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)ABEAB 2∴CG = CH + HG = 8 .易 四 形 CDEG 是矩形,∴ DE = CG = 8.CGH∴ BD DE BE2 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)(II )如 2,当点 E 在 DB 上 :DEl同理可得 CH = 5 , BE = 6 , HG = 3 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1 分)B(第 25题图 2)∴ DE CG CH HG 2 .∴BD =DE + BE = 8 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯( 1 分)上所述, BD 的 2 或 8.3.已知点 A ( 2, 2)和点 B ( 4, n )在抛物 y=ax 2( a ≠0)上.(1)求 a 的 及点 B 的坐 ;(2)点 P 在 y 上,且 △ ABP 是以 AB 直角 的三角形,求点P 的坐 ;(3)将抛物 y=ax 2(a ≠0)向右并向下平移, 平移后点 A 的 点A ′,点B 的点 B ′,若四 形 ABB ′A ′ 正方形,求此 抛物 的表达式.【考点】二次函数图象上点的坐标特征;坐标与图形变化 -平移.【分析】( 1)把点 A (2,﹣ 2)代入 y=ax 2,得到 a ,再把点 B 代入抛物线解析式即可解决问题.(2)求出直线 AB 解析式,再分别求出过点 A 垂直于 AB 的直线的解析式,过点直线 AB 的解析式即可解决问题.B 垂直于( 3)先求出点 A ′坐标,确定是如何平移的,再确定抛物线顶点的坐标即可解决问题.【解答】解:( 1)把点 A ( 2,﹣ 2)代入 y=ax 2,得到 a=﹣, ∴抛物线为 y= ﹣ x 2, ∴x= ﹣ 4 时, y= ﹣ 8, ∴点 B 坐标(﹣ 4,﹣ 8),∴a=﹣,点 B 坐标(﹣ 4,﹣ 8).(2)设直线AB为 y=kx+b ,则有,解得,∴直线 AB 为 y=x ﹣ 4,∴过点 B 垂直 AB 的直线为 y= ﹣ x ﹣ 12,与 y 轴交于点P ( 0,﹣ 12),过点 A 垂直 AB 的直线为 y= ﹣ x ,与 y 轴交于点 P ′( 0, 0),∴点 P 在 y 轴上,且 △ ABP 是以 AB 为直角边的三角形时.点 P 坐标为( 0,0),或( 0,﹣12).(3)如图四边形 ABB ′A ′是正方形,过点 A 作 y 轴的垂线,过点B 、点 A ′作 x 轴的垂线得到点 E 、 F .∵直线 AB 解析式为 y=﹣ x ﹣ 12, ∴△ ABF , △ AA ′E 都是等腰直角三角形, ∵AB=AA ′= =6 ,∴AE=A ′E=6 ,∴点 A ′坐标为( 8,﹣ 8),∴点 A 到点 A ′是向右平移 6 个单位,向下平移 6 个单位得到,∴抛物线 y=﹣ x 2的顶点( 0,0),向右平移 6 个单位,向下平移6 个单位得到( 6,﹣ 6),∴此时抛物线为 y=﹣( x ﹣ 6) 2﹣ 6.4.已知, AB=5 , tan∠ABM= ,点 C、 D、 E 为动点,其中点 C、D 在射线 BM 上(点 C 在点 D 的左侧),点 E 和点 D 分别在射线 BA 的两侧,且 AC=AD ,AB=AE ,∠ CAD= ∠BAE .(1)当点 C 与点 B 重合时(如图 1),联结 ED ,求 ED 的长;(2)当 EA ∥BM 时(如图 2),求四边形 AEBD 的面积;(3)联结 CE,当△ ACE 是等腰三角形时,求点B、 C 间的距离.【考点】三角形综合题.【分析】( 1)如图 1 中,延长 BA 交 DE 于 F,作 AH ⊥ BD 于 H ,先证明 BF⊥ DE ,EF=DF ,再利用△ ABH ∽△ DBF ,得= ,求出 DF 即可解决问题.(2)先证明四边形 ADBE 是平行四边形,根据 S 平行四边形ADBE =BD?AH ,计算即可.(3)由题意 AC≠AE ,EC≠AC,只有 EA=EC ,利用四点共圆先证明四边形ADBE 是平行四边形,求出 DH 、 CH 即可解决问题.【解答】解:( 1)如图 1 中,延长 BA 交 DE 于 F,作 AH ⊥ BD 于 H .在RT△ABH 中,∵∠AHB=90°,∴sin ∠ABH= =,∴AH=3 , BH==4,∵A B=AD ,AH ⊥BD ,∴BH=DH=4 ,在△ ABE 和△ ABD 中,,∴△ ABD ≌△ ABE ,∴B E=BD ,∠ ABE= ∠ ABD ,∴B F ⊥ DE, EF=DF ,∵∠ ABH= ∠ DBF ,∠ AHB= ∠ BFD ,∴△ ABH ∽△ DBF ,∴= ,∴D F= ,∴D E=2DF=.(2)如图 2 中,作 AH ⊥ BD 于 H.∵AC=AD , AB=AE ,∠ CAD= ∠ BAE ,∴∠ AEB= ∠ABE= ∠ACD= ∠ADC , ∵AE ∥ BD ,∴∠ AEB+ ∠EBD=180° , ∴∠ EBD+ ∠ADC=180° , ∴EB ∥AD , ∵AE ∥ BD ,∴四边形 ADBE 是平行四边形, ∴ B D=AE=AB=5 ,AH=3 , ∴S 平行四边形 ADBE =BD?AH=15 .( 3)由题意 AC ≠AE ,EC ≠AC ,只有 EA=EC .如图 3 中,∵∠ ACD= ∠ AEB (已证), ∴A 、 C 、 B 、 E 四点共圆,∵ A E=EC=AB , ∴ = , ∴ = ,∴∠ AEC= ∠ABC , ∴AE ∥ BD ,由( 2)可知四边形 ADBE 是平行四边形, ∴AE=BD=AB=5 ,∵ A H=3 , BH=4 , ∴DH=BD ﹣ BH=1 , ∵AC=AD , AH ⊥ CD , ∴ C H=HD=1 , ∴BC=BD ﹣ CD=3 .5.如图,已知二次函数y=x 2+bx +c 图象顶点为 C ,与直线 y=x +m 图象交于 AB 两点,其中A 点的坐标为( 3, 4),B 点在 y 轴上.(1)求这个二次函数的解析式;(2)联结 AC ,求∠ BAC 的正切值;(3)点 P 为直线 AB 上一点,若△ ACP 为直角三角形,求点 P 的坐标.【分析】 ( 1)先把 A 点坐标代入 y=x +m 求出 m 得到直线 AB 的解析式为 y=x +1,这可求出直线与 y 轴的交点 B 的坐标, 然后把 A 点和 B 点坐标代入 y=x 2+bx+c 中得到关于 b 、c 的方程组,再解方程组求出b 、c 即可得到抛物线解析式;(2)如图,先抛物线解析式配成顶点式得到C ( 1, 0),再利用两点间的距离公式计算出BC 2=2, AB 2=18, AC 2=20,然后利用勾股定理的逆定理可证明△ABC 为直角三角形,∠ACB=90°,于是利用正切的定义计算tan ∠ BAC 的值;(3)分类讨论:当∠ APC=90° 时,有( 2 )得点 P 在 B 点处,此时 P 点坐标为( 0, 1);当∠ ACP=90°时,利用( 2tan ∠ PAC= = ,则 PC= AC P t t 1 )中结论得,设 ( , + ), 然后利用两点间的距离公式得到方程 t 2t 1 1 220,再解方程求出t 即可得到时 P 点 +( + ﹣ ) = 坐标.【解答】解:( 1 )把 A( 3 4 )代入 y=x m 得 3 +m=4 ,解得 m=1, +∴直线 AB 的解析式为 y=x 1+ ,∵当 x=0 时, y=x +1=1,∴B ( 0,1),把 B ( 0,1), A ( 3,4)代入 y=x 2+bx+c 得,解得 ,∴抛物线解析式为y=x 2﹣ 2x+1;(2)如图,∵ y =x 2﹣ 2x+1=( x ﹣ 1)2,∴C ( 1,0),22 2 2 2 +( 4 2 2 2 2∴BC =1 +1 =2,AB =3 ﹣ 1) =18 ,AC =( 3 ﹣ 1) +4 =20,而 2+18=20,∴BC 2+AB 2=AC 2,∴△ ABC 为直角三角形,∠ ACB=90° ,∴tan∠BAC===;(3)当∠ APC=90°时,点 P 在 B 点处,此时P 点坐标为( 0, 1);当∠ ACP=90°时,∵ tan∠ PAC==,∴P C= AC ,设P( t, t+1),∴t2t 1 1220,解得 t 1=﹣, t2=(舍去),此时P 点坐标为(﹣,+( + ﹣) =﹣+ 1),综上所述,满足条件的P 点坐标为( 0, 1)或(﹣,﹣+ 1).【点评】本题考查了二次函数的综合题:熟练掌握二次函数的性质和一次函数图象上点的坐标特征;能运用待定系数法求二次函数解析式;理解坐标与图形性质,记住两点间的距离公式;能利用勾股定理的逆定理证明直角三角形.6.如图, ? ABCD 中, AB=8 ,AD=10 , sinA=,E、F分别是边AB 、BC 上动点(点 E 不与A 、B 重合),且∠ EDF= ∠ DAB , DF 延长线交射线 AB 于G.(1)若 DE⊥AB 时,求 DE 的长度;(2)设 AE=x , BG=y ,求 y 关于 x 的函数解析式,并写出函数的定义域;(3)当△ BGF 为等腰三角形时,求AE 的长度.【分析】( 1) DE⊥ AB 时,根据sinA=即可解决问题.(2)如图 2 中,作 DM ⊥AB 于 M ,根据 DG 2=DM2+MG2=AGEG ,列出等式即可解决问题.(3)分三种情形① BF=BG ,②FB=FG ,③ GB=GF ,根据 BF ∥AD ,得出比例式,列方程即可解决.【解答】解:( 1)如图 1 中,∵DE ⊥ AB ,∴sinA==,∵A D=10 ,∴DE=8 .(2)如图 2 中,作DM ⊥AB 于 M ,由( 1)可知 DM=8 , AM=6 , MG=AB ﹣ AM=8 ﹣ 6=2 ,∴DG 2=DM2+MG2,∵∠ DGE= ∠ DGA ,∠ GDE= ∠ A,∴△ DGE∽△ AGD ,∴= ,∴DG 2=AGEG ,∴DM 2+MG2=AGEG ,∴82+( 2+y)2=( 8+y)( 8+y﹣ x),∴y=(0<x<8)(3)①当 BF=FG 时,∵ BF∥ AD ,∴= ,∴AD=AG=10 ,∴y=2 ,即=2,解得 x=2 ,∴A E=2 .②当 FB=FG 时,∵ BF ∥AD ,∴=,∴A D=DG=10 ,∵DM ⊥AG ,∴A M=MB=6 ,∴A G=12 ,∴y=4 ,即=4,解得 x=.③当 GB=GF 时,∵ BF ∥ AD ,∠ GBF= ∠ BFG,∴∠ A= ∠ GBF ,∠ ADG= ∠ BFG ,∴∠ A= ∠ ADG ,∵∠ A= ∠ EDG ,∴∠ EDG= ∠ ADG ,∴此时点 E 与点 A 重合,不合题意.综上所述 AE=2 或时,△ BFG是等腰三角形.【点评】本题考查四边形综合题、锐角三角函数、相似三角形的判定和性质、平行线分线段成比例定理、勾股定理等知识,解题的关键是灵活应用这些知识解决问题,学会用方程的思想解决问题,属于中考常考题型.。
2017年挑战中考数学压轴题(全套含答案)
第一部分函数图象中点的存在性问题§1.1 因动点产生的相似三角形问题例1 2014年衡阳市中考第28题例2 2014年益阳市中考第21题例3 2015年湘西州中考第26题例4 2015年张家界市中考第25题例5 2016年常德市中考第26题例6 2016年岳阳市中考第24题例7 2016年上海市崇明县中考模拟第25题例8 2016年上海市黄浦区中考模拟第26题§1.2 因动点产生的等腰三角形问题例9 2014年长沙市中考第26题例10 2014年张家界市第25题例11 2014年邵阳市中考第26题例12 2014年娄底市中考第27题例13 2015年怀化市中考第22题例14 2015年长沙市中考第26题例15 2016年娄底市中考第26题例16 2016年上海市长宁区金山区中考模拟第25题例17 2016年河南省中考第23题例18 2016年重庆市中考第25题§1.3 因动点产生的直角三角形问题例19 2015年益阳市中考第21题例20 2015年湘潭市中考第26题例21 2016年郴州市中考第26题例22 2016年上海市松江区中考模拟第25题例23 2016年义乌市绍兴市中考第24题§1.4 因动点产生的平行四边形问题例24 2014年岳阳市中考第24题例25 2014年益阳市中考第20题例26 2014年邵阳市中考第25题例27 2015年郴州市中考第25题例28 2015年黄冈市中考第24题例29 2016年衡阳市中考第26题例30 2016年上海市嘉定区宝山区中考模拟中考第24题例31 2016年上海市徐汇区中考模拟第24题§1.5 因动点产生的面积问题例32 2014年常德市中考第25题例33 2014年永州市中考第25题例34 2014年怀化市中考第24题例35 2015年邵阳市中考第26题例36 2015年株洲市中考第23题例37 2015年衡阳市中考第28题例38 2016年益阳市中考第22题例39 2016年永州市中考第26题例40 2016年邵阳市中考第26题例41 2016年陕西省中考第25题§1.6 因动点产生的相切问题例42 2014年衡阳市中考第27题例43 2014年株洲市中考第23题例44 2015年湘潭市中考第25题例45 2015年湘西州中考第25题例46 2016年娄底市中考第25题例47 2016年湘潭市中考第26题例48 2016年上海市闵行区中考模拟第24题例49 2016年上海市普陀区中考模拟中考第25题§1.7 因动点产生的线段和差问题例50 2014年郴州市中考第26题例51 2014年湘西州中考第25题例52 2015年岳阳市中考第24题例53 2015年济南市中考第28题例54 2015年沈阳市中考第25题例55 2016年福州市中考第26题例56 2016年张家界市中考第24题例57 2016年益阳市中考第21题第二部分图形运动中的函数关系问题§2.1 由比例线段产生的函数关系问题例1 2014年常德市中考第26题例2 2014年湘潭市中考第25题例3 2014年郴州市中考第25题例4 2015年常德市中考第25题例5 2015年郴州市中考第26题例6 2015年邵阳市中考第25题例7 2015年娄底市中考第26题例8 2016年郴州市中考第25题例9 2016年湘西州中考第26题例10 2016年上海市静安区青浦区中考模拟第25题例11 2016年哈尔滨市中考第27题第三部分图形运动中的计算说理问题§3.1 代数计算及通过代数计算进行说理问题例1 2014年长沙市中考第25题例2 2014年怀化市中考第23题例3 2014年湘潭市中考第26题例4 2014年株洲市中考第24题例5 2015年衡阳市中考第27题例6 2015年娄底市中考第25题例7 2015年永州市中考第26题例8 2015年长沙市中考第25题例9 2015年株洲市中考第24题例10 2016年怀化市中考第22题例11 2016年邵阳市中考第25题例12 2016年株洲市中考第26题例13 2016年长沙市中考第25题例14 2016年长沙市中考第26题§3.2 几何证明及通过几何计算进行说理问题例15 2014年衡阳市中考第26题例16 2014年娄底市中考第26题例17 2014年岳阳市中考第23题例18 2015年常德市中考第26题例19 2015年益阳市中考第20题例20 2015年永州市中考第27题例21 2015年岳阳市中考第23题例22 2016年常德市中考第25题例23 2016年衡阳市中考第25题例24 2016年永州市中考第27题例25 2016年岳阳市中考第23题例26 2016年株洲市中考第25题例27 2016年湘潭市中考第25题第四部分图形的平移、翻折与旋转§4.1 图形的平移例1 2015年泰安市中考第15题例2 2015年咸宁市中考第14题例3 2015年株洲市中考第14题例4 2016年上海市虹口区中考模拟第18题§4.2 图形的翻折例5 2016年上海市奉贤区中考模拟第18题例6 2016年上海市静安区青浦区中考模拟第18题例7 2016年上海市闵行区中考模拟第18题例8 2016年上海市浦东新区中考模拟第18题例8 2016年上海市普陀区中考模拟第18题例10 2016年常德市中考第15题例11 2016年张家界市中考第14题例12 2016年淮安市中考第18题例13 2016年金华市中考第15题例14 2016年雅安市中考第12题§4.3 图形的旋转例15 2016年上海昂立教育中学生三模联考第18题例16 2016年上海市崇明县中考模拟第18题例17 2016年上海市黄浦区中考模拟第18题例18 2016年上海市嘉定区宝山区中考模拟第18题例19 2016年上海市闸北区中考模拟第18题例20 2016年邵阳市中考第13题例21 2016年株洲市中考第4题§4.4 三角形例22 2016年安徽省中考第10题例23 2016年武汉市中考第10题例24 2016年河北省中考第16题例25 2016年娄底市中考第10题例26 2016年苏州市中考第9题例27 2016年台州市中考第10题例28 2016年陕西省中考第14题例29 2016年内江市中考第11题例30 2016年上海市中考第18题§4.5 四边形例31 2016年湘西州中考第11题例32 2016年益阳市中考第4题例33 2016年益阳市中考第6题例34 2016年常德市中考第16题例35 2016年成都市中考第14题例36 2016年广州市中考第13题例37 2016年福州市中考第18题例38 2016年无锡市中考第17题例39 2016年台州市中考第15题§4.6 圆例40 2016年滨州市中考第16题例41 2016年宁波市中考第17题例42 2016年连云港市中考第16题例43 2016年烟台市中考第17题例44 2016年烟台市中考第18题例45 2016年无锡市中考第18题例46 2016年武汉市中考第9题例47 2016年宿迁市中考第16题例48 2016年衡阳市中考第17题例49 2016年邵阳市中考第18题例50 2016年湘西州中考第18题例51 2016年永州市中考第20题§4.7 函数的图象及性质例52 2015年荆州市中考第9题例53 2015年德州市中考第12题例54 2015年烟台市中考第12题例55 2015年中山市中考第10题例56 2015年武威市中考第10题例57 2015年呼和浩特市中考第10题例58 2016年湘潭市中考第18题例59 2016年衡阳市中考第19题例60 2016年岳阳市中考第15题例61 2016年株洲市中考第9题例62 2016年永州市中考第19题例63 2016年岳阳市中考第8题例64 2016年岳阳市中考第16题例65 2016年益阳市中考第14题例66 2016年株洲市中考第10题例67 2016年株洲市中考第17题例68 2016年东营市中考第15题例69 2016年成都市中考第13题例70 2016年泰州市中考第16题例71 2016年宿迁市中考第15题例72 2016年临沂市中考第14题例73 2016年义乌市绍兴市中考第9题例74 2016年淄博市中考第12题例75 2016年嘉兴市中考第16题§1.1 因动点产生的相似三角形问题课前导学相似三角形的判定定理有3个,其中判定定理1和判定定理2都有对应角相等的条件,因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等.判定定理2是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来,按照对应边成比例,分和两种情况列方程.应用判定定理1解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等.应用判定定理3解题不多见,根据三边对应成比例列连比式解方程(组).还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.求线段的长,要用到两点间的距离公式,而这个公式容易记错.理解记忆比较好.如图1,如果已知A、B两点的坐标,怎样求A、B两点间的距离呢?我们以AB为斜边构造直角三角形,直角边与坐标轴平行,这样用勾股定理就可以求斜边AB的长了.水平距离BC的长就是A、B两点间的水平距离,等于A、B两点的横坐标相减;竖直距离AC就是A、B两点间的竖直距离,等于A、B两点的纵坐标相减.图1例 1 2014年湖南省衡阳市中考第28题二次函数y=a x2+b x+c(a≠0)的图象与x轴交于A(-3, 0)、B(1, 0)两点,与y轴交于点C(0,-3m)(m >0),顶点为D.(1)求该二次函数的解析式(系数用含m的代数式表示);(2)如图1,当m=2时,点P为第三象限内抛物线上的一个动点,设△APC的面积为S,试求出S与点P的横坐标x之间的函数关系式及S的最大值;(3)如图2,当m取何值时,以A、D、C三点为顶点的三角形与△OBC相似?图1 图2动感体验请打开几何画板文件名“14衡阳28”,拖动点P运动,可以体验到,当点P运动到AC的中点的正下方时,△APC的面积最大.拖动y轴上表示实数m的点运动,抛物线的形状会改变,可以体验到,∠ACD和∠ADC都可以成为直角.思路点拨1.用交点式求抛物线的解析式比较简便.2.连结OP,△APC可以割补为:△AOP与△COP的和,再减去△AOC.3.讨论△ACD与△OBC相似,先确定△ACD是直角三角形,再验证两个直角三角形是否相似.4.直角三角形ACD存在两种情况.图文解析(1)因为抛物线与x轴交于A(-3, 0)、B(1, 0)两点,设y=a(x+3)(x-1).代入点C(0,-3m),得-3m=-3a.解得a=m.所以该二次函数的解析式为y=m(x+3)(x-1)=mx2+2mx-3m.(2)如图3,连结OP.当m=2时,C(0,-6),y=2x2+4x-6,那么P(x, 2x2+4x-6).由于S△AOP==(2x2+4x-6)=-3x2-6x+9,S△COP==-3x,S△AOC=9,所以S=S△APC=S△AOP+S△COP-S△AOC=-3x2-9x=.所以当时,S取得最大值,最大值为.图3 图4 图5(3)如图4,过点D作y轴的垂线,垂足为E.过点A作x轴的垂线交DE于F.由y=m(x+3)(x-1)=m(x+1)2-4m,得D(-1,-4m).在Rt△OBC中,OB∶OC=1∶3m.如果△ADC与△OBC相似,那么△ADC是直角三角形,而且两条直角边的比为1∶3m.①如图4,当∠ACD=90°时,.所以.解得m=1.此时,.所以.所以△CDA∽△OBC.②如图5,当∠ADC=90°时,.所以.解得.此时,而.因此△DCA与△OBC不相似.综上所述,当m=1时,△CDA∽△OBC.考点伸展第(2)题还可以这样割补:如图6,过点P作x轴的垂线与AC交于点H.由直线AC:y=-2x-6,可得H(x,-2x-6).又因为P(x, 2x2+4x-6),所以HP=-2x2-6x.因为△P AH与△PCH有公共底边HP,高的和为A、C两点间的水平距离3,所以S=S△APC=S△APH+S△CPH=(-2x2-6x)=.图6例 2 2014年湖南省益阳市中考第21题如图1,在直角梯形ABCD中,AB//CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A 向点B运动,设AP=x.2·1·c·n·j·y(1)求AD的长;(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.动感体验图1请打开几何画板文件名“14益阳21”,拖动点P在AB上运动,可以体验到,圆心O的运动轨迹是线段BC的垂直平分线上的一条线段.观察S随点P运动的图象,可以看到,S有最小值,此时点P看上去象是AB的中点,其实离得很近而已.思路点拨1.第(2)题先确定△PCB是直角三角形,再验证两个三角形是否相似.2.第(3)题理解△PCB的外接圆的圆心O很关键,圆心O在确定的BC的垂直平分线上,同时又在不确定的BP的垂直平分线上.而BP与AP是相关的,这样就可以以AP为自变量,求S的函数关系式.图文解析(1)如图2,作CH⊥AB于H,那么AD=CH.在Rt△BCH中,∠B=60°,BC=4,所以BH=2,CH=.所以AD=.(2)因为△APD是直角三角形,如果△APD与△PCB相似,那么△PCB一定是直角三角形.①如图3,当∠CPB=90°时,AP=10-2=8.所以==,而=.此时△APD与△PCB不相似.图2 图3 图4②如图4,当∠BCP=90°时,BP=2BC=8.所以AP=2.所以==.所以∠APD=60°.此时△APD∽△CBP.综上所述,当x=2时,△APD∽△CBP.(3)如图5,设△ADP的外接圆的圆心为G,那么点G是斜边DP的中点.设△PCB的外接圆的圆心为O,那么点O在BC边的垂直平分线上,设这条直线与BC交于点E,与AB 交于点F.设AP=2m.作OM⊥BP于M,那么BM=PM=5-m.在Rt△BEF中,BE=2,∠B=60°,所以BF=4.在Rt△OFM中,FM=BF-BM=4-(5-m)=m-1,∠OFM=30°,所以OM=.所以OB2=BM2+OM2=.在Rt△ADP中,DP2=AD2+AP2=12+4m2.所以GP2=3+m2.于是S=S1+S2=π(GP2+OB2)==.所以当时,S取得最小值,最小值为.图5 图6考点伸展关于第(3)题,我们再讨论个问题.问题1,为什么设AP=2m呢?这是因为线段AB=AP+PM+BM=AP+2BM=10.这样BM=5-m,后续可以减少一些分数运算.这不影响求S的最小值.问题2,如果圆心O在线段EF的延长线上,S关于m的解析式是什么?如图6,圆心O在线段EF的延长线上时,不同的是FM=BM-BF=(5-m)-4=1-m.此时OB2=BM2+OM2=.这并不影响S关于m的解析式.例3 2015年湖南省湘西市中考第26题如图1,已知直线y=-x+3与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,点P在线段OA上,从点O出发,向点A以每秒1个单位的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以每秒个单位的速度匀速运动,连结PQ,设运动时间为t秒.(1)求抛物线的解析式;(2)问:当t为何值时,△APQ为直角三角形;(3)过点P作PE//y轴,交AB于点E,过点Q作QF//y轴,交抛物线于点F,连结EF,当EF//PQ时,求点F的坐标;(4)设抛物线顶点为M,连结BP、BM、MQ,问:是否存在t的值,使以B、Q、M为顶点的三角形与以O、B、P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1动感体验请打开几何画板文件名“15湘西26”,拖动点P在OA上运动,可以体验到,△APQ有两个时刻可以成为直角三角形,四边形EPQF有一个时刻可以成为平行四边形,△MBQ与△BOP有一次机会相似.思路点拨1.在△APQ中,∠A=45°,夹∠A的两条边AP、AQ都可以用t表示,分两种情况讨论直角三角形APQ.2.先用含t的式子表示点P、Q的坐标,进而表示点E、F的坐标,根据PE=QF列方程就好了.3.△MBQ与△BOP都是直角三角形,根据直角边对应成比例分两种情况讨论.图文解析(1)由y=-x+3,得A(3, 0),B(0, 3).将A(3, 0)、B(0, 3)分别代入y=-x2+bx+c,得解得所以抛物线的解析式为y=-x2+2x+3.(2)在△APQ中,∠P AQ=45°,AP=3-t,AQ=t.分两种情况讨论直角三角形APQ:①当∠PQA=90°时,AP=AQ.解方程3-t=2t,得t=1(如图2).②当∠QP A=90°时,AQ=AP.解方程t=(3-t),得t=1.5(如图3).图2 图3(3)如图4,因为PE//QF,当EF//PQ时,四边形EPQF是平行四边形.所以EP=FQ.所以y E-y P=y F-y Q.因为x P=t,x Q=3-t,所以y E=3-t,y Q=t,y F=-(3-t)2+2(3-t)+3=-t2+4t.因为y E-y P=y F-y Q,解方程3-t=(-t2+4t)-t,得t=1,或t=3(舍去).所以点F的坐标为(2, 3).图4 图5(4)由y=-x2+2x+3=-(x-1)2+4,得M(1, 4).由A(3, 0)、B(0, 3),可知A、B两点间的水平距离、竖直距离相等,AB=3.由B(0, 3)、M(1, 4),可知B、M两点间的水平距离、竖直距离相等,BM=.所以∠MBQ=∠BOP=90°.因此△MBQ与△BOP相似存在两种可能:①当时,.解得(如图5).②当时,.整理,得t2-3t+3=0.此方程无实根.考点伸展第(3)题也可以用坐标平移的方法:由P(t, 0),E(t, 3-t),Q(3-t, t),按照P→E方向,将点Q向上平移,得F(3-t, 3).再将F(3-t, 3)代入y=-x2+2x+3,得t=1,或t=3.§1.2 因动点产生的等腰三角形问题课前导学我们先回顾两个画图问题:1.已知线段AB=5厘米,以线段AB为腰的等腰三角形ABC有多少个?顶点C的轨迹是什么?2.已知线段AB=6厘米,以线段AB为底边的等腰三角形ABC有多少个?顶点C的轨迹是什么?已知腰长画等腰三角形用圆规画圆,圆上除了两个点以外,都是顶点C.已知底边画等腰三角形,顶角的顶点在底边的垂直平分线上,垂足要除外.在讨论等腰三角形的存在性问题时,一般都要先分类.如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.几何法一般分三步:分类、画图、计算.哪些题目适合用几何法呢?如果△ABC的∠A(的余弦值)是确定的,夹∠A的两边AB和AC可以用含x的式子表示出来,那么就用几何法.①如图1,如果AB=AC,直接列方程;②如图2,如果BA=BC,那么;③如图3,如果CA=CB,那么.代数法一般也分三步:罗列三边长,分类列方程,解方程并检验.如果三角形的三个角都是不确定的,而三个顶点的坐标可以用含x的式子表示出来,那么根据两点间的距离公式,三边长(的平方)就可以罗列出来.图1 图2 图3例 9 2014年长沙市中考第26题如图1,抛物线y =ax 2+bx +c (a 、b 、c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和两点,点P 在该抛物线上运动,以点P 为圆心的⊙P 总经过定点A (0, 2).(1)求a 、b 、c 的值;(2)求证:在点P 运动的过程中,⊙P 始终与x 轴相交;(3)设⊙P 与x 轴相交于M (x 1, 0)、N (x 2, 0)两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标.图1动感体验请打开几何画板文件名“14长沙26”,拖动圆心P 在抛物线上运动,可以体验到,圆与x 轴总是相交的,等腰三角形AMN 存在五种情况.思路点拨1.不算不知道,一算真奇妙,原来⊙P 在x 轴上截得的弦长MN =4是定值.2.等腰三角形AMN 存在五种情况,点P 的纵坐标有三个值,根据对称性,MA =MN 和NA =NM 时,点P 的纵坐标是相等的.图文解析(1)已知抛物线的顶点为(0,0),所以y =ax 2.所以b =0,c =0. 将代入y =ax 2,得.解得(舍去了负值).(2)抛物线的解析式为,设点P 的坐标为. 已知A (0, 2),所以>.而圆心P 到x 轴的距离为,所以半径P A >圆心P 到x 轴的距离.所以在点P 运动的过程中,⊙P 始终与x 轴相交.(3)如图2,设MN 的中点为H ,那么PH 垂直平分MN ..4=2MH ,所以,中,PMH △Rt 在 所以MH =2.因此MN =4,为定值.等腰△AMN 存在三种情况:①如图3,当AM =AN 时,点P 为原点O 重合,此时点P 的纵坐标为0.图2 图3.2=OM ,所以4=AM ,2=OA 中,AOM △Rt 时,在MN =MA ,当4②如图 .的纵坐标为P .所以点2=OH =x 此时 .的纵坐标为也为P 时,根据对称性,点NM =NA ,当5如图图4 图5③如图6,当NA=NM=4时,在Rt△AON中,OA=2,AN=4,所以ON=2.此时x=OH=2.所以点P的纵坐标为.如图7,当MN=MA=4时,根据对称性,点P的纵坐标也为.图6 图7考点伸展如果点P在抛物线上运动,以点P为圆心的⊙P总经过定点B(0, 1),那么在点P运动的过程中,⊙P始终与直线y=-1相切.这是因为:设点P的坐标为.已知B(0, 1),所以.而圆心P到直线y=-1的距离也为,所以半径PB=圆心P到直线y=-1的距离.所以在点P 运动的过程中,⊙P始终与直线y=-1相切.例 10 2014年湖南省张家界市中考第25题如图1,在平面直角坐标系中,O为坐标原点,抛物线y=ax2+bx+c(a≠0)过O、B、C三点,B、C 坐标分别为(10, 0)和,以OB为直径的⊙A经过C点,直线l垂直x轴于B点.(1)求直线BC的解析式;(2)求抛物线解析式及顶点坐标;(3)点M是⊙A上一动点(不同于O、B),过点M作⊙A的切线,交y轴于点E,交直线l于点F,设线段ME长为m,MF长为n,请猜想mn的值,并证明你的结论;(4)若点P从O出发,以每秒1个单位的速度向点B作直线运动,点Q同时从B出发,以相同速度向点C作直线运动,经过t(0<t≤8)秒时恰好使△BPQ为等腰三角形,请求出满足条件的t值.图图1动感体验请打开几何画板文件名“14张家界25”,拖动点M在圆上运动,可以体验到,△EAF保持直角三角形的形状,AM是斜边上的高.拖动点Q在BC上运动,可以体验到,△BPQ有三个时刻可以成为等腰三角形.思路点拨1.从直线BC的解析式可以得到∠OBC的三角比,为讨论等腰三角形BPQ作铺垫.2.设交点式求抛物线的解析式比较简便.3.第(3)题连结AE、AF容易看到AM是直角三角形EAF斜边上的高.4.第(4)题的△PBQ中,∠B是确定的,夹∠B的两条边可以用含t的式子表示.分三种情况讨论等腰三角形.图文解析(1)直线BC的解析式为.(2)因为抛物线与x轴交于O、B(10, 0)两点,设y=ax(x-10).代入点C,得.解得.所以.抛物线的顶点为.(3)如图2,因为EF切⊙A于M,所以AM⊥EF.由AE=AE,AO=AM,可得Rt△AOE≌Rt△AME.所以∠1=∠2.同理∠3=∠4.于是可得∠EAF=90°.所以∠5=∠1.由tan∠5=tan∠1,得.所以ME·MF=MA2,即mn=25.图2(4)在△BPQ中,cos∠B=,BP=10-t,BQ=t.分三种情况讨论等腰三角形BPQ:①如图3,当BP=BQ时,10-t=t.解得t=5.②如图4,当PB=PQ时,.解方程,得.③如图5,当QB=QP时,.解方程,得.图3 图4 图5考点伸展在第(3)题条件下,以EF为直径的⊙G与x轴相切于点A.如图6,这是因为AG既是直角三角形EAF斜边上的中线,也是直角梯形EOBF的中位线,因此圆心G 到x轴的距离等于圆的半径,所以⊙G与x轴相切于点A.图6例 11 2014年湖南省邵阳市中考第26题在平面直角坐标系中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.(1)若m=2,n=1,求A、B两点的坐标;(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,-1),求∠ACB的大小;(3)若m=2,△ABC是等腰三角形,求n的值.动感体验请打开几何画板文件名“14邵阳26”,点击屏幕左下方的按钮(2),拖动点A在x轴正半轴上运动,可以体验到,△ABC保持直角三角形的形状.点击屏幕左下方的按钮(3),拖动点B在x轴上运动,观察△ABC 的顶点能否落在对边的垂直平分线上,可以体验到,等腰三角形ABC有4种情况.思路点拨1.抛物线的解析式可以化为交点式,用m,n表示点A、B、C的坐标.2.第(2)题判定直角三角形ABC,可以用勾股定理的逆定理,也可以用锐角的三角比.3.第(3)题讨论等腰三角形ABC,先把三边长(的平方)罗列出来,再分类解方程.图文解析(1)由y=x2-(m+n)x+mn=(x-m)(x-n),且m>n,点A位于点B的右侧,可知A(m, 0),B(n, 0).若m=2,n=1,那么A(2, 0),B(1, 0)..(2)如图1,由于C(0, mn),当点C的坐标是(0,-1),mn=-1,OC=1.若A、B两点分别位于y轴的两侧,那么OA·OB=m(-n)=-mn=1.所以OC2=OA·OB.所以.所以tan∠1=tan∠2.所以∠1=∠2.又因为∠1与∠3互余,所以∠2与∠3互余.所以∠ACB=90°.图1 图2 图3(3)在△ABC中,已知A(2, 0),B(n, 0),C(0, 2n).讨论等腰三角形ABC,用代数法解比较方便:由两点间的距离公式,得AB2=(n-2)2,BC2=5n2,AC2=4+4n2.①当AB=AC时,解方程(n-2)2=4+4n2,得(如图2).。
2017中考数学压轴题及答案40例(3)
2017中考数学压轴题及答案40例(3)28.如图,Rt △ABC 的顶点坐标分别为A (0,3),B (-21,23),C (1,0),∠ABC =90°,BC 与y 轴的交点为D ,D 点坐标为(0,33),以点D 为顶点、y 轴为对称轴的抛物线过点B .(1)求该抛物线的解析式;(2)将△ABC 沿AC 折叠后得到点B 的对应点B ′,求证:四边形AOCB ′是矩形,并判断点B ′是否在(1)的抛物线上;(3)延长BA 交抛物线于点E ,在线段BE 上取一点P ,过P 点作x 轴的垂线,交抛物线于点F ,是否存在这样的点P ,使四边形PADF 是平行四边形?若存在,求出点P 的坐标,若不存在,说明理由. 解:(1)∵抛物线的顶点为D (0,33) ∴可设抛物线的解析式为y =ax 2+33. ··········································· 1分 ∵B (-21,23)在抛物线上∴a (-21)2+33=23,∴a =332. ····················· 3分 ∴抛物线的解析式为y =332x 2+33. ···················· 5分(2)∵B (-21,23),C (1,0)∴BC =2223121)+()-(-=3 又B ′C =BC ,OA =3,∴B ′C =OA . ·················································· 6分∵AC =22OC OA +=2213+)(=2 ∴AB =22BC AC -=2232)-(=1又AB ′=AB ,OC =1,∴AB ′=OC . ····················································· 7分 ∴四边形AOCB ′是矩形. ···································································· 8分 ∵B ′C =3,OC =1∴点B ′ 的坐标为(1,3) ······························································ 9分 将x =1代入y =332x 2+33得y =3∴点B ′ 在抛物线上. ······································································· 10分(3)存在 ································································································· 11分理由如下:设直线AB 的解析式为y =kx +b ,则⎪⎩⎪⎨⎧32321 ==+-b b k 解得⎪⎩⎪⎨⎧33 ==b k ∴直线AB 的解析式为y =33+x ··················································· 12分 ∵P 、F 分别在直线AB 和抛物线上,且PF ∥AD∴设P (m ,33+m ),F (m ,332m 2+33)∴PF =(33+m )-(332m 2+33)=-332m 2+m 3+332AD =333-=332 若四边形PADF 是平行四边形,则有PF =AD . 即-332m 2+m 3+332=332 解得m 1=0(不合题意,舍去),m 2=23. ····································· 13分当m =23时,33+m =3×23+3=235.∴存在点P (23,235),使四边形PADF 是平行四边形. ·············· 14分29.如图1,平移抛物线F 1:y =x 2后得到抛物线F 2.已知抛物线F 2经过抛物线F 1的顶点M 和点A (2,0),且对称轴与抛物线F 1交于点B ,设抛物线F 2的顶点为N . (1)探究四边形ABMN 的形状及面积(直接写出结论);(2)若将已知条件中的“抛物线F 1:y =x 2”改为“抛物线F 1:y =ax 2”(如图2),“点A (2,0)”改为“点A (m ,0)”,其它条件不变,探究四边形ABMN 的形状及其面积,并说明理由;(3)若将已知条件中的“抛物线F 1:y =x 2”改为“抛物线F 1:y =ax 2+c ”(如图3),“点A (2,0)”改为“点A (m ,c )”其它条件不变,求直线AB 与y 轴的交点C 的坐标(直接写出结论).解:(1)四边形ABMN 是正方形,其面积为2. ···················································· 1分(2)四边形ABMN 是菱形.当m >0时,四边形ABMN 的面积为43am ;当m <0时,四边形ABMN 的面积为-43am . ·················································· 2分 (说明:如果没有说理过程,探究的结论正确的得2分)理由如下:∵平移抛物线F 1后得到抛物线F 2,且抛物线F 2经过原点O . ∴设抛物线F 2的解析式为y =ax 2+bx .∵抛物线F 2经过点A (m ,0),∴am 2+bm =0. 由题意可知m ≠0,∴b =-am .∴抛物线F 2的解析式为y =ax 2-amx . ·············································· 3分∴y =a (x -2m )2-42am∴抛物线F 2的对称轴为直线x =2m ,顶点N (2m,-42am ). ········· 4分∵抛物线F 2的对称轴与抛物线F 1的交点为B ,∴点B 的横坐标为2m. ∵点B 在抛物线F 1:y =ax 2上∴y B =a (2m )2=42am ·········································································· 5分设抛物线F 2的对称轴与x 轴交于点P ,如图1.∵a >0,∴BP =42am .∵顶点N (2m,-42am ),∴NP =|-42am |=42am .∴BP =NP . ···························································· 6分 ∵抛物线是轴对称图形,∴OP =AP .∴四边形ABMN 是平行四边形. ····························· 7分 ∵BN 是抛物线F 2的对称轴,∴BN ⊥OA .∴四边形ABMN 是菱形. ··································································· 8分∵BN =BP +NP ,∴BN =22am .∵四边形ABMN 的面积为21×OA ·BN =21×|m |×22am∴当m >0时,四边形ABMN 的面积为21×m ×22am =43am . ·········· 9分 当m <0时,四边形ABMN 的面积为21×(-m )×22am =-43am . · 10分 (3)点C 的坐标为(0,22am +c )(参考图2).30.如图,抛物线的顶点为A (2,1),且经过原点O ,与x 轴的另一个交点为B . (1)求抛物线的解析式;(2)在抛物线上求点M ,使△MOB 的面积是△AOB 面积的3倍;(3)连结OA ,AB ,在x 轴下方的抛物线上是否存在点N ,使△OBN 与△OAB 相似?若存在,求出N 点的坐标;若不存在,说明理由.解:(1)由题意,可设抛物线的解析式为y =a (x -2)2+1.∵抛物线经过原点,∴a (0-2)2+1=0,∴a =-41.∴抛物线的解析式为y =-41(x -2)2+1=-41x 2+x . ······················ 3分(2)△AOB 和所求△MOB 同底不等高,若S △MOB =3S △AOB ,则△MOB 的高是△AOB 高的3倍,即M 点的纵坐标是-3. ···································································· 5分∴-41x 2+x =-3,整理得x 2-4x -12=0,解得x 1=6,x 2=-2.∴满足条件的点有两个:M 1(6,-3),M 2(-2,-3) ·························· 7分 (3)不存在. ···························································································· 8分理由如下:由抛物线的对称性,知AO =AB ,∠AOB =∠ABO . 若△OBN ∽△OAB ,则∠BON =∠BOA =∠BNO . 设ON 交抛物线的对称轴于A ′ 点,则A ′ (2,-1).∴直线ON 的解析式为y =-21x .由21x =-41x 2+x ,得x 1=0,x 2=6. ∴N (6,-3).过点N 作NC ⊥x 轴于C .在Rt △BCN 中,BC =6-4=2,NC =3 ∴NB =2232+=13.∵OB =4,∴NB ≠OB ,∴∠BON ≠∠BNO ,∴△OBN 与△OAB 不相似. 同理,在对称轴左边的抛物线上也不存在符合条件的N 点.∴在x 轴下方的抛物线上不存在点N ,使△OBN 与△OAB 相似. ······ 10分31.如图,在直角坐标系中,点A 的坐标为(-2,0),连结OA ,将线段OA 绕原点O 顺时针旋转120°,得到线段OB .(1)求点B 的坐标;(2)求经过A 、O 、B 三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C ,使△BOC 的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由.(4)如果点P 是(2)中的抛物线上的动点,且在x 轴的下方,那么△PAB 是否有最大面积?若有,求出此时P 点的坐标及△PAB 的最大面积;若没有,请说明理由.(1)如图1,过点B 作BM ⊥x 轴于M .由旋转性质知OB =OA =2.∵∠AOB =120°,∴∠BOM =60°.∴OM =OB ·cos60°=2×21=1,BM =OB ·sin60°=2×23=3.∴点B 的坐标为(1,3). ······································ 1分 (2)设经过A 、O 、B 三点的抛物线的解析式为y =ax 2+bx +c ∵抛物线过原点,∴c =0.∴⎪⎩⎪⎨⎧=+=-3024b a b a 解得⎪⎪⎩⎪⎪⎨⎧==33233b a ∴所求抛物线的解析式为y =33x 2+332x . ·································· 3分 (3)存在. ······························································································ 4分如图2,连接AB ,交抛物线的对称轴于点C ,连接OC .∵OB 的长为定值,∴要使△BOC 的周长最小,必须BC +OC 的长最小. ∵点A 与点O 关于抛物线的对称轴对称,∴OC =AC . ∴BC +OC =BC +AC =AB .由“两点之间,线段最短”的原理可知:此时BC +OC 最小,点C 的位置即为所求.设直线AB 的解析式为y =kx +m ,将A (-2,0),B (1,3)代入,得⎪⎩⎪⎨⎧=+=+-302m k m k 解得⎪⎪⎩⎪⎪⎨⎧==33233m k∴直线AB 的解析式为y =33x +332. 抛物线的对称轴为直线x =332332⨯-=-1,即x =-1.将x =-1代入直线AB 的解析式,得y =33×(-1)+332=33. ∴点C 的坐标为(-1,33). ·························································· 6分 (4)△PAB 有最大面积. ········································································· 7分如图3,过点P 作y 轴的平行线交AB 于点D . ∵S △PAB =S △PAD +S △PBD=21(y D -y P )(x B -x A ) =21[(33x +332)-(33x 2+332x )](1+2) =-23x 2-23x +3 =-23(x +21)2+839 ∴当x =-21时,△PAB 的面积有最大值,最大值为839.·············· 8分此时y P =33×(-21)2+332×(-21)=-43. ∴此时P 点的坐标为(-21,-43). ··············································· 9分。
2017年全国各地中考数学压轴题汇编二含详细答案 推荐
湖北省武汉为明实验学校2017年全国各地中考数学压轴题汇编二(含详细答案)【11. 2017成都】28. (本小题满分l2分)如图,在平面直角坐标系xOy 中,一次函数54y x m =+ (m 为常数)的图象与x 轴交于点A(3-,0),与y 轴交于点C .以直线x=1为对称轴的抛物线2y ax bx c =++ (a b c ,, 为常数,且a ≠0)经过A ,C 两点,并与x 轴的正半轴交于点B . (1)求m 的值及抛物线的函数表达式;(2)设E 是y 轴右侧抛物线上一点,过点E 作直线AC 的平行线交x 轴于点F .是否存在这样的点E ,使得以A ,C ,E ,F 为顶点的四边形是平行四边形?若存在,求出点E 的坐标及相应的平行四边形的面积;若不存在,请说明理由;(3)若P 是抛物线对称轴上使△ACP 的周长取得最小值的点,过点P 任意作一条与y 轴不平行的直线交抛物线于111M ()x y , ,222M ()x y ,两点,试探究2112P PM M M M ⋅ 是否为定值,并写出探究过程.考点:二次函数综合题。
解答:解:(1)∵经过点(﹣3,0), ∴0=+m ,解得m=, ∴直线解析式为,C (0,).∵抛物线y=ax 2+bx+c 对称轴为x=1,且与x 轴交于A (﹣3,0),∴另一交点为B (5,0), 设抛物线解析式为y=a (x+3)(x ﹣5),∵抛物线经过C(0,),∴=a•3(﹣5),解得a=,∴抛物线解析式为y=x2+x+;(2)假设存在点E使得以A、C、E、F为顶点的四边形是平行四边形,则AC∥EF且AC=EF.如答图1,(i)当点E在点E位置时,过点E作EG⊥x轴于点G,∵AC∥EF,∴∠CAO=∠EFG,又∵,∴△CAO≌△EFG,∴EG=CO=,即y E=,∴=x E2+x E+,解得x E=2(x E=0与C点重合,舍去),∴E(2,),S▱ACEF=;(ii)当点E在点E′位置时,过点E′作E′G′⊥x轴于点G′,同理可求得E′(+1,),S▱ACE′F′=.(3)要使△ACP的周长最小,只需AP+CP最小即可.如答图2,连接BC交x=1于P点,因为点A、B关于x=1对称,根据轴对称性质以及两点之间线段最短,可知此时AP+CP最小(AP+CP最小值为线段BC的长度).∵B(5,0),C(0,),∴直线BC解析式为y=x+,∵x P=1,∴y P=3,即P(1,3).令经过点P(1,3)的直线为y=kx+3﹣k,∵y=kx+3﹣k,y=x2+x+,联立化简得:x2+(4k﹣2)x﹣4k﹣3=0,∴x1+x2=2﹣4k,x1x2=﹣4k﹣3.∵y1=kx1+3﹣k,y2=kx2+3﹣k,∴y1﹣y2=k(x1﹣x2).根据两点间距离公式得到:M1M2===∴M1M2===4(1+k2).又M1P===;同理M2P=∴M1P•M2P=(1+k2)•=(1+k2)•=(1+k2)•=4(1+k2).∴M1P•M2P=M1M2,∴=1为定值.【12.2017•聊城】25.某电子厂商投产一种新型电子厂品,每件制造成本为18元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;(2)当销售单价为多少元时,厂商每月能获得3502万元的利润?当销售单价为多少元时,厂商每月能获得最大利润?最大利润是多少?(3)根据相关部门规定,这种电子产品的销售单价不能高于32元,如果厂商要获得每月不低于350万元的利润,那么制造出这种产品每月的最低制造成本需要多少万元?考点:二次函数的应用;一次函数的应用。
2017全国中考数学压轴题——解答题部分(四)
(1)求抛物线解析式及顶点N的坐标;
(2)求证:四边形PMDA是平行四边形;
(3)求证△DPE∽△PAM,并求当它们的相似比为时的点P的坐标.
73.(湖南常德26)如图,直角△ABC中,∠BAC=90°,D在BC上,连接AD,作BF⊥AD分别交AD于E,AC于F.
(1)如图13,若BD=BA,求证:△ABE≌△DBE;
(2)如图14,若BD=4DC,取AB的中点G,连接CG交AD于M,
(2)如图,顶点在第一象限的抛物线y=m(x-1)2-4m与其伴随直线相交于点A,B(点A在点B的右侧)与x轴交于点C,D
①若∠CAB=90°求m的值;
②如果点P(x,y)是直线BC上方抛物线的一个动点,∆PBC的面积记为S,当S取得最大值时,求m的值.
70.(湖北宜昌23)正方形ABCD的边长为1,点O是BC边上的一个动点(与B,C不重合),以O为顶点在BC所在直线的上方作∠MON=90°.
(1)直接写出A、B两点的坐标;
(2)过点A、B的抛物线G与x轴的另一个交点为点C.
①若∆ABC是以BC为腰的等腰三角形,求此时抛物线的解析式;
②将抛物线G向下平移4个单位后,恰好与直线AB只有一个交点N,求点N的坐标.
77.(湖南衡阳27)如图,正方形ABCD的边长为1,点E为边AB上一动点,连结CE并将其绕点C顺时针旋转90°得到CF,连结DF,以CE、CF为邻边作矩形CFGE,GE与AD、AC分别交于点H、M,GF交CD延长线于点N.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一部分函数图象中点的存在性问题§1.1 因动点产生的相似三角形问题例1 2014年衡阳市中考第28题例2 2014年益阳市中考第21题例3 2015年湘西州中考第26题例4 2015年张家界市中考第25题例5 2016年常德市中考第26题例6 2016年岳阳市中考第24题例7 2016年上海市崇明县中考模拟第25题例8 2016年上海市黄浦区中考模拟第26题§1.2 因动点产生的等腰三角形问题例9 2014年长沙市中考第26题例10 2014年张家界市第25题例11 2014年邵阳市中考第26题例12 2014年娄底市中考第27题例13 2015年怀化市中考第22题例14 2015年长沙市中考第26题例15 2016年娄底市中考第26题例16 2016年上海市长宁区金山区中考模拟第25题例17 2016年河南省中考第23题例18 2016年重庆市中考第25题§1.3 因动点产生的直角三角形问题例19 2015年益阳市中考第21题例20 2015年湘潭市中考第26题例21 2016年郴州市中考第26题例22 2016年上海市松江区中考模拟第25题例23 2016年义乌市绍兴市中考第24题§1.4 因动点产生的平行四边形问题例24 2014年岳阳市中考第24题例25 2014年益阳市中考第20题例26 2014年邵阳市中考第25题例27 2015年郴州市中考第25题例28 2015年黄冈市中考第24题例29 2016年衡阳市中考第26题例30 2016年上海市嘉定区宝山区中考模拟中考第24题例31 2016年上海市徐汇区中考模拟第24题§1.5 因动点产生的面积问题例32 2014年常德市中考第25题例33 2014年永州市中考第25题例34 2014年怀化市中考第24题例35 2015年邵阳市中考第26题例36 2015年株洲市中考第23题例37 2015年衡阳市中考第28题例38 2016年益阳市中考第22题例39 2016年永州市中考第26题例40 2016年邵阳市中考第26题例41 2016年陕西省中考第25题§1.6 因动点产生的相切问题例42 2014年衡阳市中考第27题例43 2014年株洲市中考第23题例44 2015年湘潭市中考第25题例45 2015年湘西州中考第25题例46 2016年娄底市中考第25题例47 2016年湘潭市中考第26题例48 2016年上海市闵行区中考模拟第24题例49 2016年上海市普陀区中考模拟中考第25题§1.7 因动点产生的线段和差问题例50 2014年郴州市中考第26题例51 2014年湘西州中考第25题例52 2015年岳阳市中考第24题例53 2015年济南市中考第28题例54 2015年沈阳市中考第25题例55 2016年福州市中考第26题例56 2016年张家界市中考第24题例57 2016年益阳市中考第21题第二部分图形运动中的函数关系问题§2.1 由比例线段产生的函数关系问题例1 2014年常德市中考第26题例2 2014年湘潭市中考第25题例3 2014年郴州市中考第25题例4 2015年常德市中考第25题例5 2015年郴州市中考第26题例6 2015年邵阳市中考第25题例9 2016年湘西州中考第26题例10 2016年上海市静安区青浦区中考模拟第25题例11 2016年哈尔滨市中考第27题第三部分图形运动中的计算说理问题§3.1 代数计算及通过代数计算进行说理问题例1 2014年长沙市中考第25题例2 2014年怀化市中考第23题例3 2014年湘潭市中考第26题例4 2014年株洲市中考第24题例5 2015年衡阳市中考第27题例6 2015年娄底市中考第25题例7 2015年永州市中考第26题例8 2015年长沙市中考第25题例9 2015年株洲市中考第24题例10 2016年怀化市中考第22题例11 2016年邵阳市中考第25题例12 2016年株洲市中考第26题例13 2016年长沙市中考第25题例14 2016年长沙市中考第26题§3.2 几何证明及通过几何计算进行说理问题例15 2014年衡阳市中考第26题例16 2014年娄底市中考第26题例17 2014年岳阳市中考第23题例18 2015年常德市中考第26题例19 2015年益阳市中考第20题例20 2015年永州市中考第27题例21 2015年岳阳市中考第23题例22 2016年常德市中考第25题例23 2016年衡阳市中考第25题例24 2016年永州市中考第27题例25 2016年岳阳市中考第23题例26 2016年株洲市中考第25题例27 2016年湘潭市中考第25题第四部分图形的平移、翻折与旋转§4.1 图形的平移例3 2015年株洲市中考第14题例4 2016年上海市虹口区中考模拟第18题§4.2 图形的翻折例5 2016年上海市奉贤区中考模拟第18题例6 2016年上海市静安区青浦区中考模拟第18题例7 2016年上海市闵行区中考模拟第18题例8 2016年上海市浦东新区中考模拟第18题例8 2016年上海市普陀区中考模拟第18题例10 2016年常德市中考第15题例11 2016年张家界市中考第14题例12 2016年淮安市中考第18题例13 2016年金华市中考第15题例14 2016年雅安市中考第12题§4.3 图形的旋转例15 2016年上海昂立教育中学生三模联考第18题例16 2016年上海市崇明县中考模拟第18题例17 2016年上海市黄浦区中考模拟第18题例18 2016年上海市嘉定区宝山区中考模拟第18题例19 2016年上海市闸北区中考模拟第18题例20 2016年邵阳市中考第13题例21 2016年株洲市中考第4题§4.4 三角形例22 2016年安徽省中考第10题例23 2016年武汉市中考第10题例24 2016年河北省中考第16题例25 2016年娄底市中考第10题例26 2016年苏州市中考第9题例27 2016年台州市中考第10题例28 2016年陕西省中考第14题例29 2016年内江市中考第11题例30 2016年上海市中考第18题§4.5 四边形例31 2016年湘西州中考第11题例32 2016年益阳市中考第4题例35 2016年成都市中考第14题例36 2016年广州市中考第13题例37 2016年福州市中考第18题例38 2016年无锡市中考第17题例39 2016年台州市中考第15题§4.6 圆例40 2016年滨州市中考第16题例41 2016年宁波市中考第17题例42 2016年连云港市中考第16题例43 2016年烟台市中考第17题例44 2016年烟台市中考第18题例45 2016年无锡市中考第18题例46 2016年武汉市中考第9题例47 2016年宿迁市中考第16题例48 2016年衡阳市中考第17题例49 2016年邵阳市中考第18题例50 2016年湘西州中考第18题例51 2016年永州市中考第20题§4.7 函数的图象及性质例52 2015年荆州市中考第9题例53 2015年德州市中考第12题例54 2015年烟台市中考第12题例55 2015年中山市中考第10题例56 2015年武威市中考第10题例57 2015年呼和浩特市中考第10题例58 2016年湘潭市中考第18题例59 2016年衡阳市中考第19题例60 2016年岳阳市中考第15题例61 2016年株洲市中考第9题例62 2016年永州市中考第19题例63 2016年岳阳市中考第8题例64 2016年岳阳市中考第16题例65 2016年益阳市中考第14题例66 2016年株洲市中考第10题例67 2016年株洲市中考第17题例70 2016年泰州市中考第16题例71 2016年宿迁市中考第15题例72 2016年临沂市中考第14题例73 2016年义乌市绍兴市中考第9题例74 2016年淄博市中考第12题例75 2016年嘉兴市中考第16题§1.1 因动点产生的相似三角形问题课前导学相似三角形的判定定理有3个,其中判定定理1和判定定理2都有对应角相等的条件,因此探求两个三角形相似的动态问题,一般情况下首先寻找一组对应角相等.判定定理2是最常用的解题依据,一般分三步:寻找一组等角,分两种情况列比例方程,解方程并检验.如果已知∠A=∠D,探求△ABC与△DEF相似,只要把夹∠A和∠D的两边表示出来,按照对应边成比例,分AB DEAC DF=和AB DFAC DE=两种情况列方程.应用判定定理1解题,先寻找一组等角,再分两种情况讨论另外两组对应角相等.应用判定定理3解题不多见,根据三边对应成比例列连比式解方程(组).还有一种情况,讨论两个直角三角形相似,如果一组锐角相等,其中一个直角三角形的锐角三角比是确定的,那么就转化为讨论另一个三角形是直角三角形的问题.求线段的长,要用到两点间的距离公式,而这个公式容易记错.理解记忆比较好.如图1,如果已知A、B两点的坐标,怎样求A、B两点间的距离呢?我们以AB为斜边构造直角三角形,直角边与坐标轴平行,这样用勾股定理就可以求斜边AB的长了.水平距离BC的长就是A、B两点间的水平距离,等于A、B两点的横坐标相减;竖直距离AC就是A、B两点间的竖直距离,等于A、B两点的纵坐标相减.图1例 1 2014年湖南省衡阳市中考第28题二次函数y =a x 2+b x +c (a ≠0)的图象与x 轴交于A (-3, 0)、B (1, 0)两点,与y 轴交于点C (0,-3m )(m >0),顶点为D .(1)求该二次函数的解析式(系数用含m 的代数式表示);(2)如图1,当m =2时,点P 为第三象限内抛物线上的一个动点,设△APC 的面积为S ,试求出S 与点P 的横坐标x 之间的函数关系式及S 的最大值;(3)如图2,当m 取何值时,以A 、D 、C 三点为顶点的三角形与△OBC 相似?图1 图2动感体验请打开几何画板文件名“14衡阳28”,拖动点P 运动,可以体验到,当点P 运动到AC 的中点的正下方时,△APC 的面积最大.拖动y 轴上表示实数m 的点运动,抛物线的形状会改变,可以体验到,∠ACD 和∠ADC 都可以成为直角.思路点拨1.用交点式求抛物线的解析式比较简便.2.连结OP ,△APC 可以割补为:△AOP 与△COP 的和,再减去△AOC .3.讨论△ACD 与△OBC 相似,先确定△ACD 是直角三角形,再验证两个直角三角形是否相似. 4.直角三角形ACD 存在两种情况.图文解析(1)因为抛物线与x 轴交于A (-3, 0)、B (1, 0)两点,设y =a (x +3)(x -1). 代入点C (0,-3m ),得-3m =-3a .解得a =m .所以该二次函数的解析式为y =m (x +3)(x -1)=mx 2+2mx -3m . (2)如图3,连结OP .当m =2时,C (0,-6),y =2x 2+4x -6,那么P (x , 2x 2+4x -6).由于S △AOP =1()2P OA y ⨯-=32-(2x 2+4x -6)=-3x 2-6x +9,S △COP =1()2P OC x ⨯-=-3x ,S △AOC =9,所以S =S △APC =S △AOP +S △COP -S △AOC =-3x 2-9x =23273()24x -++.所以当32x =-时,S 取得最大值,最大值为274.图3 图4 图5(3)如图4,过点D 作y 轴的垂线,垂足为E .过点A 作x 轴的垂线交DE 于F . 由y =m (x +3)(x -1)=m (x +1)2-4m ,得D (-1,-4m ). 在Rt △OBC 中,OB ∶OC =1∶3m .如果△ADC 与△OBC 相似,那么△ADC 是直角三角形,而且两条直角边的比为1∶3m .①如图4,当∠ACD =90°时,OA OC EC ED =.所以331mm =.解得m =1. 此时3CA OC CD ED ==,3OC OB =.所以CA OC CD OB=.所以△CDA ∽△OBC . ②如图5,当∠ADC =90°时,FA FD ED EC =.所以421m m=.解得2m =. 此时222DA FD DC EC m===,而323OC m OB ==.因此△DCA 与△OBC 不相似. 综上所述,当m =1时,△CDA ∽△OBC .考点伸展第(2)题还可以这样割补:如图6,过点P 作x 轴的垂线与AC 交于点H . 由直线AC :y =-2x -6,可得H (x ,-2x -6). 又因为P (x , 2x 2+4x -6),所以HP =-2x 2-6x .因为△P AH 与△PCH 有公共底边HP ,高的和为A 、C 两点间的水平距离3,所以S =S △APC =S △APH +S △CPH=32(-2x 2-6x ) =23273()24x -++. 图6例 2 2014年湖南省益阳市中考第21题如图1,在直角梯形ABCD 中,AB //CD ,AD ⊥AB ,∠B =60°,AB =10,BC =4,点P 沿线段AB 从点A 向点B 运动,设AP =x .2·1·c·n·j·y(1)求AD 的长;(2)点P 在运动过程中,是否存在以A 、P 、D 为顶点的三角形与以P 、C 、B 为顶点的三角形相似?若存在,求出x 的值;若不存在,请说明理由;(3)设△ADP 与△PCB 的外接圆的面积分别为S 1、S 2,若S =S 1+S 2,求S 的最小值.动感体验 图1请打开几何画板文件名“14益阳21”,拖动点P 在AB 上运动,可以体验到,圆心O 的运动轨迹是线段BC 的垂直平分线上的一条线段.观察S 随点P 运动的图象,可以看到,S 有最小值,此时点P 看上去象是AB 的中点,其实离得很近而已.思路点拨1.第(2)题先确定△PCB 是直角三角形,再验证两个三角形是否相似.2.第(3)题理解△PCB 的外接圆的圆心O 很关键,圆心O 在确定的BC 的垂直平分线上,同时又在不确定的BP 的垂直平分线上.而BP 与AP 是相关的,这样就可以以AP 为自变量,求S 的函数关系式.图文解析(1)如图2,作CH ⊥AB 于H ,那么AD =CH .在Rt △BCH 中,∠B =60°,BC =4,所以BH =2,CH =23.所以AD =23.(2)因为△APD 是直角三角形,如果△APD 与△PCB 相似,那么△PCB 一定是直角三角形. ①如图3,当∠CPB =90°时,AP =10-2=8. 所以AP AD =823=433,而PCPB=3.此时△APD 与△PCB 不相似.图2 图3 图4②如图4,当∠BCP =90°时,BP =2BC =8.所以AP =2. 所以APAD =23=3.所以∠APD =60°.此时△APD ∽△CBP .综上所述,当x =2时,△APD ∽△CBP .(3)如图5,设△ADP 的外接圆的圆心为G ,那么点G 是斜边DP 的中点.设△PCB 的外接圆的圆心为O ,那么点O 在BC 边的垂直平分线上,设这条直线与BC 交于点E ,与AB 交于点F .设AP =2m .作OM ⊥BP 于M ,那么BM =PM =5-m . 在Rt △BEF 中,BE =2,∠B =60°,所以BF =4.在Rt △OFM 中,FM =BF -BM =4-(5-m )=m -1,∠OFM =30°, 所以OM =3(1)3m -. 所以OB 2=BM 2+OM 2=221(5)(1)3m m -+-.在Rt △ADP 中,DP 2=AD 2+AP 2=12+4m 2.所以GP 2=3+m 2.于是S =S 1+S 2=π(GP 2+OB 2)=22213(5)(1)3m m m π⎡⎤++-+-⎢⎥⎣⎦=2(73285)3m m π-+.所以当167m =时,S 取得最小值,最小值为1137π.图5 图6考点伸展关于第(3)题,我们再讨论个问题.问题1,为什么设AP =2m 呢?这是因为线段AB =AP +PM +BM =AP +2BM =10. 这样BM =5-m ,后续可以减少一些分数运算.这不影响求S 的最小值. 问题2,如果圆心O 在线段EF 的延长线上,S 关于m 的解析式是什么?如图6,圆心O 在线段EF 的延长线上时,不同的是FM =BM -BF =(5-m )-4=1-m .此时OB 2=BM 2+OM 2=221(5)(1)3m m -+-.这并不影响S 关于m 的解析式.例 3 2015年湖南省湘西市中考第26题如图1,已知直线y=-x+3与x轴、y轴分别交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,点P在线段OA上,从点O出发,向点A以每秒1个单位的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以每秒2个单位的速度匀速运动,连结PQ,设运动时间为t秒.(1)求抛物线的解析式;(2)问:当t为何值时,△APQ为直角三角形;(3)过点P作PE//y轴,交AB于点E,过点Q作QF//y轴,交抛物线于点F,连结EF,当EF//PQ时,求点F的坐标;(4)设抛物线顶点为M,连结BP、BM、MQ,问:是否存在t的值,使以B、Q、M为顶点的三角形与以O、B、P为顶点的三角形相似?若存在,请求出t的值;若不存在,请说明理由.图1动感体验请打开几何画板文件名“15湘西26”,拖动点P在OA上运动,可以体验到,△APQ有两个时刻可以成为直角三角形,四边形EPQF有一个时刻可以成为平行四边形,△MBQ与△BOP有一次机会相似.思路点拨1.在△APQ中,∠A=45°,夹∠A的两条边AP、AQ都可以用t表示,分两种情况讨论直角三角形APQ.2.先用含t的式子表示点P、Q的坐标,进而表示点E、F的坐标,根据PE=QF列方程就好了.3.△MBQ与△BOP都是直角三角形,根据直角边对应成比例分两种情况讨论.图文解析(1)由y=-x+3,得A(3, 0),B(0, 3).将A(3, 0)、B(0, 3)分别代入y=-x2+bx+c,得930,3.b cc-++=⎧⎨=⎩解得2,3.bc=⎧⎨=⎩所以抛物线的解析式为y=-x2+2x+3.(2)在△APQ中,∠P AQ=45°,AP=3-t,AQ=2t.分两种情况讨论直角三角形APQ:①当∠PQA=90°时,AP=2AQ.解方程3-t=2t,得t=1(如图2).②当∠QP A=90°时,AQ=2AP.解方程2t=2(3-t),得t=1.5(如图3).图2 图3(3)如图4,因为PE//QF,当EF//PQ时,四边形EPQF是平行四边形.所以EP=FQ.所以y E-y P=y F-y Q.因为x P=t,x Q=3-t,所以y E=3-t,y Q=t,y F=-(3-t)2+2(3-t)+3=-t2+4t.因为y E-y P=y F-y Q,解方程3-t=(-t2+4t)-t,得t=1,或t=3(舍去).所以点F的坐标为(2, 3).图4 图5(4)由y=-x2+2x+3=-(x-1)2+4,得M(1, 4).由A(3, 0)、B(0, 3),可知A、B两点间的水平距离、竖直距离相等,AB=2.由B(0, 3)、M(1, 4),可知B、M两点间的水平距离、竖直距离相等,BM2所以∠MBQ=∠BOP=90°.因此△MBQ与△BOP相似存在两种可能:①当BM OBBQ OP=23322tt=-.解得94t=(如图5).②当BM OPBQ OB=23322tt=-.整理,得t2-3t+3=0.此方程无实根.考点伸展第(3)题也可以用坐标平移的方法:由P(t, 0),E(t, 3-t),Q(3-t, t),按照P→E方向,将点Q向上平移,得F(3-t, 3).再将F(3-t, 3)代入y=-x2+2x+3,得t=1,或t=3.§1.2 因动点产生的等腰三角形问题课前导学我们先回顾两个画图问题:1.已知线段AB=5厘米,以线段AB为腰的等腰三角形ABC有多少个?顶点C的轨迹是什么?2.已知线段AB=6厘米,以线段AB为底边的等腰三角形ABC有多少个?顶点C的轨迹是什么?已知腰长画等腰三角形用圆规画圆,圆上除了两个点以外,都是顶点C.已知底边画等腰三角形,顶角的顶点在底边的垂直平分线上,垂足要除外.在讨论等腰三角形的存在性问题时,一般都要先分类.如果△ABC是等腰三角形,那么存在①AB=AC,②BA=BC,③CA=CB三种情况.解等腰三角形的存在性问题,有几何法和代数法,把几何法和代数法相结合,可以使得解题又好又快.几何法一般分三步:分类、画图、计算.哪些题目适合用几何法呢?如果△ABC的∠A(的余弦值)是确定的,夹∠A的两边AB和AC可以用含x的式子表示出来,那么就用几何法.①如图1,如果AB=AC,直接列方程;②如图2,如果BA=BC,那么1cos2AC AB A=∠;③如图3,如果CA=CB,那么1cos2AB AC A=∠.代数法一般也分三步:罗列三边长,分类列方程,解方程并检验.如果三角形的三个角都是不确定的,而三个顶点的坐标可以用含x的式子表示出来,那么根据两点间的距离公式,三边长(的平方)就可以罗列出来.图1 图2 图3例 9 2014年长沙市中考第26题如图1,抛物线y =ax 2+bx +c (a 、b 、c 是常数,a ≠0)的对称轴为y 轴,且经过(0,0)和1(,)16a 两点,点P 在该抛物线上运动,以点P 为圆心的⊙P 总经过定点A (0, 2).(1)求a 、b 、c 的值;(2)求证:在点P 运动的过程中,⊙P 始终与x 轴相交;(3)设⊙P 与x 轴相交于M (x 1, 0)、N (x 2, 0)两点,当△AMN 为等腰三角形时,求圆心P 的纵坐标.图1动感体验请打开几何画板文件名“14长沙26”,拖动圆心P 在抛物线上运动,可以体验到,圆与x 轴总是相交的,等腰三角形AMN 存在五种情况.思路点拨1.不算不知道,一算真奇妙,原来⊙P 在x 轴上截得的弦长MN =4是定值.2.等腰三角形AMN 存在五种情况,点P 的纵坐标有三个值,根据对称性,MA =MN 和NA =NM 时,点P 的纵坐标是相等的.图文解析(1)已知抛物线的顶点为(0,0),所以y =ax 2.所以b =0,c =0.将1(,)16a 代入y =ax 2,得2116a =.解得14a =(舍去了负值).(2)抛物线的解析式为214y x =,设点P 的坐标为21(,)4x x .已知A (0, 2),所以222411(2)4416PA x x x =+-=+>214x .而圆心P 到x 轴的距离为214x ,所以半径P A >圆心P 到x 轴的距离.所以在点P 运动的过程中,⊙P 始终与x 轴相交.(3)如图2,设MN 的中点为H ,那么PH 垂直平分MN .在Rt △PMH 中,2241416PM PA x ==+,22411()416PH x x ==,所以MH 2=4.所以MH =2.因此MN =4,为定值. 等腰△AMN 存在三种情况:①如图3,当AM =AN 时,点P 为原点O 重合,此时点P 的纵坐标为0.图2 图3②如图4,当MA =MN 时,在Rt △AOM 中,OA =2,AM =4,所以OM =3此时x =OH =32.所以点P 的纵坐标为22211(232)(31)42344x ===+如图5,当NA =NM 时,根据对称性,点P 的纵坐标为也为423+.图4 图5③如图6,当NA =NM =4时,在Rt △AON 中,OA =2,AN =4,所以ON =23.此时x =OH =232-.所以点P 的纵坐标为22211(232)(31)42344x =-=-=-.如图7,当MN =MA =4时,根据对称性,点P 的纵坐标也为423-.图6 图7考点伸展如果点P 在抛物线214y x =上运动,以点P 为圆心的⊙P 总经过定点B (0, 1),那么在点P 运动的过程中,⊙P 始终与直线y =-1相切.这是因为:设点P 的坐标为21(,)4x x .已知B (0, 1),所以222222111(1)(1)1444PB x x x x =+-++.而圆心P 到直线y =-1的距离也为2114x +,所以半径PB =圆心P 到直线y =-1的距离.所以在点P运动的过程中,⊙P 始终与直线y =-1相切.例 10 2014年湖南省张家界市中考第25题如图1,在平面直角坐标系中,O 为坐标原点,抛物线y =ax 2+bx +c (a ≠0)过O 、B 、C 三点,B 、C 坐标分别为(10, 0)和1824(,)55-,以OB 为直径的⊙A 经过C 点,直线l 垂直x 轴于B 点. (1)求直线BC 的解析式;(2)求抛物线解析式及顶点坐标;(3)点M 是⊙A 上一动点(不同于O 、B ),过点M 作⊙A 的切线,交y 轴于点E ,交直线l 于点F ,设线段ME 长为m ,MF 长为n ,请猜想mn 的值,并证明你的结论;(4)若点P 从O 出发,以每秒1个单位的速度向点B 作直线运动,点Q 同时从B 出发,以相同速度向点C 作直线运动,经过t (0<t ≤8)秒时恰好使△BPQ 为等腰三角形,请求出满足条件的t 值.图图1动感体验请打开几何画板文件名“14张家界25”,拖动点M 在圆上运动,可以体验到,△EAF 保持直角三角形的形状,AM 是斜边上的高.拖动点Q 在BC 上运动,可以体验到,△BPQ 有三个时刻可以成为等腰三角形.思路点拨1.从直线BC 的解析式可以得到∠OBC 的三角比,为讨论等腰三角形BPQ 作铺垫. 2.设交点式求抛物线的解析式比较简便.3.第(3)题连结AE 、AF 容易看到AM 是直角三角形EAF 斜边上的高.4.第(4)题的△PBQ 中,∠B 是确定的,夹∠B 的两条边可以用含t 的式子表示.分三种情况讨论等腰三角形.图文解析(1)直线BC 的解析式为31542y x =-. (2)因为抛物线与x 轴交于O 、B (10, 0)两点,设y =ax (x -10).代入点C 1824(,)55-,得241832()555a -=⨯⨯-.解得524a =. 所以2255255125(10)(5)2424122424y x x x x x =-=-=--. 抛物线的顶点为125(5,)24-.(3)如图2,因为EF 切⊙A 于M ,所以AM ⊥EF . 由AE =AE ,AO =AM ,可得Rt △AOE ≌Rt △AME . 所以∠1=∠2. 同理∠3=∠4.于是可得∠EAF =90°.所以∠5=∠1.由tan ∠5=tan ∠1,得MA MEMF MA=. 所以ME ·MF =MA 2,即mn =25.图2(4)在△BPQ 中,cos ∠B =45,BP =10-t ,BQ =t . 分三种情况讨论等腰三角形BPQ :①如图3,当BP =BQ 时,10-t =t .解得t =5.②如图4,当PB =PQ 时,1cos 2BQ BP B =∠.解方程14(10)25t t =-,得8013t =.③如图5,当QB =QP 时,1cos 2BP BQ B =∠.解方程14(10)25t t -=,得5013t =.图3 图4 图5考点伸展在第(3)题条件下,以EF 为直径的⊙G 与x 轴相切于点A .如图6,这是因为AG 既是直角三角形EAF 斜边上的中线,也是直角梯形EOBF 的中位线,因此圆心G到x轴的距离等于圆的半径,所以⊙G与x轴相切于点A.图6例 11 2014年湖南省邵阳市中考第26题在平面直角坐标系中,抛物线y=x2-(m+n)x+mn(m>n)与x轴相交于A、B两点(点A位于点B的右侧),与y轴相交于点C.(1)若m=2,n=1,求A、B两点的坐标;(2)若A、B两点分别位于y轴的两侧,C点坐标是(0,-1),求∠ACB的大小;(3)若m=2,△ABC是等腰三角形,求n的值.动感体验请打开几何画板文件名“14邵阳26”,点击屏幕左下方的按钮(2),拖动点A在x轴正半轴上运动,可以体验到,△ABC保持直角三角形的形状.点击屏幕左下方的按钮(3),拖动点B在x轴上运动,观察△ABC的顶点能否落在对边的垂直平分线上,可以体验到,等腰三角形ABC有4种情况.思路点拨1.抛物线的解析式可以化为交点式,用m,n表示点A、B、C的坐标.2.第(2)题判定直角三角形ABC,可以用勾股定理的逆定理,也可以用锐角的三角比.3.第(3)题讨论等腰三角形ABC,先把三边长(的平方)罗列出来,再分类解方程.图文解析(1)由y=x2-(m+n)x+mn=(x-m)(x-n),且m>n,点A位于点B的右侧,可知A(m, 0),B(n, 0).若m=2,n=1,那么A(2, 0),B(1, 0)..(2)如图1,由于C(0, mn),当点C的坐标是(0,-1),mn=-1,OC=1.若A、B两点分别位于y轴的两侧,那么OA·OB=m(-n)=-mn=1.所以OC2=OA·OB.所以OC OB OA OC.所以tan∠1=tan∠2.所以∠1=∠2.又因为∠1与∠3互余,所以∠2与∠3互余.所以∠ACB=90°.图1 图2 图3 (3)在△ABC中,已知A(2, 0),B(n, 0),C(0, 2n).讨论等腰三角形ABC,用代数法解比较方便:由两点间的距离公式,得AB2=(n-2)2,BC2=5n2,AC2=4+4n2.①当AB=AC时,解方程(n-2)2=4+4n2,得43n=-(如图2).。
