第二章运算方法和运算器习题答案
计算机原理第二章运算方法和运算器

算术移位时,符号位保持不变,其 余位进行相应移动。算术左移相当 于乘以2,算术右移相当于除以2并 向下取整。
乘法运算方法
原码一位乘法
将被乘数和乘数均取原码,从乘数的最低位开始逐位判断,若为1则加上被乘 数的原码,若为0则不变。重复此过程直至乘数所有位均判断完毕。
补码一位乘法
将被乘数和乘数均取补码,从乘数的最低位开始逐位判断,若为1则加上被乘数 的补码并考虑进位,若为0则只考虑进位。重复此过程直至乘数所有位均判断完 毕。
节能技术
采用节能技术,如动态电压调整、睡眠模式等, 以降低运算器在空闲或低负载时的功耗。
06
计算机中数的表示和运算 方法扩展
大数表示和运算方法
大数的概念
超出计算机基本数据类型表示范围的整数或浮点数。
大数表示方法
采用多精度表示法,将大数拆分成多个基本数据类型的数进行表示 和存储。
大数运算方法
设计相应的大数运算算法,如大数加法、减法、乘法、除法等。
转换方法
根据机器数的表示方法,通过相应的运算将其转换为真值。
定点数与浮点数
定点数
表示范围与精度
小数点位置固定的数,可表示整数或 小数。
定点数表示范围有限,精度较高;浮 点数表示范围大,但精度相对较低。
浮点数
小数点位置可变的数,由阶码和尾数 两部分组成,可表示大范围的数值。
02
基本运算方法
定点加减法运算
运算流水线设计
在算术逻辑单元(ALU)中采用流 水线技术,将复杂的运算过程分解 为多个简单的运算步骤,提高运算 速度。
超标量流水线设计
在一个周期内同时发射多条指令, 通过多个功能部件并行执行,进一 步提高处理器的性能。
计算机组成原理 第五课

例:X0X1X2X3C =10110 (奇) X0'X1'X2'X3' C' =11110 由X0'X1'X2'X3'生成C*=
(1 ⊕ 1) ⊕ (1 ⊕ 1)
=1,则
C*⊕C' =1⊕0=1 —— 出错
(4) 优缺点
优点:简单易行,省器件. 缺点:只能发现奇数位错,无纠错能力.
2.1.4 数据校验码
1. 数据校验码:
用以发现或同时能得出错误位置特征的数据编码. 计算机中的错误类型: ; (1)固定性错误---元器件故障; ) (2)突发性错误---噪声干扰. )
2. 检错码--奇偶校验码 (1) 定义
使包括一位校验位在内的数据代码,"1"的个数总是奇 (或偶)数个为合法数据的编码.
2. 补码定点减法
(1)补码减法的规则: 推论: [X-Y]补= [X+(-Y)]补 =[X]补+[-Y]补 已知 [Y]补 ,那么 [-Y]补=? (2)求补: 由[Y]补求[-Y]补,称为对Y求补. (3)求补规则 : 不管真值Y时正数还是负数,求补的方法都是将[Y]补 可见:求补时,从[Y]补的最低位开始向高位扫描,见到第 连同符号位在内各位变反, 末位加1. 一个"1",包括这个"1"的各位不变,其余各位变反 例如:[y]补=1.1010,则环冗余校验码(CRC) CRC
n位数据位和r位校验位只有1位出错,共有n+r种情况, (1) 纠正一位错所需的校验码位数r 加上没有错的一种情况,共有n+r+1种情况,而r位二进 设待编码的信息有效位数为n,则r应满足: 制的编码数为2r,因此 2r≥n+r+1 即 r>log2n n r 1 2 2~4 3 5~11 12~26 4 5
计算机组成原理.各章例题
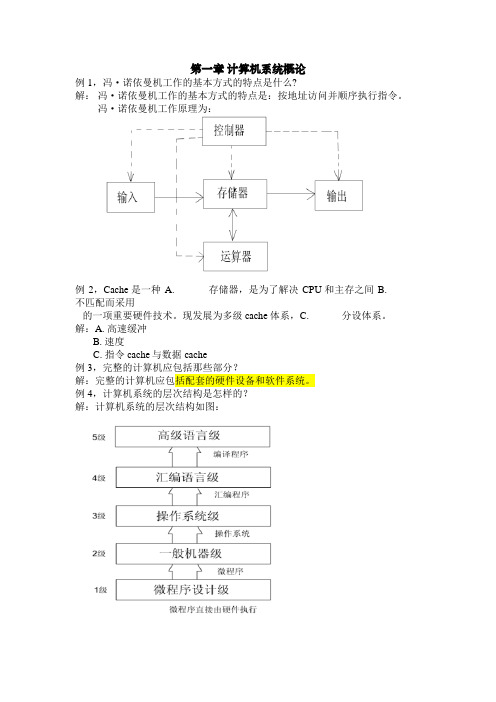
第一章计算机系统概论例1,冯·诺依曼机工作的基本方式的特点是什么?解:冯·诺依曼机工作的基本方式的特点是:按地址访问并顺序执行指令。
冯·诺依曼机工作原理为:例2,Cache是一种A. ______存储器,是为了解决CPU和主存之间B. ______不匹配而采用的一项重要硬件技术。
现发展为多级cache体系,C. ______分设体系。
解:A. 高速缓冲B. 速度C. 指令cache与数据cache例3,完整的计算机应包括那些部分?解:完整的计算机应包括配套的硬件设备和软件系统。
例4,计算机系统的层次结构是怎样的?解:计算机系统的层次结构如图:第二章 运算方法和运算器例 1.设机器字长32位,定点表示,尾数31位,数符1位,问:(1)定点原码整数表示时,最大正数是多少?最大负数是多少? (2)定点原码小数表示时,最大正数是多少?最大负数是多少? 解:(1最大正数:数值 = (231 – 1)10最大负数: 数值 = -(231 – 1)10 (2)定点原码小数表示: 最大正数值 = (1 – 231 )10最大负数值 = -(1–231 )10例2.已知 x = - 0.01111 ,y = +0.11001, 求 [ x ]补 ,[ -x ]补 ,[ y ]补 ,[ -y ]补,x + y = ? ,x – y = ?解:[ x ]原 = 1.01111 [ x ]补 = 1.10001 所以 :[ -x ]补 = 0.01111[ y ]原 = 0.11001 [ y ]补 = 0.11001 所以 :[ -y ]补 = 1.00111 [ x ]补 11.10001 [ x ]补 11.10001 + [ y ]补 00.11001 + [ -y ]补 11.00111 [ x + y ]补 00.01010 [ x - y ]补 10.11000所以: x + y = +0.01010 因为符号位相异,结果发生溢出例3.设有两个浮点数 N 1 = 2j1 × S 1 , N 2 = 2j2 × S 2 ,其中阶码2位,阶符1位,尾数四位,数符一位。
第二章 计算方法和运算器(十一)

第3位的进位输出(即整个4位运算进位输出)公式为
Cn+4=Y3+X3Cn+3=Y3+Y2X3+Y1X2X3+Y0X1X2X3+X0X1X2X3Cn
设
G=Y3+Y2X3+Y1X2X3+Y0X1X2X3
P=X0X1X2X3
则
Cn+4=G+PCn
图2-15 ALU的逻辑结构原理图
控制参数S0,S1,S2,S3分别控制输入Ai和Bi,产生Xi和Yi的函数。其中Yi是受S0,S1控制的Ai和Bi的组合函数,而Xi是受S2,S3控制的Ai和Bi的组合函数,其函数关系如表2-4所示。
表2-4Xi、Yi与控制参数和输入量的关系
S0S1
Yi
S2S3
Xi
讲授法、演示法、实践操作法
教学手段
多媒体教学
教学内容:
第二章计算方法和运算器(十一)
我们曾介绍由一位全加器(FA)构成的行波进位加法器,它可实现补码数的加法运算和减法运算。但是这种加法/减法器存在两个问题:一是由于串行进位,它的运算时间很长。假如加法器由n位全加器构成,每一位的进位延迟时间为20ns,那么最坏情况下,进位信号从最低位传递到最高位而最后输出稳定,至少需要n×20ns,这在高速计算中显然是不利的。二就是行波进位加法器本身来说,它只能完成加法和减法两种操作而不能完成逻辑操作。为此,本节我们先介绍多功能算术/逻辑运算单元(ALU),它不仅具有多种算术运算和逻辑运算的功能,而且具有先行进位逻辑,从而能实现高速运算。
根据以上表达式,用TTL器件实现的成组先行进位部件74182的逻辑电路图如图2-17所示。其中G*称为成组进位发生输出,P*称为成组进位传送输出。
图2-17成组先行进位部件74182的逻辑电路图
华南理工2017【计算机组成原理】随堂练习

9.设寄存器内容为11111111,若它等于+127,则机器码为()表示。
A、原码B、补码C、反码D、移码
参考答案:D
10.8位原码能表示的不同数据有()个。
A、15 B、16 C、255 D、256
参考答案:C
11.下列关于奇偶校验码错误的描述是()。
A、只能发现奇数位错B、无纠错能力
参考答案:C
4.在机器数的四种表示方法中,()对0的表示有两种形式。
A、原码和反码B、原码和补码C、反码和补码D、补码和移码
参考答案:A
5.n位定点补码表示的最大值是()。
A、2的n次方B、2的n次方-1 C、2的n-1次方D、2的n-1次方再-1
参考答案:B
6.将用8位二进制补码表示的十进制数-121,扩展成16位二进制补码,结果用十六进制表示为()。
参考答案:B
3.在指令格式中采用扩展码设计方案是为了()。
A、减少指令字长度B、增加指令字长度C、保持指令字长度不变而增加指令操作的数量
D、保持指令字长度不变而增加寻址空间
参考答案:C
4.某计算机存储器按字(16位)编址,每取出一条指令后PC值自动加1,说明其指令长度是()。
A、1个字节B、2个字节C、3个字节D、4个字节
A、原码B、补码和移码C、补码D、补码和反码
参考答案:B
2.二进制数-101101B的补码是()。
A、11001011B B、11010011B C、11010110B D、11110111B
参考答案:B
3.在补码表示的机器中若寄存器A中存放数9EH,经过一次()运算它可以变为CFH。
A、算术左移B、逻辑左移C、算术右移D、逻辑右移
《计算机组成原理》白中英第三版课后答案

第一章计算机系统概论习题参考答案1.比较数字计算机和模拟计算机的特点。
解: 模拟计算机的特点: 数值由连续量来表示, 运算过程是连续的;数字计算机的特点: 数值由数字量( 离散量) 来表示, 运算按位进行。
两者主要区别见P1 表1.1。
2.数字计算机如何分类? 分类的依据是什么?解: 分类: 数字计算机分为专用计算机和通用计算机。
通用计算机又分为巨型机、大型机、中型机、小型机、微型机和单片机六类。
分类依据: 专用和通用是根据计算机的效率、速度、价格、运行的经济性和适应性来划分的。
通用机的分类依据主要是体积、简易性、功率损耗、性能指标、数据存储容量、指令系统规模和机器价格等因素。
3.数字计算机有那些主要应用?( 略)4.冯. 诺依曼型计算机的主要设计思想是什么? 它包括哪些主要组成部分?课后答案网解: 冯. 诺依曼型计算机的主要设计思想是: 存储程序和程序控制。
存储程序: 将解题的程序( 指令序列) 存放到存储器中;程序控制: 控制器顺序执行存储的程序, 按指令功能控制全机协调地完成运算任务。
主要组成部分有: 控制器、运算器、存储器、输入设备、输出设备。
5.什么是存储容量? 什么是单元地址? 什么是数据字? 什么是指令字?解: 存储容量: 指存储器能够容纳的二进制信息的数量, 一般见单位KB、 MB、 GB来度量, 存储容.com量越大, 表示计算机所能存储的信息量越多, 反映了计算机存储空间的大小。
单元地址: 单元地址简称地址, 在存储器中每个存储单元都有唯一的地址编号, 称为单元地址。
数据字: 若某计算机字是运算操作的对象即代表要处理的数据, 则称数据字。
指令字: 若某计算机字代表一条指令或指令的一部分, 则称指令字。
6.什么是指令? 什么是程序?解: 指令: 计算机所执行的每一个基本的操作。
程序: 解算某一问题的一串指令序列称为该问题的计算程序, 简称程序。
7.指令和数据均存放在内存中, 计算机如何区分它们是指令还是数据?解: 一般来讲, 在取指周期中从存储器读出的信息即指令信息; 而在执行周期中从存储器中读出的信息即为数据信息。
计算机组成原理第一,二章经典习题整理

经典习题整理第一章计算机系统概论一.填空题。
1.存储______并按______顺序执行,这是______型计算机的工作原理。
解析:计算机的硬件系统是根据冯.诺依曼计算机体系结构的思想设计的,采用了存取程序的设计思想,存储程序并按地址顺序执行,是冯.诺依曼型计算机的工作原理。
2.计算机中有在流动:一股是,即操作命令,其发源地是,它分散流向各个部件;另一股是,它受的控制,从一个部件流向另一个部件,边流动边加工处理。
解析:计算机中有两股信息在流动:一股是控制信息,即操作命令,其发源地是控制器,它分散流向各个部件;另一股是数据信息,它受控制信息的控制,从一个部件流向另一个部件,边流动边加工处理。
3.程序设计语言一般可分为三类:,,。
解析:程序设计语言一般可分为三类:机器语言,汇编语言,高级语言。
4.操作系统最早出现在第代计算机。
解析:第三代计算机的主要特点:用集成电路代替了分立元件,用半导体存储器取代了磁芯存储器;在软件方面,操作系统日益成熟。
5.多媒体CPU是带有技术的处理器,它是一种技术,特别适用于处理。
解析:多媒体PC机是指具有多媒体功能的PC机。
其CPU 带有MMX技术的处理器,它是一种多媒体拓展结构技术,特别适用于图像数据处理,它以新一代奔腾CPU为代表,极大地提高了在多媒体和通信应用方面的功能。
二.选择题。
( D )1.完整的计算机应包括______。
A 运算器、存储器、控制器。
B 外部设备和主机。
C 主机和实用程序。
D 配套的硬件设备和软件系统。
( C )2.至今为止,计算机中的所有信息仍以二进制方式表示的理由是______。
A.节约元件 B 运算速度快C 物理器件的性能决定D 信息处理方便( D )3.我国在______年研制成功了第一台电子数字计算机,第一台晶体管数字计算机于______年完成。
A 1946,1958B 1950,1968C 1958,1961D 1959,1965(C )4.主机中能对指令进行译码的部件是。
经典:计算机组成原理-第2章-运算方法和运算器

第二章:运算方法和运算器
2.1 数据与文字的表示方法 2.2 定点加法、减法运算 2.3 定点乘法运算 2.4 定点除法运算 2.5 定点运算器的组成 2.6 浮点运算方法和浮点运算器
其中尾数域所表示的值是1.M。因为规格化的浮点数的尾数域最
左位(最高有效位)总是1。故这一位经常不予存储,而认为隐藏
在小数点的左边。
64位的浮点数中符号位1位,阶码域11位,尾数域52位,指数偏
移值是1023。因此规格化的64位浮点数x的真值为:
x=(-1)s ×(1.M) × 2E-1023 e=E-1023
[X]反=1.x1x2...xn 对于0,有[+0]反=[-0]反之分:
[+0]反=0.00...0
[-0]反=1.11...1
我们比较反码与补码的公式
[X]反=2-2-n+X
[X]补=2+X
可得到 [X]补=[X]反+2-n
8
若要一个负数变补码,其方法是符号位置1,其余各位0变1,1变 0,然后在最末位(2-n)上加1。
10100.10011=1.010010011*24 e=4 于是得到:S=0,E=4+127=131=10000011, M=010010011 最后得到32位浮点数的二进制存储格式为: 0100 0001 1010 0100 1100 0000 0000 0000=(41A4C000)164
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4. 将下列十进制数表示成浮点规格化数,阶码3位,用补码表示;尾数9位,用补码表示。
(1) 27/64
(2) -27/64
解:(1)27/64=11011B×=0.011011B=0.11011B×
浮点规格化数 : 1111 0110110000
(2) -27/64= -11011B×= -0.011011B= -0.11011B×
浮点规格化数 : 1111 1001010000
5. 已知X和Y, 用变形补码计算X+Y, 同时指出运算结果是否溢出。
(1)X=0.11011 Y=0.00011
(2)X= 0.11011 Y= -0.10101
(3)X=-0.10110 Y=-0.00001
解:(1)先写出x和y的变形补码再计算它们的和
[x]补=00.11011 [y]补=00.00011
[x+y]补=[x]补+[y]补=00.11011+00.00011=0.11110
∴ x+y=0.1111B 无溢出。
(2)先写出x和y的变形补码再计算它们的和
[x]补=00.11011 [y]补=11.01011
[x+y]补=[x]补+[y]补=00.11011+11.01011=00.00110
∴ x+y=0.0011B 无溢出。
(3)先写出x和y的变形补码再计算它们的和
[x]补=11.01010 [y]补=11.11111
[x+y]补=[x]补+[y]补=11.01010+11.11111=11.01001
∴ x+y= -0.10111B 无溢出
6. 已知X和Y, 用变形补码计算X-Y, 同时指出运算结果是否溢出。
(1) X=0.11011 Y= -0.11111
(2) X=0.10111 Y=0.11011
(3) X=0.11011 Y=-0.10011
解:(1)先写出x和y的变形补码,再计算它们的差
[x]补=00.11011 [y]补=11.00001 [-y]补=00.11111
[x-y]补=[x]补+[-y]补=00.11011+00.11111=01.11010
∵运算结果双符号不相等∴ 为正溢出
X-Y=+1.1101B
(2)先写出x和y的变形补码,再计算它们的差
[x]补=00.10111 [y]补=00.11011 [-y]补=11.00101
[x-y]补=00.10111+11.00101=11.11100
∴ x-y= -0.001B 无溢出
7. 用原码阵列乘法器、补码阵列乘法器分别计算X×Y。
(1)X=0.11011 Y= -0.11111
(2)X=-0.11111 Y=-0.11011
解:(1)用原码阵列乘法器计算:
[x]原=0.11011 [y]原=1.00001
1 1 0 1 1
×) 1 1 1 1 1
----------------------------------
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
1 1 0 1 1
-----------------------------------------
1 1 0 1 0 0 0 1 0 1
[x×y]原=1.101000101
∴ x×y= -0.101000101
(2)用补码阵列乘法器计算:
[x]补=0.11011 [y]补=1.00001
(0) 1 1 0 1 1
×) (1)0 0 0 0 1
----------------------------------
(0) 1 1 0 1 1
(0) 0 0 0 0 0
(0)0 0 0 0 0
(0) 0 0 0 0 0
(0) 0 0 0 0 0
(0) (1) (1) (0) (1) (1)
-----------------------------------------
(1) 0 0 1 0 1 1 1 0 1 1
[x×y]补=1.0010111011
∴ x×y= -0.1101000101
9. 设阶为5位(包括2位阶符), 尾数为8位(包括2位数符), 阶码、尾数均用补码表示, 完成下列取值的[X+Y],[X-Y]运算:
(1)X=×0.100101 Y=×(-0.011110)
(2)X=×(-0.010110) Y=×(0.010110)
解:(1)将y规格化得:y=×(-0.111100)
[x]浮=1101,00.100101 [y]浮=1101,11.000100 [-y]浮=1101,00.111100
① 对阶
[ΔE]补=[Ex]补+[-Ey]补=1101+0011=0000
∴ E x=E y
② 尾数相加
相加相减
00.100101 00.100101
+ 11.000100 + 00.111100
------------ --------------
11.101001 01.100001
[x+y]浮=1101,11.101001 左规 [x+y]浮=1100,11.010010
∴ x+y=×(-0.101110)
[x-y]浮=1101,01.100001 右规 [x-y]浮=1110,00.1100001
舍入处理得 [x-y]浮=1110,00.110001
∴ x-y=×0.110001
(2) [x]浮=1011,11.101010 [y]浮=1100,00.010110 [-y]浮=1100,11.101010
① 对阶
[ΔE]补=[Ex]补+[-Ey]补=1011+0100=1111
∴ △E= -1 [x]浮=1100,11.110101(0)
② 尾数相加
相加相减
11.110101(0) 11.110101(0)
+ 00.010110 + 11.101010
-------------- ------------------
00.001011(0) 11.011111(0)
[x+y]浮=1100,00.001011(0) 左规 [x+y]浮=1010,00.1011000
∴ x+y=×0.1011B
[x-y]浮=1100,11.011111(0)
∴ x-y=×(-0.100001B)。
