2012届高三第一轮复习(文理数) 第六章《平面向量和复数》课件1
合集下载
新教材高考数学一轮复习第6章平面向量复数微专题进阶课5平面向量与“四心”课件新人教B版

垂心问题
已知点 O 是平面上的一定点,A,B,C 是平面上不共线的
三个点,动点
P
满足O→P=O→A+λ|A→BA→|cBos
→
+
AC →
B |AC|cos
,λ∈[0,+∞), C
则动点 P 的轨迹一定通过△ABC 的( )
A.重心
B.垂心
C.外心
D.内心
B
解析:由已知得A→P=λ|A→BA→|cBos
第六章 平面向量、复数
微专题进阶课(五) 平面向量与“四心”
在平面向量的应用中,用平面向量解决平面几何问题时,首先将 几何问题中的几何元素和几何关系用向量表示,然后选择适当的基底 向量,将相关向量表示为基向量的线性组合,把问题转化为基向量的 运算问题,最后将运算的结果再还原为几何关系.应用向量相关知识, 可以巧妙地解决三角形四心所具备的一些特定的性质.
由|A→F|=|C→F|可得(y-b)2=(-a)2+y2, 所以 y=b2- 2ba2,即 F0,b2- 2ba2. 连接 AE,CE,DE,又由重心公式, 得E→A+E→D+E→C=0, 则 Ea6,2b,
所以E→F=-a6,-2ab2 , 所以C→D·E→F=-32a×-a6+b2×-2ab2 =0, 所以C→D⊥E→F,即 EF⊥CD.
重心问题
已知 O 是△ABC 所在平面上的一点,若P→O=13(P→A+P→B+
P→C)(其中 P 为平面上任意一点), 则点 O 是△ABC 的( )
A.外心
B.内心
C.重心
D.垂心
C 解析:由已知得 3P→O=O→A-O→P+O→B-O→P+O→C-O→P, 所以3P→O+3O→P=O→A+O→B+O→C, 即O→A+O→B+O→C=0, 所以点O是△ABC的重心.
高考数学一轮复习第六章平面向量复数第1节平面向量的概念及线性运算课件

解析 如图,D→C=A→B=O→B-O→A=b-a,B→C=O→C-O→B=-O→A-O→B=-a-b. 答案 b-a -a-b
6.设 D,E 分别是△ABC 的边 AB,BC 上的点,AD=12AB,BE=23BC,若D→E=λ1A→B +λ2A→C(λ1,λ2 为实数),则 λ1=________,λ2=________.
一的实数 μ,使 λa+b=μ(a+2b)成立,即 λa+b=μa+2μb,则得λ1==μ2,μ,解得 λ=μ
=12.
答案
1 2
5.(必修 4P92A12 改编)已知▱ABCD 的对角线 AC 和 BD 相交于 O,且O→A=a,O→B=b, 则D→C=______,B→C=________(用 a,b 表示).
解析 (2)若b=0,则a与c不一定平行. (3)共线向量所在的直线可以重合,也可以平行,则A,B,C,D四点不一定在一条 直线上. 答案 (1)√ (2)× (3)× (4)√ (5)√
2.给出下列命题:①零向量的长度为零,方向是任意的;②若 a,b 都是单位向量,
则 a=b;③向量A→B与B→A相等.则所有正确命题的序号是( )
第1节 平面向量的概念及线性运算
考试要求 1.了解向量的实际背景;2.理解平面向量的概念,理解两个向量相等的 含义;3.理解向量的几何表示;4.掌握向量加法、减法的运算,并理解其几何意义; 5.掌握向量的数乘运算及其几何意义,理解两个向量共线的含义;6.了解向量线性 运算的性质及其几何意义.
1.向量的有关概念 名称
B.23A→B+13A→C
C.13A→B+23A→C
D.13A→B-23A→C
解析 因为B→D=12D→C.由向量的减法运算得 2(A→D-A→B)=A→C-A→D,则A→D=
6.设 D,E 分别是△ABC 的边 AB,BC 上的点,AD=12AB,BE=23BC,若D→E=λ1A→B +λ2A→C(λ1,λ2 为实数),则 λ1=________,λ2=________.
一的实数 μ,使 λa+b=μ(a+2b)成立,即 λa+b=μa+2μb,则得λ1==μ2,μ,解得 λ=μ
=12.
答案
1 2
5.(必修 4P92A12 改编)已知▱ABCD 的对角线 AC 和 BD 相交于 O,且O→A=a,O→B=b, 则D→C=______,B→C=________(用 a,b 表示).
解析 (2)若b=0,则a与c不一定平行. (3)共线向量所在的直线可以重合,也可以平行,则A,B,C,D四点不一定在一条 直线上. 答案 (1)√ (2)× (3)× (4)√ (5)√
2.给出下列命题:①零向量的长度为零,方向是任意的;②若 a,b 都是单位向量,
则 a=b;③向量A→B与B→A相等.则所有正确命题的序号是( )
第1节 平面向量的概念及线性运算
考试要求 1.了解向量的实际背景;2.理解平面向量的概念,理解两个向量相等的 含义;3.理解向量的几何表示;4.掌握向量加法、减法的运算,并理解其几何意义; 5.掌握向量的数乘运算及其几何意义,理解两个向量共线的含义;6.了解向量线性 运算的性质及其几何意义.
1.向量的有关概念 名称
B.23A→B+13A→C
C.13A→B+23A→C
D.13A→B-23A→C
解析 因为B→D=12D→C.由向量的减法运算得 2(A→D-A→B)=A→C-A→D,则A→D=
高考数学大一轮复习第六章平面向量与复数文
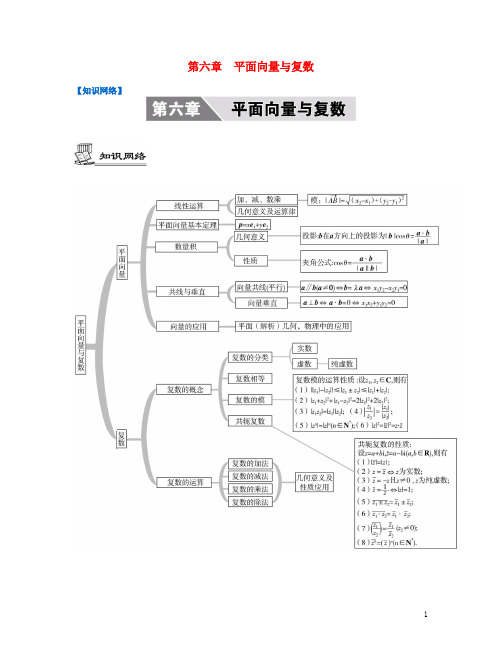
第六章 平面向量与复数
【知识网络】
【考情分析】
年份
试题
考点
备注
2013
第10题
平面向量基本定理,平面向量的数量积
运算求解
2014
第2,12题
复数的运算,向量的线性运算与数量积
向量的加、减、乘法
2015
第3,6题
复数的运算,向量的坐标运算
注重基本概念
【备考策略】
高考中以考查向量的概念与运算为主,其中共线向量、垂直向量的充要条件,向量的模与夹角的计算尤为重要.解答题会以向量为背景,与直线、圆、三角函数、不等式甚至与数列交汇出现综合题.应突出向量的工具性.
复数的考查以复数的基本概念、四则运算为主,一般以
【知识网络】
【考情分析】
年份
试题
考点
备注
2013
第10题
平面向量基本定理,平面向量的数量积
运算求解
2014
第2,12题
复数的运算,向量的线性运算与数量积
向量的加、减、乘法
2015
第3,6题
复数的运算,向量的坐标运算
注重基本概念
【备考策略】
高考中以考查向量的概念与运算为主,其中共线向量、垂直向量的充要条件,向量的模与夹角的计算尤为重要.解答题会以向量为背景,与直线、圆、三角函数、不等式甚至与数列交汇出现综合题.应突出向量的工具性.
复数的考查以复数的基本概念、四则运算为主,一般以
2025年高考数学一轮复习-第六章-平面向量、复数【课件】

(5)能用向量方法解决平面几何中平行、垂直、夹角、线段长度等问题. (6)掌握余弦定理、正弦ቤተ መጻሕፍቲ ባይዱ理可以解答的基本题型,能借助两个定理的变形进 行边角互化. (7)能用余弦定理、正弦定理解答三角形边、角、面积的复杂计算问题和实 际问题.
3.重视思想方法的应用 (1)数形结合思想:向量的几何表示,三角形法则,平行四边形法则使向量具备 “形”的特征,而向量的坐标表示和坐标运算又让向量具备“数”的特征.因此,运用数 形结合思想,可以将许多复杂的向量问题简单化. (2)化归与转化思想:用基底表示有关向量,将平面向量间的运算转化为基向量 间的运算;用余弦定理、正弦定理进行边角互化.
定理;
新高考Ⅱ卷·T18
2.能用余弦定理、正弦定理解决简单
2021年:新高考Ⅰ卷·T19
的实际问题.
新高考Ⅱ卷·T18
角度
考题 统计
考查内容
课程标准
高考真题
复数
2023年:新高考Ⅰ卷·T2
1.通过方程的解,认识复数;
新高考Ⅱ卷·T1
2.理解复数的代数表示及其几何意义,理 2022年:新高考Ⅰ卷·T2
概念的理解. (2)熟练掌握向量线性运算(加法、减法、数乘),数量积运算,并理解其几何意
义.
(3)理解向量共线的充要条件、平面向量基本定理,在此基础上体会向量坐标 表示的来龙去脉.
(4)了解向量方法推导余弦定理、正弦定理的过程,掌握两个定理及其常见变 形形式.
2.熟练掌握解决以下问题的方法规律 (1)从以下两个角度全面掌握平面向量的运算: ①几何角度:利用基底表示有关向量,转化为基向量的运算. ②坐标角度:建立平面直角坐标系,用坐标表示向量,转化为向量的坐标运算. (2)重视向量运算几何意义的理解和应用. (3)能用平面向量的线性运算解决用基底表示平面内任意向量、向量共线等 问题. (4)能用平面向量的数量积运算解决向量垂直、夹角、模等问题.
《高考调研》高三数学第一轮复习 第六章《平面向量和复数》课件6-3

→ =(1,2), (2)如图所示,在平行四边形 ABCD 中,AC → =(-3,2),则AD →· → =________. BD AC
【解析】 由于四边形 ABCD 为平行四边形,设 O 为 → =2OE → AC 与 BD 的交点,连结 O 点与 DC 的中点 E,则AD
→ → 1 AC BD 1 → → )=(-1,2),所以 AD →· → =-1 =2 + = (AC +BD AC 2 2 2 2
• 5.(2010·湖南)若非零向量a,b满足|a|= |b|,(2a+b)·b=0,则a与b的夹角为( ) • A.30° B.60° • C.120° D.150° • 答案 C
解析 (2a+b)· b=2a· b+b2=2|a|2cos〈a,b〉+a2=0 1 ⇒cos〈a,b〉=-2,所以 a,b 的夹角为 120° ,故选 C.
• • • • •
3.注意 ①两个向量的数量积是一个实数. ∴0·a=0(实数)而0·a=0 ②数量积不满足给合律(a·b)·c≠a·(b·c) ③a·b中的“·”不能省略.
• 1.(08·陕西卷)关于平面向量a,b,c,有下列三个命题: • ①若a·b=a·c,则b=c. • ②|a·b|=|a|·|b|⇔a∥b. • ③a⊥b⇔|a+b|=|a-b|; • ④|a|=|b|⇔|a·c|=|b·c|.
③当 a 与 b 的夹角为 30° 时, 3 a· b=|a||b|cos30° =2×5× 2 =5 3.
• • • •
探究1 (1)求平面向量数量积的步骤是: ①求a与b的夹角θ,θ∈[0°,180°]; ②分别求|a|和|b|; ③求数量积,即a·b=|a||b|cosθ,若知道 向量的坐标a=(x1,y1),b=(x2,y2),则求 数量积时用公式a·b=x1x2+y1y2计算. • (2)注意共线时θ=0°或180°,垂直时θ= 90°,三种特殊情况.
人教版高中总复习一轮数学精品课件 第6章 平面向量、复数 6.2 平面向量基本定理及向量的坐标表示

∵向量a+2b与2a-b平行,∴4(-2-m)=3(2m-1),
解得
1
m=-2,∴a+b=
3
- 2 ,3
.
3
- ,3
2
.
第二环节
关键能力形成
能力形成点1 平面向量基本定理的应用
例 1 (1)在▱ABCD 中,AC 与 BD 相交于点 O,E 是线段 OD 的中点,AE 的
延长线与 CD 相交于点 F.若 =a,=b,则 等于( C )
(3)坐标表示:a=(x,y)叫做向量a的坐标表示.
(4)特殊向量的坐标:i=(1,0),j=(0,1),0=(0,0).
4.平面向量线性运算的坐标表示
若向量a=(x1,y1),b=(x2,y2),则:
运算
加法
减法
向量坐
标公式
数乘向
量
文字描述
两个向量和的坐标分别等于这两个向
量相应坐标的和
两个向量差的坐标分别等于这两个向
3
3
3
2
2
1
1
1 1
= − = a- b,
6
6
6 6
1
1
1 1
2
1
∴ = + = a+ b+ a- b= a+ b,故选 C.
2
2
6 6
3
3
||
||
]
(2)设 e1,e2 是同一平面内不共线的两个向量,若=e1-λe2,=2e1+e2,
2
=3e1-e2,且 A,B,D 三点共线,则实数 λ 的值为
种形式,应视题目的具体条件而定,一般涉及坐标的应用(2).
《高考调研》高三数学第一轮复习 第六章《平面向量和复数》课件6-4

• 探究1 有向线段的定比分点坐标公式是解决有关共线问题的有 力工具,凡是与共线相联系的问题,可以考虑用这一公式来解. 用定比分点坐标公式求点的坐标时,首先要确定λ,此时一定要 分清有向线段的起点、终点和分点,尤其是要明确分点是内分点 还是外分点.若情况不定,应分类讨论,确定λ的值,一般有两 种思路:一是借助图形,数形结合求解;另一种是进行向量代数 运算,用定比分点的定义式确定λ的值.求点的坐标问题,也可 以用共线向量的充要条件求解,一般由两向量相等,建立方程组 ,解方程组即得所求点的坐标.
• 答案
22
• 命题立意 本题主要考查定比分点公式的运用和 向量的基本运算.
解析 运用定比分点公式分别求出点 E、F 的坐标为 → ,AF → 分别为(4,-1),(6,2).∴AE →· → =4×6 (5,1)、(7,4).AE AF -2=22. 失分警示 由于公式记忆不牢,出现计算上的失误.
1 7 ∴P 点坐标为( ,4)或(- ,8). 3 3 1→ → 方法 3:∵|AP|= |AB|, 3 1 → → 1 → → → → ∴AP=3(AP+PB)或AP=-3(AP+PB), 1→ → 1→ → 即AP=2PB或AP=-4PB, 1 1 → ∴点 P 分AB所成的比 λ=2或-4. (以下解法同方法二).
• 答案 A • 命题立意 本题考查线段的定比分点.
解析 如图,过点 P1 作 P1A⊥x 轴于 A,P2B⊥x 轴 → | P |P1A| 1P| → 于 B, 则点 P 分有向线段P1P2成比 λ=- =-|P B|= →2| 2 |PP 1 - . 3
2. 直角坐标平面内三点__. 若 E、 F 为线段 BC 的三等分点, 则AE AF
1→ → 方法 2:∵|AP|= |AB|,∴画出图形 3 1 1 → 由图可得,点 P 分AB所成的比 λ= 或- . 2 4 又 A(-1,6),B(3,0), 设 P(x,y),则由定比分点坐标公式得
高考数学一轮复习第6章平面向量复数1平面向量的概念及线性运算课件

(2)当a,b不共线时, 作=a,=b,则 a+b= ,如图①所示.根据三角形的
性质,有||a|-|b||<|a+b|<|a|+|b|.同理可证||a|-|b||<|a-b|<|a|+|b|.
(3)当a,b为非零向量且共线时,若向量a与b同向,则|a+b|=|a|+|b|(如图②
所示),|a-b|=||a|-|b||;若向量a,b反向,不妨设|a|>|b|,则|a+b|=|a|-|b|(如图③所
= ,
所以
1 = 2,
1
解得 λ=2.
.
第二环节
关键能力形成
能力形成点1
辨析平面向量的有关概念
例1 (1)对于非零向量a,b,“a+b=0”是“a∥b”的( A )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
若a+b=0,则a=-b,所以a∥b.
若a∥b,则a+b=0不一定成立,
1 1
A.2a+2b
1 1
C.- a- b
2 2
=
1
2
1 1
B.2a-2b
1 1
D.- a+ b
2 2
=
1
1 1
(b-a)=- a+ b,故选
2
2 2
D.
1
2
4.设向量a,b不平行,向量λa+b与a+2b平行,则实数λ=
由题意知,存在常数 t∈R,使 λa+b=t(a+2b).因为向量 a,b 不平行,
成比例等性质,把未知向量用已知向量表示出来.
性质,有||a|-|b||<|a+b|<|a|+|b|.同理可证||a|-|b||<|a-b|<|a|+|b|.
(3)当a,b为非零向量且共线时,若向量a与b同向,则|a+b|=|a|+|b|(如图②
所示),|a-b|=||a|-|b||;若向量a,b反向,不妨设|a|>|b|,则|a+b|=|a|-|b|(如图③所
= ,
所以
1 = 2,
1
解得 λ=2.
.
第二环节
关键能力形成
能力形成点1
辨析平面向量的有关概念
例1 (1)对于非零向量a,b,“a+b=0”是“a∥b”的( A )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
若a+b=0,则a=-b,所以a∥b.
若a∥b,则a+b=0不一定成立,
1 1
A.2a+2b
1 1
C.- a- b
2 2
=
1
2
1 1
B.2a-2b
1 1
D.- a+ b
2 2
=
1
1 1
(b-a)=- a+ b,故选
2
2 2
D.
1
2
4.设向量a,b不平行,向量λa+b与a+2b平行,则实数λ=
由题意知,存在常数 t∈R,使 λa+b=t(a+2b).因为向量 a,b 不平行,
成比例等性质,把未知向量用已知向量表示出来.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012 届高三第一轮复习(文理数)第六章《平面向
量和复数》课件1
1.①理解向量的概念、掌握向量的几何表示,了解共线向量的概念
②掌握向量的加法和减法
③掌握实数与向量的积,理解两个向量共线的充要条件
④了解平面向量的基本定理
2.①理解平面向量的坐标表示方法.
②掌握平面向量的和、差、实数与向量积的坐标运算,能利用向量的坐标运算解决问题.
③掌握平面向量平行的充要条件的坐标表示,并利用它解决向量平行(共线)的有关问题.
3.掌握平面向量的数量积及其几何意义,了解用平面向量的数量积可以处理有关长度、角度和垂直的问题,掌握向量垂直的充要条件.
4.掌握定比分点和中点坐标公式,并能熟练运用,掌握平移公式.
5.了解复数的有关概念及复数的代数表示和几何意义.
6.掌握复数代数形式的运算法则,能进行复数形式的加法、减法、乘法、除法运算.
一、向量的有关概念
1.向量的定义:既有又有的量叫做向量.
2.向量的长度:表示的的长度,即的大小叫做的长度或称为的模,的向量叫做零向量,记作0,的向量,叫做单位向量.大小方向
有向线段长度为0 长度等于1 个单位长度。
