物理化学第四章2
物理化学第四章-化学平衡

平衡 正向自发
ii (产物) ii (反应物) 逆向自发
自发变化的方向:反应总是从化学势较高的一边流向化 学势较低的一边。
1. 化学反应的限度
所有的化学反应既可以正向进行亦可以逆向进行, 且反应正向进行和逆向进行均有一定的程度,反应 物不会完全转化为产物。
典型例子:
H2(g)+I2(g)↔2HI C2H5OH(l)+CH3COOH(l)↔CH3COOC2H5+H2O
任意化学反应: rGm rGm RT ln Qa
rGm ii (产物) jj (反应物)
(化学反应的吉布斯自由能改变量)
rGm
i
i
(产物)
jj (反应物)
(化学反应的标准吉布斯自由能改变量)
1.rGm 是任意反应系统的吉布斯自由能变化
rGm 是任意反应系统的标准摩尔吉布斯自由能变化
rGm 指产物和反应物都处于标准态时,产物的吉布
斯函数与反应物的吉布斯函数总和之差,称为化学
反应的“标准摩尔Gibbs 自由能变化值”,只是温
度的函数。
平衡时Leabharlann gGhHa
A
b
B
r Gm
若上述反应在定温定压下进行,其中各分压是任意的而 不是平衡时的分压,此时反应的吉布斯函数变化为:
非平衡时
rGm gG hH (aA bB )
B
B
RT
ln( PB
/
P )
g[G
RT
ln(
pG
/
p
)]
h[
H
RT
ln(
pH
/
p
)]
a[
A
RT
ln(
物理化学 第4章化学平衡

当 B 0 时 K Kc Kn K y
1/31/2020
祝大家学习愉快,天天进步!
17/114
§4.2-3.有纯态凝聚相参加的理气反应 K
ΔrGm RTln K
J p
B (g)
pB p
(g)
νB(g)
K
B(g)
peq B(g) p
结论:化学反应方程中计量系数呈倍数关系,Δ r Gm
的值也呈倍数关系,而 K 值则呈指数的关系。
1/31/2020
祝大家学习愉快,天天进步!
15/114
§4.2-2.理想气体反应的 K K c K y Kn
气体的组成可用分压力,摩尔分数,浓度表 示,故平衡常数也有不同的表示方法.
K
B
2
(g)
CO
2
(g)
Δ G r m,2 RT lnK 2
(3) CO 2 (g) C(s) 2CO(g) Δ G r m,3 RT lnK3 例 4.5.1
因为: (3) = (1) 2(2)
pB p
B
e
pB yB p
K
B
pB p
B
e
B
yB p
p
B
e
B
y B B
e
B
p
p
B
Ky
p p
B
1/31/2020
祝大家学习愉快,天天进步!
16/114
§4.2—2.理想气体反应的 K K c K y Kn
物理化学中科大第四章溶液

即定温下是一常数;即若CO2溶于水的总浓度为m,则溶液中CO2分子状态的CO2浓度为: m = m(1-) (常数) 由亨利定律: P1= kmm = km m (1-) = [ km (1-) ]m = km m 式中的km也为常数,也可叫作Henry常数。
例1. CO2在水中能部分地与溶剂(水)化合形成“溶剂化物(H2CO3)”,H2CO3的电离度很小,电离常数k1= 4.3×10-7,计算时可忽略其电离部分浓度。 CO2 + H2O H2CO3 H+ + HCO3- (k1忽略) m(1-) 1 m 由
固态盐类通常是离子晶体,离子间的引力很大,只有用强极性的溶剂方能溶解,非极性溶剂不能溶解。这也说明为什么一般无机盐在水中均有一定的溶解度,而在有机溶剂的溶解度则大大降低。 上述定性规则也有不少例外,故欲知物质在一液体中的溶解度,最可靠而直接的方法还是用实际方法来测定。
温度与溶解度: 一般说来物质溶解于某一液体中时,往往有热效应,既产生吸热或放热现象,故物质的溶解度往往与温度有关: 气体溶于水多为放热,故温度升高时,气体的溶解度将减小; 固体在水中的溶解度一般随温度升高而增大(少数例外)。若固体的晶型在温度变化范围内不变,则溶解度随温度的变化曲线是光滑连续的;若在某温度点发生晶型转变,则在该温度处其溶解度会突变,溶解度—温度曲线不连续。
二、溶解现象及溶解度
以前人们认为溶解现象仅是一物理现象,现在已认识到溶液中各物质分子之间的化学相互作用对溶液性质的影响,对于稀溶液还建立了一系列定量的理论,这些理论使我们有可能根据溶液的组成来预测溶液的某些性质。
01
可是对浓溶液来说,由于互相作用的复杂性,尚未很好地解决此问题。例如,关于物质在某一液体中的溶解度问题,现在还没有找出肯定的规律,更没有理论来定量地预测。但在定性方面可有一些规律可循,如:
物理化学:第4章_多组分系统热力学_
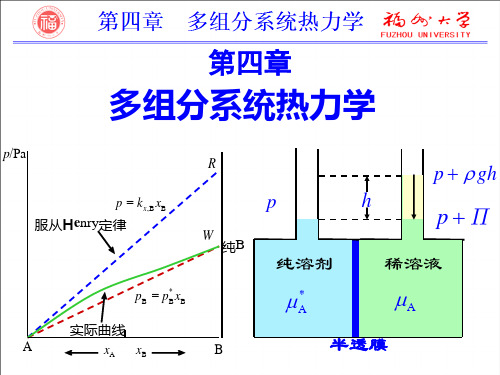
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
南京大学物理化学(第五版)04章_多组分系统热力学
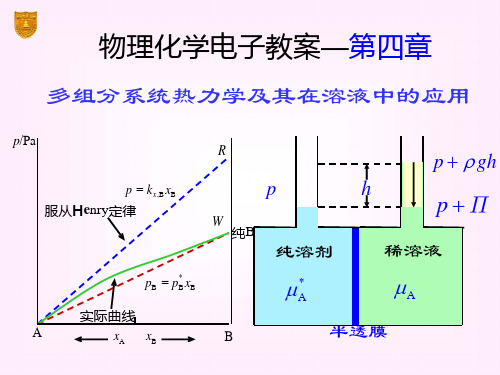
(
Gm p
)T
Vm
对多组分系统,把 Gm 换为 B ,则摩尔体积变为偏
摩尔体积 VB 。
化学势与温度的关系
(
B
T
)
p
,nB
,
nc
[ T
G ( ) ] T , p,nc p,nB ,nc nB
[ nB
G ( T ) p,nB ,nc ]T , p,nc
(S) [ nB ]T , p,nc
nk 0
dnk
k
n1Z1 n2 Z2 nk Zk nBZB B=1
偏摩尔量的加和公式
k
Z= nB ZB
B=1
这就是偏摩尔量的加和公式,说明系统的总 的容量性质等于各组分偏摩尔量的加和。
例如:系统只有两个组分,其物质的量和偏 摩尔体积分别为 n1,V1 和 n2 ,V2 ,则系统的总体积为:
(1)热力学能
设系统中有 1, 2,3, , k 个组分
所含的量分别为 n1, n2, , nk
U U (S,V , n1, n2, , nk )
化学势的定义
U U (S,V , n1, n2, , nk )
其全微分为
dU
U ( S )V ,nB dS
(
U V
)
S
,nB
dV
k U B1 ( nB )S ,V ,nc(cB) dnB
如果转移是在平衡条件下进行,则
dG 0 又
dnB dnB
所以 (B B )dnB 0
化学势在相平衡中的应用
(B B )dnB 0
因为 dnB 0 所以
B B
组分B在α,β两相中,达平衡的条件是该
大学物理化学--第四章

混合物(mixture):对系统中的各组分采用同样 的标准态和研究方法,系统中的各组分是平等的。
溶液(solution): 各组分区分为溶剂(solvent) 和溶质(solute ),并对二者采用不同的标准态和研 究方法;系统中的各组分是不平等的。
偏摩尔量
XB
(
X nB
)T
,
p
,
,下标必须是
nC
T
,
p。, nC
只有广度量才有偏摩尔量(质量除外)。
偏摩尔量是强度量。
偏摩尔量随温度、压力、组成(浓度)变化而变, 与系统的总量无关。
上一内容 下一内容 回主目录
返回
2020/8/23
§4.1 偏摩尔量
偏摩尔量的加和公式
X nB X B
B
它的含义是:在一定温度、压力下,一定组成混合
物理化学电子教案—第四章
多组分系统热力学
上一内容 下一内容 回主目录
返回
2020/8/23
第四章 多组分系统热力学
目录
§4.1 偏摩尔量 §4.2 化学势 §4.3 气体组分的化学势 §4.4 逸度及逸度因子 §4.5 拉乌尔定律和亨利定律 §4.6 理想液态混合物 §4.7 理想稀溶液
§4.8 活度及活度因子 §4.9 稀溶液的依数性
标准态 kb,B ( p p )
实际溶液 pB - bB 关系曲线
pB
O
b
上一内容 下一内容 回主目录
bB
返回
2020/8/23
4.7 理想稀溶液
理想稀溶液中溶质的化学势
B(溶 质)
0 B(溶 质)
物理化学试卷题库物化1000题第四章(2)

21.若5g 氨气通入1L水中,在常温常压下与蒸气共存,该体系的组分数K和自由度f为:A K=2,f=1B K=2,f=0C K=3,f=1D K=3,f=0BNH3(g)通入水中,有NH3(g)+H2O(l) = NH4OH(l)平衡存在,S=3,R=1,∴K=S–R–R’=3–1–0=2。
由于温度压力已定,相数为2(蒸气,溶液),按相律f=K–Φ=2–2=0。
22.I2在液态水和CCl4中分配达到平衡(无固体I2存在),此时体系的组分数K和自由度f为:A K=3,f=1B K=3,f=2C K=3,f=3D K=2,f=4C体系的物种数为3(I2,H2O,CCl4),但无化学平衡存在,∴K=S=3,体系存在二液相平衡,Φ=2,∴f=K–Φ+2=3–2+2=3。
23.体系中有Na+, Cl–,K+, NO3–,H2O(l)的平衡存在,则该体系的组分数K为:A K=2B K=3C K=4D K=5CS=5,可认为是Na+, Cl–,K+, NO3–,H2O(l),不存在化学平衡K=0,但有一浓度限制条件:正离子浓度=负离子浓度,R’=1,∴K=S–R–R’=5–0–1=4。
S=5,也可认为是NaCl,NaNO3,KCl,KNO3,H2O。
则有一化学平衡:NaCl+NaNO3=KCl +KNO3R=1,但R’=0,K=S–R–R’=5–1–0=4。
24.下列体系中,哪个自由度为2:A 298K时,H2O(l)= H2O(g)B S(方斜)= S ( l ) = S(g)C 乙醇与水的混合物D 一定量HI (g)分解对于A:K=1,f=1对于B:K=1,f=0对于C:K=2,f=3对于D:K=1,f=K– Φ+2=225.单组分物质的熔点:A 是常数B 仅是压力的函数C 同时是温度和压力的函数D 是温度压力及其他因素的函数B单组分,K=1,熔点处固液二相平衡,Φ=2,因此f=K–Φ+2=1,即熔点温度仅是压力的函数。
高等物理化学第四章

B T p ,nB ,nC
* B R ln xB T p ,nB ,nc
* m
S A,m S ( A) R ln xA SB,m S (B) R ln xB
* m
mix S S 混合后 S 混合前各组分 nB S B , m nB S ( B )
第四章: 物理化学扩展内容及应用
物理化学核心内容:化学热力学、化学动力学
扩展内容:溶液、相平衡、电化学、
界面现象、胶体化学
4.1:化学势和电化学势
封闭体系等温等压下Gibbs自由能判据: 单组分、或组成不变
组成可变的封闭体系: 相变、化学平衡 化学势 有非体积功存在 电化学、界面体系 电化学势 :
对环境做过,则 为正
由静电学原理
δ Wf n B
z B FΦ T , p ,nC
~ μ z FΦ μபைடு நூலகம்B
Φ=χ+ψ
三、化学势判据:Van’t hoff等温方程
dG SdT Vdp W f B dnB
B
dGT , p,W f 0 B dnB
* m
R nB ln xB
B
B
B
∵ xB< 1; ∴ ∆mixS >0
三、理想溶液的通性
(4): 混合Gibbs自由能
mix G RT nB ln xB
B
∆G = ∆H−T∆S
mix G mix H T mix S 0 T mix S
B
RT nB ln xB
化学势判据:∆mGT,p,Wf=0 ≤ 0 化学变化,相变化,μB ≤ 0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
10
例:在足够稀的溶液中:
n
i
n nA
W
i
W WA
ni ni ni / W A mi xi M A mi n n A n A / WA 1/ M A
(极稀溶液) …①
式中: MA(= WA / nA)为溶剂的摩尔质量(㎏/mol)。
Ci ni ni n n i i mi V W/ W WA
27
例 1 . CO2 在 水 中 能 部 分 地 与 溶 剂 ( 水 ) 化 合 形 成 “ 溶 剂 化 物 (H2CO3)”,H2CO3 的电离度很小,电离常数k1= 4.3×10-7,计算时可 忽略其电离部分浓度。
§1、引言
一、溶体
溶 液
两种以上的物质互相混合,其分散程度达到分子状态, 这样的分散体系就称为溶体。溶体是各部分的化学组成 和物理性质皆相同的均相体系。 溶体分类:按聚集状态分,溶体有: 气态溶体(混合气体) 液态溶体(溶液) 固态溶体(固溶体)
2
气态溶体: 即气体混合物,一般地不同的气体能以任意比例互相混合, 而且其分散程度达分子状态,没有相互溶解度的问题。在压 力不太大时,气体混合物可用理想气体定律来描述其行为, 并且可根据道尔顿分压定律描述气体混合物中各种气体的行 为,这些规律大家已熟知,故气态溶体不在本章中讨论了。
16
三、不挥发性溶质溶液
当溶质为不挥发性物质时,溶液的蒸气压即为溶剂的蒸气压。 可通过测定溶液与纯溶剂的蒸气压之差(PA -PA),并根
据Raoult定律求算此不挥发性溶质的摩尔分数,进而推得其
分子量:
0 PA PA n M W x1 M A m1 M A 1 A 1 0 WA WA M 1 PA
23
二、Henry定律的不同表达式
P1 = kx x1 Pi = kxi xi kxi取决于组分i与溶剂的作用。由于稀溶液,Pi足够小,可看 作理想气体。所以多组分溶质稀溶液的 P溶质 = Pi = kxi xi 在稀溶液中,由于 x 1 MAm1 (其中:km = kx MA)
因此溶剂的饱和蒸气压只与单位体积(或单位面积表 面层)中溶剂分子数成正比,而与溶质分子的性质无关, 即 PA ∝ xA, 比例系数为PA 。
15
当溶液的浓度变大后,溶质分 子对溶剂分子的作用比较显著, 此时溶剂的蒸气压不仅与溶剂的 浓度有关,还与溶质与溶剂的相 互作用,即溶质的浓度和性质有 关。例如,不同的溶质在相同的 较高浓度下对同一溶剂分子的影 响是不同的。 因此,在较高浓度下,溶剂的 蒸气压与其摩尔分数就不成正比 关系,即不遵守Raoult定律。
6
溶液中,溶质和溶剂之间也是相对的。习惯上气体 或固体溶于液体时,后者称为溶剂,前者称为溶质; 如果是液体溶于液体时,量多者为溶剂,量少者为溶 质。 本章着重讨论非电解质溶质的溶液(非电解溶 液)。至于电解质溶液,由于溶质溶解时部分或全部 解离成离子,而离子在溶液中的相互作用较复杂,不 在本章中讨论,放到下册电化学部分 “电解质溶液” 一章讨论。
4
(1)物质的结构和性质相近者,多半能互溶。如苯和甲苯互 溶;而甲苯和水就几乎完全不互溶。苯和甲苯为非极性液体, 水为极性液体。(相似相溶)。
(2)根据这一观点,醇类既有非极性官能团烃基,又有极 性官能团羟基,故其应当既可溶于水也可溶于甲苯。但随着 醇中碳链的增长,非极性官能团增大,它在水中的溶解度应随 之减小。事实上, C10以上的醇几乎不溶于水了。 (3)固态盐类通常是离子晶体,离子间的引力很大,只有 用强极性的溶剂方能溶解,非极性溶剂不能溶解。这也说明为 什么一般无机盐在水中均有一定的溶解度,而在有机溶剂的溶 解度则大大降低。 上述定性规则也有不少例外,故欲知物质在一液体中的溶 解度,最可靠而直接的方法还是用实际方法来测定。
0 W1 PA M1 ( 0 )MA W A PA PA
式中W1 、WA分别为配制溶液时溶质、溶剂的质量。
17
2003.04.14
本课内容提要
§4、亨利定律
一、亨利定律表述; 二、Henry定律的不同表达式 三、亨利定律的适用范围 一、理想溶液定义 二、理想溶液中组分的化学势(位) 三、理想溶液的热力学特性 四、理想溶液的蒸气压—组成(气、液相) 五、理想溶液与理想气体概念的比较
18
§5、理想溶液
§4、亨利定律
2003.04.14
1807年,Henry在研究一定温度下气体在溶剂中的溶 解度时,发现其溶解度与溶液液面上该气体的平衡压力 成正比; 后来进一步研究发现,这一规律对挥发性溶质(不仅 仅是气体)也适用。由此得到亨利定律:
一、亨利定律表述
定温下稀溶液中挥发性溶质的平衡分压(P1)与溶质 在溶液中的摩尔分数成正比,比例系数为某常数kx。 数学表述:
固溶体: 将在后面的多相平衡一章中讨论。 液态溶体: 本章着重讨论液态溶体——溶液,溶液的形成方式有三: 气体溶解在液体中:(气-液) 固体溶解在液体中:(固-液) 液体溶解在液体中:(液-液)
3
二、溶解现象及溶解度
以前人们认为溶解现象仅是一物理现象,现在已认识 到溶液中各物质分子之间的化学相互作用对溶液性质的 影响,对于稀溶液还建立了一系列定量的理论,这些理 论使我们有可能根据溶液的组成来预测溶液的某些性质。 可是对浓溶液来说,由于互相作用的复杂性,尚未 很好地解决此问题。例如,关于物质在某一液体中的溶 解度问题,现在还没有找出肯定的规律,更没有理论来 定量地预测。但在定性方面可有一些规律可循,如:
PA -PA = PA x1
对多溶质溶液:
o o PA PA PA ( xi (i A) ) i
推论:
稀溶液中溶剂蒸气压的降低值与溶质在溶液中的总 摩尔分数成正比。
14
二、拉乌尔定律适用范围
只有在稀溶液中,溶剂方能较准确地遵守Raoult定律。
解释:
在稀溶液中,溶剂分子之间的相互作用受溶质的影响 很小(∵溶质分子很稀疏地散布于大量溶剂中),所以溶 剂分子的周围环境与纯溶剂下几乎相同。
22
当溶液的浓度增大到一定程度时,溶质分子的周围 环境发生变化,即每个溶质分子周围不单纯只有大 量溶剂分子,部分还有溶质分子,并且随着溶液浓 度的改变而改变。 此时,每个溶质分子(在非全同环境下)逸出液相 的能力不全相同,并且随浓度变化而变化。因此其 蒸气压不仅仅只与溶液的浓度成正比关系,不再遵 守亨利定律。
分三种情况:
21
①当溶质、溶剂分子间的引力大于纯溶质分子本身之间 的引力时, kx P1 ②当溶质、溶剂分子间的引力小于纯溶质分子本身之间 的引力时,
kxP1
③当溶质分子与溶剂分子性质相近,即溶质、溶剂分子 的引力等于纯溶质分子间的引力时,
kx = P1
此时亨利定律就表现为类似拉乌尔形式: P1= P1 x1
一、拉乌尔定律表述
定温下,稀溶液中溶剂的饱和蒸气压(PA)正比于溶剂 在溶液中的摩尔分数xA,其比例系数即为该温下纯溶剂A的 饱和蒸气压(PA):
PA = PAxA
(稀溶液)
上式适用于单溶质或多溶质稀溶液。
13
对于单溶质(i =1)溶液(两组分溶液),上式可写为:
PA = PAxA = PA (1-x 1) = PA-PAx1
三、亨利定律的适用范围
1、稀溶液;
2、溶质在气相中和在溶液相中的分子状态必须相同。
26
如果溶质分子在溶液中与溶剂形成了化合物(或水 合物),而又发生了聚合或解离(电离),就不能简单 地套用亨利定律。 使用亨利定律时,溶液的浓度必须是与气相分子状 态相同的分子的浓度。 例如:SO2 在CHCl3 中,HCl在C6H6 中,H2S在H2O 中,CO2 在H2O中,通常压力下遵循亨利定律。但HCl 在水中就不遵守亨利定律(因HCl在水稀溶液中完全电 离成H+、Cl-),而SO2 在水中也不能较好的遵守亨利 定律(后面分析)。
8
二、质量(重量)摩尔浓度m i(mol/kg)(组分i的 质量摩尔浓度),溶质的摩尔数与溶剂的千克数之比:
ni ( mol ) mi W A ( k g)
(下标“A”表示溶剂)
三、体积摩尔浓度Ci(mol/dm3,mol/L,或mol/m3),
组分i的摩尔数与溶液的体积之比:
ni (mol ) Ci V (dm3 , 或m 3 )
20
定性解释:
稀溶液中,溶质分子极稀疏地散 布于大量溶剂分子中,每个溶质分子 周围几乎均被溶剂分子所包围(如 图):
溶质分子的周围环境均相同,因此其逸出液相的 能力(即蒸气压)正比于溶质的浓度。而相应的比例 系数 kx 将取决于溶质分子与周围溶剂分子的相互作用, 而不是P1(P1取决于纯溶质中溶质分子间的相互作 用)。
P1= kx x1
(稀溶液)
19
说明:
从形式上看,亨利定律与拉 乌尔定律相似,区别在于其 比例系数kx并非纯溶质在该 温度时的饱和蒸气压(P1), 即kx P1。 事实上,kx的数值在一定温 度下不仅与溶质的性质有关, 还与溶剂的性质有关,其数 值上既可大于P1,也可小于 P1。(请务必注意亨利定律 与拉乌尔定律两者比例系数 的差别)。
24
Hale Waihona Puke (稀溶液)对于多溶质稀溶液,组分i的分压:
代入 P1= kx x1 得:
P1= kxMAm1= kmm1
P1= kmm1
同理:由于
X1 MA
(稀溶液)
MA C1
C1
A
代入P1= kx x1 得:
