【原创】山东版2016届高三上学期第一次月考数学理 Word版含答案

合集下载

2016届高三上学期第一次月考数学（文）试题Word版含答案

2016届高三上学期第一次月考数学（文）试题Word版含答案2016届高三上学期第一次月考数学文试卷考试时间120分钟，满分150分一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合M ＝{x |x ≥0，x ∈R }，N ＝{x |x 2<1，x ∈R }，则M ∩N 等于( ) A ．[0,1] B ．[0,1) C ．(0,1]D ．(0,1)2．已知集合A ＝{1,2}，B ＝{1，a ，b }，则“a ＝2”是“A ?B ”的( ) A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．已知命题p ：所有有理数都是实数；命题q ：正数的对数都是负数，则下列命题中为真命题的是( ) A ．﹁p 或q B ．p 且q C ．﹁p 且﹁qD ．﹁p 或﹁q4．设函数f (x )＝x 2＋1，x ≤1，2x ，x >1，则f (f (3))等于( )A.15B ．3C.23D.1395．函数f (x )＝log 12(x 2－4)的单调递增区间是( )A ．(0，＋∞)B ．(－∞，0)C ．(2，＋∞)D ．(－∞，－2)6．已知函数f (x )为奇函数，且当x >0时，f (x )＝x 2＋1x ，则f (－1)等于( )A ．－2B ．0C ．1D ．27. 如果函数f (x )＝x 2－ax －3在区间(－∞，4]上单调递减，则实数a 满足的条件是( ) A ．a ≥8 B ．a ≤8 C ．a ≥4D ．a ≥－48. 函数f (x )＝a x －2＋1(a >0且a ≠1)的图像必经过点( ) A ．(0,1) B ．(1,1) C ．(2,0)D ．(2,2)9. 函数f (x )＝lg(|x |－1)的大致图像是( )10. 函数f (x )＝2x ＋3x 的零点所在的一个区间是( ) A ．(－2，－1) B ．(－1,0) C ．(0,1)D ．(1,2)11. 设f (x )＝x ln x ，若f ′(x 0)＝2，则x 0的值为( ) A ．e 2B ．eC.ln22D ．ln212. 函数f (x )的定义域是R ，f (0)＝2，对任意x ∈R ，f (x )＋f ′(x )>1，则不等式e x ·f (x )>e x ＋1的解集为( )．A ．{x |x >0}B ．{x |x <0}C ．{x |x <－1或x >1}D ．{x |x <－1或0<1}<="" p="">二、填空题：本大题共4小题，每题5分．13. 已知函数y ＝f (x )及其导函数y ＝f ′(x )的图像如图所示，则曲线y ＝f (x )在点P 处的切线方程是__________．14. 若函数f (x )＝x 2＋ax ＋b 的两个零点是－2和3，则不等式af (－2x )>0的解集是________． 15. 函数y ＝12x 2－ln x 的单调递减区间为________．16. 若方程4－x 2＝k (x －2)＋3有两个不等的实根，则k 的取值范围是________．三、解答题：解答应写出文字说明、证明过程或演算步骤17.(10分) 化简：(1)3131421413223b a b a ab b a -(a >0，b >0)；(2)(－278)23-＋(0.002)12-－10(5－2)－1＋(2－3)0.18．(12分)已知函数f (x )＝1a －1(a >0，x >0)，(1)求证(用单调性的定义证明)：f (x )在(0，＋∞)上是增函数； (2)若f (x )在[12，2]上的值域是[12，2]，求a 的值．19．（12分）已知定义在R 上的奇函数f (x )有最小正周期2，且当x ∈(0,1)时，f (x )＝2x4x ＋1.(1)求f (1)和f (－1)的值； (2)求f (x )在[－1,1]上的解析式．20．（12分）已知函数f (x )＝x 2＋2ax ＋3，x ∈[－4,6]． (1)当a ＝－2时，求f (x )的最值；(2)求实数a 的取值范围，使y ＝f (x )在区间[－4,6]上是单调函数；(3)当a ＝1时，求f (|x |)的单调区间． 21．（12分）已知函数f (x )＝x 3＋x －16. (1)求曲线y ＝f (x )在点(2，－6)处的切线的方程；(2)直线l 为曲线y ＝f (x )的切线，且经过原点，求直线l 的方程及切点坐标； 22．（12分）已知函数f (x )＝x 3－3ax －1，a ≠0. (1)求f (x )的单调区间；(2)若f (x )在x ＝－1处取得极值，直线y ＝m 与y ＝f (x )的图像有三个不同的交点，求m 的取值范围．2016届高三上学期第一次月考数学答题卡一、选择题（共12小题，每小题5分，共60分，每小题有一个正确答案）13、 14、15、 16、三、解答题17.(10分) 化简：(1)131421413223b a b a ab b a -(a >0，b >0)；(2)(－278)23-＋(0.002)12-－10(5－2)－1＋(2－3)0.18．(10分)已知函数f (x )＝1a －1x(a >0，x >0)，(1)求证(用单调性的定义证明)：f (x )在(0，＋∞)上是增函数； (2)若f (x )在[12，2]上的值域是[12，2]，求a 的值．19．（12分）已知定义在R 上的奇函数f (x )有最小正周期2，且当x ∈(0,1)时，f (x )＝2x4x ＋1.(1)求f (1)和f (－1)的值； (2)求f (x )在[－1,1]上的解析式．20．（12分）已知函数f(x)＝x3＋x－16.(1)求曲线y＝f(x)在点(2，－6)处的切线的方程；(2)直线l为曲线y＝f(x)的切线，且经过原点，求直线l的方程及切点坐标；21．（13分）已知函数f(x)＝x2＋2ax＋3，x∈[－4,6]．(1)当a＝－2时，求f(x)的最值；(2)求实数a的取值范围，使y＝f(x)在区间[－4,6]上是单调函数；(3)当a＝1时，求f(|x|)的单调区间．22．（13分）已知函数f(x)＝x3－3ax－1，a≠0.(1)求f(x)的单调区间；(2)若f(x)在x＝－1处取得极值，直线y＝m与y＝f(x)的图像有三个不同的交点，求m的取值范围．2016届高三上学期第一次月考数学文试卷参考答案1．B2.A3.D4.D5.D6.A7.A8.D9.B10.B11.B12.A13. x －y －2＝0 14. {x |－32<1}<="" p="">15. (0,1] 16. (512，34]17. 解 (1)原式＝121311113233211212633311233().a b a b abab ab a b+-++----==(2)原式＝(－278)23-＋(1500)12-－105－2＋1＝(－827)23＋50012－10(5＋2)＋1＝49＋105－105－20＋1＝－1679. 18. (1)证明设x 2>x 1>0，则x 2－x 1>0，x 1x 2>0，∵f (x 2)－f (x 1)＝(1a －1x 2)－(1a －1x 1)＝1x 1－1x 2＝x 2－x 1x 1x 2>0，∴f (x 2)>f (x 1)，∴f (x )在(0，＋∞)上是增函数． (2)解∵f (x )在[12，2]上的值域是[12，2]，又f (x )在[12，2]上单调递增，∴f (12)＝12，f (2)＝2.易得a ＝25.19. 解(1)∵f (x )是周期为2的奇函数，∴f (1)＝f (1－2)＝f (－1)＝－f (1)，∴f (1)＝0，f (－1)＝0. (2)由题意知，f (0)＝0. 当x ∈(－1,0)时，－x ∈(0,1)．由f (x )是奇函数，∴f (x )＝－f (－x )＝－2－x4－x ＋1＝－2x4x ＋1，综上，在[－1, 1]上，f (x )＝2x4x ＋1，x ∈(0，1)，－2x 4x＋1，x ∈(－1，0)，0，x ∈{－1，0，1}.20．解 (1)当a ＝－2时，f (x )＝x 2－4x ＋3＝(x －2)2－1，∵x ∈[－4,6]，∴f (x )在[－4,2]上单调递减，在[2,6]上单调递增，∴f (x )的最小值是f (2)＝－1，又f (－4)＝35，f (6)＝15，故f (x )的最大值是35. (2)∵函数f (x )的图像开口向上，对称轴是x ＝－a ，∴要使f (x )在[－4,6]上是单调函数，应有－a ≤－4或－a ≥6，即a ≤－6或a ≥4. (3)当a ＝1时，f (x )＝x 2＋2x ＋3，∴f (|x |)＝x 2＋2|x |＋3，此时定义域为x ∈[－6,6]，且f (x )＝?x 2＋2x ＋3，x ∈(0，6]，x 2－2x ＋3，x ∈[－6，0]，∴f (|x |)的单调递增区间是(0, 6]，单调递减区间是[－6,0]．21.解 (1)可判定点(2，－6)在曲线y ＝f (x )上．∵f ′(x )＝(x 3＋x －16)′＝3x 2＋1.∴f ′(x )在点(2，－6)处的切线的斜率为k ＝f ′(2)＝13. ∴切线的方程为y ＝13(x －2)＋(－6)，即y ＝13x －32.(2)法一设切点为(x 0，y 0)，则直线l 的斜率为f ′(x 0)＝3x 20＋1，∴直线l 的方程为y ＝(3x 20＋1)(x －x 0)＋x 30＋x 0－16，又∵直线l 过点(0,0)，∴0＝(3x 20＋1)(－x 0)＋x 30＋x 0－16，整理得，x 30＝－8，∴x 0＝－2，∴y 0＝(－2)3＋(－2)－16＝－26，k ＝3×(－2)2＋1＝13. ∴直线l 的方程为y ＝13x ，切点坐标为(－2，－26.) 法二设直线l 的方程为y ＝kx ，切点为(x 0，y 0)，则k＝y0－0x0－0＝x30＋x0－16x0又∵k＝f′(x0)＝3x20＋1，∴x30＋x0－16x0＝3x2＋1，解之得x0＝－2，∴y0＝(－2) 3＋(－2)－16＝－26，k＝3×(－2)2＋1＝13.∴直线l的方程为y＝13x，切点坐标为(－2，－26)．22.解(1)f′(x)＝3x2－3a＝3(x2－a)，当a<0时，对x∈R，有f′(x)>0，∴当a<0时，f(x)的单调增区间为(－∞，＋∞)．当a>0时，由f′(x)>0，解得x<－a或x>a.由f′(x)<0，解得－a<x<a，< p="">∴当a>0时，f(x)的单调增区间为(－∞，－a)，(a，＋∞)，单调减区间为(－a，a)．(2)∵f(x)在x＝－1处取得极值，∴f′(－1)＝3×(－1)2－3a＝0，∴a＝1.∴f(x)＝x3－3x－1，f′(x)＝3x2－3，由f′(x)＝0，解得x1＝－1，x2＝1.由(1)中f(x)的单调性可知，f(x)在x＝－1处取得极大值f(－1)＝1，在x＝1处取得极小值f(1)＝－3.∵直线y＝m与函数y＝f(x)的图像有三个不同的交点，结合如图所示f(x)的图像可知：实数m的取值范围是(－3,1)．</x<a，<>。

山东省临沂市2016届高三上学期第一次月考数学试卷(理科) 含解析

2015-2016学年山东省临沂市高三（上）第一次月考数学试卷（理科）一、选择题（本大题包括10小题，每小题5分，共50分.每小题只有一个选项符合题意) 1．已知a，b，c∈R，命题“若a+b+c=3，则a2+b2+c2≥3"的否命题是（)A．若a+b+c≠3,则a2+b2+c2＜3 B．若a+b+c=3，则a2+b2+c2＜3C．若a+b+c≠3，则a2+b2+c2≥3 D．若a2+b2+c2≥3，则a+b+c=32．已知集合A=｛1，2,3,4，5｝，B=｛(x，y）｜x∈A，y∈A，x﹣y∈A}，则B中所含元素的个数为（)A．3 B．6 C．8 D．103．已知命题p：∀x∈R,2x＜3x;命题q：∃x∈R，x3=1﹣x2，则下列命题中为真命题的是(）A．p∧q B．￢p∧q C．p∧￢q D．￢p∧￢q4．若函数y=f(x）的定义域是[0，2]，则函数g（x）=的定义域是（）A．（0，1）B．[0，1）C．[0，1）∪（1，4］D．[0，1］5．若函数f（x)=,则f（log23)=（)A．3 B．4 C．16 D．246．已知函数f(x）是定义在R上的偶函数，且在区间［0，+∞)上单调递增，若实数a满足f（log2a）+f(a)≤2f（1）,则a的取值范围是（）A． B．［1，2]C． D．（0，2]7．直线y=kx+b与曲线y=ax2+2+lnx相切于点P（1，4），则b的值为(）A．3 B．1 C．﹣1 D．﹣38．若a＜b＜c,则函数f（x）=（x﹣a）（x﹣b)+（x﹣b）（x﹣c）+（x﹣c)（x﹣a）的两个零点分别位于区间（）A．(a,b）和（b,c）内B．(﹣∞，a）和（a,b）内C．（b，c）和（c，+∞）内D．（﹣∞,a）和（c，+∞）内9．函数y=的大致图象是（）A．B．C．D．10．定义在R上的奇函数f（x）满足：对任意的x1,x2∈（﹣∞，0）（x1≠x2），有．则有（)A．f（0.32）＜f（20.3)＜f（log25) B．C．D．二、填空题（本大题共5小题，每小题5分,共25分.把答案填写在答题纸的相应位置）11．函数y=的定义域为．12．若集合A=｛x｜2x+1＞0}，B=｛x|｜x﹣1｜＜2},则A∩B=．13．定义在R上的函数f（x）是增函数，则满足f(x)＜f（2x﹣3）的取值范围是．14．过点(1,0)作曲线y=e x的切线,则切线方程为．15．已知f（x)是定义在R上的奇函数,且当x＞0时f（x)=e x+a，若f(x）在R上是单调函数，则实数a的最小值是．三、解答题（本大题共6小题，共75分,解答应写出文字说明、证明过程或演算步骤.）16．已知集合A=｛x|3≤x＜7}，B=｛2＜x＜10｝,C=｛x｜5﹣a＜x＜a}．（1）求A∪B，（∁R A）∩B；（2）若C⊆(A∪B），求a的取值范围．17．已知命题p：函数y=log0.5（x2+2x+a）的值域为R，命题q：函数y=﹣（5﹣2a）x是R上的减函数．若p或q为真命题,p且q为假命题,则实数a的取值范围是什么？18．某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元）和Q(亿元）,它们与投资额t（亿元)的关系有经验公式P=,Q=t,今该公司将5亿元投资这两个项目，其中对甲项目投资x(亿元)，投资这两个项目所获得的总利润为y（亿元)．求：(1）y关于x的函数表达式：（2）总利润的最大值．19．已知函数f（x）=，x∈［1，+∞）．（1）当a=4时,求函数f(x)的最小值；（2)若对任意x∈[1，+∞），f（x）＞0恒成立，试求实数a的取值范围．20．设f（x）=+xlnx，g(x）=x3﹣x2﹣3．（1）当a=2时，求曲线y=f（x）在x=1处的切线的斜率；（2)如果存在x1，x2∈［0，2］，使得g(x1）﹣g（x2)≥M成立，求满足上述条件的最大整数M．21．时下，网校教学越来越受到广大学生的喜爱，它已经成为学生们课外学习的一种趋势，假设某网校的套题每日的销售量y（单位:千套）与销售价格x（单位：元/套)满足的关系式，其中2＜x＜6,m为常数．已知销售价格为4元/套时，每日可售出套题21千套．（1）求m的值；（2）假设网校的员工工资，办公等所有开销折合为每套题2元（只考虑销售出的套数），试确定销售价格x的值,使网校每日销售套题所获得的利润最大．（保留1位小数）2015—2016学年山东省临沂市高三（上）第一次月考数学试卷(理科)参考答案与试题解析一、选择题（本大题包括10小题,每小题5分,共50分。

山东省威海市2016届高三一月考试数学文试题Word版含答案

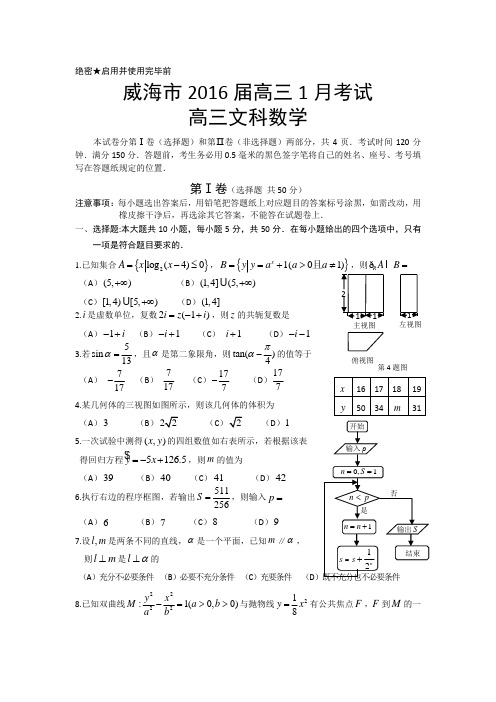
绝密★启用并使用完毕前威海市2016届高三1月考试高三文科数学本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共4页．考试时间120分钟．满分150分．答题前，考生务必用0.5毫米的黑色签字笔将自己的姓名、座号、考号填写在答题纸规定的位置．第Ⅰ卷（选择题共50分）注意事项：每小题选出答案后，用铅笔把答题纸上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，不能答在试题卷上．一、选择题:本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合{}2log (4)0A x x =-≤，{1(01)x By y a a a ==+>≠且，则R A B =ðI （A ）(5,)+∞ （B ）(1,4](5,)+∞U （C ）[1,4)[5,)+∞U （D ）(1,4]2.i 是虚数单位，复数2(1)i z i =-+，则z 的共轭复数是（A ）1i -+ （B ）1i -+ （C ） 1i + （D ）1i --3.若5sin 13α=，且α是第二象限角，则tan()4πα-的值等于（A ） 717- （B ） 717 （C ）177- （D ）1774.某几何体的三视图如图所示，则该几何体的体积为（A ）3 （B ）（C （D ）15.一次试验中测得(,)x y 的四组数值如右表所示，若根据该表得回归方程5126.5y x =-+$，则m 的值为（A ）39 （B ）40 （C ）41 （D ）426.执行右边的程序框图，若输出511256S =，则输入p =（A ）6 （B ）7 （C ）8 （D ）9 7.设,l m 是两条不同的直线，α是一个平面，已知m ∥α，则l m ⊥是l α⊥的（A ）充分不必要条件（B ）必要不充分条件（C ）充要条件（D 8.已知双曲线)0,0(1:2222>>=-b a b x a y M 与抛物线281x y =有公共焦点F ，F 到M 的一第4题图主视图左视图俯视图123456789101112131415161718192021222324252627282930313233343536124579101214161719212325262830323436.................................条渐近线的距离为3，则双曲线方程为（A ）1322=-x y （B ）1322=-y x （C ） 13722=-y x （D ）17322=-x y 9.已知()2,xf x =若(),2a b p f q f +==1(()())2r f a f b =+，其中0a b >>，则下列关系式中正确的是（A ）p r q << （B ）q p r << （C ）r p q << （D ）p q r << 10.已知直线:20l ax y -+=与圆034:22=+-+y y x M 的交点为A 、B ,点C 是圆M 上一动点，设点(0,1)P -，则||PA PB PC ++u u r u u r u u u r的最大值为（A ）12 （B ）10 （C ）9 （D ）8第Ⅱ卷（非选择题共100分）注意事项：1．请用0.5毫米的黑色签字笔将每题的答案填写在答题纸的指定位置．书写的答案如需改动，要先划掉原来的答案，然后再写上新答案．2．不在指定答题位置答题或超出答题区域书写的答案无效．在试题卷上答题无效．二、填空题:本大题共5小题，每小题5分，共25分.11.设(3,2),(1,)a b k ==-r r，若a r 与2a b +r r 共线，则k =___________.12.若函数22()log ()f x x ax =-+的图象过点(1,2)，则函数()f x 的值域为___________.13.设变量,x y 满足约束条件023,46x y x y x y -≤⎧⎪+≤⎨⎪-≥-⎩则22x yz -=的取值范围为_________.14.以下四个命题：①0,x R ∃∈使20ln(1)0x +<；②若()x k k Z π≠∈，则1sin 2sin x x+≥ ；③若命题“p ⌝”与“p 或q ”都是真命题，则命题q 一定是真命题； ④函数32xy x e =+在1x =处的切线过(0,2)-点.其中真命题的序号是（把你认为真命题的序号都填上）.15.把正整数排列成如图甲所示三角形数阵，然后擦去偶数行中的奇数和奇数行中的偶数，得到如图乙所示三角形数阵，设ij a 为图乙三角形数阵中第i 行第j 个数，若2015=mn a ，则实数对),(n m 为_____________.频率组距三、解答题:本大题共6小题，共75分．解答应写出文字说明，证明过程或演算步骤．16.（本小题满分12分）已知向量(cos ,sin )m A B =u r ，(cos ,sin )n B A =-r，cos 2m n C ⋅=-u r r，且,,A B C 分别为ABC ∆的三边,,a b c 所对的角.（Ⅰ）求角C 的大小；（Ⅱ）若2a b c +=，且 ABC ∆的面积为c 边的长.17.（本小题满分12分）某校对该校的1000名教师的年龄进行统计分析，年龄的频率分布直方图如图所示.规定年龄在[25,40)的为青年教师，年龄在[40,50)为中年教师，年龄在[50,60)为老年教师.（Ⅰ）求年龄在[30,35)、[40,45)的教师人数；（Ⅱ）现用分层抽样的方法从中、青年教师中抽取18人进行课堂展示，求抽到年龄在[35,40)的人数；（Ⅲ）在（Ⅱ）中抽取的中年教师中，随机选取2名教师进行总结交流，求抽取的中年教师中甲、乙至少有一名作总结交流的概率.18.（本小题满分12分）等比数列{}n a 满足624,a a a =⋅且2a 为12a 与312a 的等差中项．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设1(1)(1)n n n n a b a a +=--，n T 为{}n b 的前n 项和，求使20152016n T >成立时n 的最小值.19.（本小题满分12分）已知四棱台1111ABCD A B C D -的上下底面分别是边长为2和4的正方形，14AA =且1AA ⊥底面ABCD ，点P 为1DD 的中点，Q 为BC 边上一点. （Ⅰ）若PQ ∥面11A ABB ，求PQ 的长；（Ⅱ）求证：1AB ⊥面PBC .20.（本小题满分13分）设函数21()2ln 2f x x mx nx =--.A BCA 1B 1DC 1D 1 PQ（Ⅰ）若1,3m n =-=，求函数()y f x =的单调区间；（Ⅱ）若2x =是()f x 的极大值点，求m 的取值范围；（Ⅲ）在（Ⅱ）的条件下，试讨论()y f x =零点的个数．21.（本小题满分14分）已知椭圆2222:1(0)x y E a b a b+=>>，点(0,1)P在短轴CD 上，且1PC PD ⋅=-uu u r uu u r.（Ⅰ）求椭圆E 的方程；（Ⅱ）过点P 的直线l 和椭圆E 交于,A B 两点.（ⅰ）若12PB AP =uu r uu u r，求直线l 的方程；（ⅱ）已知点(0,2)Q ，证明对于任意直线l ，||||||||QA PA QB PB =恒成立.高三文科数学试题参考答案一、选择题B C C A C , C B A D B 二、填空题11. 23- ; 12.225(,log ]4-∞ ; 13. 1[,4]32 ; 14.③④ ; 15. (45,40)三、解答题16.（本小题满分12分）解：（Ⅰ） cos cos sin sin cos()cos cos2m n A B A B A B C C ⋅=-=+=-=-u r r------2分∴cos2cos C C -=-整理得22cos cos 10C C --=， ----------------------4分1cos 2C ∴=-或1， ----------------------5分∵(0,)C π∈， 23C π∴=. ----------------------6分（Ⅱ）112sin sin223ABC S ab C ab π∆=== 60ab ∴=. ------------------8分 22222cos ()2(1cos )c a b ab C a b ab C =+-=+-+ ----------------------10分将2a b c +=带入解得，220c =，∴c = ----------------------12分17．（本小题满分12分）解：（Ⅰ）年龄在[)40,45的教师人数为10000.045200⨯⨯=人； --------------------2分年龄在[)30,35的教师频率为1[1(0.070.040.03)5]0.152-++⨯=年龄在[)30,35的教师人数为10000.15150⨯=人； --------------------4分（Ⅱ）中青年教师共有1000(10.025)900⨯-⨯=,其中年龄在[)35,40中有10000.075350⨯⨯=人； --------------------6分设抽出的18人年龄在[)35,40中的有x 人则18:900:350x =，解得7x =； --------------------8分（Ⅲ）中年教师共350人，所以抽出的18人中，中年教师有7人，不妨设7名教师分别为甲、乙、A 、B 、C 、D 、E ，从7人中任意抽出两人的可能情况有（甲，乙）、（甲，A ）、（甲，B ）、（甲，C ）、（甲，D ）、（甲,E ）、（乙，A ）、（乙，B ）、（乙，C ）、（乙，D ）、（乙,E ）、（A,B ）、（A,C ）、（A,D ）、（A,E ）、（B,C ）、(B,D)、(B,E)、(C,D)、(C,E)、(D,E)共21种情况；其中甲乙至少有一人有11种情况 --------------------11分所以抽取的中年教师中甲、乙至少有一名作经验交流的概率为1121.--------------------12分 18.（本小题满分12分）解：（Ⅰ）设数列{}n a 的公比为q由624,a a a =⋅可得53111,a q a q a q =⋅解得1a q = ----------------------2分由2a 为12a 与312a 的等差中项，可得1321222a a a +=，解得2q =；---------------5分 ∴2,n n a n N *=∈ ----------------------6分（Ⅱ）11211(21)(21)2121n n n n n n b ++==----- ----------------------8分所以12231111111212121212121n n n T +=-+-++-------L 11121n +=-- --10分要使20152016n T >，即11111212016n +->--，∴122017n +>，111n +≥，∴n 的最小值为10 ----------------------12分19．（本小题满分12分）解：（Ⅰ）取1AA 中点M ，连结,BM PM∵,P M 分别为11,D D A A 的中点 ∴PM ∥AD ,∴PM ∥BC∴PMBC 四点共面 --------------------2分由PQ ∥面11A ABB ，可得PQ ∥BM∴PMBQ 为平行四边形，PQ =BM --------------------4分在Rt BAM ∆中，BM ==分（Ⅱ）1AA ⊥面ABCD ,BC ⊂面ABCD ，∴1AA ⊥BC ∵ABCD 是正方形，∴AB BC ⊥ ∴BC ⊥面11AA BB∵1AB ⊂面11AA BB ,∴1AB BC ⊥ --------------------8分通过ABM ∆≌11A B A ∆（过程略）,证得1AB BM ⊥ --------------4分 ∵BM BC B =I ,∴1AB ⊥面PBC ----------------5分 20.（本小题满分13分）解：（Ⅰ）由1,3m n =-=，得21()2ln 3,(0)2f x x x x x =+->2(1)(2)()3,(0)x x f x x x x x--'=+-=> ---------------------2分 ∴当2x >或01x <<()0f x '>；当12x <<时，()0f x '<.∴()f x 在(0,1),(2,)+∞单调递增，在(1,2)单调递减； ---------------------4分（Ⅱ）2(),(0)f x mx n x x'=-->，由已知可得(2)0f '=，整理得21m n += ---------------------5分 ∴2(2)(1)()21x mx f x mx m x x---'=-+-=---------------------6分当0m ≥时，10mx --<恒成立，当2x >时，()0f x '<，当02x <<时，()0f x '>()f x 在2x =处取得极大值，满足题意 ---------------------7分当0m <时，令()0f x '=，解得2x =或1x m=- 要使()f x 在2x =处取得极大值，只需12m ->，即102m -<< 综上所述，当12m >-时，()f x 在2x =处取得极大值. ---------------------9分（Ⅲ）由（Ⅱ）可得当0m ≥时，()f x 在(0,2)单调递增在(2,)+∞单调递减max ()(2)2ln 222f x f m ==+-QA B CA 1B 1DC 1D 1 PM当(2)0f >时，即1ln 2m >-时，()f x 有两个零点；当(2)0f =时，即1ln 2m =-时，()f x 有一个零点；当(2)0f <时，即01ln 2m ≤<-时，()f x 没有零点； ---------------------10分当102m -<<时，()f x 在1(0,2),(,)m -+∞单调递增，在1(2,)m-单调递减 (2)0f <，()f x 至多有一个零点 ---------------------11分法（1）：在1(,)m -+∞取一点2424m x m m-=-=，代入()f x 得 222214(21)422(4)2ln(4)(22)2ln(4)02m m f m m m m m m m---=--⋅+-⋅=-> ()f x 在1(,)m-+∞上必有一个零点. ---------------------12分法（2）：2l n y x =在(0,)+∞单调递增，21(12)2y mx m x =---是开口向上的二次函数，所以()f x 在1(,)m -+∞上必有正值，即()f x 在1(,)m-+∞上必有一个零点.综上所述：当1ln 2m >-时，()f x 有两个零点；当1ln 2m =-或102m -<<时，()f x 有一个零点；当01ln 2m ≤<-时，()f x 没有零点； ---------------------13分 21.（本小题满分14分）解：（Ⅰ）由题意，2c e a a ==⇒==，又(0,),(0,)C b D b -，2(1)(1)1,2PC PD b b b ∴⋅=---=-∴=u u u r u u u r，2a ∴= 所以椭圆E 的方程22142x y += ---------------------4分（Ⅱ）当直线l斜率不存在时，1,1PB AP ==u u r u u u r,12PB AP ≠uu r uu u r不符合题意，不存在这样的直线. ---------------------6分当直线l 斜率存在，设方程为11221,(,),(,)y kx A x y B x y =+，联立方程221421x y y kx ⎧+=⎪⎨⎪=+⎩，整理得22(12)420k x kx ++-=，由韦达定理得12122242,1212k x x x x k k --+==++由12PB AP =uu r uu u r 得22112111(,1)(,1),22x y x y x x -=--∴=-，---------------------7分代入韦达定理，整理得2112284,1212k x x k k-==++，解得21,14k k =∴=，所以直线l的方程为1y x =+ ---------------------8分 (ⅱ)当直线l 与x轴垂直时，||||||||QA PA QB PB ==，所以命题成立 --------------9分下面证明对任意斜率存在的直线l ，均有||||||||QA PA QB PB = 即证：y 轴为AQB ∠的角平分线所在直线.只需证明：0QB QA k k +=. ---------------------10分22222211QB y kx k k x x x --===-，11111211QA y kx k k x x x --===-， 121212112()2QB QA x x k k k k x x x x +∴+=-+=-， ---------------------12分由（1）中韦达定理得12122x x k x x +=，220QB QA k k k k ∴+=-= ---------------------13分 ∴对于任意直线l ，||||||||QA PA QB PB =恒成立. ---------------------14分。

山东省滕州市第一中学高三数学上学期第一次月考(9月)试题理

2016届山东省滕州市第一中学高三9月月考数学试卷（理科）第I 卷一、选择题：（本大题共12小题，每小题5分，满分60分.在每小题给出的四个选项中，只有一项是符合题目要求的.） 1．复数1z i =-，则1z z+对应的点所在的象限为 A ．第一象限B ．第二象限C ．第三象限D ．第四象限2．若集合{|(4)(1)0}M x x x =++=，{|(4)(1)0}N x x x =--=，则MN =A ．∅B ．{}1,4--C ．{}0D ．{}1,43. 设p ：x<3，q ：-1<x<3，则p 是q 成立的（）A ．充分必要条件B ．充分不必要条件C ．必要不充分条件D ．既不充分也不必要条件4．设f （x）＝102,0xx x ⎧-≥⎪⎨<⎪⎩，则f （f （－2））＝A ．－1B ．14 C ．12 D ．325．在等差数列{}n a 中，已知3810a a +=，则=+753a a （）A ．10B ．18C ．20D ．286.P 是双曲线1201622=-y x 上一点,21,F F 分别是双曲线左右焦点,若|1PF |=9,则|2PF |= ( )A.1B.17C.1或17D.以上答案均不对7.若某几何体的三视图如右图所示，则此几何体的体积等于（） A ．30B ．12C ．24D ．48．设函数sin cos y x x x =+的图象上的点00(,)x y 处的切线的斜率为k ，若0()k g x =，则函数0()k g x =的图象大致为（）323)0(22>=p pxy9.执行如图所示的程序框图，则输出的结果是（） A. 14B. 15C. 16D. 1710．ΔABC 中120BAC ∠=D AC AB ,1,2,==是边BC 上的一点（包括端点），则→→⋅BCAD 的取值范围是（）A ．B ．C ．D ． 11.如图过拋物线的焦点F 的直线依次交拋物线及准线于点A ，B ，C ，若|BC|＝2|BF|，且|AF|＝3，则拋物线的方程为（） A.=2y x 23B. =2y x 9 C ．=2y x 29 D ．=2y x 312.若直角坐标平面内A 、B 两点满足①点A 、B 都在函数()f x 的图象上；②点A 、B 关于原点对称，则点（A,B ）是函数()f x 的一个“姊妹点对”.点对（A,B ）与（B,A ）可看作是同一个“姊妹点对”.已知函数 ⎪⎩⎪⎨⎧≥<+=)0(,2)0(,2)(2x ex x x x f x ，则()f x 的“姊妹点对”有 ( ) A. 2个 B. 1个 C. 0个 D. 3个第Ⅱ卷本卷包括必考题和选考题两部分．第13题～第21题为必考题，每个试题考生都必须做答．第22题～第24题为选考题，考生根据要求做答．二、填空题：(本大题共4小题，每小题5分，共20分.)13.设变量y x ,满足约束条件⎪⎩⎪⎨⎧≤-+≥+-≥020120y x y x y ，则y x z +=3的最大值为 .14.在72)21(xx +-的展开式中的3x 的系数为 .15．已知1(2)xa e x dx =+⎰(e 为自然对数的底数),函数ln ,0()2,0x x x f x x ->⎧=⎨≤⎩ 则21()(log )6f a f +=.16 .已知数列{}n a 的前n 项和122+=-n n n S a ，若不等式223(5)n n n a λ--<-对*∈∀N n恒成立，则整数λ的最大值为 .三、解答题:（本大题共5小题，共计70分.解答应写出文字说明、证明过程或演算步骤.） 17. （本小题满分12分）在ABC ∆中c b a ,,,是其三个内角C B A ,,的对边且,sin 22sin 2a b A A B ≥=. (I)求角C 的大小;(II)设c =ABC ∆的面积S 的最大值. 18.（本小题满分12分）第117届中国进出品商品交易会（简称2015年秋季广交会）将于2015年8月15日在广州举行，为了搞好接待工作，组委会在广州某大学分别招募8名男志愿者和12名女志愿者，现将这20名志愿者的身高组成如下茎叶图（单位：cm ），若身高在175cm 以上（包括175cm ）定义为“高个子”，身高在175cm 以下（不包括175cm ）定义为“非高个子”. (I)计算男志愿者的平均身高和女志愿者身高的中位数（保留一位小数）.(II)若从所有“高个子”中选3名志愿者，用ξ表示所选志愿者中为女志愿者的人数，试写出ξ的分布列，并求ξ的数学期望. 19．（本小题满分12分）如图正方形ADEF 与梯形ABCD 所在的平面互相垂直,//,CD AB CD AD ⊥221===CD AD AB 点M 在线段EC 上. (I)当点M 为EC 中点时求证//:BM 平面ADEF ; (II)当平面BDM 与平面ABF 所成锐二面角的余弦值为66时，求三棱锥BDE M -的体积. 20.（本小题满分12分）椭圆)0(14222>=+b b y x 的焦点在x 轴上，其右顶点（a,0）关于直线04=+-y x 的对称点在直线ca x 2-= (c 为半焦距长) 上.（I ）求椭圆的方程；(II)过椭圆左焦点F 的直线l 交椭圆于A 、B 两点，交直线ca x 2-=于点C. 设O 为坐标原点，且,2→→→=+OB OC OA 求OAB ∆的面积. 21．（本小题满分12分）已知函数()ln f x x x =（e 为无理数， 2.718e ≈） (I)求函数()f x 在点(),()e f e 处的切线方程； (II)设实数12a e>，求函数()f x 在[],2a a 上的最小值；（III ）若k 为正整数，且()()1f x k x k >--对任意1x >恒成立，求k 的最大值．请考生在第22、23、24三题中任选一题作答，如果多做，则按所做的第一题记分．作答时请写题号．22．（本小题满分10分）【选修4—1：几何证明选讲】如图，在正△ABC 中，点D,E 分别在边AC, AB 上，且AD=13AC ， AE= 23AB ，BD ，CE 相交于点F ． (I)求证：A ，E ，F ，D 四点共圆；(II)若正△ABC 的边长为2，求，A ，E ，F ，D 所在圆的半径． 23. （本小题满分10分）【选修4—4：极坐标与参数方程】在直角坐标系中，以原点为极点，x 轴的正半轴为极轴建坐标系，已知曲线C ：ρsin 2θ=2acosθ（a ＞0），已知过点P （-2，-4）的直线l 的参数方程为24x ty tì=-+ïïíï=-+ïî，直线l 与曲线C 分别交于M ，N ．（1）写出曲线C 和直线l 的普通方程；（2）若|PM|，|MN|，|PN|成等比数列，求a 的值． 24. （本小题满分10分）【选修4-5：不等式选讲】已知a ，b ∈R +，a ＋b ＝1，1x ，2x ∈R +．(I)求12122x x a b x x ＋＋的最小值； (II)求证：122112((ax bx ax bx x x ＋)＋)≥．2016届山东省滕州市第一中学高三9月月考数学答案（理）一．选择题:二．填空题: 13. 6 14. －910 15. 7 16. 4三.解答题:17 解：（Ⅰ）∵sin22sin2,=A A B12(sin22)2sin2,2∴=A A B2sin(2)2sin2,sin(2)sin233ππ∴+=∴+=A B A B223π∴+=A B，或223ππ+=-A B，由≥a b，知≥A B，所以223π+=A B不可能成立，所以223ππ+=-A B，即3π+=A B，所以233πππ=-=C（Ⅱ）由（Ⅰ），23π=C，所以sin C1sin2=⋅⋅=S a b C22222222213cos3321 222+-+-=⇒-=⇒-=+-⇒-=+≥⇒≤a b c a bC ab a b ab a b ab abab ab即△ABC的面积S18.解：（1）根据茎叶图可得：男志愿者的平均身高为159169170175176182187191176.1()8+++++++≈cm 女志愿者身高的中位数为168169168.5()2+=cm（2）由茎叶图可知，“高个子”有8人，“非高个子”有12人，而男志愿者的“高个子”有5人，女志愿者的“高个子”有3人，ξ的可能值为0,1,2,3，故32155333881030(0),(1),5656ξξ======C C CP PC C1235333388151(2),(3),5656ξξ======C C CP PC C即ξ的分布列为：所以ξ的数学期望103015190123565656568ξ=⨯+⨯+⨯+⨯=E 19．解：（1）以直线DA 、DC 、DE 分别为x 轴、y 轴、z 轴建立空间直角坐标系，则)0,0,2(A ，)0,2,2(B )0,4,0(C ，)2,0,0(E 所以)1,2,0(M .∴)1,0,2(-=BM .........2分又，)0,4,0(=是平面ADEF 的一个法向量.∵0=⋅OC BM 即OC BM ⊥ ∴BM ∥平面ADEF .................4分（2）设),,(z y x M ，则)2,,(-=z y x ，又)2,4,0(-=设10(<<=λλEC EM ，则，λλ22,4,0-===z y x 即)22,4,0(λλ-M ...6分设),,(111z y x =是平面BDM 的一个法向量，则02211=+=⋅y x 0)22(411=-+=⋅z y n OM λλ取11=x 得 λλ-=-=12,111z y 即 )12,1,1(λλ--=n又由题设，)0,0,2(=是平面ABF 的一个法向量，......................8分 ∴2166)1(4222|||||,cos |22=⇒=-+=⋅=><λλλn OA ...................10分即点M 为EC 中点，此时，2=DEM S ∆，AD 为三棱锥DEM B -的高， ∴ =-BDE M V 342231=⋅⋅=-DEM B V ................................12分 20.解：（1）椭圆的右顶点为（2，0），设（2，0）关于直线04=+-y x 的对称点为（),00y x ，则⎪⎪⎩⎪⎪⎨⎧-=-=+-+,12,042220000x y y x ………………4分解得,1,4a ,420==-=c c c x 所以则3=b ，所求椭圆方程为13422=+y x --------------------------6分（2）设A ),,4(),,(),,(32211y C y x B y x -由,01248)4k (3),1(,1443222222=-+++⎩⎨⎧+==+k x k x x k y y x 得所以,4382221k k x x +-=+…………①，,431242221kk x x +-=…………② 因为,2OB OC OA =+即),(2),4(),(22211y x y y x =-+，所以4212-=-x x ……③……6分由①③得.434,438421222kx k k x +=++=代入②得，22222431244344384kk k k k +-=+⋅++-，整理得,05424=--k k …………8分所以,452=k 所以,47,2121-==x x ……10分由于对称性，只需求25=k 时，△OAB 的面积.此时，,583,54321-==y y 所以.5169||||2121=-⋅=∆y y OF S OAB ……12分 21.⑴∵()(0,)()ln 1,()()2f x f x x f e e f e ''+∞=+==定义域为又():2(),2y f x e y x e e y x e ∴==-+=-函数在点(，f(e))处的切线方程为即------3分（2）∵()ln 1f x x '=+()0f x '=令1x e =得10,x e ⎛⎫∈ ⎪⎝⎭ 当时,()0F x '<，()f x 单调递减；当1,x e ⎛⎫∈+∞ ⎪⎝⎭时,()0F x '>，()f x 单调递增.当min 1,()[,2],[()]()ln ,a f x a a f x f a a a e≥==时在单调递增 min 111112,[()]2a a a f x f e e e e e ⎛⎫<<<<==- ⎪⎝⎭当时,得-------------------------------6分 (3) ()(1)f x k x k >--对任意1x >恒成立，即ln x x x +(1)k x >-对任意1x >恒成立，即ln 1x x xk x +>-对任意1x >恒成立令2ln ln 2()(1)'()(1)1(1)x x x x x g x x g x x x x +--=>⇒=>-- 令1()ln 2(1)'()0()x h x x x x h x h x x-=-->⇒=>⇒在(1,)+∞上单调递增。

山东省潍坊第一中学2016届高三12月月考数学(理)试题 Word版含答案

保密★启用前2015—2016学年第一学期单元测试高三数学（理）试卷2015.12第Ⅰ卷（共50分）一、选择题：本大题共10小题，每小题5分，共50分．在每小题列出的四个选项中，有一项是符合题目要求的.1.已知全集为R ，集合A={1|()12xx ≤}，B={|2x x ≥}，B C A R =( ) A ． [0,2] B ．[0,2) C ．(1,2) D ． (1,2]2.命题“若220a b +=，则0a =且0b =”的逆否命题是( )A ．若220a b +≠，则0a ≠且0b ≠B ．若220a b +≠，则0a ≠或0b ≠C ．若0a ≠且0b ≠，则220a b +≠D ．若0a ≠或0b ≠，则220a b +≠3.偶函数()f x 在[]0,2上递减，则()12211 , log , log 42a f b f c f ⎛⎛⎫=== ⎪ ⎝⎭⎝⎭大小为 ( ) A.c a b >> B. a c b >> C. b a c >> D. a b c >> 4.平面直角坐标系内，若曲线C ：04542222=-+-++a ay ax y x 上所有的点均在第二象限内，则实数a 的取值范围为（） A ．()2,-∞-B ． ()1,-∞-C ．()+∞,1D ．()+∞,25.在空间给出下面四个命题（其中m 、n 为不同的两条直线，α、β为不同的两个平面 ①m ⊥α，n ∥α⇒m ⊥n ②m ∥n ，n ∥α⇒m ∥α③m ∥n ，n ⊥β，m ∥α⇒α⊥β④m ∩n=A ，m ∥α，m ∥β，n ∥α，n ∥β⇒α∥β 其中正确的命题个数有（） A ．1个B ．2个C ．3个D ．4个6.为了得到函数3cos 2y x =图象，只需把函数3sin 26y x π⎛⎫=+⎪⎝⎭图象上所有点（） A.向右平行移动12π个单位长度 B. 向右平行移动6π个单位长度 C.向左平行移动12π个单位长度D. 向左平行移动6π个单位长度7.已知锐角α的终边上一点P （sin 40︒，1cos 40+︒），则α等于（） A ．010 B ．020 C ． 070 D ．0808.三棱锥D ABC -中，1AB BC ==，2AD =，BD =AC =，BC AD ⊥，则三棱锥的外接球的表面积( ) A. 5π B. 94π C. 6π D. 9π9.过点()2P --的直线与圆224x y +=有公共点，则该直线倾斜角的范围是( ) A. 0,6π⎛⎫⎪⎝⎭B. 0,3π⎡⎤⎢⎥⎣⎦C. 0,6π⎡⎤⎢⎥⎣⎦D. 0,3π⎛⎤⎥⎝⎦10.对任意0,2x π⎛⎫∈ ⎪⎝⎭，不等式()()sin cos x f x x f x '⋅<⋅恒成立，则下列不等式错误．．的是( ）A. 34f ππ⎛⎫⎛⎫>⎪ ⎪⎝⎭⎝⎭B. ()cos 13f f π⎛⎫>21⋅⎪⎝⎭C. ()14f f π⎛⎫<⋅⎪⎝⎭D. 46f f ππ⎛⎫⎛⎫<⎪⎪⎝⎭⎝⎭第Ⅱ卷（非选择题共100分）二、填空题:本大题共5小题，每小题5分，共25分．11.若向量a ，b 的夹角为150,42a b a b ==+=，则___________.12.函数12y x=-的定义域是________. 13.△ABC 的面积为，且AB ＝5， AC ＝8，则BC 等于．14.已知偶函数()f x 满足)(1)1(x f x f -=+，且当[]0,1x ∈时，()f x x =，若区间[]1,3-上，函数()()g x f x kx k =--有3个零点，则实数k 的取值范围是_________.15.定义在区间[,]a b 上的连续函数()y f x =，如果[,]a b ξ∃∈，使得()()'()()f b f a f b a ξ-=-，则称ξ为区间[,]a b 上的“中值点”．下列函数中： ①()32f x x =+；②2()1f x x x =-+；③()ln(1)f x x =+；④31()()2f x x =-在区间[0,1]上“中值点”多于一个的函数序号为．（写出所有．．满足条件函数序号）三、解答题：本大题6小题，共75分．解答应写出文字说明，证明过程或演算步骤． 16．（本题满分12分）在△ABC 中，角A ，B ，C 所对的边分别()()(),,,2sin cos sin a b c f x x A x B C =-++()x R ∈，函数()f x 的图象关于点,06π⎛⎫⎪⎝⎭对称. （I ）当0,2x π⎛⎫∈ ⎪⎝⎭时，求()f x 的值域；（II ）若7a =且sin sin B C +=，求△ABC 的面积。

山东省德州市某中学2016届高三上学期1月月考数学理试题Word版含答案

高三数学（理）月考试题（2016/1/11）（时间120分钟，满分150分）一、选择题（每小题5分，共计50分）1．设i 是虚数单位，复数7412ii+=+（）A ． 32i -B ．32i +C ． 23i +D ． 23i -2．集合{}{}20,2A x x a B x x =-≥=<，若R C A B ⊆，则实数a 的取值范围是（） A ． []0,4B ．(],4-∞C ． (),4-∞D ． ()0,43.设0.50322,log 2,log 0.1a b c ===，则 A.a b c <<B. c a b <<C. c b a <<D. b c a <<4．下列四个结论：①若0x >，则sin x x >恒成立；②命题“若sin 0,0x x x -==则”的逆命题为“若0sin 0x x x ≠-≠，则”； ③“命题p q ∨为真”是“命题p q ∧为真”的充分不必要条件； ④命题“,ln 0x R x x ∀∈->”的否定是“000,ln 0x R x x ∃∈-≤”．其中正确结论的个数是（） A ．1个B ．2个C ．4个D ．3个5．直线10x my ++=与不等式组30,20,20x y x y x +-≥⎧⎪-≥⎨⎪-≤⎩表示的平面区域有公共点，则实数m 的取值范围是（）A ． 14,33⎡⎤⎢⎥⎣⎦B ． 41,33⎡⎤--⎢⎥⎣⎦C ． 3,34⎡⎤⎢⎥⎣⎦D ． 33,4⎡⎤--⎢⎥⎣⎦6．已知某几何体的三视图，则该几何体的体积是（）A ．12B ．24C ．36D ．487．设01a <<，则函数11x y a =-的图象大致为（）8．已知向量()()0,sin ,1,2cos a x b x ==，函数()()2237,22f x a bg x a b =⋅=+-，则()f x 的图象可由()g x 的图象经过怎样的变换得到（）A ．向左平移4π个单位长度 B ．向左平移2π个单位长度 C ．向右平移4π个单位长度D ．向右平移2π个单位长度9. 已知函数()()()sin 0f x A x ωϕϕπ=+<<的图象如图所示，若()00053,,sin 36f x x x ππ⎛⎫=∈ ⎪⎝⎭，则的值为D.10.设()ln f x x =，若函数()()g x f x ax =-在区间(]0,3上有三个零点，则实数a 的取值范围是 A.10,e ⎛⎫ ⎪⎝⎭B. ln 31,3e ⎡⎫⎪⎢⎣⎭C.ln 30,3⎛⎤⎥⎝⎦D.ln 3,3e ⎛⎫⎪⎝⎭二、解答题（每小题5分共计25分）11.已知()sin cos 0,,tan αααπα-=∈=则 .12.已知平面向量()()1,22,.23a b m a b a b ==-⊥+=，，且则 . 13.函数1lg 1y x ⎛⎫=-+ ⎪⎝⎭的定义域是 . 14. 设甲、乙两个圆柱的底面积分别为12S S 、，体积分别为12υυ，，若它们的侧面积相等，且1122169S S υυ=，则的值为 .15.给出下列四个命题：①命题“,cos 0x R x ∀∈>”的否定是“,cos 0x R x ∃∈≤”； ②a 、b 、c 是空间中的三条直线，a//b 的充要条件是a c b c ⊥⊥且； ③命题“在△ABC 中，若,sin sin A B A B >>则”的逆命题为假命题；④对任意实数()()()(),000x f x f x x x x ''-=>><<有，且当时，f ，则当x 0时，f . 其中的真命题是 .（写出所有真命题的编号）三、解答题：16.已知函数()()21cos cos 0,2f x x x x x R ωωωω=-->∈的图像上相邻两个最高点的距离为π.（I ）求函数()f x 的单调递增区间；（II ）若ABC ∆三个内角A 、B 、C的对边分别为()0,sin a b c c f C B ===、、，且3sin A ，求a ，b 的值.17. 已知数列{}n a 前n 项和n S 满足：21n n S a += （I ）求数列{}n a 的通项公式；（II ）设()()11211n n n n a b a a ++=++，数列{}n b 的前n 项和为n T ，求证：14n T <.18. 在如图所示的空间几何体中，平面ACD ⊥平面ABC ，ACD ACB ∆∆与是边长为2的等边三角形，BE=2，BE 和平面ABC 所成的角为60°，且点E 在平面ABC 上的射影落在ABC ∠的平分线上. （I ）求证：DE//平面ABC ；（II ）求二面角E BC A --的余弦值. 19. （本小题满分12分）如图正方形ABCD 的边长为ABCD的边长为，四边形BDEF 是平行四边形，BD 与AC交于点G ，O 为GC的中点，FO FO =⊥平面ABCD.（I ）求证:AE//平面BCF ；（II）若FO =CF ⊥平面AEF..20. （本小题满分13分）已知函数()ln ,f x x mx m R =-∈.（I ）求()f x 的单调区间；（II ）若()[)1211m f x m x-≤-++∞在，上恒成立，求实数m 的取值范围. 21（本小题满分14分）.如图，在△ABC 中，已知∠ABC=45°，O 在AB 上，且OB=OC=AB ，又PO ⊥平面ABC ，DA ∥PO ，DA=AO=PO ．（Ⅰ）求证：PD ⊥平面COD ；（Ⅱ）求二面角B ﹣DC ﹣O 的余弦值．高三数学（理）月考试题答案一、选择题1.A2.B3.C 4、D 5、D 6、A 7、B 8、C 9、D 10、D 二．填空题11. -1 12.(-4,7) 13.32[log ,)+∞ 14. 4315.①④ 三、解答题18.解析：（Ⅰ）证明：由题意知，ABC ∆，ACD ∆都是边长为2的等边三角形，取AC 中点O ，连接,BO DO ，则BO AC ⊥，DO AC ⊥，又∵平面ACD ⊥平面ABC ，∴DO ⊥平面ABC ，作EF ⊥平面ABC ，那么//EF DO ，根据题意，点F 落在BO 上， ∴60EBF ∠=︒，易求得∴四边形DEFO 是平行四边形，∴//DE OF ，∴//DE 平面 ABC …………6分（Ⅱ）建立如图所示的空间直角坐标系O xyz -，可知平面ABC 的一个法向量为(0,0,1)n =设平面BCE 的一个法向量为2(,,)n x y z =,则，2200n BC n BE ⎧⋅=⎪⎨⋅=⎪⎩可求得(3,n =- (9)分1213,13||||n n n n n n ⋅<>==⋅又由图知，所求二面角的平面角是锐角，所以二面角E BC A --的余弦值为……12分21.【解析】：（Ⅰ）证明：设OA=1，则PO=OB=2，DA=1，由DA∥PO，PO⊥平面ABC，知DA⊥平面ABC，∴DA⊥AO．从而，在△PDO中，∵PO=2，∴△PDO为直角三角形，故PD⊥DO．又∵OC=OB=2，∠ABC=45°，∴CO⊥AB，又PO⊥平面ABC，∴PO⊥OC，又PO，AB⊂平面PAB，PO∩AB=O，∴CO⊥平面PAB．故CO⊥PD．∵CO∩DO=O，∴PD⊥平面COD．-------------7分（Ⅱ）解：以OC，OB，OP所在射线分别为x，y，z轴，建立直角坐标系如图．则由（Ⅰ）知，C（2，0，0），B（0，2，0），P（0，0，2），D（0，﹣1，1），∴，由（Ⅰ）知PD⊥平面COD，∴是平面DCO的一个法向量，设平面BDC的法向量为，∴，∴，令y=1，则x=1，z=3，∴，∴，由图可知：二面角B﹣DC﹣O为锐角，二面角B﹣DC﹣O的余弦值为．--14分。

【首发】山东省新泰市第一中学2016届高三上学期第一次(10月)质量检测数学(理)试题Word版含答案

新泰一中高三年级第一次质量检测数学（理科）试题 2015年10月说明：本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）共两卷。

其中第一卷共60分，第Ⅱ卷共90分，两卷合计150分。

答题时间为120分钟。

第Ⅰ卷（选择题共60分）一、选择题：（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）1. 全集}6,5,4,3,2,1{=U ，},4,3,2{=M ，}5,4{=N ，则=}{N M C U U （）A.{1，3，5}B.{2，4，6}C.{1，5}D.{1，6}2.下列四个函数中，在区间（0，1）上是减函数的是（）A.x y 2log =B.31x y = C.x y )21(-= D.xy 1= 3.命“x x R x sin ,>∈∀”的否定是（）A.x x R x sin ,<∈∃B.x x R x sin ,≤∈∀C.x x R x sin ,≤∈∃D.x x R x sin ,<∈∀4.要得到x x y 2cos 2sin +=的图象，只需将x y 2sin 2=的图象（） A.向左移4π个单位 B.向左平移8π个单位 C.右平移4π个单位 D.向左平移8π个单位 5.函数x x f 2log )(2=与x x g )21(2)(⋅=在同一直角坐标系下的图象大致是6.若对,),0,(0R x a ∈∃-∞∈∀使a x a ≤0cos 成立，则0cos x 6π⎛⎫-= ⎪⎝⎭（）A.21B.23C.21- D.23- 7.函数x x x f cos )(-=在[0，+∞）内（） A.没有零点 B.有且仅有一个零点 C.有且仅有两个零点 D.有无穷多个零点8.同时具有性质：“①最小正周期为π；②图象关于直线3π=x 对称；③在⎥⎦⎤⎢⎣⎡-3,6ππ上是增函数”的一个函数是（） A.)62sin(π+=x y B.)32sin(π+=x y C.)62sin(π-=x y D.)652sin(π+=x y9.设)(x f 是一个三次函数，)('x f 其导函数，如图所示是函数)('x xf y =的图像的一部分，则)(x f 的极大值与极小值分别为（）A.)1(f 与)1(-fB.)1(-f 与)1(fC.)2(-f 与)2(fD.)2(f 与)2(-f10.若定义在R 上的二次函数b ax ax x f +-=4)(2在区间[0，2]上是增函数，且)0()(f m f ≥，则实数m 的取值范围是（）A.40≤≤mB.20≤≤mC.0≤mD.0≤m 或4≥m11.若对任意的R x ∈，函数)(x f 满足)2011()2012(+-=+x f x f ，且2012)2012(-=f ，则=-)1(f （）A.1B.-1C.2012D.-201212.定义在［1，+∞）上的函数)(x f 满足：①)()2(x cf x f =（c 为正常数）；②当42≤≤x 时，2)3(1)(--=x x f 。

2016届高三第一次全国大联考(山东卷)文数卷

2016年第一次全国大联考文科数学第I卷（共50分）一、选择题：本大题共是符合题目要求的. 10个小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项1•已知A {1,2,4,8,16}, B {y | y log 2X,X A}，则AI B ()A.{1,2} B -{2, 4,8} C. {1,2,4} D.{1,2,4,8}2.已知z（2i) 1 i，则z ()1 3 1 3. 1 3. 1 3.A.i B i C. i D. i5 5 5 5 5 5 5 53. 已知命题P :已知m 0，若2a2b，贝9am 2bm2.则其否命题为，()A.已知m 0,若2a2b，则am2bm2B.已知m 0，若2a2b，则am2bm2C.已知m 0，若2a 22，则am bm2D.已知m 0,若2a2b，则am2bm2r r r r r r r r4. 已知向量a (1,1)，|b| (a b) (a 3b) 1，则a,b 等于（)2 3A.- B —— C. — D.3 34 45.函数f（x） cosx log 2 | x |的图象大致为（）D6.如图为某几何体的三视图，则该几何体的体积等于（)的零点个数为（第H 卷（共100分）A. D.7.已知变量x, y 满足2x2，则 z 2x 6y 的最大值为（）如图所示是某品牌食品中微量元素含量数据的茎叶图，已知该组数据的平均数为11.5,甲小4 1则兰丄的最小值为（）a 0 a b3 1 1 9b2A. 9B. —C.8D.424ax(a 1(a 0,b 0)的两条渐近线的交点分别为 B,C ，若X C 是X B 与X F 的等比中项，则双曲线的离心率等于（B.10 3C. 2 2D. 1010.设函数yf （x ）是定义在R 上的可导函数，当x 0时，f （x ） x-f (x),则函数 2g(x) f(x)1~2xA.0B.1C.2D.0 或 2、填空题（每题5分，满分25分，将答案填在答题纸上）42~X11.函数f （x ）的定义域为In x12.ABC的三内角A 、B 、C 的对边边长分别为a 、b 、c ，若a 乎b , A2B ,C.1 A.2B.10D.120）的焦点F 作斜率为 1的直线，该直线与双曲线22x-2a9.过抛物线y 2x 21=1.量则sin B _______13. 如图是某算法的程序框图，若实数x ( 1,4)，则输出的数值不小于30的概率为.2 214. 已知直线y 2x a与圆C：x y 4x 4y 4 0相交于A, B两点，且ABC的面积S 2，则实数a _____ .ir15. 设互不相等的平面向量组a i(i 1,2, L ,n)满足：IT①| Q | 2;u in②a i a j 0 (1 i, j n).IT IT ui un UT …若T n a1 a2 L ( 1)n &，记0 |人f，则数列｛g｝的前n项和&为_____________________________ .三、解答题 (本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤.)16. (本大题满分12分)已知函数f(x) cos x(J3sin x cos x) ( 0)的两条对称轴之间的最小距离为一2(I)求的值以及f(x)的最大值；(n)已知ABC中，cosA 0,若f(A) m恒成立，求实数m的取值范围.17. (本大题满分12分)2015年山东省东部地区土豆种植形成初步规模，出口商在各地设置了大量的代收点.已知土豆收购按质量标准可分为四个等级，某代收点对等级的统计结果如下表所示：现从该代售点随机抽取了n袋土豆，其中二级品为恰有40袋.(I)求m、n的值；(n)利用分层抽样的方法从这n袋土豆中抽取10袋，剔除特级品后，再从剩余土豆中任意抽取两袋，求抽取的两袋都是一等品的概率.18. (本小题满分12分)如图几何体中，长方形ACDF所在平面与梯形BCDE所在平面垂直，且BC 2DE，DE//BC，BD AD，M为AB的中点..(I)证明：EM //平面ACDF .(n)证明：BD 平面ACDF .2已知数列｛a n ｝的前n 项和为S n ,对一切正整数n ，点巳(n,S n )在函数f(x) x {b n }单调递减，且 bib 2b 3 8, b i b 2 b 3(I )求数列｛a n ｝ , ｛b n ｝的通项公式;20.(本小题满分13分)已知 f (x) a In x ,记 g (x) f (x).(i)求证：OMN 的面积为定值;umu uur(ii)求OM ON 的最值.19.(本小题满分12分)x 的图象上；等比数列26 3(n )若C n 是a n 、b n 的等比中项，求数列2{ C n }的前n 项和T n .(I )已知函数h(x) f(x) g(x)在［1,)上单调递减，求实数 a 的取值范围;(n) (i)求证：当 a 1 时，f (x)(ii)当 a 2 时,若不等式 h(x) tg (x1) ( x [1,))恒成立，求实数t 的取值范围.21.(本小题满分14分)2 2已知椭圆C :冷占 1(a b 0)的离心率为a bf ，P(Wf)在椭圆C 上.(I )求C 的方程;(n )直线I 与椭圆C 交于不同的两点 M 、N , O 为坐标原点，且k OM k ON$ ~2. a。

山东省潍坊市高三数学上学期第一次月考试卷理(含解析)

山东省潍坊市2015届高三上学期第一次月考数学试卷（理科）一、选择题（共10小题，每小题5分，满分50分,在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知全集U=R，集合A={y|y=lg（x2+10），x∈R），集合B={x||x﹣2|＜1}，则（∁U B）∩A=（）A．{x|0≤x＜1或x＞3} B．{x|x=1或x≥3}C．{x|x＞3} D．{x|1≤x≤3}2．（5分）下列函数中，与函数定义域相同的函数为（）A．B．C．D．y=x3e x3．（5分）已知sin（α+）=，则cos（α+）=（）A．B．C．﹣D．﹣4．（5分）“a≥3”是“∀x∈[1，2]，x2﹣a≤0”为真命题的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件5．（5分）已知函数f（x）=x2+（m2﹣4）x+m是偶函数，g（x）=x m在（﹣∞，0）内单调递增，则实数m=（）A．2 B．±2C．0 D．﹣26．（5分）将函数y=cos2x+1的图象向右平移个单位，再向下平移1个单位后得到的函数图象对应的表达式为（）A．y=sin2x B．y=sin2x+2 C．y=cos2x D．y=cos（2x﹣）7．（5分）设命题p：曲线y=e﹣x在点（﹣1，e）处的切线方程：y=﹣ex；命题q：函数y=sinx+（0＜x＜π）值域为[4，+∞），则下列判断正确的是（）A．“p∨q”为真B．“￢p∨q”为真C．“￢p∧q”为真D．“￢p∧￢q”为真8．（5分）函数f（x）=﹣cosxlnx2的部分图象大致是图中的（）A．B．C．D．9．（5分）已知函数f（x）=﹣x3+ax2+bx（a，b∈R）的图象如图所示，它与x轴在原点处相切，且x轴与函数图象所围区域（图中阴影部分）的面积为，则a的值为（）A．1 B．2 C．﹣1 D．﹣210．（5分）设函数f（x）（x∈R）满足f（﹣x）=f（x），f（x）=f（2﹣x），且当x∈[0，1]时，f（x）=x3，又函数g（x）=|cos（πx）|，则函数h（x）=g（x）﹣f（x）在[﹣，]上的零点个数为（）A．8 B．7 C．6 D．5二、填空题（共5小题，每小题5分，满分25分）11．（5分）命题“若ab≤0，则a≤0或b≤0”的逆否命题是．12．（5分）已知角α的顶点与原点重合，始边与x轴的非负半轴重合，终边落在射线3x+4y=0（x＜0）上，则2sinα+cosα的值为．13．（5分）计算log2sin﹣log cos的值为．14．（5分）设函数f（x）在（0，+∞）内可导，且f（e x）=x+e2x，f′（x）的最小值为．15．（5分）如果对定义在R上的函数f（x），对任意两个不相等的实数x1，x2，都有x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1），则称函数f（x）为“H函数”．给出下列函数①y=﹣x3+x+1；②y=3x﹣2（sinx﹣cosx）；③y=e x+1；④f（x）=．以上函数是“H函数”的所有序号为．三、解答题（共6小题，满分75分）16．（12分）已知m∈R，设命题P：∃x∈{x|﹣2＜x＜2}，使等式x2﹣2x﹣m=0成立；命题Q：函数f（x）=3x2+2mx+m+有两个不同的零点．“P∨Q”为真命题，“P∧Q”为假命题，求实数m的取值范围．17．（12分）已知函数f（x）=2sin（π﹣x）•cosx+sin2x﹣cos2x，x∈R．（Ⅰ）求函数f（x）在[0，π]上的单调区间．（Ⅱ）若函数f（x）的图象向右平移m（m＞0）个单位后，得到的图象关于原点对称，求实数m的最小值．18．（12分）设函数f（x）=log2（ax2﹣2x+2）定义域为A．（Ⅰ）若A=R，求实数a的取值范围；（Ⅱ是否存在实数a，使f（x）的最大值为2？若存在求出a的值，若不存在，说明理由．19．（12分）已知函数f（x）=2cos2（ωx+φ）﹣2sin（ωx+φ）cos（ωx+φ）（ω＞0.0＜φ＜）其图象的两个相邻对称中心的距离为，且过点（﹣，2）．（Ⅰ）函数f（x）的达式；（Ⅱ）若f（﹣）=，α是第三象限角，求cosα的值．20．（13分）甲方是一农场，乙方是一工厂．由于乙方生产须占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润x （元）与年产量t（吨）满足函数关系．若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格）．（1）将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方获得最大利润的年产量；（2）甲方每年受乙生产影响的经济损失金额y=0.002t2（元），在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格s是多少？21．（14分）已知函数f（x）=lnx﹣，g（x）=f（x）+ax﹣6lnx，其中a∈R．（Ⅰ）讨论f（x）的单调性；（Ⅱ）若g（x）在其定义域内为增函数，求正实数a的取值范围；（Ⅲ）设函数h（x）=x2﹣mx+4，当a=2时，若∃x1∈（0，1），∀x2∈[1，2]，总有g（x1）≥h（x2）成立，求实数m的取值范围．山东省潍坊市2015届高三上学期第一次月考数学试卷（理科）参考答案与试题解析一、选择题（共10小题，每小题5分，满分50分,在每小题给出的四个选项中，只有一项是符合题目要求的）1．（5分）已知全集U=R，集合A={y|y=lg（x2+10），x∈R），集合B={x||x﹣2|＜1}，则（∁U B）∩A=（）A．{x|0≤x＜1或x＞3} B．{x|x=1或x≥3}C．{x|x＞3} D．{x|1≤x≤3}考点：交、并、补集的混合运算．专题：集合．分析：求出A中y的范围确定出A，求出B中不等式的解集确定出B，根据全集U=R求出B 的补集，找出B补集与A的交集即可．解答：解：由A中y=lg（x2+10）≥1，得到A={y|y≥1}，由B中不等式变形得：﹣1＜x﹣2＜1，即1＜x＜3，∴B={x|1＜x＜3}，∵全集U=R∴∁U B={x|x≤1或x≥3}，则（∁U B）∩A={x|x≥3或x=1}．故选：B．点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．2．（5分）下列函数中，与函数定义域相同的函数为（）A．B．C．D．y=x3e x考点：函数的定义域及其求法．专题：计算题；阅读型．分析：原函数的定义域是满足分母不等于0的x的取值集合，然后逐一分析给出的四个选项中函数的定义域，比较后即可得到答案．解答：解：函数定义域是{x|x≠0}．而函数的定义域为{x|x≠kπ，k∈Z}，函数的定义域是{x|x＞0}，函数的定义域是{x|x≠0}，函数y=x3e x的定义域是R．所以与函数定义域相同的函数为．故选C．点评：本题考查了函数的定义域及其求法，函数的定义域，就是使函数解析式有意义的自变量x的取值集合，是基础题．3．（5分）已知sin（α+）=，则cos（α+）=（）A．B．C．﹣D．﹣考点：运用诱导公式化简求值．专题：三角函数的求值．分析：利用三角函数间的诱导公式即可求得答案．解答：解：∵sin（α+）=，∴cos（α+）=cos[（α+）+]=﹣sin（α+）=﹣，故选：C．点评：本题考查运用诱导公式化简求值，属于基础题．4．（5分）“a≥3”是“∀x∈[1，2]，x2﹣a≤0”为真命题的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：计算题．分析：由恒成立可得a≥4，再由集合{a|a≥4}是集合{a|a≥3}的真子集，可得结论．解答：解：∵“∀x∈[1，2]，x2﹣a≤0”为真命题，∴a≥x2，在x∈[1，2]时恒成立，而当x∈[1，2]时，x2的最大值为4，故只需a≥4，因为集合{a|a≥4}是集合{a|a≥3}的真子集，故“a≥3”是“∀x∈[1，2]，x2﹣a≤0”为真命题的必要不充分条件，故选B点评：本题考查充要条件的判断，涉及恒成立问题，得出a≥4，并用集合的包含关系是解决问题的关键，属基础题．5．（5分）已知函数f（x）=x2+（m2﹣4）x+m是偶函数，g（x）=x m在（﹣∞，0）内单调递增，则实数m=（）A．2 B．±2C．0 D．﹣2考点：函数奇偶性的性质．专题：函数的性质及应用．分析：根据函数的奇偶性的性质求出m，结合幂函数的性质即可得到结论．解答：解：∵函数f（x）=x2+（m2﹣4）x+m是偶函数，∴f（﹣x）=f（x），即f（﹣x）=x2﹣（m2﹣4）x+m=x2+（m2﹣4）x+m，则﹣（m2﹣4）=m2﹣4，解得m2﹣4=0，解得m=2或﹣2，∵若m=2，g（x）=x2在（﹣∞，0）内单调递减，不满足条件，若m=﹣2，g（x）=x﹣2在（﹣∞，0）内单调递增，满足条件，故选：D点评：本题主要考查函数奇偶性的应用以及幂函数的性质，比较基础．6．（5分）将函数y=cos2x+1的图象向右平移个单位，再向下平移1个单位后得到的函数图象对应的表达式为（）A．y=sin2x B．y=sin2x+2 C．y=cos2x D．y=cos（2x﹣）考点：函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：首先把函数解析式中的x变化为，利用诱导公式整理后把函数式右边减1即可得到答案．解答：解：把函数y=cos2x+1的图象向右平移个单位，得=sin2x+1，再向下平移1个单位，得y=sin2x+1﹣1=sin2x．∴将函数y=cos2x+1的图象向右平移个单位，再向下平移1个单位后得到的函数图象对应的表达式为：y=sin2x．故选：A．点评：本题主要考查三角函数的平移．三角函数的平移原则为左加右减上加下减，是基础题．7．（5分）设命题p：曲线y=e﹣x在点（﹣1，e）处的切线方程：y=﹣ex；命题q：函数y=sinx+（0＜x＜π）值域为[4，+∞），则下列判断正确的是（）A．“p∨q”为真B．“￢p∨q”为真C．“￢p∧q”为真D．“￢p∧￢q”为真考点：复合命题的真假．专题：函数的性质及应用；三角函数的求值；不等式的解法及应用．分析：本题可以先对命题p、q进行化简转化，从而判断出其真假，再根据复合函数真假判断的规律，得到正确选项．解答：解：∵y=e﹣x，∴y′=﹣e﹣x．∴当x=﹣1时，y=e，k=y′=﹣e．∴曲线y=e﹣x在点（﹣1，e）处的切线方程为y﹣e=﹣e（x+1），∴曲线y=e﹣x在点（﹣1，e）处的切线方程：y=﹣ex，∴命题p为真命题∵y=sinx+（0＜x＜π），∴可设sinx=t，则y=t+，（0＜t≤1）．∴．∴y=t+在区间（0，1]上单调递减．当t=1时，函数有最小值y=5．∴函数y=sinx+（0＜x＜π）值域为[5+∞）．∴命题q：函数y=sinx+（0＜x＜π）值域为[4，+∞），不成立．∴命题q为假命题．∴命题p∨q为真命题．故选A．点评：本题考查了利用导函数求切线、由单调性求函数值域以及复合命题真假的判断等知识，有一定的运算量，属于中档题．8．（5分）函数f（x）=﹣cosxlnx2的部分图象大致是图中的（）A．B．C．D．考点：函数的图象．专题：图表型．分析：由于函数f（x）=﹣cosxlnx2不是基本初等函数，我们可以用排除法，排除错误答案，最后得到正确的答案，确定函数的奇偶性后，进而排除图象不关于Y轴对称的图象，判断出函数的单调后，排除不满足条件的答案，即可得到正确的结论．解答：解：∵函数f（x）=﹣cosxlnx2为偶函数，∴函数的图象关于Y轴对称，故可以排除C，D答案又∵函数f（x）=﹣cosxlnx2在区间（0，1）上为减函数故可以排除B答案．故选A点评：本题考查的知识点的图象，其中正确分析函数的性质，并根据函数的性质，判断出函数图象的形状是解答本题的关键．9．（5分）已知函数f（x）=﹣x3+ax2+bx（a，b∈R）的图象如图所示，它与x轴在原点处相切，且x轴与函数图象所围区域（图中阴影部分）的面积为，则a的值为（）A．1 B．2 C．﹣1 D．﹣2考点：定积分在求面积中的应用．专题：导数的综合应用．分析：根据导数的几何意义以及导数的基本运算，结合积分公式，即可得到结论．解答：解：∵函数f（x）=﹣x3+ax2+bx（a，b∈R）的图象如图所示，它与x轴在原点处相切，∴函数的导数f′（x）=﹣3x2+2ax+b，且f′（0）=b=0，则f（x）=﹣x3+ax2，∵x轴与函数图象所围区域（图中阴影部分）的面积为，∴由f（x）=﹣x3+ax2=0解得x=0或x=a，由图象可知a＜0，则根据积分的几何意义可得﹣=﹣（）|=，即a4=1，解得a=﹣1或a=1（舍去），故选：C点评：本题主要考查导数的几何意义的应用以及利用积分求阴影部分的面积的计算，要求熟练掌握导数的应用．10．（5分）设函数f（x）（x∈R）满足f（﹣x）=f（x），f（x）=f（2﹣x），且当x∈[0，1]时，f（x）=x3，又函数g（x）=|cos（πx）|，则函数h（x）=g（x）﹣f（x）在[﹣，]上的零点个数为（）A．8 B．7 C．6 D．5考点：函数零点的判定定理．专题：计算题；作图题；函数的性质及应用．分析：由题意函数h（x）=g（x）﹣f（x）在[﹣，]上的零点个数可化为函数g（x）与函数f（x）的交点个数，作图分析即可．解答：解：函数h（x）=g（x）﹣f（x）在[﹣，]上的零点个数可化为函数g（x）与函数f（x）的交点个数，由题意作出函数g（x）与函数f（x）的图象如下：由图可知，有5个交点，故选D．点评：本题考查了函数的零点与函数图象的交点的关系，同时考查了学生的作图能力，属于基础题．二、填空题（共5小题，每小题5分，满分25分）11．（5分）命题“若ab≤0，则a≤0或b≤0”的逆否命题是若a＞0，且b＞0，则ab＞0．考点：四种命题．分析：根据命题“若p，则q”的逆否命题是“若￢q，则￢p”，直接写出答案即可．解答：解：根据原命题与逆否命题的关系，知：命题“若ab≤0，则a≤0或b≤0”的逆否命题是“若a＞0，且b＞0，则ab＞0”．故答案为：“若a＞0，且b＞0，则ab＞0”．点评：本题考查了原命题与它的逆否命题之间的相互转化问题，解题时应明确四种命题之间的关系，是基础题．12．（5分）已知角α的顶点与原点重合，始边与x轴的非负半轴重合，终边落在射线3x+4y=0（x＜0）上，则2sinα+cosα的值为．考点：任意角的三角函数的定义．专题：三角函数的求值．分析：在角α的终边上任意取一点P（﹣4a，3a），a＞0，由任意角的三角函数的定义求得sinα=和cosα=的值，从而求得2sinα+cosα 的值．解答：解：根据角α的终边落在射线3x+4y=0（x＜0）上，在角α的终边上任意取一点P （﹣4a，3a），a＞0，则r=|OP|==5a，∴sinα===，cosα===﹣，故2sinα+cosα=﹣=，故答案为：．点评：本题主要考查任意角的三角函数的定义，两点间的距离公式的应用，属于基础题．13．（5分）计算log2sin﹣log cos的值为﹣2．考点：同角三角函数基本关系的运用．专题：三角函数的求值．分析：利用对数的运算性质与二倍角的正弦可将原式化为log2sin﹣log cos=log2sin，即可求得答案．解答：解：log2sin﹣log cos=log2sin+log2cos=log2sin==﹣2，故答案为：﹣2．点评：本题考查同角三角函数基本关系的运用，考查二倍角的正弦与对数函数的性质，属于中档题．14．（5分）设函数f（x）在（0，+∞）内可导，且f（e x）=x+e2x，f′（x）的最小值为．考点：简单复合函数的导数．专题：导数的概念及应用．分析：首先求出f（x）的解析式，再求导，最后利用基本不等式求出最小值．解答：解：∵f（e x）=x+e2x，∴f（e x）=lne x+（e x）2，∴f（x）=lnx+x2，x∈（0，+∞）∴f′（x）=≥2=2，当且仅当x=时取等号．故答案为：点评：本题主要考查了函数解析式的求法，求导的运算法则，以及基本不等式，知识点比较多，属于中档题．15．（5分）如果对定义在R上的函数f（x），对任意两个不相等的实数x1，x2，都有x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1），则称函数f（x）为“H函数”．给出下列函数①y=﹣x3+x+1；②y=3x﹣2（sinx﹣cosx）；③y=e x+1；④f（x）=．以上函数是“H函数”的所有序号为②③．考点：函数单调性的性质．专题：新定义；函数的性质及应用．分析：不等式x1f（x1）+x2f（x2）＞x1f（x2）+x2f（x1）等价为（x1﹣x2）[f（x1）﹣f（x2）]＞0，即满足条件的函数为单调递增函数，判断函数的单调性即可得到结论．解答：解：∵对于任意给定的不等实数x1，x2，不等式x1f（x1）+x2f（x2）＞x1f（x2）+x2f （x1）恒成立，∴不等式等价为（x1﹣x2）[f（x1）﹣f（x2）]＞0恒成立，即函数f（x）是定义在R上的增函数．①y=﹣x3+x+1；y'=﹣3x2+1，则函数在定义域上不单调．②y=3x﹣2（sinx﹣cosx）；y’=3﹣2（cosx+sinx）=3﹣2sin（x+）＞0，函数单调递增，满足条件．③y=e x+1为增函数，满足条件．④f（x）=．当x＞0时，函数单调递增，当x＜0时，函数单调递减，不满足条件．综上满足“H函数”的函数为②③，故答案为：②③．点评：本题主要考查函数单调性的应用，将条件转化为函数的单调性的形式是解决本题的关键．三、解答题（共6小题，满分75分）16．（12分）已知m∈R，设命题P：∃x∈{x|﹣2＜x＜2}，使等式x2﹣2x﹣m=0成立；命题Q：函数f（x）=3x2+2mx+m+有两个不同的零点．“P∨Q”为真命题，“P∧Q”为假命题，求实数m的取值范围．考点：复合命题的真假．专题：函数的性质及应用．分析：本题先对命题p、q进行化简转化，再将条件“P∨Q”为真命题，“P∧Q”为假命题，转化为命题p、q中一个命题为真，另一个命题为假，得到关于m的不等式，解不等式，得到本题结论．解答：解：命题p等价于方程x2﹣2x﹣m=0在区间（﹣2，2）上有解．记g（x）=x2﹣2x﹣m，则，∴，∴﹣1≤m＜8．命题q：由方程的根的判别式△==4m2﹣12m﹣16＞0，得m＜﹣1或m＞4．∵“P∨Q”为真命题，“P∧Q”为假命题，∴命题p、q中，一个为真，另一个为假．∴当命题p真q假时，m＜﹣1或m≥8，当命题p假q真时，﹣1≤m≤4．∴m≤4或m≥8．实数m的取值范围是（﹣∞，4]∪[8，+∞）．点评：本题考查了一元二次方程的根的存在性、“或”命题和“且”命题的真假判断，本题计算量较大，属于中档题．17．（12分）已知函数f（x）=2sin（π﹣x）•cosx+sin2x﹣cos2x，x∈R．（Ⅰ）求函数f（x）在[0，π]上的单调区间．（Ⅱ）若函数f（x）的图象向右平移m（m＞0）个单位后，得到的图象关于原点对称，求实数m的最小值．考点：三角函数中的恒等变换应用；函数y=Asin（ωx+φ）的图象变换．专题：三角函数的图像与性质．分析：利用诱导公式、二倍角公式、两角差的正弦函数公式化简解析式，（Ⅰ）根据正弦函数的单调减区间得：，求出x的范围，结合定义域求出f（x）在[0，π]上的单调区间；（Ⅱ）根据平移法则求出平移后的函数g（x）的解析式，再由图象关于原点对称得到g（0）=0，列出m的方程并化简，根据m的范围求出m的最小值．解答：解：由题意得，f（x）=2sin（π﹣x）•cosx+sin2x﹣cos2x=sin2x﹣cos2x=，（Ⅰ）令得，（k∈Z），又x∈[0，π]，所以x∈，则函数f（x）在[0，π]上的单调区间是；（Ⅱ）将函数f（x）=的图象向右平移m（m＞0）个单位后，得到函数g（x）==的图象，又其函数图象关于原点对称，则g（0）=0，即，解得m=（k∈Z），因为m＞0，令k=﹣1得m=，所以实数m的最小值是．点评：本题考查了诱导公式、二倍角公式、两角差的正弦函数公式，以及正弦函数的性质，三角函数的图象平移变换，属于中档题．18．（12分）设函数f（x）=log2（ax2﹣2x+2）定义域为A．（Ⅰ）若A=R，求实数a的取值范围；（Ⅱ是否存在实数a，使f（x）的最大值为2？若存在求出a的值，若不存在，说明理由．考点：对数函数图象与性质的综合应用．专题：函数的性质及应用．分析：（1）函数f（x）=log2（ax2﹣2x+2）定义域为R则，ax2﹣2x+2＞0在x∈R上恒成立，根据二次函数性值判断条件．（2）存在实数a，使f（x）的最大值为2，根据复合函数单调性，可判断即a＜0，g（x）max=g （）=4，即+2=4，即可求出a的值．解答：解：（1）因为A=R所以ax2﹣2x+2＞0在x∈R上恒成立．①当a=0时，由﹣2x+2＞0，得x＜1，不成了，舍去．②当a≠0时，由，a，为综上所述，实数a的取值范围：（，+∞）（2）令g（x）=ax2﹣2x+2，有题意知，要使f（x）取最大值为2，则函数g（x）需取得最大值4，抛物线开口向下，即a＜0，g（x）max=g（）=4，即+2=4，∴a=满足条件．点评：本题考查了对数函数，二次函数的性质，特别是单调性，最值问题，综合考察要求对函数理解很深刻，应用灵活．19．（12分）已知函数f（x）=2cos2（ωx+φ）﹣2sin（ωx+φ）cos（ωx+φ）（ω＞0.0＜φ＜）其图象的两个相邻对称中心的距离为，且过点（﹣，2）．（Ⅰ）函数f（x）的达式；（Ⅱ）若f（﹣）=，α是第三象限角，求cosα的值．考点：三角函数中的恒等变换应用；正弦函数的图象．专题：三角函数的求值；三角函数的图像与性质．分析：（Ⅰ）根据二倍角公式、两角和的余弦函数公式化简解析式，再由条件求出函数的周期，由周期公式求出ω的值，再把点代入结合条件和特殊角的余弦值求出φ的值，代入解析式化简即可；（Ⅱ）根据题意把代入解析式化简可得，再根据角的所在的象限和平方关系求出sin（）的值，根据两角差的余弦函数公式求出cosα=cos[（）﹣]的值．解答：解：（Ⅰ）由题意得，f（x）=2cos2（ωx+φ）﹣2sin（ωx+φ）cos（ωx+φ）=cos（ωx+φ）﹣sin（ωx+φ）+1=，由图象的两个相邻对称中心的距离为得，函数的周期T=π，所以，得ω=2，又过点（﹣，2），则=2，化简得，cosφ=，由0＜φ＜得，φ=，所以；（Ⅱ）由（Ⅰ）得，=，化简得，，因为α是第三象限角，且＜0，则角是第三象限，所以sin（）=﹣=﹣，所以cosα=cos[（）﹣]=cos（）cos+sin（）sin==．点评：本题考查了二倍角公式、两角和差的余弦函数公式，以及余弦函数的性质，考查变角在求三角函数值中的应用．20．（13分）甲方是一农场，乙方是一工厂．由于乙方生产须占用甲方的资源，因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入，在乙方不赔付甲方的情况下，乙方的年利润x （元）与年产量t（吨）满足函数关系．若乙方每生产一吨产品必须赔付甲方s元（以下称s为赔付价格）．（1）将乙方的年利润w（元）表示为年产量t（吨）的函数，并求出乙方获得最大利润的年产量；（2）甲方每年受乙生产影响的经济损失金额y=0.002t2（元），在乙方按照获得最大利润的产量进行生产的前提下，甲方要在索赔中获得最大净收入，应向乙方要求的赔付价格s是多少？考点：函数模型的选择与应用．专题：应用题．分析：（1）由已知中赔付价格为s元/吨，所以乙方的实际年利润为．我们利用导数法易求出乙方取得最大年利润的年产量（2）由已知得，若甲方净收入为v元，则v=st﹣0.002t2．再由．我们可以得到甲方净收入v与赔付价格s之间的函数关系式，利用导数法，我们易求出答案．解答：解：（1）因为赔付价格为s元/吨，所以乙方的实际年利润为．由，令w'=0，得．当t＜t0时，w'＞0；当t＞t0时，w'＜0，所以t=t0时，w取得最大值．因此乙方取得最大年利润的年产量t0为（吨）；（2）设甲方净收入为v元，则v=st﹣0.002t2．将代入上式，得到甲方净收入v与赔付价格s之间的函数关系式．又，令v'=0，得s=20．当s＜20时，v'＞0；当s＞20时，v'＜0，所以s=20时，v取得最大值．因此甲方应向乙方要求赔付价格s=20（元/吨）时，获最大净收入．点评：函数的实际应用题，我们要经过析题→建模→解模→还原四个过程，在建模时要注意实际情况对自变量x取值范围的限制，解模时也要实际问题实际考虑．将实际的最大（小）化问题，利用函数模型，转化为求函数的最大（小）是最优化问题中，最常见的思路之一．21．（14分）已知函数f（x）=lnx﹣，g（x）=f（x）+ax﹣6lnx，其中a∈R．（Ⅰ）讨论f（x）的单调性；（Ⅱ）若g（x）在其定义域内为增函数，求正实数a的取值范围；（Ⅲ）设函数h（x）=x2﹣mx+4，当a=2时，若∃x1∈（0，1），∀x2∈[1，2]，总有g（x1）≥h（x2）成立，求实数m的取值范围．考点：利用导数求闭区间上函数的最值；函数恒成立问题；利用导数研究函数的单调性．专题：综合题；压轴题．分析：（Ⅰ）f（x）的定义域为（0，+∞），且，当a≥0时，f′（x）＞0，f（x）在（x，+∞）上单调递增；当a＞0时，由f′（x）＞0，得x＞﹣a；由f′（x）＜0，得x＜﹣a．由此能够判断f（x）的单调性．（Ⅱ）由g（x）=ax﹣，定义域为（0，+∞），知﹣=，因为g（x）在其定义域内为增函数，所以∀x∈（0，+∞），g′（x）≥0，由此能够求出正实数a的取值范围．（Ⅲ）当a=2时，g（x）=2x﹣，，由g′（x）=0，得x=或x=2．当时，g′（x）≥0当x时，g′（x）＜0．所以在（0，1）上，，由此能求出实数m的取值范围．解答：解：（Ⅰ）f（x）的定义域为（0，+∞），且，①当a≥0时，f′（x）＞0，f（x）在（x，+∞）上单调递增；②当a＜0时，由f′（x）＞0，得x＞﹣a；由f′（x）＜0，得x＜﹣a；故f（x）在（0，﹣a）上单调递减，在（﹣a，+∞）上单调递增．（Ⅱ）g（x）=ax﹣，g（x）的定义域为（0，+∞），﹣=，因为g（x）在其定义域内为增函数，所以∀x∈（0，+∞），g′（x）≥0，∴ax2﹣5x+a≥0，∴a（x2+1）≥5x，即，∴．∵，当且仅当x=1时取等号，所以a．（Ⅲ）当a=2时，g（x）=2x﹣，，由g′（x）=0，得x=或x=2．当时，g′（x）≥0；当x时，g′（x）＜0．所以在（0，1）上，，而“∃x1∈（0，1），∀x2∈[1，2]，总有g（x1）≥h（x2）成立”等价于“g（x）在（0，1）上的最大值不小于h（x）在[1，2]上的最大值”而h（x）在[1，2]上的最大值为max{h（1），h（2）}，所以有，∴，∴，解得m≥8﹣5ln2，所以实数m的取值范围是[8﹣5ln2，+∞）．点评：本题考查在闭区间上求函数最值的应用，考查运算求解能力，推理论证能力；考查函数与方程思想，化归与转化思想．综合性强，难度大，有一定的探索性，对数学思维能力要求较高，是2015届高考的重点．解题时要认真审题，仔细解答．。

山东省郓城一中2016届高三上学期第一次月考数学理试题 Word版含答案[ 高考]

郓城一中高三第一次阶段性考试数学（理）试题 2015/10一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.设全集{}{}{}()2,1,0,1,2,3,0,1,2,0,1,2,3,=U U M N C M N =--==⋂则( ) A.{}012，，B.{}213--，，C.{}03，D.{}32. 设312.021231,3log =⎪⎭⎫⎝⎛==c b a ，，则（）A. c b a >>B. c a b >>C. a c b >>D. a b c >>3..下列说法正确的是 ( )A ．命题“若21x =，则1x =”的否命题为：“若21x =，则1x ≠”B ．若命题2:,210p x R x x ∃∈-->，则命题2:,210p x R x x ⌝∀∈--<C ．命题“若x y =，则sin sin x y =”的逆否命题为真命题D ．0,23x x x ∃<<4. 函数y （）A ．[0,)+∞B ．[0,4]C ．[0,4)D ．(0,4)5.设a ，b ∈R ，那么“>1ab”是“>>0a b ”的( )A 、充分不必要条件B 、必要不充分条件C 、充要条件D 、既不充分也不必要条件6设函数()sin cos f x x x x =+的图像在点(,(())t f t 处切线的斜率为k,则函数k=g(t)的部分图像为( )7. 若)2ln(21)(2++-=x b x x f 在），（∞+-1上是减函数，则b 的取值范围是( )A.[]∞+-，1B.），（∞+-1 C.]1-∞-，（ D.），（1-∞- 8. 已知函数f (x )＝sin x ＋e x ＋x 2 010，令f 1(x )＝f ′(x )，f 2(x )＝f 1′(x )，f 3(x )＝f 2′(x )，…，f n ＋1(x )＝f n ′(x )，则f 2 011(x )等于 ( )A ．sin x ＋e xB ．cos x ＋e xC ．－sin x ＋e xD ．－cos x ＋e x9.函数()22x f x a x=--的一个零点在区间()1,2内，则实数a 的取值范围是( )A.()1,3B.()1,2C.()0,3D.()0,210. 用数学归纳法证明:“(n ＋1)·(n ＋2)·…·(n ＋n )＝2n ·1·3·…·(2n －1)”，从“k 到k ＋1”左端需增乘的代数式为 ( )A ．2k ＋1B ．2(2k ＋1)C.2k ＋1k ＋1D.2k ＋3k ＋1二、填空题：本大题共5小题，每小题5分，共25分。

全国I卷2016届高三第一学期月考(二)数学(理)试卷(含答案)

第I 卷选择题（共60分）一、选择题：本大题共12小题，每小题5分，共60分在每小题给出的四个选项中，只有一项是符合题目要求的．1．设集合U ={-2，-1，0，1，2，3，4}，A={一1，0}，B={0，1，2，3，4}，则=( )A.{-2,1}B.{-2}C.{-2,0}D.{0,1,2,3,4}2．已知命题p ，q ，“pq 为真”是“p ∨q 为真”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件3. 已知向量|a |=2,| b |=l ，且a 与b 的夹角为争则a 与a +2b 的夹角为( ) A ．6π B ．3π C ．2π D ．23π 4．已知倾斜角为θ的直线，与直线x-3y+l=0垂直，则2223sin -cos θθ=( ) A ．103 B ．一103 C ．1013 D ．一1013 5．直线y= 4x 与曲线y=x 2围成的封闭区域面积为( )A ．223B ．8C ．323D ．163 6．设a=12201441(),log 2015,log 22b c ==，则( ) A. a>b>c B. b>c>a C. b>a>c D. a>c>b7．若向量m= (-1，4)与n=(2，t)的夹角为钝角，则函数f (t)=t 2—2t+1的值域是 ( )A ．()1,8181,4⎛⎫+∞ ⎪⎝⎭ B ．1,4⎛⎫+∞ ⎪⎝⎭C. [0,81) (81,+∞)D. [0,+∞)8．在△ABC 中内角A ，B ，C 的对边分别是a ，b, c ，若a b =，，则tanA=( )A B ．1 C ．3D. 9．在边长为2的正三角形ABC 中，2,3BC BD CA CE AD BE ==⋅=，则A ．1B ．-1C ．3D ．-310．若函数f (x)= sin(2x+ϕ)满足对一切x ∈R ，都有f (x)≥()7f π成立，则下列关系式中不成立的是( )11．定义在R 上的奇函数f (x)满足f (x+1)=f （一x ），当x ∈(0，1)时，1211log ||,22()10, 2x x f x x ⎧-≠⎪=⎨⎪=⎩，则f (x)在区间[1，32]内是( ) A ．增函数且f （x ）>0 B ．增函数且f (x)<oC ．减函数且f (x)>0D ．减函数且f （x ）<012．在矩形ABCD 中，,P 为矩形内一点，且(,),53A P A B A D R λμλμμ=+∈的最大值为( ’ ABCD第II 卷非选择题（共90分）二、填空题：本大题共4小题，每小题5分，共20分13．函数()1()tan 026f x x πωω⎛⎫=-> ⎪⎝⎭的最小正周期为3π，则ω= 。

精选题库2016年山东省潍坊市高三上学期期中数学试卷含解析答案(理科)

发的 B 产品，每吨原材料创造的利润为 12（ a﹣
x）万元（ a＞0）．
第 3 页（共 19 页）
（Ⅰ）若设备升级后生产这批 A 产品的利润不低于原来生产该批 A 产品的利润，求 x 的取值范围．（Ⅱ）若生产这批 B 产品的利润始终不高于设备升级后生产这批 A 产品的利润，求 a 的最大值． 20．（ 13 分）已知递增等比数列 { an} ，满足 a1=1，且 a2a4﹣2a3a5+a4a6=36．（ 1）求数列 { an} 的通项公式；（ 2）设 bn=log3an+ ，求数列 { an2?bn} 的前 n 项和 Sn；
因为 x=1 是 f （x）的极大值点，所以﹣ ＞1，解得﹣ 1＜ a＜ 0．
综合①②： a 的取值范围是 a＞﹣ 1．故选： B．
二、填空题：本大题共 5 小题，每小题 5 分，共 25 分.
11．（ 5 分）
（1﹣2sin2 ）dx= 1 ．
【解答】解：
（1﹣2sin2 ）dx= cosxdx=sinx| =1，
（Ⅰ）求 f（）的值；
（Ⅱ）将 f（x）的图象上所有点向左平移 m（m＞ 0）个长度单位，得到 y=g（x）的图象，若 y=g（x）图象的一个对称中心为（， 0），当 m 取得最小值时，求
g（x）的单调递增区间． 19．（12 分）某公司生产一批 A 产品需要原材料 500 吨，每吨原材料可创造利润 12 万元．该公司通过设备升级，生产这批 A 产品所需原材料减少了 x 吨，且每吨原材料创造的利润提高 0.5x%；若将少用的 x 吨原材料全部用于生产公司新开
11．（ 5 分）
（1﹣2sin2 ）dx=
．
12．（ 5 分）不等式 | x| ﹣| x﹣3| ＜2 的解集为

【2016年高考数学】2016届高三数学【理】上学期第二次月考试题(含答案)_7823

第二次月考数学理试题【山东版】注意事项：1．本试题分为第Ⅰ卷和第Ⅱ卷两部分，满分150 分，考试时间为120 分钟．2．禁止使用计算器．3．答卷之前将姓名、班级等信息填写在答题卡与答题纸的相应位置.4．答卷必须使用黑色0.5 毫米中性笔，使用其它类笔不给分．画图题可先用铅笔轻轻画出，确定答案后，用中性笔重描．禁止使用透明胶带，涂改液，修正带．5．选择题填涂在答题卡上，填空题的答案抄写在答题纸纸上．解答题必须写出详细的解题步骤，必须写在答题纸相应位置，否则不予计分．第Ⅰ卷（选择题共50 分）一、选择题：每小题 5 分，共10 题，50 分．1．已知集合A＝{0,1, 2,3} ，集合 B { x N || x | 2} ，则 A B =（）A．{ 3 } B．{0 ，1，2} C．{ 1 ，2} D．{0 ，1，2，3}2．若f (x ) 3，则0 limh 0f (x h) f (x h)0 0h（）A． 3 B ． 6 C ．9 D ．122 x3．函数f ( x) ln( x ) 的定义域为（）A. (0 ,1)B. [ 0,1]C. ( ,0) (1, )D. ( ,0] [1, )4．已知函数|x| 2 x a Rf (x) 5 ，g(x) ax ( ) ，若 f [g (1)] 1，则a （）A.1B. 2C. 3D. -13 x25．已知 f ( x), g( x) 分别是定义在R上的偶函数和奇函数，且 f (x) g(x) x 1，则f (1)g (1) （）A. 3B. 1C. 1D. 36．已知集合 A ={2 ，0，1，4} ，B ={ k | k R ，k2 2 A，k 2 A} ，则集合 B 中所有元素之和为（）A．2 B ．-2 C ．0 D ． 27．曲线x 1y xe 在点（1,1 ）处切线的斜率等于（）A．2e B ．e C ．2 D ． 18．若12f (x) x 2 f ( x )dx, 则1f ( x) dx （）A. 1B. 13C.13D.19．下列四个图中，函数y= 101n x 1x 1的图象可能是（）A B C D3 210．如图所示的是函数 f (x) x bx cx d 的大致图象，则2 2x1 x 等于（）2A．23B．43C．83D．163第Ⅱ卷（非选择题共100 分）二、填空题：每小题 5 分，共 5 题，25 分．t11．物体运动方程为S 2 3，则t 2 时瞬时速度为12．已知 f (x) =2lg( a)1 x是奇函数，则实数a的值是13．如图所示，已知抛物线拱形的底边弦长为a，拱高为b ，其面积为____________．14．不等式 6 ( 2) ( 2)3 2x x x x 的解集为____________．x15．已知 f (x) 为R 上增函数，且对任意x R，都有 f f (x) 3 4，则 f (2)____________．三、解答题：共 6 小题，75 分．写出必要文字说明、证明过程及演算步骤.16．(本小题满分12 分)已知函数 f (x) 的定义域为( 2, 2) ，函数g(x) f (x1) f (3 2x)（Ⅰ）求函数g( x) 的定义域；（Ⅱ）若 f (x) 是奇函数，且在定义域上单调递减，求不等式g (x) 0的解集.17．(本小题满分12 分)已知曲线 3 2y x x 在点P 处的切线l1 平行直线4x y 1 0 ，且点P0 在第三象限. 0（Ⅰ）求P的坐标；（Ⅱ）若直线l l , 且l 也过切点P0 , 求直线l 的方程.118．（本小题满分12 分）若实数x 满足f (x0) x0，则称x x0 为f (x) 的不动点．已知函数03f ( x) x bx 3，其中b 为常数．（Ⅰ）求函数 f (x) 的单调递增区间；（Ⅱ）若存在一个实数x，使得x x0 既是 f (x) 的不动点，又是 f (x) 的极值点．求实数 b 的值；19．（本小题满分12 分）统计表明，某种型号的汽车在匀速行驶中每小时的耗油量y （升）关于行驶速度x（千米/ 小时）的函数解析式可以表示为：1 33y x x 8 (0 x 120)128000 80已知甲、乙两地相距100 千米（Ⅰ）当汽车以40 千米/ 小时的速度匀速行驶时，从甲地到乙地要耗油多少升？（Ⅱ）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？20．(本小题满分13 分)已知函数f ( x) ln x (x 0), 函数( ) 1 ( )( 0)g x af x xf (x)（Ⅰ）当x 0 时, 求函数y g(x) 的表达式;（Ⅱ）若 a 0 , 函数y g(x) 在(0, ) 上的最小值是 2 , 求a的值;（Ⅲ）在（Ⅱ）的条件下, 求直线2 7y x 与函数y g(x) 的图象所围成图形的面积.3 621．（本小题满分14 分）2 mx设关于x的方程 1 0x 有两个实根, , ，函数2x m f x 。

2016届山东省青岛市平度市高三(上)12月月考数学试卷(理科)(解析版)

2015-2016学年山东省青岛市平度市高三（上）12月月考数学试卷（理科）参考答案与试题解析一、选择题：本大题共10小题．每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．若集合A={x|lg（1﹣x）＜0}，集合B={x||x﹣1|＜2}，则A∩B=（）A．（﹣1，0）B．（0，3） C．（﹣1，1）D．（0，1）【考点】交集及其运算．【专题】计算题；集合思想；定义法；不等式的解法及应用；集合．【分析】直接解对数不等式化简集合A，解绝对值不等式化简集合B，则A∩B的答案可求．【解答】解：由集合A={x|lg（1﹣x）＜0}={x|0＜x＜1}，集合B={x||x﹣1|＜2}={x|﹣1＜x ＜3}，则A∩B={x|0＜x＜1}∩{x|﹣1＜x＜3}=（0，1）．故选：D．【点评】本题考查了交集及其运算，考查了对数不等式和绝对值不等式的解法，是基础题．2．已知命题p、q，则“p且q为假”是“p或q为真”的（）A．充分不必要条件B．必要不充分条件C．充要条件 D．既不充分也不必要条件【考点】复合命题的真假．【专题】简易逻辑．【分析】根据复合命题的真假与构成其简单命题真假的关系，得出判断．【解答】解：“p且q为假”，p、q都可为假，故充分性不成立；“p或q为真”，p、q都可为真，故必要性不成立；故选D．【点评】本题考查充分、必要与充要条件的判断，属于基础题，要掌握判断充要条件的方法．3．向量，，且∥，则cos2α=（）A． B． C． D．【考点】两角和与差的余弦函数．【专题】计算题；三角函数的求值．【分析】根据向量平行的条件建立关于α的等式，利用同角三角函数的基本关系算出sinα=，再由二倍角的余弦公式加以计算，可得cos2α的值．【解答】解：∵，，且∥，∴，即，化简得sinα=，∴cos2α=1﹣2sin2α=1﹣=故选：D【点评】本题给出向量含有三角函数的坐标式，在向量互相平行的情况下求cos2α的值．着重考查了同角三角函数的基本关系、二倍角的三角函数公式和向量平行的条件等知识，属于基础题．4．设m、n是两条不同的直线，α、β是两个不同的平面，下列命题中错误的是（）A．若m⊥α，m∥n，n∥β，则α⊥βB．若α⊥β，m⊄α，m⊥β，则m∥αC．若m⊥β，m⊂α，则α⊥βD．若α⊥β，m⊂α，n⊂β，则m⊥n【考点】空间中直线与平面之间的位置关系．【分析】利用空间中线线、线面、面面间的位置关系求解．【解答】解：若m⊥α，m∥n，n∥β，则由平面与平面垂直的判定定理得α⊥β，故A正确；若α⊥β，m⊄α，m⊥β，则由直线与平面平行的判定定理得m∥α，故B正确；若m⊥β，m⊂α，则由平面与平面垂直的判定定理得α⊥β，故C正确；若α⊥β，m⊂α，n⊂β，则m与n相交、平行或异面，故D错误．故选：D．【点评】本题考查命题真假的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．5．不等式组所围成的封闭图形的面积为（）A ．B ．2C ．4D ．【考点】简单线性规划．【专题】计算题；转化思想；分割补形法；不等式．【分析】由题意画出图象，求出交点坐标，然后利用定积分求封闭图形的面积．【解答】解：由约束条件作出可行域如图，联立，解得：C （4，2），∴不等式组所围成的封闭图形的面积为：S===．故选：A ．【点评】本题考查基地的线性规划，考查了利用定积分求曲边梯形的面积，体现了数形结合的解题思想方法，是中档题．6．设实数数列{a n }，{b n }分别为等差数列与等比数列，且a 1=b 1=4，a 4=b 4=1，则以下结论正确的是（）A ．a 1＞b 2B ．a 3＜b 3C ．a 5＞b 5D ．a 6＞b 6【考点】等比数列的通项公式；等差数列的通项公式．【专题】方程思想；转化思想；等差数列与等比数列．【分析】利用等差数列与等比数列的通项公式即可得出．【解答】解：设等差数列{a n}的公差为d，等比数列{b n}的公比为q，∵a1=b1=4，a4=b4=1，∴4+3d=4q3=1，解得d=﹣1，q3=．∴a n=4﹣（n﹣1）=5﹣n，b n=4×q n﹣1=．由于b2==＜=4=a1，∴A正确，故选：A．【点评】本题考查了等差数列与等比数列的通项公式，考查了推理能力与计算能力，属于中档题．7．若正实数a，b满足a+b=1，则（）A．有最大值4 B．ab有最小值C．有最大值D．a2+b2有最小值【考点】基本不等式．【专题】计算题．【分析】由于==2+≥4，故A不正确．由基本不等式可得a+b=1≥2，可得ab≤，故B不正确．由于=1+2≤2，故≤，故C 正确．由a2+b2 =（a+b）2﹣2ab≥1﹣=，故D不正确．【解答】解：∵正实数a，b满足a+b=1，∴==2+≥2+2=4，故有最小值4，故A不正确．由基本不等式可得a+b=1≥2，∴ab≤，故ab有最大值，故B不正确．由于=a+b+2=1+2≤2，∴≤，故有最大值为，故C正确．∵a2+b2 =（a+b）2﹣2ab=1﹣2ab≥1﹣=，故a2+b2有最小值，故D不正确．故选：C．【点评】本题考查基本不等式的应用，注意检验等号成立的条件，式子的变形是解题的关键，属于基础题．8．已知函数f（x）=x2+mx+1，若命题“∃x0＞0，f（x0）＜0”为真，则m的取值范围是（）A．（﹣∞，﹣2]B．[2，+∞）C．（﹣∞，﹣2）D．（2，+∞）【考点】特称命题；命题的否定．【专题】不等式的解法及应用．【分析】根据“命题“∃x0＞0，f（x0）＜0”为真”，不等式对应的是二次函数，利用二次的图象与性质加以解决即可．【解答】解：因为函数f（x）=x2+mx+1的图象过点（0，1），若命题“∃x0＞0，f（x0）＜0”为真，则函数f（x）=x2+mx+1的图象的对称轴必在y轴的右侧，且与x轴有两个交点，∴△=m2﹣4＞0，且﹣＞0，即m＜﹣2，则m的取值范围是：（﹣∞，﹣2）．故选C．【点评】本题考查特称命题、二次不等式恒成立，解决此类问题要结合二次函数的图象处理．9．设定义在R上的奇函数y=f（x），满足对任意t∈R都有f（t）=f（1﹣t），且时，f（x）=﹣x2，则f（2015）的值等于（）A． B． C．0 D．【考点】函数的值．【专题】计算题；转化思想；函数的性质及应用．【分析】根据已知可得函数y=f（x）是周期为2的周期函数，结合时，f（x）=﹣x2，可得答案．【解答】解：∵函数y=f（x）是定义在R上的奇函数，且f（t）=f（1﹣t），∴f（x+2）=f[1﹣（x+2）]=f（﹣x﹣1）=﹣f（x+1）=﹣f[1﹣（x+1）]=﹣f（﹣x）=f（x），即函数y=f（x）是周期为2的周期函数，故f（2015）=f（1）=﹣f（0），又∵时，f（x）=﹣x2，∴f（2015）=f（1）=﹣f（0）=0，故选：C【点评】本题考查的知识点是函数的奇偶性，函数的对称性，函数的周期性，函数求值，根据已知分析出函数y=f（x）是周期为2的周期函数，是解答的关键．10．设a n=sin，S n=a1+a2+…+a n，在S1，S2，…S100中，正数的个数是（）A．25 B．50 C．75 D．100【考点】数列的求和；三角函数的周期性及其求法．【专题】计算题；压轴题．【分析】由于f（n）=sin的周期T=50，由正弦函数性质可知，a1，a2，…，a24＞0，a26，a27，…，a49＜0，f（n）=单调递减，a25=0，a26…a50都为负数，但是|a26|＜a1，|a27|＜a2，…，|a49|＜a24，从而可判断【解答】解：由于f（n）=sin的周期T=50由正弦函数性质可知，a1，a2，…，a24＞0，a25=0，a26，a27，…，a49＜0，a50=0且sin，sin…但是f（n）=单调递减a26…a49都为负数，但是|a26|＜a1，|a27|＜a2，…，|a49|＜a24∴S1，S2，…，S25中都为正，而S26，S27，…，S50都为正同理S1，S2，…，s75都为正，S1，S2，…，s75，…，s100都为正，故选D【点评】本题主要考查了三角函数的周期的应用，数列求和的应用，解题的关键是正弦函数性质的灵活应用．二、填空：本大题共5小题，每小题5分，共25分．11．已知函数f（x）=，则f（f（））的值是=﹣2．【考点】对数的运算性质；函数的值．【专题】计算题；函数的性质及应用．【分析】利于抑制投机求出f（）的值，然后求解所求表达式的值．【解答】解：∵函数，∴f（）=2+=4．=f（4）==﹣2．故答案为：﹣2．【点评】本题考查函数值的求法，指数以及对数的运算法则，解题方法是由里及外逐步求解，考查计算能力．12．在△ABC中，若=3，b2﹣a2=ac，则cosB的值为．【考点】正弦定理；余弦定理．【专题】方程思想；转化思想；解三角形．【分析】由=3，利用正弦定理可得，代入b2﹣a2=ac，可得b2=．再利用余弦定理即可得出．【解答】解：在△ABC中，∵=3，∴，∴c=3a，代入b2﹣a2=ac，解得b2=．则cosB===．故答案为：．【点评】本题考查了正弦定理余弦定理的应用，考查了推理能力与计算能力，属于中档题．13．观察下列等式：12=112﹣22=﹣312﹣22+32=612﹣22+32﹣42=﹣10…照此规律，第n个等式可为．【考点】归纳推理．【专题】压轴题；规律型．【分析】等式的左边是正整数的平方和或差，根据这一规律得第n个等式左边为12﹣22+32﹣42+…（﹣1）n﹣1n2．再分n为奇数和偶数讨论，结合分组求和法求和，最后利用字母表示即可．【解答】解：观察下列等式：12=112﹣22=﹣312﹣22+32=612﹣22+32﹣42=﹣10…分n为奇数和偶数讨论：第n个等式左边为12﹣22+32﹣42+…（﹣1）n﹣1n2．当n为偶数时，分组求和（12﹣22）+（32﹣42）+…+[（n﹣1）2﹣n2]=﹣，当n为奇数时，第n个等式左边=（12﹣22）+（32﹣42）+…+[（n﹣2）2﹣（n﹣1）2]+n2=﹣+n2=．综上，第n个等式为．故答案为：．【点评】本题考查规律型中的数字变化问题，找等式的规律时，既要分别看左右两边的规律，还要注意看左右两边之间的联系．14．一个直棱柱被一个平面截去一部分后所剩几何体的三视图如图所示，则该几何体的体积为11．【考点】由三视图求面积、体积．【专题】数形结合；数形结合法；立体几何．【分析】该几何体为长方体切去一个棱锥得到的，作出直观图，使用作差法求体积．【解答】解：由三视图可知该几何体为长方体切去一个棱锥A′﹣AMD′得到的，直观图如图所示，∴V=2×2×3﹣××1×2×3=11．故答案为11．【点评】本题考查了常见几何体的三视图和体积计算，对于不规则几何体常采用作差法，分解法等求体积．15．若函数f（x）满足：存在非零常数a，使f（x）=﹣f（2a﹣x），则称f（x）为“准奇函数”，给出下列函数：①f（x）=x2；②f（x）=（x﹣1）3；③f（x）=e x﹣1；④f（x）=cosx．则以上函数中是“准奇函数”的序号是②④．【考点】抽象函数及其应用．【专题】计算题；新定义；数形结合；函数的性质及应用．【分析】根据准奇函数的定义，先求﹣f（2a﹣x），并判断它能否等于f（x），并根据﹣f （2a﹣x）=f（x）求出a，若a≠0便得到该函数是准奇函数，若a=0便不是．按照这个方法即可判断每个选项的函数是否为准奇函数．【解答】解：A．﹣f（2a﹣x）=﹣（2a﹣x）2≤0，f（x）=x2≥0，∴f（x）=x2不是准奇函数；B．由﹣f（2a﹣x）=﹣（2a﹣x﹣1）3=（x﹣2a+1）3=（x﹣1）3得，﹣2a+1=﹣1，∴a=1，即存在a=1，使f（x）=﹣f（2a﹣x）；∴该函数为准奇函数；C．﹣f（2a﹣x）=﹣e2a﹣x﹣1＜0，而f（x）=e x﹣1＞0，∴该函数不是准奇函数；D．存在非零常数，使﹣f（2×﹣x）=﹣cos（2×﹣x）=cosx=f（x），∴该函数是准奇函数．故答案为：②④．【点评】考查对新概念﹣准奇函数的理解程度，以及根据准奇函数的定义判断一个函数是否为准奇函数的过程．三、解答题：本大题共6小题，共75分，解答时应写出必要的文字说明、证明过程或演算步骤．16．已知函数f（x）=2sinωxcosωx+2sin2ωx﹣（ω＞0）的最小正周期为π．（Ⅰ）求函数f（x）的单调增区间；（Ⅱ）将函数f（x）的图象向左平移个单位，再向上平移1个单位，得到函数y=g（x）的图象．若y=g（x）在[0，b）（b＞0）上至少含有10个零点，求b的最小值．【考点】两角和与差的正弦函数；函数的零点与方程根的关系；正弦函数的单调性；函数y=Asin（ωx+φ）的图象变换．【专题】计算题；三角函数的图像与性质．【分析】（I）根据二倍角的三角函数公式与辅助角公式化简得，利用周期公式算出ω=1，得函数解析式为．再由正弦函数单调区间的公式，解关于x的不等式即可得到函数f（x）的单调增区间；（II）根据函数图象平移的公式，得出函数g（x）的解析式为g（x）=2sin2x+1．由此解g（x）=0得sin2x=﹣，利用正弦函数的图象解出或，可见g（x）在每个周期上恰有两个零点，若g（x）在[0，b]上至少含有10个零点，则b大于或等于g（x）在原点右侧的第10个零点，由此即可算出b的最小值．【解答】解：（Ⅰ）由题意，可得f（x）==．∵函数的最小正周期为π，∴=π，解之得ω=1．由此可得函数的解析式为．令，解之得∴函数f（x）的单调增区间是．（Ⅱ）将函数f（x）的图象向左平移个单位，再向上平移1个单位，可得函数y=f（x+）+1的图象，∵∴g（x）=+1=2sin2x+1，可得y=g（x）的解析式为g（x）=2sin2x+1．令g（x）=0，得sin2x=﹣，可得2x=或2x=解之得或．∴函数g（x）在每个周期上恰有两个零点，若y=g（x）在[0，b]上至少含有10个零点，则b不小于第10个零点的横坐标即可，即b的最小值为．【点评】本题给出三角函数式满足的条件，求函数的单调区间并依此求解函数g（x）在[0，b]上零点的个数的问题．着重考查了二倍角的三角函数公式、辅助角公式与三角函数的图象与性质等知识，属于中档题．17．把边长为a的等边三角形铁皮剪去三个相同的四边形（如图阴影部分）后，用剩余部分做成一个无盖的正三棱柱形容器（不计接缝），设容器的高为x，容积为V（x）．（Ⅰ）写出函数V（x）的解析式，并求出函数的定义域；（Ⅱ）求当x为多少时，容器的容积最大？并求出最大容积．【考点】利用导数求闭区间上函数的最值；函数模型的选择与应用．【专题】综合题．【分析】（Ⅰ）根据容器的高为x，求得做成的正三棱柱形容器的底边长，从而可得函数V （x）的解析式，函数的定义域；（Ⅱ）实际问题归结为求函数V（x）在区间上的最大值点，先求V（x）的极值点，再确定极大值就是最大值即可．【解答】解：（Ⅰ）因为容器的高为x，则做成的正三棱柱形容器的底边长为﹣﹣﹣﹣．则．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣函数的定义域为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣（Ⅱ）实际问题归结为求函数V（x）在区间上的最大值点．先求V（x）的极值点．在开区间内，﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣令V'（x ）=0，即令，解得（舍去）．因为在区间内，x 1可能是极值点．当0＜x ＜x 1时，V'（x ）＞0；当时，V'（x ）＜0．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣因此x 1是极大值点，且在区间内，x 1是唯一的极值点，所以是V （x ）的最大值点，并且最大值即当正三棱柱形容器高为时，容器的容积最大为．﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣【点评】本题考查函数模型的构建，考查导数知识的运用，解题的关键是求出体积，利用导数知识求解．单峰函数，极值就是最值．18．在如图所示的空间几何体中，平面ACD ⊥平面ABC ，△ACD 与△ACB 是边长为2的等边三角形，BE=2，BE 和平面ABC 所成的角为60°，且点E 在平面ABC 上的射影落在∠ABC 的平分线上．（Ⅰ）求证：DE ∥平面ABC ；（Ⅱ）求二面角E ﹣BC ﹣A 的余弦值．【考点】用空间向量求平面间的夹角；直线与平面平行的判定；与二面角有关的立体几何综合题．【专题】空间位置关系与距离；空间向量及应用．【分析】（Ⅰ）取AC 中点O ，连接BO ，DO ，由题设条件推导出DO ⊥平面ABC ，作EF ⊥平面ABC ，由已知条件推导出∠EBF=60°，由此能证明DE ∥平面ABC ．（Ⅱ）法一：作FG⊥BC，垂足为G，连接EG，能推导出∠EGF就是二面角E﹣BC﹣A的平面角，由此能求出二面角E﹣BC﹣A的余弦值．法二：以OA为x轴，以OB为y轴，以OD为z轴，建立空间直角坐标系O﹣xyz，利用向量法能求出二面角E﹣BC﹣A的余弦值．【解答】（本小题满分12分）解：（Ⅰ）由题意知，△ABC，△ACD都是边长为2的等边三角形，取AC中点O，连接BO，DO，则BO⊥AC，DO⊥AC，…又∵平面ACD⊥平面ABC，∴DO⊥平面ABC，作EF⊥平面ABC，那么EF∥DO，根据题意，点F落在BO上，∵BE和平面ABC所成的角为60°，∴∠EBF=60°，∵BE=2，∴，…∴四边形DEFO是平行四边形，∴DE∥OF，∵DE不包含于平面ABC，OF⊂平面ABC，∴DE∥平面ABC．…（Ⅱ）解法一：作FG⊥BC，垂足为G，连接EG，∵EF⊥平面ABC，∴EF⊥BC，又EF∩FG=F，∴BC⊥平面EFG，∴EG⊥BC，∴∠EGF就是二面角E﹣BC﹣A的平面角．…Rt△EFG中，，，．∴．即二面角E﹣BC﹣A的余弦值为．…解法二：建立如图所示的空间直角坐标系O﹣xyz，B（0，，0），C（﹣1，0，0），E（0，，），∴=（﹣1，﹣，0），=（0，﹣1，），平面ABC的一个法向量为设平面BCE的一个法向量为则，∴，∴．…所以，又由图知，所求二面角的平面角是锐角，二面角E﹣BC﹣A的余弦值为．…【点评】本题考查直线与平面平行的证明，考查二面角的余弦值的求法，解题时要注意空间思维能力的培养，注意向量法的合理运用．19．设函数的图象在点（x，f（x））处的切线的斜率为k（x），且函数为偶函数．若函数k（x）满足下列条件：①k（﹣1）=0；②对一切实数x，不等式恒成立．（Ⅰ）求函数k（x）的表达式；（Ⅱ）求证：（n∈N*）．【考点】综合法与分析法(选修）；函数奇偶性的性质；函数恒成立问题；利用导数研究曲线上某点切线方程．【专题】证明题．【分析】（Ⅰ）由已知得：k（x）=f'（x），根据g（x）的奇偶性求出b，根据k（﹣1）=0，求出，再由对一切实数x恒成立，解得a、c的值，即得函数k（x）的表达式．（Ⅱ）根据，即证，把代入要证不等式的左边化简即可证得不等式成立．【解答】解：（Ⅰ）由已知得：k（x）=f'（x）=ax2+bx+c．…由为偶函数，得为偶函数，显然有．…又k（﹣1）=0，所以a﹣b+c=0，即．…又因为对一切实数x恒成立，即对一切实数x，不等式恒成立．…显然，当时，不符合题意．…当时，应满足，注意到，解得．…所以．…（Ⅱ）证明：因为，所以．…要证不等式成立，即证．…因为，…所以=．所以成立．…【点评】本题主要考查函数的奇偶性的应用，函数的恒成立问题，利用导数研究曲线在某点的切线斜率，以及用裂项法对数列进行求和，属于难题．20．设等差数列{a n}的前n项和为S n，且（c是常数，n∈N*），a2=6．（Ⅰ）求c的值及数列{a n}的通项公式；（Ⅱ）设，数列{b n}的前n项和为T n，若2T n＞m﹣2对n∈N*恒成立，求最大正整数m的值．【考点】数列的求和；数列递推式．【专题】方程思想；转化思想；综合法；等差数列与等比数列．【分析】（I）利用递推关系、等差数列的通项公式即可得出；（II）利用“错位相减法”、等比数列的前n项和公式即可得出．【解答】解：（Ⅰ）∵，当n=1时，，解得a1=2c，当n=2时，S2=a2+a2﹣c，即a1+a2=a2+a2﹣c，解得a2=3c，∴3c=6，解得c=2．则a1=4，数列{a n}的公差d=a2﹣a1=2，∴a n=a1+（n﹣1）d=2n+2．（Ⅱ）∵，∴①②①﹣②得，∴，∵，∴数列{T n}单调递增，T1最小，最小值为，∴，∴m＜3，故正整数m的最大值为2．【点评】本题考查了递推关系、“错位相减法”、等差数列与等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．21．（2015•南昌校级二模）已知函数f（x）=lnx﹣mx2，g（x）=+x，m∈R令F（x）=f（x）+g（x）．（Ⅰ）当m=时，求函数f（x）的单调递增区间；（Ⅱ）若关于x的不等式F（x）≤mx﹣1恒成立，求整数m的最小值；（Ⅲ）若m=﹣2，正实数x1，x2满足F（x1）+F（x2）+x1x2=0，证明：x1+x2．【考点】导数在最大值、最小值问题中的应用；利用导数研究函数的单调性．【专题】函数的性质及应用；导数的综合应用．【分析】（1）先求函数的定义域，然后求导，通过导数大于零得到增区间；（2）不等式恒成立问题转化为函数的最值问题，应先求导数，研究函数的单调性，然后求函数的最值；（3）联系函数的F（x）的单调性，然后证明即可．注意对函数的构造．【解答】解：（1）．由f′（x）＞0得1﹣x2＞0又x＞0，所以0＜x＜1．所以f（x）的单增区间为（0，1）．（2）令x+1．所以=．当m≤0时，因为x＞0，所以G′（x）＞0所以G（x）在（0，+∞）上是递增函数，又因为G（1）=﹣．所以关于x的不等式G（x）≤0不能恒成立．当m＞0时，．令G′（x）=0得x=，所以当时，G′（x）＞0；当时，G′（x）＜0．因此函数G（x）在是增函数，在是减函数．故函数G（x）的最大值为．令h（m）=，因为h（1）=，h（2）=．又因为h（m）在m∈（0，+∞）上是减函数，所以当m≥2时，h（m）＜0．所以整数m的最小值为2．（3）当m=﹣2时，F（x）=lnx+x2+x，x＞0．由F（x1）+F（x2）+x1x2=0，即lnx1+x12+x1+lnx2+x22+x2+x1x2=0．化简得．令t=x1x2，则由φ（t）=t﹣lnt得φ′（t）=．可知φ（t）在区间（0，1）上单调递减，在区间（1，+∞）上单调递增．所以φ（t）≥φ（1）=1．所以，即成立．【点评】本题考查了利用导数研究函数的单调性的基本思路，不等式恒成立问题转化为函数最值问题来解的方法．属于中档题，难度不大．。

【山东版】高三上学期月考(1)数学(理) Word版含答案.pdf

2015届上学期高三一轮复习第一次月考试题【版】注意事项： 1. 本试题共分22大题，全卷共150分。

考试时间为120分钟。

2．第I卷必须使用2B铅笔填涂答题纸相应题目的答案标号，修改时，要用橡皮擦干净。

3. 第II卷必须使用0.5毫米的黑色墨水签字笔书写在答题纸的指定位置，在草稿纸和本卷上答题无效。

作图时，可用2B铅笔，要求字体工整、笔迹清晰。

第I卷（共60分）选择题 (本大题共12个小题；每小题5分，共60分．在每小题给出的4个选项中，只有一项符合题目要求.) 1．已知集合,则等于（） A．B．C．D． 2．设f(x)＝lg，则f＋f的定义域为( ) A．(－4,0)∪(0,4) B．(－4，－1)∪(1,4) C．(－2，－1)∪(1,2) D．(－4，－2)∪(2,4) 3．命题“所有能被2整除的整数都是偶数”的否定是( ) A．所有不能被2整除的整数都是偶数 B．所有能被2整除的整数都不是偶数 C．存在一个不能被2整除的整数是偶数 D．存在一个能被2整除的整数不是偶数 4．设函数，则满足的x的取值范围是( ) A．，2]B．[0，2]C．[1，+)D．[0，+) 5．若函数，则下列结论正确的是（） A．，在上是增函数 B．，在上是减函数 C．，是偶函数 D．，是奇函数 6．一个篮球运动员投篮一次得3分的概率为，得2分的概率为，不得分的概率为，，已知他投篮一次得分的期望是2，则的最小值为（） A．B．C．D． 7．已知函数的定义域为,且为偶函数,则实数的值可以是（） A．B．C．D． 8．已知函数,当x=a时,取得最小值,则在直角坐标系中,函数的大致图象为 9．对于集合M、N，定义M－N＝{x|x∈M且x?N}，MN＝(M－N)∪(N－M)，设A＝{y|y＝3x，x∈R}，B＝{y|y＝－(x－1)2＋2，x∈R}，则AB等于( ) A．[0,2) B．(0,2] C．(－∞，0]∪(2，＋∞) D．(－∞，0)∪[2，＋∞) 10．已知函数在区间上有最大值3，最小值2，则的取值范围是( ) A．B．C．D． 11．对于任意两个正整数,定义某种运算“※”如下:当都为正偶数或正奇数时,※=;当中一个为正偶数,另一个为正奇数时,※=．则在此定义下,集合※中的元素个数是( ) A．10个B．15个C．16个D．18个 12．已知函数y＝f(x)的周期为2，当x∈[－1,1]时f(x)＝x2，那么函数y＝f(x)的图象与函数y＝|lgx|的图象的交点共有( ) A．10个 B．9个 C．8个 D．1个第II卷（非选择题，共90分）二、填空题(本大题共4小题，每小题4分，共16分,请将答案填在答题纸上) 13．已知集合A＝{(x，y)|}，集合B＝{(x，y)|3x＋2y－m＝0}，若A∩B≠?，则实数m的最小值等于__________． 14．若(a＋1)＜(3－2a)，则a的取值范围是__________． 15．用二分法求方程x2＝2的正实根的近似解(精确度0.001)时，如果我们选取初始区间是[1.4,1.5]，则要达到精确度要求至少需要计算的次数是__________次． 16．下列结论中是真命题的是__________(填序号)． ①f(x)＝ax2＋bx＋c在[0，＋∞)上是增函数的一个充分条件是－＜0； ②已知甲：x＋y≠3，乙：x≠1或y≠2，则甲是乙的充分不必要条件； ③数列{an}(n∈N*)是等差数列的充要条件是Pn是共线的．三、解答题:本大题共6小题，共74分，解答应写出文字说明，证明过程或演算步骤. 17. （本小题满分12分）已知集合A＝{x∈R|≥1}，集合B＝{x∈R|y＝}，若A∪B＝A，求实数m的取值范围． 18．（本小题满分12分）已知函数f(x)＝x2＋4ax＋2a＋6. (1)若函数f(x)的值域为[0，＋∞)，求a的值； (2)若函数f(x)的函数值均为非负数，求f(a)＝2－a|a＋3|的值域． 19．（本小题满分12分）已知函数为偶函数. (Ⅰ) 求的值; (Ⅱ) 若方程有且只有一个根, 求实数的取值范围. 20．（本小题满分12分）提高过江大桥的车辆通行能力可改善整个城市的交通状况．在一般情况下，大桥上的车流速度v(单位：千米/小时)是车流密度x(单位：辆/千米)的函数，当桥上的车流密度达到200辆/千米时，造成堵塞，此时车流速度为0；当车流密度不超过20辆/千米时，车流速度为60千米/小时．研究表明：当20≤x≤200时，车流速度v是车流密度x的一次函数． (1)当0≤x≤200时，求函数v(x)的表达式； (2)当车流密度x为多大时，车流量(单位时间内通过桥上某观测点的车辆数，单位：辆/小时)f(x)＝x·v(x)可以达到最大，并求出最大值．(精确到1辆/小时) 21．（本小题满分12分）已知p：?x∈R,2x＞m(x2＋1)，q：?x0∈R，x＋2x0－m－1＝0，且p∧q为真，求实数m的取值范围． 22．（本小题满分14分）设函数f (θ)＝sinθ＋cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P(x，y)，且0≤θ≤π. (1)若点P的坐标为(，)，求f(θ)的值； (2)若点P(x，y)为平面区域Ω：，上的一个动点，试确定角θ的取值范围，并求函数f(θ)的最小值和最大值．一、选择题 1. B ,所以,选B． 2. B 由，得f(x)的定义域为{x|－2＜x＜2}. 故－2＜＜2，－2＜＜2.解得x∈(－4，－1)∪(1, 4)． 3 .D 否定原题结论的同时要把量词做相应改变，故选D. 4.D 5.C 对于时有是一个偶函数. 6.D 7.B 因为函数为偶函数,所以,即函数关于对称, 所以区间关于对称,所以,即,所以选B． 8 B ,因为,所以,所以由均值不等式得,当且仅当, 即,所以时取等号,所以,所以,又,所以选B. 9. C 由题可知，集合A＝{y|y＞0}，B＝{y|y≤2}，所以A－B＝{y|y＞2}，B－A＝{y|y≤0}，所以AB＝(－∞，0]∪ (2，＋∞)，故选C. 10.D11.B 12 .A 画出两个函数图象可看出交点有10个．二、填空题 13. 5 A∩B≠?说明直线与平面区域有公共点，因此问题转化为：求当x，y满足约束条件x≥1，x≤y，2x－y≤1时，目标函数m＝3x＋2y的最小值．在平面直角坐标系中画出不等式组表示的可行域．可以求得在点(1,1)处，目标函数m＝3x＋2y取得最小值5. 14. ∵函数在定义域(0，＋∞)上递减，∴a＋1＞0，3－2a＞0，a＋1＞3－2a，即＜a＜. 15. 7 设至少需要计算n次，则n满足，即，由于，故要达到精确度要求至少需要计算7次． 16. ②③ ①f(x)＝ax2＋bx＋c在[0，＋∞)上是增函数，则必有a＞0，，故①不正确．②x＝1且y＝2，则x＋y＝3. 从而逆否命题是充分不必要条件，故②正确． ③若{an}是等差数列，则Sn＝An2＋Bn，即＝An＋B，故③正确．三、解答题 17解：由题意得：A＝{x∈R|}＝(－1,2]， B＝{x∈R|x2－x＋m－m2≤0}＝{x∈R|(x－m)(x－1＋m)≤ 0} 由A∪B＝A知B?A，得－1＜m≤2，－1＜1－m≤2，解得：－1＜m＜2. 18解：(1)∵函数的值域为[0，＋∞)， ∴Δ＝16a2－4(2a＋6)＝0, ∴2a2－a－3＝0, ∴a＝－1或a＝. (2)∵对一切x∈R函数值均为非负，∴Δ＝8 (2a2－a －3)≤0, ∴－1≤a≤，∴a＋3＞0， ∴f(a)＝2－a|a＋3|＝－a2－3a＋2＝－. ∵二次函数f(a)在上单调递减， ∴≤f(a)≤f(－1)，即－≤f(a)≤4，∴f(a)的值域为[－，4]. 19解：（1）因为为偶函数，所以即，∴ ∴，∴ (2）依题意知： ∴由得 ∴ 令，则*变为只需其有一正根. (1）不合题意 (2）*式有一正一负根，经验证满足 (3）两相等正根，经验证 20解：(1)由题意：当0≤x≤20时，v(x)＝60；当20≤x≤200时，设v(x)＝ax＋b，再由已知得200a＋b＝0，20a＋b＝60，解得a＝－，b＝. 故函数v(x)的表达式为 (2)依题意并由(1)可得 . 当0≤x≤20时，f(x)为增函数，故当x＝20时，其最大值为60×20＝1200；当20≤x≤200时，≤，当且仅当x＝200－x，即x＝100时，等号成立．所以，当x＝100时，f(x)在区间[20,200]上取得最大值. 综上，当x＝100时，f(x)在区间[0,200]上取得最大值≈3333，即当车流密度为100辆/千米时，车流量可以达到最大，最大值约为3333辆/小时． 21解：2x＞m(x2＋1) 可化为mx2－2x＋m＜0. 若p：?x∈R, 2x＞m(x2＋1)为真，则mx2－2x＋m＜0对任意的x∈R恒成立．当m＝0时，不等式可化为－2x＜0，显然不恒成立；当m≠0时，有m＜0，Δ=4－4m2＜0，∴m＜－1. 若q：?x0∈R，＋2x0－m－1＝0为真，则方程x2＋2x－m－1＝0有实根， ∴Δ=4＋4(m＋1)≥0，∴m≥－2. 又p∧q为真，故p、q 均为真命题． ∴m＜－1且m≥－2，∴－2≤m＜－1. 22解：(1)由点P的坐标和三角函数的定义可得sinθ＝，cosθ＝. 于是f(θ)＝sinθ＋cos θ＝＝2. (2)作出平面区域Ω(即三角区域ABC)如图所示，其中A(1,0)，B(1,1)，C(0,1)．于是0≤θ≤. 又f(θ)＝sinθ＋cosθ＝2sin(θ＋)，且≤θ＋≤，故当θ＋＝，即θ＝时，f(θ)取得最大值，且最大值等于2 ；当θ＋＝，即θ＝0时，f(θ)取得最小值，且最小值等于1. 。