浙江省杭州市建人高复学校2013届高三第一次月考数学(理)试题
【VIP专享】浙江省杭州建人高复学校2013届高三高考仿真模拟文科数学试题 word版
（7）把一颗骰子投掷两次，第一次得到的点数记为 a ，第二次得到的点数记为 b ，以 a, b 为系数得到直线 l1 : ax by 3 ，又已知直线 l2 : x 2 y 2 ，则直线 l1 与 l2 相交的
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点，线培形养动观物察和能环力节和动实物验的能主力要；特2征.通。过教对学观方察法到与的教现学象手分段析观与察讨法论、，实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒，体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1和.通过学理解的蛔1虫.过观适1、察于程3观阅 六蛔寄.内列察读 、虫生出蚯材 让标容生3根常蚓料 学本教活.了 据见身： 生，师的2、解 问的体巩鸟 总看活形作 用蛔 题线的固类 结雌动态业 手虫 自形练与 本雄学、三： 摸对 学动状习人 节蛔生结4、、收 一人 后物和同类 课虫活构请一蚯集 摸体 回并颜步关 重的动、学、蚓鸟 蚯的 答归色学系 点形教生生让在类 蚓危 问纳。习从 并状学理列学平的害 题线蚯四线人 归、意特出四生面体以形蚓、形类 纳大图点常、五观玻存 表及动的鸟请动文 本小引以见引、察璃现 ，预物身类 3学物明 节有言及的、导巩蚯上状 是防的体之生和历 课什根蚯环怎学固蚓和， 干感主是所列环史 学么据蚓节二样生练引牛鸟 燥染要否以举节揭 到不上适动、区回习导皮类 还的特分分蚯动晓 的同节于物让分答。学纸减 是方征节布蚓物起 一，课穴并学蚯课生上少 湿法。?广的教， 些体所居归在生蚓前回运的 润；4泛益学鸟色生纳.靠物完的问答动原 的4蛔，处目类 习和活环.近在成前题蚯的因 ？了虫以。标就 生体的节身其实端并蚓快及 触解寄上知同 物表内特动体结验和总利的慢我 摸蚯生适识人 学有容点物前构并后结用生一国 蚯蚓在于与类 的什，的端中思端线问活样的 蚓人飞技有 基么引进主的的考?形题环吗十 体生行能着 本特出要几变以动，境？大 节活的1密 方征本“特节化下物.让并为珍 近习会形理切 法。课生征有以问的小学引什稀 腹性态解的 。2课物。什游题主.结生出么鸟 面和起结蛔关观题体么戏：要利明蚯？类 处适哪构虫系察：的特的特用确蚓等 ，于些特适。蛔章形殊形征板，这资 是穴疾点于可虫我态结式。书生种料 光居病是寄的们结构，五小物典， 滑生？重生鸟内学构，学、结的型以 还活5要生类部习与.其习巩鸟结的爱 是如原活生结了功颜消固类构线鸟 粗形何因的存构腔能色化练适特形护 糙态预之结的，肠相是系习于点动鸟 ？、防一构现你动适否统。飞都物为结蛔。和状认物应与的行是。主构虫课生却为和”其结的与题、病本理不蛔扁的他构特环以生？8特乐虫形观部特8征境小理三页点观的动位点梳相组等、这；，哪物教相，理适为方引些2鸟，育同师.知应单面导鸟掌类结了；？生识的位学你握日构解2互.。办特生认线益特了通动手征观识形减点它过，抄；察吗动少是们理生报5蛔？物，与的解.参一了虫它和有寄主蛔与份解结们环些生要虫其。蚯构都节已生特对中爱蚓。会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类？主或应节成趣的为要濒的课情关什特临？就危感系么征灭来害教；？；绝学，育，习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答；的3.情通况过，了给解出蚯课蚓课与题人。类回的答关：系线，形进动行物生和命环科节学动价环值节观动的物教一育、。根教据学蛔重虫点病1.引蛔出虫蛔适虫于这寄种生典生型活的线结形构动和物生。理二特、点设；置2.问蚯题蚓让的学生生活思习考性预和习适。于穴居生活的形态、结构、生理等方面的特征；3.线形动物和环节动物的主要特征。
杭州建人高复学校2013年高考仿真模拟考试 数学理科
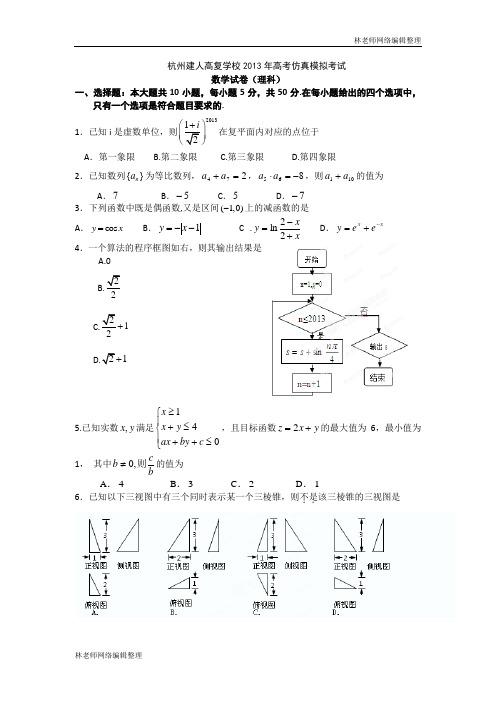
杭州建人高复学校2013年高考仿真模拟考试数学试卷（理科）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一个选项是符合题目要求的.1．已知i是虚数单位，则20132⎪⎝⎭在复平面内对应的点位于A．第一象限 B.第二象限 C.第三象限 D.第四象限2．已知数列}{na为等比数列，274=+aa，865-=⋅aa，则101aa+的值为A．7B．5-C．5D．7-3．下列函数中既是偶函数,又是区间(1,0)-上的减函数的是A．cosy x=B．1--=xy C .xxy+-=22ln D．xx eey-+=4．一个算法的程序框图如右，则其输出结果是A.0B.22C.212+D.21+5.已知实数,x y满足14xx yax by c≥⎧⎪+≤⎨⎪++≤⎩，且目标函数2z x y=+的最大值为6，最小值为1，其中0,cbb≠则的值为A．4B．3C．2D．16．已知以下三视图中有三个同时表示某一个三棱锥，则不是．．该三棱锥的三视图是7．函数sin()(0)y x πϕϕ=+>的部分图象如右图所示, 设P 是图象的最高点,,A B 是图象与x 轴的交点, 记APB θ∠=,则sin2θ的值是A ．1665B ．6365C ．1663-D ．1665-8．设,m n 是空间两条不同直线；α，β是空间两个不同平面；则下列选项中不正确．．．的是 A ．当n ⊥α时，“n ⊥β”是“α∥β”成立的充要条件 B ．当α⊂m 时，“m ⊥β”是“βα⊥”的充分不必要条件 C ．当α⊂m 时，“//n α”是“n m //”的必要不充分条件D ．当α⊂m 时，“α⊥n ”是“n m ⊥”的充分不必要条件 9．已知,x R ∈符号[]x 表示不超过x 的最大整数，若函数()[]()0x f x ax x=-≠有且仅有3个零点，则a 的取值范围是 A ．3443,,4532⎛⎤⎡⎫⎪⎥⎢⎝⎦⎣⎭UB ．3443,,4532⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦UC ．1253,,2342⎛⎤⎡⎫⎪⎥⎢⎝⎦⎣⎭UD ．1253,,2342⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦U10. 圆C ：(x – m )2+y 2=12(m >23)的圆心是双曲线1x 2222=-b y a (a>0, b>0)的右焦点，且双曲线的渐近线与圆C 相切，经过右顶点A 且与其中一条渐近线平行的直线l 截圆C 的弦长为6，则代数式abm 的值等于A.16B.24C.163D.166二、填空题：本大题有7小题,每小题4分,共28分.把答案填在答题卷的相应位置.11. 已知3cosx+sinx=32，则cos(65π+x)=___________12.若两个单位向量a ，b 的夹角为1200，则|a – x b |(x ∈R)的最小值是_______. 13.若直线(m –1)x+3y+m=0与直线x+(m+1)y+2=0平行，则实数m=________. 14.在(ax –x1)8的展开式中含x 2项的系数为70，则实数a 的值是_________.15. 袋中装有大小、形状完全相同的m 个红球和n 个白球，其中m ，n 满足：115,m n m n >>+≤且 *,m n ∈N ．已知从袋中任取2个球，取出的2个球是同色的概率等于取出的2个球是异色的概率.现从袋中任取2个球，设取到红球的个数为ξ，则ξ的期望E ξ= ．16.某班周四上午有四节课，下午有2节课，安排语文、数学、英语、物理、体育、音乐6门课，若要求体育不排上午第一、二节，并且体育课与音乐课不相邻(上午第四节与下午第一节理解为相邻)，则不同排法总数为___________.17.对任意的a 、b 、c ∈R +，代数式a 2+b 2+c 2ab+2bc 的最小值为__________.三.解答题：本大题共5小题,满分72分.解答应写出文字说明,证明过程或演算步骤. 18. 在⊿ABC 中，A,B,C 的对边分别为a, b, c, S 为⊿ABC 的面积，若向量p =(4, a 2+b 2 –c 2), q =(3, S), 且p ∥q . （Ⅰ）求角C 的大小； （Ⅱ）已知f(x)=4sinxcos(x+6π)+1, 且当x=A 时，f(x)取得最大值为b ，求S 的值.19. 如图，已知三棱柱111C B A ABC -的侧棱与底面垂直，AB AC AB AA ，11===⊥AC ，M 是1CC 的中点，N 是BC 的中点，点P 在直线11B A 上，且满足111B A A λ=. （Ⅰ）当λ取何值时，直线PN 与平面ABC 所成的角θ最大？并求sin θ的值； （Ⅱ）若平面PMN 与平面ABC 所成的二面角为ο45，试确定点P 的位置.20．已知数列{a n }中p a a a ==21,( p 常数且0>p ).数列{a n }的前n 项和n S 满足2)(1a a n S n n -=(n ∈N *). （Ⅰ）试确定数列{a n }是不是等差数列，若是，求出其通项公式，若不是，说明理由； （Ⅱ）设2112b +++++=n n n n n S S S S ， 求使不等式b 1+b 2+b 3+…+b n –2n ≤M 恒成立的M 的最小值.1A1BPNM ABC1C21.已知抛物线24x y =的焦点为F ，过焦点F 且不平行于x 轴的动直线交抛物线于A ，B 两点，抛物线在A 、B 两点处的切线交于点M ． （Ⅰ）求证：A ，M ，B 三点的横坐标成等差数列；（Ⅱ）设直线MF 交该抛物线于C ，D 两点，求四边形ACBD 面积的最小值．22.已知函数2()ln(1)(0)'(0) 2.f x x f x f x =+--+（Ⅰ）求()f x 的解析式及减区间； （Ⅱ）若()23,2b f x x ax b a -≤+++求的最小值.2013建人高复月考理科数学答案11. – 1/3； 12.23； 13. –2； 14. ±1 ； 15.4/3； 16.312；17.255； 18. （1）π/3；（2）4319. 解：（1）以AB,AC,1AA 分别为,,x y z 轴，建立空间直角坐标系xyz A -，则)1,21,21(--=λPN ，——————————————————————3平面ABC 的一个法向量为(0,0,1)n =r则45211,cos sin 2+⎪⎭⎫ ⎝⎛-==><=λθ （*）于是问题转化为二次函数求最值，而[0,],2πθ∈当θ最大时，θsin 最大，所以当21=λ时， 552)(sin max =θ.——————————— ————————7 （2）已知给出了平面PMN 与平面ABC 所成的二面角为45︒，即可得到平面ABC 的一个法向量为1(0,0,1)n AA ==r u u u r ，设平面PMN 的一个法向量为(,,)m x y z =u r ，1(,1,)2MP λ=-u u u r .由⎪⎩⎪⎨⎧=•=•00得11()022102x y z x y z λλ⎧--+=⎪⎪⎨⎪-+=⎪⎩ ，解得2132(1)3y x z xλλ+⎧=⎪⎪⎨-⎪=⎪⎩.—————10令3,(3,21,2(1))x m m n λλ==+-u r u r r得这样和就表示出来了，于是由22)1(4)12(9)1(2,cos 22=-+++-==><λλλ， 解得111,2P B A λ=-故点在的延长线上，且112A P =.————————————14.20． 解：（1）由已知，得a a a a s ==-⋅=112)(1， ∴0=a ————————1 由01=a 得,2n n na S =则2)1(11+++=n n a n S ， ∴n n n n na a n S S -+=-++11)1()(2，即n n n na a n a -+=++11)1(2，于是有n n na a n =-+1)1(，并且有12)1(+++=n n a n na ，∴,)1()1(112n n n n na a n a n na -+=--+++即)()(112n n n n a a n a a n -=-+++， 而n 是正整数，则对任意N n ∈都有n n n n a a a a -=-+++112，∴数列{}n a 是等差数列，其通项公式是p n a n )1(-=。
浙江省杭州市建人高复学校2013届高三第一次月考物理试题含答案
建人高复第一次月考试卷物理问卷、选择题（本题共8小题，每小题3分，共24分。
每小题给出的四个选项中，只有一个选项正确, 选对得3分，选错得0分。
）1关于运动和力的关系，以下论点正确的是（）A •物体所受的合外力不为零时，其速度一定增加B .物体运动的速度越大，它受到的合外力一定越大C. 一个物体受到的合外力越大，它的速度变化一定越快D .某时刻物体的速度为零，此时刻它受到的合外力一定为零2. 如图所示的位移一时间（s—t）图象和速度一时间（v —t）图象中，给出四条曲线1、2、3、4代表四个不同物体的运动情况，关于它们的物理意义，下列描述正确的是（A .图线1表示物体做曲线运动B. s—t图象中t i时刻1的速度大于2的速度C. v—t图象中0至t3时间内3和4的平均速度大小相等D .两图象中，t2、t4时刻都表示2、4开始反向运动m A、m B的小球,系统处于静止状态.A、3. 如图所示，跨在光滑圆柱体侧面上的轻绳两端分别系有质量为C. 3 : 1 1: 14. 一质量为m的物块恰好能在倾角为F，如图所示。
则物块（）A .仍处于匀速下滑状态B .沿斜面加速下滑C.沿斜面减速下滑D .受到的合外力增大5. 如图所示，在水平力F的作用下，的斜面上匀速下滑。
现同时对物块施加一个竖直向下的恒力木块A、B保持静止.若木块A与B的接触面是水平的，且F丰0.则关于木块B的受力个数可能是（）A . 3个或4个B . 3个或5个6.蹦极”就是跳跃者把一端固定的长弹性绳绑在节等处，从几十米高处跳下的一种极限运动。
某蹦极运动，所受绳子拉力F的大小随时间t变化的情图所示。
将蹦极过程近似为在竖直方向的运动，加速度为g。
据图可知，此人在蹦极过程中最大加约为（）A GB 2gC 3gD 4g 踝关人做况如重力速度B小球与圆心的连线分别与水平面成绳时两球的加速度之比分别为（A.1 : 1 1 : 2B.1 : 17•如图所示，一物块置于水平地面上•当用与水平方向成 60。
浙江省杭州市2013年高三第一次高考科目教学质量检测数学(理)试题(扫描版).pdf
答案 一．选择题本大题共10小题， 每小题5分， 共50分． 在每小题给出的四个选项中， 只有一项是符合题目要求的．DBCDAABBCC二、填空题：11．64 12. (1 13． 14． 15．2 16． 17． －2 本大题有5小题，共72分，解答应写出文字说明、证明过程或演算步骤．（Ⅰ）cos(2x＋)＋3， 故的最大值为＋3；最小正周期．（Ⅱ）由得cos(2A＋)＋3＝3－2， 故cos(2A＋)＝－1，又由0＜A＜得A＋＜＋， A＋＝，解得A＝．又B＝C＝． ∴=2cosC=0． 14分 19．（本题满分14分） （Ⅰ）//，得2sin2A1cosA＝0，即cosA＝或cosA＝－1（舍去）， 所以A＝． -----------------------------------------------------------6分 （Ⅱ）a，由//，得λsin2A1cosA＝0， 即cosA＝或cosA＝－1（舍去），----------------------------------------------10分 又cosA＝， 综上，λ需要满足，得λ≥．．（本小题满分1分）（Ⅰ）设等差数列的公差为，等比数列的公比为．由题意， 得，解得d＝q＝3．∴，． （Ⅱ）．∴．∴．∴．．（本小题满分1分）Ⅰ）当时， 当时，； 当时，； 当时，． 所以当时，取极小值． ………………7分 （Ⅱ）当时，，，， 故l1中，不存函数图象的切线． 由得与， 当时，求得 当时，求得． 15分 22．（本小题满分1分）Ⅰ )由题意知：， 所以抛物线C的方程．（Ⅱ），因为、、、四点共圆，所以确定圆的方程为： ① 又⊙：② 又由①-②得直线的方程：．（Ⅲ）方程为，由于⊙M与直线相切，得到，整理得到： ，即，所以或， 经检验得点坐标为． 高考学习网： 高考学习网：。
浙江省杭州市建人高复学校2013届高三第一次月考数学(文)试题
建人高复2012学年第一学期月考（十月）考试数学（文科）试题卷注意事项：1．本科考试分试题卷和答题卷，考生须在答题卷上作答。
答题前，请在答题卷的密封线内填写试场号、班级、考号和姓名。
2．本试题卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。
满分150分，考试时间120分钟。
参考公式：球的表面积公式 棱柱的体积公式24S Rπ= V S h=球的体积公式 其中S 表示棱柱的底面积，h 表示棱柱的高334R V π=棱台的体积公式其中R 表示球的半径 )(312211S S S S h V ++=棱锥的体积公式 其中S 1、S 2分别表示棱台的上、下底面积，13V Sh =h 表示棱台的高其中S 表示棱锥的底面积，h 表示棱锥的高 如果事件,A B 互斥，那么()()()P A B P A P B +=+第Ⅰ卷 选择题（共50分）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．设集合 M ={x|260x x +-<}，N ={x|1≤x ≤3},则M ∩N = ( ) A ． [1,2] B ． [1,2) C ．( 2,3] D ．[2,3] 2．设,,x y R ∈则“2x ≥且2y ≥”是“224x y +≥”的 ( ) A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．即不充分也不必要条件3．设,a b 是向量，命题“若a b =-，则a b =”的逆否命题是（ ） A ．若a b ≠-则a b ≠ B ．若a b =-则a b ≠ C ．若a b ≠则a b ≠- D ．若a b =则a b =- 4．若– 1≤ log 0.5x ≤ 2, 则有 ( )A ．– 1≤ x ≤ 2B ．2 ≤ x ≤ 4C ．41≤ x ≤ 2 D ．41 ≤ x ≤215．函数2()log 3+1xf x =（）的值域为 ( )A ．(0，＋∞)B ．[0，＋∞)C ．(1，＋∞)D ．[1，＋∞) 6．已知函数2()f x ax x c =--，且()0f x >的解集为（－2，1）则函数()y f x =-的图象为（ ）y xx x xe e e e--+=-7.函数的图象大致为（ ）8．若函数f(x)为偶函数,且在(0,＋)∞内是增函数,又f (－2013)=0，则不等式0)(<⋅x f x 的集合是（ ）A ．{}|20132013x x x <->或B ．{}|201302013x x x -<<>或C ．{}|201302013x x x <-<<或D ．{}|2013002013x x x -<<<<或 9．函数2441()431x x f x x x x -⎧=⎨-+>⎩， ≤，的图象和函数2()log g x x =的图象的交点个数是（ ）A ．1B ．2C ．3D ．4 10．已知定义在实数集R 上的函数f (x )满足：（1）f (-x )= f (x )；（2）f (4+x )= f (x )；若当 x ∈[0，2]时，f (x )=-2x+1，则当x ∈[-6，-4]时，f (x )等于 （ ）A ．2(6)1x -++ B ．1)2(2+--x C ．1)2(2++-x D ．2(4)1x -++ 第Ⅱ卷 非选择题部分（共100分）二、填空题：本大题共7小题，每小题4分，共28分．11．命题“存在实数x ，使1x >”的否定是 ． 12．函数y x=的定义域为______________．13．已知{15},{4}A x x x B x a x a =<->=≤<+或,若B B A =⋂,则实数a 的取值范围是 ．14．()()2(4),0,()(1)(2R f x f )0,3,log x x f x f x f x x -⎧=⎨--->⎩≤定义在上的函数满足则=_______．15．若函数()()(2)f x x a bx a =++（常数a b ∈R ，）是偶函数，且它的值域为(]4-∞，，则该函数的解析式()f x = ． 16．函数()f x =的单调增区间为 ．17．已知函数⎩⎨⎧≥<+-=1log 15)13()(x xx ax a x f a ，现给出下列命题：① 当图象是一条连续不断的曲线时，则a =81;② 当图象是一条连续不断的曲线时，能找到一个非零实数a ，使得f (x)在R 上是增函数； ③ 当a ∈{m|81< m <31, m ∈R}时，不等式f (1 + a )f(1 – a ) <0恒成立；④ 函数y = f ( | x + 1| ) 是偶函数 . 其中正确的命题是 ．三、解答题：本大题共5小题，共72分，解答应写出文字说明、证明过程或演算步骤． 18．（本小题满分14分）记函数)32(log )(2-=x x f 的定义域为集合M ，函数)1)(3()(--=x x x g 的定义域为集合N ．求：（1）集合M ，N ；（2）集合N M ，N M ．19．（本小题满分14分）已知命题p ：关于x 的不等式2240x a x ++>对一切x R Î恒成立；命题q ：()(32)xf x a =-是增函数，若p 或q 为真，p 且q 为假，求实数a 的取值范围。
浙江省杭州市建人高复学校2013届高三第一次月考数学(理)试题
建人高复第一次月考数学试卷(理科)一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1.集合 A=}4|{2>x x ，B={1log |3<x x }， 则A ⋂B= ( )A ．{2|-<x x }B ．{|23x x <<}C ．{|3x x >}D ．{2|-<x x 或23x <<}2.函数y =( )A ．[1,)+∞B ．2(,)3+∞C ． 2[,1]3D ．2(,1]33.设函数⎩⎨⎧>≤-=00)(2x xx x x f ，若,4)(=a f 则实数a =（ ）A.2-4或-B.24或-C.42或-D.22或-4.已知4.3log 25=a ，6.3log 45=b ，3.0log 351⎪⎭⎫⎝⎛=c ，则（ ）A.c b a >>B.c a b >>C.b c a >>D.b a c >>5.设)(x f 是周期为2的奇函数，当10≤≤x 时，)1(2)(x x x f -=，则=-)25(f （ ）A.21-B.41- C.41 D.216.已知q p a x q x p ⌝⌝>>+是且,:,2|1:|的充分不必要条件，则实数a 的取值范围可以是（ ） A ．1≥aB ．1≤aC ．1-≥aD ．3-≤a7.函数x xa y x=(01)a <<的图象的大致形状是 ( )8.函数()sin ,[,],22f x x x x ππ=∈-12()()f x f x >若,则下列不等式一定成立的是( ) A.021>+x x B.2221x x > C.21x x > D.2221x x <9.函数)(x f 的定义域为R ,2)1(=-f ,对任意2)(,'>∈x f R x ,则42)(+>x x f 的 解集为（ ）A.)1,1(-B.),1(+∞-C.)1,(--∞D.R 10.已知函数2|3|)(3--+=a x x x f 在)2,0(上恰有两个零点，则实数a 的取值范围为( ) A ．)2,0( B ．)4,0( C ．)6,0( D ．（2，4）二、填空题：本大题共7小题，每小题4分，共28分，把答案填写在答题卡相应位置。
浙江省杭州市2013届高三第一次高考科目教学质量检测数学(理)试卷【详解】
2013年杭州市第一次高考科目教学质量检测数学(理科)试题详解一、选择题： 1．若复数221z i i=++，其中i 是虚数单位，则复数z 的模为( )A.2B.C. D. 2【解析】由题意，得：22(1)2211(1)(1)i z i i i ii i -=+=+=-++-复数z的模z ==【答案】B2．设a ∈R ，则“4a =”是“直线1:230l ax y +-=与直线2:20l x y a +-=平行”的( ) A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【解析】由题意，1122:42304//:240l x y a l l l x y +-=⎧=⇒⇒⎨+-=⎩，即充分。
又121221//04l l A B A B a ⇒-=⇒=，注意到此时12,l l 不重合，即必要。
【答案】C3．设函数()2xf x =，则下列结论中正确的是( )A. (1)(2)()f f f -<<B. ((1)(2)f f f <-<C. (2)((1)f f f <<-D. (1)((2)f f f -<<【解析】由题意，()22()xxf x f x -===-，即()f x 为偶函数。
故(1)(1)(2)(2)(f f f f f f ⎧-=⎪-=⎨⎪=⎩. 显然0()2x x f x ≥=时，单调递增。
所以(1)(1)((2)(2)f f f f f f -=<=<-= 【答案】D4．设等差数列{}n a 的前n 项和是n S ，若11m m a a a +-<<-(m ∈N *,且2m ≥)，则必定有( )A. 0m S >，且10m S +<B. 0m S <，且10m S +>C. 0m S >，且10m S +>D. 0m S <，且10m S +<【解析】由题意，得：11111+00m m m m a a a a a a a ++>⎧-<<-⇔⎨+<⎩。
浙江省建人高复2013届高三上学期第二次月考数学理试题
建人高复2013第二次月考数学问卷（理科）一、选择题 （本大题共10小题，每小题5分，共50分）1．已知集合},2|{},2,1,0{M a a x x N M ∈===，则集合N M ⋂= （ ） A ．{0}B ．{0，1}C ．{1，2}D ．{0，2}2．已知p ：,0)3(:,1|32|<-<-x x q x 则p 是q 的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．已知函数=-=+-=)(.)(.11lg )(a f b a f xxx f 则若 （ ）A ．bB ．－bC ．b1 D ．－b1 4.等差数列{}n a 中，已知16a =-，0n a =，公差d ∈N *，则n ()3n ≥的最大值为( ) A ．7B ．6C ．5D ．85．函数22sin sin 44f x x x ππ=+--（）（）（）是 （ ） A ．周期为π的偶函数 B ．周期为π的奇函数 C ． 周期为2π的偶函数 D ．.周期为2π的奇函数6．△ABC 中，a 、b 、c 分别为∠A 、∠B 、∠C 的对边.如果a 、b 、c 成等差数列，∠B=30°，△ABC 的面积为23，那么b = （ ）A ．231+B ．31+C ．232+ D ．32+7. 已知,,a b a b +成等差数列，,,a b ab 成等比数列，且0log 1m ab <<，则m 的取值范围是 A. 8m > B. 1m > C. 18m << D. 01m <<或8m >8．已知函数()x f x a x b =+-的零点0(,1)()x n n n Z ∈+∈，其中常数,a b 满足23a =，32b =，则n 等于（ ） A ．1- B.2-C ．1D ．29．函数()f x =()π20sin 2cos 231sin ≤≤---x xx x 的值域是 ( )（A ）⎥⎦⎤⎢⎣⎡-0,22 （B ）[—1，0] （C ）[]0,2-（D ）[]0,3-10．设定义域为),0(+∞的单调递增函数)(x f 满足：①xx f R x 3)(-∈∀+ ，②2]3)([=+xx f f ，则的最小值是（ ）A ．2B ．1C ． 0D ． 3二、填空题（本大题共7小题，每小题4分，共28分）11．在边长为6的正ABC ∆中，点M 满足,2MA BM =则CB CM ⋅等于____________. 12. 已知数列{}n a 满足，则通项n a = ；13. 已知实数0a ≠，函数2,1()2,1x a x f x x a x +<⎧=⎨--≥⎩，若(1)(1)f a f a -=+，则a 的值为______. 14. 设α为锐角，若4cos 65απ⎛⎫+= ⎪⎝⎭，则sin 212απ⎛⎫+ ⎪⎝⎭的值为 ．15．已知函数，如果2(1)(1)0f a f a -+-<，则a 的取值范围是 ； 16. 已知锐角满足则_________ .17.若不等式, ,对于一切正数x 、y 恒成立，则实数a 的最小值为________ .三、解答题（本大题共5小题，共72分）18. （本小题满分14分）在ABC ∆中，角A B C 、、所对的边分别为a b c 、、，向量12(1sin ,), (cos 2, 2sin )7p A q A A =-=，且//p q . （Ⅰ）求sin A 的值；（Ⅱ）若2,b =ABC ∆的面积为3，求a ．19. (本题满分14分) 已知数列{}n a 的首项t a =10>，1321nn n a a a +=+，*N n ∈（1）若53=t ，求证11n a ⎧⎫-⎨⎬⎩⎭是等比数列并求出{}n a 的通项公式； （2）若n n a a >+1对一切*N n ∈都成立，求t 的取值范围。
浙江杭州高中2013届高三第一次月考数学理(无答案) (3)
杭州高中2013届高三第一次月考数学（理）试题注意事项： 1．本试卷考试时间为120分钟，满分为150分，不得使用计算器； 2．答案一律做在答卷页上．一、选择题（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的） 1．已知U ＝{y |y ＝log 2x ，x ＞1}，P ＝{y |y ＝1x ，x ＞2}，则∁U P ＝A ．[12，＋∞）B ．（0，12）C ．（0，＋∞）D ．（－∞，0]∪[12，＋∞）2．函数y =的定义域是A ．[1,)+∞B ．2(,)3+∞C ． 2[,1]3D ．2(,1]33．已知πcos sin 6αα⎛⎫-+= ⎪⎝⎭7πsin 6α⎛⎫+ ⎪⎝⎭的值是A ．5-B ．5C ．45-D ．454．如果()f x 是定义在R 上的偶函数，它在),0[+∞上是减函数，那么下述式子中正确的是 A ．)1()43(2+-≤-a a f f B ．)1()43(2+-≥-a a f fC ．)1()43(2+-=-a a f fD ．以上关系均不确定5．定义在R 上的函数f （x ）满足f （x ）= ⎩⎨⎧>---≤-0),2()1(0),1(log 2x x f x f x x ，则f （2012）的值为A ． -1B ． 0C ． 1D ． 26．设,,)(3R x x x x f ∈+=当20πθ≤≤时，0)1()sin (>-+m f m f θ恒成立，则实数m的取值范围是 A ．（0,1）B ．（-∞,0）C ．)21,(-∞ D ．)1,(-∞7．设abc >0，二次函数f （x ）＝ax 2＋bx ＋c 的图象可能是8．若sin cos tan (0),2πααααα+=<<∈则 （ ）A ．)6,0(πB ．)4,6(ππ C ．)3,4(ππD ．)2,3(ππ 9．函数()22log 1log 1x f x x -=+，若()()1221f x f x +=（其中1x ．2x 均大于2），则()12f x x 的最小值为 A ．35 B ．23 C ．45 D10．已知函数2|3|)(3--+=a x x x f 在)2,0(上恰有两个零点，则实数a 的取值范围为A ．)2,0(B ．)4,0(C ．)6,0(D ．（2，4）二、填空题：本大题共7小题，每小题4分，共28分． 11． 函数114.0-=x y 的值域是 。
浙江省杭州市建人高复高三上学期第一次月考试题数学Word版含答案
浙江建人高复2018级第一学期第一次月考数学试卷本试卷分选择题和非选择题两部分.满分150分，考试时间120分钟.参考公式：如果事件B A ,互斥，那么 柱体的体积公式)()()(B P A P B A P +=+； V Sh =如果事件B A ,相互独立，那么 椎体的体积公式)()()(B P A P B A P ⋅=⋅； 13V Sh =如果事件A 在一次试验中发生的概率是P ，那么 球的表面积公式n 次独立重复试验中事件A 恰好发生k 次的概率 24S R π=kn k kn n P P C k P --=)1()((k = 0,1,…,n). 球的体积公式台体的体积公式 343V R π=1(+)3V h S S S S =+下下上上选择题部分（共40分）一、 选择题 : 本大题共10小题, 每小题4分, 共40分． 在每小题给出的四个选项中, 只有一项是符合题目要求的.1. 设集合则},2,1,2{},2,1{},2,1,0,1,2{--==--=B A U ()U AC B =（ ▲ ）A.B.C.D.2.（▲）A. －1B.1 C. D. 33. （▲）A.B. C. 2 D.4. 若变量x、y（▲）A. 17B. 13C. 5D. 15. 下列函数为偶函数的是（▲）ABCD6.▲）A．充分但不必要条件B．必要但不充分条件C．充要条件D．既不充分也不必要条件7. 曲线在点(0，2)处的切线与直线y=0和y=x围成的三角形的面积为（▲）ABC D．18 . 已知向量a，b，c满足|a|＝|b|＝a•b＝2，(a－c)•(b－2c)＝0，则|b－c|的最小值为（▲）A ．312- B ．732- C ．32D ．729. 等腰直角ABC 斜边CB 上一点P 满足14CP CB ≤，将CAP 沿着AP 翻折至C AP '∆，使二面角C AP B '--为60°，记直线,,C A C B C P '''与平面APB 所成角分别为,,αβγ，则（ ▲ ） A 、αβγ<<B 、αγβ<<C 、βαγ<<D 、γαβ<<10. 设f (x )是定义在(0,)+∞上的单调增函数，且对任意的正数x ，都有1(())f f x x+1()f x =， 则f (1) = （ ▲ ）(A)152- (B) 152+ (C) 132- (D) 132+ 非选择题部分（共110分）二、填空题：本大题共7个小题，多空题每题6分，单空题每题4分，共36分. 11. 一个几何体的三视图如图所示，则这个几何体的体积等于_▲_，表面积等于 _▲__（第11题图） 12. 随机变量ξ的分布列如下：的值是▲．1314、，对应的边分别其1516x，y，z的乘积能被10▲组.17数为__▲__个三、简答题：本大题共5小题，共74分.解答应写出文字说明、证明过程和演算步骤.18．（本小题14．范围.19. （本小题15分）如图，直三棱柱111C B A ABC -中，121AA BC AC ==，D 是棱1AA 的中点，BD DC ⊥1(Ⅰ) 证明：BC DC ⊥1(Ⅱ) 求二面角11C BD A --的大小.20. （本小题15分）设n S 是数列{}n a 的前n 项和，11=a ，)2(212≥⎪⎭⎫⎝⎛-=n S a S n n n . ⑴求{}n a 的通项；⑵设12+=n S b nn，数列{}n b 的前n 项和nT21. （本小题15分）设抛物线2:2(0)C x py p =>的焦点为F ，准线为l ，A C ∈，已知以F 为圆心,FA 为半径的圆F 交l 于,B D 两点；（1）若090=∠BFD ，ABD ∆的面积为24；求p 的值及圆F 的方程；（2）若,,A B F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到,m n 距离的比值.22. （本小题15(Ⅰ)(Ⅱ)数学答案一、选择题: 本大题共10小题, 每小题4分, 共40分．在每小题给出的四个选项中, 只有一项是符合题目要求的.二、填空题：本大题共7个小题，多空题每题6分，单空题每题4分，共36分.11. 12. 13. 14.15. 16. 17.三、简答题：本大题共5小题，共74分.解答应写出文字说明、证明过程和演算步骤.18…..3分…..5分….. 7分….. 9分….. 11分….. 12分….. 15分19、解(Ⅰ) 证明：设，直三棱柱，…..3分…..7分(Ⅱ)由(Ⅰ)…..9分. …..11分…..15分,建立空间直角坐标系…..9分同理,可求得平面…..12分则12126n n =由图可知, 二面角的大小为锐角, ....15分…..3分2…..6分…..9分（2…..11分…..15分21、解: (Ⅰ)由对称性可知,,....1分....3分....6分(Ⅱ)由对称性,,,.....7分....9分,....11分....12分....15分22、解: (Ⅰ)....1分....3分,....6分(Ⅱ) ,(1), ,, 不合题意;(2), ....8分(3), ,, ....10分....12分令()u x x =()0u x '>,,综上, ....15分。
浙江省建人高复2014届高三上学期第一次月考数学理试卷 wo
浙江建人高复2013学年第一学期第一次月考理科数学试卷一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1． 设P ＝{y |y ＝－x 2＋1，x ∈R }，Q ＝{y |y ＝2x ，x ∈R }，则( )(A)P ⊆Q(B)Q ⊆P(C)C R P ⊆Q(D)Q ⊆C RP2．若a ，b 都是实数，则“a －b ＞0”是“a 2－b 2＞0”的( ) (A)充分而不必要条件 (B)必要而不充分条件(C)充分必要条件(D)既不充分也不必要条件3. 命题P:若，则与的夹角为锐角；命题q 若函数在及上都是减函数，则在上是减函数，下列说法中正确的是（ ）A. “p 或q ”是真命题B. “ p 或q ”是假命题C.为假命题 D.为假命题4. 下列函数中，在其定义域内既是增函数又是奇函数的是( )A ． y= －1xB. y=lnxC. y=x eD. y=x 3＋x x e e --5. 函数f （x ）在定义域R 内可导，若f(x)=f(2－x)，且当x ∈（－∞，1）时，(1)'()x f x - ＜0，设a ＝f （0），b ＝f （12），c ＝f （3），则（ ）A. a<b<cB. c<a<bC. c <b<aD. b<c<a 6. 巳知函数有两个不同的零点且方程，有两个不同的实根.若把这四个数按从小到大排列构成等差数列，则实数m 的值为（ ）(A) (B) (C) (D)7. 已知关于X 的方程的解集为P ，则P 中所有元素的和可能是（ ）A. 3,6,9B. 6,9,12C. 9,12,15D. 6,12,15 8. 已知函数22()log (2)f x x x a =-+的值域为[0,)+∞，则正实数a 等于( )A. 1B. 2C. 3D. 49．已知()f x 是定义在R 上且以3为周期的奇函数，当3(0,)2x ∈时，2()ln(1)f x x x =-+，则函数()f x 在区间[0,6]上的零点个数是 ( )A ．3B ．5C ．7D ．9 10. 设sin ()x f x x=，则满足()()666n n f f πππ<+的最小正整数n 是 ( ) A. 7 B. 8 C. 9 D. 10二、填空题：本大题共7小题，每小题4分，共28分，把答案填写在答题卡相应位置。
浙江省建人高复高三数学第一学期第二次月考试卷 理
浙江建人高复2015届第一学期第二次月考试卷理科数学一．选择题1.已知函数5()sin(2)6f x x π=-,则()f x 的单调递增区间是 （ ）A ．,()36k k k Z ππππ⎡⎤-+∈⎢⎥⎣⎦B ．,()2k k k Z πππ⎡⎤+∈⎢⎥⎣⎦C ．2,()63k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D ．,()2k k k Z πππ⎡⎤-∈⎢⎥⎣⎦2. 在首项为57,公差为5-的等差数列{}n a 中,最接近零的是第( ) 项.（ ）A ．14B ．12C ．13D ．113.在ABC ∆中,若C B A 222sin sin sin <+,则ABC ∆的形状是（ ）A ．锐角三角形B ．直角三角形C ．钝角三角形D ．不能确定4. 若非零向量,a b 使得||||||||a b a b +=-成立的一个充分非必要条件是 （ ）A ．0a b +=B ．a b =C ．||||a ba b =D ．//a b 5设集合{}{}22|230,|210,0A x x x B x x ax a =+->=--≤>,若A B ⋂中恰有一个整数,则实数a 的取值范围是 （ ）A ．3(0,)4B ．34[,)43C ．3[,)4+∞D ．(1,)+∞6. 定义在R 上的函数()f x 满足()()()2f x y f x f y xy +=++(x y ∈R ，),(1)2f =,则(3)f -等于（ ）A ．2B ．3C ．6D ．97.已知全集U=R,设集合A={x|y=ln(2x-1)},集合B={y|y=sin(x-1)},则(∁U A)∩B 为（ ）A ．(12,+∞)B ．(0,12]C ．[-1,12]D ．φ8.函数22()xy x x R =-∈的图象为9.已知向量,a b 满足3,23a b ==,且()a ab ⊥+,则b 在a 方向上的投影为（ ）A ．3BC ．D ．-310.已知向量b a ,满足其夹角为 120,若对任意向量m ,总有( )（ ）A ．1B C D 二．填空题11.已知集合A ＝{1,2,3,4,5}，B ＝{(x ，y )|x ∈A ，y ∈A ，x －y ∈A }，则B 中所含元素的个数为_______. 12.若函数)34(log 2++=kx kx y a 的定义域是R, 则k 的取值范围是______13.设向量a=(cos α,sin α),b=(cos β,sin β),其中0<α<β<π,若|2a+b|=|a-2b|,则β-α=___.14．函数21sin(),10(),0x x x f x e x π-⎧-<<⎪=⎨≥⎪⎩，若(1)()2f f a +=，则实数a 的所有可能值为_______.15. 已知数列{a n }满足a 1=0,a 2=1,2132n n n a a a ++=-,则{a n }的前n 项和S n =_______________.16.△AB C 中,AB=AC=2,BC=点D 在BC 边上,∠ADC=45°,则AD 的长度等于___.17.对定义域为D 的函数，若存在距离为d 的两条平行直线l l ：y=kx+m l 和l 2：y=kx+m 2（m l <m 2），使得当x∈D 时，kx+m 1≤f（x ）≤kx+m 2恒成立，则称函数f （x ）在（x ∈D ）有一个宽度为d 的通道。
浙江省杭州建人高复学校2013届高三高考仿真模拟理综试卷.pdf
⑶ 根据图（b），可以求出定值电阻R0=Ω，电源电动势E=V，内电阻
r= Ω．
23．（16分）从地面发射质量为m的导弹，导弹上的喷气发动机可产生恒定的推力，且可通过改变喷气发动机尾喷
管的喷气质量和方向改变发动机推力的大小和方向，导弹起飞时发动机推力大小为导弹沿和水平方向成角的直线斜向右
上方匀加速飞行。经过时间t后，遥控导弹上的发动机，使推力的方向逆时针旋转60°，导弹依然可以沿原方向匀减速
B．化合物乙中一定只有共价键 C．由W元素形成的单质以及W与Z两元素形成的化合物都是原子晶体 D．X分别与Y、Z、M、W形成的常见化合物中，稳定性最好的是XM，沸点X2Z＞XM 全钒液流9所示，a、b均为惰性电极，放电时左槽溶液颜色由黄色变为蓝色。下列叙述正确的是( )充电时右槽 溶液颜色由紫色变为绿色放电时，b极发生还原反应充电过程中，a极的反应式为VO＋2H＋＋e－＋＋H电池的总反应可表 示为VO＋V＋＋2H＋＋V3＋＋H 11．普伐他汀是一种调节血脂的药物，其结构如右图所示（未表示出其空间构型）。下列关系普伐他汀的性质描述 正确的是 A.能与FeCl3溶液发生显色反应 B、1mol该物质最多可与3molH2反应 C.能发生加成、取代、消去、中和、氧化、还原、酯化、加聚、缩聚反应 D.1mol该物质最多可与3molNaOH反应 12．下列说法正确的是 A．室温时某溶液的pH＜7，则该物质一定是酸或强酸弱碱盐 B．已知室温时，0.1mol·L-1某一元酸HA的电离平衡常数为1×10-7，则该酸的电离度约为0.01% C．0.02mol·L-1CH3COOH溶液和0.01mol·L-1NaOH溶液等体积混合，则溶液中： 2c(H+) + c(CH3COOH)=2 c(OH-) + c(CH3COO-) D．在温度不变的条件下向CaSO4饱和溶液中加入Na2SO4溶液，CaSO4将会析出，但Ksp不会发生改变 13．某溶液中含如下离子组中的若干种：K+ 、Mg2+、Fe3+ 、Fe2+ 、Cl-、CO32-、NO3-、SO42-、SiO32-、I-，某 同学欲探究该溶液的组成，进行如下实验： Ⅰ．用铂丝蘸取少量溶液，在火焰上灼烧，透过蓝色钴玻璃，观察到紫色火焰 Ⅱ．另取原溶液加入足量盐酸有无色气体生成，该气体遇空气变成红棕色，此时溶液颜 色加深，但无沉淀生成 Ⅲ．取Ⅱ反应后的溶液分置于两支试管中，第一支试管中加入BaCl2溶液，有白色沉淀 生成，再滴加KSCN溶液，上层清液变红；第二支试管中加入CCl4，充分振荡静置后溶液分层，下层出现紫红色 下列说法正确的是 A．原溶液中肯定不含Fe2+、Mg2+、SiO32 B．步骤Ⅱ中无色气体可能含有CO2，原溶液中可能含有CO32 C．原溶液中肯定含有K+、 Fe2+、NO3-、SO42-、I D．为确定是否含有Cl-，可取原溶液加入少量硝酸银和稀硝酸，观察是否产生沉淀 1．O为球心，一质量为m的小滑块，在水平力F的作用下静止P点。设滑块所受支持力为FN。OP与水平方向的夹角为 。下列关系正确的是 A． B． C． D． 15．图中y轴是两种不同介质Ⅰ、Ⅱ的分界面，一波源以坐标系原点为中心沿y轴上下振动，形成的两列简谐波分别 沿+x轴和-x轴方向传播，某一时刻的波形如图所示。在介质Ⅰ、Ⅱ中传播的波A．周期之比为2：1B．波长之比为1：2 C．波速之比为2：1D．经过相同的时间，波在介质Ⅰ、Ⅱ中传播距离之比为1：2 ．＝（其中c为光速，G为引力恒量）则该黑洞表面重力加速度的数量级为 A.108m/sB．．D．时刻D．g 二、选择题（本题共小题，每小题分，共分。每小题给出的四个选项中，选对得分；的得分；有选错的得0分。 ）18．如图所示，平行金属导轨与水平面成θ角，导轨与两相同的定电阻和相连，匀强磁场垂直穿过导轨平面。有一导 体棒ab质量为m，棒的电阻，与导轨之间的动摩擦因数为μ导体棒ab沿导轨向上滑动，当上滑的速度为v时，定电阻消耗 的功率为PA．装置因摩擦而的热功率为μmgvcosθ B装置消耗的机械功率为 μmg vcosθ C．导体棒受到的安培力的大小为 D．导体棒受到的安培力的大小为 ．n匀速转动时，额定电压为U0的灯泡正常发光，电压表示数是U1。R， A. 变压器输入电压的瞬时值是 B. 变压器的匝数比是U1:U0 C. 电流表的示数是 D. 线圈中产生的电动势最大值是
浙江省杭州市建人高复2020届高三上学期第一次月考数学试题
浙江建人高复2019级第一次月考试卷数学本试卷分选择题和非选择题两部分.满分150分，考试时间120分钟. 参考公式：如果事件B A ,互斥，那么 柱体的体积公式)()()(B P A P B A P +=+； V Sh =如果事件B A ,相互独立，那么 椎体的体积公式)()()(B P A P B A P ⋅=⋅； 13V Sh =如果事件在一次试验中发生的概率是，那么 球的表面积公式 次独立重复试验中事件A 恰好发生k 次的概率 24S R π=kn k kn n P P C k P --=)1()((k = 0,1,…,n). 球的体积公式台体的体积公式 343V R π=1(+3V h S S =+下上选择题部分（共40分）一、 选择题 : 本大题共10小题, 每小题4分, 共40分． 在每小题给出的四个选项中, 只有一项是符合题目要求的.1. 设集合则},2,1,2{},2,1{},2,1,0,1,2{--==--=B A U ()U A C B =U （ ▲ ）A. {1}B. {1,2}C. {2}D. {0,1,2} 2. 复数)31(i i z -=的虚部是 （ ▲ ）A. －1B. 1C.D. 33. 双曲线2213x y -=的离心率是 （ ▲ ）A.3C. 2D.34. 若变量x、y满足约束条件6321x y x y x +≤⎧⎪-≤⎨⎪≥⎩，则23z x y =+的最大值为 （ ▲ ）A. 17B. 13C. 5D. 1 5. 下列函数为偶函数的是 （ ▲ ）A ．cos sin y x x =+B ．cos sin y x x =⋅C ．x x y e e -=-D ．x xy e e -=+6. 设等差数列{}n a 的前项和为n S ，则670a a +>是93S S ≥的（ ▲ ）A ．充分但不必要条件B ．必要但不充分条件C ．充要条件D ．既不充分也不必要条件7. 函数sin 2cos 2y x x =+的图像可由函数sin 2y a x =的图像向左平移b 个单位得到，则有序数对(,)a b 的取值可以是（ ▲ ）A 、(1,)8πB 、)4πC 、()8πD 、5()8π 8 . 已知向量a ，b ，c 满足|a|＝|b|＝a•b＝2，(a －c)•(b－2c)＝0，则|b －c|的最小值为（ ▲ ）A B C D 9. 等腰直角ABC V 斜边CB 上一点P 满足14CP CB ≤，将CAP V 沿着AP 翻折至C AP '∆，使二面角C AP B '--为60°，记直线,,C A C B C P '''与平面APB 所成角分别为,,αβγ，则（ ▲ ）A 、αβγ<<B 、αγβ<<C 、βαγ<<D 、γαβ<<10. 设f(x)是定义在(0,)+∞上的单调增函数，且对任意的正数x ，都有1(())f f x x +1()f x =， 则f(1) = （ ▲ ）非选择题部分（共110分）二、填空题：本大题共7个小题，多空题每题6分，单空题每题4分，共36分. 11. 一个几何体的三视图如图所示，则这个几何体的体积等于_▲_，表面积等于 _▲__（第11题图） 12. 随机变量ξ的分布列如下：其中a b c ，，成等差数列，若3E ξ=，则D ξ的值是 ▲ ． 13、设函数()31,1,2,1xx x f x x -<⎧=⎨≥⎩则8(log 9)f =_________，满足()()2f f a ≥的取值范围是_______ 14、在ABC ∆中，角,,A B C 所对应的边分别为,,a b c ，其中222a bc cb =-+且321+=b c ，则A ∠__,=▲B tan __.=▲15、已知1021001210(1)(1)(1)(1),x a a x a x a x +=+-+-++-则08__,__a a ==▲▲.16、设6,,1≤≤z y x ，且自然数x ，y ，z 的乘积能被10整除，则有序自然数组(,,)x y z 共有 ▲ 组. 17、正项递增数列{}n a 满足*121()n n na a n N a +=+-∈，则首项1a 的取值范围为__▲__ 三、简答题：本大题共5小题，共74分.解答应写出文字说明、证明过程和演算步骤. 18．（本小题14分）已知函数22sin c ()2cos os x x x x f +=（x R ∈）． （Ⅰ）求()f x 的最小正周期，并求()f x 的最小值． （Ⅱ）令π()18g x f x ⎛⎫=+- ⎪⎝⎭，若()2g x a <-对于[,]63x ππ∈-恒成立，求实数的取值范围.19. （本小题15分）如图，直三棱柱111C B A ABC -中，121AA BC AC ==，是棱1AA 的中点，BD DC ⊥1 (Ⅰ) 证明：BC DC ⊥1(Ⅱ) 求二面角11C BD A --的大小.20. （本小题15分）设n S 是数列{}n a 的前项和，11=a ，)2(212≥⎪⎭⎫⎝⎛-=n S a S n n n .⑴求{}n S 及{}n a 的通项； ⑵设22n n S b n =+，若数列{}n b 的前项和为n T ，证明12n T <；21. （本小题15分）已知抛物线C ：2x y =.过点)5,1(M 的直线交于,两点,抛物线在点处的切线与在点处的切线交于．(Ⅰ)求抛物线C 的焦点坐标及准线方程； (Ⅱ) 求PAB ∆面积的最小值．22. （本小题15分）已知函数121()(1)(0)2x f x f e f x x -'=-+.(Ⅰ) 求)(x f 的解析式及单调区间； (Ⅱ) 若b ax x x f ++≥221)(，求b a )1(+的最大值数学试题参考答案及评分标准一、 选择题 : 本大题共10小题, 每小题4分, 共40分． 在每小题给出的四个选项中, 只有一项是符合题目要求的.二、填空题：本大题共7个小题，多空题每题6分，单空题每题4分，共36分.11. 5923a ≥ 14. 132π， 15. 1024,180 16. 72 17. 112a <<三、简答题：本大题共5小题，共74分.解答应写出文字说明、证明过程和演算步骤.18、解（Ⅰ）()sin 2cos 21214f x x x x π⎛⎫=++=++ ⎪⎝⎭， …..3分其最小正周期是22T ππ==， …..5分 又当2242x k πππ+=-+，即()38x k k Z ππ=-∈时，sin 24x π⎛⎫+ ⎪⎝⎭取得最小值1-，所以函数()x f 的最小值是1，此时的集合为3|,8x x k k Z ππ⎧⎫=-∈⎨⎬⎩⎭． ….. 7分（Ⅱ）ππ()12()228842g x f x x x x ππ⎛⎫⎛⎫⎛⎫=+-=++=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭….. 9分由[,]63x ππ∈-，得22[,]33x ππ∈-，则1cos 2[,1]2x ∈-， ….. 11分()2[2g x x ∴=∈-， ….. 12分若()2g x a <-对于[,]63x ππ∈-恒成立，则max 2()2a g x a ->> ….. 15分19、解(Ⅰ) 证明：设112AC BC AA a ===，直三棱柱111C B A ABC -， 1DC DC ∴==， 12CC a =，22211DC DC CC ∴+=，1DC DC ∴⊥. …..3分又1DC BD ⊥，1DC DC D =I ，1DC ∴⊥平面BDC . 又BC ⊂平面BDC ,1DC BC ∴⊥. …..7分(Ⅱ)由(Ⅰ)知，1DC =，1BC =，又已知BD DC ⊥1，BD ∴=.在Rt ABD △中，,,90BD AD a DAB ==∠=，AB ∴=.222AC BC AB ∴+=，AC BC ∴⊥. …..9分法一：取11A B 的中点，则易证1C E ⊥平面1BDA ，连结DE ，则1C E ⊥BD ， 已知BD DC ⊥1，BD ∴⊥平面1DC E ，BD ∴⊥DE ，1C DE ∴∠是二面角11C BD A --平面角. …..11分在1Rt C DE △中，1111sin 2C EC DE C D∠===，130C DE ∴∠=.即二面角11C BD A --的大小为30. …..15分法二：以点C 为坐标原点，为轴，CB 为轴,1CC 为轴,建立空间直角坐标系C xyz -.则()()()()11,0,2,0,,0,,0,,0,0,2A a a B a D a a C a . …..9分()()1,,,,0,DB a a a DC a a =--=-，设平面1DBC 的法向量为()1111,,n x y z =，则11111100n DB ax ay az n DC ax az ⎧=-+-=⎪⎨=-+=⎪⎩,不妨令11x =,得112,1y z ==,故可取()11,2,1n =. 同理,可求得平面1DBA 的一个法向量()21,1,0n =. …..12分 设1n 与2n 的夹角为θ,则1212cos 6n n n n θ⋅===30θ∴=. 由图可知, 二面角的大小为锐角,故二面角11C BD A --的大小为30. ....15分1211(2)11()()()22n n n n n n n n n a S S n S a S S S S --=-≥∴=-=--Q 20、解（）由题意 2111122n n n n n S S S S S --=--+ …..3分 化简得：1121n n n S S S --=+1112n n S S -∴=+ 即1{}n S 是公差为2 的等差数列，又11111S a ==，*1121,()21n n n S n N S n ∴=-=∈- …..6分 111,1,111,2,22123n n n n a n a S S n n n n -=⎧=⎧⎪∴==⎨⎨-≥-≥⎩⎪--⎩， …..8分 （2）11111()22(21)(22)(21)(21)22121n n S b n n n n n n n ==<=-+-+-+-+ …..12分12111...(1)2212n n T b b b n ∴=+++<-<+ …..15分（其他证明可酌情给分）21、解: （Ⅰ）（0，14） ，直线14y =-； …..4分 （Ⅱ）16设直线l 的方程为y ＝k(x －1)＋5，设点A(x 1，y 1)，B(x 2，y 2)．由⎩⎨⎧=+-=25)1(xy x k y ，消去y 整理得 x 2－kx ＋k －5＝0，x 1＋x 2＝k ， x 1x 2＝k －5，又因为y′＝(x 2) ′＝2x ，所以，抛物线y ＝x 2在点A ，B 处的切线方程分别为y ＝2x 1x －21x ， y ＝2x 2x －22x ．得两切线的交点P(2k ，k －5)． ….8分所以点P 到直线l 的距离为1220422++-=k k k d ． ….10分又因为|AB|204122+-+k k k ．….12分设△PAB 的面积为S ，所以S ＝12|AB|·d＝32)16)2((41+-k ≥16（当k ＝2时取到等号）．所以△PAB 面积的最小值为16． ….15分22、解: (Ⅰ) 1()(1)(0)x f x f ef x -''=-+, ....1分令1x =得,(0)1f =, 再由121()(1)(0)2x f x f ef x x -'=-+,令0x =得()1f e '=.所以)(x f 的解析式为21()2xf x e x x =-+. ....3分 ()1x f x e x '=-+,易知()1x f x e x '=-+是上的增函数,且(0)0f '=.所以()00,()00,f x x f x x ''>⇔><⇔<所以函数)(x f 的增区间为()0,+∞,减区间为(),0-∞. ....6分 (Ⅱ) 若b ax x x f ++≥221)(恒成立, 即()()21()102x h x f x x ax b e a x b =---=-+-≥恒成立， ()()1x h x e a '=-+Q ,(1)当10a +<时,()0h x '>恒成立, ()h x 为上的增函数,且当x →-∞时, ()h x →-∞,不合题意; (2)当10a +=时,()0h x >恒成立, 则0b ≤,(1)0a b +=; ....8分 (3)当10a +>时, ()()1x h x e a '=-+为增函数,由()0h x '=得()ln 1x a =+, 故()()()0ln 1,()0ln 1,f x x a f x x a ''>⇔>+<⇔<+当()ln 1x a =+时, ()h x 取最小值()()()()ln 111ln 1h a a a a b +=+-++-. ....10分 依题意有()()()()ln 111ln 10h a a a a b +=+-++-≥, 即()()11ln 1b a a a ≤+-++,10a +>Q ,()()()()22111ln 1a b a a a ∴+≤+-++, ....12分令()()22ln 0 u x x x x x =->,则()()22ln 12ln u x x x x x x x '=--=-,()00()0u x x u x x ''>⇔<<<⇔>所以当x =, ()u x 取最大值2eu=.故当12a b +==时, ()1a b +取最大值2e. 综上, 若b ax x x f ++≥221)(，则 b a )1(+的最大值为2e . ....15分。
浙江省建人高复届高三数学第一学期第二次月考试卷文
浙江建人高复2015届第一学期第二次月考试卷文科数学一.选择题（本大题共有10个小题，每小题5分，共50分）1．已知集合{}2,101，，-=A ，B {}1x ≥x ，则A B ⋂=( ) A. {2}B. {1,2}C. {1,2}-D. {1,1,2}-2．下列说法正确的是( )A ．命题“若,12=x 则1=x ”的否命题为：“若12=x ，则1≠x ”； B ．命题“若x y =，则sin sin x y =”的逆否命题为真命题． C ．命题“a 、b 都是有理数”的否定是“a 、b 都不是有理数”； D ．“1-=x ”是“0652=--x x ”的必要不充分条件；3．已知a 是函数12()2log x f x x =-的零点，若0＜x 0＜a ，则0()f x 的值满足( )A.0()f x ＜0B.0()f x =0C.0()f x ＞0D.0()f x 的符号不确定4．若△ABC 的内角A 、B 、C 所对的边a 、b 、c 满足4)(22=-+c b a ,且C = 60°,则 ab 的值为( ) A ．348-B ．1C ．34D ．32 5．设,x y ∈R ，向量(,1),(1,),(2,4)a x b y c ===-且c b c a //,⊥，则a b +=( )A ．5 B. 10 C. 25 6．将函数)26cos(x y -=π的图像向右平移12π个单位后所得的图像的一个对称轴是( )A ．6π=x B ．4π=x C ．3π=x D ．12x π=7．函数y =的图像大致是( )A ．B ．C ．D ．8．若函数tan ,0,()2(1)1,0x x f x a x x π⎧-<<⎪=⎨⎪-+≥⎩在π(,)2-+∞上单调递增，则实数a 的取值范围是( )A. (0,1]B. (0,1)C. [1,)+∞D. (0,)+∞9．已知定义在R 上的函数)(x f 满足①)()2(x f x f =- ②.(2)(2)f x f x +=- ③[]3,1,21∈x x 时，0)()(2121<--x x x f x f ，则)2016(),2015(),2014(f f f 大小关系为( )A.)2016()2015()2014(f f f >>B.)2015()2014()2016(f f f >>C.)2015()2014()2016(f f f >=D.)2016()2015()2014(f f f => 10.数列{}n a 的通项为(1)sin12nn n a n π=-⋅⋅+ 前n 项和为n S , 100S = A. 50 B. 100 C. -150 二、填空题(本大题共7小题，每小题4分，共28分．将答案填在答题卡相应的位置上)11．已知函数()()⎩⎨⎧<>=)0(,20,log 2x x x x f x ，则()241-+⎪⎭⎫⎝⎛f f 的值等于_______.12．已知tan 3,θ=则2sin 22cos θθ-=_____________. 13. 规定符号""∆表示一种运算，即,b a ab b a ++=∆其中a 、+∈R b ，则函数x x f ∆=1)(的值域 ．14．在△ABC 中，角C B A ,,所对的边分别为c b a ,,，且sin sin cos A B C =⋅， 则B =__________.若6A π=,则ac= . 15．已知21,e e 是夹角为60°的两个单位向量，若21e e +=，2124e e +-=，则与的夹角为_____________.16．等差数列{}n a 的前n 项和为n S ,且0,0501=>S a .设)(21+++∈=N n a a a b n n n n ,则当数列{}n b 的前n 项和n T 取得最大值时, n 的值是_________________ .17．如果对于函数()x f 的定义域内任意两个自变量的值21,x x ，当21x x <时，都有()()21x f x f ≤且存在两个不相等的自变量21,m m ，使得()()21m f m f =，则称()x f 为定义域上的不严格的增函数．已知函数()x g 的定义域、值域分别为A ，B ，{}3,2,1=A ，A B ⊆且()x g 为定义域A 上的不严格的增函数，那么这样的函数()x g 共有________个。
浙江省建人高复高三数学第一学期第一次月考试卷 理
浙江建人高复2014学年第一学期第一次月考试卷理科数学一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 设{}2A log ,1y y x x ==>，{}2,1,1,2B =--则下列结论正确的是 （ ） A ．}{2,1A B =--I B. ()(,0)R C A B =-∞U C ．(0,)A B =+∞UD ． }{()2,1R C A B =--I2.已知0log log ,10<<<<n m a a a ，则 ( ) A.1＜n ＜m B.1＜m ＜n C.m ＜n ＜1 D.n ＜m ＜13.下列函数既是奇函数，又在区间[]1,1-上单调递减的是 （ ） A.()sin f x x = B.()1f x x =-+ C.()1()2x x f x a a -=+ D.2()ln 2xf x x-=+ 4.下列命题错误．．的是 ( ) A ．命题“2320,1x x x -+==若则”的逆否命题为“21,320x x x ≠-+≠若则” B ．命题“0,2>-∈∃x x R x ”的否定是“0,2≤-∈∀x x R x ”C ．“0a b ⋅=r r ”是“0a =r r 或0b =r r”的必要不充分条件D ．“若b a bm am <<则,22”的逆命题为真 5.已知函数)(,||1)1()(2)(x f x x f x f x f 则满足=-的最小值是 （ ）A.32B.2C.322D. 226.)(x f 是定义在R 上的以3为周期的偶函数，且0)2(=f ，则方程)(x f =0在区间（0，6）内解的个数的最小值是 （ ）A ．5B ．4C ．3D ．27.设10<<a ，函数)22(log )(2--=xx a a a x f ，则使0)(<x f 的x 的取值范围是 （ ）A.)0,(-∞B. )3log ,(a -∞C. ),0(+∞D.),3(log +∞a8.如果函数2()(31)(01)xxf x a a a a a =-->≠且在区间[)0+，∞上是增函数，那么实数a 的取值范围是（ ）Ａ．203⎛⎤ ⎥⎝⎦， Ｂ．313⎡⎫⎪⎢⎪⎣⎭， Ｃ．(13⎤⎦，Ｄ．32⎡⎫+⎪⎢⎣⎭，∞9..若使得方程0162=---m x x有实数解，则实数m 的取值范围为 （ ）2424.≤≤-m A 244.≤≤-m B 44.≤≤-m C244.≤≤m D10.已知函数)(x f y =是定义在R 上的单调函数，对R x ∈∀，3]2)([=-xx f f 恒成立，则=)3(f （ ）A ．1B ．3C ．8D ．9二、填空题：本大题共7小题，共28分。
浙江省杭州市2013届高三第一次高考科目教学质量检测数学(理)试题
故函数存在“转点”，且是“转点”的横坐标.
(0,7) (7,0)
O x 15．在△ABC中,角A,B,C的对边分别a,b,c,若.则直线被圆
长为 ．
16．若整数满足不等式组, 则的最大值为 ．
所截得的弦
(第17题)
O A B C 17．如图,在扇形OAB中,,C为弧AB上的一个动点.若，则的取值范围是 ．
三、解答题： 18．(本题满分14分)设.
18.【解析】（I）
故的最大值为，最小正周期为.
(II)由得，
故，
又由，解得。 再由， . 19.【解析】(I)由题意知， 当且仅当时等号成立，所以，当取得最大值时. (II)当时，即甲箱中有个红球与个白球， 所以的所有可能取值为则，，,， 所以红球个数的分布列为
于是. 20.【解析】（I）证明 ， 所以数列是等差数列，，因此
值，则首项的取值范围是( )
A. B. C. D.
二、填空题：
11．二项式的展开式中第四项的系数为 ．
12．从中任取三个数字，组成无重复数字的三位数中，偶数的个数是
(用数字回答)．
13．无穷数列 的首项是，随后两项都是，接下来项都是，再接下来项
都是，…，以此类推.记该数列为，若，，则 ．
14．若正数满足，则的最小值为 ． y
(Ⅱ)若直线 与椭圆C交于A、B两点，且线段AB中点恰好在直线上，求 △OAB的面积S的最大值.(其中O为坐标原点).
22．(本题满分15分)已知函数 (Ⅰ)当时，求函数的极小值；
(Ⅱ)当时，过坐标原点作曲线的切线，设切点为，求实数的值； (Ⅲ)设定义在上的函数在点处的切线方程为当时，若在内恒成
立，则称为函数的“转点”．当时，试问函数是否存在“转点”.若存在,请
浙江省建人高复2013届高三上学期第二次月考数学理试题
建人高复2013第二次月考数学问卷（理科）一、选择题 （本大题共10小题，每小题5分，共50分）1．已知集合},2|{},2,1,0{M a a x x N M ∈===，则集合N M ⋂= （ ） A ．{0}B ．{0，1}C ．{1，2}D ．{0，2}2．已知p ：,0)3(:,1|32|<-<-x x q x 则p 是q 的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．已知函数=-=+-=)(.)(.11lg )(a f b a f xxx f 则若 （ ）A ．bB ．－bC ．b1 D ．－b1 4.等差数列{}n a 中，已知16a =-，0n a =，公差d ∈N *，则n ()3n ≥的最大值为( ) A ．7B ．6C ．5D ．85．函数22sin sin 44f x x x ππ=+--（）（）（）是 （ ） A ．周期为π的偶函数 B ．周期为π的奇函数 C ． 周期为2π的偶函数 D ．.周期为2π的奇函数6．△ABC 中，a 、b 、c 分别为∠A 、∠B 、∠C 的对边.如果a 、b 、c 成等差数列，∠B=30°，△ABC 的面积为23，那么b = （ ）A ．231+B ．31+C ．232+ D ．32+7. 已知,,a b a b +成等差数列，,,a b ab 成等比数列，且0log 1m ab <<，则m 的取值范围是 A. 8m > B. 1m > C. 18m << D. 01m <<或8m >8．已知函数()x f x a x b =+-的零点0(,1)()x n n n Z ∈+∈，其中常数,a b 满足23a =，32b =，则n 等于（ ） A ．1- B.2-C ．1D ．29．函数()f x =()π20sin 2cos 231sin ≤≤---x xx x 的值域是 ( )（A ）⎥⎦⎤⎢⎣⎡-0,22 （B ）[—1，0] （C ）[]0,2-（D ）[]0,3-10．设定义域为),0(+∞的单调递增函数)(x f 满足：①xx f R x 3)(-∈∀+ ，②2]3)([=+xx f f ，则的最小值是（ ）A ．2B ．1C ． 0D ． 3二、填空题（本大题共7小题，每小题4分，共28分）11．在边长为6的正ABC ∆中，点M 满足,2MA BM =则CB CM ⋅等于____________. 12. 已知数列{}n a 满足，则通项n a = ；13. 已知实数0a ≠，函数2,1()2,1x a x f x x a x +<⎧=⎨--≥⎩，若(1)(1)f a f a -=+，则a 的值为______. 14. 设α为锐角，若4cos 65απ⎛⎫+= ⎪⎝⎭，则sin 212απ⎛⎫+ ⎪⎝⎭的值为 ．15．已知函数，如果2(1)(1)0f a f a -+-<，则a 的取值范围是 ； 16. 已知锐角满足则_________ .17.若不等式, ,对于一切正数x 、y 恒成立，则实数a 的最小值为________ .三、解答题（本大题共5小题，共72分）18. （本小题满分14分）在ABC ∆中，角A B C 、、所对的边分别为a b c 、、，向量12(1sin ,), (cos 2, 2sin )7p A q A A =-=，且//p q . （Ⅰ）求sin A 的值；（Ⅱ）若2,b =ABC ∆的面积为3，求a ．19. (本题满分14分) 已知数列{}n a 的首项t a =10>，1321nn n a a a +=+，*N n ∈（1）若53=t ，求证11n a ⎧⎫-⎨⎬⎩⎭是等比数列并求出{}n a 的通项公式； （2）若n n a a >+1对一切*N n ∈都成立，求t 的取值范围。
浙江省建人高复高三数学第一学期第一次月考试卷 文
浙江建人高复2014学年第一学期第一次月考试卷文科数学一． 选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知全集U ＝R ，集合A ＝{x |－2≤x ≤3}，B ＝{x |x <－1或x >4}，那么集合A ∩(∁U B )等于( )A ．{x |－2≤x <4}B ．{x |x ≤3或x ≥4}C ．{x |－2≤x <－1}D ．{x |－1≤x ≤3}2．已知函数f (x )＝log 2(x ＋1)，若f (α)＝1，则α＝( )A ．0B ．1C ．2D ．33．若21log 0,12ba ⎛⎫<> ⎪⎝⎭，则( )A ．a >1，b >0B ．a >1，b <0C ．0<a <1，b >0D ．0<a <1，b <04．函数f (x )＝⎩⎪⎨⎪⎧2x －x 2，x x 2＋6x －2≤x的值域是( )A ．RB ．[1，＋∞)C ．[－8,1]D ．[－9,1]5．若函数f (x )＝log a (2x ＋1)(a >0，且a ≠1)在区间⎝ ⎛⎭⎪⎫－12，0内恒有f (x )>0，则f (x )的单调减区间是( )A.⎝ ⎛⎭⎪⎫－∞，－12B.⎝ ⎛⎭⎪⎫－12，＋∞ C ．(－∞，0) D ．(0，＋∞)6．若函数f (x )＝log a (x ＋b )的大致图象如图所示，其中a ，b (a >0且a ≠1)为常数，则函数g (x )＝a x ＋b 的大致图象为()7. 已知函数||5)(x x f =，)()(2R a x ax x g ∈-=，若1)]1([=g f ，则=a （ ）A. 1B. 2C. 3D. -18. 已知条件：x y a a <（01a <<）则它的充要条件的是( ) （A ）221111x y >++（B ）22ln(1)ln(1)x y +>+（C ）sin sin x y >（D ）3x >3y 9．(14四川)已知()ln(1)ln(1)f x x x =+--，(1,1)x ∈-。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
建人高复第一次月考数学试卷(理科)一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1.集合 A=}4|{2>x x ，B={1log |3<x x }， 则A ⋂B= ( )A ．{2|-<x x }B ．{|23x x <<}C ．{|3x x >}D ．{2|-<x x 或23x <<}2.函数y =( )A ．[1,)+∞B ．2(,)3+∞C ． 2[,1]3D ．2(,1]33.设函数⎩⎨⎧>≤-=00)(2x xx x x f ，若,4)(=a f 则实数a =（ ）A.2-4或-B.24或-C.42或-D.22或-4.已知4.3log25=a ，6.3log45=b ，3.0log351⎪⎭⎫⎝⎛=c ，则（ ）A.c b a >>B.c a b >>C.b c a >>D.b a c >>5.设)(x f 是周期为2的奇函数，当10≤≤x 时，)1(2)(x x x f -=，则=-)25(f （ ）A.21-B.41-C.41 D.216.已知q p a x q x p ⌝⌝>>+是且,:,2|1:|的充分不必要条件，则实数a 的取值范围 可以是（ ） A ．1≥a B ．1≤a C ．1-≥a D ．3-≤a7.函数xxa y x=(01)a <<的图象的大致形状是 ( )8.函数()sin ,[,],22f x x x x ππ=∈-12()()f x f x >若,则下列不等式一定成立的是( )A.021>+x xB.2221x x > C.21x x > D.2221x x <9.函数)(x f 的定义域为R ,2)1(=-f ,对任意2)(,'>∈x f R x ,则42)(+>x x f 的 解集为（ ）A.)1,1(-B.),1(+∞-C.)1,(--∞D.R 10.已知函数2|3|)(3--+=a x x x f 在)2,0(上恰有两个零点，则实数a 的取值范围为( )A ．)2,0(B ．)4,0(C ．)6,0(D ．（2，4）二、填空题：本大题共7小题，每小题4分，共28分，把答案填写在答题卡相应位置。
11. 已知直线10x y --=与抛物线2y ax =相切，则______.a =12.若对任意的实数x 都有1)2(log 1-≤+-x a e ，则a 的取值范围是___________ 13．设函数213()44f x x bx =+-,已知不论αβ、为何实数,恒有c o s 0f α≤（）,2sin 0f β-≥（）, 则b= .14．已知函数f （x ）＝⎩⎪⎨⎪⎧－x 2＋2x x >0 ，0 x ＝0 ，x 2＋mx x <0为奇函数，若函数f （x ）在区间[－1，|a |－2]上单调递增，则a 的取值范围是________． 15.对满足21≥a 的一切实数a ， 当[]1,0∈x 时，函数)()(22R c c ax x a x f ∈++-=，均有1)(≤x f 成立，则c 的取值范围是__________16.已知函数)1,0(log )(≠>-+=a a b x x x f a 且，当432<<<<b a 时，函数)(x f 的零点()1,0+∈n n x ，*∈N n ，则__________=n17. 在平面直角坐标系xoy 中，已知P 是函数)0()(>=x e x f x 的图像上的动点，该图像在点P 处的切线l ，交y 轴于点M 。
过点P 作l 的垂线交y 轴于点N 。
设线段MN 的中点纵坐标为t ，则t 的最大值是___________三．解答题：本大题共5小题，共72分，解答应写出文字说明、证明过程或演算步骤18．设p:实数x 满足22430x ax a -+<,其中0a >,命题:q 实数x 满足2260,280.x x x x ⎧--≤⎪⎨+->⎪⎩．（1）若1,a =且p q ∧为真，求实数x 的取值范围；（2）若p ⌝是⌝q 的充分不必要条件,求实数a 的取值范围．19. 设二次函数a ax x x f ++=2)(，方程0)(=-x x f 的两根21,x x 满足1021<<<x x ， （1）求实数a 的取值范围； （2）试比较)0()1()0(f f f -与161的大小，并说明理由.20.定义在R 上的奇函数()f x 有最小正周期4，且()0,2x ∈时，3()91xxf x =+。
（1）求()f x 在[]2,2-上的解析式；（2）判断()f x 在()0,2上的单调性，并给予证明；（3）当λ为何值时，关于方程()f x λ=在[]2,2-上有实数解？21. 已知函数223241)(234--++-=x axx x x f 在区间[-1,1] 上单调递减,在区间[1,2]上单调递增,(1)求实数a 的值;(2)若关于x 的方程m f x =)2(有三个不同实数解,求实数m 的取值范围.22. 已知函数()ln f x x a x =-，1(), (R).a g x a x+=-∈（1）若1a =，求函数()f x 的极值；（2）设函数()()()h x f x g x =-，求函数()h x 的单调区间； (3)若在区间[]1,e 上存在一点0x ，使得0()f x <0()g x 成立，求a 的取值范围. （e 2.718...=）第一次月考数学(理科答案)一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1.集合 A=}4|{2>x x ，B={1log |3<x x }， 则A ⋂B= ( B )A ．{2|-<x x }B ．{|23x x <<}C ．{|3x x >}D ．{2|-<x x 或23x <<}2.函数y =( D )A ．[1,)+∞B ．2(,)3+∞C ． 2[,1]3D ．2(,1]33.设函数⎩⎨⎧>≤-=00)(2x xx x x f ，若,4)(=a f 则实数a =（ B ）A.2-4或-B.24或-C.42或-D.22或-4.已知4.3log25=a ，6.3log45=b ，3.0log351⎪⎭⎫⎝⎛=c ，则（ C ）A.c b a >>B.c a b >>C.b c a >>D.b a c >>5.设)(x f 是周期为2的奇函数，当10≤≤x 时，)1(2)(x x x f -=，则=-)25(f （A ）A.21-B.41-C.41 D.216.已知q p a x q x p ⌝⌝>>+是且,:,2|1:|的充分不必要条件，则实数a 的取值范围 可以是（ A ） A ．1≥a B ．1≤a C ．1-≥a D ．3-≤a7.函数xxa y x=(01)a <<的图象的大致形状是 ( D )8.函数()sin ,[,],22f x x x x ππ=∈-12()()f x f x >若,则下列不等式一定成立的是( B )A.021>+x xB.2221x x > C.21x x > D.2221x x <9.函数)(x f 的定义域为R ,2)1(=-f ,对任意2)(,'>∈x f R x ,则42)(+>x x f 的 解集为（ B ）A.)1,1(-B.),1(+∞-C.)1,(--∞D.R 10.已知函数2|3|)(3--+=a x x x f 在)2,0(上恰有两个零点，则实数a 的取值范围为( D )A ．)2,0(B ．)4,0(C ．)6,0(D ．（2，4）二、填空题：本大题共7小题，每小题4分，共28分，把答案填写在答题卡相应位置。
11. 已知直线10x y --=与抛物线2y ax =相切，则______.a =4112.若对任意的实数x 都有1)2(log 1-≤+-x a e ，则a 的取值范围是_121<≤a __________13．设函数213()44f x x bx =+-,已知不论αβ、为何实数,恒有cos 0f α≤（）,2sin 0f β-≥（）, 则b=21 .14．已知函数f （x ）＝⎩⎪⎨⎪⎧－x 2＋2x x >0 ，0 x ＝0 ，x 2＋mx x <0为奇函数，若函数f （x ）在区间[－1，|a |－2]上单调递增，则a 的取值范围是_–3≤a<–1或1<a ≤3_______． 15.对满足21≥a 的一切实数a ， 当[]1,0∈x 时，函数)()(22R c c ax x a x f ∈++-=，均有1)(≤x f 成立，则c 的取值范围是__43≤c ________16.已知函数)1,0(log)(≠>-+=a a b x x x f a且，当432<<<<b a 时，函数)(x f 的零点()1,0+∈n n x ，*∈N n ，则2__________=n17. 在平面直角坐标系xoy 中，已知P 是函数)0()(>=x e x f x 的图像上的动点，该图像在点P 处的切线l ，交y 轴于点M 。
过点P 作l 的垂线交y 轴于点N 。
设线段MN 的中点纵坐标为t ，则t 的最大值是____ee 212+_________三．解答题：本大题共5小题，共72分，解答应写出文字说明、证明过程或演算步骤18．设p:实数x 满足22430x ax a -+<,其中0a >,命题:q 实数x 满足2260,280.x x x x ⎧--≤⎪⎨+->⎪⎩．（I ）若1,a =且p q ∧为真，求实数x 的取值范围；（II ）若p ⌝是⌝q 的充分不必要条件,求实数a 的取值范围．解：（1）P ：（x-1）(x —3)<0, 则1<x<3——————————————3 q : ⎩⎨⎧>+≤+02)-4)(x (x 02)3)(x -x （则⎩⎨⎧<>≤≤-4x 2x 32-或x 所以2<x ≤3——————6则 p q ∧为真，实数x 的取值范围 2<x<3—————————————————7(2) 若p ⌝是⌝q 的充分不必要条件, 则q 是p 的充分不必要条件——————9{x|2<x ≤3}⊆{x|a<x<3a} ————————————12所以a ≤2且3a>3 所以实数a 的取值范围1<a ≤2.————————————1419. 设二次函数a ax x x f ++=2)(，方程0)(=-x x f 的两根21,x x 满足1021<<<x x ， （1）求实数a 的取值范围； （2）试比较)0()1()0(f f f -与161的大小，并说明理由.解法1：（Ⅰ）令2()()(1)g x f x x x a x a =-=+-+， 则由题意可得01012(1)0(0)0a g g ∆>⎧⎪-⎪<<⎪⎨⎪>⎪>⎪⎩，，，，————————————3 01133a a a a ⎧>⎪⇔-<<⎨⎪<->+⎩，，或03a ⇔<<-——————————7 故所求实数a的取值范围是(03-，（II ）2(0)(1)(0)(0)(1)2f f f g g a -== ，令2()2h a a = —————————9当0a >时，()h a 单调增加，∴当03a <<-时，20()32)2322)2(17122h a h<<--—————————12 1216=<，即1(0)(1)(0)16f f f -< .——————————14 解法2：（I ）同解法1（II ） 2(0)(1)(0)(0)(1)2f f f g g a -==，由（I）知03a <<-，1170-<<∴又10+>，于是221112(321)1)0161616a a -=-=-+<，即212016a -<，故1(0)(1)(0)16f f f -<解法3：（I ）方程()0f x x -=⇔2(1)0x a x a +-+=，由韦达定理得 121x x a +=-，12x x a =，于是121212121200010(1)(1)0(1)(1)0x x x x x x x x x x ∆>⎧⎪+>⎪⎪<<<⇔>⎨⎪-+->⎪⎪-->⎩，，，，0133a a a a ⎧>⎪⇔<⎨⎪<->+⎩，，03a ⇔<<- 故所求实数a的取值范围是(03-，（II ）依题意可设12()()()g x x x x x =--，则由1201x x <<<，得12121122(0)(1)(0)(0)(1)(1)(1)[(1)][(1)]f f f g g x x x x x x x x -==--=-- 2211221112216x x x x +-+-⎛⎫⎛⎫<=⎪ ⎪⎝⎭⎝⎭，故1(0)(1)(0)16f f f -<20.定义在R 上的奇函数()f x 有最小正周期4，且()0,2x ∈时，3()91xxf x =+。