状态变量滤波器电路设计
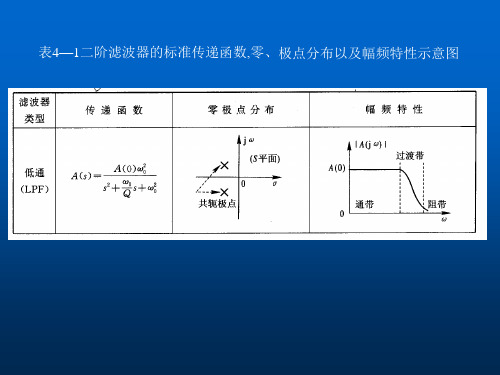
38-表41二阶滤波器的标准传递函数,零、极点分布以及幅频特性示意图
[ R ]/ 1k / 51%
10 k
12 V
74 1
10 k
12 V
图4—29 50Hz陷波器的幅频特性及输入输出波形
4—2—5
R
全通滤波器的幅频特性
是平行于频率轴的直线, 所以它对频率没有选择性。
R -
人们主要利用其相位频率 特性,作为相位校正电路
ui
+
uo
或相位均衡电路。图4—
R1
C
30所示,是一个一阶全通
滤波器或移相器,其传递 图4—30一阶全通滤波器(移相器)电路
函数为
Auf
(s)
1 1
sR1C sR1C
Auf ( j ) 1
( j ) 2 arctan RC
(4—40) (4—41a)
(4—41b)
A (ω ) 1
0 ω
(ω )
0
1 /R 1 C
R1
C4
R5
ui
-
R
C
2
3
A +
uo
Rp
(a )
图4—25带通滤波器
| A(jω) |
| A(jω) |
A(ω0) 0.707A(ω0)
R2
0
ω0
ω BW= ω0
0
ω01 ω02 ω03
ω
Q
(b)
(c)
图4—25 (a)电路;(b)幅频特性;(c)调节R2,幅频特性移动
4.3.4 带阻滤波电路(BEF)
带阻滤波器。因为
Ao s
Au
f
(s)
1
s2
Q
o s
Q
o2
带限信号的数字滤波器设计与实现

带限信号的数字滤波器设计与实现随着数字信号处理的日益发展,数字滤波器逐渐成为了数字信号处理中不可或缺的一部分。
数字滤波器主要用于对信号进行滤波,即去除干扰或保留特定频率成分,以便进一步处理。
而带限信号的数字滤波器则是常常用来处理特定频率范围内的信号。
在本文中,我们将深入探讨带限信号的数字滤波器设计与实现。
一、带限信号的概念与示例带限信号是指具有一定的低频截止频率和高频截止频率的信号,其频率范围被限制。
在实际应用中,产生带限信号的原因可能是信号源的特性或者信号在传输过程中被限定在一定的频带内。
下图是一个典型的带限信号的示例。
(图片来源:_数字信号处理(DSP)原理与应用_)二、带限信号的数字滤波器设计数字滤波器可以分为FIR(有限冲激响应)滤波器和IIR(无限冲激响应)滤波器两类。
对于带限信号的数字滤波器设计,通常选择IIR滤波器,因为它们可以比FIR滤波器更有效地利用滤波器系数,从而提供更好的性能和更低的计算复杂度。
下面,我们将介绍IIR带限信号数字滤波器设计的详细步骤。
1. 确定滤波器需求在数字滤波器设计开始之前,必须先了解所需滤波器的要求,以便选择正确的滤波器类型和设置参数。
对于带限信号的数字滤波器,主要要确定以下几个参数:- 截止频率: 包括低频截止频率和高频截止频率。
- 通带增益: 带限信号通过滤波器后的增益值。
- 阻带衰减: 滤波器在截止频率附近的衰减程度。
2. 选择合适的滤波器类型根据所需滤波器的要求,选择合适的滤波器类型。
通常,设计带限信号数字滤波器的首选是Butterworth(巴特沃斯)滤波器,因为它可以实现平滑的滤波响应,且阻带衰减比谐振响应型更好。
3. 确定滤波器阶数阶数是指滤波器中的二阶段数。
阶数越高,滤波器的斜率就越陡峭,但计算复杂度也越高。
但是,阶数也直接影响到滤波器的性能。
在确定阶数时应该如何权衡这些因素是非常关键的。
通常,滤波器的阶数越高,则滤波器性能越好。
但随着阶数的增加,滤波器的计算量也增加,可能会导致滤波器失去实用价值。
7-3有源滤波电路

U0 U 1 Au U i U i 1 j RC U0 ( s) U ( s) 1 Au( s ) ( s ) U ( s ) 1 sRC Ui i
将s换成jw,便可得到放大倍数。传递函数分母中s的 最高指数称为滤波器的阶数。电路中RC环节愈多,阶数 愈高,过渡带将愈窄。
1 UM ( S ) 1 sRC 1 1 //( R ) UM ( S ) sC sC 1 Ui ( S ) 1 R //( R ) sC sC Up ( S )
分析方法:电路引入了负反 馈利用节点电流法求解输出 电压与输入电压的关系。
(2)简单二阶LPF
一阶低通和二阶低通幅频特性曲线的区别:
Uo Ui
AF -3dB 理想低通 一阶低通 二阶低通
0
o
阶数越高,幅频特性曲线越接近理想滤波器。
运算电路与有源滤波器的比较
相同之处
电路中均引入深度负反馈,因而集成运放均工作在
线性区。 均具有“虚短”和“虚断”的特点,均可用节点电 流法求解电路。
1பைடு நூலகம்滤波电路的定义
对工作信号的频率具有选择性的电路。 功能:使指定频段的信号顺利通过,其它频率的信号被 衰减。
2、滤波电路的种类
通带:允许通过的频段称为通带 阻带:将信号衰减到零的频段为阻带
理想幅频特性 无过渡带
低通滤波器(LPF)
滤波电路的种类
高通滤波器(HPF)
阻容耦合
带通滤波器(BPF)
通信电路
有良好的隔离性。
除能滤波外,还能将信号放大,而且Av容易调节。
不适宜高电压大电流的负载,只适用于信号处理。 不适宜高频范围,一般使用频率在几十KHz以下。
各种滤波器及其典型电路

第一章滤波器1.1 滤波器的基本知识1、滤波器的基本特性定义:滤波器是一种通过一定频率的信号而阻止或衰减其他频率信号的部件.功能:滤波器是具有频率选择作用的电路或运算处理系统,具有滤除噪声和分离各种不同信号的功能。
类型:按处理信号形式分:模拟滤波器和数字滤波器。
按功能分:低通、高通、带通、带阻、带通.按电路组成分:LC无源、RC无源、由特殊元件构成的无源滤波器、RC有源滤波器按传递函数的微分方程阶数分:一阶、二阶、…高阶.如图1.1中的a、b、c、d图分别为低通滤波器、高通滤波器、带通滤波器、带阻滤波器传输函数的幅频特性曲线。
图1.1 几种滤波器传输特性曲线.2、模拟滤波器的传递函数与频率特性(一)模拟滤波器的传递函数模拟滤波电路的特性可由传递函数来描述。
传递函数是输出与输入信号电压或电流拉氏变换之比。
经分析,任意个互相隔离的线性网络级联后,总的传递函数等于各网络传递函数的乘积。
这样,任何复杂的滤波网络,可由若干简单的一阶与二阶滤波电路级联构成。
(二)模拟滤波器的频率特性模拟滤波器的传递函数H(s)表达了滤波器的输入与输出间的传递关系.若滤波器的输入信号Ui是角频率为w的单位信号,滤波器的输出Uo(jw)=H(jw)表达了在单位信号输入情况下的输出信号随频率变化的关系,称为滤波器的频率特性函数,简称频率特性。
频率特性H(jw)是一个复函数,其幅值A(w)称为幅频特性,其幅角∮(w)表示输出信号的相位相对于输入信号相位的变化,称为相频特性(三)滤波器的主要特性指标1、特征频率:(1)通带截止频f p=wp/(2)为通带与过渡带边界点的频率,在该点信号增益下降到一个人为规定的下限。
(2)阻带截止频f r=wr/(2)为阻带与过渡带边界点的频率,在该点信号衰耗(增益的倒数)下降到一人为规定的下限。
(3)转折频率f c=wc/(2)为信号功率衰减到1/2(约3dB)时的频率,在很多情况下,常以fc作为通带或阻带截频。
基于_FPGA_的卡尔曼滤波器的设计与实现

基于_FPGA_的卡尔曼滤波器的设计与实现FPGA(Field Programmable Gate Array)是一种可以重新编程的可编程逻辑器件,可以根据用户的需要进行重新配置和编程,从而实现不同的应用。
卡尔曼滤波器是一种用于估计系统状态的滤波器,能够通过利用过去观测值和当前的测量值来估计未来的状态。
在本文中,我们将探讨基于FPGA的卡尔曼滤波器的设计与实现。
卡尔曼滤波器是一种递归的估计算法,用于估计状态变量的最优估计。
它将过去的观测值和当前的测量值进行加权平均,得到对未来状态的估计。
在实时应用中,常常需要高速和高准确度的数据处理,这就需要一种高效的硬件实现方法。
基于FPGA的卡尔曼滤波器可以提供高性能的实时数据处理,同时还能够灵活地适应不同的实时应用的需求。
基于FPGA的卡尔曼滤波器的设计与实现主要包括以下几个方面:首先,需要设计FPGA的硬件结构。
硬件结构通常包括状态估计器、卡尔曼增益计算器和误差估计器等关键模块。
状态估计器用于估计当前系统的状态变量,卡尔曼增益计算器用于计算卡尔曼增益矩阵,误差估计器用于估计状态估计器的误差。
这些模块之间需要进行数据传递和计算,因此需要设计合适的数据通路和控制信号。
其次,需要进行FPGA的编程和配置。
FPGA可以通过硬件描述语言(如VHDL或Verilog)进行编程和配置。
在设计过程中,需要将卡尔曼滤波器的算法转化为相应的硬件描述,并利用FPGA的配置工具将其加载到FPGA芯片中。
然后,需要进行系统级的仿真和验证。
在设计过程中,可以通过使用仿真工具对系统进行仿真和验证。
通过仿真可以检查系统的功能和性能,并进行必要的调试和优化。
最后,需要进行性能评估和优化。
FPGA的设计和实现需要考虑多个指标,如延迟、功耗和面积等。
通过性能评估和优化可以找出系统的瓶颈,并进行相应的改进,以提高系统的性能。
总结起来,基于FPGA的卡尔曼滤波器的设计与实现是一个复杂的过程,需要进行硬件结构设计、FPGA编程和配置、系统仿真和验证以及性能评估和优化等多个步骤。
LTC1068说明文档

LTC1068说明文档1.2 程控滤波器的设计方案一:采用集成的开关电容滤波器如MAX262,开关电容滤波器可直接处理模拟信号,简化电路设计,容易实现功能。
但是此种方案不能设计较高要求的滤波器,且精度不是很高。
方案二:采用集成的连续时间滤波器如LTC1068。
可以实现对模拟信号的直接处理,电路设计也相对简单,容易实现功能,精度也比较好。
方案三:采用TI的TLC7528和运算放大器LF353组成多状态变量滤波器并通过对链路的电阻值进行改变来实现程控滤波器。
TLC7528是双8位DA转换器,转换速度快,LF353是高带宽双JEFT 输入的运算放大器,具有失调电压低。
但是此种方案电路复杂,程序控制也相对复杂。
综上所述,本设计采用方案二。
LTC1068有五种连接模式:模式1:提供二阶带通、带阻、低通输出;模式1b:模式1的变形模式,提供二阶带通、带阻、低通输出;模式2:提供二阶带通、高通带阻、低通输出;模式3:提供二阶带通、高通、低通输出;本测试使用了模式3:二阶高通:Q=0.857 信号放大倍数:Av=-(R6/R8)=-1时钟频率100KHZ,信号幅度1.06V输入信号频率(KHz)0.4 0.6 0.8 1 1.2 1.5 2 输出信号幅度(V)0.2 0.4 0.656 0.864 1 1.06 1.06时钟频率200KHZ,信号幅度1.06V输入信号频率(KHz)1 1.4 1.82 2.2 2.63 输出信号幅度(V)0.296 0.536 0.768 0.864 0.944 1.03 1.06二阶低通:Q=0.857 信号放大倍数:Av=-(R2/R8)=-1时钟频率100KHZ,信号幅度1.06V输入信号频率(KHz)0.4 0.6 0.8 1 1.2 1.5 1.8 输出信号幅度(V)1.06 1.06 1.01 0.864 0.704 0.504 0.352时钟频率200KHZ,信号幅度1.06V输入信号频率(KHz)1 1.4 1.82 2.2 2.63 输出信号幅度(V)1.06 1.05 0.994 0.864 0.776 0.616 0.496二阶带通:Q=0.857 信号放大倍数:Av=-(R3/R1)*(1/(1-(R3/(32*R4))))=-0.853时钟频率100KHZ,信号幅度1.06V输入信号频率(KHz)0.4 0.56 0.6 0.8 1 1.2 1.5 1.8 2.4 输出信号幅度(V)0.448 0.618 0.648 0.808 0.864 0.832 0.712 0.618 0.464时钟频率200KHZ,信号幅度1.06V输入信号频率(KHz)1 1.1 1.4 1.82 2.2 2.63 3.6 输出信号幅度(mV)0.552 0.618 0.746 0.864 0.864 0.864 0.802 0.728 0.618。
开关电容(SC)滤波器设计和应用

而 电流 为 :i () C t / C C v () 2t ] T ,可见 基本 开关 电容 c t =Aq () T = [1t v () / c 单元 可 以等效为 一个 电阻R cC  ̄T/ ,其优 点是在集 成 电路 中可 以用很 小的 芯
关键词 : 模拟 滤波器:开关 电容 ;音频滤波器 中图分类号 :T 7 文献标识码 :A 文章编 号:1 7 - 7 9 2 1 )0 1 0 0 0 N 1 5 7(0 0 7 0 5 - 1 6
在信 号 处理 中 ,滤 波 器 占有 十 分 重要 的地位 ,它对 实 际 信 号进 行 过 滤 ,提取 有效 信号 、抑 制干 扰噪 声 。模拟 滤波 器应 用 于各种 模拟 信 号处理
简化了开关电容电路的分析和设计 。
2开 关电窖 ( CJ S 滤波器 的设 计
l
R1
在模拟 电路 中经 常涉 及到 电路 的频率 特性 、延 时特 性等 ,这些 电路 性 能与 电路 的 时间 常数有 关 ,这些 时 间常数 多 由 电路 中 的元件 参 数 电感 、 电 阻、 电容 来确 定 。在模拟 集 成 电路 中,制 作 电感是 困难 的 ,所 以多采 用 电
图1 基本 开关 电容单 元
语音信 号 以外 的各 种杂 波 。5t 抑制 滤波 器 是话 路滤 波器 组成 部 分之 一 , 0z t 亦称 5H 陷波器 。它采 用 由加法 器和 积分 器 构成 的状 态变 量滤 波器 结构 , 0z 可 以用 来 抑制 电源 的干 扰 。 由于 陷波 频 率低 ,要 求很 大 的时 间常 数 。为节 省芯 片面 积 ,采用 开关 电容 技术 实 现 。图4 a所 示是 5H 抑制 滤波 器 的有 () 0z 源 R原 型 电路, 图4b所 示是 其对应 的 开关 电容滤 波器 电路 。 c ()
T-S模糊系统量化H∞滤波器设计

T-S模糊系统量化H∞滤波器设计赵迪;常晓恒【摘要】This paper considers the problem of H∞filter design for T-S fuzzy system with out-put quantization. Attention is focused on the design of a filter to mitigate the quantization effects, which ensured not only the asymptotical stability but also a prescribed H∞ performance. By using fuzzy Lyapunov function approach and adding slack matrix variables, a sufficient condition is presented in terms of linear matrix inequalities (LMIs) for such filter exists. Finally, a numerical example is provided to demonstrate the effectiveness of the proposed approach.%本文研究了离散T-S模糊系统H∞量化滤波问题。
主要目的是针对存在量化的T-S模糊反馈系统设计可行的滤波器算法使其在消除量化的影响下渐进稳定的并满足给定H∞性能指标。
具体是通过模糊Lyapunov函数及引入松弛变量,提出了比文献中结果保守性低的基于线性矩阵不(LMIs)的滤波器存在的充分条件。
最后,通过数值仿真例子来验证设计方案的有效性。
【期刊名称】《电子设计工程》【年(卷),期】2015(000)016【总页数】4页(P112-115)【关键词】T-S模糊系统;H∞滤波;模糊Lyapunov函数;量化;线性矩阵不等式(LMIs)【作者】赵迪;常晓恒【作者单位】渤海大学数理学院,辽宁锦州 121003;渤海大学工学院,辽宁锦州 121003【正文语种】中文【中图分类】TN964自1985 年Takagi 和Sugeno[1]提出了著名的T-S 模糊系统模型来描述复杂的非线性系统以来,T-S 模糊模型作为处理非线性系统的有效手段吸引了众多学者的关注[1-4]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
状态变量滤波器电路设计
发布: 2011-9-30 | 作者: —— | 来源:huangjiapeng| 查看: 54次| 用户关注:滤波器
到目前为止,我们所讨论的过滤器是相对简单的单运放电路或几个单运放电路级联。
状态变量的过滤器,但是,使用三个或四个运算放大器和两个反馈通路。
虽然有点复杂,状态变量的配置提供了与其他简单的过滤器没有的几个特点。
首先,所有三个过滤器类型(低通,带通和高通)可同时进行。
可以作出一
些非常有趣的反应,通过正确地总结这些输出的。
高Q带通滤波器可建。
可以电子调谐阻尼和/或临界频率。
随着IC技术的进步,现在一些厂家提供具有同时低通,高通,带通输出响应的普遍过滤器。
Notch 和全通功能也通用运算相结合,这些输出响应放大器。
由于它的多功能性,这种过滤器是所谓的普遍的过滤器。
它提供了用户容易控制的增益和品质因数。
它也被称为状态变量的过滤器。
到目前为止,我们所讨论的过滤器是相对简单的单运放电路或几个单运放电路级联。
状态变量的过滤器,但是,使用三个或四个运算放大器和两个反馈通路。
虽然有点复杂,状态变量的配置提供了与其他简单的过滤器没有的几个特点。
首先,所有三个过滤器类型(低通,带通和高通)可同时进行。
可以作出一些非常有趣的反应,通过正确地总结这些输出的。
高Q带通滤波器可建。
可以电子调谐阻尼和/或临界频率。
三运算放大器,单位增益状态变量滤波器的原理是描绘图。
运算放大器A 2和A 3是集成运算放大器与低通输出和带通输出部分输入一个1总结。
该电路实际上是一个小型模拟计算机设计,解决每一个过滤器类型的微分方程(传递函数) 。
对于正确的操作RJ = R 2 = R 3 = R,R 4 = R 5 = R;和C X = C 2 = C。
三滤的临界频率都是平等的,是为
阻尼是由R 6和R7 设置。
这就决定了低通和高通的反应类型(贝塞尔,巴特沃斯,切比雪夫)
α= 3 [R / R 6 + R 7 ]
它还设置了Q和带通滤波器的增益
Q = 1 /α和A 频段。
通= Q
状态变量的过滤器生产标准的二阶低通带通,高通响应。
每个关键频率是平等的,是由带通输出反馈和阻尼。
所有三个输出阻尼正是相同的效果(在相同的数值)为单运放滤波器。
对于低通和高通,阻尼系数的1.414提供一个Butterworth响应。
1.732阻尼提供贝塞尔响应,α= 0.766时,3分贝峰(切比雪夫) 。
高通- 3分贝频率同样是转向高通校正系数K HP = 1 / K LP
对于带通部分,改变阻尼系数成反比改变Q值和增益(临界频率)。
但关键的频率是RF和C,它不是由阻尼系数的变化而改变。
这意味着只在阻尼的变化并直接影响体重。
因此,带通滤波器的调整是非常方便的。
电阻R调整中心频率。
电阻R A和R B 调整的体重只。
在这一点上,它是至关重要的,使我们认识到从所有三个输出不能同时获得,最佳的性能。
举例来说,如果我们想在低通和高通输出的通带的最大平整度,我们必须选择一个与
α= 1.414巴特沃斯响应。
但阻尼系数的1.414给出了一个Q 和0.707 每一个F 。
带通滤波器将是非常有选择性,甚至中心频率会衰减30%。
另一方面,如果Q被选定为20,以达到合理的选择性和中心频率的增益,低通和高通输出将阻尼系数为0.05。
这将导致一个通带峰值超过25分贝。
我们可以优化输出带通或低通和高通输出。
