微积分样题1
微积分试题及答案

微积分试题及答案1. 求函数f(x) = 3x^2 - 2x + 1在x = 2处的导数。
解析:首先,我们需要求函数f(x)的导数。
对于一个二次函数 f(x) = ax^2 + bx + c,它的导数等于2ax + b。
因此,对于f(x) = 3x^2 - 2x + 1,其导数即为 f'(x) = 6x - 2。
接下来,我们需要求在 x = 2 处的导数。
将 x = 2 代入导数公式,得到 f'(2) = 6(2) - 2 = 10。
答案:函数f(x)在x = 2处的导数为10。
2. 求函数g(x) = sin(x) + cos(x)的定积分∫[0, π] g(x)dx。
解析:我们需要求函数 g(x) = sin(x) + cos(x) 在[0, π] 区间上的定积分。
首先,我们可以分别求 sin(x) 和 cos(x) 在[0, π] 区间上的定积分,然后将结果相加即可。
根据积分的基本性质,∫sin(x)dx = -cos(x) 和∫cos(x)dx = sin(x),所以:∫[0, π]sin(x)dx = [-cos(x)]|[0, π] = -cos(π) - (-cos(0)) = -(-1) - (-1) = 2∫[0, π]cos(x)dx = [sin(x)]|[0, π] = sin(π) - sin(0) = 0 - 0 = 0将上述结果相加,得到定积分的结果:∫[0, π]g(x)dx = ∫[0, π]sin(x)dx + ∫[0, π]cos(x)dx = 2 + 0 = 2答案:函数g(x) = sin(x) + cos(x)在[0, π]区间上的定积分为2。
3. 求曲线y = x^3在点(1, 1)处的切线方程。
解析:要求曲线 y = x^3 在点 (1, 1) 处的切线方程,我们需要确定切线的斜率和过切点的直线方程。
首先,我们求出这个曲线在点(1, 1)处的导数来获得切线的斜率。
微积分1(含答案)

第 1 页 共 8 页1、在二元函数的极限中,(,)P x y 趋于点000(,)P x y 的方式是任意的; ( √ )2、若(,)z f xy =在00(,)x y 处存在一阶偏导数,则(,)z f x y =在00(,)x y 处可微( × )3、“对二元函数),(y x f z =,求其在条件0),(=y x ϕ下的极值”问题的拉格朗日函数为:),(),(),,(y x y x f y x F λϕλ+=; ( √ )4、设22:14D x y ≤+≤,则3D d x d y π=⎰⎰;( √ ) 5、若级数1nn a∞=∑收敛,级数1nn b∞=∑发散,则级数1()nn n ab ∞=+∑必发散; ( √ )6、级数1nn ∞= ( × )7、级数21n n x n ∞=∑的收敛半径是2; ( × )8、2()20x y y x ''-+=是一阶微分方程. ( √ ) 1、若函数(,)f x y 点00(,)x y 处连续,则0000(,)(,)lim(,)(,)x y x y f x y f x y →=; ( √ )2、若(,)z f xy=在00(,)x y 处可微,则(,)z f x y =在00(,)x y 处存在连续偏导数( √ )3、若在驻点00(,)x y 处00(,)xx f x y ''和00(,)yy f x y ''异号,则00(,)f x y 是函数极值;( × )4、设22(,)1f x y x y =--,则(0,)是函数的极大值点; ( √ )5、(,)(cos ,sin )DDf x y d f r r drd σθθθ=⎰⎰⎰⎰;( × ) 6、若级数1nn u∞=∑收敛,则级数12nn u∞=+∑也收敛; ( √ )7、级数1(1)2nnn ∞=-∑是条件收敛; ( × ) 8、2()20y y ''-=是二阶微分方程. ( × )第 2 页 共 8 页二、填空题 1、设x z y =,则zx∂=∂ ln x y y ; 2、设22xy z e +=,则dz = 222()xy e xdx ydy ++ ;3、在极坐标系下计算二重积分有公式(,)Df x y dxdy =⎰⎰(cos ,sin )Df r r rdrd θθθ⎰⎰ ;4、设0a ≠,则当q 满足:q 1> 时,几何级数1n n aq ∞=∑收敛; 5、对任意级数1nn u∞=∑,如果1nn u∞=∑收敛,则称级数1nn u∞=∑为 绝对 收敛级数;6、1()1f x x =-展开成x 的幂级数是_______0(11)nn x x ∞=-<<∑______。
微积分数学竞赛试题及答案

微积分数学竞赛试题及答案试题一:极限问题题目:求极限 \(\lim_{x \to 0} \frac{\sin x}{x}\)。
解答:根据洛必达法则,当分子分母同时趋向于0时,可以对分子分母同时求导后再求极限。
对分子和分母分别求导得到:\[ \lim_{x \to 0} \frac{\cos x}{1} = 1 \]因此,原极限的值为1。
试题二:导数问题题目:求函数 \( f(x) = 3x^2 - 2x + 1 \) 在 \( x = 1 \) 处的导数。
解答:首先求函数 \( f(x) \) 的导数:\[ f'(x) = 6x - 2 \]然后将 \( x = 1 \) 代入导数表达式中:\[ f'(1) = 6 \times 1 - 2 = 4 \]所以,函数在 \( x = 1 \) 处的导数为4。
试题三:积分问题题目:求定积分 \(\int_{0}^{1} x^2 dx\)。
解答:使用幂函数的积分公式:\[ \int x^n dx = \frac{x^{n+1}}{n+1} + C \]对于 \( n = 2 \),我们有:\[ \int x^2 dx = \frac{x^3}{3} + C \]计算定积分的值:\[ \int_{0}^{1} x^2 dx = \left[ \frac{x^3}{3} \right]_{0}^{1}= \frac{1^3}{3} - \frac{0^3}{3} = \frac{1}{3} \]试题四:级数问题题目:判断级数 \(\sum_{n=1}^{\infty} \frac{1}{n(n+1)} \) 是否收敛。
解答:这个级数可以通过部分分式分解来简化:\[ \frac{1}{n(n+1)} = \frac{A}{n} + \frac{B}{n+1} \]解得 \( A = 1 \) 和 \( B = -1 \),因此:\[ \frac{1}{n(n+1)} = \frac{1}{n} - \frac{1}{n+1} \]将这个结果代入级数中,我们得到一个望远镜级数:\[ \sum_{n=1}^{\infty} \left( \frac{1}{n} - \frac{1}{n+1}\right) \]这个级数的项会相互抵消,只剩下第一项 \( \frac{1}{1} \),所以级数收敛,其和为1。
微积分复习题(1)(1)

《微积分》期末考试复习题第一章 函数与极限2. 求下列函数的定义域211(1)arctan ;(2);lg(1)(3); (4)arccos(2sin ).1y y x x xy y x x ==-==-6. 求下列极限:24213423(2)lim ;31(4)lim ;31(1)(2)(3)(6)lim ;5x x n x xx x x xx x n n n n →→∞→∞+-+--++++ 7若211lim 221x x ax b x →∞⎛⎫+=-- ⎪+⎝⎭,求a 和b . 9. 通过恒等变形求下列极限:2243222231016811(2)lim ;(4)lim ;15422 (5)lim log (1)113 (12)lim ;(13)lim ; (11)lim ; (1)11(1n n x x x a x x x x x x x xx x x x x x x →∞→→+∞→→→→-+⎛⎫+++ ⎪-+⎝⎭+-+⎛⎫- ⎪---⎝⎭3sin 0001sin 4)lim ; (15)lim(12); (16)lim ln .x xx x x a x x x x→→→-+11. 利用重要极限1lim(1)e uu u →+=,求下列极限:2221232cot 013(1)lim ;(2)lim ;12(3)lim(13tan );(4)lim(cos 2);xx x x xx x x x x x x x +→∞→∞→→+⎛⎫⎛⎫+ ⎪ ⎪-⎝⎭⎝⎭+12. 利用取对数的方法求下列幂指函数的极限:()1201(1)lim ;(4)lim .1e xx xx x x x →→∞⎛⎫++ ⎪⎝⎭14. 利用0sin lim1x xx→=或等价无穷小量求下列极限:000sin 1cos 2(1)lim;(3)lim ;sin sin arctan 3(5)lim ;(6)lim 2sin ;2x x n n x n mx xnx x xx x x →→→→∞-16、若0→x 时,1)1(412--ax 与x x sin 是等价无穷小,求a 的值。
微积分考试试题及答案

微积分考试试题及答案第一题:求函数 f(x) = x^3 - 3x^2 + 2x + 1 的极值点和拐点。
解析:首先,我们需要找到函数的极值点。
极值点对应于函数的导数为零的点。
对函数 f(x) 求导得到 f'(x) = 3x^2 - 6x + 2。
令导数等于零,我们得到一个二次方程 3x^2 - 6x + 2 = 0。
使用求根公式,可以解得这个二次方程的解为x = 1 ± √(2/3)。
所以函数的极值点为x = 1 + √(2/3) 和 x = 1 - √(2/3)。
接下来,我们需要找到函数的拐点。
拐点对应于函数的二阶导数为零的点。
对函数 f(x) 求二阶导数得到 f''(x) = 6x - 6。
令二阶导数等于零,我们得到 x = 1,这是函数的一个拐点。
综上所述,函数 f(x) = x^3 - 3x^2 + 2x + 1 的极值点为x = 1 + √(2/3)和 x = 1 - √(2/3),拐点为 x = 1。
第二题:已知函数 f(x) = e^x,在点 x = 0 处的切线方程为 y = mx + b,求参数 m 和 b 的值。
解析:切线方程的斜率 m 等于函数在给定点的导数。
对函数 f(x) = e^x 求导得到 f'(x) = e^x。
根据题意,在 x = 0 处求切线,所以我们需要计算函数在 x = 0 处的导数。
将 x = 0 代入函数的导数表达式中,我们得到 f'(0) = e^0 = 1。
所以切线的斜率 m = 1。
切线方程的常数项 b 可以通过将给定点的坐标代入切线方程求解。
由题意知道切线过点 (0, f(0)),即 (0, e^0) = (0, 1)。
将点 (0, 1) 代入切线方程 y = mx + b,我们得到 1 = 0 + b,解得 b = 1。
综上所述,切线方程为 y = x + 1。
第三题:计算函数f(x) = ∫(0 to x) sin(t^2) dt。
微积分练习题1(2)

微积分练习题1(2)《微积分》练习题一.单项选择题1.设f??x0?存在,则下列等式成立的有A.limf?x0??x??f?x0?f?x0??x??f?x0??f ??x0?B.lim??f??x0??x?0?x?x?0?xC .limf?x0?2h??f?x0?h?f??x D.limf?x0?2h??f?x0?1h?00?h?0h?2f??x0? 2.下列极限不存在的有A.limx?0xsin1x2?2xx2 B.xlim???x?1 12C.limxx?0e D.lim?3x?1?3x??2x6?x 3.设f(x)的一个原函数是e?2x,则f(x)? A.?2e?2x B.e?2x C.4e?2x D.?2xe?2x ?4.函数f(x)??2x,0?x?1?1,x?1在?0,???上的间断点x?1为间断点。
??1?x,x?1A.跳跃间断点;B.无穷间断点;C.可去间断点;D.振荡间断--------------------精选公文范文,管理类,工作总结类,工作计划类文档,感谢阅读下载---------------------~ 1 ~点5.设函数f?x?在?a,b?上有定义,在?a,b?内可导,则下列结论成立的有A.当f?a?f?b??0时,至少存在一点???a,b?,使f????0;B.对任何???a,b?,有limx???f?x??f?????0;C.当f?a??f?b?时,至少存在一点???a,b?,使f?????0;D.至少存在一点???a,b?,使f?b??f?a??f?????b?a?;6.已知f?x?的导数在x?a处连续,若limf??x?x?ax?a??1,则下列结论成立的有C.?a,f?a??是曲线y?f?x?的拐点;D.x?a不是f?x?的极值点,?a,f?a??也不是曲线y?f?x?的拐点;二.填空:1.设y?f?arcsin?,f可微,则y??x????1?x?2.若y?3x5?2x2?x?3,则y?6??0 3.过原点?0,1?作曲线y?e2x的切线,则切线方程为4?x?1??2的水平渐近线方程为x2 铅垂渐近线方程为4.曲线y?5.设f?(lnx)?1?x,则f??x??f?x??三.计算题:x2?1?x?2?lim2 --------------------精选公文范文,管理类,工作总结类,工作计划类文档,感谢阅读下载--------------------- ~ 2 ~lim??x?1x?2x?3x???x?x?3ln(1?x2)2lim y??ln?1?2x?? 求dy x?0xsin3x xy3e?y?5x?0 求dydxx?0四.试确定a,b,使函数f?x??? ?b?1?sinx??a?2,x?0在x?0处连续且可导。
微积分好题目1
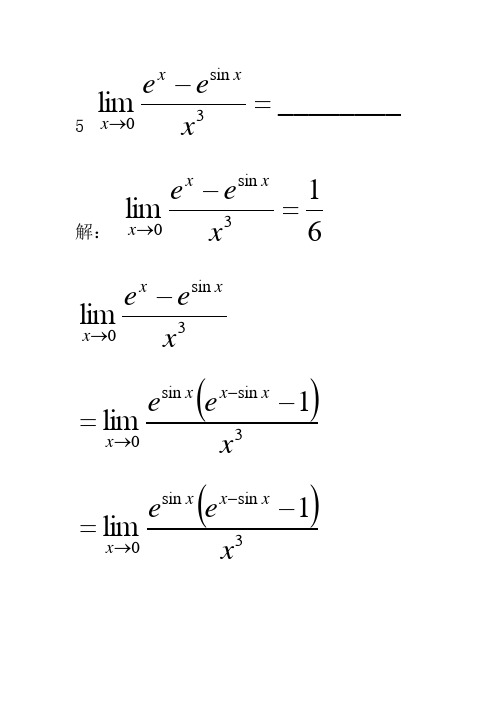
5________lim3sin 0=-→xee xx x解: 61lim3sin 0=-→xee xx x3sin 0limx ee xxx -→()3sin sin 01limx e exx xx -=-→()3sin sin 01limxeexx xx -=-→()3sin 0sin 01limlim xe exx x xx -∙=-→→()3sin 01limxexx x -=-→3sin limxx x x -=→23cos 1limxx x -=→61321lim 220==→x xx7 设⎪⎩⎪⎨⎧≤>-=0,0,arcsin 1)(2tan x ae x xe xf x x在=x 连续,则a=-----------7 1-=a解:)(x f 在0=x 连续⇒)0()0()0(f f f =+=-⇒xea xx arcsin 1lim tan 0-=+→xexx arcsin 1lim tan 0--=+→x x x tan lim 0+→-=1lim 0-=-=+→xx x8设()()x fx f 2=',则n阶导数()()x fn =-----------8 ()())(!1x fn x fn n +⋅=()())(!1111x fx f+⋅=若()())(!1x fn x fn n +⋅=成立,则 ()()()()()'=+x fx fn n 1()()'⋅=+x fn n 1!()()'⋅=+x fn n 1!())()1(!x f x f n n n'+⋅= ())()1(!2x fx f n n n+⋅=()x fn n 1)1()!1(++⋅+=∴由数学归纳法可知结论正确9若sin 2x 是()f x 的一个原函数,则___________)(=⎰dx x xf解:Cx x x dx x xf ++=⎰2cos 212sin )(sin 2x 是()f x 的一个原函数⇒)2(sin )(x d x dx x xf ⎰⎰=⇒dx x x x dx x xf ⎰⎰-=2sin 2sin )( Cx x x ++=2cos 212sin10设函数)(x y y =的导函数为x cos ,且1)0(=y ,则_________)(=x y10 1sin )(+=x x yx y cos ='⇒⎰=xdx y cos ⇒Cx y +=sin ⇒Cy +=0sin )0(⇒1=C ⇒1sin +=x y==→→xbx f xax f x x )(lim,21)(lim.10则设( A ))A a b2 )B ab 21)C 2ab)D ba23.当0→x 时,变量x x sin 是变量x cos 1-的( B ) A .等价无穷小; B .同阶但不等价无穷小; C .低阶无穷小; D .高阶无穷小。
微积分试题及答案-1

《微积分》试题 第1页(共8页)微积分试题及参考答案与评分标准一、填空题(本大题共10小题,每小题2分,共20分)1、函数21()arcsinln(1)3x f x x -=+-的定义域为 ; 2、2lim(1)x x x→∞-= ;3、若22(sin )cos ,f x x '=则()f x = ;4、设2sin(1)(),1x f x x -=-则x = 是()f x 的可去间断点; 5、若0(32)(3)1limh f h f h→--=,则(3)f '= ;6、1(arctan )x =d ;7、可导函数()f x 是偶函数,若(1)3,f '=则(1)f '-= ;8、函数()f x =[0, 3]上满足罗尔定理条件,结论中的=ξ ; 9、曲线C :2ln 1xy x =-的垂直渐近线是 ; 10、设某商品的需求函数是402Q p =-,则需求价格弹性15|p η== 。
二、单项选择题(本大题共5小题,每小题2分,共10分)1、函数)(x f 在0x 处连续是)(x f 在0x 处可导的( ).(A )必要但非充分条件; (B )充分但非必要条件;(C )充分必要条件; (D )无关条件.《微积分》试题 第2页(共8页)2、当0→x 时,2x 是x cos 1-的( )无穷小.(A )等价; (B )同阶但不等价; (C )高阶; (D )低阶.3、设函数1)(1+=xe xf ,则0=x 为)(x f 的间断点类型是( ). (A )跳跃间断点; (B )可去间断点; (C )振荡间断点; (D )无穷间断点.4、设()f x 的一个原函数是2x ,则2(1)xf x x -=⎰d ( ) (A )222(1)x C -+; (B )222(1)x C --+;(C )221(1)2x C -+; (D )221(1)2x C --+.5、函数1sin ,0()0,0x x f x xx ⎧≠⎪=⎨⎪=⎩在0x =处( ). (A )不连续; (B )极限不存在;(C )连续且可导; (D )连续但不可导.三、计算题(本大题共8小题,每小题7分,共56分)1、求极限+01lim(1)xx x→+.2、求极限11lim()1ln x x x x→--.《微积分》试题 第3页(共8页)3、设ln(x y e =,求,y y '''.4、求曲线C :2ln(1)y x =+的凹凸区间与拐点.5、求曲线C :1x y xy e ++=在0x =对应点处切线的方程.《微积分》试题 第4页(共8页)6、求函数2()1xf x x =+的单调区间和极值.7、求不定积分()112ln dx x x +⎰.8、求不定积分⎰.《微积分》试题 第5页(共8页)四、应用题(本大题共1小题,共8分)设某产品的总成本函数为:2()5,C x x =+需求函数为:120.5,x p =-其中x 为产量,p 为价格,求(1)收益最大时的产量和价格;(2)利润最大时的产量和价格。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
微积分样题1
一、 填空题(每题3分,共计15分)
1. 若0ln sin 3lim ln sin 2x x x
+→= 。
2. ⎰+dx x x )ln 31(1= 。
3. 则
2tan xdx =ò 。
4. 曲线(curve )x y x e =-的单调减少区间(interval)是 。
5. 试问a 为 时,f (x )=a sin x +
13sin 3x 在x =3π处取得极值。
二、 单项选择题(每题3分,共计15分)
6. 下列函数在给定区间[]1,e 上满足拉格朗日中值定理的有( )。
(A )ln(ln )y x = (B )ln y x = (C )1ln y x
= (D )ln(2)y x =- 7. 曲线221
x x y x +=-渐近线的条数是( )。
(A)0 (B)1 (C)2 (D)3
8. 曲线()ln 1y x x =-+( )。
(A )在(),
-∞+∞内是凹的(concave); (B )在()1,-+∞内是凹的; (C )在()1,0-内是凸的(convexity); (D )在()0,+∞内是凸的。
9. 已知()1,x f e x '=+则()f x dx =⎰( ).
(A )1ln x C ++ (B )212x x C +
+ (C )21ln ln 2
x x C ++ (D )ln x x C + 10. 设)(x f 的一个原函数是cos3x ,则()f x =( )。
(A) cos3x ; (B) sin 3x ; (C) 3sin 3x ; (D) 3sin 3x -。
三、计算下列各题:(每题9分,共54分) 11.011lim 1x x x e →⎛⎫- ⎪-⎝
⎭ 12. ()210lim cos x x x →
13. 设()arcsin ,xf x dx x C =+⎰求()
dx f x ⎰ 14.arctan xdx ⎰
15.(0)a > 16. 求y =34x -43x +1的单调区间、极值、凸凹区间和拐点.
四、应用题(9分)
17. 一房地产公司有50套公寓要出租,当租金为每月180元时,公寓可以全部租出去;当月租金每月增加10元时,就有一套公寓租不出去,而租出去的公寓每套每月需花费20元的维修费,试问公寓的月租金定为多少,房地产公司可获得最大的利益?
五、证明题 (7分)
18. 证明(prove):当0>x 时,221)1ln(x x x -
>+。
