网络图时间参数
网络图的时间参数计算
网络图的时间参数计算计算网络计划的时间参数，是编制网络计划的重要步骤，可以说，网络计划如果不计算时间参数，就不是一个完整的网络计划。
(一)计算时间参数的目的1.确定关键线路网络图从起点节点顺着箭头方向顺序通过一系列箭杆和节点，最后到达终点节点的一条条道路称为线路。
关键线路就是网络图中最重要、需时最长的线路。
关键线路上的工序叫做关键工序。
关键线路的总长度所需时间叫做总工期，一般用方框“口”标在终点节点的右方。
关键线路的工期决定整个工期的长短，它拖后一天，总工期就相应拖后一天；它提前一天，则总工期有可能提前一天。
关键线路最少必有一条，也可能有多条。
一般来讲，安排得好的计划，往往出现有关零件同时完成，组成部件；有关部件同时完成，进行总装配的情况。
这样，关键线路就不是一条了。
愈好的计划，关键线路愈多，作领导的更要全面加强管理，不然一个环节脱节会影响全局。
多条关键线路也可以作为劳动竞赛的依据。
关键线路在网络图上可以用带箭头的粗线、双线或红线表示。
2．确定非关键线路上的机动时间(或称浮动时间、富裕时间)在一份网络图中，不是关键线路的线路称非关键线路。
非关键线路上的工序，由于前后工序及平行工序的作用，使得它被限制在某一段时间之内必须完成，而当该工序的工作持续时间小于被限制的这段时间时，它就存在富裕时间(机动时间)，其大小是一个差值，因此也称为“时差”。
时差只能是正值或者为零。
一项工程的网络图画出来之后，如果要想提前完成，则要想方设法压缩关键线路的工期。
为达此目的，要调动人力物力等资源，要么从外部调整，要么从内部调整。
一般认为，从内部调整是较为经济的。
从内部调，就是从非关键线路上调。
调多少，则要看非关键线路上富裕时间的“富裕”程度，即时差有多少。
双代号网络图六个时间参数的简易计算方法
双代号网络图六个时间参数的简易计算方法
一、非常有用的要点：
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值（这点对六时参数的计算非常用用） 关键线路上相邻工作的时间间隔为零，且自由时差=总时差
在网络计划中，计算工期是根据终点节点的最早完成时间的最大值
二、双代号网络图六时参数总结的计算步骤（比书上简单多了）
① ②
t 过程
步骤一：
1．A 上再做A 下
2．做的方向从起始工作往结束工作方向；
3．起点的A 上＝0，下一个的A 上＝前一个的A 下；当遇到多指向时，要取数值大的A 下
4．A 下=A 上+t 过程（时间）
步骤二：
1．B 下再做B 上
2．做的方向从结束点往开始点
3．结束点B 下=T （需要的总时间=结束工作节点中最大的A 下）
结束点B 上=T-t 过程（时间）
关键工作：总时差最小的工作
最迟开始时间—最早开始时间（min ）
最迟完成时间—最早完成时间（min ）
4．B下=前一个的B上（这里的前一个是从终点起算的）；遇到多指出去的时，取数值小的B上
B上=B下—t过程（时间）
步骤三：总时差=B
上—A
上
=B
下
—A
下
如果不相等，你就是算错了
步骤四：自由时差=紧后工作A
上（取最小的）—本工作A
下
例：
总结起来四句话：
1．最早时间从起点开始，最早开始＝紧前最早结束的max值；
2．最迟时间总终点开始，最迟完成＝紧后最迟开始的min值；
3．总时差＝最迟－最早；
4．自由时差＝紧后最早开始的min值－最早开始
注：总时差＝自由时差＋紧后总时差的min值。
双代号网络图时间参数计算技巧
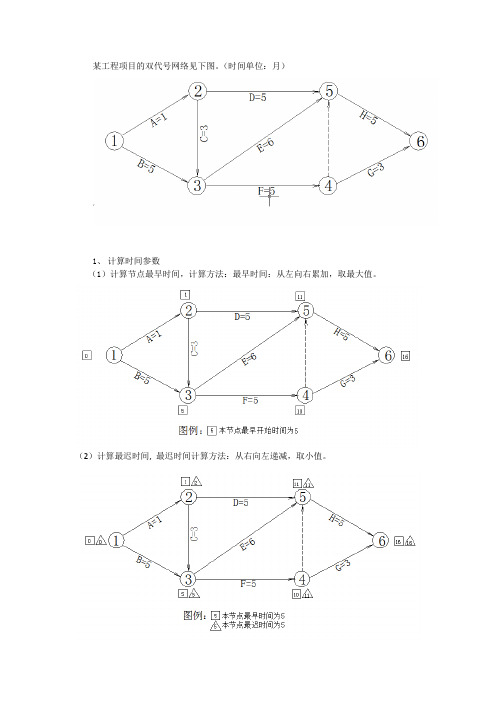
某工程项目的双代号网络见下图。
（时间单位：月）1、计算时间参数（1）计算节点最早时间，计算方法：最早时间：从左向右累加，取最大值。
（2）计算最迟时间,最迟时间计算方法：从右向左递减，取小值。
2、计算工作的六个时间参数自由时差：该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间。
总时差：该工作在不影响总工期情况下所具有的机动时间。
通过前面计算节点的最早和最迟时间，可以先确定工作的最早开始时间和最迟完成时间，根据工作持续时间，计算出最早完成时间和最迟开始时间，以F工作为例，计算F工作的4个参数（以工作计算法标示）如下：注:EF=ES+工作持续时间LF=LS+工作持续时间接下来计算F工作的总时差TF，在工作计算法中，总时差TF=LS-ES或LF-EF，在节点计算法，总时差TF可以紧后工作的最迟时间-本工作的最早完成时间，或者是紧后工作最迟时间-最早时间，以F工作为例计算它的TF：接下来计算F工作的自由时差FF，根据定义：该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间，自由时差FF=紧后工作最早（或最小）开始时间-本工作最早完成时间ES，以F工作为例，F的紧后工作为G和H，G工作的最早开始时间为10（即4节点的最早时间），H工作的最早开始时间为11（即5节点的最早时间），G工作的时间最小，所以F的自由时差FF=G工作的最早开始时间ES-F工作的最早完成时间EF：最后计算所有工作的时间参数如图：A：挖基坑。
B：垫层C：挖方D：填方：E:挡土墙F：填方G：挖方H填方通过上图我们得知：（1）关键线路为1－3－5－6，计算工期为16个月。
（2）当计划工期=计算工期时，关键工作的总时差和自由时差为0，即总时差为0的工作就是关键工作，当工作的总时差为0时，其自由时差必然为0.（3）当计划工期≠计算工期时，总时差最小的工作为关键工作。
总结：以前一直学的是工作计算法，其计算复杂且容易出错，较耗时间，本次运用节点计算法和工作计算法优点的进行综合，使更容易掌握和提高计算准确度，为后面的工期优化调整铺垫基础。
网络图中的六个时间参数.doc
2．网络图中的六个时间参数（重点）网络图中的时间参数主要有六个：最早开始时间；最早完成时间；最迟开始时间；最迟完成时间；总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后，本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后，本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下，本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下，本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下，本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下，本工作可以利用的机动时间。
3．双代号网络图中时间参数的计算(1)时间参数计算数学模型：下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天，则：工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数，则：工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中，总时差最小的工作为关键工作。
特别地，当网络计划的计划工期等于计算工期时，总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分，所以，当工作的总时差为零时，其自由时差必然为零。
即：如果网络计划中工作数量比较多，一般用项目管理软件进行计算。
如果数量不多也可用手工进行计算。
(2)计算步骤。
总时差双代号网络图时间计算参数-计算题及答案
答案：C
解析：
采用圈法最直观、简单
5、当工程网络计划的计算工期小于计划工期时，则（）。
A．单代号网络计划中关键线路上相邻工作的时间间隔为零
B．双代号网络计划中关键节点的最早时间与最迟时间相等
C．双代号网络计划中所有关键工作的自由时差全部为零
D．单代号搭接网络计划中关键线路上相邻工作的时距之和最大
总时差（用TFi-j表示），双代号网络图时间计算参数，指一项工作在不影响总工期的前提下所具有的机动时间。用工作的最迟开始时间LSi-j与最早开始时间ESi-j之差表示。
自由时差，指一项工作在不影响后续工作的情况下所拥有的机动时间。用紧后工作的最早开始时间与该工作的最早完成时间之差表示。
网络图时间参数相关概念包括：
A．FTS
B．STS
C．FTF
D．STF
答案：B
解析：
根据题意，它是从开始到开始的关系。所选B。
所以D错。
6、单代号搭接网络的计算工期由（）决定。
A．终点虚拟节点的最早完成时间
B．最后开始的工作的最早完成时间
C．最后一项工作的持续时间
D．可能由中间某个工作的最早完成时间
答案：D
解析：
根据单代号搭接网络计划时间参数的计算过程，我们应知道，其计算工期可能由中间某个工作的最早完成时间来决定．
7、在搭接网络计划中，工作之间的搭接关系是由（）决定的。
3、在工程网络计划中，判别关键工作的条件是该工作（）。
A．结束与紧后工作开始之间的时距最小
B．与其紧前工作之间的时间间隔为零
C．与其紧后工作之间的时间间隔为零
D．最迟开始时间与最早开始时间的差值最小
网络图中的六个时间参数
2．网络图中的六个时间参数（重点）网络图中的时间参数主要有六个：最早开始时间；最早完成时间；最迟开始时间；最迟完成时间；总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后，本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后，本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下，本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下，本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下，本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下，本工作可以利用的机动时间。
3．双代号网络图中时间参数的计算(1)时间参数计算数学模型：下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天，则：工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数，则：工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中，总时差最小的工作为关键工作。
特别地，当网络计划的计划工期等于计算工期时，总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分，所以，当工作的总时差为零时，其自由时差必然为零。
即：如果网络计划中工作数量比较多，一般用项目管理软件进行计算。
如果数量不多也可用手工进行计算。
(2)计算步骤。
单代号网络图时间参数计算
单代号网络图时间参数计算1.计算工作的最早开始时间和最早完成时间工作i的最早开始时间ESiT应从网络图的起点节点开始，顺着箭线方向依次逐个计算。
起点节点的最早开始时间EST1如无规定时，其值等于零，即其它工作的最早开始时间等于该工作的紧前工作的最早完成时间的最大值，即式中，EFhT──工作i的紧前工作h的最早完成时间；EShT──工作i的紧前工作h的最早开始时间；hD──工作i的紧前工作h的工作持续时间。
工作的最早完成时间EFiT等于工作的最早开始时间加该工作的持续时间，即2.计算网络计划计算工期c T式中，T n EF──终点节点n的最早完成时间。
3.计算相邻两项工作之间的时间间隔工作i→工作j之间的时间间隔T i,j LAG是工作j的最早开始时间与工作i的最早完成时间的差值，其大小按下式计算：4.计算工作最迟开始时间和最迟完成时间工作的最迟完成时间应从网络图的终点节点开始，逆着箭线方向依次逐项计算。
终点节点所代表的工作n的最迟完成时间LFnT，应按网络计划的计划工期p T或计算工期cT确定，即1=EST{}{}m axm axhEShEFhESiDTTT+==iESiEFiDTT+=EFncTT=,EFiESjLAGjiTTT-=（1-1）（1-2）（1-3）（1-4）（1-5）工作的最迟完成时间等于该工作的紧后工作的最迟开始时间的最小值，即式中，LSj T ──工作i 的紧后工作j 的最迟开始时间； LFj T ──工作i 的紧后工作j 的最迟完成时间； i D ──工作i 的紧后工作j 的持续时间。
工作的最迟开始时间等于该工作的最迟完成减去工作持续时间，即5.计算工作的总时差工作总时差应从网络图的终点节点开始，逆着箭线方向依次逐项计算。
终点节点所代表的工作n 的总时差T n F 为零，即 其他工作的总时差等于该工作与其紧后工作之间的时间间隔加该紧后工作的总时差所得之和的最小值，即 式中，T j F ──工作i 的紧后工作j 的总时差。
网络图中的六个时间参数
1.网络图中的六个时间参数（重点）
网络图中的时间参数主要有六个：最早开始时间；最早完成时间；最迟开始时间；最迟完成时间；总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ES——是指在其所有紧前工作全部完成后，本工作有可能开始的最早时刻。
(2)工作最早完成时间EF——是指在其所有紧前工作全部完成后，本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LF——是指在不影响整个任务按期完成的前提下，本工作必须完成的最迟时刻。
(4)工作最迟开始时间LS——是指在不影响整个任务按期完成的前提下，本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TF——是指在不影响总工期的前提下，本工作可以利用的机动时间。
(6)自由时差FF——是指在不影响其紧后工作最早开始时间的前提下，本工作可以利用的机动时间。
双代号网络图六个时间参数的简易计算方法[规整]
![双代号网络图六个时间参数的简易计算方法[规整]](https://img.taocdn.com/s3/m/020fa59aa1116c175f0e7cd184254b35eefd1abd.png)
双代号网络图六个时间参数的简易计算方法
一、非常有用的要点：
任何一个工作总时差≥自由时差
自由时差等于各时间间隔的最小值（这点对六时参数的计算非常用用）关键线路上相邻工作的时间间隔为零，且自由时差=
总时差
关键工作：总时差最小的工作
最迟开始时间—最早开始时间（min ）
最迟完成时间—最早完成时间（min ）
在网络计划中，计算工期是根据终点节点的最早完成时间的最大值二、双代号网络图六时参数总结的计算步骤（比书上简单多了）
①
②
t 过程
步骤一：
1．A 上再做A 下
2．做的方向从起始工作往结束工作方向；
3．起点的A 上＝0，下一个的A 上＝前一个的A 下；当遇到多指向时，要取数值大的A
下
4．A 下=A 上+t 过程（时间）
步骤二：
1．B 下再做B 上
2．做的方向从结束点往开始点
3．结束点B 下=T （需要的总时间=结束工作节点中最大的A 下）
结束点B上=T-t过程（时间）
4．B下=前一个的B上（这里的前一个是从终点起算的）；遇到多指出去的时，取数值小的B上
B上=B下—t过程（时间）
步骤三：总时差=B上—A上=B下—A下
如果不相等，你就是算错了
步骤四：自由时差=紧后工作A上（取最小的）—本工作A下
例：
总结起来四句话：
1．最早时间从起点开始，最早开始＝紧前最早结束的max值；
2．最迟时间总终点开始，最迟完成＝紧后最迟开始的min值；
3．总时差＝最迟－最早；
4．自由时差＝紧后最早开始的min值－最早开始
注：总时差＝自由时差＋紧后总时差的min值。
网络图中六个时参数
网络图中六个时参数————————————————————————————————作者：————————————————————————————————日期：2．网络图中的六个时间参数（重点）网络图中的时间参数主要有六个：最早开始时间；最早完成时间；最迟开始时间；最迟完成时间；总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后，本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后，本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下，本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下，本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下，本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下，本工作可以利用的机动时间。
3．双代号网络图中时间参数的计算(1)时间参数计算数学模型：下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天，则：工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数，则：工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中，总时差最小的工作为关键工作。
特别地，当网络计划的计划工期等于计算工期时，总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分，所以，当工作的总时差为零时，其自由时差必然为零。
网络图时间参数的计算
(一)事件最早可能发生时间(Early time ，()ET j ){}()max ()(,)ET j ET i t i j =+式中，i 和j 分别代表箭尾事件和箭头事件；t(i,j)为活动(i ，j)所需时间。
(二)事件最迟必须发生时间(Late time ，()LT i )()()LT n ET n =，其余节点最迟必须发生时间可按下式计算：{}()min ()(,)LT i LT j t i j =-（三）事件时差()S i()()()S i LT i ET i =-(四)关键路线关键路线从起始节点到终止节点顺序地将所有事件时差为零的节点连接起来的路线。
例1 计算图8.2—8所示的网络图事件时间参数（我们把图画在下面）。
解：先计算事件的最早可能发生时间。
设(10)0ET =，则(20)(10)(10,20)033ET ET t =+=+= (30)(20)(20,30)347ET ET t =+=+= (40)(20)(20,40)369ET ET t =+=+= (50)(40)(40,50)9514ET ET t =+=+={}()(60)(30)(30,60)(40)(40,60)max ,max 78,9817ET ET t ET t =++=++={}()(70)(60)(60,70)(50,70)max ,(50)max 170,14620ET ET t ET t =++=++=按这样的方式可将其余事件的最早可能发生时间计算出来，得到(100)31ET =然后计算事件最迟必须发生时间。
设(100)(100)31LT ET ==，则(90)(100)(90,100)31328LT LT t =-=-=(80)(90)(80,90)28523LT LT t =-=-={}()(70)(100)(70,100)(80)(70,80)min ,min 318,23320LT LT t LT t =--=--={}()(60)(80)(60,80)(70)(60,70)min ,min 233,20020LT LT t LT t =--=--=按同样的方式可将其余事件的最迟必须发生时间计算出来。
双代号网络图6个时间参数简单计算方法
双代号网络图6个时间参数简单计算方法双代号网络图（也称为双代号网）是一种用来表达工程项目或生产流程中各个活动之间的先后关系的工具。
它通过使用箭头来表示活动，箭头的方向表示活动的先后顺序，箭头上的时间参数表示活动的开始时间和持续时间。
在双代号网络图中，有六个重要的时间参数，分别是：最早开始时间（ES）、最早结束时间（EF）、最晚开始时间（LS）、最晚结束时间（LF）、总时差（TF）和自由时差（FF）。
1. 最早开始时间（Early Start，ES）：指一个活动可以开始的最早时间。
对于一个活动，它的最早开始时间等于它的前驱活动的最早结束时间（EF）。
2. 最早结束时间（Early Finish，EF）：指一个活动结束的最早时间。
对于一个活动，它的最早结束时间等于最早开始时间（ES）加上该活动的持续时间（D）。
3. 最晚开始时间（Late Start，LS）：指一个活动可以开始的最晚时间。
对于一个活动，它的最晚开始时间等于它的后继活动的最早开始时间（ES）减去该活动的持续时间（D）。
4. 最晚结束时间（Late Finish，LF）：指一个活动结束的最晚时间。
对于一个活动，它的最晚结束时间等于它的后继活动的最早开始时间（ES）减去15. 总时差（Total Float，TF）：指一个活动可以延迟的最长时间，而不会导致项目整体工期延长。
总时差等于最晚开始时间（LS）减去最早开始时间（ES），或等于最晚结束时间（LF）减去最早结束时间（EF）。
6. 自由时差（Free Float，FF）：指一个活动可以延迟的最长时间，而不会导致后续活动受到延迟的影响。
自由时差等于后继活动的最早开始时间（ES）减去该活动的最早结束时间（EF）减去1计算这六个时间参数的方法如下：1.计算最早开始时间（ES）和最早结束时间（EF）：根据箭头的方向，从左往右依次确定每个活动的最早开始时间和最早结束时间。
对于第一个活动，最早开始时间为0，最早结束时间为持续时间（D）。
双代号网络图六个时间参数计算口诀
双代号网络图六个时间参数计算口诀(技巧)之邯郸
勺丸创作
工作最早时间的计算: 顺着箭线, 取年夜值
工作最迟时间的计算：逆着箭线, 取小值
自由时差：后早开减本早完
1．工作最早时间的计算（包括工作最早开始时间和工作最早完成时间）：“顺着箭线计算, 依次取年夜”（最早开始时间--取
间为0. 用最早开始时间加继续时间就是该工作的最早完成时间.
3．工作最迟时间的计算（包括工作最迟完成时间和最迟开始时间）：“逆着箭线计算, 依次取小”（最迟完成时间--取紧后工作最迟开始时间的最小值）.与终点节点相连的最后一个工作的最早完成时间（计算工期）就是最后一个工作的最迟完成时间.用最迟完成时间减去工作的继续时间就是该工作的最迟开始时间.
或者最迟完成时间减最早完成时间）.注意这里都是“最迟减最
差为零的工作是“没有总时差”.
5．自由时差：“后早开减本早完”(紧后工作的最早开始时间减本工作的最早完成时间).自由时差总是小于、最多即是总时差, 不会年夜于总时差.。
3.4双代号网络图时间参数的计算(精)
2) 其他节点。其他节点i的最迟时间 为：
——工作
的箭头节点的最迟时间。
2. 工作i-j的时间参数
（1）最早时间 工作 最早开始时间 ：
工作
最早完成时间
：
（2）最迟时间 工作 的最迟完成时间 工作 的最迟开始时间
： ：
3.时差的计算
I 4
（⑥，17）
8
3
G （⑤，10） 7 7
J 5
图例： （源节点号，标号值）
对节点进行标号计算
FF i-j(Free Float Time)
• 解释：
• 第一类、最早时间参数：
• • ——是限制紧后工作提前的时间参数。 ——是限制紧前工作推迟的时间参数。 最早可能开始时间 最早可能完成时间 • 第二类、最迟时间参数：
i i
j
最迟必须开始时间 最迟必须完成时间
j
i-j 工作的工作范围
• 计算步骤： • （1）计算最早时间参数ESi-j和EFi-j。 • 计算顺序：由起始节点开始顺着箭线方向算至终点节点用 加法。 EFi-j= ESi-j+ Di-j
3．“ 最迟时间”的计算
（1）本工作最迟完成时间（LF） LFi-j＝min{LSj-k} LFi-n＝TP （2）本工作最迟开始时间（LS）： LSi-j＝LFi-j－Di-j
计算规则：“ 逆线累减，逢圈取小”
0 1 A 4 5 1 1 C 5
2
5
B 2 5
1 3 7 9 4
9 14 F 9 14 5 工期 14
5
B 2
1 3 7 9
6
4 0
网络图的时间参数计算
网络图的时间参数计算计划的重要步骤，可以说，网络计划如果不计算时间参数，就不是一个完整的网络计划。
(一)计算时间参数的目的1.确定关键线路网络图从起点节点顺着箭头方向顺序通过一系列箭杆和节点，最后到达终点节点的一条条道路称为线路。
关键线路就是网络图中最重要、需时最长的线路。
关键线路上的工序叫做关键工序。
关键线路的总长度所需时间叫做总工期，一般用方框“口”标在终点节点的右方。
关键线路的工期决定整个工期的长短，它拖后一天，总工期就相应拖后一天；它提前一天，则总工期有可能提前一天。
关键线路最少必有一条，也可能有多条。
一般来讲，安排得好的计划，往往出现有关零件同时完成，组成部件；有关部件同时完成，进行总装配的情况。
这样，关键线路就不是一条了。
愈好的计划，关键线路愈多，作领导的更要全面加强管理，不然一个环节脱节会影响全局。
多条关键线路也可以作为劳动竞赛的依据。
关键线路在网络图上可以用带箭头的粗线、双线或红线表示。
2．确定非关键线路上的机动时间(或称浮动时间、富裕时间)在一份网络图中，不是关键线路的线路称非关键线路。
非关键线路上的工序，由于前后工序及平行工序的作用，使得它被限制在某一段时间之内必须完成，而当该工序的工作持续时间小于被限制的这段时间时，它就存在富裕时间(机动时间)，其大小是一个差值，因此也称为“时差”。
时差只能是正值或者为零。
一项工程的网络图画出来之后，如果要想提前完成，则要想方设法压缩关键线路的工期。
为达此目的，要调动人力物力等资源，要么从外部调整，要么从内部调整。
一般认为，从内部调整是较为经济的。
从内部调，就是从非关键线路上调。
调多少，则要看非关键线路上富裕时间的“富裕”程度，即时差有多少。
3．时间参数的计算是网络计划调整和优化的前提通过时间参数的计算，可据以采用各种办法不断改进网络计划，使其达到在既定条件下可能达到的最好状态，以取得最佳的效果。
优化内容有时间优化、资源优化和工期优化等。
1 / 3(二)符号与计算公式1．工作时间t(或称持续时间D)工作时间是完成某项工作所需时间。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
网络图时间参数
共有十个，其内容包括：
①节点最早可能时间ET
i；②节点最迟可能时间LT
j；③工作最早开始时间ES
i-j；④工作最早结束时间EF
i-j；⑤工作最迟开始时间LS
i-j；⑥工作最迟结束时间LF
i-j；⑦公共时差PF；⑧工作自由时差FF
i-j；⑨工作独立时差IF
i-j；○
10工作总时差TF
i-j。
中英对照：
Earlist Time最早可能时间、Late Time最迟可能时间Earlist Start time最早开始时间、Earlist Finish time最早结束时间Latest Start time最迟开始时间、Latest Finish time最迟结束时间PublicFloat公共时差、FreeFloat自由时差、IndependentFloat独立时差、Total Float总时差
1）计算节点最早时间
节点最早时间就是该节点前面的全部工作全部完成，后面的工作最早可能开始的时间。
ET
1/ 3
j=max(ET
i+D
i - j)
2)节点最迟时间LTi节点最迟时间就是在不影响终点节点的最迟时间前提下，结束该节点的各工序最迟必须完成的时间。
LT
i=min(LT
i- D
i - j)
3)工作最早开始时间ES
i-j
ES
i - j=ETi4)工作最早结束时间EF
i - j
EF
i - j= ET
i+ D
i–j
5)工作最迟开始时间LS
i - j
LS
i- j=LT
2/ 3
j- D
i - j
6)工作最迟结束时间LF
i-jTj
LF
i-j= L
7)工作自由时差FF
i-j
FF
i-j= ET
j- ET
i- D
i–j
8)工作总时差TF
i-j
TF
i-j=LT
j- ET
i- D
i–j
3/ 3。