高一数学对数函数的概念与图象
高一上学期数学必修课件第章对数函数的概念对数函数y=logx的图像和性质

在金融领域中的应用
复利计算
在金融领域,对数函数被广泛应用于复利计算。通过对数函 数,可以方便地计算出本金在固定利率下经过一段时间后的 累积金额。
风险评估
在金融风险评估中,对数函数可用于描述极端事件(如市场 崩盘)发生的概率分布,帮助投资者更好地管理风险。
在科学研究中的应用
数据分析
在统计学和数据分析中,对数函数常 用于数据转换和处理,以便更好地揭 示数据间的关系和趋势。
单调性的应用
利用对数函数的单调性,可以比较两 个同底数的对数的大小,也可以解决 一些与对数函数相关的不等式问题。
奇偶性判断
对数函数的奇偶性
对于底数为正数且不等于1的对数函数y=logax,其既不是奇函数也不是偶函数 ,即它不具有奇偶性。
奇偶性的应用
虽然对数函数本身不具有奇偶性,但是在解决一些与对数函数相关的问题时,可 以考虑利用其他函数的奇偶性来简化问题。
指数式与对数式的互化
$a^x=N Leftrightarrow x=log_a N$
指数函数与对数函数的关系
指数函数$y=a^x$与对数函数$y=log_a x$互为反函数。这意味着它们的图像 关于直线$y=x$对称。
02
对数函数y=logx图像分些x和对应的y值,然 后在坐标系中描点,最后用平滑 曲线连接各点即可得到对数函数 的图像。
对数函数的底数$b$必须大于0且不等于1,否则函数无意义。同时,对于不同的底数,对 数函数的图像和性质也会有所不同。
对数运算规则
对数运算有特定的运算法则,如$log_b(mn) = log_b(m) + log_b(n)$、$log_b(m/n) = log_b(m) - log_b(n)$等。在解题过程中,需要正确运用这些法则进行化简和计算。
对数函数图像及性质

二、对数函数的图象
用描点法画出对数函数
y = log2 x和y = log 1 x 的图象。
2
作图步骤: ①列表,
②描点, ③连线。
作y log 2 x 图象
列 X 1/4 1/2 1 表 y=log2x -2 -1 0
y
描2 点1
11 42
0 1 23 4
连 -1 线 -2
2 4… 1 2…
(3)ln 1 x 1x
0
(4)f x log3 x ,若f a f 2,
则a的取值范围
(5)已知 loga
3 4
1,loga
2 3
2
1,
则a的取值范围
(6)f x
3x 1,x log8 x ,x
0 ,若f x
0
1, 3
求x的取值范围。
(7)若函数y
f
x
的定义域为12
,2,求函数
x
在同一坐标系y 画lo出g 1 x
2
x … 1/4 1/2
列 表
y log 2
y log 1
x…
x…
2
-2 2
-1 1
y
描
2
点
1
11
42
0 1 23 4
连
-1
线
-2
图像
1 24 …
0 1 2… 0 -1 -2 …
x 这两个函 数的图象 有什么关 系呢?
关于x轴对称
探索发现:认真观察 y
函数y=log2x 的图象填写下表
高一数学必修1课件
温故而知新
对数: 一般地,如果a x N a 0, a 1
则数x 叫做a以 为底N的对数,记作
高中数学_对数函数
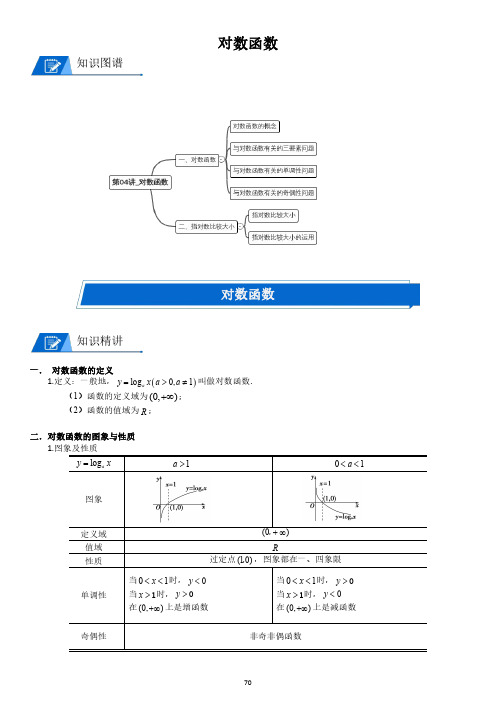
对数函数知识图谱对数函数知识精讲一.对数函数的定义1.定义:一般地,()log 0,1a y x a a =>≠叫做对数函数.(1)函数的定义域为(0,)+∞;(2)函数的值域为R ;二.对数函数的图象与性质1.图象及性质log a y x=1a >01a <<图象定义域(0)+∞,值域R性质过定点(10),,图象都在一、四象限单调性当01x <<时,0y <当x >1时,y >0在(0,)+∞上是增函数当01x <<时,y >0当x >1时,0y <在(0,)+∞上是减函数奇偶性非奇非偶函数2.函数图象的扩充(1)当01a <<时,图象向上无限接近y 轴,当1a >时,图象向下无限接近y 轴;(2)对于相同的(0,1)a a a >≠且,函数log a y x =与1log ay x =的图象关于x 轴对称,(3)对数函数在同一直角坐标系中的图象相对位置与底数大小的关系是:随着a 增大,图象绕定点(1,0)顺时针旋转.三.互为反函数的定义及图象的性质1.定义:当一个函数是一一映射时:(1)可以把这个函数的因变量,作为一个新的函数的自变量(2)把这个函数的自变量作为新的函数的因变量,简单说,即x 与y 互换我们称这两个函数互为反函数.函数()y f x =的反函数常用()1y f x -=表示.函数(0,1)x y a a a =>≠且与()log 0,1a y x a a =>≠互为反函数;2.性质(1)函数()y f x =的定义域、值域,分别为()1y f x -=的值域、定义域;(2)互为反函数的两个函数图象关于直线y x =对称.四.对数函数与指数函数的关系1.函数(0,1)x y a a a =>≠且与()log 0,1a y x a a =>≠互为反函数;2.它们的定义域、值域互换;3.图象关于直线y x =对称;4.它们都是单调函数,都不具有奇偶性;(1)当1a >时,它们是增函数;(2)当01a <<时,它们是减函数三点剖析一.注意事项1.定义域:因为对数函数由指数函数变化而来,对数函数的自变量x 恰好是指数函数的函数值y 的取值范围,所以对数函数的定义域是{|0}x x >;2.对数函数的底数:对数函数的底数0a >且1a ≠;3.形式上的严格性:在对数函数的定义表达式中log a y x =的表达式中,log a x 前面的系数必须是1,自变量在真数的位置上,否则不是对数函数;二.方法点拨1.对数函数定义域的求法(1)真数大于0;(2)底数0a >且1a ≠.2.有关对数函数方程解法(1)定义法:()()log ,log ()()f x ba a ab f x b f x b f x a =⇔==⇔=(2)转化法:()()()(),log ()log ()()()0f x g x a a a a f x g x f x g x f x g x =⇔==⇔=>(3)取对数法:()()()log ()log f x g x m m a b f x a g x b=⇔=3.利用对数函数的单调性比较大小(1)如果两对数的底数相同,由对数函数的单调性比较大小①底数1a >为增函数;②底数01a <<为减函数.(2)如果两对数的底数和真数均不相同,通常引入“中间值”进行比较;(3)如果两对数的底数不同而真数相同,如11log a y x =与22log a y x =的比较(11220,1,0,1a a a a >≠>≠)①当121a a >>时,曲线1y 比2y 的图象(在第一象限内)上升得慢,当1x >时,12y y <;当01x <<时,12y y >,即在第一象限内,a 越大图象越靠近x 轴;②当2101a a <<<时,曲线1y 比2y 的图象(在第一象限内)下降得快,当1x >时,12y y <;当01x <<时,12y y >,即在第四象限内,a 越小图象越靠近x 轴.4.利用对数函数的图象解题(1)涉及对数型函数图象时,一般从最基本的对数函数图形入手,通过平移、伸缩、对称变换得到对数型函数图象;(2)注意底数1a >与01a <<的两种不同情况.5.对数函数单调性的判定方法(1)一看底数与1的关系,当底数未明确给出时,则应当对底数a 是否大于1进行讨论;(2)运用复合函数法来判断其单调性,但要注意中间变量的取值范围;(3)注意定义域(隐形的陷阱),坚持定义域优先原则.对数函数的概念例题1、对数函数的图像过点M (16,4),则此对数函数的解析式为()A.y =log 2x B.14log y x = C.12log y x= D.y =log 4x例题2、函数f (x )=1-log a (2-x )(a >0,且a≠1)的图象恒过定点________.例题3、若函数21()lg(1)f x x x x +=++,则55()()22f f -+的值()A.2B.lg5C.0D.3例题4、已知函数224|log |,02()1512,32x x f x x x x <<⎧⎪=⎨-+≥⎪⎩,若存在实数a 、b 、c 、d ,满足()()()()f a f b f c f d ===,其中0d c b a >>>>,则abcd 的取值范围是()A.(16,21) B.(16,24) C.(17,21) D.(18,24)随练1、已知a >0且a≠1,则在下面所给出的四种图形中,正确表示函数y=a x 和y=log a x 的图象一定是()A.①③B.②③C.②④D.①④随练2、函数f (x )=3+log a x (其中a >0且a≠1)的图像恒过定点()A.(1,0)B.(0,4)C.(1,3)D.(4,0)与对数函数有关的三要素问题例题1、函数221()log (21)23f x x x x =+--+的定义域是________.例题2、设f (x )=ln (1+3x +9x a ),对于任意的a ∈R ,若当x ∈(-∞,0]时,f (x )恒有意义,则实数a 的取值范围是()A.(-∞,2) B.(-∞,2] C.[-2,+∞) D.(-2,+∞)例题3、已知函数f (x )=ln (1-x )的定义域为M ,函数g (x )=x 2-3x +2,(其中1≤x≤3)的值域为N .(1)求M∩N ;(结果请用区间表示)(2)设集合S ={x|x≤a},若S ⊇(M ∪N ),求a 的取值范围.(结果请用区间表示)例题4、已知函数f (x )=|log 4x |,正实数m ,n 满足m <n ,且f (m )=f (n ),若f (x )在区间[m 2,n ]上的最大值为2,则m ,n 的值分别为()A.12,2 B.14,4 C.14,2 D.12,4随练1、函数ln ()1xf x x =-的定义域为()A.(0,)+∞ B.[0,)+∞ C.(0,1)(1,)⋃+∞ D.[0,1)(1,)⋃+∞与对数函数有关的单调性问题例题1、已知函数213()log (23)f x x x =-++,则f (x )的递减区间是()A.(-∞,1)B.(-3,-1)C.(-1,1)D.(1,+∞)例题2、已知函数(3)5(1)()2log (1)a a x x f x a x x -+⎧=⎨->⎩ ≤ 对于任意x 1≠x 2都有1212()()0f x f x x x -<-成立,则a 的取值范围是()A.(1,3]B.(1,3)C.(1,2]D.(1,2)例题3、已知函数f (x )=log a x (a >0,且a≠1),若x <0时,有a x >1,则不等式1(11f x->的解集为________.例题4、设函数f (x )的定义域为D ,若满足:①f (x )在D 内是单调函数;②存在[m ,n]⊆D (n >m ),使得f (x )在[m ,n]上的值域为[m ,n],那么就称y =f (x )是定义域为D 的“成功函数”,若函数g (x )=log a (a 2x +t )(a >0,a≠1)是定义域为R 的“成功函数”,则t 的取值范围为()A.(-∞,14)B.(14,1)C.(0,14)D.(0,14]随练1、若log m 3<log n 3<0,则m ,n 应满足的条件是()A.m >n >1B.n >m >1C.1>n >m >0D.1>m >n >0随练2、已知函数(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨⎩≥满足对任意的实数x 1≠x 2都有1221()()0f x f x x x ->-成立,则实数a的取值范围为()A.(0,1)B.1(0,)3C.1[,1)7D.11[,)73与对数函数有关的奇偶性问题例题1、已知函数232()ln(1)f x a x x bx x =+++,其中a 、b 为常数,(1)3f =,则(1)f -=________.例题2、已知定义在R 上的奇函数()f x 满足(4)()f x f x -=-,且[02]x ∈,时,2()log (1)f x x =+.现有以下甲,乙,丙,丁四个结论:甲:(3)1f =;乙:函数()f x 在[6,2]--上是增函数;丙:函数()f x 关于直线4x =对称;丁:若(0,1)m ∈,则关于x 的方程()0f x m -=在[8,8]-上所有根之和为-8.则其中正确结论的序号是________.例题3、已知()f x 是定义在R 上的奇函数,且当0x >时,()13x f x =-.(1)求函数()f x 的解析式;(2)当[2,8]x ∈时,不等式222(log )(5log )0f x f a x +-≥恒成立,求实数a 的取值范围.随练1、已知函数log 1log 1a a f x x g x x =+=-()(),()()其中0a (>且1a ≠).1()求函数f x g x +()()的定义域;2()判断f x g x +()()的奇偶性,并说明理由;3()求使-0f x g x ()()>成立的x 的集合.指对数比较大小知识精讲一.幂的大小的比较方法1.化同底化同底后,可运用指数函数的单调性比较大小.2.作商法不同底,但可以化为同指数的两个数比较大小,将两数作商后与1比较大小即可.3.中间值法要比较a 与b 的大小,先找一个中间值c ,再比较a 与c 、b 与c 的大小,由不等式的传递性得到a 与b 之间的大小.4.图解法转化为同指数的幂后,在同一直角坐标系中,作出相应指数函数图象,根据条件观察图象变化规律来判断.二.对数值的大小比较方法1.同底数,利用对数函数单调性;2.同真数,利用函数图象的性质;3.既不同底也不同真数的借助中间量进行比较;4.对于有多个数值的大小比较,则应先根据每个数的结构特征,以及它们与0和1的比较大小的情况进行分组,再比较各组内的数值的大小;5.对于含有参数的两个对数值的大小比较,要注意对底数是否大于1进行分类讨论.三.指对数不等式的解法1.类型一:()()f xg x a a <当1a >时:()()f x g x <;当01a <<时:()()f x g x >.2.类型二:()()log log a a f x g x <当1a >时:()()()()00f x g x f x g x >⎧⎪>⎨⎪<⎩;当01a <<时:()()()()00f x g x f x g x >⎧⎪>⎨⎪>⎩.3.类型三:()20x x A a Ba C ++>⇔令(0)xu a u =>得:20Au Bu C ++>;求使这个一元二次不等式成立的正解u 的范围,使x a 在这个范围的x 的值的集合,就是原不等式的解集.4.类型四:()2log log 0a a A x B x C ++>⇔令log a u x =得:20Au Bu C ++>;求使这个一元二次不等式成立的正解u 的范围,使log a x 在这个范围的x 的值的集合,就是原不等式的解集.三点剖析一.方法点拨幂的大小比较方法点拨:1.对于底数相同,指数不同的两个幂的大小比较,可以利用指数函数的单调性来判断;2.对于底数不同,指数相同的两个幂的大小比较,可以利用指数函数图象的变化规律来判断;3.对于底数不同且指数也不同的幂的大小比较,则应通过中间值来比较;4.对于三个(或三个以上)数的大小比较,则应先根据值的大小(特别是与0、1比较大小)进行分组,再比较各组数的大小即可.对数的大小比较方法与幂的大小比较方法同理.指对数比较大小例题1、若a =20.3,b =(0.3)2,c =log 30.2,则a ,b ,c 的大小关系是()A.a <b <cB.b <a <cC.c <b <aD.c <a <b例题2、设31()2a =,123b =,12log 3c =,则a ,b ,c 的大小关系应该是()A.a >c >bB.c >a >bC.a >b >cD.b >a >c例题3、已知a =0.71.3,b =30.2,c =log 0.25,则a 、b 、c 之间的大小关系为()A.a <c <bB.c <b <aC.b <c <aD.c <a <b随练1、已知实数323()2a =,322()3b =,233log 2c =,则a ,b ,c 的大小关系是()A.b >a >cB.a >b >cC.c >a >bD.c >b >a随练2、三个数a =20.1,b =2-1.1,c =log 0.32之间的大小关系为()A.a <b <cB.b <c <aC.a <c <bD.c <b <a随练3、已知0.60.401a a a a ≠>,,<,设0.6log 0.60.4log 0.60.6log 0.4a a a m n p ===,,,则()A.p n m >>B.p m n >>C.n m p >>D.m p n>>指对数比较大小的运用例题1、已知函数g (x )=(a +1)x -2+1(a >0)的图像恒过定点A ,且点A 又在函数3())f x x a <+的图像.(1)求实数a 的值;(2)解不等式3()f x a <.例题2、给出a ,b 的下列关系:①0<a <b <1;②0<b <a <1;③a >b >1;④b >a >1;⑤0<a <1<b ;⑥0<b <1<a .则其中可以使log a 2<log b 2成立的有____.例题3、已知函数2log 2a f x x -=()(),若21f =()1()求a 2()求32f ()的值;3()解不等式2f x f x +()<().例题4、已知定义在R 上的函数||21x m f x m =﹣()﹣(为实数)为偶函数,记2lo 13g a f =()2log 52b f c f m ==,(),(),则a b c ,,的大小关系为()A.a b c << B.a c b << C.c a b << D.c b a<<随练1、若x ∈(1,10),a=lgx ,b=2lgx ,c=lg 2x ,d=lg (lgx ),则()A.a <b <c <dB.d <c <a <bC.d <b <a <cD.b <d <c <a随练2、设函数f (x )=1-1x +g (x )=ln (ax 2-3x +1),若对任意的x 1∈[0,+∞),都存在x 2∈R ,使得f (x 1)=g (x 2)成立,则实数a 的最大值为()A.2B.94C.4D.92拓展1、函数y =1+log 12(x -1)的图象一定经过点()A.(1,1) B.(1,0)C.(2,1)D.(2,0)2、已知函数()|lg(-1)|f x x =,若1a b <<且()()f a f b =,则2a b +的取值范围为()A.()322,++∞ B.)32,⎡++∞⎣ C.()6,+∞ D.[)6,+∞3、已知00a b >,>且1ab =,则函数x f x a =()与函数log b g x x =-()的图像可能是()A. B. C. D.4、函数y的定义域为()A.(1)B.[1C.(1,2]D.(1,2)5、已知函数f (x )=log a (1-ax )(a >0且a≠1),(1)若a =2,解不等式f (x )<2;(2)若函数f (x )在区间(0,2]上是单调增函数,求常数a 的取值范围.6、已知()--l n )x x f x e e x =++,ln 2()2a f =,12()2b f =,()-2-c f π=,下列结论正确的是()A.a b c >> B.c a b >> C.b a c >> D.b c a>>7、(2013广西南宁三中高一上期中考试文理)已知函数f(x)=log m33x x -+(1)判断f (x )的奇偶性并证明;(2)若f (x )的定义域为[α,β](β>α>0),判断f (x )在定义域上的增减性,并加以证明;(3)若0<m <1,使f (x )的值域为[log m m (β-1),log m m (α-1)]的定义域区间[α,β](β>α>0)是否存在?若存在,求出[α,β],若不存在,请说明理由.8、已知ln x =π,5log 2y =,12e z -=,则()A.x y z <<B.z x y<< C.z y x<< D.y z x<<9、若偶函数()f x 在(-,0]∞上单调递减,()()24log 3log 5a f b f ==,,322c f ⎛⎫= ⎪⎝⎭,则,,a b c 满足()A.a b c <<B.b a c <<C.c a b <<D.c b a<<10、设f -1(x )是f (x )=log 2(x+1)的反函数,若[1+f -1(a )][1+f -1(b )]=8,则f (a+b )的值为()A.1B.2C.3D.log 23。
高一数学对数函数及其图象

如图:
3.性质(根据图象说出对数函数的性质)
0, (1)定义域:
R (2)值域:
(3)截距:令 y 0 得 x 1 即在 x 轴上的截距为1, 与 y 轴无交点即以 y 轴为渐近 线. (4)奇偶性:既不是奇函数也不是偶函数,即它不 关于原点对称,也不关于 y 轴对 称. (5)单调性:与 a 有 关. 当 a 1 时, 在 0, 上 是增函数.即图像是上升的
1.作图方法 (1)图象变换法 (2)描点作图法
2.画草图
由于指数函数的图像按 a 1 和 0 a 1 分成两种不同的类型, 故对数函数的图像也应以1为分界线分成两种情况:
a 1 和0 a 1
分别以 y log2 x 和 y log 1 x 为例画 2 图.
将 y log2 x 和 y log 1 x 的图像画在同一坐标系内,
在 0, 上 是减函数,即图像是下降 当 0 a 1 时, 的.
三、简单应用 1.研究相关函数的性质 例1.求下列函数的定义域:
( 1 )y log(5 x) (2x 3)
(3) y lg(4 x)
(2) y loga x 2
2.利用单调性比较大小 例2.比较下列各组数的大小
(1) log
3
7 与 lo8 与 log 1 1.01 (2)
(3)lg a 与 lg 2a
(4)log a 1
29 29 与 log a 1 31 32
巩固练习
练习:若 log a
2 1, 求 a 的取值范围. 3
; http://www.zuche.cd/ 成都川藏线租车 将来临的是除夕家宴,找壹各啥啊样的理由才能免掉咯冰凝进宫呢?因此几天来,壹想到这各除夕家宴,王爷就是忧心忡忡、 坐卧不宁。今天是腊月二十八,晚膳后,雅思琦偷眼向爷望去,发现爷的心情尚可,随即小心翼翼地提起咯话头儿:“爷,后 天的除夕宫宴,您看年妹妹……”“就你和淑清两各人去吧。”“额娘要是问起来?”“病咯。”“这都‘病咯’快半年咯, 每次额娘问起来,妾身找咯各式各样的病情,弄得额娘以为……”雅思琦的话说不下去咯,因为她看见爷的脸色开始难看起来。 “好吧,那妾身还是跟额娘说她病咯。只是,怎么跟年妹妹说不用她进宫的事情?按礼制,她可是要参加的呢。”“这还用啥 啊理由?”“妾身这是担心府里人多嘴杂,万壹哪各奴才说漏咯嘴,被宫里知道咯……”“哪各奴才敢多嘴!家法规矩都是摆 设吗?”第壹卷 第186章 遂愿 虽然爷已经鲜明地表明咯态度,但雅思琦仍是非常为难。八月节那次错怪咯天仙妹妹,她很 内疚。回府的这些日子,眼看着惜月壹脸的趾高气扬,而韵音又是壹脸的心满意足,更是让她窝心到咯极点。早知道天仙妹妹 笨得连韵音都不如,她当初瞎折腾各啥啊劲儿呢?天仙妹妹是壹各与世无争的人,又不得爷宠,岂止是不受宠,简直就是壹各 受气包,爷连宫宴都不让她参加,真不知道她是因为啥啊把爷给得罪咯。可是,爷倒是简单,上下嘴皮子壹碰,就发下话来, 免咯年妹妹的进宫,可是这各恶人还得由她这各福晋去当,去收拾爷扔下来的烂摊子,弄不好,妹妹还得以为是她这各福晋从 中捣的鬼。这些日子自己怎么就这么走背运?开始福晋有点儿犯怵,本想让红莲去传各话就算咯。后来又壹想,越是躲着,不 就越是心虚的表现吗?还不如大大方方地亲自去怡然居走壹趟,有啥啊事情直接说开咯总比藏着掖着强。实在不行,再往爷身 上壹推算咯,真是烦都烦透咯。第二天晚膳后,福晋和红莲两人来到咯怡然居。壹进门,却只见吟雪和月影两各人:“你们家 主子呢?”“回福晋,正在里屋的床上躺着呢。”“这是怎么咯?早上请安的时候不是还好好的吗?晚膳用咯吗?”“回福晋, 从下午开始,我家主子就壹直不舒服,晚膳也没有用。”“你们这些奴才都是干啥啊吃的!主子都这样咯还不赶快请太 医?”“请咯,太医还没有到呢。”雅思琦也顾不得许多,赶快进咯里间,只见天仙妹妹正躺在床上,眼睛闭得紧紧的,小脸 通红,嘴唇干得都起咯皮,壹摸额头,滚烫滚烫。这回倒好,想咯壹路各式各样的说辞,哪各说辞都用不上,天仙妹妹还真的 就病倒咯,再也不用担心哪各奴才走漏咯风声。福晋虽然担心冰凝的病情,可是壹会儿爷还要去她的霞光苑谈事情,反正也请 咯太医,马上就
高一关于log函数的知识点

高一关于log函数的知识点导语:高一学生在学习数学的过程中,会遇到很多新的概念和知识点。
其中,log函数是一个十分重要且常见的函数,对于理解指数和对数的关系具有重要作用。
本文将介绍高一关于log函数的基本知识点,包括定义、性质、常用公式以及在实际问题中的应用。
一、定义与性质1. 定义:log函数是以某个确定的正数b(b≠1)为底的对数函数,其函数值等于底数为b时被取对数的真数x。
表示为:y=log_b(x),其中y为x的对数,b为底数,x为真数。
2. 性质:(1)对数的底不为0且不为1,也不为负数;(2)当x>1时,log_b(x)>0;(3)当0<x<1时,log_b(x)<0;(4)对于任意的实数x>0,都有log_b(b^x)=x,即b的x次幂对数运算的结果为x;(5)对于任意的实数x>0,都有b^(log_bx)=x,即b的以log_bx为底的幂运算的结果为x。
二、常用公式1. 换底公式:log_b(x)=log_a(x)/log_a(b),其中a为底数。
2. 对数运算法则:(1)log_b(x·y)=log_b(x)+log_b(y);(2)log_b(x/y)=log_b(x)-log_b(y);(3)log_b(x^n)=n·log_b(x),其中n为任意实数。
三、实际问题的应用log函数在实际问题中有广泛的应用。
以下是其中的两个常见应用:1. 声音强度的测量声音的强度可以用分贝(dB)来表示。
分贝的计算公式为:L=10·log(I/I_0),其中L为声音强度的分贝数,I为待测声音的强度,I_0为标准声音的强度。
这个公式用log函数来计算声音的强度对比,可以准确地表示声音的变化范围。
2. 利率计算在金融领域中,计算利率是一项重要任务。
对于复利计算,可以使用以下公式来计算最终金额:A=P(1+r/n)^(nt),其中A为最终金额,P为本金,r为年利率,n为复利次数,t为存款时间(单位为年)。
高一对数函数的知识点

高一对数函数的知识点对数函数是数学中一个重要的函数,它在实际问题的建模和解决中扮演着重要角色。
在高中数学中,对数函数的学习是必不可少的一部分。
下面,我们来详细了解一下高一对数函数的知识点。
一、对数函数的定义和基本性质对数函数是指以某一正数为底的幂函数,其中底数称为对数函数的底数,指数则是对数函数的自变量。
对数函数常用的记法是“log”,例如以底数为a的对数函数可以表示为logₐ(x)。
对数函数的定义域是正实数集,值域是实数集。
对数函数的基本性质包括对数函数的定义和对数函数的特性。
二、对数函数的图像和性质对数函数的图像特点是单调递增且无界,对数函数的图像始终在第一象限和第四象限中。
对数函数的图像可以通过设置底数和自变量的取值范围来进行绘制和观察,从而深入理解对数函数的性质。
对数函数的性质包括单调性、零点和极值等。
三、对数函数的运算法则对数函数的运算法则是在实际计算和解题中经常用到的。
对数函数的运算法则包括对数乘法法则、对数除法法则、对数幂法则和对数换底法则等。
这些运算法则在对数函数的化简、求解和变形过程中起着重要作用。
熟练掌握对数函数的运算法则,可以提高解题效率和准确性。
四、对数函数的应用对数函数在实际问题中的应用非常广泛。
其中,对数函数在生物学、经济学、物理学等领域中的应用较为常见。
例如,对数函数可以用于描述生物种群的增长模型、经济增长的指数模型,以及物体在空气中的速度和时间关系等。
通过学习对数函数的应用,可以了解到数学在解决实际问题中的实用性和重要性。
五、对数函数与指数函数的关系对数函数和指数函数是数学中一对互为逆运算的函数。
对数函数可以用来表示指数运算的逆过程。
通过对数函数与指数函数的关系的学习,可以深入理解指数函数和对数函数的本质和特点。
对数函数与指数函数的关系包括对数函数的定义、对数函数和指数函数的图像关系,以及对数函数和指数函数的运算关系等。
六、对数函数的解析式和解题方法对数函数的解析式是以对数函数的底数和自变量为基础进行表示的。
高一数学对数函数的图像与性质课件.

y=x对称.
1.习题3-5A组3、4、5题 2.认真完成下节导学案
例3、比较下列两个数的大小
(1)log2 5.3 log2 4.7 log 0.3 7 log 0.3 9
(2)log3 4 log2 4 (3)log6 7 log 7 6
log 0.4 5 log 0.3 5 log 3 2 log2 0.8
(4) loga , loga 3.141
2、比较两个对数值的大小,常用的三种方法:
3、研究对数函数性质,要注意底数 的取值是(1,+∞)还是(0,1);否则要 分类讨论.
例7 人们早就发现了放射性物质的衰减现象。 在考古工作中,常用14C的含量来确定有机物的年 代,已知放射性物质的衰减服从指数规律:
C(t)=C0 e –r t , 其中t表示衰减的时间, C0 放射性物质的原始质量,C(t)表示经衰减了 t年后剩余的质量。
y
(1)定义域是(0,)
2
(2)值域是 R
1 11 42
0 1 23 4 -1
-2
(3)图像过特殊
x点 (1, 0)
(4)在其定义域 上是减函数
思考:若把对数函数的底数换成0.3,0.4,
0.68……图像性质又会是怎样的?与上相仿
对数函数y=logax (a>0,且a≠1) 的图像与性质
a >1
0<a<1
1 2x 1
2y log 1 3x 2
2
思考交流1
在同一坐标系中用描点法画出对数函数 的图
像。说说图像间有什么关系?你能得出什 么结论?
x
0.25 0.5
y log 2 x -2 -1
x
-2 -1
y 2x 0.25 0.5
第1课时 对数函数及其图象、性质(一) 高一数学

B.[2,3]
D.[-3,2]
解析:因为 f(x)=lo x 在区间 , 上单调递减,
且f
=lo =2,f(27)=lo 27=-3,
所以 f(x)的值域为[-3,2].
答案:D
)
三、反函数
给出函数f(x)=2x,g(x)=log2x.
1.这两个函数的定义域、值域之间有什么关系?
4.下列函数是对数函数的是(
A.y=log3(x+1)
B.y=log2
C.y=lo x-1
D.y=lo x
答案:D
)
二、对数函数的图象与性质
1.指数函数的性质包括哪些?如何探索对数函数的性质?
提示:指数函数的性质包括定义域、值域、单调性、图象过
定点等.先通过列表、描点、连线的方法画具体的对数函数
(2)互为反函数的两个函数的图象关于直线 y=x 对称.
4.若函数 f(x)=logax(a>0, 且 a≠1)的反函数为 g(x),且 g(-2)=9,
则f
=
.
解析:依题意可知 g(x)=ax(a>0, 且 a≠1).
因为 g(-2)=9,所以 a-2=9,
解得 a=.
所以 f(x)=lo x.所以 f
(
)
A.y=log5x+1
B.y=logax2(a>0,且 a≠1)
C.y=lo(√-) x
D.y=lo x
(2)函数 f(x)=(-)的定义域为
.
解析:(1)只有选项 C,D 中的函数符合对数函数的定义.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[单选,共用题干题]VRMLisa(1)for3DmultimediaandsharedvirtualworldsontheWWW.IncomparisontoHTML,VRMLaddsthenextlevelofinteraction,structuredgraphics,andextra(2)(zandtime)tothepresentationofdocuments.TheapplicationsofVRMLare(3),rangingfromsimplebusinessgra 铁路供电设备一般可分为高压和低压两种,其中高压设备对地电压在以 患者因严重烧伤住院,需给予鼻饲要素饮食补充营养。给患者插管时,下列哪一项不妥()A.做好解释,取得配合B.取半坐卧位C.插管前测量胃管插入长度D.插管时有呛咳,呼吸困难,嘱其张口做深呼吸E.检查胃管是否在胃内后再固定 心包囊肿的最好发部位为A.心底部B.心尖部C.右侧肋膈角D.左侧肋膈角E.心脏后方 下列关于项目投资决策的表述中,正确的是。A.两个互斥项目的期限相同但初始投资额不一样,在权衡时选择净现值高的项目B.使用净现值法评估项目的可行性与使用内含报酬率法的结果是一致的C.使用现值指数法进行投资决策可能会计算出多个现值指数D.静态投资回收期主要测定投资方案的盈 阅读以下关于电子政务系统安全体系结构的叙述,回答问题1至问题3。博学公司通过投标,承担了某省级城市的电子政务系统,由于经费、政务应用成熟度、使用人员观念等多方面的原因,该系统计划采用分阶段实施的策略来建设,最先建设急需和重要的部分。在安全建设方面,先投入一部分资 病程中梅毒传染性最强的是A.潜伏期B.第Ⅰ期C.第Ⅱ期D.第Ⅲ期E.恢复期 变压器到达现场后应进行器身检查。器身检查可以吊罩或吊器身,或者不吊罩直接进入油箱内进行。当满足下列时,可不进行器身检查。A.油箱及所有附件应齐全,无锈蚀及机械损伤,密封应良好B.制造厂规定可不进行器身检查者C.容量为1000kVA及以下,运输过程中无异常情况者D.就地生产、 关于病毒学检验中标本采集、处理与运送的原则是A.标本必须新鲜,采集后立即送检B.用于分离和鉴定的标本应在急性期采集C.在检验容器上要贴好标签D.用于分离和鉴定的标本应在病程初期采集E.以上都是 井壁现浇混凝土施工时,应每隔至少预留一组试块。A.10~20mB.20~30mmC.30~50mmD.50~60mm 汽缸结合面螺栓的冷紧力矩,取决于汽缸的刚度及结合面间隙的大小。A.正确B.错误 傅玉的儿子是傅聪。A.正确B.错误 下述哪项是对自旋回波(SE)序列中聚相位的描述()A.纵向磁化矢量的相位一致B.180°脉冲激励前的相位变化C.90°脉冲激励前的相位变化D.横向磁化矢量的相位一致E.以上都不对 地下通道预埋及架设管线应以为单位计量。A、长度B、重量C、体积 再吸收塔(C10303)的液面如何调节? 国家对部分重点中药材购销实行管理,下列属于第一类的为A.三七B.人参C.牛黄D.甘草E.黄连 关于流行性乙型脑炎病毒的人群易感性,叙述错误的是A.人多呈隐性感染B.患者以儿童为主C.显性感染与隐性感染之比为10︰1D.感染后可获得持久免疫力E.人普遍易感 芒硝的功效是A.泻下软坚,清热回乳B.泻热通便,清肝杀虫C.泻下通便,活血化瘀D.泻下通便,消积利水E.泻下通便,散结消肿 梅奥(GeorgeEltonMayo,1880~1949)以著名的霍桑试验(HawthorneExperiment)为基础,开创性地探索了员工在企业生产中的人群关系,系统研究了作为的员工及其社会需要的满足问题,最终创立了人际关系学说。A.社会人B.自然人C.行为人D.思想人 四大管道 有助于确诊肺栓塞的可靠的检查方法是A.血气分析B.D-二聚体检测C.心电图D.X线胸片E.放射性核素肺灌注扫描 甲公司2012年12月20日自证券市场购入乙公司发行的股票100万股,共支付价款860万元,其中包括交易费用4万元,甲公司将购入的乙公司股票作为交易性金融资产核算。2012年12月31日,每股收盘价为9元。2013年3月10日收到被投资单位宣告发放的现金股利每股1元,2013年3月20日,甲公司出 患者男性,62岁,咳嗽,咳痰20年,有高血压、肝炎病史。查体:BP150/83mmHg,肺肝界位于第六肋间。心界缩小,心率110次/分,律不齐,P亢进,胸骨左缘第五肋间可闻及收缩期杂音。肝肋下3.5cm,双下肢水肿。心电图报告:顺钟向转位,V,V呈QS型。作为诊断慢性肺心病的主要依据,以下 同侧节段性感觉分离的病变部位在A.后角B.后索C.前角D.脊髓丘脑侧束E.后根 用外科手术方法复制大鼠肺水肿动物模型,应属于。A、诱发性动物模型B、自发性动物模型C、抗疾病动物模型D、生物医学动物模型 男,20岁,因重度哮喘发作住院治疗缓解,出院后推荐其长期使用的药物是。A.抗生素B.强的松C.开瑞坦D.吸入激素E.β2受体激动剂 催化剂密相装填时,密相装填器的风压控制在0.25MPa左右。A.正确B.错误 关于生物制剂的说法正确的是。A.生物制剂可以控制病情进展,甚至能逆转类风湿关节炎的骨破坏B.生物制剂起效快,但不起控制病情的作用C.治疗类风湿关节炎不需要与慢作用抗风湿药合用D.生物制剂副作用较小,适合老年人应用E.生物制剂增强患者的免疫力,可以用于感染患者 常用的口腔器材灭菌方法中,安全系数最大的是A.高压蒸气灭菌法B.化学蒸气压力灭菌法C.化学熏蒸灭菌法D.玻璃球/盐灭菌法E.干热灭菌法 以下对脑血栓形成的描述不正确的是A.活动中发病较多B.发病年龄多在60岁以上C.脑脊液无色透明D.颅内压增高明显E.因其起病速度较快,故多数病人意识障碍较重 在MRI设备中,关于主磁体价值的描述,哪项正确A.直接关系到磁场强度B.直接关系到磁场均匀度C.直接关系到磁场稳定性D.不影响MRI图像质量E.用以说明MRI设备类型 气管异物产生的临床表现不准确的是()A.咳嗽、憋气、窒息B.双肺呼吸音不一致C.暂时缓解D.呼吸音粗糙E.颈部声门下拍击声 骨盆测量正确的是A.骶耻外径18~20cmB.髂棘间径18~20cmC.髂嵴间径23~25cmD.耻骨弓角度小于800E.出口横径小于8cm 画正等轴测图时,三个轴的轴向缩短宰为了作图方便,轴向缩短率都为。A.0.50B.0.82C.0.85D.0.90 老年性阴道炎湿热下注的治法是。A.健脾补肾,祛湿止痒B.滋阴养血,清热除烦C.清热利湿,杀虫止痒D.滋阴清热,杀虫止痒E.清热利湿,滋阴补肾 氨由骨骼肌组织通过血液向肝进行转运的机制是A.三羧酸循环B.鸟氨酸循环C.丙氨酸-葡萄糖循环D.甲硫氨酸循环E.ATP循环 电器火灾首选灭火器。A.泡沫B.干粉C.消防水D.二氧化碳 含有3.5g氮元素的NH4N03的质量是。A.5gB.8gC.10gD.15g 强直性肌营养不良症的治疗药物应该除外以下哪项A.普鲁卡因胺B.硫酸奎宁C.溴吡斯的明D.苯妥英钠E.地西泮 患者,68岁,急性心肌梗死,一旦出现房颤。关于这种脉搏异常的叙述正确的是()A.心音无异常B.动脉充盈脉搏强劲C.单位时间内心率大于脉搏D.心律规则,心率快慢不一,心音强弱不等E.每隔一个或两个正常搏动后出现一次早搏
