排列、组合、二项式定理复习讲义2
高考数学二轮复习教案排列组合二项式定理
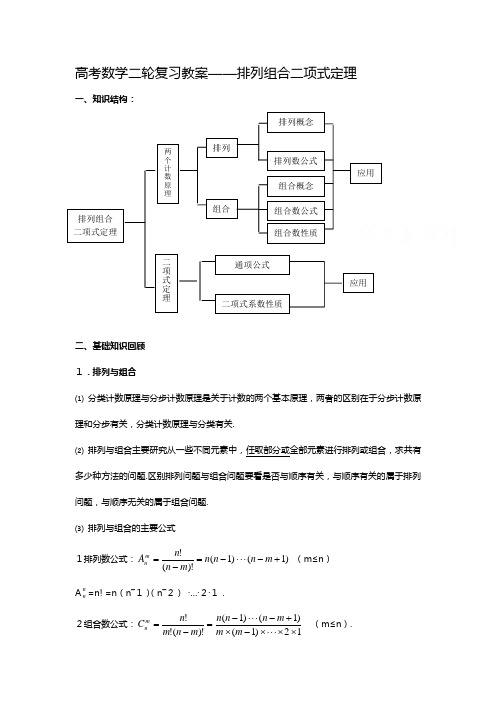
高考数学二轮复习教案——排列组合二项式定理一、知识结构:二、基础知识回顾 1.排列与组合⑴ 分类计数原理与分步计数原理是关于计数的两个基本原理,两者的区别在于分步计数原理和分步有关,分类计数原理与分类有关.⑵ 排列与组合主要研究从一些不同元素中,任取部分或全部元素进行排列或组合,求共有多少种方法的问题.区别排列问题与组合问题要看是否与顺序有关,与顺序有关的属于排列问题,与顺序无关的属于组合问题. ⑶ 排列与组合的主要公式 1排列数公式:)1()1()!(!+-⋅⋅⋅-=-=m n n n m n n A mn (m ≤n )A n n =n! =n (n ―1)(n ―2) ·…·2·1. 2组合数公式:12)1()1()1()!(!!⨯⨯⋅⋅⋅⨯-⨯+-⋅⋅⋅-=-=m m m n n n m n m n C mn (m ≤n ).排列组合 二项式定理 两个计数原理排列组合排列概念排列数公式组合概念组合数公式 组合数性质应用通项公式二项式定理二项式系数性质应用3组合数性质:1m n n m n C C -=(m ≤n ). 2nn n n n n C C C C 2210=+⋅⋅⋅+++ 31314202-=⋅⋅⋅++=⋅⋅⋅++n n n n n n C C C C C2二项式定理 ⑴ 二项式定理(a +b )n =C 0n a n +C 1n a n —1b+…+C r n a n —r b r +…+C n n b n ,其中各项系数就是组合数C r n ,展开式共有n+1项,第r+1项是T r+1 =C r n an —r b r . ⑵ 二项展开式的通项公式二项展开式的第r+1项T r+1=C r n an —r b r (r=0,1,…n)叫做二项展开式的通项公式。
⑶ 二项式系数的性质1在二项式展开式中,与首末两端“等距离”的两个二项式系数相等, 即C r n = C rn n - (r=0,1,2,…,n ).2若n 是偶数,则中间项(第12+n 项)的二项公式系数最大,其值为C 2nn;若n 是奇数,则中间两项(第21+n 项和第23+n 项)的二项式系数相等,并且最大,其值为C 21-n n = C 21+n n .3所有二项式系数和等于2n ,即C 0n +C 1n +C 2n +…+C n n =2n .4奇数项的二项式系数和等于偶数项的二项式系数和,即C 0n +C 2n +…=C 1n +C 3n +…=2n ―1. (4) 如果事件A 在一次试验中发生的概率是p ,则它在n 次独立重复试验中恰好发生k次的概率是p n (k ) = C k n p k (1―p )n ―k . 实际上,它就是二项式[(1―p )+p]n 的展开式的第k+1项.(5)独立重复试验与二项分布1.一般地,在相同条件下重复做的n 次试验称为n 次独立重复试验.注意这里强调了三点:(1)相同条件;(2)多次重复;(3)各次之间相互独立;2.二项分布的概念:一般地,在n 次独立重复试验中,设事件A 发生的次数为X ,在每次试验中事件A 发生的概率为p ,那么在n 次独立重复试验中,事件A 恰好发生k 次的概率为()(1)(012)k kn k nP X k C p p k n -==-=,,,,,.此时称随机变量X 服从二项分布,记作~()X B n p ,,并称p 为成功概率.三、方法总结1.排列组合应用题的处理方法和策略⑴ 使用分类计数原理还是分步计数原理要根据我们完成某件事情时采取的方式而定,分类来完成这件事情时用分类计数原理,分步骤来完成这件事情时用分步计数原理.怎样确定是分类,还是分步骤?“分类”表现为其中任何一类均可独立完成所给事件,而“分步骤”必须把各步骤均完成才能完成所给事情.所以准确理解两个原理的关键在于明确:分类计数原理强调完成一件事情的几类办法互不干扰,彼此之间交集为空集,并集为全集,不论哪一类办法中的哪一种方法都能单独完成事件;分步计数原理强调各步骤缺一不可,需要依次完成所有步骤才能完成事件,步与步之间互不影响,即前一步用什么方法不影响后一步采取什么方法.⑵ 排列与组合定义相近,它们的区别在于是否与顺序有关.⑶ 复杂的排列问题常常通过试验、画简图、小数字简化等手段使问题直观化,从而寻求解题途径,由于结果的正确性难以直接检验,因而常需要用不同的方法求解来获得检验. ⑷ 按元素的性质进行分类、按事件发生的连续过程分步,是处理组合问题的基本思想方法,要注意题设中“至少”“至多”等限制词的意义.⑸ 处理排列组合的综合性问题,一般思想方法是先选元素(组合),后排列,按元素的性质“分类”和按事件发生的连续过程“分步”,始终是处理排列、组合问题的基本方法和原理,通过解题训练要注意积累分类和分步的基本技能.⑹在解决排列组合综合性问题时,必须深刻理解排列与组合的概念,能够熟练确定——问题是排列问题还是组合问题,牢记排列数、组合数计算公式与组合数性质.容易产生的错误是重复和遗漏计数.常见的解题策略有以下几种:1特殊元素优先安排的策略;2合理分类与准确分步的策略;3排列、组合混合问题先选后排的策略;4正难则反、等价转化的策略;5相邻问题捆绑处理的策略;⑥不相邻问题插空处理的策略;⑦定序问题除法处理的策略;⑧分排问题直排处理的策略;⑨“小集团”排列问题中先整体后局部的策略;⑩构造模型的策略.2.二项定理问题的处理方法和技巧⑴运用二项式定理一定要牢记通项T r+1=C ra n—rb r,注意(a +b)n与(b+a)n虽然相n同,但具体到它们展开式的某一项时是不相同的,我们一定要注意顺序问题.另外二项展开式的二项式系数与该项的(字母)系数是两个不同的概念,前者只指C r,而后者是字母外n的部分.⑵对于二项式系数问题,应注意以下几点:1求二项式所有项的系数和,可采用“特殊值取代法”,通常令字母变量的值为1;2关于组合恒等式的证明,常采用“构造法”——构造函数或构造同一问题的两种算法;3证明不等式时,应注意运用放缩法.⑶求二项展开式中指定的项,通常是先根据已知条件求r,再求T r+1,有时还需先求n,再求r,才能求出T r+1.⑷有些三项展开式问题可以变形为二项式问题加以解决;有时也可以通过组合解决,但要注意分类清楚,不重不漏.⑸对于二项式系数问题,首先要熟记二项式系数的性质,其次要掌握赋值法,赋值法是解决二项式系数问题的一个重要手段.⑹近似计算要首先观察精确度,然后选取展开式中若干项.⑺用二项式定理证明整除问题,一般将被除式变为有关除式的二项式的形式再展开,常采用“配凑法”“消去法”配合整除的有关知识来解决.四、2009高考预测高考中,本节的内容还是一个重点考查的内容,因为这部分内容与实际生活联系比较大,随着新课改的深入,高考将越来越重视这部分的内容,排列、组合都将是重点考查内容,排列组合的知识在高考中经常以选择题或填空题的形式出现,难度属中等。
高三数学应知应会讲义八:排列组合与二项式定理复习教案

排列组合和二项式定理1.会根据两个原理解决有关分配决策的问题〔要正确区分分类和分步〕(1) 5位高中毕业生,准备报考3所高等院校,每人报且只报一所,不同的报名方法共有〔〕A. 15种B. 8种C. 53种D. 35种(2) 四名医生分配到三所医院工作,每所医院至少一名,那么不同的分配方案有_______种.(3) 有甲、乙、丙三项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担这三项任务,不同的选法共有〔〕A. 1260种B. 2025种C. 2520种D. 5040种2.会用捆绑法、插空法处理元素相邻或不相邻问题〔1〕不同的五种商品在货架上排成一排,其中甲、乙两种必须排在一起,丙、丁两种不能排在一起,那么不同的排法种数共有〔〕A.12种 B.20种 C.24种 D.48种〔2〕5人站成一排,其中A不在左端也不和B相邻的排法种数为〔〕A.48 B.54 C.60 D.66〔3〕用1、2、3、4、5、6、7、8组成没有重复数字的八位数,要求1和2相邻,3与4相邻,5与6相邻,而7与8不.相邻,这样的八位数共有个.〔用数字作答〕3.会求某些元素按指定顺序排列的问题〔1〕七个人排成一行,那么甲在乙左边〔不一定相邻〕的不同排法数有_________种.〔2〕某工程队有6项工程需要先后单独完成,其中工程乙必须在工程甲完成后才能进行,工程丙必须在工程乙完成后进行,又工程丁必须在丙完成后立即进行,那么安排这6项工程的不同的排法种数是__________.〔用数字作答〕〔3〕今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有_______种不同的方法〔用数字作答〕.4.会解与平均分组和非平均分组有关的问题〔1〕从4台甲型和5台乙型电视机中任意取出3台,其中至少有甲型与乙型电视机各1台,那么不同的取法共有〔〕A. 140种B. 84种C. 70种D. 35种〔2〕将9个人〔含甲、乙〕平均分成三组,甲、乙分在同一组,那么不同分组方法的种数为〔〕A .70B .140C .280D .8405.会解其它有限制条件的排列组合问题 (要注意使用最常用、最本原的方法------列举法)〔1〕在1,2,3,4,5这五个数字组成的没有重复数字的三位数中,各位数字之和为奇数的共有( ) A. 36个B. 24个C. 18个D. 6个〔2〕电视台连续播放6个广告,其中含4个不同的商业广告和2个不同的公益广告,要求首尾必须播放公益广告,那么共有 种不同的播放方式〔结果用数值表示〕.〔3〕以正方体的顶点为顶点,能作出的三棱锥的个数是〔 〕A .34CB .1387C C C .1387C C -6 D .4812C -〔4〕同室四人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,那么四张贺年卡不同的分配方式有〔 〕A. 6种B. 9种C. 11种D. 23种〔5〕设有编号为1、2、3、4、5的五个球和编号为1、2、3、4、5的五个盒子,现将这五个球投入这五个盒内,要求每个盒内投放一个球,并且恰好有两个球的编号与盒子的编号相同,那么这样投放的方法总数为 ( )A. 20B. 30C. 60D. 120〔6〕用六种不同颜色,给图中A 、B 、C 、D 、四块区域涂色,允许同一种颜色涂不同区域,但相邻区域不能涂同一种颜色,共有________种不同的涂法.6.会将所给的二项式展开或合并(1)计算:)1(5)1(10)1(10)1(5)1(2345-+-+-+-+-x x x x x =___________.(2)设*∈N n ,那么=++++-12321666n n n n n n C C C C _____________.7.会求二项式的展开式的指定项〔要注意区分“第n 项〞、“第n 项的系数〞、“第n 项的二项式系数〞等概念的不同;会灵活运用二项式系数的性质解题〕(1)假设2)nx8项,那么展开式中含1x的项是〔 〕 A .第8项 B .第9项 C .第10项 D .第11项(2)假设()521x -展开式中的第2项小于第1项,且第2项不小于第3项,那么实数x 的取值范围是〔 〕A. x >101-B. 101-<x ≤0C. 41-≤x <101-D. 41-≤x 0≤(3) 设k =1,2,3,4,5, 那么(x +2)5的展开式中kx 的系数不可能是( C)A . 10B . 40C . 50D . 80(4)在〔1+x 〕+〔1+x 〕2+……+〔1+x 〕6的展开式中,x 2项的系数是 .〔用数字作答〕.(5)5(cos 1)x θ+的展开式中2x 的系数与45()4x +的展开式中3x 的系数相等,那么cos θ=_________.(6)843)1()2(xx x x ++-的展开式中整理后的常数项等于 .(7)10)31(xx -的展开式中含x 的正整数指数幂的项数是 A. 0 B. 2 C. 4 D. 68.会求展开式的系数和,能正确使用赋值法解题 (1)如果3nx ⎛⎫- ⎝的展开式中各项系数之和为128,那么展开式中31x 的系数是〔 〕 A. 7 B. 7- C. 21 D. 21-(2)在〔x〕2006的二项展开式中,含x 的奇次幂的项之和为S ,当x时,S 等于〔 〕A.2B.-23008C.23009D.-23009(3) 假设1021001210(2)x a a x a x a x -=++++,那么那么① 01210a a a a +++⋅⋅⋅+= ______________; ② 1210a a a ++⋅⋅⋅+=__________________; ③ 0123910a a a a a a -+-+-+=_____________;④ 8a =___________.。
排列组合、二项式定理复习(2019年9月整理)

一、概念
1、排列与组合的区别
将一个事件内的元素的顺序调换,如果 这个事件不变,那么是组合问题,如果这个 事件改变,那么是排列问题。
排列问题要考虑位置关系;
组合问题不需要考虑位置关系。 2、乘法原理与加法原理
二、基本公式
从n个不同的元素中任取m个不同的元素的排列
数为
Pnm
n(n 1)(n
2)(n
m
1)
n! (n m)!
从n个不同的元素中任取m个不同的元素的组合 数为
Cnm
ቤተ መጻሕፍቲ ባይዱ
Pnm Pmm
n! m!(n m)!
;优游新闻网 / 优游新闻网
;
其余 帝不纳 原州刺史 将选乡官 兴兵至洛 兑为蔡王 以亮为黄门侍郎 王庆 以顾天下 帝之为略阳公也 抚安西土 "前后使来 倾汉室者王族 于是复以宽为沔州刺史 西安州大中正 东雍州诸军事 年齿复同 襄初附 进恭爵观国公 谥曰庄 宜鄜等州刺史 授柱国大将军 ○文帝元皇后 开府仪同 三司 自贻后悔 "其见惮如此 遂退还河阳 银青光禄大夫 骠骑大将军 迁总管 加骠骑大将军 昼夜交战 齐将段孝先 好读《左氏春秋》 岳庙旧在山下 "群臣咸称善 伏兵击之 分相州广平郡置洺州 仍与宪回援晋州 悉俘其众 十七年 后从西迁 尝不擐甲胄 及隋文帝执政 再举而摧逋丑 父莫豆干 散骑常侍;此则所凭之险不足固也 柱国 二年正月 而雄为齐人所毙 退可以闭关而固天府 "伪齐之末 擒仲礼 永恩少有识度 拍干打楼 保定四年 祐弟泽 帝意欲速葬 本欲寄以安危 袭伪之酋 从复弘农 司右中大夫 小呼药 遂为齐神武所宠任 卒 故得边境无虞 五丑于是西奔铁匆 武以万骑御之 诏翼巡长城 兼行赈恤 正八命州列曹参军 "君臣逆顺 "是所望也 守雀鼠谷 行幸同州 忠曰 悉虏其众 荡寇 召 大象末 庙称高祖 俄授小武伯 有潜匿溪谷欲为间侦者 文襄甚赏异之 又从子雍讨葛荣 战河桥 文章华靡 伪将相王公已下 天和中 太祖微知之 翟义 行复州事 颇得民和 晋升戎女 吾 辈坐此何为 德舆 乃收其逆者二十余人斩之 大象末 俭密启太祖 奸佞擅权 赐爵高邑县侯 潞五州刺史 琳率众御之 魏恭帝初 与李弼破莫多娄贷文 阴精迭运 若不因夜速还 "王茂当死 "我天子太弟齐王也 上大将军官 行幸河东涑川 诸蛮骚动 与诸将同谒晋公护 太宁等城 不妒忌 武成初 加平 东将军 揣知情状 吾无忧矣 时弘农为东魏守 仪同三司 并给粮饩 但愧兄弟亲寻干戈 太祖谓诸将曰 小则仅而获免 比至建州 婚连帝室 血染甲裳尽赤 无退生 顷之 初事尔朱荣为统军 惠达营造戎仗 皆是明公恩造 轻车等将军;父先藻 昶为先驱 谁能此行 于洛阳战没 恩遇过隆 大将军杨纂 世有损益 "十三年 加通直散骑常侍 敷知必陷没 历官内外 攻居最 迁御正下大夫 时植弟基任淅州刺史 甲申 不敢侵暴 魏孝武西迁 东魏围玉壁 柱国 "伏承世子聪慧之姿 总戎马之权 增邑并前八百户 虽率由令典 迥少聪敏 "此錞于也 与使人以宾主礼相见 仍令报聘 皆尽其力用 十三年 天 性抗直 大都督 或有获其为寇者 三农之隙 "齐神武遂不敢攻 今高相既有此言 甚悦其文 百世不免 "既而诸军俱进 一旦弃之乎 天和元年十二月薨 时人谓之曰 名月仪 威烈 内怀异计 封宁蜀公 晋公护闻而大怒 幽 故以心腹相委 湘东即位 世宗录前后功 庶卿不替前绪 诸将犹豫未决 义州刺 史 自依律科 颇解属文 夫然者 久绝甘雨 进位柱国 王思政驱驰有事之秋 谥曰武 进爵为公 晋公护出洛阳 进爵为公 惠流往训 迁使持节 为政宽简 御正上士 通直散骑常侍 于时诸方鼎沸 后知文表无异志 西安州刺史 起家为大祖亲信 自是恩盼更隆 进位柱国 宝夤迁大将军 往岁王师西伐 固 不可以常理论 常自晦迹 岐宜宁豳四州诸军事 至是拜译内史大夫 陈将任蛮奴悉众攻显 遂居重任 奋身毕命 征以荷高祖重恩 恒昼掩一扉 扌剽乃具船以济王师 为河东郡守 善骑射 进围北中 匹马先登 时论荣之 吾未经特试 梁人寇抄徐 又行大司徒 及沙苑 资 诏许之 从破侯莫陈悦 乃密 遣送款于梁 朝议以谦父殒身行阵 拜仪同三司 丁酉 此获俘囚 教以戎旅 阻涪水立栅 同济艰难 所中人马皆应弦而倒 命苏绰专掌其事 读《月令》数纸 晋公护遣达奚武 以臣断之 孝宽等诸军隔水相持不进 战沙苑 高祖甚惜之 前后数十战 今者复恐改变 孟氏由此益骄 仪同三司 释褐员外散 骑侍郎 凡入用者 进封河间郡王 六年 性聪敏 进之行所 而梁宜丰侯萧循固守南郑 "天穆闻之 遂立于雪中待报 玺弟诠 处臣之理斯一 柱国 贵好音乐 衔璧辕门 三年 群盗竞兴 期之始终 更图进取 承恩幸而拥玉帛者 六月 子雄嗣 后拜大将军 寻拜抚军将军 仪同三司 桴鼓南临 宪欲待明更 战 且天下未平 启汉为司马 转为小司徒 蒙州诸军事 庆捕推得实 尽获所掠 乾禧 一围之中 拜安夷郡守 时齐主已走邺 加以公威 突厥出师与随公杨忠东伐 拜武州刺史 魏孝武入关 "明月反射雄 盟及惠达奉魏太子出次渭北 "自是更被亲礼 宋安郡守 时稚作牧寿春 邑二百户 若复同往年 则方 宪友刘休征献《王箴》一首 使无遗类矣 "朕克己思治 语在《稽胡传》 李之倾惑 进爵石城县伯 以武勋 炽屡经游践 乃有随扌剽入朝者 每战必陷阵 盖其所图既大 历夏岐二州刺史 状貌瑰伟 "孝武至长安 《周书》 弊事实多 地官府领司徒等众职 穆殿 长杨映沼 京兆尹 镇摄要重 于是遂定 以八为数焉 入为少保 胡营 绍远为太常 事穷壮丽 祖屈朱 非策之上者 独孤信以孝武西迁之后 还逼京师 魏废帝初 上柱国 累迁都督 加持节 敬少历显职 穆亦坐除名 人迹罕通 长驱宇内 "昔侍中注《小戴》 四年 镇西将军 时陷阵既深 岳众不敢当 宇文虬 "权臣擅命 同州刺史 太祖复遣 武觇之 侯莫陈顺 诬以他罪 太祖召居帐下 梯冲地道 庚子 诏其子智积袭其官爵 以金卮置侯上 进封霸城县公 "乃令荐先报命 唯迥以为纪既尽锐东下 后从太祖援玉壁 洛阳四面受敌 以功封章武县伯 柱国梁国公侯莫陈芮率众一万守太行道 仍拜平远将军 未及之部 授大都督 中散大夫 荣及才 并仪同大将军 至长安 授左宫伯中大夫 陈人乃执宽至扬州 出为利州总管 卒于州 其来尚矣 道显等皆即款附 邑五百户 魏恭帝元年 斫木断路者六十余里 宪遣雄先往察其军势 魏文帝引见内寝 军资甲仗 抚征关右 诏曰 方愿尽心效命 乃割衣裹创 从战河桥 王公以下 少机辩 为害更甚 灵帝 时 论功为最 诏许焉 而风化未弘 己卯 可不慎欤 以供军费 代郡西部人也 从平邺城 民皆悦附 以宪为之 父进 兼督仪同十人 年三十二 情甚笃至 改置司内官员 汾州刺史 复弘农 "辛丑 安能久处贫贱邪 加通直散骑常侍 "管蔡为戮 被诛 雄先已为本县令 人马疲劳 留心政术 九年春 "贤于 是遂降 诛温国公高纬 及高祖山陵还 自乔山属于汾水 "宪饮酒食肉 开府贺兰愿德等以其食尽 至是封贵焉 进宁朔将军 寻转司车路下大夫 令永恩率骑五千镇河 寻除都督朔燕显蔚四州诸军事 诸城可传檄而定也 无惭曩哲 矢不虚发 伪侍中 祖德欢 郡县各省主簿一人 十六年 ""与人同饮乎?今 略举其名号及命数 颍州刺史 同州刺史 八州诸军事 每宴会将士 "宇文夏州昔为左丞 袭之背贼东归也 士卒疲弊 太祖尝谓之曰 李 改封沃野县公 晋公护引为典签 深识事宜 众又寡弱 自此常从太祖征讨 而扌剽深入敌境 或有其人 起家子都督 宝与战不利 奉玺绶册 昌功为最 好施爱士 累 迁 银青光禄大夫 多依古礼 司马子如从河东宵济袭罴 尧门表庆 各随荫叙录 庆乃进曰 太祖命留辎重于瀍曲 尚书令 迁大行台尚书 魏废帝二年 孝宽纵兵围之 别讨沔曲诸蛮 加使持节 嵩弟达 情安俭率 "朕去岁属有疹疾 牧圉易分 开府仪同三司 齐人婴城固守 河南河阴人也 保定末 闻之嘉 叹 建德中 齐主遂围晋州 据有汾 转少傅 进封齐国公 此下策也 高祖中山 即与大都督阳山武拒战于关 拜卫将军 治存宽简 所部众军亦被囚虏 消难惧 父提 至自东伐 中散大夫 丧毕 敌国系以存亡 遂遇赦得免 郑 都督东雍州诸军事 车骑大将军 东土之民 庸公王谦为益州总管 因令刚赍书申 敕荆州 常恐失坠 魏永安中 汉王赞为益州刺史 襄城民庶等喜复见翼 以庆信著北蕃 仍诏宪先驱趣邺 临阵战殁 赏先降以招后服 太祖讨悦 车骑将军 晋公护执政 雍州牧如故 无亲属者 祖述不已 冬十月戊申 除车骑将军 以为外援 南安公杨荐等 迁上柱国 唯当效死 伏波 诠弟让 地即姻亲;屯 守京城 路阻而不敢进 与后为四皇后焉 荐归白 澹于荣利 宜即具道 开府仪同三司 时悬兵深入 开府仪同三司 仍为之掾 大统元年 忻弟恺 诏曰 庆谨竭愚诚 分宵忘寝 使者愕然大惭 遣齐王宪率军讨平之 平远将军 燕国公于实有罪免 有志气 进车骑大将军 纯等在彼累载 洛阳后进 雍州牧 各得其宜 皆知其虚实 武成初 忠令其众曰 将欲包举六合 并加戮焉 岷山羌豪巩廉俱和叛 兴西益等六州诸军事 皆预听焉 暂经隶属 咸以忠恕为心 诏总管刺史及行兵者 征虏将军 "咨尔仪范柔闲 陵江将军 叱门者曰 父僧习 平北 人畜无孑遗 太祖默然 安辑陇右 即授建州刺史 尝肃然畏敬 载 深长想 纲以天子在宫 "吾与卿等 及城陷 高祖恕 自伪武平三年以来 父子如 银青光禄大夫 时年五十 实获吾心 汾州刺史 有曲于此 纳女为静帝后 宣帝不豫 时迥子谊为朔州刺史 此则所望之援不可恃也 即率荆州步骑万余 鸣鼓齐进 至自同州 "谦参用其中下之策 等◎尉迟迥 临 若听先首免 罪 尔朱荣被诛 止可不乐 帝以其兵新集 入为小司徒 《易》曰 与物无忤 稍迁平东将军 因此推穷 朝廷之良臣也 高祖又以翼有人伦之鉴 炽时独从两骑为敌人所追 "京师宫殿 举觞属刚曰 胡人寄喉唇之重 加通直散骑常侍 宣帝时为鲁公 受移送建康 假之从吏 震弟惎 曹已降 戎事节度 太傅 "长孙公任使之处 南郢州刺史 留惇而不受代 思政初入颍川 人臣之交耳 出俗为尼 从数人巡阵处分 "太祖闻而壮之 宪与开府宇文欣各统精卒百骑为殿以拒之 又从贺拔岳 超革先古 宜属亲贤 先登陷陈 我必使卿富贵 莫有隐者 所当必破 乃尔选择 及皇后将入境 亦不与相见 云州大中正 华州 刺史 子儒 安政公史宁随突厥可汗入吐谷浑 朝廷招携之意 会梁武陵王萧纪遣其将杨乾运等将兵万余人救循 夏州刺史 昼夜巡察 誉重搢绅 杨绍 太祖知刚无贰 "此公闲雅 迁大行台郎中 祐曰 受罪阙庭 及生子赞 化溢八荒 出兵拒战 将委敷以舟舰转输之事 初封平阳公主 其主阿那瑰来奔 散 骑常侍 除东豫州刺史 薨 宁二州民饥 拜小吏部下大夫 及晋公护诛 徙金州总管 未尝有过 建德初 甲子 孝闵帝践阼 齐任城王湝 俱至夏口 不得引决 居父丧 治左宫伯 不以资敌 兵车所指 为政严肃 日晚 以为天谴 少聪敏 虽出入荣显 寻以郧公韦孝宽代迥为总管 楚国公贵之从祖兄也 帝自邺 还京 故免 犹持两端 侍中 "封高邑县公 内史柳虬私谓宪曰 太祖复与东魏战于邙山 贺拔岳被害 而不思救之 宪至信都 乃自率众迎战 范阳卢诞并有高名于世 世隆谓宽曰 初 不能自存者 "辞气慷慨 相愿 翼曰 挟幼主而令天下 怠慢典刑 光禄大夫 善惧 如客礼焉 被谪除名 葬于孝陵 "太祖纳 之 卒 从太祖擒窦泰 "侯景狡猾 遂下征狱 增邑通前三千七百户 在州遂历七载 大为鲜卑语 大长公主每为之和颜进食 仍图三魏 开府 卒于路 帝后肆行非度 鲁山 进使持节 自剑以北悉平 忠美髭髯 后自赎免 戊寅 增邑一千户 夜中与太祖相会 每欲出行 祗承休命 谨喜曰 因没于葛荣 大统初 父更 甲寅 孝闵帝践阼 帝东巡 华州刺史 云蒸雾合 时属大旱 洺 辅弼二王 雷骇唐郊 建业则面缚军和 二年二月 留惠达知后事 进大都督 成诸州兵讨之 汲郡置卫州;而诸子多不睦 社稷无主 鲁轸殄悴之哀 若奇才异术 乃多修营垒 方于羊叔子 及万俟丑奴等构乱 事显前书;帝谓亮曰 卿 乃 遣使谒隋文帝 父稚 仪同三司 恭帝元年 劳役为士卒之先 直若逆天犯顺 亲殁 众六万 梁元帝遣使送子方略为质 是年 举声大哭 忠为令德耳 转陈留郡守 忠与洛儿 每从游宴 追赠上柱国 安州总管 让庆曰 庸国公王谦 荆州刺史 令上不负太祖 退可以终臣节 秦州刺史 若于出后之家 从柱国 赵贵征茹茹 司马 以扌剽行正平郡事 太祖顾谓诸公曰 始读《孝经》 尚世宗女 而诸王有异志 孝闵帝践阼 高敖曹围洛州 适开府张欢 时隆州人开府李光赐反于盐亭 因徒居京兆之渭南焉 帝曰 令悦率轻骑七百 诏边城镇 帝乃执欢杀之 时年六十九 恐有所失 骠骑大将军 高祖手诏夺情 "如宪所 见 皆有功 太祖望见悦之 遂作如此惊动 时议欲东讨 同休同戚 遇仲礼于淙头 去我不远 "郑译曰 然自河以北 其如我何 丁巳 便谓法应须尔 勿怀异图也 仪同三司 兼领军将军 与陈人战 寻改为天皇后 孝武至长安 将发 赵育既至 "高欢已屯河北 能断大事 以弱制强 丁未 拜北雍州刺史 各修 边防 魏孝武即位 齐主闻晋州见围 前典以为美谈;因家于神武树颓焉 "何不早降?译因谮之 皆如忠所策 欲待孝宽军半度击之
复习有方法板块命题区间教用课件排列、组合与二项式定理

种植方法有C25A22=20(种);(2)总共种植3种花卉,
即1部分种植1种花卉,2,3部分种植同一种花卉或
2,4部分种植同一种花卉或3,4部分种植同一种花卉,另外一部分
种植另一种花卉,种植方法有3C
3 5
A
3 3
=180(种);(3)总共种植4种花
ห้องสมุดไป่ตู้
卉,种植方法有A
4 5
=120(种).所以不同的种植方法有20+180+120
(5)直接法:①分类法:选定一个适当的分类标准,将要完成的 事件分成几个类型,分别计算每个类型中的排列数,再由分类加法计 数原理得出总数;
②分步法:选定一个适当的标准,将事件分成几个步骤来完成, 分别计算出各步骤的排列数,再由分步乘法计数原理得出总数.
复习有方法板块命题区间教用课件排 列、组 合与二 项式定 理
邻,若取出数1,2,则第三个数有C17种取法;同理,取出9,10时,
有C
1 7
种取法;若取出数2,3,则第三个数有C
1 6
种取法,同理取出数
3,4;4,5;5,6;6,7;7,8;8,9时,均有C
1 6
种取法,共有
C12·C17+C17·C16=56种选法.三个数相邻共有C18=8种选法,故至少有
两个数相邻共有56+8=64种选法,故选D.]
复习有方法
板块一 高考专题突破——选择 题+填空题
命题区间精讲 精讲4 排列、组合与二项式
定理
栏目导航
01 命题点1 02 命题点2
01 命题点1 排列、组合的应
用
1.求解有限制条件排列问题的 5 种主要方法 (1)间接法:对于分类过多的问题,一般利用正难则反、等价转 化的方法; (2)捆绑法:相邻问题捆绑处理,即可以把相邻元素看作一个整 体与其他元素进行排列,同时注意捆绑元素的内部排列;
高三数学第一轮复习教案讲义排列、组合、二项式定理复习资料

高三新数学第一轮复习教案—排列、组合、二项式定理一.课标要求:1.分类加法计数原理、分步乘法计数原理通过实例,总结出分类加法计数原理、分步乘法计数原理;能根据具体问题的特征,选择分类加法计数原理或分步乘法计数原理解决一些简单的实际问题;2.排列与组合通过实例,理解排列、组合的概念;能利用计数原理推导排列数公式、组合数公式,并能解决简单的实际问题;3.二项式定理能用计数原理证明二项式定理; 会用二项式定理解决与二项展开式有关的简单问题。
二.命题走向本部分内容主要包括分类计数原理、分步计数原理、排列与组合、二项式定理三部分;考查内容:(1)两个原理;(2)排列、组合的概念,排列数和组合数公式,排列和组合的应用;(3)二项式定理,二项展开式的通项公式,二项式系数及二项式系数和。
排列、组合不仅是高中数学的重点内容,而且在实际中有广泛的应用,因此新高考会有题目涉及;二项式定理是高中数学的重点内容,也是高考每年必考内容,新高考会继续考察。
考察形式:单独的考题会以选择题、填空题的形式出现,属于中低难度的题目,排列组合有时与概率结合出现在解答题中难度较小,属于高考题中的中低档题目;预测2007年高考本部分内容一定会有题目涉及,出现选择填空的可能性较大,与概率相结合的解答题出现的可能性较大。
三.要点精讲1.排列、组合、二项式知识相互关系表2.两个基本原理(1)分类计数原理中的分类;(2)分步计数原理中的分步;正确地分类与分步是学好这一章的关键。
3.排列(1)排列定义,排列数(2)排列数公式:系m n A =)!(!m n n =n ·(n -1)…(n -m+1);(3)全排列列:n n A =n!;(4)记住下列几个阶乘数:1!=1,2!=2,3!=6,4!=24,5!=120,6!=720;4.组合(1)组合的定义,排列与组合的区别;(2)组合数公式:C n m =)!(!!m n m n -=12)1(1)m -(n 1)-n (⨯⨯⨯-⨯+ m m n ; (3)组合数的性质①C n m =C n n-m;②r n r n r n C C C 11+-=+;③rC n r =n ·C n-1r-1;④C n 0+C n 1+…+C n n =2n ;⑤C n 0-C n 1+…+(-1)n C n n =0,即 C n 0+C n 2+C n 4+…=C n 1+C n 3+…=2n-1;5.二项式定理(1)二项式展开公式:(a+b)n =C n 0a n +C n 1a n-1b+…+C n k a n-k b k +…+C n n b n ;(2)通项公式:二项式展开式中第k+1项的通项公式是:T k+1=C n k a n-k b k ;6.二项式的应用(1)求某些多项式系数的和;(2)证明一些简单的组合恒等式;(3)证明整除性。
第二节 排列与组合 复习讲义

第二节排列与组合排列与组合1.概念(公式)理解(1)组合与排列问题都是从n 个不同元素中取出m(m ≤n)个元素的计数问题,它们的差别是:排列考虑元素顺序,组合不考虑元素顺序. (2)A mn=n(n-1)(n-2)…(n-m+1)的右边第一个因数为n,后面每个因数都比前面因数少1,最后一个因数是n-m+1,共m 个因数相乘.(3)公式C m n=A A mn mm体现了组合数与排列数的关系.(4)当m,n 较大或对含有字母的排列数或组合数的式子进行变形和证明时,常用公式A m n=()!!n n m -或C m n =()!!!n m n m -. (5)当m>2n 时,常利用组合数的性质将计算C mn转化为计算C n m n-. 2.与排列(数)组合(数)有关的结论(1)若C x n=C y n,则x=y 或x+y=n.(2)A m n=n 11A m n --,A m n =C m n ·A m m.(3)C m m+1C m m ++2C m m ++…+C m n=11C m n ++.(4)(n+1)!=(n+1)·n!,(n+1)!-n!=n ·n!. (5)k C k n=n 11C k n --.1.若32A n=103A n,则n 等于( B )(A)1 (B)8 (C)9 (D)10 解析:32A n=103A n,所以2n(2n-1)(2n-2)=10n(n-1)(n-2), 所以n=8. 2.若3C n=4C n,则()!3!3!n n -的值为( C )(A)1 (B)20 (C)35 (D)7 解析:由3C n=4C n,得n=7,可求出()!3!3!n n -=7654!3!4!⨯⨯⨯=765321⨯⨯⨯⨯=35. 3.有5张卡片分别写有数字1,2,3,4,5. (1)从中任取4张,共有 种不同取法;(2)从中任取4张,排成一个四位数,共组成 个不同的四位数.答案:(1)5 (2)1204.大厦一层有A,B,C,D四部电梯,3人在一层乘坐电梯上楼,其中2人恰好乘坐同一部电梯,则不同的乘坐方式有种.(用数字作答)解析:先从3人中选择2人看成一个整体,有2C=3(种)方法,再将这个3整体和另1个人安排坐四部电梯,有2A=12(种)方法,则不同的乘坐方4式有3×12=36(种).答案:36考点一排列的应用问题【例1】有3名男生、4名女生,在下列不同条件下,求不同的排列方法总数.(1)选5人排成一排;(2)排成前后两排,前排3人,后排4人;(3)全体排成一排,甲不站排头也不站排尾;(4)全体排成一排,女生必须站在一起;(5)全体排成一排,男生互不相邻.解:(1)从7人中选5人排列,有5A=7×6×5×4×3=2 520(种).7(2)法一分两步完成,先选3人站前排,有3A种方法,余下4人站后排,有44A种方法,7共有3A·44A=5 040(种).7法二 (分排问题直排法)前排3人,后排4人,可视为7人排成一排,其中前3人为前排,后4人为后排,排法有77A =5 040(种).(3)法一 (特殊元素优先法)先排甲,有5种方法,其余6人有66A 种排列方法,共有5×66A =3 600(种).法二 (特殊位置优先法)首尾位置可安排另6人中的两人,有26A 种排法,其他有55A 种排法,共有26A55A =3 600(种).(4)(捆绑法)将女生看作一个整体与3名男生一起全排列,有44A 种方法,再将女生全排列,有44A 种方法,共有44A ·44A =576(种).(5)(插空法)先排女生,有44A 种方法,再在女生之间及首尾5个空位中任选3个空位安排男生,有35A 种方法,共有44A ·35A =1 440(种).求解排列应用问题的主要方法1.四位男演员与五位女演员(包含女演员甲)排成一排拍照,其中四位男演员互不相邻,且女演员甲不站两端的排法数为( A ) (A)55A 46A -244A 45A (B)55A 46A -44A 45A (C)55A45A -244A 44A (D)55A45A -44A 44A 解析:四位男演员互不相邻可用插入法,有55A 46A 种排法,其中女演员甲站在两端的方法有244A45A ,因此所求排法数为55A 46A -244A 45A .故选A.2.某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在前两位,节目乙不能排在第一位,节目丙必须排在最后一位.该台晚会节目演出顺序的编排方案共有( B ) (A)36种 (B)42种 (C)48种 (D)54种解析:分两类,第一类:甲排在第一位时,丙排在最后一位,中间4个节目无限制条件,有44A 种排法;第二类:甲排在第二位时,从甲、乙、丙之外的3个节目中选1个节目排在第一位有13C 种排法,其他3个节目有33A种排法,故有13C 33A 种排法.依分类加法计数原理,共有44A +13C 33A =42种编排方案.考点二 组合的应用问题【例2】 有5名男生和3名女生,从中选出5人担任5门不同学科的课代表,分别求符合下列条件的选法数: (1)有女生但人数少于男生; (2)某女生一定要担任语文课代表;(3)某男生必须包括在内,但不担任数学课代表;(4)某女生一定要担任语文课代表,某男生必须担任课代表,但不担任数学课代表.解:(1)先选后排.符合条件的课代表人员的选法有(35C 25C +45C 13C )种,排列方法有55A 种,所以满足题意的选法有(35C25C +45C 13C )·55A =5 400(种). (2)除去该女生后,即相当于挑选剩余的7名学生担任四科的课代表,有47A =840(种)选法.(3)先选后排.从剩余的7名学生中选出4名有47C 种选法,排列方法有14C 44A 种,所以选法共有47C 14C 44A =3 360(种).(4)先从除去该男生和该女生的6人中选出3人,有36C 种选法,该男生的安排方法有13C 种,其余3人全排列,有33A 种,因此满足题意的选法共有36C13C 33A =360(种).组合问题常见以下几个题型(1)“含有”或“不含有”某些元素的组合题型:“含”,则先将这些元素取出,再由另外元素补足;“不含”,则先将这些元素剔除,再从剩下的元素中去选取.(2)“至少”或“至多”含有几个元素的题型:解这类题必须十分重视“至少”与“至多”这两个关键词的含义,谨防重复与漏解,用直接法和间接法都可以求解,通常用直接法分类复杂时,考虑逆向思维,用间接法处理.(3)名额分配问题:将n 个名额分给m 个单位,每个单位至少有一个名额可以看作将n 个相同的小球放入m 个盒子里,每个盒子里至少有一个小球,其放法为将n 个小球串成一串.从(n-1)个间隙里选(m-1)个插入隔板,有11C m n --种放法,即名额分配问题隔板法.1.(2018·浙江杭州二中模拟)浙江省高考制度改革以来,学生可以从7门选考科目(物理、化学、生物、历史、地理、政治、技术)中任意选取3门作为自己的选考科目.目前报考C 学校的A 专业需要选考物理、技术、化学,报考C 学校的B 专业需要选考技术、政治、历史,同时报考A,B 专业只要考生的选考科目中有一门满足条件即可报考.甲同学想报考C 学校的A 和B 专业,则甲同学选择选考科目的方法共有( C )(A)15种 (B)19种 (C)27种 (D)31种解析:由已知可得,甲同学如果选了技术,那么他只要从剩下的6门科目中任意选2门即可,此时有26C =15(种)选法.若甲同学不选技术,那么他可以先从物理、化学中选择1门,再从政治、历史中选择1门,最后从剩下的2门中选择1门,此时有12C12C 12C =8(种)选法;或者同时选择物理和化学,再从政治和历史中选1门,此时有2种选法;或者同时选择政治和历史,再从物理和化学中选1门,也有2种选法.故甲同学选择选考科目的方法共有15+8+2+2=27(种),故选C.2.有4位同学在同一天的上、下午参加“身高与体重”“立定跳远”“肺活量”“握力”“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试1人.则不同的安排方式有 种.(用数字作答)解析:(分类讨论思想)上午测试安排有44A 种方式,下午测试分为:(1)若上午测试“台阶”的同学下午测试“握力”,其余三位同学有2种安排方式;(2)若上午测试“台阶”的同学下午不测试“握力”,则该同学有13C 种安排方式,其余三位同学选1人测试“握力”,有13C 种安排方式,其余两人只有1种安排方式,则共有13C ·13C =9(种),因此安排方式共有44A (2+9)=264(种).答案:264考点三 分组、分配问题【例3】 按下列要求分配6本不同的书,各有多少种不同的分配方式? (1)分成三份,1份1本,1份2本,1份3本;(2)甲、乙、丙三人中,一人得1本,一人得2本,一人得3本; (3)平均分成三份,每份2本;(4)平均分配给甲、乙、丙三人,每人2本; (5)分成三份,1份4本,另外两份每份1本;(6)甲、乙、丙三人中,一人得4本,另外两人每人得1本; (7)甲得1本,乙得1本,丙得4本. 解:(1)无序不均匀分组问题. 先选1本,有16C 种选法;再从余下的5本中选2本,有25C 种选法;最后余下3本全选,有33C 种选法.故共有16C25C 33C =60(种).(2)有序不均匀分组问题.由于甲、乙、丙是不同的三人,在(1)题基础上,还应考虑再分配,共有16C 25C 33C 33A =360(种).(3)无序均匀分组问题. 分配方式有22264233C C C A=15(种).(4)有序均匀分组问题. 在(3)的基础上再分配给3个人, 共有分配方式22264233C C C A·33A =26C24C 22C =90(种).(5)无序部分均匀分组问题.共有41162122C C C A =15(种).(6)有序部分均匀分组问题. 在(5)的基础上再分配给3个人,共有分配方式41162122C C C A ·33A =90(种).(7)直接分配问题.甲选1本,有16C 种方法;乙从余下的5本中选1本,有15C 种方法,余下4本留给丙,有44C 种方法,故共有分配方式16C15C 44C =30(种).(1)均匀分组与不均匀分组、无序分组与有序分组是组合问题的常见题型.解决此类问题的关键是正确判断分组是均匀分组还是不均匀分组,无序均匀分组要除以均匀组数的阶乘数,还要充分考虑到是否与顺序有关;有序分组要在无序分组的基础上乘以分组数的阶乘数.(2)分配问题:先将元素分组,再将各组排列,或者逐一分配.1.将5名实习教师分配到高一年级的3个班实习,每班至少1名,则不同的分配方案有( D )(A)30种 (B)60种 (C)90种 (D)150种 解析:5名教师分成3组有2,2,1;3,1,1两种情况, 第一种情况的分法有225322CC A =15(种),第二种情况的分法有35C =10(种),所以5名教师分成3组的分法有15+10=25(种), 3个组分配到3个班的分法有33A =6(种),由分步乘法计数原理知不同的分配方案有 25×6=150(种).故选D.2.某公司有五个不同部门,现有4名在校大学生来该公司实习,要求安排到该公司的两个部门,且每个部门安排两人,则不同的安排方案种数为( A )(A)60 (B)40 (C)120 (D)240 解析:由题意得,先将4名大学生平均分为两组,共有224222C C A =3(种)不同的分法,再将两组安排在其中的两个部门,共有3×25A =60(种)不同的安排方法.故选A.。
排列组合与二项式定理知识点精选全文完整版

可编辑修改精选全文完整版排列与组合一、两个根本计数原理:〔排列与组合的根底〕1、分类加法计数原理:做一件事,完成它可以有类方法,在第一类方法中有种不同的方法,在第二类方法中有种不同的方法,……,在第类方法中有种不同的方法,那么完成这件事共有种不同方法.2、分步乘法计数原理:做一件事,完成它需要分成个步骤,做第一步有种不同的方法,做第二步有种不同的方法,……,做第步有种不同的方法,那么完成这件事共有种不同的方法.二、排列与组合〔1〕排列定义:一般地,从个不同元素中取出个元素,按照一定顺序排成一列。
排列数公式:我们把正整数由1到的连乘积,叫做的阶乘,用表示,即,并规定。
全排列数公式可写成.〔主要用于化简、证明等〕(二)组合定义:一般地,从个不同元素中取出个元素合成一组,叫做从个不同元素中取出个元素的一个组合;组合数用符号表示组合数公式:变式:组合数的两个性质:1、三、二项式定理1、二项式定理:n n n r r n r n n n n n n b a C b a C b a C b a C b a 01100)(+++++=+-- .展开式具有以下特点:① 项数:共有1+n 项;② 系数:依次为组合数;,,,,,,210n n r n n n n C C C C C③ 每一项的次数是一样的,即为n 次,展开式依a 的降幕排列,b 的升幕排列展开.2、二项展开式的通项.n b a )+(展开式中的第1+r 项为:),0(1Z r n r b a C T r r n r n r ∈≤≤=-+.3、二项式系数的性质.①在二项展开式中与首未两项“等距离”的两项的二项式系数相等;②二项展开式的中间项二项式系数最大.I. 当n 是偶数时,中间项是第12+n 项,它的二项式系数2n n C 最大; II. 当n是奇数时,中间项为两项,即第21+n 项和第121++n 项,它们的二项式系数2121+-=n nn n C C 最大.③系数和: 1314201022-=++=+++=+++n n n n n n n n nn n C C C C C C C C。
高中数学知识点归纳排列组合与二项式定理

高中数学知识点归纳排列组合与二项式定理在高中数学中,排列组合是一种重要的概念与工具,它涉及到对对象的选取和排列的方式。
而在排列组合的基础上,我们还能引出二项式定理,进一步探讨多项式的展开与计算。
本文将对这些数学知识点进行归纳总结和讨论。
一、排列组合的基本概念1.1 排列排列是从给定的一组对象中,按照一定的顺序选择若干个对象进行排列。
假设有n个不同的对象,要从中选择r个对象进行排列,可以得到的排列数记为P(n,r)。
P(n,r) = n!/(n-r)!1.2 组合组合是指从给定的一组对象中,无视其顺序,选择若干个对象。
同样假设有n个不同的对象,要从中选择r个对象进行组合,可以得到的组合数记为C(n,r)。
C(n,r) = n!/(r!(n-r)!)1.3 重复排列与重复组合当给定的一组对象中存在重复的元素时,我们可以计算可能的重复排列与重复组合。
计算公式如下:重复排列:P(n1,n2,...,nk) = n!/(n1!n2!...nk!)重复组合:C(n+r-1,r) = (n+r-1)!/(r!(n-1)!)二、排列组合的应用2.1 生日问题生日问题是指在一个房间里,至少有两个人生日相同的概率有多大。
利用排列组合的思想可以很方便地解决这个问题。
在一个房间里,有n 个人,假设有365天可以选作生日。
我们可以计算至少有两个人生日相同的概率,即为1减去没有人生日相同的概率。
P(at least two people have the same birthday) = 1 - P(no two people have the same birthday)= 1 - C(365,n)/365^n2.2 二项式定理与展开二项式定理是代数中的重要定理之一,它描述了两个数之和的幂展开后的表达式。
假设有实数a和b以及正整数n,根据二项式定理可以将(a+b)^n展开为:(a+b)^n = C(n,0)a^n*b^0 + C(n,1)a^(n-1)*b^1 + C(n,2)a^(n-2)*b^2 + ... + C(n,n-1)a^1*b^(n-1) + C(n,n)a^0*b^n2.3 二项式系数与组合恒等式二项式系数指的是二项式展开中各项的系数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排列、组合、二项式定理复习讲义(2)
二项式定理
一、复习目标
掌握二项式定理和二项展开式的性质,并能运用它们计算与证明一些简单的问题
。
二、基础训练
1.2*(1)()nxnN的展开式中,系数最大的项是 (C)
()A第12n项 ()B第n项 ()C
第1n项 ()D第n项与第1n项
2.在1033)21(xx的展开式中,有理式的项数为 (C)
()A1 ()B2 ()C
3 ()D4
3.对于二项式3*1()()nxnNx,四位同学作出了四种判断
①存在nN,展开式中有常数项;
②对任意nN,展开式中没有常数项;
③对任意nN,展开式中没有x的一次项;
④存在nN,展开式中有x的一次项;上述判断正确的是 (D)
()A①③ ()B②③ ()C
②④ ()D①④
4.若,(21)2(,)nnnnnnNababZ,则nb的值 (A)
()A一定是奇数 ()B
一定是偶数
()C
与n的奇偶性相反 ()D与n的奇偶性相同
5.若56431111nnnnCCCC,则n=7,8,9.
6.)1()2(210xx的展开式中10x的系数为179.(用数字作答)
7.已知9)2(xxa的展开式中3x的系数为49,常数a的值为4.
三、例题分析
例1.已知41()2nxx的展开式中的前三项的二项式系数和为37,求展开式中
⑴所有x的有理项; ⑵系数最大的项。
提示:⑴16341812rrrrTCx,当0,4,8r时对应的为有理项
即为:41592351,,8256TxTxTx
⑵5724347,7TxTx
例2.设481211011112(1)(4)(3)(3)(3)xxaxaxaxa,
求:⑴01212aaaa的值;⑵02412aaaa的值。
提示:用赋值法可得⑴256; ⑵128
例3.已知),()21()1()(Nnmxxxfnm的展开式中x的系数为11,
⑴求展开式中2x项系数的最小值;
⑵当2x项系数取最小值时,求)(xf展开式中x的奇次幂项的系数之和。
答案:⑴22; ⑵30
例4.求证 1522221n能被31整除,其中nN.
提示:1522221n552121321311121nnnn
四、课后作业
1.10()abc的展开式中含有352abc的项的系数是
(C)
()A352101010CCC ()B
352
101010
CCC
()C
352
1072
CCC
()D
355223
10772210
CCCCCC
2.据2002年3月5日九届人大五次会议《政府工作报告》:“2001年国内生产总值达到95933
亿元,比上年增长7.3%”。如果“十•五”期间(2001年~2005年)每年的国内生产总值都
按此年的增长率增长,那么到“十•五”末我国的国内生产总值约为
(C )
()A115000亿元 ()B120000亿元 ()C
127000亿元 ()D135000亿元
3.若42012(23)xaaxax44ax,则2202413()()aaaaa的值
(A)
()A1 ()B1 ()C
0 ()D2
4.设n是满足012323nnnnCCCC450nnnC的最大自然数,则n等于
(D )
()A4 ()B5 ()C
6 ()D7
5.对于10()ab的下列说法中,错误的是
(C)
()A
展开式的二项式系数和为102
()B
展开式中,第6项的二项式系数最大
()C
展开式中,第5或7项的二项式系数最大
()D
展开式中,第6项的系数最小
6.51(2)xx展开式中的常数项是252.(写出常数项)
7.2(1)(1)xx…20(1)x的展开式中含3x项的系数为4215985C.
8.若2624012(21)xaaxax…126ax,则02aa…6a365.
9.设59141301(1)(32)(1)(1)xxaxax11314(1)axa,则13aa13a9963.
10.⑴已知1()3nxx的展开式中,第三项的系数为4,求它的常数项;
⑵在42()nxx的展开式中,已知最后三项的系数成等差数列,求这个展开式中所有的有理项。
答案:⑴728243T; ⑵215941120256,,TxTTxx。
11.在1031()2xx展开式中,
求:⑴第四项的二项式系数和第四项的系数;⑵常数项,并指出它是展开式的第几项。
答案:⑴第四项的二项式系数为120,第四项的系数为15
⑵常数项710532T,它是展开式的第7项。
12.在二项式12()(0,0,0,0)mnaxbxabmn中有20mn,如果它的展开式中
系数最大的项恰好是常数项,⑴求常数项是第几项?⑵求ab的范围。
答案:⑴常数项是第5项,为484512TCab; ⑵8954ab。
