辽宁省沈阳市和平区2019-2020学年第二学期五年级数学期末试题图片版无答案 人教版
2019-2020学年青岛版(六三制)小学五年级下册期末考试数学试卷(二)(解析版)

2019-2020学年青岛版(六三制)小学五年级下册期末考试数学试卷一.选择题(共10小题)1.下列说法中错误的是()A.0是最小的数B.直线上﹣3在﹣1的左边C.负数比正数小2.两根同样长的铁丝,一根用去了,另一根用去了米,剩下的铁丝相比,()A.第一根长B.第二根长C.同样长D.无法比较哪根长3.能表示出意义的算式是()A.﹣=B.1﹣=C.﹣=4.小刚放学回家时往西南方向走,那么他上学时应该往()方向走.A.东北B.西北C.东南D.西南5.图中物体形状是正方体的有()A.A B.A和C C.C D.A和D6.下面四幅图中,()不是正方体的展开图.A.B.C.D.7.与点(6,5)挨着的点是()A.(5,5)B.(6,3)C.(8,5)8.+可以直接相加,是因为两个加数()A.分子相同B.分数单位相同C.都是真分数D.都是最简分数9.小兵和小花一起喝一瓶果汁,小兵喝了这瓶果汁的,小花喝的比小兵多一些,小花喝了这瓶果汁的()A.B.C.D.10.从如图的统计图中可知道,甲车间2018年平均每季度的产值是()万元.A.37.5B.55C.91.5二.填空题(共8小题)11.甲乙两人进行120米的滑板比赛,乙让甲先滑10秒.他们两人滑的路程与时间的关系如下图.(1)乙在滑完全程中,每秒钟滑行米;(2)乙滑完全程时两人相距米.12.桑植白茶远近闻名,茶香四海.为了提高桑植白茶的品质,工厂准备定制一款长与宽是20厘米、高为10厘米的精美长方体茶叶盒,制作这样一款茶叶盒至少需要平方分米的材料,这款茶叶盒的容积是升.13.和的公分母是,两个数相减的结果是.14.在﹣﹣﹣﹣里填上“>”“<”或“=”.1﹣15.把2m长的铁丝平均分成三段,每段是全长的,每段长m.16.王红在教室的位置用数对表示为(3,5),表示她在第列第行,她的同桌李华的位置用数对表示可能是(,)或(,).17.东东从0点向东行70米,表示为+70米,那么从0点向西行30米,表示为米;如果他先向东行60米,再向西行40米,这时东东的位置表示为米.18.把36升水倒入一个长8分米,宽2.5分米的长方体水箱内,正好倒满,这个水箱深分米.(水箱的厚度忽略不计)三.判断题(共5小题)19.(判断对错)(改正)20.在﹣4、﹣9、﹣1、0.1这四个数中,最大的数是﹣9.(判断对错)21.一张油饼分给两个人吃,每人吃了油饼的.(判断对错)22.以学校为参照点,甲乙二人到学校的距离相等.他们一定在同一地方.(判断对错)23.将一个正方体钢坯锻造成长方体,正方体和长方体的体积相等.(判断对错).四.计算题(共2小题)24.求下列立体图形的表面积和体积.(单位:厘米)(1)(2)25.怎样简便就怎样计算.①+++②﹣(+)③++五.应用题(共7小题)26.某食品包装袋上有“500±5g”字样,那么这种食品的正常含量应在什么范围?27.一个底面是正方形的长方体铁桶,把它的侧面展开正好得到一个边长为40厘米的正方形.如果铁桶内装半桶水,与水接触的面积是多少平方厘米?28.学校星期一用水吨,星期二用水0.35吨,星期三用水吨.29.在一幅1:500000地图上量得甲乙两地之间的距离是7厘米,一列火车以每小时200千米的速度从甲地开往乙地,需要行驶多长时间到达乙地?30.某地4月1﹣8日的气温统计如下表.(单位:℃)日期1日2日3日4日5日6日7日8日最高气温1818161925232524最低气温1112121314141516请画出折线统计图,再回答下面的问题.(1)这几天中,哪天的温差最大?哪天的温差最小?(2)这几天的最高气温是怎样变化的?最低气温呢?31.小林骑自行车去郊游,去时平均每小时行12km,小时到达.原路返回时只用了小时,返回时平均每小时行多少千米?32.一个分数约分后是,如果约分前的分子与分母的和是66,这个分数约分前是多少?参考答案与试题解析一.选择题(共10小题)1.【分析】0不是最小的数,没有最小的数,A错误;直线上﹣3<﹣1,所以﹣3在﹣1的左边,B正确;负数比所有正数都小,C正确.【解答】解:说法中错误的是“0是最小的数”.故选:A.【点评】此题考查了正负数的大小比较方法,要熟练掌握.2.【分析】可以分三种情况考虑:(1)总长小于1米时,第一根铁丝剩下:全长×,第二根剩的:总长﹣,第一根剩的长;(2)总长等于1米时,第一根剩的长度为:1×=(米);第二根剩的是:1﹣=(米),两根一样长;(3)大于1米时,第一根剩的长度:全长×;第二根剩的;全长﹣,第二根剩的长.【解答】解:分三种情况:(1)总长小于1米时,假设全长为米,则第一根剩:×=(米),第二根剩的:﹣=(米),>,第一根剩的长;(2)总长等于1米时,第一根剩的长度为:1×=(米);第二根剩的是:1﹣=(米),两根一样长;(3)总长大于1米时,假设为3米时,第一根剩的长度为:3×=2(米);第二根剩的:3﹣=(米),2<,第二根剩的长.所以无法比较.故选:D.【点评】主要考察解决实际问题时要分情况考虑,最后综合下结论.3.【分析】把一个长方形的面积看作单位“1”,平均分成6份,每份是,表示其中的5份是,减去其中的2份,就是减去,还剩下3份,就是,据此解答.【解答】解:根据题意与分析可得:能表示出意义的算式是:﹣=故选:C.【点评】考查了分数的意义以及分数减法的意义的灵活运用.4.【分析】“小刚放学回家时往西南方向走”,说明她家在学校的西南面,所以学校在她家的东北面.【解答】解:小刚放学回家时往西南方向走,那么他上学时该往东北方向走;故选:A.【点评】本题主要考查方向的辨别,注意找准观察点.5.【分析】正方体的每个面都是相同的正方形,据此选择即可.【解答】解:图中物体形状是正方体的有A、C.B是长方体,D是正方形.故选:B.【点评】此题考查了正方体的特征,要熟练掌握.6.【分析】A和C都属于正方体展开图的1﹣4﹣1型,能够折成一个正方体;D图属于正方体展开图的2﹣2﹣2型,也能够折成一个正方体;只有B不能,因为同侧的两个正方形在折的过程中会重叠,所以不是正方体展开图.【解答】解:根据分析可得:A、D、C这三个图属于正方体展开图,能够折成一个正方体;而B图不是正方体展开图.故选:B.【点评】本题重在培养学生的空间想象能力,在解答时要掌握正方体展开图的几个基本的类型,然后据此调整即可判断.7.【分析】根据用数对表示点的位置的方法,第一个数字表示列数,第二个数字表示行数,点(6,5)在第6列,第5行,与点(6,5)挨着的点要么与列,要么行与点(6,5)挨着(相差1).【解答】解:如图与点(6,5)挨着的点是(5,5).故选:A.【点评】数对中每个数字所代表的意义,在不同的题目中会有所不同,但在无特殊说明的情况下,数对中第一个数字表示列,第二个数字表示行.8.【分析】同分母分数相加(减),分子进行相加(减)得数作分子,分母不变;异分母分数相加(减),必须先通分,然后,按照同分母分数相加(减)的法则进行运算.【解答】解:+可以直接相加,是因为两个加数同分母,即分数单位相同.故选:B.【点评】此题重点考查学生对分数加减法的计算能力,同时注意计算的灵活性.9.【分析】把这瓶果汁看作单位“1”,小兵喝了这瓶果汁的,还剩下这杯果汁的1﹣=,再根据小花喝的比小兵多一些,也就是比多一些,由于大于,所以,小花喝了这瓶果汁的,据此解答.【解答】解:1﹣=;>答:小花喝了这瓶果汁的.故选:C.【点评】本题关键是把这瓶果汁看作单位“1”,根据分数的意义,求出剩下的分率,然后再根据分数大小的比较方法的进行解答.10.【分析】通过观察折线统计图可知,纵轴每格表示10万元,2018年甲车间第一季度的产值是10万元,第二季度的产值是40万元,第三季度的产值是80万元,第四季度的产值是90万元,根据求平均数的方法,用甲车间全年的产值除以4即可.【解答】解:(10+40+80+90)÷4=220÷4=55(万元)答:甲车间2018年平均每季度的产值是55万元.故选:B.【点评】此题考查的目的是理解掌握折线统计图的特点及作用,并且能够根据统计图提供的信息,解决有关的实际问题.二.填空题(共8小题)11.【分析】(1)根据折线统计图可知,虚线代表乙,实线代表甲,乙滑完120米用了55秒,甲用了65秒,根据速度=路程÷时间即可解答;(2)先求出15秒后平均速度,再用求出的平均速度乘以甲滑完全程多用的时间;即可进行解答.【解答】解:(1)120÷(55﹣10)=120÷45=2(米);答:乙在滑完全程中,每秒钟滑行2米.(2)(120﹣40)÷(65﹣15)×(65﹣55)=80÷50×10=1.6×10=16(米);答:乙滑完全程时两人相距16米.故答案为:2,16.【点评】本题主要考查了学生根据统计图分析数量关系解答问题的能力.12.【分析】根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体容积公式:V=abh,把数据分别代入公式解答.【解答】解:(20×20+20×10+20×10)×2=(400+200+200)×2=800×2=1600(平方厘米)1600平方厘米=16平方分米20×20×10=4000(立方厘米)4000立方厘米=4升答:制作这样一款茶叶盒至少需16平方分米的材料,这款茶叶盒的容积是4升.故答案为:16、4.【点评】此题主要考查长方体的表面积公式、容积(体积)公式的灵活运用,关键是熟记公式.13.【分析】先求出6和8的公倍数(一般选用最小公倍数)就是这个两个分数的公分母,然后通分,变成同分母的分数,再根据分母不变,分子相减,求出算式的结果.【解答】解:6=2×38=2×2×26和8的最小公倍数是:2×2×2×3=24和的公分母是24;﹣=﹣=两个数相减的结果是.故答案为:24,.【点评】本题考查了异分母分数加减法的计算方法:异分母分数相加减,先通分,变成同分母的分数相加减,再计算.14.【分析】根据分数加减法的计算方法以及分数混合运算的顺序与运算定律,分别求出各个算式的结果,再比较解答.【解答】解:(1)=,=,>;所以,>;(2)=1+=1=+()=+1=11<1;所以,<;(3)1﹣=1﹣()=1﹣===<;所以,1﹣<.故答案为:>,<,<.【点评】含有算式的大小比较,先求出它们的结果,然后再按照分数大小比较的方法进行解答.15.【分析】把这根铁丝的长度看作单位“1”,把它平均分成三段,每段是全长的;求每段长,用这根铁丝的长度除以平均分成的段数.【解答】解:1÷3=2÷3=(m)答:每段是全长的,每段长m.故答案为:,.【点评】解决此题关键是弄清求的是“分率”还是“具体的数量”,求分率:平均分的是单位“1”;求具体的数量:平均分的是具体的数量,要注意:分率不能带单位名称,而具体的数量要带单位名称.16.【分析】根据数对确定位置的方法:先列后行,确定王红的数对即可;因为同桌与她同一行,只是列加1或减1,据此确定李华的位置即可.【解答】解:3﹣1=23+1=4答:王红的位置是第3列第5行;李华的位置可能是(2,5)或(4,5).故答案为:3,5;2,5;4,5.【点评】此题考查了数对的写法,即先看在第几列,这个数就是数对中的第一个数;再看在第几行,这个数就是数对中的第二个数.17.【分析】此题主要用正负数来表示具有意义相反的两种量:向从0点向东记为正,则从0点向西就记为负,直接得出结论即可,先向东再西是先加后减通过计算即可.【解答】解:根据题意可知向东为正,向西30米就表示﹣30米;先向东60米是+60,再向西40米是﹣40,所以此时的位置是+20米;故答案为:﹣30米、+20米.【点评】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负.18.【分析】根据长方体的体积(容积)公式:V=abh,那么h=V÷ab,把数据代入公式解答.【解答】解:36升=36立方分米36÷(8×2.5)=36÷20=1.8(分米)答:这个水箱深1.8分米.【点评】此题主要考查长方体的体积(容积)公式的灵活运用,关键是熟记公式,注意:体积单位与容积单位之间的换算.三.判断题(共5小题)19.【分析】异分母分数相加,必须先通分,然后按照同分母分数加法的计算法则进行计算,本题没有通分,所以错误,然后改正即可.【解答】解:原题计算错误;改正:=+=故答案为:=+=.【点评】解答本题关键是掌握异分母分数加法的计算法则.20.【分析】正数>0>负数,负数大小比较就是看负号后面的数字,数字越大的反而越小,跟正数恰好相反,据此解答即可.【解答】解:因为﹣9<﹣4<﹣1<0.1,所以在﹣4、﹣9、﹣1、0.1这四个数中,最大的数是0.1.故题干的说法是错误的.故答案为:×.【点评】此题主要考查了正、负数、0的大小比较,要熟练掌握.21.【分析】一张油饼平均分给两个人吃,求每人吃油饼几分之几,平均分的是单位“1”,求的是分率;用除法计算.但此题没有“平均”两个字,所以错误.【解答】解:1÷2=但是由于没有“平均”两个字,每人吃的或多或少,就不一定是.故原题说法错误;故答案为:×.【点评】此题关键是理解分数的意义是建立在平均分的基础上的.22.【分析】到一个固定点的距离相等的点有无数个,所以以学校为参照点,甲乙二人到学校的距离相等,他们不一定在同一地方,这样的点不确定,由此判断即可.【解答】解:以学校为参照点,到学校的距离相等的点有无数个,所以以学校为参照点,甲乙二人到学校的距离相等.他们一定在同一地方,说法错误;【点评】明确到一个固定点的距离相等的点有无数个,是解答此题的关键.23.【分析】根据体积的意义,物体所占空间的大小叫做物体的体积.将一个正方体钢坯锻造成长方体,只是形状变了,但是正方体和长方体的体积相等.据此判断.【解答】解:将一个正方体钢坯锻造成长方体,只是形状变了,但是正方体和长方体的体积相等.因此,将一个正方体钢坯锻造成长方体,正方体和长方体的体积相等.这种说法是正确的.故答案为:√.【点评】此题考查的目的是理解掌握体积的意义及应用.四.计算题(共2小题)24.【分析】(1)长方体的表面积公式:S=(ab+ah+bh)×2,体积公式:V=abh,把数据分别代入公式解答.(2)根据正方体的表面积公式:S=6a2,体积公式:V=a3,把数据分别代入公式解答.【解答】解:(1)(8×6+8×3+6×3)×2=(48+24+18)×2=90×2=180(平方厘米)8×6×3=144(立方厘米)答:这个长方体的表面积是180平方厘米,体积是144立方厘米.(2)5×5×6=150(平方厘米)5×5×5=125(立方厘米)答:这个正方体的表面积是150平方厘米,体积是125立方厘米.【点评】此题主要考查长方体、正方体的表面积公式、体积公式的灵活运用,关键是熟记公式.25.【分析】①根据加法结合律和结合律进行简算;②根据减法的性质进行简算;③根据加法交换律进行简算.【解答】解:①+++=(+)+(+)=1+1=2②﹣(+)=﹣﹣=1﹣=③++=++=1+=1【点评】考查了运算定律与简便运算,四则混合运算.注意运算顺序和运算法则,灵活运用所学的运算定律进行简便计算.五.应用题(共7小题)26.【分析】先分别计算出净重的最大值和最小值,再确定合格范围,即可得出答案.【解答】解:净重的最大值是500+5=505(g);净重的最小值是500﹣5=495(g);这种食品的净重在495g~505g之间都是合格的.【点评】本题考查了正数和负数的知识,要能读懂题意,正确理解500±5克的实际意义,分别计算最大值和最小值来确定合格范围.27.【分析】它的侧面是一个边长40厘米的正方形,它的边长既是这个长方体的高,也是底面周长;再用底面周长除以4,求出底面的边长,进而求出长方体铁桶的表面积,再除以2就是与水接触的面积.【解答】解:底面边长:40÷4=10(厘米)10×10×2+40×10×4=200+1600=1800(平方厘米)1800÷2=900(平方厘米)答:与水接触的面积是900平方厘米.【点评】此题主要考查长方体的表面积公式的灵活运用,关键是求出底面边长.28.【分析】在、0.35和三个数中,其中两个分数都能化为有限小数,所以把它们化为小数进行比较大小即可.【解答】解:,,因为0.4>0.35>0.3,所以星期三用水最多.答:星期三用水最多.【点评】本题主要考查了分数大小的比较,如果分数都能化为有限小数,通常化为小数比较大小.29.【分析】此题应先求出甲、乙两地的实际距离,根据实际距离=图上距离÷比例尺即可求出;要求火车从甲地开往乙地,需要几小时,就是用距离除以速度即可.【解答】解:甲、乙两地的距离:7÷=3500000(厘米)=35(千米)从甲地开往乙地,需要:35÷200=0.175(小时)答:从甲地开往乙地,需要0.175小时.【点评】此题考查了比例尺的实际应用,以及对“时间=路程÷速度”这一关系式的掌握情况.30.【分析】根据折线统计图的绘制方法,先根据统计表中的数据分别描出各点,然后顺次连接各点即可.(1)通过观察统计表可知,5日的温差最大,3日的温差最小.(2)这几天的最高气温,1日、2日温度相同,3日有所下降,4日到5日气温呈上升趋势,6日有所下降,7日比6日有所上升,8日有下降.最低气温呈逐渐上升趋势.【解答】解:作图如下:(1)5日的温差最大,3日的温差最小.(2)这几天的最高气温,1日、2日温度相同,3日有所下降,4日到5日气温呈上升趋势,6日有所下降,7日比6日有所上升,8日有所下降.最低气温整体看呈逐渐上升趋势.【点评】此题考查的目的是理解掌握折线统计图的绘制方法及应用,并且能够根据统计图表提供的信息,解决有关的实际问题.31.【分析】首先根据速度×时间=路程,用去时的速度乘以用的时间,求出两地之间的距离是多少;然后用它除以返回用的时间,求出返回时平均每小时行多少千米即可.【解答】解:12×÷=18÷=24(千米/时)答:返回时平均每小时行24千米.【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握,解答此题的关键是求出两地之间的距离是多少.32.【分析】根据约分后的分数是,可知分子与分母的比为5:6,分别求出分子、分母各占分子与分母和的几分之几,用乘法计算即可.【解答】解:66×=3066×=36答:这个分数约分前是.【点评】此题主要利用分数的基本性质和按比例分配解决问题.。
辽宁省沈阳市沈河区2019-2020学年第二学期七年级期末考试数学试卷 (解析版)

2019-2020学年辽宁省沈阳市沈河区七年级第二学期期末数学试卷一、选择题1.计算a2•a4的结果是()A.a6B.a7C.a8D.a122.下列四个平面图形表示的图标中,属于轴对称图形的图标是()A.B.C.D.3.如图,平行线AB,CD被直线AE所截,∠1=75°,则∠2的度数是()A.75°B.95°C.105°D.115°4.三角形的两边分别为6,10,则第三边的长可能等于()A.3B.11C.16D.175.下列事件为确定事件的是()A.6张相同的小标签分别标有数字1~6,从中任意抽取一张,抽到3号签B.抛掷1枚质地均匀的硬币反面朝上C.射击运动员射击一次,命中靶心D.长度分别是4,6,8的三条线段能围成一个三角形6.如图,在△ABC中,∠B=60°,∠A=40°,分别以点B,C为圆心,大于BC长为半径画弧,两弧相交于点M,N,作直线MN,交AB于点P,连接CP,则∠ACP的度数为()A.40°B.30°C.20°D.10°7.计算(2m+3)(m﹣1)的结果是()A.2m2﹣m﹣3B.2m2+m﹣3C.2m2﹣m+3D.m2﹣m﹣38.下列说法中正确的有()①等角的余角相等;②两直线平行,同旁内角相等;③相等的角是对顶角;④同位角相等;⑤直角三角形中两锐角互余.A.1个B.2个C.3个D.4个9.如图,有三种规格的卡片,其中边长为a的正方形卡片1张,边长为b的正方形卡片4张,长、宽分别为a,b的长方形卡片m张.若使用这些卡片刚好可以拼成一个边长为a+2b的正方形,则m的值为()A.1B.2C.3D.410.如图,在△ABC中,AB=AC,∠A=112°,E,F,D分别是AB,AC,BC上的点,且BE=CD,BD=CF,则∠EDF的度数为()A.30°B.34°C.40°D.56°二、填空题(每小题3分,共18分)11.新型冠状肺炎病毒(COVID﹣19)的粒子,其直径在120~140纳米即0.00000012米~0.00000014米之间,数据0.00000012用科学记数法可以表示为.12.如图,一个转盘被分成6等分,自由转动转盘一次,停止后,指针落在阴影区域的概率是.13.如图所示,长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,余下另个长方形的面积S(cm2)与x(cm)的关系式可表示为.14.一个角的补角等于这个角的余角的4倍,这个角是.15.如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,交AB于点E,若DE=2cm,BD=3cm,则AC=cm.16.已知:如图,∠ABC=40°,点P是射线BC上一动点,把△ABP沿AP折叠,B点的对应点为点D,当直线AD垂直于BC时,∠ABD=°.三、解答题(第17小题6分,18,19小题各8分,共22分)17.计算:(﹣1)2020﹣(﹣3)﹣(7﹣π)0+(﹣)﹣1.18.计算:(3x+2y)(3x﹣2y)﹣3x(x+2y).19.先化简,再求值:[(x+y)(x﹣2y)﹣(x﹣2y)2]÷,其中x=﹣1,y=.四、(每小题8分,共16分)20.把下面的说理过程补充完整.已知:如图,∠1+∠2=180°,∠3=∠B.试判断∠AED与∠4的关系,并说明理由.结论:∠AED=∠4.理由:∵∠1+∠BDF=180°(),∠1+∠2=180°(已知)∴∠2=∠BDF.()∴EF∥AB.()∴∠3=∠ADE.()∵∠3=∠B,(已知)∴∠B=.∴DE∥BC.()∴∠AED=∠ACB.()又∵∠ACB=∠4,()∴∠AED=∠4.21.某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:(1)该班小明同学恰好抽到丙类名额的概率是;(2)该班小丽同学能有幸去参加游学活动的概率是;(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?五、(本题10分)22.如图,点A,B,C都在网格的格点上,每小方格是边长为1个单位长度的正方形.利用格点和直尺画图并填空:(1)画出格点△ABC关于直线MN轴对称的△A′B'C′;(2)画出△ABC中BC边上的高线AD;(3)若AB=5,点P是AB上一点则CP的最小值为.六、(本题10分)23.如图,点D是△ABC边AC上一点,AD=AB,过B点作BE∥AC,且BE=CD,连接CE交BD于点O,连接AO.(1)求证:AO平分∠BAC;(2)若∠ADB=70°,求∠ABE的度数.七、(本题12分)24.爷爷和他的孙子小明星期天一起去爬山.来到山脚下,小明让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小明和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小明开始爬山时开始计时),请看图回答下列问题:(1)爷爷比小明先上了米,山顶离山脚米.(2)写出图中两条线段的交点表示的实际意义.(3)小明在爬山过程中何时与爷爷相距20米?八、(本题12分)25.已知∠ACD=60°,AC=DC,MN是过点A的直线,B、E两点在直线MN上,∠BCE =60°,CB=CE.(1)问题发现:如图1,BD和EA之间的数量关系为,BD、AB、BE之间的数量关系为;(2)拓展探究:当MN绕点A旋转到如图2位置时,BD、AB、BE之间满足怎样的数量关系?请写出你的猜想,并给予证明.(3)解决问题:当MN绕点A分别旋转到如图2和如图3位置时,若当时∠CAN=50°,连接AD,则∠ADB的大小为.参考答案一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题2分,共20分)1.计算a2•a4的结果是()A.a6B.a7C.a8D.a12【分析】根据同底数幂的乘法法则,同底数幂相乘,底数不变,指数相加,即a m•a n=a m+n计算即可.解:a2•a4=a2+4=a6,故选:A.2.下列四个平面图形表示的图标中,属于轴对称图形的图标是()A.B.C.D.【分析】根据轴对称图形的概念判断即可.解:A、不是轴对称图形;B、是轴对称图形;C、不是轴对称图形;D、不是轴对称图形;故选:B.3.如图,平行线AB,CD被直线AE所截,∠1=75°,则∠2的度数是()A.75°B.95°C.105°D.115°【分析】直接利用邻补角的定义结合平行线的性质得出答案.解:∵∠1=75°,∴∠3=105°,∵AB∥CD,∴∠2=∠3=105°.故选:C.4.三角形的两边分别为6,10,则第三边的长可能等于()A.3B.11C.16D.17【分析】设第三边的长为x,根据三角形三边关系定理:三角形两边之和大于第三边,三角形的两边差小于第三边可得10﹣4<x<10+6,再解不等式即可.解:设第三边的长为x,根据三角形的三边关系得:10﹣6<x<10+6,即4<x<16,则第三边的长可能等于:11.故选:B.5.下列事件为确定事件的是()A.6张相同的小标签分别标有数字1~6,从中任意抽取一张,抽到3号签B.抛掷1枚质地均匀的硬币反面朝上C.射击运动员射击一次,命中靶心D.长度分别是4,6,8的三条线段能围成一个三角形【分析】直接利用确定事件以及随机事件的定义分析得出答案.解:A、6张相同的小标签分别标有数字1~6,从中任意抽取一张,抽到3号签,是随机事件,不合题意;B、抛掷1枚质地均匀的硬币反面朝上,是随机事件,不合题意;C、射击运动员射击一次,命中靶心,是随机事件,不合题意;D、长度分别是4,6,8的三条线段能围成一个三角形,是确定事件,符合题意;故选:D.6.如图,在△ABC中,∠B=60°,∠A=40°,分别以点B,C为圆心,大于BC长为半径画弧,两弧相交于点M,N,作直线MN,交AB于点P,连接CP,则∠ACP的度数为()A.40°B.30°C.20°D.10°【分析】由∠B=60°,∠A=40°,可得∠ACB=80°,根据作图过程可得,PN是BC 的垂直平分线,进而可求∠ACP的度数.解:∵∠B=60°,∠A=40°,∴∠ACB=80°,根据作图过程可知:PN是BC的垂直平分线,∴PB=PC,∴∠B=∠PCB=60°,∴∠ACP=∠ACB﹣∠PCB=80°﹣60°=20°.故选:C.7.计算(2m+3)(m﹣1)的结果是()A.2m2﹣m﹣3B.2m2+m﹣3C.2m2﹣m+3D.m2﹣m﹣3【分析】原式利用多项式乘以多项式法则计算即可求出值.解:原式=2m2﹣2m+3m﹣3=2m2+m﹣3,故选:B.8.下列说法中正确的有()①等角的余角相等;②两直线平行,同旁内角相等;③相等的角是对顶角;④同位角相等;⑤直角三角形中两锐角互余.A.1个B.2个C.3个D.4个【分析】分别根据余角和补角的定义、平行线的性质及直角三角形的性质对各小题进行逐一分析即可.解:①等角的余角相等,故本小题正确;②两直线平行,同旁内角互补,故本小题错误;③不符合对顶角的定义,故本小题错误;④两直线平行,同位角相等,故本小题错误;⑤符合直角三角形的性质,故本小题正确.故选:B.9.如图,有三种规格的卡片,其中边长为a的正方形卡片1张,边长为b的正方形卡片4张,长、宽分别为a,b的长方形卡片m张.若使用这些卡片刚好可以拼成一个边长为a+2b的正方形,则m的值为()A.1B.2C.3D.4【分析】根据完全平方公式解答即可.解:∵(a+2b)2=a2+4ab+4b2,∴需要长、宽分别为a,b的长方形卡片4张.即m=4.故选:D.10.如图,在△ABC中,AB=AC,∠A=112°,E,F,D分别是AB,AC,BC上的点,且BE=CD,BD=CF,则∠EDF的度数为()A.30°B.34°C.40°D.56°【分析】由等腰三角形的性质和三角形内角和定理可求∠B=∠C=34°,由“SAS”可证△BDE≌△CFD,可得∠BED=∠CDF,∠BDE=∠CFD,由外角的性质可求解.解:∵AB=AC,∠A=112°,∴∠B=∠C=34°,在△BDE和△CFD中,,∴△BDE≌△CFD(SAS),∴∠BED=∠CDF,∠BDE=∠CFD,∴∠BED+∠BDE=∠CDF+∠CFD,∵∠BED+∠B=∠CDE=∠EDF+∠CDF,∴∠B=∠EDF=34°,故选:B.二、填空题(每小题3分,共18分)11.新型冠状肺炎病毒(COVID﹣19)的粒子,其直径在120~140纳米即0.00000012米~0.00000014米之间,数据0.00000012用科学记数法可以表示为 1.2×10﹣7.【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.解:0.00 000 012=1.2×10﹣7,故答案是:1.2×10﹣7.12.如图,一个转盘被分成6等分,自由转动转盘一次,停止后,指针落在阴影区域的概率是.【分析】用阴影部分的份数除以总份数即可得.解:由图可知自由转动转盘一次,停止后,指针落在阴影区域的概率是=,故答案为:.13.如图所示,长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,余下另个长方形的面积S(cm2)与x(cm)的关系式可表示为S =﹣6x+48.【分析】直接利用已知表示出新矩形的长,进而得出其面积.解:∵长方形的长和宽分别为8cm和6cm,剪去一个长为xcm(0<x<8)的小长方形(阴影部分)后,∴余下另一个长方形的面积S(cm2)与x(cm)的关系式可表示为:S=6(8﹣x).即S=﹣6x+48.故答案为:S=﹣6x+4814.一个角的补角等于这个角的余角的4倍,这个角是60°.【分析】设这个角为x,则这个角的补角=(180°﹣x),余角=(90°﹣x),根据题意可得出方程,解出即可.解:设这个角为x,则这个角的补角=(180°﹣x),余角=(90°﹣x),由题意得,180°﹣x=4(90°﹣x),解得:x=60°.故答案为:60°.15.如图,在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,DE垂直平分AB,交AB于点E,若DE=2cm,BD=3cm,则AC=5cm.【分析】由DE垂直平分AB,根据线段垂直平分线的性质,可得AD=BD=3cm,又由在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,根据角平分线的性质,可求得CD的长,继而求得答案.解:∵DE垂直平分AB,∴AD=BD=3cm,DE⊥AB,∵在△ABC中,∠C=90°,BD平分∠ABC交AC于点D,∴CD=DE=2cm,∴AC=AD+CD=5(cm).故答案为:5.16.已知:如图,∠ABC=40°,点P是射线BC上一动点,把△ABP沿AP折叠,B点的对应点为点D,当直线AD垂直于BC时,∠ABD=65°或15°.【分析】如图1,当点P在BC上时,根据三角形的内角和定理得到∠BAD=50°,根据折叠的性质得到AB=AD,根据等腰三角形的性质得到∠ABD=∠ADB=(180°﹣∠BAD)=(180°﹣50°)=65°;如图2,当点P在线段BC的延长线上时,延长DA交BC于E,根据折叠的性质得到PB=PD,求得∠ADC=∠ABC=40°,于是得到∠ABD=∠PBD﹣∠ABC=65°﹣40°=15°.解:如图1,当点P在BC上时,∵∠ABC=40°,AD⊥BC,∴∠BAD=50°,∵把△ABP沿AP折叠,B点的对应点为点D,∴AB=AD,∴∠ABD=∠ADB=(180°﹣∠BAD)=(180°﹣50°)=65°;如图2,当点P在线段BC的延长线上时,延长DA交BC于E,∵把△ABP沿AP折叠,B点的对应点为点D,∴∠ADC=∠ABC=40°,PB=PD,∵AD⊥BC,∴∠BPD=50°,∵PB=PD,∴∠PBC=∠PCB=(180°﹣50°)=65°,∴∠ABD=∠PBD﹣∠ABC=65°﹣40°=15°,综上所述,当直线AD垂直于BC时,∠ABD=65°或15°,故答案为:65°或15.三、解答题(第17小题6分,18,19小题各8分,共22分)17.计算:(﹣1)2020﹣(﹣3)﹣(7﹣π)0+(﹣)﹣1.【分析】首先运用负整数指数幂,零指数幂运算,再进行加减运算.解:原式=1+3﹣1﹣2,=1.18.计算:(3x+2y)(3x﹣2y)﹣3x(x+2y).【分析】首先利用平方差公式和单项式乘多项式的运算法则去括号,进而合并同类项得出即可.解:(3x+2y)(3x﹣2y)﹣3x(x+2y)=9x2﹣4y2﹣3x2﹣6xy=6x2﹣6xy﹣4y2.19.先化简,再求值:[(x+y)(x﹣2y)﹣(x﹣2y)2]÷,其中x=﹣1,y=.【分析】先算括号内的乘法,再合并同类项,算除法,最后代入求出即可.解:[(x+y)(x﹣2y)﹣(x﹣2y)2]÷=[x2﹣2xy+xy﹣2y2﹣x2+4xy﹣4y2]=[3xy﹣6y2]=6x﹣12y,当x=﹣1,y=时,原式=﹣6﹣3=﹣9.四、(每小题8分,共16分)20.把下面的说理过程补充完整.已知:如图,∠1+∠2=180°,∠3=∠B.试判断∠AED与∠4的关系,并说明理由.结论:∠AED=∠4.理由:∵∠1+∠BDF=180°(邻补角的定义),∠1+∠2=180°(已知)∴∠2=∠BDF.(同角的补角相等)∴EF∥AB.(内错角相等,两直线平行)∴∠3=∠ADE.(两直线平行,内错角相等)∵∠3=∠B,(已知)∴∠B=∠ADE.∴DE∥BC.(同位角相等,两直线平行)∴∠AED=∠ACB.(两直线平行,同位角相等)又∵∠ACB=∠4,(对顶角相等)∴∠AED=∠4.【分析】依据内错角相等,两直线平行,即可判定EF∥AB,再根据平行线的性质,即可得到∠B=∠ADE,进而得出DE∥BC,再根据平行线的性质以及对顶角的性质,即可得到∠AED=∠4.解:∵∠1+∠BDF=180°(邻补角的定义),∠1+∠2=180°(已知)∴∠2=∠BDF.(同角的补角相等)∴EF∥AB.(内错角相等,两直线平行)∴∠3=∠ADE.(两直线平行,内错角相等)∵∠3=∠B,(已知)∴∠B=∠ADE.∴DE∥BC.(同位角相等,两直线平行)∴∠AED=∠ACB.(两直线平行,同位角相等)又∵∠ACB=∠4,(对顶角相等)∴∠AED=∠4.故答案为:邻补角的定义;同角的补角相等;内错角相等,两直线平行;两直线平行,内错角相等;∠ADE;同位角相等,两直线平行;两直线平行,同位角相等;对顶角相等.21.某校某次外出游学活动分为三类,因资源有限,七年级2班分配到25个名额,其中甲类4个、乙类11个、丙类10个,已知该班有50名学生,班主任准备50个签,其中甲类、乙类、丙类按名额设置和25个空签,采取抽签的方式来确定名额分配,请解决下列问题:(1)该班小明同学恰好抽到丙类名额的概率是;(2)该班小丽同学能有幸去参加游学活动的概率是;(3)后来,该班同学强烈呼吁名额太少,要求抽到甲类的概率要达到24%,则还要争取甲类名额多少个?【分析】(1)(2)直接利用概率公式计算;(3)设还要争取甲类名额x个,利用概率公式得到=24%,然后解方程求出x即可.解:(1)该班小明同学恰好抽到丙类名额的概率==.故答案为:;(2)该班小丽同学能有幸去参加实践活动的概率==.故答案为:;(3)设还要争取甲类名额x个,根据题意得=24%,解得x=8,答:要求抽到甲类的概率要达到24%,则还要争取甲类名额8个.五、(本题10分)22.如图,点A,B,C都在网格的格点上,每小方格是边长为1个单位长度的正方形.利用格点和直尺画图并填空:(1)画出格点△ABC关于直线MN轴对称的△A′B'C′;(2)画出△ABC中BC边上的高线AD;(3)若AB=5,点P是AB上一点则CP的最小值为1.【分析】(1)利用网格特点和对称的性质画出A、B、C的对称点A′、B′、C′即可;(2)利用网格特点和三角形高的定义画图;(3)利用垂线段最短,当CP⊥AB时CP最小,然后利用面积法求出此时PC的长.解:(1)如图,△A′B'C′为所作;(2)如图,AD为所作;(3)作CP⊥AB于P,如图,此时CP的长度最小,AD==,BC==,∵•CP•AB=•BC•AD,∴CP==1.故答案为1.六、(本题10分)23.如图,点D是△ABC边AC上一点,AD=AB,过B点作BE∥AC,且BE=CD,连接CE交BD于点O,连接AO.(1)求证:AO平分∠BAC;(2)若∠ADB=70°,求∠ABE的度数.【分析】(1)根据平行线和全等三角形的判定和性质即可得到结论;(2)根据等腰三角形的性质和平行线的性质即可得到结论.解:(1)∵BE∥AC,∴∠E=∠DCO,∵BE=CD,∠BOE=∠COD,∴△BOE≌△DOC(AAS),∴BO=OD,∵AB=AD,∴AO平分∠BAC;(2)∵AB=AD,∴∠ABD=∠ADB=70°,∴∠BAD=180°﹣70°﹣70°=40°,∵BE∥AC,∴∠ABE=∠BAD=40°.七、(本题12分)24.爷爷和他的孙子小明星期天一起去爬山.来到山脚下,小明让爷爷先上山,然后追赶爷爷,如图所示,两条线段分别表示小明和爷爷离开山脚的距离(米)与爬山所用时间(分)的关系(小明开始爬山时开始计时),请看图回答下列问题:(1)爷爷比小明先上了100米,山顶离山脚450米.(2)写出图中两条线段的交点表示的实际意义小明爬山10分钟时,正好追上爷爷.(3)小明在爬山过程中何时与爷爷相距20米?【分析】(1)根据函数图象中的数据,可以得到爷爷比小明先上了多少米,再根据小明10分钟上了300米,15分钟到达山顶,可以求得山顶离山脚的距离;(2)根据题意和函数图象中的数据,可以写出图中两条线段的交点表示的实际意义;(3)根据函数图象中的数据,可以得到小明和爷爷对应的函数解析式,然后即可得到相应的方程,从而可以得到小明在爬山过程中何时与爷爷相距20米.解:(1)由图象可得,爷爷比小明先上了100米,山顶离山脚300÷10×15=450(米),故答案为:100,450;(2)由题意可得,图中两条线段的交点表示的实际意义是在小明爬山10分钟时,正好追上爷爷,故答案为:小明爬山10分钟时,正好追上爷爷;(3)设爷爷对应的函数解析式为y=kx+b,,解得,,即爷爷对应的函数解析式为y=20x+100,设小明对应的函数解析式为y=ax,10a=300,解得,a=30,即小明对应的函数解析式为y=30x,令20x+100﹣30x=20或30x﹣(20x+100)=20,解得,x=8或x=12,即小明在爬山过程中第8分钟和第12分钟时与爷爷相距20米.八、(本题12分)25.已知∠ACD=60°,AC=DC,MN是过点A的直线,B、E两点在直线MN上,∠BCE =60°,CB=CE.(1)问题发现:如图1,BD和EA之间的数量关系为BD=AE,BD、AB、BE之间的数量关系为BE=BD+AB;(2)拓展探究:当MN绕点A旋转到如图2位置时,BD、AB、BE之间满足怎样的数量关系?请写出你的猜想,并给予证明.(3)解决问题:当MN绕点A分别旋转到如图2和如图3位置时,若当时∠CAN=50°,连接AD,则∠ADB的大小为10°或110°.【分析】(1)根据已知条件得到∠ACE=∠BCD,根据全等三角形的性质得到AE=BD 于是得到结论;(2)根据角的和差得到∠ACE=∠BCD,根据全等三角形的性质得到AE=BD,根据线段的和差即可得到结论;(3)根据全等三角形的性质和等边三角形的性质即可得到结论.解:(1)BD和EA之间的数量关系为BD=AE,BD、AB、BE之间的数量关系为BE =BD+AB;理由:∵∠ACD=∠BCE=60°,∴∠ACD﹣∠ACB=∠BCE﹣∠ACB,即∠ACE=∠BCD,∵AC=DC,∠CB=CE,∴△ACE≌△DCB(SAS),∴AE=BD∴BE=AE+AB=BD+AB,故答案为:BD=AE,BE=BD+AB;(2)猜想:BE=BD﹣AB,证明:∵∠ACD=∠BCE=60°,∴∠ACD+∠ACB=∠BCE+∠ACB,即∠ACE=∠BCD,∵AC=DC,∠CB=CE,∴△ACE≌△DCB(SAS),∴AE=BD,∴BE=AE﹣AB=BD﹣AB;(3)如图2,由(2)知,△ACE≌△DCB,∴∠CAN=∠CDB=50°,∵AC=CD,∠ACD=60°,∴△ACD是等边三角形,∴∠ADC=60°,∴∠ADC﹣∠BDC=10°;如图3,∵∠ACD=∠BCE=60°,∴∠ACD﹣∠DCE=∠BCE﹣∠DCE,即∠ACE=∠BCD,∵AC=DC,∠CB=CE,∴△ACE≌△DCB(SAS),∴∠CAN=∠CDB=50°,∵AC=CD,∠ACD=60°,∴△ACD是等边三角形,∴∠ADC=60°,∴∠ADC+∠BDC=110°;综上所述,∠ADB的大小为10°或110°,故答案为:10°或110°.。
人教版2019---2020学年度五年级数学上册期末试卷及答案(含两套题)

密学校 班级 姓名 学号密 封 线 内 不 得 答 题人教版小学2019—2020学年上学期五年级数学上册期末测试卷及答案(总分:100分 时间: 90分钟)一、口算。
(8分)0.6+0.54= 2.4×0.5= 10÷ 2.5=0.5×0.78×2=0.8÷0.08= 1.23÷3= 0.15×2= 4×(1.5+0.25)=二、认真读题,准确填空。
(每空1分,共11分) 1.超市购物。
(1)大米每千克5.88元,爸爸买了5kg ,估计花的钱不会超过( )元。
(2)妈妈买回1.8kg 鸡蛋,每千克鸡蛋大约有15个。
妈妈准备把这些鸡蛋放在冰箱的储蛋托中,如果每个储蛋托能放10个鸡蛋,至少需要( )个储蛋托。
2.在3.2424、3.24·、3.2424…、3.24中,最小的数是( ),最大的数是( )。
3.指针停在( )色区域的可能性最大,指针停在( )色区域的可能性最小。
4.如下面左图所示,平行四边形的面积是60cm²,那么阴影部分的面积是( )cm ²。
5.上面右图的空白部分是正方形,阴影部分的面积可以表示为( )6.买鞋的学问:如果鞋子是a 码,也就是b 厘米,它们有这样的关系:a =2b -10。
小华要穿36码的鞋子,也就是要穿( )厘米的鞋子。
7.如右图,一块形状是梯形的草坪,它的周长是28m ,两腰的长分别是6m 和7m ,这块草坪的面积是( )m ²。
8.学校召开运动会,同学们在一条直跑道一旁每隔4m 插一面小旗(起点、终点都插):共插了21面。
这条直跑道有( )m 。
三、反复比较,合理选择。
(把正确答案的序号填在括号里)(12分)1.计算8.7+3.5,商2,余数是()。
A.17B.1.7C.0.172.爸爸今年x岁,小红今年(x-26)岁,7年后,爸爸和小红相差()岁。
人教版二年级2019-2020学年度第二学期期期末数学试题及答案

密 线学校 班级 姓名 学号密 封 线 内 不 得 答 题人教版2019-2020学年度第二学期期末检测试卷二年级 数学(满分:100分 时间:60分钟)题号一 二 三 四 五 六 总分 得分一、填一填。
(第1题4分,第2、8题3分,其余每空1分,共30分)1.24个苹果平均分给5个小朋友,每人分( )个,还剩( )个。
=(个)……(个)2.填口诀,写算式。
六八三十五 3.一个数,除以7有余数,余数最大是( )。
4.看图写数、读数。
(算盘最右边的一档作为个位)写作:( ) 写作:( ) 写作:( ) 读作:( ) 读作:( ) 读作:( )5.希望小学一年级有196人,二年级有205人,两个年级大约有( )人。
6.10个一千是( );3个千、5个十合起来是( ),这个数的近似数是( )。
7.写出3个不同的除法算式。
÷=8÷=8÷=88.联系生活实际,在括号里填上合适的质量单位。
一箱牛奶重6( ),一条鱼重2000( ),一包瓜子重450( ),一盒牙膏重240( )。
9.在右面的方格中,每行、每列都有1~4这4个数,并且每个数在每行、每列都只出现一次。
A 应该是( ),B 应该是( )。
10.用、、、四张卡片摆出的四位数中,最小的数是( ),最接近9000的数是( ),最接近7000的数是( )。
二、选择。
(把正确答案的序号填在括号里)(每题2分,共10分)1.27里面最多有( )个5。
①2 ②5密 线学校 班级 姓名 学号密 封 线 内 不 得 答 题③62.一个四位数,中间有一个零或两个零时,( )。
①只读一个零 ②读两个零③一个零也不读 3.531<5129,里应填( )①0 ②1 ③24.丁丁、丽丽和园园三个小朋友分别出生在上海、北京和山东。
丁丁说:我从未到过上海。
丽丽说:在上海出生的不是我,我也不是出生在山东。
园园说:我不告诉你。
园园出生在( )。
辽宁省沈阳市和平区2019-2020学年四年级下学期数学期末试卷及参考答案

辽宁省沈阳市和平区2019-2020学年四年级下学期数学期末试卷一、填一填(共18分。
)1. 9302是由9个________,3个________和2个________组成的。
2. 把0.8扩大到原来的100倍是________,32.4缩小到原来的是________。
3. 8.5×43的积有________位小数,4.17×0.25的积有________位小数。
4. 一个三角形的两个内角分别为23°和40°,这是一个________三角形。
5. 9.52千克=________克 12时=________分8吨300千克=________吨 6角7分=________元6. 要反映蒜苗生长情况,应选择________统计图。
7. 在横线上填上“>”“<”或“=”。
3.33________33.3 0.2时________ 15分 2.3÷10________0.235.1×0.8________5.1 7.090________7.09 1.8+0.9________1.8×0.98. 三角形具有________,三角形任意两边之和________。
9. 淘气有200元钱,买书包用去a元,买钢笔用去b元,还剩下________元。
10. 东的身高是146厘米,明明和红红的身高都是140厘米,他们的平均身高是________二、辨一辨(共5分。
)11. 长方形是特殊的正方形,也是特殊的平行四边形。
()12. 任意三角形都可以密铺。
()13. 两个不为0的数相乘,积大于这两个数。
()14. 5.60的计数单位是0.1。
()15. 妈妈和爸爸今年相差3岁,再过n年,他们相差3n岁。
()三、选一选(5分。
)16. 在0.1和0.9之间的小数有()个。
A . 7B . 8C . 9D . 无数17. 下面各题中方程有()个。
2019-2020学年辽宁省沈阳市和平区七年级(下)期末数学试卷
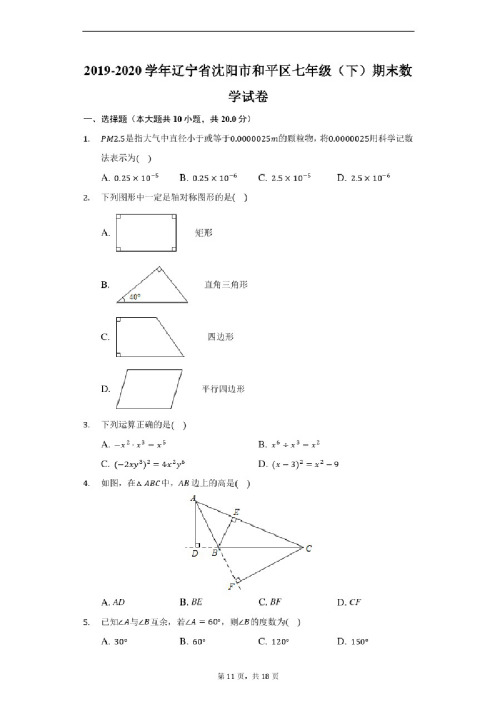
2019-2020学年辽宁省沈阳市和平区七年级(下)期末数学试卷一、选择题(本大题共10小题,共20.0分)1.PM2.5是指大气中直径小于或等于0.0000025m 的颗粒物,将0.0000025用科学记数法表示为()2.3. A. 0.25 X I 。
-' B. 0.25 X IO* C. 2.5 X 10~5 D. 2.5 X 10一6卜列图形中一定是轴对称图形的是()A.D.矩形四边形平行四边形直角三角形下列运算正确的是()A. -x 2 x 3=x 5B.4. C. (一2秒3)2 = 4x 2y 6D./一9如图,任△砧C 中,A8边上的高是()A. AD — 3)2 D. CF 5.已知"与曷互余,若乙4 =60。
,则曷的度数为()A. 30°B. 60°C. 120°D. 150°6. “任意掷一枚质地均匀的骰子,掷出的点数是偶数”这个事件是()7.A .必然事件B.不可能事件C.随机事件如图,{£Rt^ABC^9 己知ZC = 90% 边AC =8cm 98C = 10cm,点P 为边上一动点,点P 从点C 向点8运动,当点户运动到8C 中点时,AAPC 的面积是()/D.确定事件D.40A.5B. 10C. 208.在4ABC 中,匕4 =:匕B =则4 ABC 是()三角形.9. A.锐角 B.直角 C.钝角如图,以乙4。
8的顶点。
为圆心,任意长为半径画弧交OA. OB 于点G D,再分别以点为圆心,大于!CD 的长为半径画弧,两弧在COB 内部交于点P.作射线D・等腰直角A0P,则下列说法错误的是()A. △ OCP^h ODPB. 0C = DPC. l OCP = £ODPD.匕。
PC =药PD 10.研究表明,当每公顷钾肥和磷肥的施用量一定时,氮肥施用虽与上豆的产量有如表所示的关系:置肥施用量/千克03467101135202259336404471土豆产量/吨15.1821.3625.7232.2934.0539.4543.1543.4640.8330.75下列说法错误的是()A.氮肥施用量是自变量,上豆产量是因变量B.当氮肥的施用量是101千克/公顷时,上豆的产最是32.29吨/公顷C.如果不施氮肥,土豆的产量是15.18吨/公顷D.氮肥施用量404千克/公顷比氮肥施用量:336千克/公顷时的土豆的产虽更高二、填空题(本大题共6小题,共1S.0分)11.如图所示的五角星是轴对称图形,它的对称轴共有条.12.在等腰三角形A8C 中,它的两边长分别为7cm 和3cm,则它的周长为 cm.13.如图,AB//CD. EF 分别与AB. CD 交于点F,连接 AE,若£E= 30% 3 = 30% 则匕EFC =14.在一个不透明的袋中,装有一些除颜色外完全相同的红.白.绿三种颜色的球,若袋中有红球2个,白球11个,其余都是绿球.从袋中任意摸出一个球是红球的概15.率为土则袋中的绿球有.个・若。
人教版2019-2020学年五年级数学第二学期第三单元检测卷(含答案)

15.60m3沙均匀铺在长10米,宽3米的长方体沙坑内,可以铺________分米厚.
16.要拼成一个大的正方体,下边的图形至少还需要________个小正方体。
答:这个长方体的表面积是2200平方毫米。
七、应用题
27.解:40×40×6=9600(cm2)
40×40×40=64000(cm3) 64000cm3=64dm3
28.(1)解:(30×20+30×15+20×15)×2=2700(cm2)
(2)解:30÷5=6 20÷2=10 15÷3=5 6×10×5=300(块)
(1)礼盒用彩纸包装,需要多少彩纸?(重叠部分不计算)
(2)这个礼盒最多能装多少块花生酥?
29.用240厘米唱的铁丝做一个最大的正方体框架,然后用纸板将6个面包起来做一个正方体纸盒,至少需要多少平方厘米纸板?这个纸盒的体积是多少立方厘米?
30.一个正方体的棱长之和是48厘米,么它的表面积是多少平方厘米?
三、填空题(共11题;共18分)
11.5升750毫升=________毫升6000毫升=________升
12.一个长方体,如果高增加2厘米就变成一个正方体。这时表面积就比原来增加56平方厘米。原来长方体的体积是________立方厘米。
13.把一个棱长5分米的正方体的每条棱都平均分成5份,切成棱长1分米的小正方体,可以切成________个小正方体,如果排成1排长________米。
A. 20升B. 360升C. 3600升
4.把长7厘米,宽5厘米,厚3厘米的长方体肥皂两块包装在一起,用()平方厘米包装纸最节省。
2020-2021学年人教版五年级下学期期末考试数学试卷含答案

2020-2021学年五年级下学期期末数学试卷一、选择题.(请选择正确答案的序号填在括号里)(每小题2分,共10分)请将答案写在答题卡上1.(2分)下面图形中哪个不是正方体的展开图?( )A .B .C .2.(2分)将一个长9cm ,宽5cm ,高4cm 的长方体截成一个体积最大的正方体,这个正方体的体积是( )cm 3. A .25B .64C .803.(2分)如图中的x 表示( )人.A .15B .16C .174.(2分)a +15=b +0.41,那么a ( )b . A .>B .<C .=5.(2分)北偏西40°,还可以说成( ) A .南偏西40°B .西偏北50°C .西偏北40°二、填空题.(每空1分,共20分)请将答案写在答题卡上 6.(2分)在横线里填上适当的体积单位或容积单位. 一个饭盒的体积约是3 . 一个矿泉水瓶的容积约是500 . 7.(2分)把下列小数化成分数,分数化成小数. 0.7= .320= .8.(2分)同学们在美术课上折纸,淘气和笑笑共用一张纸,淘气用了这张纸的13,笑笑用了这张纸的14,他们一共用去这张纸的 ,淘气比笑笑多用去这张纸的 .9.(2分)在横线里填上“>”、“<”或“=”.411×974111119×19118×1810.(2分)一箱水果的质量是18千克,59箱水果的质量是 千克. 淘气周五晚上做家庭作业用的时间是1112时,也就是 分.11.(2分)111的倒数是 ,0.02的倒数是 .12.(2分)1.3m 3= cm 3 4600mL = L13.(2分)一个正方体的棱长总和是36cm ,它的表面积是 cm 2,体积是 cm 3. 14.(2分)某品牌汽车油箱的长是50cm ,宽是40cm ,高是30cm ,这个油箱能装 升汽油.如果每升汽油可行驶12km ,这箱油最多可供这辆汽车行驶 千米. 15.(2分)把一瓶水的13平均分给4个小朋友,每个小朋友可以得到这瓶水的 .9张同样大的圆饼,每35张一份,可以分成 份.三、计算题.(共30分)请将答案写在答题卡上 16.(6分)直接写出得数. (1)58+34= (2)1112−56= (3)745×514=(4)98÷15= (5)36×1124= (6)34÷18=17.(16分)脱式计算. (1)56−12+13(2)49−18+59(3)1−25+47(4)910−(16+23)18.(8分)解方程. (1)4.7x +3.3x =6.4 (2)x ÷14=37四、动手操作.(共10分)请将答案写在答题卡上 19.(5分)确定位置.小健要从家去神仙岛,他应该先向 走 米到达超市,再向 偏 的方向走 米到达图书馆,最后向 偏 的方向走 米到达神仙岛.20.(5分)涂一涂,算一算. 3个310相加的和是多少?五、解决问题.(每题5分,共30分)请将答案写在答题卡上21.(5分)学校图书馆去年上半年借出图书3200册,是下半年借出的89,下半年借出多少册?22.(5分)一个篮球的原价是50元,打九折后的价格是多少?23.(5分)一个长方体容器,从里面量底面长12cm ,宽15cm ,高30cm ,放入一个梨子后水面升高了1.5cm ,这个梨子的体积是多少?24.(5分)甲地到乙地的铁路线长920km .一列火车从甲地出发,每时行120km ,另一列火车从乙地开出,每时行110km .两列火车同时出发,经过几时相遇?(列方程解答) 25.(5分)学校举行广播操比赛,七位评委给五(1)班的打分如下(满分100分),去掉一个最低分和一个最高分,请算出五(1)班的最后得分是多少?6080779098708826.(5分)下面是红星超市2019年4月至9月收支情况统计表.月份 4月 5月 6月 7月 8月 9月 收入(万元) 20 25 15 16 18 22 支出(万元)1011591012(1)根据表中的数据信息,绘制复式折线统计表.(2)月份的支出最大.月份的收入和支出相差最大.(3)从图中信息可知,这个超市是盈利还是亏损?2020-2021学年五年级下学期期末数学试卷参考答案与试题解析一、选择题.(请选择正确答案的序号填在括号里)(每小题2分,共10分)请将答案写在答题卡上1.(2分)下面图形中哪个不是正方体的展开图?()A.B.C.解:、是正方体展开图;不是正方体展开图。
