16级大学物理A2复习题WORD

合集下载

《大学物理》复习题及答案

《大学物理》复习题及答案《大学物理》复习题及答案一：填空题1: 水平转台可绕通过中心的竖直轴匀速转动.角速度为?,台上放一质量为m的物体，它与平台之间的摩擦系数为?，m在距轴Ｒ处不滑动，则?满足的条件是??; 2: 质量为m的物体沿x轴正方向运动，在坐标x处的速度大小为kx，则此时物体所受力的大小为F?。

3: 质点在xoy平面内运动，任意时刻的位置矢量为r?3sin?ti?4cos?tj，其中?是正常数。

速度v?，速率v?，运动轨迹方程;物体从x?x1运动到x?x2所需的时间为4: 在合外力F?3?4x(式中F以牛顿，x以米计)的作用下，质量为6kg的物体沿x 轴运动。

如果t?0时物体的状态为，速度为x0?0,v0?0,那么物体运动了3米时，其加速度为。

2５：一质点沿半径为米的圆周运动，其转动方程为??2?t。

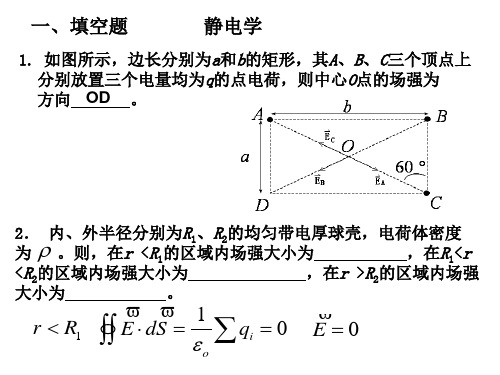
质点在第1s 末的速度为，切向加速度为6: 一质量为m?2kg的质点在力F?4ti?(2?3t)j(N)作用下以速度v0?1j(m?s?1)运动，若此力作用在质点上的时间为2s，则此力在这2s内的冲量I?在第2s末的动量P? ;质点7：一小艇原以速度v0行驶，在某时刻关闭发动机，其加速度大小与速率v成正比，但方向相反，即a??kv,k为正常数，则小艇从关闭发动机到静止这段时间内，它所经过的路程?s?，在这段时间内其速率v与时间t的关系为v? 8：两个半径分别为R1和R2的导体球，带电量都为Q,相距很远，今用一细长导线将它们相连，则两球上的带电量Q1?则球心O处的电势UO?,Q2?9:有一内外半径分别为R及2R金属球壳，在距离球心O为R处放一电量为q的点电荷，2.在离球心O为3R处的电场强度大小为E?,电势U? 2210: 空间某一区域的电势分布为U?Ax?By，其中A,B为常数，则场强分布为Ex?为，Ey? ；电势11: 两点电荷等量同号相距为a，电量为q，两电荷连线中点o处场强为；将电量为?q0的点电荷连线中点移到无穷远处电场力做功为12: 在空间有三根同样的长直导线，相互间距相等，各通以同强度同方向的电流，设除了磁相互作用外，其他影响可忽略，则三根导线将13: 一半径为R的圆中通有电流I，则圆心处的磁感应强度为第1页。

大学物理A机械振动复习题、答案与解法

参考答案：
A 中小球没有受到回复力的作用；
B 中由于是大角度，所以与 sin 不能近似相等，不能看做简谐振动；
D 中球形木块所受力 F 与位移 x 不成线性关系，故不是简谐振动。
2.如图 1 所示，以向右为正方向，用向左的力压缩一弹簧，然后松手任
k
m
其振动，若从松手时开始计时，则该弹簧振子的初相位为（D）
)
（SI），则它
们的合振动的振动方程应为（D）
(A) x 4cos5t SI
(B) x 8cos5t SI
(C) x 4 cos10t SI
2
(D) x 4 cos5t SI
2
参考答案：由于位相差为，合成后位相与 x1 同相， A A1 A2 6 2 4(m) 。
(B) 6 T 3
(C) 2T
(D) 6T
参考答案：T 2 m T 2 2m 6 T
k
3k 3
4.两相同的轻弹簧各系一物体（质量分别为 m1 、 m2 ）作简谐振动（振幅分别为 A1 、 A2 ），问下列哪一种情况两振动周期不同（B）（A） m1 m2、A1 A2,一个在光滑水平面上振动，另一个在竖直方向上振动（B） m1 2m2、A1 2A2,两个都在光滑的平面上作水平振动（C） m1 m2、A1 2A2,两个都在光滑的平面上作水平振动（D） m1 m2、A1 A2,一个在地球上作竖直振动，另一个在月球上作竖直振动
(B) 3 m s1 (D) 3 m s1
O 12
ts
参考答案： x 6 cos( t ) v 3 sin( t )
6
22
22
v(2) 3 sin(3 ) 3 (m s1) 2
10.一质量为 m 的物体与一个劲度系数为 k 的轻弹簧组成弹簧振子，当其振幅为 A 时，该弹簧

大学物理A2的重要习题

1．如计算题7-1图所示，一根铜棒长为L=0.05m ，水平放置于一竖直向上的匀强磁场中，绕位于距a 端L/5处的竖直轴OO /在水平面内旋转，每秒钟转两圈。

已知该磁场的磁感应强度B=0.50×10-4T 。

求铜棒两端a 、b 的电位差。

计算题7-1图 1. 解:建立坐标系如图所示在ab 上任取线元dx,如图。

当铜棒旋转时产生的动生电动势xdx B i dx B v d ωε=⋅⨯=)(动整根铜棒产生的动生电动势⎰--⨯===545(1071.410382L L L B xdx B 伏）动ωωε 2．如计算题7-2图所示，无限长直导线，通以电流I ，有一与之共面的直角三角形线圈ABC ，已知AC 边长为b ，与长直导线平行，BC 边长为a 若线圈以垂直于导线方向的速度向右平移，当B 点与长直导线的距离为d 时，求线圈ABC 内的感应电动势的大小和感应电动势的方向。

计算题7-2图解：建立坐标系，长直导线为Y 轴，BC 边为X 轴，原点长直导线上，则斜边的方程为abr a bx y -= 式中r 是t 时刻B 点与长直导线的距离，三角形中的磁通量⎰⎰+++-=-==r a r r a rrr a a br b I dx ax br a b I dxxyI )ln (2)(22000πμπμπμφ td r d r a a r r a a b I dt d )(ln 20+-+=-=πμφε 当r = d 时，vr a a r r a a b I )(ln 20+-+=πμε 方向：ACBA （顺时针）3．两根平行无限长直导线相距为d ，载有大小相等方向相反的电流I ，电流变化率dI/dt=α>0。

一个边长为d 的正方形线圈位于导线平面内与一根导线相距d ，如计算题7-3图所示。

求线圈中的感应电动势ε，并说明线圈中的感应电动势是顺时针还是逆时针方向。

计算题7-3图解：（1）载流为I 的无限长直导线在与其相距为r 处产生的磁感应强度为： r I B πμ20=以顺时针绕向为线圈的正方向，与线圈相距较远的导线在线圈中产生的磁通量为： 23ln22034241πμπμφId r d rI d =⋅=⎰与线圈相距较近的导线在线圈中产生的磁通量为： 2ln 2202442πμπμφIdr d rI d -=⋅-=⎰ 总磁通量34ln2021πμφφφId -=+=感应电动势为：34ln234ln 200παμπμφεd t d I d d dt d ==-=由ε>0和回路正方向为顺时针，所以ε的绕向为顺时针方向，线圈中的感应电动势亦为顺时针方向。

大学物理A2复习题2011

VP =
2q 4πε 0 r
=
2q 4πε 0 x 2 + a 2 2qQ
点电荷Q 点电荷Q在电场力的作用下移至无穷远时电场力所作的功为
A = QVP =
4πε 0 x + a
2
2
电场力所作的功转化为电荷获得的动能. 电场力所作的功转化为电荷获得的动能
20.一质量为的粒子， 20.一质量为m，电荷为q的粒子，从电势为VA的A点，在电场力作用下运动到电势为VB的B点。若粒子到达B点时的速率为vB， ______________。则它在A点时的速率vA＝______________。粒子从点移动到B点时，粒子从A点移动到B点时，电场力所做的功等于粒子的动能的增量，即
A
EI
E II
B
E III
− σ1
σ2
的正六边形每个顶点处有一个点电荷q 5. 边长为a的正六边形每个顶点处有一个点电荷q，取无限远处作为电势参考点，作为电势参考点，则六边形的中心o点电势为，o点的场强大小为。
V = 6V1 = 6
q 4πε 0 a
=
3q 2πε 0 a
由于对称性，点的场强大小为0 由于对称性，中心o点的场强大小为0。的均匀带电的薄圆盘， 6. 一个半径为R 的均匀带电的薄圆盘，电荷面密度为 σ 。在的同心圆盘，圆盘上挖去一个半径为r 的同心圆盘，则圆心处的电势。（变大或变小变大或变小）将变小。（变大或变小）的球面均匀带电， 7. 真空中一个半径为R 的球面均匀带电，面电荷密度为σ > 0，在球心处有一个带电量为q的点电荷。取无限远处作为电势参考的点电荷。点，则球内距球心r 的P 点处的电势为。不放q时均匀带电球面内是一个等势体，不放时，均匀带电球面内是一个等势体，电势与球面的电势相等：相等： q σ 4πR 2 σR

大学物理A2例题

P真空中恒定电流的磁场[例1]（如图）一长为L ，电流强度为I 的直导线AB ，求直导线外任意一点P 的磁感强度B。

P 点到直导线的距离为a ，直导线L 两端到P 点的径矢与电流正向的夹角分别为1α、2α。

[例2]（如图）半径为R 圆环电流，圆心为O ，电流强度为I ，P 为其轴线上一点，x OP =，求P 点的磁感强度。

[例3] 一根无限长导线弯成如图形状，设各线段都在同一平面内（纸面内）。

其中第二段是半径为R 的四分之一圆弧，其余为直线，导线中通有电流I ，求图中O 点处的磁感应强度。

[例4]一半径为R 的木球以细导线单层密绕，线圈彼此平行且复盖半个木球面，设总匝数为N ，通以电流I ，求球心的磁感强度B。

[例5] 有一半径cm R 0.1=无限长半圆筒形金属薄片中，沿长度方向有电流A I 0.5=通过，且横截面上电流分布均匀。

试求圆柱轴线上任一点的磁感应强度。

[例6] 有一无限长通电流的扁平铜片，宽度为a ，厚度不计，电流I 在铜片上均匀分布，在铜片外与铜片共面，离铜片右边缘为b 处的P 点（如下图）的磁感应强度B的大小为：（A ）)(20b a I+πμ。

（B ）bb a aI+ln20πμ。

（C ）bb a bI+ln20πμ。

（D ）)21(20b a I +πμ。

[例7]在图（a ）和（b ）中各有一半径相同的圆形回路1L 、2L ，圆周内有O 'Ora RI )(b )(a 3I21电流1I 、2I ，其分布相同，且均在真空中，但在（b ）图中2L 回路外有电流3I ，1P 、2P 为两圆形回路上的对应点，则； (A)，2121,P P L L B B l d B l d B =∙=∙⎰⎰(B) 2121,P P L L B B l d B l d B =∙≠∙⎰⎰(C ) 2121,P P L L B B l d B l d B ≠∙=∙⎰⎰(D) 2121,P P L L B B l d B l d B ≠∙≠∙⎰⎰[例8] 在半径为R 的长直金属圆柱体内部挖去一个半径为r 的长直圆柱体，两柱体轴线平行，其间距为a 。

光学习题课(大学物理A2)

（三）光的偏振性马吕斯定律
1.自然光和偏振光包含了各个方向的光振动，没有哪一个方向的光振动会占优势，这样的光叫自然光。自然光经过某些物质的反射、折射或吸收后，可能保留某一方向的光振动，称为线偏振光或者完全偏振光。若一个方向光振动较与之相垂直方向上的光振动占优势，则称为部分偏振光。
2.马吕斯定律光强为 I 0 的线偏振光，当其偏振方向与检偏器偏振化方向的夹角为时，则透射过检偏器后的透 I I 0 cos2 射光强为该式称为马吕斯定律
8.折射率为1.60的两块标准平面玻璃板之间形成一个劈形膜（劈尖角很小）。用波长 600 nm 的单色光垂直入射，产生等候干涉条纹。加入在劈形膜内充满 n 1.40 液体时的相邻明纹间距比劈形膜内是空报时的间距缩小 l 0.5mm ，那么劈尖角应是多少？
【分析】利用劈尖干涉中相邻条纹的间距l 2n和题给出条件可求出解劈形膜内为空气时劈形膜内为液体时则由得
光学习题课
干涉、衍射、偏振、双折射
一、内容小结
（一）光的干涉
1.相干光（1）相干条件：同频率、同振动方向、相位差恒定；（2）获得相干光方法：分波阵面、分振幅 2.光程与光程差光程：=nr ；光程差：=n2r2-n1r1 3.半波损失光从光疏介质向光密介质入射，反射光有的相位突变，相当光程增加或减少/2，称半波损失。
4.杨氏双缝干涉劳埃德镜光程差：r =r2-r1dsin dsin=k, k=0,1,2…… 明条纹 dsin=(2k+1)/2, 暗条纹条纹特点：均匀明暗相间，白光照射为彩色条纹，但中央条纹仍为白色。
r1
几何关系：D d
d

D
x r2

大学物理(64学时)期末复习及答案.docx

2016大学物理(64学时)期末复习复习一、刚体部分一、选择题1. ()两个匀质圆盘A 、B 的密度分别为和且Q A >Q B ，质量和厚度相同•两圆盘的旋转轴均通过盘心并垂直于盘面，则它们的转动惯量的关系是： A 、J A <J B B 、J A =J B C 、J A >J B D 、不能判断2. () 一力矩肱作用于飞轮上，飞轮的角加速度为河，如撤去这一力矩，飞轮的角加速3. () A 与8是两个质量相同的小球，A 球用一根不能伸长的绳子拴着，8球用橡皮筋拴着，把它们拉到水平位置，放手后两小球到达竖直位置时，绳子与橡皮筋长度相等，则6. 银河系有一可视为球体的天体，由于引力凝聚，体积不断收缩。

设它经过一万年体积收缩了 1%,而质量保持不变.则它的自转周期将： A 、增大 B 、不变 C 、减小 D 、不能判断7. () 一子弹水平射入一木棒后一同上摆.在上摆的过程中，以子弹和木棒为系统，则总角动量、总动量及总机械能是否守恒？结论是： A 、三量均不守恒 B 、三量均守恒C 、只有总机械能守恒D 、只有总动量不守恒度为— 02,则该飞轮的转动惯量为: M A 、 A nMB 、—AC 、M A - Pi此时两球的线速度 A 、匕〉％ B 、匕 <%c 、V A =V B D 、无法判断4. ()用一条皮带将两个轮子A 和8连接起来，轮与皮带间无相对滑动，8轮的半径是A 轮半径的3倍.如果两轮具有相同的角动量，则A 与B 两轮转动惯量的比值为： A 、 1:3 B 、 1:9 C 、 3:1 D 、 9:15. ()某滑冰者转动的角速度原为口°，转动惯量为人，当他收拢双臂后，转动惯量减少了 1/4.这时他转动的角速度为：8.()长为乙的均匀细杆。

肱绕水平。

轴在竖直面内自由转动，今使细杆从水平位置开始自由下摆，在细杆摆动到铅直位置的过程中，其角速度②，角加速度〃如何变化？A、勿增大，月减小B、©减小，0减小C、勿增大,0增大D、刃减小，0增大9 ()人造地球卫星绕地球作椭圆运动，地球在椭圆的一个焦点上，卫星的动量P,角动量乙及卫星与地球所组成的系统的机械能E是否守恒？A、P不守恒，乙不守恒，£不守恒B、P守恒，乙不守恒，E不守恒C、P不守恒，乙守恒，&守恒D、P守恒，乙守恒，&守恒E、P不守恒，Z守恒，&不守恒10.()如图2所示，A和8为两个相同绕着轻绳的定滑轮，A滑轮挂一质量为肱的物体，8滑轮受拉力尸，A Q H而且F = Mg,设A、B两滑轮的角加速度分别为尸A和尸B，不计滑轮轴的摩擦，则有A、P A =P BB、P A > P BC、/3A<D、开始E A=伉,以后M < 0B二、解答题1.一个可视为质点的小球和两根长均为/的细棒刚性连接成如图3所示的形状，假定小球和细棒的质量均为计算该装置绕“过。

大学物理A2 作业答案

10 静电场（1）习题解10-1 （A ）由即得 ,0dq dF ,r4)q Q (q F 20=-=πε 10-2 （C ）10-3 （C ） 0x4Q214Q ,0i r 4Q 2i 14Q E 20202020=-=-=πεπεπεπε即可得. 10-4 （A ）2220(1)2Qq k k Q ⋅⋅=⇒=- 10-5 （A ） 10-6 0 ，214S a λπε∆⋅⋅；由圆心指向S ∆方向 10-7011()4a L aλπε-+ 10-8 解：2204()dxdq dx dE a x λλπε=⇒=+1222220cos 4()()x dxxdE dE a x a x λθπε=-=⋅++ 1222220sin 4()()y dxadE dE a x a x λθπε=-=⋅++积分后得到：04x E a λπε=-；04y E a λπε=；0()4E i j aλπε=-+ 10-9 解：取宽为dx 的细长条dx λσ=该细长条在P 处产生的电场强度为002()2()dxdE a b x a b x λσππεππε==+-+- ，则P 处的电场强度为：000ln 2()2b dx a bE dE a b x aσσπεπε+===+-⎰⎰ 指向+X 方向10-10 解：θθλλd sin R dl dq 0==， 200R4d sin R dE πεθθλ=，三11 静电场（2）习题解11-1 （A ）通过半球面的电通量与以R 为半径的圆平面的电通量等. 11-2 （C ）穿进高斯面的电通量与穿出高斯面的电通量相等。

11-3 （D ）把点电荷用空间立体面包围,则电通量为q/ε0,所给平面面积为空间立体面面积的1/6, ∴电通量也为过空间立体面的1/6.11-4 （D ）作一半径为r 的高斯面(球面),包围电荷为Q a , 即可得. 11-5 q/24ε0 ;若要把A 点全部包围,需要如图的8个立方体,封闭曲面表面积为24个abcd 面.11-6 Q ΔS/16π2ε0R 4; 由球心指向ΔS. 用补偿法: 球面看成完整带正电的, 球心场强为0;ΔS 带负电,所带电量q=σΔS=Q ΔS/(4πR 2), 场强由球心指向ΔS ，即可得叠加结果.11-7 4.43×10-13（C ·m -3）.⎰⎰⎰=-=-==ππθθπελθθθπελ02000200x x 0)2(d 2sin 41R 4Rd sin cos R 4RdE E R8 d sin R 4RdE E 0002200y y ελθθπελπ-=-==⎰⎰jR8j E i E E 00y xελ-=+=∴0dE E Ry Ry ==⎰θπεθθλθsin R 4d sin R sin dE dE 200y -=-=θπεθθλθcos R4d sin R cos dE dE 200x -=-=由高斯定理 012SSh S E S E S d E ε∆ρ∆∆=-=⋅⎰h)E E (120-=ερ11-8 解：分别在r a <，a r b <<，b r <建立高斯面r a <时，110Q E d S ε⋅=⎰ ；1100Q E =⇒=a rb <<时，22222004Q Q E d S E r πεε⋅=⇒⋅=⎰；3324()3Q r a ρπ=⋅-33332204()()343r a r a E r rρπρπεε⋅--== b r <时，23333004Q Q E d S E r πεε⋅=⇒⋅=⎰，3334()3Q b a ρπ=⋅-33333204()()343b a b a E r rρπρπεε⋅--== 11-9解：空腔内可看成电荷体密度大小相等的带异号电荷的球体叠加而成. 整个大球带正电, 作高斯面过P 点,场强32Sr 34r 4'E S d 'E επρπ==⋅⎰, 00233434'ερεππρrr r E ==,OP33r 'E 00ερερ==小球带负电, 同样作过P 点高斯面,场强32'34'4''''επρπr r E S d E S-==⋅⎰,P O r E '33'''00ερερ-=-=b P O OP E E E03)'(3'''ερερ=-=+=11-10 解：因为电荷分布以纵轴对称，电场线只能沿x 轴，作柱形高斯面，在平板内（小柱面）:0SS x 2Q ES 2S d E ερε===⋅⎰ ,2dx 2d -, x E 0<<=ερ ; 在平板外（大柱面）: , dS Q ES 2S d E0Sρε===⋅⎰ 2dx 2d , d 2E 0-≤≤=ερ 12 静电场（3）习题解12-1 （D ） a 8q )a 21a 1(4q r d e r 4qV l d E V 00a a 2r20p pM M πεπεπε-=--=⋅=+⋅=⎰⎰ 12-2 （E ）12-3 （C ）均匀电场场强处处相等；电势梯度常矢量=∂∂-=n e nV E(相等).12-4 （D ） 20202422R q r d e r q l d E V R rpMπεπε⎰⎰∞=⋅=⋅= 12-5 (1)U=0；（2）E 0=0 .电势和场强分别在点叠加 0r4q (2r4q 2V 2V 2V 00=-+=+=-+πεπε）设顶角分别为a 、b 、c 、d, 中点场强： d c b a E E E E E+++=因为对角线顶点为等量同号电荷，场强相等而反向，所以0E =12-6 45(V); -15(V) . 由电势定义 B Bp p V l d E V +⋅=⎰计算即得.12-7 E x =-2Ax/(x 2+y 2) ; E y =-2Ay/(x 2+y 2) .按场强与电势梯度关系 yV E x V E y x ∂∂-=∂∂-= , 12-8 (q A -q B )d/2ε0S .12-9 解：（1）由于D ，C 在1q ，2q 产生的电场中具有对称性，故D C U U =即0DC U ∆=。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

16级大学物理A2复习题一、选择题： 1. 一质点作简谐振动，振动方程为)cos(tAx，当时间t = T/2（T为周期）时，质点的速度为 (A) sinA． (B) sinA．

(A) )21/(costmkAx (B) )21/cos(tmkAx

(C) )π21/(costkmAx (D) )21/cos(tkmAx (E) tm/kAxcos ［］ 3. 把单摆摆球从平衡位置向位移正方向拉开，使摆线与竖直方向成一微小角度 ，然后由静止放手任其振动，从放手时开始计时．若用余弦函数表示其运动方程，则该单摆振动的初相为 (A) ． (B) /2． (C) 0 ． (D) ．［］ 4. 两个质点各自作简谐振动，它们的振幅相同、周期相同．第一个质点的振动方程为x1 = Acos(t + )．当第一个质点从相对于其平衡位置的正位移处回到平衡位置时，第二个质点正在最大正位移处．则第二个质点的振动方程为

(A) )π21cos(2tAx． (B) )π21cos(2tAx．

(C) )π23cos(2tAx． (D) )cos(2tAx．［］ 5.一个弹簧振子和一个单摆（只考虑小幅度摆动），在地面上的固有振动周期分别为T1和T2．将它们拿到月球上去，相应的周期分别为1T和2T．则有 (A) 11TT且22TT． (B) 11TT且22TT．

(C) 11TT且22TT． (D) 11TT且22TT．［］ 6.一质点沿x轴作简谐振动，振动方程为 )312cos(1042tx (SI)．从t = 0时刻起，到质点位置在x = -2 cm处，且向x轴正方向运动的最短时间间隔为 (A) s81 (B) s61 (C) s41

(D) s31 (E) s21 ［］ 7.一劲度系数为k的轻弹簧，下端挂一质量为m的物体，系统的振动周期为T1．若将此弹簧截去一半的长度，下端挂一质量为m21的物体，则系统振动周期T2等于 (A) 2 T1 (B) T1 (C) T12/ (D) T1 /2 (E) T1 /4 ［］ 8.轻弹簧上端固定，下系一质量为m1的物体，稳定后在m1下边又系一质量为m2的物体，于是弹簧又伸长了x．若将m2移去，并令其振动，则振动周期为

(A) gmxmT122 ． (B) gmxmT212．

(C) gmxmT2121． (D) gmmxmT)(2212．［］ 9.一质点作简谐振动，周期为T．当它由平衡位置向x轴正方向运动时，从二分之一最大位移处到最大位移处这段路程所需要的时间为 (A) T /12． (B) T /8． (C) T /6． (D) T /4．［］ 10.两个同周期简谐振动曲线如图所示．x1的相位比x2的相位 (A) 落后/2． (B) 超前． (C) 落后． (D) 超前．［］ 11.在简谐波传播过程中，沿传播方向相距为21（为波长）的两点的振动速度必定 (A) 大小相同，而方向相反． (B) 大小和方向均相同． (C) 大小不同，方向相同． (D) 大小不同，而方向相反．［］ 12. 若一平面简谐波的表达式为 )cos(CxBtAy，式中A、B、C为正值常量，则 (A) 波速为C． (B) 周期为1/B． (C) 波长为 2 /C． (D) 角频率为2 /B．［］ 13.一横波沿绳子传播时, 波的表达式为 )104cos(05.0txy (SI)，则 (A) 其波长为0.5 m． (B) 波速为5 m/s． (C) 波速为25 m/s． (D) 频率为2 Hz．［］ 14. 机械波的表达式为y = 0.03cos6(t + 0.01x ) (SI) ，则

(A) 其振幅为3 m． (B) 其周期为s31． (C) 其波速为10 m/s． (D) 波沿x轴正向传播．［］ 15.已知一平面简谐波的表达式为 )cos(bxatAy（a、b为正值常量），则 (A) 波的频率为a． (B) 波的传播速度为 b/a． (C) 波长为  / b． (D) 波的周期为2 / a ．［］ 16.一平面简谐波在弹性媒质中传播，在某一瞬时，媒质中某质元正处于平衡位置，此时它

x1 x2 的能量是 (A) 动能为零，势能最大． (B) 动能为零，势能为零． (C) 动能最大，势能最大． (D) 动能最大，势能为零．［］ 17.一平面简谐波在弹性媒质中传播时，某一时刻媒质中某质元在负的最大位移处，则它的能量是 (A) 动能为零，势能最大． (B) 动能为零，势能为零． (C) 动能最大，势能最大． (D) 动能最大，势能为零．［］ 18.在波长为的驻波中两个相邻波节之间的距离为 (A) ． (B) 3/4． (C) /2． (D) /4．［］ 19.在波长为 的驻波中，两个相邻波腹之间的距离为 (A) /4． (B) /2． (C) 3/4． (D) ．［］ 20.在驻波中，两个相邻波节间各质点的振动 (A) 振幅相同，相位相同． (B) 振幅不同，相位相同． (C) 振幅相同，相位不同． (D) 振幅不同，相位不同．［］ 21.在相同的时间内，一束波长为的单色光在空气中和在玻璃中 (A) 传播的路程相等，走过的光程相等． (B) 传播的路程相等，走过的光程不相等． (C) 传播的路程不相等，走过的光程相等． (D) 传播的路程不相等，走过的光程不相等．［］ 22. 在真空中波长为的单色光，在折射率为n的透明介质中从A沿某路径传播到B，若A、B两点相位差为3，则此路径AB的光程为 (A) 1.5． (B) 1.5  n． (C) 1.5 n． (D) 3．［］ 23.用白光光源进行双缝实验，若用一个纯红色的滤光片遮盖一条缝，用一个纯蓝色的滤光片遮盖另一条缝，则 (A) 干涉条纹的宽度将发生改变． (B) 产生红光和蓝光的两套彩色干涉条纹． (C) 干涉条纹的亮度将发生改变． (D) 不产生干涉条纹．［］ 24.在双缝干涉实验中，设缝是水平的．若双缝所在的平板稍微向上平移，其它条件不变，则屏上的干涉条纹 (A) 向下平移，且间距不变． (B) 向上平移，且间距不变． (C) 不移动，但间距改变． (D) 向上平移，且间距改变．［］ 25.在双缝干涉实验中，为使屏上的干涉条纹间距变大，可以采取的办法是 (A) 使屏靠近双缝． (B) 使两缝的间距变小． (C) 把两个缝的宽度稍微调窄． (D) 改用波长较小的单色光源．［］ 26. 在双缝干涉实验中，两条缝的宽度原来是相等的．若其中一缝的宽度略变窄(缝中心位置不变)，则 (A) 干涉条纹的间距变宽． (B) 干涉条纹的间距变窄． (C) 干涉条纹的间距不变，但原极小处的强度不再为零． (D) 不再发生干涉现象．［］ 27.两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃慢慢地向上平移，则干涉条纹 (A) 向棱边方向平移，条纹间隔变小． (B) 向棱边方向平移，条纹间隔变大． (C) 向棱边方向平移，条纹间隔不变． (D) 向远离棱边的方向平移，条纹间隔不变． (E) 向远离棱边的方向平移，条纹间隔变小．［］ 28.两块平玻璃构成空气劈形膜，左边为棱边，用单色平行光垂直入射．若上面的平玻璃以棱边为轴，沿逆时针方向作微小转动，则干涉条纹的 (A) 间隔变小，并向棱边方向平移． (B) 间隔变大，并向远离棱边方向平移． (C) 间隔不变，向棱边方向平移． (D) 间隔变小，并向远离棱边方向平移．［］ 29. 把一平凸透镜放在平玻璃上，构成牛顿环装置．当平凸透镜慢慢地向上平移时，由反射光形成的牛顿环 (A) 向中心收缩，条纹间隔变小． (B) 向中心收缩，环心呈明暗交替变化． (C) 向外扩张，环心呈明暗交替变化． (D) 向外扩张，条纹间隔变大．［］ 30.若把牛顿环装置(都是用折射率为1.52的玻璃制成的)由空气搬入折射率为1.33的水中，则干涉条纹 (A) 中心暗斑变成亮斑． (B) 变疏． (C) 变密． (D) 间距不变．［］ 31.在单缝夫琅禾费衍射实验中波长为的单色光垂直入射到单缝上．对应于衍射角为30°的方向上，若单缝处波面可分成 3个半波带，则缝宽度a等于 (A) ． (B) 1.5． (C) 2． (D) 3．［］ 32.在单缝夫琅禾费衍射实验中，波长为的单色光垂直入射在宽度为a＝4的单缝上，对应于衍射角为30°的方向，单缝处波阵面可分成的半波带数目为 (A) 2 个． (B) 4 个． (C) 6 个． (D) 8 个．［］ 33.波长为的单色平行光垂直入射到一狭缝上，若第一级暗纹的位置对应的衍射角为=± / 6，则缝宽的大小为 (A) ． (B) ． (C) 2． (D) 3 ．［］ 34.在夫琅禾费单缝衍射实验中，对于给定的入射单色光，当缝宽度变小时，除中央亮纹的中心位置不变外，各级衍射条纹 (A) 对应的衍射角变小． (B) 对应的衍射角变大． (C) 对应的衍射角也不变． (D) 光强也不变．［］ 35.在单缝夫琅禾费衍射实验中，若增大缝宽，其他条件不变，则中央明条纹 (A) 宽度变小． (B) 宽度变大． (C) 宽度不变，且中心强度也不变． (D) 宽度不变，但中心强度增大．［］ 36.在单缝夫琅禾费衍射实验中，若减小缝宽，其他条件不变，则中央明条纹 (A) 宽度变小； (B) 宽度变大； (C) 宽度不变，且中心强度也不变； (D) 宽度不变，但中心强度变小．［］ 37.一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，偏离中央明纹最远的是 (A) 紫光． (B) 绿光． (C) 黄光． (D) 红光．［］ 38.一束白光垂直照射在一光栅上，在形成的同一级光栅光谱中，距离中央明纹最近的是 (A) 紫光． (B) 绿光． (C) 黄光． (D) 红光．［］ 39. 测量单色光的波长时，下列方法中哪一种方法最为准确？ (A) 双缝干涉． (B) 牛顿环． (C) 单缝衍射． (D) 光栅衍射．［］