实验二 积分分离数字PID调节器算法
积分分离pid算法

积分分离pid算法PID控制是一种常见的闭环控制策略,广泛应用于自动控制系统中。
而积分分离PID算法是对传统PID算法的一种改进。
本文将详细介绍积分分离PID算法的原理及应用。
积分分离PID算法的核心思想是将传统PID控制器中的积分分离出来,以避免积分饱和现象的发生。
传统PID控制器存在的问题是在控制对象存在饱和现象时,积分项会无限累积,导致系统响应不稳定。
积分分离PID算法通过将积分项分离出来独立进行计算,并通过限幅使其在合适范围内工作,从而提高系统的控制性能。
积分分离PID算法在实际控制系统中得到了广泛应用。
下面分别以电机控制和温度控制为例,介绍其应用。
1. 电机控制中的积分分离PID算法在电机控制中,积分分离PID算法能够有效解决电机启动时的过冲和饱和问题。
通过将积分项从PID控制器中分离出来,使其能够独立地对速度误差进行积分,以便更好地控制电机的速度。
这样可以提高电机系统的响应速度,减小超调量,提升控制精度。
2. 温度控制中的积分分离PID算法在温度控制中,积分分离PID算法可以有效地消除温度控制过程中的积分饱和问题。
通过将积分项从PID控制器中分离出来,对温度误差进行单独积分控制,可以更好地解决温度系统的积分累积问题。
这样可以提高温度控制系统的稳定性,减小温度波动,保证温度控制精度。
积分分离PID算法通过分离积分项来解决传统PID控制器中的积分饱和问题,从而提高控制系统的性能。
在电机控制和温度控制等领域中,积分分离PID算法得到了广泛应用,有效解决了对速度和温度等参数精确控制的需求。
通过合理应用积分分离PID算法,可以提高控制系统的稳定性和精度,实现更好的控制效果。
以上就是关于积分分离PID算法的介绍,希望对读者有所帮助。
如需进一步了解该算法的详细实现方法和应用案例,请参考相关文献和资料。
PID调节原理

PID控制的优点
①原理简单,使用方便; ②适应性强; ③鲁棒性强;
控制品质对被控对象特性的变化不大敏感。
④对模型依赖少。
比例调节的特点:
(1)比例调节的输出增量与输入增量呈一一 对应的比例关系,即:u = K e
40
50
0
60
0
20
40
60
80
100
120
Time (sec)
Time (sec)
积分调节, Ti的变化对控制效果的影响
微分调节作用:微分作用反映系统偏差信号的变化率 ,具有预见性,能预见偏差变化的趋势,因此能产生 超前的控制作用,在偏差还没有形成之前,已被微分 调节作用消除。因此,可以改善系统的动态性能。 在微分时间选择合适情况下,可以减少超调,减少调 节时间。 微分作用对噪声干扰有放大作用,因此过强的微分调 节,对系统抗干扰不利。 此外,微分反应的是变化率,而当输入没有变化时, 微分作用输出为零。 微分作用不能单独使用,需要与另外两种调节规律相 结合,组成PD或PID控制器。
1 G K TIs (s+1) (2s+1)
Amplitude Amplitude
Step Response 12
Step Response 1.8
Ti=0.5
Ti=1
10
1.6
Ti=5
8
1.4
Ti=10
6
Ti=inf
1.2
4 1
2 0.8
0 0.6
-2
0.4 -4
0.2 -6
积分分离数字pid位置算式

积分分离数字pid位置算式
积分分离数字pid位置算式是一种基于PID(比例-积分-微分)控
制原理的计算方法,它可以用来精确地控制机械系统中的位置,从而
获得最佳性能。
该算法通过对当前位置信息和期望位置信息进行比较,推断出机械系统所需要采取的正确动作,并通过PID控制进行优化,
从而达到最佳位置控制精度的效果。
其算式如下:
Position error = Desired Position – Measured Position
Proportion (P) = Kp * Position Error
Integral (I) = Ki * INT [Position Error]
Derivative (D) = Kd * d/dt[Position Error]
Total Output = P + I + D
其中,Kp,Ki和Kd是控制参数,也就是PID三个参数,分别代表
比例、积分和微分的系数。
INT[Position Error]表示积分误差,
int\[x\]表示x的积分,即不断累加的x的累积和;d/dt[Position Error]表示微分误差,d/dt\[x\]表示x的微分,即不断变化的x的增量;Total Output表示总输出,也就是PID控制器输出的控制量。
综上所述,积分分离数字pid位置算式是一种基于PID(比例-积
分-微分)控制原理的计算方法,对当前位置信息和期望位置信息进行
比较,通过控制参数Kp,Ki和Kd,积分和微分误差,以及最终总输出,从而达到最佳位置控制精度的效果。
(完整版)数字PID及其算法
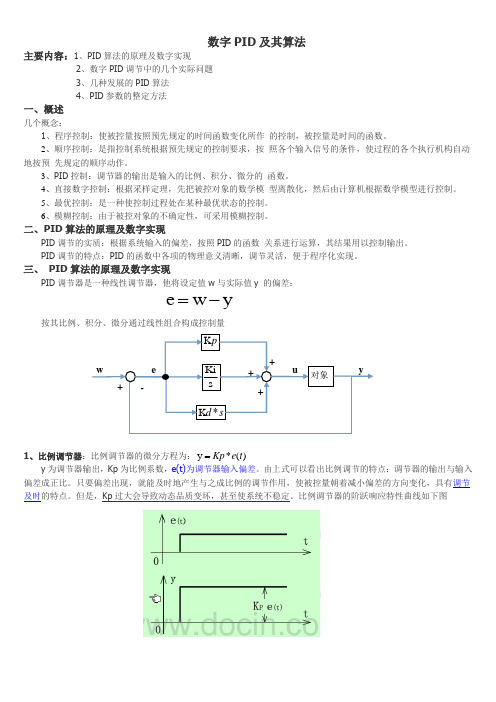
数字PID 及其算法主要内容:1、PID 算法的原理及数字实现2、数字PID 调节中的几个实际问题3、几种发展的PID 算法4、PID 参数的整定方法一、概述几个概念:1、程序控制:使被控量按照预先规定的时间函数变化所作 的控制,被控量是时间的函数。
2、顺序控制:是指控制系统根据预先规定的控制要求,按 照各个输入信号的条件,使过程的各个执行机构自动地按预 先规定的顺序动作。
3、PID 控制:调节器的输出是输入的比例、积分、微分的 函数。
4、直接数字控制:根据采样定理,先把被控对象的数学模 型离散化,然后由计算机根据数学模型进行控制。
5、最优控制:是一种使控制过程处在某种最优状态的控制。
6、模糊控制:由于被控对象的不确定性,可采用模糊控制。
二、PID 算法的原理及数字实现PID 调节的实质:根据系统输入的偏差,按照PID 的函数 关系进行运算,其结果用以控制输出。
PID 调节的特点:PID 的函数中各项的物理意义清晰,调节灵活,便于程序化实现。
三、 PID 算法的原理及数字实现PID 调节器是一种线性调节器,他将设定值w 与实际值y 的偏差:按其比例、积分、微分通过线性组合构成控制量1、比例调节器:比例调节器的微分方程为:)(*y t e Kp =y 为调节器输出,Kp 为比例系数,e(t)为调节器输入偏差。
由上式可以看出比例调节的特点:调节器的输出与输入偏差成正比。
只要偏差出现,就能及时地产生与之成比例的调节作用,使被控量朝着减小偏差的方向变化,具有调节及时的特点。
但是,Kp 过大会导致动态品质变坏,甚至使系统不稳定。
比例调节器的阶跃响应特性曲线如下图yw e -=sd *K s Ki pK 对象 we + - + + + u y2、积分调节器:积分作用是指调节器的输出与输入偏差的积分成比例的作用,其作用是消除静差。
积分方程为:TI 是积分时间常数,它表示积分速度的大小,TI 越大,积分速度越慢,积分作用越弱。
积分分离pid

积分分离pid
积分分离PID(ProportionalIntegralDerivative)是一种控制算法,它是在PID控制器中使用的一种变异形式。
其主要原理是将PID控制器中的积分环路从控制器中分离出来,使控制器更为灵活和精确。
传统的PID控制器由比例环路、积分环路和微分环路组成。
在传统PID算法中,积分环路对于系统稳定性和误差修正起着非常重要的作用。
但是在某些情况下,积分环路会导致系统过度响应和振荡。
为了避免这种情况的发生,积分分离PID控制器将积分环路从控制器中分离出来,并将其作为单独的控制器来使用。
这样可以实现控制器的更好灵活性和精确性,同时保证系统的稳定性。
积分分离PID控制器在某些应用中表现得比传统PID控制器更好。
例如,在温度控制应用中,积分分离PID控制器可以更好地控制温度波动,并避免温度过度波动。
总之,积分分离PID控制器是一种高级的控制算法,可以在某些情况下提高系统的控制精度和稳定性。
- 1 -。
pid积分分离算法

PID积分分离算法1. 简介PID(比例-积分-微分)控制是一种常用的控制算法,广泛应用于自动控制系统中。
积分分离算法是PID控制中的一种技术,用于解决传统PID控制中存在的一些问题,例如积分饱和和积分爆炸等。
PID控制器根据系统的误差、误差的积分和误差的微分来决定输出控制量,以使系统达到期望的状态。
传统的PID控制中,积分项和微分项与比例项同时作用于系统,但这样的做法可能会导致一些问题的出现。
积分分离算法通过将PID控制器的积分项和微分项分离,单独处理积分项,以解决传统PID控制中的问题。
积分分离算法可以提高系统的稳定性、响应速度和鲁棒性,广泛应用于工业控制、机器人控制等领域。
2. 传统PID控制的问题2.1 积分饱和传统的PID控制中,积分项是对误差的积分,用于消除系统的稳态误差。
但是,当系统存在饱和或限制条件时,积分项可能会导致输出超出可控范围,从而导致系统不稳定。
积分饱和是指积分项超过了设定的上限或下限,使得控制量无法继续增加或减小。
当系统处于饱和状态时,积分项的增加不会对系统产生更多的影响,从而导致系统无法快速响应。
2.2 积分爆炸在传统PID控制中,积分项是对误差的积分,如果误差一直存在,积分项会不断累积增加,导致积分爆炸的问题。
积分爆炸会导致系统产生超调、振荡或不稳定的现象。
积分爆炸的问题主要是由于积分项没有受到合适的限制或调节机制的影响,使得积分项不断增加,超过了系统的可控范围。
3. 积分分离算法原理积分分离算法通过将PID控制器的积分项和微分项分离,单独处理积分项,以解决传统PID控制中的问题。
3.1 积分项处理传统PID控制中,积分项是对误差的积分。
而在积分分离算法中,积分项的计算方式发生了改变。
积分分离算法使用积分项对系统的状态进行补偿,而不是直接对误差进行积分。
积分分离算法中的积分项计算方式如下:I(t) = I(t-1) + Ki * (SP(t) - PV(t))其中,I(t)表示当前时刻的积分项,I(t-1)表示上一时刻的积分项,Ki表示积分增益,SP(t)表示期望值,PV(t)表示当前时刻的实际值。
积分分离式pid算法实例

正文一、方案选择总体方案选择:电热锅炉温度控制系统由核心处理模块、温度采集模块、键盘显示模块、及控制执行模块等组成。
总体方案一:采用8031作为控制核心,以使用最为普遍的器件ADC0809作模数转换,控制上使用对电阻丝加电使其升温和开动风扇使其降温。
此方案简易可行,器件的价格便宜,但8031内部没有程序存储器,需要扩展,增加了电路的复杂性,且ADC0809是8位的模数转换,不能满足本题目的精度要求。
总体方案二:采用比较流行的AT89S51作为电路的控制核心,使用12位的高精度模数转换器AD574A进行数据转换,控制电路部分采用PWM控制可控硅的通断以实行对锅炉温度的连续控制,此方案电路简单并且可以满足题目中的各项要求的精度。
综上分析,我们采用方案二。
系统设计总体框图如下:图1 控制器设计总体框图根据温度变化慢,并且控制精度不易掌握的特点,我们设计了以STC89C51单片机为检测控制中心的电热锅炉温度自动控制系统。
温度控制采用改进的PID数字控制算法,显示采用3位LED静态显示。
该设计结构简单,控制算法新颖,控制精度高,有较强的通用性。
所设计的控制系统有以下功能:· 温度控制设定波动范围小于±1%,测量精度小于±1%,控制精度小于±2%,超调整量小于±4%;· 实现控制可以升温也可以降温;· 实时显示当前温度值;· 按键控制:设置复位键、运行键、功能转换键、加一键、减一键;· 越限报警。
方案一1、带死区的PID算法某些生产过程对控制精度要求不是很高但希望系统工作稳定,执行机构不要频繁动作。
针对这一类系统,带死区的PID算法应运而生。
所谓带死区的PID,实在计算机中认为的设置一个不灵敏区域β,当偏差的绝对值|e(k)|<β时,不产生新的控制增量,控制量维持不变;当偏差的绝对值|e (k)|>β时,则进行正常的PID运算后输出。
积分分离数字pid位置算式

积分分离数字pid位置算式
积分分离数字pid位置算式是一种能够实现在随机出现的要求中数字pid位置匹配的数学方法。
这种方法的基本思想是将一个数字pid (例如123)分解成几个部分,并将每个部分用积分来表示。
比如,如果一个数字pid有3位,那么它就可以分解成三部分:a,b,c,那么对应的积分分离数字pid位置算式就是:
(a*1+b*10+c*100) mod n = t
其中,a、b、c是相应的数字pid位置,n是要求的位置,t是要求的结果。
在这里,a、b、c并没有限制只能取0-9之间的数,而是可以是任意正整数。
比如,要求在数字pid 999中,最后一位数字8的位置,则可以写出积分分离数字pid位置算式:
(9*1+9*10+8*100) mod 3 = 2
因此,可以看出,最后一位8的位置为2.
此外,由于积分分离数字pid位置算式不受任何条件的限制,只要数字pid位置有变动,就可以实现准确的匹配。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二积分分离数字PID调节器算法
一、实验目的
1.学习并熟悉积分分离PID控制算法的原理。
2.掌握具有数字PID调节器控制系统的实验和调节器参数的整定方法。
二、实验内容
1.利用本实验平台,设计并构成一个用于混合仿真实验的计算机闭环实时控制系统。
2.对系统采用积分分离PID控制,并整定调节器参数。
3.利用扩充临界比例法对数字PID的参数进行整定。
三、实验接线
1.按图2-1和图2-2连接一个二阶被控对象闭环控制系统的电路。
2.该电路的输出与数据采集卡的输入端AD1相连,电路的输入与数据采集卡的输出端DA1相连。
3.将“直流稳压电源”“数据采集卡接口模块”“通用单元电路”地线全部短接在一起。
4.待检查电路接线无误后,打开实验箱的电源总开关,并将锁零单元的锁零按钮处于“解锁”状态。
2-1
2-2
四、实验结果记录Tem=37
Tem=27
Tem=12
五、实验结论
在其他参数固定不变的情况下,改变分离阈E0 会对系统的动态性能产生不同的影响。
当系统输出在门限值内才会有积分作用,在门限值外则没有积分作用,等同于微分调节器。
六、收获及建议
通过本次试验了解了积分分离法对系统的作用。
在设定值接近给定值时加入积分作用可以消除静差提高控制精度减小超调并且避免了积分的饱和作用,使系统更加稳定。
