数字PID及其参数整定方法
pid参数的整定过程

pid参数的整定过程
PID(比例-积分-微分)控制器是一种常用的反馈控制器,用于调节和稳定系统。
PID控制器的参数整定过程通常包括以下几个步骤:
1.初始参数设定:根据系统的性质和需求,设置PID控制器的初
始参数。
通常情况下,可以将三个参数(比例增益Kp、积分时
间Ti、微分时间Td)都设为一个较小的初始值。
2.比例增益调整:从零开始逐步增加比例增益Kp的数值,观察
系统响应的变化。
如果Kp过小,系统响应可能过慢;如果Kp
过大,系统可能会出现超调或不稳定的情况。
通过不断调整Kp
的数值,直到找到一个合适的值,使得系统响应快速且稳定。
3.积分时间调整:在找到合适的Kp之后,开始调整积分时间Ti
的数值。
增大Ti会增加积分作用的影响,降低控制器对于持续
偏差的敏感度。
然而,过大的Ti可能导致系统响应的延迟和振
荡。
通过逐步调整Ti的数值,找到一个使系统响应稳定且快速
的值。
4.微分时间调整:在完成比例增益和积分时间的调整后,可以开
始调整微分时间Td的数值。
微分作用可以抑制系统响应中的
过冲和振荡,并提高系统的稳定性。
然而,过大的Td可能会引
入噪声的放大。
通过逐步调整Td的数值,找到一个能够平衡系
统响应速度和稳定性的值。
5.反复迭代:整定PID参数是一个迭代的过程。
一旦完成了上述
步骤,需要对整个系统进行测试和观察,以确定参数的最佳组合。
如果发现系统仍然存在问题,可以根据实际情况再次进行参数调整,直到达到满意的控制效果。
PID控制器的参数整定

PID控制器的参数整定PID控制器是一种常用的闭环控制器,可以根据系统的输入和输出之间的误差来调整控制器的参数,从而实现对系统的稳定控制。
PID控制器的参数整定是指确定控制器的比例系数Kp、积分时间Ti和微分时间Td的过程。
下面将详细介绍PID控制器的参数整定方法和相关的考虑因素。
一、参数整定方法:1.经验整定法:根据经验将控制器的参数进行初步设定。
经验整定法通常通过试验或先验知识来确定参数,根据具体的应用场景不断调整,以达到较好的控制效果。
该方法常用与简单的控制系统或者无法获得系统数学模型的情况下。
2. Ziegler-Nichols整定法:Ziegler-Nichols整定法是一种基于试验的整定方法。
该方法首先暂时关闭积分和微分控制,只调整比例控制系数Kp,使系统达到临界稳定状态。
然后测量临界增益Ku和临界周期Pu,根据不同类型的控制系统(比例型、积分型和微分型),采用不同的参数整定公式确定Kp、Ti和Td的初始值,再根据系统的实际响应实时调整。
3. Ziegler-Nichols改进整定法(Chien-Hrones-Reswich法):该方法是对Ziegler-Nichols整定法的改进,可以更精确地测定控制器参数。
该方法同样通过测量系统的临界增益Ku和临界周期Pu,但是对参数的计算公式进行了修正,提高了参数整定的准确性。
4. 极点配置法(Pole Placement):极点配置法是一种基于系统数学模型的整定方法。
通过分析系统的传递函数,确定控制器的极点位置,从而使系统的闭环响应满足所需的性能指标。
该方法需要对系统的数学模型有较详细的了解,适用于相对复杂的控制系统。
5.自整定法:自整定法是一种自动寻优的整定方法,常用于智能控制器中。
该方法通过观察系统的动态性能,通过迭代寻找最优的参数组合。
自整定法通常采用优化算法(如遗传算法、粒子群算法等)来最优参数,在一定的性能和收敛速度之间进行权衡。
二、参数整定的考虑因素:1.系统的稳定性:控制器的参数整定应确保系统的闭环响应稳定。
PID控制原理与参数整定方法

PID控制原理与参数整定方法PID控制是一种常用的反馈控制方法,它通过测量控制系统的输出与期望输入之间的差异,计算出一个控制信号来调节控制系统的行为。
PID 控制器的主要参数有比例增益(Proportional),积分时间(Integral)和微分时间(Derivative)。
通过调节这些参数,可以实现对控制系统的动态响应和稳定性的优化。
首先,我们来了解一下PID控制器的工作原理。
PID控制器是基于控制误差和误差的变化率来计算输出控制信号的,它包含三个部分:比例控制项、积分控制项和微分控制项。
比例控制项(P项)以控制误差的比例关系来计算输出信号。
它的计算公式为:P=Kp*e(t),其中Kp为比例增益,e(t)为控制误差。
比例增益越大,控制器对误差的纠正力度越大,但过大的比例增益会引起震荡。
积分控制项(I项)以控制误差的累积值来计算输出信号。
它的计算公式为:I = Ki * ∫e(t)dt,其中Ki为积分时间,∫e(t)dt为控制误差的累积值。
积分控制项主要用于消除稳态误差,但过大的积分时间会引起超调和不稳定。
微分控制项(D项)以控制误差的变化率来计算输出信号。
它的计算公式为:D = Kd * de(t)/dt,其中Kd为微分时间,de(t)/dt为控制误差的变化率。
微分控制项主要用于抑制系统的震荡和快速响应,但过大的微分时间会引起噪声放大。
接下来,我们来介绍一下PID参数整定的方法。
在实际应用中,PID 参数的选择通常需要经验和试验。
以下是常用的PID参数整定方法。
1.经验设置法:根据经验设置PID参数的初始值,然后根据实际系统的响应进行调整。
这种方法需要经验和实践的积累,适用于经验丰富的控制工程师。
2. Ziegler-Nichols方法:这是一种基于实验步骤响应曲线的整定方法。
该方法通过观察控制系统的临界点,确定比例增益、积分时间和微分时间的初始值,然后通过试探法逐步调整,直到系统达到所需的动态响应。
PID控制器参数整定与应用

PID控制器参数整定与应用PID控制器由比例(P)、积分(I)和微分(D)三个部分组成。
比例控制器根据当前的偏差与参考值之间的差异给出一个输出。
积分控制器根据偏差随时间的累积计算输出,用于消除系统的稳态误差。
微分控制器根据偏差的变化率给出输出,用于稳定系统的动态响应。
PID控制器的输出是比例、积分和微分控制器的输出之和。
参数整定是指选择合适的PID控制器参数,使得控制系统能够稳定工作且具有良好的响应速度和抗干扰能力。
PID控制器的参数整定一般有以下几种方法:1.经验法:根据经验和实际控制系统的特点选择参数。
这种方法适用于控制系统较简单的情况,但不具有普适性。
2. Ziegler-Nichols方法:通过实验数据来确定参数。
首先将积分和微分参数设为零,逐渐增加比例参数,直到系统出现较小的超调(即超过参考值后回波的百分比),然后根据超调曲线确定比例和时间参数。
3. Chien-Hrones-Reswick方法:通过频域分析来确定参数。
首先将系统转化为频域传递函数,然后根据传递函数的特性来选择参数。
4.自整定方法:使用专门设计的算法来进行参数整定。
这些算法根据系统的频率响应和阶跃响应等特征进行参数的优化。
1.温度控制:PID控制器可以通过调节加热元件的功率来控制温度的稳定性和响应速度。
例如,在恒温恒湿箱中,通过测量温度偏差,计算出PID控制器的输出,来控制加热器的功率,使系统保持在设定温度下。
2.流量控制:PID控制器可以通过调节阀门的开度来控制液体或气体的流量。
例如,在一个水罐中,通过测量液位偏差,计算出PID控制器的输出,来控制阀门的开度,以维持设定的液位。
3.速度控制:PID控制器可以通过调节电机的输入电压或转矩来控制机械系统的速度。
例如,在一个电动机驱动的输送带系统中,PID控制器可以根据输送带的位置偏差,计算出对电机的控制信号,来控制输送带的速度。
4.位置控制:PID控制器可以通过调节电机的转矩或位置来控制机械系统的位置。
PID控制原理与参数的整定方法

PID控制原理与参数的整定方法PID控制器是一种常用的自动控制器,在工业控制中广泛应用。
它的原理很简单,即通过不断调节控制信号来使被控制物体的输出接近给定值。
PID控制器由比例(P)、积分(I)和微分(D)三个控制参数组成。
下面将详细介绍PID控制的原理和参数整定方法。
一、PID控制原理1.比例(P)控制比例控制根据被控制量的偏差的大小,按照一定比例调节控制量的大小。
当偏差较大时,调节量增大;当偏差较小时,调节量减小。
此项控制可以使系统快速响应,并减小系统稳态误差。
2.积分(I)控制积分控制根据被控制物体的偏差的积分值来调节控制量。
积分控制的作用主要是消除系统的稳态误差。
当偏差较小但持续较长时间时,积分量会逐渐增大,以减小偏差。
3.微分(D)控制微分控制根据被控制物体的偏差的变化率来调节控制量。
当偏差的变化率较大时,微分量会增大,以提前调整控制量。
微分控制可以减小系统的超调和振荡。
综合比例、积分和微分控制,PID控制器可以通过不同的控制参数整定来适应不同的被控制物体的特性。
二、PID控制参数整定方法1.经验整定法经验整定法是根据对被控制系统的调试经验和运行情况来选择控制参数的方法。
它是通过实际试验来调整控制参数,通过观察系统的响应和稳定性来判断参数的合理性。
2. Ziegler-Nichols整定法Ziegler-Nichols整定法是根据系统的临界响应来选择PID控制参数的方法。
在该方法中,首先将I和D参数设置为零,然后不断提高P控制参数直到系统发生临界振荡。
根据振荡周期和振荡增益的比值来确定P、I和D的参数值。
3.设计模型整定法设计模型整定法是根据对被控系统的数学建模来确定PID控制参数的方法。
通过建立被控系统的数学模型,分析其频率响应和稳态特性,从而设计出合理的控制参数。
4.自整定法自整定法是通过主动调节PID控制器的参数,使被控系统的输出能够接近给定值。
该方法可以通过在线自整定或离线自整定来实现。
PID参数的整定方法

PID参数的整定方法PID控制器是目前最常用的控制算法之一,其调节参数(也称为PID 参数)的合理设置对控制系统的性能起着关键作用。
下面将介绍几种常用的PID参数整定方法。
1.经验法:经验法是最为简单直接的方法,通常由经验工程师根据自身经验来设定PID参数。
这种方法适用于一些简单的控制系统,但是对于复杂的系统来说,由于经验法不能提供具体的参数值,容易出现性能较差的情况。
2. Ziegler-Nichols 整定法:Ziegler-Nichols 整定法是PID参数整定中较为经典的方法,其步骤如下:-首先将PID控制器的I和D参数设置为零。
-逐渐增大比例参数(P)直到系统出现持续且稳定的振荡。
-记录此时的比例参数为Ku。
- 根据不同的控制对象类型,Ziegler-Nichols方法会有不同的参数整定公式,常见的有:-P型系统:Kp=0.50Ku,Ti=0.50Tu,Td=0.125Tu-PI型系统:Kp=0.45Ku,Ti=0.83Tu,Td=0.125Tu-PID型系统:Kp=0.60Ku,Ti=0.50Tu,Td=0.125Tu其中Ku为临界增益值,Tu为临界周期。
3. Chien-Hrones-Reswick (CHR) 整定法:CHR整定法基于频域设计方法,通过系统的频率响应曲线来确定PID参数。
其步骤如下:-绘制系统的频率响应曲线(一些软件和仪器可以直接测量)。
-根据曲线的特征,确定比较慢的过程的时间常数τ和极点频率ωp。
-根据以下公式得到PID参数:-P参数:Kp=2/(ωpτ)-I参数:Ti=τ/2-D参数:Td=τ/8不能掉进方法的误区,如超调范围不合适,调节周期过大或周期过小时,传递函数为微分型等。
4.设计优化法:设计优化法是基于性能指标的优化算法,通过对系统的模型进行优化,得出最佳的PID参数。
这种方法较复杂,通常使用数学工具或计算机软件进行参数优化。
常见的优化算法有遗传算法、粒子群算法等。
数字PID及其参数整定方法[优质ppt]
![数字PID及其参数整定方法[优质ppt]](https://img.taocdn.com/s3/m/78ef161da5e9856a5712600f.png)
P D ( k ) K D [ E ( k ) 2 E ( k 1 ) E ( k 2 )]
则有:
P ( k ) P P ( k ) P I ( k ) P D ( k )
7.1 PID算法的原理及数字实现
左图为增量式流程框图。 说明: ⑴ 在计算之前,需要完成采 样数据处理。 ⑵按照上式分解出来的三项, 分别进行计算。 ⑶ 将计算出来的数据作为控 制量的增量与前一拍输出量相 加作为本次的输出量。
e(t)d tT D d(te )] dt
式中: P(t): e(t): Kp: Ti: Td:
调节器输出 调节器的偏差信号 比例系数 积分时间 微分时间
7.1 PID算法的原理及数字实现
PID调节器对阶跃响应特性曲线
e (t) t
0
y∞
K P K D e (t) 0
K P e (t)
K P K 1 e (t) t
把上式进一步分为P、I、D三项,:
P P(k)KpE(k)
k
PI (k) KI E( j) K IE (k ) P I(k 1 ) j0
P D ( k ) K D [ E ( k ) E ( k 1 )]
7.1 PID算法的原理及数字实现
左图为位置式流程框图。 说明: ⑴ 在计算之前,需要完成采 样数据处理。 ⑵按照上式分解出来的三项, 分别进行计算。 ⑶ 将计算出来的数据作为控 制量输出。
7.1 PID算法的原理及数字实现
对前一算式离散化,即为数字式的差分方程(7-4式):
P (k ) K P { E (k ) T T Ij k0E (j) T D E (k ) T E (k 1 )}
【值得收藏】PID控制算法精华和参数整定三大招
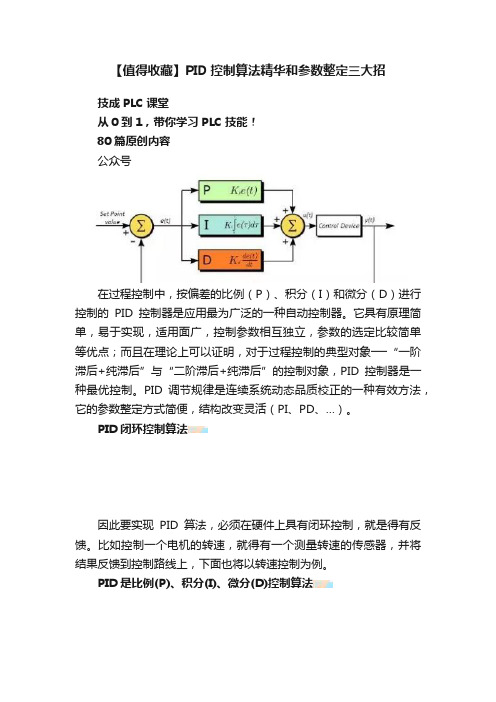
【值得收藏】PID控制算法精华和参数整定三大招技成PLC课堂从0到1,带你学习PLC技能!80篇原创内容公众号在过程控制中,按偏差的比例(P)、积分(I)和微分(D)进行控制的PID控制器是应用最为广泛的一种自动控制器。
它具有原理简单,易于实现,适用面广,控制参数相互独立,参数的选定比较简单等优点;而且在理论上可以证明,对于过程控制的典型对象──“一阶滞后+纯滞后”与“二阶滞后+纯滞后”的控制对象,PID控制器是一种最优控制。
PID调节规律是连续系统动态品质校正的一种有效方法,它的参数整定方式简便,结构改变灵活(PI、PD、…)。
PID闭环控制算法因此要实现PID算法,必须在硬件上具有闭环控制,就是得有反馈。
比如控制一个电机的转速,就得有一个测量转速的传感器,并将结果反馈到控制路线上,下面也将以转速控制为例。
PID是比例(P)、积分(I)、微分(D)控制算法但并不是必须同时具备这三种算法,也可以是PD,PI,甚至只有P算法控制。
我以前对于闭环控制的一个最朴素的想法就只有P控制,将当前结果反馈回来,再与目标相减,为正的话,就减速,为负的话就加速。
现在知道这只是最简单的闭环控制算法。
PID控制器结构考前准备PID控制系统原理结构框图对偏差信号进行比例、积分和微分运算变换后形成一种控制规律。
“利用偏差,纠正偏差”。
模拟PID控制器模拟PID控制器结构图PID控制器的输入输出关系为:比例(P)、积分(I)、微分(D)控制算法各有作用比例,反应系统的基本(当前)偏差e(t),系数大,可以加快调节,减小误差,但过大的比例使系统稳定性下降,甚至造成系统不稳定;积分,反应系统的累计偏差,使系统消除稳态误差,提高无差度,因为有误差,积分调节就进行,直至无误差;微分,反映系统偏差信号的变化率e(t)-e(t-1),具有预见性,能预见偏差变化的趋势,产生超前的控制作用,在偏差还没有形成之前,已被微分调节作用消除,因此可以改善系统的动态性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.1 PID算法的原理及数字实现
e (t) 0
y
0
t
K P e (t)
t
阶跃响应特性曲线
7.1 PID算法的原理及数字实现
式中: P(t): e(t): Kp: Ti: Td:
调节器输出 调节器的偏差信号 比例系数 积分时间 微分时间
7.1 PID算法的原理及数字实现
PID调节器对阶跃响应特性曲线
e (t) t
0
y∞
K P K D e (t) 0
K P e (t)
K P K 1 e (t) t
7.1 PID算法的原理及数字实现
7.2 数字PID调节中的几个问题
7.2.1 正、反作用问题
正、反作用问题也称为:正、逆调节问题。 正作用:当采样值大于设定值时,需要加大控制量的输 出。例如,温度控制中的制冷过程。 反作用:当采样值小于设定值时,需要加大控制量的输 出。例如,温度控制中的加热过程。 在微机控制系统中,处理正、反作用时可用对偏差值求 反来实现。
7.1.1 模拟PID调节原理
PID调节器是一种线性调节器,他将设定值w与实际值y 的偏差:
e = w-y
按其比例、积分、微分通过线性组合构成控制量。
7.1 PID算法的原理及数字实现
1. 比例调节器 比例调节器的微分方程为:y = KPe(t) 式中: y为调节器输出; Kp为比例系数; e(t)为调节器输入偏差。 由上式可以看出比例调节的特点: 调节器的输出与输入偏差成正比。只要偏差出现,就能
⑵ 有效偏差法 在 用 位 置 型 PID 算 式 算 出
的控制量超出执行范围时,控 制量实际上只能取边界值。
有效偏差法的实质:将实 际输出控制量所允许的偏差值 作为实际有效偏差进行积分。 而不是按照实际偏差来进行积 分。算法如右图示。
7.2 数字PID调节中的几个问题
⑶ 限位问题 是指在有些系统中,人
7.2 数字PID调节中的几个问题
为了消除积分饱和的影 响,可有如下几种办法: ⑴ 遇限削弱积分法
这种算法的基本思想是: 一旦控制量进入饱和区范围, 则停止增大积分项的运算而 只执行削弱积分项的运算。
这种算法的流程图如下 屏所示。
7.2 数字PID调节中的几个问题
7.2 数字PID调节中的几个问题
P ( k ) P ( k ) P ( k 1 )
(7-7)
K p [ E ( k ) E ( k 1 ) K ] I E ( k ) K D [ E ( k ) 2 E ( k 1 ) E ( k 2 )]
式中: Kp比例系数
Ki=Kp*(T/Ti)积分系数
Kd =Kp*(Td/T)微分系数。
P I(k)K IE (k)
P D ( k ) K D [ E ( k ) 2 E ( k 1 ) E ( k 2 )]
则有:
P ( k ) P P ( k ) P I ( k ) P D ( k )
7.1 PID算法的原理及数字实现
左图为增量式流程框图。 说明: ⑴ 在计算之前,需要完成采 样数据处理。 ⑵按照上式分解出来的三项, 分别进行计算。 ⑶ 将计算出来的数据作为控 制量的增量与前一拍输出量相 加作为本次的输出量。
积分分离算法的流程图见 P247
7.3 PID算法的发展
7.3.2 变速积分的PID算法
在普通的PID调节算法中,由于积分系数KI是常数,因 此,在整个调节过程中,积分增益不变。但系统对ቤተ መጻሕፍቲ ባይዱ分项的 要求是系统偏差大时积分作用减弱以至全无,而在小偏差时 则应加强。否则,积分系数取大了会产生超调,甚至积分饱 和,取小了又迟迟不能消除静差。采用变速积分可以很好地 解决这一问题。
变速积分的基本思想是:设法改变积分项的累加速度, 使其与偏差的大小相对应:偏差越大,积分越慢;偏差越小, 积分越快。
7.4 PID参数的整定方法
7.4.1 采样周期的确定
(1)根据香农采样定理,系统采样频率的下限为fs=2fmax, 此时系统可真实地恢复到原来的连续信号。 (2)从执行机构的特性要求来看,有时需要输出信号保持 一定的宽度。采样周期必须大于这一时间。 (3)从控制系统的随动和抗干扰的性能来看,要求采样周 期短些。 (4)从微机的工作量和每个调节回路的计算来看,一般要 求采样周期大些。 (5)从计算机的精度看,过短的采样周期是不合适的。
Y(t)
P
0
2
1
一般PID
开始引入积分作用
积分分离PID t
7.3 PID算法的发展
可针对这种现象采用积分分离的办法,即在控制量开始 跟踪时,屏蔽积分分量的作用,直至被调量接近给定值时才 使积分分量产生作用。
设给定值R(k),采样值M(k),允许的积分偏差值A,则积 分分离的算法为:
A时, P控 D 为制 E(k)|R(k)M (k)| A 时, PI控 为 D 制
对前一算式离散化,即为数字式的差分方程(7-4式):
Tk
E (k ) E (k 1 )
P (k ) K P { E (k ) T Ij 0E (j) T D
} T
式中:
T:
采样周期
E(k): 第k次采样时的偏差值
E(k-1): 第k-1次采样时的偏差值
k:
采样序号
P(k): 第k次采样时的调节器输出
7.0 概述
3 PID控制:调节器的输出是输入的比例、积分、微分的 函数。
4 直接数字控制:根据采样定理,先把被控对象的数学模 型离散化,然后由计算机根据数学模型进行控制。
5 最优控制:是一种使控制过程处在某种最优状态的控制。 6 模糊控制:由于被控对象的不确定性,可采用模糊控制。
7.1 PID算法的原理及数字实现
7.1 PID算法的原理及数字实现
7.1.3 PID程序设计
⑴ 位置式PID算法程序设计 由下式可改写为:
P (k ) K P { E (k ) T T Ij k 0 E (j) T D E (k ) T E (k 1 )}
k
P (k ) K p E (k ) K I E (j) K D [E (k ) E (k 1 )] j 0
2. 积分调节器 积分作用是指调节器的输出与输入偏差的积分成比例的
作用,其作用是消除静差。积分方程为:
式中: TI是积分时间常数,它表示积分速度的大小,TI越大,
积分速度越慢,积分作用越弱。积分作用的响应特性曲线, 如下图所示。
7.1 PID算法的原理及数字实现
e (t) t
0 y
t 0
积分作用响应曲线 由图中曲线看出积分作用的特点:只要偏差不为零就会 产生对应的控制量并依此影响被控量。增大Ti会减小积分作 用,即减慢消除静差的过程,减小超调,提高稳定性。
为定义了控制量的输出范围。 当计算出的控制量大于或者小 于所定义的输出范围时,则按 照定义的控制量上限或者下限 进行输出。
如右图示。
7.2 数字PID调节中的几个问题
7.2.3 手动/自动跟踪及手动后援问题
在应用系统中,控制状态由手动与自动相互切换时,必 须实现自动跟踪(柔性跟踪)。
因此,系统需要实时监测的控制状态、手动/自动的阀 位状态。称在手动状态下能够输出手动控制信号的设备为手 动后援。
7.2 数字PID调节中的几个问题
7.2.2 饱和作用的抑制
在实际控制系统中,控制量因受到执行部件的机械和物 理的约束而限制在有限的范围内时,如果计算机给出的控制 量超出上述范围,则控制系统进入输出饱和状态。
在PID控制系统中,由于积分作用的存在,会使系统的 控制输出进入饱和状态。注意理解:饱和以后所导致的对系 统的不利影响。如下图示。
7.1 PID算法的原理及数字实现
⑵ 增量式PID算法程序设计 由下式:
P ( k ) K p [ E ( k ) E ( k 1 ) K I ] E ( k ) K D [ E ( k ) 2 E ( k 1 ) E ( k 2 )]
设:
P P (k ) K p [E (k ) E (k 1 )]
7.4 PID参数的整定方法
一般采用经验法来选择采样周期,重要的是要根据系统 的实际运行状况来确定采样周期。
选择采样周期的经验数据如下表。
7.4 PID参数的整定方法
7.4.2 扩充临界比例度法
这是工程中常用的方法,也叫实验经验法,它适应于有 自平衡性的被控对象。方法如下:
首先,将调节器选为纯比例调节器,形成闭环,逐渐改 变比例系数,使系统对阶跃输入的响应达到临界振荡状态, 将此时的比例系数记为Kr,临界振荡的周期记为Tr。根据齐 格勒-尼科尔斯提供的经验公式,可由Tr、Kr得到不同类型 调节器的控制参数,如下表。
在计算机控制系统中,手动/自动跟踪以及手动后援是 保障系统可靠运行的重要功能。
实现的方法(自学)。
7.3 PID算法的发展
在计算机控制系统中,经常使用改进的PID算法以实现 更高的控制品质。
7.3.1 积分分离的PID算法
在常规的PID算法应用中,若系统的偏差较大时,由于 积分项的作用,会使系统产生较大的超调量,导致系统不断 的震荡,如下图。
7.1 PID算法的原理及数字实现
3. 微分调节器 微分调节的作用是对偏差的变化进行控制,并使偏
差消失在萌芽状态,其微分方程为:
微分作用响应曲线如下图所示。
7.1 PID算法的原理及数字实现
可见,微分分量对偏差的任何变化都会产生控制作用, 以调整系统输出,阻止偏差变化。偏差变化越快,则产生的 阻止作用越大。
7.1 PID算法的原理及数字实现
