2010年高考数学易错专题点睛:三角函数(精品)
高考数学压轴专题(易错题)备战高考《三角函数与解三角形》难题汇编含答案解析

A.2或 B. C. D. 或
【答案】D
【解析】
【分析】
根据函数 的图象关于直线 对称,则有 ,解得 ,得到函数再求最值.
【详解】
因为函数 的图象关于直线 对称,
所以 ,
即 ,
解得 或 ,
当 时, ,此时 的最大值为 ;
当 时, ,此时 的最大值为 ;
【详解】
解:双曲线 的右焦点为 ,双曲线 的右支上一点 ,它关于原点 的对称点为 ,满足 ,且 ,可得 , , ,
,所以 ,可得 ,
,
所以双曲线的离心率为: .
故选: .
【点睛】
本题考查双曲线的简单性质的应用,三角形的解法,考查转化思想以及计算能力,属于中档题.
4.已知函数 ,若方程 的解为 ( ),则 =()
【详解】
设灯塔位于 处,船开始的位置为 ,船行 后处于 ,如图所示,
可得 , ,
,
在三角形 中,利用正弦定理可得:
,
可得
故选
【点睛】
本题主要考查的是正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解决本题的关键,属于基础题.
17.函数 (ω>0)的图像过点(1,2),若f(x)相邻的两个零点x1,x2满足|x1-x2|=6,则f(x)的单调增区间为()
A. B. C. D.
【答案】C
【解析】
【分析】
由已知可得 ,结合x1<x2求出x1的范围,再由 求解即可.
【详解】
因为0<x ,∴ ,
又因为方程 的解为x1,x2(0<x1<x2<π),
∴ ,∴ ,
∴ ,
因为 ,∴0<x1 ,
∴ ,
2010届高考数学快速提升成绩题型训练——三角函数

2010届高考数学快速提升成绩题型训练——三角函数D3. 已知函数)cos (sin log )(21x x x f -=,(1)求它的定义域和值域;(2)求它的单调区间;(3)判断它的奇偶性; (4)判断它的周期性,如果是周期函数,求出它的最小正周期。
解析 (1)由题意得sinx-cosx >0即0)4sin(2>-πx ,从而得ππππ+<-<k x k 242,∴函数的定义域为),(45242ππππ++k k Z k ∈, ∵1)4sin(0≤-<πx ,故0<sinx-cosx≤2,所有函数f(x)的值域是),21[+∞-。
(2)单调递增区间是),452432[ππππ++k k Z k ∈ 单调递减区间是),(43242ππππ++k k Z k ∈,(3)因为f(x)定义域在数轴上对应的点不关于原点对称,故f(x)是非奇非偶函数。
(4)∵)()]2cos()2[sin(log )2(21x f x x x f =+-+=+πππ∴函数f(x)的最小正周期T=2π。
4. 已知向量a= (3,2),b =()cos ,2sin 2x x ωω-,()0>ω。
(1)若()f x a b =⋅,且)(x f 的最小正周期为π,求)(x f 的最大值,并求)(x f 取得最大值时x 的集合;(2)在(1)的条件下,)(x f 沿向量c 平移可得到函数,2sin 2x y =求向量c。
解析()f x a b =⋅=1)62sin(2cos 22sin 32--=-πωωωx x x ,T=π,1=ω=)(x f =1)62sin(2--πx ,1max =y ,这时x 的集合为⎭⎬⎫⎩⎨⎧∈+=Z k k x x ,3ππ (2) )(x f 的图象向左平移12π,再向上平移1个单位可得x y 2sin 2=的图象, 所以向量c=)1,12(π-。
5. 设函数x c x b a x f sin cos )(++=的图象经过两点(0,1),(1,2π),且在2|)(|20≤≤≤x f x 内π,求实数a 的的取值范围.解析 由图象过两点得1=a +b ,1=a +c ,)4sin()1(2)cos )(sin 1()(,1,1π+-+=+-+=-=-=∴x a a x x a a x f a c a b1)4sin(22,4344,20≤+≤∴≤+≤≤≤πππππx x x 则当a <1时,2|)(|,)21(2)(1≤-+≤≤x f a x f 要使, 只须2)21(2≤-+a 解得2-≥a 当1)()21(2,1≤≤-+>x f a a 时要使2)21(22|)(|-≥-+≤a x f 只须解得234+≤a ,故所求a 的范围是2342+≤≤-a6. 若函数)4sin(sin )2sin(22cos 1)(2ππ+++-+=x a x x x x f 的最大值为32+,试确定常数a 的值.解析 )4sin(sin )2sin(21cos 21)(22ππ+++--+=x a x x x x f)4sin(cos sin )4sin(sin cos 2cos 2222ππ+++=+++=x a x x x a x x x )4sin()2()4sin()4sin(222πππ++=+++=x a x a x因为)(x f 的最大值为)4sin(,32π++x 的最大值为1,则,3222+=+a所以a =7. 已知二次函数)(x f 对任意R ∈x ,都有)1()1(x f x f +=-成立,设向量=a (sin x ,2),=b (2sin x ,21),=c (cos2x ,1),=d (1,2),当∈x [0,π]时,求不等式f (⋅a b )>f (⋅c d )的解集.解析 设f (x )的二次项系数为m ,其图象上两点为(1-x ,1y )、B (1+x ,2y )因为12)1()1(=++-x x ,)1()1(x f x f +=-,所以21y y =, 由x 的任意性得f (x )的图象关于直线x =1对称,若m >0,则x ≥1时,f (x )是增函数,若m <0,则x ≥1时,f (x )是减函数. ∵ (sin x =⋅a b ,x sin 2()2⋅,11sin 2)212≥+=x ,(cos 2x =⋅c d ,1()1⋅,)2122cos ≥+=x ,∴ 当0>m 时,2()()(2sin 1)(cos 21)f f f x f x >⇔+>+⋅⋅a b c d1sin 22+⇔x 02cos 222cos 12cos 122cos <⇔+>+-⇔+>x x x x02cos <⇔x 2ππ2+⇔k 23ππ22+<<k x ,Z ∈k . ∵ π0≤≤x , ∴ 4π34π<<x .当0<m 时,同理可得4π0<≤x 或π4π3≤<x .综上()()f f >⋅⋅a b c d 的解集是当0>m 时,为}4π34π|{<<x x ;当0<m 时,为4π0|{<≤x x ,或}π4π3≤<x .8. 试判断方程sinx=π100x实数解的个数. 解析 方程sinx=π100x 实数解的个数等于函数y=sinx 与y=π100x 的图象交点个数 ∵|sinx|≤1∴|π100x|≤1, |x|≤100л当x≥0时,如右图,此时两线共有 100个交点,因y=sinx 与y=π100x都是奇函数,由对称性知当x≥0时,也有100个交点,原点是重复计数的所以只有199个交点。
高考数学易错点第8讲:三角函数与解三角形
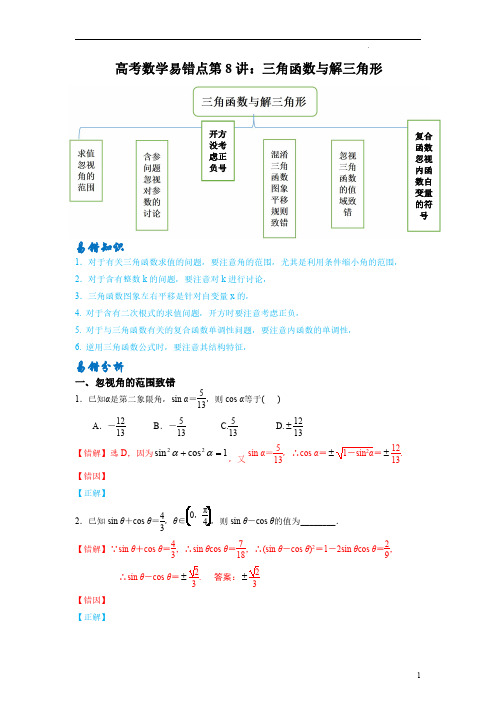
高考数学易错点第8讲:三角函数与解三角形易错知识1.对于有关三角函数求值的问题,要注意角的范围,尤其是利用条件缩小角的范围,2.对于含有整数k 的问题,要注意对k 进行讨论,3.三角函数图象左右平移是针对自变量x 的,4.对于含有二次根式的求值问题,开方时要注意考虑正负,5.对于与三角函数有关的复合函数单调性问题,要注意内函数的单调性,6.逆用三角函数公式时,要注意其结构特征,易错分析一、忽视角的范围致错1.已知α是第二象限角,sin α=513,则cos α等于()A .-1213B .-513C.513D.±1213【错解】选D ,因为1cos sin 22=+αα,又sin α=513,∴cos α=±1-sin 2α=±1213.【错因】【正解】2.已知sin θ+cos θ=43,θsin θ-cos θ的值为________.【错解】∵sin θ+cos θ=43,∴sin θcos θ=718,∴(sin θ-cos θ)2=1-2sin θcos θ=29,∴sin θ-cos θ=±23.答案:±23【错因】【正解】开方没考虑正负号复合函数忽视内函数自变量的符号3.已知θ∈(0,π),=43,则sinθ+cosθ=________.【错解】由题知=43=1+tanθ1-tanθ⇒tanθ=17,又因为θ∈(0,π),=17,sin2θ=1θ=210,θ=7210,或⎪⎪⎩⎪⎪⎨⎧-==1027cos102sinθθ,所以sinθ+cosθ=425或523-答案:425或523-【错因】【正解】4.在△ABC中,若C=3B,则cb的取值范围为()A.(0,3)B.(1,3)C.(1,3)D.(3,3)【错解】选A由正弦定理可得,cb=sin Csin B=sin3Bsin B=sin(B+2B)sin B=sin B·cos2B+cos B·sin2Bsin B =cos2B+2cos2B=4cos2B-1.又0<B<180°,∴≤0cos2B≤1,又c b>0,∴0<c b<3.【错因】【正解】二、对于含有二次根式的求值问题,开方时没有注意正负5.化简:2sin8+1+2cos8+2=()A.4cos4B.-2sin4-4cos4C.4sin4D.2sin4+4cos4【错解】选D原式=21+2sin4cos4+4cos24=2sin24+cos24+2sin4cos4+2cos4=2sin4+2cos4+2cos4=2sin4+4cos4.【错因】【正解】6.若3π2<θ<5π2,则12+1212+12cosθ等于()A.sinθ4B.cosθ4C.-sinθ4D.-cosθ4【错解】选B 由二倍角公式得12+12cos θ=1+cos θ2=cos 2θ2=cos θ2,∴12+1212+12cos θ=4cos 2212cos 21212θθ⨯=+=cos θ4【错因】【正解】三、三角函数图象左右平移时忽视自变量x 的系数致错7.为了得到函数y =sinx y =sin 2x 的图象()A .向右平移π6个单位B .向右平移π3个单位C .向左平移π6个单位D .向左平移π3个单位【错解】选B根据左加右减可知,为了得到函数y =sinx 可以将函数y =sin 2x 的图象向右平移π3个单位.【错因】【正解】8.要得到y =cos y =sin 12x 的图象()A .向左平移π3个单位B .向右平移π3个单位C .向左平移4π3个单位D .向右平移4π3个单位【错解】选A因为y =)3(21cos π+x ,故要得到y =cos只需将函数y =sin 12x 的图象向左平移π3个单位.【错因】【正解】四、涉及到整数k 的问题,忽视对k 的讨论致错9.已知角α为第一象限角,则α2是第________象限角.【错解】∵α是第一象限角,∴2k π<α<π2+2k π,k ∈Z ,∴k π<α2<π4+k π,k ∈Z ,则α2是第一象限角.答案:一【错因】【正解】10.(忽视对k 的讨论)已知A =sin (k π+α)sin α+cos (k π+α)cos α(k ∈Z),则A 的值构成的集合是________.【错解】A =sin αsin α+cos αcos α=2.答案:{2}【错因】【正解】五、含参问题忽视对参数的讨论致错11.已知角α的终边过点P (-4m,3m )(m ≠0),则2sin α+cos α=________.【错解】易知OP =(-4m )2+(3m )2=5m ,则sin α=5353=m m,cos α=5454-=-m m .故2sin α+cos α=25.答案:25【错因】【正解】六、三角函数的单调性问题中,忽视自变量x 的系数为负值致错12.函数f (x )=sin ________.【错解】要求f (x )=sin 的单调递增区间,只需令-π2+2k π≤π6-x ≤π2+2k π(k ∈Z ),可得3π-+2k π≤x ≤2π3+2k π(k ∈Z ),所以函数f (x )=sin 3[π-+2k π,2π3+2k π](k ∈Z ).答案:3[π-+2k π,2π3+2k π](k ∈Z ).【错因】【正解】七、判断三角形形状时考虑不全致错13.已知在△ABC 中,三个内角为A ,B ,C ,sin 2A =sin 2B ,则△ABC 是()A .等腰三角形B .等边三角形C .直角三角形D .等腰或直角三角形【错解】选A 因为sin 2A =sin 2B ,所以2A =2B ,解得A =B ,所以△ABC 是等腰三角形.【错因】【正解】八、忽视正切函数本身的定义域14.已知函数f(x)=lg(tan x-1)+9-x2,则f(x)的定义域是____.【错解】∵函数f(x)=lg(tan x-1)+9-x2,x-1>0,-x2≥0,∴⎪⎩⎪⎨⎧≤≤-∈+≥33,4xZkkxππ,∴x∈]343[π-,∴函数y=f(x)的定义域为]343[,π-.答案:]343[,π-【错因】【正解】易错题通关1π+π4≤α≤kπ+π2,k∈(阴影部分)是()2.在△ABC中,若sin2A=sin2C,则△ABC的形状是()A.等边三角形B.等腰三角形C.直角三角形D.等腰三角形或直角三角形3.已知角θ的顶点与原点重合,始边与x轴非负半轴重合,若A(-1,y)是角θ终边上的一点,且sinθ=-31010,则y=()A.3B.-3C.1D.-14.已知θ是第三象限角,且cos(π+θ)=13,则tanθ=()A.24B.2C.22 D.105.已知α终边与单位圆的交点α是第二象限角,则1-sin2α+2+2cos2α的值等于()A.15B.-15C.3D.-36.设α角属于第二象限,且|cosα2|=-cosα2,则α2角属于()A.第一象限B.第二象限C.第三象限D.第四象限7.已知sin α,cos α是方程x 2-2kx +k 2+k =0的两根,则k 的值为()A.1±32 B.1-32C .1±3D .1+38.若θ∈(0,π),tan θ+1tan θ=6,则sin θ+cos θ=()A .233B .-233C .±233D .239.在△ABC 中,cos A =513,sin B =35,则cos C 的值为()A.1665B .-5665C .-1665D.1665或-566510.已知cos α=255,sin β=1010,且α∈0,π2,β∈0,π2,则α+β的值是()A.3π4B.π4C.7π4D.5π411.已知φ∈R,则“φ=0”是“y =sin(x +φ)为奇函数”的()A .充分不必要条件B .充要条件C .必要不充分条件D .既不充分也不必要条件12.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a cos A =b cos B ,且c 2=a 2+b 2-ab ,则△ABC 的形状为()A .等腰三角形或直角三角形B .等腰直角三角形C .直角三角形D .等边三角形13.把函数f (x )=2cos 2x -π4的图象向左平移m (m >0)个单位,得到函数g (x )=2sin 2x -π3的图象,则m 的最小值是()A.724π B.1724π C.524π D.1924π14.已知ω>0,函数f (x )=sin ωx +π4在区间π2,π上单调递减,则实数ω的取值范围是()A.12,54B.12,34C .0,12D .(0,2]15.已知函数y =sin(ωx +φ)ω>0,|φ|<π2的图象的一部分如图所示,则ω,φ的值分别为()A .1,π3B .1,-π3C .2,-π3D .2,π316.已知函数f (x )=sinωx +π6(ω>0),对任意x ∈R ,都有f (x )≤f π3,并且f (x )在区间-π6,π3上不单调,则ω的最小值是()A .1B .3C .5D .717.(多选)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若b =23,c =3,A +3C =π,则下列结论正确的是()A .cos C =33B .sin B =23C .a =3D .S △ABC =218.(多选题)如图是函数y =sin(ωx +φ)的部分图象,则sin(ωx +φ)=()A .B .2C .xD .219.若0<α<π2,-π<β<-π2,=13,=-33,则()A .-539B.539C .-33D.3320.已知角α的终边经过点(3a -9,a +2),且cos α≤0,sin α>0,则实数a 的取值范围是________.21.已知函数f (x )=2sin(ωx +φ)(ω>0,-π<φ<0)的相邻两个零点间的距离为π2,且-2,则φ=________.22.化简sin (n π+α)cos (n π-α)cos[(n +1)π-α](n ∈Z)的结果为________.23.在锐角△ABC 中,BC =2,sin B +sin C =2sin A ,则中线AD 长的取值范围是________.24.若sin 2α=55,sin(β-α)=1010,且α∈π4,π,β∈π,3π2,则α+β的值是________.25.设f (x )=m x m -1(m ≠0).(1)若m =2,求函数f (x )的零点;(2)当x ∈0,π2时,-3≤f (x )≤4恒成立,求实数m 的取值范围.参考答案一、忽视角的范围致错1.已知α是第二象限角,sin α=513,则cos α等于()A .-1213B .-513C.513D.±1213【错解】选D ,因为1cos sin 22=+αα,又sin α=513,∴cos α=±1-sin 2α=±1213.【错因】没有注意条件α是第二象限角,【正解】选A∵α是第二象限角,则cos α>0,∴cos α=-1-sin 2α=-1213.2.已知sin θ+cos θ=43,θsin θ-cos θ的值为________.【错解】∵sin θ+cos θ=43,∴sin θcos θ=718,∴(sin θ-cos θ)2=1-2sin θcos θ=29,∴sin θ-cos θ=±23.答案:±23【错因】没有注意由条件θsin θ<cos θ,【正解】∵sin θ+cos θ=43,∴sin θcos θ=718,∴(sin θ-cos θ)2=1-2sin θcos θ=29,又θsin θ<cos θ,∴sin θ-cos θ=-23.答案:-233.已知θ∈(0,π),=43,则sin θ+cos θ=________.【错解】由题知=43=1+tan θ1-tan θ⇒tan θ=17,又因为θ∈(0,π),=17,sin 2θ=1θ=210,θ=7210,或⎪⎪⎩⎪⎪⎨⎧-==1027cos 102sin θθ,所以sin θ+cos θ=425或523-答案:425或523-【错因】没有注意由tan θ=17>0可以缩小角的范围,即可推出θ【正解】由题知=43=1+tan θ1-tan θ⇒tan θ=17,又因为θ∈(0,π),且tan θ>0,所以θ∈=17,sin 2θ=1θ=210,θ=7210,所以sin θ+cos θ=8210=425.答案:4254.在△ABC 中,若C =3B ,则cb的取值范围为()A .(0,3)B .(1,3)C .(1,3)D .(3,3)【错解】选A由正弦定理可得,c b =sin C sin B =sin 3B sin B =sin (B +2B )sin B =sin B ·cos 2B +cos B ·sin 2Bsin B=cos 2B +2cos 2B =4cos 2B -1.又0<B <180°,∴≤0cos 2B ≤1,又c b >0,∴0<cb<3.【错因】忽略了A +B +C =180°及条件C =3B ,【正解】选B由正弦定理可得,c b =sin C sin B =sin 3B sin B =sin (B +2B )sin B =sin B ·cos 2B +cos B ·sin 2Bsin B=cos 2B +2cos 2B =4cos 2B -1.又A +B +C =180°,C =3B ,∴0°<B <45°,∴22cos B <1,∴1<4cos 2B -1<3,即1<cb<3.二、对于含有二次根式的求值问题,开方时没有注意正负5.化简:2sin 8+1+2cos 8+2=()A .4cos 4B .-2sin 4-4cos 4C .4sin 4D .2sin 4+4cos 4【错解】选D原式=21+2sin 4cos 4+4cos 24=2sin 24+cos 24+2sin 4cos 4+2cos 4=2sin 4+2cos 4+2cos 4=2sin 4+4cos 4.【错因】开方时没有考虑2cos 4、sin 4+cos 4的正负,【正解】选B原式=21+2sin 4cos 4+4cos 24=2sin 24+cos 24+2sin 4cos 4+2|cos 4|=2|sin 4+cos 4|+2|cos 4|,∵π<4<3π2,∴sin 4+cos 4<0,cos 4<0,∴原式=-2(sin 4+cos 4)-2cos 4=-2sin 4-4cos 4.6.若3π2<θ<5π2,则12+1212+12cos θ等于()A .sinθ4B .cosθ4C .-sinθ4D .-cosθ4【错解】选B 由二倍角公式得12+12cos θ=1+cos θ2=cos 2θ2=cos θ2,∴12+1212+12cos θ=4cos 2212cos 21212θθ⨯=+=cos θ4【错因】没有用3π2<θ<5π2去求θ2、θ2的范围,【正解】选A∵3π2<θ<5π2,∴3π4<θ2<5π4,3π8<θ4<5π8,∴cos θ>0,cos θ2<0,sin θ4>0,∴12+12cos θ=1+cos θ2=cos 2θ2=-cos θ2,∴12+1212+12cos θ=1-cosθ22=sin 2θ4=sin θ4.三、三角函数图象左右平移时忽视自变量x 的系数致错7.为了得到函数y =sinx y =sin 2x 的图象()A .向右平移π6个单位B .向右平移π3个单位C .向左平移π6个单位D .向左平移π3个单位【错解】选B根据左加右减可知,为了得到函数y =sinx 可以将函数y =sin 2x 的图象向右平移π3个单位.x,【正解】选A ∵函数y =x sin 2∴为了得到函数y =sinx 可以将函数y =sin 2x 的图象向右平移π6个单位.8.要得到y =cos y =sin 12x 的图象()A .向左平移π3个单位B .向右平移π3个单位C .向左平移4π3个单位D .向右平移4π3个单位【错解】选A因为y =)3(21cos π+x ,故要得到y =cos只需将函数y =sin 12x 的图象向左平移π3个单位.【错因】函数图象平移变换时,没注意函数的名称是不一致的,不能直接进行平移,【正解】选Cy =+π6+y =cos图象,只需将函数y =sin 12x 的图象向左平移4π3个单位.四、涉及到整数k 的问题,忽视对k 的讨论致错9.已知角α为第一象限角,则α2是第________象限角.【错解】∵α是第一象限角,∴2k π<α<π2+2k π,k ∈Z ,∴k π<α2<π4+k π,k ∈Z ,则α2是第一象限角.答案:一【错因】没有对k 分情况讨论,【正解】∵α是第一象限角,∴2k π<α<π2+2k π,k ∈Z ,∴k π<α2<π4+k π,k ∈Z ,当k 为偶数时,α2是第一象限角;当k 为奇数时,α2是第三象限角.综上,α2是第一或第三象限角.答案:一或三10.(忽视对k 的讨论)已知A =sin (k π+α)sin α+cos (k π+α)cos α(k ∈Z),则A 的值构成的集合是________.【错解】A =sin αsin α+cos αcos α=2.答案:{2}【错因】没有对k 分情况讨论,【正解】当k 为奇数时:A =-sin αsin α-cos αcos α=-2.当k 为偶数时:A =sin αsin α+cos αcos α=2.答案:{-2,2}五、含参问题忽视对参数的讨论致错11.已知角α的终边过点P (-4m,3m )(m ≠0),则2sin α+cos α=________.【错解】易知OP =(-4m )2+(3m )2=5m ,则sin α=5353=m m,cos α=5454-=-m m .故2sin α+cos α=25.答案:25【错因】没有对参数m 分情况讨论,【正解】易知OP =(-4m )2+(3m )2=5|m |,则sin α=3m5|m |,cos α=-4m 5|m |.当m >0时,sin α=35,cos α=-45,2sin α+cos α=25;当m <0时,sin α=-35,cos α=45,∴2sin α+cos α=-25.故2sin α+cos α=±25.答案:±25六、三角函数的单调性问题中,忽视自变量x 的系数为负值致错12.函数f (x )=sin________.【错解】要求f (x )=sin的单调递增区间,只需令-π2+2k π≤π6-x ≤π2+2k π(k ∈Z ),可得3π-+2k π≤x ≤2π3+2k π(k ∈Z ),所以函数f (x )=sin3[π-+2k π,2π3+2k π](k ∈Z ).答案:3[π-+2k π,2π3+2k π](k ∈Z ).【错因】没有注意自变量x 的系数是负数,【正解】因为f (x )=f (x )=sin只需要求y =sin的单调递减区间.令π2+2k π≤x -π6≤3π2+2k π(k ∈Z ),可得2π3+2k π≤x ≤5π3+2k π(k ∈Z ),所以y =sin2π3+2k π,5π3+2k π(k ∈Z ),此即为函数f (x)=sin答案:2π3+2k π,5π3+2k π(k ∈Z )七、判断三角形形状时考虑不全致错13.已知在△ABC 中,三个内角为A ,B ,C ,sin 2A =sin 2B ,则△ABC 是()A .等腰三角形B .等边三角形C .直角三角形D .等腰或直角三角形【错解】选A因为sin 2A =sin 2B ,所以2A =2B ,解得A =B ,所以△ABC 是等腰三角形.【错因】sin 2A =sin 2B 时,有两种可能:2A =2B 或2A =π-2B ,【正解】选D因为sin 2A =sin 2B ,所以2A =2B 或2A =π-2B ,解得A =B 或A +B =π2,所以△ABC 是等腰或直角三角形.八、忽视正切函数本身的定义域14.已知函数f (x )=lg (tan x -1)+9-x 2,则f (x )的定义域是____.【错解】∵函数f (x )=lg (tan x -1)+9-x 2,x -1>0,-x 2≥0,∴⎪⎩⎪⎨⎧≤≤-∈+≥33,4x Z k k x ππ,∴x ∈]343[π-,∴函数y =f (x )的定义域为]343[,π-.答案:]343[,π-【错因】没有考虑x y tan =的定义域,【正解】∵函数f (x )=lg (tan x -1)+9-x 2,x -1>0,-x 2≥0,π+π4<x <k π+π2(k ∈Z ),3≤x ≤3,∴x -3π4,-∴函数y =f (x )-3π4,--3π4,-易错题通关1π+π4≤α≤k π+π2,k ∈(阴影部分)是()【答案】C【解析】当k =2n (n ∈Z)时,2n π+π4≤α≤2n π+π2(n ∈Z),此时α的终边和π4≤α≤π2的终边一样;当k =2n +1(n ∈Z)时,2n π+π+π4≤α≤2n π+π+π2(n ∈Z),此时α的终边和π+π4≤α≤π+π2的终边一样,结合选项知选C.2.在△ABC 中,若sin 2A =sin 2C ,则△ABC 的形状是()A .等边三角形B .等腰三角形C .直角三角形D .等腰三角形或直角三角形【答案】D【解析】因为sin 2A =sin 2C ⇒sin 2A =sin(π-2C ),所以A =C 或A +C =π2.当A =C 时,三角形为等腰三角形;当A +C =π2时,三角形为直角三角形.3.已知角θ的顶点与原点重合,始边与x 轴非负半轴重合,若A (-1,y )是角θ终边上的一点,且sin θ=-31010,则y =()A .3B .-3C .1D .-1【答案】B【解析】因为sin θ=-31010<0,A (-1,y )是角θ终边上一点,所以y <0,由三角函数的定义,得y y 2+1=-31010.解得y =-3.4.已知θ是第三象限角,且cos(π+θ)=13,则tan θ=()A.24B .2C .22 D.10【答案】C【解析】cos(π+θ)=-cos θ=13,所以cos θ=-13,又θ是第三象限角,所以sin θ=-1-cos 2θ=-=-223,所以tan θ=sin θcos θ=-223-13=22.5.已知α终边与单位圆的交点α是第二象限角,则1-sin 2α+2+2cos 2α的值等于()A.15B .-15C .3D .-3【答案】C【解析】因为α终边与单位圆的交点α是第二象限角,所以sin α=35,cos α=-45,则1-sin 2α+2+2cos 2α=1-2sin α·cos α+2(1+cos 2α)=(sin α-cos α)2|sin α-cos α|+2|cos α|=75+85=3.6.设α角属于第二象限,且|cos α2|=-cos α2,则α2角属于()A .第一象限B .第二象限C .第三象限D .第四象限【答案】C【解析】∵α是第二象限角,∴90°+k ·360<α<180°+k ·360°,k ∈Z ,∴45°+k ·180°<α2<90°+k ·180°,k ∈Z.当k =2n ,n ∈Z 时,α2在第一象限;当k =2n +1,n ∈Z 时,α2在第三象限,∴α2在第一象限或在第三象限,∵|cos α2|=-cos α2,∴cos α2<0,∴α2角在第三象限.7.已知sin α,cos α是方程x 2-2kx +k 2+k =0的两根,则k 的值为()A.1±32 B.1-32C .1±3D .1+3【答案】B【解析】α+cos α=2k ,αcos α=k 2+k ,∵sin 2α+cos 2α=(sin α+cos α)2-2sin αcos α=4k 2-2(k 2+k )=1,即2k 2-2k -1=0,解得k =2±234=1±32.∵sin α+cos α=2sin ∴sin α+cos α∈[-2,2],即2k ∈[-2,2],∴k ∈-22,22,∴k =1-32.9.若θ∈(0,π),tan θ+1tan θ=6,则sin θ+cos θ=()A .233B .-233C .±233D .23【答案】A【解析】因为tan θ+1tan θ=sin θcos θ+cos θsin θ=sin 2θ+cos 2θsin θcos θ=6,所以sin θcos θ=16,又θ∈(0,π),则sin θ>0,cos θ>0,所以sin θ+cos θ>0.所以(sin θ+cos θ)2=1+2sin θcos θ=43,所以sin θ+cos θ=233.9.在△ABC 中,cos A =513,sin B =35,则cos C 的值为()A.1665B .-5665C .-1665D.1665或-5665【答案】A【解析】在△ABC 中,由cos A =513,sin B =35,可得sin A =1-cos 2A =1213,因为sin B <sin A 且A 为锐角,则b <a ,所以A >B ,所以B 为锐角,所以cos B =1-sin 2B =45,则cos C =cos [π-(A +B )]=-cos(A +B )=-cos A cos B +sin A sin B =-513×45+1213×35=1665.10.已知cos α=255,sin β=1010,且αβα+β的值是()A.3π4B.π4C.7π4D.5π4【答案】B【解析】因为αβ所以sin α=1-cos 2α=55,cos β=1-sin 2β=31010,cos(α+β)=cos αcos β-sin αsin β=255×31010-55×1010=22.又0<α+β<π,故α+β=π4.11.已知φ∈R,则“φ=0”是“y =sin(x +φ)为奇函数”的()A .充分不必要条件B .充要条件C .必要不充分条件D .既不充分也不必要条件【答案】A【解析】当φ=0时,y =sin(x +φ)为奇函数;当y =sin(x +φ)是奇函数时,φ=k π,k ∈Z ,所以“φ=0”是“y =sin(x +φ)为奇函数”的充分不必要条件,故选A.13.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a cos A =b cos B ,且c 2=a 2+b 2-ab ,则△ABC 的形状为()A .等腰三角形或直角三角形B .等腰直角三角形C .直角三角形D .等边三角形【答案】D【解析】因为a cos A =b cos B ,所以sin A cos A =sin B cos B ,即sin 2A =sin 2B ,又A ,B ∈(0,π),故可得A =B 或A +B =π2.由c 2=a 2+b 2-ab ,得cos C =12,又C ∈(0,π),故可得C =π3.综上所述,A =B =C =π3.故三角形ABC 是等边三角形.13.把函数f (x )=2cos x m (m >0)个单位,得到函数g (x )=2sin x 图象,则m 的最小值是()A.724π B.1724π C.524π D.1924π【答案】B【解析】选B把函数f (x )=2cosx m (m >0)个单位,得到f (x )=2cos2(x +m )-π4=2cos x +2mg (x )=x 2cos π2-x 2x 由2m -π4=-5π6+2k π,k ∈Z ,得m =-7π24+k π,k ∈Z ,∵m >0,∴当k =1时,m 最小,此时m =π-7π24=17π24.14.已知ω>0,函数f (x )=sin 在区间π2,π上单调递减,则实数ω的取值范围是()A.12,54B.12,34C ,12D .(0,2]【答案】A【解析】由π2≤x ≤π,得π2ω+π4≤ωx +π4≤πω+π4,由题意π2ω+π4,πω+π4⊆2k π+π2,2k π+3π2(k ∈Z ).当k =0+π4≥π2,+π4≤3π2,得12≤ω≤54.15.已知函数y =sin(ωx +φ>0,|φ|则ω,φ的值分别为()A .1,π3B .1,-π3C .2,-π3D .2,π3【答案】D【解析】由图象知,T 4=7π12-π3=π4,即T =π,所以2πω=π,即ω=2.2×π3+φ=k π,k ∈Z ,又|φ|<π2,故φ=π3,故选D.16.已知函数f(x )=(ω>0),对任意x ∈R ,都有f (x )≤并且f (x )在区间-π6,π3上不单调,则ω的最小值是()A .1B .3C .5D .7【答案】D【解析】由题意,f f (x )的最大值,∴ωπ3+π6=2k π+π2,k ∈Z ,即ω=6k +1,k ∈Z .∵ω>0,∴k ∈N .当k =0时,ω=1,f(x )=sin 在-π6,π3上单调递增,不符合题意;当k =1时,ω=7,f(x )=sinx ω的最小值是7.17.(多选)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .若b =23,c =3,A +3C =π,则下列结论正确的是()A .cos C =33B .sin B =23C .a =3D .S△ABC =2【答案】AD【解析】选AD 由A +3C =π,得B =2C .根据正弦定理b sin B =c sin C,得23sin C =3×2sin C cos C ,又sin C >0,故cos C =33,sin C =63,故A 正确;sin B =sin 2C =2sin C cos C =223,故B 错误;由余弦定理得c 2=a 2+b 2-2ab cos C ,将b =23,c =3代入得a 2-4a +3=0,解得a =3或a =1.若a =3,则A =C =π4,且B =π2,与sin B =223矛盾,所以a =1,故C 错误;S △ABC =12ab sin C =12×1×23×63=2,故D 正确.故选A 、D.18.(多选题)如图是函数y =sin(ωx +φ)的部分图象,则sin(ωx +φ)=()A .B .2C .xD .2【答案】BC【解析】由题图可知,函数的最小正周期T =π,∴2π|ω|=π,ω=±2.当ω=2时,y =sin(2x +φ)×π6+0,∴2×π6+φ=2k π+π,k ∈Z ,即=2k π+2π3,k ∈Z ,∴y =x 故A 错误;由x sin π2sin 2B 正确;由x x +π2+cos x C 正确;由x x cos πx cos 2D 错误.综上可知,正确的选项为B 、C.20.若0<α<π2,-π<β<-π2,=13,=-33,则()A .-539B.539C .-33D.33【答案】D【解析】∵0<α<π2,-π<β<-π2,则π4<π4+α<3π4,π2<π4-β2<3π4,∴=223,=63,因此,=13×+223×63=33.20.已知角α的终边经过点(3a -9,a +2),且cos α≤0,sin α>0,则实数a 的取值范围是________.【答案】(-2,3]【解析】∵cos α≤0,sin α>0,∴角α的终边落在第二象限或y 轴的正半轴上.∴a -9≤0,+2>0,∴-2<a ≤3.21.已知函数f (x )=2sin(ωx +φ)(ω>0,-π<φ<0)的相邻两个零点间的距离为π2,且-2,则φ=________.【答案】-π4【解析】由题意T =2×π2=π,ω>0,所以ω=2πT=2,-π4+2,-π4+φ=2k π-π2,k ∈Z ,又-π<φ<0,所以φ=-π4.22.化简sin (n π+α)cos (n π-α)cos[(n +1)π-α](n ∈Z)的结果为________.【答案】(-1)n +1sin α(n ∈Z)【解析】①当n =2k (k ∈Z)时,原式=sin (2k π+α)cos (2k π-α)cos[(2k +1)π-α]=sin αcos α-cos α=-sin α.②当n =2k +1(k ∈Z)时,原式=sin[(2k +1)π+α]cos[(2k +1)π-α]cos[(2k +2)π-α]=(-sin α)(-cos α)cos α=sin α.综上,化简的结果为(-1)n +1sin α(n ∈Z).23.在锐角△ABC 中,BC =2,sin B +sin C =2sin A ,则中线AD 长的取值范围是________.【答案】3【解析】设AB =c ,AC =b ,BC =a =2,对sin B +sin C =2sin A 运用正弦定理,得b +c =2a =4,解得c =4-b ,结合该三角形为锐角三角形,得到不等式组2+c 2=b 2+(4-b )2>4,2+4=(4-b )2+4>b 2,2+4>c 2=(4-b )2,解得32<b <52,故bc =b (4-b )=-b 2+4b ,结合二次函数的性质,得到154<bc ≤4.运用向量得到AD ―→=12(AB ―→+AC ―→),所以|AD ―→|=12AB 2―→+AC 2―→+2|AB ―→|·|AC ―→|·cos ∠BAC=12b 2+c 2+2bc ·b 2+c 2-42bc=122b 2+2c 2-4=1228-4bc ,结合bc 的范围,得|AD ―→|的范围为324.若sin 2α=55,sin(β-α)=1010,且α∈π4,π,β∈π,3π2,则α+β的值是________.【答案】7π4【解析】∵α∈π4,π,β∈π,3π2,∴2α∈π2,2π,又0<sin 2α=55<12,∴2ααβ-α∴cos 2α=-1-sin 22α=-255.又sin(β-α)=1010,∴β-α∴cos(β-α)=-1-sin 2(β-α)=-31010,∴cos(α+β)=cos[2α+(β-α)]=cos 2αcos(β-α)-sin 2αsin(β-α)=-255×-55×1010=22.又αβ∈π,3π2,∴α+βα+β=7π4.25.设f (x )=m x m -1(m ≠0).(1)若m =2,求函数f (x )的零点;(2)当x ∈0,π2时,-3≤f (x )≤4恒成立,求实数m 的取值范围.解:(1)由m =2⇒f (x )=x 1,令f (x )=0,则x =-12,即2x -π3=2k π+2π3或2x -π3=2k π+4π3(k ∈Z ),解得x =k π+π2或x =k π+5π6(k ∈Z ),21∴f (x )的零点是x =k π+π2或x =k π+5π6(k ∈Z ).(2)由0≤x ≤π2可得-π3≤2x -π3≤2π3,所以-12≤x1.①当m >0时,易得m 2-1≤f (x )≤2m -1,由-3≤f (x )≤4x )min ≥-3,x )max ≤4,1≥-3,-1≤4,,解得0<m ≤52;②当m <0时,可得2m -1≤f (x )≤m 2-1,由-3≤f (x )≤4x )min ≥-3,x )max ≤4,-1≥-3,1≤4,,解得-1≤m <0.综上可得,m的取值范围是[-1,0),52.。
2010年全国高考数学试题分类汇编——三角函数

y sin(2x ) 的图像 6
(A)向左平移 个长度单位
4
(C)向左平移 个长度单位
2
(2010 陕西文数)3.函数 f (x)=2sinxcosx 是
(A)最小正周期为 2π 的奇函数
(C)最小正周期为 π 的奇函数
(B)必要而不充分条件
(D)既不充分也不必要条件
(2010 辽宁文数)(6)设 0 ,函数 y sin( x ) 2 的图像向右平移 4 个单位后
(A) f (x)
(B) f (x)
(2010 北京文数)(7)某班设计了一个八边形的班徽(如 图),它由腰长为 1,
顶角为 的四个等腰三角形,及其底边构成的正方形所组
成, 该八边形的面积为
(A) 2sin 2 cos 2 ; (B) sin 3 cos 3
(C) 3sin 3 cos 1 ; (D) 2sin cos 1
2010 年全国高考数学试题分类汇编——三角函数
(2010 上海文数)18.若△ ABC 的三个内角满足 sin A : sin B : sin C 5 :11:13 ,则△ ABC
(A)一定是锐角三角形.
(C)一定是钝角三角形.
(B)一定是直角三角形.
(D)可能是锐角三角形,也可能是钝角三角形.
(2010 福建文数)2.计算1 2 sin 22.5 的结果等于( )
第 3 页 共 12 页
(C)1200
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,通系电1,力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配,机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2,下卷而高总且中体可资配保料置障试时2卷,32调需3各控要类试在管验最路;大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷,下安要与全加过,强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中;中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整,理核或高对者中定对资值某料,些试审异卷核常弯与高扁校中度对资固图料定纸试盒,卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置,接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资,,料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气,敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术,技线以来术槽及避、系免管统不架启必等动要多方高项案中方;资式对料,整试为套卷解启突决动然高过停中程机语中。文高因电中此气资,课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试,且技合进术理行,利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。:对对在于于分调差线试动盒过保处程护,中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技,,术应作是采为指用调发金试电属人机隔员一板,变进需压行要器隔在组开事在处前发理掌生;握内同图部一纸故线资障槽料时内、,设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷,试切线验除缆报从敷告而设与采完相用毕关高,技中要术资进资料行料试检,卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
2010年全国高考数学试题分类汇编——三角函数(1)

2010年全国高考数学试题分类汇编-—三角函数(2010上海文数)18.若△ABC 的三个内角满足sin :sin :sin 5:11:13A B C =,则△ABC (A)一定是锐角三角形. (B )一定是直角三角形。
(C)一定是钝角三角形。
(D )可能是锐角三角形,也可能是钝角三角形.(2010湖南文数)7.在△ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c ,若∠C=120°,a,则A 。
a >bB 。
a <bC 。
a =bD 。
a 与b 的大小关系不能确定(2010浙江理数)(9)设函数()4sin(21)f x x x =+-,则在下列区间中函数()f x 不.存在零点的是(A )[]4,2-- (B )[]2,0- (C )[]0,2 (D )[]2,4 (2010浙江理数)(4)设02x π<<,则“2sin 1x x <”是“sin 1x x <”的(A )充分而不必要条件 (B )必要而不充分条件 (C )充分必要条件 (D)既不充分也不必要条件 (2010全国卷2理数)(7)为了得到函数sin(2)3y x π=-的图像,只需把函数sin(2)6y x π=+的图像(A )向左平移4π个长度单位 (B)向右平移4π个长度单位(C )向左平移2π个长度单位 (D )向右平移2π个长度单位(2010陕西文数)3。
函数f (x )=2sin x cos x 是(A )最小正周期为2π的奇函数 (B )最小正周期为2π的偶函数 (C)最小正周期为π的奇函数 (D)最小正周期为π的偶函数 (2010辽宁文数)(6)设0ω>,函数sin()23y x πω=++的图像向右平移43π个单位后与原图像重合,则ω的最小值是(A )23 (B ) 43 (C ) 32(D ) 3 (2010全国卷2文数)(3)已知2sin 3α=,则cos(2)x α-=(A)B)19-(C )19(D(2010江西理数)7.E,F 是等腰直角△ABC 斜边AB 上的三等分点,则tan ECF ∠=( )A 。
2010年高考数学试题三角函数部分解析及应对策略

2010年高考数学试题三角函数部分解析及应对策略一、考情分析三角函数是基本初等函数之一,三角函数与三角恒等变换结合是高考考查的重点内容之一,也是高考的热点之一。
通读2010年全国各地的高考试题发现有如下特点:1、有关三角函数的试题在客观题、主观题均有所体现,一般情况是选择题一个,填空题一个,解答题一个,解答题一般处于大题第一个题的位置。
总分值占到25分左右。
2、考小题,重在基础运用考查的重点在于基础知识:解析式、图像及图像变换、两域(定义域、值域)、四性(单调性、奇偶性、对称性、周期性)、简单的三角变换(求值、化简及比较大小)以及在三角形中结合正余弦定理考察。
3、考大题,难度明显降低有关三角函数的大题即解答题,一般都是通过降幂,或者两角和差的三角公式,最后通过辅助角公式化成标准形式b wx A y ++=)sin(φ的形式,然后再研究四性,或者求值化简。
难度明显降低,只要熟记公式即可。
4、考应用,融入三角图形之中这种题型既能考查解三角形的知识与方法,又能考查运用三角公式进行恒等变换的技能。
主要解法是充分利用三角形的内角和定理、正(余)弦定理、面积公式等,并结合三角公式进行三角变换,从而获解。
5、考综合,体现三角函数的工具性由于近年高考命题突出以能力立意,加强对知识综合性和应用性的考查,故常常在知识的交汇点处命题。
因而对三角知识的考查总是与平面向量、数列、立体几何、解析几何、导数等综合在一起来考查,突出三角的工具性作用。
二、常考题型及应对策略1、考察三角函数图像、四性(单调性、周期性、奇偶性、对称性)、最值、定义域、值域。
应对策略是利用诱导公式、降幂公式、和差角公式、辅助角公式化成标准形式b φ)Asin(wx y ++=,然后求解。
1、(2010陕西文数)函数f (x )=2sin x cos x 是[C](A)最小正周期为2π的奇函数 (B )最小正周期为2π的偶函数 (C)最小正周期为π的奇函数(D )最小正周期为π的偶函数解析:本题考查三角函数的性质f (x )=2sin x cos x=sin2x ,周期为π的奇函数 2、(2010江西理数)已知函数()()21cot sin sin sin 44f x x x m x x ππ⎛⎫⎛⎫=+++- ⎪ ⎪⎝⎭⎝⎭(1) 当m=0时,求()f x 在区间384ππ⎡⎤⎢⎥⎣⎦,上的取值范围; (2) 当tan 2a =时,()35f a =,求m 的值。
高考数学压轴专题(易错题)备战高考《三角函数与解三角形》单元汇编及答案解析

新数学复习题《三角函数与解三角形》专题解析一、选择题1.已知ABC V 的内角,,A B C 的对边分别为,,a b c ,且cos cos a B b A +=,1a =,b =c =( )A B .1CD 【答案】B 【解析】 【分析】先由正弦定理将cos cos 2cos a B b A C+=中的边转化为角,可得sin()A B +=可求出角6C π=,再利用余弦定理可求得结果.【详解】解:因为cos cos a B b A +=,所以正弦定理得,sin cos sin cos 2cos CA B B A C+=所以sin()A B +=sin C =因为sin 0C ≠,所以cos C =, 又因为(0,)C π∈,所以6C π=,因为1a =,b =所以由余弦定理得,2222cos 13211c a b ab C =+-=+-⨯=, 所以1c = 故选:B 【点睛】此题考查的是利用正、余弦定理解三角形,属于中档题.2.已知函数()sin f x a x x =的一条对称轴为56x π=,函数()f x 在区间()12,x x 上具有单调性,且()()12f x f x =-,则下述四个结论:①实数a 的值为1;②()()1,x f x 和()()22,x f x 两点关于函数()f x 图象的一条对称轴对称; ③21x x -的最大值为π, ④12x x +的最小值为23π. 其中所有正确结论的编号是( ) A .①②③ B .①③④C .①④D .③④【答案】B 【解析】 【分析】 根据56x π=是函数()f x 的一条对称轴,确定函数()f x ,再根据函数()f x 在区间()12,x x 上具有单调性,得到21x x -的最大值为2Tπ=,然后由()()12f x f x =-,得到()()11,x f x 和()()22,x f x 两点关于函数()f x 的一个对称中心对称求解验证.【详解】∵56x π=是函数()f x 的一条对称轴,∴()53f x f x π⎛⎫=- ⎪⎝⎭,令0x =,得()503f f π⎛⎫=⎪⎝⎭,即-1a =,①正确; ∴()sin 2sin 3π⎛⎫=-=- ⎪⎝⎭f x x x x .又因为函数()f x 在区间()12,x x 上具有单调性, ∴21x x -的最大值为2Tπ=,且()()12f x f x =-, ∴()()11,x f x 和()()22,x f x 两点关于函数()f x 的一个对称中心对称,∴121233223x x x x k ππ⎛⎫⎛⎫-+- ⎪ ⎪+π⎝⎭⎝⎭=-=π,k Z ∈, ∴12223x x k ππ+=+,k Z ∈,当0k =时,12x x +取最小值23π,所以①③④正确,②错误. 故选:B 【点睛】本题主要考查三角函数的图象和性质,还考查了推理论证,运算求解的能力,属于中档题.3.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a ﹣c cos B )sin A =c cos A sin B ,则△ABC 的形状一定是( ) A .钝角三角形 B .直角三角形 C .等腰三角形 D .锐角三角形【答案】C 【解析】 【分析】根据题意,由(cos )sin cos sin a c B A c A B -=变形可得sin sin a A c C =,进而由正弦定理可得22a c =,即a c =,即可得答案. 【详解】根据题意,在ABC ∆中,(cos )sin cos sin a c B A c A B -=, 变形可得:sin cos sin cos sin (cos sin cos sin )sin()sin a A c B A c A B c B A A B c A B c C =+=+=+=,即有sin sin a A c C =,又由正弦定理可得22a c =,即a c =. 故选:C . 【点睛】本题主要考查三角形的形状判断,考查正弦定理的应用,意在考查学生对这些知识点的理解掌握水平,属于基础题.4.函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象的交点横坐标的和为( ) A .53π B .2πC .76π D .π【答案】B 【解析】 【分析】根据两个函数相等,求出所有交点的横坐标,然后求和即可. 【详解】令sin cos2x x =,有2sin 12sin x x =-,所以sin 1x =-或1sin 2x =.又[],2x ππ∈-,所以2x π=-或32x π=或6x π=或56x π=,所以函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象交点的横坐标的和3522266s πππππ=-+++=,故选B. 【点睛】本题主要考查三角函数的图象及给值求角,侧重考查数学建模和数学运算的核心素养.5.如图,边长为1正方形ABCD ,射线BP 从BA 出发,绕着点B 顺时针方向旋转至BC ,在旋转的过程中,记([0,])2ABP x x π∠=∈,BP 所经过的在正方形ABCD 内的区域(阴影部分)的面积为()y f x =,则函数()f x 的图像是( )A .B .C .D .【答案】D 【解析】 【分析】根据条件列()y f x =,再根据函数图象作判断. 【详解】 当0,4x π⎡⎤∈⎢⎥⎣⎦时,()112y f x tanx ==⨯⨯; 当,42x ππ⎛⎤∈⎥⎝⎦时,()11112y f x tanx ==-⨯⨯; 根据正切函数图象可知选D. 【点睛】本题考查函数解析式以及函数图象,考查基本分析识别能力,属基本题.6.设函数f (x )=cos (x +3π),则下列结论错误的是 A .f(x)的一个周期为−2πB .y=f(x)的图像关于直线x=83π对称C .f(x+π)的一个零点为x=6π D .f(x)在(2π,π)单调递减 【答案】D 【解析】f (x )的最小正周期为2π,易知A 正确; f 8π3⎛⎫⎪⎝⎭=cos 8ππ33⎛⎫+ ⎪⎝⎭=cos3π=-1,为f (x )的最小值,故B 正确; ∵f (x +π)=cos ππ3x ⎛⎫++ ⎪⎝⎭=-cos π3x ⎛⎫+ ⎪⎝⎭,∴f ππ6⎛⎫+ ⎪⎝⎭=-cos ππ63⎛⎫+ ⎪⎝⎭=-cos 2π=0,故C 正确; 由于f 2π3⎛⎫⎪⎝⎭=cos 2ππ33⎛⎫+ ⎪⎝⎭=cosπ=-1,为f (x )的最小值,故f (x )在,2ππ⎛⎫ ⎪⎝⎭上不单调,故D 错误. 故选D.7.能使sin(2))y x x θθ=+++为奇函数,且在0,4⎡⎤⎢⎥⎣⎦π上是减函数的θ的一个值是( ) A .5π3B .43π C .23π D .3π 【答案】C 【解析】 【分析】首先利用辅助角公式化简函数,然后根据函数的奇偶性和单调性求得θ的值. 【详解】依题意π2sin 23y x θ⎛⎫=++⎪⎝⎭,由于函数为奇函数,故πππ,π33k k θθ+==-,当1,2k =时,2π3θ=或5π3θ=,由此排除B,D 两个选项.当2π3θ=时,()2sin 2π2sin 2y x x =+=-在0,4⎡⎤⎢⎥⎣⎦π上是减函数,符合题意.当5π3θ=时,()2sin 22π2sin 2y x x =+=,在0,4⎡⎤⎢⎥⎣⎦π上是增函数,不符合题意.故选C. 【点睛】本小题主要考查诱导公式的运用,考查三角函数的奇偶性和单调性,属于基础题.8.在△ABC 中,7b =,5c =,3B π∠=,则a 的值为 A .3 B .4C .7D .8【答案】D 【解析】 【分析】根据题中所给的条件两边一角,由余弦定理可得2222cos b a c ac B =+-,代入计算即可得到所求的值. 【详解】因为7,5,3b c B π==∠=,由余弦定理可得2222cos b a c ac B =+-,即214925252a a =+-⨯⨯,整理得25240a a --=, 解得8a =或5a =-(舍去),故选D. 【点睛】该题考查的是有关解三角形的问题,在解题的过程中,涉及到的知识点有余弦定理,解三角形所用的就是正弦定理和余弦定理,结合题中的条件,选择适当的方法求得结果.9.已知双曲线()222210,0x y a b a b-=>>的左右焦点分别为1F ,2F ,M 为双曲线上一点,若121cos 4F MF ∠=,122MF MF =,则此双曲线渐近线方程为( ) A.y = B.3y x =±C .y x =±D .2y x =±【答案】A 【解析】 【分析】因为M 为双曲线上一点,可得122MF MF a -=,在12F MF ∆使用余弦定理,结合已知条件即可求得答案. 【详解】Q 双曲线()222210,0x y a b a b-=>>的左右焦点分别为1F ,2F ,M 为双曲线上一点 ∴ 121222MF MF a MF MF ⎧-=⎪⎨=⎪⎩,解得:14MF a =,22MF a = 在12F MF ∆中,根据余弦定理可得:∴ 12121222122c 2os F F MF MF M MF MF F F ∠=+-⋅⋅可得:2221(2)(4)(2)2424c a a a a =+-⋅⋅⋅ 化简可得:2c a =由双曲线性质可得:22222243b c a a a a =-=-=可得:b =Q 双曲线渐近线方程为:b y x a=±则双曲线渐近线方程为: y = 故选:A. 【点睛】本题考查了求双曲线渐近线方程问题,解题关键是掌握双曲线的基本知识,数形结合,考查分析能力和计算能力,属于中档题.10.已知1F 、2F 分别为双曲线22146x y -=的左、右焦点,M 为双曲线右支上一点且满足120MF MF ⋅=u u u u v u u u u v ,若直线2MF 与双曲线的另一个交点为N ,则1MF N ∆的面积为( )A .12B .C .24D .【答案】C 【解析】 【分析】设1MF m =,2MF n =,根据双曲线的定义和12MF MF ⊥,可求出6m =,2n =,再设2NF t =,则14NF t =+根据勾股定理求出6t =即可求出三角形的面积. 【详解】解:设1MF m =,2MF n =,∵1F 、2F 分别为双曲线22146x y -=的左、右焦点,∴24m n a -==,122F F c ==∵120MF MF ⋅=u u u u v u u u u v, ∴12MF MF ⊥,∴222440m n c +==, ∴()2222m n m n mn -=+-, 即2401624mn =-=, ∴12mn =, 解得6m =,2n =,设2NF t =,则124NF a t t =+=+,在1Rt NMF ∆中可得()()222426t t +=++, 解得6t =, ∴628MN =+=, ∴1MF N ∆的面积111862422S MN MF =⋅=⨯⨯=. 故选C .【点睛】本题考查了双曲线的定义和向量的数量积和三角形的面积,考查了运算能力和转化能力,属于中档题.11.已知ππ43πsin()cos()0,322ααα++-=-<<则2πcos()3α+等于( )A 5B .35-C .45D .35【答案】C 【解析】 【分析】首先根据等式化简,得到4sin 65πα⎛⎫+=- ⎪⎝⎭,再利用诱导公式化简2cos 3πα⎛⎫+ ⎪⎝⎭求值. 【详解】解析:∵ππ43sin cos 32αα⎛⎫⎛⎫++-= ⎪ ⎪⎝⎭⎝⎭133343sin sin sin 22ααααα+== 433sin 6πα⎛⎫=+= ⎪⎝⎭ ∴π4sin 65()α+=-.又2ππππcos cos sin 32()())6(6ααα+=++=-+,∴2π4co (s 35)α+=. 故选:C 【点睛】本题考查三角恒等变换,化简求值,重点考查转化与变形,计算能力,属于基础题型.12.函数()1sin cos 1sin cos 1tan 01sin cos 1sin cos 32x x x x f x x x x x x x π+-++⎛⎫=++<< ⎪+++-⎝⎭的最小值为( ) A.13+ BCD【答案】B 【解析】 【分析】利用二倍角公式化简函数()f x ,求导数,利用导数求函数的最小值即可. 【详解】22222sin 2sin cos 2cos 2sin cos1sin cos 1sin cos 2222221sin cos 1sin cos 2cos 2sin cos 2sin 2sin cos 222222x x x x x x x x x x x x x x x xx x x x +++-+++=++++-++ 2sin sin cos 2cos sin cos sin cos 222222222sin cos sin 2cos sin cos 2sin sin cos 22222222x x x x x x x xx x x x x x x x x ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭=+=+=⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭, 则()21tan 0sin 32f x x x x π⎛⎫=+<< ⎪⎝⎭, 32222221sin 2cos 16cos cos 1()sin 3cos sin 3cos 3sin cos x x x x f x x x x x x x '''--+⎛⎫⎛⎫=+=-+= ⎪ ⎪⎝⎭⎝⎭. 令()cos 0,1t x =∈,()3261g t t t =--+为减函数,且102g ⎛⎫=⎪⎝⎭, 所以当03x π<<时,()11,02t g t <<<,从而()'0f x <; 当32x ππ<<时,()10,02t g t <<>,从而()'0f x >. 故()min 33f x f π⎛⎫== ⎪⎝⎭. 故选:A 【点睛】本题主要考查了三角函数的恒等变换,利用导数求函数的最小值,换元法,属于中档题.13.已知函数()3cos(2)2f x x π=+,若对于任意的x ∈R ,都有12()()()f x f x f x 剟成立,则12x x -的最小值为( ) A .4 B .1C .12D .2【答案】D 【解析】 【分析】由题意得出()f x 的一个最大值为()2f x ,一个最小值为()1f x ,于此得出12x x -的最小值为函数()y f x =的半个周期,于此得出答案. 【详解】对任意的x ∈R ,()()()12f x f x f x 剟成立. 所以()()2min 3f x f x ==-,()()2max 3f x f x ==,所以12min22Tx x -==,故选D . 【点睛】本题考查正余弦型函数的周期性,根据题中条件得出函数的最值是解题的关键,另外就是灵活利用正余弦型函数的周期公式,考查分析问题的能力,属于中等题.14.已知()0,απ∈,3sin 35πα⎛⎫+= ⎪⎝⎭,则cos 26πα⎛⎫+= ⎪⎝⎭( )A .2425B .2425-C .725D .725-【答案】B 【解析】 【分析】根据余弦的二倍角公式先利用sin 3πα⎛⎫+⎪⎝⎭求得2cos 23πα⎛⎫+⎪⎝⎭.再由诱导公式求出sin 26πα⎛⎫+ ⎪⎝⎭,再利用同角三角函数关系中的平方关系求得cos 26πα⎛⎫+ ⎪⎝⎭.根据角的取值范围,舍去不合要求的解即可. 【详解】因为3sin 35πα⎛⎫+= ⎪⎝⎭由余弦二倍角公式可得22237cos 212sin 1233525ππαα⎛⎫⎛⎫⎛⎫+=-+=-⨯= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭而2cos 2cos 2sin 23626ππππααα⎛⎫⎛⎫⎛⎫+=++=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭所以27sin 2cos 26325ππαα⎛⎫⎛⎫+=-+=- ⎪ ⎪⎝⎭⎝⎭由同角三角函数关系式可得24cos 2625πα⎛⎫+==± ⎪⎝⎭ 因为()0,απ∈ 则4,333πππα⎛⎫+∈ ⎪⎝⎭,而3sin 035πα⎛⎫+=> ⎪⎝⎭ 所以,33ππαπ⎛⎫+∈ ⎪⎝⎭则,33ππαπ⎛⎫+∈ ⎪⎝⎭所以22,233ππαπ⎛⎫⎛⎫+∈ ⎪ ⎪⎝⎭⎝⎭32,3262ππππα⎛⎫⎛⎫+-∈ ⎪ ⎪⎝⎭⎝⎭,即32,662πππα⎛⎫+∈ ⎪⎝⎭ 又因为7sin 20625πα⎛⎫+=-< ⎪⎝⎭,所以32,62ππαπ⎛⎫+∈ ⎪⎝⎭故cos 206πα⎛⎫+< ⎪⎝⎭所以24cos 2625πα⎛⎫+=- ⎪⎝⎭ 故选:B 【点睛】本题考查了同角三角函数关系式及诱导公式的化简应用,三角函数恒等变形及角的范围确定,综合性较强,属于中档题.15.在OAB ∆中,已知OB =u u u v 1AB u u u v=,45AOB ∠=︒,点P 满足(),OP OA OB λμλμ=+∈R u u u v u u u v u u u v ,其中λ,μ满足23λμ+=,则OP u u u v的最小值为( )A .5B C .3D .2【答案】A 【解析】 【分析】根据2OB =u u u r,1AB =uu u r ,45AOB ∠=︒,由正弦定理可得OAB ∆为等腰直角三角形,进而求得点A 坐标.结合平面向量的数乘运算与坐标加法运算,用λ,μ表示出OP u u u r.再由23λμ+=,将OP u u u r 化为关于λ的二次表达式,由二次函数性质即可求得OP u u u r的最小值.【详解】在OAB ∆中,已知2OB =u u u r,1AB =uu u r ,45AOB ∠=︒由正弦定理可得sin sin AB OBAOB OAB=∠∠u u u r u u u r 代入2sin 22OAB =∠,解得sin 1OAB ∠=即2OAB π∠=所以OAB ∆为等腰直角三角形以O 为原点,OB 所在直线为x 轴,以OB 的垂线为y 轴建立平面直角坐标系如下图所示:则点A 坐标为22⎝⎭所以22OA =⎝⎭u u u r ,)2,0OB =u u ur因为(),OP OA OB λμλμ=+∈R u u u r u u u r u u u r则)222,022OP λμ⎛ =+ ⎝⎭u u u r 222,22λμλ⎛⎫⎪ ⎪⎝⎭=则2222222OP λμλ⎛⎫=++⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭u u u r2222λλμμ=++因为23λμ+=,则32μλ=- 代入上式可得==所以当95λ=时, min OP ==u u u r 故选:A 【点睛】本题考查了平面向量基本定理的应用,正弦定理判断三角形形状,平面向量的坐标运算,属于中档题.16.我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”,用现代式子表示即为:在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,则ABC∆的面积S =根据此公式,若()cos 3cos 0a B b c A ++=,且2222a b c --=,则ABC ∆的面积为()AB .CD .【答案】A 【解析】 【分析】根据()cos 3cos 0a B b c A ++=,利用正弦定理边化为角得sin cos cos sin 3sin cos 0A B A B C A ++=,整理为()sin 13cos 0C A +=,根据sin 0C ≠,得1cos 3A =-,再由余弦定理得3bc =,又2222a b c --=,代入公式=S . 【详解】由()cos 3cos 0a B b c A ++=得sin cos cos sin 3sin cos 0A B A B C A ++=, 即()sin 3sin cos 0A B C A ++=,即()sin 13cos 0C A +=, 因为sin 0C ≠,所以1cos 3A =-, 由余弦定理22222cos 23a b c bc A bc --=-==,所以3bc =,由ABC ∆的面积公式得S ===故选:A 【点睛】本题主要考查正弦定理和余弦定理以及类比推理,还考查了运算求解的能力,属于中档题.17.已知2433sin 5cos 77ππαα⎛⎫⎛⎫+=-+ ⎪ ⎪⎝⎭⎝⎭,则tan 14πα⎛⎫-= ⎪⎝⎭( )A .53-B .35-C .35D .53【答案】B 【解析】 【分析】根据诱导公式计算得到35tan 73πα⎛⎫+= ⎪⎝⎭,故3tan tan 1472πππαα⎡⎤⎛⎫⎛⎫-=+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,解得答案. 【详解】由诱导公式可知24333sin 3sin 33sin 777πππαπαα⎡⎤⎛⎫⎛⎫⎛⎫+=++=-+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 又2433sin 5cos 77ππαα⎛⎫⎛⎫+=-+⎪ ⎪⎝⎭⎝⎭得333sin 5cos 77ππαα⎛⎫⎛⎫-+=-+ ⎪ ⎪⎝⎭⎝⎭, 所以35tan 73πα⎛⎫+= ⎪⎝⎭,313tan tan 314725tan 7πππααπα⎡⎤⎛⎫⎛⎫-=+-=-=- ⎪⎪⎢⎥⎛⎫⎝⎭⎝⎭⎣⎦+ ⎪⎝⎭. 故选:B . 【点睛】本题考查了三角恒等变换,意在考查学生的计算能力和转化能力.18.定义在R 上的函数()f x 既是偶函数又是周期函数,若()f x 的最小正周期是π,且当π0,2x ⎡⎤∈⎢⎥⎣⎦时,()sin f x x =,则5π3f ⎛⎫⎪⎝⎭的值为( ) A .12-BC .D .12【答案】B 【解析】分析:要求53f π⎛⎫⎪⎝⎭,则必须用()sin f x x =来求解,通过奇偶性和周期性,将变量转化到区间02π⎡⎤⎢⎥⎣⎦,上,再应用其解析式求解 详解:()f x Q 的最小正周期是π552333f f f ππππ⎛⎫⎛⎫⎛⎫∴=-=-⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()f x Q 是偶函数33f f ππ⎛⎫⎛⎫∴-= ⎪ ⎪⎝⎭⎝⎭,533f f ππ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭Q 当02x π⎡⎤∈⎢⎥⎣⎦,时,()sin f x x =,则5 sin 3332f f πππ⎛⎫⎛⎫===⎪ ⎪⎝⎭⎝⎭故选B点睛:本题是一道关于正弦函数的题目,掌握正弦函数的周期性是解题的关键,考查了函数的周期性和函数单调性的性质.19.ABC ∆的内角A B C 、、的对边分别是a b c 、、,若2B A =,1a =,b =c =( )A .B .2CD .1【答案】B 【解析】1sin A ===cos 2A =,所以222122c c =+-,整理得2320,c c -+=求得1c =或 2.c = 若1c =,则三角形为等腰三角形,030,60A C B ===不满足内角和定理,排除. 【考点定位】本题考查正弦定理和余弦定理的应用,考查运算能力和分类讨论思想.当求出cos A =0030,60A B ==,便于三角形的初步定型,也为排除1c =提供了依据.如果选择支中同时给出了1或2,会增大出错率.20.已知曲线1:sin C y x =,21:cos 23C y x π⎛⎫=-⎪⎝⎭,则下面结论正确的是( )A .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CC .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向左平移3π个单位长度,得到曲线2CD .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移3π个单位长度,得到曲线2C 【答案】D 【解析】 【分析】根据三角函数的周期变换和左右平移变换依次得到各选项中所得的函数解析式,从而得到正确选项. 【详解】A 中,将sin y x =横坐标缩短到原来的12倍得:sin 2y x =;向右平移3π个单位长度后得:2sin 2sin 2sin 2cos 233266y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=-- ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,A 错误;B 中,将sin y x =横坐标伸长到原来的2倍得:1sin2y x =;向右平移3π个单位长度后得:11121sin sin cos cos 232622632y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=-=-=--=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,B 错误;C 中,将sin y x =横坐标缩短到原来的12倍得:sin 2y x =;向左平移3π个单位长度后得:2sin 2sin 2sin 2cos 233266y x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫=+=+=++=+ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,C 错误;D 中,将sin y x =横坐标伸长到原来的2倍得:1sin2y x =;向左平移3π个单位长度后得:1111sin sin cos cos 232622623y x x x x πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+=+=-+=- ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,D 正确. 故选:D 【点睛】本题考查三角函数的周期变换和平移变换的问题,关键是能够准确掌握变换原则,得到变换后的函数解析式.。
高考数学压轴专题(易错题)备战高考《三角函数与解三角形》经典测试题附答案

【高中数学】数学《三角函数与解三角形》高考知识点(1)一、选择题1.在ABC ∆中,角A 、B 、C 所对的边分别为a 、b 、c ,且222b c a bc +=+若2sin sin sin B C A ⋅=,则ABC ∆的形状是()A .等腰三角形B .直角三角形C .等边三角形D .等腰直角三角形【答案】C 【解析】 【分析】直接利用余弦定理的应用求出A 的值,进一步利用正弦定理得到:b =c ,最后判断出三角形的形状. 【详解】在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c , 且b 2+c 2=a 2+bc .则:2221222b c a bc cosA bc bc +-===,由于:0<A <π,故:A 3π=.由于:sin B sin C =sin 2A , 利用正弦定理得:bc =a 2, 所以:b 2+c 2﹣2bc =0, 故:b =c ,所以:△ABC 为等边三角形. 故选C . 【点睛】本题考查了正弦定理和余弦定理及三角形面积公式的应用,主要考查学生的运算能力和转化能力,属于基础题型.2.已知函数()sin f x a x x =的一条对称轴为56x π=,函数()f x 在区间()12,x x 上具有单调性,且()()12f x f x =-,则下述四个结论:①实数a 的值为1;②()()1,x f x 和()()22,x f x 两点关于函数()f x 图象的一条对称轴对称; ③21x x -的最大值为π, ④12x x +的最小值为23π. 其中所有正确结论的编号是( )A .①②③B .①③④C .①④D .③④【答案】B 【解析】 【分析】 根据56x π=是函数()f x 的一条对称轴,确定函数()f x ,再根据函数()f x 在区间()12,x x 上具有单调性,得到21x x -的最大值为2Tπ=,然后由()()12f x f x =-,得到()()11,x f x 和()()22,x f x 两点关于函数()f x 的一个对称中心对称求解验证.【详解】 ∵56x π=是函数()f x 的一条对称轴,∴()53f x f x π⎛⎫=-⎪⎝⎭, 令0x =,得()503f f π⎛⎫=⎪⎝⎭,即-1a =,①正确; ∴()sin 2sin 3π⎛⎫=-=- ⎪⎝⎭f x x x x .又因为函数()f x 在区间()12,x x 上具有单调性, ∴21x x -的最大值为2Tπ=,且()()12f x f x =-, ∴()()11,x f x 和()()22,x f x 两点关于函数()f x 的一个对称中心对称,∴121233223x x x x k ππ⎛⎫⎛⎫-+- ⎪ ⎪+π⎝⎭⎝⎭=-=π,k Z ∈, ∴12223x x k ππ+=+,k Z ∈,当0k =时,12x x +取最小值23π,所以①③④正确,②错误. 故选:B 【点睛】本题主要考查三角函数的图象和性质,还考查了推理论证,运算求解的能力,属于中档题.3.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若(a ﹣c cos B )sin A =c cos A sin B ,则△ABC 的形状一定是( ) A .钝角三角形 B .直角三角形C .等腰三角形D .锐角三角形【答案】C 【解析】 【分析】根据题意,由(cos )sin cos sin a c B A c A B -=变形可得sin sin a A c C =,进而由正弦定理可得22a c =,即a c =,即可得答案. 【详解】根据题意,在ABC ∆中,(cos )sin cos sin a c B A c A B -=, 变形可得:sin cos sin cos sin (cos sin cos sin )sin()sin a A c B A c A B c B A A B c A B c C =+=+=+=,即有sin sin a A c C =,又由正弦定理可得22a c =,即a c =. 故选:C . 【点睛】本题主要考查三角形的形状判断,考查正弦定理的应用,意在考查学生对这些知识点的理解掌握水平,属于基础题.4.在ABC ∆中,角,,A B C 所对的边分别为,,a b c 满足,222b c a bc +-=,0AB BC ⋅>u ur u u r u u,2a =,则bc +的取值范围是( ) A .31,2⎛⎫ ⎪⎝⎭B.32⎫⎪⎪⎝⎭C .13,22⎛⎫⎪⎝⎭D .31,2⎛⎤ ⎥⎝⎦【答案】B 【解析】 【分析】利用余弦定理222cos 2b c a A bc+-=,可得3A π=,由|||cos()|0AB BC AB BC B π⋅=⋅->u u u u u u u u r u ur u r u r,可得B为钝角,由正弦定理可得sin sin(120)30)o o b c B B B ∴+=+-=+,结合B 的范围,可得解【详解】由余弦定理有:222cos 2b c a A bc+-=,又222b c a bc +-=故2221cos 222b c a bc A bc bc +-===又A 为三角形的内角,故3A π=又2a=sin sin sin(120)ob c c B C B ==- 又|||cos()|0AB BC AB BC B π⋅=⋅->u u u u u u u u r u ur u r u r故cos 0B B <∴为钝角3sin sin(120)sin 30)22o o b c B B B B B ∴+=+-=+=+(90,120)o o B ∈Q ,可得130(120150)sin(30)(,22o o o o B B +∈∴+∈,330))22o b c B ∴+=+∈ 故选:B 【点睛】本题考查了正弦定理、余弦定理和向量的综合应用,考查了学生综合分析,转化划归,数学运算能力,属于中档题5.函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象的交点横坐标的和为( ) A .53π B .2πC .76π D .π【答案】B 【解析】 【分析】根据两个函数相等,求出所有交点的横坐标,然后求和即可. 【详解】令sin cos2x x =,有2sin 12sin x x =-,所以sin 1x =-或1sin 2x =.又[],2x ππ∈-,所以2x π=-或32x π=或6x π=或56x π=,所以函数()[]()cos 2,2f x x x ππ=∈-的图象与函数()sin g x x =的图象交点的横坐标的和3522266s πππππ=-+++=,故选B. 【点睛】本题主要考查三角函数的图象及给值求角,侧重考查数学建模和数学运算的核心素养.6.在ABC ∆中,若sin :sin :sin 2:3:4A B C =,则ABC ∆是( ) A .直角三角形 B .钝角三角形C .锐角三角形D .等腰直角三角形【答案】B 【解析】 【分析】由题意利用正弦定理,推出a ,b ,c 的关系,然后利用余弦定理求出cosC 的值,即可得解. 【详解】∵sinA :sinB :sinC=2:3:4∴由正弦定理可得:a :b :c=2:3:4, ∴不妨令a=2x ,b=3x ,c=4x ,∴由余弦定理:c 2=a 2+b 2﹣2abcosC ,所以cosC=2222a b cab+-=2224916223x x x x x +-⨯⨯=﹣14, ∵0<C <π, ∴C 为钝角. 故选B . 【点睛】本题是基础题,考查正弦定理,余弦定理的应用,考查计算能力,常考题型.7.设当x θ=时,函数()sin 2cos f x x x =-取得最大值,则cos θ=()A .5-B .CD 【答案】B 【解析】 【分析】由辅助角公式可确定()max f x =sin 2cos θθ-=平方关系可构造出方程组求得结果. 【详解】()()sin 2cos f x x x x ϕ=-=+Q ,其中tan 2ϕ=- ()max f x ∴sin 2cos θθ-=又22sin cos 1θθ+= cos θ∴=【点睛】本题考查根据三角函数的最值求解三角函数值的问题,关键是能够确定三角函数的最值,从而得到关于所求三角函数值的方程,结合同角三角函数关系构造方程求得结果.8.△ABC 中,已知tanA =13,tanB =12,则∠C 等于( )A .30°B .45°C .60°D .135°【答案】D 【解析】 【分析】利用三角形内角和为180o ,可得:tan tan()tan(+)C A B A B π=--=-,利用两角和公式和已知条件,即可得解. 【详解】在△ABC 中,11tan tan 32tan tan()tan(+)=-1111tan tan 132A BC A B A B A B π++=--=-=-=---⋅,所以135C ?o .故选:D. 【点睛】本题考查了正切的两角和公式,考查了三角形内角和,考查了转化思想和计算能力,属于中档题.9.在△ABC 中,7b =,5c =,3B π∠=,则a 的值为 A .3 B .4C .7D .8【答案】D 【解析】 【分析】根据题中所给的条件两边一角,由余弦定理可得2222cos b a c ac B =+-,代入计算即可得到所求的值. 【详解】因为7,5,3b c B π==∠=,由余弦定理可得2222cos b a c ac B =+-,即214925252a a =+-⨯⨯,整理得25240a a --=, 解得8a =或5a =-(舍去),故选D. 【点睛】该题考查的是有关解三角形的问题,在解题的过程中,涉及到的知识点有余弦定理,解三角形所用的就是正弦定理和余弦定理,结合题中的条件,选择适当的方法求得结果.10.在∆ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .则“sin >sin A B ”是“a b >”的( )A .充分而不必要条件B .必要而不充分条件C .充要条件D .既不充分也不必要条件【答案】C 【解析】由正弦定理得sin sin 22a b A B a b R R>⇔>⇔> ,所以“sin sin A B >”是“a b >”的充要条件,选C.11.函数y=ππππcos sin cos -sin 4444x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦在一个周期内的图象是( ) A .B .C .D .【答案】B 【解析】 【分析】首先根据二倍角余弦公式化简得到函数的解析式,再由函数表达式得到函数的单调性和周期,进而得到选项. 【详解】根据两角和差公式展开得到: y=ππππcos sin cos -sin 4444x x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+++++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦22πππcos sin cos 2424x x x ⎛⎫⎛⎫⎛⎫+-+=+ ⎪ ⎪ ⎪⎝⎭⎝=⎝⎭⎭=-sin2x ,函数在0的右侧是单调递减的,且周期为π,故选B. 故答案选B . 【点睛】这个题目考查了三角函数的恒等变换,题型为已知函数表达式选择函数的图像,这种题目,一般是先根据函数的表达式得到函数的定义域,或者值域,进行排除;也可以根据函数的表达式判断函数的单调性,周期性等,之后结合选项选择.12.已知函数f (x )=sin 2x +sin 2(x 3π+),则f (x )的最小值为( ) A .12B .14C 3D .22【答案】A 【解析】 【分析】先通过降幂公式和辅助角法将函数转化为()11cos 223f x x π⎛⎫=-+ ⎪⎝⎭,再求最值. 【详解】已知函数f (x )=sin 2x +sin 2(x 3π+), =21cos 21cos 2322x x π⎛⎫-+⎪-⎝⎭+,=1cos 22111cos 222223x x x π⎛⎫⎛⎫--=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭, 因为[]cos 21,13x π⎛⎫+∈- ⎪⎝⎭, 所以f (x )的最小值为12. 故选:A 【点睛】本题主要考查倍角公式及两角和与差的三角函数的逆用,还考查了运算求解的能力,属于中档题.13.在OAB ∆中,已知OB =u u u v 1AB u u u v=,45AOB ∠=︒,点P 满足(),OP OA OB λμλμ=+∈R u u u v u u u v u u u v ,其中λ,μ满足23λμ+=,则OP u u u v的最小值为( )ABCD【答案】A 【解析】 【分析】根据OB =u u u r,1AB =uu u r ,45AOB ∠=︒,由正弦定理可得OAB ∆为等腰直角三角形,进而求得点A 坐标.结合平面向量的数乘运算与坐标加法运算,用λ,μ表示出OP u u u r.再由23λμ+=,将OP u u u r 化为关于λ的二次表达式,由二次函数性质即可求得OP u u u r的最小值.【详解】在OAB ∆中,已知OB =u u u r,1AB =uu u r ,45AOB ∠=︒由正弦定理可得sin sin AB OBAOB OAB=∠∠u u u r u u u rsin 2OAB =∠,解得sin 1OAB ∠=即2OAB π∠=所以OAB ∆为等腰直角三角形以O 为原点,OB 所在直线为x 轴,以OB 的垂线为y 轴建立平面直角坐标系如下图所示:则点A 坐标为22⎝⎭所以2222OA ⎛= ⎝⎭u u u r ,)2,0OB =u u u r因为(),OP OA OB λμλμ=+∈R u u u r u u u r u u u r则)222,022OP λμ⎛ =+ ⎝⎭u u u r 222,22λμλ⎛⎫⎪ ⎪⎝⎭=则2222222OP λμλ⎛⎫=++⎛⎫⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭u u u r2222λλμμ=++因为23λμ+=,则32μλ=- 代入上式可得()()22322232λλλλ+-+-218518λλ-=+299555λ⎛⎫=-+ ⎪⎝⎭所以当95λ=时, min 93555OP ==u u u r 故选:A 【点睛】本题考查了平面向量基本定理的应用,正弦定理判断三角形形状,平面向量的坐标运算,属于中档题.14.若函数tan 23y x k π⎛⎫=-+ ⎪⎝⎭,0,6x π⎛⎫∈ ⎪⎝⎭的图象都在x 轴上方,则实数k 的取值范围为( )A .)+∞ B .)+∞C .()+∞D .()【答案】A 【解析】 【分析】计算tan 203x π⎛⎫<-< ⎪⎝⎭,tan 23x k π⎛⎫->- ⎪⎝⎭恒成立,得到答案. 【详解】∵0,6x π⎛⎫∈ ⎪⎝⎭,∴2033x ππ-<-<,∴tan 203x π⎛⎫-< ⎪⎝⎭,函数tan 23y x k π⎛⎫=-+ ⎪⎝⎭,0,6x π⎛⎫∈ ⎪⎝⎭的图象都在x 轴上方, 即对任意的0,6x π⎛⎫∈ ⎪⎝⎭,都有tan 203x k π⎛⎫-+> ⎪⎝⎭,即tan 23x k π⎛⎫->- ⎪⎝⎭,∵tan 23x π⎛⎫-> ⎪⎝⎭k -≤,k ≥ 故选:A . 【点睛】本题考查了三角函数恒成立问题,转化为三角函数值域是解题的关键.15.函数()22sin 3cos 2f x x x =+-,2,36x ππ⎡⎤∈-⎢⎥⎣⎦的值域为( ) A .40,3⎡⎤⎢⎥⎣⎦B .41,3⎡⎤⎢⎥⎣⎦C .51,4⎡⎤⎢⎥⎣⎦D .50,4⎡⎤⎢⎥⎣⎦【答案】A 【解析】 【分析】化简得到()23sin 2sin 1f x x x =-++,设sin t x =,利用二次函数性质得到答案. 【详解】根据22sin cos 1x x +=,得()23sin 2sin 1f x x x =-++,2,36x ππ⎡⎤∈-⎢⎥⎣⎦, 令sin t x =,由2,36x ππ⎡⎤∈-⎢⎥⎣⎦,得1sin 1,2x ⎡⎤∈-⎢⎥⎣⎦, 故[]0,1t ∈,有2321y t t =-++,[]0,1t ∈,二次函数对称轴为13t =, 当13t =时,最大值43y =;当1t =时,最小值0y =,综上,函数()f x 的值域为40,3⎡⎤⎢⎥⎣⎦.故选:A . 【点睛】本题考查了三角函数值域,换元可以简化运算,是解题的关键.16.某船开始看见灯塔A 时,灯塔A 在船南偏东30o 方向,后来船沿南偏东60︒的方向航行45km 后,看见灯塔A 在船正西方向,则这时船与灯塔A 的距离是( ) A .152km B .30kmC .15kmD .153km【答案】D 【解析】 【分析】如图所示,设灯塔位于A 处,船开始的位置为B ,船行45km 后处于C ,根据题意求出BAC ∠与BAC ∠的大小,在三角形ABC 中,利用正弦定理算出AC 的长,可得该时刻船与灯塔的距离. 【详解】设灯塔位于A 处,船开始的位置为B ,船行45km 后处于C ,如图所示,可得60DBC ∠=︒,30ABD ∠=︒,45BC =30ABC ∴∠=︒,120BAC ∠=︒在三角形ABC 中,利用正弦定理可得:sin sin AC BCABC BAC=∠∠,可得sin 1153sin 23BC ABC AC km BAC ∠===∠ 故选D 【点睛】本题主要考查的是正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解决本题的关键,属于基础题.17.已知函数()3)(0f x x ωϕω=+>,)22ππ-<ϕ<,1(3A ,0)为()f x 图象的对称中心,B ,C 是该图象上相邻的最高点和最低点,若4BC =,则()f x 的单调递增区间是()A .2(23k -,42)3k +,k Z ∈ B .2(23k ππ-,42)3k ππ+,k Z ∈C .2(43k -,44)3k +,k Z ∈ D .2(43k ππ-,44)3k ππ+,k Z ∈【答案】C 【解析】 【分析】由三角函数图像的性质可求得:2πω=,6πϕ=-,即()sin()26f x x ππ=-,再令222262k x k ππππππ--+剟,求出函数的单调增区间即可.【详解】解:函数())(0f x x ωϕω=+>,)22ππ-<ϕ<, 因为1(3A ,0)为()f x 图象的对称中心,B ,C 是该图象上相邻的最高点和最低点,又4BC =,∴222()42T +=,即221216πω+=,求得2πω=.再根据123k πϕπ+=g ,k Z ∈,可得6πϕ=-,()3sin()26f x x ππ∴=-,令222262k x k ππππππ--+剟,求得244433k x k -+剟, 故()f x 的单调递增区间为2(43k -,44)3k +,k Z ∈, 故选:C . 【点睛】本题考查了三角函数图像的性质及单调性,属中档题.18.4cos2d cos sin xx x xπ=+⎰( )A .1)B 1C 1D .2【答案】C 【解析】 【分析】利用三角恒等变换中的倍角公式,对被积函数进行化简,再求积分. 【详解】因为22cos2cos sin cos sin cos sin cos sin x x xx x x x x x-==-++,∴4400cos 2d (cos sin )d (sin cos )14cos sin 0xx x x x x x x x πππ=-=+=+⎰⎰,故选C . 【点睛】本题考查三角恒等变换知与微积分基本定理的交汇.19.设函数()()sin f x x x x R =∈,则下列结论中错误的是( ) A .()f x 的一个周期为2π B .()f x 的最大值为2 C .()f x 在区间2,63ππ⎛⎫⎪⎝⎭上单调递减 D .3f x π⎛⎫+⎪⎝⎭的一个零点为6x π=【答案】D 【解析】 【分析】先利用两角和的正弦公式化简函数()f x ,再由奇偶性的定义判断A ;由三角函数的有界性判断B ;利用正弦函数的单调性判断C ;将6x π=代入 3f x π⎛⎫+ ⎪⎝⎭判断D .【详解】()sin f x x x = 23sin x π⎛⎫=+ ⎪⎝⎭,()f x 周期22,1T A ππ==正确; ()f x 的最大值为2,B 正确,25,,,63326x x πππππ⎛⎫⎛⎫∈∴+∈ ⎪⎪⎝⎭⎝⎭Q , ()f x ∴在2,63ππ⎛⎫⎪⎝⎭上递减,C 正确; 6x π=时,1032f x f ππ⎛⎫⎛⎫+==≠ ⎪ ⎪⎝⎭⎝⎭,6x π=不是3f x π⎛⎫+⎪⎝⎭的零点,D 不正确. 故选D. 【点睛】本题通过对多个命题真假的判断,综合考查两角和的正弦公式以及三角函数的单调性、三角函数的周期性、三角函数的最值与零点,意在考查对基础知识掌握的熟练程度,属于中档题.20.关于函数()()()sin tan cos tan f x x x =-有下述四个结论: ①()f x 是奇函数; ②()f x 在区间0,4π⎛⎫⎪⎝⎭单调递增; ③π是()f x 的周期; ④()f x 的最大值为2.其中所有正确结论的个数是( ) A .4 B .3C .2D .1【答案】C 【解析】 【分析】计算()()()sin tan cos tan f x x x -=--得到①错误,根据复合函数单调性判断法则判断②正确,()()f x f x π+=③正确,假设()f x 的最大值为2,取()2f a =,得到矛盾,④错误,得到答案. 【详解】()()()sin tan cos tan f x x x =-,()()()sin tan cos tan f x x x -=---⎡⎤⎡⎤⎣⎦⎣⎦()()sin tan cos tan x x =--,所以()f x 为非奇非偶函数,①错误;当0,4x π⎛⎫∈ ⎪⎝⎭时,令tan t x =,()0,1t ∈, 又()0,1t ∈时sin y t =单调递增,cos y t =单调递减,根据复合函数单调性判断法则, 当0,4x π⎛⎫∈ ⎪⎝⎭时,()sin tan y x =,()cos tan y x =-均为增函数, 所以()f x 在区间0,4π⎛⎫⎪⎝⎭单调递增,所以②正确; ()()()sin tan cos tan f x x x πππ+=+-+⎡⎤⎡⎤⎣⎦⎣⎦()()()sin tan cos tan x x f x =-=,所以π是()f x 的周期,所以③正确;假设()f x 的最大值为2,取()2f a =,必然()sin tan 1a =,()cos tan 1a =-, 则tan 22a k ππ=+,k Z ∈与tan 2a k ππ=+,k Z ∈矛盾,所以()f x 的最大值小于2,所以④错误. 故选:C . 【点睛】本题考查了三角函数奇偶性,单调性,周期,最值,意在考查学生对于三角函数知识的综合应用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金太阳新课标资源网 wx.jtyjy.com 第 1 页 共 12 页 金太阳新课标资源网wx.jtyjy.com 2010年高考数学易错专题点睛三:三角函数 【原题】若A、B、C是ABC的三个内角,且)2(CCBA,则下列结论中正确的个数是( ) ①.CAsinsin ②.CAcotcot ③.CAtantan ④.CAcoscos A.1 B.2 C.3 D.4 【错误分析】:CA ∴ CAsinsin,CAtantan故选B 【答案】选A 【解析】法1CA在ABC中,在大角对大边,ACacsinsin, 法2 考虑特殊情形,A为锐角,C为钝角,故排除B、C、D,所以选A . 【易错点点睛】三角形中大角对大边定理不熟悉,对函数单调性理解不到位导致应用错误 【原题】已知542cos,532sin ,试确定的象限.
【原题】已知角的终边经过)0)(3,4(aaaP,求cot,tan,cos,sin的值. 【错误分析】: 金太阳新课标资源网 wx.jtyjy.com 第 2 页 共 12 页 金太阳新课标资源网wx.jtyjy.com ayxrayax5,3,4223344sin,cos,5555aaaa
3344tan,cot4433aaaa
【答案】见解析
【解析】若0a,则ar5,且角在第二象限3344sin,cos,5555aaaa 3344tan,cot4433aaaa
若0a,则ar5,且角在第四象限3344sin,cos,5555aaaa 3344tan,cot4433aaaa
【易错点点睛】(1)给出角的终边上一点的坐标,求角的某个三解函数值常用定义求解; (2)本题由于所给字母a的符号不确定,故要对a的正负进行讨论.
【原题】已知α是第三象限角,化简sin1sin1sin1sin1。 【错误分析】:本题要求同学们熟练掌握同角三角函数之间的关系,在求值过程中特别注意三角函数值的符号。 【答案】tan2
【解析】原式=2222sin1)sin1(sin1)sin1(=cossin2cossin1sin1 又α是第三象限角,0cos所以,原式=tan2cossin2。 【易错点点睛】三角函数化简一般要求是:(1)尽可能不含分母;(2)尽可能不含根式;(3)尽可能 使三角函数名称最少;(4)尽可能求出三角函数式的值.本题的关健是如何应用基本关系式脱去根式,进行化简. 【原题】已知cot051cossin),则,(,__________ 【错误分析】:两边同时平方,由,与51cossin2512cossin得2222(sincos)sin2sincoscos4sincos497(sincos)4sincossincos255
金太阳新课标资源网 wx.jtyjy.com 第 3 页 共 12 页 金太阳新课标资源网wx.jtyjy.com ∴.cot53cos54sin,进而可求,解得:43cot 或.cot54cos53sin,进而可求,解得:34cot 【答案】43cot 【解析】),,(,051cossin 两边同时平方,有12sincos025 1sincos5与联立, 求出,,53cos54sin∴43cot 【易错点点睛】没有注意到条件),0(时,由于0cossin所以cossin的值为正而导致错误,这类问题的解决首先必须对角α的范围进行讨论,这充分体现了“函数问题,范围先行(尤其是三角函数问题)”的解题基本原则. 【原题】若函数)2cos(2sin)2sin(42cos1)(xxaxxxf的最大值为2,试确定常数a的
值. 【错误分析】:本试题将三角函数“,2”诱导公式有机地溶于式子中,考查了学生对基础知识的掌握程度,这就要求同学们在学习中要脚踏实地,狠抓基础. 【答案】15.a
【解析】222cos11()sincoscossinsin(),4cos222244xxxaafxaxxxx 2211sin4.,15.441a
aa其中角满足由已知有解之得
【易错点点睛】求三角函数的值域是常见题型.一类是xbxaycossin型,这要变形成y sin()x;二是含有三角函数复合函数,可利用换元、配方等方法转换成一元二次函数在
定区间上的值域. 【原题】已知tan2=2,求 (1)tan()4的值; (2)6sincos3sin2cos的值 【错误分析】:本题考三角函数的基本公式以及三角函数式的恒等变形等基础知识和基本运算技能 金太阳新课标资源网 wx.jtyjy.com 第 4 页 共 12 页 金太阳新课标资源网wx.jtyjy.com 【答案】(1)17(2)76
【解析】(1)∵ tan2=2, ∴ 22tan2242tan1431tan2;
所以tantantan14tan()41tan1tantan4=41134713; (2)由(I), tanα=-34, 所以6sincos3sin2cos=6tan13tan2=46()173463()23 【易错点点睛】本题设计简洁明了,入手容易,但对同角间的基本关系式要求熟练应用,运算准确.
【原题】若316sin,则232cos=( ) A.97 B.31 C.31 D.97 【错误分析】:232cos=)]23(cos[=)23cos(=1—2)6(sin2=97 【答案】选A 【解析】232cos=)]23(cos[=—)23cos(=—1+2)6(sin2=—97.故选A. 【易错点点睛】诱导公式应用符号错
【原题】求值:sincossincossinsin71587158=_______________ 【错误分析】:本题解题的思路是:方法一化同角,方法二化单角,通过角的变换的方法来解决问题。至于如何变形,先求什么,后求什么,什么情况下解题简便,只有经过不断的探索、分析、比较,逐步积累解题的经验。
【答案】23
【解析】法一 原式sin()cossincos()sinsin158158158158 金太阳新课标资源网 wx.jtyjy.com 第 5 页 共 12 页 金太阳新课标资源网wx.jtyjy.com sincoscoscos158158tan15tan(4530)133133333323 法二 1sin7(sin23sin7)sin23sin72sin15cos821cos23cos72cos15cos8cos7(cos23cos7)2原式 31333tan15tan(4530)2333313 【易错点点睛】进行必要的三角恒等变形.其通法是:发现差异(角度、函数、运算结构)寻找联系(套用、变用、活用公式,注意技巧和方法)合理转化(由因导果的综合法,由果探因的分析法)其技巧配凑角:α=(α+β)-β,β=2-2等
【原题】22221sinsincoscoscos2cos22化简 金太阳新课标资源网 wx.jtyjy.com
第 6 页 共 12 页 金太阳新课标资源网wx.jtyjy.com 法三 (从“幂”入手,利用降幂公式先降次) 原式1221221221221222coscoscoscoscoscos
14122221412222(coscoscoscos)(coscoscoscos)
1222coscos 141412 法四 (从“形”入手,利用配方法,先对二次项配方) 原式(sinsincoscos)sinsincoscoscoscos221222 cos()sinsincoscos212221222 金太阳新课标资源网 wx.jtyjy.com 第 7 页 共 12 页 金太阳新课标资源网wx.jtyjy.com cos()cos()21222cos()cos()22122112
【易错点点睛】在对三角式作变形时,以上四种方法,提供了四种变形的角度,这也是研究其他三角问题时经常要用的变形手法,常见技巧:常值代换,特别是用“1”代换;项的分拆与角的配凑;化弦(切)法;降次与升次;引入辅助角。
【原题】为了得到函数62sinxy的图像,可以将函数xy2cos的图像( ) A 向右平移6 B 向右平移3 C 向左平移6 D向左平移3 【错误分析】:A 审题不仔细,把目标函数搞错是此题最容易犯的错误 【答案】B 【解析】sin(2)6yx,cos2sin[2()]sin[2(2)]22yxxhxh所以 (2)263hh 【易错点点睛】)sin(xAy+)0,0(AB中,,,BA及,对正弦函数xysin图像的影响,应记住图像变换是对自变量而言. 如:xy2sin向右平移6个单
位,应得)6(2sinxy,而不是)62sin(xy. 【原题】当223xyxx时,函数的()sincos A. 最大值为1,最小值为-1 B. 最大值为1,最小值为12 C. 最大值为2,最小值为2 D. 最大值为2,最小值为1 【错误分析】:研究复杂三角函数的性质,一般是将这个复杂的三角函数化成y=Asin(ωx+φ)的形式再求解,这是解决所有三角函数问题的基本思路. 【答案】选D 【解析】yxxxsincossin()323,而22x
