2018年高考数学二轮复习专题1.5立体几何(练)文
2018年高考数学二轮复习专题 1.5立体几何(练)文 Word版 含答案

专题1.5 立体几何1.练高考1.【2017山东,文13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为.【答案】22π+2. 【2017课标II,文15】长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为【答案】14π.【解析】球的直径是长方体的体对角线,所以224π14π.R S R====3. 【2017课标1,文6】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是()A .B .C .D .【答案】A【解析】4. 【2017课标1,文18】如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠= .(1)证明:平面PAB ⊥平面PAD ;(2)若PA =PD =AB =DC ,90APD ∠= ,且四棱锥P-ABCD 的体积为83,求该四棱锥的侧面积. 【答案】(1)证明见解析; (2)326+.【解析】5. 【2017山东,文18】(本小题满分12分)由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E ⊥平面ABCD ,(Ⅰ)证明:1AO ∥平面B 1CD 1;(Ⅱ)设M 是OD 的中点,证明:平面A 1EM ⊥平面B 1CD 1.【答案】①证明见解析.②证明见解析.【解析】试题分析:(Ⅰ)取11B D 中点F ,证明1//AO CF ,(Ⅱ)证明11B D ⊥面1A EM .所以1,A E BD ⊥因为11//,B D BD所以11111,,EM B D A E B D ⊥⊥ 又1,A E EM ⊂平面1A EM,1A E EM E = .所以11B D ⊥平面1,A EM 又11B D ⊂平面11B CD , 所以平面1A EM ⊥平面11B CD .6. 【2017天津,文17】如图,在四棱锥P ABCD -中,AD ⊥平面PDC ,AD BC ∥,PD PB ⊥,1AD =,3BC =,4CD =,2PD =.(I )求异面直线AP 与BC 所成角的余弦值;(II )求证:PD ⊥平面PBC ;(Ⅲ)求直线AB 与平面PBC 所成角的正弦值.【答案】(ⅠⅡ . 【解析】。
2018年高考数学(理)二轮复习讲练测专题1.5立体几何(练)含解析

2018年高考数学(理)二轮复习讲练测专题五立体几何1.练高考1.【2017山东,理13】由一个长方体和两个14圆柱体构成的几何体的三视图如右图,则该几何体的体积为.【答案】22π+2.【2017天津,理10】已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为 .【答案】92π【解析】设正方体边长为a,则226183a a=⇒=,外接球直径为344279233,πππ3382R a V R====⨯=.3.【2017课标3,理16】a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b 都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:①当直线AB与a成60°角时,AB与b成30°角;②当直线AB与a成60°角时,AB与b成60°角;③直线AB与a所成角的最小值为45°;④直线AB与a所成角的最小值为60°.其中正确的是________.(填写所有正确结论的编号)【答案】②③【解析】4. 【2017课标3,理19】如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.(1)证明:平面ACD⊥平面ABC;(2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值.【答案】(1)证明略;. 【解析】(2)由题设及(1)知,,,OA OB OC 两两垂直,以O 为坐标原点,OA 的方向为x 轴正方向,OA 为单位长,建立如图所示的空间直角坐标系O xyz -.则()()()()1,0,0,3,0,1,0,0,0,0,1A B C D - 由题设知,四面体ABCE 的体积为四面体ABCD 的体积的12,从而E 到平面ABC 的距离为D 到平面ABC 的距离的12,即E 为DB 的中点,得1,22E ⎛⎫⎪ ⎪⎝⎭.故5. 【2017山东,理17】如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120︒得到的,G 是DF 的中点.(Ⅰ)设P 是CE 上的一点,且AP BE ⊥,求CBP ∠的大小; (Ⅱ)当3AB =,2AD =,求二面角E AG C --的大小.【答案】(Ⅰ)30CBP ∠=︒.(Ⅱ)60︒.思路二:以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系. 写出相关点的坐标,求平面AEG 的一个法向量111(,,)m x y z =,平面ACG 的一个法向量222(,,)n x y z =计算1cos ,||||2m n m n m n ⋅<>==⋅即得.(Ⅱ)解法一:取EC 的中点H ,连接EH ,GH ,CH . 因为120EBC ∠=︒, 所以四边形BEHC 为菱形,所以AE GE AC GC =====取AG 中点M ,连接EM ,CM ,EC . 则EM AG ⊥,CM AG ⊥,所以EMC ∠为所求二面角的平面角.又1AM =,所以EM CM ===在BEC ∆中,由于120EBC ∠=︒,由余弦定理得22222222cos12012EC =+-⨯⨯⨯︒=, 所以23EC =EMC ∆为等边三角形, 故所求的角为60︒. 解法二:以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.因此所求的角为60︒.6. 【2017北京,理16】如图,在四棱锥P-ABCD 中,底面ABCD 为正方形,平面PAD ⊥平面ABCD ,点M 在线段PB 上,PD//平面MAC ,6,AB=4. (I )求证:M 为PB 的中点; (II )求二面角B-PD-A 的大小;(III )求直线MC 与平面BDP 所成角的正弦值.【答案】(Ⅰ)详见解析:(Ⅱ)3π;(Ⅲ)【解析】(III)由题意知2(1,2,2M-,(2,4,0)D,2(3,2,2MC=-.设直线MC与平面BDP所成角为α,则||2sin|cos,|9||||MCMCMCα⋅===<>nnn.所以直线MC与平面BDP所成角的正弦值为9.2.练模拟1. 三棱锥P ABC -的四个顶点都在球O 上, PA ⊥平面ABC , 2PA =, 4AB =, 2AC =, BC =则球的表面积是( )A. 16πB. 20πC. 24πD. 28π 【答案】B【解析】由题意, AC BC ⊥, PA ⊥平面ABC ,则直径22225PA AC BC ++=则R =2420S R ππ==,故选B.2.【2018届吉林省辽源市田家炳高级中学等五校高三上期末联考】已知两条直线m n 、,两个平面αβ、,给出下面四个命题:①α∥,,m n m βαβ⊂⊂⇒∥n ; ②m ∥n , m ∥n α⇒∥α; ③m ∥n , m ⊥ n αα⇒⊥; ④α∥,m β∥,n m n αβ⊥⇒⊥。
2018高考二轮专题复习卷 立体几何专题

立体几何专题一、选择题(本大题共12题,每小题5分,共60分)1.棱锥侧面是有公共顶点的三角形,能围成一个棱锥侧面的正三角形的个数的最大值是( )A. 3B. 4C. 5D. 62. 在三棱锥S ABC -的三条侧棱,,SA SB SC 上分别任取点',','A B C ,则有( ) A .几何体'''S A B C -一定是三棱锥,几何体'''ABC A B C -一定是三棱台 B .几何体'''S A B C -一定是棱锥,几何体'''ABC A B C -不一定是棱台 C .几何体'''S A B C -不一定是棱锥,几何体'''ABC A B C -一定是棱台D .几何体'''S A B C -不一定是三棱锥,几何体'''ABC A B C -也不一定是三棱台 3.4. 用斜二侧法将四边形ABCD 画成四边形''''A B C D , 在:(1)若//AB CD ,则''//''A B C D ; (2)若AB CD =,则''''A B C D =; (3)若AB CD >,则''''A B C D >; (4)P 为AB 中点,则'P 必为''A B 中点. 中,正确的是( ) A .(1)和(2) B .(1)和(3) C .(1)和(4) D .(1)、(2)和(4)5. 已知直线21,l l 与平面α. 则下列结论正确的是( )A .若A l l =⊂αα 21,,则21,l l 为异面直线B .若α//,//121l l l ,则α//2l .C .若,,121α⊥⊥l l l 则.//2αlD .若,,21αα⊥⊥l l ,则21//l l . 6. 四棱锥的8条棱所在直线中,互为异面的直线共有( ).A .4对B .8对C .12对D .16对7. 图示最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得.现用一个竖直的平面去截这个几何体,则截得的图形可能是( )8. 四棱柱1111ABCD A BC D -底面为平行四边形,对角线1AC 与平面1A BD 相交于P .则P 是△1A BD 的( )A .重心B .内心C .外心D .垂心9. 空间四边形ABCD 的各边与两条对角线的长都是1,点P 在边AB 上移动,点Q 在CD 上移动,则点P 与Q 的最短距离为 ( ) A .12 B. 2 C .34 D .210.11. 如图,水平地面上有一个大球,现用如下方法测量球的大小:用一个锐角为450的三角板,斜边紧靠球面,一条直角边紧靠地面,并使三角板与地面垂直,P 为三角板与球的切点,如果测得PA=5cm,则球的表面积为 ( )2.100A cm π.B 2.200D c m π12. 如图所示,正四面体ABCD 中,E 在棱AB 上,F 在棱CD 上,使)0(>==λλFDCFEB AE ,设λλλαβλ,)(+=a f 表示EF 与AC 所成的角,λβ表示EF 与BD 所成的角,则( ) A.),0()(∞+在λf 上单调递增 B.),0()(∞+在λf 上单调递减 C.)1,0()(在λf 上单调递增, 而在),1(∞+上单调递减D.),0()(∞+在λf 上为常数二、填空题(本大题共4小题,每小题4分,共16分) 13. 在正方体ABCD —A 1B 1C 1D 1中,O 1为上底中心,异面直线AB 1与BC 1所成的角为 . 14.点P 是棱长为a 的正方体1111D C B A ABCD -棱11B A 上的动点,则四棱锥11D ABC P -的体积为 . 15.16. 在正四棱柱1111D C B A ABCD -中,如果底边正方形ABCD 的边长为2=AB ,侧棱21=AA ,则下列四个命题:E ADFC B①1AA 与1BC 成ο45角; ② 1AA 与1BC 的距离为2 ; ③ 二面角C AB C --1的正切值为为2; ④ ⊥D B 1平面AC D 1.则正确命题的序号为 .三、解答题(本大题共6小题, 共74分, 解答应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)把一个圆锥截成圆台,已知圆台的上、下底半径的比是1︰4,圆台的母线长是9cm ,求圆锥的母线长.18.(本小题满分12分)19.(本小题满分12分)ABCD 为空间四边形,点M 、E 、F 分别为△BAC 、△ACD 及△ADB 的重心. (1)求证:面MEF ∥面BCD ; (2)求S △MEF 与S △BCD 面积的比值.20.(本小题满分12分)如图所示,直角梯形O 2BAO 1内有一个内切半圆O ,把这个平面图形绕O 1O 2旋转一周得到圆台内有一个内切球,已知圆台全面积与球面积的比是k(k>1),求它们的体积比.21.(本小题满分12分)BC 已知P A ⊥平面ABCD ,ABCD 为矩形,P A =AD ,M 、N 分别是AB 、PC 的中点,求证:(Ⅰ)MN ∥平面P AD ; (Ⅱ)平面PMC ⊥平面PDC .22.(本小题满分14分)如图,在直三棱柱ABC —A 1B 1C 1中,AA 1=2, AC=BC=1,∠ACB=90°,点E 是AB 的中点, 点F 在侧棱BB 1上,且EF ⊥CA 1.(Ⅰ)求二面角C —A 1F —E 的大小. (Ⅱ)求点E 到平面CA 1F 的距离.1数学参考答案与解析1.C 解析:正三角形的每一个内角为600,六个这样的正三角形为侧面不能围成棱锥(顶点出发的几个内角的和应小于3600).所以最大值应有5个,故应选C.2.B 解析:由棱锥与棱台的概念可得几何体'''S A B C -一定是棱锥,几何体'''ABC A B C -不一定是棱台.故应选B.3.4.C 解析:斜二侧画法中, 若//AB CD ,则''//''A B C D ;P 为AB 中点,则'P 必为''A B 中点.正确的是(1)和(4).故应选C.5.D 解析:A 错,21,l l 也可能相交; B 错,2l 也可以能在α内;C 错, 2l 也可以能在α内; D 正确,垂直于同一条直线的两条直线平行. 综上所述,正确结论应选D.6.B 解析:每一条侧棱均与底面的2条边成异面直线,即有两对异面直线,四条侧棱共有8对互为异面的直线.7.D 解析:截面(2)(3)的外轮廓是整个的矩形,所以是错的.故排除A 、B;截面(4)圆锥的轮廓是抛物线而不是三角形,所以是错的.故选D.8.A 解析:如图所示,连接AC 、AB 1 ,可得面1A BD 与平面1A AC 交线为1A P ,1A P 所在直线为1A BD ∆ 的中线,同理可得DP 所在直线也为1A BD ∆的中线, 即点P 为1A BD ∆的重心.故应选A.9.B 解析:P 与Q 的最短距离就是异面直线AB与 DC 的距离,分别取AB 与DC 的中点,可得PQ 即 为所求,2=, 故应选B . 10.PDABC A 1B 11D 111.B 解析:如图所示,5,1)R R +=∴== 224100(3.S R cm ππ∴==+球12.D 解析:作EG ∥AC,交BC 于G,连GF,则,,EFG GEF ∠=∠=λλβαEGF ∠-=+πβαλλ,∴EGF ∠为常数.故选D.13.60°解析:如图所示, 连结AD 1,则AD 1∥BC 1 ∴∠D 1AB 1是异面直线AB 1与BC 1所成的角 ∵△D 1AB 1是正三角形,∴∠D 1AB 1=60°. 即AB 1与BC 1所成的角是60°.14.313a 解析:本题考查了正方体模型下动点条 件下锥体体积的探究.点P到面11ABC D,其底面11ABC D 的2,则其体积2311323V a a =⋅=.15.16.②③解析:①如图,连结BC 1,则BC C 1∠就是AA 1,与BC 1成的角,,22tan 1=∠BC C 则BCC 1∠不是450; ②如图,正四棱柱中,AB 就是AA 1与BC 1的距离为2; ③二面角C 1-AB-C 的平面角就是1tan 2C BC ∠=; ④因为四棱柱不是正方体,则B 1D 与平面D 1AC 不垂直. 综上所述,正确命题的序号为②③.17.解析:如图,圆锥是由直角三角形POA 绕PO 旋转而成,A BCDA 1B 1C 1D 1D则''//O A OA 知:'''O A PA OA PA=, 即1'4PA AA PA-=,'9AA =, ∴ 12PA =.即圆锥的母线长是12cm. 12分18.19.解析:(1)证明:连结AM 、AE 及AF ,分别延长使之交BC 、CD 、 DA 于G 、H 、P 三点.∵E 、F 、M 分别为三角形的重心,∴AG AM =AH AE =AP AF =32. ∴连结ME 、EF 、FM 及连结GH 、HP 、PG 后 有ME ∥GH ,EF ∥PH ,即ME ∥面BCD ,EF ∥面BCD .故面EFM ∥面BCD . 6分(2)由GH ME =32,PH EF =32知ME =32GH ,EF =32PH 而GH =21BD ,PH =21BC ,故ME =31BD ,EF =31BC , 即BD ME =BC EF =31.则BCD MEF S S ∆∆=91. 12分20.解析:设r A O =1,)(2r R R B O >=,,则圆台母线AB=BM+AM=R+r,球O 的直径 Rr r R r R O O 2)()(2221=--+=,),(2)(22222Rr r R r R r R S ++=+++=∴ππππ圆台全Rr S π4=球 6分 .222k RrRrr R S S =++=∴球圆台全故.2)(34)(23122322k Rr r Rr R Rr r Rr R Rr V V =++=++⋅=ππ球圆台 12分21. 证明:(Ⅰ)取PD 的中点为Q ,连结AQ 、QN ,∵PN =NC ,∴QN //=21DC .∵四边形ABCD 为矩形,∴QN //=AM .∴MN ∥AQ .又∵AQ ⊂平面P AD ,∴MN ∥平面P AD . 6分 (Ⅱ)∵P A ⊥平面ABCD ,∴∠P AD =90°. ∵P A =AD ,∴△P AD 为等腰直角三角形. ∵Q 为PD 中点,∴AQ ⊥PD .∵CD ⊥AD ,CD ⊥P A ,∴CD ⊥平面P AD , ∴CD ⊥AQ ,∴AQ ⊥平面PDC .由(1)MN ∥AQ ,∴MN ⊥平面PDC . 又∵MN ⊂平面PMC ,∴平面PMC ⊥平面PDC . 12分 22.解析:(Ⅰ)过E 作EG ⊥FA 1,垂足为G ,连结CG 在直三棱柱ABC —A 1B 1C 1中,面A 1B ⊥面ABC 又AC=BC ,E 为AB 中点 ∴CE ⊥AB ∴CE ⊥面A 1B , ∴CG ⊥A 1F ∴∠CGE 为二面角C —A 1F —E 的平面角 而∵CE ⊥面A 1B ∴CE ⊥EF EF ⊥CA 1 ∴EF ⊥面A 1CE ∴EF ⊥A 1E ∴△A 1AE ∽△EBF∴41222221=⨯=⋅=BE AA AE BF在Rt △A 1AE 中,A 1E=223)22(22221=+=+AE A A在Rt △EBF 中,EF=43)41()22(2222=+=+BF BE22494322349112211=⨯=⋅=∴=+=∴F A EF E A EG EF E A F A 又CE=221t a n==∠∴EG CE CGE ︒=∠∴45CGE即二面角C —A 1F —E 的大小为45° 7分(Ⅱ)设顶点E 到平面A 1CF 的距离为d ,由(1)CG=1,CE ⊥面A 1B ,A 1F ⊥EF ,EF A C CF A E V V 11--=2149121314322322312131213111=∴⋅⨯⨯⨯=⨯⨯⨯∴⋅⋅⋅⨯=⋅⋅∴d d d F A CG EF E A CE即点E 到平面CA 1F 的距离为21. 14分。
(全国各地名校好题集锦)2018年高考二轮复习理科数学专题-----立体几何

(全国各地名校好题集锦)2018年高考二轮复习理科数学专题-----立体几何一、选择题1. 【2018广西教育质量诊断性联考】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中俯视图的右边为一个半圆,则此几何体的体积为( )A. B. C. D. 【答案】B【解析】由已知可得该几何体是由一个四棱锥和半个圆锥组成的,故其体积为,故选B. 【点睛】本题主要考查三视图,属于较易题型.应注意把握三个视图的位置和尺寸:主视图在图纸的左上方,左视图在主视图的右方,俯视图在主视图的下方;主视图与俯视图长应对正(简称长对正) ,主视图与左视图高度保持平齐 (简称高平齐),左视图与俯视图宽度应相等(简称宽相等),若不按上述顺序放置,则164π+162π+484π+482π+14433⨯⨯⨯+2112316223ππ⨯⨯⨯=+应注明三个视图名称.2.【2018湖南永州市一模】关于直线l,m及平面α,β,下列命题中正确的是()A. 若l⊥α,l//β,则α⊥β B. 若l//α,m//α,则l//mC. 若l//α,l⊥m,则m⊥αD. 若l//α,α∩β=m,则l//m【答案】A【解析】对于A,若l⊥α,l//β,根据线面垂直、线面平行的性质定理以及面面垂直的判定定理得到α⊥β;故A正确;对于A,若l//α,m//α,则l与m平行、相交或者异面;故B错误;对于C,若l//α,l⊥m,则m与α可能平行,故C错误;对于D,若l//α,α∩β=m,则l与m可能相交,平行或者异面,故D 错误,故选A.3.【2018河南中原名校质检二】一棱长为6的正四面体内部有一个可以任意旋转的正方体,当正方体的棱长取最大值时,正方体的外接球的表面积是()A. 4π B. 6π C. 12π D. 24π【答案】B4.【2018衡水金卷高三联考】如图是一个空间几何体的正视图和俯视图,则它的侧视图为( )【答案】A5.【2018吉林百校联盟九月联考】如图,点是正方形外的一点,过点作直线,记直线与直线, 的夹角分别为, ,若,则满足条件的直线( )P 1111ABCD A BC D -P l l 1AC BC 1θ2θ()1sin 50θ-︒()2cos 140θ=︒-lA. 有1条B. 有2条C. 有3条D. 有4条 【答案】D6.【2018吉林百校联盟九月联考】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体的体积为( )A.B. C. D. 【答案】A()1613π+()813π+()4233π+()423π+7.【2018广东珠海高三摸底】某几何体的三视图如图所示,则该几何体的体积为( )A.B.C.D. 【答案】B【解析】作出立体图形为:故该几何体的体积为:8【2018广西柳州市一模】已知直三棱柱ABC −A 1B 1C 1的6个顶点都在球O 的球面上,若AB =3,AC =4AB ⊥AC ,AA 1=12,则球O 的半径为 ( )A.3 172B. 210C.132D. 3 10【答案】C【解析】试题分析:由已知条件可知直三棱柱的上下底面是两个相等的小圆所在的平面,且BC 和B 1C 1分别是两小圆的直径,则BC=5,设球的半径为R ,则R= (BC2)2+(AA 12)2= (52)2+(122)2=132,故选C.9.【2018辽宁沈阳育才学校一模】某几何体的三视图如图所示,则其表面积为( ) A.B. C. D. 【答案】C【解析】根据三视图恢复几何体为一个个四棱锥,其中一条侧棱垂直底面,四棱锥的表面积为 C.1112422332⨯⨯⨯⨯⨯⨯=83438+6+4228+++=+10.【2018吉林长春一模】已知矩形ABCD 的顶点都在球心为O ,半径为R 的球面上,AB =6,BC =23,且四棱锥O −ABCD 的体积为8 3,则R 等于() A. 4 B. 23C. 479D. 13【答案】A11.【2018超级全能生全国联考】若正四棱锥内接于球,且底面过球心,则球的半径与正四棱锥内切球的半径之比为( )A. B. C. D.【答案】A【点睛】求锥体的内切球半径,我们常用的方法是等体积法,求出r.12.【2018吉林长春一模】《九章算术》卷五商功中有如下问题:今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈,问积几何.刍甍:底面为矩形的屋脊状的几何体(网格纸中粗线部分为其三视图,设网格纸上每个小正方形的边P ABCD -O ABCD O O P ABCD -1211r 3V S =表长为1丈),那么该刍甍的体积为( )A. 4立方丈B. 5立方丈C. 6立方丈D. 12立方丈【解析】由已知可将刍甍切割成一个三棱柱和一个四棱锥,三棱柱的体积为3,四棱锥的体积为2,则刍甍的体积为5.故选B. 二、解答题13.【2018百校联盟高三摸底】如图所示,菱形与正三角形所在平面互相垂直, 平面,且, . (1)求证: 平面; (2)若,求几何体的体积.【答案】(1)见解析;(2)3.ABCD BCE FD ⊥ABCD 2AB =3FD =//EF ABCD 3CBA π∠=EFABCD∵平面⊥平面, 平面,平面平面,∴平面.又∵平面, ,∴.∴四边形为平行四边形,∴. ∵平面 ,平面,∴平面.(2)连接,由题意得为正三角形,∴. ∵平面⊥平面,平面,平面平面,平面.∵,平面 , 平面,∴平面,同理,由可证平面,∵, 平面, 平面, ∴平面∥平面,∴到平面的距离等于的长.∵为四棱锥的高,ABCD BCE EH ≠⊂BCE ABCD ⋂BCE BC =EH ⊥ABCD FD ⊥ABCD FD =FD EH =⊂EHDF EF HD ABCD HD ⊄ABCD EF ABCD ,,CF HA BF ABC ∆HA BC ⊥ABCD P ABCD -ABCD 22AB =2BC =P AC E F ,AB BC DE ⊥PAC PC M FM PDE PMPC∴.14.【2018江苏南京高三调研】在直三棱柱ABC-A1B1C1中,AB=AC,E是BC的中点,求证:(Ⅰ)平面AB1E⊥平面B1BCC1;(Ⅱ)A1C//平面AB1E.【答案】(1)见解析(2)见解析所以CC1 AE.因为AB=AC,E为BC的中点,所以AE BC.因为BC 平面B1BCC1,CC1 平面B1BCC1,且BC∩CC1=C,所以AE 平面B1BCC1.因为AE 平面AB1E,所以平面AB1E 平面B1BCC1.(2)连接A1B,设A1B∩AB1=F,连接EF.在直三棱柱ABC-A1B1C1中,四边形AA1B1B为平行四边形,所以F为A1B的中点.又因为E是BC的中点,所以EF∥A1C.因为EF 平面AB1E,A1C 平面AB1E,所以A1C∥平面AB1E.15.【2018衡水金卷高三联考】如图,在三棱柱ABC−A1B1C1中,AA1⊥平面ABC,AC⊥BC,AC=BC=CC1=2,点D为AB的中点.(1)证明:AC1∥平面B1CD;(2)求三棱锥A1−CDB1的体积..【答案】(1)见解析;(2)43在三棱柱ABC−A1B1C1中,四边形BCC1B1是平行四边形. ∴点O是BC1的中点.∵点D为AB的中点,∴OD∥AC1.又OD⊂平面B1CD,AC1⊄平面B1CD,∴AC1∥平面B1CD.16.【2018广东茂名五校联考】如图,在多面体ABCDFE中,四边形ADFE是正方形,在等腰梯形ABCD中,AD∥BC,AB=CD=AD=1,BC=2,G为BC中点,平面ADFE⊥平面ADCB.(1)证明:AC⊥BE;(2)求三棱锥A−GFC的体积..【答案】(1)见解析;(2)312同理可证AB∥DG,因此AC⊥AB,由于四边形ADFE为正方形,所以EA⊥AD,又平面ADFE⊥平面ABCD,平面ADFE∩平面ABCD=AD,故EA⊥平面ABCD,从而EA⊥AC,又EA∩AB=A,故AC⊥平面ABE,所以AC⊥BE..(2)因为V A−GFC=V F−AGC=V E−AGC=12V E−ABC,V E−ABC=13×1×12×1×3=36.所以,三棱锥A−GFC的体积为312.17.【2018湖南永州一模】已知三棱锥S−ABC,SA=SB,AC=BC,O为AB的中点,SO⊥平面ABC,AB=4,OC=2,N是SA中点,CN与SO所成的角为α,且tanα=2.(1)求证:OC⊥ON;(2)求三棱锥S−ABC的体积.【答案】(1)见解析;(2)45318.【2018河南中原名校质检二】在四棱锥P−ABCD中,平面PAD⊥平面ABCD,AB∥CD,ΔPAD是等边三角形,已知AD=2,BD=23,AB=2CD=4. (1)设M是PC上一点,求证:平面MBD⊥平面PAD.(2)求四棱锥P−ABCD的体积.【答案】(1)见解析(2)319.【2018湖南两市九月调研】如图,在四棱锥中, 底面,底面为菱形, , 为的中点.(1)求证: 平面;P ABCD -PA ⊥ABCD ABCD 60ABC ∠= 1,PA PB E ==PC //PA BDE(2)求三棱锥的体积.【答案】(1)见解析;(2)20.【2018广西教育质量诊断性联考】如图,在直三棱柱(侧棱与底面垂直的棱柱)中,点是的中点.(1)求证:平面;(2)若, ,求证: .【答案】(1)详见解析(2)详见解析【解析】试题分析:(1)利用三角形中位线定理可得平面;(2)先证.,再证平面,再证平面.试题解析:P BDE -P BDE V -=111ABC A B C -G AC 1//B C 1A BG AB BC =1AC 11AC A B ⊥1//OG B C ⇒1//B C 1A BG 1AA BG ⊥BG ACBG ⊥⊥111ACC A BG AC ⊥111AG AC AC ⊥⊥111A BGAC A B ⊥证明:(1)连接交于,连接.在中,因为, 分别为, 的中点,所以,21.【2018吉林百校联盟九月联考】如图所示,四棱锥中,平面平面, , , . 1AB 1A B O OG 1B AC ∆G O AC 1AB 1//OG BC S ABCD -SAD ⊥ABCD SA AD ⊥//AD BC 43SA BC AB ==24AD ==(1)证明:在线段上存在一点,使得平面;(2)若,在(1)的条件下,求三棱锥的体积.【答案】(1)见解析;(2) . 【解析】试题分析:(1)取的中点,易得:四边形是平行四边形,从而,所以平面;(2)∵是的中点,∴到平面的距离等于到平面的距离的一半从而易得三棱锥的体积.试题解析:(2)∵平面平面,平面平面, , 平面,故平面,∵是的中点,∴到平面的距离等于到平面的距离的一半,且平面,SC E //ED SAB AB AC =S AED-S AED V -=SB M AMED //ED AM //ED SAB E SC E ABCD S ABCD E ACD S AED V V --=S AED-SAD ⊥ABCD SAD ⋂ABCD AD =SA AD ⊥SA ⊂SAD SA ⊥ABCD E SC E ABCD S ABCD SA ⊥ABCD,∴三棱锥的高是2, ,在等腰中, , , 边上的高为,,∴到∴.点睛:求锥体的体积要充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解,注意求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.22.【2018辽宁沈阳育才学校一模】如图,边长为3的正方形所在平面与等腰直角三角形所在平面互相垂直, ,且, 4SA =E ACD -E ACD S AED V V --=ABC ∆3AC AB ==4BC =BC 22325-=//BC AD C AD 122ADC S ∆=⨯=123S AED V -==ABCD ABE AE AB ⊥2EM MD =.(Ⅰ)求证: 平面;(Ⅱ)求三棱锥的体积.【答案】(Ⅰ)见解析; (Ⅱ)3 3AB AN = //MN BEC E BMC-所以四边形为平行四边形,故, 而平面, 平面,所以平面; (Ⅱ)因为平面,所以:23.【2018超级全能生全国联考】如图,四边形为等腰梯形, ,将沿折起,使得平面平面, 为的中点,连接.(1)求证: ;(2)求到平面的距离.【答案】(1)证明见解析 (2)到平面NBFM //MN BF BF ⊆BEC MN ⊄BEC //MN BEC //MN BEC 1133 3.33E BMC M BEC N BEC C BEN BEN V V V V S CB ----∆====⋅=⨯⨯=1ABCD 2,1AB AD DC CB ====ADC ∆AC ADC ⊥ABC E AB ,DE DB BC AD ⊥E BCD E BCD。
2018年高考数学二轮复习 专题1.5 立体几何(讲)文
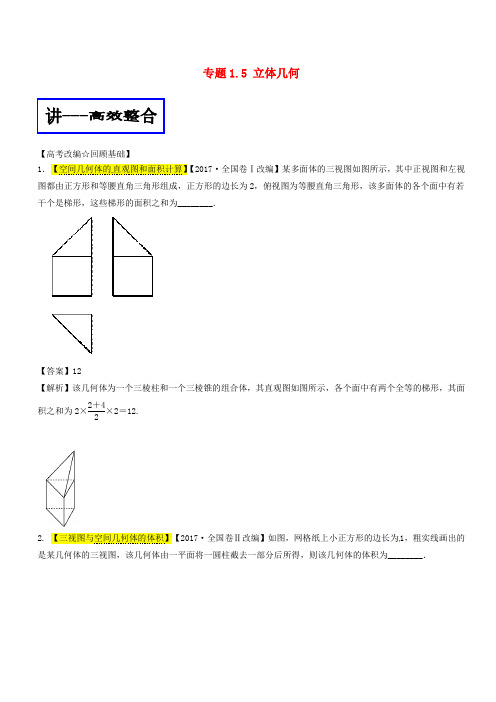
专题1.5 立体几何【高考改编☆回顾基础】1.【空间几何体的直观图和面积计算】图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为________.【答案】12【解析】该几何体为一个三棱柱和一个三棱锥的组合体,其直观图如图所示,各个面中有两个全等的梯形,其面积之和为2×2+42×2=12.【三视图与空间几何体的体积】【2017·全国卷Ⅱ改编】如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为________.2【答案】63π【解析】3. 【空间几何体的体积】【2017课标3,改编】已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为 . 【答案】3π4【解析】3【命题预测☆看准方向】1.空间几何体的三视图成为近几年高考的必考点,单独考查三视图的逐渐减少,主要考查由三视图求原几何体的面积、体积,主要以选择题、填空题的形式考查.2.对柱体、锥体、台体表面积、体积及球与多面体的切接问题中的有关几何体的表面积、体积的考查又是高考的一个热点,难度不大,主要以选择题、填空题的形式考查.3.2018年应注意抓住考查的主要题目类型进行训练,重点有三个:一是三视图中的几何体的形状及面积、体积;二是求柱体、锥体、台体及球的表面积、体积;三是求球与多面体的相切、接问题中的有关几何体的表面积、体积.【典例分析☆提升能力】【例1】17世纪日本数学家们对于数学关于体积方法的问题还不了解,他们将体积公式“V=kD 3”中的常数k 称为“立圆术”或“玉积率”,创用了求“玉积率”的独特方法“会玉术”,其中,D 为直径,类似地,对于等边圆柱(轴截面是正方形的圆柱叫做等边圆柱)、正方体也有类似的体积公式V =kD 3,其中,在等边圆柱中,D 表示底面圆的直径;在正方体中,D 表示棱长.假设运用此“会玉术”,求得的球、等边圆柱、正方体的“玉积率”分别为k 1,k 2,k 3,那么,k 1∶k 2∶k 3=( )C.【答案】D【解析】球中,等边圆柱中,正方体中, 3333,1V D k D k ==∴=;故选D. 【趁热打铁】将一个底面半径为1,高为2的圆锥形工件切割成一个圆柱体,能切割出的圆柱的最大体积为( )【答案】B【解析】【例2】【2018届河南省郑州市第一次模拟】刍薨(chuhong),中国古代算术中的一种几何形体,《九章算术》中记载“刍薨者,下有褒有广,而上有褒无广.刍,草也.薨,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱,刍薨字面意思为茅草屋顶”,如图,为一刍薨的三视图,其中正视图为等腰梯形,侧视图为等腰三角形,则搭建它(无底面,不考虑厚度)需要的茅草面积至少为()4【答案】B【趁热打铁】【2018届湖北省稳派教育高三上第二次联考】已知一个几何体的三视图如图所示,则该几何体的体积为()π+ D.C. 126【答案】A【解析】由三视图可得,该几何体为右侧的一个半圆锥和左侧的一个三棱锥拼接而成。
高三第二轮专题复习资料:立体几何题型与方法(文科)

专题二:立体几何题型与方法(文科)一、 考点回顾1.平面(1)平面的基本性质:掌握三个公理及推论,会说明共点、共线、共面问题。
(2)证明点共线的问题,一般转化为证明这些点是某两个平面的公共点(依据:由点在线上,线在面内 ,推出点在面内), 这样,可根据公理2证明这些点都在这两个平面的公共直线上。
(3)证明共点问题,一般是先证明两条直线交于一点,再证明这点在第三条直线上,而这一点是两个平面的公共点,这第三条直线是这两个平面的交线。
(4)证共面问题一般用落入法或重合法。
(5)经过不在同一条直线上的三点确定一个面. 2. 空间直线.(1)空间直线位置分三种:相交、平行、异面. 相交直线—共面有反且有一个公共点;平行直线—共面没有公共点;异面直线—不同在任一平面内。
(2)异面直线判定定理:过平面外一点与平面内一点的直线和平面内不经过该点的直线是异面直线.(不在任何一个平面内的两条直线)(3)平行公理:平行于同一条直线的两条直线互相平行.(4)等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.(5)两异面直线的距离:公垂线的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (l 1或l 2在这个做出的平面内不能叫l 1与l 2平行的平面) 3. 直线与平面平行、直线与平面垂直.(1)空间直线与平面位置分三种:相交、平行、在平面内.(2)直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行,线面平行”)(3)直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行,线线平行”)(4)直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直.● 若PA ⊥α,a ⊥AO ,得a ⊥PO (三垂线定理), 得不出α⊥PO . 因为a ⊥PO ,但PO 不垂直OA . ● 三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.(5)a.垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.[注]:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)] b.射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上。
2018立体几何专题(2018高考真题)

2018立体几何专题(文)1.已知圆柱的上、下底面的中心分别为1O ,2O ,过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A .122πB .12πC .82πD .10π2.某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M 在正视图上的对应点为A ,圆柱表面上的点N 在左视图上的对应点为B ,则在此圆柱侧面上,从M 到N 的路径中,最短路径的长度为( )A .217B .25C .3D .23.在长方体1111ABCD A B C D -中,E 为棱1CC 的中点,则异面直线AE 与CD 所成角的正切值为( ) A .2B .3 C .5 D .7 4.中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫棒头,凹进部分叫卯眼,图中木构件右边的小长方体是棒头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )5.某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )A .1 B. 2 C. 3 D. 46.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:cm 3)是( )A .2B .4C .6D .87.《九章算术》中,称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马。
设1AA 是正六棱柱的一条侧棱,如图。
若阳马以该正六棱柱的顶点为顶点、以1AA 为底面矩形的一边,则这样的阳马的个数是( ) A.4 B. 8 C. 12 D. 168.在长方体1111ABCD A B C D -中,2AB BC ==,1AC 与平面11BB C C 所成的角为30︒,则该长方体的体积为( )A .8B .62C.82D .839.设A ,B ,C ,D 是同一个半径为4的球的球面上四点,ABC △为等边三角形且其面积为93,则三棱锥D ABC -体积的最大值为( ) A .123B .183C .243D .54310.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为_______ 11.如图,已知正方体ABCD –A 1B 1C 1D 1的棱长为1,则四棱柱A 1–BB 1D 1D 的体积为__________.俯视图正视图2211A 1A12.已知圆锥的顶点为S ,母线SA ,SB 互相垂直,SA 与圆锥底面所成角为30︒,若SAB △的面积为8,则该圆锥的体积为__________13.在平行四边形ABCM 中,3AB AC ==,90ACM =︒∠,以AC 为折痕将ACM △折起,使点M 到达点D 的位置,且AB DA ⊥. ⑴证明:平面ACD ⊥平面ABC ;⑵Q 为线段AD 上一点,P 为线段BC 上一点,且23BP DQ DA ==,求三棱锥Q ABP -的体积.14.如图,在三棱锥P ABC -中,AB BC == 4PA PB PC AC ====,O 为AC 的中点.(1)证明:PO ⊥平面ABC ;(2)若点M 在棱BC 上,且2MC MB =,求点C 到平面POM 的距离.C15.在平行六面体ABCD—A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB//平面A 1B1C;(2)平面ABB1A1⊥A1BC.16.如图,矩形ABCD所在平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.(1)证明:平面AMD⊥平面BMC;(2)在线段AM上是否存在点P,使得MC∥平面PBD?说明理由.17.如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,E,F分别为AD,PB的中点.(Ⅰ)求证:PE⊥BC;(Ⅱ)求证:平面PAB⊥平面PCD;(Ⅲ)求证:EF∥平面PCD.18.如图,在四面体ABCD中,△ABC是等边三角形,平面ABC⊥平面ABD,点M为棱AB的中点,AB=2,AD=∠BAD=90°.(Ⅰ)求证:AD⊥BC;(Ⅱ)求异面直线BC与MD所成角的余弦值;(Ⅲ)求直线CD与平面ABD所成角的正弦值.19.已知圆锥的顶点为P ,底面圆心为O ,半径为2. (1)设圆锥的母线长为4,求圆锥的体积;(2)设4PO =,OA 、OB 是底面半径,且90AOB ∠=︒,M 为线段AB 的中点,如图,求异面直线PM 与OB 所成的角的大小。
2018年高考二轮复习专题——立体几何(文科)

专题五空间中的平行与垂直知识梳理:1、平面中的平行有哪些?2、空间中的平行有哪些?如何推导?(定理、性质用图示展示)3、平面中的垂直有哪些?4、空间中的垂直有哪些?如何推导?(定理、性质用图示展示)1.(2017·高考全国卷Ⅰ)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是()2.(2016·高考浙江卷)已知互相垂直的平面α,β交于直线l,若直线m,n满足m∥α,n⊥β,则() A.m∥l B.m∥n C.n⊥l D.m ⊥n3.(2016·全国卷Ⅱ)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β. ②如果m ⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β. ④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有______.(填写所有正确命题的编号)4.(2017·高考全国卷Ⅲ)如图,四面体ABCD中,△ABC是正三角形,AD=CD.(1)证明:AC⊥BD;(2)已知△ACD是直角三角形,AB=BD.若E为棱BD 上与D不重合的点,且AE⊥EC,求四面体ABCE与四面体ACDE的体积比.类型一空间线面位置关系的判断[典例1](1)已知m,n为异面直线,m⊥平面α,n ⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则() A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于l D.α与β相交,且交线平行于l(2)已知m,n表示两条不同直线,α表示平面.下列说法正确的是()A.若m∥α,n∥α,则m∥n B.若m⊥α,n⊂α,则m⊥nC.若m⊥α,m⊥n,则n∥αD.若m∥α,m⊥n,则n⊥α变式1.如本例(2)改为设m,n是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是() A.当n⊥α时,“n⊥β”是“α∥β”的充要条件B.当m⊂α时,“m⊥β”是“α⊥β”的充分不必要条件C.当m⊂α时,“n∥α”是“m∥n”的必要不充分条件D.当m⊂α时,“n⊥α”是“m⊥n”的充分不必要条件[自我挑战]1.m、n是空间中两条不同直线,α、β是两个不同平面,下面有四个命题:①m⊥α,n∥β,α∥β⇒m⊥n;②m⊥n,α∥β,m⊥α⇒n∥β;③m⊥n,α∥β,m∥α⇒n⊥β;④m⊥α,m∥n,α∥β⇒n⊥β.其中,所有真命题的序号是________.(1)证明:平面AEC⊥平面BED.(2)若∠ABC=120°,AE⊥EC,三棱锥EACD的体积为63,求该三棱锥的侧面积.自我挑战:如图,在四棱锥P ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点,求证:(1)PA⊥底面ABCD;(2)BE∥平面PAD;(3)平面BEF⊥平面PCD.[互动迁移1]在本例条件下,证明平面BEF⊥平面ABCD.[互动迁移2]在本例条件下,若AB=BC,求证:BE⊥平面PAC.[变式训练] (2017·山东卷)由四棱柱ABCDA1B1C1D1截去三棱锥C1B1CD1后得到的几何体如图所示.四边形ABCD为正方形,O为AC与BD的交点,E 为AD的中点,1A1E⊥平面ABCD.(1)证明:A1O∥平面B1CD1;(2)设M是OD的中点,证明:平面A1EM⊥平面B1CD1.类型三立体几何中的折叠、探索问题[典例3](2017·山东济南模拟)如图(1),在Rt△ABC 中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A′DE的位置,使A′C⊥CD,如图(2).(1)求证:DE∥平面A′BC;(2)求证:A′C⊥BE;(3)线段A′D上是否存在点F,使平面CFE⊥平面A′DE?若存在,求出DF的长;若不存在,请说明理由.[母题变式]本例的条件不变,在线段BE上是否存在点H,使平面A′BE⊥平面A′CH?(1)试在线段A′C上确定一点H,使FH∥平面A′BE.(2)试求三棱锥A′EBC的外接球的半径与三棱锥A′EBC的表面积.2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题1.5 立体几何1.练高考
1.【2017山东,文13】由一个长方体和两个1
4
圆柱体构成的几何体的三视图如右图,则该几何体的体积为
.
【答案】2
2
π
+
2. 【2017课标II,文15】长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为【答案】14π.
【解析】球的直径是长方体的体对角线,所以
2
24π14π.
R S R
====
3. 【2017课标1,文6】如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直接AB与平面MNQ不平行的是()
A .
B .
C .
D .
【答案】A 【解析】
4. 【2017课标1,文18】如图,在四棱锥P-ABCD 中,AB//CD ,且90BAP CDP ∠=∠=.
(1)证明:平面PAB ⊥平面PAD ;
(2)若PA =PD =AB =DC ,90APD ∠=,且四棱锥P-ABCD 的体积为8
3
,求该四棱锥的侧面积. 【答案】(1)证明见解析; (2)326+. 【解析】
5. 【2017山东,文18】(本小题满分12分)由四棱柱ABCD -A 1B 1C 1D 1截去三棱锥C 1- B 1CD 1后得到的几何体如图所示,四边形ABCD 为正方形,O 为AC 与BD 的交点,E 为AD 的中点,A 1E ⊥平面ABCD , (Ⅰ)证明:1AO ∥平面B 1CD 1;
(Ⅱ)设M 是OD 的中点,证明:平面A 1EM ⊥平面B 1CD 1.
【答案】①证明见解析.②证明见解析. 【解析】
试题分析:(Ⅰ)取11B D 中点F ,证明1
//AO CF ,(Ⅱ)证明11B D ⊥面1A EM .
所以1,A E BD ⊥ 因为11//,
B D BD
所以11111,,EM B D A E B D ⊥⊥
又1,A E EM ⊂平面1A EM ,
1A E
EM E =.
所以11B D ⊥平面1,A EM 又11B D ⊂平面11B CD ,
所以平面1A EM ⊥平面11B CD .
6. 【2017天津,文17】如图,在四棱锥P ABCD -中,AD ⊥平面PDC ,AD BC ∥,PD PB ⊥,1AD =,
3BC =,4CD =,2PD =.
(I )求异面直线AP 与BC 所成角的余弦值; (II )求证:PD ⊥平面PBC ;
(Ⅲ)求直线AB 与平面PBC 所成角的正弦值.
【答案】(ⅠⅡ . 【解析】
(Ⅱ)证明:因为AD ⊥平面PDC ,直线PD ⊂平面PDC ,所以AD ⊥PD .又因为BC //AD ,所以PD ⊥BC ,又PD ⊥PB ,所以PD ⊥平面PB C.
2.练模拟
1. 三棱锥P ABC -的四个顶点都在球O 上, PA ⊥平面ABC , 2PA =, 4AB =, 2AC =,则球的表面积是( )
A. 16π
B. 20π
C. 24π
D. 28π
【答案】B
【解析】由题意, AC BC ⊥, PA ⊥平面ABC ,则直径 ,所以表面积2420S R ππ==,故选B.
2.【2018届吉林省辽源市田家炳高级中学等五校高三上期末联考】已知两条直线m n 、,两个平面αβ、,给出下面四个命题:
①α∥,,m n m βαβ⊂⊂⇒∥n ; ②m ∥n , m ∥n α⇒∥α; ③m ∥n , m ⊥ n αα⇒⊥; ④α∥,m β∥,n m n αβ⊥⇒⊥。
其中正确命题的序号是( )
A. ①③
B. ③④
C. ①④
D. ②③ 【答案】B
故正确的是③④。
故答案为:B 。
3.在正方体1111ABCD A BC D -中,
M N 、分别为棱BC 和棱1CC 的中点,则异面直线AC 和MN 所成的角为( )
A. 30
B. 45
C. 90
D. 60
【答案】D
4.【2018届广西桂梧高中高三上第五次联考】正四面体
的所有棱长均为12,球O 是其外接球, ,M N
分别是ABC ∆与ACD ∆的重心,则球O 截直线MN 所得的弦长为( )
【答案】C
【解析】正四面体A BCD -可补全为棱长为的正方体,所以球O 是正方体的外接球,其半径
,设正四面体的高为h ,则
所以O 到直线MN 的距离为,因此球O 截直线MN 所得的弦长为
故选:C
5.【2018届甘肃省张掖市全市高三备考第一次检测】如图,四边形ABCD 是矩形
3,2,DE EC PE =⊥
(1)证明:平面PAC ⊥平面PBE ;
(2)设AC 与BE 相交于点F ,点G 在棱PB 上,且CG PB ⊥,求三棱锥F BCG -的体积.
【答案】(1)证明见解析;(2
6. 如下图,在三棱锥P ACD -中, 3AB BD =, PB ⊥底面ACD ,
(1)若E 为AC 上一点,且BE AC ⊥,证明:平面PBE ⊥平面PAC . (2)若Q 为棱PD 上一点,且//BQ 平面PAC ,求三棱锥Q ACD -的体积.
【答案】(1)见解析;(2【解析】试题分析:(1)由PB ⊥底面ACD ,得PB AC ⊥,又,BE AC BE PB B ⊥⋂=,故AC ⊥平面PBE
根据线面垂直即得面面垂直; (2)用余弦定理得AP 长,从而求得AB ,BC ,PB ,易得BQ ∥PA ,过Q 作//QH PB ,交AD 于点H ,则, 314AD AB BD =+=+=从而由三棱锥体积公式得到答案. 试题解析:
3.练原创
1. 棱长为2的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
( )
A .314
B .4
C .3
10 D .3
【答案】B 【解析】几何体如图,体积为:422
13=⨯,故选择B
2.D C B A ,,,是同一球面上的四个点,其中ABC ∆是正三角形, AD ⊥平面ABC ,4=AD ,32=AB ,则该球的表面积为( )
A.8π
B.16π
C.32π
D.64π
【答案】C
【解析】由题意画出几何体的图形如图,把D C B A ,,,扩展为三棱柱,上下底面的中心连线的中点与A 距离为球的半径,4=AD ,32=AB ,ABC ∆是正三角形,所以22,2==AO AE ,所以球的表面积
()ππ322242
=,故答案为C.
3. 已知m ,n 是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )
(A )若α,β垂直于同一平面,则α与β平行
(B )若m ,n 平行于同一平面,则m 与n 平行
(C )若α,β不平行,则在α内不存在与β平行的直线
(D )若m ,n 不平行,则m 与n 不可能垂直于同一平面
【答案】D
4.如图,已知四棱柱1111ABCD A BC D -的底面是菱形,侧棱1AA
⊥底面ABCD ,M 是AC 的中点,120BAD ∠=,1AA AB =.
(1)证明:1//MD 平面11A BC ;
(2)求直线1MA 与平面11A BC 所成的角的正弦值.
【答案】(1)详见解析;(2
5.如图,在四棱锥P-ABCD中,PA⊥CD,AD∥BC,∠ADC=∠PAB=90°,
1
2
BC CD AD
==.
(I)在平面PAD内找一点M,使得直线CM∥平面PAB,并说明理由;(II)证明:平面PAB⊥平面PBD.
【答案】(Ⅰ)取棱AD的中点M,证明详见解析;(Ⅱ)证明详见解析.。
